Abstract
We consider the problem of how to verify the security of probabilistic oblivious algorithms formally and systematically. Unfortunately, prior program logics fail to support a number of complexities that feature in the semantics and invariants needed to verify the security of many practical probabilistic oblivious algorithms. We propose an approach based on reasoning over perfectly oblivious approximations, using a program logic that combines both classical Hoare logic reasoning and probabilistic independence reasoning to support all the needed features. We formalise and prove our new logic sound in Isabelle/HOL and apply our approach to formally verify the security of several challenging case studies beyond the reach of prior methods for proving obliviousness.
This work has been supported in part by the joint CATCH MURI-AUSMURI and the Melbourne Graduate Research Scholarship.
You have full access to this open access chapter, Download conference paper PDF

1 Introduction
Side-channel attacks allow attackers to infer sensitive information by eavesdropping on a program’s execution, when the sensitive data are not directly observable (e.g. because they are encrypted). For example, sensitive documents or secret images can be reconstructed by only observing a program’s memory access pattern [15, 20, 24]. Many algorithms are charged with the protection of secrets in application contexts where such attacks are realistic, for example, cloud computing [28, 35], secure processors [8, 21] and multiparty computation [19].
The goal of an oblivious algorithm (e.g. path ORAM [32], Melbourne shuffle [25]) is to hide its secrets from an attacker that can observe memory accesses. Probabilistic oblivious algorithms aim to do so while achieving better performance than deterministic oblivious algorithms. The various programming disciplines to defend against such attacks for deterministic algorithms [1, 22] often lead to poor performance: e.g. to hide the fact that an array is accessed at a certain position, one may have to iterate over the entire array [5]. Probabilistic oblivious algorithms avoid this inefficiency by performing random choices at runtime to hide their secrets from attackers more efficiently. Unfortunately, probabilistic methods for achieving obliviousness are error prone and some have been shown insecure, as a result requiring non-trivial fixes [10, 13].
In this paper we develop a program logic to verify the security of probabilistic oblivious algorithms formally and systematically. We adopt the standard threat model for such programs, in which the attacker is assumed to be able to infer the memory access pattern (e.g. either by explicitly observing memory requests in case of untrusted/compromised operating system or by measuring the time its own memory accesses take due to shared resources like caches) [4, 9, 11, 32].
Although some previous works [3, 7, 31, 34] exist, many oblivious algorithms have complex semantics and invariants that are beyond the reach of those prior methods to reason about. For example, path ORAM [32] maintains an invariant stating that virtual addresses are independent of each other and of the program’s memory access patterns; whereas the oblivious sampling algorithm [28] contains secret- or random-variable-dependent random choices, conditional branches and loops, whose details we introduce in Sect. 2 and Sect. 5.
Also, to achieve efficiency, some oblivious algorithms [25, 30, 32] forgo perfection and have a very small probability of failure, which means that they do not perfectly hide their secrets. Fortunately, they are intentionally designed so that the failure probability is bounded by some negligible factor (e.g. of the size of the secret data), meaning that they are secure in practice. Following prior work [25, 32], this means that we can prove them secure by reasoning over perfectly oblivious approximations, the theoretical and perfect version of the practical algorithms that are free of failure by construction (Appendix A.1 of the extended version of this paper [33] justifies this claim). Proving negligible error probability bounds on oblivious algorithms is an important goal, but is out of scope of this present work.
Reasoning over the perfectly oblivious approximations requires an approach that supports for all of the following:
-
Assertions that describe probability distributions and independence;
-
Reasoning about dynamic random choices over secrets and random variables – e.g. a random choice of integers from 1 to random secret variable s;
-
Reasoning about branches that depend on secret random variables;
-
Reasoning over loops that have a random number of iterations.
Our approach addresses these challenges simultaneously.
Following preliminaries (Sect. 3), in Sect. 4 we build a program logic that combines classical and probabilistic reasoning to address the aforementioned challenges, which we prove sound in Isabelle/HOL. Our logic is situated atop the Probabilistic Separation Logic (PSL) [3]; proving the soundness of our logic revealed several oversights in PSL [3], which we fixed (see Sect. 4.4).
To our knowledge, the reasoning our logic supports is beyond all prior methods for verifying obliviousness, including PSL [3], ObliCheck [31], \(\lambda _{ OADT }\) [34], and \(\lambda _{ obliv }\) [7]. The combination of classical and probabilistic reasoning also makes our logic more expressive than previous probabilistic Hoare logics (e.g., [12], VPHL [26] and pRHL [2]) which, because they lack assertions for describing distributions and independence, are ill-suited to direct proofs of obliviousness.
Finally, we demonstrate the power of our logic by applying it on pen-and-paper to verify, for the first time, the obliviousness of several non-trivial case studies (Sect. 5). Their verification is a significant achievement in that they constitute the fundamental building blocks for secure oblivious systems.
2 Overview
2.1 Challenges for Verification
Many probabilistic oblivious algorithms use probabilistic independence as a core intermediate condition to prove their obliviousness informally on pen and paper [25, 28, 30, 32], which is intuitive and simple. However, such algorithms present a range of challenges for formally verifying their obliviousness systematically.
We have constructed the example algorithm in Fig. 1 to illustrate in a simplified form the kinds of complexities that will feature in the semantics and invariants needed to prove our case studies (Sect. 5). The teal-coloured parts show the verification and will be introduced in the next subsection. Our synthetic algorithm takes an input array S with size n containing secret elements: each either 0 or 1. The list O is empty initially but will be filled with some data later. We want to prove O will not leak any information about S. The synthetic algorithm first initialises array A with two random values sampled from the integers between 0 and 7. Its nested loop illustrates the following challenges:
-
1.
The outer loop iterates n times where the ith iteration will append A[S[i]] to O (line
 ). It simulates a simplified version of path ORAM [32], which maintains an invariant that virtual addresses are independent of each other and of the program’s memory access patterns. The secret S can be seen as a sequence of secret virtual addresses and the output O represents the memory access pattern. We need to prove an invariant that the elements in O are independent of each other and independent of each element A[S[i]] appended to O by the outer loop. Note: the assignment on line
). It simulates a simplified version of path ORAM [32], which maintains an invariant that virtual addresses are independent of each other and of the program’s memory access patterns. The secret S can be seen as a sequence of secret virtual addresses and the output O represents the memory access pattern. We need to prove an invariant that the elements in O are independent of each other and independent of each element A[S[i]] appended to O by the outer loop. Note: the assignment on line
 breaks the independence between O and A[S[i]], so lines
breaks the independence between O and A[S[i]], so lines
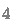 –
–
 update A[S[i]] with a fresh random value to re-establish the independence for the next loop iteration. This ensures O is independent of S and will not leak secret information.
update A[S[i]] with a fresh random value to re-establish the independence for the next loop iteration. This ensures O is independent of S and will not leak secret information. -
2.
After initialising m with 8 on line
 , we have the inner loop containing a probabilistic and secret-dependent if-conditional. Its secret dependence makes the control flow different over different values of the secret. The iteration count for the inner loop is truly random, depending on A[S[i]] (where each iteration doubles m and increases j by 1 or 2 depending on whether \(j + S[i] \% 3 = 0\)). These kinds of loops and conditionals are common in real-world oblivious algorithms (Sect. 5), yet necessarily complicate reasoning.
, we have the inner loop containing a probabilistic and secret-dependent if-conditional. Its secret dependence makes the control flow different over different values of the secret. The iteration count for the inner loop is truly random, depending on A[S[i]] (where each iteration doubles m and increases j by 1 or 2 depending on whether \(j + S[i] \% 3 = 0\)). These kinds of loops and conditionals are common in real-world oblivious algorithms (Sect. 5), yet necessarily complicate reasoning. -
3.
On line
 , the algorithm makes what we call a dynamic random choice, which is one over a truly random set (here, from 1 to the random variable m), assigning the chosen value to t. Then, (line
, the algorithm makes what we call a dynamic random choice, which is one over a truly random set (here, from 1 to the random variable m), assigning the chosen value to t. Then, (line
 ) A[S[i]] is assigned \(t~\%~8\). This requires reasoning that \(t~\%~8\) satisfies the uniform distribution on \(\{0\cdots 7\}\), because m is certainly a multiple of 8. Dynamic random choices are also common in real-world oblivious algorithms, as Sect. 5 demonstrates.
) A[S[i]] is assigned \(t~\%~8\). This requires reasoning that \(t~\%~8\) satisfies the uniform distribution on \(\{0\cdots 7\}\), because m is certainly a multiple of 8. Dynamic random choices are also common in real-world oblivious algorithms, as Sect. 5 demonstrates.
Lines
 are derived from the oblivious sampling algorithm [28] ( see Appendix C.2 of the extended version [33]) to demonstrate challenges 2 and 3.
are derived from the oblivious sampling algorithm [28] ( see Appendix C.2 of the extended version [33]) to demonstrate challenges 2 and 3.
2.2 Mixing Probabilistic and Classical Reasoning
We show how to construct a program logic that combines classical and probabilistic (and independence) reasoning over different parts of the program so that it can verify our running example, as shown in Fig. 1. Namely, certain parts of the algorithm (lines
 ) require careful probabilistic reasoning, while others do not, but that each style of reasoning can benefit the other.
) require careful probabilistic reasoning, while others do not, but that each style of reasoning can benefit the other.
Our program logic is constructed by situating these ideas in the context of the Probabilistic Separation Logic (PSL) [3]. PSL is an existing program logic for reasoning about probabilistic programs. PSL employs the separating conjunction (here written \(\star \)) familiar from separation logic [23] to capture when two probability distributions are independent. In situating our work atop PSL we extend its assertion forms with the new \(\textsf{Ct}({\cdot })\) assertion, to capture classical information. More importantly, however, we significantly extend the resulting logic with a range of novel reasoning principles for mixing classical and probabilistic reasoning embodied in a suite of new rules (Fig. 3), which we will present more fully in Sect. 4. These new rules show how classical reasoning (captured by \(\textsf{Ct}({\cdot })\) assertions) can be effectively harnessed, and allow reasoning about dynamic random choices, secret-dependent if-statements, and random loops, making our logic significantly more applicable than PSL; while leveraging PSL’s support for intuitive reasoning about probability distributions makes our logic also more expressive than prior probabilistic program logics [2, 12, 26]. We also harness the close interaction between classical and probabilistic reasoning to allow new ways to prove security (e.g., the Unif-Idp rule and the final proposition of Proposition 1, which will be introduced in Fig. 3 and Sect. 4.1), and new ways to reason about random sampling (embodied in the RSample rule, Fig. 3). Each represents a non-trivial insight, and all are necessary for reasoning about real-world oblivious algorithms (Sect. 5). The increase in expressiveness, beyond prior probabilistic program logics [2, 3, 12, 26], within a principled and clean extension of PSL attests to the careful design of our logic.
The combination of classical and probabilistic reasoning means that our logic tracks two kinds of atomic assertions, as follows.
Certain Assertions. Classical reasoning is supported by certain assertions \(\textsf{Ct}({e_r})\) that state that some property \(e_r\) (which may mention random variables) is true with absolute certainty, i.e. is true in all memories supported by the current probabilistic state of the program. With certain assertions and classical reasoning, our logic can reason about loops with random iteration numbers and randomly secret-dependent if statements. Doing so requires distinguishing classical from distribution (independence) assertions, because the latter are ill-suited for reasoning about random loops and conditionals.
For example, from line
 to
to
 , although the random loop and the probabilistic- and secret-dependent if statement complicate the algorithm, we only need classical reasoning to conclude that after the loop m is certainly a multiple of 8 (using the RLoop and RCond rules in Fig. 3, which have the classic form). This information is sufficient to verify the remainder of the algorithm.
, although the random loop and the probabilistic- and secret-dependent if statement complicate the algorithm, we only need classical reasoning to conclude that after the loop m is certainly a multiple of 8 (using the RLoop and RCond rules in Fig. 3, which have the classic form). This information is sufficient to verify the remainder of the algorithm.
Distribution Assertions. On the other hand, reasoning about probability distributions is supported by distribution assertions, which we adopt and extend from PSL: for a set expression \(e_d\) (which is allowed to mention non-random program variables), \(\textbf{U}_{e_d}[{e_r}]\) states that expression \(e_r\) is uniformly distributed over the set denoted by \(e_d\) in the sense that when \(e_r\) is evaluated in the current probabilistic state of the program it yields a uniform distribution over the evaluation of \(e_d\). We define these concepts formally later in Sect. 4.1 (see Definition 2). With this reasoning style, we support dynamic random choice (e.g. line
 , the value is sampled from a truly probabilistic set), which is not supported by previous works [2, 3, 7, 12, 26, 31, 34]. Note that we require \(e_d\) to be deterministic here because if \(e_d\) can be probabilistic, then it means a probabilistic expression satisfies a uniform distribution on a probabilistic set—a clear contradiction.
, the value is sampled from a truly probabilistic set), which is not supported by previous works [2, 3, 7, 12, 26, 31, 34]. Note that we require \(e_d\) to be deterministic here because if \(e_d\) can be probabilistic, then it means a probabilistic expression satisfies a uniform distribution on a probabilistic set—a clear contradiction.
For example, at line
 , even if we do not specify the detailed distribution of m, we can conclude \(t~\%~8\) satisfies the uniform distribution on the set \(\{0\cdots 7\}\), as m is certainly a multiple of 8, by an argument based on our concept of an even partition (Definition 4). This reasoning is supported by our novel RSample rule (Fig. 3). Here, it requires that all the possible sets (in this case, \(\{1\cdots 8\}\) or \(\{1\cdots 16\}\) or ...) over which t was sampled, can each be evenly mapped to (and thus partitioned by) the target set (here \(\{0\cdots 7\}\)) by the applied function (here \(\% 8\)). Thus \(t~\%~8\) must satisfy the uniform distribution on \(\{0\cdots 7\}\).
, even if we do not specify the detailed distribution of m, we can conclude \(t~\%~8\) satisfies the uniform distribution on the set \(\{0\cdots 7\}\), as m is certainly a multiple of 8, by an argument based on our concept of an even partition (Definition 4). This reasoning is supported by our novel RSample rule (Fig. 3). Here, it requires that all the possible sets (in this case, \(\{1\cdots 8\}\) or \(\{1\cdots 16\}\) or ...) over which t was sampled, can each be evenly mapped to (and thus partitioned by) the target set (here \(\{0\cdots 7\}\)) by the applied function (here \(\% 8\)). Thus \(t~\%~8\) must satisfy the uniform distribution on \(\{0\cdots 7\}\).
Unifying Classical and Probabilistic Independence Reasoning. Another important feature of our logic is that it allows independence to be derived by leveraging classical reasoning. For example, considering line
 , if a variable (A[S[i]]) always satisfies the same distribution (uniform distribution on \(\{0\cdots 7\}\)) over any possible values of some other variables (O and \(A[1-S[i]]\)), then the former is independent of the latter (because O and \(A[1-S[i]]\) will not influence the values of A[S[i]]). The new rule Unif-Idp (Fig. 3) embodies this reasoning (where \(\star \) denotes independence and \(\textbf{D}( )\) stands for an arbitrary distribution).Footnote 1
, if a variable (A[S[i]]) always satisfies the same distribution (uniform distribution on \(\{0\cdots 7\}\)) over any possible values of some other variables (O and \(A[1-S[i]]\)), then the former is independent of the latter (because O and \(A[1-S[i]]\) will not influence the values of A[S[i]]). The new rule Unif-Idp (Fig. 3) embodies this reasoning (where \(\star \) denotes independence and \(\textbf{D}( )\) stands for an arbitrary distribution).Footnote 1
Our logic also includes a set of useful propositions (Proposition 1) that aid deriving independence information from classical reasoning.
Returning to the example, with the conclusion that A[S[i]] is independent of other variables, we can construct the loop invariant of the outer loop (\(\textsf{inv}(i)\)) stating that the output array O always satisfies a uniform distribution following the ith iteration, which is captured by \(\textsf{eight}(i)\). We use the final proposition of Proposition 1 here. Intuitively, this proposition says given a reversible function (whose inputs can be decided by looking at its outputs, e.g. array appending), if its two inputs satisfy uniform distribution and are independent of each other, then the result of the function should satisfy the uniform distribution on the product (by the function) of the two inputs’ distribution.
By the invariant, we can conclude finally the output array always satisfies the uniform distribution on \(\textsf{eight}(n)\), regardless of secret S, which means the output will not leak any secret information.
3 Preliminaries
3.1 Programming Language and Semantics
In this paper we define a probability distribution over a countable set A is a function \(\mu :A\rightarrow [0,1]\) where \( \varSigma _{a\in A}{\mu (a)} = 1\). We write \(\mu (B)\) for \(\varSigma _{b\in B}{\mu (b)}\) where B can be any subset of A and \(\textbf{D}({A})\) for the set of all distributions over A.
The support of a distribution \(\mu \), \(\textsf{supp}({\mu })\), is the set of all elements whose probability is greater than zero, \(\{a\in A\ |\ \mu (a)>0\}\).
A unit distribution over a single element, \(\textsf{unit}({a})\), is \((\lambda x.\ \textsf{If}\ {a=x}\ \textsf{then}\ {1}\ \textsf{else}\ {0})\). A uniform distribution over a set, \(\textsf{Unif}_{S}\), is \((\lambda x.\ \textsf{If}\ {x\in S}\ \textsf{then}\ {1/|S|}\ \textsf{else}\ {0})\).
Given a distribution \(\mu \) over A and a function f from elements of A to a distribution, \(f:A\rightarrow \textbf{D}({B})\), we define \(\textsf{bind}({\mu },{f})=\lambda b.\ \varSigma _{a\in A}{\mu (a)\cdot f(a)(b)}\), used to give semantics to random selections and assignments to random variables.
Given two distributions \(\mu _A\) and \(\mu _B\) over the sets A and B, we define \(\mu _A \otimes \mu _B =\lambda a, b.\ \mu _A(a)\cdot \mu _B(b)\). Given a distribution \(\mu \) over \(A\times B\), we define \(\pi _1(\mu ) =\lambda a.\ \varSigma _{b\in B}{\mu (a,b)}\) and \(\pi _2(\mu ) =\lambda b.\ \varSigma _{a\in A}{\mu (a,b)}\). We say these two distributions are independent if and only if \(\mu = \pi _1(\mu ) \otimes \pi _2(\mu )\).
Given a distribution \(\mu \) over some set A, and \(S\subseteq A\) where \(\mu (S) > 0\), let \(E\subseteq A\), we define \((\mu | S) =\lambda E.\ \frac{\mu (E\cap S)}{\mu (S)}\), used to give semantics to conditional statements, as is the following. Given two distribution \(\mu _1, \mu _2\), and a number \(p\in [0,1]\), we define \(\mu _1\oplus _{p}\mu _2=\lambda x.\ p\cdot \mu _1(x) + (1-p)\cdot \mu _2(x)\). When p is 1 or 0, we unconditionally define the result to be \(\mu _1\) or \(\mu _2\) respectively.
Same as PSL’s memory model, we also distinguish deterministic from random variables: only the latter can be influenced by random selections (i.e. by probabilistic choices). We define \(\textbf{DV}\) as a countable set of deterministic variables and \(\textbf{RV}\) as a countable set of random variables, disjoint from \(\textbf{DV}\).
Let \(\textbf{Val}\) be the countable set of values, which we assume contains at least the values \(\textsf{true}\) and \(\textsf{false}\). When applying our logic, we will freely assume it contains integers, lists, sets, and any other standard data types as required. Let \(\textsf{op}\) be a set of operations on values, including binary functions on values of type \((\textbf{Val}\times \textbf{Val}) \rightarrow \textbf{Val}\). In practice, we will assume it includes the standard arithmetic, list and set operations, and others as required. Finally, let \(\textsf{vset}( )\) be a function of type \(\textbf{Val}\rightarrow \mathcal {P}(\textbf{Val})\), taking one value and returning a non-empty, finite set of values, for giving semantics to dynamic random choice.
Then let \(\textbf{DetM}=\textbf{DV}\rightarrow \textbf{Val}\) be the set of deterministic memories, and \(\textbf{RanM}=\textbf{RV}\rightarrow \textbf{Val}\) the set of random variable memories. A semantic configuration is a pair \((\sigma , \mu )\), where \(\sigma \in \textbf{DetM}\) and \(\mu \in \textbf{D}({\textbf{RanM}})\) (a probability distribution over \(\textbf{RanM}\)). Configurations represent program states.
As with program variables, we define sets of deterministic and random expressions, denoted \(\textbf{DE}\) and \(\textbf{RE}\) respectively. \(\textbf{DE}\) cannot mention random variables.
Definition 1 (Expressions)
Expressions are either deterministic or random, defined as follows:
Note that \(\textbf{DE}\) is a subset of \(\textbf{RE}\). Given a deterministic memory \(\sigma \) and a random variable memory m, we write \(\left[ \left[ {e_r} \right] \right] (\sigma ,m)\) as the evaluation of expression \(e_r\). Expression evaluation is entirely standard and its definition is omitted for brevity. The evaluation of deterministic expressions \(e_d\) depends only on the deterministic memory \(\sigma \) and so we often abbreviate it \(\left[ \left[ {e_d} \right] \right] \sigma \).
Following the distinction between deterministic and random variables, the programming language also distinguishes deterministic and random conditionals and loops. We define two sets of program commands for our language, where \(\textbf{C}\) is the complete set of commands and \(\textbf{RC}\) is a subset of \(\textbf{C}\) containing so-called “random” commands that cannot assign to deterministic variables. We write \(\textbf{if}_D\ {b}\ \textbf{then}\ {c}\) to abbreviate \(\textbf{if}_D\ {b}\ \textbf{then}\ {c}\ \textbf{else}\ {\textbf{skip}}\) and likewise for \(\textbf{if}_R\ {b}\ \textbf{then}\ {c}\). As with PSL, our logic is defined for programs that always terminate.

In practical verification, given an algorithm, we try to set all the variables as deterministic variables at the beginning. Then, all the variables sampled from the uniform distribution or assigned by an expression containing random variables must be random variables. All the loop and if-conditions containing random variables must be random loops/conditionals. All the variables assigned in a random loop/conditional must be random variables. We repeat the above process until no variable and loop/conditional will change their type.
The semantics (Fig. 2) of a command \(c \in \textbf{C}\) is denoted \(\left[ \left[ {c} \right] \right] \), which is a configuration transformer of type \((\textbf{DetM}\times \textbf{D}({\textbf{RanM}}))\rightarrow (\textbf{DetM}\times \textbf{D}({\textbf{RanM}}))\). Our programming language extends that of PSL by allowing dynamic random choice, in which a value is chosen from a set denoted by an random expression \(e_r \in \textbf{RE}\) rather than a constant set. We also add random loops, whose condition can depend on random expressions (rather than only deterministic expressions as in PSL). These improvements increase the expressivity of the language, necessary to capture the kinds of practical oblivious algorithms that we target in Sect. 5. Unlike PSL, which defines its loop semantics somewhat informally, ours enables direct mechanisation (in Isabelle/HOL).
4 Logic
4.1 Assertions
The assertions of our logic include those of PSL, which we extend with the certainty assertion \(\textsf{Ct}({e_r})\) while extending the uniform distribution assertion \(\textbf{U}_{e_d}[{e_r}]\) by allowing the set to be specified by an expression \(e_d\) (rather than a constant as in PSL). The free variables of an expression e are denoted \(\textsf{FV}({e})\). The domain of distribution \(\mu \) over memories, written \(\mathsf {dom({\mu })}\), is the set of random variables in the memories in the support of \(\mu \). \(\textbf{AP}\) denotes the set of atomic assertions.
For a random variable expression \(e_r\), \(\textsf{Ct}({e_r})\) asserts that \(e_r\) evaluates to true in every memory consistent with the current configuration, i.e. it holds with absolute certainty. Note that the set of random variable expressions \(e_r\) can accommodate all standard assertions from classical Hoare logic.
Definition 2 (Atomic Assertion Semantics)
The assertion \(\textbf{U}_{e_d}[{e_r}]\) asserts that the evaluation of random variable expression \(e_r\) yields the uniform distribution over the set denoted by the deterministic expression \(e_d\) when evaluated in the current deterministic memory, where the \(\textsf{vset}( )\) function is used to retrieve that denotation after evaluating \(e_d\) (Sect. 3.1). We require the expression \(e_d\) to be deterministic as otherwise this assertion can introduce contradictions (e.g. if the set expression instead denoted a truly random set including possible sets \(\{1,2\}\) and \(\{0\}\), then \(e_r\) will not be uniformly distributed on any set).
From PSL our logic inherits its other assertions and Kripke resource monoid semantics. The assertions \(\top \) (which holds always), \(\perp \) (which never holds), and connectives \(\wedge \), \(\vee \), \(\rightarrow \) have their standard meaning. The separation logic [23] connectives are \(*\), which is separating conjunction and is used to assert probabilistic independence; and \(\mathrel {\rightarrow \!\!\!*}\) is separating implication. See extended Appendix A.2 [33].
Note that \(\textsf{Ct}({P})\wedge \textsf{Ct}({Q})\) is equivalent to \(\textsf{Ct}({P\wedge Q})\), but \(\textsf{Ct}({a=1})\) \(\vee \textsf{Ct}({a=2})\) is different to \(\textsf{Ct}({a=1\vee a=2})\): the former asserts that either a is always 1 or a is always 2 (stronger); the latter asserts that always a is either 1 or 2 (weaker).
We also write \(\textbf{D}({x})\) to abbreviate \(\textsf{Ct}({x = x})\), which asserts that the variable x is in the domain of the partial configuration. Any distribution of x satisfies this assertion.
Finally, we introduce several useful propositions about assertions implication. They are very useful in the verification and reflect the interplay between classical and probabilistic independence reasoning, especially the last one.
Proposition 1
The first two are inherited from PSL. The third one generalises a similar proposition of PSL [3] over possibly different sets S and \(S'\). The fourth and fifth show the equivalence of \(\wedge \) whether inside or outside the certain assertions. The sixth shows the straightforward consequence that if e is uniformly distributed over set S, then the value of e must be in S. The seventh shows two expressions satisfy the same distribution if they are certainly equal. The eighth shows if we know that e is independent of \(e'\) and we know another variable \(x = e\) additionally, we can conclude that x is also independent of \(e'\) if x is not a free variable in \(e'\).
The last one also generalises a proposition of PSL [3] by leveraging \(\textsf{Ct}({\cdot })\) conditions: it restricts binary function f by requiring it to produce different outputs when given two different pairs of inputs. In practice, we will use this lemma letting f be the concatenation function on two arrays where S is a set of possible arrays with the same length. We conclude the concatenated array satisfies the uniform distribution on S times \(S'\) if those premises hold.
4.2 Judgements and Rules
The judgements \(\vdash \{{\phi }\}~{c}~\{{\psi }\}\) of our program logic are simple Hoare logic correctness statements, in which c is a program command and \(\phi \) and \(\psi \) are preconditions and postconditions respectively.
Definition 3 (Judgement Validity)
Given two assertions \(\phi , \psi \) and a program command c, a judgement \(\{\phi \}c\{\psi \}\) is valid if for all configuration \((\sigma ,\mu )\) satisfying \((\sigma ,\mu )\models \phi \), we have \(\left[ \left[ {c} \right] \right] (\sigma ,\mu )\models \psi \), denoted \(\vdash \{{\phi }\}~{c}~\{{\psi }\}\).
Our logic inherits all of PSL’s original rules [3] (see extended Appendix A.3 [33] for details); many of them use the \(\textsf{Ct}({\cdot })\) assertion to encode equality tests, which were encoded instead in PSL primitively.
Figure 3 depicts the rules of our logic that embody its new reasoning principles, and support the requirements listed at Sect. 2.1. The random assignment rule RAssign has the classical Hoare logic form. It requires the postcondition \(\phi \) is atomic to avoid unsound derivations, e.g. \(\{{0=0*0=0}\}~{x=0}~\{{x=x*x=x}\}\).
As mentioned in Sect. 2.2, the RSample rule is another embodiment of the general principle underlying the design of our logic, of classical and probabilistic reasoning enhancing each other. Specifically, it allows us to deduce when a randomly sampled quantity \(f(x_r)\) (a function f applied to a random variable \(x_r\)) is uniformly distributed over set \(S'\) when the random variable \(x_r\) was uniformly sampled over set S. It is especially useful when S is itself random. It relies on the function f evenly partitioning the input set S into \(S'\), as defined below.
Definition 4 (Even Partition)
Given two sets \(S, S'\) and a function f, we say that f evenly partitions S into \(S'\) if and only if \(S' = \{f(s)|s\in S\}\) and there exists an integer k such that \(\forall s'\in S'. \left| \{s\in S | f(s) = s'\}\right| = k\). In this case we write \(\textsf{EI}(f,S,S')\).
RSample allows reasoning over random choices beyond original PSL [3], and in particular dynamic random sampling from truly random sets. For example, at line
 of Fig. 1, we have \(\textsf{Ct}({\textsf{EI}(f,S,S')})\) where \(f = ~\%~8,~S = \{0\cdots m\},~S' = \{0\cdots 7\}\). Letting \(k = m/8\) with the above definition, we can prove the pre-condition implies \(\textsf{Ct}({\textsf{EI}(f,S,S')})\). Note that if \(m=9\) then \(\textsf{Ct}({\textsf{EI}(f,S,S')})\) will not hold because we cannot find k. The existence of k makes sure that S can be evenly partitioned to \(S'\) by f. Also, from our new random sample rule RSample, one can obtain PSL’s original rule by letting \(S'=S\) and \(f=(\lambda x.\ x)\).
of Fig. 1, we have \(\textsf{Ct}({\textsf{EI}(f,S,S')})\) where \(f = ~\%~8,~S = \{0\cdots m\},~S' = \{0\cdots 7\}\). Letting \(k = m/8\) with the above definition, we can prove the pre-condition implies \(\textsf{Ct}({\textsf{EI}(f,S,S')})\). Note that if \(m=9\) then \(\textsf{Ct}({\textsf{EI}(f,S,S')})\) will not hold because we cannot find k. The existence of k makes sure that S can be evenly partitioned to \(S'\) by f. Also, from our new random sample rule RSample, one can obtain PSL’s original rule by letting \(S'=S\) and \(f=(\lambda x.\ x)\).
Besides PSL’s random conditional rule, we also include the RCond rule for random conditions that operate over certainty assertions \(\textsf{Ct}({\cdot })\). It is in many cases more applicable because it does not require the branching condition to be independent of the precondition and, while it reasons only over certainty assertions, other conditions can be added by applying the Const rule [3]. The new random loop rule RLoop is straightforward, requiring proof of the invariant \(\phi \) over a random conditional.
The final new rule Unif-Idp unifies two methods to prove the independence of an algorithm’s output b from its input a: it says that if given any arbitrary distribution of a we can always prove that the result b is uniformly distributed, then a and b are independent because the distribution of a does not influence b, where \(\textsf{MV}({c})\) is the variables c may write to (same as PSL’s definition). It is useful for programs that consume their secrets by random choice at runtime (e.g. Fig. 1 we verified in Sect. 2.2 and the Oblivious Sampling algorithm [28] we verify in extended Appendix C.2 [33]).
As an example, we used this rule between line
 and line
and line
 in Fig. 1 by letting \(a = (O,~A[1-S[i]])\) and P, Q be the other information in the assertion before line
in Fig. 1 by letting \(a = (O,~A[1-S[i]])\) and P, Q be the other information in the assertion before line
 . The first premise of the rule is true because these two lines of code never modify O and \(A[1-S[i]]\). The second premise is also trivially true. The third premise is proved by the RSample and RAssign rules. This yields the conclusion that O and \(A[1-S[i]]\) are independent of A[S[i]].
. The first premise of the rule is true because these two lines of code never modify O and \(A[1-S[i]]\). The second premise is also trivially true. The third premise is proved by the RSample and RAssign rules. This yields the conclusion that O and \(A[1-S[i]]\) are independent of A[S[i]].
Note that the pre-condition \(\textsf{Ct}({a\in A})*Q \wedge \textsf{Ct}({P})\) appears in both premise and conclusion of the rule. Considering the Weak rule [3] (aka the classical consequence rule), when the precondition is in the premise, we want it be as strong as it can so that the premise is easier to be proved. When it is in conclusion, we want it be as weak as it can so that the conclusion is more useful. These two requirements guide us to design the rule with two free assertions connected by \(\wedge \) and \(*\) respectively so that it is very flexible. If we change the pre-condition to \(\textbf{D}({a})\) (deleting A, P, Q), this rule is still sound (which can be proved by letting A be the universe set and P, Q be true) but much less applicable.
4.3 Soundness
Theorem 1
All the rules in Fig. 3, plus the other original PSL rules [3], are sound, i.e. are valid according to Definition 3.
We formalised our logic and proved it sound in Isabelle/HOL (see the accompanying artifact). It constitute 7K lines of Isabelle and required approx. 8 person-months to complete. Some of our Isabelle proofs follow PSL’s pen-and-paper proofs but we also found several problems in PSL’s definitions and proofs. We briefly discuss those now, to highlight the value and importance of machine-checked proofs for establishing the soundness of program logics.
4.4 Oversights in Original PSL
Our machine-checked proofs identified various oversights in the pen-and-paper formalisation of original PSL [3]. We fixed them either by modifying specific definitions or by finding an alternative—often much more complicated, but sound—proof strategy.
PSL [3] defines the notion of when a formula \(\phi \) is supported (\(\textbf{SP}\)), requiring that for any deterministic memory \(\sigma \), there exists a distribution over random variable memories \(\mu \) such that if \((\sigma , \mu ')\models \phi \), then \(\mu \sqsubseteq \mu '\) (meaning that \(\mu \) is a marginal distribution of \(\mu '\) where \(\mathsf {dom({\mu })} \subseteq \mathsf {dom({\mu '})}\)) [3, Definition 6].
This definition aims to restrict the assertions used in PSL’s original rule for random conditionals [3, rule RCond of Fig. 3], but it is not strong enough. All the assertions satisfy it because \(\mu \) can always be instantiated with the unit distribution over the empty memory \(\textsf{unit}({\emptyset \rightarrow \textbf{Val}})\), \(\sqsubseteq \) all others. This means the second example in their paper [3, Example 2] is a counterexample to their rule for random conditionals because there is not any non-supported assertion.
We fixed this by altering their definition of \(\textbf{SP}\). Note that simply excluding the empty memory case is not enough to fix this problem. Instead, we have Definition 5 and our Isabelle proofs ensure its soundness. It does not have a big impact on adjusting the proofs strategy of relevant rules.
Definition 5 (Supported)
An assertion \(\phi \) is Supported (\(\textbf{SP}\)) if for any deterministic memory \(\sigma \), there exists a randomised memory \(\mu \) such that if \((\sigma , \mu ')\models \phi \), then \(\mu \sqsubseteq \mu '\) and \((\sigma , \mu )\models \phi \).
Additionally, key lemmas that underpin PSL’s soundness argument turned out to be true, but not for the reasons stated in their proofs [3, Lemmas 1 and 2, Appendix B]. PSL’s Lemma 1 proof has mistakes in the implication case. The second sentence of the implication case said, “there exists a distribution \(\mu \)” such that \(\ldots \)”. However \(\mu \)” may not exist because \(\mu \) and \(\mu '\) may disagree on some variables in \(\textsf{FV}({\phi _1,\phi _2})\). PSL’s Lemma 2 proof also has mistakes. They said “we have \((\sigma _1, \mu _1) \models \eta \)” on the third line of proof but this is not true because \(\sigma _1\) may not equal \(\sigma \) (the domain of \(\sigma _1\) could be smaller than \(\sigma \)). The actual proof of these needs a different strategy which we found and formalized in Isabelle.
Without mechanising the soundness of our program logic, it is unlikely we would have uncovered these issues. This shows the vital importance of mechanised soundness proofs.
5 Case Studies
We applied our program logic to verify the obliviousness of four non-trivial oblivious algorithms: the Melbourne Shuffle [25], Oblivious Sampling [28], Path ORAM [32] and Path Oblivious Heap [30]. The details are in Appendix C of the extended version of this paper [33].
While these proofs are manual, each took less than a person-day to complete, except for Path Oblivious Heap, which took approx. 2 days of proof effort.
To our knowledge, the Melbourne Shuffle, Oblivious Sampling, and Path Oblivious Heap have never been formally verified as each requires the combination of features that our approach uniquely supports. Path ORAM has received some formal verification [16, 27] (see later in Sect. 6) and also comes with an informal but rigorous proof of security [32]. We verified it to show that our logic can indeed encode existing rigorous security arguments.
In practice we need to distinguish the public memory locations and private locations, where we assume any access to public memory locations is visible to attackers. We add ghost code to record all public accesses in an array “Trace” and finally we aim to prove that array is independent of secrets.
The Melbourne Shuffle [25] (see extended Appendix C.1 [33]) is an effective oblivious shuffling algorithm used in cloud storage and also a basic building block for other higher-level algorithms (e.g. oblivious sampling [28]). Its operation is non-trivial, including rearranging array elements with dummy values and other complexities. Its verification employs much classical reasoning because, while it is probabilistic, its memory access pattern is deterministic (absent failure).
Oblivious sampling [28] (see extended Appendix C.2 [33]) is another important building block having applications in differential privacy, oblivious data analysis and machine learning. The algorithm obliviously samples from a data set, by producing a uniformly-distributed memory access pattern, and includes random and secret-dependent looping and if-statements, plus dynamic random choices (shuffling on a truly probabilistic array). Thus our logic’s interplay between classical and probabilistic reasoning is essential to verifying its security.
Path ORAM [32] (see extended Appendix C.3 [33]) is a seminal oblivious RAM algorithm with practical efficiency, providing general-purpose oblivious storage. Path oblivious heap ( extended Appendix C.4 [33]) is inspired by Path ORAM and the two share the same idea: using a binary tree with a random and virtual location table to store secret data, where the mappings between each physical and virtual location are always independent of each other and of the memory access pattern. Thus probabilistic independence is crucial to express and prove these algorithms’ key invariants.
6 Related Work
Our program logic naturally extends PSL [3] non-trivially, including support for classical reasoning, dynamic random choice, improved support for random conditionals, random loops, and random assignments. Our mechanisation of PSL identified and fixed a number of oversights (see Sect. 4.4).
Its unique synergy of classical and probabilistic independence reasoning means our program logic is more expressive not only than PSL but also prior probabilistic Hoare logics, such as [12], VPHL [26] and Easycrypt’s pRHL [2].
Probabilistic coupling (supported by pRHL and Easycrypt [2]) is another popular way for proving the security of probabilistic algorithms. It does so by proving the output distribution is equal between any pair of different secret inputs, witnessed by a bijection probabilistic coupling for each probabilistic choice. However, for dynamic random choice, the bijection probabilistic coupling may not exist or may even be undefined (e.g. Fig. 1 and [28]). Sometimes, finding the correct coupling can be far more challenging than proving the conclusion directly via probabilistic independence. Indeed, the original informal security proofs of our case studies [25, 28, 30, 32] all use probabilistic independence to argue their obliviousness, instead of coupling.
Other program logics or type systems for verifying obliviousness also exist. For example, ObliCheck [31] and \(\lambda _{\text {OADT}}\) [34] can check or prove obliviousness but only for deterministic algorithms. \(\lambda _{ obliv }\) [7] is a type system for a functional language for proving obliviousness of probabilistic algorithms but it forbids branching on secrets, which is prevalent in many oblivious algorithms including those in Sect. 5. It also forbids outputting a probabilistic value (and all other values influenced by it) more than once. Our approach suffers no such restriction.
Path ORAM has received some verification attention [16, 27]. [27] reason about this algorithm but in a non-probabilistic model, instead representing it as a nondeterministic transition system, and apply model counting to prove a security property about it. Their property says that for any observable output, there is a sufficient number of inputs to hide which particular input would have produced that output. This specification seems about the best that can be achieved for a nondeterministic model of the algorithm, but would also hold for an implementation that used biased choices (which would necessarily reveal too much of the input). Ours instead says that for each input the output is identically distributed, and would not be satisfied for such a hypothetical implementation. Nonetheless, it would be interesting to compare the strengths and weaknesses of their complementary approach to ours. Hannah Leung et al. [16] recently proposed to verify this algorithm in Coq, but as far as we are aware ours is the first verification of Path ORAM via a probabilistic program logic.
Other recent work extends PSL in different ways. Ugo Dal Lago et al. [14] extended PSL to computational security, but it cannot deal with loops (neither deterministic nor probabilistic) so their target algorithms are very different to ours. Lilac [17] also uses separating conjunction to model probabilistic independence. Crucially, it supports reasoning about conditional probability and conditional independence; John M. Li et al. [18] validated the design decisions of Lilac. However, Lilac’s programming language is functional whereas ours is imperative. Lilac does not support random loops or dynamic random choice, which are essential for our aim.
IVL [29] reasons about probabilistic programs with nondeterminism. In doing so it supports classical reasoning (e.g. for the nondeterministic parts) and probabilistic reasoning for the probabilistic parts. Our logic reasons only about probabilistic programs (with no nondeterminism) but allows using classical reasoning to reason about parts of the probabilistic program, and for the classical and probabilistic reasoning styles to interact and enhance each other.
Some oblivious algorithms and their security definition (e.g. Differentially Oblivious Algorithms [6]) are not based on independence and they are beyond the reach of our approach.
7 Conclusion and Future Work
We presented the first program logic that, to our knowledge, is able to verify the obliviousness of real-world foundational probabilistic oblivious algorithms whose implementations combine challenging features like dynamic random choice and secret- and random-variable-dependent control flow. Our logic harnesses the interplay between classical and probabilistic reasoning, is situated atop PSL [3], and proved sound in Isabelle/HOL. We applied it to several challenging case studies, beyond the reach of prior approaches.
8 Artifact Availability Statement
We published our Isabelle/HOL formalisation on
Notes
- 1.
In this case we cannot use PSL’s frame rule because m is not independent of A.
References
Almeida, J.B., Barbosa, M., Barthe, G., Dupressoir, F., Emmi, M.: Verifying constant-time implementations. In: USENIX Security Symposium, vol. 16, pp. 53–70 (2016)
Barthe, G., Dupressoir, F., Grégoire, B., Kunz, C., Schmidt, B., Strub, P.-Y.: EasyCrypt: a tutorial. In: Aldini, A., Lopez, J., Martinelli, F. (eds.) FOSAD 2012-2013. LNCS, vol. 8604, pp. 146–166. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10082-1_6
Barthe, G., Hsu, J., Liao, K.: A probabilistic separation logic. Proc. ACM Program. Lang. 4(POPL), 1–30 (2019). https://doi.org/10.1145/3371123
Bittau, A., et al.: Prochlo: strong privacy for analytics in the crowd. In: Proceedings of the 26th Symposium on Operating Systems Principles (SOSP 2017), pp. 441–459. Association for Computing Machinery, New York (2017). https://doi.org/10.1145/3132747.3132769
Cauligi, S., et al.: Fact: a DSL for timing-sensitive computation. In: Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 174–189 (2019)
Chan, T.H.H., Chung, K.M., Maggs, B., Shi, E.: Foundations of differentially oblivious algorithms. J. ACM 69(4), 1–49 (2022). https://doi.org/10.1145/3555984
Darais, D., Sweet, I., Liu, C., Hicks, M.: A language for probabilistically oblivious computation. Proc. ACM Program. Lang. 4(POPL), 1–31 (2019). https://doi.org/10.1145/3371118
Fletcher, C.W., Ren, L., Kwon, A., van Dijk, M., Stefanov, E., Devadas, S.: RAW path ORAM: a low-latency, low-area hardware ORAM controller with integrity verification. IACR Cryptol. ePrint Arch. 431 (2014). http://eprint.iacr.org/2014/431
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious rams. J. ACM 43(3), 431–473 (1996). https://doi.org/10.1145/233551.233553
Goodrich, M.T., Mitzenmacher, M.: Privacy-preserving access of outsourced data via oblivious RAM simulation. In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011. LNCS, vol. 6756, pp. 576–587. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22012-8_46
Gruss, D., Spreitzer, R., Mangard, S.: Cache template attacks: automating attacks on inclusive last-level caches. In: 24th USENIX Security Symposium (USENIX Security 15), pp. 897–912. USENIX Association, Washington, D.C. (2015). https://www.usenix.org/conference/usenixsecurity15/technical-sessions/presentation/gruss
Hartog, J.I.: Verifying probabilistic programs using a hoare like logic. In: Thiagarajan, P.S., Yap, R. (eds.) ASIAN 1999. LNCS, vol. 1742, pp. 113–125. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-46674-6_11
Kushilevitz, E., Lu, S., Ostrovsky, R.: On the (in)security of hash-based oblivious ram and a new balancing scheme. In: Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2012), pp. 143–156. Society for Industrial and Applied Mathematics (2012)
Lago, U.D., Davoli, D., Kapron, B.M.: On separation logic, computational independence, and pseudorandomness (extended version) (2024). https://arxiv.org/abs/2405.11987
Lee, S., Shih, M.W., Gera, P., Kim, T., Kim, H., Peinado, M.: Inferring fine-grained control flow inside SGX enclaves with branch shadowing. In: 26th USENIX Security Symposium (USENIX Security 17), pp. 557–574. USENIX Association, Vancouver (2017). https://www.usenix.org/conference/usenixsecurity17/technical-sessions/presentation/lee-sangho
Leung, H., Ringer, T., Fletcher, C.W.: Towards formally verified path Oram in COQ (2023). https://dependenttyp.es/pdf/oramproposal.pdf
Li, J.M., Ahmed, A., Holtzen, S.: Lilac: a modal separation logic for conditional probability. Proc. ACM Program. Lang. 7(PLDI), 148–171 (2023). https://doi.org/10.1145/3591226
Li, J.M., Aytac, J., Johnson-Freyd, P., Ahmed, A., Holtzen, S.: A nominal approach to probabilistic separation logic. In: Proceedings of the 39th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS 2024). Association for Computing Machinery, New York (2024). https://doi.org/10.1145/3661814.3662135
Liu, C., Wang, X.S., Nayak, K., Huang, Y., Shi, E.: Oblivm: a programming framework for secure computation. In: 2015 IEEE Symposium on Security and Privacy, pp. 359–376 (2015). https://doi.org/10.1109/SP.2015.29
Liu, F., Yarom, Y., Ge, Q., Heiser, G., Lee, R.B.: Last-level cache side-channel attacks are practical. In: 2015 IEEE Symposium on Security and Privacy, pp. 605–622 (2015). https://doi.org/10.1109/SP.2015.43
Maas, M., et al.: Phantom: practical oblivious computation in a secure processor. In: Proceedings of the 2013 ACM SIGSAC Conference on Computer and Communications Security (CCS 2013), pp. 311–324. Association for Computing Machinery, New York (2013). https://doi.org/10.1145/2508859.2516692
Molnar, D., Piotrowski, M., Schultz, D., Wagner, D.: The program counter security model: automatic detection and removal of control-flow side channel attacks. In: Won, D.H., Kim, S. (eds.) ICISC 2005. LNCS, vol. 3935, pp. 156–168. Springer, Heidelberg (2006). https://doi.org/10.1007/11734727_14
O’Hearn, P., Reynolds, J., Yang, H.: Local reasoning about programs that alter data structures. In: Fribourg, L. (ed.) CSL 2001. LNCS, vol. 2142, pp. 1–19. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44802-0_1
Ohrimenko, O., Costa, M., Fournet, C., Gkantsidis, C., Kohlweiss, M., Sharma, D.: Observing and preventing leakage in mapreduce. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security (CCS 2015), pp. 1570–1581. Association for Computing Machinery, New York (2015). https://doi.org/10.1145/2810103.2813695
Ohrimenko, O., Goodrich, M.T., Tamassia, R., Upfal, E.: The Melbourne shuffle: improving oblivious storage in the cloud. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8573, pp. 556–567. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43951-7_47
Rand, R., Zdancewic, S.: VPHL: a verified partial-correctness logic for probabilistic programs. Electron. Notes Theor. Comput. Sci. 319, 351–367 (2015). https://doi.org/10.1016/j.entcs.2015.12.021
Sahai, S., Subramanyan, P., Sinha, R.: Verification of quantitative hyperproperties using trace enumeration relations. In: Lahiri, S.K., Wang, C. (eds.) CAV 2020. LNCS, vol. 12224, pp. 201–224. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-53288-8_11
Sasy, S., Ohrimenko, O.: Oblivious sampling algorithms for private data analysis. In: Proceedings of the 33rd International Conference on Neural Information Processing Systems. Curran Associates Inc., Red Hook (2019)
Schröer, P., Batz, K., Kaminski, B.L., Katoen, J.P., Matheja, C.: A deductive verification infrastructure for probabilistic programs. Proc. ACM Program. Lang. 7(OOPSLA2), 2052–2082 (2023). https://doi.org/10.1145/3622870
Shi, E.: Path oblivious heap: optimal and practical oblivious priority queue. Cryptology ePrint Archive, Paper 2019/274 (2019). https://eprint.iacr.org/2019/274
Son, J., Prechter, G., Poddar, R., Popa, R.A., Sen, K.: ObliCheck: efficient verification of oblivious algorithms with unobservable state. In: 30th USENIX Security Symposium (USENIX Security 21), pp. 2219–2236. USENIX Association (2021). https://www.usenix.org/conference/usenixsecurity21/presentation/son
Stefanov, E., et al.: Path Oram: an extremely simple oblivious ram protocol. J. ACM 65(4), 1–26 (2018). https://doi.org/10.1145/3177872
Yan, P., Murray, T., Ohrimenko, O., Pham, V.T., Sison, R.: Combining classical and probabilistic independence reasoning to verify the security of oblivious algorithms (extended version). arXiv preprint arXiv:2407.00514 (2024)
Ye, Q., Delaware, B.: Oblivious algebraic data types. Proc. ACM Program. Lang. 6(POPL), 1–29 (2022). https://doi.org/10.1145/3498713
Zheng, W., Dave, A., Beekman, J.G., Popa, R.A., Gonzalez, J.E., Stoica, I.: Opaque: an oblivious and encrypted distributed analytics platform. In: 14th USENIX Symposium on Networked Systems Design and Implementation (NSDI 17), pp. 283–298. USENIX Association, Boston (2017). https://www.usenix.org/conference/nsdi17/technical-sessions/presentation/zheng
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2025 The Author(s)
About this paper
Cite this paper
Yan, P., Murray, T., Ohrimenko, O., Pham, VT., Sison, R. (2025). Combining Classical and Probabilistic Independence Reasoning to Verify the Security of Oblivious Algorithms. In: Platzer, A., Rozier, K.Y., Pradella, M., Rossi, M. (eds) Formal Methods. FM 2024. Lecture Notes in Computer Science, vol 14933. Springer, Cham. https://doi.org/10.1007/978-3-031-71162-6_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-71162-6_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-71161-9
Online ISBN: 978-3-031-71162-6
eBook Packages: Computer ScienceComputer Science (R0)



 ). It simulates a simplified version of path ORAM [
). It simulates a simplified version of path ORAM [ breaks the independence between O and A[S[i]], so lines
breaks the independence between O and A[S[i]], so lines
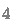 –
–
 update A[S[i]] with a fresh random value to re-establish the independence for the next loop iteration. This ensures O is independent of S and will not leak secret information.
update A[S[i]] with a fresh random value to re-establish the independence for the next loop iteration. This ensures O is independent of S and will not leak secret information. , we have the inner loop containing a probabilistic and secret-dependent if-conditional. Its secret dependence makes the control flow different over different values of the secret. The iteration count for the inner loop is truly random, depending on A[S[i]] (where each iteration doubles m and increases j by 1 or 2 depending on whether
, we have the inner loop containing a probabilistic and secret-dependent if-conditional. Its secret dependence makes the control flow different over different values of the secret. The iteration count for the inner loop is truly random, depending on A[S[i]] (where each iteration doubles m and increases j by 1 or 2 depending on whether  , the algorithm makes what we call a dynamic random choice, which is one over a truly random set (here, from 1 to the random variable m), assigning the chosen value to t. Then, (line
, the algorithm makes what we call a dynamic random choice, which is one over a truly random set (here, from 1 to the random variable m), assigning the chosen value to t. Then, (line
 ) A[S[i]] is assigned
) A[S[i]] is assigned 
