Abstract
Partially observable Markov Decision Processes (POMDPs) are a standard model for agents making decisions in uncertain environments. Most work on POMDPs focuses on synthesizing strategies based on the available capabilities. However, system designers can often control an agent’s observation capabilities, e.g. by placing or selecting sensors. This raises the question of how one should select an agent’s sensors cost-effectively such that it achieves the desired goals. In this paper, we study the novel optimal observability problem (oop): Given a POMDP \(\mathscr {M}\), how should one change \(\mathscr {M}\)’s observation capabilities within a fixed budget such that its (minimal) expected reward remains below a given threshold? We show that the problem is undecidable in general and decidable when considering positional strategies only. We present two algorithms for a decidable fragment of the oop: one based on optimal strategies of \(\mathscr {M}\)’s underlying Markov decision process and one based on parameter synthesis with SMT. We report promising results for variants of typical examples from the POMDP literature.
This work has been supported by Innovation Fund Denmark and the Digital Research Centre Denmark, through the bridge project “SIOT – Secure Internet of Things – Risk analysis in design and operation”.
You have full access to this open access chapter, Download conference paper PDF
Keywords


1 Introduction
Partially observable Markov Decision Processes (POMDPs) [1, 15, 28] are the reference model for agents making decisions in uncertain environments. They appear naturally in various application domains, including software verification [4], planning [5, 15, 16], computer security [24], and cyber-physical systems [13].
Most work on POMDPs focuses on synthesizing strategies for making decisions based on available observations. A less explored, but relevant, question for system designers is how to place or select sensors cost-effectively such that they suffice to achieve the desired goals.
To illustrate said question, consider a classical grid(world) POMDP [21], (cf. Fig. 1), where an agent is placed randomly on one of the states \(s_0\) - \(s_7\). The agent’s goal is to reach the goal state \(s_8\) (indicated with green color). The agent is free to move through the grid using the actions \(\{ left , right , up , down \}\). For simplicity, self-loops are omitted and the actions are only shown for state \(s_4\). We assume that every time the agent picks an action, (s)he takes one step. With an unlimited budget, one can achieve full observability by attaching one sensor to each state. In this case, the minimum expected number of steps the agent should take to reach the goal is 2.25.
However, the number of available sensors might be limited. Can we achieve the same optimal reward with fewer sensors? What is the minimal number of sensors needed? Where should they be located? It turns out that, in this example, 2 sensors (one in \(s_2\) and one in \(s_5\)) suffice to achieve the minimal expected number of steps, i.e., 2.25. Intuitively, the agent just needs a simple positional (aka memory-less), deterministic strategy: if no sensor is present, go right; otherwise, go down. A “symmetric” solution would be to place the sensors in \(s_6\) and \(s_7\). Any other choice for placing 2 sensors yields a higher expected number of steps. For example, placing the sensors in \(s_1\) and \(s_2\) yields a minimal expected number of steps of 2.75. The problem easily becomes more complex. Indeed, we show that this class of problems (our main focus of study) is undecidable.
The Problem. We introduce the optimal observability problem which is concerned with turning an MDP \(M\) into a POMDP \(\mathscr {M}\) such that \(\mathscr {M}\)’s expected reward remains below a given threshold and, at the same time, the number of available observations (i.e. classes of observationally-equivalent states) is limited by a given budget. We show that the problem is undecidable in the general case, by reduction to the (undecidable) policy-existence problem for POMDPs [22]. Consequently, we focus on decidable variants of the problem, where POMDPs can use positional strategies only, for which we provide complexity results, decision procedures, and experiments.
Contributions. Our main contributions can be summarized as follows:
-
1.
We introduce the novel optimal observability problem (OOP) and show that it is undecidable in general (Sect. 3) by reduction to the (undecidable) policy-existence problem for POMDPs [22]. Consequently, we study four decidable OOP variants by restricting the considered strategies and observation capabilities.
-
2.
We show in Sect. 4.1 that, when restricted to positional and deterministic strategies, the OOP becomes np-complete. Moreover, we present an algorithm that uses optimal MDP strategies to determine the minimal number of observations required to solve the OOP for the optimal threshold.
-
3.
We show in Sect. 4.2 that the OOP becomes decidable in pspace if restricted to positional, but randomized, strategies. The proofs are by a reduction to the feasibility problem for a typed extension of parametric Markov chains [12, 14].
-
4.
We provide in Sect. 5 an experimental evaluation of approaches for the decidable OOP variants on common POMDP benchmarks.
Missing proofs and additional experiments are found in an extended version of this paper, which is available online [17].
Related Work. To the best of our knowledge, this is the first work considering the optimal observability problem and its variants. The closest problem we have found in the literature is the sensor synthesis problem for POMDPs with reachability objectives presented in [6]. Said problem departs from a POMDP with a partially defined observation function and consists of finding a completion of the function by adding additional observations subject to a budget on the number of observations (as in our case) and the size of the (memory-bounded) strategies. The main difference w.r.t. our problem is in the class of POMDP objectives considered. The problem in [6] focuses on qualitative almost-sure reachability properties (which is decidable for POMDPs [7]), while we focus on quantitative optimal expected reward properties, which are generally undecidable for POMDPs [22]. This leads to different complexity results for the decision problem studied (NP-complete for [6], undecidable in our general case) and their solution methods (SAT-based in [6], SMT-based for the decidable variants we study).
Optimal placement or selection of sensors has been studied before (e.g. [18, 26, 30]). However, the only work we are aware of in this area that uses POMDPs is [30]. The problem studied in [30] is concerned with having a POMDP where the selection of k out of n sensors is part of the set of states of the POMDP together with the location of some entities in a 2D environment. At each state, the agent controlling the sensors has one of the \({n\atopwithdelims ()k}\) choices to select the next k active sensors. The goal is to synthesize and find strategies that dynamically select those sensors that optimize some objective function (e.g. increasing certainty of specific state properties). The observation function in the POMDPs used in [30] is fixed whereas we aim at synthesizing said function. The same holds for security applications of POMDPs, such as [29].
We discuss further related work, particularly about decidability results for POMDPs, parametric Markov models (cf. [12]), and related tools in the relevant subsections.
2 Preliminaries
We briefly introduce the formal models underlying our problem statements and their solution: Markov decision processes (MDPs) in Sect. 2.1 and partially observable MDPs (POMDPs) in Sect. 2.2. A comprehensive treatment is found in [2, 28].
Notation. A probability distribution over a countable set X is a function \(\mu : X \rightarrow [0,1] \subseteq \mathbb {R}\) such that the (real-valued) probabilities assigned to all elements of X sum up to one, i.e. \(\sum _{x \in X} . \mu (x) =1\). For example, the Dirac distribution \(\delta _x\) assigns probability 1 to an a-priori selected element \(x \in X\) and probability 0 to all other elements. We denote by \( Dist (X)\) the set of all probability distributions over X.
2.1 Markov Decision Processes (MDPs)
We first recap Markov decision processes with rewards and dedicated goal states.
Definition 1
(MDPs). A Markov decision process is a tuple \(M = (S, I, G, Act , P, rew )\) where S is a finite set of states, \(I \subseteq S\) is a set of (uniformly distributed) initial states, \(G \subseteq S\) is a set of goal states, \( Act \) is a finite set of actions, \(P:S \times Act \rightarrow Dist (S)\) is a transition probability function, and \( rew :S \rightarrow \mathbb {R}_{\ge 0}\) is a reward function.
Example 1
As a running example, consider an agent that is placed at one of four random locations on a line. The agent needs to reach a
 by moving to the \(\ell \)(eft) or r(ight). Whenever (s)he decides to move, (s)he successfully does so with some fixed probability \(p \in [0,1]\); with probability \(1-p\), (s)he stays at the current location due to a failure. Figure 2 depictsFootnote 1 an MDP \(M_{\text {line}}\) modeling the above scenario using five states \(s_0\)-\(s_4\). Here,
by moving to the \(\ell \)(eft) or r(ight). Whenever (s)he decides to move, (s)he successfully does so with some fixed probability \(p \in [0,1]\); with probability \(1-p\), (s)he stays at the current location due to a failure. Figure 2 depictsFootnote 1 an MDP \(M_{\text {line}}\) modeling the above scenario using five states \(s_0\)-\(s_4\). Here,
 is the single goal state. All other states are initial. An edge \(s_i \xrightarrow {\alpha : q} s_j\) indicates that \(P(s_i, \alpha )(s_j) = q\). The reward (omitted in Fig. 2) is 0 for
is the single goal state. All other states are initial. An edge \(s_i \xrightarrow {\alpha : q} s_j\) indicates that \(P(s_i, \alpha )(s_j) = q\). The reward (omitted in Fig. 2) is 0 for
 , and 1 for all other states.
, and 1 for all other states.
We often write \(S_M\), \(P_M\), and so on, to refer to the components of an MDP M. An MDP M is a Markov chain if there are no choices between actions, i.e. \(| Act _M| = 1\). We omit the set of actions when considering Markov chains. If there is more than one action, we use strategies to resolve all non-determinism.
Definition 2
(Strategy). A strategy for MDP M is a function \(\sigma :S_M^{+} \rightarrow Dist( Act _M)\) that maps non-empty finite sequences of states to distributions over actions. We denote by \(\mathfrak {S}(M)\) the set of all strategies for MDP M.
Expected rewards. We will formalize the problems studied in this paper in terms of the (minimal) expected reward \(\textsf {MinExpRew}(M)\) accumulated by an MDP M over all paths that start in one of its initial states and end in one of its goal states. Towards a formal definition, we first define paths. A path fragment of an MDP M is a finite sequence \( \pi = s_0\, \alpha _0\, s_1\, \alpha _1\, s_2\, \ldots \, \alpha _{n-1}\, s_n \) for some natural number n such that every transition from one state to the next one can be taken for the given action with non-zero probability, i.e. \(P_M(s_i,\alpha _i)(s_{i+1}) > 0\) holds for all \(i \in \{0, \ldots , n\}\). We denote by \( first (\pi ) = s_0\) (resp. \( last (\pi ) = s_n\)) the first (resp. last) state in \(\pi \). Moreover, we call \(\pi \) a path if \(s_0\) is an initial state, i.e. \(s_0 \in I_M\), and \(s_n \in G_M\) is the first encountered goal state, i.e. \(s_1, \ldots , s_{n-1} \in S_M\setminus G_M\) and \(s_n \in G_M\). We denote by \( Paths (M)\) the set of all paths of M.
The cumulative reward of a path fragment \(\pi = s_0\, \alpha _0\, \ldots \, \alpha _{n-1}\, s_n\) of \(M\) is the sum of all rewards along the path, that is,
Furthermore, for a given strategy \(\sigma \), the probability of the above path fragment \(\pi \) isFootnote 2
Put together, the expected reward of M for strategy \(\sigma \) is the sum of rewards of all paths weighted by their probabilities and divided by the number of initial states (since we assume a uniform initial distribution) – at least as long as the goal states are reachable from the initial states with probability one; otherwise, the expected reward is infinite (cf. [2]). Formally, \(\textsf {ExpRew}^{\sigma }(M) = \infty \) if \(\frac{1}{|I_M|} \cdot \sum _{\pi \in Paths (M)} P_{M}^{\sigma }(\pi ) < 1\). Otherwise,
The minimal expected reward of M (over an infinite horizon) is then the infimum among the expected rewards for all possible strategies, that is,
The (maximal) expected reward is defined analogously by taking the supremum instead of the infimum. Throughout this paper, we focus on minimal expected rewards.
Optimal, positional, and deterministic strategies. In general, strategies may choose actions randomly and based on the history of previously encountered states. We will frequently consider three subsets of strategies. First, a strategy \(\sigma \) for M is optimal if it yields the minimal expected reward, i.e. \(\textsf {ExpRew}^{\sigma }(M) = \textsf {MinExpRew}(M)\). Second, a strategy is positional if actions depend on the current state only, i.e. \(\sigma (ws) = \sigma (s)\) for all \(w \in S_M^*\) and \(s \in S_M\). Third, a strategy is deterministic if the strategy always chooses exactly one action, i.e. for all \(w \in S_M^+\) there is an \(a \in Act _M\) such that \(\sigma (w) = \delta _a\).
Example 2
(cntd.). An optimal, positional, and deterministic strategy \(\sigma \) for the MDP \(M_{\text {line}}\) (Fig. 2) chooses action r(ight) for states \(s_0\), \(s_1\) and \(\ell \)(eft) for \(s_3\), \(s_4\). For \(p = 2/3\), the (minimal) expected number of steps until reaching
 is \(\textsf {ExpRew}^{\sigma }(M_{\text {line}}) = 3\).
is \(\textsf {ExpRew}^{\sigma }(M_{\text {line}}) = 3\).
Every positional strategy for an MDP M induces a Markov chain over the same states.
Definition 3
(Induced Markov Chain). The induced Markov chain of an MDP M and a positional strategy \(\sigma \) of M is given by \(M[\sigma ] = (S_M, I_M, G_M, P, rew _M)\), where the transition probability function P is given by
For MDPs, there always exists an optimal strategy that is also positional and deterministic (cf. [2]). Hence, the minimal expected reward of such an MDP \(M\) can alternatively be defined in terms of the expected rewards of its induced Markov chains:
2.2 Partially Observable Markov Decision Processes
A partially observable Markov decision process (POMDP) is an MDP with imperfect information about the current state, that is, certain states are indistinguishable.
Definition 4
(POMDPs). A partially observable Markov decision process is a tuple \(\mathscr {M}= (M, O, obs )\), where \(M = (S, I, G, Act , P, rew )\) is an MDP, O is a finite set of observations, and
 is an observation function such that
is an observation function such that
 Footnote 3
Footnote 3
For simplicity, we use a dedicated observation
 for goal states and only consider observation functions of the above kind. We write
for goal states and only consider observation functions of the above kind. We write
 as a shortcut for
as a shortcut for
 .
.
Example 3
(cntd.). The colors in Fig. 2 indicate a POMDP obtained from \(M_{\text {line}}\) by assigning observations
 to \(s_0\) and \(s_4\),
to \(s_0\) and \(s_4\),
 to \(s_1\) and \(s_4\), and
to \(s_1\) and \(s_4\), and
 to
to
 . Hence, we know how far away from the goal state
. Hence, we know how far away from the goal state
 we are but not which action leads to the goal.
we are but not which action leads to the goal.
In a POMDP \(\mathscr {M}\), we assume that we cannot directly see a state, say s, but only its assigned observation \( obs _\mathscr {M}(s)\) – all states in \( obs ^{-1}_{\mathscr {M}}(o) = \{ s ~|~ obs _\mathscr {M}(s) = o \}\) thus become indistinguishable. Consequently, multiple path fragments in the underlying MDP M might also become indistinguishable. More formally, the observation path fragment \( obs _\mathscr {M}(\pi )\) of a path fragment \(\pi = s_0 \alpha _0 s_1 \ldots s_n \in Paths (M)\) is defined as
We denote by \( OPaths (\mathscr {M})\) the set of all observation paths obtained from the paths of \(\mathscr {M}\)’s underlying MDP M, i.e. \( OPaths (\mathscr {M}) = \{ obs _\mathscr {M}(\pi ) ~|~ \pi \in Paths (M) \}\). Strategies for POMDPs are defined as for their underlying MDPs. However, POMDP strategies must be observation-based, that is, they have to make the same decisions for path fragments that have the same observation path fragment.
Definition 5
(Observation-Based Strategies). An observation-based strategy \(\sigma \) for a POMDP \(\mathscr {M}= (M, O, obs )\) is a function \(\sigma : OPaths (\mathscr {M}) \rightarrow Dist ( Act _M)\) such that:
-
\(\sigma \) is a strategy for the MDP M, i.e. \(\sigma \in \mathfrak {S}(M)\) and
-
for all path fragments \(\pi = s_0 \alpha _0 s_1 ... s_n\) and \(\pi ' = s_0' \alpha _0' s_1' ... s_n'\), if \( obs (\pi ) = obs (\pi ')\), then \(\sigma (s_0 s_1 \ldots s_n) = \sigma (s_0' s_1' \ldots s_n')\).
We denote by \(\mathfrak {O}(\mathscr {M})\) the set of all observation-based strategies of \(\mathscr {M}\). The minimal expected reward of a POMDP \(\mathscr {M}= (M, O, obs )\) is defined analogously to the expected reward of the MDP M when considering only observation-based strategies:
Strategies for POMDPs. Optimal, positional, and deterministic observation-based strategies for POMDPs are defined analogously to their counterparts for MDPs. Furthermore, given a positional strategy \(\sigma \), we denote by \(\mathscr {M}[\sigma ] = (M_\mathscr {M}[\sigma ], O_\mathscr {M}, obs _\mathscr {M})\) the POMDP in which the underlying MDP M is changed to the Markov chain induced by M and \(\sigma \).
When computing expected rewards, we can view a POMDP as an MDP whose strategies are restricted to observation-based ones. Hence, the minimal expected reward of a POMDP is always greater than or equal to the minimal expected reward of its underlying MDP. In particular, if there is one observation-based strategy that is also optimal for the MDP, then the POMDP and the MDP have the same expected reward.
Example 4
(cntd.). Consider the POMDP \(\mathscr {M}\) in Fig. 2 for \(p=1/2\). For the underlying MDP \(M_{\text {line}}\), we have \(\textsf {MinExpRew}(M_{\text {line}}) = 4\). Since we cannot reach
 from
from
 and
and
 by choosing the same action, every positional and deterministic observation-based strategy \(\sigma \) yields \(\textsf {ExpRew}^{\sigma }(\mathscr {M}) = \infty \). An observation-based positional strategy \(\sigma '\) can choose each action with probability \(1/2\), which yields \(\textsf {ExpRew}^{\sigma '}(\mathscr {M}) = 10\). Moreover, for deterministic, but not necessarily positional, strategies, \(\textsf {MinExpRew}(\mathscr {M}) \approx 4.74.\)Footnote 4
by choosing the same action, every positional and deterministic observation-based strategy \(\sigma \) yields \(\textsf {ExpRew}^{\sigma }(\mathscr {M}) = \infty \). An observation-based positional strategy \(\sigma '\) can choose each action with probability \(1/2\), which yields \(\textsf {ExpRew}^{\sigma '}(\mathscr {M}) = 10\). Moreover, for deterministic, but not necessarily positional, strategies, \(\textsf {MinExpRew}(\mathscr {M}) \approx 4.74.\)Footnote 4
Notation for (PO)MDPs. Given a POMDP \(\mathscr {M}= (M, O, obs )\) and an observation function
 , we denote by \(\mathscr {M}\langle { obs '}\rangle \) the POMDP obtained from \(\mathscr {M}\) by setting the observation function to \( obs '\), i.e. \(\mathscr {M}\langle { obs '}\rangle = (M, O', obs ')\). We call \(\mathscr {M}\) fully observable if all states can be distinguished from one another, i.e. \(s_1 \ne s_2\) implies \( obs (s_1) \ne obs (s_2)\) for all \(s_1,s_2 \in S_M\). Throughout this paper, we do not distinguish between a fully-observable POMDP \(\mathscr {M}\) and its underlying MDP M. Hence, we use notation introduced for POMDPs, such as \(\mathscr {M}\langle { obs '}\rangle \), also for MDPs.
, we denote by \(\mathscr {M}\langle { obs '}\rangle \) the POMDP obtained from \(\mathscr {M}\) by setting the observation function to \( obs '\), i.e. \(\mathscr {M}\langle { obs '}\rangle = (M, O', obs ')\). We call \(\mathscr {M}\) fully observable if all states can be distinguished from one another, i.e. \(s_1 \ne s_2\) implies \( obs (s_1) \ne obs (s_2)\) for all \(s_1,s_2 \in S_M\). Throughout this paper, we do not distinguish between a fully-observable POMDP \(\mathscr {M}\) and its underlying MDP M. Hence, we use notation introduced for POMDPs, such as \(\mathscr {M}\langle { obs '}\rangle \), also for MDPs.
3 The Optimal Observability Problem
We now introduce and discuss observability problems of the form “what should be observable for a POMDP such that a property of interest can still be guaranteed?”.
As a simple example, assume we want to turn an MDP \(M\) into a POMDP \(\mathscr {M}= (M,O, obs )\) by selecting an observation function
 such that \(M\) and \(\mathscr {M}\) have the same expected reward, that is, \(\textsf {MinExpRew}(M) = \textsf {MinExpRew}(\mathscr {M})\). Since every MDP is also a POMDP, this problem has a trivial solution: We can introduce one observation for every non-goal state, i.e. \(O = (S_M\setminus G_M)\), and encode full observability, i.e. \( obs (s) = s\) if \(s \in S_M\setminus G_M\) and
such that \(M\) and \(\mathscr {M}\) have the same expected reward, that is, \(\textsf {MinExpRew}(M) = \textsf {MinExpRew}(\mathscr {M})\). Since every MDP is also a POMDP, this problem has a trivial solution: We can introduce one observation for every non-goal state, i.e. \(O = (S_M\setminus G_M)\), and encode full observability, i.e. \( obs (s) = s\) if \(s \in S_M\setminus G_M\) and
 if \(s \in G_M\). However, we will see that the above problem becomes significantly more involved if we add objectives or restrict the space of admissible observation functions \( obs \).
if \(s \in G_M\). However, we will see that the above problem becomes significantly more involved if we add objectives or restrict the space of admissible observation functions \( obs \).
In particular, we will define in Sect. 3.1 the optimal observability problem which is concerned with turning an MDP \(M\) into a POMDP \(\mathscr {M}\) such that \(\mathscr {M}\)’s expected reward remains below a given threshold and, at the same time, the number of available observations, i.e. how many non-goal states can be distinguished with certainty, is limited by a budget. In Sect. 3.2, we show that the problem is undecidable.
3.1 Problem Statement
Formally, the optimal observability problem is the following decision problem:
Definition 6
(Optimal Observability Problem (OOP)). Given an MDP \(M\), a budget \(B \in \mathbb {N}_{\ge 1}\), and a (rational) threshold \(\tau \in \mathbb {Q}_{\ge 0}\), is there an observation function
 with \(|O|\le B\) such that \(\textsf {MinExpRew}(M\langle { obs }\rangle ) \le \tau \)?
with \(|O|\le B\) such that \(\textsf {MinExpRew}(M\langle { obs }\rangle ) \le \tau \)?
Example 5
(cntd.). Recall from Fig. 2 the MDP \(M_{\text {line}}\) and consider the OOP-instance \((M_{\text {line}},B,\tau )\) for \(p = 1/2\), \(B = 2\), and \(\tau = \textsf {MinExpRew}(M_{\text {line}}) = 4\). As discussed in Example 4, the observation function given by the colors in Fig. 2 is not a solution. However, there is a solution: For \( obs (s_0) = obs (s_1) = o_1\),
 , and \( obs (s_2) = obs (s_3) = o_2\), we have \(\textsf {MinExpRew}(M_{\text {line}}\langle { obs }\rangle ) = 4\), because the optimal strategy for \(M_{\text {line}}\) discussed in Example 2 is also observation-based for \(M_{\text {line}}\langle { obs }\rangle \).
, and \( obs (s_2) = obs (s_3) = o_2\), we have \(\textsf {MinExpRew}(M_{\text {line}}\langle { obs }\rangle ) = 4\), because the optimal strategy for \(M_{\text {line}}\) discussed in Example 2 is also observation-based for \(M_{\text {line}}\langle { obs }\rangle \).
3.2 Undecidability
We now show that the optimal observability problem (Definition 6) is undecidable.
Theorem 1
(Undecidability). The optimal observability problem is undecidable.
The proof is by reduction to the policy-existence problem for POMDPs [22].
Definition 7
(Policy-Existence Problem). Given a POMDP \(\mathscr {M}\) and a rational threshold \(\tau \in \mathbb {Q}_{\ge 0}\), does \(\textsf {MinExpRew}(\mathscr {M}) \le \tau \) hold?
Proposition 1
(Madani et al. [22]). The policy-existence problem is undecidable.
Sketch of the MDP \(M'\) constructed in the undecidability proof (Theorem 1). We assume the original POMDP \(\mathscr {M}\) uses actions \( Act = \{\alpha , \beta \}\) and observations \(O = \{o,\tilde{o}\}\). Edges with a black dot indicate the probability distribution selected for the action(s) next to it. Edges without a black dot are taken with probability one. Concrete probabilities, rewards, and transitions of unnamed states have been omitted for simplicity.
Formal construction of the MDP \(M'\) in the proof of Theorem 1. Here, \(M'\) is derived from the POMDP \(\mathscr {M}= (M, O, obs )\), where \(M= (S, I, G, Act , P, rew )\). Moreover, \( uniform (S'')\) assigns probability \(1/|S''|\) to states in \(S''\) and probability 0, otherwise.
Proof
(of Theorem 1). By reduction to the policy-existence problem. Let \((\mathscr {M},\tau )\) be an instance of said problem, where \(\mathscr {M}= (M, O, obs )\) is a POMDP, \(M= (S, I, G, Act , P, rew )\) is the underlying MDP, and \(\tau \in \mathbb {Q}_{\ge 0}\) is a threshold. Without loss of generality, we assume that G is non-empty and that \(| range (obs)| = |O|+1\), where \( range (obs) = \{ obs (s) ~|~ s \in S \}\). We construct an OOP-instance \((M', B, \tau )\), where \(B = |O|\), to decide whether \(\textsf {MinExpRew}(\mathscr {M}) \le \tau \) holds.
Construction of \(M'\). Figure 3 illustrates the construction of \(M'\); a formal definition is found in Fig. 4. Our construction extends \(M\) in three ways: First, we add a sink state \(s_{\infty }\) such that reaching \(s_{\infty }\) with some positive probability immediately leads to an infinite total expected reward. Second, we add a new initial state \(s_o\) for every observation \(o \in O\). Those new initial states can only reach each other, the sink state \(s_{\infty }\), or the goal states via the new state \(s_{\tau }\). Third, we tag every action \(\alpha \in Act\) with an observation from O, i.e. for all \(\alpha \in Act \) and \(o \in O\), we introduce an action \(\alpha _o\). For every state \(s \in S \setminus G\), taking actions tagged with \( obs (s)\) behaves as in the original POMDP \(\mathscr {M}\). Taking an action with any other tag leads to the sink state. Intuitively, strategies for \(M'\) thus have to pick actions with the same tags for states with the same observation in \(\mathscr {M}\). However, it could be possible that a different observation function than the original \( obs \) could be chosen. To prevent this, every newly introduced initial state \(s_o\) (for each observation \(o \in O\)) leads to \(s_{\infty }\) if we take an action that is not tagged with o. Each \(s_o\) thus represents one observable, namely o. To rule out observation functions with less than |O| observations, our transition probability function moves from every new initial state \(s_o \in S_O\) to every \(s_o' \in S_O\) and to \(s_{\tau }\) with some positive probability (uniformly distributed for convenience). If we would assign the same observation to two states in \(s_o, s_o' \in S_O\), then there would be two identical observation-based paths to \(s_o\) and \(s_o'\). Hence, any observation-based strategy inevitably has to pick an action with a tag that leads to \(s_{\infty }\). In summary, the additional initial states enforce that – up to a potential renaming of observations – we have to use the same observation function as in the original POMDP.
Clearly, the MDP \(M'\) is computable (even in polynomial time). Our construction also yields a correct reduction (see [17, Appendix A.1] for details), i.e. we have

4 Optimal Observability for Positional Strategies
Since the optimal observability problem is undecidable in general (cf. Theorem 1), we consider restricted versions. In particular, we focus on positional strategies throughout the remainder of this paper. We show in Sect. 4.1 that the optimal observability problem becomes np-complete when restricted to positional and deterministic strategies. Furthermore, one can determine the minimal required budget that still yields the exact minimal expected reward by analyzing the underlying MDP (Sect. 4.1). In Sect. 4.2, we explore variants of the optimal observability problem, where the budget is lower than the minimal required one. We show that an extension of parameter synthesis techniques can be used to solve those variants.
4.1 Positional and Deterministic Strategies
We now consider a version of the optimal observability problem in which only positional and deterministic strategies are taken into account. Recall that a positional and deterministic strategy for \(\mathscr {M}\) assigns one action to every state, i.e. it is of the form \(\sigma :S_\mathscr {M}\rightarrow Act _\mathscr {M}\). Formally, let \(\mathfrak {S}_{pd}(\mathscr {M})\) denote the set of all positional and deterministic strategies for \(\mathscr {M}\). The minimal expected reward over strategies in \(\mathfrak {S}_{pd}(\mathscr {M})\) is
The optimal observability problem for positional and deterministic strategies is then defined as in Definition 6, but using \(\textsf {MinExpRew}_{pd}(\mathscr {M})\) instead of \(\textsf {MinExpRew}(\mathscr {M})\):
Definition 8
(Positional Deterministic Optimal Observability Problem (PDOOP)). Given an MDP \(M\), \(B \in \mathbb {N}_{\ge 1}\), and \(\tau \in \mathbb {Q}_{\ge 0}\), does there exist an observation function
 with \(|O| \le B\) such that \(\textsf {MinExpRew}_{pd}(\mathscr {M}\langle { obs }\rangle ) \le \tau \)?
with \(|O| \le B\) such that \(\textsf {MinExpRew}_{pd}(\mathscr {M}\langle { obs }\rangle ) \le \tau \)?
Example 6
(ctnd.). Consider the PDOOP-instance \((M_{\text {line}},2,4)\), where \(M_{\text {line}}\) is the MDP in Fig. 2 for \(p = 1/2\). Then there is a solution by assigning the observation \(o_1\) to \(s_0\) and \(s_1\) (and moving r(ight) for \(o_1\)), and \(o_2\) to \(s_3\) and \(s_4\) (and moving \(\ell \)(eft) for \(o_2\)).
Analogously, we restrict the policy-existence problem (cf. Definition 7) to positional and deterministic strategies.
Definition 9
(Positional Deterministic Policy-Existence Problem (PDPEP)). Given a POMDP \(\mathscr {M}\) and \(\tau \in \mathbb {Q}_{\ge 0}\), does \(\textsf {MinExpRew}_{pd}(\mathscr {M}) \le \tau \) hold?
Proposition 2
(Sec. 3 from [20]). PDPEP is np-complete.
np-hardness of PDOOP then follows by a reduction from PDPEP, which is similar to the reduction in our undecidability proof for arbitrary strategies (cf. Theorem 1). In fact, PDOOP is not only np-hard but also in np.
Theorem 2
(NP-completeness). PDOOP is np-complete.
Proof
(Sketch). To see that PDOOP is in np, consider a PDOOP-instance \((M,B,\tau )\). We guess an observation function
 and a positional and deterministic strategy \(\sigma :S_M\rightarrow Act _M\). Both are clearly polynomial in the size of \(M\) and B. Then \( obs \) is a solution for the PDOOP-instance \((M,B,\tau )\) iff (a) \(\sigma \) is an observation-based strategy and (b) \(\textsf {ExpRew}^{\sigma }(M\langle { obs }\rangle ) \le \tau \). Since \(\sigma \) is positional and deterministic, property (a) amounts to checking whether \( obs (s) = obs (t)\) implies \(\sigma (s) = \sigma (t)\) for all states \(s,t \in S_M\), which can be solved in time quadratic in the size of \(M\). To check property (b), we construct the induced Markov chain \(M\langle { obs }\rangle [\sigma ]\), which is linear in the size of \(M\) (see Definition 3). Using linear programming (cf. [2]), we can determine the Markov chain’s expected reward in polynomial time, i.e. we can check that
and a positional and deterministic strategy \(\sigma :S_M\rightarrow Act _M\). Both are clearly polynomial in the size of \(M\) and B. Then \( obs \) is a solution for the PDOOP-instance \((M,B,\tau )\) iff (a) \(\sigma \) is an observation-based strategy and (b) \(\textsf {ExpRew}^{\sigma }(M\langle { obs }\rangle ) \le \tau \). Since \(\sigma \) is positional and deterministic, property (a) amounts to checking whether \( obs (s) = obs (t)\) implies \(\sigma (s) = \sigma (t)\) for all states \(s,t \in S_M\), which can be solved in time quadratic in the size of \(M\). To check property (b), we construct the induced Markov chain \(M\langle { obs }\rangle [\sigma ]\), which is linear in the size of \(M\) (see Definition 3). Using linear programming (cf. [2]), we can determine the Markov chain’s expected reward in polynomial time, i.e. we can check that
We show np-hardness by polynomial-time reduction from PDPEP to PDOOP. The reduction is similar to the proof of Theorem 1 but uses Proposition 2 instead of Proposition 1. We refer to [17, Appendix A.3] for details. In particular, notice that the construction in Fig. 4 is polynomial in the size of the input \(\mathscr {M}\), because the constructed MDP \(M'\) has \(|S|+|O_\mathscr {M}| + 2\) states and \(| Act _\mathscr {M}| \cdot |O_\mathscr {M}|\) actions. \(\square \)
Before we turn to the optimal observability problem for possibly randomized strategies, we remark that, for positional and deterministic strategies, we can also solve a stronger problem than optimal observability: how many observables are needed to turn an MDP into POMDP with the same minimal expected reward?
Definition 10
(Minimal Positional Budget Problem (MPBP)). Given an MDP \(M\), determine an observation function
 such that
such that
-
\(\textsf {MinExpRew}_{pd}(M\langle { obs }\rangle ) = \textsf {MinExpRew}_{pd}(M)\) and
-
\(\textsf {MinExpRew}_{pd}(M\langle { obs }\rangle ) < \textsf {MinExpRew}_{pd}(M\langle { obs '}\rangle )\) for all observation functions
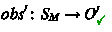 with \(|O'| < |O|\).
with \(|O'| < |O|\).
The main idea for solving the problem MPBP is that every optimal, positional, and deterministic (opd, for short) strategy \(\sigma :S_M\rightarrow Act _M\) for an MDP \(M\) also solves PDOOP for \(M\) with threshold \(\tau = \textsf {MinExpRew}_{p}(M)\) and budget \(B = | range (\sigma )|\): A suitable observation function \( obs :S_M\rightarrow range (\sigma )\) assigns action \(\alpha \) to every state \(s \in S_M\) with \(\sigma (s) = \alpha \). It thus suffices to find an opd strategy for \(M\) that uses a minimal set of actions. A brute-force approach to finding such a strategy iterates over all subsets of actions \(A \subseteq Act _M\): For each A, we construct an MDP \(M_A\) from \(M\) that keeps only the actions in A, and determine an opd strategy \(\sigma _A\) for \(M_A\). The desired strategy is then given by the strategy for the smallest set A such that \(\textsf {ExpRew}^{\sigma _A}(M_A) = \textsf {MinExpRew}_{p}(M)\). Since finding an opd strategy for a MDP is possible in polynomial time (cf. [2]), the problem MPBP can be solved in \(O(2^{| Act _M|} \cdot \textit{poly(size(M)))}\).
Example 7
(ctnd.). An opd strategy \(\sigma \) for the MDP \(M_{\text {line}}\) in Fig. 2 with \(p=1\) is given by \(\sigma (s_0) = \sigma (s_1) = r\) and \(\sigma (s_3) = \sigma (s_4) = \ell \). Since this strategy maps to two different actions, two observations suffice for selecting an observation function \( obs \) such that \(\textsf {MinExpRew}_{pd}(M_{\text {line}}\langle { obs }\rangle ) = \textsf {MinExpRew}_{pd}(M_{\text {line}}) = 3/2\).
4.2 Positional Randomized Strategies
In the remainder of this section, we will remove the restriction to deterministic strategies, i.e. we will study the optimal observability problem for positional and possibly randomized strategies. Our approach builds upon a typed extension of parameter synthesis techniques for Markov chains, which we briefly introduce first. For a comprehensive overview of parameter synthesis techniques, we refer to [12, 14].
Typed Parametric Markov Chains. A typed parametric Markov chain (tpMC) admits expressions instead of constants as transition probabilities. We admit variables (also called parameters) of different types in expressions. The types \(\mathbb {R}\) and \(\mathbb {B}\) represent real-valued and \(\{0,1\}\)-valued variables, respectively. We denote by \(\mathbb {R}_{=C}\) (resp. \(\mathbb {B}_{=C}\)) a type for real-valued (resp. \(\{0,1\}\)-valued) variables such that the values of all variables of this type sum up to some fixed constant C.Footnote 5 Furthermore, we denote by V(T) the subset of V consisting of all variables of type T. Moreover, \(\mathbb {Q}[V]\) is the set of multivariate polynomials with rational coefficients over variables taken from V.
Definition 11
(Typed Parametric Markov Chains). A typed parametric Markov chain is a tuple \(\mathscr {D}= (S, I, G, V, P, rew )\), where S is a finite set of states, \(I \subseteq S\) is a set of initial states, \(G \subseteq S\) is a set of goal states, V is a finite set of typed variables, \(P:S \times S \rightarrow \mathbb {Q}[V]\) is a parametric transition probability function, and \( rew :S \rightarrow \mathbb {R}_{\ge 0}\) is a reward function.
An instantiation of a tpMC \(\mathscr {D}\) is a function \(\iota :V_\mathscr {D}\rightarrow \mathbb {R}\) such that
-
for all \(x \in V_\mathscr {D}(\mathbb {B}) \cup V_\mathscr {D}(\mathbb {B}_{= C})\), we have \(\iota (x) \in \{0,1\}\);
-
for all \(V_\mathscr {D}(\mathbb {D}_{= C}) = \{ x_1,\ldots ,x_n \} \ne \emptyset \) with \(\mathbb {D} \in \{\mathbb {B},\mathbb {R}\}\), we have \(\sum _{i=1}^{n} \iota (x_i) = C\).
Given a polynomial \(q \in \mathbb {Q}[V_{\mathscr {D}}]\), we denote by \(q[\iota ]\) the real value obtained from replacing in q every variable \(x \in V_{\mathscr {D}}\) by \(\iota (x)\). We lift this notation to transition probability functions by setting \(P_\mathscr {D}[\iota ](s,s') = P_\mathscr {D}(s,s')[\iota ]\) for all states \(s, s' \in S_\mathscr {D}\). An instantiation \(\iota \) is well-defined if it yields a well-defined transition probability function, i.e. if \(\sum _{s' \in S_\mathscr {D}} P_\mathscr {D}[\iota ](s,s') = 1\) for all \(s \in S_\mathscr {D}\). Every well-defined instantiation \(\iota \) induces a Markov chain \(\mathscr {D}[\iota ] = (S_\mathscr {D}, I_\mathscr {D}, G_\mathscr {D}, P[\iota ], rew _\mathscr {D})\).
We focus on the feasibility problem – is there a well-defined instantiation satisfying a given property? – for tpMCs, because of a closed connection to POMDPs.
Definition 12
(Feasibility Problem for tpMCs). Given a tpMC \(\mathscr {D}\) and a threshold \(\tau \in \mathbb {Q}_{\ge 0}\), does there exist a well-defined instantiation \(\iota \) such that \(\textsf {ExpRew}(\mathscr {D}[\iota ]) \le \tau \).
Junges [14] studied decision problems for parametric Markov chains (pMCs) over real-typed variables. In particular, he showed that the feasibility problem for pMCs over real-typed variables is etr-complete. Here, ETR refers to the Existential Theory of Reals, i.e. all true sentences of the form \(\exists x_1 \ldots \exists x_n . P(x_1,...,x_n)\), where P is a quantifier-free first-order formula over (in)equalities between polynomials with real coefficients and free variables \(x_1, \ldots , x_n\). The complexity class etr consists of all problems that can be reduced to the etr in polynomial time. We extend this result to tpMCs.
Lemma 1
The feasibility problem for tpMCs is etr-complete.
A proof is found in [17, Appendix A.5]. Since etr lies between \(\textsc {np}\) and \(\textsc {pspace}\) (cf. [3]), decidability immediately follows:
Theorem 3
The feasibility problem for tpMCs is decidable in pspace.
Positional Optimal Observability via Parameter Synthesis. We are now ready to show that the optimal observability problem over positional strategies is decidable. Formally, let \(\mathfrak {S}_{p}(\mathscr {M})\) denote the set of all positional strategies for \(\mathscr {M}\). The minimal expected reward over strategies in \(\mathfrak {S}_{p}(\mathscr {M})\) is then given by
Definition 13
(Positional Observability Problem (POP)). Given an MDP \(M\), a budget \(B \in \mathbb {N}_{\ge 1}\), and a threshold \(\tau \in \mathbb {Q}_{\ge 0}\), is there a function
 with \(|O| \le B\) such that \(\textsf {MinExpRew}_{p}(M\langle { obs }\rangle ) \le \tau \)?
with \(|O| \le B\) such that \(\textsf {MinExpRew}_{p}(M\langle { obs }\rangle ) \le \tau \)?
To solve a POP-instance \((M,B,\tau )\), we construct a tpMC \(\mathscr {D}\) such that every well-defined instantiation corresponds to an induced Markov chain \(M\langle { obs }\rangle [\sigma ]\) obtained by selecting an observation function
 and a positional strategy \(\sigma \). Then the POP-instance \((M,B,\tau )\) has a solution iff the feasibility problem for \((\mathscr {D}, \tau )\) has a solution, which is decidable by Theorem 3.
and a positional strategy \(\sigma \). Then the POP-instance \((M,B,\tau )\) has a solution iff the feasibility problem for \((\mathscr {D}, \tau )\) has a solution, which is decidable by Theorem 3.
Our construction of \(\mathscr {D}\) is inspired by [14]. The main idea is that a positional randomized POMDP strategy takes every action with some probability depending on the given observation. Since the precise probabilities are unknown, we represent the probability of selecting action \(\alpha \) given observation o by a parameter \(x_{o,\alpha }\). Those parameters must form a probability distribution for every observation o, i.e. they will be of type \(\mathbb {R}^{o}_{=\,1}\). In the transition probability function, we then pick each action with the probability given by the parameter for the action and the current observation. To encode observation function \( obs \), we introduce a Boolean variable \(y_{s,o}\) for every state s and observation o that evaluates to 1 iff \( obs (s) = o\). Formally, the tpMC \(\mathscr {D}\) is constructed as follows:
Definition 14
(Observation tpMC of an MDP). For an MDP \(M\) and a budget \(B \in \mathbb {N}_{\ge 1}\), the corresponding observation tpMC \(\mathscr {D}_{M} = (S_M, I_M, G_M, V, P, rew _M)\) is given by
where, to avoid case distinctions, we define \(y_{s,o}\) as the constant 1 for all \(s \in G_M\).
Our construction is sound in the sense that every Markov chain obtained from an MDP \(M\) by selecting an observation function and an observation-based positional strategy corresponds to a well-defined instantiation of the observation tpMC of \(M\).
Lemma 2
Let \(M\) be an MDP and \(\mathscr {D}\) the observation tpMC of \(M\) for budget \(B \in \mathbb {N}_{\ge 1}\). Moreover, let \(O = \{1,\ldots ,B\}\). Then, the following sets are identical:

Proof
Intuitively, the values of \(y_{s,o}\) determine the observation function \( obs \), and the values of \(x_{s,\alpha }\) determine the positional strategy. See [17, Appendix A.6] for details. \(\square \)
Put together, Lemma 2 and Theorem 3 yield a decision procedure for the positional observability problem: Given a POP-instance (\(M,B,\tau )\), construct the observation tpMC \(\mathscr {D}\) of \(M\) for budget B. By Theorem 3, it is decidable in etr whether there exists a well-defined instantiation \(\iota \) such that \(\textsf {ExpRew}(\mathscr {D}[\iota ]) \le \tau \), which, by Lemma 2, holds iff there exists an observation function
 and a positional strategy \(\sigma \in \mathfrak {S}_{p}(M\langle { obs }\rangle )\) such that \(\textsf {MinExpRew}_{p}(M\langle { obs }\rangle ) \le \textsf {ExpRew}^{\sigma }(M\langle { obs }\rangle ) \le \tau \). Hence,
and a positional strategy \(\sigma \in \mathfrak {S}_{p}(M\langle { obs }\rangle )\) such that \(\textsf {MinExpRew}_{p}(M\langle { obs }\rangle ) \le \textsf {ExpRew}^{\sigma }(M\langle { obs }\rangle ) \le \tau \). Hence,
Theorem 4
The positional observability problem POP is decidable in etr.
In fact, POP is etr-complete because the policy-existence problem for POMDPs is etr-complete when restricted to positional strategies [14, Theorem 7.7]. The hardness proof is similar to the reduction in Sect. 3.2. Details are found in [17, Appendix A.3].
Example 8
(ctnd.). Figure 5 depicts the observation tpMC of the MDP \(M_{\text {line}}\) in Fig. 2 for \(p = 1\) and budget \(B = 2\). The Boolean variable \(y_{s,o}\) is true if we observe o for state s. Moreover, \(x_{o,\alpha }\) represents the rate of choosing action \(\alpha \) when o is been observed. As is standard for Markov models [27], including parametric ones [14], the expected reward can be expressed as a set of recursive Bellman equations (parametric in our case). For the present example those equations yield the following etr constraints:
where \(r_i\) is the expected reward for paths starting at \(s_i\), i.e. \(r_i = \sum _{\pi \in Paths (M_{\text {line}}) \mid \pi [0]=s_i} P_{M_{\text {line}}}^{\sigma }(\pi ) \cdot rew _{M_{\text {line}}}(\pi )\). Note that \(\textsf {ExpRew}^{\sigma }(M_{\text {line}}) = \frac{1}{4} \cdot (r_0 + r_1 + r_3 + r_4)\) for the strategy \(\sigma \) defined by the parameters \(x_{o,\alpha }\).
Observation tpMC for the MDP \(M_{\text {line}}\) in Fig. 2 with \(p=1\) and budget 2.
Sensor Selection Problem. We finally consider a variant of the positional observability problem in which observations can only be made through a fixed set of location sensors that can be turned on or off for every state. In this scenario, a POMDP can either observe its position (i.e. the current state) or nothing at all (represented by \(\bot \)).Footnote 6 Formally, we consider location POMDPs \(\mathscr {M}\) with observations \(O_\mathscr {M}= D \uplus \{ \bot \}\), where \(D \subseteq \{ @s \mid s \in (S_\mathscr {M}\setminus G_\mathscr {M}) \}\) are the observable locations and the observation function is

Example 9
(ctnd.). Consider the MDP \(M_{\text {line}}\) with \(p=1\) and location sensors assigned as in Fig. 2. With a budget of 2 we can only select 2 of the 4 location sensors. For example, we can turn on the sensors on one side, say \(@s_0\), \(@s_1\). The observation function is then given by \( obs (s_0)=@s_1\), \( obs (s_1)=@s_2\), and \( obs (s_3)= obs (s_4) = \bot \). This is an optimal sensor selection as it reveals whether one is located left or right of the goal.
The sensor selection problem aims at turning an MDP into a location POMDP with a limited number of observations such that the expected reward stays below a threshold.
Definition 15
(Sensor Selection Problem (SSP)). Given an MDP \(M\), a budget \(B \in \mathbb {N}_{\ge 1}\), and \(\tau \in \mathbb {Q}_{\ge 0}\), is there an observation function
 with \(|O| \le B\) such that \(\mathscr {M}= (M,O, obs )\) is a location POMDP and \(\textsf {MinExpRew}_{p}(\mathscr {M}) \le \tau \)?
with \(|O| \le B\) such that \(\mathscr {M}= (M,O, obs )\) is a location POMDP and \(\textsf {MinExpRew}_{p}(\mathscr {M}) \le \tau \)?
To solve the SSP, we construct a tpMC similar to Definition 14. The main difference is that we use a Boolean variable \(y_i\) to model whether the location sensor \(@s_i\) is on (1) or off (0). Moreover, we require that at most B sensors are turned on.
Definition 16
(Location tpMC of an MDP). For an MDP \(M\) and a budget \(B \in \mathbb {N}_{\ge 1}\), the corresponding location tpMC \(\mathscr {D}_{M} = (S_M, I_M, G_M, V, P, rew _M)\) is given by
where, to avoid case distinctions, we define \(y_s\) as the constant 1 for all \(s \in G_M\).
Analogously, to Lemma 2 and Theorem 5, soundness of the above construction then yields a decision procedure in pspace for the sensor selection problem (see [17, Appendix A.7]).
Lemma 3
Let \(M\) be an MDP and \(\mathscr {D}\) the location tpMC of \(M\) for budget \(B \in \mathbb {N}_{\ge 1}\). Moreover, let \( LocObs \) be the set of observation functions
 such that \(M\langle { obs }\rangle \) is a location MDP. Then, the following sets are identical:
such that \(M\langle { obs }\rangle \) is a location MDP. Then, the following sets are identical:
Theorem 5
The sensor selection problem SSP is decidable in etr, and thus in pspace.
Example 10
Figure 6 shows the location tpMC of the location POMDP in Fig. 2 for \(p=1\) and budget 2. The Boolean variable \(y_{s}\) indicates if the sensor @s is be turned on, while the variables \(x_{s,\alpha }\) indicates the rate of choosing action \(\alpha \) if sensor @s is turned on; otherwise, i.e. if sensor @s is turned off, \(x_{\bot ,\alpha }\) is used, which is the rate of choosing action \(\alpha \) for unknown locations.
Location tpMC for the location POMDP in Fig. 2 with \(p=1\) and budget 2.
5 Implementation and Experimental Evaluation
Our approaches for solving the optimal observability problem and its variants fall into two categories: (a) parameter synthesis (cf. Section 4.2) and (b) brute-force enumeration of observation functions combined with probabilistic model checking (cf. Theorem 2). In this section, we evaluate the feasibility of both approaches. Regarding approach (a), we argue in Sect. 5.1 why existing parameter synthesis tools cannot be applied out-of-the-box to the optimal observability problem. Instead, we performed SMT-backed experiments based on direct etr-encodings (see Theorems 4 and 5); the implementation and experimental setup is described in Sect. 5.2. Section 5.3 presents experimental results using our etr-encodings for approach (a) and, for comparison, an implementation of approach (b) using the probabilistic model checker prism [19].
5.1 Solving Optimal Observability Problems with Parameter Synthesis Tools
Existing tools that can solve parameter synthesis problems for Markov models, such as param [10], prophesy [8, 9, 12], and storm [11], are, to the best of our knowledge, restricted to (1) real-valued parameters and (2) graph-preserving models. Restriction (1) means that they do not support typed parametric Markov chains, which are needed to model the search for an observation function and budget constraints. Restriction (2) means that the choice of synthesized parameter values may not affect the graph structure of the considered Markov chain. For example, it is not allowed to set the probability of a transition to zero, which effectively means that the transition is removed. While the restriction to graph-preserving models is sensible for performance reasons, it rules out Boolean-typed variables, which we require in our tpMC-encodings of the positional observability problem (Definition 13) and the sensor selection problem (Definition 15). For example, the tpMCs in Fig. 5 and Fig. 6, which resulted from our running example, are not graph-preserving models. It remains an open problem whether the same efficient techniques developed for parameter synthesis of graph-preserving models can be applied to typed parametric Markov chains. It is also worth mentioning that for both POP and SSP the typed extension for pMCs is not strictly necessary. However, the types simplify the presentation and are straightforward to encode into etr. Alternatively, one can encode Boolean variables in ordinary pMCs as in [14, Fig. 5.23 on page 144]. We opted for the typed version of pMCs to highlight what is challenging for existing parameter synthesis tools.
5.2 Implementation and Setup
As outlined above, parameter synthesis tools are currently unsuited for solving the positional observability (POP, Definition 13) and the sensor selection problem (SSP, Definition 15). We thus implemented direct etr-encodings of POP and SSP instances for positional, but randomized, strategies based on the approach described in Sect. 4.2. We also consider the positional-deterministic observability problem (PDOOP, Definition 8) by adding constraints to our implementation for the POP to rule out randomized strategies. Our code is written in Python with z3 [25] as a backend. More precisely, for every tpMC parameter in Definition 14 and Definition 16 there is a corresponding variable in the z3 encoding. For example, if a z3 model assigns 1 to the z3 variable ys01, which corresponds to the tpMC parameter \(y_{s_0,o_1}\) (Definition 14), we have \( obs (s_0) = o_1\). Thus, we can directly construct the observation function. Similarly, we can map the results for the SSP. Furthermore, the expected reward for each state is computed using standard techniques based on Bellmann equations as explained in Example 8.
For comparison, we also implemented a brute-force approach for positional and deterministic strategies described in Sect. 4.1, which enumerates all observation functions and corresponding observation-based strategies, hence analyzing the resulting induced DTMCs with prism [19].Footnote 7 Our code and all examples are available online.Footnote 8
Benchmark Selection. To evaluate our approaches for P(D)OP and SSP, we created variants (with different state space sizes, probabilities, and thresholds) of two standard benchmarks from the POMDP literature, grid(world) [21] and maze [23], and our running example (cf. Example 1). Overall, we considered 26 variants for each problem.
Setup. All experiments were performed on an HP EliteBook 840 G8 with an 11th Gen Intel(R) Core(TM) i7@3.00GHz and 32GB RAM. We use Ubuntu 20.04.6 LTS, Python 3.8.10, z3 version 4.12.4, and prism 4.8 with default parameters (except for using exact model checking). We use a timeout of 15 min for each individual execution.
5.3 Experimental Results
Tables 1 and 2 show an excerpt of our experiments for selected variants of the three benchmarks, including the largest variant of each benchmark that can be solved for randomized and deterministic strategies, respectively. The full tables containing the results of all experiments are found in [17, Appendix A.10]. The left-hand side of Tables 1 and 2 show our results for the P(D)OP, whereas the right-hand side shows our results for the SSP. We briefly go over the columns used in both tables.
The considered variant is given by the columns model, threshold and budget. There are three kinds of models. We denote by L(k) a variant of our running example MDP \(M_{\text {line}}\) scaled up to k states. We choose k as an odd number such that the goal is always in the middle of the line. Likewise, we write G(k) to refer to an \(k \times k\) grid model, where the goal state is in the bottom right corner. Finally, M(k) refers to the maze model, where k is the (odd) number of states; an example is found in [17, Appendix A.4].
The column z3 represents the runtime for our direct etr-encoding with z3 as a backend. The column PRISM shows the runtime for the brute-force approach. All runtimes are in seconds. We write t.o. if a variant exceeds the timeout. If the (expected) reward is not available due to a timeout, we write N/A in the respective column. In both cases, we color the corresponding cells grey. If our implementation manages to prove that there is no solution, we also write N/A, but leave the cell white.
We choose three different threshold constraints in each problem, if the optimal cumulative expected reward is \(\tau \) we use the threshold constraints \(\le 2\tau \), \(\le \tau \), and \(< \tau \). The last one should yield no solution. The budget is always the minimal optimal one.
Randomised Strategies. Table 1 shows that our implementation can solve several non-trivial POP/SSP-instances for randomized strategies. Performance is better when the given thresholds are closer to the optimal one (namely \(\le \tau \) and \(< \tau \)). For large thresholds (\(\le 2\tau \)) the implementation times out earlier (see [17, Appendix A.10] for details). We comment on this phenomenon in more detail later.
Deterministic Strategies. Table 2 shows our results for deterministic strategies. We observe that we can solve larger instances for deterministic strategies than for randomized ones. Considering the performances of both tools, the SMT-backed approach outperforms the brute-force PRISM-based one. For the PDOOP, we observe that z3 can solve some of the problems for the L(377) states, whereas PRISM times our for instances larger than L(9). Also, z3 is capable of solving problems for grid instances G(y) up to \(k = 24\) and maze instances M(k) up to \(k = 39\), while PRISM cannot solve any problem instance of these models. For the SSP, we can see that z3 manages to solve L(y) instances up to \(k = 193\), whereas PRISM gives up after \(k = 7\).
On The Impact of Thresholds. For both randomized and deterministic strategies we observe that larger thresholds yield considerably longer solver runtimes and often lead to a time-out. At first, this behavior appears peculiar because larger thresholds allow for more possible solutions. To investigate this peculiar further, we studied the benchmark L(7) considering the PDOOP with thresholds \(\le \tau \), for \(\tau \) ranging from 1 to 1000. An excerpt of the considered thresholds and verification times is provided in Table 3. For the optimal threshold 2, z3 finds a solution in 0.079 s. Increasing the threshold (step size 0.25) until 4.5 leads to a steady increase in verification time up to 15.027 s. Verification requires more than 10min for thresholds in [4.75, 5.5]. For larger thresholds, verification time drops to less than 0.1 s. Hence, increasing the threshold first decreases performance, but at some point, performance becomes better again. We have no definitive answers on the threshold’s impact, but we conjecture that a larger threshold increases the search space, which might decrease performance. At the same time, a larger threshold can also admit more models, which might increase performance.
Discussion. Our experiments demonstrate that SMT solvers, specifically z3, can be used out-of-the-box to solve small-to-medium sized POP- and SSP-instances that have been derived from standard examples in the POMDP literature. In particular, for deterministic strategies, the SMT-backed approach clearly outperforms a brute-force approach based on (exact) probabilistic model checking.
Although the considered problem instances are, admittedly, small-to-medium sizedFootnote 9, they are promising for several reasons: First, our SMT-backed approach is a faithful, yet naive, etr-encoding of the POP, and leaves plenty of room for optimization. Second, z3 does, to the best of our knowledge, not use a decision procedure specifically for etr, which might further hurt performance. Finally, we showed in Sect. 4.2 that POP can be encoded as a feasibility problem for (typed) parametric Markov chains. Recent advances in parameter synthesis techniques (cf. [8, 12]) demonstrate that those techniques can scale to parametric Markov chains with tens of thousands of states. While the available tools cannot be used out-of-the-box for solving observability problems because of the graph-preservation assumption, it might be possible to extend them in future work.
It is also worth mentioning that our implementation not only provides an answer to the decidability problems P(D)OP and SSP, but it also synthesizes the corresponding observation function and the strategy if they exist. However, the decision problem and the problem of synthesising such observation function have the same complexities.
6 Conclusion and Future Work
We have introduced the novel optimal observability problem (OOP). The problem is undecidable in general, np-complete when restricted to positional and deterministic strategies. We have also shown that the OOP becomes decidable in pspace if restricted to positional, but randomized, strategies, and that it can be reduced to parameter synthesis on a novel typed extension of parametric Markov chains [12, 14], which we exploit in our SMT-based implementation. Our experiments show that SMT solvers can be used out-of-the-box to solve small-to-medium-sized instances of observability problems derived from POMDP examples found in the literature. Although we have focused on proving upper bounds on minimal expected rewards, our techniques also apply to other observability problems on POMDPs that can be encoded as a query on tpMCs, based on our faithful encoding of POMDPs as tpMCs with the observation function as a parameter. For example, the sensor synthesis for almost-sure reachability properties [6] can be encoded. Moreover, one obtains dual results for proving lower bounds on maximal expected rewards. For future work, we believe that scalability could be significantly improved by extending parameter synthesis tools such that they can deal with typed and non-graph-preserving parametric Markov chains.
Notes
- 1.
The red and blue colors as well as the @s-labels will become relevant later.
- 2.
If \(\pi \) is a path, notice that our definition does not include the probability of starting in \( first (\pi )\).
- 3.
Here, \(A \uplus B\) denotes the union \(A \cup B\) of sets A and B if \(A \cap B = \emptyset \); otherwise, it is undefined.
- 4.
Approximate solution provided by prism’s POMDP solver.
- 5.
We allow using multiple types with different names of this form. For example, \(\mathbb {R}^{1}_{= 1}\) and \(\mathbb {R}^{2}_{= 1}\) are types for two different sets of variables whose values must sum up to one.
- 6.
We provide a generalized version for multiple sensors per state in [17, Appendix A.8].
- 7.
Brute-force enumeration of POMDPs has not been considered as PRISM’s POMDP solver uses approximation techniques and does not allow to restrict to positional strategies.
- 8.
- 9.
At least for notoriously-hard POMDP problems; some instances have ca. 600 states.
References
Åström, K.J.: Optimal control of Markov processes with incomplete state information I. J. Math. Anal. Appl. 10, 174–205 (1965)
Baier, C., Katoen, J.-P.: Principles of Model Checking. MIT press (2008)
Canny, J.F.: Some algebraic and geometric computations in PSPACE. In: STOC, pp. 460–467. ACM (1988)
Černý, P., Chatterjee, K., Henzinger, T.A., Radhakrishna, A., Singh, R.: Quantitative synthesis for concurrent programs. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 243–259. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_20
Chades, I., Carwardine, J., Martin, T.G., Nicol, S., Sabbadin, R., Buffet, O.: MOMDPs: a solution for modelling adaptive management problems. In: AAAI, pp. 267–273. AAAI Press (2012)
Chatterjee, K., Chmelik, M., Topcu, U.: Sensor synthesis for POMDPs with reachability objectives. In: Proceedings of the International Conference on Automated Planning and Scheduling, vol. 28, pp. 47–55 (2018)
Chatterjee, K., Doyen, L., Henzinger, T.A.: Qualitative analysis of partially-observable Markov decision processes. In: Hliněný, P., Kučera, A. (eds.) MFCS 2010. LNCS, vol. 6281, pp. 258–269. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15155-2_24
Cubuktepe, M., Jansen, N., Junges, S., Katoen, J.-P., Topcu, U.: Synthesis in pMDPs: a tale of 1001 parameters. In: Lahiri, S.K., Wang, C. (eds.) ATVA 2018. LNCS, vol. 11138, pp. 160–176. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01090-4_10
Dehnert, C., et al.: PROPhESY: a PRObabilistic ParamEter SYnthesis tool. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 214–231. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21690-4_13
Hahn, E.M., Hermanns, H., Zhang, L.: Probabilistic reachability for parametric Markov models. Int. J. Softw. Tools Technol. Transf. 13(1), 3–19 (2011)
Hensel, C., Junges, S., Katoen, J.-P., Quatmann, T., Volk, M.: The probabilistic model checker storm. Int. J. Softw. Tools Technol. Transfer 24(4), 589–610 (2022). https://doi.org/10.1007/s10009-021-00633-z, https://doi.org/10.1007/s10009-021-00633-z
Jansen, N., Junges, S., Katoen, J.-P.: Parameter synthesis in Markov models: a gentle survey. In: Raskin, JF., Chatterjee, K., Doyen, L., Majumdar, R. (eds.) Principles of Systems Design: Essays Dedicated to Thomas A. Henzinger on the Occasion of His 60th Birthday, vol. 13660, pp. 407–437 (2022). https://doi.org/10.1007/978-3-031-22337-2_20
Jdeed, M., et al.: The CPSwarm technology for designing swarms of cyber-physical systems. In: STAF (Co-Located Events). CEUR Workshop Proceedings, vol. 2405, pp. 85–90. CEUR-WS.org (2019)
Junges, S.: Parameter synthesis in Markov models. Ph.D. thesis, Dissertation, RWTH Aachen University, 2020 (2020)
Kaelbling, L.P., Littman, M.L., Cassandra, A.R.: Planning and acting in partially observable stochastic domains. Artif. Intell. 101(1), 99–134 (1998). https://doi.org/10.1016/S0004-3702(98)00023-X, https://www.sciencedirect.com/science/article/pii/S000437029800023X
Kochenderfer, M.J.: Decision Making Under Uncertainty: Theory and Application. MIT press (2015)
Konsta, A.M., Lafuente, A.L., Matheja, C.: What should be observed for optimal reward in pomdps? arXiv preprint arXiv:2405.10768 (2024)
Krause, A., Singh, A.P., Guestrin, C.: Near-optimal sensor placements in gaussian processes: theory, efficient algorithms and empirical studies. J. Mach. Learn. Res. 9, 235–284 (2008). https://doi.org/10.5555/1390681.1390689, https://dl.acm.org/doi/10.5555/1390681.1390689
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
Littman, M.L.: Memoryless policies: theoretical limitations and practical results. In: From Animals to Animats 3: Proceedings of the third International Conference on Simulation of Adaptive Behavior, vol. 3, p. 238. MIT Press Cambridge, MA, USA (1994)
Littman, M.L., Cassandra, A.R., Kaelbling, L.P.: Learning policies for partially observable environments: scaling up. In: Prieditis, A., Russell, S. (eds.) Machine Learning Proceedings 1995, pp. 362–370. Morgan Kaufmann, San Francisco (CA) (1995). https://doi.org/10.1016/B978-1-55860-377-6.50052-9, https://www.sciencedirect.com/science/article/pii/B9781558603776500529
Madani, O., Hanks, S., Condon, A.: On the undecidability of probabilistic planning and infinite-horizon partially observable Markov decision problems. In: AAAI/IAAI, pp. 541–548 (1999)
McCallum, R.A.: Overcoming incomplete perception with utile distinction memory. In: Machine Learning Proceedings 1993, pp. 190–196. Morgan Kaufmann, San Francisco (CA) (1993). https://doi.org/10.1016/B978-1-55860-307-3.50031-9, https://www.sciencedirect.com/science/article/pii/B9781558603073500319
Miehling, E., Rasouli, M., Teneketzis, D.: A POMDP approach to the dynamic defense of large-scale cyber networks. IEEE Trans. Inf. Forensics Secur. 13(10), 2490–2505 (2018)
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Pahalawatta, P., Pappas, T., Katsaggelos, A.: Optimal sensor selection for video-based target tracking in a wireless sensor network. In: 2004 International Conference on Image Processing, 2004. ICIP 2004, vol. 5, pp. 3073–3076 (2004). https://doi.org/10.1109/ICIP.2004.1421762
Puterman, M.L.: Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley Series in Probability and Statistics, Wiley (1994). https://doi.org/10.1002/9780470316887, https://doi.org/10.1002/9780470316887
Russell, S., Norvig, P.: Artificial Intelligence: A Modern Approach, 4th edn. Pearson (2020)
Sheyner, O., Haines, J., Jha, S., Lippmann, R., Wing, J.: Automated generation and analysis of attack graphs. In: Proceedings 2002 IEEE Symposium on Security and Privacy, pp. 273–284 (2002). https://doi.org/10.1109/SECPRI.2002.1004377
Spaan, M., Lima, P.: A decision-theoretic approach to dynamic sensor selection in camera networks. In: Proceedings of the International Conference on Automated Planning and Scheduling, vol. 19, pp. 297–304 (2009)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Konsta, AM., Lluch Lafuente, A., Matheja, C. (2024). What Should Be Observed for Optimal Reward in POMDPs?. In: Gurfinkel, A., Ganesh, V. (eds) Computer Aided Verification. CAV 2024. Lecture Notes in Computer Science, vol 14683. Springer, Cham. https://doi.org/10.1007/978-3-031-65633-0_17
Download citation
DOI: https://doi.org/10.1007/978-3-031-65633-0_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-65632-3
Online ISBN: 978-3-031-65633-0
eBook Packages: Computer ScienceComputer Science (R0)






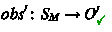 with
with 
