Abstract
Stateless model checking is a fully automatic verification technique for concurrent programs that checks for safety violations by exploring all possible thread schedulings. It becomes effective when coupled with Dynamic Partial Order Reduction (DPOR), which introduces an equivalence on schedulings and reduces the amount of needed exploration. DPOR algorithms that are optimal are particularly effective in that they guarantee to explore exactly one execution from each equivalence class. Unfortunately, existing sequence-based optimal algorithms may in the worst case consume memory that is exponential in the size of the analyzed program. In this paper, we present Parsimonious-OPtimal DPOR (POP), an optimal DPOR algorithm for analyzing multi-threaded programs under sequential consistency, whose space consumption is polynomial in the worst case. POP combines several novel algorithmic techniques, including (i) a parsimonious race reversal strategy, which avoids multiple reversals of the same race, (ii) an eager race reversal strategy to avoid storing initial fragments of to-be-explored executions, and (iii) a space-efficient scheme for preventing redundant exploration, which replaces the use of sleep sets. Our implementation in Nidhugg shows that these techniques can significantly speed up the analysis of concurrent programs, and do so with low memory consumption. Comparison to TruSt, a related optimal DPOR algorithm that represents executions as graphs, shows that POP ’s implementation achieves similar performance for smaller benchmarks, and scales much better than TruSt ’s on programs with long executions.
You have full access to this open access chapter, Download conference paper PDF


1 Introduction
Testing and verification of multi-threaded programs is challenging, since it requires reasoning about all the ways in which operations executed by different threads can interfere. A successful technique for finding concurrency bugs in multithreaded programs and for verifying their absence is stateless model checking (SMC) [20]. Given a terminating program and fixed input data, SMC systematically explores the set of all thread schedulings that are possible during program runs. A dedicated runtime scheduler drives the SMC exploration by making decisions on scheduling whenever such choices may affect the interaction between threads. Given enough time, the exploration covers all possible executions and detects any unexpected program results, program crashes, or assertion violations. The technique is entirely automatic, has no false positives, does not consume excessive memory, and can reproduce the concurrency bugs it detects. SMC has been implemented in many tools (e.g., VeriSoft [21], Chess [39], Concuerror [15], Nidhugg [2], rInspect [48], CDSChecker [41], RCMC [28], and GenMC [34]), and successfully applied to realistic programs (e.g., [22] and [32]).
To reduce the number of explored executions, SMC tools typically employ dynamic partial order reduction (DPOR) [1, 18, 28]. DPOR defines an equivalence relation on executions, typically Mazurkiewicz trace equivalence [36], which preserves many important correctness properties, such as reachability of local states and assertion violations, and explores at least one execution in each equivalence class. Thus, to analyze a program, it suffices to explore one execution from each equivalence class. DPOR was originally developed [18] for models of concurrency where executions are expressed as sequences of interactions between threads/processes and shared objects. Subsequently, sequence-based DPOR has been adapted and refined to a number of programming models, including actor programs [46], abstract computational models [27], event driven programs [4, 24, 35], and MPI programs [42]; it has been extended with features for efficiently handling spinloops and blocking constructs [25], and been adapted for weak concurrency memory models, such as TSO and PSO [2, 48]. DPOR has also been adapted for weak memory models by representing executions as graphs, where nodes represent read and write operations, and edges represent reads-from and coherence relations; this allows the algorithm to be parametric on a specific memory model, at the cost of calling a memory-model oracle [28, 30]
An important improvement has been the introduction of optimal DPOR algorithms, which are efficient in that they guarantee to explore exactly one execution from each equivalence class. The first optimal DPOR algorithm was designed for the sequence-based representation [1]. Subsequently, optimal DPOR algorithms for even weaker equivalences than Mazurkiewicz trace equivalence have been developed [6, 9, 11]. In some DPOR algorithms [1, 9, 11], optimality comes at the price of added memory consumption which in the worst case can be exponential in the size of the program [3]. Even though most benchmarks in the literature show a modest memory overhead as the price for optimality, it would be desirable to have an optimal DPOR algorithm whose memory consumption is guaranteed to be polynomial in the size of the program. Such an algorithm, called TruSt [29], was recently presented, but for a graph-based setting [30]. It would be desirable to develop a polynomial-space optimal DPOR algorithm also for sequence-based settings. One reason is that a majority of past work on DPOR is sequence-based; hence such an algorithm could be adapted to various programming models and features, some of which were recalled above. Another reason is that sequence-based models represent computations adhering to sequential consistency (SC) and TSO more naturally than graph-based models. For SC, representing executions as sequences of events makes executions consistent by construction and alleviates the need to resort to a potentially expensive memory-model oracle for SC.
In this paper, we present the Parsimonious-OPtimal DPOR (POP) algorithm for analyzing multi-threaded programs under SC (Sect. 4). POP is designed for programs in which threads interact by atomic reads, writes, and RMWs to shared variables, and combines several novel algorithmic techniques.
-
A parsimonious race reversal technique (Sect. 4.1), which considers a race if and only if its reversal will generate a previously unexplored execution; in contrast, most existing DPOR algorithms reverse races indiscriminately, only to thereafter discard redundant reversals (e.g., by sleep sets or similar mechanisms).
-
An eager race reversal strategy (Sect. 4.2), which immediately starts exploration of the new execution resulting from a race reversal; this prevents accumulation of a potentially exponential number of execution fragments generated by race reversals.
-
In order to avoid exploring several executions in the same equivalence class, a naïve realization of POP would employ an adaptation of sleep sets [19]. However, these can in the worst case become exponentially large. Therefore, POP employs a parsimonious characterization of sleep sets (Sect. 4.3): instead of representing the elements of the sleep set explicitly, POP uses a characterization of them, which allows to detect and prevent redundant exploration, and uses at most polynomial space. This sleep set characterization is computed only from its generating race, implying that explorations of different executions share no state, making POP suitable for parallelization.
We prove (in the appendices of the longer version of this paper [5]) that the POP algorithm is correct (explores at least one execution in each equivalence class), optimal (explores exactly one execution in each equivalence class), does not suffer from blocked explorations, and requires only polynomial size memory.
We have implemented POP DPOR in an extension of the Nidhugg tool [2]. Using a wide variety of benchmarks (Sect. 6), which are available in the paper’s artifact, we show that POP ’s implementation indeed has its claimed properties, it always outperforms Optimal DPOR ’s implementation, and offers performance which is on par with TruSt ’s, the state-of-the-art graph-based DPOR algorithm. Moreover, by being sequence-based, it scales much better than TruSt ’s implementation on programs with long executions.
2 Main Concepts
In this section, we informally present the core principles of our approach, in particular the three novel algorithmic techniques of parsimonious race reversal, eager race reversal, and parsimonious characterization of sleep sets, along with how they relate to previous sequence-based DPOR algorithms, on a simple example, shown in Fig. 1. In this code, four threads (p, q, r, s) access three shared variables (g, x, y, z), using five thread-local registers (\(a, b, c, d, e\)).Footnote 1 DPOR algorithms typically first explore an arbitrary execution, which is then inspected to detect races. Assume that this execution is \(E_1\) (the leftmost execution in Fig. 2). To detect races in an execution \(E\), one first computes its happens-before order, denoted
 , which is the smallest transitive relation that orders two events that (i) are in the same thread, or (ii) access a common shared variable and at least one of them is a write. A race consists of two events in different threads that are adjacent in the
, which is the smallest transitive relation that orders two events that (i) are in the same thread, or (ii) access a common shared variable and at least one of them is a write. A race consists of two events in different threads that are adjacent in the
 order. In execution \(E_1\) there are two races on \(\texttt {x}\), two races on \(\texttt {y}\), and one race on \(\texttt {z}\). The two races on \(\texttt {y}\) are marked with yellow arrows, as we are going to discuss them now. POP first reverses the race between events
order. In execution \(E_1\) there are two races on \(\texttt {x}\), two races on \(\texttt {y}\), and one race on \(\texttt {z}\). The two races on \(\texttt {y}\) are marked with yellow arrows, as we are going to discuss them now. POP first reverses the race between events
 and
and
 . For each race, a DPOR algorithm constructs an initial fragment of an alternative execution, called a schedule, which reverses the race and branches off from the explored execution just before the race. POP constructs a minimal schedule consisting of the events that happen before (in the
. For each race, a DPOR algorithm constructs an initial fragment of an alternative execution, called a schedule, which reverses the race and branches off from the explored execution just before the race. POP constructs a minimal schedule consisting of the events that happen before (in the
 order) the second event followed by the second event of the race, while omitting the first event of the race, resulting in the event sequence
order) the second event followed by the second event of the race, while omitting the first event of the race, resulting in the event sequence
 , which is inserted as an alternative continuation after
, which is inserted as an alternative continuation after
 (the branch to the right of
(the branch to the right of
 ).
).
Part of the exploration tree for the program in Fig. 1. Completed executions are denoted \(E_i\); truncated subtrees are denoted \(T_i\).
In comparison, early DPOR algorithms, including the “classic” DPOR algorithm by Flanagan and Godefroid [18] and the Source DPOR algorithm of Abdulla et al. [1] construct a schedule consisting of just one event that can initiate an execution which reverses the race (
 in this case). Storing just one event saves space, but the execution afterwards is uncontrolled and may deviate from the path towards the second racing event
in this case). Storing just one event saves space, but the execution afterwards is uncontrolled and may deviate from the path towards the second racing event
 , potentially leading to redundant exploration. To avoid redundancy, we need schedules which consist of paths to the second racing event.
, potentially leading to redundant exploration. To avoid redundancy, we need schedules which consist of paths to the second racing event.
Eager Race Reversal: Following an eager race reversal strategy, POP continues the exploration with this branch and explores \(E_2\). POP can in principle be implemented so that the schedules constructed as alternative continuations of an event are all collected before they are explored. However, such a strategy can in the worst case consume memory that is exponential in the program size. The reason is that, for some programs, the number of schedules that branch off at a particular point in an execution may become exponential in the size of the program; this was first observed by Abdulla et al. [3, Sect. 9]; an illustrating shared-variable program is given by Kokologiannakis et al. [29, Sect. 2.3]. POP avoids this problem by exploring schedules eagerly: immediately after the creation of a schedule, exploration switches to continuations of that schedule. This strategy can be realized by an algorithm that calls a recursive function to initiate exploration of a new schedule. We establish, in Lemma 1, that the recursion depth of such an algorithm is at most \(n(n-1)/2\), where n is the length of the longest execution of the program.
Continuing exploration, POP encounters the race on \(\texttt {x}\) in \(E_2\) involving events
 and
and
 . (In Fig. 2, we show races by red arrows.) POP constructs the schedule \(\sigma _1:=\)
. (In Fig. 2, we show races by red arrows.) POP constructs the schedule \(\sigma _1:=\)
 (second branch from the root) and explores the subsequent part of \(T_4\) (tree \(T_4\) represents all the extensions after \(\sigma _1\)). After exploring \(T_4\) (second branch from the root), POP comes back to \(E_2\).
(second branch from the root) and explores the subsequent part of \(T_4\) (tree \(T_4\) represents all the extensions after \(\sigma _1\)). After exploring \(T_4\) (second branch from the root), POP comes back to \(E_2\).
Parsimonious Race Reversal: To illustrate POP ’s mechanism for reversing each race only once, let us next consider races in execution \(E_2\). There is one race on y, between
 and
and
 in \(E_2\), for which POP would construct the schedule
in \(E_2\), for which POP would construct the schedule
 However, a prefix of \(\sigma \), namely
However, a prefix of \(\sigma \), namely
 will be constructed from a race in \(E_1\) between
will be constructed from a race in \(E_1\) between
 and
and
 and inserted as an alternative continuation after
and inserted as an alternative continuation after
 (the rightmost child of
(the rightmost child of
 in Fig. 2). Thus, any continuation of \(\sigma \) after
in Fig. 2). Thus, any continuation of \(\sigma \) after
 can also be explored as a continuation after the rightmost child of
can also be explored as a continuation after the rightmost child of
 , implying that inserting \(\sigma \) as an alternative continuation after
, implying that inserting \(\sigma \) as an alternative continuation after
 would lead to redundant exploration. POP avoids such redundant exploration by forbidding to consider races whose first event (in this case
would lead to redundant exploration. POP avoids such redundant exploration by forbidding to consider races whose first event (in this case
 ) is in some schedule: reversing a race whose first event is in a schedule yields a fragment that is explored in some other execution. The execution \(E_2\) also exhibits two races on x, both including
) is in some schedule: reversing a race whose first event is in a schedule yields a fragment that is explored in some other execution. The execution \(E_2\) also exhibits two races on x, both including
 , with the events
, with the events
 and
and
 These races have already occurred in \(E_1\), and should therefore not be considered, since the schedules they would generate will be generated from the corresponding races in \(E_1\). POP achieves this by forbidding to consider races whose second event is not fresh. A second event of a race is fresh if it happens-after (in the
These races have already occurred in \(E_1\), and should therefore not be considered, since the schedules they would generate will be generated from the corresponding races in \(E_1\). POP achieves this by forbidding to consider races whose second event is not fresh. A second event of a race is fresh if it happens-after (in the
 order) the last event of each schedule that appears between the two racing events. Returning to the two races on x in \(E_2\), their second events are not fresh, and hence they are not reversed.
order) the last event of each schedule that appears between the two racing events. Returning to the two races on x in \(E_2\), their second events are not fresh, and hence they are not reversed.
Let us continue the exploration of \(E_2\) in Fig. 2 to illustrate how the eager race reversal strategy affects the order in which branches are explored. In \(E_2\), there are two more races, on \(\texttt {y}\) and \(\texttt {z}\), whose reversals produce two branches after
 and
and
 , denoted by wavy edges. After their exploration, since there are no more races in \(E_2\), POP returns to \(E_1\), where the race between events
, denoted by wavy edges. After their exploration, since there are no more races in \(E_2\), POP returns to \(E_1\), where the race between events
 and
and
 induces the schedule
induces the schedule
 , initiating exploration of \(E_3\). While exploring \(E_3\), the race inolving events
, initiating exploration of \(E_3\). While exploring \(E_3\), the race inolving events
 and
and
 in \(E_3\) induces the schedule
in \(E_3\) induces the schedule
 , initiating exploration of the subtree \(T_5\), during which the race on \(\texttt {x}\) involving
, initiating exploration of the subtree \(T_5\), during which the race on \(\texttt {x}\) involving
 and
and
 induces the schedule \(\sigma _2:=\)
induces the schedule \(\sigma _2:=\)
 , and explores the subsequent part of the tree \(T_6\). After finishing exploration of \(T_6\) and \(T_5\), POP comes back to \(E_3\), where the race involving events
, and explores the subsequent part of the tree \(T_6\). After finishing exploration of \(T_6\) and \(T_5\), POP comes back to \(E_3\), where the race involving events
 and
and
 induces the schedule \(\sigma _3:=\)
induces the schedule \(\sigma _3:=\)
 initiating exploration of \(T_7\), whereafter exploration of \(E_3\) resumes.
initiating exploration of \(T_7\), whereafter exploration of \(E_3\) resumes.
Parsimonious Characterization of Sleep Sets: Even though the parsimonious race reversal strategy guarantees that the initial fragments of alternative executions are inequivalent, one must prevent that their continuations become equivalent. This happens when POP continues after a read schedule, generated from a race whose second event is a read event. To illustrate this problem, let us consider the race involving events
 and
and
 in \(E_3\), which produces the read schedule \(\sigma _4:=\)
in \(E_3\), which produces the read schedule \(\sigma _4:=\)
 , initiating exploration of \(T_8\). Note that the schedule \(\sigma _4\) is not conflicting with the read schedules \(\sigma _2\) and \(\sigma _3\). At this point, we need to be careful: there is a danger that \(\sigma _4\) will be continued using the other two schedules (\(\sigma _2\) and \(\sigma _3\)), whereas the explorations starting with schedules \(\sigma _2\) and \(\sigma _3\) can be continued using \(\sigma _4\); we would then explore equivalent executions, consisting of these three schedules in either order. The same problem occurs with \(\sigma _1\) and \(\sigma _3\), as they do not conflict. The DPOR technique for avoiding such redundant exploration is sleep sets [19]. In its standard form, a sleep set is a set of events that should not be performed before some conflicting event. Since POP uses schedules as beginnings of alternative explorations, the appropriate adaptation would be to let a sleep set be a set of read schedules that should not be performed unless some conflicting event is performed before that. In Fig. 2, this would mean that after exploring the continuations of \(\sigma _2\) and \(\sigma _3\), these schedules are added to the sleep set when starting to explore the continuations of \(\sigma _4\), and \(\sigma _1\) is added to the sleep set when starting to explore the continuations of \(\sigma _3\). This mechanism is simple to combine with parsimonious race reversal and eager exploration of schedules. Unfortunately, there are programs where the number of read schedules that would be added to such a sleep set is exponential in the size of the program, whence the worst-case memory consumption may be exponential in the size of the program. POP avoids this problem by a parsimonious characterization of sleep sets, which consumes memory that is polynomial in the size of the program. The idea is to totally order the read schedules. When continuing exploration after a read schedule \(\sigma \), the read schedules that precede \(\sigma \) in this order are represented by POP ’s parsimonious characterization in polynomial space, even though the number of represented schedules may be exponential. In principle, there are several ways to order the read schedules. POP uses one such ordering, namely \(\sigma _1\), \(\sigma _2\), \(\sigma _3\) and \(\sigma _4\). We provide the details about this representation in Sect. 4.3.
, initiating exploration of \(T_8\). Note that the schedule \(\sigma _4\) is not conflicting with the read schedules \(\sigma _2\) and \(\sigma _3\). At this point, we need to be careful: there is a danger that \(\sigma _4\) will be continued using the other two schedules (\(\sigma _2\) and \(\sigma _3\)), whereas the explorations starting with schedules \(\sigma _2\) and \(\sigma _3\) can be continued using \(\sigma _4\); we would then explore equivalent executions, consisting of these three schedules in either order. The same problem occurs with \(\sigma _1\) and \(\sigma _3\), as they do not conflict. The DPOR technique for avoiding such redundant exploration is sleep sets [19]. In its standard form, a sleep set is a set of events that should not be performed before some conflicting event. Since POP uses schedules as beginnings of alternative explorations, the appropriate adaptation would be to let a sleep set be a set of read schedules that should not be performed unless some conflicting event is performed before that. In Fig. 2, this would mean that after exploring the continuations of \(\sigma _2\) and \(\sigma _3\), these schedules are added to the sleep set when starting to explore the continuations of \(\sigma _4\), and \(\sigma _1\) is added to the sleep set when starting to explore the continuations of \(\sigma _3\). This mechanism is simple to combine with parsimonious race reversal and eager exploration of schedules. Unfortunately, there are programs where the number of read schedules that would be added to such a sleep set is exponential in the size of the program, whence the worst-case memory consumption may be exponential in the size of the program. POP avoids this problem by a parsimonious characterization of sleep sets, which consumes memory that is polynomial in the size of the program. The idea is to totally order the read schedules. When continuing exploration after a read schedule \(\sigma \), the read schedules that precede \(\sigma \) in this order are represented by POP ’s parsimonious characterization in polynomial space, even though the number of represented schedules may be exponential. In principle, there are several ways to order the read schedules. POP uses one such ordering, namely \(\sigma _1\), \(\sigma _2\), \(\sigma _3\) and \(\sigma _4\). We provide the details about this representation in Sect. 4.3.
3 Programs, Executions, and Equivalence
We consider programs consisting of a finite set of threads that share a finite set of (shared) variables. Each thread has a finite set of local registers and runs a deterministic code, built in a standard way from expressions (over local registers) and atomic commands, using standard control flow constructs (sequential composition, selection, and bounded loop constructs). Atomic commands either write the value of an expression to a shared variable, or assign the value of a shared variable to a register, or can atomically both read and modify a shared variable. Conditional control flow constructs can branch on the value of an expression. From here on, we use \(t\) to range over threads, and x, y, z to range over shared variables. The local state of a thread is defined as usual by its program counter and the contents of its registers. The global state of a program consists of the local state of each thread together with the valuation of the shared variables. The program has a unique initial state, in which shared variables have predefined initial values. We assume that memory is sequentially consistent.
The execution of a program statement is an event, which affects or is affected by the global state of the program. An event is represented by a tuple
 , where \(t\) is the thread performing the event, i is a positive integer, denoting that the event results from the i-th execution step in thread \(t\).
, where \(t\) is the thread performing the event, i is a positive integer, denoting that the event results from the i-th execution step in thread \(t\).
 is the type of the event (either \(\texttt{R}\) for read or \(\texttt{W}\) for write and read-modify-write), and \(x\) is the accessed variable. If \(e\) is the event
is the type of the event (either \(\texttt{R}\) for read or \(\texttt{W}\) for write and read-modify-write), and \(x\) is the accessed variable. If \(e\) is the event
 , we write \(e. th \) for \(t\),
, we write \(e. th \) for \(t\),
 for
for
 , and \(e. var \) for \(x\). An access is a pair
, and \(e. var \) for \(x\). An access is a pair
 consisting of a type and a variable. We write \(e. acc \) for
consisting of a type and a variable. We write \(e. acc \) for
 . We say that two accesses
. We say that two accesses
 and
and
 are dependent, denoted
are dependent, denoted
 , if \(x= x'\) and at least one of
, if \(x= x'\) and at least one of
 and
and
 is \(\texttt{W}\). We say that two events \(e\) and \(e'\) are dependent, denoted \(e\bowtie e\), if \(e. th = e'. th \) or \(e. acc \bowtie e'. acc \). As is customary in DPOR algorithms, we can let an event represent the combined effect of a sequence of statements, if at most one of them accesses a shared variable.
is \(\texttt{W}\). We say that two events \(e\) and \(e'\) are dependent, denoted \(e\bowtie e\), if \(e. th = e'. th \) or \(e. acc \bowtie e'. acc \). As is customary in DPOR algorithms, we can let an event represent the combined effect of a sequence of statements, if at most one of them accesses a shared variable.
An execution sequence (or just execution) \(E\) is a finite sequence of events, starting from the initial state of the program. We let \(\texttt{enabled}\left( E\right) \) denote the set of events that can be performed in the state to which E leads. An execution \(E\) is maximal if \(\texttt{enabled}\left( E\right) = \emptyset \). We let \({{\texttt{dom}}}\left( E\right) \) denote the set of events in \(E\); we also write \(e \in E\) to denote \(e \in {{\texttt{dom}}}\left( E\right) \). We use u and w, possibly with superscripts, to range over sequences of events (not necessarily starting from the initial state), \(\langle \rangle \) to denote the empty sequence, and \(\langle e \rangle \) to denote the sequence with only the event \(e\). We let \(w \cdot w'\) denote the concatenation of sequences w and \(w'\), and let \(w \! \setminus \!e\) denote the sequence w with the first occurrence of \(e\) (if any) removed. For a sequence \(u = e_1 \cdot e_2 \cdot \ldots \cdot e_m\), we let \(w \! \setminus \!u\) denote \(( \cdots ((w \! \setminus \!e_1) \! \setminus \!e_2) \! \setminus \!\cdots ) \! \setminus \!e_m\).
The basis for a DPOR algorithm is an equivalence relation on the set of execution sequences. The definition of this equivalence is based on a happens-before relation on the events of each execution sequence, which captures the data and control dependencies that must be respected by any equivalent execution.
Definition 1
(Happens-before). Given an execution sequence \(E\), we define the happens-before relation on E, denoted
 , as the smallest irreflexive partial order on \({{\texttt{dom}}}\left( E\right) \) such that
, as the smallest irreflexive partial order on \({{\texttt{dom}}}\left( E\right) \) such that
 if \(e\) occurs before \(e'\) in \(E\), and \(e\bowtie e'\).
if \(e\) occurs before \(e'\) in \(E\), and \(e\bowtie e'\).
The
 -trace (or trace for short) of E is the directed graph
-trace (or trace for short) of E is the directed graph
 .
.
Definition 2
(Equivalence). Two execution sequences E and \(E'\) are equivalent, denoted \(E \simeq E'\), if they have the same
 -trace. We let \([E]_{\simeq }\) denote the equivalence class of E.
-trace. We let \([E]_{\simeq }\) denote the equivalence class of E.
The equivalence relation \(\simeq \) partitions the set of execution sequences into equivalence classes, paving the way for an optimal DPOR algorithm which explores precisely one execution in each equivalence class.
4 Design of the POP Algorithm
In this section, we explain the design of POP, which is optimal in the sense that it explores precisely one execution in each equivalence class defined by Definition 2. We first need some auxiliary definitions
Definition 3
(Compatible sequences and happens-before prefix). For two execution sequences \(E\cdot w\) and \(E\cdot w'\),
-
the sequences \(w\) and \(w'\) are compatible, denoted \(w\sim w'\), iff there are sequences \(w''\) and \(w'''\) s.t. \(E\cdot w\cdot w''\simeq E\cdot w'\cdot w'''\),
-
the sequence \(w\) is a happens-before prefix of \(w'\), denoted \(w\sqsubseteq w'\), iff there is a sequence \(w''\) s.t. \(E\cdot w\cdot w''\simeq E\cdot w'\).
We illustrate the definition on the example in Fig. 2. Assuming
 , it is true that \(\sigma _4\sqsubseteq w'\), since
, it is true that \(\sigma _4\sqsubseteq w'\), since
 , where \(w''\) is the sequence
, where \(w''\) is the sequence
 . However, \(\sigma _1\not \sim \sigma _4\), since \(\sigma _1\)’s access to \(\texttt {y}\) and \(\sigma _4\)’s second access to \(\texttt {y}\) are in conflict.
. However, \(\sigma _1\not \sim \sigma _4\), since \(\sigma _1\)’s access to \(\texttt {y}\) and \(\sigma _4\)’s second access to \(\texttt {y}\) are in conflict.
Definition 4
(Schedule). A sequence of events \(\sigma \) is called a schedule if all its events happen-before its last one, i.e.,
 where \(e\) is its last event, and \(e'\) is any other event in \(\sigma \). The last event \(e\) of a schedule \(\sigma \) is called the head of \(\sigma \), sometimes denoted \({hd}\left( \sigma \right) \). For an execution sequence \(E\cdot w\) and event \(e\in w\), define the schedule \({e}\downarrow ^{w}\) to be the subsequence \(w'\) of \(w\) such that (i) \(e\in w'\), and (ii) for each \(e'\in w\) it holds that \(e'\in w'\) iff
where \(e\) is its last event, and \(e'\) is any other event in \(\sigma \). The last event \(e\) of a schedule \(\sigma \) is called the head of \(\sigma \), sometimes denoted \({hd}\left( \sigma \right) \). For an execution sequence \(E\cdot w\) and event \(e\in w\), define the schedule \({e}\downarrow ^{w}\) to be the subsequence \(w'\) of \(w\) such that (i) \(e\in w'\), and (ii) for each \(e'\in w\) it holds that \(e'\in w'\) iff
 .
.
4.1 Parsimonious Race Reversals
A central mechanism of many DPOR algorithms is to detect and reverse races. Intuitively, a race is a conflict between two consecutive accesses to a shared variable, where at least one access writes to the variable (i.e., it is a write or a read-modify-write).
Definition 5
(Race). Let E be an execution sequence. Two events e and \(e'\) in E are racing in E if (i) e and \(e'\) are performed by different threads, (ii)
 . (iii) there is no other event \(e''\) with
. (iii) there is no other event \(e''\) with
 .
.
Intuitively, a race arises when two different threads perform dependent accesses to a shared variable, which are adjacent in the
 order. If e and \(e'\) are racing in E, then to reverse the race, E is decomposed as \(E=E_1\cdot e\cdot E_2\) with \(e'\) in \(E_2\), thereafter the schedule \(\sigma = {e'}\downarrow ^{E_2}\) is formed as the initial fragment of an alternative execution, which extends \(E_1\).
order. If e and \(e'\) are racing in E, then to reverse the race, E is decomposed as \(E=E_1\cdot e\cdot E_2\) with \(e'\) in \(E_2\), thereafter the schedule \(\sigma = {e'}\downarrow ^{E_2}\) is formed as the initial fragment of an alternative execution, which extends \(E_1\).
The key idea of parsimonious race reversal is to reverse a race only if such a reversal generates an execution that has not been explored before. To be able to do so, POP remembers whenever an event in a new execution is in a schedule, and whether it is a schedule head. This can be done, e.g., by marking events in schedules, and specifically marking the schedule head. From now on, we consider such markings to be included in the events of executions. They play an important role in selecting races.
Definition 6
(Fresh event). For an execution \(E\cdot w\cdot e'\cdot w'\), the event \(e'\) is called fresh in \(w\cdot e'\cdot w'\) after \(E\) if (i) if \(e'\) is in a schedule, then it is the head of that schedule, and (ii) for each head \(e_h\) of a schedule in \(w\) it is the case that
 .
.
Definition 7
(Parsimonious race). Let E be an execution sequence. Two events e and \(e'\) in E are in a parsimonious race, denoted \({e}{\mathtt {\lesssim }}_{E}{e'}\) if (i) e and \(e'\) are racing in E, (ii) \(e\) is not in a schedule in E, and (iii) \(e'\) is fresh in \(w\cdot e'\) after \(E_1\), where \(E=E_1\cdot e\cdot w\cdot e'\cdot w'\)
Conditions (ii) and (iii) are the additional conditions for a race to be parsimonious. They filter out races, whose reversals would lead to previously explored executions. Let us provide the intuition behind these conditions. (ii) If \(e\) is in a schedule, then that schedule, call it \(\sigma \), was generated by a race in an earlier explored execution \(E'\). Hence \(\sigma \) was contained in \(E'\). Moreover \(e'\) would race with the head of \(\sigma \) also in \(E'\); if \(e'\) appeared after \(\sigma \) the resulting new schedule had been generated already in \(E'\); if \(e'\) appeared before \(\sigma \), then we would only undo a previous race reversal. This is illustrated in Fig. 2 by the race on y, between
 and
and
 in \(E_2\). (iii) If \(e'\) is not fresh, then \(e'\) appeared with the same happens-before predecessors in an earlier explored execution \(E'\), where it was in a race that would generate the same schedule as in \(E\). This is illustrated in Fig. 2 by the race on x, between
in \(E_2\). (iii) If \(e'\) is not fresh, then \(e'\) appeared with the same happens-before predecessors in an earlier explored execution \(E'\), where it was in a race that would generate the same schedule as in \(E\). This is illustrated in Fig. 2 by the race on x, between
 and
and
 . in \(E_2\), which was considered already in \(E_1\).
. in \(E_2\), which was considered already in \(E_1\).
4.2 The Parsimonious-OPtimal DPOR (POP) Algorithm
We will now describe the mechanism of the POP algorithm, without going into details regarding its handling of sleep sets (this will be done in Sect. 4.3). In particular, we will show how the eager race reversal strategy is represented in pseudo-code. Recall from Sect. 2 that a DPOR algorithm with parsimonious race reversal could be implemented so that the schedules that constructed from races with a particular event \(e\) are all collected before they are explored. However, for some programs, the number of schedules created from races with an event \(e\) can be exponential in the length of the longest program execution. In order not to consume exponential memory, POP explores schedules eagerly: immediately after the creation of a schedule, exploration switches to continuations of that schedule.

The POP algorithm is shown as Algorithm 1, where lines without background shading are concerned with the exploration and race handling, and the other lines, which are marked with green background, are concerned with sleep sets. POP takes an input program, and explores its executions by repeated calls to the procedure \({\texttt{Explore}}\). For each prefix \(E'\) of an execution that is under exploration, the algorithm maintains a characterization \( SSChar [E']\) of the sleep set at \(E'\), to be described in Sect. 4.3, in order to prevent redundant exploration of read schedules. This characterization is manipulated by POP through two functions:
-
\({\texttt{MkSchedChar}}(\sigma ,E_1,e,E_2)\) constructs a characterization of the sleep set for a newly constructed \(\sigma \), constructed from a race \({e}{\mathtt {\lesssim }}_{E_1\cdot e\cdot E_2}{{\texttt{last}}\left( E_2\right) }\),
-
\({\texttt{UpdSeq}}(w, SSChar )\) updates the sleep set characterization \( SSChar \) wrt. processing of the sequence \(w\). However, if a characterized read schedule (i.e., a schedule in the sleep set) would be performed while exploring \(w\), the function returns block instead of the updated characterization.
The algorithm first picks an enabled event \(e\) (line 1), initializes the characterizations of sleep sets of \(\langle \rangle \) and \(\langle e \rangle \) (line 2), whereafter it calls \({\texttt{Explore}}(\langle e \rangle )\) (line 3). Each call to \({\texttt{Explore}}(E)\) consists of a race reversal phase (lines 5 to 13) and an exploration phase (lines 14 to 16). In the race reversal phase, POP considers all parsimonious races between an event \(e\) in \(E\) and the last event \(e'\) of \(E\) (line 5). For each such race, of form \({e}{\mathtt {\lesssim }}_{E}{e'}\), POP decomposes \(E\) as \(E_1\cdot e\cdot E_2\) (line 6), and forms the schedule \(\sigma \) that reverses the race as \({e'}\downarrow ^{E_2}\) (line 7). It then intends to call \({\texttt{Explore}}(E_1\cdot \sigma )\) in order to recursively switch the exploration to the newly reversed race, according to the eager race reversal strategy. Before that it checks whether exploring \(E_1\cdot \sigma \) will complete a schedule in the sleep set by calling \({\texttt{UpdSeq}}(\sigma , SSChar [E_1])\) (line 8). If not, \( SSChar [E_1\cdot \sigma ]\) is computed (line 9), and if \(e'\) is a read event also extended with the new sleep set for \(\sigma \) (lines 11 to 12). After these preparations, \({\texttt{Explore}}(E_1\cdot \sigma )\) is called recursively (line 13). After the return of all recursive calls initiated in the race reversal phase, \({\texttt{Explore}}\) enters the exploration phase. There it picks an event \(e\) that is enabled for execution, and check that \(e\) is not the head of a schedule in the sleep set by calling \({\texttt{UpdSeq}}(\langle e\rangle , SSChar [E])\) (line 14) If the check succeeds, exploration of \(e\) is prepared by updating \( SSChar [E_1\cdot e]\) (line 15) and then performed by calling \({\texttt{Explore}}(E\cdot e)\)(line 16).
We establish (in Lemma 1) that the recursion depth of Algorithm 1 is at most \(n(n-1)/2\), where n is the length of the longest execution of the analyzed program.
4.3 Parsimonious Sleep Set Characterization
As described in Sect. 2, POP needs a sleep set mechanism to avoid redundant exploration of read schedules. Such a mechanism is needed whenever POP explores reversals of races with a write event \(e_W\) that appears after an execution \(E_1\). Then each parsimonious race \({e_W}{\mathtt {\lesssim }}_{E'}{e_R}\) between \(e_W\) and a read event \(e_R\) results in a schedule \(\sigma \), which will be explored as a continuation of \(E_1\). For any two such schedules, \(\sigma \) and \(\sigma '\), POP must ensure that either the exploration starting with \(\sigma \) does not continue in a way that includes \(\sigma '\), or (vice versa) that the exploration starting with \(\sigma '\) does not continue in a way that includes \(\sigma \). In Sect. 2, it was further described that to achieve this, POP must for each such explored write event \(e_W\) establish a total order between the read schedules resulting from races with \(e_W\), and ensure that an exploration starting with \(\sigma \) does not continue in a way that includes another schedule \(\sigma '\) which precedes \(\sigma \) in this order. It was also observed that, since there can be an exponential number of such schedules, the naïve approach of enumerating the schedules that precede \(\sigma \) can in the worst case consume space exponentical in the length of the longest execution.
In this section, we will describe one way to realize such a sleep set mechanism. We first define, for each explored write event \(e_W\), a total order between the read-schedules resulting from races with \(e_W\). Thereafter we define a succinct (polynomial-space) characterization of all schedules that precede any given such schedule \(\sigma \). Finally, we define a polynomial-space mechanism for POP to monitor exploration so that exploration after the schedule \(\sigma \) does not explore another read schedule which precedes \(\sigma \) in the order.
First, for a variable \(x\), we define a read-\(x\)-schedule to be a schedule whose head is a read on \(x\), and which does not contain any other read or write on \(x\). A read-schedule is a read-\(x\)-schedule for some variable \(x\). Then a read-\(x\)-schedule is a schedule that may be formed when reversing a parsimonious race between a write on \(x\) and a read on \(x\). Such a schedule \(\sigma \) cannot include a write on \(x\), since then it could not have been formed from a race. Also, it cannot include a read on \(x\), since that extra read will both happen-before \({hd}\left( \sigma \right) \), and happen-after the write on \(x\), contradicting that there was a race between the write and \({hd}\left( \sigma \right) \).
Let us now define the order \(\propto \), which for each write event \(e_W\) totally orders the schedules that result from parsimonious races between \(e_W\) and a subsequent read. Let \(\sigma \) be formed from a race \({e_W}{\mathtt {\lesssim }}_{E}{e_R}\) between \(e_W\) and another read event \(e_R\) in \(E\) and \(\sigma '\) be formed from a race \({e_W}{\mathtt {\lesssim }}_{E'}{e_R'}\) between \(e_W\) and another read event \(e_R'\). Then \(\sigma ' \propto \sigma \) if either
-
(A)
\(E'\) is a prefix of \(E\), i.e., \(e_R'\) occurs before \(e_R\) in \(E\), or
-
(B)
for the longest common prefix \(\hat{E}\) of \(E\) and \(E'\), \(E\) has a prefix of form \(\hat{E} \cdot \hat{e}\) for some non-schedule event \(\hat{e}\), whereas \(E'\) has a prefix of form \(\hat{E} \cdot \hat{\sigma }\) for some schedule \(\hat{\sigma }\) (which is induced by a race whose first event is \(\hat{e}\)), or
-
(C)
for the longest common prefix \(\hat{E}\) of \(E\) and \(E'\), \(E\) has a prefix of form \(\hat{E} \cdot \sigma _i\) for some schedule \(\sigma _i\), whereas \(E'\) has a prefix of form \(\hat{E} \cdot \sigma _i'\) for some schedule \(\sigma _i'\), and \(\sigma _i' \propto \sigma _i\).
Schedules of form (A) are called contained schedules (wrt. \(\sigma \)). An example can be found in Fig. 2. Consider the schedules
 from the race
from the race
 in \(E_3\), and
in \(E_3\), and
 from the race
from the race
 in \(E_3\). As
in \(E_3\). As
 occurs before
occurs before
 in \(E_3\), (A) implies that \(\sigma _3\propto \sigma _4\). Schedules of form (B) are called conflicting schedules, because \(e'\) occurs in an execution which branches off from (thus conflicts with) \(E\) because of a race involving an event \(\hat{e}\) in \(E\). For example, consider the schedules
in \(E_3\), (A) implies that \(\sigma _3\propto \sigma _4\). Schedules of form (B) are called conflicting schedules, because \(e'\) occurs in an execution which branches off from (thus conflicts with) \(E\) because of a race involving an event \(\hat{e}\) in \(E\). For example, consider the schedules
 , which is constructed from the race between
, which is constructed from the race between
 and
and
 in \(T_5\), and \(\sigma _4\) constructed from the race
in \(T_5\), and \(\sigma _4\) constructed from the race
 in \(E_3\). Since \(T_5\) branches off from (and thus conflicts with) \(E_3\) after the prefix
in \(E_3\). Since \(T_5\) branches off from (and thus conflicts with) \(E_3\) after the prefix
 with the schedule
with the schedule
 , we have \(\sigma _2\propto \sigma _4\) according to case (B). Schedules of form (C) are called inherited schedules, because the order \(\sigma '\propto \sigma \) is inherited from the order \(\sigma _i'\propto \sigma _i\). For example, consider the schedules
, we have \(\sigma _2\propto \sigma _4\) according to case (B). Schedules of form (C) are called inherited schedules, because the order \(\sigma '\propto \sigma \) is inherited from the order \(\sigma _i'\propto \sigma _i\). For example, consider the schedules
 (second branch after
(second branch after
 ), and
), and
 (third branch after
(third branch after
 ), for which
), for which
 because of (A). Now consider the schedules \(\sigma _1:=\)
because of (A). Now consider the schedules \(\sigma _1:=\)
 from the race
from the race
 in \(E_2\), and \(\sigma _2\) from the race between the events
in \(E_2\), and \(\sigma _2\) from the race between the events
 and
and
 from an execution in \(T_5\). As
from an execution in \(T_5\). As
 is a prefix of \(\sigma _1\) and
is a prefix of \(\sigma _1\) and
 is a prefix of \(\sigma _2\), according to (C), the order
is a prefix of \(\sigma _2\), according to (C), the order
 is inherited as \(\sigma _1\propto \sigma _2\).
is inherited as \(\sigma _1\propto \sigma _2\).
It is clear that these rules define a total order on the read schedules that branch off after \(E_1\). We next define a succinct way to characterize, for a given schedule \(\sigma \), the set of schedules \(\sigma '\) such that \(\sigma ' \propto \sigma \). Given \(E= E_1 \cdot e_W \cdot w \cdot e_R\) and \(\sigma \) formed from the race \({e_W}{\mathtt {\lesssim }}_{E}{e_R}\), let \(w = w_0\cdot \sigma _1\cdot w_1\cdot \sigma _2 \cdot \cdots \sigma _m\cdot w_m\), where \(\sigma _1, \ldots , \sigma _m\) are the schedules in \(w\). We note that \(\sigma \), since \({e_W}{\mathtt {\lesssim }}_{E}{e_R}\) is parsimonious, includes all \(\sigma _i\) (including their heads) for \(1 \le i \le m\), and may also include events in the sequences \(w_0, \ldots , w_m\). This means that \(w\! \setminus \!\sigma \) is of form \(w_0' \cdot \ldots \cdot w_m'\), where \(w_i'\) is the sequence remaining in \(w_i\) after removing \(\sigma \); in particular \(w\! \setminus \!\sigma \) does not contain any events in any schedule \(\sigma _i\). The following proposition characterizes how to detect a schedule \(\sigma '\) with \(\sigma ' \propto \sigma \) in an exploration that is initiated as a continuation of \(E_1\cdot \sigma \).
Proposition 1
Let \(E= E_1 \cdot e_W \cdot w \cdot e_R\), let \(w= w_0\cdot \sigma _1\cdot w_1 \cdot \cdots \cdot \cdot w_m\), and let \(\sigma \) be formed from \({e_W}{\mathtt {\lesssim }}_{E}{e_R}\). Let \(w_j' = w_j\! \setminus \!\sigma \) for \(j = 0, \ldots , m\), and \(e_j = {hd}\left( \sigma _j\right) \) for \(j = 1, \ldots , m\). Let \(E_1 \cdot \sigma \cdot u\cdot e_R'\) be an execution where \(e_R'\) is a read event on \(x\), and let \(\sigma ' = {e_R'}\downarrow ^{\sigma \cdot u\cdot e_R'}\). Then \(\sigma ' \propto \sigma \) iff \(\sigma '\) is a read-\(x\)-schedule such that either
-
(A)
(i) \(({e_R'}\downarrow ^{u\cdot e_R'}) \sqsubseteq w\! \setminus \!\sigma \), and (ii) if \(e_R'\) is in \(w_j'\) then
 for \(1 \le k \le j\),
for \(1 \le k \le j\), -
(B)
for some j with \(0 \le j \le m\) we have (i) \(({e_R'}\downarrow ^{u\cdot e_R'})\ \not \sim w_0' \cdot \ldots \cdot w_{j}'\), and (ii) if j is the smallest index s.t. (i) holds, then
 for \(1 \le k \le j\), or
for \(1 \le k \le j\), or -
(C)
for some i with \(1\le i \le m\) s.t. \(\sigma _i\) is a read-schedule, and \(\sigma _i'\) with \(\sigma _i' \propto \sigma _i\)
-
1)
if \({hd}\left( \sigma _i\right) . var \ne x\) then (i) \(({{hd}\left( \sigma _i'\right) }\downarrow ^{w_0' \cdot \ldots \cdot w_i' \cdot \sigma _i'}) \sqsubseteq u\), (ii)
 , and (iii)
, and (iii)
 for \(1 \le k \le i\).
for \(1 \le k \le i\). -
2)
if \({hd}\left( \sigma _i\right) . var = x\) then (i) \(({{hd}\left( \sigma _i'\right) }\downarrow ^{w_0' \cdot \ldots \cdot w_i' \cdot \sigma _i'}) \sqsubseteq u\cdot e_R'\), (ii) \({hd}\left( \sigma _i'\right) = e_R'\), and (iii)
 for \(1 \le k \le i\). \(\square \)
for \(1 \le k \le i\). \(\square \)
-
1)
Let us motivate this proposition.
-
(A)
Since \(\sigma \sqsubseteq w\cdot e_R\), condition (i) implies that \(\sigma ' = {e_R'}\downarrow ^{\sigma \cdot u\cdot e_R'} \ \sqsubseteq w\), implying that \(\sigma '\) is a contained schedule (wrt. \(\sigma \)).
-
(B)
Since \(\sigma \sqsubseteq w\cdot e_R\), condition (i) implies that \(\sigma ' = {e_R'}\downarrow ^{\sigma \cdot u\cdot e_R'} \ \not \sim w_0 \cdot \sigma _1 \cdot \ldots \cdot \sigma _j \cdot w_{j}\), implying that \(\sigma '\) is a conflicting schedule.
-
(C)
Let us first consider case 1). Since \(\sigma \sqsubseteq w\cdot e_R\), condition (i) implies that \(({{hd}\left( \sigma _i'\right) }\downarrow ^{w_0 \cdot \sigma _1 \cdot \ldots \cdot \sigma _j \cdot w_{j} \cdot \sigma _i'}) \ \sqsubseteq \sigma \cdot u\), implying that \(\sigma '\) is an inherited schedule. Condition (ii) ensures that \(e_R'\) appears in the exploration that follows \({hd}\left( \sigma _i'\right) \), in which case
 is necessary for \(e_R'\) to be fresh. Case 2) is a slight modification for these case that the head of \(\sigma _i'\) and \(e_R'\) read from the same variable, in which case \(e_R'\) must be \({hd}\left( \sigma _i'\right) \) (since a read-\(x\)-schedule cannot contain another read on \(x\)).
is necessary for \(e_R'\) to be fresh. Case 2) is a slight modification for these case that the head of \(\sigma _i'\) and \(e_R'\) read from the same variable, in which case \(e_R'\) must be \({hd}\left( \sigma _i'\right) \) (since a read-\(x\)-schedule cannot contain another read on \(x\)).
In each case, the last condition ensures that \(e_R'\) is fresh, and thus part of a parsimonious race.
Let us illustrate, using Fig. 2, how some continuations of read schedules can be characterized according to Proposition 1. First, consider \(\sigma _4\) (top right in Fig. 2), derived from the race
 in \(E_3\). Decomposing \(E_3\) as
in \(E_3\). Decomposing \(E_3\) as
 , where
, where
 , we obtain
, we obtain
 .
.
-
(A)
Assume that the exploration continues after \(\sigma _4\) as
 . Letting u be
. Letting u be
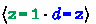 and \(e_R'\) be
and \(e_R'\) be
 , we see that \(\sigma ' = u\cdot e_R'\) matches the conditions in case (A), since (i) \(\sigma ' \sqsubseteq w\setminus \sigma _4\) and (ii) \(e_R'\) happens-after the head of the only schedule
, we see that \(\sigma ' = u\cdot e_R'\) matches the conditions in case (A), since (i) \(\sigma ' \sqsubseteq w\setminus \sigma _4\) and (ii) \(e_R'\) happens-after the head of the only schedule
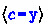 in \(E_3\).
in \(E_3\). -
(B)
Assume next that the exploration continues after \(\sigma _4\) as
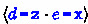 . Letting u be
. Letting u be
 and \(e_R'\) be
and \(e_R'\) be
 , we see that \(\sigma ' = u\cdot e_R'\) matches the conditions in case (B), since (i)
, we see that \(\sigma ' = u\cdot e_R'\) matches the conditions in case (B), since (i)
 and
and
 , and (ii)
, and (ii)
 happens-after the head of the only schedule
happens-after the head of the only schedule
 in \(E_3\).
in \(E_3\). -
(C)
Let us next consider \(\sigma _2\) (top middle in Fig. 2), derived from the race
 in the first explored execution \(E'\) from \(T_5\). Decomposing \(E'\) as
in the first explored execution \(E'\) from \(T_5\). Decomposing \(E'\) as
 , where
, where
 we obtain
we obtain
 . Assume next that the exploration continues after \(\sigma _2\) as
. Assume next that the exploration continues after \(\sigma _2\) as
 . Letting u be
. Letting u be
 and \(e_R'\) be
and \(e_R'\) be
 , we see that \(\sigma ' = u\cdot e_R'\) matches the conditions in case (C)1), since there is the schedule
, we see that \(\sigma ' = u\cdot e_R'\) matches the conditions in case (C)1), since there is the schedule
 for which there is another schedule
for which there is another schedule
 with \(\sigma _i'\propto \sigma _i\). The conditions in case (C)1) are satisfied, since (i)
with \(\sigma _i'\propto \sigma _i\). The conditions in case (C)1) are satisfied, since (i)
 , (ii)
, (ii)
 , and (iii) there is no schedule before the event
, and (iii) there is no schedule before the event
 in \(E'\).
in \(E'\).
Based on Proposition 1, we now describe a technique to monitor the exploration of executions in order to detect when it is about to explore a schedule in a sleep set. It is based on annotating each newly constructed read schedule \(\sigma \) with a characterization of the schedules \(\sigma '\) with \(\sigma ' \propto \sigma \) that must be avoided in the exploration that continues after \(\sigma \). We use the same notation and set-up as for Proposition 1. For \(i= 0 , \ldots , m\), let \(P_i\) denote \(P_i = w_0'\{e_1\}w_1' \cdots \{e_i\}w_i'\), where \(w_j'\) is \(w_j \! \setminus \!\sigma \) for \(j = 0, \ldots , i\), and \(e_j\) is \({hd}\left( \sigma _j\right) \) for \(j = 1, \ldots , i\). From Proposition 1 we see that (i) \(P_m\) and \(x\) contains sufficient information to characterize the contained and conflicting schedules that must be avoided, and (ii) for each \(i = 1, \ldots , m\), such that \(\sigma _i\) is a read-schedule, \(P_{i-1}\) together with a characterization of the schedules \(\sigma _i'\) with \(\sigma _i' \propto \sigma _i\) contain sufficient information to characterize the schedules inherited from schedules \(\sigma _i'\) with \(\sigma _i' \propto \sigma _i\) that must be avoided. Let us therefore define a schedule expression as an expression of form (i) \(P_m \rhd x\), characterizing the set of contained and conflicting read-\(x\)-schedules, according to cases (A) and (B) in Proposition 1, or of form (ii) \(P_{i-1} [\varphi _i] \rhd x\) for some \(i = 1, \ldots , m\), such that \(\sigma _i\) is a read-schedule, and \(\varphi _i\) is a schedule expression characterizing schedules \(\sigma _i'\) with \(\sigma _i' \propto \sigma _i\). Let us go through one example of each form of schedule expressions using Fig. 2. While exploring continuations of \(\sigma _4\), POP creates two schedule expressions; (i)
 representing the schedules \(\sigma _2\) and \(\sigma _3\), and (ii)
representing the schedules \(\sigma _2\) and \(\sigma _3\), and (ii)
 , representing only \(\sigma _1\). Notice that, expression (ii) is useless in this case as \(\sigma _1\) is conflicting with \(\sigma _4\), i.e., \(\sigma _1\) is not a feasible continuation after \(\sigma _4\). However, the same expression is useful to prevent doing \(\sigma _1\), when exploring a continuation of \(\sigma _2\).
, representing only \(\sigma _1\). Notice that, expression (ii) is useless in this case as \(\sigma _1\) is conflicting with \(\sigma _4\), i.e., \(\sigma _1\) is not a feasible continuation after \(\sigma _4\). However, the same expression is useful to prevent doing \(\sigma _1\), when exploring a continuation of \(\sigma _2\).
In order to detect when exploration is about to explore a schedule that must be avoided, the “state” of each schedule expression will during exploration be maintained by POP in a sleep set expression, which is obtained from a schedule expression \(\varphi \) by (i) augmenting each event \(e\) which occurs in some sequence \(w_i\) in \(\varphi \) (i.e., not inside brackets \(\{\cdot \}\)) with a conflict set (denoted C) of encountered events that conflict with e or happen-after an event that conflicts with e; we use the notation \(e^{C}\) to denote such an augmented event, (ii) augmenting each enclosed subexpression of form \(P \rhd x\) or \(P[\varphi ] \rhd x\) with the set (denoted D) of encountered read-\(x\)-events that are heads of read-schedules that are characterized by \(P \rhd x\); we use the notation \([P \rhd x]^D\) (or \([P[\varphi ] \rhd x]^D\)), and (iii) augmenting each occuring variable \(x\) that occurs after \(\rhd \) in a subexpression of form \(P \rhd x\) or \(P[\varphi ] \rhd x\) with the set of previously encountered read events on \(x\); we use the notation \(\rhd x^{R}\), where R is this set of read events. If a read on \(x\) happens-after a read in R, it cannot be the head of a read-\(x\)-schedule, and should thus not be blocked (recall from the definition of read-\(x\)-schedules that its head cannot happen-after another read on the same variable). When a sleep set expression is created and initialized, its augmenting sets are empty. We identify a schedule expression with its initialized sleep set expression. We use \(\psi \), possibly with sub- or superscripts, to range over sleep set expressions.

Algorithm 2 shows POP ’s implementation of the sleep set expression manipulation functions \({\texttt{MkSchedChar}}(\sigma ,E_1,e,E_2)\) and \({\texttt{UpdSeq}}(w, SSChar )\), which are called by Algorithm 1. A set of sleep set expressions is called a sleep set characterization. The function \({\texttt{MkSchedChar}}(\sigma ,E_1,e,E_2)\) (line 1), constructs the set of schedule expressions (which can be seen as initialized sleep set expressions) for \(\sigma \) according to the description given earlier in this section. The function \({\texttt{UpdSeq}}(w, SSChar )\) updates the sleep set characterization \( SSChar \) wrt. processing of the sequence \(w\). At its top level, \({\texttt{UpdSeq}}(w, SSChar )\) updates each sleep set expression \(\psi \) in \( SSChar \) with the sequence of events in \(w\), one by one, each time calling \({\texttt{UpdSE}}(e,\psi )\). If \(e\) is a write on a variable \(y\), then in this process, all sleep set expressions containing \(\rhd y\) are discarded, since it is from now impossible to complete a read-\(y\)-schedule. The function \({\texttt{UpdSE}}(e,\psi )\) comes in two versions (at line 12 and line 15). Both versions first call \({\texttt{UpdP}}(e,P,x,R)\), which updates the sleep set expressions with respect to contained and conflicting read-\(x\)-schedules characterized by \(P\rhd x^R\). If e is the head of such a schedule, then \({\texttt{UpdP}}(e,P,x,R)\) returns block; if e is independent with all of \(P\), then \({\texttt{UpdP}}(e,P,x,R)\) returns indep; otherwise it returns the updated version of \(P\). In the code for \({\texttt{UpdP}}\), we let let \(e\leftrightarrow e'\) denote that e and \(e'\) are performed by different threads and access the same variable and at least one of e and \(e'\) writes. For an event \(e\) and a set C of events, let \(e\bowtie C\) denote that there is some \(e' \in C\) with \(e\bowtie e'\). When called, \({\texttt{UpdP}}(e,P,x,R)\) traverses the sequences \(w_0', \ldots , w_i'\), one event at a time, and stops at the first event \(e_l^{C_l}\) such that either (i) \(e\) conflicts with \(e_l\) or depends with an event in \(C_l\), in which case \(e\) is added to \(C_l\) (line 29), or (ii) \(e= e_l\), in which case \(e\) is removed from the sequence (of form \(w_j'\)) (line 30). If in addition \(e\) is a read on \(x\) and happens after the relevant schedule heads among \(e_1', \ldots , e_i'\) for being fresh, then if \(e\) does not happen after a read in R, \({\texttt{UpdP}}(e,P,x,R)\) returns blocked (since in case (i) it is the head of a conflicting schedule and in case (ii) of a contained schedule), else \(e\) is added to R (line 33). If on the other hand, \(e\) is not a read on \(x\) or does not happen after the relevant schedule heads among \(e_1', \ldots , e_i'\), then \({\texttt{UpdP}}(e,P,x,R)\) returns the updated version of \(P\). Finally, if there is no event \(e_l^{C_l}\) in \(w_0', \ldots , w_i'\) satisfying conditions (i) or (ii), then \({\texttt{UpdP}}\) returns indep (line 31).
Let us now consider \({\texttt{UpdSE}}(e,\psi )\), which comes in two versions, depending on the form of \(\psi \). If \(\psi \) is of form \(P\rhd x^R\) (line 12), it calls \({\texttt{UpdP}}(e,P,x,R)\) and forwards its return value. If \(\psi \) is of form \(P[\psi ']^D\rhd x^R)\) (line 15), it also calls \({\texttt{UpdP}}(e,P,x,R)\). Also this version forwards the return value block. In addition, if \({\texttt{UpdP}}(e,P,x,R)\) returns indep, meaning that \(e\) is independent of \(P\), then (i) if some event already in D (being the head of a schedule characterized by \(\psi '\)) happens-before \(e\) (or is the same as \(e\) if it reads from \(x\)), and \(e\) is a read on \(x\), then if \(e\) does not happen after a read in R, the function returns blocked (since \(e\) is the head of an inherited schedule), else \(e\) is added to R (line 19), (ii) otherwise, processing is continued recursively on \(\psi '\) by calling \({\texttt{UpdSE}}(e,\psi ')\). If this call returns blocked, then \(e\) is added to D (line 21), otherwise the inner sleep set expression \(\psi '\) is updated. Finally, if \({\texttt{UpdP}}(e,P,x,R)\) returns neither blocked nor indep, the updated sleep set expression is returned (line 23).
5 Correctness and Space Complexity
In this section, we state theorems of correctness, optimality, and space complexity of \(\text{ POP } \). We first consider correctness and optimality.
Theorem 1
For a terminating program \(P\), the POP algorithm has the properties that (i) for each maximal execution E of \(P\), it explores some execution \(E'\) with \(E' \simeq E\), and (ii) it never explores two different but equivalent maximal executions, and (iii) it is never blocked (at line 14) unless it has explored a maximal execution.
We thereafter consider space complexity.
Lemma 1
The number of nested recursive calls to \({\texttt{Explore}}\) at line 13 is at most \(n(n-1)/2\), where n is the length of the longest execution of the program.
Note that in this lemma, we do not count the calls at line 16, since they are considered as normal exploration of some execution. Only the calls at line 13 start the exploration of a new execution.
Theorem 2
Algorithm 1 needs space which is polynomial in n, where n is the length of the longest execution of the analyzed program.
6 Implementation and Evaluation
Our implementation, which is available in the artifact of this paper, was done in a fork of Nidhugg. Nidhugg is a state-of-the-art stateless model checker for C/C++ programs with Pthreads, which works at the level of LLVM Intermediate Representation, typically produced by the Clang compiler. Nidhugg comes with a selection of DPOR algorithms, one of which is Optimal DPOR [1] nowadays also enhanced with Partial Loop Purity elimination and support for await statements [25]. In our Nidhugg fork, we have added the POP algorithm as another selection. Its implementation involved: (i) designing an efficient data structure to simulate recursive calls to \({\texttt{Explore}}\), i.e., follow the next schedule to explore and backtrack to the previous execution when no further races to reverse, (ii) developing a procedure to filter out races that are not parsimonious, and (iii) implementing a more optimized data structure than Algorithm 2 that stores sleep set characterizations as trees.
In this section, we evaluate the performance of POP ’s implementation and compare it, in terms of time and memory, against the implementations of Optimal DPOR in Nidhugg commit 5805d77 and the graph-based Truly Stateless (TruSt) Optimal DPOR algorithm [29] as implemented in GenMC v0.10.0 using options -sc –disable-instruction-caching. All tools employed LLVM 14.0.6, and the numbers we present are measured on a desktop with a Ryzen 7950X CPU running Debian 12.4.
Table 1 contains the results of our evaluation. Its first nine benchmarks are from the DPOR literature, and are all parametric on the number of threads (shown in parentheses). The last benchmark, length-param, is synthetic and is additionally parametric on the length of its executions. Since these DPOR algorithms are optimal, they explore the same number of executions (2nd column) in all ten benchmarks. We will analyze the results in five groups (cf. Table 1).
The first group consists of three programs (circular-buffer from SCTBench [47], fib-bench from SV-Comp [45], and the linuxrwlocks from SATCheck [16]). Here, all algorithms consume memory that stays constant as the size of the program and the number of executions explored increase. We can therefore compare the raw performance of the implementation of these three DPOR algorithms. POP ’s implementation is fastest on circular-buffer, while TruSt ’s is fastest on the two other programs. However, notice that all three implementations scale similarly.
The second group consists of the two benchmarks (filesystem and indexer) from the “classic” DPOR paper of Flanagan and Godefroid [18]. Here, Optimal DPOR shows an increase in memory consumption (measured in MB), while the other two algorithms use constant memory. POP is fastest here by approximately \(2\times \).
The third group, consisting of lastzero [1] and exp-mem3,Footnote 2 two synthetic benchmarks also used in the TruSt paper [29, Table 1], shows a similar picture in terms of memory consumption: Optimal DPOR ’s increases more noticeably here, while the two other algorithms use memory that stays constant. Time-wise, TruSt is 2–5\(\times \) faster than POP, which in turn is \(2\times \) faster than Optimal.
The fourth group, consisting of two concurrent data structure programs (dispatcher and poke) from the Quasi-Optimal POR paper [40], shows Optimal’s memory explosion more profoundly, and provides further evidence of the good memory performance of the TruSt and POP algorithms. Time-wise, there is no clear winner here, with TruSt ’s implementation being a bit faster on dispatcher, and with POP ’s being faster and scaling slightly better than TruSt ’s on poke.
Finally, let us examine the algorithms’ performance on length-param(T , N), a synthetic but simple program in which a number of threads (just two here) issue N stores and loads to thread-specific global variables, followed by a store and a load to a variable shared between threads. The total number of executions is just four here, but the executions grow in length. One can clearly see the superior time performance of sequence-based DPOR algorithms, such as Optimal and POP, compared to TruSt ’s graph-based algorithm that needs to perform consistency checks for the executions it constructs. As can be seen, these checks can become quite expensive (esp. if their implementation has sub-optimal complexity, as it is probably the case here). In contrast, sequence-based DPOR algorithms naturally generate consistent executions (for memory models such as SC). We can also notice that POP performs slightly better than Optimal in terms of memory.
Wrapping up our evaluation, we can make the following two general claims:
-
1.
Both POP and TruSt live up to their promise about performing SMC exploration which is optimal (w.r.t. the Mazurkiewicz equivalence) but also with polynomial (in fact, in practice, constant) space consumption.
-
2.
The implementation of the POP algorithm consistently outperforms that of Optimal DPOR in Nidhugg. This is mostly due to increased simplicity.
7 Related Work
Since its introduction in the tools Verisoft [20, 21] and CHESS [39], stateless model checking has been an important technique for analyzing correctness of concurrent programs. Dynamic partial order reduction [18, 44] has enabled a significantly increased efficiency for covering all interleavings, which has been adapted to many different settings and computational models, including actor programs [46], abstract computational models [27], event driven programs [4, 24, 35], and MPI programs [42]. DPOR has been adapted for weak memory models including TSO [2, 16, 48], Release-Acquire [8], POWER [7], and C11 [28], and also been applied to real life programs [32]. DPOR has been extended with features for efficiently handling spinloops and blocking constructs [25, 31],
An important advancement has been the introduction of optimal DPOR algorithms, which guarantee to explore exactly one execution from each equivalence class [1], and therefore achieve exponential-time reduction over non-optimal algorithms. This saving came at the cost of worst-case exponential (in the size of the program) memory consumption [3]. The strive for covering the space of all interleavings with fewer representative executions inspired DPOR algorithms for even weaker equivalences than Mazurkiewicz trace equivalence, such as equivalence based on observers [11], reads-from equivalence [6, 13, 14], conditional independence [10], context-sensitive independence and observers [9], or on the maximal causal model [23]. These approaches explore fewer traces than approaches based on Mazurkiewicz trace equivalence at the cost of potentially expensive (often NP-hard) consistency checks. Another line of work uses unfoldings [37] to further reduce the number of interleavings that must be considered [26, 40, 43]; these techniques incur significantly larger cost per test execution than the previously mentioned ones.
DPOR has also been adapted for weak memory models using an approach in which executions are represented as graphs, where nodes represent read and write operations, and edges represent reads-from and coherence relations; this allows the algorithm to be parametric on a specific memory model, at the cost of calling a memory-model oracle [28, 30, 33]. For this graph-based setting, an optimal DPOR algorithm with worst-case polynomial space consumption, called TruSt, was recently presented [29]. POP is also optimal with worst-case polynomial space consumption. Since it is designed for a sequence-based representation of executions, POP must be designed differently. In analogy with the parsimonious race reversal technique, TruSt has a technique for reversing each race only once, which is based on a maximal extension criterion. POP adapts TruSt ’s strategy of eager race reversal to avoid potentially space-consuming accumulation of schedules. Finally, since TruSt operates in a graph-based setting, it reverses write-read races by changing the source of a read-from relation in the graph, instead of constructing a new schedule. Therefore redundant exploration of read-schedules is prevented by careful book-keeping instead of using sleep sets, which POP represents in a compact parsimonious way. The experimental results show that TruSt and POP have comparable performance for small and modest-size programs, but that POP is superior for programs with long executions, since the graph-based approach has difficulties to scale for long executions.
An alternative to DPOR for limiting the number of explored executions is to cover only a subset of all executions. Various heuristics for choosing this subset have been developed, including delay bounding [17], preemption bounding [38], and probabilistic strategies [12]. Such techniques can be effective in finding bugs in concurrent programs, but not prove their absence.
8 Conclusion
In this paper, we have presented POP, a new optimal DPOR algorithm for analyzing multi-threaded programs under SC. POP combines several novel algorithmic techniques, which allow efficiency improvements over previous such DPOR algorithms, both in time and space. In particular, its space consumption is polynomial in the size of the analyzed program. Our experiments on a wide variety of benchmarks show that POP always outperforms Optimal DPOR, the state-of-the-art sequence-based optimal DPOR algorithm, and offers performance comparable with TruSt, the state-of-the-art graph-based DPOR algorithm. Moreover, by being sequence-based, its implementation scales much better than TruSt ’s on programs with long executions.
As future work, it would be interesting to investigate the effect of applying POP ’s novel algorithmic techniques on DPOR algorithms tailored for different computational models, and for analyzing programs under weak concurrency memory models such as TSO and PSO.
Notes
- 1.
Throughout this paper, we assume that threads are spawned by a main thread, and that all shared variables get initialized to 0, also by the main thread.
- 2.
exp-mem3 is slight variant of the exp-mem program used in the TruSt paper. It uses atomic stores and loads instead of fetch-and-adds (FAAs), because the current implementation of Optimal DPOR (and POP) in Nidhugg employs an optimization which treats independent FAAs as non-conflicting [25] and explores only one trace on the exp-mem program independently of the benchmark’s parameter.
References
Abdulla, P., Aronis, S., Jonsson, B., Sagonas, K.: Optimal dynamic partial order reduction. In: Symposium on Principles of Programming Languages, pp. 373–384. POPL 2014, ACM, New York, NY, USA (2014). https://doi.org/10.1145/2535838.2535845
Abdulla, P.A., Aronis, S., Atig, M.F., Jonsson, B., Leonardsson, C., Sagonas, K.: Stateless model checking for TSO and PSO. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 353–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_28
Abdulla, P.A., Aronis, S., Jonsson, B., Sagonas, K.: Source sets: a foundation for optimal dynamic partial order reduction. J. ACM 64(4), 25:1–25:49 (2017). https://doi.org/10.1145/3073408
Abdulla, P.A., Atig, M.F., Bønneland, F.M., Das, S., Jonsson, B., Lång, M., Sagonas, K.: Tailoring stateless model checking for event-driven multi-threaded programs. In: André, É., Sun, J. (eds.) Automated Technology for Verification and Analysis - 21st International Symposium, ATVA 2023, Proceedings, Part II. LNCS, vol. 14216, pp. 176–198. Springer (2023). https://doi.org/10.1007/978-3-031-45332-8_9
Abdulla, P.A., Atig, M.F., Das, S., Jonsson, B., Sagonas, K.: Parsimonious optimal dynamic partial order reduction (2024). https://doi.org/10.48550/arXiv.2405.11128, https://doi.org/10.48550/arXiv.2405.11128, Extended Version with Proofs
Abdulla, P.A., Atig, M.F., Jonsson, B., Lång, M., Ngo, T.P., Sagonas, K.: Optimal stateless model checking for reads-from equivalence under sequential consistency. Proc. ACM Program. Lang. 3(OOPSLA), 150:1–150:29 (2019). https://doi.org/10.1145/3360576
Abdulla, P.A., Atig, M.F., Jonsson, B., Leonardsson, C.: Stateless model checking for POWER. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 134–156. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_8
Abdulla, P.A., Atig, M.F., Jonsson, B., Ngo, T.P.: Optimal stateless model checking under the release-acquire semantics. Proc. ACM on Program. Lang. 2(OOPSLA), 135:1–135:29 (2018). https://doi.org/10.1145/3276505
Albert, E., de la Banda, M.G., Gómez-Zamalloa, M., Isabel, M., Stuckey, P.J.: Optimal dynamic partial order reduction with context-sensitive independence and observers. J. Syst. Softw. 202, 111730 (2023). https://doi.org/10.1016/J.JSS.2023.111730
Albert, E., Gómez-Zamalloa, M., Isabel, M., Rubio, A.: Constrained dynamic partial order reduction. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10982, pp. 392–410. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96142-2_24
Aronis, S., Jonsson, B., Lång, M., Sagonas, K.: Optimal dynamic partial order reduction with observers. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10806, pp. 229–248. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_14
Burckhardt, S., Kothari, P., Musuvathi, M., Nagarakatte, S.: A randomized scheduler with probabilistic guarantees of finding bugs. In: Proceedings of the Fifteenth Edition of ASPLOS on Architectural Support for Programming Languages and Operating Systems, pp. 167–178. ASPLOS XV, ACM, New York, NY, USA (2010). https://doi.org/10.1145/1736020.1736040
Chalupa, M., Chatterjee, K., Pavlogiannis, A., Sinha, N., Vaidya, K.: Data-centric dynamic partial order reduction. Proc. ACM on Program. Lang. 2(POPL), 31:1–31:30 (2018). https://doi.org/10.1145/3158119
Chatterjee, K., Pavlogiannis, A., Toman, V.: Value-centric dynamic partial order reduction. Proc. ACM Program. Lang. 3(OOPSLA), 124:1–124:29 (2019). https://doi.org/10.1145/3360550
Christakis, M., Gotovos, A., Sagonas, K.: Systematic testing for detecting concurrency errors in Erlang programs. In: Sixth IEEE International Conference on Software Testing, Verification and Validation, pp. 154–163. ICST 2013, IEEE, Los Alamitos, CA, USA (2013). https://doi.org/10.1109/ICST.2013.50
Demsky, B., Lam, P.: SATCheck: SAT-directed stateless model checking for SC and TSO. In: Proceedings of the 2015 ACM SIGPLAN International Conference on Object-Oriented Programming, Systems, Languages, and Applications, pp. 20–36. OOPSLA 2015, ACM, New York, NY, USA (2015). https://doi.org/10.1145/2814270.2814297
Emmi, M., Qadeer, S., Rakamaric, Z.: Delay-bounded scheduling. In: Proceedings of the 38th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 411–422. POPL 2011, ACM (2011). https://doi.org/10.1145/1926385.1926432
Flanagan, C., Godefroid, P.: Dynamic partial-order reduction for model checking software. In: Principles of Programming Languages, (POPL), pp. 110–121. ACM, New York, NY, USA (2005). https://doi.org/10.1145/1040305.1040315
Godefroid, P. (ed.): Partial-Order Methods for the Verification of Concurrent Systems. LNCS, vol. 1032. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-60761-7
Godefroid, P.: Model checking for programming languages using VeriSoft. In: Principles of Programming Languages, (POPL), pp. 174–186. ACM Press, New York, NY, USA (1997). https://doi.org/10.1145/263699.263717
Godefroid, P.: Software model checking: the VeriSoft approach. Formal Methods Syst. Des. 26(2), 77–101 (2005). https://doi.org/10.1007/s10703-005-1489-x
Godefroid, P., Hanmer, R.S., Jagadeesan, L.: Model checking without a model: an analysis of the heart-beat monitor of a telephone switch using VeriSoft. In: Proceedings of the ACM SIGSOFT International Symposium on Software Testing and Analysis, pp. 124–133. ISSTA, ACM, New York, NY, USA (1998). https://doi.org/10.1145/271771.271800
Huang, J.: Stateless model checking concurrent programs with maximal causality reduction. In: Proceedings of the 36th ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 165–174. PLDI 2015, ACM, New York, NY, USA (2015). https://doi.org/10.1145/2737924.2737975
Jensen, C.S., Møller, A., Raychev, V., Dimitrov, D., Vechev, M.T.: Stateless model checking of event-driven applications. In: Proceedings of the 2015 ACM SIGPLAN International Conference on Object-Oriented Programming, Systems, Languages, and Applications, pp. 57–73. OOPSLA 2015, ACM, New York, NY, USA (2015). https://doi.org/10.1145/2814270.2814282
Jonsson, B., Lång, M., Sagonas, K.: Awaiting for godot: stateless model checking that avoids executions where nothing happens. In: Griggio, A., Rungta, N. (eds.) 22nd Formal Methods in Computer-Aided Design, pp. 284–293. FMCAD 2022, IEEE (2022). https://doi.org/10.34727/2022/ISBN.978-3-85448-053-2_35
Kähkönen, K., Saarikivi, O., Heljanko, K.: Using unfoldings in automated testing of multithreaded programs. In: IEEE/ACM International Conference on Automated Software Engineering, pp. 150–159. ASE’12, ACM, New York, NY, USA (2012). https://doi.org/10.1145/2351676.2351698, http://dl.acm.org/citation.cfm?id=2351676
Kastenberg, H., Rensink, A.: Dynamic partial order reduction using probe sets. In: van Breugel, F., Chechik, M. (eds.) CONCUR 2008. LNCS, vol. 5201, pp. 233–247. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85361-9_21
Kokologiannakis, M., Lahav, O., Sagonas, K., Vafeiadis, V.: Effective stateless model checking for C/C++ concurrency. Proc. ACM on Program. Lang. 2(POPL), 17:1–17:32 (2018). https://doi.org/10.1145/3158105
Kokologiannakis, M., Marmanis, I., Gladstein, V., Vafeiadis, V.: Truly stateless, optimal dynamic partial order reduction. Proc. ACM Program. Lang. 6(POPL), 1–28 (2022). https://doi.org/10.1145/3498711
Kokologiannakis, M., Raad, A., Vafeiadis, V.: Model checking for weakly consistent libraries. In: Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 96–110. PLDI 2019, ACM, New York, NY, USA (2019). https://doi.org/10.1145/3314221.3314609
Kokologiannakis, M., Ren, X., Vafeiadis, V.: Dynamic partial order reductions for Spinloops. In: Formal Methods in Computer Aided Design, pp. 163–172. FMCAD 2021, IEEE (2021). https://doi.org/10.34727/2021/isbn.978-3-85448-046-4_25
Kokologiannakis, M., Sagonas, K.: Stateless model checking of the Linux kernel’s read-copy update (RCU). Softw. Tools Technol. Transf. 21(3), 287–306 (2019). https://doi.org/10.1007/s10009-019-00514-6
Kokologiannakis, M., Vafeiadis, V.: HMC: model checking for hardware memory models. In: Larus, J.R., Ceze, L., Strauss, K. (eds.) Architectural Support for Programming Languages and Operating Systems, pp. 1157–1171. ASPLOS ’20, ACM (2020). https://doi.org/10.1145/3373376.3378480
Kokologiannakis, M., Vafeiadis, V.: GenMC: a model checker for weak memory models. In: Silva, A., Leino, K.R.M. (eds.) CAV 2021. LNCS, vol. 12759, pp. 427–440. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-81685-8_20
Maiya, P., Gupta, R., Kanade, A., Majumdar, R.: Partial order reduction for event-driven multi-threaded programs. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 680–697. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_44
Mazurkiewicz, A.: Trace theory. In: Brauer, W., Reisig, W., Rozenberg, G. (eds.) ACPN 1986. LNCS, vol. 255, pp. 278–324. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-17906-2_30
McMillan, K.L.: A technique of a state space search based on unfolding. Formal Methods Syst. Des. 6(1), 45–65 (1995). https://doi.org/10.1007/BF01384314
Musuvathi, M., Qadeer, S.: Iterative context bounding for systematic testing of multithreaded programs. In: Proceedings of the ACM SIGPLAN 2007 Conference on Programming Language Design and Implementation, pp. 446–455. PLDI 2007, ACM (2007). https://doi.org/10.1145/1250734.1250785
Musuvathi, M., Qadeer, S., Ball, T., Basler, G., Nainar, P.A., Neamtiu, I.: Finding and reproducing heisenbugs in concurrent programs. In: Proceedings of the 8th USENIX Symposium on Operating Systems Design and Implementation, pp. 267–280. OSDI ’08, USENIX Association, Berkeley, CA, USA (2008). http://dl.acm.org/citation.cfm?id=1855741.1855760
Nguyen, H.T.T., Rodríguez, C., Sousa, M., Coti, C., Petrucci, L.: Quasi-optimal partial order reduction. In: Chockler, H., Weissenbacher, G. (eds.) CAV 2018. LNCS, vol. 10982, pp. 354–371. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96142-2_22
Norris, B., Demsky, B.: A practical approach for model checking C/C++11 code. ACM Trans. Program. Lang. Syst. 38(3), 10:1–10:51 (2016). https://doi.org/10.1145/2806886
Palmer, R., Gopalakrishnan, G., Kirby, R.M.: Semantics driven dynamic partial-order reduction of MPI-based parallel programs. In: Ur, S., Farchi, E. (eds.) Proceedings of the 5th Workshop on Parallel and Distributed Systems: Testing, Analysis, and Debugging, pp. 43–53. PADTAD 2007, ACM (2007). https://doi.org/10.1145/1273647.1273657
Rodríguez, C., Sousa, M., Sharma, S., Kroening, D.: Unfolding-based partial order reduction. In: 26th International Conference on Concurrency Theory (CONCUR 2015). LIPIcs, vol. 42, pp. 456–469. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik (2015). https://doi.org/10.4230/LIPIcs.CONCUR.2015.456
Sen, K., Agha, G.: A race-detection and flipping algorithm for automated testing of multi-threaded programs. In: Bin, E., Ziv, A., Ur, S. (eds.) HVC 2006. LNCS, vol. 4383, pp. 166–182. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70889-6_13
SV-COMP: Competition on Software Verification (2019). https://sv-comp.sosy-lab.org/2019. Accessed 24 Mar 2019
Tasharofi, S., Karmani, R.K., Lauterburg, S., Legay, A., Marinov, D., Agha, G.: TransDPOR: a novel dynamic partial-order reduction technique for testing actor programs. In: Giese, H., Rosu, G. (eds.) FMOODS/FORTE -2012. LNCS, vol. 7273, pp. 219–234. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30793-5_14
Thomson, P., Donaldson, A.F., Betts, A.: Concurrency testing using controlled schedulers: An empirical study. ACM Trans. Parallel Comput. 2(4), 23:1–23:37 (2016). https://doi.org/10.1145/2858651
Zhang, N., Kusano, M., Wang, C.: Dynamic partial order reduction for relaxed memory models. In: Programming Language Design and Implementation (PLDI), pp. 250–259. ACM, New York, NY, USA (2015). https://doi.org/10.1145/2737924.2737956
Acknowledgements
This research was partially funded by research grants from the Swedish Research Council (Vetenskapsrådet) and from the Swedish Foundation for Strategic Research through project aSSIsT. We thank these funding agencies and the anonymous CAV 2024 reviewers for their comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Abdulla, P.A., Atig, M.F., Das, S., Jonsson, B., Sagonas, K. (2024). Parsimonious Optimal Dynamic Partial Order Reduction. In: Gurfinkel, A., Ganesh, V. (eds) Computer Aided Verification. CAV 2024. Lecture Notes in Computer Science, vol 14682. Springer, Cham. https://doi.org/10.1007/978-3-031-65630-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-65630-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-65629-3
Online ISBN: 978-3-031-65630-9
eBook Packages: Computer ScienceComputer Science (R0)




 for
for  for
for  , and (iii)
, and (iii)
 for
for  for
for  is necessary for
is necessary for  . Letting u be
. Letting u be
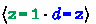 and
and  , we see that
, we see that 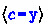 in
in 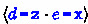 . Letting u be
. Letting u be
 and
and  , we see that
, we see that  and
and
 , and (ii)
, and (ii)
 happens-after the head of the only schedule
happens-after the head of the only schedule
 in
in  in the first explored execution
in the first explored execution  , where
, where
 we obtain
we obtain
 . Assume next that the exploration continues after
. Assume next that the exploration continues after  . Letting u be
. Letting u be
 and
and  , we see that
, we see that  for which there is another schedule
for which there is another schedule
 with
with  , (ii)
, (ii)
 , and (iii) there is no schedule before the event
, and (iii) there is no schedule before the event
 in
in