Abstract
We present a new angle on solving quantified linear integer arithmetic based on combining the automata-based approach, where numbers are understood as bitvectors, with ideas from (nowadays prevalent) algebraic approaches, which work directly with numbers. This combination is enabled by a fine-grained version of the duality between automata and arithmetic formulae. In particular, we employ a construction where states of automaton are obtained as derivatives of arithmetic formulae: then every state corresponds to a formula. Optimizations based on techniques and ideas transferred from the world of algebraic methods are used on thousands of automata states, which dramatically amplifies their effect. The merit of this combination of automata with algebraic methods is demonstrated by our prototype implementation being competitive to and even superior to state-of-the-art SMT solvers.
You have full access to this open access chapter, Download conference paper PDF


1 Introduction
Linear integer arithmetic (LIA), also known as Presburger arithmetic, is the first-order theory of integers with addition. Its applications include e.g. databases [60], program analysis [61], synthesis [59], and it is an essential component of every aspiring SMT solver. Many other types of constraints can either be reduced to LIA, or are decided using a tight collaboration of a solver for the theory and a LIA solver, e.g., in the theory of bitvectors [71], strings [19], or arrays [37]. Current SMT solvers are strong enough in solving large quantifier-free LIA formulae. Their ability to handle quantifiers is, however, problematic to the extent of being impractical. Even a tiny formula with two quantifier alternations can be a show stopper for them. Handling quantifiers is an area of lively research with numerous application possibilities waiting for a practical solution, e.g., software model checking [46], program synthesis [67], or theorem proving [49].
Among existing techniques for handling quantifiers, the complete approaches based on quantifier elimination [23, 64] and automata [13, 17, 79] have been mostly deemed not scalable and abandoned in practice. Current SMT solvers use mainly incomplete techniques originating, e.g., from solving the theory of uninterpreted functions [66] and algebraic techniques, such as the simplex algorithm for quantifier-free formulae [25].
This work is the first step in leveraging a recent renaissance of practically competitive automata technology for solving LIA. This trend that has recently emerged in string constraint solving (e.g. [2, 7, 8, 18, 20]), processing regular expressions [21, 24, 74], reasoning about the SMT theory of bitvectors [54], or regex matching (e.g. [40, 53, 62, 78]). The new advances are rooted in paradigms such as usage of non-determinism and alternation, various flavours of symbolic representations, and combination with/or integration into SAT/SMT frameworks and with algebraic techniques.
We particularly show that the automata-based procedure provides unique opportunities to amplify certain algebraic optimizations that reason over the semantic of formulae. These optimizations then boost the inherent strong points of the automata-based approach to the extent that it is able to overcome modern SMT solvers. The core strong points of automata are orthogonal to those of algebraic methods, mainly due to treating numbers as strings of bits regardless of their numerical values. Automata can thus represent large sets of solutions succinctly and can use powerful techniques, such as minimization, that have no counterpart in the algebraic world. This makes automata more efficient than the algebraic approaches already in their basic form, implemented e.g. in [13, 79], on some classes of problems such as the Frobenius coin problem [41]. In many practical cases, the automata construction, however, explodes. The explosion usually happens when constructing an intermediate automaton for a sub-formula, although the minimal automaton for the entire formula is almost always small. The plot in Fig. 1 shows that the gap between sizes of final and intermediate automata in our benchmark is always several orders of magnitude large, offering opportunities for optimizations. In this paper, we present a basic approach to breaching this gap by transferring techniques and ideas from the algebraic world to automata and using them to prune the vast state space.
Comparison of the peak intermediate automaton size and the size of the minimized DFA for the entire formula on the SMT-LIB benchmark (cf. Sect. 9).
To this end, we combine the classical inductive automata construction with constructing formula derivatives, similar to derivatives of regular expressions [3, 15, 74] or WS1S/WSkS formulae [32, 45, 77]. Our construction directly generates states of an automaton of a nested formula, without the need to construct intermediate automata for sub-formulae first. Although the derivative construction is not better than the inductive construction by itself, it gives an opportunity to optimize the state space on the fly, before it gets a chance to explode. The optimization itself is negotiated by the fine-grained version of the well-known automaton-formula duality. In the derivative construction, every state corresponds to a LIA formula. Applying equivalence-preserving formula rewriting on state formulae has the effect of merging or pruning states, similar to what DFA minimization could achieve after the entire automaton were constructed.
Our equivalence-preserving rewriting uses known algebraic techniques or ideas originating from them. First, we use basic formula simplification techniques, such as propagating true or false values or antiprenexing. Despite being simple, these simplifications have a large impact on performance. Second, we use disjunction pruning, which replaces \(\varphi _1 \vee \varphi _2 \vee \cdots \vee \varphi _k\) by \(\varphi _2 \vee \cdots \vee \varphi _k\) if \(\varphi _1\) is entailed by the rest of the formula (this is close to the state pruning techniques used in [28, 32, 38]). We also adopt the principle of quantifier instantiation [26, 36, 68], where we detect cases when a quantified variable can be substituted by one or several values, or when a linear congruence can be simplified to a linear equation. We particularly use ideas from Cooper’s quantifier elimination [23], where a quantifier is expanded into a disjunction over a finite number of values, and from Omega test [65], where a variable with a one-side unbounded range is substituted by the least restrictive value.
It is noteworthy that in the purely algebraic setting, the same techniques could only be applied once on the input formula, with a negligible effect. In the automata-based procedure, their power is amplified since they are used on thousands of derivative states generated deep within automata after reading several bits of the solution.
Our prototype implementation is competitive with the best SMT solvers on benchmarks from SMT-LIB, and, importantly, it is superior on quantifier-intensive instances. We believe that more connections along the outlined direction, based on the fine-grained duality between automata and formulae, can be found, and that the work in this paper is the first step in bridging the worlds of automata and algebraic approaches. Many challenges in incorporating automata-based LIA reasoning into SMT solvers still await but, we believe, can be tackled, as witnessed e.g. within the recent successes of the integration of automata-based string solvers [7, 18, 19].
2 Preliminaries
We use \(\mathbb {Z}\) to denote the set of integers, \(\mathbb {Z}^+\) to denote the set of positive integers, and \(\mathbb {B}\) to denote the set of binary digits \(\{0,1\}\). For \(x, y \in \mathbb {Z}\) and \(m \in \mathbb {Z}^+\), we use \(x \mathrel {\equiv _{m}} y\) to denote that x is congruent with y modulo m, i.e., there exists \(z \in \mathbb {Z}\) s.t. \(z \cdot m + x = y\); and x|y to denote that there exists \(z' \in \mathbb {Z}\) s.t. \(y = z' \cdot x\). Furthermore, we use \(\left[ x\right] _{m}\) to denote the unique integer s.t. \(0 \le \left[ x\right] _{m} < m\) and \(x \mathrel {\equiv _{m}} \left[ x\right] _{m}\). The following notation will be used for intervals of integers: for \(a,b \in \mathbb {Z}\), the set \(\{x \in \mathbb {Z}\mid a \le x \le b\}\) is denoted as [a, b], the set \(\{x \in \mathbb {Z}\mid a \le x\}\) is denoted as \([a, {+\infty })\), and the set \(\{x \in \mathbb {Z}\mid x \le b\}\) is denoted as \(({-\infty }, b]\). The greatest common divisor of \(a,b \in \mathbb {Z}\), denoted as \(\gcd (a,b)\), is the largest integer such that \(\gcd (a,b)|a\) and \(\gcd (a,b)|b\) (note that \(\gcd (a,0) = |a|\)); if \(\gcd (a,b) = 1\), we say that a and b are coprime. For a real number y, \(\lfloor y \rfloor \) denotes the floor of y, i.e., the integer \(\max \{z \in \mathbb {Z}\mid z \le y\}\), and \(\lceil y \rceil \) denotes the ceiling of y, i.e., the integer \(\min \{z \in \mathbb {Z}\mid z \ge y\}\).
An alphabet \(\varSigma \) is a finite non-empty set of symbols and a word \(w = a_1 \ldots a_n\) of length n over \(\varSigma \) is a finite sequence of symbols from \(\varSigma \). If \(n = 0\), we call w the empty word and denote it \(\epsilon \). \(\varSigma ^+\) is the set of all non-empty words over \(\varSigma \) and \(\varSigma ^* = \varSigma ^+ \cup \{\epsilon \}\).
Finite Automata. In order to simplify constructions in the paper, we use a variation of finite automata with accepting transitions instead of states. A (final transition acceptance-based) nondeterministic finite automaton (FA) is a five-tuple \(\mathcal {A}= (Q, \varSigma , \delta , I, Acc )\) where Q is a finite set of states, \(\varSigma \) is an alphabet, \(\delta \subseteq Q \times \varSigma \times Q\) is a transition relation, \(I \subseteq Q\) is a set of initial states, and \( Acc :\delta \rightarrow \{ true , false \}\) is a transition-based acceptance condition. We often use \(q \xrightarrow {a} p\) to denote that \((q,a,p) \in \delta \). A run of \(\mathcal {A}\) over a word \(w = a_1 \ldots a_n\) is a sequence of states \(\rho = q_0 q_1 \ldots q_n \in Q^{n+1}\) such that for all \(1 \le i \le n\) it holds that \(q_{i-1} \xrightarrow {a_i} q_i\) and \(q_0 \in I\). The run \(\rho \) is accepting if \(n \ge 1\) and \( Acc (q_{n-1} \xrightarrow {a_n} q_n)\) (i.e., if the last transition in the run is accepting)Footnote 1. The language of \(\mathcal {A}\), denoted as \(\mathcal {L}(\mathcal {A})\), is defined as \(\mathcal {L}(\mathcal {A})= \{w \in \varSigma ^* \mid \text {there is an accepting run of } \mathcal {A}\text { on } w\}\). We further use \(\mathcal {L}_\mathcal {A}(q)\) to denote the language of the FA obtained from \(\mathcal {A}\) by setting its set of initial states to \(\{q\}\) (if the context is clear, we use just \(\mathcal {L}(q)\)).
\(\mathcal {A}\) is deterministic (a DFA) if \(|I| \le 1\) and for all states \(q \in Q\) and symbols \(a \in \varSigma \), it holds that if \(q \xrightarrow {a} p\) and \(q \xrightarrow {a} r\), then \(p=r\). On the other hand, \(\mathcal {A}\) is complete if \(|I| \ge 1\) and for all states \(q \in Q\) and symbols \(a \in \varSigma \), there is at least one state \(p \in Q\) such that \(q \xrightarrow {a} p\). For a deterministic and complete \(\mathcal {A}\), we abuse notation and treat \(\delta \) as a function \(\delta :Q \times \varSigma \rightarrow Q\). A DFA \(\mathcal {A}\) is minimal if \(\forall q \in Q:\mathcal {L}(q) \ne \emptyset \wedge \forall p \in Q:p \ne q \Rightarrow \mathcal {L}(q) \ne \mathcal {L}(p)\). Hopcroft’s [51] and Brzozowski’s [14] algorithms for obtaining a minimal DFA can be modified for our definition of FAs .
Linear Integer Arithmetic. Let \(\mathbb {X}= \{x_1, \ldots , x_n\}\) be a (finite) set of integer variables. We will use \(\vec {x}\) to denote the vector \((x_1, \ldots , x_n)\). Sometimes, we will treat \(\vec {x}\) as a set, e.g., \(y \in \vec {x}\) denotes \(y \in \{x_1, \ldots , x_n\}\). A linear integer arithmetic (LIA) formula
 over \(\mathbb {X}\) is obtained using the following grammar:
over \(\mathbb {X}\) is obtained using the following grammar:

where \(\vec {a}\) is a vector of n integer coefficients \((a_1, \ldots , a_n) \in \mathbb {Z}^n\), \(c \in \mathbb {Z}\) is a constant, \(m\in \mathbb {Z}^+\) is a modulus, and \(y \in \mathbb {X}\) (one can derive the other connectives \(\top \), \(\rightarrow \), \(\leftrightarrow \), \(\forall \), ...in the standard way)Footnote 2. Free variables of
 are denoted as
are denoted as
 . Given a formula
. Given a formula
 , we say that an assignment \(\nu :\mathbb {X}\rightarrow \mathbb {Z}\) is a model of
, we say that an assignment \(\nu :\mathbb {X}\rightarrow \mathbb {Z}\) is a model of
 , denoted as
, denoted as
 , if \(\nu \) satisfies
, if \(\nu \) satisfies
 in the standard way. Note that we use the same symbols \(=, \le , \mathrel {\equiv _{m}}, \lnot , \wedge , \vee , \exists , \ldots \) in the syntactical language (where they are not to be interpreted, with the exception of evaluation of constant expressions) of the logic as well as in the meta-language. In order to avoid ambiguity, we use the style
in the standard way. Note that we use the same symbols \(=, \le , \mathrel {\equiv _{m}}, \lnot , \wedge , \vee , \exists , \ldots \) in the syntactical language (where they are not to be interpreted, with the exception of evaluation of constant expressions) of the logic as well as in the meta-language. In order to avoid ambiguity, we use the style
 for a syntactic formula. W.l.o.g. we assume that variables in
for a syntactic formula. W.l.o.g. we assume that variables in
 are unique, i.e., there is no overlap between quantified variables and also between free and quantified variables.
are unique, i.e., there is no overlap between quantified variables and also between free and quantified variables.
In our decision procedure we represent integers as non-empty sequences of binary digits \(a_0 \ldots a_n \in \mathbb {B}^+\) using the two’s complement with the least-significant bit first (LSBF) encoding (i.e., the right-most bit denotes the sign). Formally, the decoding of a binary word represents the integer
For instance, \(\textsf{dec}(0101) = -6\) and \(\textsf{dec}(010) = 2\). Note that any integer has infinitely many representations in this encoding: the shortest one and others obtained by repeating the sign bit any number of times. In this paper, we work with the so-called binary assignments. A binary assignment is an assignment \(\nu :\mathbb {X}\rightarrow \mathbb {B}^+\) s.t. for each \(x_1, x_2 \in \mathbb {X}\) the lengths of the words assigned to \(x_1\) and \(x_2\) match, i.e., \(|\nu (x_1)| = |\nu (x_2)|\). We overload the decoding operator \(\langle \cdot \rangle \) to binary assignments such that \(\langle \nu \rangle :\mathbb {X}\rightarrow \mathbb {Z}\) is defined as \(\langle \nu \rangle = \{ x \mapsto \langle y\rangle \mid \nu (x) = y \}\). A binary model of a formula
 is a binary assignment \(\nu \) such that \(\langle \nu \rangle \models \varphi \). We denote the set of all binary models of a LIA formula
is a binary assignment \(\nu \) such that \(\langle \nu \rangle \models \varphi \). We denote the set of all binary models of a LIA formula
 as
as
 and we write
and we write
 to denote
to denote
 and
and
 to denote
to denote
 .
.
3 Classical Automata-Based Decision Procedure for LIA
The following classical decision procedure is due to Boudet and Comon [13] (based on the ideas of [16]) with an extension to modulo constraints by Durand-Gasselin and Habermehl [29]. Given a set of variables \(\mathbb {X}\), a symbol \(\sigma \) is a mapping \(\sigma :\mathbb {X}\rightarrow \mathbb {B}\) and \(\varSigma _{\mathbb {X}}\) denotes the set of all symbols over \(\mathbb {X}\). For a symbol \(\sigma \in \varSigma _{\mathbb {X}}\) and a variable \(x\in \mathbb {X}\) we define the projection \(\pi _x(\sigma ) = \{ \sigma '\in \varSigma _{\mathbb {X}} \mid \sigma '_{|\mathbb {X}\setminus \{x\}} = \sigma _{\left| \mathbb {X}\setminus \{x\}\right. } \}\) where \(\sigma _{|\mathbb {X}\setminus \{x\}}\) is the restriction of the function \(\sigma \) to the domain \(\mathbb {X}\setminus \{x\}\).
For a LIA formula \(\varphi \), the classical automata-based decision procedure builds an FA \(\mathcal {A}_\varphi \) encoding all binary models of \(\varphi \). We use a modification which uses automata with accepting edges instead of states. It allows to construct deterministic automata for atomic formulae, later in Sect. 4 also for complex formulae, and to eliminate an artificial final state present in the original construction that does not correspond to any arithmetic formula. The construction proceeds inductively as follows:
Base Case. First, an FA \(\mathcal {A}_{\varphi _{ atom }}\) is constructed for each atomic formula \(\varphi _{ atom }\) in \(\varphi \). The states of \(\mathcal {A}_{\varphi _{ atom }}\) are LIA formulae with
 being the (only) initial state. \(\mathcal {A}_{\varphi _{ atom }}\)’s structure is given by the transition function \( Post \), implemented via a derivative
being the (only) initial state. \(\mathcal {A}_{\varphi _{ atom }}\)’s structure is given by the transition function \( Post \), implemented via a derivative
 of \(\varphi _{ atom }\) w.r.t. symbols \(\sigma \in \varSigma _{\mathbb {X}}\) as given in Fig. 2 (an example will follow).
of \(\varphi _{ atom }\) w.r.t. symbols \(\sigma \in \varSigma _{\mathbb {X}}\) as given in Fig. 2 (an example will follow).
Intuitively, for
 , the next state after reading \(\sigma \) is given by taking the least significant bits (LSBs) of all variables (\(\vec {x}\)) after being multiplied with the respective coefficients (\(\vec {a}\)) and subtracting this value from c. If the parity of the result is odd, we can reject the input word (\(\vec {a} \cdot \vec {x}\) and c have a different LSB, so they cannot match), otherwise we can remove the LSB of the result, set it as a new c, and continue. One can imagine this process as performing a long addition of several binary numbers at once with c being the result (the subtraction from c can be seen as working with carry). The intuition for a formula
, the next state after reading \(\sigma \) is given by taking the least significant bits (LSBs) of all variables (\(\vec {x}\)) after being multiplied with the respective coefficients (\(\vec {a}\)) and subtracting this value from c. If the parity of the result is odd, we can reject the input word (\(\vec {a} \cdot \vec {x}\) and c have a different LSB, so they cannot match), otherwise we can remove the LSB of the result, set it as a new c, and continue. One can imagine this process as performing a long addition of several binary numbers at once with c being the result (the subtraction from c can be seen as working with carry). The intuition for a formula
 is similar. On the other hand, for a formula
is similar. On the other hand, for a formula
 , i.e., a congruence with an even modulus, if the parity of the left-hand side (\(\vec {a} \cdot \vec {x}\)) and the right-hand side (c) does not match (in other words, \(c - \vec {a} \cdot \vec {x}\) is odd), we can reject the input word (this is because the modulus is even, so the parities of the two sides of the congruence need to be the same). Otherwise, we remove the LSB of the modulus (i.e., divide it by two). Lastly, let us mention the second case for the rule for a formula of the form
, i.e., a congruence with an even modulus, if the parity of the left-hand side (\(\vec {a} \cdot \vec {x}\)) and the right-hand side (c) does not match (in other words, \(c - \vec {a} \cdot \vec {x}\) is odd), we can reject the input word (this is because the modulus is even, so the parities of the two sides of the congruence need to be the same). Otherwise, we remove the LSB of the modulus (i.e., divide it by two). Lastly, let us mention the second case for the rule for a formula of the form
 . Here, since \(\kappa \) is odd, we cannot divide it by two; however, adding the modulus (\(2m+1\)) to \(\kappa \) yields an even value equivalent to \(\kappa \).
. Here, since \(\kappa \) is odd, we cannot divide it by two; however, adding the modulus (\(2m+1\)) to \(\kappa \) yields an even value equivalent to \(\kappa \).
The states of \(\mathcal {A}_{\varphi _{ atom }}\) are then all reachable formulae obtained from the application of \( Post \) from the initial state. The reachability from a set of formulae S using symbols from \(\varGamma \) is given using the least fixpoint operator \(\mu \) as follows:

Lemma 1
 is finite for an atomic formula
is finite for an atomic formula
 .
.
Proof
The cases for linear equations and inequations follow from [13, Proposition 1] and [13, Proposition 3] respectively. For moduli, the lemma follows from the fact that in the definition of \( Post \), the right-hand side of a modulo is an integer from \([0,m-1]\). \(\square \)
\( Post \) is deterministic, so it suffices to define the acceptance condition for the derivatives only for each state and symbol, as given in Fig. 3. E.g., a transition from
 over \(\sigma = \big [{\begin{matrix} 1 \\ 1 \end{matrix}}\big ]\) is accepting; the intuition is similar as for \( Post \) with the difference that the last bit is the sign bit (cf. Eq. (1)), so it is treated in the opposite way to other bits (therefore, there is the “\(+\)” sign on the right-hand sides of the definitions rather than the “−” sign as in Fig. 2). If we substitute into the example, we obtain \(2 \cdot (-1) - 7 \cdot (-1) = -2 +7 = 5\). The acceptance condition \( Acc \) is then defined as
over \(\sigma = \big [{\begin{matrix} 1 \\ 1 \end{matrix}}\big ]\) is accepting; the intuition is similar as for \( Post \) with the difference that the last bit is the sign bit (cf. Eq. (1)), so it is treated in the opposite way to other bits (therefore, there is the “\(+\)” sign on the right-hand sides of the definitions rather than the “−” sign as in Fig. 2). If we substitute into the example, we obtain \(2 \cdot (-1) - 7 \cdot (-1) = -2 +7 = 5\). The acceptance condition \( Acc \) is then defined as
 and \(\mathcal {A}_{\varphi _{ atom }}\) is defined as the FA
and \(\mathcal {A}_{\varphi _{ atom }}\) is defined as the FA

Note that if an FA accepts a word w, it also accepts all words obtained by appending any number of copies of the most significant bit (the sign) to w.
Example 1
Figure 4 gives examples of FAs for
 and
and
 . For the case of the FA for
. For the case of the FA for
 , consider for instance the state
, consider for instance the state
 (denoted by the state “\(-1\)” in Fig. 4a). We show computation of the \( Post \) of this state over the symbol \(\sigma = \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ]\). From the definition in Fig. 2, we have
(denoted by the state “\(-1\)” in Fig. 4a). We show computation of the \( Post \) of this state over the symbol \(\sigma = \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ]\). From the definition in Fig. 2, we have
 where \(k = \lfloor \frac{1}{2} (-1 - (1,2) \cdot \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] ) \rfloor = \lfloor \frac{1}{2} (-2) \rfloor = -1\). Moreover, since
where \(k = \lfloor \frac{1}{2} (-1 - (1,2) \cdot \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] ) \rfloor = \lfloor \frac{1}{2} (-2) \rfloor = -1\). Moreover, since
 , this transition is marked as accepting (cf. Fig. 3).
, this transition is marked as accepting (cf. Fig. 3).
For the case of the second FA, consider for instance the state
 (denoted by the state “\(0_{\mathrel {\equiv _{3}}}\)” in Fig. 4b). Similarly to the previous example, we show computation of \( Post \) of this state over the symbol \(\sigma = \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ]\). From the definition in Fig. 2, we have
(denoted by the state “\(0_{\mathrel {\equiv _{3}}}\)” in Fig. 4b). Similarly to the previous example, we show computation of \( Post \) of this state over the symbol \(\sigma = \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ]\). From the definition in Fig. 2, we have
 where \(\ell = \left[ \frac{1}{2} ( 0- (1,2) \cdot \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] + 3)\right] _{3} = 1\).
where \(\ell = \left[ \frac{1}{2} ( 0- (1,2) \cdot \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] + 3)\right] _{3} = 1\).
 , so this transition is not accepting. \(\square \)
, so this transition is not accepting. \(\square \)
Inductive Case. The inductive cases for Boolean connectives are defined in the standard way: conjunction of two formulae is implemented by taking the intersection of the two corresponding FAs, disjunction by taking their union, and negation is implemented by taking the complement (which may involve determinization via the subset construction). Formally, let \(\mathcal {A}_{\varphi _i} = (Q_{\varphi _i},\varSigma _{\mathbb {X}}, \delta _{\varphi _i}, I_{\varphi _i}, Acc _{\varphi _i})\) for \(i \in \{1,2\}\) with \(Q_{\varphi _1} \cap Q_{\varphi _2} = \emptyset \) be complete FAs. Then,
-
\(\mathcal {A}_{\varphi _1 \wedge \varphi _2} = (Q_{\varphi _1} \times Q_{\varphi _2},\varSigma _{\mathbb {X}}, \delta _{\varphi _1 \wedge \varphi _2}, I_{\varphi _1} \times I_{\varphi _2}, Acc _{\varphi _1 \wedge \varphi _2})\) where
-
\(\delta _{\varphi _1 \wedge \varphi _2} = \{(q_1, q_2) \xrightarrow {\sigma }(p_1, p_2) \mid q_1 \xrightarrow {\sigma }p_1 \in \delta _{\varphi _1}, q_2 \xrightarrow {\sigma }p_2 \in \delta _{\varphi _2}\}\) and
-
\( Acc _{\varphi _1 \wedge \varphi _2}((q_1, q_2) \xrightarrow {\sigma }(p_1, p_2)) \mathrel {{\mathop {\Leftrightarrow }\limits ^{\text {def}}}} Acc _{\varphi _1}(q_1 \xrightarrow {\sigma }p_1) \wedge Acc _{\varphi _2}(q_2 \xrightarrow {\sigma }p_2)\).
-
-
\(\mathcal {A}_{\varphi _1 \vee \varphi _2} = (Q_{\varphi _1} \times Q_{\varphi _2},\varSigma _{\mathbb {X}}, \delta _{\varphi _1 \vee \varphi _2}, I_{\varphi _1} \times I_{\varphi _2}, Acc _{\varphi _1 \vee \varphi _2})\) where
-
\(\delta _{\varphi _1 \vee \varphi _2} = \{(q_1, q_2) \xrightarrow {\sigma }(p_1, p_2) \mid q_1 \xrightarrow {\sigma }p_1 \in \delta _{\varphi _1}, q_2 \xrightarrow {\sigma }p_2 \in \delta _{\varphi _2}\}\) and
-
\( Acc _{\varphi _1 \vee \varphi _2}((q_1, q_2) \xrightarrow {\sigma }(p_1, p_2)) \mathrel {{\mathop {\Leftrightarrow }\limits ^{\text {def}}}} Acc _{\varphi _1}(q_1 \xrightarrow {\sigma }p_1) \vee Acc _{\varphi _2}(q_2 \xrightarrow {\sigma }p_2)\).
-
-
\(\mathcal {A}_{\lnot \varphi _1} = (2^{Q_{\varphi _1}}, \varSigma _{\mathbb {X}}, \delta _{\lnot \varphi _1},\{I_{\varphi _1}\}, Acc _{\lnot \varphi _1})\) where
-
\(\delta _{\lnot \varphi _1} = \{S \xrightarrow {\sigma }T \mid T = \{p \in Q_{\varphi _1} \mid \exists q \in S:q \xrightarrow {\sigma }p \in \delta _{\varphi _1}\}\) and
-
\( Acc _{\lnot \varphi _1}(S \xrightarrow {\sigma }T) \mathrel {{\mathop {\Leftrightarrow }\limits ^{\text {def}}}}\forall q \in S\,\forall p \in T:\lnot Acc _{\varphi _1}(q \xrightarrow {\sigma }p)\).
-
Existential quantification is more complicated. Given a formula
 and the FA \(\mathcal {A}_{\varphi } = (Q_{\varphi }, \varSigma _{\mathbb {X}}, \delta _\varphi , I_{\varphi }, Acc _\varphi )\), a word w should be accepted by \(\mathcal {A}_{\exists x(\varphi )}\) iff there is a word \(w'\) accepted by \(\mathcal {A}_{\varphi }\) s.t. w and \(w'\) are the same on all tracks except the track for x. One can perform projection of x out of \(\mathcal {A}_{\varphi }\), i.e., remove the x track from all its transitions. This is, however, insufficient. For instance, consider the model \(\{x \mapsto 7, y \mapsto -4\}\), encoded into the (shortest) word \(\big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] \big [{\begin{matrix} 1 \\ 1 \end{matrix}}\big ] \big [{\begin{matrix} 0 \\ 1 \end{matrix}}\big ]\) (we use the notation \(\big [{\begin{matrix} x \\ y \end{matrix}}\big ]\)). When we remove the x-track from the word, we obtain \({\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 1\right] \end{matrix}}\!\! {\begin{matrix}\left[ 1\right] \end{matrix}}\), which encodes the assignment \(\{y \mapsto -4\}\). It is, however, not the shortest encoding of the assignment; the shortest encoding is \({\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 1\right] \end{matrix}}\). Therefore, we further need to modify the FA obtained after projection to also accept words that would be accepted if their sign bit were arbitrarily extended, which we do by reachability analysis on the FA. Formally, \(\mathcal {A}_{\exists x(\varphi )} = (Q_{\varphi }, \varSigma _{\mathbb {X}}, \delta _{\exists x(\varphi )}, I_{\varphi }, Acc _{\exists x(\varphi )})\) where
and the FA \(\mathcal {A}_{\varphi } = (Q_{\varphi }, \varSigma _{\mathbb {X}}, \delta _\varphi , I_{\varphi }, Acc _\varphi )\), a word w should be accepted by \(\mathcal {A}_{\exists x(\varphi )}\) iff there is a word \(w'\) accepted by \(\mathcal {A}_{\varphi }\) s.t. w and \(w'\) are the same on all tracks except the track for x. One can perform projection of x out of \(\mathcal {A}_{\varphi }\), i.e., remove the x track from all its transitions. This is, however, insufficient. For instance, consider the model \(\{x \mapsto 7, y \mapsto -4\}\), encoded into the (shortest) word \(\big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] \big [{\begin{matrix} 1 \\ 0 \end{matrix}}\big ] \big [{\begin{matrix} 1 \\ 1 \end{matrix}}\big ] \big [{\begin{matrix} 0 \\ 1 \end{matrix}}\big ]\) (we use the notation \(\big [{\begin{matrix} x \\ y \end{matrix}}\big ]\)). When we remove the x-track from the word, we obtain \({\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 1\right] \end{matrix}}\!\! {\begin{matrix}\left[ 1\right] \end{matrix}}\), which encodes the assignment \(\{y \mapsto -4\}\). It is, however, not the shortest encoding of the assignment; the shortest encoding is \({\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 0\right] \end{matrix}}\!\! {\begin{matrix}\left[ 1\right] \end{matrix}}\). Therefore, we further need to modify the FA obtained after projection to also accept words that would be accepted if their sign bit were arbitrarily extended, which we do by reachability analysis on the FA. Formally, \(\mathcal {A}_{\exists x(\varphi )} = (Q_{\varphi }, \varSigma _{\mathbb {X}}, \delta _{\exists x(\varphi )}, I_{\varphi }, Acc _{\exists x(\varphi )})\) where
-
\(\delta _{\exists x(\varphi )} = \{q \xrightarrow {\sigma '} p \mid \exists q \xrightarrow {\sigma }p \in \delta _{\varphi }:\sigma ' \in \pi _x(\sigma )\}\) and
-
\( Acc _{\exists x(\varphi )}(q \xrightarrow {\sigma }p) \mathrel {{\mathop {\Leftrightarrow }\limits ^{\text {def}}}}\displaystyle \bigvee _{\sigma '\in \pi _x(\sigma )} Acc _\varphi (q \xrightarrow {\sigma '} p) \vee \exists r,s \in Reach (\{p\}, \pi _x(\sigma )) :\displaystyle \bigvee _{\sigma '\in \pi _x(\sigma )} Acc _\varphi (r \xrightarrow {\sigma '} s).\)
After defining the base and inductive cases for constructing the FA \(\mathcal {A}_{\varphi }\), we can establish the connection between its language and the models of \(\varphi \). For a word \(w = a_1\dots a_n \in \varSigma _{\mathbb {X}}\) and a variable \(x \in \mathbb {X}\), we define \(w_x = a_1(x)\dots a_n(x)\), i.e., \(w_x\) extracts the binary number assigned to variable x in w. For a binary assignment \(\nu \) of a LIA formula \(\varphi \), we define its language as \(\mathcal {L}(\nu ) = \{ w \in \varSigma _{\mathbb {X}}^* \mid \forall x \in \mathbb {X}:w_x = \nu (x) \}\). We lift the language to sets of binary assignments as usual.
Theorem 1
Let \(\varphi \) be a LIA formula. Then
 .
.
Proof
Follows from [13, Lemma 5].
4 Derivative-Based Construction for Nested Formulae
This section lays down the basics of our approach to interconnecting automata with the algebraic approach for quantified LIA. We aim at using methods and ideas from the algebraic approach to circumvent the large intermediate automata constructed along the way before obtaining the small DFAs (cf. Fig. 1). To do that, we need a variation of the automata-based decision procedure that exposes the states of the target automata without the need of generating the complete state space of the intermediate automata first. To achieve this, we generalize the post-image function \( Post \) (and the acceptance condition \( Fin \)) from Sect. 3 to general non-atomic formulae using an approach similar to that of [32, 45, 76], which introduced derivatives of WS1S/WSkS formulae. Computing formula derivatives produces automata states that are at the same time LIA formulae, and can be manipulated as such using algebraic methods and reasoning about their integer semantics. We will then use basic Boolean simplification, antiprenexing, and also ideas from Cooper’s quantifier elimination algorithm and Omega test [23, 65] to prune and simplify the state-formulae. The techniques will be discussed in Sects. 5 to 7.
Example 2
In Fig. 6, we show an intuitive example of rewriting state formulae when constructing the FA for
 (which is written in the basic syntax as
(which is written in the basic syntax as
 ). After reading the first symbol \({\begin{matrix}\left[ 0\right] \end{matrix}}\), the obtained formula is a conjunction of the three following \( Post \)s:
). After reading the first symbol \({\begin{matrix}\left[ 0\right] \end{matrix}}\), the obtained formula is a conjunction of the three following \( Post \)s:
-
 ,
, -
 , and
, and -
 .
.
We can write the resulting formula as
 , which is satisfied only by \(x=256\). We can therefore rewrite the formula into an equivalent formula
, which is satisfied only by \(x=256\). We can therefore rewrite the formula into an equivalent formula
 . Similar rewriting can be applied to the state obtained after reading \({\begin{matrix}\left[ 1\right] \end{matrix}}\!\!{\begin{matrix}\left[ 0\right] \end{matrix}}\) and \({\begin{matrix}\left[ 1\right] \end{matrix}}\!\!{{\begin{matrix}\left[ 1\right] \end{matrix}}}\). The rest of the automaton constructed from the rewritten states
. Similar rewriting can be applied to the state obtained after reading \({\begin{matrix}\left[ 1\right] \end{matrix}}\!\!{\begin{matrix}\left[ 0\right] \end{matrix}}\) and \({\begin{matrix}\left[ 1\right] \end{matrix}}\!\!{{\begin{matrix}\left[ 1\right] \end{matrix}}}\). The rest of the automaton constructed from the rewritten states
 ,
,
 , and
, and
 is then of a logarithmic size (each state in the rest will have only one successor based on the binary encoding of 256, 192, or 63 respectively, while if we did not perform the rewriting, the states would have two successors and the size would be linear). \(\square \)
is then of a logarithmic size (each state in the rest will have only one successor based on the binary encoding of 256, 192, or 63 respectively, while if we did not perform the rewriting, the states would have two successors and the size would be linear). \(\square \)
In Fig. 5, we extend the derivative post-image function \( Post \) and the acceptance condition \( Fin \) (cf. Figs. 2 and 3) to non-atomic formulae. The derivatives mimic the automata constructions in Sect. 3, with the exception that at every step, the derivative (and therefore also the state in the constructed FA) is a LIA formula and can be treated as such. One notable exception is
 , which, since the \( Post \) function is deterministic, in addition to the projection, also mimics determinisation. One can see the obtained disjunction-structure as a set of states from the standard subset construction in automata. Correctness of the construction is stated in the following.
, which, since the \( Post \) function is deterministic, in addition to the projection, also mimics determinisation. One can see the obtained disjunction-structure as a set of states from the standard subset construction in automata. Correctness of the construction is stated in the following.
Lemma 2
Let
 be a LIA formula and let \(\mathcal {A}_{\varphi }\) be the FA constructed by the procedure in this section or any combination of it and the classical one. Then
be a LIA formula and let \(\mathcal {A}_{\varphi }\) be the FA constructed by the procedure in this section or any combination of it and the classical one. Then
 .
.
Proof
Follows from preservation of languages of the states/formulae. \(\square \)
Without optimizations, the derivative-based construction would generate a larger FA than the one obtained from the classical construction, which can perform minimization of the intermediate automata. The derivative-based construction cannot minimize the intermediate automata since they are not available; they are in a sense constructed on the fly within the construction of the automaton for the entire formula. Our algebraic optimizations mimic some effect of the minimization on the fly, while constructing the automaton, by simplifying the state formulae and detecting entailment between them.
In principle, when we construct a state q of \(\mathcal {A}_{\psi }\) as a result of \( Post \), we could test whether some state p was already constructed such that
 and, if so, we could merge p and q (drop q and redirect the edges to p). This would guarantee us to directly obtain the minimal DFA for
and, if so, we could merge p and q (drop q and redirect the edges to p). This would guarantee us to directly obtain the minimal DFA for
 (no two states would be language-equivalent).
(no two states would be language-equivalent).
Solving the LIA equivalence queries precisely is, however, as hard as solving the original problem. Even when we restrict ourselves to quantifier-free formulae, the equivalence problem is \({\textbf {co-NP}}\)-complete. Our algebraic optimizations are thus a cheaper and more practical alternative capable of merging at least some equivalent states. We discuss the optimizations in detail in Sects. 5 to 7 and also give a comprehensive example of their effect in Sect. 8.
5 Simple Rewriting Rules
The simplest rewriting rules are just common simplifications generally applicable in predicate logic. Despite their simplicity, they are quite powerful, since their use enables to apply the other optimizations (Sects. 6 and 7) more often.
-
1.
We apply the propositional laws of identity (
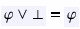 and
and
 ) and annihilation (
) and annihilation (
 and
and
 ) to simplify the formulae.
) to simplify the formulae. -
2.
We use antiprenexing [30, 44] (i.e., pushing quantifiers as deep as possible using inverses of prenexing rules [69, Chapter 5]). This is helpful, e.g., after a range-based quantifier instantiation (cf. Sect. 7.2), which yields a disjunction. Since our formula analysis framework (Sect. 7) only works over conjunctions below existential quantifiers, we need to first push existential quantifiers inside the disjunctions to allow further applications of the heuristics.
-
3.
Since negation is implemented as automaton complementation, we apply De Morgan’s laws (
 and
and
 ) to push negation as deep as possible. The motivation is that small subformulae are likely to have small corresponding automata. As complementation requires the underlying automaton to be deterministic, complementing smaller automata helps to mitigate the exponential blow-up of determinization.
) to push negation as deep as possible. The motivation is that small subformulae are likely to have small corresponding automata. As complementation requires the underlying automaton to be deterministic, complementing smaller automata helps to mitigate the exponential blow-up of determinization.
Moreover, we also employ the following simplifications valid for LIA:
-
4.
We apply simple reasoning based on variable bounds to simplify the formula, e.g.,
 , and to prune away some parts of the formula, e.g.,
, and to prune away some parts of the formula, e.g.,
 .
. -
5.
We employ rewriting rules aimed at accelerating the automata construction by minimizing the number of variables used in a formula, and, thus, avoiding constructing complicated transition relations, e.g.,
 where
where
 , or
, or
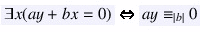 .
. -
6.
We detect conflicts by identifying small isomorphic subformulae, i.e., subformulae that have the same abstract syntax tree, except for renaming of quantified variables, for example,
 . One can see this as a variant of DAGification used in Mona [57].
. One can see this as a variant of DAGification used in Mona [57].
6 Disjunction Pruning
We prune disjunctions by removing disjunct implied by other disjuncts. That is, if it holds that
 , then
, then
 can be replaced by just
can be replaced by just
 . Testing the entailment precisely is hard, so we use a stronger but cheaper relation of subsumpion. Our subsumption is a preorder (a reflexive and transitive relation) \(\preceq _{\textsf{s}}\) between LIA formulae in Fig. 7Footnote 3. When we encounter the said macrostate and establish
. Testing the entailment precisely is hard, so we use a stronger but cheaper relation of subsumpion. Our subsumption is a preorder (a reflexive and transitive relation) \(\preceq _{\textsf{s}}\) between LIA formulae in Fig. 7Footnote 3. When we encounter the said macrostate and establish
 , we perform the rewriting. This optimization has effect mainly in formulae of the form
, we perform the rewriting. This optimization has effect mainly in formulae of the form
 : their \( Post \) contains a disjunction of formulae of a similar structure.
: their \( Post \) contains a disjunction of formulae of a similar structure.
Lemma 3
For LIA formulae
 and
and
 , if
, if
 , then
, then
 .
.
Example 3
In Fig. 8, we show an example of pruning disjunctions in the FA for the formula
 . \(\square \)
. \(\square \)
7 Quantifier Instantiation
The next optimization is an instance of quantifier instantiation, a well known class of algebraic techniques. We gather information about the formulae with a focus on the way a particular variable, usually a quantified one, affects the models of the whole formula. If one can find “the best” value for such a variable (e.g., a value such that using it preserves all models of the formula), then the (quantified) variable can be substituted with a concrete value. For instance, let
 . The variable y is quantified so we can think about instantiating it (it will not occur in a model). The first atom
. The variable y is quantified so we can think about instantiating it (it will not occur in a model). The first atom
 says that we want to pick y as large as possible (larger y’s have higher chance to satisfy the inequation), but, on the other hand, the second atom
says that we want to pick y as large as possible (larger y’s have higher chance to satisfy the inequation), but, on the other hand, the second atom
 says that y can be at most 12. The last atom
says that y can be at most 12. The last atom
 adds an additional constraint on y. Intuitively, we can see that the best value of y—i.e., the value that preserves all models of
adds an additional constraint on y. Intuitively, we can see that the best value of y—i.e., the value that preserves all models of
 —would be 9, allowing to rewrite
—would be 9, allowing to rewrite
 to
to
 .
.
To define the particular ways of gathering such kind of information in a uniform way, we introduce the following formula analysis framework that uses the function \(\textsf{FA}\) to extract information from formulae. Consider a meet-semilattice \((\mathbb {D}, \sqcap )\) where \( undef \in \mathbb {D}\) is the bottom element. Let \(\textsf{atom}\) be a function that, given an atomic formula
 and a variable \(y\in \mathbb {X}\), outputs an element of \(\mathbb {D}\) that represents the behavior of y in
and a variable \(y\in \mathbb {X}\), outputs an element of \(\mathbb {D}\) that represents the behavior of y in
 (e.g., bounds on y). The function \(\textsf{FA}\) then aggregates the information from atoms into an information about the behavior of y in the whole formula using the meet operator \(\sqcap \) recursively as follows:
(e.g., bounds on y). The function \(\textsf{FA}\) then aggregates the information from atoms into an information about the behavior of y in the whole formula using the meet operator \(\sqcap \) recursively as follows:


(By default, a missing case in the pattern matching evaluates to \( undef \).) We note that the framework is defined only for conjunctions of formulae, which is the structure of subformulae that was usually causing troubles in our experiments (cf. Sect. 9).
The optimizations defined later are based on substituting certain variables in a formula with concrete values to obtain an equivalent (simpler) formula. For this, we extend standard substitution as follows. Let
 be a formula with free variables \(\vec {x} = (x_1, \ldots , x_n)\) and \(y \notin \vec {x}\). For \(k \in \mathbb {Z}\), substituting k for y in
be a formula with free variables \(\vec {x} = (x_1, \ldots , x_n)\) and \(y \notin \vec {x}\). For \(k \in \mathbb {Z}\), substituting k for y in
 yields the formula
yields the formula
 obtained in the usual way (with all constant expressions being evaluated). For \(k = \pm \infty \), the resulting formula is obtained for inequalities containing y as
obtained in the usual way (with all constant expressions being evaluated). For \(k = \pm \infty \), the resulting formula is obtained for inequalities containing y as

and is undefined for all other atomic formulae.
7.1 Quantifier Instantiation Based on Formula Monotonicity
The first optimization based on quantifier instantiation uses the so-called monotonicity of formulae w.r.t. some variables (a similar technique is used in the Omega test [65]). Consider the following two formulae:

where
 does not contain occurrences of y, and x, z are free variables in
does not contain occurrences of y, and x, z are free variables in
 . For
. For
 , since y is existentially quantified, the inequation
, since y is existentially quantified, the inequation
 can be always satisfied by picking an arbitrarily large value for y, so
can be always satisfied by picking an arbitrarily large value for y, so
 can be simplified to just
can be simplified to just
 . On the other hand, for
. On the other hand, for
 , we cannot pick an arbitrarily large y because of the other inequation
, we cannot pick an arbitrarily large y because of the other inequation
 . We can, however, observe, that \(\lfloor \frac{42}{5}\rfloor = 8\) is the largest value that we can substitute for y to satisfy
. We can, however, observe, that \(\lfloor \frac{42}{5}\rfloor = 8\) is the largest value that we can substitute for y to satisfy
 . As a consequence, since the possible value of y in
. As a consequence, since the possible value of y in
 is not bounded from above, we can substitute y by the value 8, i.e.,
is not bounded from above, we can substitute y by the value 8, i.e.,
 can be simplified to
can be simplified to
 .
.
Formally, let \(c \in \mathbb {Z}\cup \{{+\infty }\}\) and \(y \in \mathbb {X}\). We say that a formula
 is c-best from below w.r.t. y if (i)
is c-best from below w.r.t. y if (i)
 for all \(y_1 \le y_2 \le c\) (for \(c \in \mathbb {Z}\)) or for all \(y_1 \le y_2\) (for \(c = {+\infty }\)) and (ii)
for all \(y_1 \le y_2 \le c\) (for \(c \in \mathbb {Z}\)) or for all \(y_1 \le y_2\) (for \(c = {+\infty }\)) and (ii)
 for all \(y' > c\). Intuitively, substituting bigger values for y (up to c) in
for all \(y' > c\). Intuitively, substituting bigger values for y (up to c) in
 preserves all models obtained by substituting smaller values, so c can be seen as the most conservative limit of y (and for \(c= {+\infty }\), this means that y does not have an upper bound, so it can be chosen arbitrarily large for concrete values of other variables). Similarly,
preserves all models obtained by substituting smaller values, so c can be seen as the most conservative limit of y (and for \(c= {+\infty }\), this means that y does not have an upper bound, so it can be chosen arbitrarily large for concrete values of other variables). Similarly,
 is called c-best from above (w.r.t. y) for \(c \in \mathbb {Z}\cup \{{-\infty }\}\) if (i)
is called c-best from above (w.r.t. y) for \(c \in \mathbb {Z}\cup \{{-\infty }\}\) if (i)
 for all \(y_1 \ge y_2 \ge c\) (for \(c \in \mathbb {Z}\)) or for all \(y_1 \ge y_2\) (for \(c = {-\infty }\)) and (ii)
for all \(y_1 \ge y_2 \ge c\) (for \(c \in \mathbb {Z}\)) or for all \(y_1 \ge y_2\) (for \(c = {-\infty }\)) and (ii)
 for all \(y' < c\). If a formula is c-best from below or above, we call it c-monotone (w.r.t. y).
for all \(y' < c\). If a formula is c-best from below or above, we call it c-monotone (w.r.t. y).
Lemma 4
Let \(c \in \mathbb {Z}\cup \{\pm \infty \}\) and
 be a formula c-monotone w.r.t. y such that
be a formula c-monotone w.r.t. y such that
 is defined. Then the formula
is defined. Then the formula
 is equivalent to the formula
is equivalent to the formula
 .
.
Moreover, the following lemma utilizes formula monotonicity to provide a tool for simplification of formulae containing a modulo atom.
Lemma 5
Let \(c\in \mathbb {Z}\) and
 be a formula c-monotone w.r.t. y for \(c\in \mathbb {Z}\). Then, the formula
be a formula c-monotone w.r.t. y for \(c\in \mathbb {Z}\). Then, the formula
 is equivalent to the formula
is equivalent to the formula
 where (i) \(c' = \max \{ \ell \in \mathbb {Z}\mid \ell \mathrel {\equiv _{m}} k, \ell \le c \}\) if
where (i) \(c' = \max \{ \ell \in \mathbb {Z}\mid \ell \mathrel {\equiv _{m}} k, \ell \le c \}\) if
 is c-best from below, and (ii) \(c' = \min \{ \ell \in \mathbb {Z}\mid \ell \mathrel {\equiv _{m}} k, \ell \ge c \}\) if
is c-best from below, and (ii) \(c' = \min \{ \ell \in \mathbb {Z}\mid \ell \mathrel {\equiv _{m}} k, \ell \ge c \}\) if
 is c-best from above.
is c-best from above.
In general, it is, however, expensive to decide whether a formula is c-monotone and find the tight c. Therefore, we propose a cheap approximation working on the structure of LIA formulae, which uses the formula analysis function \(\textsf{FA}\) introduced above. First, we propose the partial function
 (whose result is in \(\mathbb {Z}\cup \{+\infty \}\)) estimating the c for atomic formulae c-best from above w.r.t. y:
(whose result is in \(\mathbb {Z}\cup \{+\infty \}\)) estimating the c for atomic formulae c-best from above w.r.t. y:


Intuitively, if y is in an inequation
 without any other variable and \(a > 0\), then y’s value is bounded from above by \(\left\lfloor \frac{c}{a}\right\rfloor \). On the other hand, if \(y=x_i\) is in an inequation
without any other variable and \(a > 0\), then y’s value is bounded from above by \(\left\lfloor \frac{c}{a}\right\rfloor \). On the other hand, if \(y=x_i\) is in an inequation
 where \(\vec {a}\) has at least two nonzero coefficients and y’s coefficient is negative, or y does not appear in the inequation at all, then y’s value is not bounded (larger values of y make it easier to satisfy the inequation). The value for other cases is undefined.
where \(\vec {a}\) has at least two nonzero coefficients and y’s coefficient is negative, or y does not appear in the inequation at all, then y’s value is not bounded (larger values of y make it easier to satisfy the inequation). The value for other cases is undefined.
Similarly,
 (with the result in \(\mathbb {Z}\cup \{-\infty \}\)) estimates the c for atomic formulae c-best from above:
(with the result in \(\mathbb {Z}\cup \{-\infty \}\)) estimates the c for atomic formulae c-best from above:


Based on \(\textsf{blw}_{ atom }\) and \(\textsf{abv}_{ atom }\) and using the \(\textsf{FA}\) framework, we define the functions \(\textsf{blw}\) and \(\textsf{abv}\) estimating the c for general formulae c-best from below and above as

For a formula
 , the simplification algorithm then determines whether \(\varphi \) is c-monotone for some c, which is done using the \(\textsf{abv}\) and \(\textsf{blw}\) functions. In particular, if
, the simplification algorithm then determines whether \(\varphi \) is c-monotone for some c, which is done using the \(\textsf{abv}\) and \(\textsf{blw}\) functions. In particular, if
 for some \(c\in \mathbb {Z}\cup \{\pm \infty \}\), we have that
for some \(c\in \mathbb {Z}\cup \{\pm \infty \}\), we have that
 is c-best from below w.r.t. y (analogously for \(\textsf{abv}\)). Then, in the positive case and if \(c\in \mathbb {Z}\), we apply Lemma 5 to simplify the formula
is c-best from below w.r.t. y (analogously for \(\textsf{abv}\)). Then, in the positive case and if \(c\in \mathbb {Z}\), we apply Lemma 5 to simplify the formula
 . If
. If
 is of the simple form
is of the simple form
 where
where
 is c-monotone w.r.t. y, we can directly use Lemma 4 to simplify
is c-monotone w.r.t. y, we can directly use Lemma 4 to simplify
 to
to
 .
.
Example 4
Consider the formula
 . In order to simplify \(\psi \), we first need to check if the formula
. In order to simplify \(\psi \), we first need to check if the formula
 is c-monotone. Using \(\textsf{blw}\), we can deduce that
is c-monotone. Using \(\textsf{blw}\), we can deduce that
 ,
,
 , and hence
, and hence
 meaning that \(\varphi \) is (\(-1\))-best from below w.r.t. y (
meaning that \(\varphi \) is (\(-1\))-best from below w.r.t. y (
 is undefined). Lemma 5 yields that
is undefined). Lemma 5 yields that
 is equivalent to
is equivalent to
 (using \(c' = -5\)). \(\square \)
(using \(c' = -5\)). \(\square \)
7.2 Range-Based Quantifier Instantiation
Similarly as in Cooper’s elimination algoroithm [23], we can compute the range of possible values for a given variable y and instantiating y with all values in the range. For instance,
 can be simplified into
can be simplified into
 .
.
To obtain the range of possible values of y in the formula
 , we use the formula analysis framework with the following function \(\textsf{range}_{ atom }\) (whose result is an interval of integers) defined for atomic formulae as follows:
, we use the formula analysis framework with the following function \(\textsf{range}_{ atom }\) (whose result is an interval of integers) defined for atomic formulae as follows:



We then employ our formula analysis framework to get the range of y in
 using the function
using the function
 .
.
Lemma 6
Let
 be a formula such that
be a formula such that
 with \(a,b \in \mathbb {Z}\). Then
with \(a,b \in \mathbb {Z}\). Then
 is equivalent to the formula
is equivalent to the formula
 .
.
Proof
It suffices to notice that for all \(c \notin [a,b]\) we have
 . \(\square \)
. \(\square \)
In our decision procedure, given a formula
 , if
, if
 for \(a,b\in \mathbb {Z}\) and \(b-a \le N\) for a parameter N (set by the user), we simplify
for \(a,b\in \mathbb {Z}\) and \(b-a \le N\) for a parameter N (set by the user), we simplify
 to
to
 . In our experiments, we set \(N=0\).
. In our experiments, we set \(N=0\).
7.3 Modulo Linearization
The next optimization is more complex and helps mainly in practical cases in the benchmarks containing congruences with large moduli. It does not substitute the value of a variable by a constant, but, instead, substitutes a congruence with an equation.
Let
 such that
such that
 is 17-best from below w.r.t. y and
is 17-best from below w.r.t. y and
 . Since the modulo constraint
. Since the modulo constraint
 contains two variables (y and m), we cannot use the optimization from Sect. 7.1. From the modulo constraint and the fact that
contains two variables (y and m), we cannot use the optimization from Sect. 7.1. From the modulo constraint and the fact that
 is 17-best from below w.r.t. y, we can infer that it is sufficient to consider y only in the interval \([-19,17]\) (we obtained \(-19\) as \(17-37+1\)). The reason is that any other y can be mapped to a \(y'\) from the same congruence class (modulo 37) that is in the interval and, therefore, gives the same result in the modulo constraint. This, together with the other fact (i.e.,
is 17-best from below w.r.t. y, we can infer that it is sufficient to consider y only in the interval \([-19,17]\) (we obtained \(-19\) as \(17-37+1\)). The reason is that any other y can be mapped to a \(y'\) from the same congruence class (modulo 37) that is in the interval and, therefore, gives the same result in the modulo constraint. This, together with the other fact (i.e.,
 ) tells us that it is sufficient to only consider the (possibly multiple) linear relations between y and m in the rectangle \([-19,17] \times [1,50]\) (cf. Fig. 9). The modulo constraint can, therefore, be substituted by the linear relations to obtain the formula
) tells us that it is sufficient to only consider the (possibly multiple) linear relations between y and m in the rectangle \([-19,17] \times [1,50]\) (cf. Fig. 9). The modulo constraint can, therefore, be substituted by the linear relations to obtain the formula

Although the formula seems more complex than the original one, it avoids the large FA to be generated for the modulo constraint (a modulo constraint with \(\mathrel {\equiv _{k}}\) needs an FA with k states) and, instead, generates the usually much smaller FAs for the (in)equalities.
The general rewriting rule can be given by the following lemma:
Lemma 7
Let
 be a formula s.t.
be a formula s.t.
 for \(r,s \in \mathbb {Z}\), let
for \(r,s \in \mathbb {Z}\), let
 , with \(a_y \ne 0 \ne a_m\), and \(\alpha = \frac{M}{\gcd (a_y, M)}\). If
, with \(a_y \ne 0 \ne a_m\), and \(\alpha = \frac{M}{\gcd (a_y, M)}\). If
 is c-best from below w.r.t. y, then
is c-best from below w.r.t. y, then
 is equivalent to the formula
is equivalent to the formula

where
and
Due to space constraints, we omit a similar lemma for the case when
 is c-best from above. In our implementation, we use the linearization if the N from Lemma 7 is 1, which is sufficient with many practical cases with large moduli.
is c-best from above. In our implementation, we use the linearization if the N from Lemma 7 is 1, which is sufficient with many practical cases with large moduli.
8 A Comprehensive Example of Our Optimizations
Consider the formula

and see Fig. 10 for a part of the generated FA (for simplicity, we only consider a fragment of the constructed automaton to demonstrate our technique).
Let us focus on the configuration after reading the word \(x:\!{\begin{matrix}\left[ 0\right] \end{matrix}}\!\!{\begin{matrix}\left[ 0\right] \end{matrix}}\):
 . First, we examine the relation between
. First, we examine the relation between
 and
and
 . We notice that the two formulae look similar with the only difference being in two pairs of atoms:
. We notice that the two formulae look similar with the only difference being in two pairs of atoms:
 and
and
 , and
, and
 and
and
 respectively. Since \(0 \le 1\) there are structural subsumptions
respectively. Since \(0 \le 1\) there are structural subsumptions
 and
and
 , which yields
, which yields
 , and we can therefore use disjunction pruning (Sect. 6) to simplify
, and we can therefore use disjunction pruning (Sect. 6) to simplify
 to
to
 .
.
Next, we analyze
 . First, we compute
. First, we compute
 (cf. Sect. 7.2) and, based on that, perform the substitution
(cf. Sect. 7.2) and, based on that, perform the substitution
 , obtaining (after simplifications) the formula
, obtaining (after simplifications) the formula
 . Then, we analyze the behaviour of y in
. Then, we analyze the behaviour of y in
 by computing
by computing
 . Based on this, we know that
. Based on this, we know that
 is \((-1)\)-best from below (cf. Sect. 7.1), so we can use Lemma 5 to instantiate y in
is \((-1)\)-best from below (cf. Sect. 7.1), so we can use Lemma 5 to instantiate y in
 with \(-5\) (the largest number less than \(-1\) satisfying the modulo constraint), obtaining the (quantifier-free) formula
with \(-5\) (the largest number less than \(-1\) satisfying the modulo constraint), obtaining the (quantifier-free) formula
 .
.
Finally, we focus on
 again. First, we compute
again. First, we compute
 and rewrite
and rewrite
 to
to
 . After antiprenexing, this will be changed to
. After antiprenexing, this will be changed to
 . Using similar reasoning as in the previous paragraph, we can analyze the two disjuncts in the formula to obtain the formula
. Using similar reasoning as in the previous paragraph, we can analyze the two disjuncts in the formula to obtain the formula
 . With disjunction pruning, we obtain the final result of simplification of
. With disjunction pruning, we obtain the final result of simplification of
 as the formula
as the formula
 . In the end, again using disjunction pruning (Sect. 6), the whole formula
. In the end, again using disjunction pruning (Sect. 6), the whole formula
 can be simplified to
can be simplified to
 .
.
9 Experimental Evaluation
We implemented the proposed procedure in a prototype tool called Amaya [48]. Amaya is written in Python and contains a basic automata library with alphabets encoded using multi-terminal binary decision diagrams (MTBDDs), for which it uses the C-based Sylvan library [27] (implementation details can be found in [42]). We ran all our experiments on Debian GNU/Linux 12 system with Intel(R) Xeon(R) CPU E5-2620 v3 @ 2.40 GHz and 32 GiB of RAM with the timeout of 60 s.
Tools. We selected the following tools for comparison: Z3 [63] (version 4.12.2), cvc5 [4] (version 1.0.5), Princess [70] (version 2023-06-19), and Lash [80] (version 0.92). Out of these, only Lash is an automata-based LIA solver; the other tools are general purpose SMT solvers with the LIA theory.
Benchmarks. Our main benchmark comes from SMT-LIB [5], in particular, the categories LIA [72] and NIA (nonlinear integer arithmetic) [73]. We concentrate on formulae in directories UltimateAutomizer and (20190429-)UltimateAutomizer
Svcomp2019 of these categories (the main difference between LIA and NIA is that LIA formulae are not allowed to use the modulo operator) and remove formulae from NIA that contain multiplication between variables, giving us 372 formulae. We denote this benchmark as SMT-LIB. The formulae come from verification of real-world C programs using Ultimate Automizer [46]. Other benchmarks in the categories, tptp and psyco, were omitted. Namely, tptp is easy for all tools (every tool finished within 1.3 s on each formula). The psyco benchmark resembles Boolean reasoning more than integer reasoning. In particular, its formulae contain simple integer constraints (e.g., \(x = y + 1\) or just \(x = y\)) and complex Boolean structure with ite operators and quantified Boolean variables. Our prototype is not optimized for these features, but with a naive implementation of unwinding of ite and with encoding of Boolean variables in a special automaton track, Amaya could solve 46 out of the 196 formulae in psyco.
Our second benchmark consists of the Frobenius coin problem [41] asking the following question: Given a pair of coins of certain coprime denominations a and b, what is the largest number not obtainable as a sum of values of these coins? Or, as a formula,
Each formula is specified by a pair of denominations (a, b), e.g., (3, 7) for which the model is 11. Apart from theoretical interest, the Frobenius coin problem can be used, e.g., for liveness checking of markings of conservative weighted circuits (a variant of Petri nets) [22] or reasoning about automata with counters [50, 52, 78]. We created a family of 55 formulae encoding the problem with various increasing coin denominations. We denote this benchmark as Frobenius. The input format of the benchmarks is SMT-LIB [5], which all tools can handle except Lash—for this, we implemented a simple translator in Amaya for translating LIA problems in SMT-LIB into Lash ’s input format (the time of translation is not included in the runtime of Lash).
Results. We show the results in Table 1. For each benchmark we show the run time statistics together with the number of timeouts and the number of wins/losses for each competitor of Amaya (e.g., the value “354 (40)” in the row for Princess in SMT-LIB means that Amaya was faster than Princess on 354 SMT-LIB formulae and in 40 cases out of these, this was because Princess timed out). Note that statistics about times tend to be biased in favour of tools that timed out more since the timeouts are not counted.
The first part of the table contains automata-based solvers and the second part contains general SMT solvers. We also measure the effect of our optimizations against \(\textsc {Amaya} _{\text {noopt}}\), a version of the tool that only performs the classical automata-based procedure from Sect. 3 without our optimizations.
Discussion. In the comparison with other SMT solvers, from Table 1, automata-based approaches are clearly superior to current SMT solvers on Frobenius (confirming the conjecture made in [41]). cvc5 fails already for denominations (3, 5) (where the result is 7) and Z3 follows suite soon; Princess can solve significantly more formulae than Z3 and cvc5, but is still clearly dominated by Amaya. Details can be found in [42].
On the SMT-LIB benchmark, Amaya can solve the most formulae among all tools. It has 17 timeouts, followed by cvc5 with 28 timeouts (out of 372 formulae). On individual examples, the comparison of Amaya against Z3 and cvc5 almost always falls under one of the two cases: (i) the solver is one or two orders of magnitude faster than Amaya or (ii) the solver times out. This probably corresponds to specific heuristics of Z3 and cvc5 taking effect or not, while Amaya has a more robust performance, but is still a prototype and nowhere near as optimized. The performance of Princess is, however, usually much worse. Amaya is often complementary to the SMT solvers and was able to solve 6 formulae that no SMT solver did.
Comparison with \(\textsc {Amaya} _{\text {noopt}}\) (cf. Fig. 11) shows that the optimizations introduced in this paper have a profound effect on the number of solved cases (which is a proper superset of the cases solved without them). This is most visible on the SMT-LIB benchmark, where Amaya has 56 TOs less than \(\textsc {Amaya} _{\text {noopt}}\). On the Frobenius benchmark, the results of \(\textsc {Amaya} _{\text {noopt}}\) and Amaya are comparable. Our optimizations had limited impact here since the formulae are built only from a small number of simple atoms (cf. Eq. (21)). In some cases, Amaya takes even longer than \(\textsc {Amaya} _{\text {noopt}}\); this is because the lazy construction explores parts of the state space that would be pruned by the classical construction (e.g., when doing an intersection with a minimized FA with an empty language). This could be possibly solved by algebraic rules tailored for lightweight unsatisfiability checking.
We also tried to evaluate the effect of individual optimizations by selectively turning them off. It turns out that the most critical optimizations are the simple rewriting rules (Sect. 5; when turned off, Amaya gave additional 33 timeouts) and quantifier instantiation (Sect. 7; when turned off, Amaya gave additional 28 timeouts). On the other hand, surprisingly, turning off disjunction pruning (Sect. 6) did not have a significant effect on the result. By itself (without other optimizations), it can help the basic procedure solve some hard formulae, but its effect is diluted when used with the rest of the optimizations. Still, even though it comes with an additional cost, it still has a sufficient effect to compensate for this overhead.
Comparing with the older automata-based solver Lash, Amaya solves more examples in both benchmarks; Lash has 123 TOs in total compared to 22 TOs of Amaya. The lower median of Lash on SMT-LIB is partially caused by the facts that (i) Lash is a compiled C code while Amaya uses a Python frontend, which has a non-negligible overhead and (ii) Lash times out on harder formulae.
10 Related Work
The decidability of Presburger arithmetic was established already at the beginning of the 20th century by Presburger [64] via quantifier elimination. Over time, more efficient quantifier-elimination-based decision procedures occurred, such as the one of Cooper [23] or the one used within the Omega test [65] (which can be seen as a variation of Fourier-Motzkin variable elimination for linear real arithmetic [58, Section 5.4]). The complexity bounds of 2-\({\textbf {NEXP}}\)-hardness and 2-\({\textbf {EXPSPACE}}\) membership for satisfiability checking were obtained by Fischer and Rabin [35] and Berman [6] respectively. Quantifier elimination is often considered impractical due to the blow up in the size of the resulting formula. Counterexample-guided quantifier instantiation [66] is a proof-theoretical approach to establish (one-shot) satisfiability of LIA formulae, which can be seen as a lazy version of Cooper’s algorithm [23]. It is based on approximating a quantified formula by a set of formulae with the approximation being refined in case it is found too coarse. The approach focuses on formulae with one alternation, but is also extended to any number of alternations (according to the authors, the procedure was implemented in CVC4).
The first automata-based decision procedure for Presburger arithmetic can be obtained from Büchi’s decision procedure for the second-order logic WS1S [17] by noticing that addition is WS1S-definable. A similar construction for LIA is used by Wolper and Boigelot in [79], except that they avoid performing explicit automata product constructions by using the notion of concurrent number automata, which are essentially tuples of synchronized FAs.
Boudet and Comon [13] propose a more direct construction of automata for atomic constraints of the form \(a_1 x_1 + \ldots + a_n x_n \sim c\) (for \({\sim } \in \{=, \le \}\)) over natural numbers; we use a construction similar to theirs extended to integers (as used, e.g., in [29]). Moreover, they give a direct construction for a conjunction of equations, which can be seen as a special case of our construction from Sect. 4. Wolper and Boigelot in [80] discuss optimizations of the procedure from [13] (they use the most-significant bit first encoding though), in particular how to remove some states in the construction for automata for inequations based on subsumption obtained syntactically from the formula representing the state (a restricted version of disjunction pruning, cf. Sect. 6). The works [9,10,11,12] extend the techniques from [80] to solve the mixed linear integer real arithmetic (LIRA) using weak Büchi automata, implemented in Lash [1].
WS1S [17] is a closely related logic with an automata-based procedure similar to the one discussed in this paper (as mentioned above, Presburger arithmetic can be encoded into WS1S). The automata-based decision procedure for WS1S is, however, of nonelementary complexity (which is also a lower bound for the logic), it was, however, postulated that the sizes of the obtained automata (when reduced or minimized) describing Presburger-definable sets of integers are bounded by a tower of exponentials of a fixed height. (3-\({\textbf {EXPSPACE}}\)). This postulate was proven by Klaedtke [55] (refined later by Durand-Gasselin and Habermehl [29] who show that all automata during the construction do not exceed size 3-\({\textbf {EXP}}\)). The automata-based decision procedure for WS1S itself has been a subject of extensive study, making many pioneering contributions in the area of automata engineering [31,32,33,34, 39, 44, 45, 47, 56, 57, 75], showcasing in the well-known tool Mona [31, 47, 56, 57].
Data Availability Statement
An environment with the tools and data used for the experimental evaluation in the current study is available at [43].
Notes
- 1.
Note that our FAs cannot accept the empty word \(\epsilon \), which corresponds in our use to the fact that in the two’s complement encoding of integers, one needs at least one bit (the sign bit) to represent a number, see further.
- 2.
Although the modulo constraint
 could be safely removed without affecting the expressivity of the input language, keeping it allows a more efficient automata construction and application of certain heuristics (cf. Sect. 7.1).
could be safely removed without affecting the expressivity of the input language, keeping it allows a more efficient automata construction and application of certain heuristics (cf. Sect. 7.1). - 3.
The subsumption is similar to the one used in efficient decision procedures for WS1S/WSkS [32, 45] with two important differences: (i) it can look inside atomic formulae and use semantics of states and (ii) it does not depend on the initial structure of the initial formula. (iii) Both of these make the subsumption relation larger.
References
The Liège automata-based symbolic handler (Lash). https://people.montefiore.uliege.be/boigelot/research/lash/
Abdulla, P.A., et al.: Trau: SMT solver for string constraints. In: Bjørner, N.S., Gurfinkel, A. (eds.) 2018 Formal Methods in Computer Aided Design, FMCAD 2018, Austin, TX, USA, October 30 – November 2, 2018, pp. 1–5. IEEE (2018). https://doi.org/10.23919/FMCAD.2018.8602997
Antimirov, V.: Partial derivatives of regular expressions and finite automaton constructions. Theoret. Comput. Sci. 155(2), 291–319 (1996). https://doi.org/10.1016/0304-3975(95)00182-4, http://www.sciencedirect.com/science/article/pii/0304397595001824
Barbosa, H., et al.: cvc5: a versatile and industrial-strength SMT solver. In: Fisman, D., Rosu, G. (eds.) ETAPS 2022, Part I. LNCS, vol. 13243, pp. 415–442. Springer (2022). https://doi.org/10.1007/978-3-030-99524-9_24
Barrett, C., Fontaine, P., Tinelli, C.: The Satisfiability Modulo Theories Library (SMT-LIB) (2016). www.SMT-LIB.org
Berman, L.: The complexity of logical theories. Theoret. Comput. Sci. 11(1), 71–77 (1980). https://doi.org/10.1016/0304-3975(80)90037-7
Berzish, M., et al.: Towards more efficient methods for solving regular-expression heavy string constraints. Theor. Comput. Sci. 943, 50–72 (2023). https://doi.org/10.1016/j.tcs.2022.12.009
Blahoudek, F., et al.: Word equations in synergy with regular constraints. In: Chechik, M., Katoen, J.P., Leucker, M. (eds.) FM 2023. LNCS, vol. 14000, pp. 403–423. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-27481-7_23
Boigelot, B., Jodogne, S., Wolper, P.: On the use of weak automata for deciding linear arithmetic with integer and real variables. In: Goré, R., Leitsch, A., Nipkow, T. (eds.) IJCAR 2001. LNCS, vol. 2083, pp. 611–625. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45744-5_50
Boigelot, B., Jodogne, S., Wolper, P.: An effective decision procedure for linear arithmetic over the integers and reals. ACM Trans. Comput. Log. 6(3), 614–633 (2005). https://doi.org/10.1145/1071596.1071601
Boigelot, B., Rassart, S., Wolper, P.: On the expressiveness of real and integer arithmetic automata. In: Larsen, K.G., Skyum, S., Winskel, G. (eds.) ICALP 1998. LNCS, vol. 1443, pp. 152–163. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055049
Boigelot, B., Wolper, P.: Representing arithmetic constraints with finite automata: an overview. In: Stuckey, P.J. (ed.) ICLP 2002. LNCS, vol. 2401, pp. 1–20. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45619-8_1
Boudet, A., Comon, H.: Diophantine equations, Presburger arithmetic and finite automata. In: Kirchner, H. (ed.) CAAP 1996. LNCS, vol. 1059, pp. 30–43. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-61064-2_27
Brzozowski, J.A.: Canonical regular expressions and minimal state graphs for definite events. In: Proceedings of the Symposium Mathematics Theory of Automata (New York, 1962), Microwave Research Institute Symposia Series, Brooklyn, NY, vol. XII, pp. 529–561. Polytechnic (1963)
Brzozowski, J.A.: Derivatives of regular expressions. J. ACM 11(4), 481–494 (1964). https://doi.org/10.1145/321239.321249
Büchi, J.R.: On a decision method in restricted second order arithmetic. In: Proceedings of International Congress on Logic, Method, and Philosophy of Science 1960. Stanford Univ. Press, Stanford (1962)
Büchi, J.R.: Weak second-order arithmetic and finite automata. Zeitscrift fur mathematische Logic und Grundlagen der Mathematik 6, 66–92 (1960)
Chen, T., et al.: Solving string constraints with regex-dependent functions through transducers with priorities and variables. Proc. ACM Program. Lang. 6(POPL), 1–31 (2022). https://doi.org/10.1145/3498707
Chen, Y.F., Chocholatý, D., Havlena, V., Holík, L., Lengál, O., Síč, J.: Solving string constraints with lengths by stabilization. Proc. ACM Program. Lang. 7(OOPSLA2) (oct 2023). https://doi.org/10.1145/3622872
Chen, Y.F., Chocholatý, D., Havlena, V., Holík, L., Lengál, O., Síč, J.: Z3-noodler: an automata-based string solver (technical report). CoRR abs/2310.08327 (2023). https://doi.org/10.48550/arXiv.2310.08327
Chocholatý, D., et al.: Mata: a fast and simple finite automata library (technical report). CoRR abs/2310.10136 (2023). https://doi.org/10.48550/arXiv.2310.10136, To appear at TACAS’23
Chrzastowski-Wachtel, P., Raczunas, M.: Liveness of weighted circuits and the diophantine problem of Frobenius. In: Ésik, Z. (ed.) FCT 1993. LNCS, vol. 710, pp. 171–180. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57163-9_13
Cooper, D.: Theorem proving in arithmetic without multiplication. Mach. Intell. 7, 91–99 (1972)
Cox, A., Leasure, J.: Model checking regular language constraints. CoRR abs/1708.09073 (2017)
Dantzig, G.B.: Inductive proof of the simplex method. IBM J. Res. Dev. 4(5), 505–506 (1960). https://doi.org/10.1147/RD.45.0505
Detlefs, D., Nelson, G., Saxe, J.B.: Simplify: a theorem prover for program checking. J. ACM 52(3), 365–473 (2005). https://doi.org/10.1145/1066100.1066102
van Dijk, T., van de Pol, J.: SYLVAN: multi-core framework for decision diagrams. Int. J. Softw. Tools Technol. Transf. 19(6), 675–696 (2017). https://doi.org/10.1007/s10009-016-0433-2
Doyen, L., Raskin, J.-F.: Antichain algorithms for finite automata. In: Esparza, J., Majumdar, R. (eds.) TACAS 2010. LNCS, vol. 6015, pp. 2–22. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-12002-2_2
Durand-Gasselin, A., Habermehl, P.: On the use of non-deterministic automata for Presburger arithmetic. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 373–387. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15375-4_26
Egly, U.: On the value of antiprenexing. In: Pfenning, F. (ed.) LPAR 1994. LNCS, vol. 822, pp. 69–83. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-58216-9_30
Elgaard, J., Klarlund, N., Møller, A.: MONA 1.x: new techniques for WS1S and WS2S. In: Hu, A.J., Vardi, M.Y. (eds.) CAV 1998. LNCS, vol. 1427, pp. 516–520. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0028773
Fiedor, T., Holík, L., Janků, P., Lengál, O., Vojnar, T.: Lazy automata techniques for WS1S. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 407–425. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_24
Fiedor, T., Holík, L., Lengál, O., Vojnar, T.: Nested antichains for WS1S. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 658–674. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_59
Fiedor, T., Holík, L., Lengál, O., Vojnar, T.: Nested antichains for WS1S. Acta Informatica 56(3), 205–228 (2019). https://doi.org/10.1007/s00236-018-0331-z
Fischer, M.J., Rabin, M.O.: Super-exponential complexity of Presburger arithmetic. In: Proceedings of the SIAM-AMS Symposium in Applied Mathematics, vol. 7, pp. 27—41 (1974)
Ge, Y., de Moura, L.: Complete instantiation for quantified formulas in satisfiabiliby modulo theories. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 306–320. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02658-4_25
Ghilardi, S., Nicolini, E., Ranise, S., Zucchelli, D.: Decision procedures for extensions of the theory of arrays. Ann. Math. Artif. Intell. 50(3–4), 231–254 (2007). https://doi.org/10.1007/s10472-007-9078-x
van Glabbeek, R., Ploeger, B.: Five determinisation algorithms. In: Ibarra, O.H., Ravikumar, B. (eds.) CIAA 2008. LNCS, vol. 5148, pp. 161–170. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70844-5_17
Glenn, J., Gasarch, W.: Implementing WS1S via finite automata. In: Raymond, D., Wood, D., Yu, S. (eds.) WIA 1996. LNCS, vol. 1260, pp. 50–63. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63174-7_5
Google: RE2. https://github.com/google/re2
Haase, C.: A survival guide to Presburger arithmetic. ACM SIGLOG News 5(3), 67–82 (2018). https://doi.org/10.1145/3242953.3242964
Habermehl, P., Havlena, V., Holík, L., Hečko, M., Lengál, O.: Algebraic reasoning meets automata in solving linear integer arithmetic (technical report). CoRR abs/2403.18995 (2024). https://doi.org/10.48550/arXiv.2403.18995
Habermehl, P., Havlena, V., Holík, L., Hečko, M., Lengál, O.: Artifact for the cav’24 paper “Algebraic reasoning meets automata in solving linear integer arithmetic” (2024). https://doi.org/10.5281/zenodo.10996343
Havlena, V., Holík, L., Lengál, O., Vales, O., Vojnar, T.: Antiprenexing for WSkS: a little goes a long way. In: Albert, E., Kovács, L. (eds.) LPAR 2020: 23rd International Conference on Logic for Programming, Artificial Intelligence and Reasoning, Alicante, Spain, May 22–27, 2020. EPiC Series in Computing, vol. 73, pp. 298–316. EasyChair (2020). https://doi.org/10.29007/6bfc
Havlena, V., Holík, L., Lengál, O., Vojnar, T.: Automata terms in a lazy WSkS decision procedure. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 300–318. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_18
Heizmann, M., Hoenicke, J., Podelski, A.: Software model checking for people who love automata. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 36–52. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_2
Henriksen, J.G., et al.: Mona: monadic second-order logic in practice. In: Brinksma, E., Cleaveland, W.R., Larsen, K.G., Margaria, T., Steffen, B. (eds.) TACAS 1995. LNCS, vol. 1019, pp. 89–110. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60630-0_5
Hečko, M.: Amaya (2024). https://github.com/MichalHe/amaya
Hieronymi, P., Ma, D., Oei, R., Schaeffer, L., Schulz, C., Shallit, J.O.: Decidability for Sturmian words. In: Manea, F., Simpson, A. (eds.) 30th EACSL Annual Conference on Computer Science Logic, CSL 2022, February 14-19, 2022, Göttingen, Germany (Virtual Conference). LIPIcs, vol. 216, pp. 24:1–24:23. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2022). https://doi.org/10.4230/LIPICS.CSL.2022.24
Holík, L., Lengál, O., Saarikivi, O., Turoňová, L., Veanes, M., Vojnar, T.: Succinct determinisation of counting automata via sphere construction. In: Lin, A.W. (ed.) APLAS 2019. LNCS, vol. 11893, pp. 468–489. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34175-6_24
Hopcroft, J.: An \(n\) log \(n\) algorithm for minimizing states in a finite automaton. In: Theory of Machines and Computations (Proc. Internat. Sympos., Technion, Haifa, 1971), pp. 189–196. Academic Press, New York-London (1971)
Hu, D., Wu, Z.: String constraints with regex-counting and string-length solved more efficiently. In: Hermanns, H., Sun, J., Bu, L. (eds.) SETTA 2023. LNCS, vol. 14464, pp. 1–20. Springer, Cham (2023). https://doi.org/10.1007/978-981-99-8664-4_1
Hyperscan.io (2021). https://www.hyperscan.io/
Jonáš, M., Strejček, J.: Q3B: an efficient BDD-based SMT solver for quantified bit-vectors. In: Dillig, I., Tasiran, S. (eds.) CAV 2019. LNCS, vol. 11562, pp. 64–73. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-25543-5_4
Klaedtke, F.: Bounds on the automata size for presburger arithmetic. ACM Trans. Comput. Log. 9(2), 11:1-11:34 (2008). https://doi.org/10.1145/1342991.1342995
Klarlund, N.: A theory of restrictions for logics and automata. In: Halbwachs, N., Peled, D. (eds.) CAV 1999. LNCS, vol. 1633, pp. 406–417. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48683-6_35
Klarlund, N., Møller, A., Schwartzbach, M.I.: Mona implementation secrets. Int. J. Found. Comput. Sci. 13(4), 571–586 (2002)
Kroening, D., Strichman, O.: Decision Procedures - An Algorithmic Point of View, Second Edition. Texts in Theoretical Computer Science. An EATCS Series. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-50497-0
Kuncak, V., Mayer, M., Piskac, R., Suter, P.: Software synthesis procedures. Commun. ACM 55(2), 103–111 (2012). https://doi.org/10.1145/2076450.2076472
Kuper, G.M., Libkin, L., Paredaens, J. (eds.): Constraint Databases. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-662-04031-7
Monniaux, D.: Automatic modular abstractions for linear constraints. In: Shao, Z., Pierce, B.C. (eds.) Proceedings of the 36th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2009, Savannah, GA, USA, January 21-23, 2009. pp. 140–151. ACM (2009). https://doi.org/10.1145/1480881.1480899
Moseley, D., et al.: Derivative based nonbacktracking real-world regex matching with backtracking semantics. Proc. ACM Program. Lang. 7(PLDI), 1026–1049 (2023). https://doi.org/10.1145/3591262
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Presburger, M.: Über die vollständigkeit eines gewissen systems der arithmetik ganzer zahlen, in welchem die addition als einzige operation hervortritt. In: Comptes Rendus du I congrès de Mathématiciens des Pays Slaves, pp. 92—101 (1929)
Pugh, W.W.: The omega test: a fast and practical integer programming algorithm for dependence analysis. In: Martin, J.L. (ed.) Proceedings Supercomputing ’91, Albuquerque, NM, USA, November 18–22, 1991, pp. 4–13. ACM (1991). https://doi.org/10.1145/125826.125848
Reynolds, A., King, T., Kuncak, V.: Solving quantified linear arithmetic by counterexample-guided instantiation. Formal Methods Syst. Des. 51(3), 500–532 (2017). https://doi.org/10.1007/s10703-017-0290-y
Reynolds, A., Kuncak, V., Tinelli, C., Barrett, C.W., Deters, M.: Refutation-based synthesis in SMT. Formal Methods Syst. Des. 55(2), 73–102 (2019). https://doi.org/10.1007/S10703-017-0270-2
Reynolds, A., Tinelli, C., de Moura, L.: Finding conflicting instances of quantified formulas in SMT. In: Proceedings of the 14th Conference on Formal Methods in Computer-Aided Design. FMCAD ’14, Austin, Texas, pp. 195-202. FMCAD Inc. (2014)
Robinson, J.A., Voronkov, A. (eds.): Handbook of Automated Reasoning (in 2 volumes). Elsevier and MIT Press (2001). https://www.sciencedirect.com/book/9780444508133/handbook-of-automated-reasoning
Rümmer, P.: A constraint sequent calculus for first-order logic with linear integer arithmetic. In: Cervesato, I., Veith, H., Voronkov, A. (eds.) LPAR 2008. LNCS (LNAI), vol. 5330, pp. 274–289. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89439-1_20
Schuele, T., Schneider, K.: Verification of data paths using unbounded integers: automata strike back. In: Bin, E., Ziv, A., Ur, S. (eds.) HVC 2006. LNCS, vol. 4383, pp. 65–80. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70889-6_5
SMT-LIB: LIA (2023). https://clc-gitlab.cs.uiowa.edu:2443/SMT-LIB-benchmarks/LIA
SMT-LIB: NIA (2023). https://clc-gitlab.cs.uiowa.edu:2443/SMT-LIB-benchmarks/NIA
Stanford, C., Veanes, M., Bjørner, N.: Symbolic Boolean derivatives for efficiently solving extended regular expression constraints. In: Proceedings of the 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation. PLDI 2021, New York, NY, USA, pp. 620–635. Association for Computing Machinery (2021). https://doi.org/10.1145/3453483.3454066
Topnik, C., Wilhelm, E., Margaria, T., Steffen, B.: jMosel: a stand-alone tool and jABC plugin for M2L(Str). In: Valmari, A. (ed.) SPIN 2006. LNCS, vol. 3925, pp. 293–298. Springer, Heidelberg (2006). https://doi.org/10.1007/11691617_18
Traytel, D.: A coalgebraic decision procedure for WS1S. In: Kreutzer, S. (ed.) 24th EACSL Annual Conference on Computer Science Logic, CSL 2015, September 7-10, 2015, Berlin, Germany. LIPIcs, vol. 41, pp. 487–503. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2015). https://doi.org/10.4230/LIPIcs.CSL.2015.487
Traytel, D., Nipkow, T.: Verified decision procedures for MSO on words based on derivatives of regular expressions. J. Funct. Program. 25 (2015). https://doi.org/10.1017/S0956796815000246
Turonová, L., Holík, L., Lengál, O., Saarikivi, O., Veanes, M., Vojnar, T.: Regex matching with counting-set automata. Proc. ACM Program. Lang. 4(OOPSLA), 218:1–218:30 (2020). https://doi.org/10.1145/3428286
Wolper, P., Boigelot, B.: An automata-theoretic approach to Presburger arithmetic constraints. In: Mycroft, A. (ed.) SAS 1995. LNCS, vol. 983, pp. 21–32. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60360-3_30
Wolper, P., Boigelot, B.: On the construction of automata from linear arithmetic constraints. In: Graf, S., Schwartzbach, M. (eds.) TACAS 2000. LNCS, vol. 1785, pp. 1–19. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46419-0_1
Acknowledgments
This work has been supported by the Czech Ministry of Education, Youth and Sports ERC.CZ project LL1908, the Czech Science Foundation project 23-07565S, and the FIT BUT internal project FIT-S-23-8151.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Habermehl, P., Havlena, V., Hečko, M., Holík, L., Lengál, O. (2024). Algebraic Reasoning Meets Automata in Solving Linear Integer Arithmetic. In: Gurfinkel, A., Ganesh, V. (eds) Computer Aided Verification. CAV 2024. Lecture Notes in Computer Science, vol 14681. Springer, Cham. https://doi.org/10.1007/978-3-031-65627-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-65627-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-65626-2
Online ISBN: 978-3-031-65627-9
eBook Packages: Computer ScienceComputer Science (R0)








 .
. ,
, , and
, and .
.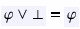 and
and
 ) and annihilation (
) and annihilation (
 and
and
 ) to simplify the formulae.
) to simplify the formulae. and
and
 ) to push negation as deep as possible. The motivation is that small subformulae are likely to have small corresponding automata. As complementation requires the underlying automaton to be deterministic, complementing smaller automata helps to mitigate the exponential blow-up of determinization.
) to push negation as deep as possible. The motivation is that small subformulae are likely to have small corresponding automata. As complementation requires the underlying automaton to be deterministic, complementing smaller automata helps to mitigate the exponential blow-up of determinization. , and to prune away some parts of the formula, e.g.,
, and to prune away some parts of the formula, e.g.,
 .
. where
where
 , or
, or
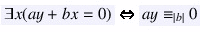 .
. . One can see this as a variant of DAGification used in
. One can see this as a variant of DAGification used in 

 .
.





 could be safely removed without affecting the expressivity of the input language, keeping it allows a more efficient automata construction and application of certain heuristics (cf. Sect.
could be safely removed without affecting the expressivity of the input language, keeping it allows a more efficient automata construction and application of certain heuristics (cf. Sect.