Abstract
The predicate definitions in Separation Logic (SL) play an important role: they capture a large spectrum of unbounded heap shapes due to their inductiveness. This expressiveness power comes with a limitation: the entailment problem is undecidable if predicates have general inductive definitions (ID). Iosif et al. [8] proposed syntactic and semantic conditions, called PCE, on the ID of predicates to ensure the decidability of the entailment problem. We provide a (possibly nonterminating) algorithm to transform arbitrary ID into equivalent PCE definitions when possible. We show that the existence of an equivalent PCE definition for a given ID is undecidable, but we identify necessary conditions that are decidable. The algorithm has been implemented, and experimental results are reported on a benchmark, including significant examples from SL-COMP.
This work has been partially funded by the French National Research Agency project ANR-21-CE48-0011.
You have full access to this open access chapter, Download conference paper PDF
Keywords
- Separation logic
- Inductive definitions
- Bounded treewidth fragment
- PCE fragment
- Symbolic heaps
- Decision procedures
1 Introduction
Separation logic (SL) [9, 11] is widely used in verification to reason about programs manipulating dynamically allocated memory. Formulas in SL are defined from atoms of the form \(x\rightarrow (y_1,\dots ,y_k)\), stating that at location (i.e., a memory address), x is allocated a memory block containing the tuple built from values of \(y_1,\dots ,y_k\), and \(\texttt{emp}\), stating that the heap is empty, i.e., that there are no allocated locations. SL includes the standard logical connectives and quantifiers, together with a special connective \(\varphi _1 \star \varphi _2\), called separating conjunction, asserting that formulas \(\varphi _1\) and \(\varphi _2\) are satisfied on disjoint parts of the heap. This particular feature of the logic ensures the scalability of program analyses by enabling local reasoning: the properties of a program may be asserted and established by referring only to the part of the heap that is affected by the program. To specify recursive data structures, the SL formulas include predicate atoms defined by inductive rules with a fixpoint semantics. For instance, list segments from x to y may be defined by the following rules:
Many problems in verification boil down to checking the validity of entailments between formulas in SL. In general, unsurprisingly, entailment is undecidable. However, several fragments have been identified for which the entailment problem is decidable. Among these fragments, the so-called PCE fragment is one of the most expressive ones [8]. Decidability was initially established by reduction to monadic second-order logic on graphs with bounded treewidth. Later, more efficient algorithms were proposed [4, 10], and the problem turned out to be 2-Exptime-complete [3]. The PCE fragment is defined by restricting the syntax and the semantics of the inductive rules defining the predicates. Each rule is required to satisfy three properties (formally defined later): (P)rogress, (C)onnectivity and (E)stablishment. Informally, the conditions respectively assert that: (P) every rule allocates exactly one location; (C) the allocated locations have a tree-shaped structure which mimics the call tree of the predicates, and (E) every location not associated with a free variable is (eventually) allocated. A PCE formula is a formula in which all predicates are defined by PCE rules. Most usual data structures in programming can be defined using PCE rules. However, the PCE conditions impose rigid constraints on the rules’ syntax, which are not necessarily satisfied in practice by user-provided rules. For instance, the above rules of \(\texttt{ls}\) (Eq. (1)) are not PCE (because the first rule of \(\texttt{ls}\) allocates no location), while the following ones, although specifying non-empty list segments, are PCE:
The non-PCE formula \(\texttt{ls}(x,y)\) can then be written as a PCE formula \((\texttt{emp}\star x \approx y) \vee \texttt{ls}^+(x,y)\). Other, rather natural, definitions of \(\texttt{ls}^+\) can be given, which are not PCE (the second rule of \(\texttt{ls}^m\) allocates no location, and the second rule of \(\texttt{ls}^e\) is not connected):
Similarly, the following definition of lists of odd length is not PCE:
but it is clear that it can be transformed into a PCE definition by replacing the inductive rule (at right) with the following ones:
A natural question thus arises, which has not been investigated so far: can algorithms be provided to identify whether a formula can be rewritten into an equivalent PCE formula and to effectively compute such a formula (and the associated inductive rules) if possible? The present paper aims to address these issues.
Contributions. We first observe that the PCE problem — i.e., the problem of testing whether a given formula admits an equivalent PCE formula — is undecidable. The result follows from the undecidability of testing whether context-free grammar is regular. Then, we provide a procedure for transforming some formulas that do not satisfy the PCE conditions into equivalent PCE formulas. Equivalence is guaranteed in all cases, but the procedure does not always terminate. We also identify cases for which the formulas cannot possibly admit any equivalent PCE formula. More precisely, we identify a property called PCE-compatibility, which is strictly weaker than PCE, in the sense that any formula that is equivalent to a PCE formula is PCE-compatible, but the converse does not hold, and we prove that this property is decidable. To sum up, given a formula \(\varphi \), the procedure may either terminate with a negative answer (if \(\varphi \) is not PCE-compatible) or may terminate with a positive answer and output a PCE formula equivalent to \(\varphi \) or may diverge (if \(\varphi \) is PCE-compatible, but no equivalent PCE formula can be obtained).
To our knowledge, there is no published work on this topic. In [7], the authors proposed inductive definitions (ID, termed “recursive definitions” in [8]) with syntactic restrictions incomparable to PCE since they require linearity and compositionality of the ID to obtain decidability of the entailment problem. This class of ID (disregarding data constraints) may be translated by our procedure into PCE form, i.e., they are PCE-compatible. In [5], other decidable fragments of entailment problems are considered, which do not fulfil the PCE conditions but can be reduced to PCE entailment. Unlike the present approach, the reduction proposed in [5] does not preserve the equivalence of formulas. In [4], the establishment condition is replaced by a condition on the equalities occurring in the problem.
2 Separation Logic with Inductive Definitions
We recall the definition of the syntax and semantics of SL with inductive definitions. Missing definitions, further explanations and examples can be found in [8]. We briefly review standard notations: \({{\,\textrm{card}\,}}(A)\) denotes the cardinality of set A, and \(A \uplus B\) denotes the disjoint union of sets A and B. The set \(\{ x \in \mathbb {Z}\;\vert \;i \le x \le j \}\) is denoted by \(\llbracket {i,j}\rrbracket \). The domain of a function f is written \({{\,\textrm{dom}\,}}(f)\). The equivalence class of an element x w.r.t. some equivalence relation
 is written
is written
 , and the set
, and the set
 is written
is written
 . The relation
. The relation
 will sometimes be omitted if it is clear from the context. We often identify an equivalence relation
will sometimes be omitted if it is clear from the context. We often identify an equivalence relation
 with the set of its equivalence classes. For any binary relation \(\rightarrow \), we denote by \(\rightarrow ^*\) its reflexive and transitive closure. A set R is a set of roots for \(\rightarrow \) if for all elements x, y such that \(x \rightarrow y\), there exists \(r \in R\) such that \(r \rightarrow ^*x\). It is minimal if, moreover, there is no set of roots \(R'\) such that \(R' \subset R\) (where \(\subset \) denotes strict inclusion).
with the set of its equivalence classes. For any binary relation \(\rightarrow \), we denote by \(\rightarrow ^*\) its reflexive and transitive closure. A set R is a set of roots for \(\rightarrow \) if for all elements x, y such that \(x \rightarrow y\), there exists \(r \in R\) such that \(r \rightarrow ^*x\). It is minimal if, moreover, there is no set of roots \(R'\) such that \(R' \subset R\) (where \(\subset \) denotes strict inclusion).
Definition 1
(SL formulas). Let \(\mathcal {V}\) be a countably infinite set of variables, and let \(\mathcal {P}\) be a set of spatial predicate symbols, where each symbol \(p\in \mathcal {P}\) is associated with a unique arity \(\#(p)\) (with countably infinite sets of predicate symbols of each arity). The set of SL-formulas (or simply formulas) \(\varphi \) is inductively defined as follows:
where \(\varphi _1,\varphi _2\) are formulas, \(p\in \mathcal {P}\), \(k \in \mathbb {N}\) and \(x,y,x_1,\dots ,x_{\#(p)}, y_1,\dots ,y_{k} \in \mathcal {V}\).
Note that negations are not supported. The considered fragment is similar to that of [4] (with disjunctions added), with the slight difference that points-to atoms \(x\rightarrow (y_1,\dots ,y_k)\) contain tuples of arbitrary length \(k \ge 0\). Let \( fv (\varphi )\) be the set of free variables in \(\varphi \). A substitution \(\sigma \) is a function from variables to variables; its domain \({{\,\textrm{dom}\,}}(\sigma )\) is the set of variables x such that \(\sigma (x)\ne x\), and its image \({{\,\textrm{img}\,}}(\sigma )=\sigma ({{\,\textrm{dom}\,}}(\sigma ))\). For any expression (variable, tuple or set of variables, or formula) e, we denote by \(e\sigma \) the expression obtained from e by replacing every free occurrence of a variable x by \(\sigma (x)\). A symbolic heap is a formula containing no occurrence of \(\vee \). By distributivity of \(\star \) and \(\exists \) over \(\vee \), any formula \(\varphi \) can be reduced to an equivalent disjunction of symbolic heaps, denoted by \( dnf (\varphi )\). An inductive rule associated with the predicate p has the form \(p(x_1,\dots ,x_n) \Leftarrow \varphi \), where \(x_1,\dots ,x_n\) are pairwise distinct variables, \(n = \#(p)\), and \(\varphi \) is a formula with \( fv (\varphi ) \subseteq \{ x_1,\dots ,x_n\}\). If \(\varphi \) is not a symbolic heap, then \(p(x_1,\dots ,x_n) \Leftarrow \varphi \) may be replaced by the rules \(\{p(x_1,\dots ,x_n) \Leftarrow \varphi _i \;\vert \;i \in \llbracket {1,m}\rrbracket \}\), where \(\varphi _1,\dots ,\varphi _m\) are symbolic heaps such that \(\bigvee _{i=1}^m \varphi _i\) is \( dnf (\varphi )\). We assume in the following that this transformation is applied eagerly to every rule. A set of inductive definitions (SID) \(\mathcal {R}\) is a set of inductive rules such that, for all predicates p, \(\mathcal {R}\) contains finitely many rules associated with p. We write \(p(y_1,\dots ,y_n) \Leftarrow _{\mathcal {R}} \psi \) if \(\mathcal {R}\) contains a rule \(p(x_1,\dots ,x_n) \Leftarrow \varphi \), with \(\psi = \varphi \{ x_i \mapsto y_i \;\vert \;i \in \llbracket {1,n}\rrbracket \}\).
Definition 2
(SL structure). Let \(\mathcal {L}\) be a countably infinite set of so-called locations. An SL-structure is a pair \((\mathfrak {s}, \mathfrak {h})\) where \(\mathfrak {s}\) is a store, i.e., a partial function from \(\mathcal {V}\) to \(\mathcal {L}\), and \(\mathfrak {h}\) is a heap, i.e., a partial finite function from \(\mathcal {L}\) to \(\mathcal {L}^*\), which can be written as a relation: \(\mathfrak {h}(\ell )= (\ell _1,\dots ,\ell _k)\) iff \((\ell ,\ell _1,\dots , \ell _k) \in \mathfrak {h}, k\in \mathbb {N}\).
For any heap \(\mathfrak {h}\), we let \( ref (\mathfrak {h}) = \{\ell \;\vert \;\ell _0 \in {{\,\textrm{dom}\,}}(\mathfrak {h}),\ell \text { occurs in } \mathfrak {h}(\ell _0)\}\), \( loc (\mathfrak {h}) = ref (\mathfrak {h}) \cup {{\,\textrm{dom}\,}}(\mathfrak {h})\) and \( dgl (\mathfrak {h}) = loc (\mathfrak {h}) \smallsetminus {{\,\textrm{dom}\,}}(\mathfrak {h})\) (for “dangling pointers”). Locations in \({{\,\textrm{dom}\,}}(\mathfrak {h})\) and variables x such that \(\mathfrak {s}(x)\in {{\,\textrm{dom}\,}}(\mathfrak {h})\) are allocated. We write \(\ell \rightarrow _{\mathfrak {h}} \ell '\) iff \(\ell \in {{\,\textrm{dom}\,}}(\mathfrak {h})\), and \(\ell '\) occurs in \(\mathfrak {h}(\ell )\).
Definition 3
(SL semantics). Given a formula \(\varphi \), a SID \(\mathcal {R}\) and a structure \((\mathfrak {s},\mathfrak {h})\) with \( fv (\varphi ) \subseteq {{\,\textrm{dom}\,}}(\mathfrak {s})\), the satisfaction relation \(\models _{\mathcal {R}}\) is inductively defined as the least relation such that \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\varphi \) iff one of the following conditions holds:
-
\(\varphi = \texttt{emp}\) and \(\mathfrak {h}=\emptyset \); or \(\varphi = (x\rightarrow (y_1,\dots ,y_k))\) and \(\mathfrak {h}= \{(\mathfrak {s}(x),\mathfrak {s}(y_1),\dots ,\mathfrak {s}(y_k)) \}\);
-
\(\varphi = (x \approx y)\), \(\mathfrak {s}(x) = \mathfrak {s}(y)\) and \(\mathfrak {h}= \emptyset \); or \(\varphi = (x \not \approx y)\), \(\mathfrak {s}(x) \not = \mathfrak {s}(y)\) and \(\mathfrak {h}= \emptyset \);
-
\(\varphi = \varphi _1 \vee \varphi _2\) and \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\varphi _i\), for some \(i\in \{1,2\}\); or \(\varphi =\varphi _1 \star \varphi _2\) and there exist disjoint domain heaps \(\mathfrak {h}_1,\mathfrak {h}_2\) such that \(\mathfrak {h}= \mathfrak {h}_1 \uplus \mathfrak {h}_2\) and \((\mathfrak {s},\mathfrak {h}_i) \models _{\mathcal {R}}\varphi _i\), for all \(i\in \{1,2\}\);
-
\(\varphi = \exists x.\,\psi \) and \((\mathfrak {s}',\mathfrak {h}) \models _{\mathcal {R}}\psi \), for some \(\mathfrak {s}'\) matching \(\mathfrak {s}\) on all variables distinct from x;
-
\(\varphi = p(x_1,\dots ,x_{\#(p)})\), \(p \in \mathcal {P}\) and \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\psi \) for some \(\psi \) such that \(\varphi \Leftarrow _{\mathcal {R}} \psi \).
We write \(\varphi \models _{\mathcal {R}}\psi \) if for every structure \((\mathfrak {s},\mathfrak {h})\) we have \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\varphi \implies (\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\psi \). If both \(\varphi \models _{\mathcal {R}}\psi \) and \(\psi \models _{\mathcal {R}}\varphi \) hold, then we write \(\varphi \equiv _{\mathcal {R}}\psi \).
Definition 4
(SL model). An \(\mathcal {R}\)-model of \(\varphi \) is a structure \((\mathfrak {s},\mathfrak {h})\) such that \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\varphi \). Given two pairs \((\varphi ,\mathcal {R})\) and \((\varphi ',\mathcal {R}')\), where \(\varphi ,\varphi '\) are formulas and \(\mathcal {R},\mathcal {R}'\) are SID, we write \((\varphi ,\mathcal {R}) \equiv (\varphi ',\mathcal {R}')\) iff \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}} \varphi \iff (\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}'} \varphi '\) holds for all structures \((\mathfrak {s},\mathfrak {h})\).
We emphasize that the atoms \(x \approx y\) or \(x \not \approx y\) only hold for empty heaps (this convention simplifies notations as it avoids the use of standard conjunction). Formulas are taken modulo the usual properties of SL connectives: associativity and commutativity of \(\star \) and \(\vee \), neutrality of \(\texttt{emp}\) for \(\star \), commutativity of \(\approx ,\not \approx \), and also modulo prenex form and \(\alpha \)-renaming. We also assume that bound variables are renamed to avoid any name collision. Rules are defined up to a renaming of free variables.
3 The PCE Problem
We now recall the conditions from [8], ensuring the decidability of the entailment problem.
Definition 5
(PCE rule and SID). Let \(r\) be a function mapping every spatial predicate \(p \in \mathcal {P}\) to an element of \(\llbracket {1,\#(p)}\rrbracket \). For any atom \(p(x_1,\dots ,x_n)\), the variable \(x_{r(p)}\) is the root of \(p(x_1,\dots ,x_n)\), and the root of an atom \(x\rightarrow (y_1,\dots ,y_k)\) is x. A rule \(p(x_1,\dots ,x_n) \Leftarrow \varphi \) is PCE w.r.t. some SID \(\mathcal {R}\) if it is:
-
progressing, i.e., \(\varphi \) is of the form \(\exists u_1, \dots ,u_m.\, (x_i\rightarrow (y_1,\dots ,y_k) \star \psi )\), where \(m \ge 0\), \(\psi \) is a formula with no occurrence of \(\rightarrow ,\exists ,\vee \), and \(i = r(p)\);
-
connected, i.e., moreover, all spatial predicate atoms occurring in \(\psi \) are of the form \(q(z_1,\dots ,z_{\#(q)})\) with \(z_{r(q)} \in \{y_1,\dots ,y_k\}\);
-
established, i.e., moreover, for all \(i \in \llbracket {1,m}\rrbracket \), and for all structures \((\mathfrak {s},\mathfrak {h})\) such that \((\mathfrak {s},\mathfrak {h}) \models _{\mathcal {R}}\psi \), either \(\mathfrak {s}(u_i) \in {{\,\textrm{dom}\,}}(\mathfrak {h})\) or \(\mathfrak {s}(u_i) \in \{\mathfrak {s}(x_j) \;\vert \;j \in \llbracket {1,n}\rrbracket \}\).
A SID \(\mathcal {R}\) is PCE if every rule is PCE w.r.t. \(\mathcal {R}\). A formula \(\varphi \) is PCE if every predicate used in \(\varphi \) is defined by PCE rules.
The problem we are investigating in the present paper is the following:
Definition 6
(PCE problem). Given a pair \((\varphi , \mathcal {R})\), the PCE problem lies in deciding whether there exists a formula \(\varphi '\) and a PCE SID \(\mathcal {R}'\) such that \((\varphi ,\mathcal {R}) \equiv (\varphi ',\mathcal {R}')\).
Assuming that \(\varphi \) is atomic is sufficient (complex formulas may be introduced by inductive rules), but the possibility that \(\varphi '\) is non-atomic allows for greater expressiveness. If one restricts oneself to list-shaped structures denoting words, then the PCE conditions essentially state that the set of denoted words is regular. This entails the following result, obtained by reduction from the regularity of context-free languages:
Theorem 1
The PCE problem is undecidable.
It may be observed that the structures \((\mathfrak {s},\mathfrak {h})\) satisfying PCE pairs \((\varphi ,\mathcal {R})\) necessarily satisfy two essential properties. First, due to the connectivity condition, these structures necessarily admit a bounded number of roots, which correspond to locations assigned by \(\mathfrak {s}\) to (possibly quantified) variables occurring inside \(\varphi \) (at some root position in a predicate or points-to atom, as defined in Definition 5).
Structures with multiple roots are permitted (e.g., doubly linked lists), but due to the connectivity condition, if x is the root of an atom \(\varphi \), then, for every model \((\mathfrak {s},\mathfrak {h})\) of \(\varphi \), the singleton \(\{\mathfrak {s}(x)\}\) is a set of roots for \(\rightarrow _{\mathfrak {h}}\) (i.e., all locations in \( loc (\mathfrak {h})\) must be accessible from \(\mathfrak {s}(x)\)). Disjoint structures built in parallel (such as two lists with the same length) are not allowedFootnote 1. Second, these structures also admit a bounded number of “dangling pointers” (i.e., elements of \( dgl (\mathfrak {h})\)), which again correspond (by \(\mathfrak {s}\)) to variables occurring in \(\varphi \), since all the variables introduced by unfolding rules must be allocated due to the establishment property. The latter property turned out to be essential for decidability [6]. This yields the definition of a property called PCE-compatibility:
Definition 7
(PCE-compatibility). Let \(k \in \mathbb {N}\). A structure \((\mathfrak {s},\mathfrak {h})\) is k-PCE-compatible if (i) \({{\,\textrm{card}\,}}( dgl (\mathfrak {h})) \le k\) and (ii) there exists a set of roots R for \(\rightarrow _{\mathfrak {h}}\) with \({{\,\textrm{card}\,}}(R) \le k\). A pair \((\varphi ,\mathcal {R})\) is k-PCE-compatible if every \(\mathcal {R}\)-model of \(\varphi \) is \(k\)-PCE-compatible.
Proposition 1
Let \(\varphi \) be a formula, and \(\mathcal {R}\) be a PCE SID. Every \(\mathcal {R}\)-model \((\mathfrak {s},\mathfrak {h})\) of \(\varphi \) is \(k\)-PCE-compatible, where k is the number of (free or bound) variables in \(\varphi \).
Example 1
Let us consider the formula \(\varphi = p(x,y)\) and the SID \(\mathcal {R}_1\) below. For readability, we employ the same variable names in predicate definitions and predicate calls to avoid introducing the renaming of variables:
The SID \(\mathcal {R}_1\), and thus \((\varphi ,\mathcal {R}_1)\), are not PCE. In the first rule for p, z is root but not a free variable, the rule defining q is not established for the existential variable u and the rule defining r does not respect the progress condition as it has two points-to atoms.
4 Overview of Our Procedure
The (nonterminating) algorithm for transforming a pair \((\varPhi ,\mathcal {R})\) into an equivalent PCE pair is divided into four main steps (from now on, we denote the target formula by \(\varPhi \), whereas the meta-variable \(\varphi \) is reserved for formulas occurring in inductive rules).
Step 1: We compute abstractions of the models of \(\varPhi \) (and of all relevant predicate atoms). The aim is to extract relevant information about the constraints satisfied by these models concerning (dis)equalities, heap reachability and allocated locations. The abstractions are constructed over a set of variables that includes the variables freely occurring in the formulas, together with some additional variables — the so-called invisible variables — that correspond to existential variables that either occur in \(\varPhi \) or are introduced by unfolding inductive rules. The usefulness of invisible variables will be demonstrated later. The computation does not terminate in general, as the set of abstractions is infinite (due to the presence of invisible variables). However, we prove that the computation terminates exactly when the considered formula is \(k\)-PCE-compatible (for some \(k \in \mathbb {N}\)). Furthermore, we introduce a technique — the so-called ISIV condition — to detect when the formula is not \(k\)-PCE-compatible during the computation of the abstractions. This ensures termination in all cases and also proves that the problem of deciding whether a given pair is \(k\)-PCE-compatible, for some k, is decidable. This step is detailed in Sect. 5.
Step 2: We transform the set of rules in order to ensure that every predicate is associated with a unique abstraction, in which all invisible variables are replaced by visible ones. This step always terminates. It adds some combinatorial explosion that could be reduced by a smart transformation, but it greatly simplifies the technical developments. This step is detailed in Sect. 6.
Step 3: We apply some transformations on the SID to ensure that every abstraction admits exactly one root. This step may fail in the case where the structures described by the rules do not have this property. See Sect. 7.
Step 4: We recursively transform any rule
 into a PCE rule by decomposing \(\varphi \) into a separating conjunction \(y\rightarrow (z_1,\dots ,z_k) \star \varphi _1 \star \dots \star \varphi _k\) where y is the root of the structure and every \(\varphi _i\) encodes a structure of root \(z_i\). Each of these formulas \(\varphi _i\) may then be associated with fresh predicate atoms if needed. The process is repeated until one gets a fixpoint. Equivalence is always preserved, but termination is not guaranteed. This step is detailed in Sect. 8.
into a PCE rule by decomposing \(\varphi \) into a separating conjunction \(y\rightarrow (z_1,\dots ,z_k) \star \varphi _1 \star \dots \star \varphi _k\) where y is the root of the structure and every \(\varphi _i\) encodes a structure of root \(z_i\). Each of these formulas \(\varphi _i\) may then be associated with fresh predicate atoms if needed. The process is repeated until one gets a fixpoint. Equivalence is always preserved, but termination is not guaranteed. This step is detailed in Sect. 8.
Before describing all these steps, we wish to convey some general explanations about the difficulties that arise when one tries to enforce each condition in Definition 5.
The progress condition can often be enforced by introducing additional predicates to ensure that each rule allocates exactly one location. For instance, the definition of lists of odd length in Eq. (5) is not PCE, but it can be transformed into a PCE definition by replacing the inductive rule (at right) with the two inductive rules given in Eq. (6) (introducing a new predicate \(\texttt{ls}^{2}(x,y)\)). The key point is that the root of the structure must be associated with a parameter of the predicate, which sometimes requires the addition of new existential variables in the formula. For instance, the formula p(x) with \(p(x) \Leftarrow \exists y.\, y\rightarrow (x)\) will be written: \(\exists y.\,p'(x,y)\) with \(p'(x,y) \Leftarrow y\rightarrow (x)\). The set of roots is computed in Step 1 above, and invisible roots (like y in the above example) are made visible during Step 2. Note that this technique is applicable only if the number of such roots is bounded; the ISIV condition will ensure that this constraint is satisfied.
The connectivity condition is enforced by using the abstract reachability relation computed during Step 1 to identify the predicate atoms that do not satisfy this condition and by modifying the rules to delay the call to these predicates until the connectivity condition is satisfied. For instance, the first rule below is modified into the second one:
where \(q'(y_1,y_3)\) is defined similarly to \(\texttt{ls}^+(y_1,y_3)\) in Eq. (2) except the first rule:
The establishment condition may be enforced in two ways. If the considered existential variable only occurs in pure atoms (disequalities or equalities), then it can be eliminated using usual quantifier elimination techniques. For instance, the predicate \(r(x) \Leftarrow \exists y.\, x\rightarrow () \star x\not \approx y\) can be reduced into \(r(x) \Leftarrow x\rightarrow ()\) since a location y distinct from x always exists (recall that the equational atom \(x\not \approx y\) only holds for empty heaps). Otherwise, one must collect the set of all variables that are reachable but not allocated and associate them with new existential variables in \(\varphi \) (and parameters of predicates). For instance, the formula \(r'(x)\) with \(r'(x) \Leftarrow \exists y.\, x\rightarrow (y)\) is transformed into \(\exists y.\, r''(x,y)\) with \(r''(x,y) \Leftarrow x\rightarrow (y)\). These variables correspond to invisible variables computed during Step 1 and transformed into visible variables in Step 2. Again, the ISIV condition ensures that the number of such variables is bounded.
5 Abstracting Models and Formulas
We formalize the notion of abstraction that summarizes the main features (locations defined and allocated, reachability, etc.) of models and SL-formulas. Then, we define two relations between abstractions and SL-structures. Finally, we define the abstraction process for a formula, i.e., how we attach a set of abstractions to an SL-formula.
Definition 8
(Abstraction). An abstraction is a tuple
 where: (i) V is a set of variables and \(\backsim \) is an equivalence relation on V; (ii)
where: (i) V is a set of variables and \(\backsim \) is an equivalence relation on V; (ii)
 (disequality relation) is a symmetric and irreflexive binary relation on \(\overline{V}\); (iii) \(V_v\subseteq V\) is a finite set of variables called visible variables; (iv) \(\overline{V}_a\subseteq \overline{V}\) is a subset of classes of variables called allocated variables; (v) \(h:\overline{V}_a\longrightarrow \overline{V}^*\) is a partial heap mapping which associates a tuple of classes of variables of arbitrary size to some class of allocated variables; (vi) \(\rightsquigarrow \subseteq \overline{V}\times \overline{V}\) is a reachability relation which is a relation such that \(\forall \left[ x\right] \in \overline{V}_a\) and \(\forall \left[ y\right] \in h(\left[ x\right] )\), \((\left[ x\right] ,\left[ y\right] )\in \rightsquigarrow \). The set of all abstractions is denoted by \(\mathcal {A}\). We designate the components of an abstraction A using the dotted notation by
(disequality relation) is a symmetric and irreflexive binary relation on \(\overline{V}\); (iii) \(V_v\subseteq V\) is a finite set of variables called visible variables; (iv) \(\overline{V}_a\subseteq \overline{V}\) is a subset of classes of variables called allocated variables; (v) \(h:\overline{V}_a\longrightarrow \overline{V}^*\) is a partial heap mapping which associates a tuple of classes of variables of arbitrary size to some class of allocated variables; (vi) \(\rightsquigarrow \subseteq \overline{V}\times \overline{V}\) is a reachability relation which is a relation such that \(\forall \left[ x\right] \in \overline{V}_a\) and \(\forall \left[ y\right] \in h(\left[ x\right] )\), \((\left[ x\right] ,\left[ y\right] )\in \rightsquigarrow \). The set of all abstractions is denoted by \(\mathcal {A}\). We designate the components of an abstraction A using the dotted notation by
 ,
,
 , etc. The set of invisible variables of A is
, etc. The set of invisible variables of A is
 .
.
Abstractions are taken modulo renaming of invisible variables: two abstractions, \(A_1\) and \(A_2\), are considered equal, denoted \(A_1=A_2\), if there exists a renaming \(\sigma \) of invisible variables such that \(A_1 = A_2\sigma \).
Example 2
Figure 1 graphically represents three abstractions denoted \(A^p_1\), \(A^r_1\) and \(A^q_1\). Equivalence classes are represented by circles and are labelled by variable names. Allocated classes are filled grey; invisible variables are prefixed with \(\exists \), and [ ] are omitted. Disequalities are represented with dashed lines, while heap and reachability relations are represented with tick resp. snaked arrows.
An SL-structure is a model of an abstraction if its store is coherent with the abstraction (i.e., it maps equal variables to the same location and disequal variables to different locations) and its heap contains at least all the reachability relations of the abstraction. However, the model may contain more allocated locations and paths between locations. On the other hand, an abstraction of an SL-structure captures exactly the visibility of variables in the store, the equivalence between variables and the reachability of locations in the heap; it abstracts the paths between locations labelled by (visible or invisible) variables and going through locations not labelled by some variable.
Definition 9
(Model and Abstraction). A structure \((\mathfrak {s},\mathfrak {h})\) is a model of an abstraction A, denoted by \((\mathfrak {s},\mathfrak {h}) \models A\), if there exists a functional extension \(\dot{\mathfrak {s}}\) of \(\mathfrak {s}\) satisfying the following conditions: (i)
 and
and
 ; (ii) If
; (ii) If
 then \(\dot{\mathfrak {s}}(x) = \dot{\mathfrak {s}}(y)\); (iii) If
then \(\dot{\mathfrak {s}}(x) = \dot{\mathfrak {s}}(y)\); (iii) If
 then \(\dot{\mathfrak {s}}(x) \ne \dot{\mathfrak {s}}(y)\); (iv) For all
then \(\dot{\mathfrak {s}}(x) \ne \dot{\mathfrak {s}}(y)\); (iv) For all
 , if
, if
 then \(\dot{\mathfrak {s}}(x) \in {{\,\textrm{dom}\,}}(\mathfrak {h})\); (v) For all
then \(\dot{\mathfrak {s}}(x) \in {{\,\textrm{dom}\,}}(\mathfrak {h})\); (v) For all
 if
if
 then \(\mathfrak {h}(\dot{\mathfrak {s}}(x)) = (\dot{\mathfrak {s}}(y_1),\dots ,\dot{\mathfrak {s}}(y_k))\); (vi) For all \(x,y\in V\), if
then \(\mathfrak {h}(\dot{\mathfrak {s}}(x)) = (\dot{\mathfrak {s}}(y_1),\dots ,\dot{\mathfrak {s}}(y_k))\); (vi) For all \(x,y\in V\), if
 then there exists a path \(\ell _0 \rightarrow _{\mathfrak {h}} \cdots \rightarrow _{\mathfrak {h}} \ell _n\) in \(\mathfrak {h}\) such that \(\ell _0=\dot{\mathfrak {s}}(x)\), \(\ell _n = \dot{\mathfrak {s}}(y)\) and \(\{\ell _1,\dots ,\ell _{n-1}\} \cap {{\,\textrm{img}\,}}(\dot{\mathfrak {s}}) = \emptyset \). If \((\mathfrak {s},\mathfrak {h}) \models A\) and the converses of Items (ii), (iii) and (vi) hold, then A is an abstraction of \((\mathfrak {s},\mathfrak {h})\). The set of all abstractions of \((\mathfrak {s},\mathfrak {h})\) is denoted by \(\mathfrak {abs}(\mathfrak {s},\mathfrak {h})\).
then there exists a path \(\ell _0 \rightarrow _{\mathfrak {h}} \cdots \rightarrow _{\mathfrak {h}} \ell _n\) in \(\mathfrak {h}\) such that \(\ell _0=\dot{\mathfrak {s}}(x)\), \(\ell _n = \dot{\mathfrak {s}}(y)\) and \(\{\ell _1,\dots ,\ell _{n-1}\} \cap {{\,\textrm{img}\,}}(\dot{\mathfrak {s}}) = \emptyset \). If \((\mathfrak {s},\mathfrak {h}) \models A\) and the converses of Items (ii), (iii) and (vi) hold, then A is an abstraction of \((\mathfrak {s},\mathfrak {h})\). The set of all abstractions of \((\mathfrak {s},\mathfrak {h})\) is denoted by \(\mathfrak {abs}(\mathfrak {s},\mathfrak {h})\).
Example 3
Consider the structure \((\mathfrak {s}_1,\mathfrak {h}_1)\) defined over the set of variables \(\{x,y\}\) with \(\mathfrak {s}_1(x)=\ell _1\), \(\mathfrak {s}_1(y)= \ell _2\ne \ell _1\), \(\mathfrak {h}_1(\ell _0)= (\ell _1,\ell _2)\). \(A^p_1\) from Fig. 1 is an abstraction of \((\mathfrak {s}_1,\mathfrak {h}_1)\) for \(\dot{\mathfrak {s}}_1(z)=\ell _0\). Moreover, \(A^p_1\) has as model \((\mathfrak {s}_2,\mathfrak {h}_2)\) with \(\mathfrak {s}_1(x)=\mathfrak {s}_1(y) = \ell _1\), \(\mathfrak {h}_1(\ell _0)= (\ell _1,\ell _1)\).
The following operations on abstractions are used in our abstraction process.
Definition 10
(Pure abstractions). The empty abstraction, denoted \(A_\texttt{emp}\), has all its components empty sets. Let \(V_0\) be a set of variables. The abstraction of equalities over \(V_0\), denoted \(A_{\approx }(V_0)\), is \(\langle V_0,\{V_0\},\emptyset ,V_0,\emptyset ,\emptyset ,\emptyset \rangle \), i.e., all variables are visible and in the same equivalence class. The abstraction of disequalities over \(V_0\) is \(A_{\not \approx }(V_0) = \langle V_0,\texttt{Id}_{V_0},V_0^2\smallsetminus \texttt{Id}_{V_0}, V_0,\emptyset ,\emptyset , \emptyset \rangle \), i.e., all variables are visible and pairwise distinct, and none is allocated.
Note that we identify equivalence relations with the set of their equivalence classes so that \(\{V_0\}\) denotes the relation \(\{(x,y) \;\vert \;x,y \in V_0\}\).
Definition 11
(Quantified abstractions). Let
 be a set of variables. The hiding of \(V_0\) in A, denoted by \(A_{\exists (V_0)}\), is the abstraction having the same components as A except the set of visible variables, i.e.,
be a set of variables. The hiding of \(V_0\) in A, denoted by \(A_{\exists (V_0)}\), is the abstraction having the same components as A except the set of visible variables, i.e.,
 .
.
Definition 12
(Separated abstractions). Let \(A_1\) and \(A_2\) be two abstractions; w.l.o.g., we consider that
 , i.e., the sets of invisible variables are disjoint (modulo renaming). Let
, i.e., the sets of invisible variables are disjoint (modulo renaming). Let
 and the equivalence relation \(\backsim _\star \) over \(V^\star \) defined by the transitive closure of
and the equivalence relation \(\backsim _\star \) over \(V^\star \) defined by the transitive closure of
 . Consider now the relation
. Consider now the relation
 over \(\overline{V^\star }_{\backsim _\star }\) (the set of equivalence classes of \(\backsim _\star \)) defined by the symmetric closure of the relation:
over \(\overline{V^\star }_{\backsim _\star }\) (the set of equivalence classes of \(\backsim _\star \)) defined by the symmetric closure of the relation:
 . If
. If
 is irreflexive, then \(A_1\) and \(A_2\) are separated.
is irreflexive, then \(A_1\) and \(A_2\) are separated.
Definition 13
(Separating abstractions). The separating composition \(A_1\star A_2\) of two separated abstractions \(A_1\) and \(A_2\) is the abstraction \(A_\star \) such that:
-
 ;
;
 ;
;
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 .
.
The following definitions are used to build the reachability relation in abstractions by replacing chains \(\left[ x_0\right] \mapsto \left[ x_1\right] \mapsto \ldots \mapsto \left[ x_{n-1}\right] \mapsto \left[ x_n\right] \) related by
 with the tuple \((\left[ x_0\right] ,\left[ x_n\right] )\) in
with the tuple \((\left[ x_0\right] ,\left[ x_n\right] )\) in
 if the variables \(x_i\) with \(i\in [1,n-1]\) are not “special ” for A.
if the variables \(x_i\) with \(i\in [1,n-1]\) are not “special ” for A.
Definition 14
(Roots). The roots of an abstraction A, \({{\,\textrm{root}\,}}(A)\), is the set of minimal sets of roots of
 . We denote by \(x\in _\forall {{\,\textrm{root}\,}}(A)\) or \(\left[ x\right] \in _\forall {{\,\textrm{root}\,}}(A)\) that \(\left[ x\right] \) belongs to all sets in \({{\,\textrm{root}\,}}(A)\) and by \(x\in _\exists {{\,\textrm{root}\,}}(A)\) or \(\left[ x\right] \in _\exists {{\,\textrm{root}\,}}(A)\) that \(\left[ x\right] \) belongs to at least one set in \({{\,\textrm{root}\,}}(A)\).
. We denote by \(x\in _\forall {{\,\textrm{root}\,}}(A)\) or \(\left[ x\right] \in _\forall {{\,\textrm{root}\,}}(A)\) that \(\left[ x\right] \) belongs to all sets in \({{\,\textrm{root}\,}}(A)\) and by \(x\in _\exists {{\,\textrm{root}\,}}(A)\) or \(\left[ x\right] \in _\exists {{\,\textrm{root}\,}}(A)\) that \(\left[ x\right] \) belongs to at least one set in \({{\,\textrm{root}\,}}(A)\).
As
 may contain cycles, roots are not uniquely defined. However, the algorithm for computing abstractions will ensure that \({{\,\textrm{root}\,}}(A)\) is always non-empty.
may contain cycles, roots are not uniquely defined. However, the algorithm for computing abstractions will ensure that \({{\,\textrm{root}\,}}(A)\) is always non-empty.
Definition 15
(Special and persistent variables). A variable
 is special if its equivalence class is a singleton and it satisfies one of the following conditions: (i) \(x\in _\forall {{\,\textrm{root}\,}}(A)\), i.e., x occurs in all sets of roots of A; (ii)
is special if its equivalence class is a singleton and it satisfies one of the following conditions: (i) \(x\in _\forall {{\,\textrm{root}\,}}(A)\), i.e., x occurs in all sets of roots of A; (ii)
 , i.e., x is not allocated, and there exists
, i.e., x is not allocated, and there exists
 such that
such that
 , i.e., x is reachable from an allocated variable; (iii) there exists
, i.e., x is reachable from an allocated variable; (iii) there exists
 such that \(y \in _\exists {{\,\textrm{root}\,}}(A)\) and
such that \(y \in _\exists {{\,\textrm{root}\,}}(A)\) and
 , i.e., x is pointed to by a possible root that is visible; (iv) there exists
, i.e., x is pointed to by a possible root that is visible; (iv) there exists
 such that \(\left[ y\right] \in _\forall {{\,\textrm{root}\,}}(A)\) and
such that \(\left[ y\right] \in _\forall {{\,\textrm{root}\,}}(A)\) and
 , i.e., x is pointed to by a necessary root that is visible or invisible. An invisible variable is persistent if it satisfies one of the items \((i)\) or \((ii)\) above. The set of persistent variables is denoted by
, i.e., x is pointed to by a necessary root that is visible or invisible. An invisible variable is persistent if it satisfies one of the items \((i)\) or \((ii)\) above. The set of persistent variables is denoted by
 .
.
Example 4
Abstractions \(A^p_1\) and \(A^q_1\) in Fig. 1 have a singleton set of roots built from one class: \({{\,\textrm{root}\,}}(A^p_1)=\{\{\left[ z\right] \}\}\) and \({{\,\textrm{root}\,}}(A^q_1)=\{\{\left[ y\right] \}\}\), while \(A^r_1\) has a unique set of roots but containing two classes \({{\,\textrm{root}\,}}(A^r_1)=\{\{\left[ z\right] ,\left[ t\right] \}\}\). The variable z is not visible in \(A^p_1\), but it is special and persistent since it fulfils the condition (i) of Definition 15. All the variables in \(A^q_1\) are special, but only y and u are persistent.
Definition 16
(Disconnected variable). A variable
 is disconnected if it satisfies the following two conditions: (1)
is disconnected if it satisfies the following two conditions: (1)
 , i.e., x is not allocated; and (2) for all
, i.e., x is not allocated; and (2) for all
 , i.e., x is not pointed by an allocated variable.
, i.e., x is not pointed by an allocated variable.
If a variable is disconnected, any variable in its equivalence class is also disconnected. Moreover, a disconnected variable cannot be special. For any equivalence relation
 , we denote by
, we denote by
 the restriction of
the restriction of
 to the elements distinct from x. Similarly, \(\overline{S} \smallsetminus x\) denotes the set \(\{\left[ y\right] \;\vert \;y \in S, y \ne x\}\), and for any relation \(\rightarrow \) on equivalence classes of
to the elements distinct from x. Similarly, \(\overline{S} \smallsetminus x\) denotes the set \(\{\left[ y\right] \;\vert \;y \in S, y \ne x\}\), and for any relation \(\rightarrow \) on equivalence classes of
 , \({\rightarrow } \smallsetminus x\) is the corresponding relation on equivalence classes of
, \({\rightarrow } \smallsetminus x\) is the corresponding relation on equivalence classes of
 .
.
Definition 17
(Deletion of variables not special). Let A be an abstraction and
 a variable that is not special. We define \({{\,\textrm{rem}\,}}(A,x)\), the abstraction obtained by deleting x from A as follows:
a variable that is not special. We define \({{\,\textrm{rem}\,}}(A,x)\), the abstraction obtained by deleting x from A as follows:
 with
with
 . We denote by \({{\,\textrm{rem}\,}}(A)\) the abstraction obtained by removing all variables not special in A.
. We denote by \({{\,\textrm{rem}\,}}(A)\) the abstraction obtained by removing all variables not special in A.
Definition 18
(Set of abstractions of a symbolic heap). Let \(\varphi \) be a symbolic heap formula of SL. The set of abstractions of a formula \(\varphi \), denoted \({{\,\textrm{abs}\,}}(\varphi )\), is inductively constructed using the rules in Tab. 1.
Example 5
Consider the pair \((\varphi ,\mathcal {R})\) introduced by Example 1. The abstractions of \(\varphi \) are built by firstly building the abstractions of the predicates r(z, u, t) and then q(y) — that calls r — defined by the rules in Eq. (7). Then \(\varphi = p(x,y)\) has two abstractions. The first is \(A^p_1\) from Fig. 1, obtained from the non-recursive rule of p. The second is \(A^p_2\) in Fig. 2, obtained from \(A_2\) by removing variables z and t using the procedure in Definition 17 because they are not special. The abstraction \(A_2\) is obtained by applying the rule [Sep] on \(A^q_1\) in Fig. 1, which is an abstraction of q(y), and the abstraction obtained by the rule [Pto] for \(x\rightarrow (y)\).
Given \(A\in {{\,\textrm{abs}\,}}(\varphi )\), we consider the implicit tree of construction of A using rules in Definition 18: every node of this tree is an abstraction created by one of the rules [Ex], [Pred] and [Sep], and every leaf is an abstraction of an atomic formula. Therefore, every node of this tree is associated with a formula, which is a sub-formula of an unfolding of \(\varphi \).
Definition 19
(Condition “Infinite Set of Invisible Variables” (ISIV)). The abstraction \(A\in {{\,\textrm{abs}\,}}(p(x_1,\dots ,x_n))\) satisfies the condition ISIV if there exists an abstraction \(A'\) in the construction tree of A such that:
-
1.
\(A'\) is associated with a renaming \(p(y_1,\dots ,y_n)\) of \(p(x_1,\dots ,x_n)\);
-
2.
A has strictly more persistent variables than \(A'\):
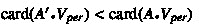 ;
; -
3.
the projections of abstractions A and \(A'\) on their visible variables are equal (modulo a renaming of the arguments \(x_i \leftarrow y_i\)).
Intuitively, the condition asserts that a “loop” exists in the unfolding tree of p, where persistent variables are introduced inside the loop. As one can go through the loop an arbitrary number of times, this entails that some branch exists with an unbounded number of persistent variables, which in turn entails that non-\(k\)-PCE-compatible models exist. If this condition is satisfied by one abstraction built during this step, the algorithm fails. The following theorem states that the algorithm is correct and complete:
Theorem 2
Let \(\varphi \) be a formula and let \(\mathcal {R}\) be an SID. We suppose that the construction of abstractions terminates without failing. If \(A \in {{\,\textrm{abs}\,}}(\varphi )\), then there exists a model \((\mathfrak {s}, \mathfrak {h})\) of \(\varphi \) such that A is an abstraction of \((\mathfrak {s}, \mathfrak {h})\). Moreover, if \(\varphi \) admits a model \((\mathfrak {s},\mathfrak {h})\), then there exists an abstraction A of \(\varphi \) such that \((\mathfrak {s},\mathfrak {h}) \models A\).
We also show that the algorithm terminates, provided the ISIV condition is used to dismiss pairs \((\varphi ,\mathcal {R})\) that are not \(k\)-PCE-compatible (thus that cannot admit any equivalent PCE pair, by Proposition 1):
Theorem 3
Let \(\varphi \) be a formula and let \(\mathcal {R}\) be an SID. If there exists \(k \in \mathbb {N}\) such that \((\varphi ,\mathcal {R})\) is \(k\)-PCE-compatible, then the computation of \({{\,\textrm{abs}\,}}(\varphi )\) terminates without failure (hence the ISIV condition is never fulfilled). Otherwise, the ISIV condition eventually applies during the computation of \({{\,\textrm{abs}\,}}(\varphi )\). Consequently, the problem of testing whether \((\varphi ,\mathcal {R})\) is k-PCE-compatible for some \(k \in \mathbb {N}\) is decidable.
6 Predicates with Exactly One Abstraction
We describe an algorithm reducing any pair \((\varPhi ,\mathcal {R})\) into an equivalent pair \((\varPhi ^\dagger ,\mathcal {R}^\dagger )\) such that every predicate atom admits exactly one abstraction with no invisible variables. We also get rid of some existential variables when possible. The eventual goal is to ensure that the rules that were obtained are established (in the sense of Definition 5). We need to introduce some definitions and notations. A disconnected set for an n-ary predicate p and an abstraction \(A\in {{\,\textrm{abs}\,}}(p(x_1,\dots ,x_n))\) is any subset I of \(\{ 1,\dots ,n\}\) such that all variables \(x_i\) for \(i\in I\) are disconnected in A. Let \(\mathcal {R}\) be an SID. Let \(x_1,\dots ,x_n,\dots \) be an infinite sequence of pairwise distinct variables, which will be used to denote the formal parameters of the predicates. For each n-ary predicate p occurring in \(\mathcal {R}\), for each abstraction \(A \in {{\,\textrm{abs}\,}}(p(x_1,\dots ,x_n))\) and for all disconnected sets I for p, A, we introduce a fresh predicate \(p^A_I\), of arity \(n+m-{{\,\textrm{card}\,}}(I)\), where
 . Intuitively, \(p^A_I\) will denote some “projection” of the structures corresponding to the abstraction A. The additional arguments will denote the invisible variables. The removed arguments correspond to disconnected variables.
. Intuitively, \(p^A_I\) will denote some “projection” of the structures corresponding to the abstraction A. The additional arguments will denote the invisible variables. The removed arguments correspond to disconnected variables.
Example 6
The predicate p, defined by rules on the left in Example 1, has two abstractions (one by rule), \(A^p_1\) and \(A^p_2\), where all roots are connected. In the same example, predicates q and r also have only one abstraction. For all these predicates, the sets I are always \(\emptyset \).
The rules associated with \(p^A_I\) are obtained from those associated with p as follows. For every formula \(\varphi \) such that \(p(x_1,\dots ,x_n)\Leftarrow _{\mathcal {R}}\varphi \), where \(\varphi \) is of the form
 and \(\varphi '\) contains no predicate symbol, and for all abstractions \(A_i \in {{\,\textrm{abs}\,}}(q_i(x_1,\dots ,x_{\#(q_i)}))\) (for \(i \in \llbracket {1,k}\rrbracket \)), we add the rule:
and \(\varphi '\) contains no predicate symbol, and for all abstractions \(A_i \in {{\,\textrm{abs}\,}}(q_i(x_1,\dots ,x_{\#(q_i)}))\) (for \(i \in \llbracket {1,k}\rrbracket \)), we add the rule:

if all the following conditions hold:
-
A is the abstraction computed from \(\varphi \) as explained in Definition 18, selecting \(A_i\) for the abstraction of \(q_i(x_1,\dots ,x_{\#(q_i)})\), i.e.,
 , where \(\{A''\} ={{\,\textrm{abs}\,}}(\varphi ')\) (since \(\varphi '\) contains no predicate) and \(A' = A_1\star \dots \star A_k\star A''\) is the abstraction computed from the matrix
, where \(\{A''\} ={{\,\textrm{abs}\,}}(\varphi ')\) (since \(\varphi '\) contains no predicate) and \(A' = A_1\star \dots \star A_k\star A''\) is the abstraction computed from the matrix
 of \(\varphi \).
of \(\varphi \). -
 (resp.
(resp.
 ) is the subsequence of \(x_1,\dots ,x_n\) (resp. of
) is the subsequence of \(x_1,\dots ,x_n\) (resp. of
 ) obtained by removing all components of rank \(j \in I\) (resp. \(j\in J_i\)). Intuitively, I and \(J_i\) denote the parameters that are removed from the arguments of p and \(q_i\), respectively.
) obtained by removing all components of rank \(j \in I\) (resp. \(j\in J_i\)). Intuitively, I and \(J_i\) denote the parameters that are removed from the arguments of p and \(q_i\), respectively. -
\(J_i\) is a subset of \(\{ 1,\dots ,\#(q_i)\}\), and for all variables z occurring as the j-th component of
 , the following equivalence holds: \(j \in J_i\) iff
, the following equivalence holds: \(j \in J_i\) iff
 and z is disconnected in \(A'\). Note that the last condition entails that the j-th component of
and z is disconnected in \(A'\). Note that the last condition entails that the j-th component of
 is also disconnected in \(A_i\); hence the predicate \({q_i}^{A_i}_{J_i}\) exists. Intuitively, a variable is removed if it is disconnected, and either it is existentially quantified in the rule, or it is a free variable that was removed from the argument of p.
is also disconnected in \(A_i\); hence the predicate \({q_i}^{A_i}_{J_i}\) exists. Intuitively, a variable is removed if it is disconnected, and either it is existentially quantified in the rule, or it is a free variable that was removed from the argument of p. -
\((x_1',\dots ,x_m')\) and
 are the sequences of invisible variables in A and \(A_i\), respectively (the order is irrelevant and can be chosen arbitrarily). We assume by renaming that the
are the sequences of invisible variables in A and \(A_i\), respectively (the order is irrelevant and can be chosen arbitrarily). We assume by renaming that the
 are pairwise disjoint.
are pairwise disjoint. -
\(\sigma \) is any substitution with
 and
and
 such that for all
such that for all
 and for all
and for all
 :
:
 . Intuitively, \(\sigma \) is applied to get rid of superfluous existential variables by instantiating them when it is possible, i.e., when the variable is known to be equal to a free variable or another existential variableFootnote 2.
. Intuitively, \(\sigma \) is applied to get rid of superfluous existential variables by instantiating them when it is possible, i.e., when the variable is known to be equal to a free variable or another existential variableFootnote 2. -
\(\varphi ''\) is obtained from \(\varphi '\) by removing all pure atoms containing a variable that is disconnected in \(A'\) and does not occur in
 .
. -
 is the sequence of variables occurring either in the formula \(\varphi ''\) or in the sequences
is the sequence of variables occurring either in the formula \(\varphi ''\) or in the sequences
 or
or
 (for some \(i \in \llbracket {1,k}\rrbracket \)) but not in \(\{x_1,\dots ,x_n,x_1',\dots ,x_m'\} \cup {{\,\textrm{dom}\,}}(\sigma )\) (again, the order is irrelevant). These variables correspond to variables from
(for some \(i \in \llbracket {1,k}\rrbracket \)) but not in \(\{x_1,\dots ,x_n,x_1',\dots ,x_m'\} \cup {{\,\textrm{dom}\,}}(\sigma )\) (again, the order is irrelevant). These variables correspond to variables from
 or
or
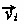 that can be eliminated during the computation of A using the rule introduced in Definition 17.
that can be eliminated during the computation of A using the rule introduced in Definition 17.
The obtained set of rules is denoted by \(\mathcal {R}^\dagger \). It is clear that \(\mathcal {R}^\dagger \) is finite (up to \(\alpha \)-renaming) if \(\mathcal {R}\) is finite and \({{\,\textrm{abs}\,}}(p(x_1,\dots ,x_n))\) is finite for all n-ary predicates p in \(\mathcal {R}\).
Example 7
The new rules for p, q, and r defined in the SID \(\mathcal {R}_1\) in Ex. 1 are given below:
The arity of predicates \(p_\emptyset ^{A^p_2}\) and \(q_\emptyset ^{A^q_1}\) has been changed to include the invisible but special variable u, and the predicate \(p_\emptyset ^{A^p_1}\) now does not have an invisible root any more.
Example 8
In this example, we show how disconnected variables may be eliminated. Let p, q be predicates defined by the rules: \(p(x,y) \Leftarrow \exists z.\, (x\rightarrow (y) \star q(x,z))\), \(q(x,y) \Leftarrow x \not \approx y\). \(p(x_1,x_2)\) and \(q(x_1,x_2)\) both admit one abstraction, \(A_p\) and \(A_q\), respectively, defined by:
The above transformation produces the rules: \(p^{A_p}_{\emptyset }(x,y) \Leftarrow (x\rightarrow (y)\star q^{A_q}_{\{2\}}(x))\) and \(q^{A_r}_{\{ 2\}}(x) \Leftarrow \texttt{emp}\). The variable z is eliminated, as it is disconnected in the abstraction corresponding to \(x\rightarrow (y) \star q(x,z)\). This yields the introduction of a predicate \(q^{A_r}_{\{2\}}\) in which the second argument of q is dismissed.
The above transformation may be applied to the formulas \(\varPhi \) occurring in pairs \((\varPhi ,\mathcal {R})\). Since the establishment condition applies only to the variables occurring in the rule and not to the existential variables of \(\varPhi \), there is no need to eliminate any predicate argument in this case; thus, we may simply take \(I = \emptyset \) for the predicates \(p^A_I\) such that p appears in \(\varPhi \). Predicates of the form \(q^B_I\) with \(I \ne \emptyset \) will never appear at the root level in \(\varPhi \), but they may appear in the rules of the predicates \(p^A_\emptyset \) (in practice, such rules will be computed on demand). More precisely, we denote by \(\varPhi ^\dagger \) the formula obtained from \(\varPhi \) by replacing every atom \(p(y_1,\dots ,y_n)\) in \(\varPhi \) by the formula
 , where
, where
 is the sequence of variables in
is the sequence of variables in
 (with arbitrary order). Note that in the case where \({{\,\textrm{abs}\,}}(p(x_1,\dots ,x_n)) = \emptyset \), \(p(y_1,\dots ,y_n)\) is replaced by an empty disjunction, i.e., by \({{\,\textrm{false}\,}}\). The properties of this transformation are stated by the following result:
(with arbitrary order). Note that in the case where \({{\,\textrm{abs}\,}}(p(x_1,\dots ,x_n)) = \emptyset \), \(p(y_1,\dots ,y_n)\) is replaced by an empty disjunction, i.e., by \({{\,\textrm{false}\,}}\). The properties of this transformation are stated by the following result:
Theorem 4
\((\varPhi ,\mathcal {R}) \equiv (\varPhi ^\dagger ,\mathcal {R}^\dagger )\). Moreover, for all predicates \(p_I^A\) defined in \(\mathcal {R}^\dagger \), the set
 contains exactly one abstraction.
contains exactly one abstraction.
7 Abstractions with Exactly One Root
We introduce an algorithm that transforms the considered SID by introducing and removing predicates such that the abstraction of each predicate p defined by the new \(\mathcal {R}\) has only one root. This transformation is done in two steps: first, change predicates with an abstraction without roots, and then change predicates with an abstraction with more than one root. The transformation may fail if the structures corresponding to a given recursive predicate have multiple roots, as such structures cannot be defined by PCE rules (e.g., two parallel lists of the same length).
Removal of Abstractions Without Root: Let us consider every predicate p such that its abstraction
 satisfies \({{\,\textrm{root}\,}}(A_p) = \emptyset \). Because the abstraction of p has no root, the associated structure has no allocated locations, and the predicate can only be unfolded into formulas that do not contain points-to. Thus, for each unfolding of p of abstraction A, which cannot be unfolded any more, it only contains equalities and disequalities that are abstracted in A by
satisfies \({{\,\textrm{root}\,}}(A_p) = \emptyset \). Because the abstraction of p has no root, the associated structure has no allocated locations, and the predicate can only be unfolded into formulas that do not contain points-to. Thus, for each unfolding of p of abstraction A, which cannot be unfolded any more, it only contains equalities and disequalities that are abstracted in A by
 and
and
 . As a consequence, we can create a formula \(\varphi _A = (\star _{i,j\in I_{\approx }}a_i\approx a_j) \star (\star _{i,j\in I_{\not \approx }}b_i \not \approx b_j)\) with
. As a consequence, we can create a formula \(\varphi _A = (\star _{i,j\in I_{\approx }}a_i\approx a_j) \star (\star _{i,j\in I_{\not \approx }}b_i \not \approx b_j)\) with
 and
and
 . We can then replace every occurrence of p with \(\varphi _A\).
. We can then replace every occurrence of p with \(\varphi _A\).
Removal of Abstractions With Several Roots: We suppose now that for all predicates p, the abstraction
 verifies \({{\,\textrm{root}\,}}(A_p)\ne \emptyset \). Now let us consider every predicate p such that its abstraction
verifies \({{\,\textrm{root}\,}}(A_p)\ne \emptyset \). Now let us consider every predicate p such that its abstraction
 has at least two roots, i.e., for all \(R\in {{\,\textrm{root}\,}}(A_p), {{\,\textrm{card}\,}}(R)\ge 2\). If p does not call itself, we unfold p by replacing each occurrence of p with its definition using the rules in SID. Otherwise, the transformation is considered impossible, and it fails.
has at least two roots, i.e., for all \(R\in {{\,\textrm{root}\,}}(A_p), {{\,\textrm{card}\,}}(R)\ge 2\). If p does not call itself, we unfold p by replacing each occurrence of p with its definition using the rules in SID. Otherwise, the transformation is considered impossible, and it fails.
At this point, if the transformation does not fail, we obtain:
Proposition 2
(Every abstraction has a single root). After applying the transformation in this section, for all predicates p, for all abstractions
 , there exists a set \(R\in {{\,\textrm{root}\,}}(A)\) such that \({{\,\textrm{card}\,}}(R) = 1\).
, there exists a set \(R\in {{\,\textrm{root}\,}}(A)\) such that \({{\,\textrm{card}\,}}(R) = 1\).
Remark 1
We wish to emphasize that the failure of the above operation does not imply that the transformation is unfeasible. For instance, one could, in principle, define two lists of arbitrary (possibly distinct) lengths using one single inductive predicate, adding elements in one of the lists in a non-deterministic way, although such a definition is very unlikely to occur in practice. Then, our algorithm would fail (as it will detect that the structure has two roots), although a PCE presentation exists. Extending the algorithm to cover such cases is part of future work.
8 Transformation into PCE Rules
The last step of the transformation is a procedure reducing any pair \((\varPhi ^\dagger ,\mathcal {R}^\dagger )\) into an equivalent pair \((\varPhi ^\ddagger ,\mathcal {R}^\ddagger )\) such that \(\varPhi ^\ddagger \) and \(\mathcal {R}^\ddagger \) are PCE formula resp. SID.
To this aim, we first introduce so-called derived predicates (adapted and extended from [4]), the rules of which can be computed from the rules defining predicate symbols. The aim is to extract from the call tree of a spatial atom the part that corresponds to another atom. Given a SID \(\mathcal {R}\) and two spatial atoms \(\gamma \) and \(\lambda \), we denote by \(\gamma {-}\!\!{\bullet }\lambda \) the atom defined by the following rules:

We assume that all such rules occur in \(\mathcal {R}\). Intuitively, \(\gamma {-}\!\!{\bullet }\lambda \) encodes a structure defined as the atom \(\lambda \) but in which a call to \(\gamma \) is removed. It is easy to see that \(\gamma {-}\!\!{\bullet }\lambda \) is unsatisfiable if \(\lambda \) is a points-to atom and \(\gamma \) is a predicate atom. By definition, \((x_1\rightarrow (x_2,\dots ,x_n)) {-}\!\!{\bullet }(y_1\rightarrow (y_2,\dots ,y_m))\) is equivalent to \(x_1 \approx y_1 \star \cdots \star x_n \approx y_n\) if \(m = n\) and unsatisfiable otherwise. These remarks can be used to simplify the rules above (e.g., by removing rules with unsatisfiable bodies).
For instance, given the rules \(p(x) \Leftarrow \exists y.\, (x\rightarrow (y) \star p(y))\) and \(p(x) \Leftarrow x\rightarrow ()\), the derived atoms \(p(x') {-}\!\!{\bullet }p(x)\) and \((x'\rightarrow ()) {-}\!\!{\bullet }p(x)\) both denote a list segment from x to \(x'\), whereas \((x'\rightarrow (x'')) {-}\!\!{\bullet }p(x)\) denotes a list with a “hole” at \(x'\). The corresponding rules are, after simplification:
The operator \({-}\!\!{\bullet }\) can be nested, for instance \((x_1 \rightarrow (x_1')) {-}\!\!{\bullet }(p(x_2) {-}\!\!{\bullet }p(x))\) denotes a list segment from x to \(x_2\) with a hole at \(x_1\).
Consider a rule \(\rho = p(x_1,\dots ,x_n) \Leftarrow \varphi \), where \(\varphi '\) denotes the quantifier-free formula such that
 . By Theorem 4, the formulas \(\varphi \) and \(\varphi '\) have unique abstractions \(A_\varphi \) and \(A_{\varphi '}\), respectively (in what follows the notations \(\left[ x\right] \) and \(\rightsquigarrow \) always refer to abstraction \(A_{\varphi '}\)). Recall that, at this point, establishment is ensured, and all roots are visible. As \(\varphi \) only has a unique abstraction, there is a unique \(k \in \llbracket {1,n}\rrbracket \) such that \(\left[ x_k\right] \) is the root of \(A_{\varphi }\) and the tuple pointed to by the location associated with \(x_k\) contains only locations associated with variables \(y_1,\dots ,y_m\) that are visible or special in \(A_\varphi \), with
. By Theorem 4, the formulas \(\varphi \) and \(\varphi '\) have unique abstractions \(A_\varphi \) and \(A_{\varphi '}\), respectively (in what follows the notations \(\left[ x\right] \) and \(\rightsquigarrow \) always refer to abstraction \(A_{\varphi '}\)). Recall that, at this point, establishment is ensured, and all roots are visible. As \(\varphi \) only has a unique abstraction, there is a unique \(k \in \llbracket {1,n}\rrbracket \) such that \(\left[ x_k\right] \) is the root of \(A_{\varphi }\) and the tuple pointed to by the location associated with \(x_k\) contains only locations associated with variables \(y_1,\dots ,y_m\) that are visible or special in \(A_\varphi \), with
 . To make the rule \(\rho \) PCE, it must be rewritten to have the form
. To make the rule \(\rho \) PCE, it must be rewritten to have the form
 , where \(\psi \) is a pure formula, and the root of each atom
, where \(\psi \) is a pure formula, and the root of each atom
 is in \(\{ y_1,\dots ,y_m\}\). There are two cases:
is in \(\{ y_1,\dots ,y_m\}\). There are two cases:
Case 1: Assume that \(\varphi \) contains a points-to atom \(x_k'\rightarrow (y_1',\dots ,y_l')\), with \(\left[ x_k'\right] =\left[ x_k\right] \) and \(\left[ y_i'\right] = \left[ y_i\right] \) for all \(i \in \llbracket {1,l}\rrbracket \). The formula \(\varphi '\) is of the form \(x_k'\rightarrow (y_1',\dots ,y_m') \star \psi \star \psi '\), where \(\psi \) contains only points-to and predicate atoms and \(\psi '\) is a pure formula. The formula \(\psi \) may be decomposed into \(\varphi _1\star \dots \star \varphi _{l'}\), where each formula \(\varphi _i\) allocates only variables z such that \(\left[ y_{j_i}\right] \rightsquigarrow ^* \left[ z\right] \), where \(y_{j_1}, \dots , y_{j_{l'}}\) are variables in \(\{ y_1,\dots ,y_l\}\) such that the \(\left[ y_{j_i}\right] \) are pairwise distinct. Such a decomposition necessarily existsFootnote 3 since \(\left[ x_k\right] \) is the root of \(\rightsquigarrow \), and every class reachable from \(\left[ x_k\right] \) must be reachable from one of the \(\left[ y_i\right] \). For \(i\in \llbracket {1,l'}\rrbracket \), if \(\varphi _i\) is not a predicate atom, then we create a fresh predicate \(q_i\) whose arguments are all the variables
 that appear in \(\varphi _i\), we create the rule
that appear in \(\varphi _i\), we create the rule
 , and we replace in \(\varphi \) the formula \(\varphi _i\) by
, and we replace in \(\varphi \) the formula \(\varphi _i\) by
 . We get a rule \(\rho '\) that is now PCE.
. We get a rule \(\rho '\) that is now PCE.
Case 2: Now assume that \(\varphi \) contains no such points-to atom \(x_k'\rightarrow (y_1',\dots ,y_l')\). We have to extract this points-to from some rule that, when unfolded, creates it and add it to a new rule equivalent to \(\rho \). Because \(A_\varphi \) is unique and because every predicate also has a unique abstraction, only one atom can allocate \(x_k\), and this atom must be a predicate atom (because of case 1). Thus \(\varphi '\) is of the form \(q(\vec {w}) \star \varphi ''\), where \(x_k\) is allocated in every model of \(q(\vec {w})\). By the previous construction, the atom \(q(\vec {w})\) may be replaced by \(x_k\rightarrow (y_1,\dots ,y_l) \star (x_k\rightarrow (y_1,\dots ,y_l) {-}\!\!{\bullet }q(\vec {w}))\). We get a new rule
 which fulfils the previous condition, and we may apply the transformation described in the previous item to \(\rho '\). The new rules associated with
which fulfils the previous condition, and we may apply the transformation described in the previous item to \(\rho '\). The new rules associated with
 are added to the set of rules.
are added to the set of rules.
The above transformations are applied until all rules are PCE. Note that termination is not guaranteed (indeed, not all \(k\)-PCE-compatible pairs \((\varPhi ,\mathcal {R})\) admit an equivalent PCE pair, and the existence of such a pair is undecidable by Theorem 1). To enforce termination in some cases, a form of memoization may be used: the predicates introduced above may be reused if the corresponding formulas are equivalent. As logical equivalence is hard to test (undecidable in general), we only check that the rules associated with both predicates are identical up to a renaming of existential variables and spatial predicates. In practice, termination may be ensured by imposing limitations on the number of rules or predicates. We show that if the transformation terminates, we obtain the desired result.
Theorem 5
Let \((\varPhi ^\dagger ,\mathcal {R}^\dagger )\) be any pair obtained by applying the transformations in Secs. 6 and 7. If the computation of \((\varPhi ^\ddagger ,\mathcal {R}^\ddagger )\) terminates, then \((\varPhi ^\dagger ,\mathcal {R}^\dagger ) \equiv (\varPhi ^\ddagger ,\mathcal {R}^\ddagger )\). Also, the SID \(\mathcal {R}^\ddagger \), and thus \(\varPhi ^\ddagger \), are PCE.
9 Experimental Evaluation and Conclusion
We devised an algorithm to construct PCE rules for a given formula (if possible). The existence of such a presentation is undecidable, but we identify a property called PCE-compatibility, which is decidable and weaker. Our algorithm helps to relax the rigid conditions on the PCE presentations. It is also able to construct PCE rules in some more complex cases by performing deep, global transformations on the rules. We have implemented an initial version of the algorithm in OCaml using the Cyclist [2] framework and applied it to benchmarks taken from this framework and SL-COMP [1]. The program comprises approximately 3000 lines of code. To ensure efficiency, the implemented procedure is somewhat simplified compared to the algorithm described in this paper: in Step Sect. 8, we avoid the use of derived predicates and instead employ a fixed-depth unfolding of predicate atoms (the other sections strictly adhere to the theoretical definitions). All tests are performed with a timeout of 30 seconds. The running time is low in most examples. In the 145 tested examples, 105 are successfully transformed into equivalent PCE-formulas, 20 trigger the ISIV condition (the structures are not \(k\)-PCE-compatible), 3 examples fail at Step Sect. 7 (recursive structures with multiple roots) and 17 other timeout. The program and input data are available at https://hal.science/hal-04549937. We find the results highly encouraging, as about 86% of the tested examples are successfully managed. Therefore, this tool may be used to provide a measure of the difficulty of the examples in the SL-COMP benchmark.
We end the paper by identifying some lines of future work. For efficiency, we first plan to refine the transformation by avoiding the systematic reduction to one-abstraction predicates given in Sect. 6. Indeed, this transformation is very convenient from a theoretical point of view but introduces some additional computational blow-up, which could be avoided in some cases. We wish to strengthen the definition of \(k\)-PCE-compatible ID in order to capture additional properties of PCE definitions. Notice that the semi-decidability of the PCE problem is an open question. Finally, it could also be interesting to extend the transformation to E-restricted IDs, a fragment of non-established IDs introduced in [4], for which the entailment is decidable.
Notes
- 1.
Indeed, to satisfy the connectivity condition the two lists must be defined in distinct atoms (as they are not connected). But then it is impossible to ensure that they have the same number of elements.
- 2.
In the latter case several substitutions exist, one of them can be chosen arbitrarily (the resulting rules are identical up to \(\alpha \)-renaming, e.g., \(\exists x \exists y (x \approx y \star q(x,y))\) can be written \(\exists x (x \approx y \star q(x,y)) \{ y \leftarrow x \}\) or \(\exists y (x \approx y \star q(x,y)) \{ x \leftarrow y \}\)).
- 3.
If several decompositions exist, then one of them is chosen arbitrarily.
References
SL-COMP website. https://sl-comp.github.io/
Brotherston, J., Gorogiannis, N., Petersen, R.L.: A generic cyclic theorem prover. In: Jhala, R., Igarashi, A. (eds.) APLAS 2012. LNCS, vol. 7705, pp. 350–367. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35182-2_25
Echenim, M., Iosif, R., Peltier, N.: Entailment checking in separation logic with inductive definitions is 2-EXPTIME hard. In: Albert, E., Kovacs, L. (eds.) LPAR23. LPAR-23: 23rd International Conference on Logic for Programming, Artificial Intelligence and Reasoning, vol. 73. EPiC Series in Computing, pp. 191–211. EasyChair, May 2020. ISSN: 2398-7340. https://easychair.org/publications/paper/DdNg, https://doi.org/10.29007/f5wh
Echenim, M., Iosif, R., Peltier., N.: Decidable entailments in separation logic with inductive definitions: beyond establishment. In: Baier, C., Goubault-Larrecq, J. (eds.) 29th EACSL Annual Conference on Computer Science Logic (CSL 2021), vol. 183. Leibniz International Proceedings in Informatics (LIPIcs), pp. 20:1–20:18, Dagstuhl, Germany, 2021. Schloss Dagstuhl - Leibniz-Zentrum für Informatik. https://drops.dagstuhl.de/entities/document/10.4230/ LIPIcs.CSL.2021.20, https://doi.org/10.4230/LIPIcs.CSL.2021.20
Echenim, M., Iosif, R., Peltier, N.: Unifying decidable entailments in separation logic with inductive definitions. In: Platzer, A., Sutcliffe, G. (eds.) CADE 2021. LNCS (LNAI), vol. 12699, pp. 183–199. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-79876-5_11
Echenim, M., Iosif, R., Peltier, N.: Entailment is Undecidable for Symbolic Heap Separation Logic Formulæ with Non-Established Inductive Rules. Inf. Process. Lett. 173:106169, January 2022. https://www.sciencedirect.com/science/article/pii/ S0020019021000843, https://doi.org/10.1016/j.ipl.2021.106169
Gu, X., Chen, T., Wu, Z.: A complete decision procedure for linearly compositional separation logic with data constraints. In: Olivetti, N., Tiwari, A. (eds.) IJCAR 2016. LNCS (LNAI), vol. 9706, pp. 532–549. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40229-1_36
Iosif, R., Rogalewicz, A., Simacek, J.: The tree width of separation logic with recursive definitions. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 21–38. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_2
Ishtiaq, S.S., O’Hearn, P.W.: BI as an assertion language for mutable data structures. In: Proceedings of the 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2001, pp. 14–26. Association for Computing Machinery, New York, January 2001. https://doi.org/10.1145/360204.375719
Matheja, C., Pagel, J., Zuleger, F.: A decision procedure for guarded separation logic complete entailment checking for separation logic with inductive definitions. ACM Trans. Comput. Logic 24(1), 1:1–1:76 (2023). https://doi.org/10.1145/3534927
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: Proceedings 17th Annual IEEE Symposium on Logic in Computer Science, pp. 55–74, Copenhagen, Denmark, July 2002. ISSN: 1043-6871. https://ieeexplore.ieee.org/document/1029817, https://doi.org/10.1109/LICS.2002.1029817
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Bozec, T., Peltier, N., Petitjean, Q., Sighireanu, M. (2024). What Is Decidable in Separation Logic Beyond Progress, Connectivity and Establishment?. In: Benzmüller, C., Heule, M.J., Schmidt, R.A. (eds) Automated Reasoning. IJCAR 2024. Lecture Notes in Computer Science(), vol 14740. Springer, Cham. https://doi.org/10.1007/978-3-031-63501-4_9
Download citation
DOI: https://doi.org/10.1007/978-3-031-63501-4_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63500-7
Online ISBN: 978-3-031-63501-4
eBook Packages: Computer ScienceComputer Science (R0)



 ;
;
 ;
;
 ;
; ;
; ;
; ;
; .
.
 ;
; , where
, where  of
of  (resp.
(resp.
 ) is the subsequence of
) is the subsequence of  ) obtained by removing all components of rank
) obtained by removing all components of rank  , the following equivalence holds:
, the following equivalence holds:  and z is disconnected in
and z is disconnected in  is also disconnected in
is also disconnected in  are the sequences of invisible variables in A and
are the sequences of invisible variables in A and  are pairwise disjoint.
are pairwise disjoint. and
and
 such that for all
such that for all
 and for all
and for all
 :
:
 . Intuitively,
. Intuitively,  .
. is the sequence of variables occurring either in the formula
is the sequence of variables occurring either in the formula  or
or
 (for some
(for some  or
or
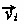 that can be eliminated during the computation of A using the rule introduced in Definition
that can be eliminated during the computation of A using the rule introduced in Definition