Abstract
This paper introduces a uniform substitution calculus for differential refinement logic dRL. The logic dRL extends the differential dynamic logic dL such that one can simultaneously reason about properties of and relations between hybrid systems. Refinements are useful e.g. for simplifying proofs by relating a concrete hybrid system to an abstract one from which the property can be proved more easily. Uniform substitution is the key to parsimonious prover microkernels. It enables the verbatim use of single axiom formulas instead of axiom schemata with soundness-critical side conditions scattered across the proof calculus. The uniform substitution rule can then be used to instantiate all axioms soundly. Access to differential variables in dRL enables more control over the notion of refinement, which is shown to be decidable on a fragment of hybrid programs.
Funding has been provided by an Alexander von Humboldt Professorship and the pilot program Core Informatics (KiKIT) of the Helmholtz Association (HGF).
You have full access to this open access chapter, Download conference paper PDF
Keywords
1 Introduction
Hybrid systems modeled by joint discrete dynamics and continuous dynamics are important and subtle systems in need of sound proofs [26] on account of their important applications [15, 16, 20, 22, 32]. Since such systems are important to get right, hybrid systems verification techniques themselves should be sound. Uniform substitution [24, 25, 27, 28], originally phrased by Church for first-order logic [10, §35,40], has been identified as the key technique reducing the soundness-critical core to a prover microkernel and is behind the KeYmaera X prover [14].
This paper designs a corresponding uniform substitution proof calculus for differential refinement logic (dRL) [19]. The logic dRL is unique in its capabilities of proving simultaneous hybrid systems properties and hybrid systems refinement relations. This ability of dRL has been shown to be beneficial for establishing refinement relations of system implementations to verification abstractions and for relating time-triggered implementation models to event-triggered verification models [18]. The latter relation overcomes a stark divide in embedded system design principles while combining ease of verification with ease of implementation in ways that neither design paradigm alone supports. But such proving power only helps practical system verification if the theoretical proof calculi are implemented in a sound way and, in fact, dRL has not yet been implemented at all. Such an implementation is significantly simplified and significantly easier to get sound by identifying a uniform substitution calculus, which has no axiom schemata with their usual side conditions (and the algorithms implementing them) but merely a finite list of concrete dRL formulas as axioms. Reasoning directly with these concrete formulas also makes the proofs easier as the conditions are checked only when uniform substitution is used. This means that a direct consequence of the axioms could have more admissible substitution instances than the axioms themselves, whereas with schemata, the side conditions would pile up and not generalize as well. Other beneficial side effects include the fact that dRL now acquires a Hilbert-style proof calculus that is significantly more flexible and also more modular than dRL ’s previous sequent calculus.
Challenges include the fact that uniform substitution calculi for hybrid systems give a differential-form semantics to differentials and differential symbols [25], which is critical to obtain logic-based decision procedures for differential equation invariants [30], but also renders some sequent calculus proof rules of dRL unsound due to the resulting finer-grained view on differential equations. The flip side is that this finer view distinguishes widely different classes of differential equations better, thereby making it easier to tell apart different differential equations that merely coincide on the overall reachable set while having different temporal behavior. This difference is exploited here to obtain a decidability result for refinement for a fragment of hybrid systems. Other challenges to overcome are the unexpected definition of free variables of refinements, which are required for soundness. The core of the resulting calculus has been implemented in KeYmaera XFootnote 1, extending the prover microkernel in 4 h of work with about 300 lines of code, mostly spent on writing down all the new axioms.
2 Related Work
Hybrid programs in dRL form a Kleene algebra with tests [17]. Program equivalence for Kleene algebra with tests is known to be decidable for abstract atomic programs. Refinement \(\alpha \le \beta \) can be recovered and defined as \({\alpha }\cup {\beta } =\beta \), but that duplicates reasoning about \(\beta \). Certain classes of hypotheses can be added to the theory, e.g. Hoare-like triples \(?p;\alpha ;?\lnot q ={? false }\), without breaking the decidability [11]. This however does not extend when limited commutativity is allowed, which arises even in the discrete fragment: \(({x}{:}{=}{2};{y}{:}{=}{3}) =({y}{:}{=}{3};{x}{:}{=}{2})\) but \(({x}{:}{=}{2};{x}{:}{=}{3}) \ne ({x}{:}{=}{3};{x}{:}{=}{2})\). KAT with only discrete assignments has been studied as Schematic KAT [4]. dRL can derive the axioms of Schematic KAT, but also allows reasoning with continuous dynamics and differential equations.
The Event-B method [1] is a formalism for reasoning about discrete models where the primary mechanism is refinement to check the conformance between abstract models and more detailed ones. Multiple different formalisms have been proposed. Hybrid Event-B [2, 5, 6] is an extension with tool support [8] for hybrid systems with events corresponding to discrete and continuous evolutions. These continuous steps are however abstracted by the invariants they are assumed to satisfy. Event-B can also be extended with theories [9]. By adding some axioms about differential equations, it allows refinement reasoning with some continuous dynamics [3, 12]. In contrast, dRL captures the continuous dynamics directly and proves the invariants as a consequence of the continuous dynamics.
Uniform substitution was proposed by Alonzo Church for first-order logic to capture axioms instead of axiom schemata [10, §35,40]. Modern uniform substitution originated for dL to support hybrid systems theorem proving in simple ways [25], extended to hybrid games in differential game logic dGL [27], and to communicating parallel programs \(\textsf {dL} {}_{\text {CHP}}\) [7]. This work is complementing the approach by adding refinement reasoning in a uniform substitution calculus for hybrid systems. Developing uniform substitution calculi are key to the design of small soundness-critical prover microkernels such as KeYmaera X [14].
3 Differential Refinement Logic dRL
Differential refinement logic dRL [19] extends the differential dynamic logic dL for hybrid systems [23] with a first-class refinement operator \(\le \) on hybrid systems. This section presents differential-form dRL, which prepares dRL for the features needed for dL ’s uniform substitution axiomatization, most notably the inclusion of differential terms alongside function symbols, predicate symbols, and program constant symbols, but also the requisite inclusion of differential variable symbols. Differential terms \((\theta )'\) are the fundamental logical device with which to enable sound [25] and complete [29, 30] reasoning about differential equations.
3.1 Syntax
This section defines the syntax of the differential refinement logic dRL. The set of all variables is \(\mathcal {V}\). To each variable \(x \in \mathcal {V}\) is associated a differential symbol \({x}^{\prime }\) which is also in \(\mathcal {V}\). Its purpose is to use \({x}^{\prime }\) to refer to the time-derivative of variable x during a differential equation, but also to cleverly relay that information to surrounding formulas in a sound way [25]. It is this (crucial) presence of differential symbols, that gives differential-form dRL a refined notion of refinement, especially of differential equations, compared to its sequent calculus predecessor [19].
Definition 1
(Terms). Terms are defined by the grammar below where \(x \in \mathcal {V}\) is a variable,
 is a function symbol of arity n and \(\theta ,\eta ,\theta _{1},\dots ,\theta _{n}\) are terms:
is a function symbol of arity n and \(\theta ,\eta ,\theta _{1},\dots ,\theta _{n}\) are terms:

Terms have the usual arithmetic operations and function symbols. They also have differentials of terms \((\theta )'\) which describe how the value of \(\theta \) changes locally depending on the values of the differential symbols associated to the variables of \(\theta \).
Definition 2
(Formulas). Formulas are defined by the grammar below where \(\theta ,\eta ,\theta _{1},\dots ,\theta _{n}\) are terms, \(p\) is a predicate symbol of arity \(n,\phi ,\psi \) are formulas and \(\alpha , \beta \) are hybrid programs (Definition 3):

In addition to the operators of first-order logic of real arithmetic, formulas also contain the dL modality
 which expresses that the formula \(\phi \) holds after all possible runs of the hybrid program \(\alpha \). dRL extends dL with the refinement operator \(\alpha \le \beta \) which expresses that \(\alpha \) refines \(\beta \) as \(\beta \) has more behaviors than \(\alpha \): it is true in a state \(\nu \) if all states reachable by hybrid program \(\alpha \) from \(\nu \) can be reached by hybrid program \(\beta \). The program equivalence \(\alpha =\beta \) is shorthand for \(\alpha \le \beta \wedge \beta \le \alpha \). This will be made explicit by axiom (\(=\)) in Sect. 5.
which expresses that the formula \(\phi \) holds after all possible runs of the hybrid program \(\alpha \). dRL extends dL with the refinement operator \(\alpha \le \beta \) which expresses that \(\alpha \) refines \(\beta \) as \(\beta \) has more behaviors than \(\alpha \): it is true in a state \(\nu \) if all states reachable by hybrid program \(\alpha \) from \(\nu \) can be reached by hybrid program \(\beta \). The program equivalence \(\alpha =\beta \) is shorthand for \(\alpha \le \beta \wedge \beta \le \alpha \). This will be made explicit by axiom (\(=\)) in Sect. 5.
Note the fundamental difference between dRL modal formula
 , which expresses that all runs of hybrid program \(\alpha \) satisfy dRL formula \(\phi \), compared to the dRL refinement formula \(\alpha \le \beta \), which expresses that all runs of hybrid program \(\alpha \) are also runs of hybrid program \(\beta \). Both dRL formulas refer to the runs of a hybrid program \(\alpha \), but only the former states a property of the (final) states reached, while only the latter relates the overall transition behavior of hybrid program \(\alpha \) to that of another program. Just like
, which expresses that all runs of hybrid program \(\alpha \) satisfy dRL formula \(\phi \), compared to the dRL refinement formula \(\alpha \le \beta \), which expresses that all runs of hybrid program \(\alpha \) are also runs of hybrid program \(\beta \). Both dRL formulas refer to the runs of a hybrid program \(\alpha \), but only the former states a property of the (final) states reached, while only the latter relates the overall transition behavior of hybrid program \(\alpha \) to that of another program. Just like
 , formula \(\alpha \le \beta \) is a dRL formula and not just a judgment, so it can be true in some states and false in others. This makes it possible to easily express conditional refinement as \(\phi \rightarrow \alpha \le \beta \) meaning that if \(\phi \) is true initially, then \(\alpha \) refines \(\beta \). The logic dRL is closed under all operators. For example the dRL formula
, formula \(\alpha \le \beta \) is a dRL formula and not just a judgment, so it can be true in some states and false in others. This makes it possible to easily express conditional refinement as \(\phi \rightarrow \alpha \le \beta \) meaning that if \(\phi \) is true initially, then \(\alpha \) refines \(\beta \). The logic dRL is closed under all operators. For example the dRL formula
 expresses that after all runs of \(\alpha \) it is the case that all runs of \(\beta \) are also runs of \(\gamma \). Just like in an ordinary implication, \(\phi \rightarrow \alpha \le \beta \) says nothing about what happens when the initial state does not satisfy \(\phi \). Just like ordinary dynamic logic modalities,
expresses that after all runs of \(\alpha \) it is the case that all runs of \(\beta \) are also runs of \(\gamma \). Just like in an ordinary implication, \(\phi \rightarrow \alpha \le \beta \) says nothing about what happens when the initial state does not satisfy \(\phi \). Just like ordinary dynamic logic modalities,
 says nothing about what happens before program \(\alpha \) ran. Indeed, this extended capabilities that dRL is closed under all operators will add to its expressibility and the eloquence of its uniform substitution proof calculus.
says nothing about what happens before program \(\alpha \) ran. Indeed, this extended capabilities that dRL is closed under all operators will add to its expressibility and the eloquence of its uniform substitution proof calculus.
Definition 3
(Hybrid Programs). Hybrid programs are defined by the grammar below where x is a variable, \(\theta \) is a term, \(a\) is a program constant, \(\psi \) is a differential-free formula and \(\alpha ,\beta \) are hybrid programs:

The test \(?\psi \) behaves like a skip if the formula \(\psi \) is true in the current state and blocks the system otherwise. The assignment
 instantaneously updates the value of the variable x to the value of the term \(\theta \). The nondeterministic assignment
instantaneously updates the value of the variable x to the value of the term \(\theta \). The nondeterministic assignment
 updates the value of the variable x to an arbitrary value. The differential equation
updates the value of the variable x to an arbitrary value. The differential equation
 behaves like a continuous evolution where both the differential equation \({x}^{\prime }=\theta \) and the evolution domain \(\psi \) holds. The nondeterministic choice \({\alpha }\cup {\beta }\) can behave like either \(\alpha \) or \(\beta \). The sequence \(\alpha ;\beta \) behaves like \(\alpha \) followed by \(\beta \). The nondeterministic repetition \(\alpha ^{*}\) behaves like \(\alpha \) repeated an arbitrary natural number of times.
behaves like a continuous evolution where both the differential equation \({x}^{\prime }=\theta \) and the evolution domain \(\psi \) holds. The nondeterministic choice \({\alpha }\cup {\beta }\) can behave like either \(\alpha \) or \(\beta \). The sequence \(\alpha ;\beta \) behaves like \(\alpha \) followed by \(\beta \). The nondeterministic repetition \(\alpha ^{*}\) behaves like \(\alpha \) repeated an arbitrary natural number of times.
Example 1
(Modelling safe breaking). Let us consider a car that needs to stop before a wall at distance m. It starts from a safe position and can accelerate with acceleration A if some safety condition \(\text {safe}_T(x)\) is true or brake with braking force B. The controller is run at most every T seconds. Proving its safety can be achieved by proving the following dRL formula:

Such system, called time-triggered, can be refined to a event-triggered system where the controller is sure to run before a critical event, leaving the domain E(x), occurs. Event-triggered systems are easier to verify but less realistic. With dRL and the axiom ([\(\le \)]) below, the time-triggered system can be proved safe by proving the safety of the event-triggered system and the refinement between the two systems:

3.2 Semantics
A state \(\nu \) is a mapping \(\mathcal {V}\rightarrow \mathbb {R}\). The state
 agrees with the state \(\nu \) except for the variable x whose value is \(r\in \mathbb {R}\). State \(\omega \) is a U-variation of \(\nu \) if \(\omega \) and \(\nu \) are equal on the complement \(U^\complement \) of that set of variables U. For instance,
agrees with the state \(\nu \) except for the variable x whose value is \(r\in \mathbb {R}\). State \(\omega \) is a U-variation of \(\nu \) if \(\omega \) and \(\nu \) are equal on the complement \(U^\complement \) of that set of variables U. For instance,
 is an \(\{x\}\)-variation of \(\nu \). The set of all states is \(\mathcal {S}\). The interpretation of a function symbol of arity n in interpretation I is a smooth function \(I{(f)}: \mathbb {R}^n\rightarrow \mathbb {R}\).
is an \(\{x\}\)-variation of \(\nu \). The set of all states is \(\mathcal {S}\). The interpretation of a function symbol of arity n in interpretation I is a smooth function \(I{(f)}: \mathbb {R}^n\rightarrow \mathbb {R}\).
Definition 4
(Term semantics). The semantics of a term \(\theta \) in interpretation I and state \(\nu \) is its value \(I\nu \llbracket {\theta }\rrbracket \in \mathbb {R}\) and is defined as follows:
-
1.
\(I\nu \llbracket {x} \rrbracket = \nu (x)\)
-
2.
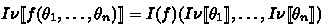
-
3.
\(I\nu \llbracket {\theta + \eta } \rrbracket = I\nu \llbracket {\theta }\rrbracket + I\nu \llbracket {\eta }\rrbracket \)
-
4.
\(I\nu \llbracket {\theta \cdot \eta }\rrbracket = I\nu \llbracket {\theta }\rrbracket \cdot I\nu \llbracket {\eta }\rrbracket \)
-
5.

The partial derivative \(\frac{\mathrm {\partial }I\nu \llbracket {\theta }\rrbracket }{\mathrm {\partial }x} \) corresponds to the derivative of the one-dimensional function \(X \mapsto I\nu ^{X}_{x}\llbracket {\theta }\rrbracket \) at \(X=\nu (x)\). Since \(I\nu \llbracket {\theta }\rrbracket \) denotes a smooth function, the derivative always exists.
Since hybrid programs appear in formulas and vice versa, the interpretation of hybrid programs and formulas is defined by simultaneous induction. The interpretation of a predicate symbol of arity n in interpretation I is an n-ary relation
 . The interpretation of a program constant symbol \(a\) in interpretation I is a state-transition relation
. The interpretation of a program constant symbol \(a\) in interpretation I is a state-transition relation
 where \( (\nu ,\omega ) \in I \llbracket {a}\rrbracket \) iff the program constant \(a\) can reach the state \(\omega \) starting from the state \(\nu \).
where \( (\nu ,\omega ) \in I \llbracket {a}\rrbracket \) iff the program constant \(a\) can reach the state \(\omega \) starting from the state \(\nu \).
Definition 5
(dRL semantics). The semantics of a formula \(\phi \) for an interpretation I is the subset \(I\llbracket {\phi }\rrbracket \subseteq \mathcal {S}\) of states in which \(\phi \) is true and defined as:
-
1.
\(\nu \in I \llbracket {\theta \le \eta }\rrbracket \) iff \(I\nu \llbracket {\theta }\rrbracket \le I\nu \llbracket {\eta }\rrbracket \)
-
2.

-
3.
\(\nu \in I \llbracket {\lnot \phi }\rrbracket \) iff \(\nu \notin I \llbracket {\phi }\rrbracket \)
-
4.
\(\nu \in I \llbracket {\phi \wedge \psi }\rrbracket \) iff \(\nu \in I \llbracket {\phi }\rrbracket \) and \(\nu \in I \llbracket {\psi }\rrbracket \)
-
5.
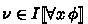 iff \( \nu ^{r}_{x} \in I \llbracket {\phi }\rrbracket \) for all \(r\in \mathbb {R}\)
iff \( \nu ^{r}_{x} \in I \llbracket {\phi }\rrbracket \) for all \(r\in \mathbb {R}\) -
6.
 iff \(\omega \in I \llbracket {\phi }\rrbracket \) for all \((\nu ,\omega )\in I \llbracket \alpha \rrbracket \)
iff \(\omega \in I \llbracket {\phi }\rrbracket \) for all \((\nu ,\omega )\in I \llbracket \alpha \rrbracket \) -
7.
\(\nu \in I \llbracket {\alpha \le \beta }\rrbracket \) iff \((\nu ,\omega )\in I \llbracket \beta \rrbracket \) for all \((\nu ,\omega )\in I \llbracket \alpha \rrbracket \)
A formula \(\phi \) is valid in I if \(I \llbracket {\phi }\rrbracket = \mathcal {S}\). A formula \(\phi \) is valid if it is valid in all interpretations.
Definition 6
(Transition semantics of programs). The semantics of a hybrid program \(\alpha \) for an interpretation I is the transition relation \(I \llbracket \alpha \rrbracket \subseteq \mathcal {S}\times \mathcal {S}\) and is defined as follows:
-
1.

-
2.

-
3.

-
4.

-
5.

-
6.
\( I \llbracket {\alpha }\cup {\beta } \rrbracket = I \llbracket \alpha \rrbracket \cup I \llbracket \beta \rrbracket \)
-
7.

-
8.

Most importantly, \(\alpha \le \beta \) is true in a state \(\nu \) iff all states \(\omega \) reachable from \(\nu \) by running program \(\alpha \) are also reachable by running \(\beta \) from \(\nu \).
The transition for a differential equation
 synchronizes the differential symbol \({x}^{\prime }\) with the current time-derivative of x, i.e. \(\theta \), and then evolves the system continuously along the solution \(\varphi \) of the differential equation \({x}^{\prime }=\theta \) within the domain \(\psi \). Differential equations are the only hybrid programs that intrinsically relate variables with their associated differential symbol.
synchronizes the differential symbol \({x}^{\prime }\) with the current time-derivative of x, i.e. \(\theta \), and then evolves the system continuously along the solution \(\varphi \) of the differential equation \({x}^{\prime }=\theta \) within the domain \(\psi \). Differential equations are the only hybrid programs that intrinsically relate variables with their associated differential symbol.
As differential equations effectively change the value of differential symbols, this is taken into account in the semantics of refinements. The differential equations \({x}^{\prime } = 1\) and \({x}^{\prime } = 2\) are not equivalent: although both can reach the same values for x, their respective end states will always have a different value for \({x}^{\prime }\). This behavior differs from the original semantics of dRL [19]. Intuitively, this notion of refinement corresponds to assuming that differential equations evolve with a global time \({t}^{\prime }=1\). Other extensions of dL like \(\textsf {dL} {}_{\text {CHP}}\) [7] already assume the presence of such global time. This property allows to express refinements of differential equations as a dL formula as shown in the axiom (ODE) below.
3.3 Static Semantics
Uniform substitution relies on the notions of free and bound variables to prevent any unsound substitution attempts. Static semantics gives a definition for free and bound variables of terms, formulas and hybrid programs based on their (dynamic) semantics, which can be defined as in dL [25]:
Definition 7
(Static semantics). The static semantics defines the free variables \(\textsf{FV}(\theta )\), \(\textsf{FV}(\phi )\) and \(\textsf{FV}(\alpha )\), which are the variables whose values the expression depends on, and the bound variables \(\textsf{BV}(\alpha )\), which are the variables whose values may change during the execution of \(\alpha \). They are defined formally as follows:

Free and bounds variables are the only information needed about the logic to ensure that the result of uniform substitution is only defined when sound. The coincidence lemmas [25] show that the truth-values of formulas only depend on their free variables and the interpretation of the symbols appearing in them (similarly for terms and hybrid programs). The set of function, predicate, and program symbols appearing in a formula, term or hybrid program is denoted \(\varSigma ({\cdot })\).
Lemma 1
(Coincidence for terms [25]). The set \(\textsf{FV}(\theta )\) is the smallest set with the coincidence property for \(\theta \): If
 on \(V\supseteq \textsf{FV}(\theta )\) and
on \(V\supseteq \textsf{FV}(\theta )\) and
 on \(\varSigma (\theta )\), then \(I\nu \llbracket {\theta }\rrbracket = J\tilde{\nu } \llbracket {\theta }\rrbracket \).
on \(\varSigma (\theta )\), then \(I\nu \llbracket {\theta }\rrbracket = J\tilde{\nu } \llbracket {\theta }\rrbracket \).
Lemma 2
(Coincidence for formulas [25]). The set \(\textsf{FV}(\phi )\) is the smallest set with the coincidence property for \(\phi \): If
 on \(V\supseteq \textsf{FV}(\phi )\) and
on \(V\supseteq \textsf{FV}(\phi )\) and
 on \(\varSigma (\phi )\), then \(\nu \in I \llbracket {\phi } \rrbracket \) iff \(\tilde{\nu } \in J \llbracket {\phi } \rrbracket \).
on \(\varSigma (\phi )\), then \(\nu \in I \llbracket {\phi } \rrbracket \) iff \(\tilde{\nu } \in J \llbracket {\phi } \rrbracket \).
Lemma 3
(Coincidence for hybrid programs [25]). The set \(\textsf{FV}(\alpha )\) is the smallest set with the coincidence property for \(\alpha \): If
 on \(V\supseteq \textsf{FV}(\alpha )\) and
on \(V\supseteq \textsf{FV}(\alpha )\) and
 on \(\varSigma (\alpha )\), then \((\nu ,\omega ) \in I \llbracket \alpha \rrbracket \) implies \((\tilde{\nu }, \tilde{\omega }) \in J \llbracket \alpha \rrbracket \) for some
on \(\varSigma (\alpha )\), then \((\nu ,\omega ) \in I \llbracket \alpha \rrbracket \) implies \((\tilde{\nu }, \tilde{\omega }) \in J \llbracket \alpha \rrbracket \) for some
 with
with
 on V.
on V.
The proof [25] requires a mutual induction on the structure of the formula and hybrid program to show that \(I \llbracket {\phi }\rrbracket = J \llbracket {\phi }\rrbracket \) and \(I \llbracket \alpha \rrbracket = J \llbracket \alpha \rrbracket \) which extends to the refinement case. The rest is done by induction on the set of variables S where the states \(\nu \) and
 can differ.
can differ.
Lemma 4
(Bound effect [25]). The set \(\textsf{BV}(\alpha )\) is the smallest set with the bound effect property for \(\alpha \): If \((\nu ,\omega ) \in I \llbracket \alpha \rrbracket \), then \(\nu = \omega \) on \(\textsf{BV}(\alpha )^\complement \).
These sets are the smallest sets with the coincidence property, which means that all conservative extensions of these sets can also be used soundly. We define \(\mathop {\text {FV}}(\theta ),\mathop {\text {FV}}(\phi ),\mathop {\text {FV}}(\alpha )\) and \(\mathop {\text {BV}}(\alpha )\) as such overapproximations that can be computed syntactically. Computing the free variables for a formula
 requires the must-bound variables of the hybrid program \(\alpha \), written \(\text {MBV}(\alpha )\). They represent the variables that will be written in all executions of \(\alpha \). These sets are given in [31] and are constructed in a standard way [25], except for the new refinement operator.
requires the must-bound variables of the hybrid program \(\alpha \), written \(\text {MBV}(\alpha )\). They represent the variables that will be written in all executions of \(\alpha \). These sets are given in [31] and are constructed in a standard way [25], except for the new refinement operator.
Since the behavior of hybrid program \(\alpha \) and \(\beta \) only depends on their respective free variables (Lemma 3), it would be tempting to define \(\mathop {\text {FV}}(\alpha \le \beta ) = \mathop {\text {FV}}(\alpha )\cup \mathop {\text {FV}}(\beta )\) stating that the refinement depends on the variables for which either program depends on. Somewhat surprisingly, this would be unsound for reasons that truly touch on the nature of refinement. Take the refinement formula
 and a state \(\nu \) with \(\nu (x) = 0\). Then
and a state \(\nu \) with \(\nu (x) = 0\). Then
 . However if the initial value of x is 1, then the refinement holds:
. However if the initial value of x is 1, then the refinement holds:
 , because the assignment
, because the assignment
 has no effect. In fact
has no effect. In fact
 even though
even though
 . To obtain a sound definition of \(\mathop {\text {FV}}(\alpha \le \beta )\), one needs to take into account the variables that may be written in one program, \(\mathop {\text {BV}}(\alpha )\cup \mathop {\text {BV}}(\beta )\), but that can also remain unmodified (which makes them depend on their initial values), so not in \(\text {MBV}(\alpha )\cap \text {MBV}(\beta )\). Hence, the (syntactic) free variables of a refinement are defined as follows:
. To obtain a sound definition of \(\mathop {\text {FV}}(\alpha \le \beta )\), one needs to take into account the variables that may be written in one program, \(\mathop {\text {BV}}(\alpha )\cup \mathop {\text {BV}}(\beta )\), but that can also remain unmodified (which makes them depend on their initial values), so not in \(\text {MBV}(\alpha )\cap \text {MBV}(\beta )\). Hence, the (syntactic) free variables of a refinement are defined as follows:
With this definition for refinements as the only but notable outlier to an otherwise standard definition of the syntatic computations for a static semantics [25], the static semantics \(\mathop {\text {FV}}(\phi )\) etc. can be proved to be sound overapproximations of the static semantics \(\textsf{FV}(\phi )\) from Definition 7 and thereby enjoy the coincidence Lemmas 1–3 and the bound effect Lemma 4, respectively.
Lemma 5
(Soundness of static semantics). For all terms \(\theta \), formulas \(\phi \) and hybrid programs \(\alpha \):
The proof of \(\mathop {\text {FV}}(\cdot )\supseteq \textsf{FV}(\cdot )\) for formulas and hybrid programs is the only case affected by the addition of refinement operators compared to prior proofs [25, Lem. 17]. It is proved by induction on the structure of the formulas and hybrid programs. For hybrid programs, the property shown for \(\mathop {\text {FV}}(\alpha )\) is stronger than the coincidence property from Lemma 3, enforcing
 on \(V\cup \text {MBV}(\alpha )\) rather than V.
on \(V\cup \text {MBV}(\alpha )\) rather than V.
For the case of the refinement operator \(\alpha \le \beta \), the main insight is visible when proving that \(\tilde{\nu }\in J \llbracket {\alpha \le \beta }\rrbracket \) implies \( \nu \in I \llbracket {\alpha \le \beta }\rrbracket \) with
 on V and
on V and
 on \(\varSigma (\alpha \le \beta )\). For any \((\nu ,\omega )\in I \llbracket \alpha \rrbracket \), we have \((\tilde{\nu },\tilde{\omega }) \in J \llbracket \alpha \rrbracket \), \((\tilde{\nu },\tilde{\omega }) \in J \llbracket \beta \rrbracket \) and \((\nu ,\mu )\in I\llbracket \beta \rrbracket \) for some states
on \(\varSigma (\alpha \le \beta )\). For any \((\nu ,\omega )\in I \llbracket \alpha \rrbracket \), we have \((\tilde{\nu },\tilde{\omega }) \in J \llbracket \alpha \rrbracket \), \((\tilde{\nu },\tilde{\omega }) \in J \llbracket \beta \rrbracket \) and \((\nu ,\mu )\in I\llbracket \beta \rrbracket \) for some states
 by repeated use of the induction hypothesis and the definition of refinement. Both the induction hypothesis and Lemma 4 give us information on
by repeated use of the induction hypothesis and the definition of refinement. Both the induction hypothesis and Lemma 4 give us information on
 and
and
 . As \(V \supseteq \mathop {\text {FV}}(\alpha \le \beta )\), the definition of \(\mathop {\text {FV}}(\alpha \le \beta )\) is crucial for ensuring that this knowledge is enough to fully determine
. As \(V \supseteq \mathop {\text {FV}}(\alpha \le \beta )\), the definition of \(\mathop {\text {FV}}(\alpha \le \beta )\) is crucial for ensuring that this knowledge is enough to fully determine
 and
and
 from \(\nu ,\omega \) and
from \(\nu ,\omega \) and
 , and then that
, and then that
 .
.
4 Uniform Substitution
A uniform substitution \(\sigma \) is a mapping from terms of the form
 , from formulas of the form
, from formulas of the form
 to formulas
to formulas
 , and from program constants \(a\) to hybrid programs \(\sigma (a)\). The reserved 0-ary function symbol
, and from program constants \(a\) to hybrid programs \(\sigma (a)\). The reserved 0-ary function symbol
 marks the position where the argument, e.g. \(\theta \) in
marks the position where the argument, e.g. \(\theta \) in
 , will be substituted in the resulting expression. Soundness of such substitutions requires that the substitution does not introduce new free variables in a context where they are bound [10].
, will be substituted in the resulting expression. Soundness of such substitutions requires that the substitution does not introduce new free variables in a context where they are bound [10].
Figure 1 defines the result \({\sigma }^{U}{\phi }\) of applying a uniform substitution \(\sigma \) with taboo set \(U\subseteq \mathcal {V}\) to a formula \(\phi \) (or term \(\theta \), or hybrid programs \(\alpha \) respectively) [28]. For hybrid programs \(\alpha \), the substitution result \({\sigma }^{U}_{V}{\alpha }\) for input taboo \(U\subseteq \mathcal {V}\) also outputs a taboo set \(V\subseteq \mathcal {V}\), written in subscript notation, that will be tabooed after program \(\alpha \). Taboos U, V are sets of variables that cannot be substituted in free during the application of the substitution, because they have been bound within the context and, thus, potentially changed their meaning compared to the original substitution \(\sigma \). The difference is that the input U is already taboo when the substitution \(\sigma \) is applied to \(\alpha \) while V is the new output taboo after \(\alpha \). Finally, \(\sigma (\phi )\) is short for \({\sigma }^{\emptyset }{\phi }\) started without initial taboos. The key advantage to working with uniform substitution applications with taboo passing is that they enable an efficient one-pass substitution [28] compared to the classical Church-style uniform substitution application mechanism that checks admissibility at every binding operator along the way [25]. One-pass uniform substitution postpones admissibility checks till the actual substitutions of function and predicate symbols according to explicit taboos carried around.
Despite the surprising definition of the free variables of a refinement, defining uniform substitution for the refinement case is standard, the input taboo U is given to both programs except that their output taboos V, W are discarded:
The reason is two-fold:
-
1.
Unlike quantifiers and modalities, refinements do not subsequently bind any variables.
-
2.
The free variables of a refinement introduced by a substitution can only be introduced free in the programs, and thus checking these against the input taboo set U is sufficient.
This last statement is a consequence of \(\mathop {\text {BV}}({\sigma }^{}_{}{\alpha }) \subseteq \mathop {\text {BV}}(\alpha )\) and \(\text {MBV}({\sigma }^{}_{}{\alpha }) \supseteq \text {MBV}(\alpha )\), which is proved by a direct induction.
4.1 Uniform Substitutions and Adjoint Interpretations
The proof of the soundness of uniform substitution follows the same structure as the proof of the uniform substitution lemma for dGL [28] but adapted to hybrid programs instead of hybrid games and generalized to the presence of refinements. The output taboo V of a uniform substitution \({\sigma }^{U}_{V}{\alpha }\) will include the original taboo set U and all variables bound in the program \(\alpha \).
Lemma 6
(Taboo set computation [28]). If \({\sigma }^{U}_{V}{\alpha }\) is defined, then \(V \supseteq U \cup \textsf{BV}({\sigma }^{U}_{V}{\alpha })\).
Whereas uniform substitutions are syntactic transformations on expressions, their semantic counterparts are semantic transformations on interpretations. The two are related by Lemmas 7 and 8. Let
 denote the interpretation that agrees with interpretation I except for the constant function symbol
denote the interpretation that agrees with interpretation I except for the constant function symbol
 which is interpreted as the constant \(d\in \mathbb {R}\).
which is interpreted as the constant \(d\in \mathbb {R}\).
Definition 8
(Adjoint interpretation). For an interpretation I and a state \(\omega \), the adjoint interpretation \(\sigma ^{*}_{\omega }I\) modifies the interpretation of each function symbol
 , predicate symbol \(p\in \sigma \) and program constant \(a\in \sigma \) as follows:
, predicate symbol \(p\in \sigma \) and program constant \(a\in \sigma \) as follows:

Lemma 7
(Uniform substitution for terms [28]). The uniform substitution \(\sigma \) for taboo \(U \subseteq \mathcal {V}\) and its adjoint interpretation \(\sigma ^{*}_{\omega }I\) for \(I,\omega \) have the same semantics on U-variations \(\nu \) of \(\omega \) for all terms \(\theta \):
Lemma 8
(Uniform substitution for formulas, programs). Uniform substitution \(\sigma \) for taboo \(U \subseteq \mathcal {V}\) and its adjoint interpretation \(\sigma ^{*}_{\omega }I\) for \(I,\omega \) have the same semantics on U-variations \(\nu \) of \(\omega \) for all formulas \(\phi \) and hybrid programs \(\alpha \):
The proof is done by simultaneous induction on the structure of \(\sigma \), \(\alpha \) and \(\phi \) for all \(U,\nu ,\omega \) and \(\mu \) [31]. The use of U-variations is critical when the induction hypothesis needs to be used in a state other than \(\nu \), e.g. for quantifiers and modalities. Without considering the extension of the refinement operator, this result was previously proved in a weaker form (\(U = \emptyset \)) for dL [25] or for more complex semantics like hybrid games [28].
4.2 Soundness of Uniform Substitution
Lemma 8 is essentially all that is required to ensure the sound application of uniform substitution. First, uniform substitution can be used to have a sound instantiation of the axioms, using the uniform substitution rule (US). A proof rule is sound if the validity of the premises implies the validity of the conclusion.
Theorem 1
(Soundness of uniform substitution [28]). The proof rule (US) is sound.
Uniform substitution can also be used on rules or whole inferences, as long as they are locally sound, i.e. the conclusion is valid in any interpretation where the premises are valid. Locally sound inferences are also sound.
Theorem 2
(Soundness of uniform substitution for rules [28]). All locally sound inferences remain locally sound when substituted with a uniform substitution \(\sigma \) with taboo set \(\mathcal {V}\).
 locally sound implies
locally sound implies
 locally sound.
locally sound.
5 Proof Calculus
Most notably, uniform substitution makes it possible to use concrete dRL formulas as axioms instead of axiom schemata that accept infinitely many formulas as axioms. Axioms are finite syntactic objects, and are thus easy to implement, while axiom schemata are ultimately algorithms accepting certain formulas as input while rejecting others [25]. Figure 2 lists the axioms of dRL. dRL also satisfies the axioms of KAT [17], Schematic KAT [4] and the axioms of dL [31]. Some axioms use the reverse implication \(\phi \leftarrow \psi \) instead of \(\psi \rightarrow \phi \) for emphasis.
In the axiom ([\(\le \)]), \(\bar{x}\) stands for the (finite) vector of all relevant variables (alternative treatments [25, 28] of \(p(\bar{x})\) use quantifier symbols or additional program constants instead, but are not necessary for this paper). This characteristic axiom of dRL expresses that if formula \(p(\bar{x})\) holds after all runs of hybrid program \(b\), then it also holds after any refinement \(a\). Thus, as long as a proof of the refinement is given, it is possible to replace hybrid programs inside modalities. In general, axioms are meant to be applied to the axiom key (marked
 ).
).
Refinement is transitive (\(\le _{t}\)), allowing the introduction of intermediate refinements \(c\) similar to the role that cuts play in first-order logic.
Axioms (\(\cup _l\)) and (\(\cup _r\)) decompose the choice operator using logical connectives. As the choice \({a}\cup {b}\) can behave like either subprograms, whenever it refines a program \(c\), both \(a\) and \(b\) must refine \(c\). Axiom (\(\cup _r\)) is not an equivalence though. \(a\le b\vee a\le c\) says that for each initial state, one of the two refinement holds. However, when \(a\) is nondeterministic, and so can have multiple end states for one initial state, it may not be the case despite the left-hand side being true.
Axiom (;) helps proving a refinement between two sequences of programs (\(a;b\le c;d\)) by proving the refinement of the first programs (\(a\le c\)) and the refinement of the second programs, but only after all executions of \(a\)
 . Axioms (?\(_{\text {det}}\)) and (\(:=_{\text {det}}\)) are particular cases of the axiom (;) where the implication can be strengthened to an equivalence. As such, the implication from right to left is not required for both axioms [31].
. Axioms (?\(_{\text {det}}\)) and (\(:=_{\text {det}}\)) are particular cases of the axiom (;) where the implication can be strengthened to an equivalence. As such, the implication from right to left is not required for both axioms [31].
Axioms (\(\text {loop}_l\)), (\(\text {loop}_r\)) and (\(\text {unloop}\)) are used to prove refinements of loops. The first two state that if adding a program before or after only leads to less executions, then adding an unbounded number of executions, i.e. a loop, will also lead to less executions. The axiom (\(\text {unloop}\)) is useful for comparing two loops, as it allows to reduce the problem to comparing the loop bodies. Both axioms (\(\text {loop}_l\)) and (\(\text {unloop}\)) need a box modality when proving the refinement of the loop body, as the refinement must be proved after any number of iterations of a.
The axiom (ODE) describes how to prove refinements between differential equations. A refinement
 is true iff throughout the execution of the former ODE, it always satisfies the latter differential equation and evolution domain. Along with the axioms (\(\text {DW}_{=}\)) and (\(\text {DE}_{=}\)), these axioms subsume differential cut (DC), differential weakening (DW) and differential effect (DE) from dL [31]. The equivalence in the axiom (ODE) effectively means that refinements of differential equations can always be reduced to standard dL formulas, which is essential to our decidability result.
is true iff throughout the execution of the former ODE, it always satisfies the latter differential equation and evolution domain. Along with the axioms (\(\text {DW}_{=}\)) and (\(\text {DE}_{=}\)), these axioms subsume differential cut (DC), differential weakening (DW) and differential effect (DE) from dL [31]. The equivalence in the axiom (ODE) effectively means that refinements of differential equations can always be reduced to standard dL formulas, which is essential to our decidability result.
The axiom (DX) states that a differential equation always has a solution for the interval [0, 0]. In that case, the execution succeeds only if the domain holds, and the correct value
 is assigned to the differential variable \({x}^{\prime }\). The axiom (\(\text {ODE}_\text {idemp}\)) states that following the same differential equation twice in a row is equivalent to following it only once, because the concatenation of solutions of the same differential equation is still a solution of the same differential equation.
is assigned to the differential variable \({x}^{\prime }\). The axiom (\(\text {ODE}_\text {idemp}\)) states that following the same differential equation twice in a row is equivalent to following it only once, because the concatenation of solutions of the same differential equation is still a solution of the same differential equation.
Compared to the original sequent calculus for dRL [19], the proof rule schemata matching infinitely many instances are now replaced by a finite number of axioms that are concrete dRL formulas rather than standing for infinitely many instances. The infinitely many possible instances can then be recovered soundly using the uniform substitution rule (US). Because of this two-step mechanism, reasoning with the axioms can be done without considering the possible instantiations. Take for instance the sound equivalence
 . The proof can be done by transitivity (\(\le _{t}\)) with
. The proof can be done by transitivity (\(\le _{t}\)) with
 as intermediate step [31]. But the same proof cannot be done by replacing
as intermediate step [31]. But the same proof cannot be done by replacing
 by any term \(\theta \): the intermediate program is not always equivalent to the other two (e.g. for \(\theta = x+1\)). On the other hand, by proving the equivalence for
by any term \(\theta \): the intermediate program is not always equivalent to the other two (e.g. for \(\theta = x+1\)). On the other hand, by proving the equivalence for
 and then using rule (US), the equivalence can be proved for all terms \(\theta \).
and then using rule (US), the equivalence can be proved for all terms \(\theta \).
The dRL axioms are also more modular than its cast-in-stone sequent calculus rules. For instance, with rule (G) and axiom (K), any implication \(\phi \rightarrow \psi \), e.g. (\(\cup _r\)), can be used to prove
 . This would not fit the shape of the corresponding sequent rule, which requires \(\psi \) at the top level. The lack of differential symbols in the original sequent calculus [19] changes the soundness of some rules: the match direction field rule (MDF) would allow rescaling the right-hand side of a differential equation, which is unsound here as it would change the resulting differential symbols. Conversely, only the reverse implication of the axiom (ODE) would be sound in the original calculus, again for lack of differential symbols. The dRL axioms are proved sound [31]:
. This would not fit the shape of the corresponding sequent rule, which requires \(\psi \) at the top level. The lack of differential symbols in the original sequent calculus [19] changes the soundness of some rules: the match direction field rule (MDF) would allow rescaling the right-hand side of a differential equation, which is unsound here as it would change the resulting differential symbols. Conversely, only the reverse implication of the axiom (ODE) would be sound in the original calculus, again for lack of differential symbols. The dRL axioms are proved sound [31]:
Theorem 3
(Soundness of dRL axioms). All axioms of dRL are sound.
6 Decidability of Refinement for a Fragment of dRL
This section identifies a subset of hybrid programs for which the refinement problem is decidable. It is focused on concrete programs, i.e. programs without function symbols, predicate symbols or program constants. They have the following high-level structure: \((ctrl;plant)^{*}\) where a discrete, loop-free program ctrl, modelling a controller that sets some parameters \(\bar{u}\), then a continuous program plant that describes the dynamics of the variables \(\bar{y}\) according to the choice of the parameters \(\bar{u}\). These steps are then repeated nondeterministically. The continuous variables \(\bar{y}\) (and by extension \({\bar{y}}^{\prime }\)) are expected to be distinct from the discrete variables \(\bar{u}\) and also contain a global clock t which follows the differential equation \({t}^{\prime }=1\). The presence of the clock t is not needed for comparing the differential equations, but to distinguish between discrete executions and hybrid executions.
For two such programs, \((ctrl_a;plant_a)^{*}\) and \((ctrl_b;plant_b)^{*}\), a canonical proof of the refinement has the following shape (omitting uses of MP for brevity):

This means that proving the refinement of the whole programs is reduced to proving the refinement of the controllers, \(ctrl_a \le ctrl_b\) and the refinement of the plants after all \(ctrl_a\) executions,
 . With our restrictions on the controllers, the first refinement is always decidable.
. With our restrictions on the controllers, the first refinement is always decidable.
Lemma 9
For concrete, discrete and loop-free controllers \(ctrl_a\) and \(ctrl_b\), the validity of \(ctrl_a \le ctrl_b\) is decidable by dRL proof.
Given a controller \(ctrl_a\), it is possible to synthesize a first-order formula \(\phi _a(x,x^+)\) that characterizes the behavior of \(ctrl_a\), where x (resp. \(x^+\)) corresponds to the variables after (resp. before) the controller [21]. Using the dRL axioms, \(ctrl_a \le ctrl_b\) is provable from \(\phi _a(x,x^+) \rightarrow \phi _b(x,x^+)\). The validity of the latter is decidable as it is first-order real arithmetic [33]. The full proof is in [31].
The second refinement,
 , is more complex. Let us write the two plants as
, is more complex. Let us write the two plants as
 and
and
 for some polynomials \(p(\bar{y},\bar{u}), q(\bar{y},\bar{u})\) and formulas Q, R. The axiom ODE entails that we must prove
for some polynomials \(p(\bar{y},\bar{u}), q(\bar{y},\bar{u})\) and formulas Q, R. The axiom ODE entails that we must prove
 , which no longer contains any refinement. For the decidability result (Theorem 4) to hold, we require that the validity of this formula is decidable.
, which no longer contains any refinement. For the decidability result (Theorem 4) to hold, we require that the validity of this formula is decidable.
There are two cases which always ensure this. First, if the differential equation \(plant_a\) admits a solution expressible in dRL (e.g. a polynomial), then using standard dL reasoning, the formula can be reduced to a first-order formula and thus its validity can be decided. The differential equation from Example 1, \({x}^{\prime } = v,{v}^{\prime } = a\), is such a case.
The second case is when domain R is algebraic, i.e. of the form \(\bigwedge _i\bigvee _j p_{ij}(x) = 0\) for some polynomial \(p_{ij}\) and Q, the domain of \(plant_a\), is a semialgebraic set [30].
The remaining question is now to show that the approach presented above is complete, meaning it always succeeds when the refinement holds. The only additional constraint we require is that the controller \(ctrl_b\) is idempotent.
Definition 9
(Idempotent controller). A controller ctrl is idempotent if it satisfies \(ctrl;ctrl =ctrl\).
An idempotent controller cannot reach more states by executing multiple times without any continuous dynamics happening. Pure reactive controllers, i.e. controllers for which the parameters’ values only depend on the values of the continuous variables, are always idempotent. This is the case for the controllers in Example 1:
 . On the other hand, counting the number of times the controller has been executed would not be idempotent.
. On the other hand, counting the number of times the controller has been executed would not be idempotent.
Lemma 10
This derived rule is invertible, if \(ctrl_b\) is idempotent.

The derivation of the rule is given in the canonical proof. The converse, that the conclusion implies the premise, is more involved [31]. Proving \(ctrl_a;plant_a \le (ctrl_b;plant_b)^{*}\) from \((ctrl_a;plant_a)^{*} \le (ctrl_b;plant_b)^{*}\) is done by unfolding the loop on the left. To get rid of the loop on the right, we use the fact that \(ctrl_b\) is idempotent. It means that if the global time is not modified, then we can assume without loss of generality that the controller (and thus also the plant) is executed only once. The case when the global time is modified additionally considers the value of the derivative to ensure that there is an execution of the right program that does not require looping.
With the above lemma, we can now state the decidability result.
Theorem 4
(Decidability of refinement for idempotent controllers). For concrete hybrid programs \(ctrl_a;plant_a\) and \(ctrl_b;plant_b\) discrete loop-free \(ctrl_a, ctrl_b\) and with
 and
and
 , if \(ctrl_b\) is idempotent, and the validity of
, if \(ctrl_b\) is idempotent, and the validity of
 is decidable, then the validity of \((ctrl_a;plant_a)^{*} \le (ctrl_b;plant_b)^{*}\) is also decidable.
is decidable, then the validity of \((ctrl_a;plant_a)^{*} \le (ctrl_b;plant_b)^{*}\) is also decidable.
In particular, the theorem applies to the event-triggered model and the time-triggered model templates used to show how to prove that the latter refines the former [19]. Indeed, their controller template is loop-free and idempotent and the differential equation are assumed to be solvable. Theorem 4 strengthens their result by showing the completeness of the approach.
7 Conclusion
This paper introduced a uniform substitution proof calculus for differential refinement logic dRL. This yields a parsimonious prover microkernel for hybrid systems verification that simultaneously works for properties of and relations between hybrid systems. The handling of refinement relations between hybrid systems is subtle even only in its static semantics, which makes the correctness proofs of this paper particularly interesting. The uniform substitution is one-pass [28] giving it respectable performance advantages compared to Church-style uniform substitutions. While the joint presence of differential equations reasoning and refinement reasoning causes challenges, a resulting benefit besides soundness is that a finer notion of differential equation refinement is obtained with logical decidability properties on a fragment of hybrid systems refinements.
Future work involves improving the implementation of the uniform substitution calculus in KeYmaera X. Although the prover microkernel was straightforward following the uniform substitution process and list of dRL ’s uniform substitution axioms, the prover would benefit from quality of life features, e.g. using the axioms to rewrite on subprograms, and an implementation of the refinement decision algorithm for the decidable fragment. Another axis of research is to combine refinements with hybrid games, with a proper semantics and adapt the new axioms of dRL to games, some of which would not be sound as is.
References
Abrial, J.: Modeling in Event-B - System and Software Engineering. Cambridge University Press, Cambridge (2010). https://doi.org/10.1017/CBO9781139195881
Abrial, J.-R., Su, W., Zhu, H.: Formalizing hybrid systems with Event-B. In: Derrick, J., et al. (eds.) ABZ 2012. LNCS, vol. 7316, pp. 178–193. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30885-7_13
Afendi, M., Laleau, R., Mammar, A.: Modelling hybrid programs with Event-B. In: Raschke, A., Méry, D., Houdek, F. (eds.) ABZ 2020. LNCS, vol. 12071, pp. 139–154. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-48077-6_10
Angus, A., Kozen, D.: Kleene algebra with tests and program schematology. Technical report TR2001-1844, Cornell University, USA (2001). https://ecommons.cornell.edu/items/b376f0d0-ca43-4896-b8b3-4c8a31e24ab1
Banach, R., Butler, M.J., Qin, S., Verma, N., Zhu, H.: Core hybrid Event-B I: single hybrid Event-B machines. Sci. Comput. Program. 105, 92–123 (2015). https://doi.org/10.1016/J.SCICO.2015.02.003
Banach, R., Zhu, H., Su, W., Huang, R.: Continuous KAOS, ASM, and formal control system design across the continuous/discrete modeling interface: a simple train stopping application. Formal Aspects Comput. 26(2), 319–366 (2014). https://doi.org/10.1007/S00165-012-0263-2
Brieger, M., Mitsch, S., Platzer, A.: Uniform substitution for dynamic logic with communicating hybrid programs. In: Pientka, B., Tinelli, C. (eds.) CADE 2023. LNCS, vol. 14132, pp. 96–115. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-38499-8_6
Butler, M.J., Abrial, J., Banach, R.: Modelling and refining hybrid systems in Event-B and Rodin. In: Petre, L., Sekerinski, E. (eds.) From Action Systems to Distributed Systems - The Refinement Approach, pp. 29–42. Chapman and Hall/CRC (2016). https://doi.org/10.1201/B20053-5
Butler, M., Maamria, I.: Practical theory extension in Event-B. In: Liu, Z., Woodcock, J., Zhu, H. (eds.) Theories of Programming and Formal Methods. LNCS, vol. 8051, pp. 67–81. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39698-4_5
Church, A.: Introduction to Mathematical Logic. Princeton University Press, Princeton (1956)
Doumane, A., Kuperberg, D., Pous, D., Pradic, P.: Kleene algebra with hypotheses. In: Bojańczyk, M., Simpson, A. (eds.) FoSSaCS 2019. LNCS, vol. 11425, pp. 207–223. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17127-8_12
Dupont, G.: Correct-by-Construction Design of Hybrid Systems Based on Refinement and Proof. (Conception correcte par construction de systèmes hybrides basée sur le raffinement et la preuve). Ph.D. thesis, National Polytechnic Institute of Toulouse, France (2021). https://tel.archives-ouvertes.fr/tel-04165215
Felty, A., Middeldorp, A. (eds.): Automated Deduction, CADE-25. LNCS, vol. 9195. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6
Fulton, N., Mitsch, S., Quesel, J.D., Völp, M., Platzer, A.: KeYmaera X: an axiomatic tactical theorem prover for hybrid systems. In: Felty and Middeldorp [13], pp. 527–538. https://doi.org/10.1007/978-3-319-21401-6_36
Jeannin, J., et al.: A formally verified hybrid system for safe advisories in the next-generation airborne collision avoidance system. STTT 19(6), 717–741 (2017). https://doi.org/10.1007/s10009-016-0434-1
Kabra, A., Mitsch, S., Platzer, A.: Verified train controllers for the Federal Railroad Administration train kinematics model: balancing competing brake and track forces. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 41(11), 4409–4420 (2022). https://doi.org/10.1109/TCAD.2022.3197690
Kozen, D.: Kleene algebra with tests. ACM Trans. Program. Lang. Syst. 19(3), 427–443 (1997). https://doi.org/10.1145/256167.256195
Loos, S.M.: Differential refinement logic. Ph.D. thesis, Computer Science Department, School of Computer Science, Carnegie Mellon University (2016). http://reports-archive.adm.cs.cmu.edu/anon/2015/CMU-CS-15-144.pdf
Loos, S.M., Platzer, A.: Differential refinement logic. In: Grohe, M., Koskinen, E., Shankar, N. (eds.) LICS, pp. 505–514. ACM, New York (2016). https://doi.org/10.1145/2933575.2934555
Mitsch, S., Ghorbal, K., Vogelbacher, D., Platzer, A.: Formal verification of obstacle avoidance and navigation of ground robots. I. J. Robot. Res. 36(12), 1312–1340 (2017). https://doi.org/10.1177/0278364917733549
Mitsch, S., Platzer, A.: ModelPlex: verified runtime validation of verified cyber-physical system models. Form. Methods Syst. Des. 49(1-2), 33–74 (2016). https://doi.org/10.1007/s10703-016-0241-z. Special issue of selected papers from RV’14
Pereira, A., Baumann, M., Gerstner, J., Althoff, M.: Improving efficiency of human-robot coexistence while guaranteeing safety: theory and user study. IEEE Trans. Autom. Sci. Eng. 20(4), 2706–2719 (2023)
Platzer, A.: Differential dynamic logic for hybrid systems. J. Autom. Reas. 41(2), 143–189 (2008). https://doi.org/10.1007/s10817-008-9103-8
Platzer, A.: A uniform substitution calculus for differential dynamic logic. In: Felty and Middeldorp [13], pp. 467–481. https://doi.org/10.1007/978-3-319-21401-6_32
Platzer, A.: A complete uniform substitution calculus for differential dynamic logic. J. Autom. Reas. 59(2), 219–265 (2017). https://doi.org/10.1007/s10817-016-9385-1
Platzer, A.: Logical Foundations of Cyber-Physical Systems. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-63588-0
Platzer, A.: Uniform substitution for differential game logic. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 211–227. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_15
Platzer, A.: Uniform substitution at one fell swoop. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 425–441. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_25
Platzer, A., Tan, Y.K.: Differential equation axiomatization: the impressive power of differential ghosts. In: Dawar, A., Grädel, E. (eds.) LICS, pp. 819–828. ACM, New York (2018). https://doi.org/10.1145/3209108.3209147
Platzer, A., Tan, Y.K.: Differential equation invariance axiomatization. J. ACM 67(1), 6:1–6:66 (2020). https://doi.org/10.1145/3380825
Prebet, E., Platzer, A.: Uniform substitution for differential refinement logic (2024). https://doi.org/10.48550/arXiv.2404.16734
Stauner, T., Müller, O., Fuchs, M.: Using HyTech to verify an automotive control system. In: Maler, O. (ed.) HART 1997. LNCS, vol. 1201, pp. 139–153. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0014722
Tarski, A., McKinsey, J.C.C.: A Decision Method for Elementary Algebra and Geometry. University of California Press, Berkeley (1951). https://doi.org/10.1525/9780520348097
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Additional dRL Axioms
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Prebet, E., Platzer, A. (2024). Uniform Substitution for Differential Refinement Logic. In: Benzmüller, C., Heule, M.J., Schmidt, R.A. (eds) Automated Reasoning. IJCAR 2024. Lecture Notes in Computer Science(), vol 14740. Springer, Cham. https://doi.org/10.1007/978-3-031-63501-4_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-63501-4_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63500-7
Online ISBN: 978-3-031-63501-4
eBook Packages: Computer ScienceComputer Science (R0)


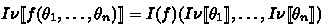


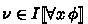 iff
iff  iff
iff 








