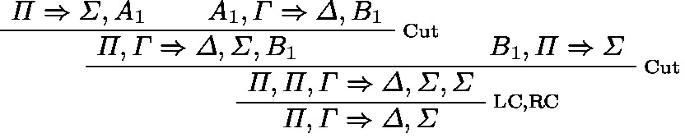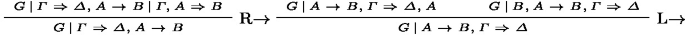Abstract
Enhancing cut-free expressiveness through minimal structural additions to sequent calculus is a natural step. We focus on Åqvist’s system \(\textbf{F}\) with cautious monotonicity (CM), a deontic logic extension of \(\textbf{S5}\), for which we define a sequent calculus employing (semi) analytic cuts.The transition to hypersequents is key to develop modular and cut-free calculi for \(\mathbf{F + (CM)}\) and \(\textbf{G}\), also supporting countermodel construction.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Normative reasoning is crucial across various fields, including law and artificial intelligence. It is effectively formalized by deontic logic, the branch of logic that deals with obligations and related concepts. Numerous deontic logics have emerged, and they can be broadly classified into preference-based and norm-based systems [11]. The latter analyse deontic modalities with reference to a set of explicit norms, while the former employ possible world semantics. Preference-based systems are particularly useful to model contrary to duty obligations (i.e., obligations that come into force when some other obligation is violated) and defeasible deontic conditionals. Åqvist’s landmark systems [1] \(\textbf{E}\), \(\textbf{F}\), and \(\textbf{G}\), fall into this category. Semantically, they are characterized by preference models using relations to represent the betterness of states. They extend the modal logic \(\textbf{S5}\) with a dyadic obligation \(\bigcirc (B/A)\) (“B is obligatory, given A") which is true when the best A-worlds are all B-worlds. A more recent addition to the family [27] is \(\textbf{F}\) with the addition of cautious monotonicity (CM) from the non-monotonic literature [12, 18]. \(\textbf{E}\), \(\textbf{F}\), \(\mathbf{F + (CM)}\), and \(\textbf{G}\) are modular systems with increasing deductive strength w.r.t. the sets of theorems they derive. The last two systems correspond to well-known conditional logics: \(\textbf{G}\) is \(\textbf{VTA}\) [13], one of Lewis’ logics, while \(\mathbf{F + (CM)}\) corresponds to Preferential Conditional Logic \(\textbf{PCL}\) [6] supplemented with the absoluteness axiom, that reflects the fact that the ranking is not world-relative. \(\textbf{PCL}\) contains as a fragment the KLM preferential logic P [18] for default reasoning.
Reasoning necessitates (finding) derivations and countermodels. The exploration of the proof theory for these logics has only recently become a focal point. Prior to that, the only available calculi for them were Hilbert systems, which are unsuitable for the mentioned tasks. Since Gentzen’s introduction in 1935, sequent calculi in which the cut rule is admissible (or eliminable) have been employed for these purposes. Although crucial to simulate modus ponens, the cut rule poses a hindrance to proof search. Cut-free sequent systems are not available for Åqvist’s systems insofar as they contain an \(\textbf{S5}\) modality which impedes their formulationFootnote 1. Many sequent calculus generalizations, like hypersequents, nested, and labelled sequents, have been introduced to capture logics without cut-free formulations. Notably, hypersequents are characterized by less complex objects and expressiveness compared to nested sequents, which, in turn, are less complex and expressive than labelled sequents, see e.g. [22]. Using hypersequents, modular cut-free calculi have been introduced for \(\textbf{E}\) and \(\textbf{F}\) in [8, 9]. The situation for \(\textbf{G}\) and \(\mathbf{F + (CM)}\) is less clear. Although \(\textbf{G}\) semantically arises by imposing to \(\mathbf{F + (CM)}\) totality on frames, this is not reflected in their calculi: (forms of) labelled sequents [20, 24] have been employed for \(\textbf{PCL}\), and a hypersequent calculus with blocks (incorporating a shallow form of nesting) [14] for \(\textbf{G}\).
This leaves open the question whether modular and cut-free calculi, using a simpler framework, can be defined for \(\mathbf{F + (CM)}\) and \(\textbf{G}\). Simplicity in the proof formalism is advantageous for proving meta-logical results and streamlining the proof search space. Indeed the introduction of additional structure in the basic objects manipulated by the formalism often poses obstacles in these endeavors.
Our positive answer to the question relies on the use of an alternative semantics (w.r.t. preference models) [28]. We first introduce a sequent calculus \(\textbf{SFcm}\) for \(\mathbf{F + (CM)}\). Like the calculus in [25] for \(\textbf{S5}\), \(\textbf{SFcm}\) lacks completeness without cuts. Nevertheless, we show that a restricted form of cuts, we call them semi-analytic, suffices. We present a syntactic procedure, akin to cut-elimination, to transform \(\textbf{SFcm}\) proofs with arbitrary cuts into proofs with semi-analytic cuts, simplifying the method in [7]. Extending \(\textbf{SFcm}\) to encompass \(\textbf{G}\) would be hard, if possible at all. Sequent calculi, are indeed known to be inadequate for capturing modal logics with linear frames (Ch.9 in [15]). To achieve modular and cut-free calculi for \(\mathbf{F + (CM)}\) and \(\textbf{G}\), we shift from the sequent to the hypersequent framework. The use of hypersequents (which are sequents working in parallel) enables the definition of structural rules operating across multiple sequents. In particular, adapting the peculiar hypersequent rule for \(\textbf{S5}\) from [4] simplifies the rules for \(\textbf{SFcm}\), resulting in a cut-free hypersequent calculus for \(\mathbf{F + (CM)}\). A calculus for \(\textbf{G}\) is obtained by adding (a version of) the communication rule from [3], designed to capture Gödel logic [10]. We prove cut-elimination for both calculi and modify them into proof-search oriented calculi, providing proofs of decidability and countermodel construction from failed derivations.
Similarly to the calculi for \(\textbf{E}\) and \(\textbf{F}\) in [8, 9] we encode maximality by a (S4-type) modal operator. \(\bigcirc (B/A)\) can be indirectly defined as \(\Box (A\rightarrow \lnot \mathcal {Bet}\lnot (A \wedge \mathcal {Bet}(A\rightarrow B))) \). \(\mathcal {Bet}\) is not part of the language of \(\mathbf{F + (CM)}\) and \(\textbf{G}\), but is used at the meta-level in the calculi to define rules for the dyadic obligation.
2 F + (CM) and G in a Nutshell
We present the logics \(\mathbf{F + (CM)}\) and \(\textbf{G}\) both syntactically and semantically. Let \(\text{ PropVar }\) be a countable set of atomic formulas. Their language is defined by the following BNF:
\(\Box A\) is read as “A is settled as true”, and \(\bigcirc (B/A)\) as “B is obligatory, given A”. The Boolean connectives other than \(\lnot \) and \(\rightarrow \) are defined as usual.
Definition 1
\(\textbf{F}\) consists of any Hilbert system for S5 augmented with:

\(\mathbf{F + (CM)}\) and \(\textbf{G}\) extend \(\textbf{F}\) with axioms (CM) and (RM) respectively:
(COK) is the analogue of axiom \(\textbf{K}\), (Sh) expresses a “half” of deduction theorem (or residuation property). The absoluteness axiom (Abs) of [21] corresponds to the removal of world-relative accessibility relations. (O-Nec) is the deontic counterpart of the necessitation rule. (Ext) enables the substitution of necessarily equivalent sentences in the antecedent of deontic conditionals. (Id) is the deontic analogue of the identity principle. These axioms define the logic \(\textbf{E}\).
\(\textbf{F}\) extends \(\textbf{E}\) with (D\(^{\star }\)) that rules out conflicts between obligations for possible antecedents. (CM) and (RM) are cautious and rational monotony from the non-monotonic literature [18]. Introduced in [12] (CM) expresses a weakened form of strengthening of the antecedent, while (RM) a stronger form: if B is permitted given A, and C is obligatory given A, then C is obligatory given \(A \wedge B\).
Semantics for the logics \(\textbf{E}\), \(\textbf{F}\), \(\mathbf{F + (CM)}\) and \(\textbf{G}\) can be given in terms of preference models, see [28]. This semantics was used in [8, 9] to define cut-free hypersequent calculi for \(\textbf{E}\) and \(\textbf{F}\). With preference models, structures are easily described, but they come with complex model theoretic conditions on the valuation function. In this paper we adopt a different semantics. This semantics has a more complex truth condition for the deontic operator, involving a \(\forall \exists \forall \) nesting of quantifiers [28], but simpler frame and valuation conditions.
The original language does not include the modality \(\mathcal {Bet}\), but we add it to the semantic explanation of connectives for clarity.
Definition 2
A preference model for \(\mathbf{F + (CM)}\) is a triple \(\langle W, \le , v\rangle \), where \(\le \) is a reflexive and transitive order on W and \(v:{\text{ PropVar }}\rightarrow \mathcal {P}(W)\) a valuation function. The truth conditions for a formula in a world are defined as:
-
\(x\Vdash P\) if and only if \(x\in v(P)\).
-
\(x\Vdash \lnot A\) if and only if \(x\nVdash A\).
-
\(x\Vdash A\rightarrow B\) if and only if \(x\nVdash A\) or \(x\Vdash B\).
-
\(x\Vdash \mathcal {Bet}A\) if and only if \(\forall y (x\le y\Rightarrow y\Vdash A)\).
-
\(x\Vdash \square A\) if and only if \(\forall y (y\Vdash A)\).
-
\(x\Vdash \bigcirc (B/A)\) if and only if \( \forall y (y\Vdash A\Rightarrow \exists z (y\le z \, \& \, \, z\Vdash A\, \& \, \, \forall u (z\le u\Rightarrow u\Vdash A\rightarrow B))).\)
Models for \(\textbf{G}\) are obtained by imposing totality, i.e., \(\forall x \forall y (x\le y \vee y\le x)\).
Theorem 1 ([28])
[28]] \(\mathbf{F + (CM)}\) (resp. \(\textbf{G}\)) is sound and complete with respect to the semantics of (resp. total) preference models.
Note that the truth condition for the operator \(\bigcirc (B/A)\) can be rewritten, using the conditions for \(\square ,\rightarrow ,\lnot \) and \(\mathcal {Bet}\), as:
3 A Sequent Calculus for \(\mathbf{F + (CM)}\)
We introduce a sequent calculus \(\textbf{SFcm}\) for \(\mathbf{F + (CM)}\), whose completeness relies on the use of cuts of a restricted form.
\(\textbf{SFcm}\) is obtained by adding the rules for the deontic modality and for the betterness operator to a (slightly modifiedFootnote 2 version of) the sequent calculus in [25] for \(\textbf{S5}\). The cuts required in \(\textbf{SFcm}\) are a generalization of analytic cuts (arising from the calculus for \(\textbf{S5}\) [30]), due to the shape of the rules for the deontic modalityFootnote 3. We use \(\varGamma ,\varDelta ,\varPi ,...\) as metavariables for multisets of formulas.
Definition 3
The sequent calculus \(\textbf{SFcm}\) consists of a variant of Gentzen’s calculus LK for classical logic, with axioms \(\varGamma , p \Rightarrow p, \varDelta \), extended with the rules below


where \(\varGamma ^{b}=\{\mathcal {Bet}A\,|\, \mathcal {Bet}A\in \varGamma \}\) and \(\varGamma ^{\square \bigcirc }= \{\square A\,|\, \square A\in \varGamma \}\cup \{\bigcirc (B/A)\,|\, \bigcirc (B/A)\in \varGamma \}\).
The notion of derivation, principal formulas and height of a derivation are as usual. The derived rules for conjunction and disjunction are as in Genten’s LK and the generalization of initial sequents to arbitrary formulas is provable. A rule is (height-preserving) admissible if, whenever the premises are derivable, so is the conclusion (with at most the same height). In \(\textbf{SFcm}\) the weakening rules (
 ) are height-preserving admissible. The rules of contraction (
) are height-preserving admissible. The rules of contraction (
 ) are explicitly present.
) are explicitly present.
Theorem 2 (Soundness)
[Soundness] \(\textbf{SFcm}\) is sound for \(\mathbf{F + (CM)}\).
Proof
By induction on the height of the \(\textbf{SFcm}\) derivation distinguishing cases according to the last rule applied. Initial sequents are clearly sound. We discuss only the cases of the right rules for the modal operator \(\mathcal {Bet}\) and \(\bigcirc (A/B)\).
R\(\mathcal {Bet}\): Let us assume that the sequent \(\varGamma ^{\square \bigcirc },\varGamma ^{b}\Rightarrow \varDelta ^{\square \bigcirc }, A\) is valid. Let x, y be worlds such that \(x\le y\) and we assume that \(x\Vdash \bigwedge \varGamma \). Hence we get \(y\Vdash \bigwedge \varGamma ^{\square \bigcirc }\wedge \bigwedge \varGamma ^{b}\) (by transitivity of \(\le \)) which yields (i) \(y\Vdash \bigvee \varDelta ^{\square \bigcirc }\) or (ii) \(y\Vdash A\). In (i), we get \(x\Vdash \bigvee \varDelta \), in (ii) \(x\Vdash \mathcal {Bet}A\), giving the desired conclusion.
R\(\bigcirc \): Assume that \( \varGamma ^{\square \bigcirc },A,\mathcal {Bet}\lnot (A\wedge \mathcal {Bet}(A\rightarrow B))\Rightarrow \varDelta ^{\square \bigcirc }\) is valid. We argue by contradiction assuming that the conclusion \( \varGamma \Rightarrow \varDelta ,\bigcirc (B/A)\) is not valid. Hence there is a world x which satisfies every formula in \(\varGamma \) and falsifies every formula in \(\varDelta \) and \(\bigcirc (B/A)\). By definition there is y s.t.: \(y\Vdash A\) and there is not a world z such that \(y\le z\) and \(z\Vdash A\) and \(z\Vdash \mathcal {Bet}(A\rightarrow B)\). Since \(x\Vdash \bigwedge \varGamma ^{\square \bigcirc }\), we get that \(y\Vdash \bigwedge \varGamma ^{\square \bigcirc }\). We also have \(y\Vdash A\) and \(y\Vdash \mathcal {Bet}\lnot (A\wedge \mathcal {Bet}(A\rightarrow B))\). As a consequence of the validity of \( \varGamma ^{\square \bigcirc },A,\mathcal {Bet}\lnot (A\wedge \mathcal {Bet}(A\rightarrow B))\Rightarrow \varDelta ^{\square \bigcirc }\), we get that \(y\Vdash \bigvee \varDelta ^{\square \bigcirc }\), which entails \(x\Vdash \bigvee \varDelta ^{\square \bigcirc } \), a contradiction.
Theorem 3 (Completeness with cut)
[Completeness with cut] Each theorem of \(\mathbf{F + (CM)}\) has a proof in \(\textbf{SFcm}\) with the addition of the cut rule.
Proof
It suffices to show that all the axioms of \(\mathbf{F + (CM)}\) are provable in \(\textbf{SFcm}\). Modus Ponens corresponds to the provability of \(A, A \rightarrow B \Rightarrow B\) and two applications of cut. The necessity rule is a particular case of \( R\square \). The axioms of classical logic are clearly derivable. In what follows, we omit to write trivially derivable premises to increase the readability of the derivations.
-
A derivation of (CM) is as follow (omitting trivially derivable premises)

-
The \(\textbf{S4}\) axioms are trivially derivable. The characteristic axiom of \(\textbf{S5}\) is derivable using analytic cuts, as follows

The cut on \(\lnot \square \lnot A\) is analytic because it is a subformula of \( \square \lnot \square \lnot A\).
-
The axiom (D\(^*\)) \(\bigcirc (\bot /A)\rightarrow \square \lnot A\) is derivable in \(\textbf{SFcm}\) as follow

item The axiom (Sh) \(\bigcirc (C/A\wedge B)\Rightarrow \bigcirc (B\rightarrow C/A)\) is derivable in \(\textbf{SFcm}\). We construct the following derivation (the topmost sequent is clearly derivable).

-
The axiom (COK) \(\bigcirc (B\rightarrow C/A), \bigcirc (B/A)\Rightarrow \bigcirc (C/A)\) is derivable in \(\textbf{SFcm}\). We construct the following derivation.

The topmost sequent is clearly derivable.
The derivations in \(\textbf{SFcm}\) of axioms (Id) \(\bigcirc (A/A)\) and (Abs) \(\bigcirc (B/A)\rightarrow \square \bigcirc (B/A)\) are evident. Also the extensionality axiom \(\square (A\leftrightarrow B)\rightarrow (\bigcirc (C/A)\leftrightarrow \bigcirc (C/B))\) is easy to derive.
3.1 From Cuts to Semi-analytic Cuts
We provide a syntactic procedure to restrict cuts in \(\textbf{SFcm}\) to semi-analytic cuts, where an instance of the cut rule

is semi-analytic if C is a generalized subformula of the conclusion, i.e. \(C\in \textsf{SUB}(\varGamma \cup \varSigma \cup \varDelta \cup \varPi )\), where for any formula A, \(\textsf{SUB}(A)\) is inductively defined as
-
\(A\in \textsf{SUB}(A)\); If \(B\rightarrow C\in \textsf{SUB}(A)\), then \(B,C\in \textsf{SUB}(A)\)
-
If \(\square B,\lnot B,\mathcal {Bet}B\in \textsf{SUB}(A)\), then \(B\in \textsf{SUB}(A)\)
-
\(\bigcirc (C/B)\in \textsf{SUB}(A)\), then \(\mathcal {Bet}\lnot (B\wedge \mathcal {Bet}(B\rightarrow C))\in \textsf{SUB}(A)\)
The notion of generalized subformula naturally extends to multisets of formulas.
To restrict the use of cuts to semi-analytic cuts we reformulate, simplify and also broaden the applicability of the method in [7] to apply to rules more general than so-called simple rules. Specifically, the inherent (almost) local structure of the proof below could seamlessly accommodate rules having more than one principal formula, as well as rules that do not obey the subformula property. Prior to [7], proofs of restriction of cuts to analytic cuts, e.g., [17, 26, 30, 31] were all logic-tailored and, with the exception of [30], relied on semantic arguments.
Proof Idea: We start considering an uppermost non semi-analytic cut (semi-analytic cuts are left in the derivation). Cuts on boolean connectives are handled using rule invertibilities (and reduced in the usual way). Non semi-analytic cuts with cut-formulas \(\Box A\), \(\mathcal {Bet}\ A\) and \(\bigcirc (B / A)\) need a different approach as their rules are not invertible; we shift them upwards until their cut formulas are principal (and then reduced). Notice that the rules R\(\mathcal {Bet}\), R\(\square \) and R\(\bigcirc \) do not allow to shift any cut upwards; however they permit to permute upward any cut in which (\(*\)) the other premise is a right rule introducing the cut formula \(\mathcal {Bet}A\), \(\square A\) or \(\bigcirc (B/A)\) (because of the “good” contexts of these rules). To reach the scenario (\(*\)) we need to bring the considered cut beyond the rules that do not allow the permutation, jumping directly to the point where the cut-formula is introduced. We do that by tracing (bottom up) all the ancestorsFootnote 4 of the cut formulas on the right hand side (RHS), and replacing the cut (actually we consider mix) by new semi-analytic cuts. Following [7], the premises of these new semi-analytic cuts are obtained by replacing the cut-formulas in the original derivation with the contexts of the right rules introducing the cut-formulas (switching their side of the sequent), taking care that the resulting proof is still a correct derivation.
Smaller cuts are cuts of lesser degrees, according to the following definition.
Definition 4
The degree of a formula A, \(\texttt{dg}(A)\) is inductively defined:
-
\(\texttt{dg}(p)=0\) if \(A=p\) atomic; \(\texttt{dg}(B\rightarrow C)=\texttt{dg}(B)+\texttt{dg}(C)+1\)
-
\(\texttt{dg}(\lnot B)=\texttt{dg}(\square B)=\texttt{dg}(Bet B)=\texttt{dg}(B)+1\)
-
\(\texttt{dg}(\bigcirc (C/B))=3\cdot \texttt{dg}(B)+\texttt{dg}(C)+7\)
Definition 5
The non-analytic cut rank \(\sigma (\mathcal {D})\) of a proof is the maximal degree +1 of non-semi analytic cut formulas in \(\mathcal {D}\). The cut rank of a proof \(\rho (\mathcal {D})\) is the maximal degree +1 of cut formulas in \(\mathcal {D}\).
By \(A^n\) we denote n-repetitions of the formula A. As here we focus on the elimination of cuts that are non semi-analytic, we use the non-analytic cut rank.
Lemma 1
The rules for \(\rightarrow \) and \(\lnot \) are height and (non-analytic) rank-preserving invertible.
Lemma 2
Given derivations \(\mathcal {D}_1\) and \(\mathcal {D}_2\) of \(\varGamma \Rightarrow \varDelta , X\) and \(X,\varPi \Rightarrow \varSigma \) with \(\sigma (\mathcal {D}_1),\sigma (\mathcal {D}_2)\le \texttt{dg}(X)\) and with X principal in the last rule applied in \(\mathcal {D}_1\) and \(\mathcal {D}_2\), there is a derivation \(\mathcal {D}\) of \(\varGamma ,\varPi \Rightarrow \varDelta ,\varSigma \) with \(\sigma (\mathcal {D})\le \texttt{dg}(X)\).
Proof
Easy in case of the propositional connectives, \(\mathcal {Bet}\), and \(\square \).
If the cut formula is principal in applications of the rule for \(\bigcirc \), we have:

We construct the following derivation:

The modified version of the rules \( R\square \), \( R\bigcirc \) and \( R\mathcal {Bet}\) in the lemma below will be used to simplify the presentation of case (B) in the proof of Theorem 4: when shifting upward a non semi-analytic cut over the right rules for \(\Box \), \(\mathcal {Bet}\) or \(\bigcirc \).
Lemma 3
The versions \( R'\square \), \( R'\bigcirc \) and \( R'\mathcal {Bet}\) of the rules \( R\square \), \( R\bigcirc \) and \( R\mathcal {Bet}\) with \(\bigvee \varSigma _{1}^{\square \bigcirc },\hdots ,\bigvee \varSigma _{m}^{\square \bigcirc }\) (resp. \(\bigwedge \varPi _{1}^{\square \bigcirc },\hdots ,\bigwedge \varPi _{n}^{\square \bigcirc }\)) in their antecedent (resp. consequent) are admissible.
Proof
(\( R'\square \)): Given \(\bigvee \varSigma _{1}^{\square \bigcirc },\hdots ,\bigvee \varSigma _{m}^{\square \bigcirc },\varGamma ^{\square \bigcirc }\Rightarrow \varDelta ^{\square \bigcirc },\bigwedge \varPi _{1}^{\square \bigcirc },\hdots ,\bigwedge \varPi _{n}^{\square \bigcirc }, B \), we first apply the invertibility of the derived rules for \(\bigwedge \) and \(\bigvee \) (Lemma 1). The \( R'\square \) conclusion \(\bigvee \varSigma _{1}^{\square \bigcirc },\hdots ,\bigvee \varSigma _{m}^{\square \bigcirc },\varGamma ^{\square \bigcirc }\Rightarrow \varDelta ^{\square \bigcirc }, \bigwedge \varPi _{1}^{\square \bigcirc },\hdots ,\bigwedge \varPi _{n}^{\square \bigcirc }, \square B \) is obtained by multiple applications of \( R\square \), and of the logical rules. The proof for \( R'\bigcirc \) and \( R'\mathcal {Bet}\) is analogous.
Theorem 4
Given the derivations \(\mathcal {D}_1\) of \(\varGamma \Rightarrow \varDelta , X^m\) and \(\mathcal {D}_2\) of \(X^n,\varPi \Rightarrow \varSigma \) containing only semi-analytic cuts, there is a derivation \(\mathcal {D}\) of \(\varGamma ,\varPi \Rightarrow \varDelta ,\varSigma \) with \(\sigma (\mathcal {D})\le \texttt{dg}(X)\).
Proof
We first replace all (analytic) cuts on X in \(\mathcal {D}_1\) and \(\mathcal {D}_2\), by applications of contraction. The theorem’s claim is proved by induction on the sum of the height of the derivations \(\mathcal {D}_1\) and \(\mathcal {D}_2\). If the cut-formula is a connective of classical logic the claim follows by Lemmas 1 and 2. We consider \(\mathcal {D}_1\) and distinguish two cases: the cut formula is principal in the last rule applied or it is not.
(A) The cut formula is principal in the last rule applied in \(\mathcal {D}_1\). We consider cases according to the last rule (r) applied in \(\mathcal {D}_2\):
-
(r)is an initial sequent, hence the cut is analytic.
-
(r)is a rule introducing the cut formula. We use Lemma 2 (with obvious adjustments given by the use of mix).
-
(r)is any rule different from R\(\bigcirc \) , R\(\square \) , and R\(\mathcal {Bet}\). The cut can be permuted upwards.
-
(r)is R\(\mathcal {Bet}\) , R\(\square \)or R\(\bigcirc \). Note that these rules’ contexts permit moving the cut upward in \(\mathcal {D}_2\). As an example, consider the case in which the cut formula is of the shape \(\mathcal {Bet}B\) and the last rule applied in \(\mathcal {D}_2\) is R\(\mathcal {Bet}\), as in:

(B) The cut formula is not principal in the last rule applied in \(\mathcal {D}_1\) . We distinguish sub-cases according to the last rule (r) applied in \(\mathcal {D}_1\).
-
(r)is an initial sequent, then the required derivation follows by weakening.
-
(r)is any rule different from R\(\bigcirc \) , R\(\square \) , and R\(\mathcal {Bet}\), then we simply permute the cut upwards.
-
(r)is R\(\bigcirc \) , R\(\square \) , or R\(\mathcal {Bet}\) . This is the key case, which requires peculiar proof transformations and the introduction of new semi-analytic cuts. We focus on cases where the cut formula is \(\square A\) or \( \bigcirc (B/A)\), as other cases are trivial due to the removal of formulas from the RHS with different shapes by the application of (r). We detail the case \(\square A\) (the case with cut formula \(\bigcirc (B/A)\) is analogous), assuming, for illustration purposes, that the last applied rule is R\(\mathcal {Bet}\). We trace the cut formula in \(\mathcal {D}_1\), till it is introduced a first time (in each branch), as in

For the sake of simplicity we first consider the case in which the cut formula is principal only in one branch of \(\mathcal {D}_1\) (w.l.o.g. the one displayed above); the general case is handled in the same way with an additional combinatorial argument. The cut is replaced by (\(\varTheta ^{\square \bigcirc }_{i}\Rightarrow \bigwedge \varTheta ^{\square \bigcirc }_{i} \) and \(\bigvee \varLambda ^{\square \bigcirc }_i \Rightarrow \varLambda ^{\square \bigcirc }_{i}\) are clearly derivable):

The first derivation above, say \(\mathcal {D}'_1\) is obtained from \(\mathcal {D}_1\) by substituting all occurrences of the cut formulas with \(\bigwedge \varTheta ^{\square \bigcirc }_{i} \), and the second derivation \(\mathcal {D}''_1\) by removing the cut formula from the RHS and adding \(\bigvee \varLambda ^{\square \bigcirc }_i\) to the LHS. The correctness of the application of the rules in these sub-derivations is guaranteed by Lemma 3. The cut between \(\varTheta ^{\square \bigcirc }_{i}\Rightarrow \varLambda ^{\square \bigcirc }_i,\square A^{l_{i}} \) and \( \square A^{m},\varPi \Rightarrow \varSigma \) is handled by induction hypothesis. The rule Cut\(^{*}\) can be replaced by new semi-analytic cuts (see Lemma 4 below, in the particular case \(n=1\)). The argument which ensures the semi-analyticity of the new cuts is at the end of the proof. In the general case, there may be k branches in which the cut formula is principal, with the following conclusions of \( R\square \) rules introducing \(\square A\)’s:
$$\{\varTheta _{j}^{\square \bigcirc }\Rightarrow \varLambda _{j}^{\square \bigcirc },\square A^{l_j}\,|\, j\in \{1,\hdots ,k\} \}.$$We now need to construct - following the pattern detailed for \(\mathcal {D}'_1\) and \(\mathcal {D}''_1\) - derivations with all the possible combinations of length k of the contexts \(\bigwedge \varTheta ^{\square \bigcirc }_{k_1}\) and \(\bigvee \varLambda ^{\square \bigcirc }_{k_2}\), with \(k_1\ne k_2\) and \(k_1,k_2\in \{1,\hdots ,k\}\), inverting their polarities, i.e. their position w.r.t. the sequent arrow. To witness a concrete example, if \(k=2\), we construct the derivations of the sequents: \(\bigvee \varLambda _{1}^{\square \bigcirc }, \bigvee \varLambda _{2}^{\square \bigcirc },\varGamma \Rightarrow \varDelta ,\mathcal {Bet}B\); \(\bigvee \varLambda _{1}^{\square \bigcirc },\varGamma \Rightarrow \varDelta ,\mathcal {Bet}B,\bigwedge \varTheta _{2}^{\square \bigcirc }\); \(\bigvee \varLambda _{2}^{\square \bigcirc },\varGamma \Rightarrow \varDelta ,\mathcal {Bet}B,\bigwedge \varTheta _{1}^{\square \bigcirc }\) and \( \varGamma \Rightarrow \varDelta ,\mathcal {Bet}B,\bigwedge \varTheta _{1}^{\square \bigcirc },\bigwedge \varTheta _{2}^{\square \bigcirc }\). In general, by suitably replacing all the occurrences of the cut formulas in \(\mathcal {D}_1\) we obtain \(2^k\) derivations of \(\varUpsilon ,\varGamma \Rightarrow \varDelta ,\mathcal {Bet}B, \Xi \), for any multiset \(\varUpsilon \) and \(\Xi \) s.t. \( C_j\in \varUpsilon \) if and only if \(C_j=\bigvee \varLambda _{j}^{\square \bigcirc }\) and \(C_j\in \Xi \) if and only if \(C_j=\bigwedge \varTheta _{j}^{\square \bigcirc }\) for some j, \(|\varUpsilon \cup \Xi |= k\) and if \(C_j,C_l\in \varUpsilon \cup \Xi \), then \(j\ne l\). The correctness of the resulting derivations follows again by Lemma 3. The desired sequent \(\varGamma , \varPi \Rightarrow \varDelta ,\mathcal {Bet}B, \varSigma \) is obtained by using the derived rule Cut\(^{*}\) (Lemma 4 below) also with the k derivations of \( \varTheta _{j}^{\square \bigcirc }, \varPi \Rightarrow \varLambda _{j}^{\square \bigcirc },\varSigma \) obtained by the induction hypothesis. It remains to show that all cut-formulas of the newly introduced cuts are generalized subformulas, i.e. that \(E\in \textsf{SUB}(\varGamma ,\varDelta )\) for every \(E\in \varTheta _{j}^{\square \bigcirc }\cup \varLambda _{j}^{\square \bigcirc }\), and hence that the newly introduced cuts are semi-analytic (by Lemma 4). Indeed, by assumption every formula in \(\mathcal {D}_1\) is in \(\textsf{SUB}(\varGamma ,\varDelta , X)\). Therefore the only case to be excluded is that E is \(\square A\). Assume by contradiction that this is the case. The \(\square A\) cannot change side of the sequent, and is not in \(\textsf{SUB}(\varGamma ,\varDelta )\) by hypothesis. As there is no cut on \(\square A\) in \(\mathcal {D}_1\) (being all these cuts replaced by contractions), the only remaining possibility is that \(\square A\) has been removed by a cut on a formula containing \(\square A\) as a subformula, but this cannot be the case by hypothesis.
The lemma below shows that cuts on conjunctions and disjunctions of generalized subformulas can be simulated by semi-analytic cuts.
Lemma 4
Let \(\varTheta =A_1,...,A_n, \varLambda =B_1,...,B_n\) be conjunctions and disjunctions of formulas in \(\textsf{SUB}(\varGamma , \varPi ,\varDelta ,\varSigma )\), the rule, with \(\varLambda _j \subseteq \varLambda \), \(\varTheta _j\subseteq \varTheta \), \(|\varLambda _j\cup \varTheta _j|=n\):

is admissible in \(\textbf{SFcm}\) without using non semi-analytic cuts.
Proof
We first show that the rule Cut\(^*\) is admissible using arbitrary cuts on the formulas \(A_i,B_i\)s and the contraction rules. The proof is by induction on n.
-
If \(n=1\), then the proof follows applying twice the cut rule:
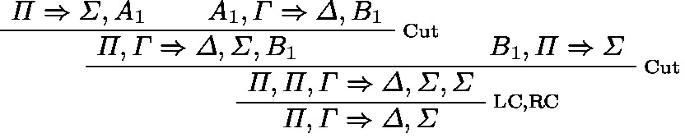
-
Let \(n=k+1\) and assume that the claim holds for k. We have \(\varTheta =A_1,...,A_k,A_{k+1} , \varLambda =B_1,...,B_k,B_{k+1} \) and the \(2^{k+1}\) left premises of the rule can be rewritten as: \(\{ \varLambda _j,\varPi \Rightarrow \varSigma , \varTheta _j, A_{k+1}\,|\,\,\, for\,\, all\,\, C_l,C_t\in \varLambda _j\cup \varTheta _j(l\ne t)\}\cup \) \(\{B_{k+1},\varLambda _j,\varPi \Rightarrow \varSigma , \varTheta _j\,|\, \,\, for\,\, all\,\, C_l,C_t\in \varLambda _j\cup \varTheta _j(l\ne t)\}\) with \(\varTheta _j\subseteq \{A_1,\hdots , A_k\}\) and \(\varLambda _j\subseteq \{A_1,\hdots , A_k\}\). Hence we proceed as follows:

the application of Cut\(^{*}\) is admissible by induction hypothesis. Analogously, we construct a derivation of \( B_{k+1},\varPi ,\varGamma \Rightarrow \varDelta ,\varSigma \):

applying the induction hypothesis. The conclusion now follows from two applications of the cut rule with the sequent \( A_{k+1},\varPi \Rightarrow \varSigma , B_{k+1} \) followed by contraction.
The claim of the lemma is now obtained observing that cuts on \(A_i\) and \(B_i\) can be transformed into semi-analytic cuts by exploiting the invertibility of the derived rules for \(\wedge \) and \(\vee \), because by hypothesis \(A_i, B_j\in \textsf{SUB}(\varGamma ,\varPi ,\varDelta ,\varSigma )\).
Theorem 5
Any \(\textbf{SFcm}\) proof with cuts can be transformed into a proof of the same sequent that only uses semi-analytic cuts.
Proof
Let \(\mathcal {D}\) be an \(\textbf{SFcm}\) proof with \(\sigma (\mathcal {D}) > 0\). We proceed by a double induction on \(\langle \sigma (\mathcal {D}), n\sigma (\mathcal {D}) \rangle \), where \(n\sigma (\mathcal {D})\) is the number of applications of cut in \(\mathcal {D}\) with non-analytic cut rank \(\sigma (\mathcal {D})\). Consider an uppermost application of non-analytic (cut) in \(\mathcal {D}\) with rank \(\sigma (\mathcal {D})\). By applying Theorem 4 to its premises either \(\sigma (\mathcal {D})\) or \(n\sigma (\mathcal {D})\) decreases.
Remark 1
The above result can be adapted to define sequent calculi with restricted cuts for the sequent calculus version of the calculi for \(\textbf{E}\) and \(\textbf{F}\) in [8, 9]. These calculi would be obtained by replacing in \(\textbf{SFcm}\) the rules for \(\mathcal {Bet}\) and \(\bigcirc (B/A)\) with the corresponding sequent rules for \(\textbf{E}\) and \(\textbf{F}\).
4 A Hypersequent Calculus for \(\mathbf{F + (CM)}\) and \(\textbf{G}\)
The calculus \(\textbf{SFcm}\) uses semi-analytic cuts, and is not easily extendable to capture \(\textbf{G}\)Footnote 5. Additionally, it would be challenging, if possible at all, to adapt it into a proof-search-oriented calculus for \(\mathbf{F + (CM)}\). Inspired by the transition in [4, 19, 23] from sequent calculus with analytic cuts [25] for the logic \(\textbf{S5}\) to a cut-free hypersequent calculus, we shift from the sequent to the hypersequent framework. Hypersequents are arguably the easiest generalization of sequents [2,3,4], consisting of multisets of sequents (called components) working in parallel and separated by the symbol “\(\mid \)”. We introduce a cut-free hypersequent calculus \(\textbf{HFcm}\) for \(\mathbf{F + (CM)}\). \(\textbf{HFcm}\) incorporates the sequent calculus for the logic \(\textbf{S4}\) as a sub-calculus and adds an additional layer of information by considering a single sequent to live in the context of hypersequents. Axioms and rules (including cut) of \(\textbf{HFcm}\) are obtained by adding to each sequent in \(\textbf{SFcm}\) a context G or H, standing for a (possibly empty) hypersequent, and simplifying the right rules for \(\square \), \(\mathcal {Bet}\) and \(\bigcirc \), as follows (with explicit weakening rules):

To manipulate the additional structure w.r.t. sequents, any hypersequent calculus contains external structural rules that operate on whole sequents. Standard rules are ext. weakening (ew) and ext. contraction (ec) (see below), which behave like weakening and contraction over whole sequents. The hypersequent structure opens the possibility to define new rules that allow the “exchange of information” between different components. These rules increase the expressive power of hypersequent calculi compared to sequent calculi, enabling the definition of cut-free calculi for logics that escape a cut-free sequent formulation; in the case of \(\textbf{S5}\) this is done using the rule (\(s5'\)) below (the \(\bigcirc \) is added to deal with \(\mathbf{F + (CM)}\))

Hence the crucial difference w.r.t. the calculus \(\textbf{SFcm}\) is that, due to the structural rules (ec) and \((s5')\), we can now restrict to single-succedent modal right rules without impairing cut-free completeness.
Remark 2
A cut-free hypersequent calculus for \(\textbf{F}\) was introduced in [9] by adding one rule to the calculus for \(\textbf{E}\) [8]. While \(\mathbf{F + (CM)}\) extends \(\textbf{F}\) (and \(\textbf{E}\)), our calculus is not a modular extension of these two. Indeed \(\textbf{HFcm}\) stems from an alternative semantics definition. Note that the premise \(A,\mathcal {Bet}\lnot A\Rightarrow B \) of the right rule for \(\bigcirc \) in these calculi would be trivially derivable in \(\textbf{HFcm}\).
Given a hypersequent \(\varGamma _1\Rightarrow \varDelta _1\,|\, \hdots \,|\, \varGamma _n\Rightarrow \varDelta _n\), its interpretation \(\iota \) is defined:
\((\varGamma _1\Rightarrow \varDelta _1\,|\, \hdots \,|\, \varGamma _n\Rightarrow \varDelta _n)^\iota := \square (\bigwedge \varGamma _1\rightarrow \bigvee \varDelta _1)\vee \hdots \vee \square (\bigwedge \varGamma _n\rightarrow \bigvee \varDelta _n)\)
Theorem 6
\(\textbf{HFcm}\) is sound and complete with cuts w.r.t. \(\mathbf{F + (CM)}\).
Proof
The soundness proof follows the pattern detailed for \(\textbf{SFcm}\). Completeness is ensured by the derivation of (CM).
A calculus for \(\textbf{G}\) is obtained in a modular way by adding an external structural rule to the calculus \(\textbf{HFcm}\) for \(\mathbf{F + (CM)}\). The additional rule is a slightly modified version of the well known communication rule, introduced by Avron [3] for capturing Gödel logic, and used in [16] for the modal logic S4.3:

Theorem 7
\(\textbf{HG}\) is sound and complete in presence of cuts w.r.t. \(\textbf{G}\)
Proof
Soundness: By induction on the height of the derivation. We only consider the case of the rule com. If the conclusion is not valid, then there are worlds x and y where x (y) forces every formula in \(\varGamma \) (\(\varPi \)) and x (y) falsifies every formula in \(\varDelta \) (\(\varSigma \)). By totality \(x\le y\) or \(y\le x\). If \(x\le y\), then y forces all the \(\square \), \(\bigcirc \) and \(\mathcal {Bet}\) formulas in \(\varGamma \) and thus, by the validity of the premise \( G \, | \, \varGamma ^{\square \bigcirc },\varGamma ^{b},\varPi \Rightarrow \varSigma \), we get an immediate contradiction. The other case is symmetrical.
Completeness in Presence of Cuts: follows by the derivability of axiom (RM) (the topmost sequent is derivable).

one premise of the rule com is omitted for space reasons.
5 Cut-Elimination for \(\textbf{HFcm}\) and \(\textbf{HG}\)
We prove that the calculus \(\textbf{HG}\) (and hence \(\textbf{HFcm}\)) admits cut-elimination. The strategy is the same as for the hypersequent calculus for \(\textbf{E}\) in [8].
Proof idea: As for the cut-reduction proof of \(\textbf{SFcm}\), cuts on a formula of the form \(\lnot A\) or \(A \rightarrow B\) are reduced using invertibility. In contrast with \(\textbf{SFcm}\), we can shift cuts with cut-formulas of the form \(\Box A\), \(\mathcal {Bet}\ A\) and \(\bigcirc (B / A)\) upwards until the cut formula is principal, using a specific order. First over the premise containing the cut formula on the right hand side (Lemma 6), due to the change made w.r.t. \(\textbf{SFcm}\) to the right rules of \(\mathcal {Bet}\), \(\square \), and \(\bigcirc \). Afterwards, over the other premise (Lemma 7). Note that when a rule introducing the cut formula on the right hand side is reached, the context has a shape that matches with the other premise of the cut and allows us to permute the cut upwards, similarly to case \(\mathbf {(A)}\) from Theorem 4. When the cut formula becomes principal also on the left hand side, it can be replaced by cuts on smaller formulas.
Henceforth we use the same inductive measure of the degree of formulas as in Sect. 3, while the rank of a derivation \(\mathcal {D}\) is now \(\rho (\mathcal {D})\) (Definition 5). The following lemmas refer to derivations in \(\textbf{HG}\) (and hence in \(\textbf{HFcm}\)).
The invertibility of the hypersequent version of the rules for \(\rightarrow \) and \(\lnot \) (Lemma 1) also holds in \(\textbf{HG}\) and is rank-preserving.
Lemma 5
Given derivations \(\mathcal {D}_1\) of \(G\,|\,\varGamma \Rightarrow \varDelta ,X\) and \(\mathcal {D}_2\) of \(H\,|\, X,\varPi \Rightarrow \varSigma \) with X principal in a logical, modal or deontic rule in both premises and \(\rho (\mathcal {D}_i) \le \texttt{dg}(X)\), there is a derivation \(\mathcal {D}\) of \(G\,|\,H\,|\, \varGamma ,\varPi \Rightarrow \varDelta ,\varSigma \) with \(\rho (\mathcal {D})\le \texttt{dg}(X)\).
Proof
As in Lemma 2 (the hypersequent structure plays no role).
The following lemmas are formulated in order to prove the admissibility of cuts on multiple occurrences of formulas taking into account the presence of explicit rules for contraction, both internal and external.
Lemma 6 (Right shift)
[Right shift] Given \(\mathcal {D}_1\) of \(H\,|\, \varPi _1\Rightarrow \varSigma _1, X^{n_1}\,|\,\hdots \,|\, \varPi _m\Rightarrow \varSigma _m,X^{n_m}\) in \(\textbf{HG}(\textbf{HFcm})\) and \(\mathcal {D}_2\) of \(G\,|\, X,\varGamma \Rightarrow \varDelta \) with \(\rho (\mathcal {D}_1),\rho (\mathcal {D}_2)\le \texttt{dg}(X)\), there is a derivation \(\mathcal {D}\), with \(\rho (\mathcal {D})\le \texttt{dg}(X)\), of
Proof
By induction on the height of \(\mathcal {D}_1\). If it is an initial sequent or the last applied rule acts on sequents in H, the proof is trivial. If the cut formula is principal in a logical (modal, deontic) rule, then we use Lemma 7. Assume that the cut formula is not principal. If the rule is R\(\bigcirc \), R\(\mathcal {Bet}\) and R\(\square \), then the claim follows by internal and external weakening (because such rules permit a single formula in the RHS). Otherwise, the cut is permuted and removed by induction hypothesis (note that the RHS of the rules \((s5')\) and (com), if present, remains unchanged in the premises, along with the associated context on the LHS).
Once we have reached the right rule introducing the cut formula \(\mathcal {Bet}A\), \(\bigcirc (A/B)\), or \(\square A\), we can shift the cut upward over the other premise of the cut, as shown in the next lemma.
Lemma 7 (Left shift)
[Left shift] Given \(\mathcal {D}_2\) of \(G\,|\, X^{n_1},\varGamma _1\Rightarrow \varDelta _1\,|\,\hdots \,|\, X^{n_m},\varGamma _m\Rightarrow \varDelta _m\) and \(\mathcal {D}_1\) of \(H\,|\,\varPi \Rightarrow \varSigma , X\) where X is principal in the last rule applied in \(\mathcal {D}_1\) with \(\rho (\mathcal {D}_1),\rho (\mathcal {D}_2)\le \texttt{dg}(X)\), there is a derivation \(\mathcal {D}\) with \(\rho (\mathcal {D} )\le \texttt{dg}(X)\) of
Proof
By induction on the height of the derivation \(\mathcal {D}_2\). The proof is similar to case (A) in Theorem 4. The hypersequent structure does not alter the proof, the only additional cases to consider are those involving hypersequent structural rules. See, e.g. [8] for \((s5')\). We consider the case of (com) where the cut formula moves from a component to another. W.l.o.g. we show a case in which we have two components in \(\mathcal {D}_2\), as in:

assuming that one of the active components does not contain the cut formula (the other case is analogous). We construct the following derivation:

where cuts are removed by induction hypothesis on the height of the derivation.
Theorem 8
Any \(\textbf{HFcm}\) \((\textbf{HG})\) proof with cuts can be transformed into a proof of the same hypersequent that does not use cuts.
Corollary 1
\(\textbf{HFcm}\) and \(\textbf{HG}\) are cut-free complete w.r.t. \(\mathbf{F + (CM)}\) and \(\textbf{G}\).
6 Proof Search Oriented Calculi for \(\mathbf{F + (CM)}\) and \(\textbf{G}\)
We transform the hypersequent calculi \(\textbf{HFcm}\) and \(\textbf{HG}\) into proof-search oriented calculi. The resulting systems feature reversible rules, with structural rules absorbed into logical ones, allowing for the construction of countermodels. This process follows the pattern established, e.g., for system \(\textbf{E}\) in [8].
Definition 6
The \(\textbf{HFcm}^{ps}\) calculus consists of the initial hypersequents of the shape \(G\, | \, \varGamma , p \Rightarrow \varDelta , p \), the (usual) rules for the propositional connectives that repeat the introduced formulas in the premises, together with:
The proof search oriented calculus \(\textbf{HG}^{ps}\) for \(\textbf{G}\) extends \(\textbf{HFcm}^{ps}\) with the rule:

Notice the peculiar shape of the rules L\(\bigcirc _2\) and L\(\square _2\), designed to absorb the hypersequent structural rule \({(s5')}\). The rule com acts only on \(\mathcal {Bet}\) formulas. This depends on the fact that \(\bigcirc \) and \(\square \) are governed by rules which introduce bottom-up formulas in every component.
Lemma 8
The rules of (internal and external weakening) and contraction are height-preserving admissible in \(\textbf{HFcm}^{ps}\). Every rule of the calculus is height-preserving invertible in \(\textbf{HFcm}^{ps}\).
Proof
The height-preserving admissibility of internal and external weakening follows from a straightforward induction on the height of the derivation. Invertibility follows from weakening. The contraction rules are admissible due to the repetition of every formula and component in each premise.
Theorem 9 (Soundness of \(\textbf{HFcm}^{ps}\) \((\textbf{HG}^{ps})\))
[Soundness of \(\textbf{HFcm}^{ps}\) \((\textbf{HG}^{ps})\)] If a hypersequent G is derivable in \(\textbf{HFcm}^{ps}\) \((\textbf{HG}^{ps})\), then so is in \(\textbf{HFcm}\) \((\textbf{HG})\).
Proof
Follows from the structural rules of \(\textbf{HFcm}\).
6.1 Decidability and Countermodel Construction
We define a proof search procedure which terminates for every sequent. If the proof search fails, we show how to extract a countermodel out of it.
Definition 7
A hypersequent H is saturated w.r.t. the system \(\textbf{HFcm}^{ps}\) if it is not an initial sequent and for every component \(\varGamma \Rightarrow \varDelta \) in H, whenever \(\varGamma \Rightarrow \varDelta \) contains the principal formulas in the conclusion of a rule (r), then H also contains the formulas introduced by one of the premisses of (r) for every rule (r). For example, in the case of \(\mathcal {Bet}\), we have:
-
(L\(\mathcal {Bet}\)). If \(\varGamma ,\mathcal {Bet}A\Rightarrow \varDelta \in H\), then \(A\in \varGamma \).
-
(R\(\mathcal {Bet}\)). If \(\varGamma \Rightarrow \varDelta ,\mathcal {Bet}A\in H\), then \(\varPi ,\varGamma ^{b} \Rightarrow \varSigma ,A\in H\) for some \(\varPi ,\varSigma \).
The saturation condition w.r.t. \(\textbf{HG}^{ps}\) is defined adding the condition:
-
(com). If \(\varGamma \Rightarrow \varDelta \in H\) and \( \varPi \Rightarrow \varSigma \in H\) then either \(\varPi ^{b}\) in \(\varGamma \) or \(\varGamma ^{b}\) in \(\varPi \).
Theorem 10
Given \(\Rightarrow A\) there is a derivation or a saturated hypersequent.
Proof
We start showing that the number of hypersequent components can be bounded in any derivation \(\mathcal {D}\) of \(\Rightarrow A\). Indeed, the rules which introduce new components are R\(\square \), R\(\bigcirc \) and R\(\mathcal {Bet}\). Consider first R\(\square \): we show that this rule is applied exactly once to each formula (say \(\square B\)), occurring in the consequent of a component and creates only one new component, no matter if \(\square B\) appears in the consequent of many components. To illustrate the situation, consider, e.g.,

Hence the number of components created by R\(\square \) is bounded by the number of boxed subformulas of A, whence it is O(n). The situation for R\(\bigcirc \) is similar.
R\(\mathcal {Bet}\) requires more care, being \(\mathcal {Bet}\) an S4 modality. In this case, having bounded the number of applications of R\(\square \) and R\(\bigcirc \), we assume that if there is an infinite introduction bottom-up of components these are introduced by the rule R\(\mathcal {Bet}\). Hence, since the number of possible sequents is finite (in particular \(2^{|2^{|\textsf{SUB}(A)|}|}\)), there has to be a repetition. In this case, we have met the saturation condition for the rule R\(\mathcal {Bet}\). Thus the number of components is finite. Since we can rule out rule applications for which the saturation condition has already been met (due to the admissibility of contraction), every rule introduces bottom-up a new component or new formulas in the components, hence the length of every branch of a putative derivation of A is bounded and the derivation is finite.
The next theorem ensures the completeness of our calculi and show how to extract countermodels out of a failed proof search.
Theorem 11
If A is valid in \(\mathbf{F + (CM)}\) (\(\textbf{G}\)), is derivable in \(\textbf{HFcm}^{ps}\) (\(\textbf{HG}^{ps}\)).
Proof
By contraposition. If A is not derivable, by Theorem 10 there is a saturated hypersequent: \(\varGamma _1\Rightarrow \varDelta _1\,|\,\hdots \,|\,\varGamma _n\Rightarrow \varDelta _n\). We assign labels to the components \(i:\varGamma _i\Rightarrow \varDelta _i\) (\(i\in \{1,\hdots , n\}\)) and consider the model: \(\mathcal {M}=\langle \{1,\hdots ,n\}, \le , v\rangle \) with \(i\le j\) if and only if \(\varGamma _{i}^{b}\subseteq \varGamma _{j}\) and \(i\in v(p)\) if and only if \(p\in \varGamma _i\).
We have to check that the model is reflexive and transitive in the case of \(\textbf{HFcm}^{ps}\) and total in the case of \(\textbf{HG}^{ps}\). The relation \(\le \) is reflexive and transitive, because set inclusion is reflexive and transitive. As regards totality, we observe that the saturation condition for (com) ensures that for every i and j, \(\varGamma _{i}^{b}\subseteq \varGamma _{j}\) or \(\varGamma _{j}^{b}\subseteq \varGamma _i\) which gives by definition \(i\le j\) or \(j\le i\).
We now show that for every i in the model \(\mathcal {M}\) we have \( i\Vdash B\) if \(B\in \varGamma _i\) and \(i\nVdash B\) if \(B\in \varDelta _i\). We argue by induction on the degree of the formulas.
-
If B is atomic, the claim stems from the definition of the valuation function and by the saturation condition.
-
If B is a compound formula, the proof follows from the use of the induction hypothesis and saturation. We deal with the case in which B is \(\mathcal {Bet}C\); the other cases are handled similarly. If \(\mathcal {Bet}C\in \varGamma _i\), suppose \(i\le j\), then \(\varGamma ^{b}_{i}\subseteq \varGamma _j\). By the saturation condition for L\(\mathcal {Bet}\), we get \({C}\in \varGamma _j\) and by induction hypothesis we have \(j\Vdash {C}\), hence the desired conclusion. If \(\mathcal {Bet}C\in \varDelta _i\), then by definition of saturation there is \(\varGamma _j\Rightarrow \varDelta _j, C\) with \(\varGamma ^{b}_{i}\subseteq \varGamma _j\) so \(i\le j\), and by induction hypothesis \( i\nVdash C\), so the desired conclusion follows.
Remark 3
The above countermodel construction can be adaptedFootnote 6 to define a proof-search-oriented calculus for Gödel-Dummett logic [10].
Concluding Remark: we demonstrated that for \(\mathbf{F + (CM)}\) (and Åqvist systems \(\textbf{E}\) and \(\textbf{F}\)), while it is possible to define sequent calculi that use semi-analytic cuts, the hypersequent framework provides a modular and cut-free approach, enabling the capture of \(\mathbf{F + (CM)}\) and \(\textbf{G}\), and supporting countermodel construction.
Notes
- 1.
- 2.
Our \(R\square \) rule derives the absoluteness axiom.
- 3.
\(\bigcirc (B/A)\) could have been introduced as a defined operator. However, since our main concern is the investigation of dyadic deontic logics we preferred to retain the obligation connective as a primitive element, and generalize the notion of analytic cut. .
- 4.
This is the familiar parametric ancestor relation of [5].
- 5.
- 6.
Using the multiple conclusion version of calculus in [3] (whose rule com moves any multiset of formulas) in which the rules for \(\rightarrow \) are replaced by:
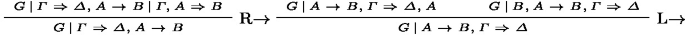
.
References
Åqvist, L.: Deontic logic. In: Gabbay, D., Guenthner, F. (eds.) Handbook of Philosophical Logic. Synthese Library, vol. 165, pp. 605–714. Springer, Dordrecht (1984). https://doi.org/10.1007/978-94-009-6259-0_11
Avron, A.: A constructive analysis of RM. J. Symb. Logic 52(4), 939–951 (1987)
Avron, A.: Hypersequents, logical consequence and intermediate logics for concurrency. Ann. Math. Artif. Intell. 4, 225–248 (1991)
Avron, A.: The method of hypersequents in the proof theory of propositional non-classical logics. In: Logic: From Foundations to Applications, pp. 1–32. OUP, New York (1996)
Belnap, N.D., Jr.: Display logic. J. Philos. Logic 11(4), 375–417 (1982)
Burgess, J.: Quick completeness proofs for some logics of conditionals. Notre Dame J. Formal Logic 22(3), 76–84 (1981)
Ciabattoni, A., Lang, T., Ramanayake, R.: Cut-restriction: from cuts to analytic cuts. In: LICS, pp. 1–13 (2023)
Ciabattoni, A., Olivetti, N., Parent, X.: Dyadic obligations: proofs and countermodels via hypersequents. In: Aydoğan, R., Criado, N., Lang, J., Sanchez-Anguix, V., Serramia, M. (eds.) PRIMA 2022. LNCS, vol. 13753, pp. 54–71. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-21203-1_4
Ciabattoni, A., Olivetti, N., Parent, X., Ramanayake, R., Rozplokhas, D.: Analytic proof theory for Aqvist’s system F. In: Maranhão, J., Peterson, C., Straßer, C., van der Torre, L. (eds.) DEON 2023, pp. 79–98 (2023)
Dummett, M.: A propositional logic with denumerable matrix. J. Symb. Log. 24, 96–107 (1959)
Gabbay, D., Horty, J., Parent, X., van der Torre, L., van der Meyden, R. (eds.) Handbook of Deontic Logic and Normative Systems, vol. 2. College Publications, London (2021)
Gabbay, D.M.: Theoretical foundations for non-monotonic reasoning in expert systems. In: Apt, K.R. (ed.) Logics and Models of Concurrent Systems. NATO ASI Series, vol. 13, pp. 439–457. Springer, Heidelberg (1985). https://doi.org/10.1007/978-3-642-82453-1_15
Giordano, L., Gliozzi, V., Olivetti, N., Pozzato, G.L.: Analytic tableaux calculi for KLM logics of nonmonotonic reasoning. ACM Trans. Comput. Log. 10(3), 18:1–18:47 (2009)
Girlando, M., Lellmann, B., Olivetti, N., Pozzato, G.L.: Hypersequent calculi for Lewis’ conditional logics with uniformity and reflexivity. In: Proceedings of Tableaux (2017)
Indrzejczak, A.: Natural Deduction, Hybrid Systems and Modal Logics. Springer, Dordrecht (2010). https://doi.org/10.1007/978-90-481-8785-0
Indrzejczak, A.: Cut-free hypersequent calculus for S4.3. Bull. Sect. Logic Univ. Łódź 41(1–2), 89–104 (2012)
Kowalski, T., Ono, H.: Analytic cut and interpolation for bi-intuitionistic logic. Rev. Symb. Log. 10(2), 259–283 (2017)
Kraus, S., Lehmann, D., Magidor, M.: Nonmonotonic reasoning, preferential models and cumulative logics. Artif. Intell. 44(1–2), 167–207 (1990)
Kurokawa, H.: Hypersequent calculi for modal logics extending S4. In: Nakano, Y., Satoh, K., Bekki, D. (eds.) JSAI-isAI 2013. LNCS (LNAI), vol. 8417, pp. 51–68. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10061-6_4
Schröder, L., Pattinson, D., Hausmann, D.: Optimal tableaux for conditional logics with cautious monotonicity. In: Wooldridge, M. Coelho, H., Studer, R. (eds.) Proceedings of the 2010 conference on ECAI 2010: 19th European Conference on Artificial Intelligence, pp. 707–712. IOS Press, Amsterdam (2010)
Lewis, D.: Counterfactuals. Blackwell, Oxford (1973)
Lyon, T.S., et al.: Internal and external calculi: ordering the jungle without being lost in translations. CoRR, abs/2312.03426 (2023)
Minc, G.: Some calculi of modal logic. Trudy Mat. Inst. Steklov 98, 88–111 (1968)
Negri, S., Olivetti, N.: A sequent calculus for preferential conditional logic based on neighbourhood semantics. In: Proceedings of Tableaux, vol. 9323, pp. 115–134 (2015)
Ohnishi, M., Matsumoto, K.: Gentzen method in modal calculi. Osaka Math. J. 9, 113–130 (1957)
Ono, H., Sano, K.: Analytic cut and Mints’ symmetric interpolation method for Bi-intuitionistic tense logic. In: Advances in Modal Logic, pp. 601–624. College Publications (2022)
Parent, X.: Maximality vs. optimality in dyadic deontic logic. J. Philos. Log. 43(6), 1101–1128 (2014)
Parent, X.: Preference semantics for Hansson-type dyadic deontic logic: a survey of results. In: Gabbay, et al. [11], pp. 7–70
Smullyan, R.M.: Analytic cut. J. Symb. Log. 33, 560–564 (1968)
Takano, M.: Subformula property as a substitute for cut-elimination in modal propositional logics. Math. Japon. 37, 1129–1145 (1992)
Takano, M.: New modification of the subformula property for a modal logic. Bull. Sect. Log. 49, 08 (2020)
Acknowledgements
Work supported by the FWF project I 6372-N.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Ciabattoni, A., Tesi, M. (2024). Sequents vs Hypersequents for Åqvist Systems. In: Benzmüller, C., Heule, M.J., Schmidt, R.A. (eds) Automated Reasoning. IJCAR 2024. Lecture Notes in Computer Science(), vol 14740. Springer, Cham. https://doi.org/10.1007/978-3-031-63501-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-63501-4_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63500-7
Online ISBN: 978-3-031-63501-4
eBook Packages: Computer ScienceComputer Science (R0)