Keywords

1 Introduction

SAT solvers are highly complex and highly optimized programs, which are used to verify critical properties of other systems. To increase the trust in them, SAT solvers produce certificates that can be independently checked by formally verified checkers [5, 9, 10, 16, 23, 34, 35]. Here, the focus is on certificates for unsatisfiability, as certificates for satisfiability are (considered) trivial.

Typically, certificate checking proceeds in two phases: An unverified elaborator adds additional information to the certificate produced by the SAT solver, and then a formally verified checker checks the elaborated certificate against the original formula. This approach moves some complicated and computationally expensive tasks into the unverified elaborator, making checking of the elaborated certificate simpler and less expensive.

However, the elaborator has to recompute information which is, in principle, known to the solver, and elaboration typically takes as long as solving. More recent techniques accelerate elaboration by including this information into the certificate [2]. The most recent development are solvers that directly produce elaborated certificates [29]. This allows for streaming the certificates from the solver into the checker: solving and checking are done in parallel, and the potentially large certificates need not be stored on disk. When implemented appropriately, the memory footprint of the checker is similar to that of the solver.

There are different formats for elaborated unsatisfiability certificates, such as PB [4] and GRAT [23]. The de-facto standard is the LRUP format [10], and its backwards compatible generalizations LRAT [9] and LPR [35]. These correspond to the non-elaborated DRUP [17], DRAT [36], and DPR [35] formats. With an exception in 2023, LRUP is sufficient for all top performing solvers in the SAT competitions of the last years [29].

In this paper, we present a formally verified checker that can stream LRUP certificates. We benchmark our tool on the CaDiCaL solver [29], where it only causes a minimal additional computation overhead, and has a memory usage similar to that of the solver. Our checker is as fast as the highly optimized unverified lrat-trim checker [29], and at least one order of magnitude faster than any other verified checker we know of. Using the Isabelle Refinement Framework [22], our checker is verified down to the LLVM intermediate representation [26] of its code, and against a formal grammar of the DIMACS CNF format, which is the standard for representing CNF formulas [32]. To the best of our knowledge, our checker is the first that comes with a verified parser. Our tool and benchmark data is available at https://github.com/lammich/lrat_isa.

In the rest of this paper, we describe our formal specification (Sect. 2), the abstract certificate checking algorithm (Sect. 3), and its implementation (Sect. 4). We then report on our benchmark results (Sect. 5). Finally we conclude the paper and discuss related and future work (Sect. 6).

2 Specification

We prove soundness of our checker, i.e., it accepts a string only if it is a representation of an unsatisfiable formula in DIMACS CNF formatFootnote 1. In this section we present the formalization of this specification.

2.1 Conjunctive Normal Form

Throughout this paper, we will use some simplified Isabelle/HOL notation, and explain unusual notations where they first occur. For definitions we use \(\equiv \). Data types are written in prefix notation, e.g., lit set for a set of literals. Function application is denoted as \(f\ x_1\ \dots \ x_n\).

The following is the abstract syntax and semantics of CNF, taken from the GRAT tool [23] and slightly adapted to our needs:

figure a

A variable is a positive natural number, a literal is a positive or negative variable, a clause is a set of literals, and a cnf-formula is a set of clauses. A valuation assigns truth values to variables. For a valuation \(\sigma \), the semantics assigns truth values to literals (sem_lit) and formulas (sem_cnf): a positive literal is true iff its variable is true, and a negative literal is true iff its variable is false. A formula is true iff every clause contains a true literal, and it is satisfiable if there is a valuation for which it is true.

Fig. 1.
figure 1

Example formula in DIMACS CNF

Full size image

2.2 Specification of the DIMACS CNF Format

DIMACS CNF is the de-facto standard format for representing CNF formulas. Figure 1 displays an example: the file can start with optional comment lines, indicated by a heading ‘c’. After the comments, there is a header of the form p cnf n m, where n is the maximum variable, and m is the number of clauses. Then the clauses follow, encoded as zero-terminated sequences of integers, where a positive integer represents a positive literal, and a negative integer represents a negative literal. We need to specify how a word in DIMACS format corresponds to a formula. While a language is a set of words, we use a relation between words and corresponding abstract syntax. By slight abuse of naming, we call such relations grammars. We shallowly embed regular grammars into Isabelle HOL’s logic:

figure b

Here, \((w,r)\in g\) means that the grammar g relates the word w to the result r. The empty relation corresponds to the empty language. The relation \(\texttt {return}\ x\) relates the empty word to the result x. It corresponds to the language of only the empty word. The relation \(\langle C \rangle \) relates single-character words to the corresponding character from the set C. Finally, the relation \(\texttt {bind}\ g\ f\) relates a word \(w_1w_2\) to a result r, if g relates \(w_1\) to some intermediate result x, and f x relates \(w_2\) to r. This corresponds to concatenation of languages.

The type gM is a monad, and we use the usual shortcut notation for bind:

figure e

We also define shortcuts to apply a function to the result of a monad, to lift a binary function into a monad, and to concatenate two grammars, ignoring the result of the latter:

figure f

We then define the relational versions of the power function and the Kleene star:

figure g

where x#xs prepends the element x to the list xs. That is, \(g\_pow\ g\ n\) and \(g^*\) relate the input to lists, the elements being the results produced by g. We also define .

Using the grammar monad, we specify a grammar for the simplified DIMACS format as used by SAT competitions since 2009 [32]. We start with defining sets of ASCII characters:

figure i

Here, 8 word is the 8-bit word type from Isabelle’s machine word library [3, 11]. Note whitespace includes all 6 ASCII whitespace characters. Based on this, we define a grammar :

figure k

Here, converts a string to a natural number, and yields the set of elements in a list.

Note that we do not check the contents of the header, which contains auxiliary information for parsing, but does not affect the represented formula. We also accept multiple clauses per line and clauses spanning several lines, as well as extra whitespace anywhere in the file. Many SAT solvers support similar relaxations of the format, and we wanted this flexibility in our tool, too.

As a sanity check, we prove that our grammar is unambiguous, i.e., that it relates the same word to at most one formula:

figure n

2.3 Correctness Specification

At this point, we can formalize the postcondition for our checker’s specification: \(\exists F.\ (w,F) \in g\_dimacs \wedge \lnot sat\ F\) means that the sequence of bytes w is a valid DIMACS CNF representation of an unsatisfiable formula.

3 Certificates for Unsatisfiability

RUP (reverse unit propagation) certificates contain the clauses learned by the solver. The checker justifies that addition of each clause preserves satisfiability. For an unsatisfiable formula, the last learned clause is the empty clause. Adding the empty clause yields an unsatisfiable formula, and, as each clause addition is justified to preserve satisfiability, the original formula is unsatisfiable, too.

Justification is done by reverse unit propagation [14]: a clause C can be added to the formula F, if the formula \(F \wedge \lnot C\) is unsatisfiable, and if this can be shown by generating an empty clause via unit propagation. For RUP, the checker has to implement unit propagation itself, for example with a two-watched-literals data structure [28]. LRUP (linear RUP) certificates annotate each clause addition, with the relevant unit clauses in the order they become unit, and the final conflict clause. This makes the checker simpler and more efficient, as it only needs to check if clauses are unit, rather then find unit clauses.

The certificates also contain clauses deleted by the solver. This allows the checker to also delete those clauses from its data structures, freeing up memory. Note that deleting a clause trivially preserves satisfiability.

The actual LRUP format uses natural numbers to identify clauses, rather than spelling them out whenever they are referenced. The n clauses of the initial formula implicitly get the ids \([1,\ldots ,n]\). A clause addition has the form . It consists of the id under which this clause shall be added, a zero-terminated list of the literals of the clause, and a zero terminated list of the unit clauses and the conflict clause to justify the addition. A clause deletion has the form , and consists of a zero terminated list of the ids of the clauses to be deleted. There is an ASCII and a more compact binary encoding for LRUP certificates.

3.1 Abstract Checker

In this section, we present our formalization of the abstract checker algorithm. We start with defining some basic concepts:

figure q

The literal \(-l\) is the negation of the literal l. A partial assignment (pan) characterizes a set of literals that are assigned (to true). It is consistent if it does not assign both a literal and its negation. A formula F is satisfiable w.r.t. a partial assignment A (sat_wrt F A), if A can be extended to a satisfying valuation; A is in conflict with a clause C (conflict A C), if the negations of all the clause’s literals are assigned. The clause C is unit or true w.r.t. A and a literal l (is_uot A C l), if l is the only literal in C whose negation is not assigned. A clause is a tautology (taut C), if it contains both a literal and its negation.

Correctness of a RUP step adding C to F is implied by the following lemmas:

  1. (1)

    Let C be a non-tautological clause. Then, the initial assignment , which assigns the negated version of each literal in C, is consistent, and \(F\, \wedge \, \lnot C\) is satisfiable iff F is satisfiable w.r.t. the initial assignment:

    figure s
  2. (2)

    If the formula contains a unit or true clause, assigning its literal preserves consistency and does not change satisfiability:

    figure t
  3. (3)

    If the formula contains a conflict clause, it is unsatisfiable:

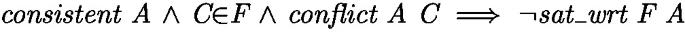
    figure u

    Note that the learned clause cannot be a tautology. While adding tautologies trivially preserves satisfiability, they yield an inconsistent initial assignment. Instead of spending computation time to detect tautologies, we let our checker run with the inconsistent assignment: should it succeed, we add the clause, which is safe.

We formalize the abstract checker as a transition system over the state:

figure v

The transition relation \(\rightarrow \) is the least relation that satisfies the following rules:

figure w

The checker starts in state CNF F, with some formula F. To delete clauses (del_clauses), they are removed from F. A clause addition is split into multiple smaller steps: First, we initiate adding a clause by going to state CLS (start_clause). We also maintain a partial assignment, starting with the empty assignment \(\lambda \_.\ \textit{False}\). We then add the literals of the clause, one by one (add_lit). For each added literal l, we assign the negated literal \(-l\). When all literals have been added, we start the proof (start_proof) going to state PRF. During the proof, we add unit clauses, assigning the unit literal (add_unit). When we have added enough unit clauses, we add a conflict clause (add_conflict), going to state PDN (proof done). From there, we either go to state UNSAT if we have proved the empty clause (finish_proof_unsat), or back to state CNF with the new clause added to the formula (finish_proof). We can always go to FAIL (to_fail), indicating that the proof failed.

With the above Lemmas 1–3, some bookkeeping that add_lit steps construct the correct initial assignment, and a special case for tautologies, we prove:

Theorem 1

(Soundness of Abstract Checker). If the abstract checker can reach UNSAT from the initial state CNF F, then the formula F is unsatisfiable: \(\textit{CNF}\ F \rightarrow ^* \textit{UNSAT} \implies \lnot \textit{sat}\ F\)

Note that we do not yet model clause identifiers on this level. They will be introduced in a later refinement step.

4 Implementation

We have specified a grammar to relate strings in DIMACS format to formulas, a semantics to define satisfiability of formulas, and an abstract certificate checker. We now refine these to the actual implementation of a certificate checker.

We use the Isabelle Refinement Framework [24], which supports refinement in multiple steps and in a modular fashion. Each step focuses on a different aspect of the algorithm, thus structuring the correctness proof, and making it manageable in the first place. In this section, we first describe the data structures that we use in our implementation, to represent abstract concepts such as literals and clauses (cf. Sect. 2.1). We then describe how we implement the abstract checker algorithm (cd. Sect. 3.1), using these data structures. Finally, we describe how we integrate the checker with the parser, to obtain the actual verified tool.

4.1 Basic Concepts and Data Structures

We use data structures such as arrays, dynamic arrays, and array lists from Isabelle LLVM’s library [22]. For technical reasons, sizes and counters are implemented as non-negative signed 64-bit integers, or, equivalently, as unsigned 64-bit integers less than \(2^{63}\). Formally, refinement relations between concrete and abstract types are used. For example, relates non-negative 64-bit signed integers to natural numbers. Similarly, Booleans are implemented by 1-bit words, via the relation .

Clause identifiers are modelled as 64-bit unsigned integers less than \(2^{63}-1\), via the relation . This bound allows us to use clause identifiers as indexes into an array whose length is represented by a size.

Literals are first refined to natural numbers via , where a number \(n>1\) represents the variable \(\lfloor n/2\rfloor \), and the literal is negative iff n is odd. The natural numbers are further refined to unsigned 32-bit integers, via . When we compose the two refinement relations, we get a relation between 32-bit integers and literals: \(\textit{ulit}\_\textit{rel} \equiv \textit{u32}\_\textit{rel}\ \textit{O}\ \textit{nlit}\_\textit{rel}\). Using 0 for None, we can also refine optional literals to 32-bit integers via the relation . For each operation on the abstract data type, we define a corresponding operation on the concrete data type. For example, we define:

figure ad

We show that the concrete operations refine their abstract counterparts:

figure ae

Here, is a shorthand notation for . Combining these refinement theorems yields .

Clauses are implemented as zero-terminated arrays of 32-bit words, via the relation . As arrays are stored on the heap, this relation is expressed as separation logic assertion (assn). By convention, pure refinement relations have the suffix _rel, while those that use the heap have the suffix _assn.

A clause database \(\textit{cdb} \equiv \textit{nat} \Rightarrow \textit{clause}\ \textit{option}\) is a partial function from clause identifiers to clauses. It is implemented by a dynamic array of pointers to clauses \(\textit{cdbi} \equiv \textit{32}\ \textit{word}\ \textit{ptr}\ \textit{larray}\), via . The array is indexed by the clause identifier. For clause identifiers not in the database, the array contains a null pointer. Consider the abstract operation cdb_ins cid C db that inserts a clause C with identifier cid into the database db, its concrete version cdb_ins_impl, and the corresponding refinement theorem:

figure ak

The concrete operation destructively updates the array, thus the abstract cdb parameter does no longer correspond to any concrete value. Also, the ownership of the inserted clause is transferred into the clause database, thus the abstract clause parameter does no longer correspond to any (visible) concrete value. We call those parameters destroyed, indicated by a \({}^d\) in the refinement theorem [21].

4.2 Data Structures with Capacity Bounds

Several data structures in our checker use counters. For example, during parsing, the literals of a clause are collected in an array list, which uses a counter for its size. We prove non-overflow of these counters from the bounded size of the CNF file, and a limit on how many literals we can read from the certificate before the checker rejects itFootnote 2. While we elide the details, we note that some abstract data structures have a capacity bound field. This is a ghost field, i.e., it is not present in the implementation.

The clause builder uses a dynamic array to store the literals of the clause that is currently parsed, and also keeps track of the maximum literal encountered so far. Its abstract type is \(\textit{cbld} \equiv \textit{nat} \times \textit{lit}\ \textit{list} \times \textit{nat}\). A clause builder consists of the maximum encountered literal ml, the current list of literals ls, and a (ghost) bound bnd that limits the length of ls. We define a data type invariant that characterizes valid clause builders (i.e., the bound and maximum literal are consistent with the list of literals). The relation implements clause builders.

A partial assignment (cf. Sect. 3.1) is implemented by an array of bits indexed by the literals, as well as an array list that contains all set literals. This array list allows for efficiently resetting the assignment in between proof steps. We use the type for the implementation, and for the functional representation, related by . The last field of rpan is a (ghost) capacity bound. The type rpan comes with an invariant rpan_inv, and an abstraction function to the encoded partial assignment.

4.3 Proof Checker Implementation

We implement the abstract checker state (Sect. 3.1) by the following types:

figure as

All data structures start with an error flag, which indicates a failed proof (abstract state FAIL). Outside a proof, i.e., in abstract states CNF and UNSAT, the checker state is represented by a tuple , where unsat indicates that the formula has been proved unsatisfiable and db is the clause database holding the formula. The builder state bld and assignment A are unused here, but threaded through such that they can be reused when the next proof begins. When building a clause (abstract state CLS), the state is represented as . Finally, inside a proof (abstract states PRF and PDN), the state is . Here, confl indicates that a conflict clause has been found.

We define invariants cs_op_inv, cs_bc_inv, cs_ip_inv; and abstraction functions \(\textit{cs}\_\textit{op}\_\alpha \), \(\textit{cs}\_\textit{bc}\_\alpha \), \(\textit{cs}\_\textit{ip}\_\alpha \) to the abstract checker state. We then show that the functions on the concrete states preserve the invariants and implement the transition relation \(\rightarrow ^*\) on the corresponding abstract states. For example, the following function handles a proof step, adding a unit or a conflict clause:

figure aw

Here, ’a nres is the Isabelle Refinement Framework’s type of programs that return a result of type ’a, and \(P \implies c \le \texttt {spec}\ r.\ Q\ r\) is a Hoare-triple with pre- condition P, program c, and postcondition Q [24]. That is, if the concrete checker state cs has some capacity left, then the cs_prf_step function preserves the invariant cs_ip_inv and implements the abstract transition relation \(\rightarrow \). The available capacity of the checker state decreases by one.

Fig. 2.
figure 2

Function to check if a clause is unit, true, or conflict.

Full size image

The implementation of cs_prf_step uses a function to check if a clause is unit, true, or a conflict. It is displayed in Fig. 2. It first checks (l. 3) if the clause identifier is valid, and looks it up in the database (l. 4). Then (l. 6), it loops over the literals of the clause, maintaining a state consisting of an optional literal and an error flag (ul,err). Initially (l. 11), the state is (None,False). The loop assigns to ul the first literal that is not false (l. 9). If a second non-false literal is encountered, the error flag is set (l. 10). The function returns the state after the loop, or (None,True) if the clause was invalid (l. 12). Note that we assume (l. 5) a finite clause. On the abstract level, we can use this to justify termination of the loop. When implementing the function, we have to prove finiteness, which is trivial, as the clause is stored in an array. Dually, we assert (l. 7) that the literals of the clause are in bounds of the assignment. This has to be proved on the abstract level. When implementing, we can use it to justify that the array access for looking up the literal is in bounds. This way, assertions and assumptions are used to pass proof obligations up and down the refinement chain, proving them at the most convenient abstraction level.

The loop in check_uot is the innermost loop of the checker, and special care has been taken to optimize it: while an actual certificate always contains unit clauses, we also allow clauses with one true literal (cf. is_uot in Sect. 3.1). This avoids indexing both A(l) and \(A(-l)\) to distinguish between the two cases.

The correctness theorem for check_uot is as follows:

figure ax

I.e., if the partial assignment satisfies its invariant, the clause identifier identifies clause C, and the clause database contains only variables within the bounds of the partial assignment, then the function will either return an error, or some literal l such that C is unit or true w.r.t. l, or None and C is a conflict clause.

4.4 A Verified DIMACS Parser

We present the parsing function’s signature and correctness theorem. Its implementation is elided due to page limit constraints:

figure ay

This function parses a string, and returns a checker state. On a parsing error, the checker state corresponds to the abstract state FAIL. Otherwise, it corresponds to CNF F for the formula F parsed from the string. The function also returns the capacity left for the certificate after parsing the formula.

4.5 Assembling the Whole Program

Having implemented functions for the proof steps, we combine them with a parser (details elided) for LRAT proofs, resulting in a function that reads an LRAT proof from a buffered reader (brd_rs), performs the corresponding transitions on the proof state, and finally checks if the proof state has reached UNSAT:

figure az
Fig. 3.
figure 3

The checker program.

Full size image

The certificate checker, displayed in Fig. 3, combines the main checker loop with the DIMACS parser. It takes a string cnf, parses it as formula (l. 3), initializes a buffered reader for the certificate stream (l. 5), and runs the main checker loop with that reader (l. 6). From the correctness of the parser (Sect. 4.4), the fact that all proof steps in main_checker_loop implement the abstract checker, and the fact that the abstract checker is sound (Theorem 1), we prove:

Theorem 2

(Soundness of Functional Checker). If read_check_lrat cnf returns true, then cnf is a valid representation of an unsatisfiable formula:

figure ba

4.6 Refinement to LLVM Code

In Sect. 4.1 and Sect. 4.2 we have indicated how we implement the basic data structures of our checker. Then, we have mostly presented functional code. Given implementations of the data structures, refining this functional code to imperative code is mostly straightforward. Actually, much of this process can be automated by the Sepref tool [22], which we use to generate implementations for each data structure and algorithm. For example, for the function check_uot (cf. Sect. 4.3):

figure bb

This generates the function check_uot_impl and proves the refinement theorem:

figure bc

To read the certificate, we use an external C function based on fread:

figure bd

Inside Isabelle, this function is specified by:

figure be

Where htriple is the Hoare triple for LLVM programs and \(\star \) is the separating conjunction. This matches the specification of POSIX’s fread function [30], except that we do not specify what data is read. This is sound, as it is a valid over-approximation of the actual behaviour.

4.7 Soundness Theorem

Finally, we generate an implementation of read_check_lrat (Sect. 4.5), obtaining:

figure bf

Here, inp_assn implements the input string by an array and its length. In order to smoothly interface this function from C/C++, we eliminate the tuple type and return a byte instead of a bit. We define:

figure bg

Isabelle LLVM’s code generator creates LLVM code, and a matching header file:

figure bh

We link this with a small C program that reads the command line, memory-maps the formula file, provides the function fread_from_certificate (cf. Sect. 4.6), calls the verified checker, and prints the result.

Chaining together the correctness of the functional checker (Theorem 2) and the refinement theorem for read_check_lrat, and unfolding some definitions yields:

Theorem 3

(Soundness of Implementation). When we pass the checker a pointer cp to an array of size cszi holding the bytes c, then the checker will terminate with the array being unchanged, and if the result is not zero, the bytes c in the array are a syntactically correct encoding of an unsatisfiable CNF:

figure bi

Note that this theorem does not depend on any complex data structures or refinements. Apart from the basic notions of Hoare triples, separation logic, machine words, and pointers to arrays, it only depends on our semantics of formulas (Sect. 2.1), and our grammar for the DIMACS format (Sect. 2.2).

5 Benchmarks

For our benchmarks, we have used the latest stable versions of the tools available at the time of writing: CaDiCaL 1.9.4 [7], lrat-trim 0.2.0 [27], cake_lpr 7a207e9 [8], gratchk dc6dd9d [15], lrat-check 9ee016c [12], and lrat-acl2 (incremental) 8.5 [1] on gcl 2.6.13pre [13]. We used an AMD Ryzen 9 7950X3D machine with 128 GB DDR5 RAM and a 2.0 TB Samsung 990 Pro SSD disk.

We have used problems from the 2022 SAT competitionFootnote 3 [33]: out of the 156 problems proved unsatisfiable in the main track, CaDiCaL timed out on 5 after 5000 s. The remaining 151 problems form our benchmark set.

Table 1. Benchmark results in streaming mode. The table displays the averages over the successfully certified problems (n).
Full size table

First, we let the checker run in parallel to CaDiCaL, streaming the certificate directly into the checker. We used our checker and cake_lprFootnote 4. We measure the computing times (the sum of user and system time) that were allocated to the sat solver (\(t_s\)) and checker (\(t_c\)). The ratio \(t_c/t_s\) indicates how the work is distributed between solver and checker. The smaller this ratio, the less time the checker needs in comparison to the solver. Next, we measure the average CPU loads allocated to the solver (\(l_s\)) and checker (\(l_c\)). A solver load less than 100% indicates that the solver was slowed down. The less load the checker produces, the fewer additional computing power is needed for checking. We also measure the peak memory consumption (maximum resident set size) of the solver (\(m_s\)) and checker (\(m_c\)). The ratio \(m_c/m_s\) indicates the additional memory required for checking. Finally, we measure the wall-clock time until certification finishes (w), and compare that to the time required by the solver to solve the problem and write the certificate to a file (\(w_f\)), and to the solving time without producing a certificate at all (\(w_b\)). The ratios \(w/w_f\) and \(w/w_b\) indicate the observed extra time required for certification. The results are displayed in Table 1: Our checker verified all problems, adding about 6% more computation time and 80% more memory on top of solving and certificate producing. It does not significantly slow down the solver, which runs at 97% CPU load. Compared to writing the certificate to a file, streaming it directly to the checker is 2% slower, and the overhead added by the whole certification process is 10%. The cake_lpr checker failed to certify 13 problemsFootnote 5. For the remaining problems, it added 61% of computation time, and the solver only ran at 85% load. Streaming the certificate to cake_lpr is 30% slower than writing the certificate to a file, and 43% slower than solving without producing a certificate. Moreover, for each cake_lpr run, maximum heap and stack sizes have to be determined upfront, and cake_lpr is likely to use all available heapFootnote 6. Without prior knowledge of the problem, it is impossible to guess good sizes. For our experiments, we used 8 GiB stack and 16 GiB heap, based on the maximum of 11 GiB that our tool needed. With this, cake_lpr ran out of memory for six problems, and maxed out at around 16 GiB memory usage for most of the remaining problems (131/138). On average, it needed 162 times more memory than the solver.

Table 2. Benchmark results in file mode.
Full size table

To measure the performance of just the checker, we ran it on certificates stored in files. For this experiment we also included the gratchk tool, which is reported to be faster than cake_lpr [35], the lrat-acl2 tool, and the unverified checker implementations lrat-trim (forward) and lrat-check, to compare our verified tool against unverified but highly optimized implementations. For the garbage collected tools (gratchk, cake_lpr, lrat-acl2), we set a heap limit of 16GiB. If possible, we used binary LRAT encoding (our tool and lrat-trim), and did not include conversion time from LRAT to GRAT (gratchk). Using our tool as baseline (100%), we display the ratio of the total computation times over all problems (\(t_{tot}\)), and the average ratios of computation time and peak memory usage per problem (\(t_{avg}\) and \(m_{avg}\)). The results are displayed in Table 2: our tool is slightly faster but uses slightly more memory than lrat-trim. It is significantly faster and uses less memory than any other verified or unverified tool we tested. After 14:30h, lrat-acl2 had processed 66 problems and succeeded on 57. The same problems took 3:25m to check by our tool. We aborted the experiment at that point, as, by extrapolation, it would have taken 5 more days to complete.

6 Conclusion

We have used the Isabelle LLVM framework to formally verify soundness of an unsatisfiability certificate checker. Our checker is verified w.r.t. a grammar of the DIMACS format, a semantics of CNF, and down to the LLVM code that implements the checker. Completeness of the checker has been empirically verified by showing that it accepts a large set of benchmarks. Our checker accepts the LRUP fragment of the LRAT format, which makes it suitable for checking certificates from many top-performing SAT solvers. For solvers that support streaming of LRAT certificates, our tool can be run in parallel to the solver, eliminating the need to store the potentially large certificate, and coming back with the certification result the moment the solver is finished. For CaDiCaL, this is only 10% slower than running just the solver, and 2% slower than writing the certificate to a file without checking it. Our implementation is slightly faster and uses only 4% more memory than the unverified and highly optimized lrat-trim checker. It is significantly faster and more memory efficient than any other LRAT checker we know of, verified or unverified. This makes it possible to routinely run the checker with the solver, increasing the confidence at low cost.

To design our checker, we first implemented and profiled prototypes in C++ to determine the important optimizations. This took roughly 40 person hours. We then used the Isabelle Refinement Framework to produce a verified version of the checker. This was done in a top-down refinement process, which was guided by the experience from the unverified prototypes. This took another 200 h.

6.1 Related Work

The closest work to ours is the verified cake_lpr checker [34, 35]. It supports streaming certificatesFootnote 7 and the full LPR format. The cake_lpr checker is verified down to assembly code (with a thin C wrapper around it), while our checker is verified down to LLVM intermediate code. While verifying an LLVM compiler is orthogonal to this project, we would immediately profit from such a verified compiler, further reducing our trusted code base. Moreover, our checker is verified w.r.t. a grammar of DIMACS CNF, while cake-lpr’s parser is not verified. It only comes with a sanity check, showing that the parser is left inverse to a pretty printer. Our checker is significantly faster than cake_lpr, and only allocates as much memory as needed, while cake-lpr’s memory size has to be set upfront, making it uncontrollable without background information about the problem. In particular in streaming mode, such information is not available. Finally, cake_lpr uses the ASCII encoding of LRAT, while our checker uses the more compact binary encoding.Footnote 8

There are other verified certificate checkers [5, 9, 16, 23], which, however, do not support streaming or are significantly slower than cake_lpr.

6.2 Future Work

There are no principle problems to extend our tool to the more powerful LRAT and LPR formats. We leave this to future work, as we are not aware of any solver that would support streaming these formats.

While our parser was manually implemented and then verified, there is work on verified parser generators [6, 18,19,20, 25, 31]. We leave it to future work to integrate similar techniques into the Isabelle LLVM workflow.

While faster than parsing the ASCII encoding, decompression of the binary encoding is a hot-spot in our checker. In streaming mode, we could probably use a less compact but faster to read format, which we leave to future work.