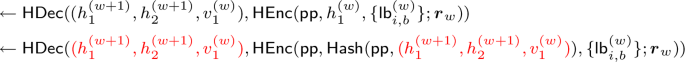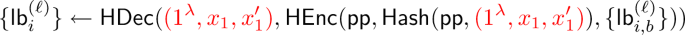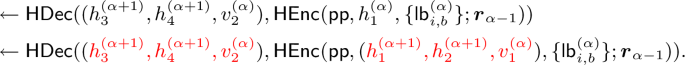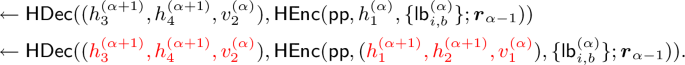Laconic Branching Programs from the Diffie-Hellman Assumption

Abstract

Laconic cryptography enables secure two-party computation (2PC) on unbalanced inputs with asymptotically-optimal communication in just two rounds of communication. In particular, the receiver (who sends the first-round message) holds a long input and the sender (who sends the second-round message) holds a short input, and the size of their communication to securely compute a function on their joint inputs only grows with the size of the sender’s input and is independent of the receiver’s input size. The work on laconic oblivious transfer (OT) [Cho et al. CRYPTO 2017] and laconic private set intersection (PSI) [Alamati et al. TCC 2021] shows how to achieve secure laconic computation for OT and PSI from the Diffie-Hellman assumption.

In this work, we push the limits further and achieve laconic branching programs from the Diffie-Hellman assumption. In particular, the receiver holds a large branching program P and the sender holds a short input x. We present a two-round 2PC protocol that allows the receiver to learn x iff $P(x) =1$, and nothing else. The communication only grows with the size of x and the depth of P, and does not further depend on the size of P.

1 Introduction

Suppose a server holds a large set of elements Y (which could be exponentially large) that can be represented as a polynomial-sized branching program P, that is, $y \in Y$ iff $P(y) = 1$. The server would like to publish a succinct digest of Y such that any client who holds a small set X can send a short message to the server to allow her to learn the set intersection $X \cap Y$ but nothing beyond that.

This is a special case of the secure two-party computation (2PC) [Yao86] problem, where two mutually distrustful parties, each holding a private input x and y respectively, would like to jointly compute a function f over their private inputs without revealing anything beyond the output of the computation. Garbled circuits [Yao86] together with oblivious transfer (OT) [Rab81, Rab05] enables 2PC for any function f with two rounds of communication: one message from the receiver to the sender and another message from the sender back to the receiver. This approach achieves the optimal round complexity; nevertheless, it requires the communication complexity to grow with the size of f. In particular, if we represent f as a Boolean circuit, then the communication grows with the number of gates in the circuit, which grows at least with the size of the inputs x and y. For unbalanced input lengths (i.e., $|x| \gg |y|$ or $|x| \ll |y|$), is it possible to make the communication only grow with the shorter input and independent of the longer input?

Long Sender Input. When the sender has a long input, i.e. $|x| \gg |y|$, we can use fully homomorphic encryption (FHE) [Gen09] to achieve communication that only grows with the receiver’s input length |y| plus the output length. This technique works for any function but can only be based on variants of the learning with errors (LWE) assumption [GSW13]. For simpler functions that can be represented by a branching program, in particular, if the sender holds a private large branching program P and the receiver holds a private short input y, the work of Ishai and Paskin [IP07] illustrates how to construct 2PC for P(y) where the communication only grows with |y| and the depth of P, and does not further depend on the size of P. Their construction is generic from a primitive called rate-1 OT, which can be built based on a variety of assumptions such as DCR, DDH, QR, and LWE assumptions with varying efficiency parameters [IP07, DGI+19, GHO20, CGH+21]. In this setting, there are works in secure BP evaluation for applications in machine learning and medicine [BPSW07, BFK+09, KNL+19, CDPP22]. Our results concern the dual setting, in which the receiver has the longer input and is the party that learns the output. Moreover, this should be achieved in only two rounds of communication.

Long Receiver Input. When the receiver has a long input, i.e. $|x| \ll |y|$, a recent line of work on laconic cryptography [CDG+17, QWW18, DGGM19, ABD+21, ALOS22] focuses on realizing secure 2PC with asymptotically-optimal communication in two rounds. In particular, the receiver has a large input and the size of her protocol message only depends on the security parameter and not her input size. The second message (sent by the sender) as well as the sender’s computation may grow with the size of the sender’s input, but should be independent of the receiver’s input size.

In this dual setting, the work of Quach, Wee, and Wichs [QWW18] shows how to realize laconic 2PC for general functionalities using LWE. Regarding laconic 2PC for simpler functions from assumptions other than LWE, much less is known compared to the setting of long sender inputs.

The work of Cho et al. [CDG+17] introduced the notion of laconic oblivious transfer (laconic OT), where the receiver holds a large input $D \in \{0,1\}^n$, the sender holds an input $(i \in [n] , m_0, m_1)$, and the two-round protocol allows the receiver to learn $(i, m_{D[i]})$ and nothing more. The communication complexity as well as the sender’s computation only grow with the security parameter and is independent of the size of D. Besides LWE [QWW18], laconic OT can be built from DDH, CDH, and QR [CDG+17, DG17].¹ Recent work [ABD+21, ALOS22] extends the functionality to laconic private set intersection (laconic PSI), where the sender and receiver each holds a private set of elements X and Y respectively ($|X| \ll |Y|$), and the two-round protocol allows the receiver to learn the set intersection $X \cap Y$ and nothing more. The communication complexity and the sender’s computational complexity are both independent of |Y|. Laconic PSI can be built from CDH/LWE [ABD+21] or pairings [ALOS22].

Both laconic OT and laconic PSI can be viewed as special cases of a branching program. Recall that in the setting of long sender input, where a sender has a large branching program, we have generic constructions from rate-1 OT, which can be built from various assumptions. However, in the dual setting of long receiver input, we no longer have such a generic construction. Laconic OT seems to be a counterpart building block in the dual setting, but it does not give us laconic branching programs. Given the gap between the two settings, we ask the following question:

Can we achieve laconic branching programs from assumptions other than LWE?

This diversifies the set of assumptions from which laconic MPC can be realized. It also increases our understanding of how far each assumption allows us to expand the functionality, which helps in gaining insights into the theoretical limits of the assumptions themselves.

1.1 Our Results

We answer the above question in the affirmative. In particular, as a natural counterpart to the aforementioned setting of long sender input, when the receiver holds a private large branching program $\textrm{BP}$ and the sender holds a private short input x, we construct a two-round 2PC protocol allowing the receiver to learn x iff $\textrm{BP}(x) =1$, and nothing else. The communication only grows with |x| and the depth of $\textrm{BP}$, and does not further depend on the size of $\textrm{BP}$. Furthermore, the sender’s computation also only grows with |x| and the depth of $\textrm{BP}$. The receiver’s computation grows with the number of BP nodes and the number of root-to-leaf paths. Our construction is based on anonymous hash encryption schemes [BLSV18], which can in turn be based on CDH/LWE [DG17, BLSV18].

Sender Security. We achieve what we call weak sender security which says if $\textrm{BP}(x)=0$, then no information about x is leaked; else, there are no privacy guarantees for x. A stronger security requirement would be that in the latter case, the receiver only learns $\textrm{BP}(x)$, and no other information about x. Unfortunately, realizing strong sender security is too difficult in light of known barriers: it generically implies a notion called private laconic OT [CDG+17, DGI+19]. Private laconic OT is laconic OT in which the index i chosen by the sender is also kept hidden from the receiver. The only existing construction of private laconic OT with polylogarithmic communication uses techniques from laconic secure function evaluation and is based on LWE [QWW18]. In particular, it is not known if private laconic OT can be realized using Diffie-Hellman assumptions.

Strong sender security allows one to achieve laconic PSI cardinality, a generalization of laconic PSI. In the PSI cardinality problem, the receiver learns only the size of the intersection and nothing about the intersection set itself. Strong sender security for a receiver with a large set S and a sender with a single element x would allow the receiver to only learn whether or not $x \in S$. This immediately implies laconic PSI cardinality by having the sender send a second-round protocol message for each element in its set. Laconic PSI cardinality generically implies private laconic OT, establishing a barrier. The same barriers prevented [DKL+23] from building laconic PSI cardinality. We can get laconic PSI as an application of our results (and other applications discussed below), but our results do not allow us to realize laconic PSI cardinality. More specifically, after receiving the second-round message from the sender, the receiver in our protocol works by checking which path in their BP tree (if any) decrypts to “accept”. If there is an accepting path, then $\textrm{BP}(x)=1$, where x is the sender’s input. But this reveals the value of x since the receiver knows which path resulted in acceptance.

Applications. Our laconic branching program construction directly implies laconic OT and laconic PSI, as their functionalities can be represented as branching programs. Moreover, we can capture other functionalities not considered by previous work, such as private-set unions (PSU). A branching program for PSU can be obtained by making local changes to a branching program for PSI. (See Sect. 5.) This demonstrates the versatility of our approach, giving a unifying construction for all these functionalities. In contrast, the accumulator-based PSI constructions in [ABD+21, ALOS22, DKL+23] are crucially tied to the PSI setting, and do not seem to extend to the PSU setting. This is because the sender’s message to the receiver only provides enough information to indicate which element (if any) in the receiver’s set is also held by the sender. In essence, only the index of this element within the receiver’s set needs to be conveyed in the sender’s message. In the PSU setting, on the other hand, there could be elements in the union that do not exist in the receiver’s set. So, the sender’s message needs to contain more information than an index. If the sender’s element is not in the receiver’s set, the receiver needs to be able to recover the sender’s element from the message.

Our techniques can be used in unbalanced PSI where the receiver holds a large set (possibly of exponential size) that can be represented as a branching program. For instance, a recent work by Garimella et al. [GRS22] introduced the notion of structure-aware PSI where one party’s (potentially large) set Y is publicly known to have a certain structure. As long as the publicly known structure can be represented as a branching program, our techniques can be used to achieve a two-round fuzzy-matching PSI protocol where the communication only grows with the size of the smaller set |X| and the depth of the branching program, and does not further depend on |Y|, which could potentially be exponentially large.

2 Technical Overview

Our constructions are based on hash encryption (HE) schemes [DG17, BLSV18]. An HE scheme, parameterized by $n = n(\lambda )$ (where $\lambda$ is the security parameter), consists of a hash function $\textsf{Hash}(\textsf{pp}, \cdot ): \{0,1\}^n \rightarrow \{0,1\}^\lambda$ and associated $\textsf{HEnc}$ and $\textsf{HDec}$ functions. One can encrypt n pairs of plaintexts $\textbf{m} := (m_{i,b})$ (for $i \in [n]$ and $b\in \{0,1\}$) with respect to $h := \textsf{Hash}(\textsf{pp}, z)$ to get $\mathbf {\textsf{cth}} \leftarrow \textsf{HEnc}(h, \textbf{m})$.² The ciphertext $\textsf{cth}$ is such that given z, one may recover $(m_{1,z_1}, \dots , m_{n, z_n})$ from $\mathbf {\textsf{cth}}$, while maintaining semantic security for $(m_{i, 1-z_i})$ even in the presence of z. HE can be realized using CDH/LWE [DG17, BLSV18].

Consider a simple example where the receiver R has a depth-one BP on bits (see Definition 3 for branching programs) where the root node encodes index $i^*\in [n]$ and its left child encodes accept ($b_0 := \textsf {acpt}$) and its right child encodes reject ($b_1 := \textsf {rjct}$). This BP evaluates an input x by checking the bit value at index $i^*$. If $x[i^*] = 0$, then the value of left child is output: $b_0 = \textsf {acpt}$. If $x[i^*] = 1$, then the value of right child is output: $b_1 = \textsf {rjct}$. As a starting point, suppose R only wants to learn if $\textsf{BP}(x) = 1$, where x is the sender’s input. The receiver hashes $h := \textsf{Hash}(\textsf{pp}, (i^*, b_0, b_1 ))$, padding the input if necessary, and sends h to the sender, S. S has the following circuit $\textsf{F}[x]$ with their input x hardwired: on input $(j, q_0 , q_1)$, $\textsf{F}[x]$ outputs $q_{x[j]}$. S garbles $\textsf{F}[x]$ to get a garbled circuit $\widetilde{\textsf{F}}$ and corresponding labels $(\textsf{lb}_{i,b})$. S uses the hash value, h, from R to compute $\textsf{cth}\leftarrow \textsf{HEnc}(h, (\textsf{lb}_{i,b}))$. Finally, S sends $(\widetilde{\textsf{F}} , \textsf{cth})$ to R. The receiver, given her hash pre-image value $z := (i^*, \textsf {acpt} , \textsf {rjct} )$ can only recover $(\textsf{lb}_{i, z[i]})$, allowing her in turn to learn $\textsf{F}[x](z)$ from the garbled circuit, outputting either accept ($\textsf{BP}(x) = 1$) or reject ($\textsf{BP}(x) = 0$).

Beyond Depth 1. Next, consider the $\textrm{BP}$ of depth 2 in Fig. 1 held by the receiver, R. Each internal node encodes an index, $\textsf{rot}, \textsf{lft}, \textsf{rgt}\in [n]$. The four leaves have values with variables $(b_{00}, b_{01}, b_{10}, b_{11})$. For $i,j \in \{0,1\}$, $b_{ij}\in \{\textsf {acpt, rjct}\}$. Suppose $x[\textsf{rot}]=0$, where x is the sender’s input, so the root-leaf path induced by $\textsf{BP}(x)$ first goes left. If the sender, S, ‘by some miracle’ knows the hash value $h_{0} := \textsf{Hash}(\textsf{pp}, (\textsf{lft}, b_{00} , b_{01}))$, he can, as above, send a garbled circuit for $\textsf{F}[x]$ and an HE ciphertext wrt $h_0$ of the underlying labels, allowing R to evaluate $\textsf{F}[x](\textsf{lft}, b_{00} , b_{01})$. But S does not know the value of $h_0$, nor does he know whether the first move is left or right, because the $\textrm{BP}$ is hidden from S. Moreover, R cannot send both $h_{0} := \textsf{Hash}(\textsf{pp}, (\textsf{lft},b_{00} , b_{01}))$ and $h_{1} := \textsf{Hash}(\textsf{pp}, (\textsf{rgt}, b_{10} , b_{11}))$ because (a) there will be a size blowup (the communication will grow with the size, and not the depth, of the BP), and (b) R will learn more information than necessary because S does not know a priori whether the induced computation travels left or right, so he has to encrypt the labels under both $h_0$ and $h_1$. But encrypting the labels $(\textsf{lb}_{i,b})$ under both $h_0$ and $h_1$ will allow the receiver to recover two labels for an index on which $(\textsf{lft},b_{00} , b_{01})$ and $(\textsf{rgt},b_{10} , b_{11})$ differ, destroying garbled-circuit security.

Fig. 1.

Depth 2 BP example

Fixing Size Blow-Up via Deferred Encryption. We fix the above issue via deferred encryption techniques [DG17, BLSV18, GHMR18, ABD+21], allowing the sender to defer the HE encryptions of $(\textsf{lb}_{i,b})$ labels to the receiver herself at decryption time! To enable this technique, the receiver further hashes $(h_0, h_1)$ such that during decryption, the receiver, through the evaluation of a garbled circuit, will obtain an HE encryption of $(\textsf{lb}_{i,b})$ labels with respect to $h_{x[\textsf{rot}]}$, where $(\textsf{lb}_{i,b})$ and $(h_0, h_1)$ are as above. To do this, we have to explain how the receiver further hashes down $h_0$ and $h_1$, and how she can later perform deferred encryption. First, the receiver R computes the hash value $\textsf{hr} := \textsf{Hash}(\textsf{pp},(h_0, h_1, \textsf{rot}))$, and sends $\textsf{hr}$ to S. Next the sender S(x) garbles $\textsf{F}[x]$ to get $(\widetilde{\textsf{F}} , \textsf{lb}_{i,b})$ as above. Then, he forms a circuit $\textsf{G}[x , (\textsf{lb}_{i,b})]$ with x and $(\textsf{lb}_{i,b})$ hardwired, which on an input $(h'_0, h'_1 , u)$ outputs $\textsf{HEnc}( h'_{x_u} , (\textsf{lb}_{i,b}))$. The sender garbles $\textsf{G}[x , (\textsf{lb}_{i,b})]$ to get $(\widetilde{\textsf{G}} , (\textsf{lb}'_{i,b}))$. Before proceeding, let us consider R’s perspective. If R is given $\widetilde{\textsf{G}}$ and the labels $(\textsf{lb}'_{i, z'[i]})$, where $z' := (h_0, h_1 , \textsf{rot})$, she can evaluate $\widetilde{\textsf{G}}$ on these labels, which will in turn release an HE encryption of labels $(\textsf{lb}_{i,b})$ under $h_{x_{\textsf{rot}}}$, as desired. To ensure R only gets the $(\textsf{lb}'_{i, z'[i]})$ labels, S encrypts the $\{\textsf{lb}'_{i,b} \}$ labels under $\textsf{hr}$, and sends the resulting HE ciphertext $\textsf{cth}'$, as well as $\widetilde{\textsf{F}}$ and $\widetilde{\textsf{G}}$ to R. From $\textsf{cth}'$ and $z' := (h_0, h_1 , \textsf{rot})$, R can only recover the labels $(\textsf{lb}'_{i, z'[i]})$, as desired.

How Can the Receiver Decrypt? The receiver will evaluate $\widetilde{\textsf{G}}$ on the decrypted $(\textsf{lb}'_{i, z'[i]})$ labels, releasing an HE encryption $\textsf{cth}$ of $(\textsf{lb}_{i,b})$ labels under $h_{x_{\textsf{rot}}}$. The receiver does not know whether $\textsf{cth}$ is encrypted under $h_0$ or $h_1$, so she tries to decrypt with respect to the pre-images of both hash values and checks which one (if any) is valid. However, this results in the following security issue: an HE scheme is not guaranteed to hide the underlying hash value with respect to which an HE ciphertext was made. For example, imagine an HE scheme where $\textsf{HEnc}(h , (m_{i,b}))$ appends h to the ciphertext. Employing such an HE scheme (which is semantically secure) in the above construction will signal to the receiver if $\textsf{cth}'$ was encrypted under $h_0$ or $h_1$, namely the bit value of $x[\textsf{rot}]$. This breaks sender security if $\textsf{BP}(x)=0$. Moreover, even if the HE encryption scheme is anonymous in the sense of hiding h, decrypting an $h_b$-formed HE encryption under the pre-image of $h_{1-b}$ may result in $\bot$, or in junk labels that do not work on $\widetilde{\textsf{F}}$. We use the same technique as in [ABD+21] of using anonymous hash encryption and garbled circuits to resolve this issue.

Signalling the Correct Output of $\textsf{F}$. In the above examples, $\textsf{F}[x]$ outputs either $\textsf {acpt}$ or $\textsf {rjct}$, indicating if $\textsf{BP}(x)$ equals 1 or 0, respectively. But, in the desired functionality, $\textsf{F}[x]$ outputs x if $\textsf{BP}(x)=1$. We cannot simply modify $\textsf{F}[x]$ to output x if $q_{x_j}=\textsf {acpt}$ since in that case if the receiver evaluates $\widetilde{\textsf{F}}$ on junk labels she will not be able to tell the difference between the junk output and x. Similar to [ABD+21], we address this problem by having S include a signal value in the ciphertext and in their message to R. Then we can modify $\textsf{F}[x]$ to output x and the decrypted signal value. The receiver compares this output signal value with the true value. If they are equal, R knows that output x is not junk.

Handling Unbalanced Branching Programs. The above discussion can be naturally extended to the balanced BP setting, wherein we have a full binary tree of depth d. When the BP is unbalanced, like our BPs for PSI and PSU, the above approach does not work, because the sender does not know a priori which branches stop prematurely. We solve this issue via the following technique. We design the circuit $\textsf{G}$ to work in two modes: normal mode (as explained above) and halting mode, which is triggered when its input signals a leaf node. In halting mode, the circuit $\textsf{G}$ will release its hardwired input x, assuming the halt is an accept. Executing the above blueprint requires striking a delicate balance to have both correctness and security.

Comparison with  [ABD+21]. At a high level, the garbled-circuit-based laconic PSI construction of [ABD+21] is an ad hoc and specific instantiation of our general methodology. In particular, for a receiver with $m = 2^k$ elements (for $k := \textsf{polylog}(\lambda )$), the construction of [ABD+21] builds a full binary tree of depth k, with the m elements appearing sorted in the leaves, Merkle hashed all the way up in a specific way. In particular, the pre-image of each node’s hash value is comprised of its two children’s hashes as well as some additional encoded information about its sub-tree, enabling an evaluator, with an input x, to make a deterministic left-or-right downward choice at each intermediate node. This is a very specific BP instantiation of PSI, where the intermediate BP nodes, instead of running index predicates (e.g., going left/right if the ith bit is 0/1), they run full-input predicates $\varPhi : x \mapsto \{0,1\}$, where $\varPhi$ is defined based on the left sub-tree of the node. Our approach, on the other hand, handles branching programs for index predicates, and we subsume the results of [ABD+21] as a special case. In particular, we show how to design simple index-predicate BPs for PSI, PSU, and wildcard matching, the latter two problems are not considered by [ABD+21].

In summary, our construction generalizes and simplifies the approach of [ABD+21], getting much more mileage out of the garbled-circuit based approach. For example, [ABD+21] builds a secure protocol for a specific PSI-based BP which is in fact a decision tree: namely, the in-degree of all internal nodes is one. On the other hand, we generalize this concept to handle all decision trees and even the broader class of branching programs, in which the in-degree of intermediates nodes can be greater than one. Moreover, we introduce some new techniques (e.g., for handling unbalanced BPs) that may be of independent interest.

Comparison with  [DGGM19]. The work of Döttling, Garg, Goyal, and Malavolta [DGGM19] builds laconic conditional disclosure of secrets (CDS) involving a sender holding an NP instance x and a message m, and a receiver holding x and a potential witness w for x. If $R(x,w) = 1$, where R is the corresponding relation R, the receiver learns m; else, the receiver learns no information about m. They show how to build two-round laconic CDS protocols from CDH/LWE with polylogarithmic communication and polylogarithmic sender computation. The CDS setting is incomparable to ours. The closest resemblance is to think of x, the BP input, as the NP instance, and of the BP as the NP witness w. But then under CDS, the input x is not kept hidden from the receiver. In particular, it is not even clear whether laconic CDS implies laconic PSI.

3 Preliminaries

Throughout this work, $\lambda$ denotes the security parameter. $\textsf{negl}{\left( \lambda \right) }$ denotes a negligible function in $\lambda$, that is, a function that vanishes faster than any inverse polynomial in $\lambda$.

For $n\in \mathbb {N}$, [n] denotes the set $\{1,\dots ,n\}$. If $x \in \{0,1\}^n$ then the bits of x can be indexed as $x[i] := x_i$ for $i \in [n]$, where $x= x_1 \dots x_n$ (note that indexing begins at 1, not 0). $x:=y$ is used to denote the assignment of variable x to the value y. If $\mathcal {A}$ is a deterministic algorithm, $y\leftarrow \mathcal {A}(x)$ denotes the assignment of the output of $\mathcal {A}(x)$ to variable y. If $\mathcal {A}$ is randomized, $y{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\mathcal {A}(x)$ is used. If S is a (finite) set, $x{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}S$ denotes the experiment of sampling uniformly at random an element x from S. If D is a distribution over S, $x{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}D$ denotes the element x sampled from S according to D. If $D_0,D_1$ are distributions, we say that $D_0$ is statistically (resp. computationally) indistinguishable from $D_1$, denoted by $D_0\approx _{s}D_1$ (resp. $D_0 {\mathop {\equiv }\limits ^{c}}D_1$), if no unbounded (resp. PPT) adversary can distinguish between the distributions except with probability at most $\textsf{negl}(\lambda )$.

If $\varPi$ is a two-round two-party protocol, then $(\textsf{m}_1, \textsf{m}_2) \leftarrow \textsf{tr}^\varPi (x_0, x_1, \lambda )$ denotes the protocol transcript, where $x_i$ is party $P_i$’s input for $i \in \{0,1\}$. For $i \in \{0,1\}$, $(x_i, r_i, \textsf{m}_1, \textsf{m}_2) \leftarrow \textsf{view}^\varPi _i(x_0, x_1, \lambda )$ denotes $P_i$’s “view” of the execution of $\varPi$, consisting of their input, random coins, and the protocol transcript.

Definition 1

(Computational Diffie-Hellman). Let $\mathcal {G}(\lambda )$ be an algorithm that outputs $(\mathbb {G},p,g)$ where $\mathbb {G}$ is a group of prime order p and g is a generator of the group. The CDH assumption holds for generator $\mathcal {G}$ if for all PPT adversaries $\mathcal {A}$

Definition 2

(Learning with Errors). Let $q,k\in \mathbb {N}$ where $k\in \textsf{poly}(\lambda )$, $\textbf{A}\in \mathbb {Z}_q^{k\times n}$ and $\beta \in \mathbb {R}$. For any $n=\textsf{poly}(k\log q)$, the LWE assumption holds if for every PPT algorithm $\mathcal {A}$ we have

$$\left| \Pr \left[ 1\leftarrow \mathcal {A}(\textbf{A},\textbf{s}\textbf{A}+\textbf{e}) \right] -\Pr \left[ 1\leftarrow \mathcal {A}(\textbf{A},\textbf{y}) \right] \right| \le \textsf{negl}{\left( \lambda \right) }$$

for $\textbf{s}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^k$, $\textbf{e}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}D_{\mathbb {Z}^n,\beta }$ and $\textbf{y}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^n$, where $D_{\mathbb {Z}^n,\beta }$ is some error distribution.

The following definitions related to branching programs are modified from [IP07].

Definition 3

(Branching Program (BP)). A (deterministic) branching program over the input domain $\{0,1\}^\lambda$ and output domain $\{0,1\}$ is defined by a tuple $(V, E, T, \textsf{Val})$ where:

• $G:=(V,E)$ is a directed acyclic graph of depth d.

• Two types of nodes partition V:

  • Interior nodes: Have outdegree 2.³ The root node, denoted $v_1^{(0)}$, has indegree 0.

  • Terminal/leaf nodes: Have outdegree 0. T denotes the set of terminal nodes. Leaf nodes are labeled as $T= \{u_1, \dots , u_{|T|}\}$. Each $u_i \in T$ encodes a value in $\{0,1\}$.

• For every non-root node $u \in V \setminus \{v_1^{(0)}\}$ there exists a path from $v_1^{(0)}$ to u.

• Each node in V encodes a value in $[\lambda ]$. These values are stored in the array $\textsf{Val}$ such that for all $v \in V$, $\textsf{Val}[v]=i$ for some $i\in [\lambda ]$.

• The elements of the edge set E are formatted as an ordered tuple $(v, v', b)$ indicating a directed edge from $v\in V$ to $v'\in V$ with label $b \in \{0,1\}$. If $b=0$ (resp. $b=1$), $v'$ is the left (resp. right) child of v.

BP Evaluation. The output of a branching program is defined by the function $\textsf{BP}: \{0,1\}^\lambda \rightarrow \{0,1\}$, which on input $x\in \{0,1\}^\lambda$ outputs a bit. Evaluation of $\textsf{BP}$ (see Fig. 2, right, and relevant function definitions below) follows the unique path in G induced by x from the root $v_1^{(0)}$ to a leaf node $u\in T$. The output of $\textsf{BP}$ is the value encoded in u, $\textsf{Val}[u]$.

• $\varGamma : V \setminus T \times \{0,1\}\rightarrow V$ takes as input an internal node v and a bit b and outputs v’s left child if $b=0$ and v’s right child if $b=1$.

• $\textsf{Eval}_\textsf{int}: V \setminus T \times \{0,1\}^\lambda \rightarrow V$ takes as input an interior node v and a string of length $\lambda$ and outputs either v’s left or right child ($\varGamma (v,0)$ or $\varGamma (v,1)$, respectively). See Fig. 2, left.

• $\textsf{Eval}_\textsf{leaf}: T \rightarrow \{0,1\}$ takes as input a terminal node $u \in T$ and outputs the value $\textsf{Val}[u]$.

Fig. 2.

Interior node evaluation function $\textsf{Eval}_\textsf{int}$ and BP evaluation function $\textsf{BP}$.

Definition 4

(Layered BP). A BP of depth d is layered if the node set V can be partitioned into $d + 1$ disjoint levels $V = \bigcup _{i=0}^d V^{(i)}$, such that $V^{(0)} = \{v_1^{(0)}\}$, $V^{(d)} = T$, and for every edge $e = (u, v)$ we have $u \in V^{(i)}$, $v \in V^{(i+1)}$ for some level $i\in \{0, \dots , d\}$. We refer to $V^{(i)}$ as the i-th level of the BP, or the level at depth i. Nodes on level i are labelled from leftmost to rightmost: $V^{(i)} = \{v_1^{(i)}, \dots , v_{|V^{(i)}|}^{(i)}\}$.

We require that all branching programs in this work are layered.

4 Semi-honest Laconic 2PC with Branching Programs

Our construction uses hash encryption schemes with garbled circuits. The following definitions are taken directly from [ABD+21].

Definition 5

(Hash Encryption [DG17, BLSV18]). A hash encryption scheme $\textsf{HE}= (\textsf{HGen}, \textsf{Hash}, \textsf{HEnc}, \textsf{HDec})$ and associated security notions are defined as follows.

• $\textsf{HGen}(1^\lambda , n)$: Takes as input a security parameter $1^\lambda$ and an input size n and outputs a hash key $\textsf{pp}$.

• $\textsf{Hash}(\textsf{pp}, z)$: Takes as input a hash key $\textsf{pp}$ and $z \in \{0,1\}^n$, and deterministically outputs $h \in \{0,1\}^\lambda$.

• $\textsf{HEnc}(\textsf{pp}, h, \{m_{i,b} \}_{i \in [n], b \in \{0,1\}} ; \{r_{i,b} \})$: Takes as input a hash key $\textsf{pp}$, a hash output h, messages $\{ m_{i,b}\}$ and randomness $\{r_{i,b} \}$, and outputs $\{ \textsf{cth}_{i,b}\}_{i \in [n], b \in \{0,1\}}$, (written concisely as $\{ \textsf{cth}_{i,b}\}$). Each ciphertext $\textsf{cth}_{i,b}$ is computed as $\textsf{cth}_{i,b} = \textsf{HEnc}(\textsf{pp}, h , m_{i,b} , (i,b); r_{i,b})$, where we have overloaded the $\textsf{HEnc}$ notation.

• $\textsf{HDec}(z, \{ \textsf{cth}_{i,b} \})$: Takes as input a hash input z and $\{\textsf{cth}_{i,b} \}$ and outputs n messages $(m_1, \dots , m_n)$. Correctness is required such that for the variables above, $(m_1, \dots , m_n) = (m_{1, z[1]} , \dots , m_{n , z[n]})$.

• Semantic Security: Given $z \in \{0,1\}^n$, no adversary can distinguish between encryptions of messages made to indices $(i, \bar{z_{i}})$. For any PPT $\mathcal {A}$, sampling $\textsf{pp}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HGen}(1^\lambda , n)$, if $(z , \{m_{i,b}\} , \{m'_{i,b} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\mathcal {A}(\textsf{pp})$ and if $m_{i, z[i]} = m'_{i, z[i]}$ for all $i \in [n]$, then $\mathcal {A}$ cannot distinguish between $\textsf{HEnc}(\textsf{pp}, h, \{m_{i,b} \})$ and $\textsf{HEnc}(\textsf{pp}, h, \{m'_{i,b} \})$, where $h \leftarrow \textsf{Hash}(\textsf{pp}, z)$.

• Anonymous Semantic Security: For a random $\{ m_{i,b}\}$ with equal rows (i.e., $m_{i,0} = m_{i , 1}$), the output of $\textsf{HEnc}(\textsf{pp}, h , \{m_{i,b}\})$ is pseudorandom even in the presence of the hash input. Formally, for any $z \in \{0,1\}^n$, sampling $\textsf{pp}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HGen}(1^\lambda , n)$, $h \leftarrow \textsf{Hash}(\textsf{pp}, z)$, and sampling $\{m_{i,b}\}$ uniformly at random with the same rows, then $\boldsymbol{v} :=(\textsf{pp}, z, \textsf{HEnc}(\textsf{pp}, h , \{m_{i,b}\}) )$ is indistinguishable from another tuple in which we replace the hash-encryption component of $\boldsymbol{v}$ with a random string.

The following results are from [BLSV18, GGH19].

Lemma 1

Assuming CDH/LWE there exists anonymous hash encryption schemes, where $n = 3\lambda$ (i.e., $\textsf{Hash}(\textsf{pp}, \cdot ) :\{0,1\}^{3 \lambda } \mapsto \{0,1\}^\lambda$).⁴ Moreover, the hash function $\textsf{Hash}$ satisfies robustness in the following sense: for any input distribution on z which samples at least $2 \lambda$ bits of z uniformly at random, $(\textsf{pp}, \textsf{Hash}(\textsf{pp}, z))$ and $(\textsf{pp}, u)$ are statistically close, where $\textsf{pp}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HGen}(1^\lambda , 3 \lambda )$ and $u {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$.

We also review garbled circuits and the anonymous property, as defined in [BLSV18].

Definition 6

(Garbled Circuits). A garbling scheme for a class of circuits $\mathcal {C} :=\{ \textsf{C} :\{0,1\}^n \mapsto \{0,1\}^m \}$ consists of $(\textsf{Garb},\textsf{Eval}, \textsf{Sim})$ satisfying the following.

• Correctness: For all $\textsf{C} \in \mathcal {C}$, $\textsf{m}\in \{0,1\}^n$, $\Pr [\textsf{Eval}(\widetilde{\textsf{C}}, \{ \textsf{lb}_{i , \textsf{m}[i]} \}) = \textsf{C}(\textsf{m})] = 1$, where $(\widetilde{\textsf{C}} , \{ \textsf{lb}_{i,b} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(1^\lambda ,\textsf{C})$.

• Simulation Security: For any $\textsf{C} \in \mathcal {C}$ and $\textsf{m}\in \{0,1\}^n$: $(\widetilde{\textsf{C}}, \{ \textsf{lb}_{i , \textsf{m}[i]} \}) {\mathop {\equiv }\limits ^{c}}\textsf{Sim}(1^\lambda , \textsf{C}, \textsf{C}(\textsf{m}))$, where $(\widetilde{\textsf{C}} , \{ \textsf{lb}_{i,b} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(1^\lambda ,\textsf{C})$.

• Anonymous Security⁵ [BLSV18]: For any $\textsf{C} \in \mathcal {C}$, if the output of $\textsf{C}(x)$ for $x\in \{0,1\}^n$ is uniformly random, then the output of $\textsf{Sim}(1^\lambda , \textsf{C},y)$ is pseudorandom.

Lemma 2

([BLSV18]). Anonymous garbled circuits can be built from one-way functions.

Hash Encryption Notation. We assume $\textsf{Hash}(\textsf{pp}, \cdot ) :\{0,1\}^{n} \mapsto \{0,1\}^\lambda$, where $n = 3 \lambda$. $\{\textsf{lb}_{i,b} \}$ denotes a sequence of pairs of labels, where $i \in [n]$ and $b \in \{0,1\}$. For $\boldsymbol{r} :=\{r_{i,b} \}$, $\textsf{HEnc}(\textsf{pp}, h, \{\textsf{lb}_{i,b} \}; \boldsymbol{r})$ denotes ciphertexts $\{\textsf{cth}_{i,b} \}$, where $\textsf{cth}_{i,b} = \textsf{HEnc}(\textsf{pp}, h,\textsf{lb}_{i,b} , (i,b); r_{i,b})$. We overload notation as follows. $\{ \textsf{lb}_i \}$ denotes a sequence of $3 \lambda$ elements. For $\boldsymbol{r} :=\{r_{i,b} \}$, $\textsf{HEnc}(\textsf{pp}, h, \{\textsf{lb}_{i} \} ; \boldsymbol{r})$ denotes a hash encryption where both plaintext rows are $\{\textsf{lb}_i\}$; namely, ciphertexts $\{\textsf{cth}_{i,b} \}$, where $\textsf{cth}_{i,b} = \textsf{HEnc}(\textsf{pp}, h, \{ m_{i,b}\}; r_{i,b})$ and $m_{i,0} = m_{i,1} = \textsf{lb}_i$, for all i.

Definition 7

($\textsf{BP}\text{- }\textsf{2PC}$ Functionality). We define the evaluation of a branching program in the two-party communication setting ($\textsf{BP}\text{- }\textsf{2PC}$) to be a two-round protocol between a receiver R and a sender S such that:

• R holds a branching program $\textrm{BP}$ with evaluation function $\textsf{BP}: \{0,1\}^\lambda \rightarrow \{0,1\}$ and S holds a string $\textsf{id}\in \{0,1\}^\lambda$. In the first round of the protocol, R sends the message $\textsf{m}_1$ to S. In the second round S sends $\textsf{m}_2$ to R.

• Correctness: If $\textsf{BP}(\textsf{id}) = 1$, then R outputs $\textsf{id}$. Otherwise, R outputs $\bot$.

• Computational (resp., statistical) receiver security: $\textsf{BP}\text{- }\textsf{2PC}$ achieves receiver security if for all $\textsf{id}\in \{0,1\}^\lambda$, and all pairs of branching programs $\textrm{BP}_0, \textrm{BP}_1$ we have that $\textsf{view}_S^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}_0, \textsf{id}, \lambda ) \approx \textsf{view}_S^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}_1, \textsf{id}, \lambda )$. If the distributions are computationally (resp., statistically) indistinguishable then we have computational (resp., statistical) security.

• Computational (resp., statistical) sender security: $\textsf{BP}\text{- }\textsf{2PC}$ achieves sender security if for all branching programs $\textrm{BP}$, and all pairs $\textsf{id}_0, \textsf{id}_1 \in \{0,1\}^\lambda$ with $\textsf{BP}(\textsf{id}_0) =0 = \textsf{BP}(\textsf{id}_1)$, we have that $\textsf{view}_R^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}, \textsf{id}_0,\lambda ) \approx \textsf{view}_R^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}, \textsf{id}_1, \lambda )$. If the distributions are computationally (resp. statistically) indistinguishable, we have computational (resp. statistical) security.

4.1 The $\textsf{BP}\text{- }\textsf{2PC}$ Construction

In this section, we give a construction for a $\textsf{BP}\text{- }\textsf{2PC}$ protocol, inspired by laconic OT techniques [CDG+17, ABD+21]. Construction 1 uses hash encryption and garbling schemes. A high-level overview is as follows.

• 1. The receiver party R hashes their branching program in a ‘specific way’ from the leaf level up to the root. R then sends the message $\textsf{m}_1 = ({\textsf{d}_\textsf{m}}, \mathsf {h_{root}})$ to the sender, where ${\textsf{d}_\textsf{m}}$ is the maximum BP depth and $\mathsf {h_{root}}$ is the hash value of the root node of the hashed BP.

• 2. The sender party S gets the message $\textsf{m}_1 = ({\textsf{d}_\textsf{m}}, \mathsf {h_{root}})$ and garbles one circuit for every possible level of the hash tree, (i.e., generates ${\textsf{d}_\textsf{m}}$ garbled circuits). S starts with the leaf level and garbles circuit $\textsf{F}$ (Fig. 3). $\textsf{F}$ takes as input a leaf node value and two random strings. If the leaf node value is 1, $\textsf{F}$ outputs the hardcoded sender element $\textsf{id}$ and a random, fixed, signal string r. Otherwise, $\textsf{F}$ outputs two random strings $(\textsf{id}', r')$. Then for every level from the leaf parents to the root, S garbles the circuit $\textsf{V}$ (also in Fig. 3). Each $\textsf{V}$ garbled by the sender has the labels of the previously generated garbled circuit hardcoded. After garbling, S computes a hash encryption of the root-level garbled circuit labels using the hash image $\mathsf {h_{root}}$. Finally, S sends $\textsf{m}_2 :=(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_0, \{\textsf{cth}_{i,b}^{(0)}\}, r)$ to R, where $\widetilde{\textsf{C}}_w$ is the garbled circuit associated with level w, $\{\textsf{cth}_{i,b}^{(0)}\}$ is the encryption of the labels for $\widetilde{\textsf{C}}_0$, and r is the signal value.

• 3. For all root-to-leaf paths through the BP, R runs $\textsf{DecPath}$ (Fig. 3, bottom) on $\textsf{m}_2$ searching for the path that will decrypt to a signal value equal to r from $\textsf{m}_2$. On input a path $\textsf{pth}$ and $\textsf{m}_2$, $\textsf{DecPath}$ outputs a pair $(\textsf{id}_\textsf{pth}, r_\textsf{pth})$ to R. If $r_\textsf{pth}= r$, then R takes $\textsf{id}_\textsf{pth}$ to be S’s element.

Construction 1

($\textsf{BP}\text{- }\textsf{2PC}$). We require the following ingredients for the two-round, two-party communication BP construction.

• 1. An anonymous and robust hash encryption scheme $\textsf{HE}= (\textsf{HGen}, \textsf{Hash}, \textsf{HEnc},\textsf{HDec})$, where $\textsf{Hash}(\textsf{pp}, \cdot ) :\{0,1\}^{3\lambda } \mapsto \{0,1\}^\lambda$.

• 2. An anonymous garbling scheme $\textsf{GS}= (\textsf{Garb}, \textsf{Eval}, \textsf{Sim})$.

• 3. Circuits $\textsf{F}$, $\textsf{V}$, and procedure $\textsf{DecPath}$, defined in Fig. 3.

The receiver holds a-potentially unbalanced-branching program BP of depth $d \le \lambda +1$ as defined in Definition 3. The sender has a single element $\textsf{id}\in \{0,1\}^\lambda$. $\textsf{BP}\text{- }\textsf{2PC}:= (\textsf{GenCRS}, \textsf{R}_1, \textsf{S}, \textsf{R}_2)$ is a triple of algorithms built as follows.

$\textsf{GenCRS}(1^\lambda )$: Return $\textsf{crs}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HGen}(1^\lambda , 3\lambda )$.

$\textsf{R}_1(\textsf{crs},\textsf{BP})$: BP has terminal node set $T = \{u_1, \dots , u_{|T|}\}$. Nodes in level $0 \le w\le d$ are labelled from leftmost to rightmost: $V^{(w)} = \{v_1^{(w)}, \dots , v_{|V^{(w)}|}^{(w)}\}$.

• Parse $\textsf{crs}:=\textsf{pp}$. The receiver creates a hashed version of BP, beginning at the leaf level: For $j \in [|T|]$, sample $x_j, x_j' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$ and compute $h_j^{(d)}\leftarrow \textsf{Hash}(\textsf{pp}, (\textsf{Val}[u_j]^{\times \lambda }, x_j, x_j'))$. $\textsf{Val}[u_j]^{\times \lambda }$ indicates that $\textsf{Val}[u_j]$ is copied $\lambda$ times to obtain either the all zeros or all ones string of length $\lambda$. The remaining levels are hashed from level $d-1$ up to 0 (the root):

  • 1. For w from $d-1$ to 0, $|V^{(w)}|$ nodes are added to level w. The hash value of each node is the hash of the concatenation of its left child, right child, and the index encoded in the current node. Formally: For $j \in [|V^{(w)}|]$, set $h^{(w)}_j \leftarrow \textsf{Hash}(\textsf{pp}, (h^{(w+1)}_{2j-1}, h^{(w+1)}_{2j}, \textsf{Val}[v^{(w)}_j]))$, where $\textsf{Val}[v^{(w)}_j]$ is the value of the bit encoded in the j-th node of level w. If needed, padding is added so that $|\textsf{Val}[v^{(w)}_j]| = \lambda$.

  • 2. Let $\textsf{m}_1 :=({\textsf{d}_\textsf{m}}, \mathsf {h_{root}})$, where ${\textsf{d}_\textsf{m}}= \lambda +1$ is the maximum tree depth and $\mathsf {h_{root}}:=h_1^{(0)}$ is the root hash value. For all $i \in [|T|]$, $w \in \{0, \dots , d\}$, and $j \in [|V^{(w)}|]$, set $\textsf{st}:=(\{x_i\}, \{x'_i\}, \{v_j^{(w)} \})$. Send $\textsf{m}_1$ to $\textsf{S}$.

$\textsf{S}(\textsf{crs}, \textsf{id},\textsf{m}_1)$:

• Parse $\textsf{m}_1 :=({\textsf{d}_\textsf{m}}, \mathsf {h_{root}})$ and $\textsf{crs}:=\textsf{pp}$. Sample $r,\textsf{id}',r' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$ and padding $\textsf{pad}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{2(n-1)}$. Let $\textsf{C}_{\textsf{d}_\textsf{m}}:=\textsf{F}[\textsf{id},\textsf{id}', r,r']$ (Fig. 3). Garble $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_{i,b}^{({\textsf{d}_\textsf{m}})} \}){\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{C}_{\textsf{d}_\textsf{m}})$. For w from ${\textsf{d}_\textsf{m}}-1$ to 0 do:

  • 1. Sample random $\boldsymbol{r}_w$ and let $\textsf{C}_w :=\textsf{V}[\textsf{pp}, \textsf{id}, \{\textsf{lb}_{i,b}^{(w+1)}\}, \boldsymbol{r}_w, r,\textsf{id}',r',\textsf{pad}]$.

  • 2. Garble $(\widetilde{\textsf{C}}_w , \{\textsf{lb}_{i,b}^{(w)} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{C}_w)$.

• Let $\{\textsf{cth}^{(0)}_{i,b}\} {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HEnc}(\textsf{pp}, \mathsf {h_{root}}, \{\textsf{lb}_{i,b}^{(0)} \})$.

• Send $\textsf{m}_2 :=(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0} , \{\textsf{cth}_{i,b}^{(0)}\}, r)$ to $\textsf{R}_2$.

$\textsf{R}_2(\textsf{crs}, \textsf{st}, \textsf{m}_2)$: Parse $\textsf{st}:=(\{x_i\}, \{x'_i\}, \{v_j^{(w)} \})$ and $\textsf{m}_2 :=(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0}, \{\textsf{cth}_{i,b}^{(0)}\}, r )$. $\forall$ leaves $u \in T$, let $\textsf{pth}_u :=((\textsf{Val}[u]^{\times \lambda },x, x'),\dots , \mathsf {h_{root}})$ be the root to leaf u path in BP. Let $\ell$ be the length of $\textsf{pth}_u$ and let

$$\begin{aligned} (\textsf{id}_u, r_u) \leftarrow \textsf{DecPath}(\textsf{pth}_u, \widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0}, \{\textsf{cth}_{i,b}^{(0)} \} ). \end{aligned}$$

If $r_u = r$, then output $\textsf{id}_u$ and halt. If for all $u\in T$, $r_u\ne r$, then output $\bot$.

Fig. 3.

Circuits $\textsf{F}, \textsf{V}$ and procedure $\textsf{DecPath}$ for construction 1. Circuits based on those in Table 1 of [ABD+21].

$\textsf{R}_2$ must run $\textsf{DecPath}$ on every root-to-leaf path. $\textsf{R}_2$ is written above as if there is a unique path from the root to each leaf. But since we allow nodes to have in-degree $>1$, a leaf may be reachable from more than one path. In such a case, the path iteration in $\textsf{R}_2$ should be modified so that all paths are explored.

Communication Costs. The first message $\textsf{m}_1$ is output by $\textsf{R}_1$ and sent to $\textsf{S}$. $\textsf{m}_1$ consists of the maximum depth ${\textsf{d}_\textsf{m}}$ and the hash digest $\mathsf {h_{root}}$, which are $O(\log \lambda )$ and $\lambda$ bits, respectively. So the receiver’s communication cost is $\textsf{poly}({\textsf{d}_\textsf{m}}, \lambda )$, and since we assume ${\textsf{d}_\textsf{m}}= \lambda +1$, this is $\textsf{poly}({\textsf{d}_\textsf{m}}, \lambda )$.Next, $\textsf{m}_2$ is output by $\textsf{S}$ and sent to $\textsf{R}_2$. $\textsf{m}_2$ consists of $\widetilde{\textsf{C}}_{0}$, $\widetilde{\textsf{C}}_{i}$ for $i \in [{\textsf{d}_\textsf{m}}]$, $\{\textsf{cth}_{i,b}^{(0)}\}_{i\in [n], b\in \{0,1\}}$, and r. So the sender’s communication cost grows with $\textsf{poly}(\lambda , {\textsf{d}_\textsf{m}}, |\textsf{id}|)$, which is $\textsf{poly}(\lambda )$.

Computation Costs. $\textsf{R}_1$: performs |V| $\textsf{Hash}$ evaluations and samples 2|T| random strings of length $\lambda$. $\textsf{S}$: samples $\textsf{poly}(\lambda , {\textsf{d}_\textsf{m}})$ random bits, garbles an $\textsf{F}$ circuit, garbles ${\textsf{d}_\textsf{m}}$ $\textsf{V}$ circuits, and performs a hash encryption of $6\lambda$ garbled labels. The sender’s computation cost is $\textsf{poly}(\lambda , {\textsf{d}_\textsf{m}})$. $\textsf{R}_2$: runs $\textsf{DecPath}$ for every root-leaf path. Each iteration of $\textsf{DecPath}$ requires at most ${\textsf{d}_\textsf{m}}+1$ $\textsf{HDec}$ and $\textsf{GS}.\textsf{Eval}$ evaluations. In total, R’s computation cost is $O(\lambda , {\textsf{d}_\textsf{m}}, |V|, |\textsf {PTH}|)$, where $|\textsf {PTH}|$ is the total number of root-to-leaf paths in the BP. So we require |V| and $|\textsf {PTH}|$ to be $\textsf{poly}(\lambda )$.

Lemma 3

Construction 1 is correct in the sense that (1) if $\textsf{BP}(\textsf{id}) = 1$, then with overwhelming probability $\textsf{R}_2$ outputs $\textsf{id}$ and (2) if $\textsf{BP}(\textsf{id}) = 0$, then with overwhelming probability $\textsf{R}_2$ outputs $\bot$.

Theorem 1

If $\textsf{HE}$ is an anonymous and robust hash encryption (defined in Lemma 1), and $\textsf{GS}$ is an anonymous garbling scheme, then the $\textsf{BP}\text{- }\textsf{2PC}$ protocol of Construction 1 provides statistical security for the receiver and semi-honest security for the sender.

The proofs of Lemma 3 and Theorem 1 are in Sects. 6 and 7, respectively.

5 Applications

Construction 1 can be used to realize multiple functionalities by reducing the desired functionality to an instance of $\textsf{BP}\text{- }\textsf{2PC}$. One step of the reductions involves constructing a branching program based on a set of bit strings.

At a high level, $\textsf{SetBP}$ (Fig. 4) creates a branching program for a set of elements $S:=\{x_1,\dots , x_m\}$ in three main steps. For concreteness, suppose the goal is to use this BP for a private set intersection.

First, for every prefix $a \in \{\epsilon \} \cup \{0,1\}\cup \{0,1\}^2 \cup \dots \cup \{0,1\}^\lambda$ of the elements in S, a node $v_a$ is added to the set of nodes V. If $a\in S$, then the value encoded in $v_a$ is set to 1; this is an ‘accept’ leaf. If $|a| < \lambda$, then the encoded value is set to $|a|+1$. When the BP is being evaluated on some input, $|a|+1$ will indicate the bit following prefix a. Next, edges are created between the BP levels. For $|a|< \lambda$, if for $b\in \{0,1\}$, node $v_{a\Vert b}$ exists in V, then a b-labelled edge is added from $v_a$ to $v_{a\Vert b}$. For $b\in \{0,1\}$, if $v_{a\Vert b}\notin V$, then node $v_{a\Vert b}$ is added to V with an encoded bit 0. This is a ‘reject’ leaf. Then a b-labelled edge is added from $v_a$ to $v_{a\Vert b}$. Finally, the BP is pruned. If two sibling leaves are both encoded with the same value, they are deleted and their parent becomes a leaf encoding that same value.

The definition below generalizes this concept by allowing us to capture both PSI and PSI via an indicator bit $b_\textsf{pth}$. In the description above, $b_\textsf{pth}$ is set to 1 for the PSI setting. For PSU we set $b_\textsf{pth}= 0$.

Construction 2

(Set to branching program). Figure 4 defines a procedure to create a branching program from an input set S. $\textsf{SetBP}(S, b_\textsf{pth})$ takes as input a set $S:=\{x_1, \dots , x_m\}$ of m strings, all of length $\lambda$ and a bit $b_\textsf{pth}$ and outputs a tuple $(V, E, T, \textsf{Val})$ defining a branching program. The output BP is such that if $x\in S$, then $\textsf{BP}(x) = b_\textsf{pth}$, and if $x\notin S$, then $\textsf{BP}(x) = 1- b_\textsf{pth}$.

Procedure $\textsf{SetBP}$ runs in time $O(\lambda |S|)$. In particular, when $|S|= \textsf{poly}(\lambda )$, $\textsf{SetBP}$ generates the BP in time $O(\textsf{poly}(\lambda ))$. The output BP has depth $d \le \lambda +1$ and the number of nodes is $2d+1 \le |V| \le 2^{d+1}-1$. Evaluation of $\textsf{BP}(x)$ for arbitrary $x \in \{0,1\}^\lambda$ takes time $O(\textsf{poly}(\lambda ))$.

BP Evaluation Runtime: Recall the BP evaluation algorithm in Fig. 2. Each loop iteration moves down the tree one level. The number of iterations is at most the tree depth, which is $\le \lambda +1$ for a BP created in Fig. 4. Each iteration takes constant time, so evaluation of $\textsf{BP}(x)$ for any $x \in \{0,1\}^\lambda$ takes time $O(\textsf{poly}(\lambda ))$.

Fig. 4.

Procedure for constructing a BP from a set of m $\lambda$-bit strings. See Construction 2. Based on a description in [CGH+21].

5.1 Private Set Intersection (PSI)

Assume a sender party has a set $S_\textsf{S}=\{\textsf{id}\}$ where $\textsf{id}\in \{0,1\}^\lambda$ and a receiver has a polynomial-sized set $S_\textsf{R}\subset \{0,1\}^\lambda$. In this setting, we define PSI as follows.

Definition 8

(Private set Intersection (PSI) functionality with $|S_\textsf{S}|=1$). Let $\varPi$ be a two-party communication protocol. Let R be the receiver holding set $S_\textsf{R}\subset \{0,1\}^\lambda$ and let S be the sender holding singleton set $S_\textsf{S}=\{\textsf{id}\}$, with $\textsf{id}\in \{0,1\}^\lambda$. $\varPi$ is a PSI protocol if the following hold after it is executed.

• Correctness: R learns $S_\textsf{R}\cap \{\textsf{id}\}$ if and only if $\textsf{id}\in S_\textsf{R}$.

• Receiver security: $\varPi$ achieves receiver security if $\forall \textsf{id}\in \{0,1\}^\lambda$, and all pairs $S_{\textsf{R}0}, S_{\textsf{R}1} \subset \{0,1\}^\lambda$ we have that $\textsf{view}_S^\varPi (S_{\textsf{R}0}, \textsf{id}, \lambda ) \approx \textsf{view}_S^\varPi (S_{\textsf{R}1}, \textsf{id}, \lambda )$. If the distributions are computationally (resp., statistically) indistinguishable then we have computational (resp., statistical) security.

• Sender security: $\varPi$ achieves sender security if $\forall \lambda \in \mathbb {N}$, $S_\textsf{R}\subset \{0,1\}^\lambda$, and all pairs $\textsf{id}_0, \textsf{id}_1 \in \{0,1\}^\lambda \setminus S_\textsf{R}$ we have that $\textsf{view}_R^\varPi (S_\textsf{R}, \textsf{id}_0, \lambda ) \approx \textsf{view}_R^\varPi (S_\textsf{R}, \textsf{id}_1, \lambda )$. If the distributions are computationally (resp., statistically) indistinguishable then we have computational (resp., statistical) security.

The PSI functionality can be achieved by casting it as an instance of $\textsf{BP}\text{- }\textsf{2PC}$:

• 1. R runs $\textsf{SetBP}(S_\textsf{R}, 1)$ (Fig. 4) to generate a branching program $\textrm{BP}_\text {psi}$ such that $\textsf{BP}_\text {psi}(x) = 1$ if $x \in S_\textsf{R}$ and $\textsf{BP}_\text {psi}(x) = 0$ otherwise.

• 2. R and S run $\textsf{BP}\text{- }\textsf{2PC}$ with inputs $\textrm{BP}_\text {psi}$ and $\textsf{id}$, respectively. By construction of $\textsf{BP}\text{- }\textsf{2PC}$:

  $$\begin{aligned} {\left\{ \begin{array}{ll} R \text { learns } \textsf{id}&{} \text {if } \textrm{BP}_\textrm{psi}(\textsf{id}) = 1 \implies \textsf{id}\in S_\textsf{R}\\ R \text { does not learn } \textsf{id}&{} \text {if } \textrm{BP}_\textrm{psi}(\textsf{id}) = 0 \implies \textsf{id}\notin S_\textsf{R}\end{array}\right. }, \end{aligned}$$

  which satisfies the PSI correctness condition and security follows from the security of Construction 1 for $\textsf{BP}\text{- }\textsf{2PC}$.

The computation and communication costs of the receiver and sender do not depend on $|S_\textsf{R}|$. If the receiver holds a polynomial-sized BP describing a set $S_\textsf{R}$ of exponential size, then this PSI protocol can run in polynomial time.⁶

5.2 Private Set Union (PSU)

As before, assume the sender has a singleton set $S_\textsf{S}=\{\textsf{id}\}$ where $\textsf{id}\in \{0,1\}^\lambda$ and the receiver has a set $S_\textsf{R}$. In this setting, we define PSU as follows.

Definition 9

(Private set union (PSU) functionality with $|S_\textsf{S}|=1$). Let $\varPi$ be a two-party communication protocol. Let R be the receiver holding set $S_\textsf{R}\subset \{0,1\}^\lambda$ and let S be the sender holding singleton set $S_\textsf{S}=\{\textsf{id}\}$, with $\textsf{id}\in \{0,1\}^\lambda$. $\varPi$ is a PSU protocol if the following hold after execution of the protocol.

• Correctness: R learns $S_\textsf{R}\cup \{\textsf{id}\}$.

• Receiver security: $\varPi$ achieves receiver security if $\forall \textsf{id}\in \{0,1\}^\lambda$, and all pairs $S_{\textsf{R}0}, S_{\textsf{R}1} \subset \{0,1\}^\lambda$ we have that $\textsf{view}_S^\varPi (S_{\textsf{R}0}, \textsf{id}, \lambda ) \approx \textsf{view}_S^\varPi (S_{\textsf{R}1}, \textsf{id}, \lambda )$. If the distributions are computationally (resp., statistically) indistinguishable then we have computational (resp., statistical) security.

• Sender security: $\varPi$ achieves sender security if $\forall S_\textsf{R}\subset \{0,1\}^\lambda$, and all pairs $\textsf{id}_0, \textsf{id}_1 \in S_\textsf{R}$ we have that $\textsf{view}_R^\varPi (S_\textsf{R}, \textsf{id}_0, \lambda ) \approx \textsf{view}_R^\varPi (S_\textsf{R}, \textsf{id}_1, \lambda )$. If the distributions are computationally (resp., statistically) indistinguishable then we have computational (resp., statistical) security.

The PSU functionality can be achieved by casting it as an instance of $\textsf{BP}\text{- }\textsf{2PC}$:

• 1. R runs $\textsf{SetBP}(S_\textsf{R}, 0)$ (Fig. 4) to generate a branching program $\textrm{BP}_\textrm{psu}$ such that $\textsf{BP}_\text {psu}(x) = 1$ if $x \notin S_\textsf{R}$ and $\textsf{BP}_\text {psu}(x) = 0$ otherwise.

• 2. R and S run $\textsf{BP}\text{- }\textsf{2PC}$ with inputs $\textrm{BP}_\textrm{psu}$ and $\textsf{id}$, respectively. By construction of $\textsf{BP}\text{- }\textsf{2PC}$:

  $$\begin{aligned} {\left\{ \begin{array}{ll} R \text { learns } \textsf{id}&{} \text {if } \textrm{BP}_\textrm{psu}(\textsf{id}) = 1 \implies \textsf{id}\notin S_\textsf{R}\\ R \text { does not learn } \textsf{id}&{} \text {if } \textrm{BP}_\textrm{psu}(\textsf{id}) = 0 \implies \textsf{id}\in S_\textsf{R}\end{array}\right. }, \end{aligned}$$

  which satisfies the PSU correctness condition and security follows from the security of Construction 1 for $\textsf{BP}\text{- }\textsf{2PC}$.

The computation and communication costs of the receiver and sender do not depend on $|S_\textsf{R}|$. If the receiver holds a polynomial-sized BP describing a set $S_\textsf{R}$ of exponential size, then this PSU protocol can run in polynomial time.⁷

5.3 Wildcards

Definition 10

(Wildcard). In a bit string a wildcard, denoted by an asterisk $*$, is used in place of a bit to indicate that its position may hold either bit value. In particular, the wildcard character replaces only a single bit, not a string. (E.g. $00*=\{000, 001\}$ and $**0 = \{000,010,100,110\}$.)

$\textsf{SetBP}$ in Fig. 4 creates a branching program based on a set that does not contain strings with wildcards. Figure 5 presents a modified version called $\textsf{SetBP}^*$ which creates a BP based on a singleton set containing a string with wildcard elements. Using $\textsf{SetBP}^*$ instead of $\textsf{SetBP}$ in the constructions for PSI and PSU above allows the receiver’s set to contain wildcards.

$\textsf{SetBP}^*$ runs in $O(\lambda )$ time. The resulting BP has depth $\overline{k}$, or $\lambda -k$, where k is the number of wildcard indices, and will contain $2\overline{k}+1$ nodes, where $\overline{k}\le \lambda$ is the number of non-wildcard indices. Since the depth leaks the number of wildcards in x, the receiver’s message $\textsf{m}_1$ to the sender in Construction 1 contains the maximum depth ${\textsf{d}_\textsf{m}}$, instead of the true depth.

Fig. 5.

Procedure for constructing a BP from a singleton set with a $\lambda$-bit string with wildcards. See Construction 2 and Sect. 5.3.

Overview of $\textsf{SetBP}^*$. $\textsf{SetBP}^*$ (Fig. 5) starts by forming an ordered ascending list of all indices of x without wildcards. Then it loops over each of these indices. A node is added to the BP for every prefix of x ending with an explicit (as opposed to *) bit value. Each node value is set to the index of the next non-wildcard bit in x. The node representing the final non-wildcard index is given value $b_\textsf{pth}$. For example, if $x= 0*1*0$, then we add prefix nodes $v_\epsilon , v_0, v_{0*1}, v_{0*1*0}$, (where $v_\epsilon$ is the root), and set their values to $1,3, 5, b_\textsf{pth}$, respectively.

Each iteration adds an edge from the previous prefix node to the one just created. This edge is labelled with the bit value at the current non-wildcard index. Continuing with the example, in the iteration that node $v_{0*1}$ is created, an edge from $v_{0}$ to $v_{0*1}$ is added with label 1. Since $S_\textsf{R}$ only contains one element, we also create a $1-b_\textsf{pth}$ leaf representing the prefix of the current interior node with the final bit flipped. An edge labelled with this flipped bit is also added from the previous node. In the example, $v_{0*0}$ is created with value $1-b_\textsf{pth}$ and edge $(v_{0*}, v_{0*0}, 0)$ is added. Once all non-wildcard indices of x have been considered, the BP is returned. If $|S_\textsf{R}|>1$, $\textsf{SetBP}^*$ can be run multiple times to add more leaf nodes to the BP. After the first $\textsf{SetBP}^*$ run, the zero-set initialization of V, E, T should be omitted.

5.4 Fuzzy Matching

A fuzzy match [GRS22] in our PSI setting refers to the inclusion of an element $x\in S_\textsf{R}$ in the intersection $S_\textsf{R}\cap S_\textsf{S}$ if $S_\textsf{S}$ contains an element that is $\delta$-close to x. The receiver sets a distance threshold $\delta$, which defines an $\ell _\infty$ ball of radius $\delta$ around all points in $S_\textsf{R}$. If an element in $S_\textsf{S}$ falls within any of these balls, it counts as a match and the point in $S_\textsf{R}$ at the center of this ball will be included in the intersection set. Construction 1 can be used for PSI with fuzzy matches defined with the $\ell _\infty$-norm as the distance metric (as considered in the structure-aware PSI [GRS22]). This may be accomplished if the receiver’s BP can be modified with the addition of wildcards to allow any BP input within an $\ell _\infty$ ball centred at a point of $S_\textsf{R}$ to be accepted as a fuzzy match.

6 Proof of Lemma 3

Proof

(Condition (1): $\textsf{BP}(\textsf{id}) =1 \Rightarrow \textsf{R}_2$ outputs $\textsf{id}$ w.o.p.)

Claim 1: When $\textsf{DecPath}$ is evaluated on the correct path, it will output $(\textsf{id},r)$.

Proof of claim 1: Consider the root-to-leaf path of length $\ell$ induced by the evaluation of $\textsf{BP}(\textsf{id})$. By hypothesis $\textsf{BP}(\textsf{id})=1$, so the path leaf node encodes the value 1. For concreteness, suppose the induced path has the leftmost leaf of the BP, $u_1\in T$, as the leaf endpoint. With this in mind, denote the path as,

$$\begin{aligned} \textsf{pth}[u_1] :=((\underbrace{1^{\lambda }, x_1, x'_1}_{z_{\ell }}), (\underbrace{h_1^{(\ell )}, h_2^{(\ell ) }, \textsf{Val}[v_1^{(\ell -1)}]}_{z_{\ell -1}} ), \dots ,(\underbrace{h_1^{(1)}, h_2^{(1)}, \textsf{Val}[v_1^{(0)}]}_{z_0}) ,\mathsf {h_{root}}). \end{aligned}$$

(1)

For the remainder of the proof, node labels v will be identified with their encoded values $\textsf{Val}[v]$ to save space. Let $(\textsf{id}_{u_1}, r_{u_1}) \leftarrow \textsf{DecPath}(\textsf{pth}[u_1], \widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0}, \{\textsf{cth}_{i,b}^{(0)} \} )$, where $\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_0, \{\textsf{cth}_{i,b}^{(0)} \}$ are defined as in the construction. Then it suffices to show that $r_{u_1} =r$. Consider an arbitrary iteration $w \in \{0,\dots , \ell - 2\}$ of the loop in step 2 of $\textsf{DecPath}$:

• 2. (a) $\{\textsf{lb}_{i}^{(w)}\} \leftarrow \textsf{HDec}(z_{w}, \{\textsf{cth}_{i,b}^{(w)} \})$

  

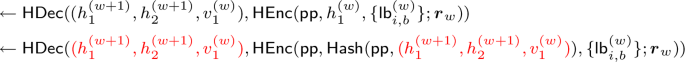
Since the two terms indicated are equal, the labels $\{\textsf{lb}_{i}^{(w)}\}$ output by $\textsf{HDec}$ are the subset of $\{\textsf{lb}_{i,b}^{(w)}\}$ corresponding to the bits of $z_{w} :=(h_1^{(w+1)}, h_2^{(w+1)},v_1^{(w)} )$. More precisely, $\textsf{lb}_{i,0}^{(w)} :=\textsf{lb}_{i, z_{w}[i]}^{(w)}$ and $\textsf{lb}_{i,1}^{(w)} :=\textsf{lb}_{i, z_{w}[i]}^{(w)}$ for all $i \in [n]$.

• 2. (b) $\{\textsf{cth}_{i,b}^{(w+1)} \} \leftarrow \textsf{Eval}(\widetilde{\textsf{C}}_{w}, \{\textsf{lb}_{i}^{(w)} \})$.

  $$\begin{aligned} \{\textsf{cth}_{i,b}^{(w+1)} \} &\leftarrow \textsf{V}[\textsf{pp}, \textsf{id}, \{\textsf{lb}_{i,b}^{(w+1)}\}, \boldsymbol{r}_{w}, r,\textsf{id}', r',\textsf{pad}](h_1^{(w+1)}, h_2^{(w+1)}, v_1^{(w)}) & \nonumber \\ \{\textsf{cth}_{i,b}^{(w+1)} \} &\leftarrow \textsf{HEnc}(\textsf{pp}, \ \underbrace{h_1^{(w+1)}}_{ { \quad \quad =\textsf{Hash}(\textsf{pp}, (h_1^{(w+2)}, h_2^{(w+2)}, v_1^{(w+1)} ))}} \ , \{\textsf{lb}_{i,b}^{(w+1)}\}; \boldsymbol{r}_{w}) & \end{aligned}$$

  (2)

The first input $h_1^{(w+1)}$ is used in the input to $\textsf{HEnc}$ because $\textsf{pth}[u_1]$ was defined to have the leftmost leaf as an endpoint. In other words, travelling from the root, $\textsf{pth}[u_1]$ always progresses to the left child.

In the final iteration of the loop, when $w = \ell -1$, the steps expanded above remain the same except for Eq. 2. When $w=\ell - 1$, Eq. 2 is instead

$$\begin{aligned} \{\textsf{cth}_{i,b}^{(\ell )} \} &\leftarrow \textsf{HEnc}(\textsf{pp}, \ \ \underbrace{h_1^{(\ell )}}_{{ =\textsf{Hash}(\textsf{pp}, (1^\lambda , x_1, x_1' ))}} ,\ \ \{\textsf{lb}_{i,b}^{(\ell )}\}; \boldsymbol{r}_{\ell -1}). \end{aligned}$$

With this in mind, the final two steps of $\textsf{DecPath}$ are as follows.

• 3. $\{\textsf{lb}_{i}^{(\ell )}\} \leftarrow \textsf{HDec}(z_{\ell }, \{\textsf{cth}_{i,b}^{(\ell )} \})$

  

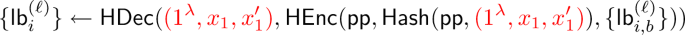
Since the two terms indicated above are equal, the labels $\{\textsf{lb}_{i}^{(\ell )}\}$ output by $\textsf{HDec}$ are the subset of labels $\{\textsf{lb}_{i,b}^{(\ell )}\}$ used in the input to $\textsf{HEnc}$, where the subset corresponds to the bits of $z_{\ell } = (1^\lambda , x_1, x_1')$.

• 4. $\{\textsf{id}_{u_1}, r_{u_1},\textsf{pad}\} \leftarrow \textsf{Eval}(\widetilde{\textsf{C}}_{\ell }, \{\textsf{lb}_{i}^{(\ell )} \})$

  $$\begin{aligned} & \{\textsf{id}_{u_1}, r_{u_1},\textsf{pad}\} \leftarrow \textsf{V}[\textsf{pp}, \textsf{id}, \{\textsf{lb}_{i,b}^{(\ell + 1)}\}, \boldsymbol{r}_{\ell }, r, \textsf{id}',r',\textsf{pad}](1^\lambda , x_1, x_1') & \\ & \{\textsf{id}_{u_1}, r_{u_1},\textsf{pad}\} \leftarrow \{\textsf{id}_{u_1} \leftarrow \textsf{id}, r_{u_1} \leftarrow r, \text { and } \textsf{pad}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{2(n-1)}\} & \end{aligned}$$

Then return $(\textsf{id}_{u_1}, r_{u_1})$ to the receiver. The first input to $\textsf{V}$ is $1^\lambda$, so the tuple $(\textsf{id}_{u_1}, r_{u_1})$ is equal to $(\textsf{id}, r)$.

The receiver compares $r_{u_1}$ from $\textsf{DecPath}$ with r in $\textsf{m}_2$. Since these strings are equal, the receiver takes $\textsf{id}_{u_1}$ output from $\textsf{DecPath}$ as the sender’s element. Hence, the receiver learns $\textsf{id}$ when $\textsf{BP}(\textsf{id}) =1$, completing the proof of claim 1.

In the above, we made use of the correctness properties of garbled circuit evaluation and $\textsf{HE}$ decryption. These guarantees give us that $\text {Pr}[\textsf{id}_{u_1} = \textsf{id}\wedge r_{u_1} = r \ | \ [1] (\textsf{id}_{u_1}, r_{u_1}) \leftarrow \textsf{DecPath}(\textsf{pth}[u_1], \textsf{m}_2)] = 1$ when $\textsf{pth}[u_1]$ is the correct path through the $\textrm{BP}$. In order for the correctness condition (1) to be met, it must also be true that there does not exist any other path $\textsf{pth}[u'] \ne \textsf{pth}[u_1]$ such that $r_{u'} = r$ where $(\textsf{id}_{u'}, r_{u'}) \leftarrow \textsf{DecPath}(\textsf{pth}[u'], \textsf{m}_2)$. In other words, there must not exist an incorrect path that decrypts the correct signal value r.

Claim 2: With at most negligible probability, there exists an incorrect path that when input to $\textsf{DecPath}$, decrypts to the correct signal value r.

Proof of claim 2: To show that occurs with negligible probability, consider running $\textsf{DecPath}$ on an incorrect path $\textsf{pth}[u'] \ne \textsf{pth}[u_1]$. Let $\textsf{pth}[u_1]$ and $\textsf{pth}[u']$ have lengths $\ell$ and $\ell '$, respectively where $1\le \ell , \ell '\le d$. Suppose these paths are equal at level $\alpha -1$ and differ at level $\alpha$ onward, for some $\alpha \in \{0,\dots , \min \{\ell , \ell '\}\}$. Suppose $u_1 \in T$ is the leftmost leaf, as above, and $u'\in T\setminus \{u_1\}$ is the leaf endpoint of $\textsf{pth}[u']$. Let these paths be given by the following.

$$\begin{aligned} \textsf{pth}[u_1] &:=((\underbrace{u_1^{(\ell )\times \lambda }, x_1, x_1'}_{z_{\ell }}), (\underbrace{h_1^{(\ell )}, h_2^{(\ell ) }, v_1^{(\ell -1)}}_{z_{\ell -1}} ), \dots , (\underbrace{h_1^{(\alpha +1)}, h_2^{(\alpha +1) }, v_1^{(\alpha )}}_{z_{\alpha }} ), \nonumber \\ & \quad \quad (\underbrace{h_1^{(\alpha )}, h_2^{(\alpha ) }, v_1^{(\alpha -1 )}}_{z_{\alpha -1}} ), \dots , (\underbrace{h_1^{(1)}, h_2^{(1)}, v_1^{(0)}}_{z_0}) , \mathsf {h_{root}}) \end{aligned}$$

(3)

$$\begin{aligned} \textsf{pth}[u'] & :=((\underbrace{u^{\prime (\ell ')\times \lambda }, x, x'}_{z'_{\ell '}}), (\underbrace{h^{(\ell ')}, h^{\prime (\ell ') }, v^{(\ell ' -1)}}_{z'_{\ell ' -1}} ), \dots , (\underbrace{h_3^{(\alpha +1)}, h_4^{(\alpha +1) }, v_2^{(\alpha )}}_{z'_{\alpha }} ), \nonumber \\ & \quad \quad (\underbrace{h_1^{(\alpha )}, h_2^{(\alpha ) }, v_1^{(\alpha -1 )}}_{z'_{\alpha -1}} ), \dots , (\underbrace{h_1^{(1)}, h_2^{(1)}, v_1^{(0)}}_{z'_0}) , \mathsf {h_{root}}). \end{aligned}$$

(4)

Since $\textsf{pth}[u']$ differs from the correct path at level $\alpha$, the steps of $\textsf{DecPath}(\textsf{pth}[u'],\textsf{m}_2)$ and $\textsf{DecPath}(\textsf{pth}[u_1], \textsf{m}_2)$ will be identical until loop iteration $w=\alpha$. Consider iteration $w=\alpha -1$ of $\textsf{DecPath}(\textsf{pth}[u'], \textsf{m}_2)$:

• 2. (a) $\{\textsf{lb}_{i}^{\prime (\alpha )}\} \leftarrow \textsf{HDec}(z'_\alpha , \{\textsf{cth}_{i,b}^{(\alpha )}\})$

  

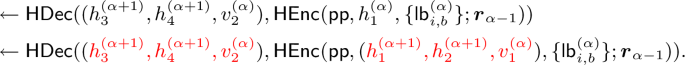
Since the indicated terms are equal, the $\{\textsf{lb}_{i}^{(\alpha -1)} \}$ labels output are the labels of circuit $\widetilde{\textsf{C}}_{\alpha -1}$ corresponding to the bits of $z'_{\alpha -1}$.

• 2. (b) $\{\textsf{cth}_{i,b}^{(\alpha )} \} \leftarrow \textsf{Eval}(\widetilde{\textsf{C}}_{\alpha -1}, \{\textsf{lb}_{i}^{(\alpha -1)} \})$

  $$\begin{aligned} \quad \quad \quad \ \ & \leftarrow \textsf{V}[\textsf{pp}, \textsf{id}, \{\textsf{lb}_{i,b}^{(\alpha )}\}, \boldsymbol{r}_{\alpha -1}, r, \textsf{id}',r', \textsf{pad}](h_1^{(\alpha )}, h_2^{(\alpha )}, v_1^{(\alpha -1)}) & \\ & \leftarrow \textsf{HEnc}(\textsf{pp}, h_1^{(\alpha )}, \{\textsf{lb}_{i,b}^{(\alpha )}\}; \boldsymbol{r}_{\alpha -1}). & \end{aligned}$$

In the last line, $h_1^{(\alpha )}$ is used in the hash encryption due to the assumption that the correct path has the leftmost leaf as an endpoint, meaning $\textsf{id}[v_1^{(\alpha +1)}]=0$.⁸ Next, the $w=\alpha$ iteration of the loop proceeds as follows.

• 2. (a) $\{\textsf{lb}_{i}^{\prime (\alpha )}\} \leftarrow \textsf{HDec}(z'_\alpha , \{\textsf{cth}_{i,b}^{(\alpha )}\})$

  

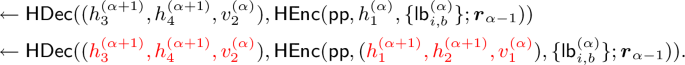
The two indicated terms are not equal. Decrypting an $\textsf{HE}$ ciphertext with an incorrect hash preimage produces an output containing no PPT-accessible information about the encrypted plaintext. For this reason, a prime was added above to the LHS labels to differentiate them from the labels encrypted on the RHS. Thus $\{\textsf{lb}_{i}^{\prime (\alpha )}\}$ provides no information about $\{\textsf{lb}_{i,b}^{(\alpha )}\}$.

• 2. (b) $\{\textsf{cth}_{i,b}^{(\alpha +1)}\} \leftarrow \textsf{Eval}(\widetilde{\textsf{C}}_\alpha , \{\textsf{lb}_{i}^{\prime (\alpha )}\})$.

Note that $\{\textsf{lb}_{i}^{ \prime (\alpha )}\}$ are not labels of $\widetilde{\textsf{C}}_\alpha$, and certainly not a subset of those labels corresponding to a meaningful input. So the output $\{\textsf{cth}_{i,b}^{(\alpha +1)}\}$ is a meaningless set of strings, not a ciphertext.

For w from $\alpha$ to $\ell '$, every $\textsf{HDec}$ operation will output $\{\textsf{lb}_i^{\prime (w)}\}$ which are not circuit labels for $\widetilde{\textsf{C}}_w$ and every evaluation $\textsf{Eval}(\widetilde{\textsf{C}}_w,\{\textsf{lb}_i^{\prime (w)}\})$ will output strings with no relation to $\widetilde{\textsf{C}}_w$. In step 4, $\{\textsf{id}_{u'}, r_{u'}, \textsf{pad}\} \leftarrow \textsf{Eval}(\widetilde{\textsf{C}}_{\ell '}, \{\textsf{lb}_i^{\prime (\ell ')}\} )$ is computed. Since $\{\textsf{lb}_i^{\prime (\ell ')}\}$ are not labels, the evaluation output is meaningless. In particular, the tuple $(\textsf{id}_{u'}, r_{u'})$ output to $\textsf{R}_2$ contains no PPT-accessible information about $(\textsf{id}, r)$. Hence ${\text {Pr}}\left[ r_{u'} = r\right] \le 2^{-\lambda }+\textsf{negl}(\lambda )$. By assumption on the size of BP, there are a polynomial number of root-to-leaf paths, thus by the union bound the probability that any incorrect root-to-path causes $\textsf{DecPath}$ to output r is,

$$\begin{aligned} \text {Pr}[\exists \ u \in T \setminus \{u_1\} \text { s.t. } r_u = r \ | \ (\textsf{id}_u, r_u) \leftarrow \textsf{DecPath}(\textsf{pth}[u], \textsf{m}_2)] \le \frac{\textsf{poly}(\lambda )}{2^\lambda } + \textsf{negl}(\lambda ). \end{aligned}$$

The probability that $\textsf{R}_2$ outputs $\textsf{id}$ when $\textsf{BP}(\textsf{id}) =1$ is the probability that none of the incorrect paths output a signal value equal to r:

$$\begin{aligned} {\text {Pr}}\left[ \textsf{R}_2 \text { outputs } \textsf{id}\ | \ \textsf{BP}(\textsf{id}) = 1\right] \ge 1 - \frac{\textsf{poly}(\lambda )}{2^\lambda } - \textsf{negl}(\lambda ). \end{aligned}$$

Thus proving claim 2 and correctness condition (1).

(Condition (2): $\textsf{BP}(\textsf{id}) =0 \Rightarrow \textsf{R}_2$ outputs $\bot$ w.o.p.) In the proof of Theorem 1 we will show that when $\textsf{BP}(\textsf{id})=0$,

$$\begin{aligned} (\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0}, \{\textsf{cth}^{(0)}_{i,b} \} , r) {\mathop {\equiv }\limits ^{c}}(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}', \dots , \widetilde{\textsf{C}}_{0}', \{\textsf{cth}^{\prime (0)}_{i,b} \} , r'), \end{aligned}$$

(5)

where all primed values are sampled uniformly random. On the LHS, the circuits all have r hardcoded, while the RHS is independent of r. So, for all fixed $u \in T$,

$$\begin{aligned} {\text {Pr}}\left[ r_u = r \ | \ (\textsf{id}_u, r_u) \leftarrow \textsf{DecPath}(\textsf{pth}[u], (\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}' , \dots ,\widetilde{\textsf{C}}_0', \{\textsf{cth}^{\prime (0)}_{i,b} \} , r')) \right] \le \frac{1}{2^\lambda }, \end{aligned}$$

where $\textsf{pth}[u]$ denotes the path from the root to leaf u. By assumption on the size of $\textrm{BP}$, there are a polynomial number of root-to-leaf paths, thus by the union bound the probability that any root-to-leaf paths decrypt to output r is,

$$\begin{aligned} {\text {Pr}}\left[ \exists \, u \in T \ \mathrm {s.t.}\ r_u = r \ | \ (\textsf{id}_u, r_u) \leftarrow \textsf{DecPath}(\textsf{pth}[u], (\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}', \dots , \widetilde{\textsf{C}}_{0}', \{\textsf{cth}^{\prime (0)}_{i,b} \} , r')) \right] \\ \le \frac{\textsf{poly}(\lambda )}{2^\lambda }. \end{aligned}$$

By Eq. 5, we must also have that the analogous probability for inputs $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_0, \{\textsf{cth}^{(0)}_{i,b} \} , r)$ is computationally indistinguishable. Thus,

$$\begin{aligned} {\text {Pr}}\left[ \exists \, u \in T \ \mathrm {s.t.}\ r_u = r \ | \ (\textsf{id}_u, r_u) \leftarrow \textsf{DecPath}(\textsf{pth}[u], (\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0}, \{\textsf{cth}^{(0)}_{i,b} \} , r)) \right] \\ \le \frac{\textsf{poly}(\lambda )}{2^\lambda }+ \textsf{negl}(\lambda ). \end{aligned}$$

If $\textsf{R}_2$ receives $r_u$ from $\textsf{DecPath}$ s.t. $r_u=r$, then $\textsf{R}_2$ outputs $\textsf{id}_u$. It follows that,

$$\begin{aligned} {\text {Pr}}\left[ \textsf{R}_2 \text { outputs } \bot \ | \ \textsf{BP}(\textsf{id}) = 0\right] &\ge 1- \frac{\textsf{poly}(\lambda )}{2^\lambda } - \textsf{negl}(\lambda ), \end{aligned}$$

which completes the proof of Lemma 3.    $\square$

7 Proof of Theorem 1

Proof

(Theorem 1 receiver security proof). Note that node labels will be identified with their encoded values to save space. Following Definition 7, for any pair $(\textrm{BP}_0, \textrm{BP}_1)$ consider the distribution below for $i \in \{0,1\}$.

where $\boldsymbol{r}_\textsf{S}$ are the sender’s random coins, $\textsf{h}_{\textsf{root}_i}$ is the root hash, and ${\textsf{d}_\textsf{m}}$ is the maximum depth of branching program $\textrm{BP}_i$. Since both BPs have security parameter $\lambda$, both will have ${\textsf{d}_\textsf{m}}=\lambda +1$. Let $d_i$ be the depth of $\textrm{BP}_i$.

Robustness of $\textsf{HE}$ implies that for all $\textsf{pp}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HGen}(1^\lambda , 3 \lambda )$ and $u \in T$, the distribution $(\textsf{pp}, \textsf{Hash}(\textsf{pp}, (u^{\lambda }, x,x')))$, where $x,x'{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{\lambda }$, is statistically close to $(\textsf{pp}, h_\$)$ where $h_\$ {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$. Hence $\textsf{Hash}(\textsf{pp}, (u^{\lambda }, x, x'))$ statistically hides u. At level $d_i$, $\textrm{BP}_i$ will have at least two leaf nodes with the same parent. Let $u_1,u_2$ be two such leaves and let $v^{(d_i-1)}$ be the parent. Node $v^{(d_i-1)}$ will then have hash value,

$$\begin{aligned} h^{(d_i-1)} & \leftarrow \textsf{Hash}(\textsf{pp}, (h_1^{(d_i)}, h_2^{(d_i)}, v^{(d_i-1)} )) \\ & \leftarrow \textsf{Hash}(\textsf{pp}, (\textsf{Hash}(\textsf{pp}, (u_1^{\lambda }, x_1, x_1')), \textsf{Hash}(\textsf{pp}, (u_2^{\lambda }, x_2, x_2')), v^{(d_i-1)} )). \end{aligned}$$

Since $h_1^{(d_i)}$ and $h_2^{(d_i)}$ are both statistically close to uniform, we have that $h^{(d_i-1)}$ is also statistically close to uniform. Continuing up the tree in this way, we see that the root hash $\textsf{h}_{\textsf{root}_i}$ is also indistinguishable from random. Thus $\textsf{h}_{\textsf{root}_0} \approx _s \textsf{h}_{\textsf{root}_1}$, which gives us $\textsf{view}_S^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}_0, \textsf{id}, \lambda ) \approx _s \textsf{view}_S^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}_1, \textsf{id}, \lambda )$.    $\square$

Proof

(Theorem 1 sender security proof).

Sender security will be proved through a sequence of indistinguishable hybrids in two main steps. First, all garbled circuits in the sender’s message $\textsf{m}_2$ are replaced one at a time with simulated circuits. Then $\textsf{m}_2$ is switched to random.

Sender security only applies when $\textsf{BP}(\textsf{id})=0$, so this will be assumed for the proof. For concreteness, suppose the path induced on the BP by evaluating $\textsf{id}$ has the leftmost leaf as an endpoint. In particular, let

$$\begin{aligned} \textsf{pth}:=((\underbrace{\textsf{Val}[v_1^{(\ell )}]^{\times \lambda }, x_1, x'_1}_{z_{\ell }}), (\underbrace{h_1^{(\ell )}, h_2^{(\ell ) }, \textsf{Val}[v_1^{(\ell -1)}]}_{z_{\ell -1}} ), \dots ,(\underbrace{h_1^{(1)}, h_2^{(1)}, \textsf{Val}[v_1^{(0)}]}_{z_0}) ,\mathsf {h_{root}}) \end{aligned}$$

(6)

be the leaf-root path induced on the hashed BP by evaluation of $\textsf{id}$, where $\ell$ is the path length and d is the BP depth.⁹ Since $\textsf{BP}(\textsf{id}) = 0$, the terminal node encodes value 0, i.e., $\textsf{Val}[v_1^{(\ell )}] = 0$. We let $\mathsf {h_{root}}\leftarrow \textsf{Hash}(\textsf{pp}, z_0)$ and $h_1^{(i)} \leftarrow \textsf{Hash}(\textsf{pp}, z_i)$ for all $1\le i\le \ell$, where the $z_i$ values are defined as in Eq. 6. To save space, often node labels v will be identified with their encoded index values $\textsf{Val}[v]$ and the padding superscript will be omitted from leaf node values.

$\mathsf {\textbf{Hyb}}_0$: [Fig. 6 left] The sender’s message $\textsf{m}_2:=(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}},\dots , \widetilde{\textsf{C}}_0,\{\textsf{cth}_{i,b}^{(0)}\}, r)$ is formed as described in the construction.

$\mathsf {\textbf{Hyb}}_1$: [Fig. 6 right] All circuits are simulated. The circuits are simulated so that if R runs $\textsf{DecPath}$ on $\textsf{pth}$ with simulated circuits, then every step occurs, from the view of R, as it would in $\mathsf {\textbf{Hyb}}_0$. This requires knowledge of $\textsf{pth}$ and the correct sequence of hash preimages $z_{\ell },\dots , z_0$, where $z_{\ell } = (0^\lambda , x_1, x_1')$ and $z_{j} = (h_1^{(j+1)}, h_2^{(j+1)}, v_1^{(j)})$ for $j\in \{0,\dots , \ell -1\}$. By assumption of $\textsf{pth}$, every evaluation $\textsf{Eval}(\widetilde{\textsf{C}}_j, \{\textsf{lb}_i^{(j)}\})$, where $\{\textsf{lb}_i^{(j)}\}\leftarrow \textsf{HDec}(z_j, \{\textsf{cth}_{i,b}^{(j)}\})$, done in $\textsf{DecPath}$ for $j \in \{0,\dots , \ell -1\}$ will output ciphertexts $\textsf{HEnc}(\textsf{pp}, h_1^{(j+1)}, \{\textsf{lb}_{i,b}^{(j+1)}\}; \boldsymbol{r}_j)$¹⁰. Moreover, evaluation of $\textsf{Eval}(\widetilde{\textsf{C}}_{\ell }, \{\textsf{lb}_i^{(\ell )}\})$ outputs $\{\textsf{id}', r', \textsf{pad}\}$ for random $\textsf{id}', r' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$ and $\textsf{pad}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{2(n-1)}$. Simulating circuits $\widetilde{\textsf{C}}_{\ell },\dots , \widetilde{\textsf{C}}_0$ is straightforward.

Fig. 6.

$\mathsf {\textbf{Hyb}}_0$ and $\mathsf {\textbf{Hyb}}_1$ for the proof of Theorem 1.

To simulate circuits $\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{\ell +1}$ note that none of these circuits can be used by R in $\textsf{DecPath}$ to obtain a meaningful output. Only this behaviour needs to be mimicked. To this end, we define “ghost” values $z_{\textsf{d}_\textsf{m}},\dots , z_{\ell + 1}$ with their associated hash values. The deepest is defined to be uniformly random: $z_{\textsf{d}_\textsf{m}}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{3\lambda }$. Then for $j\in \{{\textsf{d}_\textsf{m}}-1,\dots , \ell +1\}$ define,

$$\begin{aligned} h^{\prime (j)} := \textsf{Hash}(\textsf{pp}, (\overbrace{\underbrace{\ h^{\prime (j+1)}}_{{\textsf{Hash}(\textsf{pp}, z_{j+1})}} \ , h^{\prime (j+1)}, v^{\prime (j)}}^{z_j})) \end{aligned}$$

where $v_j' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$. In this way, two-thirds of the $z_j$ preimage is uniformly random which allows us to invoke the $\textsf{HE}$ robustness property. Moreover, the $z_j$ values create a chain of preimages similar to the $z_j$ values for $0\le j\le \ell -1$.

Lemma 4

Hybrids $\mathsf {\textbf{Hyb}}_0$ and $\mathsf {\textbf{Hyb}}_1$ are computationally indistinguishable.

Fig. 7.

Method of generating circuits in $\mathsf {\textbf{Hyb}}_{1.p}$ depending on the value of $p-1$ relative to the value of $\ell$. Use of $h_1^{(w+1)}$ in $\textsf{HEnc}$ on the LHS is from the assumption that $\textsf{pth}$ has the leftmost leaf as an endpoint. $''$ is the ditto symbol.

$\mathsf {\textbf{Hyb}}_2$: Sample $\textsf{m}_2$ at random.

Lemma 5

Hybrids $\mathsf {\textbf{Hyb}}_1$ and $\mathsf {\textbf{Hyb}}_2$ are computationally indistinguishable.

If $\textsf{m}_2$ is pseudorandom to the receiver, then $\textsf{m}_2$ created with some $\textsf{id}_0$ is computationally indistinguishable from $\textsf{m}_2$ created with some other $\textsf{id}_1$. Therefore we have $\textsf{view}_R^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}, \textsf{id}_0, \lambda ) {\mathop {\equiv }\limits ^{c}}\textsf{view}_R^\textsf{BP}\text{- }\textsf{2PC}(\textrm{BP}, \textsf{id}_1, \lambda )$, hence the above two lemmas establish computational sender security.

7.1 Proof of Lemma 4

To prove that $\mathsf {\textbf{Hyb}}_0 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_1$, we define a chain of ${\textsf{d}_\textsf{m}}+1$ hybrids between $\mathsf {\textbf{Hyb}}_0$ and $\mathsf {\textbf{Hyb}}_1$. Then we prove each game hop is indistinguishable.

$\mathsf {\textbf{Hyb}}_{1.p}$ for $0 \le p \le {\textsf{d}_\textsf{m}}$ (Fig. 8 ): Let $\textsf{pth}$ be as in Eq. 6 and recall we assume that $\textsf{Val}[v_1^{(\ell )}] = 0$. In $\mathsf {\textbf{Hyb}}_{1.p}$ circuits $\widetilde{\textsf{C}}_{0},\dots , \widetilde{\textsf{C}}_{p-1}$ are simulated and circuits $\widetilde{\textsf{C}}_p,\dots , \widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}$ are honestly generated (as in $\mathsf {\textbf{Hyb}}_{0}$). In $\mathsf {\textbf{Hyb}}_{1.0}$, all circuits are generated honestly¹¹ and in $\mathsf {\textbf{Hyb}}_{1.{\textsf{d}_\textsf{m}}}$ all circuits are simulated except for $\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}$. The way a particular circuit $\widetilde{\textsf{C}}_i$ for $i \le p-1$ is simulated depends on if $i< \ell$, $i = \ell$, or $i > \ell$, where $\ell$ is the length of path induced by $\textsf{id}$. These differences are shown in Fig. 7. As in $\mathsf {\textbf{Hyb}}_1$, simulating circuits $\widetilde{\textsf{C}}_{\ell +1},\dots , \widetilde{\textsf{C}}_{{\textsf{d}_\textsf{m}}-1}$ is done using ciphertexts created with “ghost” z values.

Fig. 8.

$\mathsf {\textbf{Hyb}}_{1.p}$ for $0\le p \le {\textsf{d}_\textsf{m}}$. The last $p+1$ circuits in $\mathsf {\textbf{Hyb}}_{1.p}$ are generated honestly and the remainder are simulated. See Lemma 4.

Lemma 6

$\mathsf {\textbf{Hyb}}_0 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.0 }$ and $\mathsf {\textbf{Hyb}}_1 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.{\textsf{d}_\textsf{m}}}$.

Proof

First we will prove $\mathsf {\textbf{Hyb}}_0 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.0}$ (Fig. 6 and Fig. 8). In both hybrids all circuits are honestly generated, but they differ in two ways. The first is in how the labels $\{\textsf{lb}^{({\textsf{d}_\textsf{m}})}\}$ are formed. Both hybrids generate the tuple $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_{i,b}^{({\textsf{d}_\textsf{m}})}\}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{F}[\textsf{id},\textsf{id}',r,r'])$ but $\mathsf {\textbf{Hyb}}_{1.0}$ additionally does $\{\textsf{lb}_{i}^{({\textsf{d}_\textsf{m}})}\} :=\{\textsf{lb}_{i,z_{\textsf{d}_\textsf{m}}[i]}^{({\textsf{d}_\textsf{m}})}\}$. If $\ell < {\textsf{d}_\textsf{m}}$, then $z_{\textsf{d}_\textsf{m}}$ is random. In that case, $\textsf{Eval}(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}},\{\textsf{lb}_{i, z_{\textsf{d}_\textsf{m}}[i]}^{({\textsf{d}_\textsf{m}})}\})$ will return $\{\textsf{id}', r^\prime \}$ w.o.p. If $\ell = {\textsf{d}_\textsf{m}}$ then $z_{\textsf{d}_\textsf{m}}:=(0^{\lambda }, x_1,x'_1)$ and so $\textsf{Eval}(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_{i, z_{\textsf{d}_\textsf{m}}[i]}^{({\textsf{d}_\textsf{m}})}\})$ will return $\{\textsf{id}', r^\prime \}$ with probability 1. Hence the difference between the sets of labels is indistinguishable by the $\textsf{BP}(\textsf{id}) = 0$ assumption.

The second difference between $\mathsf {\textbf{Hyb}}_0$ and $\mathsf {\textbf{Hyb}}_{1.0}$ is in how $\{ \textsf{cth}^{(0)}_{i,b}\}$ is formed. In $\mathsf {\textbf{Hyb}}_0$ we define $\{ \textsf{cth}_{i,b}^{(0)}\} {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HEnc}(\textsf{pp}, \mathsf {h_{root}}, \{\textsf{lb}_{i,b}^{(0)} \} )$. While $\mathsf {\textbf{Hyb}}_{1.0}$ does $\{ \textsf{cth}_{i,b}^{(0)}\} {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HEnc}(\textsf{pp}, \mathsf {h_{root}}, \{\textsf{lb}_{i}^{(0)} \} )$, where $\{\textsf{lb}_{i}^{(0)} \} :=\{\textsf{lb}_{i, z_0[i]}^{(0)} \}$. Since $\mathsf {h_{root}}\leftarrow \textsf{Hash}(\textsf{pp}, z_0)$, by semantic security of hash encryption we have that $\textsf{HEnc}(\textsf{pp}, \mathsf {h_{root}}, \{\textsf{lb}_{i}^{(0)} \} ) {\mathop {\equiv }\limits ^{c}}\textsf{HEnc}(\textsf{pp},\mathsf {h_{root}}, \{\textsf{lb}_{i,b}^{(0)} \} )$, completing the proof of $\mathsf {\textbf{Hyb}}_0 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.0}$.

Next we prove $\mathsf {\textbf{Hyb}}_1 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.{\textsf{d}_\textsf{m}}}$. In $\mathsf {\textbf{Hyb}}_1$ (Fig. 6) all circuits are simulated. In $\mathsf {\textbf{Hyb}}_{1.{\textsf{d}_\textsf{m}}}$ (Fig. 8) all circuits except for $\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}$ are simulated. The hybrids are the same after constructing $\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}$ and its labels. So, either hybrid can be simulated with r, the induced path $\textsf{pth}$, and $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_i^{({\textsf{d}_\textsf{m}})} \})$. For brevity, let $(\widetilde{\textsf{C}} , \{\textsf{lb}_i \})$ and $(\widetilde{\textsf{C}}^\prime , \{\textsf{lb}'_i \})$ denote the distribution of $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_i^{({\textsf{d}_\textsf{m}})} \})$ in $\mathsf {\textbf{Hyb}}_1$ and $\mathsf {\textbf{Hyb}}_{1.0}$, respectively. Then $(\widetilde{\textsf{C}} , \{\textsf{lb}_i \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{F} , \{ \textsf{id}',r'\})$ for random $\textsf{id}', r' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$. In $\mathsf {\textbf{Hyb}}_{1.0}$, letting $\textsf{C}_{\textsf{d}_\textsf{m}}:=\textsf{F}[\textsf{id},\textsf{id}', r,r' ]$ for random r, we have $(\widetilde{\textsf{C}'} , \{\textsf{lb}_{i,b} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{C}_{\textsf{d}_\textsf{m}})$ and $\{\textsf{lb}'_i \} :=\{ \textsf{lb}_{i, z_{\textsf{d}_\textsf{m}}[i]}\}$, where $z_{\textsf{d}_\textsf{m}}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{3\lambda }$ if $\ell < {\textsf{d}_\textsf{m}}$ and $z_{\textsf{d}_\textsf{m}}:=(\textsf{Val}[v_1^{({\textsf{d}_\textsf{m}})}]^{\times \lambda }, x_1,x'_1)$ otherwise, where $\textsf{Val}[v_1^{({\textsf{d}_\textsf{m}})}]^{\times \lambda } = 0^\lambda$. By garbling simulation security $(\widetilde{\textsf{C}'} , \{\textsf{lb}'_i \} ) {\mathop {\equiv }\limits ^{c}}\textsf{Sim}(\textsf{F} , \textsf{C}_{{\textsf{d}_\textsf{m}}}(z_{{\textsf{d}_\textsf{m}}}) ) {\mathop {\equiv }\limits ^{c}}\textsf{Sim}(\textsf{F} , \{\textsf{id}',r' \} )$. If $\ell < {\textsf{d}_\textsf{m}}$ and $z_{\textsf{d}_\textsf{m}}$ is random, then $\textsf{C}_{{\textsf{d}_\textsf{m}}}(z_{{\textsf{d}_\textsf{m}}}) =\{\textsf{id},r \}$ with probability $2^{-\lambda }$. If $\ell = {\textsf{d}_\textsf{m}}$ and $z_{\textsf{d}_\textsf{m}}:=(0^{\lambda }, x_1,x'_1)$ then $\textsf{C}_{{\textsf{d}_\textsf{m}}}(z_{{\textsf{d}_\textsf{m}}}) =\{\textsf{id}',r' \}$ with probability 1. Thus, $(r,\textsf{pth}, \widetilde{\textsf{C}} , \{\textsf{lb}_i \}) {\mathop {\equiv }\limits ^{c}}(r,\textsf{pth}, \widetilde{\textsf{C}'} , \{\textsf{lb}'_i \})$, proving $\mathsf {\textbf{Hyb}}_1 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.0}$ and completing the proof of Lemma 6.    $\square$

Lemma 7

For all $p \in \{0, \dots , {\textsf{d}_\textsf{m}}-1\}$, $\mathsf {\textbf{Hyb}}_{1.p}{\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_{1.p+1}$.

Proof

First, consider the circuits created in either hybrid:

$\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}^{({\textsf{d}_\textsf{m}})}_{i,b} \}, \dots , \widetilde{\textsf{C}}_{p+1}, \{\textsf{lb}^{(p+1)}_{i,b} \}$ are the same in both hybrids. They differ only in the distribution of $(\widetilde{\textsf{C}}_p, \{\textsf{lb}_i^{(p)}\})$; it is generated honestly in $\mathsf {\textbf{Hyb}}_{1.p}$ and simulated in $\mathsf {\textbf{Hyb}}_{1.p+1}$. There are three possible ways $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})$ can be simulated in $\mathsf {\textbf{Hyb}}_{1.p+1}$ depending on the value of p relative to $\ell$ (see Fig. 7, but note that it shows $\mathsf {\textbf{Hyb}}_{1.p}$, not $\mathsf {\textbf{Hyb}}_{1.p+1}$). First, if $p< \ell$, then $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})$ is simulated using a hash encryption of $\{\textsf{lb}_i^{(p+1)}\}$ with $z_{p+1}$. If $p = \ell$, then $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})$ is simulated using random output since $\textsf{BP}(\textsf{id}) = 0$. Finally, if $p > \ell$, then $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})$ is simulated using a hash encryption of $\{\textsf{lb}_i^{(p+1)}\}$ using “ghost” value $z_{p+1}$. We will prove that in each case it holds that $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p}} {\mathop {\equiv }\limits ^{c}}(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p+1}}$.

• 1. If $p< \ell$:

  $$\begin{aligned} \mathsf {\textbf{Hyb}}_{1.p} & : {\left\{ \begin{array}{ll} (\widetilde{\textsf{C}}_p, \{\textsf{lb}_{i,b}^{(p)}\} ) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{V}[\textsf{pp},\textsf{id}, \{\textsf{lb}_{i,b}^{(p+1)}\},\boldsymbol{r}_p, r, \textsf{id}', r', \textsf{pad}]) \\[0.5ex] \{\textsf{lb}_i^{(p)} \} :=\{\textsf{lb}_{i, z_p[i]}^{(p)} \} \quad \text {where } z_p = (h_1^{(p+1)}, h_2^{(p+1)}, v_1^{(p)} ) \end{array}\right. } \nonumber \\ \mathsf {\textbf{Hyb}}_{1.p+1} & : {\left\{ \begin{array}{ll} \{\textsf{cth}_{i,b}^{(p+1)}\} \leftarrow \textsf{HEnc}(\textsf{pp}, h_1^{(p+1)} , \{\textsf{lb}_{i}^{(p+1)} \} ; \boldsymbol{r}_p) \\[0.5ex] (\widetilde{\textsf{C}}_{p} , \{\textsf{lb}_{i}^{(p)} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{V}, \{\textsf{cth}_{i,b}^{(p+1)} \}) \end{array}\right. } \end{aligned}$$

  (7)

  By simulation security of garbled circuits,

  $$\begin{aligned} (\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p}} &{\mathop {\equiv }\limits ^{c}}\textsf{Sim}(\textsf{V}, \textsf{C}_{p}(z_{p}) ) \nonumber \\ &{\mathop {\equiv }\limits ^{c}}\textsf{Sim}(\textsf{V}, \textsf{HEnc}(\textsf{pp}, h_1^{(p+1)}, \{\textsf{lb}_{i,b}^{(p+1)}\} ; \boldsymbol{r}_{p} ) ). \end{aligned}$$

  (8)

  The use of $h_1^{(p+1)}$ in Eq. 8 is due to the assumption that the path induced by $\textsf{id}$ has the leftmost node as its terminal node. So by definition of $\textsf{C}_{p}$, its hardwired labels $\{\textsf{lb}_{i,b}^{(p+1)}\}$ will be encrypted under $h_1^{(p+1)}$. Equation 8 is identical to the RHS of Eq. 7, and thus when $p > \ell$ we have $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p}} {\mathop {\equiv }\limits ^{c}}(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p+1}}$.

• 2. If $p= \ell$:

  $$\begin{aligned} \mathsf {\textbf{Hyb}}_{1.p} & : {\left\{ \begin{array}{ll} (\widetilde{\textsf{C}}_p, \{\textsf{lb}_{i,b}^{(p)}\} ) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{V}[\textsf{pp},\textsf{id}, \{\textsf{lb}_{i,b}^{(p+1)}\},\boldsymbol{r}_p, r, \textsf{id}', r', \textsf{pad}]) \\[0.5ex] \{\textsf{lb}_i^{(p)} \} :=\{\textsf{lb}_{i, z_p[i]}^{(p)} \} \quad \text {where } z_p = (0^\lambda , x_1, x_1' ) \end{array}\right. } \nonumber \\ \mathsf {\textbf{Hyb}}_{1.p+1} & : {\left\{ \begin{array}{ll} (\widetilde{\textsf{C}}_{p} , \{\textsf{lb}_{i}^{(p)} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{V}, \{\textsf{id}', r', \textsf{pad}\}) \\[0.5ex] \text {where } \textsf{id}', r' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda {\, ; \,}\textsf{pad}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{2(n-1)} \end{array}\right. } \end{aligned}$$

  (9)

  By simulation security of garbled circuits,

  $$\begin{aligned} (\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p}} &{\mathop {\equiv }\limits ^{c}}\textsf{Sim}(\textsf{V}, \textsf{C}_{p}(z_{p}) ){\mathop {\equiv }\limits ^{c}}\textsf{Sim}(\textsf{V},\{\textsf{id}', r', \textsf{pad}\}). \end{aligned}$$

  (10)

  When $p = \ell$, $z_{p} = (0^\lambda , x_1, x_1')$ which causes $\textsf{C}_{p}(z_{p})$ to output a random ID and signal string. So, the RHS of Eq. 10 is identical to the first line of Eq. 9. Thus if $p = \ell$, we have $(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p}} {\mathop {\equiv }\limits ^{c}}(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p+1}}$.

• 3. If $p> \ell$:

  $$\begin{aligned} \mathsf {\textbf{Hyb}}_{1.p} & : {\left\{ \begin{array}{ll} (\widetilde{\textsf{C}}_p, \{\textsf{lb}_{i,b}^{(p)}\} ) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Garb}(\textsf{V}[\textsf{pp},\textsf{id}, \{\textsf{lb}_{i,b}^{(p+1)}\},\boldsymbol{r}_p, r, \textsf{id}', r', \textsf{pad}]) \\[0.5ex] \{\textsf{lb}_i^{(p)} \} :=\{\textsf{lb}_{i, z_p[i]}^{(p)} \} \quad \text {where } z_p = (h^{\prime (p+1)}, h^{\prime (p+1)}, v^{\prime (p)} ) \end{array}\right. } \nonumber \\ \mathsf {\textbf{Hyb}}_{1.p+1} & : {\left\{ \begin{array}{ll} \{\textsf{cth}_{i,b}^{(p+1)} \} \leftarrow \textsf{HEnc}(\textsf{pp}, h^{\prime (p+1)}, \{\textsf{lb}_{i}^{(p+1)} \}; \boldsymbol{r}_p ) \\ (\widetilde{\textsf{C}}_{p} , \{\textsf{lb}_{i}^{(p)} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{V}, \{\textsf{cth}_{i,b}^{(p+1)} \}) \\ \text {where } h^{\prime (p+1)} \leftarrow \textsf{Hash}(\textsf{pp}, z_{p+1}) \text { is pseudorandom} \end{array}\right. } \end{aligned}$$

  (11)

  Consider evaluating $\widetilde{\textsf{C}}_{p}$ on labels $\{\textsf{lb}_{i,z_{p}[i]}^{(p)} \}$ as in $\mathsf {\textbf{Hyb}}_{1.p}$:

  $$\begin{aligned} \textsf{Eval}(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}_{i,z_{p}[i]}^{(p)} \}) &= \textsf{V}[\textsf{pp}, \textsf{id}, \{\textsf{lb}_{i,b}^{(p+1)}\}, \boldsymbol{r}_{p}, r,\textsf{id}',r',\textsf{pad}]( h^{\prime (p+1)}, h^{\prime (p+1)}, v^{\prime (p)} ) \nonumber \\ & = {\left\{ \begin{array}{ll} \textsf{HEnc}(\textsf{pp}, h^{\prime (p+1)}, \{\textsf{lb}_{i,b}^{(p+1)}\};\boldsymbol{r}_{p}) &{} \text { if } \textsf{id}[v_{p}'] = 0\\ \textsf{HEnc}(\textsf{pp}, h^{\prime (p+1)}, \{\textsf{lb}_{i,b}^{(p+1)}\};\boldsymbol{r}_{p}) &{} \text { otherwise } \end{array}\right. } \nonumber \\ & = \textsf{HEnc}(\textsf{pp}, h^{\prime (p+1)}, \{\textsf{lb}_{i,b}^{(p+1)}\};\boldsymbol{r}_{p}). \end{aligned}$$

  (12)

Equation 12 is identical to the RHS of Eq. 11 (first), up to the labels $\{\textsf{lb}_i^{(p+1)}\}$ in Eq. 11 vs. $\{\textsf{lb}_{i,b}^{(p+1)}\}$ in Eq. 12. By simulation security, the labels $\{\textsf{lb}_i^{(p+1)}\}$ in Eq. 11 are computationally indistinguishable from labels $\{\textsf{lb}_{i, z_{p+1}[i]}^{(p+1)}\}$. Thus $\{\textsf{lb}_{i,z_{p+1}[i]}^{(p+1)}\}_{\mathsf {\textbf{Hyb}}_{1.p}} {\mathop {\equiv }\limits ^{c}}\{\textsf{lb}_{i}^{(p+1)}\}_{\mathsf {\textbf{Hyb}}_{1.p+1}}$. By $\textsf{HE}$ semantic security, $\textsf{HEnc}(\textsf{pp}, h^{\prime (p+1)},\{\textsf{lb}_{i,b}^{(p+1)}\};\boldsymbol{r}_{p}) {\mathop {\equiv }\limits ^{c}}\textsf{HEnc}(\textsf{pp}, h^{\prime (p+1)},\{\textsf{lb}_{i}^{(p+1)}\}; \boldsymbol{r}_{p})$, and hence $(\widetilde{\textsf{C}}_{p},\{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p}} {\mathop {\equiv }\limits ^{c}}(\widetilde{\textsf{C}}_{p}, \{\textsf{lb}^{(p)}_i \})_{\mathsf {\textbf{Hyb}}_{1.p+1}}$ when $p>\ell$, which completes the proof of Lemma 7.    $\square$

7.2 Proof of Lemma 5

Lemma 5 states that $\mathsf {\textbf{Hyb}}_1 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_2$. So, we must show that $\textsf{m}_2 :=(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \dots , \widetilde{\textsf{C}}_{0} , \{\textsf{cth}^{(0)}_{i,b} \} , r)$, as sampled in $\mathsf {\textbf{Hyb}}_1$, is computationally indistinguishable from random. We will argue that each element of $\textsf{m}_2$ is pseudorandom.

First consider the circuit $\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}$. It is formed as $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_i^{({\textsf{d}_\textsf{m}})} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{F} , \{\textsf{id}',r'\})$ where $\textsf{id}',r' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$. Since the inputs $\textsf{id}',r'$ are random, by anonymous security of garbled circuits the distribution $(\widetilde{\textsf{C}}_{\textsf{d}_\textsf{m}}, \{\textsf{lb}_i^{({\textsf{d}_\textsf{m}})} \})$ is pseudorandom.

For w from ${\textsf{d}_\textsf{m}}-1$ to $\ell +1$ the circuits are formed as $(\widetilde{\textsf{C}}_w , \{\textsf{lb}_{i}^{(w)} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{V}, \{\textsf{cth}_{i,b}^{(w+1)}\})$ where $\{\textsf{cth}_{i,b}^{(w+1)}\} {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HEnc}(\textsf{pp}, h^{\prime (w+1)} , \{\textsf{lb}_{i}^{(w+1)}\})$. $\{\textsf{cth}_{i,b}^{(w+1)}\}$ is pseudorandom by anonymous semantic security of $\textsf{HE}$, and so by anonymous security of $\textsf{GS}$, $(\widetilde{\textsf{C}}_w , \{\textsf{lb}_{i}^{(w)} \})$ is also pseudorandom.

For $w = \ell$ we have $(\widetilde{\textsf{C}}_{\ell } , \{\textsf{lb}_i^{(\ell )} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{V}, \{\textsf{id}',r', \textsf{pad}\})$ where $\textsf{id}',r' {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^\lambda$, $\textsf{pad}{\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\{0,1\}^{2(n-1)}$, so again by anonymous security of garbled circuits, the distribution $(\widetilde{\textsf{C}}_{\ell } , \{\textsf{lb}_i^{(\ell )} \})$ is pseudorandom.

For w from $\ell -1$ to 0 we have $\{\textsf{cth}^{(w+1)}_{i,b}\} {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HEnc}(\textsf{pp}, h_1^{(w+1)} ,\{\textsf{lb}_i^{(w+1)} \} )$ and $(\widetilde{\textsf{C}}_w , \{\textsf{lb}_{i}^{(w)} \}) {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{Sim}(\textsf{V},\{\textsf{cth}_{i,b}^{(w+1)}\})$. Where, again, the use of $h_1^{(w+1)}$ in $\textsf{HEnc}$ is from the assumption on $\textsf{pth}$. For all w from $\ell -1$ to 0, $\{\textsf{cth}^{(w+1)}_{i,b}\}$ is pseudorandom by anonymous semantic security of $\textsf{HE}$, and thus by anonymous security of $\textsf{GS}$, $(\widetilde{\textsf{C}}_w , \{\textsf{lb}_{i}^{(w)} \})$ is also pseudorandom.

Next in $\textsf{m}_2$ is the ciphertext, which in $\mathsf {\textbf{Hyb}}_1$ is formed as $\{\textsf{cth}^{(0)}_{i,b} \} {\, \overset{\scriptscriptstyle \$}{\scriptstyle \leftarrow }\,}\textsf{HEnc}(\textsf{pp},\mathsf {h_{root}}, \{\textsf{lb}_{i}^{(0)} \} )$. $\{\textsf{cth}^{(0)}_{i,b} \}$ is pseudorandom by anonymous semantic security of $\textsf{HE}$. The final element of $\textsf{m}_2$ is the signal string r, which is sampled uniformly at random. Hence $\textsf{m}_2$ is pseudorandom in the view of $\textsf{R}$, proving $\mathsf {\textbf{Hyb}}_1 {\mathop {\equiv }\limits ^{c}}\mathsf {\textbf{Hyb}}_2$ and completing the proof.    $\square$

Remark 1

In the proofs above, we assumed that the path induced by evaluating $\textsf{BP}(\textsf{id})$ always travelled to the left child. In the general case, the path in Eq. 6 ending in $v_1^{(\ell )}$ just needs to be changed to the path induced by $\textsf{BP}(\textsf{id})$ ending in the appropriate leaf $u \in T$. The proofs should then be updated accordingly.