Specifying and Verifying Persistent Libraries

Abstract

We present a general framework for specifying and verifying persistent libraries, that is, libraries of data structures that provide some persistency guarantees upon a failure of the machine they are executing on. Our framework enables modular reasoning about the correctness of individual libraries (horizontal and vertical compositionality) and is general enough to encompass all existing persistent library specifications ranging from hardware architectural specifications to correctness conditions such as durable linearizability. As case studies, we specify the FliT and Mirror libraries, verify their implementations over , and use them to build higher-level durably linearizable libraries, all within our framework. We also specify and verify a persistent transaction library that highlights some of the technical challenges which are specific to persistent memory compared to weak memory and how they are handled by our framework.

1 Introduction

Persistent memory (PM), also known as non-volatile memory (NVM), is a new kind of memory, which can be used to extend the capacity of regular RAM, with the added benefit that its contents are preserved after a crash (e.g. a power failure). Employing PM can boost the performance of any program with access to data that needs to survive power failures, be it a complex database or a plain text editor.

Nevertheless, doing so is far from trivial. Data stored in PM is mediated through the processors’ caching hierarchy, which generally does not propagate all memory accesses to the PM in the order issued by the processor, but rather performs these accesses on the cache and only propagates them to the memory asynchronously when necessary (i.e. upon a cache miss or when the cache has reached its capacity limit). Caches, moreover, do not preserve their contents upon a power failure, which results in rather complex persistency models describing when and how stores issued by a program are guaranteed to survive a power failure. To ensure correctness of their implementations, programmers have to use low-level primitives, such as flushes of individual cache lines, fences that enforce ordering of instructions, and non-temporal stores that bypass the cache hierarchy.

These primitives are often used to implement higher-level abstractions, packaged into persistent libraries, i.e. collections of data structures that must guarantee to preserve their contents after a power failure. Persistent libraries can be thought of as the analogue of concurrent libraries for persistency. And just as concurrent libraries require a specification, so do persistent libraries.

The question naturally arises: what is the right specification for persistent libraries? Prior work has suggested a number of candidate definitions, such as durable linearizability, buffered durable linearizability [17], and strict linearizability [1], which are all extensions of the well-known correctness condition for concurrent data structures (i.e. linearizability [15]). In general, these definitions stipulate the existence of a total order among all executed library operations, a contiguous prefix of which is persisted upon a crash: the various definitions differ in exactly what this prefix should be, e.g. whether it is further constrained to include all fully executed operations.

Even though these specifications have a nice compositionality property, we argue that none of them are the right specification pattern for every persistent concurrent library. While for high-level persistent data structures, such as stacks and queues, a strong specification such as durable or strict linearizability would be most appropriate, this is certainly not the case for a collection of low-level primitives. Take, for instance, a library whose interface simply exposes the exact primitives of the underlying platform: memory accesses, fences and flushes. Their semantics, recently formalized in [19, 28, 30] in the case of the architecture and in [5, 31] in the case of the architecture, quite clearly do not fit into the framework of the durable linearizability definitions. More generally, there are useful concurrent libraries (especially in the context of weak memory consistency) that are not linearizable [26]; it is, therefore, conceivable that making those libraries persistent will require weak specifications.

Another key problem with attempting to specify persistent libraries modularly is that they often break the usual abstraction boundaries. Indeed, some models such as epoch persistency [6, 24] provide a global persistency barrier that affects all memory locations, and therefore all libraries using them. Such global operations also occur at higher abstraction layers: persistent transactional libraries often require memory locations to be registered with the library in order for them to be used inside transactions. As such, to ensure compatibility with such transactional libraries, implementers of other libraries must register all locations they use and ensure that any component libraries they use do the same.

In this paper, we introduce a general declarative framework that addresses both of these challenges. Our framework provides a very flexible way of specifying persistent libraries, allowing each library to have a very different specification—be it durable linearizability or a more complex specification in the style of the hardware architecture persistency models. Further, to handle libraries that have a global effect (such as persistent barriers above) or, more generally, that make some assumptions about the internals of all other libraries, we introduce a tag system, allowing us to describe these assumptions modularly.

Our framework supports both horizontal and vertical compositionality. That is, we can verify an execution containing multiple libraries by verifying each library separately (horizontal compositionality). Moreover, we can completely verify the implementation of a library over a set of other libraries using the specifications of its constituent libraries without referring to their implementations (vertical compositionality). To achieve the latter, we define a semantic notion of substitution in terms of execution graphs, which replaces each library node by a suitably constrained set of nodes (its implementation).

For simplicity, in §2, we develop a first version of our framework over the classical notion of an execution history [15], which we extend with a notion of crashes. This basic version of our framework includes full support for weak persistency models but assumes an interleaving semantics of concurrency; i.e. sequential consistency (SC) [23].

Subsequently, in §3 we generalise and extend our framework to handle weak consistency models such as x86-TSO [32] and RC11 [22], thereby allowing us to represent hardware persistency models such as [30] and [31], in our framework. To do so, we rebase our formal development over execution graphs using Yacovet [26] as a means of specifying the consistency properties of concurrent libraries.

We illustrate the utility of our framework by encoding in it a number of existing persistency models, ranging from actual hardware models such as [30], to general-purpose correctness conditions such as durable linearizability [17]. We further consider two case studies, chosen to demonstrate the expressiveness of our framework beyond the kind of case studies that have been worked out in the consistency setting.

First, in §4 we use our framework to develop the first formal specifications of the FliT [35] and Mirror [10] libraries and establish the correctness of not only their implementations against their respective specifications, but also their associated constructions for turning a linearizable library into a durably linearizable one. This generic theorem is new compared to the case studies in [26], and leverages our ‘semantic’ approach in §3. Moreover, our proofs of these constructions are the first to establish this result in a weak consistency setting.

Second, in §5 we specify and prove an implementation of a persistent transactional library $\textsf{L}_{\textsf {trans}}$, which provides a high-level construction to persist a set of writes atomically. The $\textsf{L}_{\textsf {trans}}$ library illustrates the need for a ‘well-formedness’ specification (in addition to its consistency and persistency specifications) that requires clients of the $\textsf{L}_{\textsf {trans}}$ library to ensure e.g. that $\textsf{L}_{\textsf {trans}}$ writes appear only inside transactions. Moreover, it demonstrates the use of our tagging system to enable other libraries to interoperate with it.

Contributions and Outline. The remainder of this article is organised as follows.

• §2 We present our general framework for specifying and verifying persistent libraries in the strong sequential consistency setting.

• §3 We further generalise our framework to account for weaker consistency models.

• §4 We use our framework to develop the first formal specifications of the FliT and Mirror libraries, verify their implementations against their specifications and prove their general construction theorems for turning linearizable libraries to durably linearizable ones.

• §5 We specify a persistent transactional library $\textsf{L}_{\textsf {trans}}$, develop an implementation of $\textsf{L}_{\textsf {trans}}$ (over the Intel-x86 architecture) and verify it against its specification. We then consider two case studies of vertical and horizontal composition in our framework using $\textsf{L}_{\textsf {trans}}$.

We conclude and discuss related and future work in §6. The full proofs of all theorems stated in the paper are given in the technical appendix.

2 A General Framework for Persistency

We present our framework for specifying and verifying persistent libraries, which are collections of methods that operate on durable data structures. Following Herlihy et al. [15], we will represent program histories over a collection of libraries $\varLambda$ as $\varLambda$-histories, i.e. as sequences of calls to the methods of $\varLambda$, which we will then gradually enhance to model persistency semantics. Throughout this section, we assume an underlying sequential consistency semantics; in §3 we will generalize our framework to account for weaker consistency models.

In the following, we assume the following infinite domains: $\textbf{Meth}$ of method names, $\textbf{Loc}$ of memory locations, $\textbf{Tid}$ of thread identifiers, and $\textbf{Val}\supseteq \textbf{Loc}\cup \textbf{Tid}$ of values. We let m range over method names, x over memory locations, $\textsf{t}$ over thread identifiers, and v over values. An optional value ${v_\bot }\in \textbf{Val}_\bot$ is either a value $v \in \textbf{Val}$ or $\bot \notin \textbf{Val}$.

2.1 Library Interfaces

A library interface declares a set of method invocations of the form $m(\vec{v})$. Some methods are are designated as constructors; a constructor returns a location pointing to the new library instance (object), which is passed as an argument to other library methods. An interface additionally contains a function, $\textrm{loc}$, which extracts these locations from the arguments and return values of its method calls.

Definition 1

A library interface $L$ is a tuple $\langle \mathcal {M}, \mathcal {M}_\textrm{c}, \textrm{loc} \rangle$, where the set of method invocations $\mathcal {M}$ is a subset of $\mathcal {P}\left( \textbf{Meth}\times \textbf{Val}^*\right)$, $\mathcal {M}_\textrm{c}\subseteq \mathcal {M}$ is the set of constructors, and $\textrm{loc}: \mathcal {M}\times \textbf{Val}_\bot \rightarrow \mathcal {P}\left( \textbf{Loc}\right)$ is the location function.

Example 1

(Queue library interface). The queue library interface, $\textsf{L}_\textsf {Queue}$, has three methods: a constructor $\textsf{QueueNew}()$, which returns a new empty queue; $\textsf{QueueEnq}(x, v)$ which adds value v to the end of queue x; and $\textsf{QueueDeq}(x)$ which removes the head entry in queue x. We define $\textrm{loc}(\textsf{QueueNew}(), x) = \textrm{loc}(\textsf{QueueEnq}(x, \_), \_) = \textrm{loc}(\textsf{QueueDeq}(x), \_) = \{ x \}$.

A collection $\varLambda$ is a set of library interfaces with disjoint method names. When $\varLambda$ consists of a single library interface $L$, we often write $L$ instead of $\{L\}$.

2.2 Histories

Given a collection $\varLambda$, an event $e \in \textbf{Events}(\varLambda )$ of $\varLambda$ is either a method invocation $m(\vec{v})_\textsf{t}$ with $m(\vec{v}) \in \bigcup _{L\in \varLambda } L{.}\mathcal {M}$ and $\textsf{t}\in \textbf{Tid}$ or method response (return) event $\textbf{ret}(v)_\textsf{t}$.

A $\varLambda$-history is a sequence of events of $\varLambda$ whose projection to each thread is an alternating sequence of invocation and return events which starts with an invocation.

Definition 2

(Sequential event sequences). A sequence of events $e_1 \ldots e_n$ is sequential if all its odd-numbered events $e_1,e_3,\ldots$ are invocation events and all its even-numbered events $e_2,e_4,\ldots$ are return events.

Definition 3

(Histories). A $\varLambda$-history is a finite sequence of events $H\in \textbf{Events}(\varLambda )^*$, such that for every thread $\textsf{t}$, the sub-sequence $H[\textsf{t}]$ comprising only of $\textsf{t}$ events is sequential. The set $\textbf{Hist}(\varLambda )$ denotes the set of all $\varLambda$-histories.

When clear from the context, we refer to occurrences of events in a history by their corresponding events. For example, if $H= e_1 \dots e_n$ and $i < j$, we say that $e_i$ precedes $e_j$ and that $e_j$ succeeds $e_i$. Given an invocation $m(\vec{v})_\textsf{t}$ in $H$, its matching return (when it exists) is the first event of the form $\textbf{ret}(v)_\textsf{t}$ that succeeds it (they share the same thread). A call is a pair $m(\vec{v})_{\textsf{t}}{:}{{v_\bot }}$ of an invocation and either its matching return ${v_\bot }\in \textbf{Val}$ (complete call) or ${v_\bot }= \bot$ (incomplete call).

A library (specification) comprises an interface and a set of consistent histories. The latter captures the allowed behaviors of the library, which is a guarantee made by the library implementation.

Definition 4

A library specification (or simply a library) $\textsf{L}$ is a tuple $\langle L, \mathcal {S}_{\textsf {c}} \rangle$, where $L$ is a library interface, and $\mathcal {S}_{\textsf {c}}\subseteq \textbf{Hist}(L)$ denotes its set of consistent histories.

2.3 Linearizability

Linearizability [15] is a standard way of specifying concurrent libraries that have a sequential specification S, denoting a set of finite sequences of complete calls. Given a sequential specification S, a concurrent library $\textsf{L}$ is linearizable under S if each consistent history of $\textsf{L}$ can be linearized into a sequential one in S, while respecting the happens before order, which captures causality between calls. It is sufficient to consider consistent executions because inconsistent executions are, by definition, guaranteed by the library to never happen. Happens-before is defined as follows.

Definition 5

(Happens-Before). A method call $C_1$ happens before another method call $C_2$ in a history $H$, written $C_1 \prec _HC_2$ if the response of $C_1$ precedes the invocation of $C_2$ in $H$. When the choice of $H$ is clear from the context, we drop the $H$ subscript from $\prec$.

A history $H$ is linearizable under a sequential specification S if there exists a linearization (in the order-theoretic sense) of $\prec _H$ that belongs to S. The subtlety is the treatment of incomplete calls, which may or may not have taken effect. We write $\textsf{compl}(H)$ for the set of histories obtained from a history $H$ by appending zero or more matching return events. We write $\textsf{trunc}(H)$ for the history obtained from $H$ by removing its incomplete calls. We can then define linearizability as follows [14].

Definition 6

A sequential history $H_\ell$ is a sequentialization of a history $H$ if there exists $H' \in \textsf{trunc}(\textsf{compl}(H))$ such that $H_\ell$ is a linearization of $\prec _{H'}$. A history $H$ is linearizable under S if there exists a sequentialization of $H$ that belongs to S. A library $\textsf{L}$ is linearizable under S if all its consistent histories are linearizable under S.

For instance, we can specify the notion of linearizable queues as those that linearizable under the following sequential queue specification, $S_\textsf {Queue}$.

Example 2

(Sequential queue specification). The behaviors of a sequential queue, $S_\textsf {Queue}$, is expressed as a set of sequential histories as follows. Given a history $H$ of $L_\textsf {Queue}$ and a location $x \in \textbf{Loc}$, let $H[x]$ denote the sub-history containing calls c such that $\textrm{loc}(c) = \{x\}$. We define $S_\textsf {Queue}$ as the set of all sequential histories $H$ of $L_\textsf {Queue}$ such that for all $x \in \textbf{Loc}$, $H[x]$ is of the form $\textsf{QueueNew}()_{\textsf{t}_0}{:}{x} \; e_1 \; \cdots \; e_n$, where each $\textsf{QueueDeq}$ call in $e_1 \; \cdots \; e_n$ returns the value of the k-th $\textsf{QueueEnq}$ call, if it exists and precedes the $\textsf{QueueDeq}$, where k is the number of preceding $\textsf{QueueDeq}$ calls returning non-null values; otherwise, it returns null.

2.4 Adding Failures

Our framework so far does not support reasoning about persistency as it lacks the ability to describe the persistent state of a library after a failure. Our first extension is thus to extend the set of events of a collection, $\textbf{Events}(\varLambda )$, with another type of event, a crash event .

Crash events allow us to specify the durability guarantees of a library. For instance, a library that does not persist any of its data may specify that a history with crash events is consistent if all of its sub-histories between crashes are (independently) consistent. In other words, in such a library, the method calls before a crash have no effect on the consistency of the history after the crash. We modify the definition of happens-before accordingly by treating it both as an invocation and a return event. We also assume that, after a crash, the thread ids of the new threads are distinct from that of all the pre-crash threads. For libraries that do persist their data, a useful generic specification is durable linearizability [17], defined as follows.

Definition 7

Given a history $H$, let $\textsf{ops}(H)$ denote the sub-history obtained from $H$ by removing all its crash markers. A history $H$ is durably linearizable under S if there exists a sequentialization $H_\ell$ of $\textsf{ops}(H)$ such that $H_\ell \in S$.

Intuitively, this ensures that operations persist before they return, and they persist in the same order as they take effect before a crash.

Although durable linearizability can specify a large range of persistent data-structures, it can be too strong. For example, consider a (memory) register library $\textsf{L}_{\textsf {wreg}}$ that only guarantees that writes to the same location are persisted in the order they are observed by concurrent reads. The $\textsf{L}_{\textsf {wreg}}$ methods comprise $\textsf{RegNew}()$ to allocate a new register, $\textsf{RegWrite}(x, v)$ to write v to register x, and $\textsf{RegRead}(x)$ to read from register x. The sequential specification $S_{\textsf {wreg}}$ is simple: once a register is allocated, a read R on x returns the latest value written to x, or 0 if R happens before all writes. The associated durable linearizability specification requires that writes be persisted in the linearization order; however, this is often not the case on existing hardware, e.g. in (the Intel-x86 persistency model) [30].

A more relaxed and realistic specification would consider two linearizations of the events: the standard volatile order $\prec$ and a persistent order  expressing the order in which events are persisted. The next sections will handle this more refined model, this paragraph only gives a quick tastes of the kind of models that are implemented by hardware. To capture the same-location guarantees, we stipulate a per-location ordering on writes that is respected by both linearizations. Specifically, we require an ordering  of the write calls such that for all locations x: 1) restricting to x, written , totally orders writes to x; and 2) and . Given a history $H$, we can then combine these two linearizations by using $\prec$ after the last crash and before.

Formally, a history $H$ with $n{-}1$ crashes can be decomposed into n (crash-free) eras; i.e. where each $H_i$ is crash-free. Let us write $\prec _i$ for $\prec \cap (H_i \times H_i)$ and so forth. We then consider k-sequentializations of the form $H^k_\ell = H_\ell ^{(1)} \cdots H_\ell ^{(k-1)} \cdot H_\ell ^{(k)}$, where $H_\ell ^{(k)}$ is a sequentialization of $E_k$ w.r.t. $\prec _k$ and $H^{(i)}_\ell$ is a sequentialization of $E_i$ w.r.t. , for $i<k$. We can now specify our weak register library as follows, where $H$ comprises n eras:

$$\begin{aligned} H\in \textsf{L}_{\textsf {wreg}}{.}\mathcal {S}_{\textsf {c}}\iff \forall k \le n.\;\exists H^k_\ell k\text { -seq. of } H.\; H^k_\ell \in S_{\textsf {wreg}}\end{aligned}$$

Example 3

The following history is valid according to this specification but not according to the durably linearizable one:

While the writes to x ($W_{\textsf{t}_1}(x, 1)$) and y ($W_{\textsf{t}_2}(y, 1)$) are executing, thread $\textsf{t}_3$ observes the new value (1) of y but the old value (0) of x; i.e. $\prec$ must order $W_{\textsf{t}_2}(y, 1)$ before $W_{\textsf{t}_1}(x, 1)$. By contrast, after the crash the new value (1) of x but the old value of y (0) is visible; i.e. must order the two writes in the opposite order to $\prec$ ($W_{\textsf{t}_1}(x, 1)$ before $W_{\textsf{t}_2}(y, 1)$).

Persist Instructions. The persistent registers described above are too weak to be practical, as there is no way to control how writes to different locations are persisted. In realistic hardware models such as , this control is afforded to the programmer using per-location persist instructions (e.g. CLFLUSH), ensuring that all writes on a location x persist before a write-back on x. Here, we consider a coarser (stronger) variant, denoted by , that ensures that all writes (on all locations) that happen before a are persisted. Later in §3 we describe how to specify the behavior of per-location persist operations.

Formally, we specify by extending the specification of $\textsf{L}_{\textsf {wreg}}$ as follows: given history $H$, write call $c_w$ and event $c_f$, if $c_w \prec _Hc_f$, then .

Example 4

Consider the history obtained from example 3 by adding a :

This history is no longer consistent according to the extended specification of $\textsf{L}_{\textsf {wreg}}$: as has completed (returned), all its $\prec$-previous writes must have persisted and thus must be visible after the crash (which is not the case for $W_{t_2}(y,1)$).

2.5 Adding Well-formedness Constraints

Our next extension is to allow library specifications to constrain the usage of the library methods by the client of the library. For example, a library for a mutual exclusion lock may require that the “release lock” method is only called by a thread that previously acquired the lock and has not released it in between. Another example is a transactional library, which may require that transactional read and write methods are only called within transactions, i.e. between a “transaction-begin” and a “transaction-end” method call.

We call such constraints library well-formedness constraints, and extend the library specifications with another component, $\mathcal {S}_{\textsf {wf}}\subseteq \textbf{Hist}(L)$, which records the set of well-formed histories of the library. Ensuring that a program produces only well-formed histories of a certain library is an obligation of the clients of that library, so that the library implementation can rely upon well-formedness being satisfied.

2.6 Tags and Global Specifications

The goal of our framework is not only to specify libraries in isolation, but also to express how a library can enforce persistency guarantees across other libraries. For example, consider a library $\textsf{L}_{\textsf {trans}}$ for persistent transactions, where all operations wrapped within a transaction persist together atomically; i.e. either all or none of the operations in a transaction persist.

The $\textsf{L}_{\textsf {trans}}$ methods are: to allocate a register that can be accessed (read/written) within a transaction; and to start and end a transaction, respectively; and to read from and write to $\textsf{L}_{\textsf {trans}}$ register , respectively; and to restore the atomicity of transactions whose histories were interrupted by a crash.

Consider the snippet below, where the (enqueuing into persistent queue ) and (adding to persistent set ) are wrapped within an $\textsf{L}_{\textsf {trans}}$ transaction and thus should take effect atomically and at the latest after the end of the call to .

Such guarantees are not offered by existing hardware primitives e.g. on Intel-x86 or ARMv8 [30, 31] architectures. As such, to ensure atomicity, the persistent queue and set implementations cannot directly use hardware reads/writes; rather, they must use those provided by the transactional library whose implementation could use e.g. an undo-log to provide atomicity.

Our framework as described so far cannot express such cross-library persistency guarantees. The difficulty is that the transactional library relies on other libraries using certain primitives. This, however, is against the spirit of compositional specification, which precludes the transactional library from referring to other libraries (e.g. the queue or set libraries). Specifically, there are two challenges. First, both well-formedness requirements and consistency guarantees of $\textsf{L}_{\textsf {trans}}$ must apply to any method call that is designed to use (transitively) the primitives of $\textsf{L}_{\textsf {trans}}$. Second, we must formally express atomicity (“all operations persist atomically”), without $\textsf{L}_{\textsf {trans}}$ knowing what it means for a method of an arbitrary library to persist. In other words, $\textsf{L}_{\textsf {trans}}$ needs to introduce an abstract notion of ‘having persisted’ for an operation, and guarantee that all methods in a transaction ‘persist’ atomically.

To remedy this, we introduce the notion of tags. Specifically, to address the first challenge, the transactional library provides the tag $\textsc {t}$ to designate those operations that are ‘transaction-aware’ and as such must be used inside a transaction. To address the second challenge, the transaction library provides the tag $\textsc {p} ^{\textsf{tr}}$, denoting an operation that has abstractly persisted. The specification of $\textsf{L}_{\textsf {trans}}$ then guarantees that all operations tagged with $\textsc {t}$ inside a transaction persist atomically, in that either they are all tagged with $\textsc {p} ^{\textsf{tr}}$ of none of them are. Dually, using the well-formedness condition, $\textsf{L}_{\textsf {trans}}$ requires that all operations tagged with $\textsc {t}$ appear inside a transaction. Note that as the persistent queue and set libraries tag their operations with $\textsc {t}$, verifying their implementations incurs related proof obligations; we will revisit this later when we formalize the notion of library implementations.

Remark 1 (Why bespoke persistency?)

The reader may question why ‘having persisted’ is not a primitive notion in our framework, as in an existing model of  [19] where histories track the set P of persisted events. This is because associating a Boolean (‘having persisted’) flag with an operation may not be sufficient to describe whether it has persisted. To see this, consider a library $\textsf{L}_{\textsf {pair}}$ with operations $\textsf{Write}(x, l, r)$ (writing (l, r) to pair x), $\textsf{Readl}(x)$ and $\textsf{Readr}(x)$ (reading the left and right components of x, respectively). Suppose $\textsf{L}_{\textsf {pair}}$ is implemented by storing the left component in an $\textsf{L}_{\textsf {trans}}$ register and the right component in a  $\textsf{L}_{\textsf {wreg}}$ register. The specification of $\textsf{L}_{\textsf {pair}}$ would need to track the persistence of each component separately, and hence a single set P of persisted events would not suffice.

Let us see how libraries can use these tags in global well-formedness and consistency specifications. The dilemma is, on the one hand, the specification of $\textsf{L}_{\textsf {trans}}$ needs to refer to events from other libraries, but on the other hand, it should not depend on other libraries to preserve encapsulation. Our idea is to anonymize these external events such that the global specification depends only on their relevant tags. A library should only rely on the tags it introduces itself, as well as the tags of the libraries it uses.

We now revisit several of our definitions to account for tags and global specifications. A library interface now additionally holds the tags it introduces as well as those it uses. For instance, the $\textsf{L}_{\textsf {trans}}$ library described above depends on no tag and introduces tags $\textsc {t}$ and $\textsc {p} ^{\textsf{tr}}$.

Definition 8

(Interfaces). An interface is a tuple $L= \langle \mathcal {M}, \mathcal {M}_\textrm{c}, \textrm{loc}, \textsc {Tags}_{\textrm{new}}, \textsc {Tags}_{\textrm{dep}} \rangle$, where $\mathcal {M}$, $\mathcal {M}_\textrm{c}$, and $\textrm{loc}$ are as in Def. 1, $\textsc {Tags}_{\textrm{new}}$ is the set of tags $L$ introduces, and $\textsc {Tags}_{\textrm{dep}}$ is the set of tags $L$ uses. The set of tags usable by $L$ is $\textsc {Tags}(L) \triangleq L{.}\textsc {Tags}_{\textrm{new}}\cup L{.}\textsc {Tags}_{\textrm{dep}}$.

We next define the notion of tagged method invocations (where a method invocation is associated with a set of tags). Hereafter, our notions of events, history (and so forth) use tagged method invocations (rather than methods invocations).

Definition 9

Given a library interface $L$, a tagged method invocation is of the form ${m}(\vec{v})^{T}_{\textsf{t}}{:}\,{{v_\bot }}$, where the new component is a set of tags $T \subseteq \textsc {Tags}(L)$.

A global specification of a library interface $L$ is a set of histories with some “anonymized” events. These are formalized using a designated library interface, $\star _{L}$ (with a single method $\star$), which can be tagged with any tag from $\textsc {Tags}(L)$.

Definition 10

Given an interface $L$, the interface $\star _{L}$ is $\langle \{\star \}, \emptyset , \emptyset , \emptyset , \textsc {Tags}(L) \rangle$.

Now, given any history $H\in \textbf{Hist}(\{L\} \cup \varLambda )$, let $\pi _{L}(H) \in \textbf{Hist}(\{L, \star _{L}\})$ denote the anonymization of $H$ such that each non-$\textsf{L}$ event e in $H$ labelled with a method ${m}(\vec{v})^{T}_{\textsf{t}}{:}\,{{v_\bot }}$ of $L' \in \varLambda$ is replaced with $\star ^T_\textsf{t}$ of $\star _{L}$ if $T\ne \emptyset$ and is discarded otherwise. It is then straightforward to extend the notion of libraries with global specifications as follows.

Definition 11

A library specification $\textsf{L}$ is a tuple $\langle L, \varLambda _{\textrm{tags}}, \mathcal {S}_{\textsf {c}}, \mathcal {S}_{\textsf {wf}}, \mathcal {T}_{\textsf {c}}, \mathcal {T}_{\textsf {wf}} \rangle$, where $L$, $\mathcal {S}_{\textsf {c}}$ and $\mathcal {S}_{\textsf {wf}}$ are as in Def. 4; $\mathcal {T}_{\textsf {c}}$ and $\mathcal {T}_{\textsf {wf}}\subseteq \textbf{Hist}(\{L, \star _{L}\})$ are the globally consistent and globally well-formed histories, respectively; and $\varLambda _{\textrm{tags}}$ denotes the tag-dependencies, i.e. a collection of libraries that provide all tags that $\textsf{L}$ uses: $L.\textsc {Tags}_{\textrm{dep}}\subseteq \bigcup _{\textsf{L}' \in \varLambda _{\textrm{tags}}} \textsf{L}'.\textsc {Tags}_{\textrm{new}}$. Both $\mathcal {T}_{\textsf {wf}}$ and $\mathcal {T}_{\textsf {c}}$ contain the empty history.

In the context of a history, we write $\lfloor \textsc {t} \rfloor$ for the set of events or calls tagged with the tag $\textsc {t}$ (we consider a return event tagged the same way as its unique matching invocation).

For the $\textsf{L}_{\textsf {trans}}$ library, the globally well-formed set $\textsf{L}_{\textsf {trans}}{.}\mathcal {T}_{\textsf {wf}}$ comprises histories $H$ such that for each thread $\textsf{t}$, $E[\textsf{t}]$ restricted to PTBegin, PTEnd and events of the form $\textsc {t}$-tagged events is of the form described by the regular expression $(\textsf {PTBegin}.\lfloor \textsc {t} \rfloor \!{}^*. \textsf {PTEnd})^*$. In particular, transaction nesting is disallowed in our simple $\textsf{L}_{\textsf {trans}}$ library.

To define global consistency, we need to know when two operations are part of the same transaction. Given a history $H$, we define the same-transaction relation, , relating pairs of $e, e' \in \lfloor \textsc {t} \rfloor \cup \textsf {PTEnd} \cup \textsf {PTBegin}$ executed by the same thread $\textsf{t}$ such that there is no $\textsf {PTBegin}$ or $\textsf {PTEnd}$ executed by $\textsf{t}$ between them. The set $\textsf{L}_{\textsf {trans}}{.}\mathcal {T}_{\textsf {c}}$ of globally consistent histories contains histories $H$ such that , and all completed $\textsf {PTEnd}$ calls are in $\lfloor \textsc {p} ^{\textsf{tr}}\rfloor$. Since the PTEnd call is related to all events inside its transaction, this specification does express that (1) a transaction persist by the time the call to PTEnd finishes and (2) all events persist atomically.

Finally, we need to define the local consistency predicate $\textsf{L}_{\textsf {trans}}.\mathcal {S}_{\textsf {c}}$ describing the behavior of the registers provided by $\textsf{L}_{\textsf {trans}}$. This is where the we define the concrete meaning of ‘having persisted’ for these registers. Let S be the sequential specification of a register. Let $H\in \textbf{Hist}(\textsf{L}_{\textsf {trans}})$ be a history decomposed into k eras as . Then $H\in \textsf{L}_{\textsf {trans}}.\mathcal {S}_{\textsf {c}}$ iff all events are tagged with $\textsc {t}$, and there exists a $\prec$-linearization $H_\ell$ of such that $H_\ell \in S$, where $\lfloor \textsc {p} ^{\textsf{tr}}\rfloor$ is the set of events of $H$ tagged with $\textsc {p} ^{\textsf{tr}}$. In other words, a write operation is seen after a crash iff it has persisted. The requirement that such operations must appear within transactions and the guarantee that they persist at the same time in a transaction are covered by the global specifications.

2.7 Library Implementations

We have described how to specify persistent libraries in our framework, and next describe how to implement persistent libraries. This is formalized by the judgment $\varLambda \vdash I : \textsf{L}$, stating that I is a correct implementation of library $\textsf{L}$ and only uses calls in the collection of libraries $\varLambda$. As usual in such ‘layered’ frameworks [13, 26], the base layer, which represents the primitives of the hardware, is specified as a library, keeping the framework uniform. This judgement can be composed vertically as follows, where $I[I_L]$ denotes replacing the calls to library $\textsf{L}$ in $I$ with their implementations given by $I_L$ (which in turn calls libraries $\varLambda '$):

As we describe later, this judgment denotes contextual refinement and is impractical to prove directly. We define a stronger notion that is compositional and more practical to use.

Definition 12

(Implementation). Given a collection $\varLambda$ of libraries and a library $\textsf{L}$, an implementation $I$ of $\textsf{L}$ over $\varLambda$ is a map, $I \;\;:\;\; \textsf{L}{.}\mathcal {M}\times \textbf{Val}_\bot \;\;\longrightarrow \;\; \mathcal {P}(\textbf{Hist}(\varLambda ))$, such that it is downward-closed: 1) if $H\in I(m(\vec{v})_\textsf{t}, {v_\bot })$ and $H'$ is a prefix of $H$, then $H' \in I(m(\vec{v}), \bot )$; and 2) each $I(m(\vec{v})_{\textsf{t}}{:}{{v_\bot }})$ history only contain events by thread $\textsf{t}$.

Intuitively, $I(m(\vec{v}), {v_\bot })$ contains the histories corresponding to a call $m(\vec{v})$ with outcome ${v_\bot }$, where ${v_\bot }= \bot$ denotes that the call has not terminated yet and ${v_\bot }= v\in \textbf{Val}$ denotes the return value. Downward-closure means that an implementation contains all partial histories. We use a concrete programming language to write these implementations; its syntax and semantics are standard and given in the appendix [34].

Fig. 1.

Implementation of $\textsf{L}_{\textsf {trans}}$

For example, the implementation of $\textsf{L}_{\textsf {trans}}$ over $\textsf{L}_{\textsf {wreg}}$ and $\textsf{L}_\textsf {Queue}$ is given in Fig. 1. The idea is to keep an undo-log as a persistent queue that tracks the values of the variables before the transaction begins. At the end of a transaction, and after all its writes have persisted, we write the sentinel value to the log to indicate that the transaction was completed successfully. After a crash, the recovery routine returns the undo-log and undoes the operations of incomplete transactions by writing their previous values.

Histories and Implementations. An implementation I of $\textsf{L}$ over $\varLambda$ is correct if for all histories $H\in \textbf{Hist}(\{\textsf{L}\} \cup \varLambda ')$ that use library $\textsf{L}$ as well as those in $\varLambda '$, and all histories $H'$ obtained by replacing calls to $\textsf{L}$ methods with their implementation in I, if $H'$ is consistent, then so is $H$ (it satisfies the $\textsf{L}$ specification).

We define the action $H\cdot I$ of an implementation I on an abstract history $H$ in a ‘relational’ way: $H' \in H\cdot I$ when we can match each operation $m'(\vec{v})$ in $H'$ with some operation $f(m'(\vec{v}))$ in $H$ in such a way that the collection $f{}^{-1}(m(\vec{v})_{\textsf{t}}{:}{{v_\bot }})$ of operations corresponding to some call $m(\vec{v})_{\textsf{t}}{:}{{v_\bot }}$ in $H$ agrees with $I(m(\vec{v})_{\textsf{t}}{:}{{v_\bot }})$.

Definition 13

Let $I$ be an implementation of $\textsf{L}$ over $\varLambda$; let $H\in \textbf{Hist}(\{\textsf{L}\} \cup \varLambda ')$ and $H' \in \textbf{Hist}(\varLambda \cup \varLambda ')$ be two histories. Given a map $f: \{1, \ldots , | H' |\} \rightarrow \{1, \ldots , | H | \}$, $H'$ (I, f)-matches $H$ if the following hold:

• 1. f is surjective;

• 2. for all invocations of $H$, if $m(\vec{v})_\textsf{t}\notin \textsf{L}{.}\mathcal {M}$, then $f(m(\vec{v})_\textsf{t}) = m(\vec{v})_\textsf{t}$;

• 3. for all threads $\textsf{t}$, if $e_1$ precedes $e_2$ in $H'[\textsf{t}]$, then $f(e_1)$ precedes $f(e_2)$ in $H[\textsf{t}]$;

• 4. for all calls $m(\vec{v})_{\textsf{t}}{:}{{v_\bot }}$ of $H$, the set $f{}^{-1}(m(\vec{v})_\textsf{t})$ corresponds to a substring $H'_m$ of $H'[\textsf{t}]$ and $H'_m \in I(m(\vec{v})_{\textsf{t}}{:}{{v_\bot }})$, where ${v_\bot }$ is the (optional) return value of $m(\vec{v})_\textsf{t}$ in $H$.

The action of $I$ on a history $H$ is defined as follows:

$$ H\cdot I\triangleq \{ H' \mid \exists f.\;{H' (I,f)\text {-matches } H} \}. $$

Condition 1 ensures that all events of the abstract history are matched with an implementation event; condition 2 ensures that the events that do not belong to the library being implemented ($\textsf{L}$) are left untouched, and condition 3 ensures that the thread-local order of events in the implementation agrees with the one in the specification. The last condition (4) states that the events corresponding to the implementation of a call $m(\vec{v})$ are consecutive in the history of the executing thread $\textsf{t}$, and correspond to the implementation $I$.

Well-formedness and Consistency. Recall that libraries specify both how they should be used (well-formedness), and what they guarantee if used correctly (consistency). Using these specifications (expressed as sets of histories) to define implementation correctness is more subtle than one might expect. Specifically, if we view a program using a library $\textsf{L}$ as a downward-closed set of histories in $\textbf{Hist}(\textsf{L})$, we cannot assume all its histories are in the set $\textsf{L}{.}\mathcal {S}_{\textsf {wf}}$ of well-formed histories, as the semantics of the program will contain unreachable traces (see [26]). To formalize reachability at a semantic level, we define hereditary consistency, stating that each step in the history was consistent, and thus the current ‘state’ is reachable.

Definition 14

(Consistency). History $H\!\in \! \textbf{Hist}(\varLambda )$ is consistent if for all $\textsf{L}\!\in \! \varLambda$, $H[\textsf{L}] \!\in \! \textsf{L}{.}\mathcal {S}_{\textsf {c}}$ and $\pi _{\textsf{L}}(H) \!\in \! \textsf{L}{.}\mathcal {T}_{\textsf {c}}$. It is hereditarily consistent if all $H[1..k]$ are consistent, for $k \le | H |$.

This definition uses the ‘anonymization’ operator $\pi _{\textsf{L}}$ defined in §2.6 to test that the history $H$ follows the global consistency predicates of every $\textsf{L}\in \varLambda$.

We further require that programs using libraries respect encapsulation, defined below, stating that locations obtained from a library constructor are only used by that library instance. Specifically, the first condition ensures that distinct constructor calls return distinct locations. The second condition ensures that a non-constructor call e of $\textsf{L}$ uses locations that have been allocated by an earlier call c ($c \prec e$) to an $\textsf{L}$ constructor.

Definition 15

(Encapsulation). A history $H\in \textbf{Hist}(\varLambda )$ is encapsulated if the following hold, where C denotes the set of calls to constructors in $H$:

• 1. for all $c, c' \in C$, if $c \ne c'$, then $\textrm{loc}(c) \cap \textrm{loc}(c') = \emptyset$;

• 2. for all $e \in H\setminus C$, if $\textrm{loc}(e) \ne \emptyset$, then there exist $c \in C$, $\textsf{L}\in \varLambda$ such that $e, c \in \textsf{L}.\mathcal {M}$, $c \prec e$ and $\textrm{loc}(e) \subseteq \textrm{loc}(c)$.

We can now define when a history of $\varLambda$ is immediately well-formed: it must be encapsulated and be well-formed according to each library in $\varLambda$ and all the tags it uses.

Definition 16

History $H\in \textbf{Hist}(\varLambda )$ is immediately well-formed if the following hold:

• 1. $H$ is encapsulated;

• 2. $H[\textsf{L}] \in \textsf{L}{.}\mathcal {S}_{\textsf {wf}}$, for all $\textsf{L}\in \varLambda$; and

• 3. $\pi _{\textsf{L}}(H) \in \textsf{L}{.}\mathcal {T}_{\textsf {wf}}$ for all $\textsf{L}\in \textsf{TagDep}(\varLambda )$, where the immediate dependencies $\textsf{TagDep}(\varLambda )$ is defined as $\bigcup _{\textsf{L}\in \varLambda } \{ \textsf{L}\} \cup \varLambda _{\textrm{tags}}(\textsf{L})$.

We finally have the notions required to define a correct implementation.

Implementation Correctness. As usual, an implementation is correct if all behaviors of the implementation are allowed by the specification. In our setting, this means that if a concrete history is hereditarily consistent, so should the abstract history. Moreover, assuming the abstract history is well-formed, all corresponding concrete histories should also be well-formed; this corresponds to the requirement that the library implementation uses its dependencies correctly, under the assumption that the program itself uses its libraries correctly.

Definition 17

(Correct implementation). An implementation $I$ of $\textsf{L}$ over $\varLambda$ is correct, written $\varLambda \vdash I : \textsf{L}$, if for all collections $\varLambda '$, all ‘abstract’ histories $H\in \textbf{Hist}(\{\textsf{L}\} \cup \varLambda ')$ and all ‘concrete’ histories $H' \in H\cdot I\subseteq \textbf{Hist}(\varLambda \cup \varLambda ')$, the following hold:

• 1. if $H$ is immediately well-formed, then $H'$ is also immediately well-formed; and

• 2. if $H'$ is immediately well-formed and hereditarily consistent, then $H$ is consistent.

This definition is similar to contextual refinement in that it quantifies over all contexts: it considers histories that use arbitrary libraries as well as those that concern $I$ directly. We now present a more convenient, compositional method for proving an implementation correct, which allows one to only consider libraries and tags that are used by the implemented library.

2.8 Compositionally Proving Implementation Correctness

Recall that in this section we present our framework in a simplified sequentially consistent setting; later in §3 we generalize our framework to the weak memory setting. We introduce the notion of compositional correctness, simplifying the global correctness conditions in Def. 17. Specifically, while Def. 17 considers histories with arbitrary libraries that may use tags introduced by $\textsf{L}$, our compositional condition requires one to prove that only those $\textsf{L}$ methods that are $\textsf{L}$-tagged satisfy $\textsf{L}.\mathcal {T}_{\textsf {c}}$.

Definition 18

(Compositional correctness). An implementation $I$ of $\textsf{L}$ over $\varLambda$ is compositionally correct if the following hold:

• 1. For all $\varLambda '$, $H\in \textbf{Hist}(\{\textsf{L}\} \cup \varLambda )$ and $H' \in H\cdot I\subseteq \textbf{Hist}(\varLambda \cup \varLambda ')$, if $H'$ is well-formed, then $H$ is well-formed;

• 2. For all $H\in \textbf{Hist}(\textsf{L})$ and $H' \in H\cdot I\subseteq \textbf{Hist}(\varLambda )$, if $H'$ is well-formed and hereditarily consistent, then $H\in \textsf{L}.\mathcal {S}_{\textsf {c}}\cap \textsf{L}.\mathcal {T}_{\textsf {c}}$; and

• 3. For all $\textsf{L}' \in \varLambda$, $H\in \textbf{Hist}(\{\textsf{L}, \textsf{L}', \star _{\textsf{L}'}\})$ and $H' \in H\cdot I$, if $\pi _{\textsf{L}'}(H') \in \textsf{L}'.\mathcal {T}_{\textsf {wf}}\cap \textsf{L}'.\mathcal {T}_{\textsf {c}}$, then $\pi _{\textsf{L}'}(H) \in \textsf{L}'.\mathcal {T}_{\textsf {c}}$.

The preservation of well-formedness (condition 1) does not change compared to its counterpart in Def. 17, as in practice this condition is easy to prove directly. Condition 2 requires one to prove that the implementation is correct in isolation (without $\varLambda '$). Condition 3 requires one to prove that global consistency requirements are maintained for all dependencies of the implementation. In practice, this corresponds to proving that those $\textsf{L}$ operations tagged with existing tags in $\varLambda$ obey the global specifications associated with these tags. Intuitively, the onus is on the library that uses a tag for its methods to prove the associated global consistency predicate: we need not consider unknown methods tagged with tags in $\textsf{L}.\textsc {Tags}_{\textrm{new}}$.

Finally, we show that it is sufficient to show an implementation $I$ is compositionally correct as it implies that $I$ is correct.

Theorem 1 (Correctness)

If an implementation $I$ of $\textsf{L}$ over $\varLambda$ is compositionally correct (Def. 18), then it is also correct (Def. 17).

Example 5

(Transactional Library ). Consider the implementation $I_{\textsf {trans}}$ of $\textsf{L}_{\textsf {trans}}$ over $\varLambda = \{\textsf{L}_{\textsf {wreg}}, \textsf{L}_\textsf {Queue} \}$ given in Fig. 1, and let us assume we were to show that $I_{\textsf {trans}}$ is compositionally correct. Our aim here is only to outline the proof obligations that must be discharged; later in §5 we give a full proof in the more general weak memory setting.

• 1. For the first condition of compositional correctness, we must show $I_{\textsf {trans}}$ preserves well-formedness: if the abstract history $H$ is well-formed, then so is any corresponding concrete history $H' \in H\cdot I_{\textsf {trans}}$. This is straightforward as the well-formedness conditions of $\textsf{L}_{\textsf {wreg}}$ and $\textsf{L}_\textsf {Queue}$ are trivial, and $\textsf{L}_{\textsf {trans}}$ does not use any existing tag.

• 2. For the second condition of compositional correctness, we must show that $I_{\textsf {trans}}$ preserves consistency in the other direction: keeping the notations as above, assuming $H'$ is consistent for $\varLambda$, then $H$ is consistent as specified by $\textsf{L}_{\textsf {trans}}$. There are two parts to this obligation, as we also have to show that the $\textsf{L}_{\textsf {trans}}$’s operations tagged with $\textsc {t}$ satisfy the global consistency predicate of the library.

• 3. The last condition holds vacuously as $\textsf{L}_{\textsf {trans}}$ does not use any existing tags.

Example 6

(A Client of $\textsf{L}_{\textsf {trans}}$). To see how the global consistency specifications work, consider a simple min-max counter library, $\textsf{L}_\textsf{mmcnt}$, tracking the maximal and minimal integer it has been given. The $\textsf{L}_\textsf{mmcnt}$ is to be used within $\textsf{L}_{\textsf {trans}}$ transactions, and provides four methods: $\texttt {mmNew}()$ to construct a min-max counter, $\texttt {mmAdd}(x, n)$, to add integer n to the min-max counter, and $\texttt {mmMin}(x)$ and $\texttt {mmMax}(x)$ to read the respective values.

We present the $I_\textsf{mmcnt}$ implementation over $\textsf{L}_{\textsf {trans}}$ in Fig. 2.

Fig. 2.

Implementation $I_\textsf{mmcnt}$ of $\textsf{L}_\textsf{mmcnt}$

The idea is simply to track two integers denoting the minimal and maximal values of the numbers that have been added. Interestingly, even though they are stored in $\textsf{L}_{\textsf {trans}}$ registers, the implementation does not begin or end transactions: this is the responsibility of the client to avoid nesting transactions. This is enforced by $\textsf{L}_\textsf{mmcnt}$ using a global well-formedness predicate. Moreover, the $\texttt {mmAdd}$ operation is tagged with $\textsc {t}$ from the $\textsf{L}_{\textsf {trans}}$ library, ensuring that it behaves well w.r.t. transactions. A non-example is a version of $I_\textsf{mmcnt}$ where the minimum is in a $\textsf{L}_{\textsf {trans}}$ register, but the max is in a “normal” $\textsf{L}_{\textsf {wreg}}$ register. This breaks the atomicity guarantee of transactions.

Formally, the interface $L_\textsf{mmcnt}$ has four methods as above, where $\texttt {mmNew}$ is the only constructor. The set of used tags is $\textsc {Tags}_{\textrm{dep}}= \{ \textsc {t}, \textsc {p} ^{\textsf{tr}}\}$, and all $L_\textsf{mmcnt}$ methods are tagged with $\textsc {t}$ as they all use primitives from $\textsf{L}_{\textsf {trans}}$. The consistency predicate is defined using the obvious sequential specification $S_\textsf{mmcnt}$, which states that calls to $\texttt {mmMin}$ return the minimum of all integers previously given to $\texttt {mmAdd}$ in the sequential history. We lift this to (concurrent) histories as follows. A history $H\in \textbf{Hist}(\textsf{L}_\textsf{mmcnt})$ is in $\textsf{L}_\textsf{mmcnt}.\mathcal {S}_{\textsf {c}}$ if there exists $E_\ell \in S_\textsf{mmcnt}$ that is a $\prec$-linearization of $E_1[\textsc {p} ^{\textsf{tr}}] \cdot E_2[\textsc {p} ^{\textsf{tr}}] \cdots E_{n-1} \cdot E_n[\textsc {p} ^{\textsf{tr}}]$, where $H$ constructs n eras decomposed as (recall that $E[\textsc {p} ^{\textsf{tr}}]$ denotes the sub-history with events tagged with $\textsc {p} ^{\textsf{tr}}$, that is, persisted events.). The global specification and well-formedness conditions of $\textsf{L}_\textsf{mmcnt}$ are trivial. Because $\textsf{L}_\textsf{mmcnt}$ uses tag $\textsc {t}$ of $\textsf{L}_{\textsf {trans}}$, a well-formed history of $\textsf{L}_\textsf{mmcnt}$ must satisfy $\textsf{L}_{\textsf {trans}}.\mathcal {T}_{\textsf {wf}}$, which requires that all operations tagged with $\textsc {t}$ be inside transactions, and $\textsf{L}_{\textsf {trans}}.\mathcal {T}_{\textsf {c}}$ guarantees that $\textsf{L}_\textsf{mmcnt}$ operations persist atomically in a transaction.

When proving that the implementation in Figure 2 satisfies $\textsf{L}_\textsf{mmcnt}$ using compositional correctness, one proof obligation is to show that, given histories $H\in \textbf{Hist}(\{\textsf{L}_{\textsf {trans}}, \textsf{L}_\textsf{mmcnt}, \star _{\textsf{L}_{\textsf {trans}}}\})$ and $H' \in H\cdot I_\textsf{mmcnt}\subseteq \textbf{Hist}(\{\textsf{L}_{\textsf {trans}}, \star _{\textsf{L}_{\textsf {trans}}}\})$, if $\pi _{\textsf{L}_{\textsf {trans}}}(H') \in \textsf{L}_{\textsf {trans}}.\mathcal {T}_{\textsf {c}}$, then $\pi _{\textsf{L}_{\textsf {trans}}}(H) \in \textsf{L}_{\textsf {trans}}.\mathcal {T}_{\textsf {c}}$. This corresponds precisely to the fact that min-max counter operations persist atomically in a transaction, assuming the primitives it uses do as well.

2.9 Generic Durable Persistency Theorems

We consider another family of libraries with persistent reads/writes guaranteeing the following:

if one replaces regular (volatile) reads/writes in a linearizable implementation with persistent ones, then the implementation obtained is durably linearizable.

We consider two such such libraries: FliT  [35] and Mirror  [10]. Thanks to our framework, we formalise the statement above for the first time and prove it for both Flit and Mirror against a realistic consistency (concurrency) model (see §4).

3 Generalization to weak-memory

This section sketches how we generalize the framework presented in the previous section to the weak memory, where events generated by the program are not totally ordered. For lack of space, the technical details, which largely follow that of the previous section, are relegated to the Appendix [34]. The purpose of this section is to give an idea of how executions, a standard tool in the semantics of weak memory, generalize the histories we used in the Overview section, and to give enough context for the case studies that follow.

Fig. 3.

An execution of the program $\textsf{P}$: $a = x;\; y = 2 \parallel a = y;\; x = 5$

Unlike the histories that we discussed in the previous section, in which events are totally ordered by a notion of time, events in executions are only partially ordered, reflecting that instructions executed in parallel are not naturally ordered. Formally, an execution is thus a set of events equipped with a partial order which represents the ordering between events from the same thread. This partial order, written , for program-order, is depicted with black arrows in Fig. 3, where it orders minimally the initial event, and the two events of each thread according to the source code. Additional edges indicate, for each read-event returning the value v, the write-event that provided the value v: in that case, an -edge from the write-event to the read-event is added to the execution.

To be able to reason about synchronization, the notion of happens-before needs to be adapted to this setting. It is defined using and an additional type of edge, synchronizes-with, written , which denotes that two events synchronize with each other, and in particular that one happens before the other. Usually, , for example between a release-write and an acquire-read in the C11 memory model. Given these edges, the happens-before order they induce, which generalizes $\prec$ from the previous section is defined as the transitive closure . This is not sufficient however, because we consider partial executions G where the focus is on a subset of the libraries in some unknown global execution $G'$, that is: $G = G' \downharpoonleft {\textsf{L}}$. Therefore, external events (in $G'$ but not in G) may induce happens-before relations between events of G, yet we want to specify library $\textsf{L}$ without referring to any such execution $G'$ that contains it. To solve this issue, we use the technique of [26], and we add a final type of edge to executions: , which corresponds to both the external and the internal synchronization. Because of the latter, it must contain the internal synchronization: .

To summarize, an execution is a tuple comprised of a set E of events, and of the relations we just described. A library specification is the same as in the previous section, mutatis mutandis. The sets of executions that are parts of specifications are defined using a formalism developed in the weak memory model literature. A set $\mathcal S$ of executions is described with conditions about relations built from , , etc. Given a set V of events, we denote by [V] the relation $V \times V$, and we denote by $R_1; R_2$ the standard composition of two relations $R_1$ and $R_2$. For example, if R denotes the set of read-events of an execution and W the set of write-events, the condition states that if there is a -edges between two events $e_1 \in W$ and $e_2 \in R$ of an execution, there must also be a synchronization edge between $e_1$ and $e_2$.

As in the previous section, the tag system allows the library specification to state which events must have been persisted in a valid execution. The semantics of a program is a set of executions that contain events from all the libraries used by the program; and whose happens-before order satisfy , as there are no external synchronization in the executions of the whole program. The Appendix [34] details how our framework is defined in this more general setting.

4 Case Study: Durable Linearizability with FliT and Mirror

We consider a family of libraries that provide a simple interface with persistent memory accesses (reads and writes), allowing one to convert any linearisable implementation to a durably linearisable one by replacing regular (volatile) accesses with persistent ones supplied by the library. Specifically, we consider two such libraries FliT  [35] and Mirror  [10]; we specify them both in our framework, prove their implementations sound against their respective specifications, and further prove their general result for converting data structures.

4.1 The FliT Library

FliT [35] is a persistent library that provides a simple interface very close to , but with stronger persistency guarantees, which make it easier to implement durable data structures. Specifically, a FliT object $\ell$ can be accessed via write and read methods, $\texttt{wr}_{\pi }(\ell , v)$ and $\texttt{rd}_{\pi }(\ell )$, as well as standard read-modify-write methods. Each write (resp. read) operation has two variants, denoted by the type $\pi \in \{\textsf{p}, \textsf{v}\}$. This type specifies if the write (resp. read) is persistent ($\pi = \textsf{p}$) in that its effects must be persisted, or volatile ($\pi =\textsf{v}$) in that its persistency has been optimised and offers weaker guarantees. The default access type is persistent ($\textsf{p}$), and the volatile accesses may be used as optimizations when weaker guarantees suffice. Wei et al. [35] introduce a notion of dependency between different operations as follows. If a (persistent or volatile) write w depends on a persistent write $w'$, then $w'$ persists before w. If a persistent read r reads from a persistent write w, then r depends on w and thus w must be persisted upon reading if it has not already persisted. Though simple, FliT provides a strong guarantee as captured by a general result for correctly converting volatile data structures to persistent ones: if one replaces every memory access in the implementation of a linearizable data-structure with the corresponding persistent FliT access, then the resulting data structure is durably linearizable.

Fig. 4.

$\textsf {FliT}$ library implementation in

Compared to the original FliT development, our soundness proof is more formal and detailed: it is established against a formal specification (rather than an English description) and with respect to the formal model.

Interface. The FliT interface uses the  from  and contains a single constructor, new, allocating a new FliT location, as well as three other methods below, the last two of which are durable:

• $\texttt{rd}_{\pi }(\ell )$ with $\pi \!\in \! \{\textsf{p}, \textsf{v}\}$, for a $\pi$-read from $\ell$;

• $\texttt{wr}_{\pi }(\ell , v)$ with $\pi \!\in \! \{\textsf{p}, \textsf{v}\}$, denoting a $\pi$-write of value $v \in \textbf{Val}$ to $\ell$; and

• $\texttt {finishOp}$, which waits for previously executed operations to persist.

We write R and W respectively for the read and write events, and add the superscript $\pi$ (e.g. $R^{\textsf{p}}$) to denote such events with the given persistency mode.

Specification. We develop a formal specification of FliT in our framework, based on its original informal description. The correctness of FliT executions is described via a dependency relation that contains the program order and the total execution (linearization) order restricted to persistent write-read operations on the same location. Note that this dependency notion is stronger than the customary definitions that use a relation (as in the specification) instead of , because a persistent read may not read directly from a persistent write w, but rather from another later (-after w) write.

Definition 19

( execution Correctness). A FliT execution $\mathcal {G}$ is correct if there exists a ‘reads-from’ relation  and a total order on $\mathcal {G}.E$ and an order  such that:

• 1. Each read event reads from the most recent previous write to the same location:

  

• 2. Reads return the value written by the write they read from:

  

• 3. Persistent writes persist before every other later dependent write:

  

• 4. Persistent writes before a $\texttt {finishOp}$ persist:

  

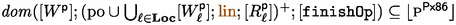
• 5. And is a persist order: .

implementation of . The implementation of FliT methods is given in Fig. 4. Whereas a naive implementation of this interface would have to issue a flush instruction both after persistent writes and in persistent reads, the implementation shown associates each location with a counter to avoid performing superfluous flushes when reading from a location whose value has already persisted. Specifically, a persistent write on $\ell$ increments its counter before writing to and flushing it, and decrements the counter afterwards. As such, persistent reads only need to issue a flush if the counter is positive (i.e. if there is a concurrent write that has not executed its flush yet).

Theorem 2

The implementation of FliT in Fig. 4 is correct.

and Durable Linearizability. Given a data structure implementation I, let p(I) denote the implementation obtained from I by 1) replacing reads/writes in the implementation with their corresponding persistent FliT instructions, and 2) adding a call to $\texttt {finishOp}$ right before the end of each method. We then show that given an implementation I, if I is linearizable, then p(I) is durably linearizable¹. We assume that all method implementations are single-threaded, i.e. all plain executions $I(m(\vec{v}))$ are totally ordered.

Theorem 3

If , then $\textsf {FliT} \vDash p(I) : \textsf {DurLin}(S)$.

4.2 The Mirror Library

The Mirror [10] persistent library has similar goals to FliT. The main difference between the two is that Mirror operations do not offer two variants, and their operations are implemented differently from those of FliT. Specifically, in Mirror each location has two copies: one in persistent memory to ensure durability, and one in volatile memory for fast access. As such, read operations are implemented as simple loads from volatile memory, while writes have a more involved implementation than those of FliT.

We present the Mirror specification and implementation in the technical appendix where we also prove that its implementation is correct against its specification. As with FliT, we further prove that Mirror can be used to convert linearizable data structures to durably linearizable ones, as described above.

5 Case Study: Persistent Transactional Library

We revisit the $\textsf{L}_{\textsf {trans}}$ transactional library, develop its formal specification and verify its implementation (Fig. 1) against it. Recall the simple $\textsf{L}_{\textsf {trans}}$ implementation in Fig. 1 and that we do not allow for nested transactions. The implementation uses an undo-log which records the former values of persistent registers (locations) modified in a transaction. If, after a crash, the recovery mechanism detects a partially persisted transaction (i.e. the last entry in the undo log is not ), then it can use the undo-log to restore registers to their former values. The implementation uses a durably linearizable queue library² $\textsf {Q}$, and assumes that it is externally synchronized: the user is responsible for ensuring no two transactions are executed in parallel. We formalize this using a global well-formedness condition.

Later in §5.2 we develop a wrapper library $\textsf{L}_{\textsf {Strans}}$ for $\textsf{L}_{\textsf {trans}}$ that additionally provides synchronization using locks and prove that our implementation of this library is correct. To do this, we need to make small modifications to the structure of the specification: the specification in §2 requires that any ‘transaction-aware operation’ (i.e. those tagged with $\textsc {t}$) be enclosed in calls to $\texttt {PTBegin}$ and $\texttt {PTEnd}$. Since $\textsf{L}_{\textsf {Strans}}$ wraps the calls to $\texttt {PTBegin}$ and $\texttt {PTEnd}$, the well-formedness condition needs to be generalized to allow operations tagged with $\textsc {t}$ to appear between calls to operations that behave like $\texttt {PTBegin}$ and $\texttt {PTEnd}$. To that end, we add two new tags $\textsc {b}$ and $\textsc {e}$ to denote such operations, respectively.

5.1 Specification

The $\textsf{L}_{\textsf {trans}}$ library provides four tags: 1) $\textsc {t}$ for transaction-aware ‘client’ operations; 2) $\textsc {p} ^{\textsf{tr}}$ for operations that have persisted using transactions; and 3) $\textsc {b}, \textsc {e}$ for operations that begin and end transactions, respectively. We write $\mathcal {R}, \mathcal {W}, \mathcal {B}, \mathcal {E}, \mathcal{R}\mathcal{C}$ respectively for the sets of events labeled with read, write, begin, end and recovery methods. As before, we write e.g. $\lfloor \textsc {t} \rfloor$ for the set of events tagged with $\textsc {t}$. Note that while $\mathcal {B}$ denotes the set of the begin events in library $\textsf{L}_{\textsf {trans}}$, the $\lfloor \textsc {b}\rfloor$ denotes the set of all events that are tagged with $\textsc {b}$, which includes $\mathcal {B}$ (of library $\textsf{L}_{\textsf {trans}}$) as well as events of other (non-$\textsf{L}_{\textsf {trans}}$) libraries that may be tagged with $\textsc {b}$; similarly for $\mathcal {E}$ and $\lfloor \textsc {e}\rfloor$. As such, our local specifications below (i.e. local well-formedness and consistency) are defined in terms of $\mathcal {B}$ and $\mathcal {E}$, whereas our global specifications are defined in terms of $\lfloor \textsc {b}\rfloor$ and $\lfloor \textsc {e}\rfloor$. As before, for brevity we write e.g. $[ \textsc {t} ]$ as a shorthand for the relation $[ \lfloor \textsc {t} \rfloor ]$. We next define the ‘same-transaction’ relation :

An execution is locally well-formed iff the following hold:

• 1. A transaction must be opened before it is closed:

• 2. Transactions are not nested and are matching: and

• 3. Transactions must be externally synchronized:

• 4. The recovery routine must be called after each crash before using the library:

• 5. Events are correctly tagged: $\mathcal {W} \cup \mathcal {R} \subseteq \lfloor \textsc {t} \rfloor$

An execution is globally well-formed if client operations are inside transactions:

• 6.
• 7.

An execution is locally-consistent if there exists a relation  satisfying:

• 8. 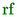relates writes to reads, , such that each read is related to exactly one write (i.e. is total and functional).

• 9. Reads access the most recent write:

• 10. External reads (reading from a different transaction) read from persisted writes:

An execution is globally-consistent if there exists an order  over $\lfloor \textsc {t} \rfloor$ satisfying:

• 11. Transactions are -ordered:

• 12. is the persistance order: ;

• 13. Either all the events or none of the events in a transaction persist (atomicity):

• 14. All events of a completed transaction (ones with an associated end event) persist: $\lfloor \textsc {e}\rfloor ^c \subseteq \lfloor \textsc {p} ^{\textsf{tr}}\rfloor$, where $\lfloor \textsc {e}\rfloor ^c$ denotes the set of method calls tagged with $\textsc {e}$ which have completed.

Theorem 4

The $\textsf{L}_{\textsf {trans}}$ implementation in Fig. 1 over  is correct.

5.2 Vertical Library Composition: Adding Internal Synchronization

We next demonstrate how our framework can be used for vertical library composition, where an implementation of one library comprises calls to other libraries with non-trivial global specifications. To this end, we develop $\textsf{L}_{\textsf {Strans}}$, a wrapper library around $\textsf{L}_{\textsf {trans}}$ that is meant to be simpler to use by providing synchronization internally: rather than the user ensuring synchronization for $\textsf{L}_{\textsf {trans}}$, one can use $\textsf{L}_{\textsf {Strans}}$ to prevent two transactions from executing in parallel. More formally, the well-formedness condition (3) of $\textsf{L}_{\textsf {trans}}$ becomes a correctness guarantee of $\textsf{L}_{\textsf {Strans}}$. We consider a simple implementation of $\textsf{L}_{\textsf {Strans}}$ that uses a global lock acquired at the beginning of each transaction and released at the end as shown below.

Theorem 5

The implementation of $\textsf{L}_{\textsf {Strans}}$ above is correct.

Using compositional correctness, the main proof obligation is the condition stipulating that the implementation be well-formed, ensuring that $\textsf{L}_{\textsf {trans}}$ is used correctly by the $\textsf{L}_{\textsf {Strans}}$ implementation. This is straightforward as we can assume there exists an immediate prefix that is consistent. The existence of the -ordering of calls to $\texttt {PTBegin}$ and $\texttt {PTEnd}$ follows from the consistency of the global lock used by the implementation.

5.3 Horizontal Library Composition

We next demonstrate how our framework can be used for horizontal library composition, where a client program comprises calls to multiple libraries. To this end, we develop a simple library, $\textsf{L}_{\textsf{cntr}}$, providing a persistent counter to be used in sequential (single-threaded) settings: If a client uses $\textsf{L}_{\textsf{cntr}}$ in concurrent settings, it must call its methods within critical sections. The $\textsf{L}_{\textsf{cntr}}$ provides three operations to create (), increment () and read a counter (). The specification and implementation of $\textsf{L}_{\textsf{cntr}}$ are given in [34]

As $\textsf{L}_{\textsf{cntr}}$ uses the tags of $\textsf{L}_{\textsf {trans}}$, we define $\textsf{L}_{\textsf{cntr}}{.}\varLambda _{\textrm{tags}}\triangleq \{ \textsf{L}_{\textsf {trans}}\}$. The all the operations are tagged with $\textsc {t}$. As such, $\textsf{L}_{\textsf{cntr}}$ inherits the global well-formedness condition of $\textsf{L}_{\textsf {trans}}$, meaning that $\textsf{L}_{\textsf{cntr}}$ operations must be used within transactions (i.e. -between operations respectively tagged with $\textsc {b}$ and $\textsc {e}$). Putting it all together, the following client code snippet uses $\textsf{L}_{\textsf{cntr}}$ in a correct way, even though $\textsf{L}_{\textsf{cntr}}$ has no knowledge of the existence of $\textsf{L}_{\textsf {Strans}}$.

Specifically, the above is an instance of horizontal library composition (as the client comprises calls to both $\textsf{L}_{\textsf {Strans}}$ and $\textsf{L}_{\textsf{cntr}}$), facilitated in our framework through global specifications.

6 Conclusions, Related and Future Work

We presented a framework for specifying and verifying persistent libraries, and demonstrated its utility and generality by encoding existing correctness notions within it and proving the correctness of the FliT and Mirror libraries, as well as a persistent transactional library.

Related Work. The most closely related body of work to ours is [26]. However, while their framework can be used for specifying only the consistency guarantees of a library, ours can be used to specify both consistency and persistency guarantees. More generally, our tag system extends the expressivity of [26] with support for global effects such as some types of fences.

Existing literature includes several works on formal persistency models, both for hardware [5, 6, 19, 25, 28,29,30,31] and software [4, 11, 21], as well as correctness conditions for persistent libraries such as durable linearizability [17]. As we showed in §3, such models can be specified in our framework.

There have been works [33] to specify libraries using an operational approach instead of the declarative approach that we advocate for here. While it is not generic in the memory model, it support weak memory, with a fragment of the C++ 11 memory model, and supports synchronization that is internal and external to the library. Another framework for formalizing behavior of concurrent objects in the presence of weak memory is [18], which is more syntactic as our framework: they use a process calculus, which allows them to handle callbacks between the library and the client. Extending our framework, which is more semantic, to handle this setting would probably require shifting from executions/histories to something similar to game semantics.

Additionally, there are several works on implementing and verifying algorithms that operate on NVM. [9] and [36] respectively developed persistent queue and set implementations in . [8] provided a formal correctness proof of the implementation in [36]. All three of [8, 9, 36] assume that the underlying concurrency model is SC [23], rather than that of (namely TSO). As we demonstrated in §4–§5 we can use our framework to verify persistent implementations modularly while remaining faithful to the underlying concurrency model. [2, 27] have developed persistent program logics for verifying programs under . [20] recently formalized the consistency and persistency semantics of the Linux ext4 file system, and developed a model-checking algorithm and tool for verifying the consistency and persistency behaviors of ext4 applications such as text editors.

Recently, and independently to this work, Bodenmüller et al [3] have proved the correctness of the Flit library under TSO. They used an operational approach, and modeled the libraries and the memory and persistency models operationally using automata, and proved a simulation result using KIV a specialized proof assistant. As for this paper, they proved that a linearizable library using Flit becomes durably linearizable.

Future Work. We believe our framework will pave the way for further work on verifying persistent libraries, whether manually (as done here), possibly with the assistance of an interactive theorem prover and/or program logics such as those of [2, 7, 27], or automatically via model checking. The work of [7] uses the framework of [26] to specify data structures in a program logic, and it would be natural to extend it to our framework for persistency. Existing work in the latter research direction, e.g. [12, 20], has so far only considered low-level properties, such as the absence of races or the preservation of user-supplied invariants. It has not yet considered higher-level functional correctness properties, such as durable linearizability and its variants. We believe our framework will be helpful in that regard. In a more theoretical direction, it would be interesting to understand how our compositional correctness theorem fits in general settings for abstract logical relations such as [16].