Abstract
Invertible programming languages specify transformations to be run in two directions, such as compression/decompression or encryption/decryption. Two key concepts in invertible programming languages are partial invertibility and local invertibility. Partial invertibility lets invertible code be parameterized by the results of non-invertible code, whereas local invertibility requires all code to be invertible. The former allows for more flexible programming, while the latter has connections to domains such as low-energy computing and quantum computing. We find that existing approaches lack a satisfying treatment of partial invertibility, leaving the connection to local invertibility unclear.
In this paper, we identify four core constructs for partially invertible programming, and show how to give them a locally invertible interpretation. We show the expressiveness of the constructs by designing the functional invertible language Kalpis, and show how to give them a locally invertible semantics using the novel arrow combinator language \(\textsc {rrArr}\)—the key idea is viewing partial invertibility as an invertible effect. By formalizing the two systems and giving Kalpis semantics by translation to \(\textsc {rrArr}\), we reconcile partial and local invertibility, solving an open problem in the field. All formal developments are mechanized in Agda.
You have full access to this open access chapter, Download conference paper PDF
Keywords


1 Introduction
An invertible computation can be run in two ways: forward in the conventional way, or backward to recover an input given the output. Such processes appear frequently and prominently in a variety of contexts, enabling the shape of information to be adapted to different purposes, while preserving the essential content. For instance, (lossless) compression shrinks the size of a piece of information to facilitate efficient storage, encryption transforms it to be inaccessible to third parties, and serialization reshapes it to enable storage or transmission. The property of invertibility is crucial, as it guarantees that the data can always be refit to its original purpose.
For example, consider the function \( autokey \) below, which computes a variant of the Autokey cipher (see e.g., [50]). The cipher takes a primer character \( k \), and interprets it as an integer (e.g., \(\texttt {'A'} \mapsto 0, \texttt {'B'} \mapsto 1, \ldots , \texttt {'Z'} \mapsto 25\)) determining a shift to apply to the first element of the input. Each consecutive character in the input is similarly shifted by the amount given by its predecessor. For instance, \( autokey \;\texttt {'F'} \;\texttt {"HELLO"} = \texttt {"CXHAD"}\), as ’F’ represents a (cyclic left) shift of 5 characters, mapping ’H’ to ’C’, and ’H’ a shift of 7 characters, mapping ’E’ to ’X’, and so on.
The corresponding decryption function \( autokey ^\prime \) is given to the right, and shifts backward to restore the original input. We assume \( shift : \textsf{Int} \rightarrow \textsf{Char} \rightarrow \textsf{Char}\) performing the cyclic shift is previously defined. This is a simple example, but it serves as a toy model of more advanced encryption schemes and has a few interesting features which we highlight momentarily.
In traditional unidirectional languages, each direction of an invertible algorithm has to be specified separately in this way, and there is no easy way of ensuring that the two programs really constitute each other’s inverses. Furthermore, there is a maintenance concern—when one direction is updated, the other has to be updated accordingly. An alternative, more scalable approach is to let a single program denote both directions at the same time—intuitively, the inverse is derived by “reading the original code right-to-left”. Invertible programming languages implement this approach, letting each program be executed in either of two directions, which are guaranteed to form a pair of inverse functions. Some examples of invertible languages include Janus [35, 53], R [17], Inv [43], \(\varPi \) [10, 26], RFun [54], Theseus [27], \(\textsf{CoreFun}\) [25] and Sparcl [39, 40].
These languages traditionally require each individual step of computation to be invertible, which can be ensured, e.g., by providing a set of invertible combinators as basic building blocks, or by imposing various syntactic restrictions. This form of local invertibility has several benefits, in addition to being a simple foundation for building programming languages. For example, it was observed early on that discarding information fundamentally results in heat dissipation, meaning that a machine executing only invertible instructions could in principle operate at lower energy levels than a conventional computer [32]. Moreover, locally invertible languages serve as a foundation when considering other domains with similar requirements, such as quantum computing, where computations are composed of individually invertible quantum gates along with irreversible measurements [22, 48]. Despite these benefits, the local flavor of invertibility severely limits the flexibility of the programmer. In particular, our example function \( autokey \) is not actually invertible up front! The case \(~ autokey \;k \;[\,]= [\,]~\) discards the value of \( k \), which means we cannot simply read the definition right-to-left. Of course, the primer \( k \) is not intended to be treated as part of the invertible input to \( autokey \), but rather as a parameter determining the bijection between input and output strings. However, this cannot be naturally expressed in a language adhering strictly to the (locally) invertible paradigm, where the parameter would need to be preserved in the result.
The property of becoming invertible when some parameters are fixed is known as partial invertibility [39, 40, 44, 47], and many previous languages offer some form of support for partially invertible definitions. However, the level of support varies from more limited (e.g., [25, 27, 35]) to more complete (e.g., [39, 40]), and the previous work largely lacks a systematic treatment. The case of \( autokey \) is especially tricky, since its invertible input \( h \) flows to the unidirectional parameter \( k \) in the recursive call. To our knowledge, only Sparcl [39, 40] handles cases like this in a systematic way, but it does so through an advanced language foundation quite different from that of traditional invertible languages, and its connection to the locally invertible paradigm is not well-understood. Thus, it is an open question whether it is possible to support fully expressive partial invertibility while maintaining a compositional locally invertible interpretation.
It is theoretically known that any (partially) invertible computation can be simulated in a locally invertible system [8]; however, this simulation gives poor control over the invertible behavior and is inefficient in both time and space. There has been research on inversion of arbitrary programs (e.g., [41, 44, 49]), and on logic languages with no fixed direction of execution, like Prolog and Curry, which use (lazy) generate-and-test to find inputs corresponding to a given output [4]. Yet, these approaches lack the guarantee of invertibility, which is the main motivation of an invertible language.
1.1 Contributions and Organization
In this paper, we identify a core set of constructs for partially invertible programming, and explain them in terms of a locally invertible semantics. These constructs are sufficient to allow expressive partially-invertible and higher-order computation, thus solving an open problem in the invertible programming literature. The constructs include (1) partially invertible branching, (2) pinning invertible inputs, (3) partially invertible composition, and (4) abstraction and application of invertible computations.
We demonstrate the above findings by designing and formalizing two systems based on these constructs, KalpisFootnote 1 and \(\textsc {rrArr}\). Kalpis is a typed functional programming language accommodating expressive partially-invertible and higher-order computation, and \(\textsc {rrArr}\) is an arrow combinator language intended to capture the essence of partially invertible programs. Kalpis is given semantics via \(\textsc {rrArr}\), which captures partial invertibility as an effect on top of ‘pure’ invertible computations, intuitively adjoining a parameter to an invertible function, analogously to the reader monad in unidirectional computation. By interpreting terms of Kalpis as parameterized bijections, we are able to give a translation into \(\textsc {rrArr}\) combinators, giving a compositional embedding into a locally invertible setting. Thus, we present a simple and rigorous take on partial invertibility which bridges the gap between previous work in the field.
The core constructs for partial invertibility that we present are not new per se, and the features of Kalpis largely coincide with those of Sparcl [39, 40]. However, the goal of this paper is not to present Kalpis as such, but rather to describe partial invertibility from first principles and give a simpler semantics which is compatible with local invertibility. There are key technical differences between the two languages, and the fact that they are still similar should be taken as a sign that we have achieved our goal without a significant loss of expressiveness.
In summary, our main contributions are:
-
We identify a core set of partially invertible programming constructs (Section 2), which we demonstrate to be sufficient to achieve a level of expressiveness similar to the state-of-the-art.
-
We showcase the constructs through the design of the invertible functional language Kalpis, including a formal type system and operational semantics (Section 3).
-
We present \(\textsc {rrArr}\), an extension of the irreversibility effect [26] and the reversible reader [23] (Section 4) as a core calculus for partially invertible computation with a locally invertible interpretation.
-
We give a compositional translation from Kalpis into \(\textsc {rrArr}\) (Section 5).
-
We prove type safety and invertibility properties (Section 3), and prove the correctness of the arrow translation (Sections 4 and 5).
-
Our developments come with a formalization in Agda including proofs of all theorems,Footnote 2 and a prototype implementation of Kalpis.Footnote 3
Section 6 discusses the results in relation to previous work, and Section 7 concludes.
2 Constructs for Partially Invertible Programming
In this section, we introduce a set of core constructs for partially invertible programming and explain their intuitive idea using programming examples in our partially invertible language Kalpis, which we introduce formally in Section 3. The constructs include (1) partially invertible branching, (2) pinning invertible inputs, (3) partially invertible composition, and (4) abstraction and application of invertible computations. We explain them each in turn, and show how they can be understood as operations on parameterized bijections, which we exploit in later sections to embed them into a locally invertible setting.
These constructs act as a form of glue, allowing invertible and unidirectional computations to be run in tandem. Thus, we also assume some traditional invertible constructs taken from the existing literature, like invertible pattern matching, which we briefly explain where necessary.
2.1 Partially Invertible Branching
As a first example, we define partially invertible addition. In particular, the function \(x \mapsto x + n\) has inverse \(x \mapsto x - n\) for any \(n \in \mathbb {N}\). Kalpis supports recursive type definitions, and we can define the naturals as follows.
Now, addition is implemented naturally by the following function \( add \), taking an \( n \) to produce the corresponding bijection.
The language uses a functional syntax, and features elements typical to invertible programming: a bijection type \(A \leftrightarrow B\), bijection definition \(\textbf{def} ^\bullet \), and bijection application \(f \diamond x\). The functional types associate to the right, so the type of
indicates a partially invertible function taking a \(\textsf{Nat}\) to produce a bijection \(\textsf{Nat} \leftrightarrow \textsf{Nat}\). The \(\textbf{case}\) form showcases our first core construct, partially invertible branching. If \( n \) is zero, \( x \) is returned unchanged, and otherwise \(\textsf{S}\) is applied to the result of a recursive computation. The resulting function appends \( n \) copies of \(\textsf{S}\) to \( x \) in the forward direction, or peels them off in the backward direction.
What is interesting is that \(\textbf{case}\) results in a loss of information: without prior knowledge of \( n \), it is impossible to determine which branch to choose when executing backwards. This corresponds to the fact that one cannot uniquely determine \( n \) and \( x \) given \( y = n + x\). However, when \( n \) is fixed beforehand, we can refer to its value regardless of executing forwards or backwards, which is what motivates the \(\textbf{case}\) construct. For example, we get the following results when applying \( add \) to some example inputs, where the primitive operator \((\cdot )^\dagger : (A \leftrightarrow B) \rightarrow (B \leftrightarrow A)\) lets us compute the inverse.
As the type \(\textsf{Nat} \leftrightarrow \textsf{Nat}\) requires, the argument \( x \) in the definition of \( add \) must be treated linearly, i.e., must be used exactly once in any successful evaluation (see e.g., [51]) in order to ensure invertibility. For instance, changing the first case above to \(\textsf{Z} \rightarrow \textsf{Z}\) gives an error, as x is unused in the case body. Indeed, if \(x\) is never used, there is no way to recover its value in the backward direction. While allowing more than one use does not directly prevent invertibility, it requires implicit copying of values, which may induce unintended runtime failures in the backward execution. Similarly, we cannot branch on \( x \) using \(\textbf{case}\) for the reasons mentioned above; instead, an invertible \(\textbf{case} ^\bullet \) form is available, explained later.
Note that \( add \) is not a total function: e.g., the application \(( add \;(\textsf{S} \;\textsf{Z}))^\dagger \diamond \textsf{Z}\) will try to peel an \(\textsf{S}\) when there is none, resulting in a runtime error.Footnote 4 The guarantee given by Kalpis is that whenever evaluating a bijection f on argument v gives \(v^\prime \) in the forward direction, then evaluating f on \(v^\prime \) gives v in the backward direction, and vice versa (this is made formal in Section 3).
Mathematically, \( add \) represents a parameterized bijection, a family of (partial) one-to-one mappings \(f_n : \mathbb {N} \rightarrow \mathbb {N}\) (such that \(f_n(x) = x + n\)). This view will underpin our explanation of partially invertible computations in later sections, and each of the core constructs in this section can also be understood from this viewpoint. Seen from this perspective, the \(\textbf{case}\) construct allows definitions of the form
where \( g \) and \( h \) are also parameterized bijections.
2.2 Pinning Invertible Inputs
As a second example, we consider a program \( fib \) computing pairs of Fibonacci numbers (defined by the equations \(F_0 = F_1 = 1\) and \(F_{n+1} = F_{n} + F_{n-1}\) for \(n > 0\)), a classic in the invertible programming literature (e.g., [18, 53]). We can compute \( fib \;n\) by case distinction on \( n \); if \( n = 0\), we return \((F_0, F_1)\), and otherwise we recursively obtain \( fib \;(n - 1) = (F_{n-1}, F_n)\), with which we compute the next pair \((F_n, F_n + F_{n - 1})\).
However, if we try to implement this algorithm invertibly using the function \( add \) above, we encounter an issue: we cannot make the call \(~ add \;F_n \diamond F_{n - 1},~\) as \( add \) does not treat its first argument invertibly. Since \(F_n\) comes from the invertible input \( n \), we need an operation that is properly invertible in both inputs. To this end, we can define an invertible addition \( add' \) such that \(~ add' \diamond (x, y) = (x, x + y).~\) By preserving a copy of \( x \) in the output, the same \( x \) can be used to recover \( y \) by subtraction in the inverse direction. Indeed, \( add' \diamond (F_{n}, F_{n-1})\) gives just the result we need. In Kalpis, \( add' \) can be derived from \( add \) automatically using our second core construct, \( pin \).
Here, the operator \(~ pin : (c \rightarrow a \leftrightarrow b) \rightarrow (c, a) \leftrightarrow (c, b)~\) lifts a partially invertible function to operate on invertible data; we refer to this as pinning the invertible input \( x \), allowing it to be used in a unidirectional position. This construct (inherited from Sparcl [39, 40]) is crucial in practical programming, as it lets unidirectional computations depend on invertible data in a controlled manner. With \( add' \) defined, \( fib \) can be written as follows.

This example is defined by invertible pattern matching (\(\textbf{case} ^\bullet \)), a construct inherited from previous languages like Janus [35, 53] and \(\varPsi \)-Lisp [7]. When branching on the input to a bijection (as opposed to a fixed parameter), postconditions marked by the keyword \(\textbf{with}\) ensure that the execution can determine which branch to take in the backward direction. Each postcondition is a boolean function that must return \(\textsf{True}\) for any result of its branch and \(\textsf{False}\) for any result of the branches below it (this is checked at runtime following the symmetric first-match policy [54]). The backward evaluation tests each condition in turn, selecting the first branch whose condition is true. Here, \( is11 \) is used to distinguish the base case where the output is \((\textsf{S}\;\textsf{Z},\textsf{S}\;\textsf{Z})\).
The inverse behavior of \( fib \) computes \( n \) given a pair \((F_n, F_{n+1})\). Specifically, by computing \(F_{n+1} - F_n\), we obtain \(F_{n-1}\), and repeating the process until we reach the start of the sequence lets us deduce the index of the initial pair. Kalpis runs \( fib \) as below.

Again, \( fib \) is non-total: running it backwards on a pair not constituting two consecutive Fibonacci numbers will cause the computation to fail.
Viewed as an operation on parameterized bijections, \( pin \) lets part of an invertible input be shifted to the parameter position if a copy is returned in the end. Formally, we have \( pin (f)_n(x,y) = (x, f_{(n,x)}(y))\); in our example, \(f_{(n,x)}\) corresponds to addition by \( x \), ignoring a trivial \( n \) representing variables captured in the \( pin \) form.
2.3 Partially Invertible Composition
We now return to the example of the introduction, \( autokey \). It can be defined in Kalpis as follows:

The structure is very similar to the unidirectional version in Section 1, but uses the invertible branching and pinning constructs explained previously. We assume primitives \( chrToInt : \textsf{Char} \rightarrow \textsf{Int}\) and \( shift : \textsf{Int} \rightarrow \textsf{Char} \leftrightarrow \textsf{Char}\) for computing and performing the cyclical shifts, respectively. We omit the \(\textbf{with}\)-conditions of the invertible match by convention, as the syntactically distinct branch bodies can act as patterns to guide backward branching.
This example features our third core construct, partially invertible composition. This simply refers to the fact that we can modify the parameter of a bijection unidirectionally, as in \( shift \;( chrToInt \;k)\diamond h\). In this case, the (irreversible) function \( chrToInt \) is applied to \( k \) inside the (invertible) call to \( shift \). In other words, the parameter part of an invertible computation is allowed to depend freely on unidirectional computations, greatly enhancing the flexibility when programming. The reason we call it composition is because from the perspective of parameterized bijections, this corresponds to the composition of a parameterized bijection \( f \) with an (arbitrary) function \( g \) on the parameter part, i.e., \((f \circ g)_n(x) = f_{g(n)}(x)\). In our example, we have \( f \) corresponding to \( shift \) and \( g \) corresponding to \( chrToInt \).
The example also further highlights the utility of \( pin \). As noted in the introduction, \( autokey \) is tricky to express since each character in the invertible output depends unidirectionally on the preceding character in the corresponding input. Similar patterns also appear in more advanced examples; for instance, consider an adaptive compression method where each character in the input must be treated invertibly, and yet also be used as part of the (unidirectional) compression table. \( pin \) enables this sort of dependency in a safe way, letting us use \( h \) in the recursive call to \( autokey \) and returning a copy to use in the output.
Again, Kalpis lets us execute \( autokey \) in either direction, and guarantees that the two are inverses.
2.4 Abstraction and Application of Invertible Computations
Our final core construct of partially invertible programming is the ability to abstract and apply invertible computations. Although the examples we have seen so far have defined (partially) invertible computations using the \(\textbf{def} ^\bullet \) keyword in a style close to traditional invertible languages, Kalpis actually features bijections as first-class values and supports proper higher-order programming. Bijections can be constructed with an invertible \(\lambda \)-form \(\lambda ^\bullet x. e\) analogous to that typical for ordinary functions, and the form \(\textbf{def} ^\bullet ~f\;x_1\;x_2~\ldots ~x_n = e\) is simply syntactic sugar for \(f = \lambda x_1.\lambda x_2 \ldots \lambda ^\bullet x_n.~e\). To our knowledge, only Sparcl [39, 40] shares this feature, with most invertible languages being limited to first-order computation.
For example, we are able to define multiple variants of the typical \( map \) function for lists in Kalpis.
Here, \( map \) is defined as usual, and maps a function over each element of a list, while \( mapBij \) makes use of the language’s invertible constructs, taking a bijection argument to produce a bijection on lists. For example, using \( mapBij \), the Caesar cipher (which shifts each character in the input a fixed number of steps) can be defined with a one-liner, as below to the left.
The function on the right, \( vig \) (from Vigenère), takes a list of keys, shifting each character in the input using the corresponding key—the definition relies on \( apBij : [a \leftrightarrow b] \rightarrow [a] \leftrightarrow [b]\) to apply a list of bijections pointwise to a list of inputs (assuming the two have equal lengths). The latter example demonstrates that bijections can even occur inside data structures such as lists.
Some restrictions must be observed when dealing with higher-order computation in Kalpis. The language distinguishes between unidirectional and invertible terms, and carefully controls the interaction between the two. The restrictions mean that the invertible fragment of the language is essentially first-order; a formal account is given in Section 3.
Viewed from the perspective of parameterized bijections, abstraction corresponds to forming the function \(n \mapsto f_n\), witnessing that each choice of parameter \(n\) induces a bijection \(f_n\) which can be treated as a standalone value. On the other hand, application of a bijection \(\alpha \) corresponds to forming the parameterized bijection \( app _\alpha (x) = \alpha (x)\), where the parameter determining the bijection is \(\alpha \) itself.
This concludes Section 2; for more programming examples in Kalpis, we refer to the prototype implementation,Footnote 5 which contains a number of nontrivial programs, including implementations of Huffman coding and sliding-window compression.
3 The Kalpis Core System
In this section, we formally define the Kalpis core system and state the essential metatheoretic properties. A salient feature of the system is the clear separation between unidirectional and invertible terms: we have two main syntactic categories, two typing relations, and three evaluation relations (one for unidirectional terms, and one in each direction for invertible terms). The unidirectional terms are a conservative extension of a standard simply-typed call-by-value \(\lambda \)-calculus, and the invertible terms add support for (partially) invertible computation.
After introducing the syntax and reviewing some examples, Sections 3.4 and 3.5 give a formal semantics which suggests an interpretation of Kalpis terms as parameterized bijections. This view is made precise in Sections 4 and 5, which define a translation from Kalpis into the arrow language \(\textsc {rrArr}\), enabling a locally invertible interpretation.
3.1 Syntax
The syntax of Kalpis core is given below, where \( u \) denotes unidirectional terms, \( r \) denotes invertible terms, and \( p \) denotes patterns. The vector notation \(\overline{t}\) denotes an ordered sequence of elements \(t_i\), whose length we will refer to by \(|\overline{t}|\).
The syntax of unidirectional terms include the standard cases for variables, abstraction and application, along with data constructors and pattern matching. In addition, there is the invertible abstraction \(\lambda ^\bullet x. r\) and application \(u_1 \diamond u_2\) explained in the previous section. Note that while the body \(r\) is an invertible term, the abstraction itself is unidirectional.
The syntax of invertible terms resembles a first-order functional language, but with a couple of key additions. We have bijection application \(u \diamond r\), where the bijection is unidirectional whereas the argument is invertible. We also have fully applied versions of the \((\cdot )^\dagger \) and \( pin \) operators explained in the previous section (this is without loss of generality, as e.g., the higher-order version of \( pin \) can be recovered as \(\lambda f.\lambda ^\bullet x.~ pin \;f \diamond x\)). Partially invertible branching is represented by the \(\textbf{case} \) form, whose scrutinee \( u \) is unidirectional. The \(\textbf{case} ^\bullet \) form deconstructs an invertible term, and has a \(\textbf{with}\)-condition for invertible branching, following Janus [35, 53] and \(\varPsi \)-Lisp [7]. The core constructs of the previous section are all featured explicitly in the syntax, except for partially invertible composition, which is implicitly performed whenever a unidirectional term \( u \) occurs in an invertible context.
3.2 Types
Next, we define the types of Kalpis core.
The types include constructors \(\textsf{T} \;\overline{B}\), functions \(A \rightarrow B\), bijections \(A \leftrightarrow B\) and type variables X. The types are conventional with the exception of invertible computations \(A \leftrightarrow B\); this simplicity is a design feature of Kalpis. With each type constructor \(\textsf{T}\) we associate an arity k and a set of constructors \(\textsf{C}\) with signatures \( \textsf{C} : A_1 \rightarrow A_2 \rightarrow \cdots \rightarrow A_n \rightarrow \textsf{T} \;\overline{B}, \) where \(|\overline{B}| = k\). We will assume the type constructors include at least the unit \(\textsf{1}\), products \(\otimes \), and sums \(\oplus \) with constructors
for any A, B. We use \(\textsf{Bool}\) as a shorthand for \(\textsf{1} \oplus \textsf{1}\), and \(\textsf{True}\), \(\textsf{False}\) as shorthands for \(\textsf{InL}\;\mathsf {()}, \textsf{InR}\;\mathsf {()}\), respectively.
Types can be (mutually) recursive via constructors; for example, the type \(\textsf{Nat}\) has constructors \(\textsf{Z} : \textsf{Nat}\) and \(\textsf{S} : \textsf{Nat} \rightarrow \textsf{Nat}.\) In general, for any fixed A, the recursive type \(\mu X.A\) can be represented with a nullary type constructor \(\textsf{Rec}_A\), with constructor
For instance, \(\textsf{Rec}_{\textsf{1} \oplus X}\) has constructor \(\textsf{Roll} : \textsf{1} \oplus \textsf{Rec}_{\textsf{1} \oplus X} \rightarrow \textsf{Rec}_{\textsf{1} \oplus X}\), making it isomorphic to \(\textsf{Nat}\). Technically, we consider a variable X implicitly bound in the annotation to \(\textsf{Rec}\), and assume all other types are closed.
3.3 Correspondence to the Surface Language
The correspondence between the core syntax and the examples of Section 2 should be clear. For instance, the examples of addition and Fibonacci number calculation can be written as follows:

Here, \( add \) is a unidirectional term defined using a fixpoint operator \( fix \), and the structure is similar to the version presented in Section 2.1. The function \( fib \) is similarly defined, but uses the fixpoint operator \( fixBij \) instead of \( fix \), which works for bijections instead of functions. We omit the definition of \( is11 : \textsf{Nat} \otimes \textsf{Nat} \rightarrow \textsf{Bool}\) in the interest of space. The term \( fixBij \) (and analogously \( fix \)) is defined as below, making use of the language’s recursive types.
The type system we define in the next section will assign these terms the following types as expected.
3.4 Type System
Figure 1 shows the typing rules for unidirectional (\(\varGamma \vdash u : A\)) and invertible (\(\varGamma ;\varTheta \vdash r : A\)) terms. The latter relation uses two contexts \(\varGamma \) and \(\varTheta \); intuitively, \(\varGamma \) contains variables for unidirectional data, which may be discarded or duplicated freely, whereas \(\varTheta \) contains variables for data that must be treated in an invertible way. This use of a dual context system [13] is inspired by previous work such as \(\textsf{CoreFun}\) [25] and Sparcl [39, 40]. Formally, we define the typing contexts as \( \varGamma , \varTheta :\,\!:= \varepsilon \mid \varGamma , x : A, \) and assume names \(x\) are unique within a context. We let \(\varGamma _1 , \varGamma _2\) denote the concatenation of two contexts.
The rules for \(\varGamma \vdash u : A\) are mostly straightforward. \(\textsc {T}\hbox {-}\textsc {Abs}^\bullet \) pushes the parameter x of \(\lambda ^\bullet x.r\) into \(\varTheta \) instead of \(\varGamma \) to ensure that the variable is used in an invertible way in r, and \(\textsc {T}\hbox {-}\textsc {Run}\) gives a rule for bijection application analogous to \(\textsc {T}\hbox {-}\textsc {App}\). In the Case rules, we implicitly require that patterns are disjoint and exhaustive.
In the rules for \(\varGamma ; \varTheta \vdash r : A\), the variables in the \(\varTheta \) environments must be used exactly once to ensure invertibility. Hence, we need to separate \(\varTheta \) into, e.g., \(\varTheta = \varTheta _1 \uplus \varTheta _2\) for typing subterms, where \(\uplus \) is used analogously to a linear type system (see, e.g., [9]). The rules follow the intuition that r denotes a bijection between \(\varTheta \) and A parameterized by \(\varGamma \). This highlights the difference between the pattern matching rules, T-UCase and T-RCase: the bound variables \(\varGamma _i\) in the former are parameters for the bijection that \(r_i\) defines, while in the latter, the variables \(\varTheta _i\) are part of the inputs of \(r_i\), so that \(\textbf{case} ^\bullet \) performs a composition of two invertible computations.
As stated in Section 2.4, there are some restrictions on how unidirectional and invertible terms can interact. Note that the unidirectional subterms occurring in the invertible typing rules are only typed using \(\varGamma \), and not \(\varTheta \). For instance, since the left-hand side in rule T-RApp is unidirectional, it cannot depend directly on invertible variables, ruling out terms like \(\lambda ^\bullet x. (x \diamond \textsf{True})\). This is a natural restriction, as we cannot generally deduce which function was used to produce some given result. Conversely, there is no rule for directly accessing \(\varGamma \) from the invertible typing relation; instead, unidirectional data can only affect the computation through rules like T-UCase and T-RApp. Both \(\lambda \)-forms are unidirectional, meaning they can neither capture invertible variables nor be returned from an invertible computation. In this sense, the invertible fragment of the language is first-order.
We note that there are no particular restrictions on unidirectional terms, and the approach presented could be used to augment any standard functional language with invertible computations \(\lambda ^\bullet x. r\) and \(u_1 \diamond u_2\). The prototype implementation further adds \(\textbf{let}\)-polymorphism as an orthogonal extension.
3.5 Operational Semantics
We first define the set of values as below.
Here, \(\gamma \) is a value environment, i.e., a mapping from variables to their values. Formally, we define \(\gamma , \theta :\,\!:= \emptyset \mid \gamma , x \mapsto v\), with \(\gamma \) and \(\theta \) corresponding to \(\varGamma \) and \(\varTheta \). We use the disjoint union \(\theta _1 \uplus \theta _2\) to concatenate two environments \(\theta _1\) and \(\theta _2\), which is defined only when \(\textsf{dom}(\theta _1)\) and \(\textsf{dom}(\theta _2)\) are disjoint. The values include constructors and two closure forms \(\langle \lambda x. u, \gamma \rangle \) and \(\langle \lambda ^\bullet x. r, \gamma \rangle \), corresponding to unidirectional and invertible computations. We type the values in analogy with the terms, with the rules for closures as follows:

Here, we write \(\gamma : \varGamma \) to mean that \(\textsf{dom}(\gamma ) = \textsf{dom}(\varGamma )\) and \(\gamma (x) : \varGamma (x)\) for all \(x \in \textsf{dom}(\varGamma )\). For p a pattern, we write \(p \gamma \) to denote the value obtained by applying the substitution \(\gamma \) to p’s variables. In addition, we use the shorthand \(\widehat{i = j} \triangleq \left\{ \begin{array}{ll} \textsf{True}\quad &{}\text {if}~i = j\\ \textsf{False}&{} \text {otherwise} \end{array}\right. \).
We now present in Figure 2 the operational semantics of Kalpis core, which consists of three evaluation relations: unidirectional, forward, and backward. The unidirectional evaluation relation \(\gamma \vdash u \Downarrow v\) reads that under \(\gamma \) term u evaluates to value v, as usual. In contrast, the forward and backward evaluation relations define a bijection. The former relation \(\gamma ; \theta \vdash r \Rightarrow v\) reads that under \(\gamma \) the forward evaluation of r maps \(\theta \) to v, and the latter relation \(\gamma ; v \vdash r \Leftarrow \theta \) reads that under \(\gamma \) the backward evaluation of r maps v to \(\theta \). As one can see, \(\gamma \) serves as parameter for this bijection that defines a one-to-one correspondence between \(\theta \) and v. Due to the space limitations, we omitted the rules for backward evaluation, as they are completely symmetric to forward evaluation. That is, for each rule of the forward evaluation, the corresponding backward rule is obtained by swapping each occurrence \(\gamma ; \theta \vdash r \Rightarrow v\) with \(\gamma ; v \vdash r \Leftarrow \theta \), and vice versa. Crucially, the evaluation relations are mutually dependent, and when a unidirectional term is embedded in an invertible computation, the unidirectional evaluation will be invoked to evaluate the term in the same way regardless of whether executing forwards or backwards.
We encourage the reader to study the rules for partially invertible \(\textbf{case}\) and invertible \(\textbf{case} ^\bullet \) especially. The former branches based on a unidirectional term, which is evaluated first regardless of the direction of execution. The latter branches based on an invertible term, which is evaluated first in the forward direction but last in the backward direction. In the backward direction, the \(\textbf{with}\)-conditions \(\overline{u}\) are instead evaluated first; the condition \(\widehat{i=j}\) for \(j \le i\) encodes the branch selection and the runtime check of postconditions mentioned previously.
There is a subtlety in the backward evaluation rule for constructors \(\textsf{C}\;\overline{r}\), where the same \(\textsf{C}\) occurs both in the term \(\textsf{C} \;\overline{r}\) and the input \(\textsf{C} \;\overline{v}\), meaning that evaluation fails if the value does not match the constructor \(\textsf{C}\). This corresponds to, e.g., the term \((\lambda ^\bullet x.~\textsf{S} \;x)^\dagger \diamond \textsf{Z}\) failing as it tries to subtract one from zero.
3.6 Metatheory
In this section, we briefly state the essential properties of the core system. The propositions in this section have been formalized mechanically, by implementing and reasoning about a definitional interpreter [46] in Agda. The implementation follows the presentation of the paper closely, but uses intrinsically-typed terms and nameless variables, and relies on the sized delay monad [1, 11].
Theorem 1 (Subject reduction)
[Subject reduction]
-
If \(\varGamma \vdash u : A\), \(\gamma : \varGamma \) and \(\gamma \vdash u \Downarrow v\), then v : A.
-
If \(\varGamma ; \varTheta \vdash r : A\), \(\gamma : \varGamma \), \(\theta : \varTheta \) and \(\gamma ; \theta \vdash r \Rightarrow v\), then v : A.
-
If \(\varGamma ; \varTheta \vdash r : A\), \(\gamma : \varGamma \), v : A and \(\gamma ; v \vdash r \Leftarrow \theta \), then \(\theta : \varTheta \).
Proof
Directly from the existence and type of the definitional interpreter in Agda.
Theorem 2 (Invertibility)
[Invertibility] If \(\varGamma ; \varTheta \vdash r : A\), \(\gamma : \varGamma \), \(\theta : \varTheta \) and v : A, then
Proof
By simultaneous induction on the term r and the step count of evaluation; simple induction on the term r is not enough as the language has general recursion. The proof is otherwise straightforward, since the evaluation relations are completely symmetric.
Remark on Progress. We have chosen to give the semantics in a big-step style in this paper. This choice was made both because the invertibility property is more natural to state about a big-step semantics, which relates input to output directly, and to make the step to a denotational semantics smaller—as mentioned, the evaluation relations suggest an interpretation of invertible terms as parameterized bijections.
Thus, the progress property typically proven for a small-step semantics, meaning that evaluation never gets “stuck” given a valid input (see, e.g., [45]), is not direct to state in our case. However, we get a similar guarantee from the implementation in Agda, whose type checker asserts that no uncontrolled run-time errors are possible. Indeed, the only errors that can occur during evaluation are those caused by imprecise \(\textbf{with}\)-conditions or mismatched constructors.
4 Arrows for Partial and Local Invertibility
While the core system of Kalpis presented in the previous section is simple and illuminating, it only offers an operational understanding of the language. Furthermore, it depends on a unidirectional evaluation, which does not fit in a locally invertible setting. We want to get at the essence of partially invertible programming, and show that partial and local invertibility can be reconciled, which is the focus of this section.
In what follows, we define \(\textsc {rrArr}\), a low-level language based on arrow combinators, intended to capture the essence of partially invertible computation. The operations of \(\textsc {rrArr}\) directly correspond to the core constructs of Section 2, and have an immediate interpretation in terms of abstract functions and parameterized bijections. What is more, we show that they have an alternative, compositional and locally invertible interpretation using an idea similar to the reader monad in unidirectional computation (based on the irreversibility effect [26] and the reversible reader [23]). This property is not obvious for Kalpis, not to mention earlier work such as Sparcl [39, 40].
We begin by explaining the syntax and semantics of a first-order fragment of \(\textsc {rrArr}\), before proceeding to give its locally invertible interpretation. We then extend this fragment to match the full expressiveness of Kalpis in Section 4.5 with operations for higher-order computation. In Section 5, we top it all off by giving a formal translation from Kalpis core to \(\textsc {rrArr}\).
4.1 Syntax and Type System of \(\textsc {rrArr}\)
Figure 3 shows the syntax and type system of \(\textsc {rrArr}\) (where base bijections c of type \(A \leftrightharpoons B\) are kept abstract). The language involves unidirectional (\(\mu \)) and invertible (\(\alpha \)) terms, similarly to Kalpis. Both kinds of terms form arrows over bijections, through the combinators \( arr \), \(\ggg \), and \( first \).
The former arrow, denoted by \(\mu : A \rightsquigarrow B\), intuitively represents an ordinary function; \( arr _\textrm{u} \;c\) extracts the forward semantics of a bijection c, \(\mu _1 \ggg _\textrm{u} \mu _2\) composes two functions \(\mu _1\) and \(\mu _2\), and \( first _\textrm{u} \;\mu \) simply applies \(\mu \) to the first component of the input. The unidirectional arrows also feature \( left _\textrm{u}\), the sum counterpart of \( first \), and allow copying data through \( clone \).
The latter arrow, denoted by  , represents bijections between A and B parameterized by C; \( arr _\textrm{r} \;c\) constructs a parameterized bijection that behaves as the bijection c ignoring any parameter, \(\alpha _1 \ggg _\textrm{r} \alpha _2\) composes the two bijections obtained by passing the parameter to both \(\alpha _1\) and \(\alpha _2\), and \( first _\textrm{r} \;\alpha \) applies the bijection determined by \(\alpha \) to the first component of the input. These arrows also support \( left _\textrm{r}\), and form an inverse arrow [23] through a dagger operator \(\alpha ^\dagger \), that undoes \(\alpha \) and its effect.
, represents bijections between A and B parameterized by C; \( arr _\textrm{r} \;c\) constructs a parameterized bijection that behaves as the bijection c ignoring any parameter, \(\alpha _1 \ggg _\textrm{r} \alpha _2\) composes the two bijections obtained by passing the parameter to both \(\alpha _1\) and \(\alpha _2\), and \( first _\textrm{r} \;\alpha \) applies the bijection determined by \(\alpha \) to the first component of the input. These arrows also support \( left _\textrm{r}\), and form an inverse arrow [23] through a dagger operator \(\alpha ^\dagger \), that undoes \(\alpha \) and its effect.
What is special in \(\textsc {rrArr}\) is the communication between the two arrows through \( case! \), \( pin \), \(\mathbin {\gg !}\), and \( run \), where the former three directly correspond to the core constructs of Section 2. The term \( case! ~\alpha _1~\alpha _2\) performs partially invertible branching, running \(\alpha _1\) or \(\alpha _2\) depending on the value of its parameter. The term \( pin ~\alpha \) corresponds to the pinning construct; in \(\textsc {rrArr}\), this operation moves part of the input (D) into the parameter (\(C \otimes D\)) of \(\alpha \). The term \(\mu \mathbin {\gg !}\alpha \) represents partially invertible composition of the function \(\mu \) with the parameterized bijection \(\alpha \). Finally, the operator \( run \) allows converting a parameterized bijection  to a function \(C\otimes A \rightsquigarrow B\) by extracting its forward semantics. This can be seen as a special case of applying invertible computations (in a unidirectional context); the treatment of abstraction and application supporting higher-order computation is left for Section 4.5, as it requires a slight extension.
to a function \(C\otimes A \rightsquigarrow B\) by extracting its forward semantics. This can be seen as a special case of applying invertible computations (in a unidirectional context); the treatment of abstraction and application supporting higher-order computation is left for Section 4.5, as it requires a slight extension.
It is worth noting that invertible arrows are inherently allowed to ignore their parameter (through \( arr _\textrm{r}\)), a fact that can be used to derive the crucial erasure operation in unidirectional arrows. In particular, supposing \( id : A \leftrightharpoons A\), we get the term \( run ~( arr _\textrm{r}~ id ) : C \otimes \textsf{1} \rightsquigarrow \textsf{1}\), which ignores any input C to return \(\mathsf {()}\).
4.2 Semantics of \(\textsc {rrArr}\)
We now formalize the intuitive interpretation through the semantics presented in Figure 4. We define a base set of values containing unit, pairs, and tagged values, which we type in the conventional way. Recursively typed values \(\textbf{roll} ~w\) are only manipulated by the base invertible combinators c.
The semantics of \(\textsc {rrArr}\) again takes the form of three relations: one for unidirectional arrows and two for invertible arrows. The first (\(\mu ~w_1 \mapsto w_2\)) reads that \(\mu \) maps \(w_1\) to \(w_2\), confirming the intuition that unidirectional arrows represent functions. The second (\(\alpha ~w ; w_1 \mapsto w_2\)) and third ( ) read that given parameter w, \(\alpha \) maps \(w_1\) to \(w_2\) under the forward (resp. backward) evaluation, confirming the intuition that our invertible arrows correspond to parameterized bijections. The rules closely follow the informal descriptions presented in the previous section. We assume a base invertible semantics for combinators c of the form \(c~w_1\mapsto w_2\), invoked by the rules concerning \( arr \) for each arrow.
) read that given parameter w, \(\alpha \) maps \(w_1\) to \(w_2\) under the forward (resp. backward) evaluation, confirming the intuition that our invertible arrows correspond to parameterized bijections. The rules closely follow the informal descriptions presented in the previous section. We assume a base invertible semantics for combinators c of the form \(c~w_1\mapsto w_2\), invoked by the rules concerning \( arr \) for each arrow.
The semantics satisfies the desired properties of subject reduction and invertibility, although we refer to our mechanized formalization for the details.Footnote 6
4.3 Locally Invertible Interpretation
Recall that our goal is to define a locally invertible interpretation, whereas the straightforward semantics of Section 4.2 depended on a unidirectional evaluation. In this section, we give an alternative interpretation of \(\textsc {rrArr}\), utilizing the reversible reader (\(\textsf{RReader}\)) [23] to interpret the invertible arrow combinators.

Here, \(\textsf{RReader} \;C \;A \;B\) consists of the bijections of type \(C \otimes A \leftrightharpoons C \otimes B\) that keep the C part unchanged. This arrow was originally introduced with the intention of modelling a bijection with some “static” input C [23]. Regarding \(\rightsquigarrow \), we use the irreversibility effect [26] that leverages the fact that every unidirectional computation can be simulated by a locally invertible computation yielding “garbage” [8], as:
Combining these two effects is a novel point of \(\textsc {rrArr}\); in particular, we contribute the core constructs of \( case! \), \(\mathbin {\gg !}\), \( pin \) and \( run \), which enable communication between the two. Locally invertible interpretations of the primitives in each system have been given in the existing results. Here, we extend the results with the operations novel to \(\textsc {rrArr}\), to show that the two systems together give a locally invertible model of partially invertible computations.
As our target invertible language, we use \(\varPi ^o\) [26], whose combinators c constitute a minimal set of (non-total) invertible operations. The combinators support sequential composition ( ), parallel composition (\(c_1 \otimes c_2\) and \(c_1 \oplus c_2\)), and importantly, a local inversion operator (\(c^\dagger \)) such that
), parallel composition (\(c_1 \otimes c_2\) and \(c_1 \oplus c_2\)), and importantly, a local inversion operator (\(c^\dagger \)) such that  . Figure 5 shows a summary of the primitives; their behavior should be obvious from the types (see the Agda formalization for details).
. Figure 5 shows a summary of the primitives; their behavior should be obvious from the types (see the Agda formalization for details).
We now proceed to give another interpretation of the core constructs of \(\textsc {rrArr}\).
-
Partially invertible branching. Given \(\alpha _1\) and \(\alpha _2\) with \(\llbracket \alpha _1 \rrbracket : C \otimes A \leftrightharpoons C \otimes B\) and \(\llbracket \alpha _2 \rrbracket : D \otimes A \leftrightharpoons D \otimes B\), we must construct
$$ \llbracket case! ~\alpha _1~\alpha _2 \rrbracket : (C \oplus D) \otimes A \leftrightharpoons (C \oplus D) \otimes B. $$Using \( distr \), we can convert \((C \oplus D) \otimes A\) to \(C \otimes A \oplus D \otimes A\), after which \(\llbracket \alpha _1 \rrbracket \) and \(\llbracket \alpha _2 \rrbracket \) can be run in parallel. Factoring out the B, we get the required transformation.

-
Pinning. Given \(\alpha \) with \(\llbracket \alpha \rrbracket : (C \otimes D) \otimes A \leftrightharpoons (C \otimes D) \otimes B\) , we must produce
$$ \llbracket pin \;\alpha \rrbracket : C \otimes (D \otimes A) \leftrightharpoons C \otimes (D \otimes B). $$As the reversible reader arrow \(\llbracket \alpha \rrbracket \) already returns the context C unchanged, we only need to shuffle the inputs and outputs appropriately.

-
Partially invertible composition. Given \(\mu \) and \(\alpha \) with \(\llbracket \mu \rrbracket : C \leftrightharpoons G \otimes D\) and \(\llbracket \alpha \rrbracket : D \otimes A \leftrightharpoons D \otimes B\), we must construct
$$ \llbracket \mu \mathbin {\gg !}~ \alpha \rrbracket : C \otimes A \leftrightharpoons C \otimes B. $$The basic idea is to run \(\llbracket \mu \rrbracket \) to produce a D-typed value to run \(\llbracket \alpha \rrbracket \) on, however, this brings with it unwanted garbage. Fortunately, since \(\llbracket \alpha \rrbracket \) is a reversible reader arrow, it is guaranteed to preserve the D-component, meaning that after running it we have the same D and G-values available to us as before. These can be turned back into the original C value by running \(\llbracket \mu \rrbracket \) backwards, giving the transformation required.

Note that this is precisely the construction underlying the reversible updates [5] of imperative reversible languages, and that \(\llbracket \alpha \rrbracket \) preserving the context is crucial for the construction to succeed.
-
Running invertible computations. Given \(\alpha \) with \(\llbracket \alpha \rrbracket : C \otimes A \leftrightharpoons C \otimes B\), we must produce
$$ \llbracket run ~\alpha \rrbracket : C \otimes A \leftrightharpoons G \otimes B, $$for some G. Clearly it suffices to take \(\llbracket \alpha \rrbracket \) with \(G = C\), and we are done.
4.4 Correctness
We now state the desired correctness properties of our locally invertible interpretation, which show that it is equivalent to the direct semantics of Figure 4 and that \(\llbracket \alpha \rrbracket \) is indeed a reversible reader arrow (i.e., it preserves the context C).
Theorem 3
(rrArr\(\dashrightarrow \varPi ^o\) Soundness).
-
\(\mu ~w_1 \mapsto w_2\) implies \(\llbracket \mu \rrbracket ~w_1 \mapsto (g, w_2)\) for some g.
-
\(\alpha ~w; w_1 \mapsto w_2\) implies \(\llbracket \alpha \rrbracket ~(w, w_1) \mapsto (w, w_2)\). \(\square \)
Theorem 4
(rrArr\(\dashrightarrow \varPi ^o\) Completeness).
-
\(\llbracket \mu \rrbracket ~w_1 \mapsto (g, w_2)\) implies \(\mu ~w_1 \mapsto w_2\).
-
\(\llbracket \alpha \rrbracket ~(w, w_1) \mapsto (w', w_2)\) implies \(w = w'\) and \(\alpha ~w;w_1 \mapsto w_2\). \(\square \)
The theorems do not refer to the backward evaluation directly, utilizing the invertibility of both \(\textsc {rrArr}\) and \(\varPi ^o\).
4.5 Higher-order Computation
The previous sections laid out the fundamental ideas for representing partial invertibility in a locally invertible setting. However, with \(\textsc {rrArr}\) being first-order, it is not sufficient to be able to interpret Kalpis in a simple way. In this section, we extend the language with four new combinators enabling proper higher-order computation, shown in Figure 6.
The combinators \( curry \) and \( app \) are the standard currying and evaluation maps, creating and applying functions \(A \rightarrow B\). Their invertible counterparts \( curry ^\bullet \) and \( app ^\bullet \) provide the final core construct from Section 2: abstraction and application of invertible computations. They operate over parameterized bijections, abstracting the parameter to get a bijection value \(A \leftrightarrow B\). The values are extended accordingly with two new closure forms \(\langle \mu , w \rangle : A \rightarrow B\) and \(\langle \alpha , w \rangle : A \leftrightarrow B\), where \(\mu : C \otimes A \rightsquigarrow B\),  , and w : C, representing staged unidirectional and invertible computations, respectively.
, and w : C, representing staged unidirectional and invertible computations, respectively.
Having higher-order computation in the invertible setting has been challenging [2, 12, 39, 40]. Borrowing the idea from [39, 40], we address the issue by leveraging the fact that the function and bijection values are only part of invertible computations as parameters of parameterized bijections; hence, we only need a limited form of higher-orderness. We extend \(\varPi ^o\) with two additional primitive operations:

The former takes a combinator with an auxiliary piece of “state” C, and abstracts it into a bijection given a value of C. The latter applies a bijection, and saves it to enable reversing the operation later. To represent the values of type \(A \leftrightarrow B\) in \(\varPi ^o\), we introduce a third form of closure \(\langle f, w \rangle \), where we have \(f : C \otimes A \leftrightharpoons C \otimes B\) and w : C. Then, the semantics of \( app_\leftrightharpoons \) and \( curry_\leftrightharpoons \) are as follows:

As before, the inverse semantics is symmetric; e.g., \(( curry_\leftrightharpoons ~f)^\dagger ~(w, clos ) \mapsto w \; \text {if} \; clos = \langle f, w \rangle \). The (non-total) invertibility of \( curry_\leftrightharpoons \) is trivial, as its inverse fails unless its input matches the corresponding output; it is essentially a unidirectional function embedded in the invertible world. Since observational equality of closure values is undecidable, the equality check must rely on some other, intensional (e.g., syntactic) equality. Practically, this means that the combinator can only be used to create a closure and then subsequently undo the very same closure. However, this does not pose an issue for the translation from \(\textsc {rrArr}\), where closures will only result from uses of \( curry \) and \( curry ^\bullet \), both of which are unidirectional arrows (\(\rightsquigarrow \)). These unidirectional arrows will only be executed backwards as part of partially invertible compositions (\(\mathbin {\gg !}\)), which ensures that the input is the same as the corresponding output.
Now, we can interpret \(\llbracket app \rrbracket = app_\leftrightharpoons \), \(\llbracket app ^\bullet \rrbracket = app_\leftrightharpoons \), and

The former construction curries \(\llbracket \mu \rrbracket : C \otimes A \leftrightharpoons G \otimes B\) given w : C by creating a one-shot closure \(\langle f , \textbf{inl} ~w \rangle \) which turns into \(\langle f , \textbf{inr} ~g \rangle \) for g : G when first applied, and fails on a second application.
The theorems of Section 4.4 extend without difficulty to the higher-order combinators, although the statement is somewhat more intricate due to the differing set of closure values between \(\textsc {rrArr}\) and \(\varPi ^o\). We refer to the mechanized formalization in Agda for details.
5 Interpreting Kalpis with Arrows
Theorem 1 (Section 3.6) suggests that a unidirectional term-in-context \(\varGamma \vdash u : A\) can be seen as a function from \(\varGamma \) to A, and that an invertible term-in-context \(\varGamma ; \varTheta \vdash r : A\) can be seen as a bijection between \(\varTheta \) and A parameterized by \(\varGamma \). Then, it is natural that they be related with the two arrows \(({-} \rightsquigarrow {-})\) and  of \(\textsc {rrArr}\), respectively. In this section, we give a formal account of this relation by translating terms of Kalpis into \(\textsc {rrArr}\), giving by extension a compositional locally invertible interpretation of Kalpis.
of \(\textsc {rrArr}\), respectively. In this section, we give a formal account of this relation by translating terms of Kalpis into \(\textsc {rrArr}\), giving by extension a compositional locally invertible interpretation of Kalpis.
We first define some operations on typing contexts. We define \(\varGamma ^\times \) as
It is straightforward to define an operator \( lookup _x : \varGamma ^\times \rightsquigarrow A\) provided that \(\varGamma (x) = A\). We also use a combinator \( split _{\varTheta _1,\varTheta _2} : (\varTheta _1 \uplus \varTheta _2)^\times \leftrightharpoons \varTheta _1^\times \otimes \varTheta _2^\times \) for splitting the linear environments. Then, we give two type-directed transformations: \(\varGamma \vdash u : A \dashrightarrow \mu \) that transforms u to \(\mu \) of type \(\varGamma ^\times \rightsquigarrow A\), and \(\varGamma ; \varTheta \vdash r : A \dashrightarrow \alpha \) that transforms r to \(\alpha \) of type  . For the purposes of the translation, we consider a fixed set of type constructors \(\textsf{T}~\overline{B} :\,\!:= \textsf{1} \mid A \otimes B \mid A \oplus B \mid \textsf{Rec}_A\), identifying \(\mu X. A\) with \(\textsf{Rec}_A\).
. For the purposes of the translation, we consider a fixed set of type constructors \(\textsf{T}~\overline{B} :\,\!:= \textsf{1} \mid A \otimes B \mid A \oplus B \mid \textsf{Rec}_A\), identifying \(\mu X. A\) with \(\textsf{Rec}_A\).
Without loss of generality, we drop unnecessary \(\textbf{with}\)-conditions, so that a \(\textbf{case} ^\bullet \)-expression with one branch needs no \(\textbf{with}\)-clause, and one with two branches needs only one clause. Due to the space limitations, we present only the most representative cases here, and point the interested reader to the mechanized formalization in Agda.Footnote 7
-
Case T-UCase (\(A \oplus B\)).

We can duplicate \(\varGamma ^\times \) using \( clone \) and use one copy to construct \(A \oplus B\) with \(\mu \). Using \( distl : A \otimes (B \oplus C) \leftrightharpoons A \otimes B \oplus A \otimes C\), which is easily derived, we distribute the second copy of \(\varGamma \) over the sum. Then, the required combinator can be constructed through a combination of partially invertible composition (\(\mathbin {\gg !}\)) and branching (\( case! \)), where we have
 .
. -
Case T-RCase (\(A \oplus B\)).

The idea is similar to T-UCase, but we now operate in the invertible world, so we split \((\varTheta _1 \uplus \varTheta _2)^\times \) instead of duplicating \(\varGamma \), and compose using \(\ggg _\textrm{r}\) instead of \(\gg !\). The combinator \( case ~\alpha _1~\alpha _2~\alpha _3 \triangleq left _\textrm{r}~\alpha _1 \ggg _\textrm{r} right _\textrm{r}~\alpha _2 \ggg _\textrm{r} \alpha _3^\dagger \) with type
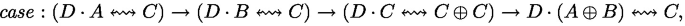
provides an invertible branching operator analogous to \( case! \), with a postcondition for merging the branches. We convert \(\mu : \varGamma ^\times \rightsquigarrow (C \rightarrow \textsf{Bool})\) to an arrow
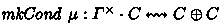 through the \( mkCond \) operator, which can be defined using \( pin \), \( case! \) and \( app \) in tandem.
through the \( mkCond \) operator, which can be defined using \( pin \), \( case! \) and \( app \) in tandem. -
Cases \(\textsc {T-Abs}^\bullet \), T-RApp.

For \(\textsc {T-Abs}^\bullet \), we get
 , which we \( curry ^\bullet \) after handling the unit. For T-RApp, \(\alpha \) transforms \(\varTheta ^\times \) to A, letting \(\mu \) be applied through a partially invertible composition (\(\mathbin {\gg !}\)) with \( app ^\bullet \).
, which we \( curry ^\bullet \) after handling the unit. For T-RApp, \(\alpha \) transforms \(\varTheta ^\times \) to A, letting \(\mu \) be applied through a partially invertible composition (\(\mathbin {\gg !}\)) with \( app ^\bullet \). -
Case T-Pin.

We have \(\alpha \) producing \(C \otimes A\), and with parameter \(\varGamma ^\times \otimes C\), we can apply \(\mu \) to produce B. Thus, we must shift C from the output into the parameter, and \( pin \) achieves just that.
Correctness. Finally, we show the correctness of the translation with respect to the semantics of Sections 3.5 and 4.2. Before we state correctness, we must first define a translation of the values, since they differ between Kalpis and \(\textsc {rrArr}\).
The base values are translated trivially, whereas the closures are translated according to the type-directed translation given above (cf. Case \(\textsc {T-Abs}^\bullet \)). We also define a translation of value environments \(\gamma \) in the obvious way.
Then, we can state the correctness of the translation as below.
Theorem 5
(Kalpis\(\dashrightarrow \textsc {rrArr} \) Soundness).
-
\(\varGamma \vdash u : A \dashrightarrow \mu \) and \(\gamma \vdash u \Downarrow v\) implies \(\mu ~\llbracket \gamma \rrbracket \mapsto \llbracket v \rrbracket \)
-
\(\varGamma ; \varTheta \vdash r : A \dashrightarrow \alpha \) and \(\gamma ; \theta \vdash r \Rightarrow v\) implies \(\alpha ~\llbracket \gamma \rrbracket ; \llbracket \theta \rrbracket \mapsto \llbracket v \rrbracket \). \(\square \)
This theorem does not refer to the backward evaluation directly, utilizing the invertibility of both Kalpis and \(\textsc {rrArr}\). The completeness part, on the other hand, does need a separate statement for the backward direction, since there is no a priori guarantee that the output w is of the form \(\llbracket \theta \rrbracket \).
Theorem 6
(Kalpis\(\dashrightarrow \textsc {rrArr} \) Completeness).
-
\(\varGamma \vdash u : A \dashrightarrow \mu \) and \(\mu ~\llbracket \gamma \rrbracket \mapsto w\) implies \(\gamma \vdash u \Downarrow v\) for v with \(\llbracket v \rrbracket = w\).
-
\(\varGamma ; \varTheta \vdash r : A \dashrightarrow \alpha \) and \(\alpha ~\llbracket \gamma \rrbracket ;\llbracket \theta \rrbracket \mapsto w\) implies \(\gamma ; \theta \vdash r \Rightarrow v\) for v with \(\llbracket v \rrbracket = w\).
-
\(\varGamma ; \varTheta \vdash r : A \dashrightarrow \alpha \) and
 implies \(\gamma ; v \vdash r \Leftarrow \theta \) for \(\theta \) with \(\llbracket \theta \rrbracket = w\). \(\square \)
implies \(\gamma ; v \vdash r \Leftarrow \theta \) for \(\theta \) with \(\llbracket \theta \rrbracket = w\). \(\square \)
We refer to the Agda code in the supplementary material for the proofs.
6 Related Work
Kalpis and \(\textsc {rrArr}\) are not the first to support partial invertibility. In the imperative setting, languages such as Janus [35, 53], Frank’s R [17], and R-While [19] support a limited form of partial invertibility via reversible update operators [6]. An example of a reversible update statement is \(x \mathbin {\texttt {+=}} e\), whose effect can be reverted by the corresponding inverse statement \(x \mathbin {\texttt {-=}} e\). Both statements use the same e, which need not be invertible (e.g., \(x \mathbin {\texttt {+=}} yz\) is reverted by \(x \mathbin {\texttt {-=}} yz\), and vice versa). In the functional setting, Theseus [27] allows a bijection to take additional parameters, but only provided that they are available at compile time. RFun version 2,Footnote 8 an extension to the original RFun [54], and CoreFun [25] allow more flexibility via so-called ancilla parameters, which are translated to auxiliary inputs and outputs of the invertible computation. Their approach is similar to Kalpis ’s but more restrictive since they lack support for the \( pin \) operator and higher-order computation. Jeopardy [31] is a recent invertible language where even irreversible functions can be inverted in certain contexts depending on implicitly available information. However, this is still work in progress, and seems to lean closer to program inversion methods than the lightweight type-based approach we employ.
Sparcl [39, 40] is the most flexible system that supports partial invertibility to our knowledge, which is realized through a more advanced language foundation. Instead of bijections \(A \leftrightarrow B\), Sparcl features invertible data marked by the type \(A^\bullet \), which implicitly corresponds to some bijection \(S \leftrightarrow A\). This idea of invertible data is inherited from the HOBiT language [38], which represents lens combinators [15, 16] as higher-order functions to achieve applicative-style higher-order bidirectional programming [36, 37]. The type system of Sparcl ensures that a closed linear function between invertible data \(!(A^\bullet \multimap B^\bullet )\) is isomorphic to a (non-total) bijection between A and B, so that partial invertibility can be represented as a function that takes both unidirectional and invertible data \(C \rightarrow A^\bullet \multimap B^\bullet \). This representation affords more flexibility than Kalpis does: invertible data is allowed to be captured in abstractions, and can even appear in subcomponents of datatypes (e.g., \(\textsf{Int} \otimes (\textsf{Int}^\bullet )\) or \(\textsf{Int} \oplus (\textsf{Int}^\bullet )\) are both valid types). However, this flexibility comes at the cost of complexity, requiring a semantics that interleaves partial evaluation and invertible computation, making a locally invertible interpretation difficult. We remark that the holed residuals \(\langle x. E \rangle \) featured in Sparcl’s core system bear a strong resemblance to bijections \(\lambda ^\bullet x. r\) in Kalpis.
Our combinator language \(\textsc {rrArr}\) can be seen as an extension of \(\textsf {ML}_{\varPi }\), an arrow metalanguage on top of the invertible language \(\varPi \) treating information creation and loss (non-totality and irreversibility) as an effect [26]. By combining their work with the reversible reader arrow [23], we are able to give erasing (weakening) as a derived operation defined via the operator \( run \) (as demonstrated in Section 4). Further research on the nontrivial interaction between the arrows, such as an equational characterization and a denotational model, is left for future work. While the previous work is able to treat non-totality as part of an effect, we assume some non-total operations in the underlying invertible system due to the inclusion of recursive and functional types.
The design of Kalpis is inspired by the arrow calculus of Lindley, Wadler, and Yallop [33], which is a metalanguage for the conventional representation of arrows [24], analogous to the monad metalanguage [42]. In a sense, Kalpis can be seen as a counterpart to the arrow calculus for \(\textsc {rrArr}\). For example, the treatment of \(\lambda ^\bullet x. r\) is actually inherited from the arrow calculus, where arrows cannot be nested in general [34], unless the underlying arrow supports application to form a monad [24]. To the best of our knowledge, a monad-based programming system for invertible/reversible computation does not exist, though there are some closely related results, including monads for nondeterministic computation (such as [14]) and a monadic programming framework for bidirectional transformations [20, 52]. However, these existing approaches lack the guarantee of bijectivity—a motivation to use invertible languages.
The importance of partial invertibility has been recognized in the neighboring literature on program inversion—program transformations that derive a program of \(f^{-1}\) for a given program of f. Partial inversion [44, 47] essentially applies a binding-time analysis [21, 28] to an input program, where the static data can be treated as unidirectional inputs. The technique is further extended to treat results of inverses as unidirectional [3, 29, 30]. This treatment is similar to the role of \( pin \) in Kalpis and Sparcl [39, 40] in that it converts invertible data into “static” parameters. Some approaches to program inversion are more liberal: semi inversion [41] essentially converts a program into a logic program, where there is no clear boundary between unidirectional and invertible data, and the PINS system [49], in addition to an original program, can take a control structure of an inverse program to effectively synthesize inverses that may not mirror the control structures of the original. The main limitation of program inversion is that as a program transformation it may fail, often for reasons that are not obvious to programmers.
7 Conclusion
We have presented a set of four core constructs for partially invertible programming, demonstrated their expressiveness through examples, and shown that they can be given a locally invertible interpretation, thus solving an open problem in the field. The four constructs are (1) partially invertible branching, (2) pinning invertible inputs, (3) partially invertible composition, and (4) abstraction and application of invertible computations. We designed the partially invertible language Kalpis on top of these constructs and formalized its syntax, type system and operational semantics. We then presented \(\textsc {rrArr}\), a low-level arrow language with primitives directly corresponding to the constructs, and gave it a locally invertible interpretation based on two effects—the irreversibility effect [26] and the reversible reader [23]. Finally, we presented a type-directed translation from Kalpis to \(\textsc {rrArr}\), showing how to support expressive partial invertibility on top of a locally invertible foundation. Proofs of all theorems stated in the paper are formalized by the accompanying Agda code.Footnote 9
Notes
- 1.
The name stands for “Kalpis—an Arrow-based Locally and Partially Invertible System”.
- 2.
- 3.
- 4.
The loss of totality is unavoidable in order to achieve r-Turing completeness [5], i.e., the ability to define all computable bijections.
- 5.
- 6.
- 7.
- 8.
- 9.
References
Abel, A., Chapman, J.: Normalization by evaluation in the delay monad: A case study for coinduction via copatterns and sized types. In: Levy, P., Krishnaswami, N. (eds.) Proceedings 5th Workshop on Mathematically Structured Functional Programming, MSFP@ETAPS 2014, Grenoble, France, 12 April 2014. EPTCS, vol. 153, pp. 51–67 (2014). https://doi.org/10.4204/EPTCS.153.4
Abramsky, S.: A structural approach to reversible computation. Theor. Comput. Sci. 347(3), 441–464 (2005). https://doi.org/10.1016/j.tcs.2005.07.002
Almendros-Jiménez, J.M., Vidal, G.: Automatic partial inversion of inductively sequential functions. In: Horváth, Z., Zsók, V., Butterfield, A. (eds.) Implementation and Application of Functional Languages, 18th International Symp osium, IFL 2006, Budapest, Hungary, September 4-6, 2006, Revised Selected Papers. Lecture Notes in Computer Science, vol. 4449, pp. 253–270. Springer (2006). https://doi.org/10.1007/978-3-540-74130-5_15
Antoy, S., Echahed, R., Hanus, M.: A needed narrowing strategy. J. ACM 47(4), 776–822 (2000). https://doi.org/10.1145/347476.347484
Axelsen, H.B., Glück, R.: What do reversible programs compute? In: Hofmann, M. (ed.) Foundations of Software Science and Computational Structures - 14th International Conference, FOSSACS 2011, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2011, Saarbrücken, Germany, March 26-April 3, 2011. Proceedings. Lecture Notes in Computer Science, vol. 6604, pp. 42–56. Springer (2011). https://doi.org/10.1007/978-3-642-19805-2_4
Axelsen, H.B., Glück, R., Yokoyama, T.: Reversible machine code and its abstract processor architecture. In: Diekert, V., Volkov, M.V., Voronkov, A. (eds.) Computer Science - Theory and Applications, Second International Symposium on Computer Science in Russia, CSR 2007, Ekaterinburg, Russia, September 3-7, 2007, Proceedings. Lecture Notes in Computer Science, vol. 4649, pp. 56–69. Springer (2007). https://doi.org/10.1007/978-3-540-74510-5_9
Baker, H.G.: NREVERSAL of fortune - the thermodynamics of garbage collection. In: Bekkers, Y., Cohen, J. (eds.) Memory Management, International Workshop IWMM 92, St. Malo, France, September 17-19, 1992, Proceedings. Lecture Notes in Computer Science, vol. 637, pp. 507–524. Springer (1992). https://doi.org/10.1007/BFb0017210
Bennett, C.H.: Logical reversibility of computation. IBM Journal of Research and Development 17(6), 525–532 (11 1973). https://doi.org/10.1147/rd.176.0525
Bernardy, J., Boespflug, M., Newton, R.R., Peyton Jones, S., Spiwack, A.: Linear haskell: practical linearity in a higher-order polymorphic language. PACMPL 2(POPL), 5:1–5:29 (2018). https://doi.org/10.1145/3158093
Bowman, W.J., James, R.P., Sabry, A.: Dagger traced symmetric monoidal categories and reversible programming. Work-in-progress report in the 3rd Workshop on Reversible Computation (July 2011), available from https://www.williamjbowman.com/resources/cat-rev.pdf (visited Jan 23, 2024)
Capretta, V.: General recursion via coinductive types. Logical Methods in Computer Science 1(2), Article No. 1 (2005). https://doi.org/10.2168/LMCS-1(2:1)2005
Chen, C., Sabry, A.: A computational interpretation of compact closed categories: reversible programming with negative and fractional types. Proc. ACM Program. Lang. 5(POPL), 1–29 (2021). https://doi.org/10.1145/3434290
Davies, R., Pfenning, F.: A modal analysis of staged computation. J. ACM 48(3), 555–604 (2001). https://doi.org/10.1145/382780.382785
Fischer, S., Kiselyov, O., Shan, C.: Purely functional lazy nondeterministic programming. J. Funct. Program. 21(4-5), 413–465 (2011). https://doi.org/10.1017/S0956796811000189
Foster, J.N., Greenwald, M.B., Moore, J.T., Pierce, B.C., Schmitt, A.: Combinators for bi-directional tree transformations: a linguistic approach to the view update problem. In: Palsberg, J., Abadi, M. (eds.) Proceedings of the 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2005, Long Beach, California, USA, January 12-14, 2005. pp. 233–246. ACM (2005). https://doi.org/10.1145/1040305.1040325
Foster, J.N., Greenwald, M.B., Moore, J.T., Pierce, B.C., Schmitt, A.: Combinators for bidirectional tree transformations: A linguistic approach to the view-update problem. ACM Trans. Program. Lang. Syst. 29(3), Article No. 17 (2007). https://doi.org/10.1145/1232420.1232424
Frank, M.P.: The R programming language and compiler. MIT Reversible Computing Project Memo #M8, MIT AI Lab (7 1997), available on: https://github.com/mikepfrank/Rlang-compiler/blob/master/docs/MIT-RCP-MemoM8-RProgLang.pdf
Glück, R., Kawabe, M.: A program inverter for a functional language with equality and constructors. In: Ohori, A. (ed.) Programming Languages and Systems, First Asian Symposium, APLAS 2003, Beijing, China, November 27-29, 2003, Proceedings. Lecture Notes in Computer Science, vol. 2895, pp. 246–264. Springer (2003). https://doi.org/10.1007/978-3-540-40018-9_17
Glück, R., Yokoyama, T.: A linear-time self-interpreter of a reversible imperative language. Computer Software 33(3), 3_108–3_128 (2016). https://doi.org/10.11309/jssst.33.3_108
Goldstein, H., Frohlich, S., Wang, M., Pierce, B.C.: Reflecting on random generation. Proc. ACM Program. Lang. 7(ICFP) (aug 2023). https://doi.org/10.1145/3607842
Gomard, C.K., Jones, N.D.: A partial evaluator for the untyped lambda-calculus. J. Funct. Program. 1(1), 21–69 (1991). https://doi.org/10.1017/S0956796800000058
Heunen, C., Kaarsgaard, R.: Quantum information effects. Proc. ACM Program. Lang. 6(POPL), 1–27 (2022). https://doi.org/10.1145/3498663
Heunen, C., Kaarsgaard, R., Karvonen, M.: Reversible effects as inverse arrows. Electronic Notes in Theoretical Computer Science 341, 179–199 (2018). https://doi.org/10.1016/j.entcs.2018.11.009
Hughes, J.: Generalising monads to arrows. Sci. Comput. Program. 37(1-3), 67–111 (2000). https://doi.org/10.1016/S0167-6423(99)00023-4
Jacobsen, P.A.H., Kaarsgaard, R., Thomsen, M.K.: \(\sf CoreFun\) : A typed functional reversible core language. In: Kari, J., Ulidowski, I. (eds.) Reversible Computation - 10th International Conference, RC 2018, Leicester, UK, September 12-14, 2018, Proceedings. Lecture Notes in Computer Science, vol. 11106, pp. 304–321. Springer (2018). https://doi.org/10.1007/978-3-319-99498-7_21
James, R.P., Sabry, A.: Information effects. In: Field, J., Hicks, M. (eds.) Proceedings of the 39th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2012, Philadelphia, Pennsylvania, USA, January 22-28, 2012. pp. 73–84. ACM (2012). https://doi.org/10.1145/2103656.2103667
James, R.P., Sabry, A.: Theseus: a high level language for reversible computing. Work-in-progress report in the 6th Conference on Reversible Computation (2014), available from https://legacy.cs.indiana.edu/~sabry/papers/theseus.pdf (visited Jan 23, 2024)
Jones, N.D., Gomard, C.K., Sestoft, P.: Partial evaluation and automatic program generation. Prentice Hall international series in computer science, Prentice Hall (1993)
Kirkeby, M.H., Glück, R.: Inversion framework: Reasoning about inversion by conditional term rewriting systems. In: PPDP ’20: 22nd International Symposium on Principles and Practice of Declarative Programming, Bologna, Italy, 9-10 September, 2020. pp. 9:1–9:14. ACM (2020). https://doi.org/10.1145/3414080.3414089
Kirkeby, M.H., Glück, R.: Semi-inversion of conditional constructor term rewriting systems. In: Gabbrielli, M. (ed.) Logic-Based Program Synthesis and Transformation - 29th International Symposium, LOPSTR 2019, Porto, Portugal, October 8-10, 2019, Revised Selected Papers. Lecture Notes in Computer Science, vol. 12042, pp. 243–259. Springer (2019). https://doi.org/10.1007/978-3-030-45260-5_15
Kristensen, J.T., Kaarsgaard, R., Thomsen, M.K.: Jeopardy: An invertible functional programming language. Work-in-progress paper presented at 34th Symposium on Implementation and Application of Functional Languages abs/2209.02422 (2022). https://doi.org/10.48550/arXiv.2209.02422
Landauer, R.: Irreversibility and heat generation in the computing process. IBM Journal of Research and Development 5(3), 183–191 (1961). https://doi.org/10.1147/rd.53.0183
Lindley, S., Wadler, P., Yallop, J.: The arrow calculus. J. Funct. Program. 20(1), 51–69 (2010). https://doi.org/10.1017/S095679680999027X
Lindley, S., Wadler, P., Yallop, J.: Idioms are oblivious, arrows are meticulous, monads are promiscuous. Electron. Notes Theor. Comput. Sci. 229(5), 97–117 (2011). https://doi.org/10.1016/j.entcs.2011.02.018
Lutz, C.: Janus: a time-reversible language (1986), Letter to R. Landauer. Available on: http://tetsuo.jp/ref/janus.pdf
Matsuda, K., Wang, M.: Applicative bidirectional programming with lenses. In: Fisher, K., Reppy, J.H. (eds.) ICFP. pp. 62–74. ACM (2015). https://doi.org/10.1145/2784731.2784750
Matsuda, K., Wang, M.: Applicative bidirectional programming: Mixing lenses and semantic bidirectionalization. J. Funct. Program. 28, e15 (2018). https://doi.org/10.1017/S0956796818000096
Matsuda, K., Wang, M.: Hobit: Programming lenses without using lens combinators. In: Ahmed, A. (ed.) ESOP. Lecture Notes in Computer Science, vol. 10801, pp. 31–59. Springer (2018). https://doi.org/10.1007/978-3-319-89884-1_2
Matsuda, K., Wang, M.: Sparcl: A language for partially-invertible computation. Proc. ACM Program. Lang. 4(ICFP) (8 2020). https://doi.org/10.1145/3409000
Matsuda, K., Wang, M.: Sparcl: A language for partially-invertible computation. J. Funct. Program. (in press). https://doi.org/10.1017/S0956796823000126
Mogensen, T.Æ.: Semi-inversion of guarded equations. In: Glück, R., Lowry, M.R. (eds.) Generative Programming and Component Engineering, 4th International Conference, GPCE 2005, Tallinn, Estonia, September 29 - October 1, 2005, Proceedings. Lecture Notes in Computer Science, vol. 3676, pp. 189–204. Springer (2005). https://doi.org/10.1007/11561347_14
Moggi, E.: Notions of computation and monads. Inf. Comput. 93(1), 55–92 (1991). https://doi.org/10.1016/0890-5401(91)90052-4
Mu, S., Hu, Z., Takeichi, M.: An injective language for reversible computation. In: Kozen, D., Shankland, C. (eds.) Mathematics of Program Construction, 7th International Conference, MPC 2004, Stirling, Scotland, UK, July 12-14, 2004, Proceedings. Lecture Notes in Computer Science, vol. 3125, pp. 289–313. Springer (2004). https://doi.org/10.1007/978-3-540-27764-4_16
Nishida, N., Sakai, M., Sakabe, T.: Partial inversion of constructor term rewriting systems. In: Giesl, J. (ed.) Term Rewriting and Applications, 16th International Conference, RTA 2005, Nara, Japan, April 19-21, 2005, Proceedings. Lecture Notes in Computer Science, vol. 3467, pp. 264–278. Springer (2005). https://doi.org/10.1007/978-3-540-32033-3_20
Pierce, B.C.: Types and programming languages. MIT Press (2002)
Reynolds, J.C.: Definitional interpreters for higher-order programming languages. Higher-Order and Symbolic Computation 11(4), 363–397 (1998). https://doi.org/10.1023/A:1010027404223
Romanenko, A.: Inversion and metacomputation. In: Consel, C., Danvy, O. (eds.) Proceedings of the Symposium on Partial Evaluation and Semantics-Based Program Manipulation, PEPM’91, Yale University, New Haven, Connecticut, USA, June 17-19, 1991. pp. 12–22. ACM (1991). https://doi.org/10.1145/115865.115868
Sabry, A., Valiron, B., Vizzotto, J.K.: From symmetric pattern-matching to quantum control. In: Baier, C., Lago, U.D. (eds.) Foundations of Software Science and Computation Structures - 21st International Conference, FOSSACS 2018, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2018, Thessaloniki, Greece, April 14-20, 2018, Proceedings. Lecture Notes in Computer Science, vol. 10803, pp. 348–364. Springer (2018). https://doi.org/10.1007/978-3-319-89366-2_19
Srivastava, S., Gulwani, S., Chaudhuri, S., Foster, J.S.: Path-based inductive synthesis for program inversion. In: Hall, M.W., Padua, D.A. (eds.) Proceedings of the 32nd ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2011, San Jose, CA, USA, June 4-8, 2011. pp. 492–503. ACM (2011). https://doi.org/10.1145/1993498.1993557
Stinson, D., Paterson, M.: Cryptography: Theory and Practice. Textbooks in Mathematics, CRC Press (2018)
Wadler, P.: A taste of linear logic. In: Borzyszkowski, A.M., Sokolowski, S. (eds.) Mathematical Foundations of Computer Science 1993, 18th International Symposium, MFCS’93, Gdansk, Poland, August 30 - September 3, 1993, Proceedings. Lecture Notes in Computer Science, vol. 711, pp. 185–210. Springer (1993). https://doi.org/10.1007/3-540-57182-5_12
Xia, L., Orchard, D., Wang, M.: Composing bidirectional programs monadically. In: Caires, L. (ed.) Programming Languages and Systems - 28th European Symposium on Programming, ESOP 2019, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2019, Prague, Czech Republic, April 6-11, 2019, Proceedings. Lecture Notes in Computer Science, vol. 11423, pp. 147–175. Springer (2019). https://doi.org/10.1007/978-3-030-17184-1_6
Yokoyama, T., Axelsen, H.B., Glück, R.: Principles of a reversible programming language. In: Ramírez, A., Bilardi, G., Gschwind, M. (eds.) Proceedings of the 5th Conference on Computing Frontiers, 2008, Ischia, Italy, May 5-7, 2008. pp. 43–54. ACM (2008). https://doi.org/10.1145/1366230.1366239
Yokoyama, T., Axelsen, H.B., Glück, R.: Towards a reversible functional language. In: Vos, A.D., Wille, R. (eds.) RC. Lecture Notes in Computer Science, vol. 7165, pp. 14–29. Springer (2011). https://doi.org/10.1007/978-3-642-29517-1_2
Acknowledgments
We thank Eijiro Sumii, Oleg Kiselyov, and other Sumii-Matsuda Lab members for useful feedback on a preliminary version of this research. This work is partially supported by JSPS KAKENHI Grant Numbers, JP19K11892, JP20H04161, and JP22H03562, EPSRC Grant EXHIBIT: Expressive High-Level Languages for Bidirectional Transformations (EP/T008911/1), and Royal Society Grant Bidirectional Compiler for Software Evolution (IES\(\backslash \) R3\(\backslash \) 170104). This work was also partially supported by a scholarship awarded to the first author by the Marianne and Marcus Wallenberg Foundation (SJF application BA21-0019).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
Data Availability
The accompanying artifact that contains the prototype implementation of Kalpis and the Agda formalization mentioned in this paper is available from https://doi.org/10.5281/zenodo.10511566.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Ågren Thuné, A., Matsuda, K., Wang, M. (2024). Reconciling Partial and Local Invertibility. In: Weirich, S. (eds) Programming Languages and Systems. ESOP 2024. Lecture Notes in Computer Science, vol 14577. Springer, Cham. https://doi.org/10.1007/978-3-031-57267-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-57267-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57266-1
Online ISBN: 978-3-031-57267-8
eBook Packages: Computer ScienceComputer Science (R0)












 .
.
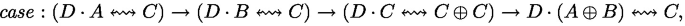
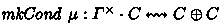 through the
through the 
 , which we
, which we 
 implies
implies 