Abstract
Inlining is a crucial optimisation when compiling functional programming languages. This paper describes how we have implemented and verified function inlining and loop specialisation for PureCake, a verified compiler for a Haskell-like (purely functional, lazy) programming language. A novel aspect of our formalisation is that we justify inlining by pushing and pulling  -bindings. All of our work has been mechanised in the HOL4 interactive theorem prover.
-bindings. All of our work has been mechanised in the HOL4 interactive theorem prover.
You have full access to this open access chapter, Download conference paper PDF
Keywords


1 Introduction
It can be tricky to generate high-quality code from lazy, purely functional programs for a number of reasons. One of these reasons is that functional programming encourages a brief declarative style that makes heavy use of shorthands (e.g., for partially-applied functions) and higher-order functions [8]. Producing good code from such input requires a well-developed inliner, as noted [17] by the developers of the Glasgow Haskell Compiler (GHC):
“One of the trickiest aspects of a compiler for a functional language is the handling of inlining. [...] Effective inlining is particularly crucial in getting good performance.”
This paper is about implementing and verifying an inliner that can specialise loops for PureCake, an end-to-end verified compiler for a Haskell-like language [10].
The inliner by example. The following simple example demonstrates what our inliner does. Imagine that a programmer is to write a function that increments every element of a list of integers. The programmer should write:

Here, the programmer has relied on the library function  below to perform the necessary list traversal.
below to perform the necessary list traversal.

To generate high-quality code for  , the compiler must both inline and specialise
, the compiler must both inline and specialise  . Our inliner takes the definition of
. Our inliner takes the definition of  above and produces the following code.
above and produces the following code.

In particular, the inliner has combined the following code transformations:
-
selective expansion of function definitions at call sites; and
-
loop specialisation of recursive functions with known arguments (e.g., argument f to
 is always
is always  in
in  ).
).
Contributions. Our work adds verified inlining and loop specialisation to PureCake. Our inliner is capable of optimisations such as the one above. More specifically, we make the following contributions:
-
1.
We define and prove sound a relation that encapsulates an envelope of semantics-preserving inlinings (§ 4). This relation is independent of the heuristics of any real implementation. It is proved sound using a novel formalisation of inlining as pushing/pulling of
 -bindings.
-bindings. -
2.
We derive sound equational principles that allow us to lift out arguments which remain constant during recursion, such as f in
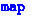 in the example above (§ 5). These principles are phrased such that they can be used in the relation above and have the effect of specialising loops.
in the example above (§ 5). These principles are phrased such that they can be used in the relation above and have the effect of specialising loops. -
3.
We implement an inliner that can specialise loops and verify that its action preserves semantics, relying on the formalisations above (§ 6).
-
4.
We integrate our inliner into the PureCake compiler and its verification (§ 7).
All of our work is mechanised using the HOL4 interactive theorem prover, and our development is open-source.Footnote 1 To the best of our knowledge, ours is the first verified inliner for a lazy functional programming language, and the first verified loop specialiser for any functional language.
2 The Inliner by Example
We begin with a high-level explanation of how our inliner works, before diving into verification details in later sections. We will show the transformations the inliner performs step-by-step. As a running example, we use the code from the previous section with one modification: we lift  to a separate function
to a separate function  for clarity. The input code after this modification is as follows:
for clarity. The input code after this modification is as follows:

Our inliner is installed very early in the PureCake compiler, directly after parsing and binding group analysis. Binding group analysis processes the program above to the code below, breaking up the mutually recursive bindings into a nesting of  -expressions. Note that there is no dependency between add1 and map, so their definitions could be reordered; for this example we put add1 first.
-expressions. Note that there is no dependency between add1 and map, so their definitions could be reordered; for this example we put add1 first.

The inliner receives this program as input. As it traverses the program, it records known definitions that it may wish to inline later on. In particular, it maintains a mapping from names to their definitions, which starts off empty. Therefore, after processing line 18 (i.e., the definition of add1), the mapping contains only the definition of add1, that is,  .
.
The inliner then moves to line 19, the  -expression that defines map. The definition of map is recursive, so the inliner analyses it to determine whether any of its arguments remain constant over all recursive calls. In the case of map, it finds that the first argument, f, remains constant. This means that it can loop specialise map to produce the following equivalent definition.
-expression that defines map. The definition of map is recursive, so the inliner analyses it to determine whether any of its arguments remain constant over all recursive calls. In the case of map, it finds that the first argument, f, remains constant. This means that it can loop specialise map to produce the following equivalent definition.

Our inliner does not alter the definition of map in the program, but it does add this equivalent definition to its mapping of known definitions. We will very soon see why it is useful to pull out the constant argument f.
The inliner moves on to the definition of suc_list on line 22.

After pulling out the constant argument f above, the inliner considers map to be a single-argument function. Therefore, the application map add1 here seems fully applied and the inliner will rewrite it. First, it transforms map add1 into the following.

Notice the use of a binding  to assign the constant argument f of map. Then, the inliner recurses into this expression, replacing f by add1 in the second row of the pattern match:
to assign the constant argument f of map. Then, the inliner recurses into this expression, replacing f by add1 in the second row of the pattern match:

The inliner recurses again into the modified subexpression add1 x, and realises that add1 (which is mapped to  ) is fully applied. Therefore, it inlines add1 too:
) is fully applied. Therefore, it inlines add1 too:

Once again, the inliner recurses on the modified subexpression, turning the innermost i into x:

The final code produced by the inliner is below. The definition of suc_list has been rewritten so extensively that it now resembles a copy of map which has been specialised to the add1 function.

Some dead code remains, e.g.,  (line 46) and
(line 46) and  (line 49). We perform a simple dead code elimination pass immediately after the inliner to remove these.
(line 49). We perform a simple dead code elimination pass immediately after the inliner to remove these.
Single-pass optimisation. Note that our inliner does not make multiple passes over input code, in contrast to the presentation above. It performs a single top-down pass over its input, calling itself recursively only on function applications or variables that it has successfully rewritten. The depth of this recursion is bounded by a simple user-configurable recursion limit.
3 Setting: PureCake
We implement and verify our inlining and specialisation optimisations as part of the verified compiler PureCake. In this section, we describe both the PureCake project at a high level, and the key aspects of its formalisation on which we rely.
What is PureCake? PureCake [10] is an end-to-end verified compiler for a Haskell-like language known as PureLang. Here, a “Haskell-like” language is one which: is purely functional with monadic effects; evaluates lazily; and has a syntax resembling that of Haskell. PureCake compiles PureLang to the CakeML language, which is call-by-value and ML-like, and has an end-to-end verified compiler [12, 14]. CakeML targets machine code, so PureCake and CakeML can be composed to produce end-to-end guarantees for the compilation of PureLang to machine code [10, §6].
The PureCake compiler is designed to be realistic: it accepts a featureful input language and generates performant code. This makes it an ideal setting for verified inlining and specialisation optimisations. We add these to PureCake as PureLang-to-PureLang transformations.
Formalisation details. PureLang is formalised using two ASTs: compiler expressions and semantic expressions, denoted \( ce \) and \( e \) respectively [10, §3.2]. The compiler implementation uses compiler expressions, and their semantics is given by desugaring into semantic expressions (denoted desugar, of type \( ce \rightarrow e \)).
The call-by-name operational semantics of PureLang is defined over its simpler semantic expressions [10, §3.3]. This semantics admits an equational theory [10, §3.4] which is sound and complete with respect to contextual equivalence. Its equivalence relation, \( e_{{\textrm{1}}} \, \cong \, e_{{\textrm{2}}} \), is based on an untyped applicative bisimulation from Abramsky’s lazy \(\lambda \)-calculus [1] and is proved congruent via Howe’s method [7], i.e., expressions composed of equivalent subexpressions are themselves equivalent.
PureCake’s compiler passes are verified in two stages.
-
1.
A binary syntactic relation is defined over semantic expressions (\(e_1\; \mathcal {R}\; e_2\)). The relation is proved to imply \( e_{{\textrm{1}}} \, \cong \, e_{{\textrm{2}}} \), so \(e_1\) and \(e_2\) have identical observable behaviour in all contexts. Intuitively, the syntactic relation carves out an envelope of possible valid transformations, independent of the heuristics of any real implementation.
-
2.
The implementation is then defined over compiler expressions, with concrete heuristics. It is verified to perform only those valid transformations expressed by the syntactic relation.
Composition of the two stages produces the overall proof that the action of the compiler implementation preserves semantics. A key benefit of this approach is that heuristics remain an implementation detail in stage 2, and can be changed without incurring the significant proof obligations of stage 1.
Approach and paper outline. We can now describe more precisely the steps we took to add inlining and loop specialisation to the PureCake compiler.
-
§ 4 (stage 1) We defined a relation which captures an envelope of valid inlining transformations, and proved that this relation preserves semantics.
-
§ 5 We formalised loop specialisation using PureLang’s equational theory such that it can be used in the envelope mentioned above.
-
§ 6 (stage 2) We implemented the overall inlining and specialisation transformations over compiler expressions, verifying that they fit the envelopes.
-
§ 7 We integrated our inliner into the PureCake compiler pipeline and its top-level correctness result.
-
§ 8 We benchmarked the performance of the output of the inliner.
4 Inlining as a Relational Envelope
In this section, we define a relation which characterises all the inlinings that we wish to perform. We then prove that any code transformation contained within this relational envelope must preserve semantics.
4.1 Understanding the relation
We begin by describing the intuition behind our relation.
Inlining is not substitution. Inlining is a more complex transformation than substitution or \(\beta \)-conversion. If we were to view inlining as a special case of these, we would generate unsatisfactory code. In particular, consider the example below: inlining based on substitution must replace all three occurrences of f with its definition; inlining based on \(\beta \)-conversion would remove the  -binding.
-binding.

By contrast, a real inliner must be able to choose whether to inline a definition per use of that definition. In other words, the inliner should decide which usages of a given definition are rewritten on a case-by-case basis. For the example above, a real inliner should produce the code below. Note that it chooses to inline the function f only at the usage which fully applies it.

Of course, a real inliner would further transform  into
into  (this is in fact a \(\beta \)-conversion). For clarity in this example, we do not show that step.
(this is in fact a \(\beta \)-conversion). For clarity in this example, we do not show that step.
Inlining is a series of  transformations. The key intuition behind our inlining transformations is as follows. We push \(\textbf{let}\)-bindings into expressions as far as possible, rewrite the result, then pull the bindings out again. We illustrate this by example below, starting from the same initial code as above.
transformations. The key intuition behind our inlining transformations is as follows. We push \(\textbf{let}\)-bindings into expressions as far as possible, rewrite the result, then pull the bindings out again. We illustrate this by example below, starting from the same initial code as above.

We now push in the  -binding which defines f to produce a series of equivalent expressions. First, we push it in one step past the list constructor
-binding which defines f to produce a series of equivalent expressions. First, we push it in one step past the list constructor  :
:

Next, we push it in through the function application f  :
:

Now, we choose to rewrite the use of f under the first  to
to  :
:

Note that we have chosen not to perform any other rewrites of f, because other uses of f are not fully applied.
We can now reverse the pushing in of  -bindings, i.e., we pull them out instead. The final result is as follows, where f is inlined exactly as we wanted:
-bindings, i.e., we pull them out instead. The final result is as follows, where f is inlined exactly as we wanted:

Stacking  transformations. Above, our example shows how we can inline a single
transformations. Above, our example shows how we can inline a single  -binding: we push it inwards, use it for rewriting, and pull it outwards back to its original position. We can generalise this straightforwardly to handle a list of
-binding: we push it inwards, use it for rewriting, and pull it outwards back to its original position. We can generalise this straightforwardly to handle a list of  -bindings. This mimics the implementation of a real inliner, which must carry with it a collection of definitions it may wish to inline.
-bindings. This mimics the implementation of a real inliner, which must carry with it a collection of definitions it may wish to inline.
Consider the following example, in which an inliner attempts to rewrite the expression  and carries definitions
and carries definitions  .
.

Just as with a single  -binding, we can push in the stack of
-binding, we can push in the stack of  -bindings, rewrite, and pull them out again. This produces the following expression.
-bindings, rewrite, and pull them out again. This produces the following expression.

The only complication in generalising to a stack of  -bindings is that some definitions can depend on others. In the example above, the definition of g depends on f. This is why we model the bindings as a list: this preserves scoping correctly, ensuring we do not break any dependencies between definitions.
-bindings is that some definitions can depend on others. In the example above, the definition of g depends on f. This is why we model the bindings as a list: this preserves scoping correctly, ensuring we do not break any dependencies between definitions.
Note that this intuition of pushing in and pulling out of  -bindings applies only to the formalisation that justifies our inlining rewrites. The implementation of our inliner performs no such push/pull transformations: as one might expect, it merely carries around a simple (unordered) map of variable names to their definitions. This map represents exactly the set of definitions that the inliner may wish to use for rewriting at usage sites.
-bindings applies only to the formalisation that justifies our inlining rewrites. The implementation of our inliner performs no such push/pull transformations: as one might expect, it merely carries around a simple (unordered) map of variable names to their definitions. This map represents exactly the set of definitions that the inliner may wish to use for rewriting at usage sites.
4.2 Defining a Semantics-Preserving Envelope
We now describe an inductive relation, \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \), which characterises all of the inlining transformations that we perform. We prove that any transformation described by the relation lies within the equational theory of PureLang (\(\cong \), § 3). Therefore, the relation describes only semantics-preserving transformations.
The relation \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \) should be read as follows: expression \( e_{{\textrm{1}}} \) can be transformed into expression \( e_{{\textrm{2}}} \) under the definitions in the list l. Both \( e_{{\textrm{1}}} \) and \( e_{{\textrm{2}}} \) are PureLang semantic expressions, and l is a list of definitions. Each such definition is of the form \( x \leftarrow e \), associating name x with semantic expression e. We will first describe the formal meaning of \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \), which is best understood via its soundness theorem, Theorem 1. Then in following subsections, we describe key parts of the definition of \(\leadsto \).
Theorem 1 relates derivations of \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \) with \(\cong \), PureLang’s equational theory, assuming pre and lets_ok. The definitions of pre and lets_ok are shown in Figure 1—they enforce distinct variable names between both the expression \( e_{{\textrm{1}}} \) and each of the definitions in l to avoid inadvertent clashes or capture.
Theorem 1
Soundness of \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \).
where  and
and 
In particular, expressions \( e_{{\textrm{1}}} \) and \( e_{{\textrm{2}}} \) related in the context of definitions l produce equal expressions (according to \(\cong \)) under the stack of \(\textbf{let}\)-bindings corresponding to l. The latter correspondence is encapsulated by the definition of \(\textbf{lets}\), which nests \(\textbf{let}\)-bindings. This theorem is proved by induction over the derivation of \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \). In upcoming subsections, we will examine key rules of \(\leadsto \) and their cases in this inductive proof.
When the inliner is first invoked, it is passed an entire PureLang program and has no knowledge of any definitions. In other words, its mapping of variable names to known definitions is empty, corresponding to the list l being empty ([]). In this case, we can simplify Theorem 1 by instantiating \(l \mapsto []\), and unfolding the definitions of \({\textsf {pre}}\; l\) and \({\textsf {lets\_ok}}\; l\). This produces the following theorem:
Theorem 2
Soundness of \([] \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \).
We can read this as follows: if we can transform some closed \( e_{{\textrm{1}}} \) which satisfies barendregt to some \( e_{{\textrm{2}}} \) according to \(\leadsto \), then \( e_{{\textrm{1}}} \) and \( e_{{\textrm{2}}} \) are equivalent. The barendregt predicate restricts the variable naming convention within \( e_{{\textrm{1}}} \) to avoid problems with variable capture, because PureLang has explicit names. In particular, barendregt is the well known Barendregt variable convention that enforces unique free/bound variable names across an entire program [3].
The precise definition of barendregt is not necessary here. Suffice it to say that in order to discharge this assumption, our inliner implementation will rely on a freshening pass. This pass \(\alpha \)-renames programs such that they obey the Barendregt variable convention, and therefore satisfy barendregt.
Reflexivity. We must allow the inliner to choose whether to rewrite a usage site on a case-by-case basis (§ 4.1). Therefore, the inliner must be allowed not to inline, i.e., it must be able to leave an expression unchanged. Therefore the \(\leadsto \) relation has a reflexivity rule:

The refl case of the proof of Theorem 1 boils down to showing the equation \(\textbf{lets} \, l \, e \, \cong \, \textbf{lets} \, l \, e \), which is trivial due to reflexivity of \(\cong \).
Inlining. The simplest rule for inlining uses a definition found in the list l (where mem denotes list membership) to rewrite a variable:

In particular, if l associates name x with definition e, then the variable \(\textbf{var} \, x \) can be replaced by expression e. The inline case of Theorem 1 requires establishing:
Proof outline
We first derive a lemma that allows us to duplicate a \(\textbf{let}\)-binding from l, assuming lets_ok (defined in Figure 1 such that it enables this lemma):
Equipped with the Let-dup lemma, we proceed as follows:

\(\square \)
Let. We can now inline known definitions, but we must be able to learn those definitions in the first place. The rule Let allows us to add a \(\textbf{let}\)-bound definition to the stack l, using the append operator (\(\mathbin {++}{}\)).

Proof outline
Let case of Theorem 1.

\(\square \)
Above, we can push and pull \(\textbf{lets}\) through \(\textbf{let}\) because the precondition pre enforces sufficiently distinct variable names.
Note that this rule records the unmodified expression \( e_{{\textrm{1}}} \) in the stack of known definitions l. It could instead use the \(\leadsto \)-transformed expression \( e'_{{\textrm{1}}} \). The proof strategy with this modification is essentially unchanged, except we must reverse our applications of the inductive hypotheses.
Congruences. We must be able to apply \(\leadsto \) within subexpressions. Therefore, we have several congruence rules, such as the following:

Each such case in Theorem 1 requires showing that we can push/pull \(\textbf{lets}\) into/out of subexpressions. Once again, the precondition pre permits this by enforcing sufficiently distinct variable names. The remainder of the proof follows from congruence of \(\cong \).
Simplification. The following rule allows \(\leadsto \) to carry out any transformation that preserves \(\cong \):

The simp case in Theorem 1 is a direct consequence of the transitivity of \(\cong \).
This rule permits the inliner to modify (and in particular, simplify) generated expressions during its operation. There are two important uses of this ability:
-
Turning fully applied \(\lambda \)-abstractions into a stack of \(\textbf{let}\)-bindings. This allows recursive applications of inlining (see rule trans below).

-
Freshening names of bound variables (i.e., \(\alpha \)-renaming). This happens directly before application of the rule trans below.
Transitivity. To permit recursion into recently inlined expressions, \(\leadsto \) has a transitivity rule:

In particular, \( e_{{\textrm{1}}} \) can be transformed to \( e_{{\textrm{3}}} \) if there is some intervening \( e_{{\textrm{2}}} \) which can act as a stepping stone.
Unusually, we require precondition pre to hold of intermediate expression \( e_{{\textrm{2}}} \). This is demanded by the proof of Theorem 1, in which we can only instantiate inductive hypotheses if we first establish pre. Unfortunately, \( l \Vdash e_{{\textrm{1}}} \leadsto e_{{\textrm{2}}} \) and \({\textsf {pre}}\; l\; e_{{\textrm{1}}} \) are not enough to derive \({\textsf {pre}}\; l\; e_{{\textrm{2}}} \). Fortunately, we can freshen bound variable names (i.e., \(\alpha \)-rename) sufficiently to establish pre, and justify this freshening using rule simp above.
Specialisation. The \(\leadsto \) relation must be able to support loop specialisation, as described for the map function in § 2. Therefore, it has a rule spec which permits conversion of a \(\textbf{letrec}\) into a \(\textbf{let}\), as long as there is a proof that the conversion preserves \(\cong \).

That is, if we can \(\cong \)-convert some \(\textbf{letrec}\; x = e_{{\textrm{1}}} \) to some \(\textbf{let}\; x = e_{{\textrm{2}}} \), then we can append \( x \leftarrow e_{{\textrm{2}}} \) to the stack of known definitions when processing \(\textbf{letrec}\) body \( e_{{\textrm{3}}} \). Again, we require restrictions on variable naming: the variables bound in \( e_{{\textrm{2}}} \) and \( e_{{\textrm{3}}} \) must be disjoint, and the bound variable x must not appear free in \( e_{{\textrm{2}}} \).
Proof outline
spec case of Theorem 1.

\(\square \)
5 Specialisation of Recursive Bindings
Our example in § 2 showed that our inliner can specialise applications of recursive functions such as map to known arguments such as add1. This is possible whenever constant arguments such as f can be pulled out of the recursion. That is, whenever we can transform recursive functions like map (left) into equivalent code which makes the constant argument explicit using map’ (right):

In this section, we describe how we prove correctness of such transformations. Critically, our proofs can be used in the spec rule of \(\leadsto \) from the previous section.
5.1 Understanding Specialisation
Like \(\leadsto \), our specialisation transformation is justified using equational reasoning. We illustrate the equational steps below, again noting that the implementation is much more direct. We use the map example of § 1, eliding parts not relevant to specialisation. The input is therefore as follows:

We first make a local copy of the recursive definition map, named map’:

We then \(\eta \)-expand the final usage of the copy map’:

Next, we pull out the new \(\lambda \)-abstractions to the top-level:

We then \(\alpha \)-rename the constant argument in the copy (here, f becomes g):

The first major step (transform 1) replaces the constant argument g with the known value to which the function map’ is always applied, f:

The second major step (transform 2) deletes the now unused argument g. It removes the argument from both the definition of map’ and all calls to map’:

We push back in some of the top-level \(\lambda \)-abstractions, in this case just l:

Finally, \(\eta \)-contraction removes the \(\lambda \)-abstraction over l:

Most of the steps are straightforwardly justified in PureLang’s equational theory. However, the steps marked transform 1 and transform 2 are more involved. We discuss these below.
5.2 Key Lemmas for Specialisation
Both transform 1 and transform 2 require a substitution-like traversal of the entire subexpression under consideration. It is not clear how to justify these traversals using simple equational reasoning in PureLang’s theory. Therefore, we resort to more cumbersome simulation proofs to establish \(\cong \) by appealing to its definition in terms of PureLang’s operational semantics.
For transform 1, we prove a theorem of the following form. Here call_with_arg holds only if every application of f in e is applied to \(\textbf{var} \, y \) after n arguments, and the names f and y are never rebound within e.

Though the variable w is free in the theorem above, it is a closed constant expression in most parts of the proof, which simplifies the derivation of this theorem. This is because \(\cong \) is defined over open terms in terms of closing substitution and a relation over closed terms. The proof of this theorem is a large simulation based on the semantics of PureLang.
For transform 2, we prove a theorem with a similar shape. This time, remove_call_arg is an inductive relation that ensures y never appears in \(e_1\) and relates \(e_1\) to a second expression \(e_2\) in which the relevant argument has been removed from each application of f.
We prove this theorem by a large simulation too. The simulation strategy is necessary because \(\textbf{letrec}\) causes (potentially non-terminating) recursion.
6 Implementing a Correct Inliner
In this section, we describe the implementation of our inliner and the proof that its action lies within the \(\leadsto \) relation described in § 4. We also touch on three other transformations mentioned previously: specialisation, freshening of bound variables, and dead code elimination. Our inliner relies on all three.
6.1 Preliminaries
We implement our inliner within a state monad with the following type:

Here, name set is a set of variable names; we will see its usage shortly. This monad has standard return/bind operators, and we will use Haskell-style do-notation to show definitions written within the monad.
The inliner itself has the following signature:
In other words, the inliner transforms compiler expressions to compiler expressions within the state monad, requiring several other inputs:
-
An unordered mapping m from names to expressions. This is the “memory” of the inliner: the set of known definitions which it can use for rewriting.
-
Heuristic h decides whether to “remember” a definition for future inlining. It accepts an expression \( ce \) and returns a boolean: if true, the definition should be remembered.
-
Natural number k is the recursion limit for the inliner, used to bound its recursion into rewritten expressions.
-
The name set parameter hidden within the monad keeps track of all variable names (whether bound or free) in input expression \( ce \). It is used to ensure that sufficiently fresh variable names are chosen when freshening the names of bound variables.
6.2 Inliner implementation
The inliner traverses compiler expressions top-down. During the traversal, it performs two key operations: rewriting a variable to a known definition from memory, and adding a new definition to memory.
Rewriting a variable. There are two kinds of expressions in which the inliner will attempt to rewrite a variable. The first is a lone variable (of the form \(\textbf{var} \, x \)), and the second is an application of a variable to some arguments (of the form \(\left( \textbf{var} \, x \right) \cdot \ldots \)). The latter case is used to inline fully applied functions only.
In the lone variable case, the inliner is defined as follows:

That is, on encountering a free variable x the inliner does one of the following:
-
Leaves the variable unchanged if the definition of x is unknown, or the recursion limit has been reached, or the definition of x is known to be a \(\lambda \)-abstraction. The last case may seem unusual, but note we do not rewrite variables to \(\lambda \)-abstractions unless the result will be fully applied. This is handled in the application case below.
-
Rewrites the variable by inserting the expression \( ce \) found in memory, and then recurses into \( ce \) with a decremented recursion limit.
In the application case, the inliner is defined as follows:

That is, on encountering a free variable x applied to n arguments the inliner does the following:
-
1.
Recurses into the arguments to produce n new arguments.
-
2.
Searches for variable x in memory and checks the recursion limit. If x is not found or the recursion limit has been reached, the inliner returns variable x applied to the n new arguments.
-
3.
Rewrites x using its definition from memory, m(x).
-
4.
Freshens the resulting application of m(x) to the n new arguments.
-
5.
Attempts to convert the freshened application to a series of \(\textbf{let}\)-bindings. This is precisely the conversion shown in eq. () (pg. 11). Note that the conversion fails (returns None) if m(x) is not fully applied, in which case the inliner bails out of inlining the definition of x.
-
6.
Recurses into the newly produced series of \(\textbf{let}\)-bindings with a decremented recursion limit.
The conversion into \(\textbf{let}\)-bindings is critical: it allows the inliner to learn the definitions of the applied arguments \( ce'_{{\textrm{1}}} ,\; \ldots ,\; ce'_{ n } \) for future inlining within the function body of m(x). Note that we only decrement the recursion limit when the size of the input expression may not have strictly decreased. This happens only when performing non-structural recursions, which only occur when we recurse into a definition rewritten from memory.
Remembering a new definition. The inliner can remember \(\textbf{let}\)- or \(\textbf{letrec}\)-bound expressions.
In the \(\textbf{let}\) case, it is defined as follows:

That is, the inliner recurses into \( ce_{{\textrm{1}}} \) (without decrementing the recursion limit), before memorising the definition \( x \leftarrow ce_{{\textrm{1}}} \) and recursing into \( ce_{{\textrm{2}}} \) with the augmented memory. The function remember records the definition only when two conditions are satisfied: the definition is cheap, and heuristic h returns true.
As the name suggests, cheap is a predicate that determines whether a definition is cheap to compute, and so will not slow the program down or cause loss of value sharing when inlined. The definition of cheap is as follows:

In the \(\textbf{letrec}\) case, the inliner must also perform specialisation. Its action is defined as follows:

This mirrors the \(\textbf{let}\) case almost exactly. The key difference is the use of remember_rec instead of remember: this does not check cheap, but does attempt specialisation (and bails out if it fails). We examine specialisation in the upcoming subsection.
Heuristics. So far, we have only implemented one heuristic based on expression size: the inliner only remembers definitions that are smaller than a user-configurable bound. Our implementation can accept any heuristic function as an input, making it straightforward to support new kinds of heuristic.
Implementing specialisation. Above, specialise transforms a \(\textbf{letrec}\)-binding into a \(\textbf{let}\)-binding before adding it to memory. We rely on two helper functions: can_specialise and extract_const_args.
The test can_specialise simply checks if we are able to specialise a recursive body. The body must be a \(\lambda \)-abstraction with some constant arguments. Then, extract_const_args will extract these constant arguments. It accepts a definition \( x \leftarrow ce \), where we know \( ce \) is a \(\lambda \)-abstraction of the form \(\lambda \, \overline{ x_{ n } }^{\, n } \, .\; ce \). It splits the formal parameters \(\overline{x_n}\) into \(x_1 \ldots x_m\) and \(x_{m + 1} \ldots x_n\), where m is the minimum number of arguments that x is invoked with recursively in body \( ce \). It further annotates the \(x_1 \ldots x_m\) with annotations \(a_1 \ldots a_m\), which describe whether the arguments remain constant for each recursive call. In the implementation of inline above, this has produced the annotated variables \(w_i^{a_i}\) and left the remainder of the \(\lambda \)-abstraction untouched (\(\lambda \, \overline{ y_{ m } }^{\, m } \, .\; ce' \)).
Then, specialise is defined as follows.

That is, it processes each annotated variable in turn, updating their call sites in body \( ce \) (i.e., performing transform 1 and transform 2 from § 5 simultaneously using specialise_each), producing a new set of formal parameters \(\overline{x_n}\). It determines which of these can be \(\eta \)-contracted (the final step in § 5) with a call to drop_common_suffix, and then returns the new \(\textbf{letrec}\) which accepts constant arguments \(\overline{y_i}\) at the top-level, and has \(\eta \)-contracted constant arguments \(\overline{z_j}\) applied directly already.
Freshening and Dead-Let Elimination. Our inliner assumes that its input expression has a variable naming convention which is sufficient to prevent it from accidentally capturing variables during operation. Therefore, we only give the inliner expressions which obey the Barendregt variable convention, which asserts unique bound variable names and disjoint bound/free names [3]. This is achieved by freshening (\(\alpha \)-renaming) bound variables directly before inlining, and further freshening before recursing into subexpressions taken from the inliner’s memory. For example, the inliner invokes freshen in eq. () (pg. 16) above. This is precisely why the inliner carries around a name set in its state monad: this set contains all variable names (whether bound or free) of the input expression. Freshening avoids names in this set when inventing fresh names, and returns an updated set each time it runs.
The output of the inliner also contains various unused \(\textbf{let}\)-bindings. We showed such bindings in the example of § 1 (namely, f and i). To remove such bindings, we run a dead-\(\textbf{let}\) elimination pass directly after the inliner.
Including these two auxiliary passes, the top-level definition of the inliner is as follows:

That is, the inliner freshens names, inlines definitions top-down starting with an empty (\(\varnothing \)) memory, then removes dead \(\textbf{let}\)s. Note that the top-level definition expects to receive only closed expressions, which is why it only passes bound variables (boundvars) to freshen. This respects our invariant that the name set contains all bound and free variable names, as there are no free variables.
6.3 Inliner correctness
In this section, we prove that the inliner implementation is correct. In the context of PureCake’s proof strategy as described in § 3:
-
(stage 1) Theorem 2 above (pg. 9) proved that \(\leadsto \) preserves semantics.
-
(stage 2) Theorem 3 below will prove that any transformation performed by the inliner lies within the \(\leadsto \) relation of § 4.
We then compose these results to produce our final soundness theorem: the output expression of the inliner is equivalent to its corresponding input.
Theorem 3
inline satisfies \(\leadsto \).
That is, after desugaring compiler expressions into semantic expressions (desugar, see § 3), the action of the inliner for input \( ce \), memory m, and name set \( ns \) lies within \(\leadsto \) for some stacked \(\textbf{let}\)s l when the following hold:
-
(memory_rel) m and l contain the same definitions, and each such definition both satisfies \({\textsf {wf}}\) below and has bound/free variables within \( ns \);
-
(barendregt) bound names in \( ce \) are unique, and disjoint from free names;
-
the bound variables of \( ce \) do not shadow (are disjoint from, \(\#\)) any variables with known definitions, i.e., those in the domain of m;
-
all bound/free variables of \( ce \) are within \( ns \); and
-
(\({\textsf {wf}}\)) \( ce \) is well-formed.
Proof outline
Induction over the implementation function inline. For each case of the proof, we apply rules of \(\leadsto \) to justify each atomic inlining operation. \(\square \)
Theorem 4
Top-level correctness of inliner.
Proof outline
Composition of Theorem 3 above with Theorem 2 (pg. 9), the soundness theorem for \(\leadsto \). Unfolding the definition of inliner, we use the soundness theorem of freshen, the closed assumption, and the application of inline to empty memory \(\varnothing \) to discharge the preconditions on Theorem 3. \(\square \)
7 Integration into the PureCake Compiler
We insert the inliner and its associated cleanup of dead \(\textbf{let}\)-bindings as PureLang-to-PureLang transformations early in the PureCake compiler. In particular, directly after parsing and binding group analysis, as shown in Figure 2. Elimination of dead \(\textbf{let}\)s happens directly afterwards.
Unusually, the inliner runs before type inference. Ideally, it would take place afterwards: it changes program structure significantly, and type inference should execute on code resembling user input to allow direct error-reporting. The reasoning behind this design choice is PureCake’s demand analysis, which facilitates strictness optimisations by annotating variables that can be evaluated eagerly. We found that running the inliner before demand analysis produces significantly better performance (§ 8, Figure 4). However, the soundness proof for demand analysis requires it to receive only well-typed input code. To run the inliner after type inference and before demand analysis, we would have to prove that it preserves well-typing, which is a significant undertaking due to PureLang’s untyped AST. Future iterations of PureLang’s AST are intended to be typed; therefore, we could consider proving type preservation in future work.
To update PureCake’s compiler correctness theorem after integrating our inliner, we must establish that the inliner preserves both semantics and various syntactic invariants. We have already presented our proof of semantics preservation in § 6. The latter syntactic invariants guarantee that compiler expressions are closed and satisfy well-formedness properties which are checked as part of parsing. For example, PureLang forbids degenerate function applications to zero arguments: this can be expressed in the AST for PureLang compiler expressions but is ill-formed. Establishing preservation of the invariants is mostly mechanical, but quite tedious and long-winded.
Graphs showing the performance impact of our inliner when executed after PureCake’s demand analysis. Performance is clearly worse compared to Figure 3; therefore we do not pursue this approach.
8 Benchmarks
In this section we measure the efficacy of our inliner. In particular, we benchmark code generated by PureCake to determine how much the addition of the inliner improves runtime and memory overhead.
Methodology. We evaluate the performance of several benchmark programs with and without the inliner enabled, using an Intel® Xeon® E-2186G and 64 GB RAM. We consider the same programs as presented by the PureCake developers in prior work [10, §7.1]. We also add a new suc_list program, which repeatedly applies the suc_list function shown in § 1 to a list of natural numbers. Like the PureCake developers, we measure wall-clock runtime and total heap allocations as reported by the CakeML runtime. Our measurements are facilitated by existing benchmarking scripts found in the PureCake development.
Results. Figure 3 shows our results, plotted as two bar graphs: the left shows runtime speedup, the right shows allocation reduction. In many cases, our inliner significantly improves performance; in all cases it does not worsen performance. The value for each plot is obtained by taking the base-2 logarithm of a ratio: the measurement without the inliner enabled (i.e., the longer duration or greater allocation) divided by the measurement with the inliner enabled. Expressed as a percentage, the most significant improvements are: a \({\sim }20\%\) reduction in the runtime of life, a \({\sim }15\%\) reduction in the allocations of suc_list.
Inliner placement. We noted in § 7 that our inliner should run before PureCake’s demand analysis. Here, we justify that design choice. In particular, we benchmark a version of the PureCake compiler which runs our inliner directly after demand analysis. The results are shown in Figure 4. The improvements in runtime and memory overhead are reduced for several benchmarks, and in some cases runtime even worsens overall. Therefore, our inliner should run before demand analysis for maximum benefit.
Code size and compile times. Simple measurements of code size show that our inliner can produce significantly larger CakeML programs (\({\sim }50\%\) increase); however CakeML’s efficient handling of inserted \(\textbf{let}\)s reduces the effect for binaries (\(<15\%\) overall increase). Compile times are unaffected: these remain dominated by PureCake’s type-checking and CakeML’s register allocation.
Line counts. Our work adds to PureCake significantly. Figure 1 shows line counts for each part of our development, measured using wc -l.
9 Related Work
Verified inlining in functional languages. CakeML [12] compiles a subset of Standard ML (strict, impure) to several mainstream architectures with end-to-end guarantees. It performs function inlining in its second intermediate language, ClosLang, which has first-class closures. A flow analysis discovers invocations of known functions, and simultaneously inlines closed functions which themselves do not contain closures. Use of de Bruijn indices sidesteps reasoning about shadowing and freshening. As in our work, recursive applications of inlining improve the performance of higher-order functions; we go one step further with specialisation and the inlining of open terms which can contain \(\lambda \)-abstractions.
CertiCoq [2] verifiably compiles Gallina (the metalanguage of Coq) to C light, an intermediate language early in CompCert’s pipeline. One of its passes [4] performs several shrink reductions simultaneously: transformations that only reduce code size. One such reduction is the inlining of functions which are applied exactly once; in this case, inlining is \(\beta \)-reduction, contrary to our discussion in § 4.1. Restriction to shrink reductions further removes the need for a recursion limit as code size strictly decreases on each recursive call. Their verification relies on a more general rewrite system which permits inlining of functions which are used multiple times. A separate pass [16] further inlines small non-recursive functions which can be applied multiple times; here a key concern is maintenance of A-normal form expressions. In all proofs, the Barendregt variable convention (i.e., barendregt) is used to avoid name clashes.
Pilsner [15] compiles a strict impure language to an idealised assembly, inlining select top-level functions in its intermediate representation. Recursive functions can be unrolled in this way, but not specialised. Again, the Barendregt variable convention is enforced. The focus here is on the novel proof technique of parametric inter-language simulations (PILS) to enable compositional compiler correctness, where PureCake focuses on mechanised whole-program compiler correctness for a realistic language.
Other verified inlining passes. CompCert [13] compiles a subset of C99, performing function inlining in its register transfer language (RTL). This control flow graph (CFG) representation differs considerably from the functional PureLang; inlining considers only top-level function declarations in the RTL setting. Rather than using a recursion limit, CompCert guarantees termination by forbidding inlining of functions within their own bodies.
CompCert also performs lazy code motion [19] within RTL. A special case of this transformation is loop-invariant code motion, which loosely resembles our specialisation: both are concerned with moving constant expressions out of loops, but in our functional setting loops are expressed as recursive functions. Their verification uses translation validation [18]: an unverified tool transforms code, and then per-run automation proves that semantics has been preserved.
The Plutus Tx language from the Cardano blockchain platform resembles a subset of Haskell, and is compiled to a custom language known as Plutus Core. The compiler is implemented as a GHC plugin: GHC machinery first lowers Plutus Tx to a System F-like language, which is then optimised and compiled further. The compiler is verified using translation certification [11], which aims to make translation validation approaches less brittle by combining automated and manual proof. As in PureCake, syntactic relations are used to encapsulate semantics-preserving transformations: automated proof shows that unverified code transformations inhabit the relations, and manual proof shows that the relations preserve semantics. Translation certification is robust to evolving compiler implementations because the syntactic proofs are more amenable to automated verification than the semantic ones. A syntactic relation akin to § 4 justifies inlining; however, semantic verification is ongoing work at the time of writing. The Barendregt variable convention is enforced in this work too.
Verified optimisation of realistic Haskell-like languages. The CoreSpec projectFootnote 2 tackles verified variants of Haskell as implemented by GHC. For example, GHC’s dependent types extensions were proposed using formal specifications of the syntax, semantics, and typing rules of GHC’s Core language [20]. The unverified tool hs-to-coq [6] translates Haskell code to Gallina (Coq’s metalanguage), leveraging Coq’s logic to enable equational reasoning about real-world programs. A future aim of the project is to derive Coq models of Core automatically from GHC’s implementation, prove correctness of optimisations within Coq, and integrate the resulting verified code back into GHC as a plugin. Where CoreSpec focuses on accurate modelling of GHC with the loss of some trust, PureCake instead sacrifices faithfulness for end-to-end guarantees.
GHC’s arity analysis pass [5] \(\eta \)-expands functions to avoid excessive thunk allocations. Its mechanised proof of correctness for a simplified Core language relies on an explicitly call-by-need semantics to show performance preservation, i.e., that \(\eta \)-expansion does not reduce value-sharing.
10 Summary and Future Work
This paper has described our work on a verified inlining and loop specialisation pass for PureLang, a lazy functional programming language. First, we verified a syntactic relation which defines an envelope of permitted inlining transformations, independent of heuristic choices. We used a novel phrasing of inlining as the pushing in and pulling out of  -bindings to prove the relation sound using PureLang’s equational theory. Our inliner implementation is then proven to remain within this envelope. We have integrated our work into the PureCake compiler, an end-to-end verified compiler, and demonstrated significant performance improvements. To the best of our knowledge, ours is the first verified function inliner for a lazy functional programming language, and the first verified loop specialiser for any functional language.
-bindings to prove the relation sound using PureLang’s equational theory. Our inliner implementation is then proven to remain within this envelope. We have integrated our work into the PureCake compiler, an end-to-end verified compiler, and demonstrated significant performance improvements. To the best of our knowledge, ours is the first verified function inliner for a lazy functional programming language, and the first verified loop specialiser for any functional language.
In future work, we intend to support loop unrolling and develop better heuristics that decide when to do inlining. Loop unrolling will probably involve augmenting the definition of \(\textbf{lets}\) so that it can hold both \(\textbf{let}\) expressions and \(\textbf{letrec}\)s. Developing good heuristics will require some careful experimentation with the compiler implementation. We do not expect adjustment to the inliner’s heuristics to impact our correctness proofs in any significant way, since the proofs are designed to be independent of heuristic choices.
Data Availability Statement
An artifact supporting the results presented in this paper is openly available on Zenodo [9]. The latest development version of PureCake is available on GitHub (https://github.com/cakeml/pure).
Notes
- 1.
https://github.com/cakeml/pure, see also our artifact hosted on Zenodo [9].
- 2.
References
Abramsky, S.: The lazy \(\lambda \)-calculus. In: Research Topics in Functional Programming. Addison Wesley (1990)
Anand, A., Appel, A.W., Morrisett, G., Paraskevopoulou, Z., Pollack, R., Bélanger, O.S., Sozeau, M., Weaver, M.Z.: CertiCoq: A verified compiler for Coq. In: Workshop on Coq for Programming Languages (CoqPL) (2017), https://popl17.sigplan.org/details/main/9/CertiCoq-A-verified-compiler-for-Coq
Barendregt, H.P.: The lambda calculus - its syntax and semantics, Studies in logic and the foundations of mathematics, vol. 103. North-Holland (1985)
Bélanger, O.S., Appel, A.W.: Shrink fast correctly! In: Principles and Practice of Declarative Programming (PPDP). ACM (2017). https://doi.org/10.1145/3131851.3131859
Breitner, J.: Formally proving a compiler transformation safe. In: Symposium on Haskell. ACM (2015). https://doi.org/10.1145/2804302.2804312
Breitner, J., Spector-Zabusky, A., Li, Y., Rizkallah, C., Wiegley, J., Weirich, S.: Ready, set, verify! Applying hs-to-coq to real-world Haskell code (experience report). Proc. ACM Program. Lang. 2(ICFP) (2018). https://doi.org/10.1145/3236784
Howe, D.J.: Proving congruence of bisimulation in functional programming languages. Inf. Comput. 124(2) (1996). https://doi.org/10.1006/inco.1996.0008
Hughes, J.: Why functional programming matters. Comput. J. 32(2) (1989). https://doi.org/10.1093/comjnl/32.2.98
Kanabar, H., Korban, K., Myreen, M.O.: Artifact for “Verified Inlining and Specialisation for PureCake” (2024). https://doi.org/10.5281/zenodo.10456887
Kanabar, H., Vivien, S., Abrahamsson, O., Myreen, M.O., Norrish, M., Åman Pohjola, J., Zanetti, R.: PureCake: A verified compiler for a lazy functional language. In: Programming Language Design and Implementation (PLDI). ACM (2023). https://doi.org/10.1145/3591259
Krijnen, J.O.G., Chakravarty, M.M.T., Keller, G., Swierstra, W.: Translation certification for smart contracts. In: Functional and Logic Programming (FLOPS). Lecture Notes in Computer Science, vol. 13215. Springer (2022). https://doi.org/10.1007/978-3-030-99461-7_6
Kumar, R., Myreen, M.O., Norrish, M., Owens, S.: CakeML: a verified implementation of ML. In: Principles of Programming Languages (POPL). ACM (2014). https://doi.org/10.1145/2535838.2535841
Leroy, X.: Formal verification of a realistic compiler. Commun. ACM 52(7) (2009). https://doi.org/10.1145/1538788.1538814
Myreen, M.O.: The CakeML project’s quest for ever stronger correctness theorems (invited paper). In: Interactive Theorem Proving (ITP). LIPIcs, vol. 193. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.ITP.2021.1
Neis, G., Hur, C., Kaiser, J., McLaughlin, C., Dreyer, D., Vafeiadis, V.: Pilsner: a compositionally verified compiler for a higher-order imperative language. In: International Conference on Functional Programming (ICFP). ACM (2015). https://doi.org/10.1145/2784731.2784764
Paraskevopoulou, Z., Li, J.M., Appel, A.W.: Compositional optimizations for CertiCoq. Proc. ACM Program. Lang. 5(ICFP) (2021). https://doi.org/10.1145/3473591
Peyton Jones, S.L., Marlow, S.: Secrets of the Glasgow Haskell Compiler inliner. Journal of Functional Programming 12 (2002)
Pnueli, A., Siegel, M., Singerman, E.: Translation validation. In: Tools and Algorithms for Construction and Analysis of Systems (TACAS). Lecture Notes in Computer Science, vol. 1384. Springer (1998). https://doi.org/10.1007/BFb0054170
Tristan, J., Leroy, X.: Verified validation of lazy code motion. In: Programming Language Design and Implementation (PLDI). ACM (2009). https://doi.org/10.1145/1542476.1542512
Weirich, S., Voizard, A., de Amorim, P.H.A., Eisenberg, R.A.: A specification for dependent types in Haskell. Proc. ACM Program. Lang. 1(ICFP) (2017). https://doi.org/10.1145/3110275
Acknowledgements
Hrutvik Kanabar was supported by the UK Research Institute in Verified Trustworthy Software Systems (VeTSS). Magnus Myreen was supported by Swedish Research Council grant 2021-05165.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Kanabar, H., Korban, K., Myreen, M.O. (2024). Verified Inlining and Specialisation for PureCake. In: Weirich, S. (eds) Programming Languages and Systems. ESOP 2024. Lecture Notes in Computer Science, vol 14577. Springer, Cham. https://doi.org/10.1007/978-3-031-57267-8_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-57267-8_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57266-1
Online ISBN: 978-3-031-57267-8
eBook Packages: Computer ScienceComputer Science (R0)


 is always
is always  in
in  ).
). -bindings.
-bindings.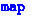 in the example above (§
in the example above (§ 
 .
.


 . Error bars are too small to be visible.
. Error bars are too small to be visible.
