Abstract
There has been much progress in designing bidirectional type systems and associated type synthesis algorithms, but mainly on a case-by-case basis. To remedy the situation, this paper develops a general and formal theory of bidirectional typing for simply typed languages: for every signature that specifies a mode-correct bidirectionally typed language, there exists a proof-relevant type synthesiser which, given an input abstract syntax tree, constructs a typing derivation if any, gives its refutation if not, or reports that the input does not have enough type annotations. Sufficient conditions for deriving a type synthesiser such as soundness, completeness, and mode-correctness are studied universally for all signatures. We propose a preprocessing step called mode decoration, which helps the user to deal with missing type annotations. The entire theory is formally implemented in Agda, so we provide a verified generator of proof-relevant type synthesisers as a by-product of our formalism.
You have full access to this open access chapter, Download conference paper PDF


1 Introduction
c Type inference is an important mechanism for the transition to well-typed programs from untyped abstract syntax trees, which we call raw terms. Here ‘type inference’ refers specifically to algorithms that ascertain the type of any raw term without type annotations. However, full parametric polymorphism entails undecidability in type inference, as do dependent types [9, 31]. In light of these limitations, bidirectional type synthesis emerged as a viable alternative, deciding the types of raw terms that meet some syntactic criteria and typically contain annotations. In their survey paper [10], Dunfield and Krishnaswami summarised the principles of bidirectional type synthesis and its wide coverage of languages with simple, polymorphic, dependent, and gradual types, among others.
While type inference is not decidable in general, for certain kinds of terms it is still possible to synthesise their types. For example, the type of a variable can be looked up in the context. Bidirectional type synthesis combines type synthesis on this subset of terms with type checking (based on a given type) on the rest. Formally, every judgement in a bidirectional type system is extended with a mode: (i)  for synthesis and (ii)
for synthesis and (ii)  for checking.
for checking.
The former indicates that the type A is an output, using both the context \(\varGamma \) and the term t as input, while for the latter, all three of \(\varGamma \), t, and A are input. The algorithm of a bidirectional type synthesiser can often be ‘read off’ from a well-designed bidirectional type system: as the synthesiser traverses a raw term, it switches between synthesis and checking, following the modes assigned to the judgements in the typing rules.
Despite sharing the same basic idea, bidirectional typing has been mostly developed on a case-by-case basis. Dunfield and Krishnaswami present informal design principles learned from individual bidirectional type systems, but in addition to crafting special techniques for individual systems, we should start to consolidate concepts common to a class of bidirectional type systems into a general and formal theory that gives mathematically precise definitions and proves theorems for the class of systems once and for all. In this paper, we develop such a theory of bidirectional typing with the proof assistant Agda.
Proof-relevant type synthesis Our work adopts a proof-relevant approach to (bidirectional) type synthesis, as illustrated by Wadler et al. [30] for PCF. The proof-relevant formulation deviates from the usual one: traditionally, a type synthesis algorithm is presented as algorithmic rules, for example in the form  , which denotes that
, which denotes that  in the surface language can be transformed to a well-typed term
in the surface language can be transformed to a well-typed term  of type A in the core language [24]. Such an algorithm is accompanied by soundness and completeness assertions that the algorithm correctly synthesises the type of a raw term, and every typable term can be synthesised. By contrast, the proof-relevant approach exploits the simultaneously computational and logical nature of Martin-Löf type theory, and formulates algorithmic soundness, completeness, and decidability in one go.
of type A in the core language [24]. Such an algorithm is accompanied by soundness and completeness assertions that the algorithm correctly synthesises the type of a raw term, and every typable term can be synthesised. By contrast, the proof-relevant approach exploits the simultaneously computational and logical nature of Martin-Löf type theory, and formulates algorithmic soundness, completeness, and decidability in one go.
Recall that the law of excluded middle \(P + \lnot P\) does not hold as an axiom for every P constructively, and we say that P is logically decidable if the law holds for P. Since Martin-Löf type theory is logical and computational, a decidability proof is a proof-relevant decision procedure that computes a yes-or-no answer with a proof of P or its refutation, so logical decidability is algorithmic decidability. More specifically, consider the statement of the type inference problem
‘for a context \(\varGamma \) and a raw term t, either a typing derivation of \(\varGamma |- t : A\) exists for some type A or any derivation of \(\varGamma |- t : A\) for some type A leads to a contradiction’,
which can be rephrased more succinctly as
‘It is decidable for any \(\varGamma \) and t whether \(\varGamma |- t : A\) is derivable for some A’.
A proof of this statement would also be a program that produces either a typing derivation for the given raw term  or a negation proof that such a derivation is impossible. The first case is algorithmic soundness, while the second case is algorithmic completeness in contrapositive form (which implies the original form due to the decidability). Therefore, proving the statement is the same as constructing a verified proof-relevant type inference algorithm, which returns not only an answer but also a proof justifying that answer. This is an economic way to bridge the gap between theory and practice, where proofs double as verified programs, in contrast to separately exhibiting a theory and an implementation that are loosely related.
or a negation proof that such a derivation is impossible. The first case is algorithmic soundness, while the second case is algorithmic completeness in contrapositive form (which implies the original form due to the decidability). Therefore, proving the statement is the same as constructing a verified proof-relevant type inference algorithm, which returns not only an answer but also a proof justifying that answer. This is an economic way to bridge the gap between theory and practice, where proofs double as verified programs, in contrast to separately exhibiting a theory and an implementation that are loosely related.
Annotations in the type synthesis problem As we mentioned in the beginning, with bidirectional typing we avoid the generally undecidable problem of type inference, and instead solve the simpler problem about the typability of ‘sufficiently annotated’ raw terms, which we call the type synthesis problem to distinguish it from type inference. Annotations therefore play an important role even in the definition of the problem solved by bidirectional typing, but have not received enough attention. In our theory, we define mode derivations to explicitly take annotations into account, and formulate the type synthesis problem with sufficiently annotated raw terms. Accordingly, a preprocessing step called mode decoration is proposed to help the user to work with annotations.
The type synthesis problem is not just about deciding whether a raw term is typable—there is a third possibility that the term does not have sufficient annotations. Thus, before attempting to decide typability (using a bidirectional type synthesiser), we should first decide if the raw term has sufficient annotations, which corresponds to whether the term has a mode derivation. Our theory gives a proof-relevant mode decorator, which either (i) construct a mode derivation for a raw term, or (ii) provides information that refutes the existence of any mode derivation and pinpoints missing annotations.
Then a bidirectional type synthesiser is only required to decide the typability of mode-decorated raw terms. Soundness and completeness of bidirectional typing is reformulated as a one-to-one correspondence between bidirectional typing derivations and pairs of a typing derivation and a mode derivation for the same raw term. Our completeness is simpler and more useful than annotatability, which is a typical formulation of completeness in the literature of bidirectional typing [10, Section 3.2].
Mode-correctness and general definitions of languages The most essential characteristics of bidirectional typing is mode-correctness, since an algorithm can often be ‘read off’ from the definition of a bidirectionally typed language if mode-correct. As illustrated by Dunfield and Krishnaswami [10], it seems that the implications of mode-correctness have only been addressed informally so far, and mode-correctness is not yet formally defined as a property of languages.
In order to make the notion of mode-correctness precise, we first give a general definition of bidirectional simple type systems, called bidirectional binding signature, extending the typed version of Aczel’s binding signature [1] with modes. A general definition of typed languages allows us to define mode-correctness and to investigate its consequences rigorously: the uniqueness of synthesised types and the decidability of bidirectional type synthesis for mode-correct signatures. The proof of the latter theorem amounts to a generator of proof-relevant bidirectional type synthesisers (analogous to a parser generator working for unambiguous or disambiguated grammars).
To make our exposition accessible, the theory in this paper focuses on simply typed languages with a syntax-directed bidirectional type system, so that the decidability of bidirectional type synthesis can be established without any other technical assumptions. It should be possible to extend the theory to deal with more expressive types and assumptions other than mode-correctness. For instance, we briefly discuss how the theory can be extended to handle polymorphically typed languages such as System F, System \(\textsf{F}_{\mathsf {<:}}\), and those systems using implicit type applications with additional assumptions in Section 7.
Contributions and plan of this paper In short, we develop a general and formal theory of bidirectional type synthesis for simply typed languages, including
-
1.
general definitions for bidirectional type systems and mode-correctness;
-
2.
mode derivations for explicitly dealing with annotations in the theory, and mode decoration for helping the user to work with annotations in practice;
-
3.
rigorously proven consequences of mode-correctness, including the uniqueness of synthesised types and the decidability of bidirectional type synthesis, which amounts to
-
4.
a fully verified generator of proof-relevant type-synthesisers.
Our theory is fully formally developed with Agda, but is translated to the mathematical vernacular for presentation in this paper. The formal theory doubles as a verified implementation, which is available publicly on Zenodo [8].
This paper is structured as follows. We present a concrete overview of our theory using simply typed \(\lambda \)-calculus in Section 2, prior to developing a general framework for specifying bidirectional type systems in Section 3. Following this, we discuss mode decoration and related properties in Section 4. The main technical contribution lies in Section 5, where we introduce mode-correctness and bidirectional type synthesis. Some examples other than simply typed \(\lambda \)-calculus are given in Section 6, and further developments are discussed in Section 7.
2 Bidirectional type synthesis for simply typed \(\lambda \)calculus
We start with an overview of our theory by instantiating it to simply typed \(\lambda \)-calculus. Roughly speaking, the problem of type synthesis requires us to take a raw term as input, and produce a typing derivation for the term if possible. To give more precise definitions: the raw terms for simply typed \(\lambda \)-calculus are definedFootnote 1 in Figure 1; besides the standard constructs, there is an Anno rule that allows the user to insert type annotations to facilitate type synthesis.
Correspondingly, the definition of typing derivationsFootnote 2 in Figure 2 has an Anno rule enforcing that the type of an annotated term does match the annotation.
Now we can define what it means to solve the type synthesis problem.
Definition 2.1
Parametrised by an ‘excuse’ predicate E on raw terms, a type synthesiser takes a context \(\varGamma \) and a raw term \(\left| \varGamma \right| \vdash t\) (where \(\left| \varGamma \right| \) is the list of variables in \(\varGamma \)) as input, and establishes one of the following outcomes:
-
1.
there exists a derivation of \(\varGamma \vdash t : A\) for some type A,
-
2.
there does not exist a derivation \(\varGamma \vdash t : A\) for any type A, or
-
3.
E holds for t.
It is crucial to allow the third outcome, without which we would be requiring the type synthesis problem to be decidable, but this requirement would quickly become impossible to meet when the theory is extended to handle more complex types. If a type synthesiser cannot decide whether there is a typing derivation, it is allowed to give an excuse instead of an answer. Acceptable excuses are defined by the predicate E, which describes what is wrong with an input term, for example, not having enough type annotations.
Now our goal is to use Definition 2.1 as a specification and implement it using a bidirectional type synthesiser, which attempts to produce bidirectional typing derivations defined in Figure 3. It is often said that a type synthesis algorithm can be ‘read off’ from well-designed bidirectional typing rules. Take the  rule as an example: to synthesise the type of an application
rule as an example: to synthesise the type of an application  , we first synthesise the type of
, we first synthesise the type of  , which should have the form \(A \mathbin {\boldsymbol{\supset }}B\), from which we can extract the expected type of
, which should have the form \(A \mathbin {\boldsymbol{\supset }}B\), from which we can extract the expected type of  , namely A, and perform checking; then the type of the whole application, namely B, can also be extracted from the type \(A \mathbin {\boldsymbol{\supset }}B\). Note that the synthesiser is able to figure out the type A for checking u and the type B to be synthesised for \(t\;u\) because they have been computed when synthesising the type \(A \mathbin {\boldsymbol{\supset }}B\) of t. In general, there should be a flow of type information in each rule that allows us to determine unknown types (e.g. types to be checked) from known ones (e.g. types previously synthesised). This is called mode-correctness, which we will formally define in Section 5.1.
, namely A, and perform checking; then the type of the whole application, namely B, can also be extracted from the type \(A \mathbin {\boldsymbol{\supset }}B\). Note that the synthesiser is able to figure out the type A for checking u and the type B to be synthesised for \(t\;u\) because they have been computed when synthesising the type \(A \mathbin {\boldsymbol{\supset }}B\) of t. In general, there should be a flow of type information in each rule that allows us to determine unknown types (e.g. types to be checked) from known ones (e.g. types previously synthesised). This is called mode-correctness, which we will formally define in Section 5.1.
While it is possible for a bidirectional type synthesiser to do its job in one go, which can be thought of as adding both mode and typing information to a raw term and arriving at a bidirectional typing derivation, it is beneficial to have a preprocessing step which adds only mode information, based on which the synthesiser then continues to add typing information. More precisely, the preprocessing step, which we call mode decoration, attempts to produce mode derivations as defined in Figure 4, where the rules are exactly the mode part of the bidirectional typing rules (Figure 3).
Definition 2.2
A mode decorator decides for a raw term  whether
whether  .
.
One (less important) benefit of mode decoration is that it helps to simplify the synthesiser, whose computation can be partly directed by a mode derivation. More importantly, whether there is a mode derivation for a term is actually very useful information to the user, because it corresponds to whether the term has enough type annotations: observe that the  and
and  rules allow us to switch between the synthesising and checking modes; the switch from synthesising to checking is free, whereas the opposite direction requires a type annotation. That is, any term in synthesising mode is also in checking mode, but not necessarily vice versa. A type annotation is required wherever a term that can only be in checking mode is required to be in synthesising mode, and a term does not have a mode derivation if and only if type annotations are missing in such places. (We will treat all these more rigorously in Section 4.) For example, an abstraction is strictly in checking mode, but the left sub-term of an application has to be synthesising, so a term of the form
rules allow us to switch between the synthesising and checking modes; the switch from synthesising to checking is free, whereas the opposite direction requires a type annotation. That is, any term in synthesising mode is also in checking mode, but not necessarily vice versa. A type annotation is required wherever a term that can only be in checking mode is required to be in synthesising mode, and a term does not have a mode derivation if and only if type annotations are missing in such places. (We will treat all these more rigorously in Section 4.) For example, an abstraction is strictly in checking mode, but the left sub-term of an application has to be synthesising, so a term of the form  does not have a mode derivation unless we annotate the abstraction.
does not have a mode derivation unless we annotate the abstraction.
Perhaps most importantly, mode derivations enable us to give bidirectional type synthesisers a tight definition: if we restrict the domain of a synthesiser to terms in synthesising mode (i.e. having enough type annotations for performing synthesis), then it is possible for the synthesiser to decide whether there is a suitable typing derivation.
Definition 2.3
A bidirectional type synthesiser decides for any context \(\varGamma \) and synthesising term  whether
whether  for some type A.
for some type A.
Now we can get back to implementing a type synthesiser (Definition 2.1).
Theorem 2.4
A type synthesiser using ‘not in synthesising mode’ as its excuse can be constructed from a mode decorator and a bidirectional type synthesiser.
The construction is straightforward: run the mode decorator on the input term \(\left| \varGamma \right| \vdash t\). If there is no synthesising mode derivation, report that t is not in synthesising mode (the third outcome). Otherwise  , and we can run the bidirectional type synthesiser. If it finds a derivation of
, and we can run the bidirectional type synthesiser. If it finds a derivation of  for some type A, return a derivation of \(\varGamma \vdash t : A\) (the first outcome), which is possible because the bidirectional typing (Figure 3) is sound with respect to the original typing (Figure 2); if there is no derivation of
for some type A, return a derivation of \(\varGamma \vdash t : A\) (the first outcome), which is possible because the bidirectional typing (Figure 3) is sound with respect to the original typing (Figure 2); if there is no derivation of  for any type A, then there is no derivation of \(\varGamma \vdash t : A\) for any A either (the second outcome), because the bidirectional typing is complete:
for any type A, then there is no derivation of \(\varGamma \vdash t : A\) for any A either (the second outcome), because the bidirectional typing is complete:
Theorem 2.5
(Soundness and Completeness). if and only if
if and only if  and \(\varGamma \vdash t : A\).
and \(\varGamma \vdash t : A\).
We will construct a mode decorator (Section 4.2) and a bidirectional type synthesiser (Section 5) and prove the above theorem for all syntax-directed bidirectional simple type systems (Section 4.1). To quantify over all such systems, we need their general definitions, which we formulate next.
3 Bidirectionally simply typed languages
This section provides general definitions of simple types, simply typed languages, and bidirectional type systems, and uses the simply typed \(\lambda \)-calculus in Section 2 as our running example. These definitions may look dense, especially on first reading. The reader may choose to skim through this section, in particular the figures, and still get some rough ideas from later sections.
The definitions are formulated in two steps: (i) first we introduce a notion of arity and a notion of signature which includes a setFootnote 3 of operation symbols and an assignment of arities to symbols; (ii) then, given a signature, we define raw terms and typing derivations inductively by primitive rules such as Var and a rule schema for constructs \(\textsf{op}_o\) indexed by an operation symbol o. As we move from simple types to bidirectional typing, the notion of arity, initially as the number of arguments of an operation, is enriched to incorporate an extension context for variable binding and the mode for the direction of type information flow.
3.1 Signatures and simple types
For simple types, the only datum needed for specifying a type construct is its number of arguments:
Definition 3.1
A signature \(\varSigma \) for simple types consists of a set I with a decidable equality and an arity function \( ar :I \rightarrow \mathbb {N}\). For a signature \(\varSigma \), a type \(A : \textsf{Ty}_{\varSigma }(\varXi )\) over a variable set \(\varXi \) is either
-
1.
a variable in \(\varXi \) or
-
2.
\(\textsf{op}_{i}(A_1, \ldots , A_n)\) for some i : I with \( ar (i) = n\) and types \(A_1,\ldots , A_n\).
Example 3.2
Function types \(A \mathbin {\boldsymbol{\supset }}B\) and typically a base type \(\texttt{b}\) are included in simply typed \(\lambda \)-calculus, and can be specified by the type signature \(\varSigma _{\mathbin {\boldsymbol{\supset }}}\) consisting of operations \(\textsf{fun}\) and \(\textsf{b}\) where \( ar (\textsf{fun}) = 2\) and \( ar (\textsf{b}) = 0\). Then, all types in simply typed \(\lambda \)-calculus can be given as \(\varSigma _{\mathbin {\boldsymbol{\supset }}}\)-types over the empty set, with \(A \mathbin {\boldsymbol{\supset }}B\) introduced as \(\textsf{op}_{\textsf{fun}}(A, B)\) and \(\texttt{b}\) as \(\textsf{op}_{\textsf{b}}\).
Definition 3.3
The substitution for a function \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\varXi ')\), denoted by \(\rho :\textsf{Sub}_{\varSigma }(\varXi ,\varXi ')\), is a map which sends a type \(A : \textsf{Ty}_{\varSigma }(\varXi )\) to  and is defined as usual.
and is defined as usual.
3.2 Binding signatures and simply typed languages
A simply typed language specifies (i) a family of sets of raw terms  indexed by a list V of variables (that are currently in scope), where each construct is allowed to bind some variables like Abs and to take multiple arguments like App; (ii) a family of sets of typing derivations indexed by a typing context \(\varGamma \), a raw term
indexed by a list V of variables (that are currently in scope), where each construct is allowed to bind some variables like Abs and to take multiple arguments like App; (ii) a family of sets of typing derivations indexed by a typing context \(\varGamma \), a raw term  , and a type A. Therefore, to specify a term construct, we enrich the notion of arity with some set of types for typing and extension context for variable binding.
, and a type A. Therefore, to specify a term construct, we enrich the notion of arity with some set of types for typing and extension context for variable binding.
Definition 3.4
([13], p. 322). A binding arity with a set T of types is an inhabitant of \(\left( T^* \times T\right) ^* \times T\), where \(T^*\) is the set of lists over T. In a binding arity \((((\varDelta _1, A_1), \ldots , (\varDelta _n, A_n)), A)\), every \(\varDelta _i\) and \(A_i\) refers to the extension context and the type of the i-th argument, respectively, and A the target type. For brevity, it is denoted by \([\varDelta _{1}]A_{1}, \ldots , [\varDelta _{n}]A_{n}\rightarrow A\), where \([\varDelta _i]\) is omitted if empty.
Example 3.5
Observe that the Abs and App rules in Figure 2 can be read as

if the empty context \(\cdot \) is added verbosely, so they can be specified by arities \({[A]B} \rightarrow {(A \mathbin {\boldsymbol{\supset }}B)}\) and \({(A \mathbin {\boldsymbol{\supset }}B), A} \rightarrow {B}\), respectively, with \(\textsf{Ty}_{\varSigma _{\mathbin {\boldsymbol{\supset }}}}(A, B)\) as types.
Next, akin to a signature, a binding signature \(\varOmega \) consists of a set of operation symbols along with their respective binding arities:
Definition 3.6
For a type signature \(\varSigma \), a binding signature \(\varOmega \) is a set O with a function
That is, each inhabitant o : O is associated with a set \(\varXi \) of type variables and an arity \( ar (o)\) with \(\textsf{Ty}_{\varSigma }(\varXi )\) as types denoted by \(o:\varXi \mathrel {\rhd } [\varDelta _{1}]A_{1}, \ldots , [\varDelta _{n}]A_{n} \rightarrow A_0\).
The set \(\varXi \) of type variables for each operation, called its local context, plays an important role. To use a rule like Abs in an actual typing derivation, we need to substitute concrete types, i.e. types without any type variables, for variables A, B. In our formulation of substitution (3.3), we must first identify which type variables to substitute for. As such, this information forms part of the arity of an operation, and typing derivations, defined subsequently, will include functions \(\rho \) from \(\varXi \) to concrete types specifying how to instantiate typing rules by substitution.
By a simply typed language \((\varSigma , \varOmega )\), we mean a pair of a type signature \(\varSigma \) and a binding signature \(\varOmega \). Now, we define raw terms for \((\varSigma , \varOmega )\) first.
Definition 3.7
For a simply typed language \((\varSigma , \varOmega )\), the family of sets of raw terms indexed by a list V of variables consists of (i) (indices of) variables in V, (ii) annotations  for some raw term t in V and a type A, and (iii) a construct
for some raw term t in V and a type A, and (iii) a construct  for some \(o:\varXi \mathrel {\rhd } [\varDelta _{1}]A_{1}, \ldots , [\varDelta _{n}]A_{n} \rightarrow A_0\) in O, where
for some \(o:\varXi \mathrel {\rhd } [\varDelta _{1}]A_{1}, \ldots , [\varDelta _{n}]A_{n} \rightarrow A_0\) in O, where  ’s are lists of variables whose length is equal to the length of \(\varDelta _i\), and \(t_i\)’s are raw terms in the variable list
’s are lists of variables whose length is equal to the length of \(\varDelta _i\), and \(t_i\)’s are raw terms in the variable list  . These correspond to rules Var, Anno, and Op in Figure 5 respectively.
. These correspond to rules Var, Anno, and Op in Figure 5 respectively.
Before defining typing derivations, we need a definition of typing contexts.
Definition 3.8
A typing context \(\varGamma :\textsf{Cxt}_{\varSigma }\) is formed by \(\cdot \) for the empty context and \(\varGamma , x : A\) for an additional variable x with a concrete type \(A : \textsf{Ty}_{\varSigma }(\emptyset )\). The list of variables in \(\varGamma \) is denoted \(\left| \varGamma \right| \).
The definition of typing derivations is a bit more involved. We need some information to compare types on the object level during type synthesis and substitute those type variables in a typing derivation of  for an operation o in \(\varOmega \) at some point. Here we choose to include a substitution \(\rho \) from the local context \(\varXi \) to \(\emptyset \) as part of its typing derivation explicitly:
for an operation o in \(\varOmega \) at some point. Here we choose to include a substitution \(\rho \) from the local context \(\varXi \) to \(\emptyset \) as part of its typing derivation explicitly:
Definition 3.9
For a simply typed language \((\varSigma , \varOmega )\), the family of sets of typing derivations of  , indexed by a typing context \(\varGamma : \textsf{Cxt}_\varSigma \), a raw term
, indexed by a typing context \(\varGamma : \textsf{Cxt}_\varSigma \), a raw term  with free variables in \(\left| \varGamma \right| \), and a type \(A : \textsf{Ty}_\varSigma (\emptyset )\), consists of
with free variables in \(\left| \varGamma \right| \), and a type \(A : \textsf{Ty}_\varSigma (\emptyset )\), consists of
-
1.
a derivation of \(\varGamma |-_{\varSigma , \varOmega } x : A\) if x : A is in \(\varGamma \),
-
2.
a derivation of
 if
if  has a derivation, and
has a derivation, and -
3.
a derivation of
 for some operation \(o:\varXi \mathrel {\rhd } [\varDelta _{1}]A_{1}, \ldots , [\varDelta _{n}]A_{n} \rightarrow A_0\) if there exist \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\) and a derivation of
for some operation \(o:\varXi \mathrel {\rhd } [\varDelta _{1}]A_{1}, \ldots , [\varDelta _{n}]A_{n} \rightarrow A_0\) if there exist \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\) and a derivation of  for each i,
for each i,
corresponding to rules Var, Anno, and Op in Figure 6 respectively.
Example 3.10
Raw terms (Figure 1) and typing derivations (Figure 2) for simply typed \(\lambda \)-calculus can be specified by the type signature \(\varSigma _{\mathbin {\boldsymbol{\supset }}}\) (Example 3.2) and the binding signature consisting of \(\textsf{app}:A, B \mathrel {\rhd } (A \mathbin {\boldsymbol{\supset }}B), A \rightarrow B\) and \(\textsf{abs}:A , B \mathrel {\rhd } [A]B \rightarrow (A \mathbin {\boldsymbol{\supset }}B)\). Rules Abs and App in simply typed \(\lambda \)-calculus are subsumed by the Op rule schema, as applications \(t\;u\) and abstractions  can be introduced uniformly as \(\textsf{op}_{\textsf{app}}(t, u)\) and \(\textsf{op}_{\textsf{abs}}(x.t)\), respectively.
can be introduced uniformly as \(\textsf{op}_{\textsf{app}}(t, u)\) and \(\textsf{op}_{\textsf{abs}}(x.t)\), respectively.
3.3 Bidirectional binding signatures and bidirectional type systems
Typing judgements for a bidirectional type system appear in two forms:  and
and  . These two typing judgements can be considered as a single typing judgement
. These two typing judgements can be considered as a single typing judgement  indexed by a mode \(d : \textsf{Mode}\), which can be either
indexed by a mode \(d : \textsf{Mode}\), which can be either  or
or  . Therefore, to define a bidirectional type system, we enrich the concept of binding arity to bidirectional binding arity, which further specifies the mode for each of its arguments and for the conclusion:
. Therefore, to define a bidirectional type system, we enrich the concept of binding arity to bidirectional binding arity, which further specifies the mode for each of its arguments and for the conclusion:
Definition 3.11
A bidirectional binding arity with a set T of types is an inhabitant of
For clarity, an arity is denoted by  .
.
Example 3.12
Consider the  rule (Figure 3) for
rule (Figure 3) for  . It has the arity
. It has the arity  , indicating additionally that both
, indicating additionally that both  and its argument t are checking. Likewise, the
and its argument t are checking. Likewise, the  rule has the arity
rule has the arity  .
.
Definition 3.13
For a type signature \(\varSigma \), a bidirectional binding signature \(\varOmega \) is a set O with
We write  for an operation o with a variable set \(\varXi \) and its bidirectional binding arity with \(\textsf{Ty}_{\varSigma }(\varXi )\) as types. We call it checking if d is
for an operation o with a variable set \(\varXi \) and its bidirectional binding arity with \(\textsf{Ty}_{\varSigma }(\varXi )\) as types. We call it checking if d is  or synthesising if d is
or synthesising if d is  ; similarly, its i-th argument is checking if \(d_i\) is
; similarly, its i-th argument is checking if \(d_i\) is  and synthesising if \(d_i\) is
and synthesising if \(d_i\) is  . A bidirectional type system \((\varSigma , \varOmega )\) refers to a pair of a type signature \(\varSigma \) and a bidirectional binding signature \(\varOmega \).
. A bidirectional type system \((\varSigma , \varOmega )\) refers to a pair of a type signature \(\varSigma \) and a bidirectional binding signature \(\varOmega \).
Definition 3.14
For a bidirectional type system \((\varSigma , \varOmega )\),
-
the set of bidirectional typing derivations of
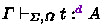 , indexed by a typing context \(\varGamma \), a raw term
, indexed by a typing context \(\varGamma \), a raw term  under \(\left| \varGamma \right| \), a mode
under \(\left| \varGamma \right| \), a mode  , and a type A, is defined in Figure 7, and particularly
, and a type A, is defined in Figure 7, and particularly 
has a derivation for
 in \(\varOmega \) if there is \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\) and a derivation of
in \(\varOmega \) if there is \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\) and a derivation of  for each i;
for each i; -
the set of mode derivations of
 , indexed by a list V of variables, a raw term
, indexed by a list V of variables, a raw term 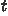 under V, and a mode d, is defined in Figure 8.
under V, and a mode d, is defined in Figure 8.
The two judgements  and
and  stand for
stand for  and
and  , respectively. A typing rule is checking if its conclusion mode is
, respectively. A typing rule is checking if its conclusion mode is  or synthesising otherwise.
or synthesising otherwise.
Every bidirectional binding signature \(\varOmega \) gives rise to a binding signature \(\left| \varOmega \right| \) if we erase modes from \(\varOmega \), called the (mode) erasure of \(\varOmega \). Hence a bidirectional type system \((\varSigma , \varOmega )\) also specifies a simply typed language \((\varSigma , \left| \varOmega \right| )\), including raw terms and typing derivations.
Example 3.15
Having established generic definitions, we can now specify simply typed \(\lambda \)-calculus and its bidirectional type system—including raw terms, (bidirectional) typing derivations, and mode derivations—using just a pair of signatures \(\varSigma _{\mathbin {\boldsymbol{\supset }}}\) (Example 3.2) and \(\varOmega ^{\Leftrightarrow }_\varLambda \) which consists of

More importantly, we are able to reason about constructions and properties that hold for any simply typed language with a bidirectional type system once and for all by quantifying over \((\varSigma , \varOmega )\).
4 Mode decoration and related properties
Our first important construction is mode decoration in Section 4.2, which is in fact generalised to pinpoint any missing type annotations in a given raw term. We discuss some related properties: by bringing mode derivations into the picture, we are able to give a natural formulation of soundness and completeness of a bidirectional type system with respect to its erasure to an ordinary type system in Section 4.1. We also reformulate annotatability [10, Section 3.2] and compare it with our completeness and generalised mode decoration in Section 4.3.
4.1 Soundness and completeness
Erasure of a bidirectional binding signature removes modes and keeps everything else intact; this can be straightforwardly extended by induction to remove modes from a bidirectional typing derivation and arrive at an ordinary typing derivation, which is soundness. Alternatively, we can remove typing and retain modes, arriving at a mode derivation. Conversely, if we have both mode and typing derivations for the same term, we can combine them to form a bidirectional typing derivation, which is completeness. In short, soundness and completeness are merely the separation and combination of mode and typing information carried by the three kinds of derivations while keeping their basic structure, directed by the same raw term. All these can be summarised in one theorem and proved by induction.
Theorem 4.1
 if and only if both
if and only if both  and \(\varGamma |-_{\varSigma , \left| \varOmega \right| } t : A\).
and \(\varGamma |-_{\varSigma , \left| \varOmega \right| } t : A\).
4.2 Generalised mode decoration
The goal of this section is to construct a mode decorator, which decides for any raw term \(V |-_{\varSigma ,\left| \varOmega \right| } t\) and mode  whether
whether  or not. In fact we shall do better: if a mode decorator returns a proof that no mode derivation exists, that negation proof does not give useful information for the user. It will be helpful if a decorator can produce an explanation of why no mode derivation exists, and even how to fix the input term to have a mode derivation. We will construct such a generalised mode decorator (Theorem 4.4), which can be weakened to an ordinary mode decorator (Corollary 4.6) if the additional explanation is not needed.Footnote 4
or not. In fact we shall do better: if a mode decorator returns a proof that no mode derivation exists, that negation proof does not give useful information for the user. It will be helpful if a decorator can produce an explanation of why no mode derivation exists, and even how to fix the input term to have a mode derivation. We will construct such a generalised mode decorator (Theorem 4.4), which can be weakened to an ordinary mode decorator (Corollary 4.6) if the additional explanation is not needed.Footnote 4
Intuitively, a term does not have a mode derivation exactly when there are not enough type annotations, but such negative formulations convey little information. Instead, we can provide more information by pointing out the places in the term that require annotations. For a bidirectional type system, an annotation is required wherever a term is ‘strictly’ (which we will define shortly) in checking mode but required to be in synthesising mode, in which case there is no rule for switching from checking to synthesising, and thus there is no way to construct a mode derivation. We can, however, consider generalised mode derivations (Figure 9) that allow the use of an additional  rule for such switching, so that a derivation can always be constructed. Given a generalised mode derivation, if it uses
rule for such switching, so that a derivation can always be constructed. Given a generalised mode derivation, if it uses  in some places, then those places are exactly where annotations should be supplied; if it does not use
in some places, then those places are exactly where annotations should be supplied; if it does not use  , then the derivation is genuine in the sense that it corresponds directly to an original mode derivation. This can be succinctly formulated as Lemma 4.2 below by encoding genuineness as a boolean g in the generalised mode judgement, which is set to \(\textbf{F}\) only by the
, then the derivation is genuine in the sense that it corresponds directly to an original mode derivation. This can be succinctly formulated as Lemma 4.2 below by encoding genuineness as a boolean g in the generalised mode judgement, which is set to \(\textbf{F}\) only by the  rule. (Ignore the boolean s for now.)
rule. (Ignore the boolean s for now.)
Lemma 4.2
If  , then
, then  .
.
We also want a lemma that covers the case where \(g = \textbf{F}\).
Lemma 4.3
If  , then
, then  .
.
This lemma would be wrong if the ‘strictness’ boolean s was left out of the rules: having both  and
and  , which we call mode casts, it would be possible to switch between the two modes freely, which unfortunately means that we could insert a pair of
, which we call mode casts, it would be possible to switch between the two modes freely, which unfortunately means that we could insert a pair of  and
and  anywhere, constructing a non-genuine derivation even when there is in fact a genuine one. The ‘strictness’ boolean s can be thought of as disrupting the formation of such pairs of mode casts: every rule other than the mode casts sets s to \(\textbf{T}\), meaning that a term is strictly in the mode assigned by the rule (i.e. not altered by a mode cast), whereas the mode casts set s to \(\textbf{F}\). Furthermore, the sub-derivation of a mode cast has to be strict, so it is impossible to have consecutive mode casts. Another way to understand the role of s is that it makes the
anywhere, constructing a non-genuine derivation even when there is in fact a genuine one. The ‘strictness’ boolean s can be thought of as disrupting the formation of such pairs of mode casts: every rule other than the mode casts sets s to \(\textbf{T}\), meaning that a term is strictly in the mode assigned by the rule (i.e. not altered by a mode cast), whereas the mode casts set s to \(\textbf{F}\). Furthermore, the sub-derivation of a mode cast has to be strict, so it is impossible to have consecutive mode casts. Another way to understand the role of s is that it makes the  rule precise: an annotation is truly missing only when a term is strictly in checking mode but is required to be in synthesising mode. The explicit formulation of strictness makes non-genuine derivations ‘truly non-genuine’, and Lemma 4.3 can be proved.
rule precise: an annotation is truly missing only when a term is strictly in checking mode but is required to be in synthesising mode. The explicit formulation of strictness makes non-genuine derivations ‘truly non-genuine’, and Lemma 4.3 can be proved.
Now we are ready to construct a generalised mode decorator.
Theorem 4.4
(Generalised mode decoration). For any raw term \(V |-_{\varSigma ,\left| \varOmega \right| } t\) and mode  , there is a derivation of
, there is a derivation of  for some g and s.
for some g and s.
The theorem could be proved directly, but that would mix up two case analyses which respectively inspect the input term  and apply mode casts depending on which mode
and apply mode casts depending on which mode  is required. Instead, we distill the case analysis on
is required. Instead, we distill the case analysis on  that deals with mode casts into the following Lemma 4.5, whose antecedent ((1)) is then established by induction on
that deals with mode casts into the following Lemma 4.5, whose antecedent ((1)) is then established by induction on  in the proof of Theorem 4.4.
in the proof of Theorem 4.4.
Lemma 4.5
For any raw term \(V |-_{\varSigma ,\left| \varOmega \right| } t\), if

then for any mode  , there is a derivation of
, there is a derivation of  for some g and s.
for some g and s.
With a generalised mode decorator, it is now easy to derive an ordinary one.
Corollary 4.6
(Mode decoration). It is decidable whether  .
.
4.3 Annotatability
Dunfield and Krishnaswami [10, Section 3.2] formulated completeness differently from our Theorem 4.1 and proposed annotatability as a more suitable name. In our theory, we may reformulate annotatability as follows.
Proposition 4.7
(Annotatability). If \(\varGamma |-_{\varSigma ,\left| \varOmega \right| } t : A\), then there exists \(t'\) such that \(t' \sqsupseteq t\) and  for some
for some  .
.
Defined in Figure 10, the ‘annotation ordering’ \(t' \sqsupseteq t\) means that \(t'\) has the same or more annotations than t. In a sense, annotatability is a reasonable form of completeness: if a term of a simply typed language \((\varSigma , \left| \varOmega \right| )\) is typable in the ordinary type system, it may not be directly typable in the bidirectional type system \((\varSigma , \varOmega )\) due to some missing annotations, but will be if those annotations are added correctly. In our theory, Proposition 4.7 can be straightforwardly proved by induction on the derivation given by generalised mode decoration (Theorem 4.4) to construct a bidirectional typing derivation in the same mode. The interesting case is  , which is mapped to
, which is mapped to  , adding to the term a type annotation that comes from the given typing derivation.
, adding to the term a type annotation that comes from the given typing derivation.
On the other hand, when using a bidirectional type synthesiser to implement a type synthesiser, for example in Theorem 2.4, if the bidirectional type synthesiser concludes that there does not exist a bidirectional typing derivation, we use the contrapositive form of completeness to establish that such an ordinary typing derivation does not exist either. Now, annotatability is a kind of completeness because (roughly speaking) it turns an ordinary typing derivation bidirectional. Hence, it is conceivable that we could use annotatability in place of completeness in the proof of Theorem 2.4. However, in the contrapositive form of annotatability, the antecedent is ‘there does not exist \(t'\) that is more annotated than t and has a bidirectional typing derivation’, which is more complex than the bidirectional type synthesiser would have to produce. Annotatability also does not help the user to deal with missing annotations: although annotatability seems capable of determining where annotations are missing and even filling them in correctly, its antecedent requires a typing derivation, which is what the user is trying to construct and does not have yet. Therefore we believe that our theory offers simpler and more useful alternatives than the notion of annotatability.
5 Bidirectional type synthesis and checking
This section focuses on defining mode-correctness and deriving bidirectional type synthesis for any mode-correct bidirectional type system \((\varSigma , \varOmega )\). We start with Section 5.1 by defining mode-correctness and showing the uniqueness of synthesised types. This uniqueness means that any two synthesised types for the same raw term t under the same context \(\varGamma \) have to be equal. It will be used especially in Section 5.2 for the proof of the decidability of bidirectional type synthesis and checking. Then, we conclude this section with the trichotomy on raw terms in Section 5.3.
5.1 Mode correctness
As Dunfield and Krishnaswami [10] outlined, mode-correctness for a bidirectional typing rule means that (i) each ‘input’ type variable in a premise must be an ‘output’ variable in ‘earlier’ premises, or provided by the conclusion if the rule is checking; (ii) each ‘output’ type variable in the conclusion should be some ‘output’ variable in a premise if the rule is synthesising.
Here ‘input’ variables refer to variables in an extension context and in a checking premise. It is important to note that the order of premises in a bidirectional typing rule also matters, since synthesised type variables are instantiated incrementally during type synthesis.
Consider the rule  (Figure 3) as an example. This rule is mode-correct, as the type variables A and B in its only premise are already provided by its conclusion \(A \mathbin {\boldsymbol{\supset }}B\). Likewise, the rule
(Figure 3) as an example. This rule is mode-correct, as the type variables A and B in its only premise are already provided by its conclusion \(A \mathbin {\boldsymbol{\supset }}B\). Likewise, the rule  for an application term
for an application term  is mode-correct because: (i) the type \(A \mathbin {\boldsymbol{\supset }}B\) of the first argument t is synthesised, thereby ensuring type variables A and B must be known if successfully synthesised; (ii) the type of the second argument u is checked against A, which has been synthesised earlier; (iii) as a result, the type of an application \(t\;u\) can be synthesised.
is mode-correct because: (i) the type \(A \mathbin {\boldsymbol{\supset }}B\) of the first argument t is synthesised, thereby ensuring type variables A and B must be known if successfully synthesised; (ii) the type of the second argument u is checked against A, which has been synthesised earlier; (iii) as a result, the type of an application \(t\;u\) can be synthesised.
Now let us define mode-correctness rigorously. As we have outlined, the condition of mode-correctness for a synthesising rule is different from that of a checking rule, and the argument order also matters. Defining the condition directly for a rule, and thus in our setting for an operation, can be somewhat intricate. Instead, we choose to define the conditions for the argument list—more specifically, triples  of an extension context \(\varDelta _i\), a type \(A_i\), and a mode
of an extension context \(\varDelta _i\), a type \(A_i\), and a mode  —pertaining to an operation, for an operation, and subsequently for a signature. We also need some auxiliary definitions for the subset of variables of a type and of an extension context, and the set of variables that have been synthesised:
—pertaining to an operation, for an operation, and subsequently for a signature. We also need some auxiliary definitions for the subset of variables of a type and of an extension context, and the set of variables that have been synthesised:
Definition 5.1
The finite subsetsFootnote 5 of (free) variables of a type A and of variables in an extension context \(\varDelta \) are denoted by \( fv (A)\) and \( fv (\varDelta )\) respectively. For an argument list  , the set of type variables
, the set of type variables  with \(d_i\) being
with \(d_i\) being  is denoted by
is denoted by  , i.e.
, i.e.  gives the set of type variables that will be synthesised during type synthesis.
gives the set of type variables that will be synthesised during type synthesis.
Definition 5.2
The mode-correctness  for an argument list
for an argument list  with respect to a subset S of \(\varXi \) is a predicate defined by
with respect to a subset S of \(\varXi \) is a predicate defined by

where \(\textsf{MC}_{ as }( \cdot ) = \top \) means that an empty list is always mode-correct.
This definition encapsulates the idea that every ‘input’ type variable, possibly derived from an extension context \(\varDelta _n\) or a checking argument \(A_n\), must be an ‘output’ variable from  or, if the rule is checking, belong to the set S of ‘input’ variables in its conclusion. This condition must also be met for every tail of the argument list to ensure that ‘output’ variables accessible at each argument are from preceding arguments only, hence an inductive definition.
or, if the rule is checking, belong to the set S of ‘input’ variables in its conclusion. This condition must also be met for every tail of the argument list to ensure that ‘output’ variables accessible at each argument are from preceding arguments only, hence an inductive definition.
Definition 5.3
An arity  is mode-correct if
is mode-correct if
-
1.
either d is
 , its argument list is mode-correct with respect to \( fv (A_0)\), and the union
, its argument list is mode-correct with respect to \( fv (A_0)\), and the union  contains every inhabitant of \(\varXi \);
contains every inhabitant of \(\varXi \); -
2.
or d is
 , its argument list is mode-correct with respect to \(\emptyset \), and
, its argument list is mode-correct with respect to \(\emptyset \), and 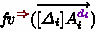 contains every inhabitant of \(\varXi \) and, particularly, \( fv (A_0)\).
contains every inhabitant of \(\varXi \) and, particularly, \( fv (A_0)\).
A bidirectional binding signature \(\varOmega \) is mode-correct if every operation’s arity is mode-correct.
For a checking operation, an ‘input’ variable of an argument could be derived from \(A_0\), as these are known during type checking as an input. Since every inhabitant of \(\varXi \) can be located in either \(A_0\) or synthesised variables, we can determine a concrete type for each inhabitant of \(\varXi \) during type synthesis. On the other hand, for a synthesising operation, we do not have any known variables at the onset of type synthesis, so the argument list should be mode-correct with respect to \(\emptyset \). Also, the set of synthesised variables alone should include every type variable in \(\varXi \) and particularly in \(A_n\).
Remark 5.4
Mode-correctness is fundamentally a condition for bidirectional typing rules, not for derivations. Thus, this property cannot be formulated without treating rules as some mathematical object such as those general definitions in Section 3. This contrasts with the properties in Section 4, which can still be specified for individual systems in the absence of a general definition.
It is easy to check the bidirectional type system \((\varSigma _{\mathbin {\boldsymbol{\supset }}}, \varOmega ^{\Leftrightarrow }_{\varLambda }\)) for simply typed \(\lambda \)-calculus is mode-correct by definition or by the following lemma:
Lemma 5.5
For any bidirectional binding arity  , it is decidable whether it is mode-correct.
, it is decidable whether it is mode-correct.
Now, we set out to show the uniqueness of synthesised types for a mode-correct bidirectional type system. For a specific system, its proof is typically a straightforward induction on the typing derivations. However, since mode-correctness is inductively defined on the argument list, our proof proceeds by induction on both the typing derivations and the argument list:
Lemma 5.6
(Uniqueness of synthesised types). In a mode-correct bidirectional type system \((\varSigma , \varOmega )\), the synthesised types of any two derivations

for the same term t must be equal, i.e. \(A = B\).
Proof
We prove the statement by induction on derivations \(d_1\) and \(d_2\) for  and
and  . Our system is syntax-directed, so \(d_1\) and \(d_2\) must be derived from the same rule:
. Our system is syntax-directed, so \(d_1\) and \(d_2\) must be derived from the same rule:
-
 follows from the fact that each variable as a raw term refers to the same variable in its context.
follows from the fact that each variable as a raw term refers to the same variable in its context. -
 holds trivially, since the synthesised type A is from the term
holds trivially, since the synthesised type A is from the term  in question.
in question. -
Op: Recall that a derivation of
 contains a substitution \(\rho \) from the local context \(\varXi \) to concrete types. To prove that any two typing derivations has the same synthesised type, it suffices to show that those substitutions \(\rho _1\) and \(\rho _2\) of \(d_1\) and \(d_2\), respectively, agree on variables in
contains a substitution \(\rho \) from the local context \(\varXi \) to concrete types. To prove that any two typing derivations has the same synthesised type, it suffices to show that those substitutions \(\rho _1\) and \(\rho _2\) of \(d_1\) and \(d_2\), respectively, agree on variables in  so that
so that  . We prove it by induction on the argument list:
. We prove it by induction on the argument list: -
1.
For the empty list, the statement is vacuously true.
-
2.
If
 is
is  , then the statement holds by induction hypothesis.
, then the statement holds by induction hypothesis. -
3.
If
 is
is  , then
, then  by induction hypothesis (of the list). Therefore, under the same context
by induction hypothesis (of the list). Therefore, under the same context  the term \(t_{i+1}\) must have the same synthesised type
the term \(t_{i+1}\) must have the same synthesised type  by induction hypothesis (of the typing derivation), so \(\rho _1\) and \(\rho _2\) agree on \( fv (A_{i+1})\) in addition to
by induction hypothesis (of the typing derivation), so \(\rho _1\) and \(\rho _2\) agree on \( fv (A_{i+1})\) in addition to  .
.
-
1.
\(\square \)
5.2 Decidability of bidirectional type synthesis and checking
We have arrived at the main technical contribution of this paper.
Theorem 5.7
In a mode-correct bidirectional type system \((\varSigma , \varOmega )\),
-
1.
if
 , then it is decidable whether
, then it is decidable whether  for some A;
for some A; -
2.
if
 , then it is decidable for any A whether
, then it is decidable for any A whether  .
.
The interesting part of the theorem is the case for the Op rule. We shall give its insight first instead of jumping into the details. Recall that a typing derivation for  contains a substitution \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\). The goal of type synthesis for this case is exactly to define such a substitution \(\rho \), and we have to start with an ‘accumulating’ substitution: a substitution \(\rho _0\) that is partially defined on \( fv (A_0)\) if d is
contains a substitution \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\). The goal of type synthesis for this case is exactly to define such a substitution \(\rho \), and we have to start with an ‘accumulating’ substitution: a substitution \(\rho _0\) that is partially defined on \( fv (A_0)\) if d is  or otherwise nowhere. By mode-correctness, the accumulating substitution \(\rho _i\) will be defined on enough synthesised variables so that type synthesis or checking can be performed on \(t_{i}\) with the context
or otherwise nowhere. By mode-correctness, the accumulating substitution \(\rho _i\) will be defined on enough synthesised variables so that type synthesis or checking can be performed on \(t_{i}\) with the context  based on its mode derivation
based on its mode derivation  . If we visit a synthesising argument
. If we visit a synthesising argument  , then we may extend the domain of \(\rho _i\) to \(\rho _{i+1}\) with the synthesised variables \( fv (A_{i + 1})\), provided that type synthesis is successful and that the synthesised type can be unified with \(A_{i+ 1}\). If we go through every \(t_i\) successfully, then we will have a total substitution \(\rho _n\) by mode-correctness and a derivation of
, then we may extend the domain of \(\rho _i\) to \(\rho _{i+1}\) with the synthesised variables \( fv (A_{i + 1})\), provided that type synthesis is successful and that the synthesised type can be unified with \(A_{i+ 1}\). If we go through every \(t_i\) successfully, then we will have a total substitution \(\rho _n\) by mode-correctness and a derivation of  for each sub-term \(t_i\).
for each sub-term \(t_i\).
Remark 5.8
To make the argument above sound, it is necessary to compare types and solve a unification problem. Hence, we assume that the set \(\varXi \) of type variables has a decidable equality, thereby ensuring that the set \(\textsf{Ty}_{\varSigma }(\varXi )\) of types also has a decidable equality.Footnote 6
We need some auxiliary definitions for the notion of extension to state the unification problem:
Definition 5.9
By an extension \(\sigma \ge \rho \) of a partial substitution \(\rho \) we mean that the domain \( dom (\sigma )\) of \(\sigma \) contains the domain of \(\rho \) and \(\sigma (x) = \rho (x)\) for every x in \( dom (\rho )\). By a minimal extension \(\bar{\rho }\) of \(\rho \) satisfying P we mean an extension \(\bar{\rho } \ge \rho \) with \(P(\bar{\rho })\) such that \(\sigma \ge \bar{\rho }\) whenever \(\sigma \ge \rho \) and \(P(\sigma )\).
Lemma 5.10
For any A of \(\textsf{Ty}_{\varSigma }(\varXi )\), B of \(\textsf{Ty}_{\varSigma }(\emptyset )\), and a partial substitution \(\rho :\varXi \rightarrow \textsf{Ty}_{\varSigma }(\emptyset )\), either
-
1.
there is a minimal extension \(\bar{\rho }\) of \(\rho \) such that
 , or
, or -
2.
there is no extension \(\sigma \) of \(\rho \) such that

This lemma can be derived from the correctness of first-order unification [21, 22], or be proved directly without unification. We are now ready for Theorem 5.7:
Proof
(of Theorem 5.7) We prove this statement by induction on the mode derivation  . The two cases
. The two cases  and
and  are straightforward and independent of mode-correctness. The case
are straightforward and independent of mode-correctness. The case  invokes the uniqueness of synthesised types to refute the case that
invokes the uniqueness of synthesised types to refute the case that  but \(A \ne B\) for a given type A. The first three cases follow essentially the same reasoning provided by Wadler et al. [30], so we only detail the last case Op, which is new (but has been discussed informally above). For brevity we omit the subscript \((\varSigma , \varOmega )\). For a mode derivation of
but \(A \ne B\) for a given type A. The first three cases follow essentially the same reasoning provided by Wadler et al. [30], so we only detail the last case Op, which is new (but has been discussed informally above). For brevity we omit the subscript \((\varSigma , \varOmega )\). For a mode derivation of  , we first claim:
, we first claim:
Claim
For an argument list  and any partial substitution \(\rho \) from \(\varXi \) to \(\emptyset \), either
and any partial substitution \(\rho \) from \(\varXi \) to \(\emptyset \), either
-
1.
there is a minimal extension \(\bar{\rho }\) of \(\rho \) such that
 (2)
(2)for \(i = 1, \ldots , n\), or
-
2.
there is no extension \(\sigma \) of \(\rho \) such that (2) holds.
Then, we proceed with a case analysis on  in the mode derivation:
in the mode derivation:
-
 is
is  : We apply our claim with the partial substitution \(\rho _0\) defined nowhere.
: We apply our claim with the partial substitution \(\rho _0\) defined nowhere.-
1.
If there is no \(\sigma \ge \rho \) such that (2) holds but
 for some A, then by inversion we have \(\rho :\textsf{Sub}_{\varSigma }(\varXi ,\emptyset )\) such that
for some A, then by inversion we have \(\rho :\textsf{Sub}_{\varSigma }(\varXi ,\emptyset )\) such that 
for every i. Obviously, \(\rho \ge \rho _0\) and
 for every i, which contradict the assumption that no such extension exists.
for every i, which contradict the assumption that no such extension exists. -
2.
If there exists a minimal \(\bar{\rho } \ge \rho _0\) defined on
 such that (2) holds, then by mode-correctness \(\bar{\rho }\) is total, and thus
such that (2) holds, then by mode-correctness \(\bar{\rho }\) is total, and thus 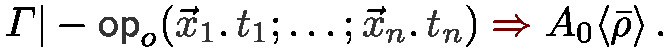
-
1.
-
 is
is  : Let A be a type and apply Lemma 5.10 with \(\rho _0\) defined nowhere.
: Let A be a type and apply Lemma 5.10 with \(\rho _0\) defined nowhere.-
1.
If there is no \(\sigma \ge \rho _0\) s.t.
 but
but 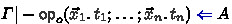 , then inversion gives us a substitution \(\rho \) s.t.
, then inversion gives us a substitution \(\rho \) s.t.  —a contradiction.
—a contradiction. -
2.
If there is a minimal \(\bar{\rho } \ge \rho _0\) s.t.
 , then apply our claim with \(\bar{\rho }\):
, then apply our claim with \(\bar{\rho }\): -
(a)
If no \(\sigma \ge \bar{\rho }\) satisfies (2) but
 , then by inversion there is \(\gamma \) s.t.
, then by inversion there is \(\gamma \) s.t.  and
and  for every i. Given that \(\bar{\rho } \ge \rho \) is minimal s.t.
for every i. Given that \(\bar{\rho } \ge \rho \) is minimal s.t.  , it follows that \(\gamma \) is an extension of \(\bar{\rho }\), but by assumption no such an extension satisfying
, it follows that \(\gamma \) is an extension of \(\bar{\rho }\), but by assumption no such an extension satisfying  exists, thus a contradiction.
exists, thus a contradiction. -
(b)
If there is a minimal \(\bar{\bar{\rho }} \ge \bar{\rho }\) s.t. (2), then by mode-correctness \(\bar{\bar{\rho }}\) is total and

where
 since \(\bar{\bar{\rho }}(x) = \bar{\rho }\) for every x in \( dom (\bar{\rho })\).
since \(\bar{\bar{\rho }}(x) = \bar{\rho }\) for every x in \( dom (\bar{\rho })\).
-
(a)
-
1.
We have proved the decidability by induction on the derivation of  , assuming the claim.
, assuming the claim.
Proof
(of Claim). We prove it by induction on the list  :
:
-
1.
For the empty list, \(\rho \) is the minimal extension of \(\rho \) itself satisfying (2) trivially.
-
2.
For
 , by induction hypothesis on the list, we have two cases:
, by induction hypothesis on the list, we have two cases: -
(a)
If there is no \(\sigma \ge \rho \) s.t. (2) holds for all \(1 \le i \le m\) but a minimal \(\gamma \ge \rho \) such that (2) holds for all \(1 \le i \le m + 1\), then we have a contradiction.
-
(b)
There is a minimal \(\bar{\rho } \ge \rho \) s.t. (2) holds for \(1 \le i \le m\). By case analysis on
 :
:-
 is
is  : By mode-correctness,
: By mode-correctness,  and
and 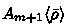 are defined. By the ind. hyp.
are defined. By the ind. hyp.  is decidable. Clearly, if
is decidable. Clearly, if  then the desired statement is proved; otherwise we easily derive a contradiction.
then the desired statement is proved; otherwise we easily derive a contradiction. -
 is
is  : By mode-correctness,
: By mode-correctness, 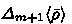 is defined. By the ind. hyp., ‘
is defined. By the ind. hyp., ‘ for some A’ is decidable:
for some A’ is decidable: -
i.
If
 for any A but there is \(\gamma \ge \rho \) s.t. (2) holds for \(1 \le i \le m+1\), then \(\gamma \ge \bar{\rho }\). Therefore
for any A but there is \(\gamma \ge \rho \) s.t. (2) holds for \(1 \le i \le m+1\), then \(\gamma \ge \bar{\rho }\). Therefore  , and we derive a contradiction because
, and we derive a contradiction because  .
. -
ii.
If
 for some A, then Lemma 5.10 gives the following two cases:
for some A, then Lemma 5.10 gives the following two cases:-
Suppose no \(\sigma \ge \bar{\rho }\) s.t.
 but an extension \(\gamma \ge \rho \) s.t. (2) holds for \(1 \le i \le m + 1\). Then, \(\gamma \ge \bar{\rho }\) by the minimality of \(\bar{\rho }\) and thus
but an extension \(\gamma \ge \rho \) s.t. (2) holds for \(1 \le i \le m + 1\). Then, \(\gamma \ge \bar{\rho }\) by the minimality of \(\bar{\rho }\) and thus  . However, by Lemma 5.6, the synthesised type
. However, by Lemma 5.6, the synthesised type  must be unique, so \(\gamma \) is an extension of \(\bar{\rho }\) s.t.
must be unique, so \(\gamma \) is an extension of \(\bar{\rho }\) s.t. 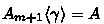 , i.e. a contradiction.
, i.e. a contradiction. -
If there is a minimal \(\bar{\bar{\rho }} \ge \bar{\rho }\) such that
 , then it is not hard to show that \(\bar{\bar{\rho }}\) is also the minimal extension of \(\rho \) such that (2) holds for all \(1 \le i \le m + 1\).
, then it is not hard to show that \(\bar{\bar{\rho }}\) is also the minimal extension of \(\rho \) such that (2) holds for all \(1 \le i \le m + 1\).
-
-
i.
-
-
(a)
We have proved our claim for any argument list by induction.\(\blacksquare \)
We have completed the proof of Theorem 5.7. \(\square \)
The formal counterpart of the above proof in Agda functions as two top-level programs for type checking and synthesis. These programs provide either the typing derivation or its negation proof. Each case analysis branches depending on the outcomes of bidirectional type synthesis and checking for each sub-term, as well as the unification process. If a negation proof is not of interest in practice, these programs can be simplified by discarding the cases that yield negation proofs. Alternatively, we could consider generalising typing derivations instead, like our generalised mode derivations (Figure 9), to reformulate negation proofs positively to deliver more informative error messages. This would assist programmers in resolving issues with ill-typed terms, rather than returning a blatant ‘no’.
5.3 Trichotomy on raw terms by type synthesis
Combining the bidirectional type synthesiser with the mode decorator, soundness, and completeness from Section 4, we derive a type synthesiser parameterised by \((\varSigma , \varOmega )\), generalising Theorem 2.4.
Corollary 5.11
(Trichotomy on raw terms). For any mode-correct bidirectional type system \((\varSigma , \varOmega )\), exactly one of the following holds:
-
1.
 and
and  for some type A,
for some type A, -
2.
 but
but  for any type A, or
for any type A, or -
3.
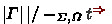 .
.
6 Examples
To exhibit the applicability of our approach, we discuss two more examples: one has infinitely many operations and the other includes many more constructs than simply typed \(\lambda \)-calculus, exhibiting the practical side of a general treatment.
6.1 Spine application
A spine application \(t\;u_1\;\ldots \;u_n\) is a form of application that consists of a head term t and an indeterminate number of arguments \(u_1\), \(u_2\), ..., \(u_n\). This arrangement allows direct access to the head term, making it practical in various applications, and has been used by Agda ’s core language.
At first glance, accommodating this form of application may seem impossible, given that the number of arguments for a construct is finite and has to be fixed. Nonetheless, the total number of operation symbols in a signature need not be finite, allowing us to establish a corresponding construct for each number n of arguments, i.e. viewing the following rule

as a rule schema parametrised by n, so the signature \(\varOmega _{\varLambda }^{\Leftrightarrow }\) can be extended with

Each application \(t\;u_1\;\ldots \;u_n\) can be introduced as \(\textsf{op}_{\textsf{app}_n}(t; u_1; \ldots ; u_n)\), thereby exhibiting the necessity of having an arbitrary set for operation symbols.
6.2 Computational calculi
Implementing a stand-alone type synthesiser for a simply typed language is typically a straightforward task. However, the code size increases proportionally to the number of type constructs and of arguments associated with each term construct. For example, when dealing with a fixed number n of type constructs, for each synthesising construct there are two cases for a checking argument but \(n + 1\) cases for each synthesising argument: the successful synthesis of the expected type, an instance where it fails, or \(n-1\) cases where the expected type does not match. Thus, having a generator is helpful and can significantly reduce the effort for implementation.
For illustrative purposes, consider a computational calculus [23] with naturals, sums, products, and general recursion.
The extended language has ‘only’ 15 constructs, including pairing, projections, injections, and so on, and this number of constructs is still far fewer than what a realistic programming language would have. Even for this small calculus, there are already nearly 100 possible cases to consider in bidirectional type synthesis.
On the other hand, similar to a parser generator, only one specification is needed for a type-synthesiser generator from the user to produce a corresponding type synthesiser. Such a specification can be derived by extending \((\varSigma _{\mathbin {\boldsymbol{\supset }}}, \varOmega _{\varLambda }^{\Leftrightarrow })\) accordingly for additional types and constructs with mode-correctness proved by applying Lemma 5.5, so its type synthesiser follows from Corollary 5.11 directly.
7 Discussion
We believe that our formal treatment lays a foundation for further investigation, as the essential aspects of bidirectional typing have been studied rigorously. While our current development is based on simply typed languages to highlight the core ideas, it is evident that many concepts and aspects remain untouched.
Language formalisation frameworks The idea of presenting logics universally at least date back to universal algebra and model theory, where structures are studied for certain notions of arities and signatures. In programming language theory, Aczel’s binding signature [1] is an example which has been used to prove a general confluence theorem. Many general definitions and frameworks for defining logics and type theories have been proposed and can be classified into two groups by where signatures reside—the meta level or the object level of a meta-language:
-
1.
Harper et al.’s logical framework LF [17] and its family of variants [5, 11, 18, 25] are extensions of Martin-Löf type theory, where signatures are on the meta level and naturally capable of specifying dependent type theories;
-
2.
general dependent type theories [6, 7, 19, 28], categorical semantics [4, 12,13,14,15,16, 26, 27] (which includes the syntactic model as a special case), and frameworks for substructural systems [26, 27, 32] are developed within a meta-theory (set theory or type theory), where signatures are on the object level and their expressiveness varies depending on their target languages.
The LF family is expressive, but each extension is a different metalanguage and requires a different implementation to check formal LF proofs. Formalising LF and its variants is at least as complicated as formalising a dependent type theory, and they are mostly implemented separately from their theory and unverified.
For the second group, theories developed in set theory can often be restated in type theory and thus manageable for formalisation in a type-theoretic proof assistant. Such examples include frameworks developed by Ahrens et al. [2],Allais et al. [3], Fiore and Szamozvancev [14], although these formal implementations are limited to simply typed theories for now.
Our work belongs to the second group, as we aim for a formalism in a type theory to minimise the gap between theory and implementation.
Beyond simple types Bidirectional type synthesis plays a crucial role in handling more complex types than simple types, and we sketch how our theory can be extended to treat a broader class of languages. First, we need a general definition of languages in question (Sections 3.1 and 3.2). Then, this definition can be augmented with modes (Section 3.3) and the definition of mode-correctness (Definition 5.3) can be adapted accordingly. Soundness and completeness (Theorem 4.1) should still hold, as they amount to the separation and combination of mode and typing information for a given raw term (in a syntax-directed formulation). Mode decoration (Section 4.2), which annotates a raw term with modes and marks missing annotations, should also work. As for the decidability of bidirectional type synthesis, we discuss two cases involving polymorphic types and dependent types below.
Polymorphic types In the case of languages like System F and others that permit type-level variable binding, we can start with the notion of polymorphic signature, as introduced by Hamana [16]—(i) each type construct in a signature is specified by a binding arity with only one type \(*\), and (ii) a term construct can employ a pair of extension contexts for term variables and type variables.
Extending general definitions for bidirectional typing and mode derivations from Hamana’s work is straightforward. For example, the universal type \(\forall \alpha .\, A\) and type abstraction in System F can be specified as operations \(\textsf{all} : * \rhd [*] * \rightarrow *\) and  .
.
The decidability of bidirectional type synthesis (Theorem 5.7) should also carry over, as no equations are imposed on types and no guessing (for type application) is required. Adding subtyping \(A \mathrel {<:} B\) to languages can be done by replacing type equality with a subtyping relation \(\mathrel {<:}\) and type equality check with subtyping check, so polymorphically typed languages with subtyping such as System \(\textsf{F}_{\mathsf {<:}}\) can be specified. The main idea of bidirectional typing does not change, so it should be possible to extend the formal theory without further assumptions too.
However, explicit type application in System F and System \(\textsf{F}_{\mathsf {<:}}\) is impractical but its implicit version results in a stationary rule [20] which is not syntax-directed. By translating the rule to subtyping, we have the instantiation problem that requires guessing B in \(\forall \alpha . A <: A[B/\alpha ]\). A theory that accommodates various solutions to the problem is left as future work.
Dependent types Logical frameworks with bidirectional typing are proposed by Reed [25] and Felicissimo [11]. Felicissimo’s framework is more expressive than Reed’s, due to its ability to specify rewriting rules. Both frameworks extend LF, enabling generic bidirectional type checking for dependent type theories. They also incorporate notions of signatures and mode-correctness (called strictness and validity, respectively, in their contexts) but differ from ours in several ways.
First, the number of operations introduced by a signature in LF is finite, so constructs like spine application seem impossible to define. Second, Reed and Felicissimo deal with decorated raw terms only, while our theory bridges the gap between ordinary and decorated raw terms by mode decoration. Lastly, Felicissimo classifies operations a priori into introduction and elimination rules, and follows the Pfenning recipe assigning, for example, the synthesising mode to each elimination rule and its principal argument. As pointed out by Dunfield and Krishnaswami that bidirectional typing is essentially about managing information flow, and that some systems remarkably deviate from this recipe, we do not enforce it but establish our results on any reasonable information flow.
Beyond syntax-directedness To relax the assumption of syntax-directedness, we could start from a simple but common case where the ordinary typing part is still syntax-directed, but each typing rule is refined to multiple bidirectional variants, including different orders of its premises. In such cases, the mode decorator would need to backtrack and find all mode derivations, but the type synthesiser should still work in a syntax-directed manner on each mode derivation. Completeness could still take the simple form presented in this paper too.
Next, we could consider systems where each construct can have multiple typing rules, which can further have multiple bidirectional variants. In this setting, the bidirectional type synthesiser will also need to backtrack. It is still possible to treat soundness as the separation of mode and type information, but completeness will pose a problem: for every raw term, a mode derivation chooses a mode assignment while a typing derivation chooses a typing rule, but there may not be a bidirectional typing rule for this particular combination. A solution might be refining completeness to say that any typing derivation can be combined with one of the possible mode derivations into a bidirectional typing derivation.
Towards a richer formal theory There are more principles and techniques in bidirectional typing that could be formally studied in general, with one notable example being the Pfenning recipe for bidirectionalising typing rules [10, Section 4]. There are also concepts that may be hard to fully formalise, for example ‘annotation character’ [10, Section 3.4], which is roughly about how easy it is for the user to write annotated programs, but it would be interesting to explore to what extent such concepts can be formalised.
Notes
- 1.
The usual conditions about named representations of variables are omitted.
- 2.
We write ‘\(\mathbin {\boldsymbol{\supset }}\)’ instead of ‘\(\rightarrow \)’ for the function types of simply typed \(\lambda \)-calculus to avoid confusion with the function types in our type-theoretic meta-language.
- 3.
Even though our theory is developed in Martin-Löf type theory, the term ‘set’ is used instead of ‘type’ to avoid the obvious confusion. Indeed, as we assume Axiom K, all types are legitimately sets in the sense of homotopy type theory [29, Definition 3.1.1].
- 4.
For the sake of simplicity, we use ordinary mode decoration elsewhere in this paper.
- 5.
There are various definitions for finite subsets of a set within type theory, but for our purposes the choice among these definitions is not a matter of concern.
- 6.
To simplify our choice, we may confine \(\varXi \) to any set within the family of sets \(\textsf{Fin}(n)\) of naturals less than n, given that these sets have a decidable equality and the arity of a type construct is finite. Indeed, in our formalisation, we adopt \(\textsf{Fin}(n)\) as the set of type variables in the definition of \(\textsf{Ty}_{\varSigma }\). For the sake of clarity in presentation, though, we just use named variables and assume that \(\varXi \) has a decidable equality.
References
Aczel, P.: A general Church–Rosser theorem (1978),http://www.ens-lyon.fr/LIP/REWRITING/MISC/AGeneralChurch-RosserTheorem.pdf
Ahrens, B., Matthes, R., Mörtberg, A.: Implementing a category-theoretic
Allais, G., Atkey, R., Chapman, J., McBride, C., McKinna, J.: A type- andscope-safe universe of syntaxes with binding: their semantics and proofs.Journal of Functional Programming 31, e22:1–55 (2021),https://doi.org/10.1017/S0956796820000076
Arkor, N., Fiore, M.: Algebraic models of simple type theories: a polynomialapproach. In: Symposium on Logic in Computer Science (LICS), pp. 88–101, ACM(2020), https://doi.org/10.1145/3373718.3394771
Assaf, A., Burel, G., Cauderlier, R., Delahaye, D., Dowek, G., Dubois, C.,
Bauer, A., Haselwarter, P.G., Lumsdaine, P.L.: A general definition ofdependent type theories (2020), https://doi.org/10.48550/arXiv.2009.05539
Bauer, A., Komel, A.P.: An extensible equality checking algorithm for dependenttype theories. Logical Methods in Computer Science 18(1), 17:1–42(2022), https://doi.org/10.46298/lmcs-18(1:17)2022
Chen, L.T., Ko, H.S.: A formal treatment of bidirectional typing (artefact)(2024), https://doi.org/10.5281/zenodo.10458840
Dowek, G.: The undecidability of typability in the lambda-pi-calculus. In:International Conference on Typed Lambda Calculi and Applications (TLCA),Lecture Notes in Computer Science, vol. 664, pp. 139–145, Springer (1993),https://doi.org/10.1007/BFb0037103
Dunfield, J., Krishnaswami, N.: Bidirectional typing. ACM Computing Surveys54(5), 98:1–38 (2021), https://doi.org/10.1145/3450952
Felicissimo, T.: Generic bidirectional typing for dependent type theories(2023), https://doi.org/10.48550/arXiv.2307.08523
Fiore, M., Hamana, M.: Multiversal polymorphic algebraic theories: syntax,semantics, translations, and equational logic. In: Symposium on Logic inComputer Science (LICS), pp. 520–529, IEEE (2013),https://doi.org/10.1109/LICS.2013.59
Fiore, M., Hur, C.K.: Second-order equational logic (extended abstract). In:International Workshop on Computer Science Logic (CSL), Lecture Notes inComputer Science, vol. 6247, pp. 320–335, Springer (2010),https://doi.org/10.1007/978-3-642-15205-4_26
Fiore, M., Szamozvancev, D.: Formal metatheory of second-order abstract syntax.Proceedings of the ACM on Programming Languages 6(POPL), 53:1–29(2022), https://doi.org/10.1145/3498715
Fiore, M.P., Plotkin, G.D., Turi, D.: Abstract syntax and variable binding. In:Symposium on Logic in Computer Science (LICS), pp. 193–202, IEEE (1999),https://doi.org/10.1109/LICS.1999.782615
Hamana, M.: Polymorphic abstract syntax via Grothendieck construction. In:International Conference on Foundations of Software Science and ComputationalStructures (FoSSaCS), Lecture Notes in Computer Science, vol. 6604, pp.381–395, Springer (2011), https://doi.org/10.1007/978-3-642-19805-2_26
Harper, R., Honsell, F., Plotkin, G.: A framework for defining logics. Journalof the ACM 40(1), 143–184 (1993), https://doi.org/10.1145/138027.138060
Harper, R., Licata, D.R.: Mechanizing metatheory in a logical framework.Journal of Functional Programming 17(4–5), 613–673 (2007),https://doi.org/10.1017/S0956796807006430
Haselwarter, P.G., Bauer, A.: Finitary type theories with and without contexts(2021), https://doi.org/10.48550/arXiv.2112.00539
Leivant, D.: Typing and computational properties of lambda expressions.Theoretical Computer Science 44, 51–68 (1986),https://doi.org/10.1016/0304-3975(86)90109-X
McBride, C.: First-order unification by structural recursion. Journal ofFunctional Programming 13(6), 1061–1075 (2003a),https://doi.org/10.1017/S0956796803004957
McBride, C.: First-order unification by structural recursion: correctness proof(2003b),http://www.strictlypositive.org/foubsr-website/
Moggi, E.: Computational lambda-calculus and monads. In: Symposium on Logic inComputer Science (LICS), pp. 14–23, IEEE (1989),https://doi.org/10.1109/LICS.1989.39155
Pierce, B.C., Turner, D.N.: Local type inference. ACM Transactions onProgramming Languages and Systems 22(1), 1–44 (2000),https://doi.org/10.1145/345099.345100
Reed, J.: Redundancy elimination for LF. In: International Workshop onLogical Frameworks and Meta-Languages (LFM 2004), vol. 199, pp. 89–106(2008), https://doi.org/10.1016/j.entcs.2007.11.014
Tanaka, M., Power, A.J.: Pseudo-distributive laws and axiomatics for variablebinding. Higher-Order and Symbolic Computation 19(2–3), 305–337(2006a), https://doi.org/10.1007/s10990-006-8750-x
Tanaka, M., Power, J.: A unified category-theoretic semantics for bindingsignatures in substructural logic. Journal of Logic and Computation16(1), 5–25 (2006b), https://doi.org/10.1093/logcom/exi070
Uemura, T.: Abstract and Concrete Type Theories. Ph.D. thesis, University ofAmsterdam (2021),https://hdl.handle.net/11245.1/41ff0b60-64d4-4003-8182-c244a9afab3b
Univalent Foundations Program, T.: Homotopy Type Theory: UnivalentFoundations of Mathematics. Institute for Advanced Study (2013),https://homotopytypetheory.org/book
Wadler, P., Kokke, W., Siek, J.G.: Programming Language Foundations inAgda (2022), https://plfa.inf.ed.ac.uk/22.08/
Wells, J.B.: Typability and type checking in System F are equivalent andundecidable. Annals of Pure and Applied Logic 98(1–3), 111–156(1999), https://doi.org/10.1016/S0168-0072(98)00047-5
Wood, J., Atkey, R.: A framework for substructural type systems. In: EuropeanSymposium on Programming (ESOP), Lecture Notes in Computer Science, vol.13240, pp. 376–402, Springer (2022), https://doi.org/10.1007/978-3-030-99336-8_14
Acknowledgement
We thank Kuen-Bang Hou (Favonia) and anonymous reviewers for their comments and suggestions. The work was supported by the National Science and Technology Council of Taiwan under grant NSTC 112-2221-E-001-003-MY3.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Chen, LT., Ko, HS. (2024). A Formal Treatment of Bidirectional Typing. In: Weirich, S. (eds) Programming Languages and Systems. ESOP 2024. Lecture Notes in Computer Science, vol 14576. Springer, Cham. https://doi.org/10.1007/978-3-031-57262-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-57262-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57261-6
Online ISBN: 978-3-031-57262-3
eBook Packages: Computer ScienceComputer Science (R0)







 if
if  has a derivation, and
has a derivation, and for some operation
for some operation  for each i,
for each i,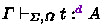 , indexed by a typing context
, indexed by a typing context  under
under  , and a type A, is defined in Figure
, and a type A, is defined in Figure 
 in
in  for each i;
for each i; , indexed by a list V of variables, a raw term
, indexed by a list V of variables, a raw term 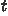 under V, and a mode d, is defined in Figure
under V, and a mode d, is defined in Figure 




 , its argument list is mode-correct with respect to
, its argument list is mode-correct with respect to  contains every inhabitant of
contains every inhabitant of  , its argument list is mode-correct with respect to
, its argument list is mode-correct with respect to 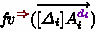 contains every inhabitant of
contains every inhabitant of  follows from the fact that each variable as a raw term refers to the same variable in its context.
follows from the fact that each variable as a raw term refers to the same variable in its context. holds trivially, since the synthesised type A is from the term
holds trivially, since the synthesised type A is from the term  in question.
in question. contains a substitution
contains a substitution  so that
so that  . We prove it by induction on the argument list:
. We prove it by induction on the argument list:  is
is  , then the statement holds by induction hypothesis.
, then the statement holds by induction hypothesis. is
is  , then
, then  by induction hypothesis (of the list). Therefore, under the same context
by induction hypothesis (of the list). Therefore, under the same context  the term
the term  by induction hypothesis (of the typing derivation), so
by induction hypothesis (of the typing derivation), so  .
. , then it is decidable whether
, then it is decidable whether  for some A;
for some A; , then it is decidable for any A whether
, then it is decidable for any A whether  .
. , or
, or

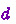 is
is  : We apply our claim with the partial substitution
: We apply our claim with the partial substitution  for some A, then by inversion we have
for some A, then by inversion we have 
 for every i, which contradict the assumption that no such extension exists.
for every i, which contradict the assumption that no such extension exists. such that (
such that (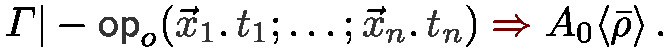
 is
is  : Let A be a type and apply Lemma
: Let A be a type and apply Lemma  but
but 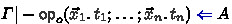 , then inversion gives us a substitution
, then inversion gives us a substitution  —a contradiction.
—a contradiction. , then apply our claim with
, then apply our claim with  , then by inversion there is
, then by inversion there is  and
and  for every i. Given that
for every i. Given that  , it follows that
, it follows that  exists, thus a contradiction.
exists, thus a contradiction.
 since
since  , by induction hypothesis on the list, we have two cases:
, by induction hypothesis on the list, we have two cases:  :
: is
is  : By mode-correctness,
: By mode-correctness,  and
and 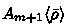 are defined. By the ind. hyp.
are defined. By the ind. hyp.  is decidable. Clearly, if
is decidable. Clearly, if  then the desired statement is proved; otherwise we easily derive a contradiction.
then the desired statement is proved; otherwise we easily derive a contradiction. is
is  : By mode-correctness,
: By mode-correctness, 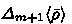 is defined. By the ind. hyp., ‘
is defined. By the ind. hyp., ‘ for some A’ is decidable:
for some A’ is decidable:  for any A but there is
for any A but there is  , and we derive a contradiction because
, and we derive a contradiction because  .
. for some A, then Lemma
for some A, then Lemma  but an extension
but an extension  . However, by Lemma
. However, by Lemma  must be unique, so
must be unique, so 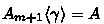 , i.e. a contradiction.
, i.e. a contradiction. , then it is not hard to show that
, then it is not hard to show that  and
and  for some type A,
for some type A, but
but  for any type A, or
for any type A, or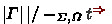 .
.