Abstract
This article presents Trocq, a new proof transfer framework for dependent type theory. Trocq is based on a novel formulation of type equivalence, used to generalize the univalent parametricity translation. This framework takes care of avoiding dependency on the axiom of univalence when possible, and may be used with more relations than just equivalences. We have implemented a corresponding plugin for the Coq interactive theorem prover, in the Coq-Elpi meta-language.
This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No.101001995).
You have full access to this open access chapter, Download conference paper PDF
Keywords


1 Introduction
Formalizing mathematics provides every object and statement of the mathematical literature with an explicit data structure, in a certain choice of foundational formalism. As one would expect, several such explicit representations are most often needed for a same mathematical concept. Sometimes, these different choices are already made explicit on paper: multivariate polynomials can for instance be represented as lists of coefficient-monomial pairs, e.g., when computing Gröbner bases, but also as univariate polynomials with polynomial coefficients, e.g., for the purpose of projecting algebraic varieties. The conversion between these equivalent data structures however remains implicit on paper, as they code in fact for the same free commutative algebra. In some other cases, implementation details are just ignored on paper, e.g., when a proof involves both reasoning with Peano arithmetic and computing with large integers.
Example 1 (Proof-oriented vs. computation-oriented data structures)
[Proof-oriented vs. computation-oriented data structures] The standard library of the Coq interactive theorem prover [32] has two data structures for representing natural numbers. Type \(\mathbb {N}\) is the base-1 number system and the associated elimination principle  is the usual recurrence scheme:
is the usual recurrence scheme:

On the other hand, type  provides a binary representation
provides a binary representation  of non-negative integers, as sequences of bits with a head 1, and is thus better suited for coding efficient arithmetic operations. The successor function
of non-negative integers, as sequences of bits with a head 1, and is thus better suited for coding efficient arithmetic operations. The successor function  is no longer a constructor of the type, but can be implemented as a program, via an auxiliary successor function
is no longer a constructor of the type, but can be implemented as a program, via an auxiliary successor function  for type
for type  .
.

This successor function is useful to implement conversions \(\uparrow _{\mathbb {N}}\ :\ \texttt {N}\ \rightarrow \ \mathbb {N}\) and \(\downarrow _{\mathbb {N}}\ :\ \mathbb {N}\ \rightarrow \ \texttt {N}\) between the unary and binary representations. These conversion functions are in fact inverses of each other. The natural recurrence scheme on natural numbers thus transfers to type  :
:

Incidentally,  can be proved from
can be proved from  by using only the fact that \(\downarrow _{\mathbb {N}}\) is a left inverse of \(\uparrow _{\mathbb {N}}\), and the following compatibility lemmas:
by using only the fact that \(\downarrow _{\mathbb {N}}\) is a left inverse of \(\uparrow _{\mathbb {N}}\), and the following compatibility lemmas:
Proof transfer issues are not tied to program verification. For instance, the formal study of summation and integration, in basic real analysis, provides a classic example of frustrating bureaucracy.
Example 2 (Extended domains)
[Extended domains] Given a sequence \((u_n)_{n\in \mathbb {N}}\) of non-negative real numbers, i.e., a function \(u\ : \ \mathbb {N} \rightarrow [0,+\infty [\), u is said to be summable when the sequence \((\sum _{k=0}^nu_k)_{n\in \mathbb {N}}\) has a finite limit, denoted \(\sum u\). Now for two summable sequences u and v, it is easy to see that \(u + v\), the sequence obtained by point-wise addition of u and v, is also a summable sequence, and that:
As expression \(\sum u\) only makes sense when u is a summable sequence, any algebraic operation “under the sum”, e.g., rewriting \(\sum (u + (v + w))\) into \(\sum ((w + u) + v)\), a priori requires a proof of summability for every rewriting step. In a classical setting, the standard approach rather assigns a default value to the case of an infinite sum, and introduces an extended domain \([0,+\infty ]\). Algebraic operations on real numbers, like addition, are extended to the extra \(+\infty \) case. Now for a sequence \(u\ : \ \mathbb {N} \rightarrow [0,+\infty ]\), the limit \(\sum u\) is always defined, as increasing partial sums either converge to a finite limit, or diverge to \(+\infty \). The road map is then to first prove that Equation 1 holds for any two sequences of extended non-negative numbers. The result is then transferred to the special case of summable sequences of non-negative numbers. Major libraries of formalized mathematics including Lean’s mathlib [1], Isabelle/HOL’s Archive of Formal Proofs, coq-interval [20] or Coq’s mathcomp-analysis [2], resort to such extended domains and transfer steps, notably for defining measure theory. Yet, as reported by expert users [18], the associated transfer bureaucracy is essentially done manually and thus significantly clutters formal developments in real and complex analysis, probabilities, etc.
Users of interactive theorem provers should be allowed to elude mundane arguments pertaining to proof transfer, as they would on paper, and spare themselves the related bureaucracy. Yet, they still need to convince the proof checker and thus have to provide explicit transfer proofs, albeit ideally automatically generated ones. The present work aims at providing a general method for implementing this nature of automation, for a diverse range of proof transfer problems.
In this paper, we focus on interactive theorem provers based on dependent type theory, such as Coq, Agda [24] or Lean [22]. These proof management systems are genuine functional programming languages, with full-spectrum dependent types, a context in which representation independence meta-theorems can be turned into concrete instruments for achieving program and proof transfer.
Seminal results on the contextual equivalence of distinct implementations of a same abstract interface were obtained for System F, using logical relations [21] and parametricity meta-theorems [26, 35]. In the context of type theory, such meta-theorems can be turned into syntactic translations of the type theory of interest into itself, automating this way the generation of the statement and proof of parametricity properties for type families and for programs. Such syntactic relational models can accommodate dependent types [10], inductive types [9] and scale to the Calculus of Inductive Constructions, with an impredicative sort [19].
In particular, the univalent parametricity translation [30] leverages the univalence axiom [33] so as to transfer statements using established equivalences of types. This approach crucially removes the need for devising an explicit common interface for the types in relation. In presence of an internalized univalence axiom and of higher-inductive types, the structure identity principle provides internal representations of independence results, for more general relations between types than equivalences [5]. This last approach is thus particularly relevant in cubical type theory [12, 34]. Indeed, a computational interpretation of the univalence axiom brings computational adequacy to otherwise possibly stuck terms, those resulting from a transfer involving an axiomatized univalence principle.
Yet taming the bureaucracy of proof transfer remains hard in practice for users of Coq, Lean or Agda. Examples 1 and 2 actually illustrate fundamental limitations of the existing approaches:
Univalence is overkill Both univalent parametricity and the structure identity principle can be used to derive the statement and the proof of the induction principle  of Example 1, from the elimination scheme of type \(\mathbb {N}\). But up to our knowledge, all the existing methods for automating this implication pull in the univalence principle in the proof, although it can be obtained by hand by very elementary means. This limitation is especially unsatisfactory for developers of libraries formalizing classical mathematics, and notably Lean’s mathlib. These libraries indeed typically assume a strong form of proof irrelevance, which is incompatible with univalence, and thus with univalent parametricity.
of Example 1, from the elimination scheme of type \(\mathbb {N}\). But up to our knowledge, all the existing methods for automating this implication pull in the univalence principle in the proof, although it can be obtained by hand by very elementary means. This limitation is especially unsatisfactory for developers of libraries formalizing classical mathematics, and notably Lean’s mathlib. These libraries indeed typically assume a strong form of proof irrelevance, which is incompatible with univalence, and thus with univalent parametricity.
Equivalences are not enough, neither are quotients Univalent parametricity cannot help with Example 2, as type \([0,+\infty [\) is not equivalent to its extended version \([0,+\infty ]\). In fact, we are not aware of any tool able to automate this proof transfer. In particular, the structure identity principle [5] would not apply as such.
Contributions In short, existing techniques for transferring results from one type to another, e.g., from  to
to  or from extended real numbers to real numbers, are either not suitable for dependent types, or too coarse to track the exact amount of data needed in a given proof, and not more. This paper presents three contributions improving this unfortunate state of affairs:
or from extended real numbers to real numbers, are either not suitable for dependent types, or too coarse to track the exact amount of data needed in a given proof, and not more. This paper presents three contributions improving this unfortunate state of affairs:
-
A parametricity framework à la carte, that generalizes the univalent parametricity translation [30], as well as refinements à la CoqEAL [14] and generalized rewriting [28]. Its pivotal ingredient is a variant of Altenkirch and Kaposi’s symmetrical presentation of type equivalence [3].
-
A conservative subtyping extension of \(CC_{\omega }\) [15], used to formulate an inference algorithm for the synthesis of parametricity proofs.
-
The implementation of a new parametricity plugin for the Coq interactive theorem prover, using the Coq-Elpi [31] meta-language. This plugin rests on original formal proofs, conducted on top of the HoTT library [8], and is distributed with a collection of application examples.
Outline The rest of this paper is organized as follows. Section 2 introduces proof transfer and recalls the principle, strengths and weaknesses of the univalent parametricity translation. In Section 3, we present a new definition of type equivalence, motivating a hierarchy of structures for relations preserved by parametricity. Section 4 then presents variants of parametricity translations. In Section 5, we discuss a few examples of applications and we conclude in Section 6.
2 Strengths and limits of univalent parametricity
We first clarify the essence of proof transfer in dependent type theory (§ 2.1) and briefly recall a few concepts related to type equivalence and univalence (§ 2.2). We then review and discuss the limits of univalent parametricity (§ 2.3).
2.1 Proof transfer in type theory
We recall the syntax of the Calculus of Constructions, \(CC_{\omega }\), a \(\lambda \)-calculus with dependent function types and a predicative hierarchy of universes, denoted \(\square _{i}\):
We omit the typing rules of the calculus, and refer the reader to standard references (e.g., [23, 25]). We also use the standard equality type, called propositional equality, as well as dependent pairs, denoted \(\varSigma x : A.\,B\). We write \(t \equiv u\) the definitional equality between two terms t and u. Interactive theorem provers like Coq, Agda and Lean are based on various extensions of this core, notably with inductive types or with an impredicative sort. When the universe level does not matter, we casually remove the annotation and use notation \(\square _{}\).
In this context, proof transfer from type \(T_1\) to type \(T_2\) roughly amounts to synthesizing a new type former \(W : T_2 \rightarrow \square _{}\), i.e., a type parametric in some type \(T_2\), from an initial type former \(V : T_1 \rightarrow \square _{}\), i.e., a type parametric in some type \(T_1\), so as to ensure that for some given relations \(R_{T} : T_1 \rightarrow T_2 \rightarrow \square _{}\) and \(R_{\square _{}} : \square _{} \rightarrow \square _{} \rightarrow \square _{}\), there is a proof w that:
for a suitable context \(\varGamma \). This setting generalizes as expected to k-ary type formers, and to more pairs of related types. In practice, relation \(R_{\square _{}}\) is often a right-to-left arrow, i.e., \(R_{\square _{}}\ A\ B \triangleq B \rightarrow A\), as in this case the proof w substantiates a proof step turning a goal clause \(\varGamma \vdash V\ t_1\) into \(\varGamma \vdash W\ t_2\).
Phrased as such, this synthesis problem is arguably quite loosely specified. Consider for instance the transfer problem discussed in Example 1. A first possible formalization involves the design of an appropriate common interface structure for types \(\mathbb {N}\) and \(\texttt {N}\), for instance by setting both \(T_1\) and \(T_2\) as \(\varSigma N : \square _{}. N \times (N \rightarrow N)\), and both V and W as: \(\lambda X : T_1.\, \varPi P : X.1 \rightarrow \Box .\, P\ X.2 \rightarrow (\varPi n : X.1.\, P\ n \rightarrow P\ (X.3\ n)) \rightarrow \varPi n : X.1.\, P\ n\), where X.i denotes the i-th item in the dependent tuple X. In this case, relation \(R_T\) may characterize isomorphic instances of the structure. Such instances of proof transfer are elegantly addressed in cubical type theories via internal representation independence results [5]. In the context of \(CC_{\omega }\), the hassle of devising explicit structures by hand has been termed the anticipation problem [30].
Another option is to consider two different types \(T_1 \triangleq \mathbb {N} \times (\mathbb {N} \rightarrow \mathbb {N})\) and \(T_2 \triangleq \textrm{N} \times (\textrm{N} \rightarrow \textrm{N})\) and
where one would typically expect \(R_T\) to be a type equivalence between \(T_1\) and \(T_2\), so as to transport \((V'\ t_1)\) to \((W'\ t_2)\), along this equivalence.
Note that some solutions of given instances of proof transfer problems are in fact too trivial to be of interest. Consider for example the case of a functional relation between \(T_2\) and \(T_1\), with \(R_T \ t_1\ t_2\) defined as \(t_1 = \phi \ t_2\), for some \(\phi : T_2 \rightarrow T_1\). In this case, the composition \(V \circ \phi \) is an obvious candidate for W, but is often uninformative. Indeed, this composition can only propagate structural arguments, blind to the additional mathematical proofs of program equivalences potentially available in the context. For instance, here is a useless variant of \(W'\):
Automation devices dedicated to proof transfer thus typically consist of a meta-program which attempts to compute type former W and proof w by induction on the structure of V, by composing registered canonical pairs of related terms, and the corresponding proofs. These tools differ by the nature of relations they can accommodate, and by the class of type formers they are able to synthesize. For instance, generalized rewriting [28], which provides essential support to formalizations based on setoids [7], addresses the case of homogeneous (and reflexive) relations, i.e., when \(T_1\) and \(T_2\) coincide. The CoqEAL library [14] provides another example of such transfer automation tool, geared towards refinements, typically from a proof-oriented data-structure to a computation-oriented one. It is thus specialized to heterogeneous, functional relations but restricted to closed, quantifier-free type formers. We now discuss the few transfer methods which can accommodate dependent types and heterogeneous relations.
2.2 Type equivalences, univalence
Let us first focus on the special case of types related by an equivalence, and start with a few standard definitions, notations and lemmas. Omitted details can be found in the usual references, like the Homotopy Type Theory book [33]. Two functions \(f,g : A \rightarrow B\) are point-wise equal, denoted \(f \doteqdot g\) when their values coincide on all arguments, that is \(f \doteqdot g \triangleq \varPi a : A.\,f\ a = g\ a\). For any type A, \(id_A\) denotes \(\lambda a : A.\,a\), the identity function on A, and we write id when the implicit type A is not ambiguous.
Definition 1 (Type isomorphism, type equivalence)
[Type isomorphism, type equivalence] A function \(f : A \rightarrow B\) is an isomorphism, denoted \(\textsf {IsIso}(f)\), if there exists a function \(g : B \rightarrow A\) which satisfies the section and retraction properties, i.e., g is respectively a point-wise left and right inverse of f. A function f is an equivalence, denoted \(\textsf {IsEquiv}(f)\), when it moreover enjoys a coherence property, relating the proofs of the section and retraction properties and ensuring that \(\textsf {IsEquiv}(f)\) is proof-irrelevant.
Types A and B are equivalent, denoted \(A \simeq B\), when there is an equivalence \(f : A \rightarrow B\):
Lemma 1
Any isomorphism \(f : A \rightarrow B\) is also an equivalence.
The data of an equivalence \(e : A \simeq B\) thus include two transport functions, denoted respectively \(\uparrow _e\ : A \rightarrow B\) and \(\downarrow _e\ : B \rightarrow A\). They can be used for proof transfer from A to B, using \(\uparrow _e\) at covariant occurrences, and \(\downarrow _e\) at contravariant ones. The univalence principle asserts that equivalent types are interchangeable, in the sense that all universes are univalent.
Definition 2 (Univalent universe)
[Univalent universe] A universe \(\mathcal {U}\) is univalent if for any two types A and B in \(\mathcal {U}\), the canonical map \(A = B \rightarrow A \simeq B\) is an equivalence.
In variants of \(CC_{\omega }\), the univalence axiom has no explicit computational content: it just postulates that all universes \(\Box _i\) are univalent, as for instance in the HoTT library for the Coq interactive theorem prover [8]. Some more recent variants of dependent type theory [4, 12] feature a built-in computational univalence principle. They are used to implement experimental interactive theorem provers, such as Cubical Agda [34]. In both cases, the univalence principle provides a powerful proof transfer principle from \(\square _{}\) to \(\square _{}\), as for any two types A and B such that \(A \simeq B\), and any \(P : \square _{} \rightarrow \square _{}\), we can obtain that \(P\ A \simeq P\ B\) as a direct corollary of univalence. Concretely, \(P\ B\) is obtained from \(P\ A\) by appropriately allocating the transfer functions provided by the equivalence data, a transfer process typically useful in the context of proof engineering [27].
Going back to our example from § 2.1, transferring along an equivalence \(\mathbb {N} \simeq \texttt {N}\) thus produces \(W''\) from \(V'\). Assuming univalence, one may achieve the more informative transport from \(V'\) to \(W'\), using a method called univalent parametricity [30], which we discuss in the next section.
2.3 Parametricity translations
Univalent parametricity strengthens the transfer principle provided by the univalence axiom by combining it with parametricity. In \(CC_{\omega }\), the essence of parametricity, which is to devise a relational interpretation of types, can be turned into an actual syntactic translation, as relations can themselves be modeled as \(\lambda \)-terms in \(CC_{\omega }\). The seminal work of Bernardy, Lasson et al. [9, 10, 19] combine in what we refer to as the raw parametricity translation, which essentially defines inductively a logical relation \(\llbracket \,T\,\rrbracket \) for any type T, as described on Figure 1. This presentation uses the standard convention that \(t'\) is the term obtained from a term t by replacing every variable x in t with a fresh variable \(x'\). A variable x is translated into a variable \(x_R\), where \(x_R\) is a fresh name. Parametricity follows from the associated fundamental theorem, also called abstraction theorem [26]:
Theorem 1
If \(\ \varGamma \vdash t : T\) then the following hold: \(\ \llbracket \,\varGamma \,\rrbracket \vdash t : T\), \(\ \llbracket \,\varGamma \,\rrbracket \vdash t' : T'\) and \(\ \llbracket \,\varGamma \,\rrbracket \vdash \llbracket \,t\,\rrbracket : \llbracket \,T\,\rrbracket \ t\ t'\).
Proof
By structural induction on the typing judgment, see for instance [19].
A key, albeit mundane ingredient of Theorem 1 is the fact that the rules of Figure 1 ensure that:
This translation precisely generates the statements expected from a parametric type family or program. For instance, the translation of a \(\varPi \)-type, given by Equation 8, is a type of relations on functions that relate those producing related outputs from related inputs. Concrete implementations of this translation are available [19, 31]; they generate and prove parametricity properties for type families or for constants, improved induction schemes, etc.
Univalent parametricity follows from the observation that the abstraction theorem still holds when restricting to relations that are in fact (heterogeneous) equivalences. This however requires some care in the translation of universes:
where \(\llbracket \,\cdot \,\rrbracket \) now refers to the univalent parametricity translation, replacing the notation introduced for the raw variant. For any two types A and B, \(\llbracket \,\square _{i}\,\rrbracket \ A\ B\) packages a relation R and an equivalence e such that R is equivalent to the functional relation associated with \(\downarrow _e\). Crucially, assuming univalence, \(\llbracket \,\square _{i}\,\rrbracket \) is equivalent to type equivalence, that is, for any two types A and B:
This observation is actually an instance of a more general technique available for constructing syntactic models of type theory [11], based on attaching extra intensional specifications to negative type constructors. In these models, a standard way to recover the abstraction theorem consists of refining the translation into two variants, for any term \(T : \square _{i}\), that is also a type. The translation of such a T as a term, denoted \([\,T\,]\), is a dependent pair, which equips a relation with the additional data prescribed by the interpretation \(\llbracket \,\square _{i}\,\rrbracket \) of the universe. The translation \(\llbracket \,T\,\rrbracket \) of T as a type is the relation itself, that is, the projection of the dependent pair \([\,T\,]\) onto its first component, denoted \(\textsf {rel}([\,T\,])\). We refer to the original article [30, Figure 4] for a complete description of the translation.
We now state the abstraction theorem of the univalent parametricity translation [30], where \(\vdash _u\) denotes a typing judgment of \(CC_{\omega }\) assuming univalence:
Theorem 2
If \(\ \varGamma \vdash t : T\) then \(\llbracket \,\varGamma \,\rrbracket \vdash _u [\,t\,]\ :\ \llbracket \,T\,\rrbracket \ t\ t'\).
Note that proving the abstraction theorem 2 involves in particular proving that:
The definition of relation \([\,\square _{i}\,]\) relies on the univalence principle in a crucial way, in order to prove that the relation in the universe is equivalent to equality on the universe, i.e., to prove that:
Importantly, this univalent parametricity translation can be seamlessly extended so as to also make use of a global context of user-defined equivalences.
Yet because of the interpretation of universes given by Equation 10, univalent parametricity can only automate proof transfer based on type equivalences. This is too strong a requirement in many cases, e.g., to deduce properties of natural numbers from that of integers, or more generally for refinement relations. Even in the case of equivalent types, this restriction may be problematic, as Equation 11 may incur unnecessary dependencies on the univalence axiom, as in Example 1.
3 Type equivalence in kit
In this section, we propose (§ 3.1) an equivalent, modular presentation of type equivalence, phrased as a nested sigma type. Then (§ 3.2), we carve a hierarchy of structures on relations out of this dependent tuple, selectively picking pieces. Last, we revisit (§ 3.3) parametricity translations through the lens of this finer grained analysis of the relational interpretations of types.
3.1 Disassembling type equivalence
Let us first observe that the Definition 1, of type equivalence, is quite asymmetrical, although this fact is somehow swept under the rug by the infix \(A \simeq B\) notation. First, the data of an equivalence \(e : A \simeq B\) privileges the left-to-right direction, as \(\uparrow _e\) is directly accessible from e as its first projection, while accessing the right-to-left transport requires an additional projection. Second, the statement of the coherence property, which we eluded in Definition 1, is actually:
where \(\textsf {ap}_f (t)\) is the term \(f\ u = f\ v\), for any identity proof \(t : u = v\). This statement uses proofs s and r, respectively of the section and retraction properties of e, but not in a symmetrical way, although swapping them leads to an equivalent definition. This entanglement prevents tracing the respective roles of each direction of transport, left-to-right or right-to-left, during the course of a given univalent parametricity translation. Exercise 4.2 in the HoTT book [33] however suggests a symmetrical definition of type equivalence, via functional relations.
Definition 3
A relation \(R : A \rightarrow B \rightarrow \square _{i}\), is functional when:
where for any type T, \(\textsf {IsContr}(T)\) is the standard contractibility predicate \(\varSigma t : T.\,\varPi t' : T.\,t = t'\). This property is denoted \(\textsf {IsFun}(R)\).
We can now obtain an equivalent but symmetrical characterization of type equivalence, as a functional relation whose symmetrization is also functional.
Lemma 2
For any types \(A, B : \square _{}\), type \(A \simeq B\) is equivalent to:
where \({R}^{-1} : B \rightarrow A \rightarrow \square _{}\) just swaps the arguments of relation \(R : A \rightarrow B \rightarrow \square _{}\).
We sketch below a proof of this result, left as an exercise in [33]. The essential argument is the following characterization of functional relations:
Lemma 3
The type of functions is equivalent to the type of functional relations; i.e., for any types \(A, B\ :\ \square _{}\), we have \((A \rightarrow B) \, \simeq \, \varSigma R : A \rightarrow B \rightarrow \square _{}.\,\textsf {IsFun}(R)\).
Proof
The proof goes by chaining the following equivalences:
Proof
(of Lemma 2). The proof goes by chaining the following equivalences, where the type of f is always \(A \rightarrow B\) and the type of R is \(A \rightarrow B \rightarrow \square _{}\):
However, the definition of type equivalence provided by Lemma 2 does not expose explicitly the two transfer functions in its data, although this computational content can be extracted via first projections of contractibility proofs. In fact, it is possible to devise a definition of type equivalence which directly provides the two transport functions in its data, while remaining symmetrical. This variant follows from an alternative characterization of functional relations.
Definition 4
For any types \(A, B : \square _{}\), a relation \(R : A \rightarrow B \rightarrow \square _{}\), is a univalent map, denoted \(\textsf {IsUmap}(R)\) when there exists a function \(m : A \rightarrow B\) together with:
Now comes the crux lemma of this section.
Lemma 4
For any types \(A, B : \square _{}\) and any relation \(R : A \rightarrow B \rightarrow \square _{}\)
Proof
The proof goes by rewording the left hand side, in the following way:
After a suitable reorganization of the sigma types we are left to show that
which proof we do not detail, referring the reader to the supplementary material.
As a direct corollary, we obtain a novel characterization of type equivalence:
Theorem 3
For any types \(A, B : \square _{i}\), we have:

where the relation  is defined as:
is defined as:
The collection of data packed in a term of type  is now symmetrical, as the right-to-left direction of the equivalence based on univalent maps can be obtained from the left-to-right by flipping the relation and swapping the two functionality proofs. If the \(\eta \)-rule for records is verified, symmetry is even definitionally involutive.
is now symmetrical, as the right-to-left direction of the equivalence based on univalent maps can be obtained from the left-to-right by flipping the relation and swapping the two functionality proofs. If the \(\eta \)-rule for records is verified, symmetry is even definitionally involutive.
3.2 Reassembling type equivalence
Definition 4 of univalent maps and the resulting rephrasing of type equivalence suggest introducing a hierarchy of structures for heterogeneous relations, which explains how close a given relation is to type equivalence. In turn, this distance is described in terms of structure available respectively on the left-to-right and right-to-left transport functions.
Definition 5
For \(n, k \in \{0, 1, 2_{\text {a}}, 2_{\text {b}}, 3, 4\}\), and \(\alpha =(n,k)\), relation  , is defined as:
, is defined as:

where the map class \(\textsf {Class}_{\alpha }\ R\) itself unfolds to a pair type \((\textsf {M}_{n}\ R) \times (\textsf {M}_{k}\ {R}^{-1})\), with \(\textsf {M}_{i}\) defined as:Footnote 1
For any types A and B, and any  we use notations \(\textsf {rel}(r)\), \(\textsf {map}(r)\) and \(\textsf {comap}(r)\) to refer respectively to the relation, map of type \(A \rightarrow B\), map of type \(B \rightarrow A\), included in the data of r, for a suitable \(\alpha \).
we use notations \(\textsf {rel}(r)\), \(\textsf {map}(r)\) and \(\textsf {comap}(r)\) to refer respectively to the relation, map of type \(A \rightarrow B\), map of type \(B \rightarrow A\), included in the data of r, for a suitable \(\alpha \).
Definition 6
We denote \(\mathcal {A}\) the set \(\{0, 1, 2_{\text {a}}, 2_{\text {b}}, 3, 4\}^2\), used to index map classes in Definition 5. This set is partially ordered for the product order defined from the partial order \(0 < 1 < 2_{*} < 3 < 4\) for \(2_{*}\) either \(2_\text {a}\) or \(2_\text {b}\), and with \(2_\text {a}\) and \(2_\text {b}\) being incomparable.
Remark 1
Relation  of Definition 5 coincides with the relation
of Definition 5 coincides with the relation  introduced in Theorem 3. Similarly, we denote
introduced in Theorem 3. Similarly, we denote  the relation
the relation  .
.
Remark 2
Definition 5 is associated with the following dictionary. For r of type:
-
 , \(\textsf {map}(r)\) is an arbitrary function \(f : A \rightarrow B\);
, \(\textsf {map}(r)\) is an arbitrary function \(f : A \rightarrow B\); -
 , \(\textsf {rel}(r)\) is a univalent map, in the sense of Definition 4;
, \(\textsf {rel}(r)\) is a univalent map, in the sense of Definition 4; -
 , \(\textsf {rel}(r)\) is the graph of a retraction (i.e., a subjective univalent map with an explicit partial left inverse) of type \(A \rightarrow B\);
, \(\textsf {rel}(r)\) is the graph of a retraction (i.e., a subjective univalent map with an explicit partial left inverse) of type \(A \rightarrow B\); -
 , \(\textsf {rel}(r)\) is the graph of a section (i.e., an injective univalent map with explicit partial right inverse) of type \(A \rightarrow B\);
, \(\textsf {rel}(r)\) is the graph of a section (i.e., an injective univalent map with explicit partial right inverse) of type \(A \rightarrow B\); -
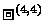 , r is an equivalence between A and B;
, r is an equivalence between A and B; -
 , r is an isomorphism between A and B.
, r is an isomorphism between A and B.
Observe that  coincides, up to equivalence, with
coincides, up to equivalence, with  . Other classes, while not corresponding to a meaningful mathematical definition, may arise in concrete runs of proof transfer: see also Section 4 for explicit examples.
. Other classes, while not corresponding to a meaningful mathematical definition, may arise in concrete runs of proof transfer: see also Section 4 for explicit examples.
The corresponding lattice to the collection of \(\textsf {M}_{n}\) is implemented as a hierarchy of dependent tuples, more precisely, of record types.
3.3 Populating the hierarchy of relations
We shall now revisit the parametricity translations of Section 2.3. In particular, combining Theorem 3 with Equation 11, crux of the abstraction theorem for univalent parametricity, ensures the existence of a term \(p_{\square _{i}}\) such that:

Otherwise said, relation  can be endowed with a
can be endowed with a  structure, assuming univalence. Similarly, Equation 9, for the raw parametricity translation, can be read as the fact that relation
structure, assuming univalence. Similarly, Equation 9, for the raw parametricity translation, can be read as the fact that relation  on universes can be endowed with a
on universes can be endowed with a  structure.
structure.
Now the hierarchy of structures introduced by Definition 5 enables a finer grained analysis of the possible relational interpretations of universes. Not only would this put the raw and univalent parametricity translations under the same hood, but it would also allow for generalizing parametricity to a larger class of relations. For this purpose, we generalize the previous observation, on the key ingredient for translating universes: for each \(\alpha \in \mathcal {A}\), relation  may be endowed with several structures from the lattice, and we need to study which ones, depending on \(\alpha \). Otherwise said, we need to identify the pairs \((\alpha , \beta )\in \mathcal {A}^2\) for which it is possible to construct a term \(p_\Box ^{\alpha , \beta }\) such that:
may be endowed with several structures from the lattice, and we need to study which ones, depending on \(\alpha \). Otherwise said, we need to identify the pairs \((\alpha , \beta )\in \mathcal {A}^2\) for which it is possible to construct a term \(p_\Box ^{\alpha , \beta }\) such that:

Note that we aim here at a definitional equality between \(\textsf {rel}(p_\Box ^{\alpha , \beta })\) and  , rather than at an equivalence. It is easy to see that a term \(p_\Box ^{\alpha , \bot }\) exists for any \(\alpha \in \mathcal {A}\), as
, rather than at an equivalence. It is easy to see that a term \(p_\Box ^{\alpha , \bot }\) exists for any \(\alpha \in \mathcal {A}\), as  requires no structure on the relation. On the other hand, it is not possible to construct a term \(p_\Box ^{\bot , \top }\), i.e., to turn an arbitrary relation into a type equivalence.
requires no structure on the relation. On the other hand, it is not possible to construct a term \(p_\Box ^{\bot , \top }\), i.e., to turn an arbitrary relation into a type equivalence.
Definition 7
We denote \(\mathcal {D}_\Box \) the following subset of \(\mathcal {A}^2\):
The supplementary material constructs terms \(p_\Box ^{\alpha , \beta }\) for every pair \((\alpha ,\beta )\in \mathcal {D}_\Box \), using a meta-program to generate them from a minimal collection of manual definitions. In particular, assuming univalence, it is possible to construct a term \(p_{\square _{}}^{\top ,\top }\), which can be seen as an analogue of the translation [ \(\square _{}\) ] of univalent parametricity. More generally, the provided terms \(p_\Box ^{\alpha , \beta }\) depend on univalence if and only if \(\beta \notin \{0, 1, 2_{\text {a}}\}^2\).
The next natural question concerns the possible structures  endowing the relational interpretation of a product type \(\varPi x : A.\, B\), given relational interpretation for types A and B respectively equipped with structures
endowing the relational interpretation of a product type \(\varPi x : A.\, B\), given relational interpretation for types A and B respectively equipped with structures  and
and  .
.
Otherwise said, we need to identify the triples \((\alpha ,\beta ,\gamma )\in \mathcal {A}^3\) for which it is possible to construct a term \(p_{\varPi }^{\gamma }\) such that the following statements both hold:

The corresponding collection of triples can actually be described as a function \(\mathcal {D}_\varPi : \mathcal {A}\rightarrow \mathcal {A}^2\), such that \(\mathcal {D}_\varPi (\gamma ) = (\alpha , \beta )\) provides the minimal requirements on the structures associated with A and B, with respect to the partial order on \(\mathcal {A}^2\). The supplementary material provides a corresponding collection of terms \(p_\varPi ^{\gamma }\) for each \(\gamma \in \mathcal {A}\), as well as all the associated weakenings. Once again, these definitions are generated by a meta-program. Observe in particular that by symmetry, \(p_\varPi ^{(m, n)}\) can be obtained from \(p_\varPi ^{(m, 0)}\) and \(p_\varPi ^{(n, 0)}\) by swapping the latter and glueing it to the former. Therefore, the values of \(p_\varPi ^\gamma \) and \(\mathcal {D}_\varPi (\gamma )\) are completely determined by those of \(p_\varPi ^{(m, 0)}\) and \(\mathcal {D}_\varPi (m, 0)\). In particular, for any \((m, n)\in \mathcal {A}\):
where \(m_A, n_A, m_B, n_B\in \mathcal {A}\) are such that \(\mathcal {D}_\varPi (m, 0) = \left( (0, n_A), (m_B, 0)\right) \) and \(\mathcal {D}_\varPi (n, 0) = \left( (0, m_A), (n_B, 0)\right) \). We sum up in Figure 2 the values of \(\mathcal {D}_\varPi (m, 0)\).
Note that in the case of a non-dependent product, constructing \(p_\rightarrow ^\gamma \) requires less structure on the domain A of an arrow type \(A \rightarrow B\), which motivates the introduction of function \(\mathcal {D}_\rightarrow (\gamma )\). Using the combinator for dependent products to interpret an arrow type, albeit correct, potentially pulls in unnecessary structure (and axiom) requirements. The supplementary material includes a construction of terms \(p_\rightarrow ^\gamma \) for any \(\gamma \in \mathcal {A}\).
The two tables in Figure 2 show how requirements on levels stay the same on the right hand side of both \(\varPi \) and \(\rightarrow \), stay the same up to symmetries (exchange of variance and of \(2_\text {a}\) and \(2_\text {b}\)) on the left hand side of a \(\rightarrow \) and increase on the left hand side of a \(\varPi \). This elegant arithmetic justifies our hierarchy of relations.
4 A calculus for proof transfer
This section introduces Trocq, a framework for proof transfer designed as a generalization of parametricity translations, so as to allow for interpreting types as instances of the structures introduced in Section 3.2. We adopt a sequent style presentation, which fits closely the type system of \(CC_{\omega }\), while explaining in a consistent way the transformations of terms and contexts. This choice of presentation departs from the standard literature about parametricity in pure type systems. Yet, it brings the presentation closer to actual implementations, whose necessary management of parametricity contexts is swept under the rug by notational conventions (e.g., the primes of Section 2.3).
For this purpose, we successively introduce four calculi, of increasing sophistication. We start (§ 4.1) with introducing this sequent style presentation by rephrasing the raw parametricity translation, and the univalent parametricity one (§ 4.2). We then introduce \(CC_{\omega }^+\) (§ 4.3), a Calculus of Constructions with annotations on sorts and subtyping, before defining (§ 4.4) the Trocq calculus.
4.1 Raw parametricity sequents
We introduce parametricity contexts, under the form of a list of triples packaging two variables x and \(x'\) together with a third one \(x_R\). The latter \(x_R\) is a witness (a proof) that x and \(x'\) are related:
We write \((x, x', x_R) \in \varXi \) when \(\varXi = \varXi ',\; x\,\sim \,x'\ \because \ x_R,\; \varXi ''\) for some \(\varXi '\) and \(\varXi ''\).
We denote \(\textrm{Var}(\varXi )\) the sequence of variables related in a parametricity context \(\varXi \), with multiplicities:
A parametricity context \(\varXi \) is well-formed, written \(\varXi \vdash \), if the sequence \(\textrm{Var}(\varXi )\) is duplicate-free. In this case, we use the notation \(\varXi (x)=(x', x_R)\) as a synonym of \((x, x', x_R) \in \varXi \).
A parametricity judgment relates a parametricity context \(\varXi \) and three terms \(M, M', M_R\) of \(CC_{\omega }\). Parametricity judgments, denoted as:
are defined by rules of Figure 3 and read in context \(\varXi \), term M translates to the term \(M'\), because \(M_R\).
Lemma 5
The relation associating a term M with pairs \((M', M_R)\) such that \(\varXi \vdash M\,\sim \,M'\ \because \ M_R\) holds, with \(\varXi \) a well-formed parametricity context, is functional. More precisely, for any well-formed parametricity context \(\varXi \):
Proof
Immediate by induction on the syntax of M.
This presentation of parametricity thus provides an alternative definition of translation \(\llbracket \,\cdot \,\rrbracket \) from Figure 1, and accounts for the prime-based notational convention used in the latter.
Definition 8
A parametricity context \(\varXi \) is admissible for a well-formed typing context \(\varGamma \), denoted \({\varGamma }\rhd {\varXi }\), when \(\varXi \) and \(\varGamma \) are well-formed as a parametricity context and \(\varGamma \) provides coherent type annotations for all terms in \(\varXi \), that is, for any variables \(x, x', x_R\) such that \( \varXi (x) = (x', x_R)\), and for any terms \(A'\) and \(A_R\):
We can now state and prove an abstraction theorem:
Theorem 4 (Abstraction theorem)
[Abstraction theorem]

Proof
By induction on the derivation of \(\varXi \vdash M\,\sim \,M'\ \because \ M_R\).
4.2 Univalent parametricity sequents
We now propose in Figure 4 a rephrased version of the univalent parametricity translation [30], using the same sequent style and replacing the translation of universes with the equivalent relation  . Parametricity judgments are denoted:
. Parametricity judgments are denoted:
where \(\varXi \) is a parametricity context and M, \(M'\), and \(M_R\) are terms of \(CC_{\omega }\). The u index is a reminder that typing judgments \(\varGamma \vdash _u M : A\) involved in the associated abstraction theorem assume the univalence axiom Fig. 4.
We can now rephrase the abstraction theorem for univalent parametricity.
Theorem 5 (Univalent abstraction theorem)
[Univalent abstraction theorem]

Proof
By induction on the derivation of \(\varXi \vdash _{u} M\,\sim \,M'\ \because \ M_R\).
Remark 3
In Theorem 5, \(\textsf {rel}(A_R)\) is a term of type \(A \rightarrow A' \rightarrow \Box \). Indeed:

entails \(A_R\) has type

4.3 Annotated type theory
We are now ready to generalize the relational interpretation of types provided by the univalent parametricity translation, so as to allow for interpreting sorts with instances of weaker structures than equivalence. For this purpose, we introduce a variant \(CC_{\omega }^+\) of \(CC_{\omega }\) where each universe is annotated with a label indicating the structure available on its relational interpretation. Recall from Section 3.2 that we have used annotations \(\alpha \in \mathcal {A}\) to identify the different structures of the lattice disassembling type equivalence: these are the labels annotating sorts of \(CC_{\omega }^+\) , so that if A has type \(\Box ^\alpha \), then the associated relation \(A_R\) has type  . The syntax of \(CC_{\omega }^+\) is thus:
. The syntax of \(CC_{\omega }^+\) is thus:
Before completing the actual formal definition of the Trocq proof transfer framework, let us informally illustrate how these annotations shall drive the interpretation of terms, and in particular, of a dependent product \(\varPi x : A.\,B\). In this case, before translating B, three terms representing the bound variable x, its translation \(x'\), and the parametricity witness \(x_R\) are added to the context. The type of \(x_R\) is \(\textsf {rel}(A_R)\ x\ x'\) where \(A_R\) is the parametricity witness relating A to its translation \(A'\). The role of annotation \(\alpha \) on the sort typing type A is thus to to govern the amount of information available in witness \(x_R\), by determining the type of \(A_R\). This intent is reflected in the typing rules of \(CC_{\omega }^+\) , which rely on the definition of the loci \(\mathcal {D}_{\Box }\), \(\mathcal {D}_{\rightarrow }\) and \(\mathcal {D}_{\varPi }\), introduced in §3.3.
Contexts are defined as usual, but typing terms in \(CC_{\omega }^+\) requires defining a subtyping relation \(\preccurlyeq \), defined by the rules of Figure 5. The typing rules of \(CC_{\omega }^+\) are available in Figure 6 and follow standard presentations [6]. The \(\equiv \) relation in the (SubConv) rule is the conversion relation, defined as the closure of \(\alpha \)-equivalence and \(\beta \)-reduction. The two types of judgment in \(CC_{\omega }^+\) are thus:
where M, A and B are terms in \(CC_{\omega }^+ \) and \(\varGamma \) is a context in \(CC_{\omega }^+ \).
Due to space constraints, we omit the direct proof that \(CC_{\omega }^+\) is a conservative extension over \(CC_{\omega }\). It goes by defining an erasure function for terms \(\left| \,\,\cdot \,\,\right| ^- : \mathcal {T}_{CC_{\omega }^+ } \rightarrow \mathcal {T}_{CC_{\omega }}\) and the associated erasure function for contexts.
4.4 The Trocq calculus
The final stage of the announced generalization consists in building an analogue to the parametricity translations available in pure type systems, but for the annotated type theory of § 4.3. This analogue is geared towards proof transfer, as discussed in § 2.1, and therefore designed to synthesize the output of the translation from its input, rather than to check that certain pairs of terms are in relation. However, splitting up the interpretation of universes into a lattice of possible relation structures means that the source term of the translation is not enough to characterize the desired output: the translation needs to be informed with some extra information about the expected outcome of the translation. In the Trocq calculus, this extra information is a type of \(CC_{\omega }^+ \).
We thus define Trocq contexts as lists of quadruples:
and introduce a conversion function \(\gamma \) from Trocq contexts to \(CC_{\omega }^+\) contexts:
Now, a Trocq judgment is a 4-ary relation of the form \(\varDelta \vdash _t M\ @\ A\,\sim \,M'\ \because \ M_R\), which is read in context \(\varDelta \), term M of annotated type A translates to term \(M'\), because \(M_R\) and \(M_R\) is called a parametricity witness. Trocq judgments are defined by the rules of Figure 7. This definition involves a weakening function for parametricity witnesses, defined as follows.
Definition 9
For all \(p, q \in \{0, 1, 2_{\text {a}}, 2_{\text {b}}, 3, 4\}\), such that \(p \ge q\), we define map \(\downarrow ^p_q : \textsf {M}_{p} \rightarrow \textsf {M}_{q}\), which forgets the fields from class \(\textsf {M}_{p}\) that are not in \(\textsf {M}_{q}\).
For all \(\alpha , \beta \in \mathcal {A}\), such that \(\alpha \ge \beta \), function  is defined by:
is defined by:
The weakening function on parametricity witnesses is defined on Figure 8 by extending function \(\downdownarrows ^\alpha _\beta \) to all relevant pairs of types of \(CC_{\omega }^+\) , i.e., \(\Downarrow ^T_U\) is defined for \(T, U \in \mathcal {T}_{CC_{\omega }^+ }\) as soon as \(T \preccurlyeq U\).
An abstraction theorem relates Trocq judgments and typing in \(CC_{\omega }^+\) .
Theorem 6
(Trocq abstraction theorem).

Proof
By induction on derivation \(\varDelta \vdash _t M\ @\ A\,\sim \,M'\ \because \ M_R\).
Note that type A in the typing hypothesis \(\gamma (\varDelta ) \vdash _{+} M : A\) of the abstraction theorem is exactly the extra information passed to the translation. The latter can thus also be seen as an inference algorithm, which infers annotations for the output of the translation from that of the input.
Remark 4
Since by definition of \(p_\Box ^{\alpha ,\beta }\) (Equation 12), we have \(\vdash _t \Box ^\alpha \ @\ \Box ^\beta \,\sim \,\Box ^\alpha \ \because \ p_\Box ^{\alpha ,\beta }\), by applying Theorem 6 with \(\gamma (\varDelta ) \vdash _{+} A : \Box ^\alpha \), we get:

Now by the same definition, for any \(\beta \in \mathcal {A}\),  , hence
, hence  , as expected by the type annotation \(A : \Box ^\alpha \) in the premise of the rule.
, as expected by the type annotation \(A : \Box ^\alpha \) in the premise of the rule.
Remark 5
By applying the Remark 4 with \(\vdash _{+} \Box ^\alpha : \Box ^\beta \), we indeed obtain that  as expected, provided that \((\alpha , \beta ) \in \mathcal {D}_\Box \).
as expected, provided that \((\alpha , \beta ) \in \mathcal {D}_\Box \).
4.5 Constants
Concrete applications require extending Trocq with constants. Constants are similar to variables, except that they are stored in a global context instead of a typing context. A crucial difference though is that a constant may be assigned several different annotated types in \(CC_{\omega }^+\) .
Consider for example, a constant \(\texttt {list}\), standing for the type of polymorphic lists. As \(\texttt {list}\ A\) is the type of lists with elements of type A, it can be annotated with type \(\Box ^\alpha \rightarrow \Box ^\alpha \) for any \(\alpha \in \mathcal {A}\).
Every constant declared in the global environment has an associated collection of possible annotated types \( T_{c} \subset \mathcal {T}_{CC_{\omega }^+ }\). We require that all the annotated types of a same constant share the same erasure in \(CC_{\omega }\), i.e., \(\forall c, \forall A, \forall B,\ A, B \in T_{c} \Rightarrow \left| \,A\,\right| ^- = \left| \,B\,\right| ^-\). For example, \(T_{\texttt {list}} = \left\{ \Box ^\alpha \rightarrow \Box ^\alpha \ \left| \ \alpha \in \mathcal {A}\right. \right\} .\)
In addition, we provide translations \(\mathcal {D}_c(A)\) for each possible annotated type A of each constant c in the global context. For example, \(\mathcal {D}_{\texttt {list}}(\Box ^{(1,0)} \rightarrow \Box ^{(1,0)})\) is equal to \(\left( \texttt {list},\ \lambda A\,A'\,A_R.\,\left( \texttt {List.All2}\ A_R,\; \texttt {List.map}\ \left( \texttt {map}\ A_R\right) \right) \right) \), where relation List.All2 \(A_R\) relates lists of the same length, whose elements are pair-wise related via \(A_R\), \(\texttt {List.map}\) is the usual map function on lists and \(\texttt {map}\ A_R : A \rightarrow A'\) extracts the map projection of the record \(A_R\) of type  . Part of these translations can be generated automatically by weakening.
. Part of these translations can be generated automatically by weakening.
We describe in Figure 9 the additional rules for constants in \(CC_{\omega }^+\) and Trocq. Note that for an input term featuring constants, an unfortunate choice of annotation may lead to a stuck translation.
We describe in Figure 9 the additional rules for constants in \(CC_{\omega }^+\) and Trocq. Note that for an input term featuring constants, an unfortunate choice of annotation may lead to a stuck translation.
5 Implementation and applications
The Trocq plugin [13] turns the material presented in Section 4 into an actual tactic, called  , for automating proof transfer in Coq. This tactic synthesizes a new goal from the current one, as well as a proof that the former implies the latter. User-defined relations between constants, registered via specific vernacular commands, inform this synthesis. The core of the plugin implements each rule of the Trocq calculus in the Elpi meta-programming language [17, 31], on top of Coq libraries formalizing the contents of Section 3. In the logic programming paradigm of Elpi, each rule of Figure 7 translates gracefully into a corresponding \(\lambda \) Prolog predicate, making the corresponding source code very close to the presentation of §4.4. However, the Trocq plugin also implements a much less straightforward annotation inference algorithm, so as to hide the management of sort annotations to Coq users completely. This section illustrates the usage of the
, for automating proof transfer in Coq. This tactic synthesizes a new goal from the current one, as well as a proof that the former implies the latter. User-defined relations between constants, registered via specific vernacular commands, inform this synthesis. The core of the plugin implements each rule of the Trocq calculus in the Elpi meta-programming language [17, 31], on top of Coq libraries formalizing the contents of Section 3. In the logic programming paradigm of Elpi, each rule of Figure 7 translates gracefully into a corresponding \(\lambda \) Prolog predicate, making the corresponding source code very close to the presentation of §4.4. However, the Trocq plugin also implements a much less straightforward annotation inference algorithm, so as to hide the management of sort annotations to Coq users completely. This section illustrates the usage of the  tactic on various concrete examples.
tactic on various concrete examples.
5.1 Isomorphisms
Bitvectors (code). Here are two possible encodings of bitvectors in Coq:

We can prove that these representations are equivalent by combining two proofs by transitivity: the proof that  is related to
is related to  for a given
for a given  , and the proof that
, and the proof that  is related to itself. We also make use of the equivalence relations
is related to itself. We also make use of the equivalence relations  and
and  , which respectively relate type
, which respectively relate type  and
and  with themselves:
with themselves:

Now, suppose we would like to transfer the following result from the bounded natural numbers to the vector-based encoding:

As this goal involves  and
and  operations on bitvectors, and the order and equality relations on type
operations on bitvectors, and the order and equality relations on type  , we inform Trocq with the associated operations
, we inform Trocq with the associated operations  and
and  on the vector encoding. E.g., for
on the vector encoding. E.g., for  and
and  , we prove:
, we prove:

We can now use proof transfer from bitvectors to bounded natural numbers:

Induction principle on integers. (code). Recall that the problem from Example 1 is to obtain the following elimination scheme, from that available on type \(\mathbb {N}\):

We first inform Trocq that  and
and  are isomorphic, by providing proofs that the two conversions \(\uparrow _{\mathbb {N}}\ :\ \texttt {N}\ \rightarrow \ \mathbb {N}\) and \(\downarrow _{\mathbb {N}}\ :\ \mathbb {N}\ \rightarrow \ \texttt {N}\) are mutual inverses. Using lemma
are isomorphic, by providing proofs that the two conversions \(\uparrow _{\mathbb {N}}\ :\ \texttt {N}\ \rightarrow \ \mathbb {N}\) and \(\downarrow _{\mathbb {N}}\ :\ \mathbb {N}\ \rightarrow \ \texttt {N}\) are mutual inverses. Using lemma  , we can deduce an equivalence
, we can deduce an equivalence  , i.e.,
, i.e.,  . We also prove and register that zeros and successors are related:
. We also prove and register that zeros and successors are related:

Trocq is now able to generate, prove and apply the desired implication:

Inspecting this proof confirms that only information up to level \((2_\text {a}, 3)\) has been extracted from the equivalence proof  . It is thus possible to run the exact proof transfer, but with a weaker relation, as illustrated in the code for an abstract type I with a zero and a successor constants, and a retraction \(\mathbb {N} \rightarrow I\).
. It is thus possible to run the exact proof transfer, but with a weaker relation, as illustrated in the code for an abstract type I with a zero and a successor constants, and a retraction \(\mathbb {N} \rightarrow I\).
5.2 Sections, retractions
Modular arithmetic (code).
A typical application of modular arithmetic is to show that some statement on \(\mathbb {Z}\) can be reduced to statements on \(\mathbb {Z}/p\mathbb {Z}\) Let us show how Trocq can synthesize and prove the following implication:

where scope  is for the usual product and zero on type
is for the usual product and zero on type  , for \(\mathbb {Z}/p\mathbb {Z}\), scope
, for \(\mathbb {Z}/p\mathbb {Z}\), scope  for those on type
for those on type  , for \(\mathbb {Z}\), and
, for \(\mathbb {Z}\), and  is an equality test modulo p on type
is an equality test modulo p on type  . Observe that the implication deduces a lemma on \(\mathbb {Z}\) from its modular analogues. Type
. Observe that the implication deduces a lemma on \(\mathbb {Z}\) from its modular analogues. Type  and
and  are obviously not equivalent, but a retraction is actually enough for this proof transfer. We have:
are obviously not equivalent, but a retraction is actually enough for this proof transfer. We have:

where  , (a proof that
, (a proof that  ), is obtained from
), is obtained from  via lemma
via lemma  . Proving lemma
. Proving lemma  by
by  now just requires relating the respective zeroes, multiplications, and equalities of the two types:
now just requires relating the respective zeroes, multiplications, and equalities of the two types:

where  (
( is the Coq name for
is the Coq name for  ) is
) is  . Note that by definition of the relation given by
. Note that by definition of the relation given by  , lemma
, lemma  amounts to:
amounts to:

Summable sequences. (code). Example 2 involves two instances of subtypes: type \({\overline{\mathbb {R}}_{\ge 0}}\) extends a type \({{\mathbb {R}}_{\ge 0}}\) of positive real numbers with an abstract element and type  is for provably convergent sequences of positive real numbers:
is for provably convergent sequences of positive real numbers:

Type \({\overline{\mathbb {R}}_{\ge 0}}\) and \({{\mathbb {R}}_{\ge 0}}\) are related at level \((4,2_\text {b})\): e.g.,  provides a partial inverse to the
provides a partial inverse to the  injection by sending the extra
injection by sending the extra  to zero. Types
to zero. Types  and
and  are also related at level \((4,2_\text {b})\), via the relation:
are also related at level \((4,2_\text {b})\), via the relation:

where  transforms a summable sequence into a sequence of extended positive reals in the obvious way. Now
transforms a summable sequence into a sequence of extended positive reals in the obvious way. Now  is the sum of a sequence
is the sum of a sequence  of extended positive reals, and we also define the sum of a sequence of positive reals, as a positive real, again by defaulting infinite sums to zero. For the purpose of the example, we only do so for summable sequences:
of extended positive reals, and we also define the sum of a sequence of positive reals, as a positive real, again by defaulting infinite sums to zero. For the purpose of the example, we only do so for summable sequences:

These two notions of sums are related via  , and so are the respective additions of positive (resp. extended positive) reals and the respective pointwise additions of sequences. Once Trocq is informed of these relations, the tactic is able to transfer the statement from the much easier variant on extended reals:
, and so are the respective additions of positive (resp. extended positive) reals and the respective pointwise additions of sequences. Once Trocq is informed of these relations, the tactic is able to transfer the statement from the much easier variant on extended reals:

5.3 Polymorphic, dependent types
Polymorphic parameters (code). Suppose we want to transfer a goal involving lists along an equivalence between the types of the values contained in the lists. We first prove that the  type former is equivalent to itself, and register this fact:
type former is equivalent to itself, and register this fact:

We also need to relate with themselves all operations on type  involved in the goal, including constructors, and to register these facts, before Trocq is able to transfer any goal, e.g., about
involved in the goal, including constructors, and to register these facts, before Trocq is able to transfer any goal, e.g., about  to its analogue on
to its analogue on  .
.
Note that lemma  requires an equivalence between its parameters. If this does not hold, as in the case of type
requires an equivalence between its parameters. If this does not hold, as in the case of type  and
and  from Section 5.1, the translation is stuck: weakening does not apply here. In order to avoid stuck translation, we need several versions of
from Section 5.1, the translation is stuck: weakening does not apply here. In order to avoid stuck translation, we need several versions of  to cover all cases. For instance, the following lemma is required for proof transfers from
to cover all cases. For instance, the following lemma is required for proof transfers from  to
to  .
.

Dependent and polymorphic types (code). Fixed-size vectors can be represented by iterated tuples, an alternative to the inductive type  , from Coq’s standard library, as follows.
, from Coq’s standard library, as follows.

On the following mockup example, Trocq transfers a lemma on  to its analogue on
to its analogue on  , about a function
, about a function  , and a function
, and a function  creating a constant vector, and simultaneously refines integers into the integers modulo p from Section 5.1:
creating a constant vector, and simultaneously refines integers into the integers modulo p from Section 5.1:

This automated proof only requires proving (and registering) that  and
and  are related to their analogue
are related to their analogue  and
and  , from Coq’s standard library. Note that the proof uses the equivalence between
, from Coq’s standard library. Note that the proof uses the equivalence between  and
and  but only requires a retraction between parameter types.
but only requires a retraction between parameter types.
6 Conclusion
The Trocq framework can be seen as a generalization of the univalent parametricity translation [30]. It allows for weaker relations than equivalence, thanks to a fine-grained control of the data propagated by the translation. This analysis is enabled by skolemizing the usual symmetrical presentation of equivalence, so as to expose the data, and by introducing a hierarchy of algebraic structures for relations. This scrutiny allows in particular to get rid of the univalence axiom for a larger class of equivalence proofs [29], and to deal with refinement relations for arbitrary terms, unlike the CoqEAL library [14]. Altenkirch and Kaposi already proposed a symmetrical, skolemized phrasing of type equivalence [3], but for different purposes. In particular, they did not study the resulting hierarchy of structures. Definition 4 however slightly differs from theirs: by reducing the amount of transport involved, it eases formal proofs significantly in practice, both in the internal library of Trocq and for end-users of the tactic.
The concrete output of this work is a plugin [13] that consists of about 3000 l. of original Coq proofs and 1200 l. of meta-programming, in the Elpi meta-language, excluding white lines and comments. This plugin goes beyond the state of the art in two ways. First, it demonstrates that a single implementation of this parametricity framework covers the core features of several existing other tactics, for refinements [14, 16], generalized rewriting [28], and proof transfer [30]. Second, it addresses use cases, such as Example 2, that are beyond the skills of any existing tool in any proof assistant based on type theory. The prototype plugin arguably needs an improved user interface so as to reach the maturity of some of the aforementioned existing tactics. It would also benefit from an automated generation of equivalence proofs, such as Pumpkin Pi [27].
Notes
- 1.
For the sake of readability, we omit implicit arguments, e.g., although \(\textsf {M}_{i}\) has type \(\lambda (T_1\ T_2 \,:\, \square _{}).\,(T_1 \rightarrow T_2 \rightarrow \square _{}) \rightarrow \square _{}\), we write \(\textsf {M}_{n}\ R\) for \((\textsf {M}_{n}\ A\ B\ R)\).
References
The lean mathematical library. In: Blanchette, J., Hritcu, C. (eds.) Proceedings of the 9th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2020, New Orleans, LA, USA, January 20-21, 2020. pp. 367–381. ACM (2020). https://doi.org/10.1145/3372885.3373824, https://doi.org/10.1145/3372885.3373824
Affeldt, R., Cohen, C.: Measure construction by extension in dependent type theory with application to integration (2023), accepted for publication in JAR
Altenkirch, T., Kaposi, A.: Towards a cubical type theory without an interval. In: TYPES. LIPIcs, vol. 69, pp. 3:1–3:27. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2015)
Angiuli, C., Brunerie, G., Coquand, T., Harper, R., (Favonia), K.H., Licata, D.R.: Syntax and models of cartesian cubical type theory. Math. Struct. Comput. Sci. 31(4), 424–468 (2021). https://doi.org/10.1017/S0960129521000347, https://doi.org/10.1017/S0960129521000347
Angiuli, C., Cavallo, E., Mörtberg, A., Zeuner, M.: Internalizing representation independence with univalence. Proc. ACM Program. Lang. 5(POPL), 1–30 (2021). https://doi.org/10.1145/3434293, https://doi.org/10.1145/3434293
Aspinall, D., Compagnoni, A.B.: Subtyping dependent types. Theor. Comput. Sci. 266(1-2), 273–309 (2001). https://doi.org/10.1016/S0304-3975(00)00175-4, https://doi.org/10.1016/S0304-3975(00)00175-4
Barthe, G., Capretta, V., Pons, O.: Setoids in type theory. J. Funct. Program. 13(2), 261–293 (2003). https://doi.org/10.1017/S0956796802004501, https://doi.org/10.1017/S0956796802004501
Bauer, A., Gross, J., Lumsdaine, P.L., Shulman, M., Sozeau, M., Spitters, B.: The hott library: a formalization of homotopy type theory in coq. In: Bertot, Y., Vafeiadis, V. (eds.) Proceedings of the 6th ACM SIGPLAN Conference on Certified Programs and Proofs, CPP 2017, Paris, France, January 16-17, 2017. pp. 164–172. ACM (2017). https://doi.org/10.1145/3018610.3018615, https://doi.org/10.1145/3018610.3018615
Bernardy, J., Jansson, P., Paterson, R.: Proofs for free - parametricity for dependent types. J. Funct. Program. 22(2), 107–152 (2012). https://doi.org/10.1017/S0956796812000056, https://doi.org/10.1017/S0956796812000056
Bernardy, J., Lasson, M.: Realizability and parametricity in pure type systems. In: Hofmann, M. (ed.) Foundations of Software Science and Computational Structures - 14th International Conference, FOSSACS 2011, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2011, Saarbrücken, Germany, March 26-April 3, 2011. Proceedings. Lecture Notes in Computer Science, vol. 6604, pp. 108–122. Springer (2011). https://doi.org/10.1007/978-3-642-19805-2_8, https://doi.org/10.1007/978-3-642-19805-2_8
Boulier, S., Pédrot, P., Tabareau, N.: The next 700 syntactical models of type theory. In: Bertot, Y., Vafeiadis, V. (eds.) Proceedings of the 6th ACM SIGPLAN Conference on Certified Programs and Proofs, CPP 2017, Paris, France, January 16-17, 2017. pp. 182–194. ACM (2017). https://doi.org/10.1145/3018610.3018620, https://doi.org/10.1145/3018610.3018620
Cohen, C., Coquand, T., Huber, S., Mörtberg, A.: Cubical type theory: A constructive interpretation of the univalence axiom. FLAP 4(10), 3127–3170 (2017), http://collegepublications.co.uk/ifcolog/?00019
Cohen, C., Crance, E., Mahboubi, A.: coq-community/trocq: Trocq 0.1.5 (Jan 2024). https://doi.org/10.5281/zenodo.10563382, https://doi.org/10.5281/zenodo.10563382
Cohen, C., Dénès, M., Mörtberg, A.: Refinements for free! In: Gonthier, G., Norrish, M. (eds.) Certified Programs and Proofs - Third International Conference, CPP 2013, Melbourne, VIC, Australia, December 11-13, 2013, Proceedings. Lecture Notes in Computer Science, vol. 8307, pp. 147–162. Springer (2013). https://doi.org/10.1007/978-3-319-03545-1_10, https://doi.org/10.1007/978-3-319-03545-1_10
Coquand, T., Huet, G.P.: The calculus of constructions. Inf. Comput. 76(2/3), 95–120 (1988). https://doi.org/10.1016/0890-5401(88)90005-3, https://doi.org/10.1016/0890-5401(88)90005-3
Dénès, M., Mörtberg, A., Siles, V.: A refinement-based approach to computational algebra in coq. In: Beringer, L., Felty, A. (eds.) Interactive Theorem Proving. pp. 83–98. Springer Berlin Heidelberg, Berlin, Heidelberg (2012)
Dunchev, C., Guidi, F., Coen, C.S., Tassi, E.: ELPI: fast, embeddable, \(\lambda \)prolog interpreter. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) Logic for Programming, Artificial Intelligence, and Reasoning - 20th International Conference, LPAR-20 2015, Suva, Fiji, November 24-28, 2015, Proceedings. Lecture Notes in Computer Science, vol. 9450, pp. 460–468. Springer (2015). https://doi.org/10.1007/978-3-662-48899-7_32, https://doi.org/10.1007/978-3-662-48899-7_32
Gouëzel, S.: Vitali-carathéodory theorem in mathlib. https://leanprover-community.github.io/mathlib_docs/measure_theory/integral/vitali_caratheodory.html (2021)
Keller, C., Lasson, M.: Parametricity in an impredicative sort. In: Cégielski, P., Durand, A. (eds.) Computer Science Logic (CSL’12) - 26th International Workshop/21st Annual Conference of the EACSL, CSL 2012, September 3-6, 2012, Fontainebleau, France. LIPIcs, vol. 16, pp. 381–395. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2012). https://doi.org/10.4230/LIPIcs.CSL.2012.381, https://doi.org/10.4230/LIPIcs.CSL.2012.381
Martin-Dorel, É., Melquiond, G.: Proving tight bounds on univariate expressions with elementary functions in coq. J. Autom. Reason. 57(3), 187–217 (2016). https://doi.org/10.1007/s10817-015-9350-4, https://doi.org/10.1007/s10817-015-9350-4
Mitchell, J.C.: Representation independence and data abstraction. In: Conference Record of the Thirteenth Annual ACM Symposium on Principles of Programming Languages, St. Petersburg Beach, Florida, USA, January 1986. pp. 263–276. ACM Press (1986). https://doi.org/10.1145/512644.512669, https://doi.org/10.1145/512644.512669
de Moura, L., Ullrich, S.: The lean 4 theorem prover and programming language. In: Platzer, A., Sutcliffe, G. (eds.) Automated Deduction - CADE 28 - 28th International Conference on Automated Deduction, Virtual Event, July 12-15, 2021, Proceedings. Lecture Notes in Computer Science, vol. 12699, pp. 625–635. Springer (2021). https://doi.org/10.1007/978-3-030-79876-5_37, https://doi.org/10.1007/978-3-030-79876-5_37
Nederpelt, R., Geuvers, H.: Type Theory and Formal Proof: An Introduction. Cambridge University Press (2014). https://doi.org/10.1017/CBO9781139567725
Norell, U.: Dependently typed programming in agda. In: Koopman, P.W.M., Plasmeijer, R., Swierstra, S.D. (eds.) Advanced Functional Programming, 6th International School, AFP 2008, Heijen, The Netherlands, May 2008, Revised Lectures. Lecture Notes in Computer Science, vol. 5832, pp. 230–266. Springer (2008). https://doi.org/10.1007/978-3-642-04652-0_5, https://doi.org/10.1007/978-3-642-04652-0_5
Paulin-Mohring, C.: Introduction to the Calculus of Inductive Constructions. In: Paleo, B.W., Delahaye, D. (eds.) All about Proofs, Proofs for All, Studies in Logic (Mathematical logic and foundations), vol. 55. College Publications (Jan 2015), https://inria.hal.science/hal-01094195
Reynolds, J.C.: Types, abstraction and parametric polymorphism. In: Mason, R.E.A. (ed.) Information Processing 83, Proceedings of the IFIP 9th World Computer Congress, Paris, France, September 19-23, 1983. pp. 513–523. North-Holland/IFIP (1983)
Ringer, T., Porter, R., Yazdani, N., Leo, J., Grossman, D.: Proof repair across type equivalences. In: Freund, S.N., Yahav, E. (eds.) PLDI ’21: 42nd ACM SIGPLAN International Conference on Programming Language Design and Implementation, Virtual Event, Canada, June 20-25, 2021. pp. 112–127. ACM (2021). https://doi.org/10.1145/3453483.3454033, https://doi.org/10.1145/3453483.3454033
Sozeau, M.: A new look at generalized rewriting in type theory. J. Formaliz. Reason. 2(1), 41–62 (2009). https://doi.org/10.6092/issn.1972-5787/1574, https://doi.org/10.6092/issn.1972-5787/1574
Tabareau, N., Tanter, É., Sozeau, M.: Equivalences for free: univalent parametricity for effective transport. Proceedings of the ACM on Programming Languages 2(ICFP), 1–29 (2018)
Tabareau, N., Tanter, É., Sozeau, M.: The marriage of univalence and parametricity. Journal of the ACM (JACM) 68(1), 1–44 (2021)
Tassi, E.: Deriving proved equality tests in Coq-elpi: Stronger induction principles for containers in Coq. In: ITP 2019 - 10th International Conference on Interactive Theorem Proving. Portland, United States (Sep 2019). https://doi.org/10.4230/LIPIcs.CVIT.2016.23, https://inria.hal.science/hal-01897468
The Coq Development Team: The coq proof assistant (Sep 2022). https://doi.org/10.5281/zenodo.7313584, https://doi.org/10.5281/zenodo.7313584
Univalent Foundations Program, T.: Homotopy Type Theory: Univalent Foundations of Mathematics. https://homotopytypetheory.org/book, Institute for Advanced Study (2013)
Vezzosi, A., Mörtberg, A., Abel, A.: Cubical agda: a dependently typed programming language with univalence and higher inductive types. Proc. ACM Program. Lang. 3(ICFP), 87:1–87:29 (2019). https://doi.org/10.1145/3341691, https://doi.org/10.1145/3341691
Wadler, P.: Theorems for free! In: Stoy, J.E. (ed.) Proceedings of the fourth international conference on Functional programming languages and computer architecture, FPCA 1989, London, UK, September 11-13, 1989. pp. 347–359. ACM (1989). https://doi.org/10.1145/99370.99404, https://doi.org/10.1145/99370.99404
Acknowledgments
The authors would like to thank András Kovács, Kenji Maillard, Enrico Tassi, Quentin Vermande, Théo Winterhalter, and anonymous reviewers, whose comments greatly helped us improve this article.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Ethics declarations
Disclosure of Interests
None.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Cohen, C., Crance, E., Mahboubi, A. (2024). Trocq: Proof Transfer for Free, With or Without Univalence. In: Weirich, S. (eds) Programming Languages and Systems. ESOP 2024. Lecture Notes in Computer Science, vol 14576. Springer, Cham. https://doi.org/10.1007/978-3-031-57262-3_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-57262-3_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57261-6
Online ISBN: 978-3-031-57262-3
eBook Packages: Computer ScienceComputer Science (R0)



 ,
,  ,
,  ,
,  ,
, 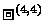 , r is an equivalence between A and B;
, r is an equivalence between A and B; , r is an isomorphism between A and B.
, r is an isomorphism between A and B.







