Abstract
Petri nets constitute a well-studied model to verify and study concurrent systems, among others, and computing the coverability set is one of the most fundamental problems about Petri nets. Using the proof assistant Coq, we certified the correctness and termination of the MinCov algorithm by Finkel, Haddad, and Khmelnitsky (FOSSACS 2020). This algorithm is the most recent algorithm in the literature that computes the minimal basis of the coverability set, a problem known to be prone to subtle bugs. Apart from the intrinsic interest of a computer-checked proof, our certification provides new insights on the MinCov algorithm. In particular, we introduce as an intermediate algorithm a small-step variant of MinCov of independent interest.
You have full access to this open access chapter, Download conference paper PDF
Keywords

1 Introduction
Petri nets constitute a well-studied model to verify and study concurrent systems, with several applications in other domains, like in chemical [1] and biological process [2, 26] (see [31] for additional applications). Formally, a Petri net is given by a finite set of places and a finite set of transitions. Each place is marked with a natural number that can be incremented or decremented by the transitions. A function that maps places to the marked numbers is called a marking. The reachability set of a Petri net from an initial marking is the set of markings that can be obtained by executing a sequence of transitions from the initial marking.
The central problem about Petri nets is the reachability problem that consists in deciding whether a final marking is in the reachability set. Many important computational problems in logic and complexity reduce or are even equivalent to this problem [15, 31]. The reachability problem is known to be Ackermann-complete [5, 6, 20, 23]. On positive instances, it can be decided with efficient directed exploration strategies [3], but general complete algorithms deciding the problem are complex [24], and require a lot of implementation efforts [7].
This high complexity is not always a barrier in practice since many problems related to Petri nets can be decided by introducing an over-approximation of the reachability set, called the coverability set [18]. This set is defined by introducing the cover relation over the markings, defined by \(x\le y\) if x is less than or equal to y component-wise, i.e., on each place. The coverability set is then defined as the downward-closure of the reachability set. It provides a way to decide a variant of the reachability problem, called the coverability problem. This latter problem can be solved by computing what is called a basis of the coverability set. Its definition uses the notion of \(\omega \)-markings, an extension of markings that allows to mark places with a special symbol denoted by \(\omega \), and interpreted as an infinite number. The well-quasi-order theory [11] shows that any downward-closed set of markings can be symbolically represented by a finite set of \(\omega \)-markings, called a basis. Moreover, this theory also proves that there exists a unique minimal one for the inclusion relation.
The computation of bases of coverability sets is exactly the purpose of the Karp-Miller algorithm introduced in [19]. This algorithm inductively computes trees where nodes are labeled by \(\omega \)-markings. When the algorithm stops, those labels form a basis of the coverability set. Karp-Miller algorithms (including all variants) are not optimal in worst-case complexity for deciding the coverability problem. In fact, those algorithms have an Ackermannian computational complexity [8, 25] while the coverability problem is known to be Expspace-complete [28]. There exist other algorithms, based on backward computations from the final marking, that are optimal in worst-case [4, 21]. However, Karp-Miller algorithms outperform backward computation algorithms in practice (see [3] for benchmarks). Moreover, the computation of the coverability set bases provides ways to decide other properties than the coverability problem, like the termination and boundedness problems, as well as some liveness properties. It follows that this algorithm is central for analyzing Petri nets.
Bases computed by the Karp-Miller algorithm are not minimal (for the inclusion relation) since they may contain distinct \(\omega \)-markings x, y with \(x\le y\). Naturally, the unique minimal basis of the coverability set can be computed by first invoking the Karp-Miller algorithm, and then applying a simple reduction algorithm. However, such a computation is not optimal in practice since it requires computing several \(\omega \)-markings that will be discarded only at the end of the computation. A first attempt to avoid this problem was introduced by Alain Finkel in [9]. This algorithm is an optimization of the original Karp-Miller algorithm that seems very natural. However, a subtle problem when the computation is performed on a very particular instance was discovered only 14 years later in [10]. Several authors tried to find patches for that bug by proposing various solutions [13, 27, 29, 30]. Finally, in [12], an efficient algorithm removing on-the-fly useless basis elements was proved to be correct with a pen-and-paper proof. This algorithm, called MinCov, is a state-of-the-art algorithm for computing the minimal basis of the coverability set. It can be seen as a variant of the Karp-Miller algorithm based on the new notions of abstractions and accelerations. Since algorithms a la Karp-Miller are prone to subtle bugs, formal proofs certified by proof assistants are called for.
Our Contributions.
-
We developed a complete formal proof in Coq of the correctness and termination of the MinCov algorithm, via an intermediate algorithm called AbstractMinCov. We follow the Coq formalization of Petri nets and markings introduced in [33], built on top of the Mathematical Components library [14] (MathComp). This formalization contains several formal proofs and basic concepts related to Petri nets and markings that we extended to handle recent notions. Our proofs are based on this code to take benefits from those developments, but also to easily measure the gap between Coq formal proofs of two algorithms that compute coverability set bases: the original Karp-Miller algorithm and a state-of-the-art one.
-
We provide two new characterizations of the central notion of abstractions used by the MinCov algorithm. A simple mathematical one, and an algebraic one that shows that three operators on abstractions (weakening, contraction, and acceleration) provide a complete set of rules for generating any abstraction starting from the Petri net transitions. The proof of this result is based on the Jančar well-quasi-order on executions [17, 22].
-
We introduce as an intermediate algorithm a small-step variant of MinCov, called AbstractMinCov. We implemented in Coq proofs of the correctness and termination of AbstractMinCov. Since the original MinCov algorithm can be simulated by our algorithm, the proof that the original MinCov algorithm is correct and terminates is obtained at the cost of a simple Coq proof. Compared to a direct proof, our approach provides more succinct proofs in Coq, because proving that some properties are invariant is usually easier for a small step than for a big step. Additionally, our algorithm provides room for optimization by decorrelating some transformations performed by the original algorithm (this is discussed in the conclusion).
Outline. Our Coq formalization of Petri nets, markings, and \(\omega \)-markings are given in Section 2, while the ones on abstractions and accelerations are given in Section 3. The Coq modelization of MinCov is provided in Section 4, and our small-step algorithm AbstractMinCov is presented in Section 5. The code is available on Software Heritage [16].
2 Petri Nets
A Petri net is a tuple \(\mathcal {P}=\langle P,T,{\text {Pre}},{\text {Post}}\rangle \) where P, T are two finite sets of elements called respectively places and transitions, and \({\text {Pre}},{\text {Post}}\) are two mappings from T to \(\mathbb {N}^P\). An element \(x \in \mathbb {N}^P\) is called a marking. We denote by x(p) the value of x at the place p. Markings \({\text {Pre}}(t)\) and \({\text {Post}}(t)\), where t is a transition in T are called respectively the precondition and the postcondition of t.
We follow the Coq formalization of Petri nets and markings introduced in [33]. That formalization was introduced to prove the correctness and termination of the original Karp-Miller algorithm. This formalization is built on top of the Mathematical Components library [14] (MathComp). This library provides finite types (see the Coq keyword
 below) that provides a useful type for Petri net places and transitions, but also functions with finite domain (see
below) that provides a useful type for Petri net places and transitions, but also functions with finite domain (see
 ). Markings are conveniently represented by these functions. More precisely, in our Coq proofs, Petri nets and markings are defined as follows.
). Markings are conveniently represented by these functions. More precisely, in our Coq proofs, Petri nets and markings are defined as follows.

Now, let us provide some elements of Petri net semantics. Given a Petri net \(\mathcal {P}\), a transition \(t \in T\) is said to be fireable from a marking x if \({\text {Pre}}(t) \le x\); where \(\le \) is the component-wise extension of the usual order \(\le \) on \(\mathbb {N}\), i.e. \(x\le m\) iff \(x(p)\le m(p)\) for every place \(p\in P\). In that case we write \(x \xrightarrow {t} y\) where \(y=x - {\text {Pre}}(t) + {\text {Post}}(t)\) is called the marking obtained after firing t from x. We extend the notion of fireability to a sequence \(\sigma =t_1\ldots t_k\) of transitions \(t_1,\ldots ,t_k\in T\) by \(x \xrightarrow {\sigma } y\) if there exists a sequence \(x_0,\ldots ,x_k\) of markings such that \(x_0=x\), \(x_k=y\) and \(x_{j-1}\xrightarrow {t_j}x_j\) for every \(1\le j\le k\). In that case, we say that \(\sigma \) is fireable from x and y is naturally called the marking obtained after firing \(\sigma \) from x. When such a sequence \(\sigma \) exists, we say that y is reachable from x (for the Petri net \(\mathcal {P}\)).
The Petri net reachability problem consists in deciding, given a Petri net \(\mathcal {P}\) and two markings x, y, whether y is reachable from x. The reachability problem is Ackermann-complete [5, 6, 20, 23] and algorithms deciding the problem are complex [24]. However, this high lower bound is not always a barrier in practice since many problems related to Petri nets can be decided by computing an over-approximation of the reachability property, called the coverability, obtained by introducing the downward-closed sets.
More formally, the downward closure of a set M of markings is defined as the set \(\{x \in \mathbb {N}^P \mid \exists y \in M, ~x \le y \}\). We say that M is downward-closed if it is equal to its downward closure. Downward-closed sets can be finitely represented by introducing the notion of \(\omega \)-markings, a notion also known as the ideal representation of downward-closed sets (see [11] for extra results). We first introduce the set \(\mathbb {N}_\omega \) defined as \(\mathbb {N}\cup \{\omega \}\), where \(\omega \) is a special symbol not in \(\mathbb {N}\) that is interpreted as an infinite number. This interpretation is defined by extending the total order \(\le \) over \(\mathbb {N}\) into a total order on \(\mathbb {N}_\omega \) by \(n\le \omega \) for every \(n\in \mathbb {N}_\omega \). An \(\omega \)-marking is an element of \(x\in \mathbb {N}_\omega ^P\). In [33] and in our Coq proofs, \(\omega \)-markings are defined with the type
 as follows.
as follows.

We associate with an \(\omega \)-marking x the downward-closed set \(\mathord {\downarrow }x\) of markings defined as \(\{y\in \mathbb {N}^P \mid y\le x\}\). We also denote by \(\mathord {\downarrow }B\), where B is a finite set of \(\omega \)-markings, the downward-closed set \(\bigcup _{x\in B}\mathord {\downarrow }x\). Let us recall from the well-quasi-order theory [11] that any downward-closed set M of markings admits a finite set B of \(\omega \)-markings, called a basis of M, such that \(M=\mathord {\downarrow }B\). Bases provide finite descriptions of downward-closed sets. Naturally a downward-closed set can have several bases. However, among all the bases of a downward-closed set, the unique minimal one (for the inclusion relation) can be computed from any basis as follows. We say that a finite set B of \(\omega \)-markings forms an antichain if for every \(x,y\in B\) such that \(x\le y\), we have \(x=y\). Notice that if B is a basis of a downward-closed set M that is not an antichain, then there exist \(x,y\in B\) such that \(x<y\). Since in that case \(B\backslash \{x\}\) is also a basis of M, it follows that by recursively removing from B the \(\omega \)-markings that are strictly smaller than another one in B, we derive from any basis another one that is an antichain. One can prove that this antichain is the unique minimal basis of M (for the inclusion relation).
Given a Petri net \(\mathcal {P}\), we say that a marking \(z\in \mathbb {N}^P\) is coverable from a marking \(x_0\) if there exists a marking \(y\ge z\) reachable from \(x_0\). The set of coverable markings is called the coverability set.
Since coverability sets are downward-closed, they can be described by bases. The computation of such those bases is exactly the purpose of Karp-Miller algorithms. While \(\omega \) components were introduced in the original Karp-Miller algorithm [19] with some algorithmic techniques, this notion was abstracted away in [12] as kind of meta-transitions, called accelerations and abstractions. Those notions are recalled in the next section. They are used to compute the minimal basis of the coverability set, called the clover in [12]. In our Coq proofs, we encode the clover as a list of \(\omega \)-markings (a list is denoted by
 ). The definition uses the
). The definition uses the
 predicate defined in [33].
predicate defined in [33].

3 Abstractions and Accelerations
Abstractions provide a simple way to explain why some markings can be covered from other ones. In this section we first recall the definition and semantics of \(\omega \)-transitions. Then we introduce the abstractions following the definition introduced in [12], based on \(\omega \)-transitions. We show that this rather technical definition is in fact equivalent to a new simpler one. Whereas the proof of equivalence between the two definitions is simple, we think that our definition provides interesting intuitions on abstractions. Finally, in the last part of this section we show that three operators on abstractions (weakening, contraction, and acceleration) provides a complete set of rules for generating any abstraction starting from the Petri net transitions. The proof is based on the Jančar well-quasi-order on executions [17, 22].
Since our Coq proofs for this part are obtained by series of case analyses (not complicated but lengthy in Coq), we do not provide additional information concerning that part of our implementation. All proofs can be found in the file New_transitions.v.
3.1 \(\omega \)-Transitions
An \(\omega \)-transition t is a pair \(t=(x,y)\) where \(x,y\in \mathbb {N}_\omega ^P\) are \(\omega \)-markings such that \(x(p)=\omega \Rightarrow y(p)=\omega \) for every place \(p\in P\). The \(\omega \)-markings x and y are respectively denoted by \({\text {Pre}}(t)\) and \({\text {Post}}(t)\) and they are called respectively the precondition and the postcondition of t. This notation provides a natural way to identify transitions of a Petri net as particular \(\omega \)-transitions. We implemented \(\omega \)-transitions in Coq with the dependent datatype
 as follows.
as follows.

We introduce the operator \(\ominus :\mathbb {N}_\omega ^P\times \mathbb {N}_\omega ^P\rightarrow \mathbb {N}_\omega ^P\) defined component-wise by \(x\ominus y =0\) if \(x\le y\), \(\omega \) if \(x=\omega \) and \(y\in \mathbb {N}\), and \(x-y\) otherwise. As expected, an \(\omega \)-transition t is said to be fireable from an \(\omega \)-marking x if \({\text {Pre}}(t) \le x\). In that case, we write \(x \xrightarrow {t} y\) where \(y=(x \ominus {\text {Pre}}(t)) + {\text {Post}}(t)\) is called the \(\omega \)-marking obtained after firing t from x.
In order to provide a way to manipulate a sequence of \(\omega \)-transitions as just one single \(\omega \)-transition, the notion of Hurdle [15], known by the Petri net community for sequences of transitions, was extended to sequences of \(\omega \)-transitions [12]. More formally, we introduce an internal binary operator \(\otimes \) on \(\omega \)-transitions, called the contraction, as follows:
We implemented in Coq the contraction operator and we formally proved the following lemma.
Lemma 1
For every \(\omega \)-markings \(x,z\in \mathbb {N}_\omega ^P\), the \(\omega \)-transition \(s\otimes t\) satisfies:
In the sequel, given a sequence of \(\omega \)-transitions \(\sigma =t_1\ldots t_k\), we call the \(\omega \)-transition \(t=t_1\otimes \cdots \otimes t_k\) the contraction of \(\sigma \) and, when there is no ambiguity, we identify \(\sigma \) with its contraction. It follows that \({\text {Pre}}(\sigma )\) and \({\text {Post}}(\sigma )\) are well defined.
3.2 Abstractions
Following [12], an abstraction is an \(\omega \)-transition a such that for all \(n \ge 0\), there exists \(\sigma _n \in T^*\) such that for all \(p \in P\) with \({\text {Pre}}(a)(p) \in \mathbb {N}\):
-
\( {\text {Pre}}(\sigma _n)(p) \le {\text {Pre}}(a)(p)\)
-
If \({\text {Post}}(a)(p) \in \mathbb {N}\) then \({\text {Post}}(a)(p) +{\text {Pre}}(\sigma _n)(p) \le {\text {Post}}(\sigma _n)(p) +{\text {Pre}}(a)(p) \)
-
If \({\text {Post}}(a)(p)= \omega \) then \({\text {Pre}}(\sigma _n)(p) + n \le {\text {Post}}(\sigma _n)(p) \)
Our Coq implementation of abstractions is a direct translation of the previous definition. We provide the code just below. In that code, note that
 is a function that maps sequences of transitions to their contractions. Also, we provide a simplification of the actual code in which we use the same symbols for comparisons and operations independently of whether
is a function that maps sequences of transitions to their contractions. Also, we provide a simplification of the actual code in which we use the same symbols for comparisons and operations independently of whether
 ,
,
 , or a mix of the two, are used. Similarly, we assume in the sequel implicit coercions from
, or a mix of the two, are used. Similarly, we assume in the sequel implicit coercions from
 ,
,
 , or
, or
 to
to
 .
.

The previous definition of abstraction is in fact equivalent to the following simpler one, where \({\text {Cover}}(x,\mathcal {P})\) for some \(\omega \)-marking x denotes the set of markings z such that \(x\xrightarrow {\sigma } y\) for some word \(\sigma \) of transitions and some \(\omega \)-marking \(y\ge z\).
Lemma 2
A given \(\omega \)-transition a is an abstraction if, and only if, it satisfies \(\mathord {\downarrow }{\text {Post}}(a)\subseteq {\text {Cover}}({\text {Pre}}(a),\mathcal {P})\).
Note that this new characterization provides a way to constructively check whether an \(\omega \)-transition is an abstraction. This would allow us to declare abstractions as an
 in a future work.
in a future work.
We also recall the following lemma proved in [12]. This result is central for the correctness of the algorithm MinCov. We implemented its proof in Coq in the file New_transitions.v.
Lemma 3
(Lemma 1 in [12]). Let \(x_0\) be a marking of a Petri net \(\mathcal {P}\). For every \(\omega \)-markings x, y such that \(x\xrightarrow {a}y\) for some abstraction a, we have:
3.3 Abstraction Builder
In this last part, we show that any abstraction can be built from Petri net transitions by applying three operators: weakening, contraction, and acceleration.
Let us first start with the simplest operator, called the weakening. We introduce a partial order \(\sqsubseteq \) on the \(\omega \)-transitions defined by \(s\sqsubseteq t\) if \({\text {Pre}}(t)\le {\text {Pre}}(s)\) and \({\text {Post}}(s)+{\text {Pre}}(t)\le {\text {Post}}(t)+{\text {Pre}}(s)\). The second inequality intuitively means that the effect of t is larger than or equal to the effect of s (component-wise). Based on Lemma 2, we deduce that if t is an abstraction and s an \(\omega \)-transition such that \(s\sqsubseteq t\), then s is also an abstraction. Based on this observation, we introduce a weakening operator that just replaces an abstraction t by any other abstraction \(s\sqsubseteq t\).
The second simplest operator is the contraction. Based on Lemmas 1 and 2, we can deduce that if s, t are two abstractions, then \(s\otimes t\) is also an abstraction.
The last operator, called the acceleration, associates with an \(\omega \)-transition t the \(\omega \)-transition \(t^\omega \) that intuitively corresponds to the infinite firing of t. More formally, \(t^\omega \) is defined as follows for every place \(p\in P\):
In [12], it is proved that if a is an abstraction then \(a^\omega \) is also an abstraction.
Notice that \(t^\omega =t\) if, and only if, \({\text {Post}}(t)(p)\in \{{\text {Pre}}(t)(p),\omega \}\) for every \(p\in P\). If a is an abstraction and \(a^\omega =a\), we say that a is an acceleration. Since accelerations play a central role in the MinCov algorithm, we implemented them in Coq as follows.

The following Lemma 4 is one of the main result of this section. It shows that any abstraction can be derived from the Petri net transitions by applying the previously mentioned operators.
Lemma 4
An \(\omega \)-transition a is an abstraction if, and only if, there exist \(w_0\), \(t_1,w_1,\ldots ,t_k,w_k\) where \(w_0,\ldots ,w_k\in T^*\) and \(t_1,\ldots ,t_k\in T\) such that:
4 The Original MinCov Algorithm
In this section, we present our Coq implementation of the MinCov algorithm. We tried to be as close as possible to the algorithm introduced in [12], to provide convincing evidence that it is correct and terminating. We however omitted the trunc function used in the MinCov pseudocode presented in [12] but not in their Python implementation. In practice this function differs from the identity function only when numbers computed by the algorithm are larger than the number of atoms in the universe.
4.1 Explicit Coverability Trees
As already mentioned, this algorithm computes the minimal basis of the coverability set of a Petri net \(\mathcal {P}\) from an initial \(\omega \)-marking \(x_0\). Similarly to the original Karp-Miller algorithm, it computes inductively a tree \(\mathcal {T}\) such that nodes are labeled by \(\omega \)-markings, and edges by transitions. In the case of MinCov, the constructed tree, called an explicit coverability tree, contains additional labels that are explained a bit later. We implement explicit coverability trees in Coq as the following inductive definition
 :
:

A node obtained with the constructor
 is called empty, whereas a node obtained with the constructor
is called empty, whereas a node obtained with the constructor
 is called valid. The first line of the constructor
is called valid. The first line of the constructor
 of a valid node N provides the \(\omega \)-marking denoted by \(\lambda (N)\) that labels the node N. The fourth line provides a function that inductively maps each transition t to a subtree. The root node of that subtree is denoted by N.t and called the child of N following t. Given a node, we call the unique word \(\sigma \in T^*\) that labels the edges of the tree from the root to that node the address of that node. A word \(\sigma \in T^*\) is called a valid address if it is the address of a valid node. This node is denoted by \(N_\sigma \) in that case. A node is called a leaf if it is valid and if N.t is an empty node for every transition t.
of a valid node N provides the \(\omega \)-marking denoted by \(\lambda (N)\) that labels the node N. The fourth line provides a function that inductively maps each transition t to a subtree. The root node of that subtree is denoted by N.t and called the child of N following t. Given a node, we call the unique word \(\sigma \in T^*\) that labels the edges of the tree from the root to that node the address of that node. A word \(\sigma \in T^*\) is called a valid address if it is the address of a valid node. This node is denoted by \(N_\sigma \) in that case. A node is called a leaf if it is valid and if N.t is an empty node for every transition t.
Compared to trees computed by the Karp-Miller algorithm, explicit coverability trees computed by the MinCov algorithm have two additional pieces of information on each valid node, provided by the second and third lines of the constructor
 . First of all, since trees may be partially destroyed when a subtree corresponding to redundant computations is detected, the computation is no longer a DFS exploration. In order to keep track of nodes that are waiting for further exploration, called front nodes, each valid node is marked with a boolean flag that is assigned to true when it is a front one. The set of front nodes of an explicit coverability tree \(\mathcal {T}\) is denoted by \({\text {Front}}(\mathcal {T})\). Last but not least, explicit coverability trees contain additional information to recover the way the node labels were generated. To do so, the second line of the constructor
. First of all, since trees may be partially destroyed when a subtree corresponding to redundant computations is detected, the computation is no longer a DFS exploration. In order to keep track of nodes that are waiting for further exploration, called front nodes, each valid node is marked with a boolean flag that is assigned to true when it is a front one. The set of front nodes of an explicit coverability tree \(\mathcal {T}\) is denoted by \({\text {Front}}(\mathcal {T})\). Last but not least, explicit coverability trees contain additional information to recover the way the node labels were generated. To do so, the second line of the constructor
 of a valid node N provides a sequence \(a_1\ldots a_k\) of accelerations denoted by \(\mu (N)\).
of a valid node N provides a sequence \(a_1\ldots a_k\) of accelerations denoted by \(\mu (N)\).
In our implementation, we prove that the following properties (called invariant properties in the sequel) are maintained throughout any execution of the algorithm.
-
Front nodes are always leaves (predicate
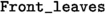 ).
). -
Non-front node labels form an antichain (predicate
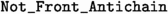 ).
). -
The root node is valid, and \(x_0\xrightarrow {\mu (N_\varepsilon )}\lambda (N_\varepsilon )\) (predicate
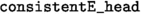 ).
). -
If a valid node N is not the root, i.e. \(N=N'.t\) for some node \(N'\) and some transition t, then \(\lambda (N')\xrightarrow {t \mu (N)}\lambda (N)\) (predicate
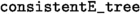 ).
).
4.2 Step Relation
The MinCov algorithm is a while loop algorithm that updates a pair \((\mathcal {T},A)\), where \(\mathcal {T}\) is an explicit coverability tree, and A is a (finite) sequence of accelerations. Accelerations that occur in \(\mathcal {T}\) (in the \(\mu \) labeling) are taken from A. Moreover, the sequence A can only grow with new discovered accelerations. Initially, the MinCov algorithm begins with the pair \((\mathcal {T}, A)\) where A is the empty sequence \(\varepsilon \) and \(\mathcal {T}\) is the explicit coverability tree reduced to a single valid front node \(N_\varepsilon \) labeled by \(\lambda (N_\varepsilon )=x_0\) and \(\mu (N_\varepsilon )=\varepsilon \). The algorithm picks nondeterministically a front node at each iteration of the while loop to transform the tree. It terminates when the set of front nodes is empty and, at that point, returns the current \(\mathcal {T}\) (the set A is discarded at the end). Our Coq implementation of this algorithm is defined by introducing a binary relation
 on those pairs \((\mathcal {T},A)\). Such a one-step encoding provides all the possible nondeterministic behaviors of the algorithm. It follows that our proofs of correctness and termination are valid whatever the implemented particular exploration heuristic.
on those pairs \((\mathcal {T},A)\). Such a one-step encoding provides all the possible nondeterministic behaviors of the algorithm. It follows that our proofs of correctness and termination are valid whatever the implemented particular exploration heuristic.
Formally, the relation
 is defined as follows, with three constructors
is defined as follows, with three constructors
 ,
,
 , and
, and
 that are defined later in this section:
that are defined later in this section:

As will be discussed later, the termination of the MinCov algorithm is proved by certifying that the relation
 is well-founded. For that reason,
is well-founded. For that reason,
 corresponds to a step of the MinCov algorithm from \((\mathcal {T},A)\) to \((\mathcal {T}',A')\), and not the other way around.
corresponds to a step of the MinCov algorithm from \((\mathcal {T},A)\) to \((\mathcal {T}',A')\), and not the other way around.
One central notion of the algorithm is the definition of saturated \(\omega \)-markings. An \(\omega \)-marking x is saturated for a sequence A of accelerations if, for every acceleration \(a\in A\) such that \(x\xrightarrow {a}y\) for some \(\omega \)-marking y, we have \(x=y\). When an \(\omega \)-marking is not saturated for a sequence A, it can be saturated with respect to A as follows. Note that in general, given two \(\omega \)-markings x, y such that \(x\xrightarrow {a}y\) for some acceleration a, then \(y(p)\in \{x(p),\omega \}\) for every place p. It means that y is obtained from x by setting to \(\omega \) some places of x. In particular, if \(x\not =y\), then the number of places with natural numbers is strictly decreasing from x to y. It follows that an algorithm that tries to apply in a round-robin fashion all the accelerations in A eventually terminates on a fixed point in at most |P| rounds. We implement this algorithm in Coq with a function
 that takes as input a sequence A of accelerations, an explicit coverability tree \(\mathcal {T}\), and a valid address \(\sigma \in T^*\) (denoted by
that takes as input a sequence A of accelerations, an explicit coverability tree \(\mathcal {T}\), and a valid address \(\sigma \in T^*\) (denoted by
 ), and returns the explicit coverability tree obtained from \(\mathcal {T}\) by saturating \(\lambda (N_\sigma )\) with respect to A, and by appending to \(\mu (N_\sigma )\) the sequence of accelerations used by the round-robin saturation algorithm.
), and returns the explicit coverability tree obtained from \(\mathcal {T}\) by saturating \(\lambda (N_\sigma )\) with respect to A, and by appending to \(\mu (N_\sigma )\) the sequence of accelerations used by the round-robin saturation algorithm.
The MinCov algorithm is implemented in such a way the labels of the non-front valid nodes form an antichain. To enforce that property, the cleaning operation takes as input two explicit coverability trees \(\mathcal {T}\) and \(\mathcal {T}'\), a sequence A of accelerations, and an address \(\sigma \) (denoted by
 below), and checks if \(\sigma \) is the address of a front node, if \(\mathcal {T}'\) is the tree obtained from \(\mathcal {T}\) by saturating \(N_\sigma \) with respect to A (see above), and if there exists a non-front node \(N'\) such that \(\lambda (N_{\sigma }) \le \lambda (N')\) in \(\mathcal {T}'\) (predicate
below), and checks if \(\sigma \) is the address of a front node, if \(\mathcal {T}'\) is the tree obtained from \(\mathcal {T}\) by saturating \(N_\sigma \) with respect to A (see above), and if there exists a non-front node \(N'\) such that \(\lambda (N_{\sigma }) \le \lambda (N')\) in \(\mathcal {T}'\) (predicate
 below). In that case, the cleaning operation puts in the relation
below). In that case, the cleaning operation puts in the relation
 the pair \((\mathcal {T},A)\) with \((\mathcal {T}'',A)\), where \(\mathcal {T}''\) is obtained from \(\mathcal {T}'\) by removing the node at address \(\sigma \) (implemented by
the pair \((\mathcal {T},A)\) with \((\mathcal {T}'',A)\), where \(\mathcal {T}''\) is obtained from \(\mathcal {T}'\) by removing the node at address \(\sigma \) (implemented by
 ).
).

When the previous cleaning operation cannot be applied on a front node with address \(\sigma \) (
 denotes the negation, and
denotes the negation, and
 and
and
 in the code refer to \(\sigma \) and \(\sigma '\)), the algorithm checks if this front node, once saturated, is labeled by an \(\omega \)-marking larger than the label of an ancestor with address \(\sigma '\) (through the predicate
in the code refer to \(\sigma \) and \(\sigma '\)), the algorithm checks if this front node, once saturated, is labeled by an \(\omega \)-marking larger than the label of an ancestor with address \(\sigma '\) (through the predicate
 , which also checks that \(\sigma '\) is the prefix of \(\sigma \)). If so, an accelerating operation is performed. It consists first in computing the acceleration corresponding to the path between the two nodes. More precisely,
, which also checks that \(\sigma '\) is the prefix of \(\sigma \)). If so, an accelerating operation is performed. It consists first in computing the acceleration corresponding to the path between the two nodes. More precisely,
 computes the acceleration \(a=(t_1\sigma _1\ldots t_k\sigma _k)^\omega \), where \(\sigma =\sigma 't_1\ldots t_k\) for a sequence \(t_1\ldots t_k\) of transitions, and \(\sigma _1,\ldots ,\sigma _k\) are the sequences of accelerations that occur in \(\mathcal {T}'\) from \(\sigma \) to \(\sigma '\), i.e. \(\sigma _j=\mu (N_{\sigma 't_1\ldots t_j})\). In that case, the accelerating operation puts in the relation
computes the acceleration \(a=(t_1\sigma _1\ldots t_k\sigma _k)^\omega \), where \(\sigma =\sigma 't_1\ldots t_k\) for a sequence \(t_1\ldots t_k\) of transitions, and \(\sigma _1,\ldots ,\sigma _k\) are the sequences of accelerations that occur in \(\mathcal {T}'\) from \(\sigma \) to \(\sigma '\), i.e. \(\sigma _j=\mu (N_{\sigma 't_1\ldots t_j})\). In that case, the accelerating operation puts in the relation
 the pair \((\mathcal {T},A)\) with \((\mathcal {T}'',A')\), where \(A'\) is the sequence obtained by adding a to A, and \(\mathcal {T}''\) is obtained from \(\mathcal {T}'\) by removing the subtree of \(\mathcal {T}'\) from \(N_{\sigma '}\) and by setting that node as a front node (
the pair \((\mathcal {T},A)\) with \((\mathcal {T}'',A')\), where \(A'\) is the sequence obtained by adding a to A, and \(\mathcal {T}''\) is obtained from \(\mathcal {T}'\) by removing the subtree of \(\mathcal {T}'\) from \(N_{\sigma '}\) and by setting that node as a front node (
 below).
below).

When the previous cleaning and accelerating operations cannot be applied on a front node (tested through
 for the accelerating operation), the algorithm performs an exploration from that front node by trying to fire all the transitions from the label of that node. This label x is computed after saturation via the function
for the accelerating operation), the algorithm performs an exploration from that front node by trying to fire all the transitions from the label of that node. This label x is computed after saturation via the function
 , from the tree and the address \(\sigma \) (denoted by
, from the tree and the address \(\sigma \) (denoted by
 below) of the node. The exploring operation (see
below) of the node. The exploring operation (see
 below) puts in the relation
below) puts in the relation
 the pair \((\mathcal {T},A)\) with \((\mathcal {T}''',A)\), where \(\mathcal {T}''\) is the tree obtained from \(\mathcal {T}'\) by removing valid nodes labeled by an \(\omega \)-marking smaller than x (implemented by
the pair \((\mathcal {T},A)\) with \((\mathcal {T}''',A)\), where \(\mathcal {T}''\) is the tree obtained from \(\mathcal {T}'\) by removing valid nodes labeled by an \(\omega \)-marking smaller than x (implemented by
 ), and \(\mathcal {T}'''\) is obtained from \(\mathcal {T}''\) by removing the node at address \(\sigma \) from the front list, and by creating, for each transition t such that there exists an \(\omega \)-marking y such that \(x\xrightarrow {t}y\), a front node \(N_{\sigma t}\) labeled by \(\lambda (N_{\sigma t})=y\) and \(\mu (N_{\sigma t})=\varepsilon \) (this last operation is implemented by
), and \(\mathcal {T}'''\) is obtained from \(\mathcal {T}''\) by removing the node at address \(\sigma \) from the front list, and by creating, for each transition t such that there exists an \(\omega \)-marking y such that \(x\xrightarrow {t}y\), a front node \(N_{\sigma t}\) labeled by \(\lambda (N_{\sigma t})=y\) and \(\mu (N_{\sigma t})=\varepsilon \) (this last operation is implemented by
 ).
).

5 The AbstractMinCov Algorithm
The Coq proofs of correctness and termination of the MinCov algorithm are obtained by introducing a variant of that algorithm, called AbstractMinCov. This new algorithm takes a small-step approach obtained by decomposing the three main operations (cleaning, accelerating, and exploring) of the original MinCov into sequences of five small-step operations presented in this section.
We implemented in Coq a formalization of AbstractMinCov and proved the correctness and termination of that algorithm. Since the original MinCov algorithm can be simulated by our algorithm, we obtain at the cost of a simple Coq proof of simulation that the original MinCov algorithm is correct and terminates. Compared to a direct proof, our approach provides more succinct proofs in Coq, because proving that some properties are invariant is usually easier for a small step than for a big step.
Compared to the original MinCov algorithm, which performs the three main operations in a strict order, the five operations of AbstractMinCov can be executed in any order. It follows that new exploration heuristics, for instance the early discarding of subtrees after the discovering of an acceleration, can be implemented without rewriting any proof of correctness or termination.
In Section 5.1, we introduce the (implicit) coverability trees, the central data structure of the AbstractMinCov algorithm. In Section 5.2, we present the five operations of the AbstractMinCov algorithm. Finally, in Section 5.3 we provide some elements of our termination and correctness Coq proofs.
5.1 Coverability Trees
We implement the (implicit) coverability trees in Coq as the following inductive definition
 :
:

As one can see, they are nearly the same as explicit coverability trees: we just remove the sequence of accelerations that was previously part of the label of a node. The invariant properties introduced for explicit coverability trees (see the end of Section 4.1) have straightforward counterparts for the coverability trees, which are similarly maintained throughout any execution of AbstractMinCov.
5.2 The Algorithm
AbstractMinCov also consists of a main while loop that updates a pair (\(\mathcal {T},A\)), where \(\mathcal {T}\) is a coverability tree instead of an explicit one, and A a finite sequence of accelerations. Initially, the AbstractMinCov algorithm begins with the pair \((\mathcal {T}, A)\) where A is the empty sequence \(\varepsilon \) and \(\mathcal {T}\) is the coverability tree reduced to a single valid front node \(N_\varepsilon \) labeled by \(\lambda (N_\varepsilon )=x_0\). This tree is built by the Coq function
 . Then, at each round of the loop, it picks one of the five operations it can apply on the pair, the one whose precondition is met, and apply it. It terminates when none of the operations have preconditions satisfied by the pair (\(\mathcal {T},A\)). At the end, A is discarded and only \(\mathcal {T}\) is returned. As AbstractMinCov is nondeterministic, we implement it as a relation, like we do for MinCov. More precisely, we implement it in Coq as a binary relation
. Then, at each round of the loop, it picks one of the five operations it can apply on the pair, the one whose precondition is met, and apply it. It terminates when none of the operations have preconditions satisfied by the pair (\(\mathcal {T},A\)). At the end, A is discarded and only \(\mathcal {T}\) is returned. As AbstractMinCov is nondeterministic, we implement it as a relation, like we do for MinCov. More precisely, we implement it in Coq as a binary relation
 on those pairs \((\mathcal {T},A)\) such that
on those pairs \((\mathcal {T},A)\) such that
 corresponds to a step of AbstractMinCov from \((\mathcal {T},A)\) to \((\mathcal {T}',A')\). Hence all possible executions of AbstractMinCov are encoded into decreasing sequences of
corresponds to a step of AbstractMinCov from \((\mathcal {T},A)\) to \((\mathcal {T}',A')\). Hence all possible executions of AbstractMinCov are encoded into decreasing sequences of
 . Hence, by proving its well-foundedness and its correctness, we prove that every execution of the AbstractMinCov algorithm is correct and terminates.
. Hence, by proving its well-foundedness and its correctness, we prove that every execution of the AbstractMinCov algorithm is correct and terminates.

In the file MinCov.v, operations of MinCov are proved to be simulated by sequences of AbstractMinCov operations matching the following regular expressions (for readability, the prefixes
 and
and
 are removed):
are removed):

In MinCov, accelerations are added to the set A only during the accelerating operation, and the added acceleration comes from the considered branch of the tree. On the contrary, the five operations of AbstractMinCov allow new accelerations to be added to A. Such accelerations could be computed from the tree like in MinCov, but they could also be discovered by running an external heuristic algorithm for example.
The saturating operation is a small-step version of the already seen function
 , applying only one acceleration at a time instead of applying as many accelerations as possible. It can be performed on any front node N of label x and address
, applying only one acceleration at a time instead of applying as many accelerations as possible. It can be performed on any front node N of label x and address
 such that \(x \xrightarrow {a} y\) (i.e.
such that \(x \xrightarrow {a} y\) (i.e.
 ) and \(x \ne y\), for some \(a \in A\) and some \(\omega \)-marking y. The saturating operation simply sets \(\lambda (N)\) to y (which is what the function
) and \(x \ne y\), for some \(a \in A\) and some \(\omega \)-marking y. The saturating operation simply sets \(\lambda (N)\) to y (which is what the function
 does).
does).

The cleaning operation is basically the same as the one of MinCov. The difference is that now the \(\omega \)-marking of the considered node is required to be already saturated (which can be obtained via the
 operation). Also note that the
operation). Also note that the
 function has been replaced by the
function has been replaced by the
 function (with the same behavior) because of the change from
function (with the same behavior) because of the change from
 to
to
 . This is also the case for several other functions in the other operations.
. This is also the case for several other functions in the other operations.

The accelerating operation is abstracted compared to the MinCov equivalent operation. More precisely, the acceleration used to justify the cut of the branch via the
 function may come from previous stages of the algorithm, or be guessed during the operation. In the latter case, the acceleration may be computed as in MinCov. It follows that subtrees rooted in non-saturated nodes can be discarded earlier than in MinCov.
function may come from previous stages of the algorithm, or be guessed during the operation. In the latter case, the acceleration may be computed as in MinCov. It follows that subtrees rooted in non-saturated nodes can be discarded earlier than in MinCov.

The covering operation removes a node of \(\mathcal {T}\) when it is covered by a node in \({\text {Front}}(\mathcal {T})\). It corresponds to a part of the exploring operation of MinCov. The non-prefix requirement is here to ensure that a front node does not trigger its own deletion.

The exploring operation is an abstracted version of the one in MinCov. It only performs the extension of some front node N without any additional transformation. However, stronger requirements are needed. Namely, N must be already saturated (this can be obtained thanks to the saturating operation), and the non-front nodes must satisfy the
 property once the front flag of N is switched to
property once the front flag of N is switched to
 (this can be obtained thanks to the covering operation).
(this can be obtained thanks to the covering operation).

5.3 Certification
Termination proofs of Karp-Miller algorithms are usually based on the fact that \(\le \) is a well-quasi-order over the set of \(\omega \)-markings. As in [33], we replace this classical notion with the notion of almost-full relation [32]. This order is however just an ingredient and further arguments are needed. This is especially true for MinCov, because the tree maintained in this algorithm may not only grow, as in the original Karp-Miller algorithm, but also shrink. The code can be found in the file Termination.v, including the following theorem, where
 is the predicate of the Coq standard library used in the constructive definition of well-foundedness.
is the predicate of the Coq standard library used in the constructive definition of well-foundedness.

This theorem is proved thanks to a general well-founded rewriting relation on trees described in the file wbr_tree.v.
Our correctness proof in Coq is close to the pen-and-paper one of MinCov [12]. Whereas the correctness proof of the original Karp-Miller algorithm is based on branches, operations on trees performed by MinCov depend on the complete tree. The correctness proof can be found in the file Correctness.v, whose main theorem is the following one, where
 is the predicate for the reflexive and transitive closure, and
is the predicate for the reflexive and transitive closure, and
 computes the list of all \(\omega \)-markings of the input coverability tree.
computes the list of all \(\omega \)-markings of the input coverability tree.

As in [12], this theorem is a corollary of two results, corresponding to the two directions of the equivalence in the
 definition.
definition.
The main theorem of the file KMTrees.v, shown below, provides the first direction by observing that the desired implication follows from the consistent properties mentioned in Sections 4.1 and 5.1. The fact that these properties are invariant (proved in file AbstractMinCov.v) implies that this implication is in fact satisfied throughout the execution and not just when the algorithm has terminated.

The other direction is the main theorem of file Completeness.v.

The following table summarizes the size of [33]’s and our formalizations. We import and use all files from [33] except the Karp-Miller part.
[33] (commit bbb0668) | Technical tools | 631 lines |
|---|---|---|
Petri net | 1226 lines | |
Karp-Miller | 775 lines | |
[This paper] | Technical tools | 1790 lines |
Petri net extension | 1869 lines | |
MinCov and AbstractMinCov | 5590 lines |
6 Conclusion
We provide a complete Coq certification of MinCov, an algorithm that computes the minimal basis of the coverability set (of a Petri net with an initial marking). Our development is obtained by introducing a small-step variant of that algorithm, called AbstractMinCov. This variant consists of smaller and more abstract steps than in MinCov, and which can be performed in any order. This gives a lot of freedom to an actual implementation of the algorithm, leaving room for heuristics. In particular, the step
 can prune any subtree rooted on a non-saturated node. Note that such a subtree is necessarily removed at some step of the MinCov algorithm, since every node is saturated when the algorithm terminates. This early removal will decrease the total number of node comparisons that are performed by operations maintaining the antichain property (
can prune any subtree rooted on a non-saturated node. Note that such a subtree is necessarily removed at some step of the MinCov algorithm, since every node is saturated when the algorithm terminates. This early removal will decrease the total number of node comparisons that are performed by operations maintaining the antichain property (
 and
and
 ). It would be interesting to quantify the actual impact of such a strategy, and more generally, of all the heuristics permitted by our AbstractMinCov algorithm.
). It would be interesting to quantify the actual impact of such a strategy, and more generally, of all the heuristics permitted by our AbstractMinCov algorithm.
The constructive logic of Coq provides automatic correct-by-construction Ocaml code extraction. This is however not currently possible because we use relations to describe the algorithms in order to preserve their non-determinism. It should be interesting in a future work to implement choice functions and boolean versions of our
 predicates, and to benchmark the extracted code against the existing Python implementation of MinCov. Since most of our predicates are already boolean functions (although their boolean natures are hidden by a coercion), we think that obtaining an OCaml extraction would be reasonably easy. However, obtaining an efficient one would require a significant additional amount of work.
predicates, and to benchmark the extracted code against the existing Python implementation of MinCov. Since most of our predicates are already boolean functions (although their boolean natures are hidden by a coercion), we think that obtaining an OCaml extraction would be reasonably easy. However, obtaining an efficient one would require a significant additional amount of work.
References
Angeli, D., Leenheer, P.D., Sontag, E.D.: Persistence results for chemical reaction networks with time-dependent kinetics and no global conservation laws. SIAM Journal on Applied Mathematics 71(1), 128–146 (2011). https://doi.org/10.1137/090779401, http://www.jstor.org/stable/41111581
Baldan, P., Cocco, N., Marin, A., Simeoni, M.: Petri nets for modelling metabolic pathways: A survey. Natural Computing 9, 955–989 (12 2010). https://doi.org/10.1007/s11047-010-9180-6
Blondin, M., Haase, C., Offtermatt, P.: Directed Reachability for Infinite-State Systems. In: Groote, J.F., Larsen, K.G. (eds.) Tools and Algorithms for the Construction and Analysis of Systems - 27th International Conference, TACAS 2021, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2021, Luxembourg City, Luxembourg, March 27 - April 1, 2021, Proceedings, Part II. Lecture Notes in Computer Science, vol. 12652, pp. 3–23. Springer (2021). https://doi.org/10.1007/978-3-030-72013-1_1
Bozzelli, L., Ganty, P.: Complexity Analysis of the Backward Coverability Algorithm for VASS. In: Delzanno, G., Potapov, I. (eds.) Reachability Problems - 5th International Workshop, RP 2011, Genoa, Italy, September 28-30, 2011. Proceedings. Lecture Notes in Computer Science, vol. 6945, pp. 96–109. Springer (2011). https://doi.org/10.1007/978-3-642-24288-5_10
Czerwinski, W., Lasota, S., Lazic, R., Leroux, J., Mazowiecki, F.: The reachability problem for Petri nets is not elementary. In: Charikar, M., Cohen, E. (eds.) Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, STOC 2019, Phoenix, AZ, USA, June 23-26, 2019. pp. 24–33. ACM (2019). https://doi.org/10.1145/3313276.3316369
Czerwinski, W., Orlikowski, L.: Reachability in Vector Addition Systems is Ackermann-complete. In: 62nd IEEE Annual Symposium on Foundations of Computer Science, FOCS 2021, Denver, CO, USA, February 7-10, 2022. pp. 1229–1240. IEEE (2021). https://doi.org/10.1109/FOCS52979.2021.00120
Dixon, A., Lazic, R.: KReach: A Tool for Reachability in Petri Nets. In: Biere, A., Parker, D. (eds.) Tools and Algorithms for the Construction and Analysis of Systems - 26th International Conference, TACAS 2020, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2020, Dublin, Ireland, April 25-30, 2020, Proceedings, Part I. Lecture Notes in Computer Science, vol. 12078, pp. 405–412. Springer (2020). https://doi.org/10.1007/978-3-030-45190-5_22
Figueira, D., Figueira, S., Schmitz, S., Schnoebelen, P.: Ackermannian and Primitive-Recursive Bounds with Dickson’s Lemma. In: Proceedings of the 26th Annual IEEE Symposium on Logic in Computer Science, LICS 2011, June 21-24, 2011, Toronto, Ontario, Canada. pp. 269–278. IEEE Computer Society (2011). https://doi.org/10.1109/LICS.2011.39
Finkel, A.: The Minimal Coverability Graph for Petri Nets. In: Rozenberg, G. (ed.) Advances in Petri Nets 1993, Papers from the 12th International Conference on Applications and Theory of Petri Nets, Gjern, Denmark, June 1991. Lecture Notes in Computer Science, vol. 674, pp. 210–243. Springer (1991). https://doi.org/10.1007/3-540-56689-9_45
Finkel, A., Geeraerts, G., Raskin, J.F., Van Begin, L.: A counter-example to the minimal coverability tree algorithm. Université Libre de Bruxelles, Tech. Rep 535 (2005)
Finkel, A., Goubault-Larrecq, J.: Forward analysis for WSTS, part I: completions. Math. Struct. Comput. Sci. 30(7), 752–832 (2020). https://doi.org/10.1017/S0960129520000195
Finkel, A., Haddad, S., Khmelnitsky, I.: Minimal Coverability Tree Construction Made Complete and Efficient. In: Goubault-Larrecq, J., König, B. (eds.) Foundations of Software Science and Computation Structures - 23rd International Conference, FOSSACS 2020, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2020, Dublin, Ireland, April 25-30, 2020, Proceedings. Lecture Notes in Computer Science, vol. 12077, pp. 237–256. Springer (2020). https://doi.org/10.1007/978-3-030-45231-5_13
Geeraerts, G., Raskin, J.F., Van Begin, L.: On the Efficient Computation of the Minimal Coverability Set for Petri Nets. In: Namjoshi, K.S., Yoneda, T., Higashino, T., Okamura, Y. (eds.) Automated Technology for Verification and Analysis. pp. 98–113. Springer Berlin Heidelberg, Berlin, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75596-8_9
Gonthier, G., Mahboubi, A., Tassi, E.: A small scale reflection extension for the Coq system. Ph.D. thesis, Inria Saclay Ile de France (2016)
Hack, M.: Decidability Questions for Petri Nets. Outstanding Dissertations in the Computer Sciences, Garland Publishing, New York (1975)
Hilaire, T., Ilcinkas, D., Leroux, J.: Petri-net-in-coq (2024), https://archive.softwareheritage.org/swh:1:rev:7b5523e30026266c471c73e911f0fda525c6f900; origin=https://gitub.u-bordeaux.fr/thhilaire/petri-net-in-coq.git
Jančar, P.: Decidability of a Temporal Logic Problem for Petri Nets. Theor. Comput. Sci. 74(1), 71–93 (1990). https://doi.org/10.1016/0304-3975(90)90006-4
Kaiser, A., Kroening, D., Wahl, T.: Efficient Coverability Analysis by Proof Minimization. In: Koutny, M., Ulidowski, I. (eds.) CONCUR 2012 - Concurrency Theory - 23rd International Conference, CONCUR 2012, Newcastle upon Tyne, UK, September 4-7, 2012. Proceedings. Lecture Notes in Computer Science, vol. 7454, pp. 500–515. Springer (2012). https://doi.org/10.1007/978-3-642-32940-1_35
Karp, R.M., Miller, R.E.: Parallel Program Schemata. J. Comput. Syst. Sci. 3(2), 147–195 (1969). https://doi.org/10.1016/S0022-0000(69)80011-5
Lasota, S.: Improved Ackermannian Lower Bound for the Petri Nets Reachability Problem. In: Berenbrink, P., Monmege, B. (eds.) 39th International Symposium on Theoretical Aspects of Computer Science, STACS 2022, March 15-18, 2022, Marseille, France (Virtual Conference). LIPIcs, vol. 219, pp. 46:1–46:15. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2022). https://doi.org/10.4230/LIPIcs.STACS.2022.46
Lazic, R., Schmitz, S.: The ideal view on Rackoff’s coverability technique. Inf. Comput. 277, 104582 (2021). https://doi.org/10.1016/j.ic.2020.104582
Leroux, J.: Vector addition system reachability problem: a short self-contained proof. In: Ball, T., Sagiv, M. (eds.) Proceedings of the 38th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2011, Austin, TX, USA, January 26-28, 2011. pp. 307–316. ACM (2011). https://doi.org/10.1145/1926385.1926421
Leroux, J.: The Reachability Problem for Petri Nets is Not Primitive Recursive. In: 62nd IEEE Annual Symposium on Foundations of Computer Science, FOCS 2021, Denver, CO, USA, February 7-10, 2022. pp. 1241–1252. IEEE (2021). https://doi.org/10.1109/FOCS52979.2021.00121
Leroux, J., Schmitz, S.: Reachability in Vector Addition Systems is Primitive-Recursive in Fixed Dimension. In: 34th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2019, Vancouver, BC, Canada, June 24-27, 2019. pp. 1–13. IEEE (2019). https://doi.org/10.1109/LICS.2019.8785796
Mayr, E.W., Meyer, A.R.: The Complexity of the Finite Containment Problem for Petri Nets. J. ACM 28(3), 561–576 (1981). https://doi.org/10.1145/322261.322271
Peleg, M., Rubin, D., Altman, R.B.: Using Petri Net Tools to Study Properties and Dynamics of Biological Systems. Journal of the American Medical Informatics Association 12(2), 181–199 (03 2005). https://doi.org/10.1197/jamia.M1637
Piipponen, A., Valmari, A.: Constructing Minimal Coverability Sets. Fundam. Informaticae 143(3-4), 393–414 (2016). https://doi.org/10.3233/FI-2016-1319
Rackoff, C.: The Covering and Boundedness Problems for Vector Addition Systems. Theor. Comput. Sci. 6, 223–231 (1978). https://doi.org/10.1016/0304-3975(78)90036-1
Reynier, P.A., Servais, F.: Minimal coverability set for petri nets: Karp and miller algorithm with pruning. In: International Conference on Application and Theory of Petri Nets and Concurrency. pp. 69–88. Springer (2011). https://doi.org/10.1007/978-3-642-21834-7_5
Reynier, P., Servais, F.: On the Computation of the Minimal Coverability Set of Petri Nets. In: Filiot, E., Jungers, R.M., Potapov, I. (eds.) Reachability Problems - 13th International Conference, RP 2019, Brussels, Belgium, September 11-13, 2019, Proceedings. Lecture Notes in Computer Science, vol. 11674, pp. 164–177. Springer (2019). https://doi.org/10.1007/978-3-030-30806-3_13
Schmitz, S.: The complexity of reachability in vector addition systems. ACM SIGLOG News 3(1), 4–21 (2016). https://doi.org/10.1145/2893582.2893585
Vytiniotis, D., Coquand, T., Wahlstedt, D.: Stop When You Are Almost-Full - Adventures in Constructive Termination. In: Beringer, L., Felty, A.P. (eds.) Interactive Theorem Proving - Third International Conference, ITP 2012, Princeton, NJ, USA, August 13-15, 2012. Proceedings. Lecture Notes in Computer Science, vol. 7406, pp. 250–265. Springer (2012). https://doi.org/10.1007/978-3-642-32347-8_17
Yamamoto, M., Sekine, S., Matsumoto, S.: Formalization of Karp-Miller tree construction on petri nets. In: Bertot, Y., Vafeiadis, V. (eds.) Proceedings of the 6th ACM SIGPLAN Conference on Certified Programs and Proofs, CPP 2017, Paris, France, January 16-17, 2017. pp. 66–78. ACM (2017). https://doi.org/10.1145/3018610.3018626
Acknowledgments
We thank the anonymous reviewers for their numerous and very interesting remarks.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Hilaire, T., Ilcinkas, D., Leroux, J. (2024). A State-of-the-Art Karp-Miller Algorithm Certified in Coq. In: Finkbeiner, B., Kovács, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2024. Lecture Notes in Computer Science, vol 14570. Springer, Cham. https://doi.org/10.1007/978-3-031-57246-3_21
Download citation
DOI: https://doi.org/10.1007/978-3-031-57246-3_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57245-6
Online ISBN: 978-3-031-57246-3
eBook Packages: Computer ScienceComputer Science (R0)


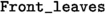 ).
).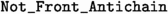 ).
).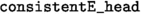 ).
).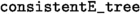 ).
).