Abstract
In this experience report, we present the complete formal verification of a Java implementation of inplace superscalar sample sort (
 ) using the KeY program verification system. As
) using the KeY program verification system. As
 is one of the fastest general purpose sorting algorithms, this is an important step towards a collection of basic toolbox components that are both provably correct and highly efficient. At the same time, it is an important case study of how careful, highly efficient implementations of complicated algorithms can be formally verified directly. We provide an analysis of which features of the KeY system and its verification calculus are instrumental in enabling algorithm verification without any compromise on algorithm efficiency.
is one of the fastest general purpose sorting algorithms, this is an important step towards a collection of basic toolbox components that are both provably correct and highly efficient. At the same time, it is an important case study of how careful, highly efficient implementations of complicated algorithms can be formally verified directly. We provide an analysis of which features of the KeY system and its verification calculus are instrumental in enabling algorithm verification without any compromise on algorithm efficiency.
You have full access to this open access chapter, Download conference paper PDF


1 Introduction
The core task of computer scientists can be seen as writing correct and efficient computer programs. However, although both correctness and efficiency have been intensively studied, there is comparably little work on fully combining both features. We would like formally verified code that is efficient on modern machines. We believe that a library of verified high-performance implementations of the basic toolbox of most frequently used algorithms and data structures is a crucial step towards this goal: often, these components take a considerable part of the overall computation time, and they have a simple specification which allows reusing their verified functionality in a large number of programs. Since the remaining code may be simpler from an algorithmic point of view, verifying such programs could thus be considerably simplified.
To make progress in this direction, we perform a case study on sorting, which is one of the most frequently used basic toolbox algorithms. For example, a recent study identified hundreds of performance relevant sorting calls in Google’s central software depot [36]. Taking correctness of even standard library routines for granted is also not an option. For example, during a verification attempt of the built-in sorting routine of the OpenJDK TimSort routine, researchers were able to detect a bug, using the KeY verifier [11].
Although some sorters have been formally verified [4, 12, 20], it turns out that these do not achieve state-of-the-art performance because only rather simple combinations and variants of quicksort, mergesort, or heapsort have been used that lack cache efficiency when applied to large data sets and have performance bottlenecks that limit instruction parallelism. The best available sorters are considerably more complex (\(\approx \) 1000 lines of code) and even more likely to contain bugs when not formally verified. Moreover, previous verifications do not prove all required properties or they operate only on an abstraction of the code, which makes it difficult to relate to highly tuned implementations.
For our verification of a state-of-the-art sorter, we consider
 (in-place super scalar sample sort) [2]. Sample sort [10] generalises quicksort by partitioning the data into many pieces in a single pass over the data, which makes it more cache efficient (indeed I/O-optimal up to lower order terms). Additionally,
(in-place super scalar sample sort) [2]. Sample sort [10] generalises quicksort by partitioning the data into many pieces in a single pass over the data, which makes it more cache efficient (indeed I/O-optimal up to lower order terms). Additionally,
 works in-place (an important requirement for standard libraries and large inputs), avoids branch mispredictions, and allows high instruction parallelism by reducing data dependencies in the innermost loops. The algorithm also has an efficient parallelisation and parts of it can be used for fast integer sorting [2, 36]. Extensive experiments indicate that a C++ implementation of
works in-place (an important requirement for standard libraries and large inputs), avoids branch mispredictions, and allows high instruction parallelism by reducing data dependencies in the innermost loops. The algorithm also has an efficient parallelisation and parts of it can be used for fast integer sorting [2, 36]. Extensive experiments indicate that a C++ implementation of
 considerably outperforms quicksort, mergesort and heapsort on large inputs and is several times faster than adaptive sorters such as TimSort on inputs that are not already almost sorted [2]. Our experiments in Sec. 5 indicate that the verified Java implementation is 1.3 to 1.8 times faster than the standard library sorter of OpenJDK 20 for large inputs on three different architectures.
considerably outperforms quicksort, mergesort and heapsort on large inputs and is several times faster than adaptive sorters such as TimSort on inputs that are not already almost sorted [2]. Our experiments in Sec. 5 indicate that the verified Java implementation is 1.3 to 1.8 times faster than the standard library sorter of OpenJDK 20 for large inputs on three different architectures.
We use the Java Modeling Language (JML) [22] to directly specify the efficient Java implementation of sequential
 . We obtain a largely automated proof using the KeY theorem prover [1] in part aided by external theory solvers (in particular Z3 [33]) and KeY ’s support for interactively guiding the proof construction process. This yields a full functional correctness proof of the full Java implementation of
. We obtain a largely automated proof using the KeY theorem prover [1] in part aided by external theory solvers (in particular Z3 [33]) and KeY ’s support for interactively guiding the proof construction process. This yields a full functional correctness proof of the full Java implementation of
 showing, for all possible inputs, sortedness, the permutation property, exception safety, memory safety, termination, and absence of arithmetic overflows. The complete 8-line specification of the toplevel sorting method can be seen in Fig. 1.
showing, for all possible inputs, sortedness, the permutation property, exception safety, memory safety, termination, and absence of arithmetic overflows. The complete 8-line specification of the toplevel sorting method can be seen in Fig. 1.
The verified code is available for downloadFootnote 1 and can easily be used in real-world Java applications (through the maven packaging mechanism). It spans over 900 lines of Java code with the main properties specified on 8 lines of JML, annotated with some 2500 lines of JML auxiliary annotations for prover guidance. The project required a total of 1 million proof steps (of which 4000 were performed manually) on 179 proof obligations (with one or more proof obligation per Java method). The project required about 4 person months.
The verification revealed a subtle bug in the original version, where the algorithm would not terminate if presented with an array containing the same single value many times.Footnote 2 This flaw was subsequently fixed. Moreover, the formal verification revealed that the code could be simplified at one point.
This case study demonstrates that competitive code hand-optimised for the application on modern processors can be deductively verified within a reasonable time frame. It resulted from a fruitful collaboration of experts in program verification and experts in algorithm engineering. An extended version of this paper [3] is available containing more in-depth information about the specification and verification.
2 Background
2.1 Formal Specification with the Java Modeling Language
The Java Modeling Language (JML) [22] is a behavioural interface specification language [15] following the paradigm of design-by-contract [29]. JML is the de-facto standard for the formal specification of Java programs. The main artefact of JML specifications are method contracts comprised of preconditions (specified via requires clauses), postconditions (ensures) and a frame condition (assignable) which describes the set of heap locations to which a method invocation is allowed to write. A contract specifies that, if a method starts in a state satisfying its preconditions, then it must terminate and the postcondition must be satisfied in the post-state of the method invocation. Additionally, any modified heap location already allocated at invocation time must lie within the specified assignable clause. Termination witnesses (measured_by clauses) are used to reason about the termination of recursive methods. Java loops can be annotated with invariants (loop_invariant), which must be true whenever the loop condition is evaluated, termination witnesses (decreases), and frame conditions (assignable) that limit the heap locations the loop body may modify. Loop specifications and method contracts of internal methods allow one to conduct proofs modularly and inductively.
Expressions in JML are a superset of side-effect-free Java expressions. In particular, JML allows the use of field references and the invocation of pure methods in specifications. JML-specific syntax includes first-order quantifiers (
 and
and
 ) and generalised quantifiers. One generalised quantifier is the construct
) and generalised quantifiers. One generalised quantifier is the construct
 which evaluates to the number of elements of type T that satisfy the condition \(\varphi \) (if that number is finite).
which evaluates to the number of elements of type T that satisfy the condition \(\varphi \) (if that number is finite).
 sums the expression e over all values of type T satisfying \(\varphi \). Quantifiers in JML support range predicates to constrain the bound variable; the expression
sums the expression e over all values of type T satisfying \(\varphi \). Quantifiers in JML support range predicates to constrain the bound variable; the expression
 is hence equivalent to
is hence equivalent to
 .
.
JML specifications are annotated in the Java source code directly and enclosed in special comments beginning with /*@ or //@ to allow them to be compiled by a standard Java compiler. JML supports the definition of verification-only (model and ghost) entities within JML comments that are only visible at verification time and do not influence runtime behaviour (see also Sec. 4.1).
Fig. 1 shows the specification of the top-level sort method as an example. Since that JML contract is labelled normal_behaviour, it requires (in addition to satisfying the pre-post contract) that the method does not terminate abruptly by throwing an exception.
2.2 Deductive Verification with the KeY System
The KeY verification tool [1] is a deductive theorem prover which can be used to verify Java programs against JML specifications. KeY translates JML specifications into proof obligations formalised in the dynamic logic [13] variant JavaDL, in which Java program fragments can occur within formulas. The JavaDL formula \(\varphi \rightarrow \langle \texttt {o.m();}\rangle \psi \) is similar to the total Hoare triple \([ \varphi ]\ \texttt {o.m();}\ [ \psi ]\), with both stating that the method invocation o.m() terminates in a state satisfying \(\psi \) if started in a state satisfying \(\varphi \). Proofs in KeY are conducted by applying inference rules in a sequent calculus. Using a set of inference rules for Java statements, the Java code (\(\langle \texttt {o.m()}\rangle \psi \) in the above statement) is symbolically executed such that the approach yields the weakest precondition for o.m() and \(\psi \) as a formula in first-order predicate logic. KeY can settle many proof obligations automatically, but also allows interactive rule application and invocation of external provers like satisfiability modulo theories (SMT) solvers.
3 Our Java Implementation of
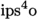
3.1 The Algorithm
In-place (parallel) super scalar sample sort (
 ), is a state-of-the-art general sorting algorithm [2]. Sample sorting can be seen as a generalisation of quick sort, where instead of choosing a single pivot to partition elements into two parts, we choose a sorted sequence of \(k-1\) splitters which define k buckets consisting of the elements lying between adjacent splitters. One advantage of this is the reduced recursion depth and the resulting better cache efficiency. “Super-scalar” refers to enabling instruction parallelism by avoiding branches and reducing data dependencies while classifying elements into buckets. “In-place” means that the algorithm needs only logarithmic space in addition to the input. Although
), is a state-of-the-art general sorting algorithm [2]. Sample sorting can be seen as a generalisation of quick sort, where instead of choosing a single pivot to partition elements into two parts, we choose a sorted sequence of \(k-1\) splitters which define k buckets consisting of the elements lying between adjacent splitters. One advantage of this is the reduced recursion depth and the resulting better cache efficiency. “Super-scalar” refers to enabling instruction parallelism by avoiding branches and reducing data dependencies while classifying elements into buckets. “In-place” means that the algorithm needs only logarithmic space in addition to the input. Although
 has a parallel version, this work is concerned with the sequential case.
has a parallel version, this work is concerned with the sequential case.
The algorithm works by recursively partitioning the input into buckets; when the sub-problems are small enough, they are sorted using insertion sort. The maximum number of buckets \(k_\text {max}\) and the base-case size, i.e., the maximum problem size for insertion sort, are configuration parameters. In our implementation, we chose \(k_\text {max} = 256\) and base-case size 128 experimentally. Partitioning consists of four steps: Sampling, classification, permutation, and cleanup.
Sampling. This step finds the splitters as equally spaced elements from a (recursively) sorted random sample of the current subproblem. There are special cases to handle small or skewed inputs. These are fully handled in our proof, but to simplify the exposition, we will assume in this summary that \(k=k_\text {max}\) distinctFootnote 3 splitters are found this way.
Classification. The goal of the classification step is two-fold: (1) to assign each element to one of the k buckets defined by the splitters, and (2) to presort elements into fixed-size blocks such that all elements in a block belong to the same bucket. To find the right bucket for each element, the largest splitter element smaller than that element must be identified. A number of algorithm engineering optimisations make the classification efficient: it is implemented using an implicit perfect binary search tree with logarithmic lookup complexity. Moreover, the tree data structure also supports an implementation without branching statements and unrolled loops that eliminates branch mispredictions and facilitates high instruction parallelism and the use of SIMD instruction. We will come back to this classification tree implementation in Sect. 4.2 where we discuss how this efficiency choice was dealt with in the formal proof.
After classification is done, the input array consists of blocks in which all elements belong to the same bucket, followed by some empty space, with the remaining elements still remaining in the (partially filled) buffers. The block size B is chosen experimentally to be 1 KiB. Fig. 2.b shows the output of this step.
Overview of all steps of
 : (a) input with elements classifying as the four classes blue, green, orange and red, (b) After classification (\(B=2\)); bucket sizes are indicated by brackets and white elements are empty, (c) after permutation, (d) the operations done by the cleanup step, (e) partitioned output.
: (a) input with elements classifying as the four classes blue, green, orange and red, (b) After classification (\(B=2\)); bucket sizes are indicated by brackets and white elements are empty, (c) after permutation, (d) the operations done by the cleanup step, (e) partitioned output.
Permutation. By now, it is known how many elements are in each bucket, and therefore where in the array each bucket begins and ends after partitioning is done. The objective of the permutation step is to rearrange the blocks so that each block starts in the correct bucket. Then, if the block is not already correctly placed, it is moved to its bucket, possibly displacing another (incorrectly placed) block, which is then similarly moved. Refer to Fig. 2.c for the state of the input array after this step.
Cleanup. In general, bucket boundaries will not coincide with block boundaries. Since the permutation step works on block granularity, there may be overlap where elements spill into an adjacent bucket. These elements are corrected in the cleanup step. In addition, the remaining elements in the buffers from the classification step are written back into the input array. Fig. 2.d shows an example of the steps performed during cleanup.
3.2 Algorithm Engineering for Java
While the original implementation of
 was written in C++, the verification target of this case study is a translation by one of the authors of the original code to Java. No performance-relevant compromises where made, e.g., to achieve easier verification. We started with a Java implementation as close as possible to the C++ implementation. We then performed profiling-driven tuning. Adjusting configuration parameters improved performance by 12%. The only algorithmically significant change resulting from tuning is when small sub-problems are sorted. In the C++ implementation this is done during cleanup in order to improve cache locality. In Java it turned out to be better to remove this special case, i.e., to sort all sub-problems in the recursion step. This improved performance by a further 4%.
was written in C++, the verification target of this case study is a translation by one of the authors of the original code to Java. No performance-relevant compromises where made, e.g., to achieve easier verification. We started with a Java implementation as close as possible to the C++ implementation. We then performed profiling-driven tuning. Adjusting configuration parameters improved performance by 12%. The only algorithmically significant change resulting from tuning is when small sub-problems are sorted. In the C++ implementation this is done during cleanup in order to improve cache locality. In Java it turned out to be better to remove this special case, i.e., to sort all sub-problems in the recursion step. This improved performance by a further 4%.
4 Specification and Verification
In this case study, the following properties of the Java
 implementation have been specified and successfully verified:
implementation have been specified and successfully verified:
-
Sorting Property: The array is sorted after the method invocation.
-
Permutation Property: The content of the input array after sorting is a permutation of the initial content.
-
Exception Safety: No uncaught exceptions are thrown.
-
Memory Safety: The implementation does not modify any previously allocated memory location except the entries of the input array.
-
Termination: Every method invocation terminates.
-
Absence of Overflows: During the execution of the method, no integer operation will overflow or underflow.
We assume that no out-of-memory or stack-overflow errors can ever occur at runtime. Since the algorithm is in-place, and the recursion depth is in
 , this is a reasonable assumption to make.
, this is a reasonable assumption to make.
Fig. 1 shows the JML specification of the entry method sort of the
 implementation, i.e., the top-level requirements specification of the sorting algorithm. The annotation normal_behaviour in line 1 specifies exception safety (i.e. the absence of both explicitly and implicitly thrown uncaught exceptions). Memory safety is required by the framing condition in line 5. The permutation and sorting property are formulated as postconditions in lines 3 resp. 4. Termination is a default specification case with JML (unless explicitly specified otherwise). The absence of overflows is not specified in JML, but is an option that can be switched on in KeY. The precondition in line 1 of the method contract ensures that there are no overflows and is of little practical restriction since it is very close to the maximum integer value (\(\texttt {MAX\_LEN} = 2^{31} - 256\)).
implementation, i.e., the top-level requirements specification of the sorting algorithm. The annotation normal_behaviour in line 1 specifies exception safety (i.e. the absence of both explicitly and implicitly thrown uncaught exceptions). Memory safety is required by the framing condition in line 5. The permutation and sorting property are formulated as postconditions in lines 3 resp. 4. Termination is a default specification case with JML (unless explicitly specified otherwise). The absence of overflows is not specified in JML, but is an option that can be switched on in KeY. The precondition in line 1 of the method contract ensures that there are no overflows and is of little practical restriction since it is very close to the maximum integer value (\(\texttt {MAX\_LEN} = 2^{31} - 256\)).
The implementation of Java
 comprises 900 lines of code, annotated with 2500 lines in JML. Besides the requirement specification, this comprises auxiliary specifications such as method contracts for (sub-)methods, class and loop invariants, function or predicate definitions and lemmata. We will focus on selected specification items and emphasise the algorithm’s classification step since it has sophisticated, interesting loop invariants that are at the same time comprehensible, exemplifying the techniques we were using.
comprises 900 lines of code, annotated with 2500 lines in JML. Besides the requirement specification, this comprises auxiliary specifications such as method contracts for (sub-)methods, class and loop invariants, function or predicate definitions and lemmata. We will focus on selected specification items and emphasise the algorithm’s classification step since it has sophisticated, interesting loop invariants that are at the same time comprehensible, exemplifying the techniques we were using.
4.1 Enabling KeY Features
A few advanced features of KeY were essential for completing the proof. They are needed to abstract from sophisticated algorithmic concepts and to decompose larger proofs into more manageable units.
We followed a mostly autoactive program verification approach [25] with as much automation as possible while supporting interactive prover guidance in form of source code annotations (e.g. assertions). This concept has been widely adapted throughout the program verification community [9, 24, 31, 35]. Most program verification tools only allow guidance by source code annotations. However, the KeY theorem prover also supports an interactive proof mode in which inference rules can be applied manually – and we resorted also to this way of proof construction where needed.
Model methods. Due to the scale of the project, it was useful to encapsulate important properties of the data structures into named abstract predicates or functions. The vehicle to formulate such abstraction in JML are model methods [32], which are side-effect free (pure) methods defined within JML annotations. For
 , around 100 different model methods were used.
, around 100 different model methods were used.
The benefits of using model methods are two-fold: (1) They structure and decompose specifications making them more comprehensible and (2) they simplify resp. enable automated verification by abstraction of the proof state. An example for a widely used (50 occurrences) model method is shown in Fig. 3.
Ghost fields and variables provide further abstractions from the memory state by defining verification-only memory locations. In the present case study, all Java classes except simple pure data containers required at least one ghost field. Sec. 4.2 reports a challenge were ghost variables and ghost code (i.e. assignments to ghost variables) made verification possible in the first place.
Assertions are the main proof-guidance tool in autoactive verification as they provide means to formulate intermediate proof targets that the automation can discharge more easily and that thus may provide a deductive chain completing the proof. This corresponds to making case distinctions or to introducing intermediate goals in a manual proof. In the present case study, assertions avoided many tedious interactive proof steps as the annotations in the source code guide the proof search such that it now runs automatically.
Block contracts. Much like method contracts, block contracts abstract from details in control flow and implementation details of a Java code block they annotate (similar to a method contract). Block contracts can decompose large and complex method implementation and allow one to focus on the relevant effects of individual components (i.e., code blocks) formalised in the postconditions of the block contracts.
4.2 Central Ideas Used in the Proofs of the Steps of
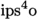
In this section we zoom in on a few central concepts from the proofs of the algorithm. We mainly focus on the classification step which (1) establishes the most relevant invariants of the recursion step, and (2) showcases a particular proof technique related to the verification of the efficient algorithm implementation used in this case study.
Relevant Invariants. During classification, the algorithm rearranges the input elements into blocks (of a given size B) such that all elements in a block are classified into the same bucket. Furthermore, it counts the elements in each bucket. Fig. 4 shows an intermediate state of the classification step. It is checked to which bucket the next element belongs, that bucket’s buffer is flushed if needed, and then the element is pushed to the buffer according to its classification. This is done in batches of m elements at once such that the classification can take advantage of batched queries (that allow the CPU to apply instruction parallelism).
After classifying all elements, the count of all elements in each bucket’s buffer is added to get the full element count for each bucket. We define the written slice to be the elements that were already flushed to the input array.
To exemplify the nature of the specification used in this case study, we discuss the inductive loop invariants of the classification loop which allowed us to close the proof for this step. Fig. 5 shows the corresponding JML annotationsFootnote 4.
-
1.
The buffers contain only bucket elements of their respective bucket.
-
2.
The written slice is made up of blocks of size B where each block contains only elements of exactly one bucket.
-
3.
The permutation property is maintained.
-
4.
The per bucket element counts are exactly the number of elements of the corresponding bucket in the written slice.
-
5.
The sum of all per bucket element counts equals the size of the written slice.
-
6.
The buffer size of each bucket is valid.
-
7.
The spacings are well formed:
-
(a)
The total element count in all buffers equals the length of the free slice.
-
(b)
The start offset of the current batch is a multiple of m.
-
(c)
The length of the written slice is a multiple of B.
-
(a)
Invariants 1 and 2 straightforwardly encode the block structure during classification from the abstract algorithm. They are also needed as preconditions for the following partitioning step. The permutation invariant 3 ensures that no elements are lost during classification by stating that the original array content is a permutation of the union of all elements not yet handled, the written slice and the union of all buffers. Invariants 4 and 5 are needed to show that the bucket element counts are correct and to show that all elements of the input will have been taken into account eventually. These invariants were engineered by translating the ideas from the abstract algorithm into the Java situation. The remaining two invariants were discovered later in the verification process: The validity invariant 6 was only discovered during the proof of the cleanup step (where it becomes relevant). A buffer is called valid, if (1) the number of elements written back during classification is a multiple of the block size B and (2) empty buffers are only allowed when nothing has yet been written back. Invariant 7 was discovered last by inspecting the open proof goals of failed attempts, and is mostly needed to show that write operations to the heap remain in bounds.
Invariant 5, while in principle derivable from the other invariants, simplifies the proof that the sum of all bucket element counts is the size of the input after termination. Adding it as a redundant loop invariant avoids having to prove the same statement repeatedly using the other invariants.
When flushing a buffer, the algorithm must not overwrite the batch that it is currently processing nor the elements that were not processed yet. This property is captured in invariant 7. First and foremost, 7a ensures that there is enough space to write a whole buffer if a buffer is full. When pushing the elements of the current batch to their buckets, the algorithm makes sure that the start of the batch will never be overwritten. However, this was not provable from the scope of this loop: For example, let there be B total elements in all buffers, all of which are in the buffer of some bucket b when we are trying to push the second element of a batch to b’s buffer. A flush may then happen before the push which would illegally overwrite the first element of the batch. This case is shown to be impossible by adding invariants 7b and 7c. In general, this holds for any values where B is a multiple of the batch size m.
Classification Search Tree. As mentioned in Sec. 3, classification employs an implicit binary search-tree data structure to find the bucket to which an element belongs. This is a complete binary tree where the root of a subtree stores the median of the splitters belonging to the subtree. The splitters are stored in an array with the root at index one. The children of the node stored at index i are stored at indices 2i and \(2i+1\). Fig. 6 shows the branch-free loop to compute the bucket c(e) for an element e.
It was difficult to verify this routine with hard to find loop invariants. On the other hand, an implementation using binary search on a linearly sorted array would have been easier to verify; but without the benefits of branch-freedom. Hence, this optimisation is an example where algorithm engineering decisions make verification more complicated. Our solution to the problem was to implement the binary search algorithm on the array of indices in parallel next to the efficient tree search by means of ghost variables and ghost code. A set of coupling invariants set the variables of heap and array into relation. Fig. 7 illustrates the relationship between the search in the binary heap and the search in the ghost code sorted index array.
Visualisation of finding the classification for an element; in the binary heap search tree (left) and in a linearly sorted array (right) for \(k=8\) buckets. The red path indicates the same classification as a path on the heap tree and a nesting of intervals for the binary search. The circled numbers indicate the index in the array representing the search tree; the italic numbers show the bucket number and the upright numbers the index of the splitters against which is compared.
Besides Classification. The algorithm’s initial step of drawing samples and determining the splitters to be used in the recursion step operates on a fixed number of elements such that most of the properties of this step can be shown by an exhaustive bounded analysisFootnote 5. The permutation and cleanup steps build upon the same general principles already established during classification, but require more and additional book keeping to relate different indices into the array. The implementation consists of four quadruply nested loops and the innermost loop has three different exit paths. Hence, verifying the permutation and cleanup part needed the most proof rule applications to close.
4.3 Selected Cross-cutting Concerns of the Proofs
While constructing the correctness proofs for
 , we made the following noteworthy observations.
, we made the following noteworthy observations.
Non-trivial termination proofs. For many algorithms, termination is an easy to show property. However, even though
 follows essentially an array-based divide-and-conquer strategy, its termination proofs are non-trivial. We exemplify this on the termination of the partitioning step.
follows essentially an array-based divide-and-conquer strategy, its termination proofs are non-trivial. We exemplify this on the termination of the partitioning step.
The textbook version of quicksort removes the splitter element (pivot) from the partitions. Hence, the partition size is a variant (termination witness) as each recursive call receives a strictly smaller slice to work on. For our
 implementation, however, this is not the case as the splitter elements remain within the partitions. It is the following observation that ensures termination: If there are two elements \(e_1, e_2\) in the input slice that are classified into two different buckets (\(c(e_1) \ne c(e_2)\)), then the number of elements in each bucket is strictly below the size of the input slice. While this observation may look trivial to a human reader, it requires a non-trivial interactive proof in KeY. One has to reason that for every bucket \(b_1\), there is a different non-empty bucket \(b_2\) implying that \(b_1\) is smaller than the input slice. This variant allows proving the termination of the recursion.
implementation, however, this is not the case as the splitter elements remain within the partitions. It is the following observation that ensures termination: If there are two elements \(e_1, e_2\) in the input slice that are classified into two different buckets (\(c(e_1) \ne c(e_2)\)), then the number of elements in each bucket is strictly below the size of the input slice. While this observation may look trivial to a human reader, it requires a non-trivial interactive proof in KeY. One has to reason that for every bucket \(b_1\), there is a different non-empty bucket \(b_2\) implying that \(b_1\) is smaller than the input slice. This variant allows proving the termination of the recursion.
Multiple variants of property formalisations. One important insight from the case study is that for some properties it pays off to have not one but two (or multiple) syntactically different, yet semantically equivalent formalisations at hand and to be able to use them at different places in the proofs. We give examples on sortedness and permutation properties.
Sortedness of an array can be expressed in first-order logic by either of the following equivalent formulae:
While (1) compares every array element with its successor, (2) allows comparison between arbitrary indices in the array. In the case study, when proving sortedness, (1) is used. However, when assuming sortedness in a proof (e.g., in preconditions), the transitive representation (2) is more useful. Technically, both representations are formulated as model methods and their equivalence has been shown using a simple inductive argument, which allowed us to switch between representations as needed.
A similar effect with two formalisation variations can be observed for the permutation property: For two sequences \(s_1, s_2\), the expression \(\texttt {seqPerm}(s_1, s_2)\) formulates that there exists a bijection \(\pi \) between the indices of \(s_1\) and \(s_2\) such that \(s_1[\pi (i)] = s_2[i]\) for all indices i. This straightforward formulation of the property using an explicit permutation witness \(\pi \) proved helpful to show statements like \(\sum _{i=0}^n s_1[i] = \sum _{i=0}^n s_2[i]\) under the assumption that \(s_1\) and \(s_2\) are permutations of one another. However, proving the permutation property using this definition can be difficult since one has to provide the explicit witness for \(\pi \). Therefore, an alternative formulation has been used based on the fact that two sequences are permutations of one another iff they are equal when considered as multisets, i.e., iff every element occurs equally often in both sequencesFootnote 6. The equivalence of the two notions is made available to KeY as an (proved) axiom.
Proving frame conditions. To reason that the memory footprints of different data structures do not overlap, KeY supports the concept of dynamic frames [18]. To be cache-efficient, the
 implementation uses a number of auxiliary buffers, realised as Java arrays. In the Java language, array variables may alias. In the case study, methods have up to 11 array parameters which all must not alias with each other. JML possesses an operator
implementation uses a number of auxiliary buffers, realised as Java arrays. In the Java language, array variables may alias. In the case study, methods have up to 11 array parameters which all must not alias with each other. JML possesses an operator
 which can be used to specify that the sets of memory locations provided as arguments must be disjoint. KeY then generates the (quadratically many) inequalities capturing the non-aliasing. KeY is not slowed down since all generated formulas are inequalities between identifiers. We used an auxiliary class to group all arrays for reuse during the recursion which reduced the required specification overhead. This shows that dynamic frames are an adequate formalism to deal with the framing problem for this type of algorithmic verification challenge.
which can be used to specify that the sets of memory locations provided as arguments must be disjoint. KeY then generates the (quadratically many) inequalities capturing the non-aliasing. KeY is not slowed down since all generated formulas are inequalities between identifiers. We used an auxiliary class to group all arrays for reuse during the recursion which reduced the required specification overhead. This shows that dynamic frames are an adequate formalism to deal with the framing problem for this type of algorithmic verification challenge.
Integer overflow. As mentioned above, KeY uses mathematical integers to model machine int values. For this to be sound, arithmetic expressions must not over- or underflow the ranges of their respective primitive type. We hence verified the absence of integer overflows in all methods proved in KeY. Corresponding assertions are automatically generated by KeY during symbolic execution: every arithmetic operation generates a new goal where the absence of overflow for this operation is checked. There were only a few lines of additional specification required. The overwhelming majority of those proofs closed without interactions since they could be derived from already proven invariants.
Performance and Verifiability. Optimisations to the code in the case study sometimes had an impact on the required effort to verify and sometimes did not: verifying the binary search tree optimisation explained in Sec. 4.2 was pretty costly whereas the reverification of the project after the optimisations mentioned in Sec. 3.2 went through pretty automatically. Both optimisations bought a noteworthy bit of performance. A key factor for the complexity of the verification is how much the optimisation modifies data representation.
4.4 Proof Statistics
Table 1 gives an overview of the size of the proofs in this case study. A rule application in the KeY system may be part of the symbolic execution of Java code, part of first-order or theory reasoning.
The overall ratio between specification and source code lines is about 3:1, which since many model methods were declared, is still quite low. Using models methods to formulate lemmas deduplicating the proofs allowed us to obtain an overall proof with only \(10^6\) steps. Consider in comparison a recent case study [5] performed with KeY: The numbers of branches and rule applications are in the same order of magnitude; but our case study has \(6\times \) as many the lines of code, and \(7\times \) as many lines of specification. However it also required twice the number of manual interactions.
The specification consists of 179 JML contracts of which 114 could be verified with fewer than ten manual interactions. However, some methods require extensive interaction. Most interactions were needed to prove the contract of a method wrapping an inner loop from the permutation stepwith 836 interactions and the cleanup method with 475. Those were also the biggest proofs for method contracts with about 125 000 and 110 000 rule applications, respectively. Without heavy usage of lemma methods, those proofs would have been multiple times larger. Notably, most of the interactions for constructing these proofs were unpacking model methods, using their contracts, simplifying the sequent and using observer dependencies, see Table 2.
5 Performance of the
 Java Version
Java Version
As our stated goal is an implementation that is both verified and has state-of-the-art efficiency, we performed experiments to measure the performance of our Java implementation of
 . Our experimental setup is similar to that of the original
. Our experimental setup is similar to that of the original
 paper [2] – in particular, we use all of the same input distributions in our evaluation:
paper [2] – in particular, we use all of the same input distributions in our evaluation:
-
Uniform: Values are pseudo-random numbers in
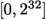 .
. -
Ones: All values are 1.
-
Sorted: Values are increasing.
-
Reversed: Values are decreasing.
-
Unsorted-Tail: Like Sorted, except the last
 elements are shuffled.
elements are shuffled. -
Almost-Sorted: Like Sorted, except
 random adjacent pairs are swapped.
random adjacent pairs are swapped. -
Exponential: Values are distributed exponentially.
-
RootDup: Sets
 .
. -
TwoDup: Sets
 , where
, where
 .
. -
EightDup: Sets
 , where
, where
 .
.
We performed experiments using OpenJDK 20 on three different machines/CPUs: An Intel i7 11700 at 4.8 GHz, an AMD Ryzen 3950X at 3.5 Ghz, and an Ampere Altra Q80-30 ARM processor at 3 GHz. We repeated each measurement multiple times and report the mean execution times of all iterations. For input sizes
 , we took 1000 measurements, for
, we took 1000 measurements, for
 we took 25 measurements, and for
we took 25 measurements, and for
 we took 5 measurements. In addition, we repeated the entire benchmark 5 times to get results across different invocations of the JVM. This means that there are between 25 and 5000 data points for each input size, distribution, and architecture.
we took 5 measurements. In addition, we repeated the entire benchmark 5 times to get results across different invocations of the JVM. This means that there are between 25 and 5000 data points for each input size, distribution, and architecture.
On all three machines,
 outperforms OpenJDK’s Arrays.sort() for int by a factor of 1.33 to 1.83 for large inputs on the Uniform distribution. These results can be found in Fig. 8. For comparison, Fig. 9 shows the runtimes, including the C++ implementation of
outperforms OpenJDK’s Arrays.sort() for int by a factor of 1.33 to 1.83 for large inputs on the Uniform distribution. These results can be found in Fig. 8. For comparison, Fig. 9 shows the runtimes, including the C++ implementation of
 , on the Intel machine.
, on the Intel machine.
Most other distributions show similar results (with a speedup factor of up to 2.27), with the exception of pre-sorted or almost sorted inputs. These distributions – which include Ones, Sorted, Reversed, and Almost-Sorted, but not Unsorted-Tail – are detected by the adaptive implementation of Arrays.sort() and are not actually sorted by the default dual-pivot quicksort, but by a specialised merging algorithm, which ends up doing almost no work on these distributions.
In summary, our experiments show that the verified Java implementation of
 outperforms the standard dual-pivot quicksort algorithm across a variety of input distributions and hardware. The same opportunistic merging algorithm currently implemented by Arrays.sort() could be used in conjunction with
outperforms the standard dual-pivot quicksort algorithm across a variety of input distributions and hardware. The same opportunistic merging algorithm currently implemented by Arrays.sort() could be used in conjunction with
 , which would shortcut the work in case the input is already (almost) sorted.
, which would shortcut the work in case the input is already (almost) sorted.
6 Related Work
JML and KeY have been used previously to verify sorting algorithms. Besides the verifications of nontrivial proof-of-concept implementations like Counting Sort and Radixsort [12], KeY has been used to verify the sorting algorithms deployed with OpenJDK: The formal analysis with KeY revealed a relevant bug in the TimSort implementation shipped with the JDK as the standard algorithm for generic data types [11]. A bugfix was proposed and it was shown that the fixed code does not throw exceptions (but sortedness or permutation were not shown). For the Dual Pivot Quicksort implementation of the JDK (used to sort arrays of primitive values), the sorting and permutation property were successfully specified and verified using KeY [4]. However, the complexity and size of those verification proofs are considerably smaller than our
 case study. Other pivotal classes of the JDK were also successfully verified using KeY [5, 16].
case study. Other pivotal classes of the JDK were also successfully verified using KeY [5, 16].
Lammich et al. [14, 20] verified efficient sorting routines by proving functional propertieson abstract high-level algorithmic descriptions in the Isabelle/HOL theorem prover and then refining them down to LLVM code. In that framework, even parallelised implementations can be analysed to some degree if no shared memory is used [21]. While the verified algorithms are on par with the performance of the standard library, they do not reach the efficiency of
 , and the authors explicitly list sample sorting as future work. Mohsen and Huisman [34] provide a general framework for the formal verification of swap-based sequential and parallel sorting routines, but restrict it to the analysis of the permutation property. Since
, and the authors explicitly list sample sorting as future work. Mohsen and Huisman [34] provide a general framework for the formal verification of swap-based sequential and parallel sorting routines, but restrict it to the analysis of the permutation property. Since
 is not entirely swap-based (due to the external buffers in the classification step), it is not covered by their approach.
is not entirely swap-based (due to the external buffers in the classification step), it is not covered by their approach.
There exists a large number of prominent algorithm verification case studies that focus on the challenges provided by the verification and do not consider the performance of the implementation [6,7,8, 17, 26,27,28, 30].
Finally, there are several large-scale verification projects like the verified microkernel L4.verified [19], the CertiOS framework [37] for the verification of preemptive OS kernels, or the verified Hypervisor Hyper-V [23] that easily top this case study w.r.t. both verified lines of code and invested person years. However, they target a completely different type of system to be verified and have their focus on operating-system-related challenges, like handling concurrent low-level data structures or concurrent accesses to resources. While they also address similar performance questions, the algorithmic aspects are considerably different
7 Conclusions and Future Work
We have demonstrated that a state-of-the-art sorting algorithm like
 can be formally verified starting directly with an efficient implementation that has not been modified to ease verification. The involved effort of several person months was considerable but seems worthwhile for a widely used basic toolbox function with potential to become part of the standard library of important programming languages. Parts of this verification or at least the basic approach can be reused for related algorithms like radix sort, semisorting, aggregation, hash-join, random permutations, index construction etc.
can be formally verified starting directly with an efficient implementation that has not been modified to ease verification. The involved effort of several person months was considerable but seems worthwhile for a widely used basic toolbox function with potential to become part of the standard library of important programming languages. Parts of this verification or at least the basic approach can be reused for related algorithms like radix sort, semisorting, aggregation, hash-join, random permutations, index construction etc.
Future work could look at parallel versions of
 or implementations that use advanced features such as vector-instructions (e.g., as in [36]). Of course, further basic toolbox components like collection classes (hash tables, search trees etc.) should also be considered.
or implementations that use advanced features such as vector-instructions (e.g., as in [36]). Of course, further basic toolbox components like collection classes (hash tables, search trees etc.) should also be considered.
On the methodology side it would be interesting to compare our approach of direct verification with approaches that start from a verified abstraction of the actual code that is later refined to an implementation. Besides the required effort for verification and the efficiency of the resulting code, a comparison should also consider the ease of communicating with algorithm engineers, which on the one hand may benefit from an abstraction but on the other hand is easier when based on their original implementation. Our case study involved both experts in program verification and experts in algorithm engineering, which proved essential to its success.
For much of the desirable future work, verification tools and methods need further development, in particular for efficient parallel programs and high-performance languages like C++ or Rust. It is also important to better support evolution of the implementation, since it is quite rare that one wants to keep an implementation over decades – algorithm libraries have to evolve with added functionality and changes in hardware, compilers or operating systems.
Notes
- 1.
at the github repository https://github.com/KeYProject/ips4o-verify
- 2.
The bug was latently present in the original C++-code also. However, it cannot occur when the default parameter values are used in C++.
- 3.
If equal splitters do appear, duplicates are removed and equality buckets are used that do not require recursive sorting. Details can be found in the extended version [3].
- 4.
In the actual implementation, the invariants are grouped in several model methods.
- 5.
The extended version [3] elaborates on this.
- 6.
which is a standard formalisation often used in proofs of sorting algorithms
References
Ahrendt, W., Beckert, B., Bubel, R., Hähnle, R., Schmitt, P.H., Ulbrich, M. (eds.): Deductive Software Verification - The KeY Book - From Theory to Practice, Lecture Notes in Computer Science, vol. 10001. Springer (2016). https://doi.org/10.1007/978-3-319-49812-6
Axtmann, M., Ferizovic, D., Sanders, P., Witt, S.: Engineering in-place (shared-memory) sorting algorithms. ACM Transaction on Parallel Computing 9(1), 2:1–2:62 (2022), see also github.com/ips4o. Conference version in ESA 2017
Beckert, B., Sanders, P., Ulbrich, M., Wiesler, J., Witt, S.: Formally verifying an efficient sorter, extended version. Tech. rep., Karlsruhe Institute of Technology (2024). https://doi.org/10.5445/IR/1000167846
Beckert, B., Schiffl, J., Schmitt, P.H., Ulbrich, M.: Proving JDK’s dual pivot quicksort correct. In: Working Conference on Verified Software: Theories, Tools, and Experiments. pp. 35–48. Springer (2017)
Boer, M.d., Gouw, S.d., Klamroth, J., Jung, C., Ulbrich, M., Weigl, A.: Formal specification and verification of JDK’s identity hash map implementation. In: International Conference on Integrated Formal Methods. pp. 45–62.Springer (2022)
Bottesch, R., Haslbeck, M.W., Thiemann, R.: A verified efficient implementation of the LLL basis reduction algorithm. In: LPAR-22. 22nd International Conference on Logic for Programming, Artificial Intelligence and Reasoning, Awassa, Ethiopia, 16-21 November 2018. pp. 164–180 (2018). https://doi.org/10.29007/xwwh
Broy, M., Pepper, P.: Combining algebraic and algorithmic reasoning: An approach to the schorr-waite algorithm. ACM Trans. Program. Lang. Syst. 4(3), 362–381 (1982). https://doi.org/10.1145/357172.357175
Bubel, R.: The Schorr-Waite-algorithm. In: Verification of Object-Oriented Software. The KeY Approach - Foreword by K. Rustan M. Leino, pp. 569–587 (2007). https://doi.org/10.1007/978-3-540-69061-0_15
Filliâtre, J., Paskevich, A.: Why3 - where programs meet provers. In: Programming Languages and Systems - 22nd European Symposium on Programming, ESOP 2013, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2013, Rome, Italy, March 16-24, 2013. Proceedings. pp. 125–128 (2013). https://doi.org/10.1007/978-3-642-37036-6_8
Frazer, W.D., McKellar, A.C.: Samplesort: A sampling approach to minimal storage tree sorting. Journal of the ACM (JACM) 17(3), 496–507 (1970)
de Gouw, S., de Boer, F.S., Bubel, R., Hähnle, R., Rot, J., Steinhöfel, D.: Verifying OpenJDK’s sort method for generic collections. Journal of Automated Reasoning 62(1), 93–126 (2019)
de Gouw, S., de Boer, F.S., Rot, J.: Verification of counting sort and radix sort. In: Deductive Software Verification - The KeY Book - From Theory to Practice, pp. 609–618 (2016). https://doi.org/10.1007/978-3-319-49812-6_19
Harel, D., Kozen, D., Tiuryn, J.: Dynamic Logic. MIT Press (2000)
Haslbeck, M.P.L., Lammich, P.: For a few dollars more: Verified fine-grained algorithm analysis down to LLVM. ACM Trans. Program. Lang. Syst. 44(3), 14:1–14:36 (2022). https://doi.org/10.1145/3486169
Hatcliff, J., Leavens, G.T., Leino, K.R.M., Müller, P., Parkinson, M.J.: Behavioral interface specification languages. ACM Comput. Surv. 44(3), 16:1–16:58 (2012). https://doi.org/10.1145/2187671.2187678
Hiep, H.A., Maathuis, O., Bian, J., de Boer, F.S., de Gouw, S.: Verifying OpenJDK’s linkedlist using key (extended paper). Int. J. Softw. Tools Technol. Transf. 24(5), 783–802 (2022). https://doi.org/10.1007/s10009-022-00679-7
Hubert, T., Marché, C.: A case study of C source code verification: the Schorr-Waite algorithm. In: Third IEEE International Conference on Software Engineering and Formal Methods (SEFM 2005), 7-9 September 2005, Koblenz, Germany. pp. 190–199 (2005). https://doi.org/10.1109/SEFM.2005.1
Kassios, I.T.: The dynamic frames theory. Formal Aspects Comput. 23(3), 267–288 (2011). https://doi.org/10.1007/s00165-010-0152-5
Klein, G., Elphinstone, K., Heiser, G., Andronick, J., Cock, D.A., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolanski, R., Norrish, M., Sewell, T., Tuch, H., Winwood, S.: seL4: formal verification of an OS kernel. In: Proceedings of the 22nd ACM Symposium on Operating Systems Principles 2009, SOSP 2009, Big Sky, Montana, USA, October 11-14, 2009. pp. 207–220 (2009). https://doi.org/10.1145/1629575.1629596
Lammich, P.: Efficient verified implementation of introsort and pdqsort. In: Automated Reasoning - 10th International Joint Conference, IJCAR 2020, Paris, France, July 1-4, 2020, Proceedings, Part II. pp. 307–323 (2020). https://doi.org/10.1007/978-3-030-51054-1_18
Lammich, P.: Refinement of parallel algorithms down to LLVM. In: 13th International Conference on Interactive Theorem Proving, ITP 2022, August 7-10, 2022, Haifa, Israel. pp. 24:1–24:18 (2022). https://doi.org/10.4230/LIPIcs.ITP.2022.24
Leavens, G.T., Poll, E., Clifton, C., Cheon, Y., Ruby, C., Cok, D., Müller, P., Kiniry, J., Chalin, P., Zimmerman, D.M., et al.: JML reference manual (2008)
Leinenbach, D., Santen, T.: Verifying the microsoft Hyper-V hypervisor with VCC. In: FM 2009: Formal Methods, Second World Congress, Eindhoven, The Netherlands, November 2-6, 2009. Proceedings. pp. 806–809 (2009). https://doi.org/10.1007/978-3-642-05089-3_51
Leino, K.R.M.: Accessible software verification with Dafny. IEEE Softw. 34(6), 94–97 (2017). https://doi.org/10.1109/MS.2017.4121212
Leino, K.R.M., Moskal, M.: Usable auto-active verification. Usable Verification Workshop, Redmond, WS (2010)
Mahboubi, A.: Proving formally the implementation of an efficient gcd algorithm for polynomials. In: Automated Reasoning, Third International Joint Conference, IJCAR 2006, Seattle, WA, USA, August 17-20, 2006, Proceedings. pp. 438–452 (2006). https://doi.org/10.1007/11814771_37
Medina-Bulo, I., Palomo-Lozano, F., Ruiz-Reina, J.: A verified common lisp implementation of Buchberger’s algorithm in ACL2. J. Symb. Comput. 45(1), 96–123 (2010). https://doi.org/10.1016/j.jsc.2009.07.002
Mehta, F., Nipkow, T.: Proving pointer programs in higher-order logic. In: Automated Deduction - CADE-19, 19th International Conference on Automated Deduction Miami Beach, FL, USA, July 28 - August 2, 2003, Proceedings. pp. 121–135 (2003). https://doi.org/10.1007/978-3-540-45085-6_10
Meyer, B.: Applying "design by contract". Computer 25(10), 40–51 (1992). https://doi.org/10.1109/2.161279
Mohan, A., Leow, W.X., Hobor, A.: Functional correctness of C implementations of Dijkstra’s, Kruskal’s, and Prim’s algorithms. In: Computer Aided Verification - 33rd International Conference, CAV 2021, Virtual Event, July 20-23, 2021, Proceedings, Part II. pp. 801–826 (2021). https://doi.org/10.1007/978-3-030-81688-9_37
Mommen, N., Jacobs, B.: Verification of C++ programs with VeriFast. CoRR abs/2212.13754 (2022). https://doi.org/10.48550/arXiv.2212.13754
Mostowski, W., Ulbrich, M.: Dynamic dispatch for method contracts through abstract predicates. LNCS Trans. Modul. Compos. 1, 238–267 (2016). https://doi.org/10.1007/978-3-319-46969-0_7
de Moura, L.M., Bjørner, N.S.: Z3: an efficient SMT solver. In: Tools and Algorithms for the Construction and Analysis of Systems, 14th International Conference, TACAS 2008, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2008, Budapest, Hungary, March 29-April 6, 2008. Proceedings. pp. 337–340 (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Safari, M., Huisman, M.: A generic approach to the verification of the permutation property of sequential and parallel swap-based sorting algorithms. In: Integrated Formal Methods - 16th International Conference, IFM 2020, Lugano, Switzerland, November 16-20, 2020, Proceedings. pp. 257–275 (2020). https://doi.org/10.1007/978-3-030-63461-2_14
Tschannen, J., Furia, C.A., Nordio, M., Polikarpova, N.: Autoproof: Auto-active functional verification of object-oriented programs. In: Tools and Algorithms for the Construction and Analysis of Systems - 21st International Conference, TACAS 2015, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2015, London, UK, April 11-18, 2015. Proceedings. pp. 566–580 (2015). https://doi.org/10.1007/978-3-662-46681-0_53
Wassenberg, J., Blacher, M., Giesen, J., Sanders, P.: Vectorized and performance-portable quicksort. Softw. Pract. Exp. 52(12), 2684–2699 (2022). https://doi.org/10.1002/spe.3142
Xu, F., Fu, M., Feng, X., Zhang, X., Zhang, H., Li, Z.: A practical verification framework for preemptive OS kernels. In: Computer Aided Verification - 28th International Conference, CAV 2016, Toronto, ON, Canada, July 17-23, 2016, Proceedings, Part II. pp. 59–79 (2016). https://doi.org/10.1007/978-3-319-41540-6_4
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2024 The Author(s)
About this paper
Cite this paper
Beckert, B., Sanders, P., Ulbrich, M., Wiesler, J., Witt, S. (2024). Formally Verifying an Efficient Sorter. In: Finkbeiner, B., Kovács, L. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2024. Lecture Notes in Computer Science, vol 14570. Springer, Cham. https://doi.org/10.1007/978-3-031-57246-3_15
Download citation
DOI: https://doi.org/10.1007/978-3-031-57246-3_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-57245-6
Online ISBN: 978-3-031-57246-3
eBook Packages: Computer ScienceComputer Science (R0)





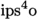




 Java Version
Java Version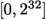 .
. elements are shuffled.
elements are shuffled. random adjacent pairs are swapped.
random adjacent pairs are swapped. .
. , where
, where
 .
. , where
, where
 .
.
 over
over 
