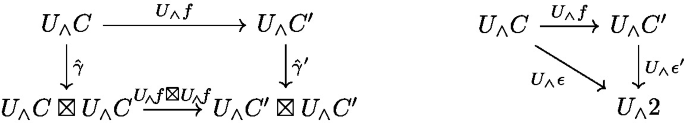Monoidal Extended Stone Duality

Abstract

Extensions of Stone-type dualities have a long history in algebraic logic and have also been instrumental for proving results in algebraic language theory. We show how to extend abstract categorical dualities via monoidal adjunctions, subsuming various incarnations of classical extended Stone and Priestley duality as a special case. Guided by these categorical foundations, we investigate residuation algebras, which are algebraic models of language derivatives, and show the subcategory of derivation algebras to be dually equivalent to the category of profinite ordered monoids, restricting to a duality between boolean residuation algebras and profinite monoids. We further extend this duality to capture relational morphisms of profinite ordered monoids, which dualize to natural morphisms of residuation algebras.

All authors are supported by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project 470467389

1 Introduction

Marshall H. Stone’s representation theorem for boolean algebras, the foundation for the so called Stone duality between boolean algebras and Stone spaces, manifests a tight connection between logic and topology. It has thus become an ubiquitous tool in various areas of theoretical computer science, not only in logic, but also for example in domain theory and automata theory.

From algebraic logic arose the need for extending Stone duality to capture boolean algebras equipped with additional operators (modelling quantifiers or modalities). Originating in Jónsson and Tarski’s representation theorem for boolean algebras with operators [21, 22], a representation in the spirit of Stone was proven by Halmos [17]; the general categorical picture of the duality of Kripke frames and modal algebras is based on an adjunction between operators and continuous relations developed by Sambin and Vaccaro [31].

In the study of regular languages, the need for extensions of Stone duality was not discovered until this millenium: while Pippenger [27] has already shown that the boolean algebra of regular languages on an alphabet $\varSigma$ corresponds, under Stone duality, to the Stone space $\widehat{\varSigma ^{*}}$ of profinite words, Gehrke et al. [15] discovered that, under Goldblatt’s form of extended Priestley duality [16], the residuals of language concatenation dualize to multiplication on the space of profinite words. But while categorical frameworks have identified Stone-type dualities to be one of the cornerstones of algebraic language theory [30, 36], the correspondence between residuals and multiplication via extended duality has not yet been placed in the categorical big picture. One reason is that, despite some progress in recent years [6, 18], extended (Stone) dualities for (co-)algebras are themselves not fully understood as instances of a crisp categorical idea.

Therefore we introduce as our first main contribution a simple, yet powerful framework to extend any categorical duality $\textbf{C} \simeq ^{\textrm{op}}\mathbf {\hat{C}}$ via monoidal adjunctions: For a given adjunction on $\textbf{C}$ with a strong monoidal right adjoint $U$ we prove a dual equivalence between the category of $U$-operators on $\textbf{C}$ to dual operators in the Kleisli category of the monad on $\mathbf {\hat{C}}$ arising from the dual of the given adjunction. We show how to instantiate the abstract extended duality to Priestley duality, which not only recovers Goldblatt’s original duality for distributive lattices with operators [16] but also applies more generally to bialgebraic operators with relational morphisms. Guided by our categorical foundations for extended Stone duality we investigate the correspondence between language derivatives and multiplication of profinite words in the setting of residuation algebras originally studied by Gehrke [14]. The key observation is that on finite distributive lattices the residuals are equivalent to a coalgebraic operator on the lattice, and we show how to lift this correspondence to locally finite structures, i.e. structures built up from finite substructures. By identifying suitable non-full subcategories – derivation algebras and locally finite comonoids, respectively – and an appropriate definition of morphism for residuation algebras, we augment Gehrke’s characterization of Stone-topological algebras in terms of residuation algebras to a duality between the categories of derivation algebras and that of profinite ordered monoids:

$$\begin{aligned} \textbf{Der} \cong \textbf{Comon} _{\textrm{lf}} \simeq ^{\textrm{op}}\textbf{ProfOrdMon}. \end{aligned}$$

(1.1)

The above duality clarifies the relation between Gehrke’s results and the duality by Rhodes and Steinberg [29] between profinite monoids and counital boolean bialgebras. The extended duality now suggests that the dual equivalence between profinite ordered monoids on one side and locally finite comonoids as well as derivation algebras on the other side extends to a more general duality capturing morphisms of relational type of profinite ordered monoids. To this end, we identify a natural notion of relational morphism for residuation algebras and comonoids, and use our abstract extended duality theorem to obtain the dual equivalence

$$\begin{aligned} \textbf{RelDer} \cong \textbf{RelComon} _{\textrm{lf}} \simeq ^{\textrm{op}}\textbf{RelProfOrdMon} \end{aligned}$$

which extends (1.1) to relational morphisms. To our knowledge, this is the first duality result for relational morphisms of profinite monoids, which have become an ubiquitous tool in algebraic language theory [26] and semigroup theory [29]. Full proof details can be found in the full version [5] of this paper.

Related Work. Duality for (complete) boolean algebras with operators goes back to Jónsson and Tarski [21, 22]. This duality was refined by the topological approach via Stone spaces taken by Halmos [17], which allowed to characterize the relations arising as the duals of operators, namely boolean relations. Halmos’ duality was extended to distributive lattices with ($n$-ary) operators by Goldblatt [16] and Cignoli [7]. Kupke et al. [24] recognized that boolean relations elegantly describe descriptive frames as coalgebras for the (underlying functor of) the Vietoris monad on Stone spaces; notions of bisimulation for these coalgebras were investigated by Bezhanishvili et al. [2]. Bosangue et al. [6] introduced a framework for dualities over distributive lattices equipped with a theory of operators for a signature, which are dual to certain coalgebras. Hofmann and Nora [18] have taken a categorical approach to extend natural dualities to algebras for a signature equipped with unary operators preserving only some of the operations prescribed by the signature; they relate these to coalgebras for (the underlying functor of) a suitable monad $T$. In their framework $T$ is a parameter required to satisfy certain conditions for the duality to work, while in our work T is already determined by the adjunction. The recent work by Bezhanishvili et al. [1] clarifies the relation between free constructions on distributive lattices and the different versions of the Vietoris monad to derive several dualities between distributive lattices with different types of operators and their corresponding Priestley relations.

Residuated boolean algebras, i.e. boolean algebras with a residuated binary operator,were explicitly considered by Jónsson and Tsinakis [23] to highlight the roles of the residuals in relation algebra. Gehrke et al. [15] discovered the connection between the residuals of the concatenation of regular languages and the multiplication on profinite words and investigated applications to automata theory, most notably a duality-theoretic proof of Eilenberg’s variety theorem [8]. The duality theory behind the correspondence of general residuation algebras and Priestley-topological algebras was given via canonical extensions [11, 12] and Goldblatt’s extended Stone duality [16] by Gehrke [14]. She has also provided conditions under which the dual relations of the residuals is functional; Fussner and Palmigiano [10] have shown that functionality of the dual relation is not equationally definable in the language of residuation algebras.

2 Preliminaries

Readers are assumed to be familiar with basic category theory, such as functors, natural transformations, adjunctions and monoidal categories [25]. We briefly recall the foundations of Stone duality [34] and Priestley duality [28]. By the latter we mean the dual equivalence $\textbf{DL} \simeq ^{\textrm{op}}\textbf{Priest}$ between the category $\textbf{DL}$ of bounded distributive lattices and lattice homomorphisms, and the category $\textbf{Priest}$ of Priestley spaces (ordered compact topological spaces in which for every $x\not \le y$ there exists a clopen up-set containing x but not y) and continuous monotone maps. The duality sends a distributive lattice D to the pointwise-ordered space $\textbf{DL} (D, 2)$ of homomorphisms into the two-element lattice (equivalently prime filters, ordered by inclusion), and topologized via pointwise convergence. In the reverse direction, it sends a Priestley space X to the distributive lattice $\textbf{Priest} (X, 2)$ of continuous maps into the two-element poset $2=\{0\le 1\}$ with discrete topology (equivalently clopen upsets), with the pointwise lattice structure. Priestley duality restricts to Stone duality $\textbf{BA} \simeq ^{\textrm{op}}\textbf{Stone}$ between the full subcategories $\textbf{BA}$ of boolean algebras and $\textbf{Stone}$ of Stone spaces (discretely ordered Priestley spaces). Moreover, it restricts to Birkhoff duality [3] $\textbf{DL} _{\textrm{f}} \simeq ^{\textrm{op}}\textbf{Pos} _{\textrm{f}}$ between finite distributive lattices and finite posets, sending a finite distributive lattice to its poset of join-irreducibles and a poset to its lattice of upsets – note that the pointwise order on homorphisms induces the reverse order on join-irreducibles. For a comprehensive introduction to ordered structures and their dualities, see the first two chapters of the classic textbook by Johnstone [20].

3 Extending Dualities

We present the first contribution of our paper, a general categorical framework for extending Stone-type dualities via monoidal adjunctions, motivated by the extension of Priestley duality to operators due to Goldblatt [16] recovered in Section 4. It serves as the basis for our duality results in the next two sections.

Notation 3.1

• (1) For $U :\textbf{C} \rightarrow \textbf{D}$ being right adjoint to $F :\textbf{D} \rightarrow \textbf{C}$ we write . We denote the unit and counit by $\eta$ and $\varepsilon$ and the transposing isomorphisms by

  

• (2) For dually equivalent categories $\textbf{C}$ and $\hat{\textbf{C}}$ we denote the equivalence functors in both directions by $(\hat{-}):\textbf{C} \xrightarrow {\simeq } \mathbf {\hat{C}}$ and $(\hat{-}):\mathbf {\hat{C}} \xrightarrow {\simeq } \textbf{ C}$. Moreover, if if $F :\textbf{C} \rightarrow \textbf{D}$ is a functor and $\mathbf {\hat{D}}$ is dual to $\textbf{D}$, we denote its dual by $\hat{F} = (\hat{-}) \circ F \circ (\hat{-}) :\hat{\textbf{C}} \rightarrow \hat{\textbf{D}}$.

• (3) The Kleisli category of a monad $(T,\eta ,\mu )$ on $\textbf{C}$ is denoted by $\textbf{C} _{T}$. It has the same objects as $\textbf{C}$ and $\textbf{C} _{T}(X, Y) = \textbf{C} (X, TY)$ with Kleisli composition $g \circ f = \mu \cdot Tg \cdot f$. A morphism $f :C \rightarrow T D$ of the Kleisli category is pure if $f=\eta \cdot f'$ for some $f':C \rightarrow D$ in $\textbf{C}$. (We omit the components of $\eta$ and $\mu$.)

Assumptions 3.2

We fix monoidal categories $\textbf{C}, \textbf{D}$ with dually equivalent categories $\mathbf {\hat{C}}, \mathbf {\hat{D}}$; we regard $\mathbf {\hat{C}}, \mathbf {\hat{D}}$ as monoidal categories with tensor products $\hat{\otimes }$ dual to the tensor products $\otimes$ of $\textbf{C}, \textbf{D}$. Moreover, we fix an adjunction with unit $\eta :{{\,\mathrm{\textrm{Id}}\,}}\rightarrow UF$ and counit $\varepsilon :FU \rightarrow {{\,\mathrm{\textrm{Id}}\,}}$, and assume that $U$ is a strong monoidal functor with associated natural isomorphisms $\lambda :UX \otimes UY \cong U(X \otimes Y)$ and $\epsilon :I_{\textbf{D}} \cong UI_{\textbf{C}}$. One can extend $\lambda$ to an isomorphism $\lambda :\bigotimes _{i=1}^{n} UX_{i} \cong U(\bigotimes _{i=1}^{n}X_{i})$ for all finite n. The dual functor $\hat{U} :\hat{\textbf{C}} \rightarrow \hat{\textbf{D}}$ is a strong monoidal left adjoint to $\hat{F}$ and the unit and counit of this dual adjunction are $\hat{\varepsilon }$ and $\hat{\eta }$. We denote the monad dual to the comonad $FU$ by $T = \hat{F}\hat{U}$ with unit $e = \hat{\varepsilon } :{{\,\mathrm{\textrm{Id}}\,}}\rightarrow T$ and multiplication $m = \hat{F}\hat{\eta }\hat{U} :TT \rightarrow T$.

Remark 3.3

Since $\hat{U}$ is strong monoidal with ${\hat{\epsilon }} :\hat{I}_{\textbf{D}} \cong \hat{U} \hat{I}_{\textbf{C}}$ and $\hat{\lambda } :\hat{U}X \hat{\otimes } \hat{U}Y \cong \hat{U}(X \hat{\otimes } Y)$ its right adjoint $\hat{F}$ is (lax) monoidal (see e.g. [32, p. 17]) with

$$\begin{aligned} ((\hat{\eta } \hat{\otimes } \hat{\eta }) \cdot \hat{\lambda }^{-1})^{-} :\hat{F}X \hat{\otimes } \hat{F}Y \rightarrow \hat{F}(X \hat{\otimes } Y) \quad {\text {and}} \quad (\hat{\varepsilon }^{-1})^{-} :\hat{I}_{\textbf{C}} \rightarrow \hat{F} \hat{I}_{\textbf{D}}. \end{aligned}$$

This makes $\hat{U} \dashv \hat{F}$ a monoidal adjunction, which then induces a monoidal monad $T = \hat{F}\hat{U}$ on $\mathbf {\hat{C}}$. Let $\delta :TX {\hat{\otimes }} T Y \rightarrow T(X {\hat{\otimes }} Y)$ denote the witnessing natural transformation, which also extends to any arity. The tensor product ${\hat{\otimes }}$ of $\mathbf {\hat{C}}$ lifts to the Kleisli category $\mathbf {\hat{C}} _{T}$; the lifting sends a pair $(f:X \rightarrow TY, g:X'\rightarrow TY')$ of $\mathbf {\hat{C}} _{T}$-morphisms to the $\mathbf {\hat{C}} _{T}$-morphism $\delta \cdot (f{\hat{\otimes }} g) :X {\hat{\otimes }} X' \rightarrow TY {\hat{\otimes }} TY' \rightarrow T(Y {\hat{\otimes }} Y')$. This makes $\mathbf {\hat{C}} _T$ itself a monoidal category [33, Prop. 1.2.2] with tensor $\hat{\otimes }$ and the canonical left adjoint $J_T:\mathbf {\hat{C}} \rightarrow \mathbf {\hat{C}} _T$ a strict monoidal functor.

Definition 3.4

Let $G:{\textbf{A}}\rightarrow {\textbf{B}}$ be a functor between monoidal categories, and let $m, n \in \mathbb {N}$. An $(m, n)$-ary $G$-operator consists of an object $A \in \textbf{A}$ and a morphism $a :(GA)^{\otimes m} \rightarrow (GA)^{\otimes n}$ of $\textbf{B}$. An $(m, n)$-ary $G$-operator morphism from $(A, b)$ to $(B, b)$ is a morphism $h:GA\rightarrow GB$ of $\textbf{B}$ such that

commutes. The category of $(m, n)$-ary $G$-operators is denoted by ${{\,\mathrm{\textrm{Op}}\,}}_{G}^{m, n}( \textbf{A} )$. We call $(m, 1)$-ary $G$-operators $G$-algebras and $(1, n)$-ary $G$-operators $G$-coalgebras. If $G$ is strong monoidal we call an operator pure if it is of the form $\lambda ^{-1} \cdot Ga' \cdot \lambda$, for $\lambda$ analogous to Assumptions 3.2, and an operator morphism pure if it is of the form $Gh'$.

Note that the full subcategory of $\textbf{B}$ consisting of the objects in the image of $G$ fully embeds into ${{\,\mathrm{\textrm{Op}}\,}}_{G}^{1,1}(\textbf{A})$ via $GA \mapsto (GA, \textrm{id}_{GA})$.

Theorem 3.5

(Abstract Extended Duality). The category of $(m, n)$-ary $U$-operators is dually equivalent to the category of $(n, m)$-ary $J_T$-operators:

$$\begin{aligned} {{\,\mathrm{\textrm{Op}}\,}}_{U}^{m, n}(\textbf{C}) \simeq ^{\textrm{op}}{{\,\mathrm{\textrm{Op}}\,}}_{J_T}^{n, m}(\mathbf {\hat{C}}). \end{aligned}$$

Proof

(Sketch). The functor ${{\,\mathrm{\textrm{Op}}\,}}_{J_{T}}^{n, m}(\mathbf {\hat{C}}) \rightarrow {{\,\mathrm{\textrm{Op}}\,}}_{U}^{m, n}(\textbf{C})$ is defined as follows. An object of ${{\,\mathrm{\textrm{Op}}\,}}_{J_{T}}^{n, m}(\mathbf {\hat{C}})$ is an operator $\hat{a} :\hat{A}^{\hat{\otimes } n} \rightarrow T \hat{A}^{\hat{\otimes } m}$. By dualization, transposition and conjugation with $\lambda$ it is mapped to

$$\lambda ^{-1} \cdot a^{-} \cdot \lambda :(UA)^{\otimes m} \cong UA^{\otimes m} \rightarrow UA^{\otimes n} \cong (UA)^{\otimes n}.$$

An operator morphism $\hat{f} :(\hat{A}, \hat{a}) \rightarrow (\hat{B}, \hat{b})$ is mapped to $f^{-} :UB \rightarrow UA$, the dual of its transpose; a diagram chase shows that this is indeed an operator morphism. One then proves that this yields a dual equivalence    $\square$

An advantage of extending dualities via adjunctions is that adjunctions compose, making the extensions modular: let $\textbf{E}$ be a monoidal category with monoidal adjunctions and splitting $F \dashv U$, i.e., $F = F_{1} F_{2}$ and $U = U_{2}U_{1}$ and $\lambda = U_{2} \lambda _{1} \cdot \lambda _2U_{1}$. Then the following lifting property applies to operators (set $A=B$) as well as operator morphisms (set $m=n=1$):

Proposition 3.6

A morphism $a :(UA)^{\otimes m} \rightarrow (UB)^{\otimes n}$ in $\textbf{D}$ lifts to a morphism $b :(U_{1}A)^{\otimes m} \rightarrow (U_{1}B)^{\otimes n}$ with $a = \lambda _{2}^{-1} \cdot U_{2} b \cdot \lambda _{2}$ iff the dual of $a$ factors through the canonical monad morphism $\hat{F_{1}}\hat{\varepsilon }_{2}\hat{U_{1}} :T_{1} \rightarrow T$, where $T_1=\hat{F_1} \hat{U}_1$.

Remark 3.7

• (1) A special case of Proposition 3.6 proves that extended dualities preserve purity: splitting $F \dashv U$ into $F_{1} = {{\,\mathrm{\textrm{Id}}\,}}\dashv {{\,\mathrm{\textrm{Id}}\,}}= U_{1}$ and $F_{2}= F \dashv U = U_{2}$ we see that a $U$-operator (or operator morphism) $a$ is pure iff its dual $f$ is pure as a Kleisli morphism, i.e. factors through the unit $e$ of $T$.

• (2) The right adjoint $U_{2}$ often is faithful and in this case $\hat{F_{1}}\hat{\varepsilon }_{2}\hat{U_{1}}$ is monic, i.e. $T_{1}$ is a submonad of $T$: faithfulness of $U_{2}$ is equivalent to having an epic counit $\varepsilon _{2}$, hence $\hat{\varepsilon }_{2}\hat{U}_{1}$ is mono, and the right adjoint $\hat{F_{1}}$ preserves monos. In particular, if $T$ is “powerset-like”, then $\hat{\textbf{C}}_{T}$ is a category of relations, and we think of U-operators (or operator morphisms) of the form $a = \lambda _{2}^{-1} \cdot U_{2}b \cdot \lambda _{2}$ as dualizing to “more functional” relations. The examples of Section 4.2 illustrate this idea.

4 Example: Extended Priestley Duality

As a first application of our adjoint framework, we investigate the classical Priestley duality (Section 2) and derive a generalized version of Goldblatt’s duality [16] between distributive lattices with operators and relational Priestley spaces. We instantiate (3.1) to the following categories and functors, which we will subsequently explain in detail:

Categories The upper duality is Hofman-Mislove-Stralka duality [19] between the category of join-semilattices with bottom and the category of Stone semilattices (i.e. topological join-semilattices with bottom whose underlying topological space is a Stone space) and continuous semilattice homomorphisms. The duality maps a join-semilattice $J$ to the Stone semilattice $\textbf{JSL} (J, 2)$ of semilattice homomorphisms into the two-element semilattice, topologized by pointwise convergence. Equivalently, $\textbf{JSL} (J, 2)$ is the space ${{\,\textrm{Idl}\,}}(J)$ of ideals (downwards closed and upwards directed subsets) of $J$, ordered by reverse inclusion, with topology generated by the subbasic open sets $\sigma (j) = \{I \in {{\,\textrm{Idl}\,}}(J) \mid j \in I\}$ and their complements for $j \in J$. In the other direction, a Stone semilattice $X$ is mapped to its semilattice $\textbf{StoneJSL} (X, 2)$ of clopen ideals, ordered by inclusion.

Functors The functor $U :\textbf{DL} \rightarrow \textbf{JSL}$ is the obvious forgetful functor. Its left adjoint $F :\textbf{JSL} \rightarrow \textbf{DL}$ maps a join-semilattice to the set $\mathcal {U}_{\textrm{fg}}^{\circ }(J)$ of finitely generated upsets of $J$ ordered by reverse inclusion. The dual right adjoint $\hat{F}$ of the left adjoint $F$ is the forgetful functor mapping a Stone semilattice to its underlying Priestley space. Indeed, as $U2 = 2$ we compute for the underlying Priestley space $|X|$ of a Stone semilattice $X$ that

$$\hat{F} X = \textbf{DL} (F(\textbf{StoneJSL} (X, 2)), 2) \cong |\textbf{JSL} (\textbf{StoneJSL} (X, 2), U2)| \cong |X|,$$

and this bijection is a homeomorphism. Its left adjoint $\hat{U} :\textbf{Priest} \rightarrow \textbf{StoneJSL}$ maps a Priestley space $X$ to the space

$$\widehat{U \hat{X}} = \textbf{JSL} (U(\textbf{Priest} (X, 2)), 2) \cong {{\,\textrm{Idl}\,}}({{\,\mathrm{\textrm{Cl}}\,}}_{\uparrow } X) \cong \mathbb {V}_{\!\downarrow }X$$

of ideals of clopen upsets of $X$. This space is isomorphic to the (downset) Vietoris hyperspace $\mathbb {V}_{\!\downarrow }X$ of $X$ that has as carrier the set of closed downsets of $X$. The isomorphism ${{\,\textrm{Idl}\,}}({{\,\mathrm{\textrm{Cl}}\,}}_{\uparrow }X) \cong \mathbb {V}_{\!\downarrow }X$ maps an ideal $I$ to the intersection $\bigcap _{U \in I} X \setminus U$; its inverse sends a closed downset $C$ to the ideal $\{U \in {{\,\mathrm{\textrm{Cl}}\,}}_{\uparrow }X \mid C \subseteq X \setminus U\}$ of complements of the basic clopen downsets that contain it. The topology of pointwise convergence on $\textbf{JSL} (U(\textbf{Priest} (X, 2)), 2)$ translates to the hit-or-miss topology on $\mathbb {V}_{\!\downarrow }X$ generated by the subbasic open sets

$$ \{A \subseteq X \text { closed } \mid A \cap U \ne \emptyset \} \quad {\text {for}} \quad U \in {{\,\mathrm{\textrm{Cl}}\,}}_{\uparrow }X$$

and their complements. For a detailed exposition of these results we refer the reader to the recent work by Bezhanishvili et al. [1]; the free join-semilattice structure on $\mathbb {V}_{\!\downarrow }X$ was already observed by Johnstone [20, Sec. 4.8]. The unit $e :X \rightarrow \mathbb {V}_{\!\downarrow }X$ of the Vietoris monad is given by $x \mapsto {\downarrow }x$ and multiplication is given by union [18]. The monad $\mathbb {V}_{\!\downarrow }$ restricts to the full subcategory $\textbf{Stone}$ of Stone spaces. We denote the restriction of this monad simply by $\mathbb {V}$.

Remark 4.1

(Continuous Relations). Continuous maps in $\textbf{Priest}$ of the form $\rho :X \rightarrow \mathbb {V}_{\!\downarrow }Y$ have a variety of names, we use the term Priestley relation as in [7, 16] or Stone relation if $X, Y$ are Stone spaces. We write $x\mathbin {\rho } y$ for $y\in \rho (x)$, and sometimes identify $\rho$ with a subset of $X\times Y$. Let us note that some authors (e.g. [29]) call a relation $R\subseteq X\times Y$ between topological spaces continuous if it is closed as a subspace of $X\times Y$. Every Priestley relation is continuous, but a continuous relation between Priestley spaces is generally not a Priestley relation.

Monoidal Structure The category $\textbf{JSL}$ of join-semilattices has a tensor product $\otimes$ with the universal property that it extends join-bilinear maps:

$$\begin{aligned} \textrm{Bilin}(J\times J', K) \cong \textbf{JSL} (J \otimes J', K). \end{aligned}$$

Join-bilinear maps $J\times J'\rightarrow K$ and their corresponding $\textbf{JSL}$-morphisms $J\otimes J'\rightarrow K$ are often tacitly identified. The tensor product $\otimes$ makes $\textbf{JSL}$ a monoidal category with unit $2$, i.e. $2 \otimes J \cong J$. The tensor product has a representation by the generators $\{j \otimes j' \mid j \in J, j' \in J'\}$ and relations

$$\begin{aligned} j \otimes 0 = 0 \otimes j' = 0, \quad (j_{1} \vee j_{2})\otimes k = j_{1} \otimes k \vee j_{2} \otimes k \quad \text {and}\quad j \otimes (k_{1} \vee k_{2}) = j \otimes k_{1} \vee j \otimes k_{2}. \end{aligned}$$

We call generating elements $j \otimes j'$ pure tensors. If $D, D'$ are bounded distributive lattices then so is $UD \otimes UD'$ [9], with meet given on pure tensors as $(d \otimes d') \wedge (e \otimes e') = (d \wedge e) \otimes (d' \wedge e')$. The lattice $UD \otimes UD'$ moreover is the coproduct of $D, D'$ in $\textbf{DL}$: the coproduct injections are $\iota (d) = d \otimes 1'$ and $\iota '(d') = 1 \otimes d'$ for $d \in D, d' \in D'$, and the copairing of lattice homomorphisms $f :D \rightarrow E, f' :D' \rightarrow E$ is given by the extension of the join-bilinar map

$$\begin{aligned} \wedge \cdot (f \times f') :D \times D' \rightarrow E,\qquad (d, d') \mapsto f(d)\wedge f(d'). \end{aligned}$$

Taking coproducts yields a monoidal structure on $\textbf{DL}$ and since $U(D + D') = UD \otimes UD'$ the functor $U$ is strong monoidal. The dual monoidal structure on $\textbf{Priest}$ takes binary products, and the natural transformation $\delta$ of Remark 3.3 is the expected product of sets

$$\begin{aligned} \delta :\mathbb {V}_{\!\downarrow }X \times \mathbb {V}_{\!\downarrow }Y \rightarrow \mathbb {V}_{\!\downarrow }(X \times Y), \qquad (C, D) \mapsto C \times D. \end{aligned}$$

Spelling out Definition 3.4, the category ${{\,\mathrm{\textrm{Op}}\,}}_{J_{\mathbb {V}_{\!\downarrow }}}^{n,m}(\textbf{Priest})$ is given as follows:

Definition 4.2

A ($(n, m)$-ary) relational Priestley space consists of a carrier Priestley space $X$ and a Priestley relation $\rho :X^{n} \rightarrow \mathbb {V}_{\!\downarrow }X^{m}$. A relational morphism from a relational Priestley space $(X, \rho )$ to $(X', \rho ')$ is given by a Priestley relation $\beta :X \rightarrow \mathbb {V}_{\!\downarrow }Y$ such that, for all $\textbf{x} \in X^{n}, \textbf{y} \in X^{m}, \textbf{y}' \in X'^{m}$,

$$ \textbf{x} \mathrel {\rho } \textbf{y} \wedge (\forall i :y_{i} \mathrel {\beta } y_{i}') \Rightarrow \exists \textbf{x}' :(\forall i :x_{i} \mathrel {\beta } x_{i}') \wedge \textbf{x}' \mathrel {\rho '} \textbf{y}', $$

and, for all $\textbf{x} \in X^{n}, \textbf{x}' \in X'^{n}, \textbf{y}' \in X'^{m}$,

$$ (\forall i :x_{i} \mathrel {\beta } x_{i}') \wedge \textbf{x}' \mathrel {\rho '} \textbf{y}' \Rightarrow \exists \textbf{y} :\textbf{x} \mathrel {\rho } \textbf{y} \wedge (\forall i :y_{i} \mathrel {\beta } y_{i}'). $$

We let ${{\,\mathrm{\textrm{Op}}\,}}_{J_{\mathbb {V}_{\!\downarrow }}}^{n,m}(\textbf{Priest})$ denote the category of (n, m)-ary relational Priestley operators and relational morphisms.

Then Theorem 3.5 instantiates to the following result:

Theorem 4.3

(Extended Priestley duality). The category of $(m, n)$-ary U-operators of distributive lattices is dually equivalent to the category of $(n, m)$-ary relational Priestley spaces and relational morphisms:

$$\begin{aligned} {{\,\mathrm{\textrm{Op}}\,}}_{U}^{m,n}(\textbf{DL}) \simeq ^{\textrm{op}}{{\,\mathrm{\textrm{Op}}\,}}_{J_{\mathbb {V}_{\!\downarrow }}}^{n,m}(\textbf{Priest}). \end{aligned}$$

By taking $n = 1$ and restricting the operator morphisms to be pure, we recover Goldblatt’s duality [16]. Here, pure relational morphisms are called bounded morphisms and n-ary U-algebras $(UD)^{\otimes n}\rightarrow UD$ in $\textbf{JSL}$ are called $n$-ary join-hemimorphisms.

Corollary 4.4

(Goldblatt, 1989). The category of distributive lattices with n-ary join-hemimorphisms, and pure morphisms between them, is dually equivalent to the category of $(1, n)$-relational Priestley spaces and bounded morphisms.

4.1 Deriving Concrete Formulas

We proceed to show how an enriched extension of our adjoint framework can be used to methodically derive concrete (i.e. element-based) formulas for the dual join operator of a continuous relation and vice versa. Let us first observe that all involved categories are order-enriched, i.e. the homsets are (pointwise) partially ordered; for $\textbf{JSL}$ and $\textbf{DL}$ this is clear and relations $X \rightarrow \mathbb {V}_{\!\downarrow }Y$ are ordered by inclusion, as usual. Moreover, from the definitions it is clear that the transposing isomorphisms of the adjunction $F \dashv U$ and the duality $\textbf{DL} \simeq ^{\textrm{op}}\textbf{Priest}$ are order-isomorphisms.

Second, in $\textbf{Priest}$ we can represent an element $\hat{x}$ of a space $\hat{X}$ as a continuous function $1 \rightarrow X$ that we also denote by $\hat{x}$; on the lattice side, elements of a join-semilattice $J$ correspond bijectively to $\textbf{JSL}$-morphisms $2\rightarrow J$.

For the rest of the section we fix a U-algebra $h :(UX)^{\otimes n} \rightarrow U X$ with dual Priestley relation $\rho :\hat{X} \rightarrow \mathbb {V}_{\!\downarrow }\hat{X}^{n}$. We first show how to express $\rho$ in terms of h. Two elements $\hat{x} \in \hat{X}, \mathbf {\hat{x}} \in \hat{X}^{n}$ are related by $\rho$ (i.e. $\hat{x} \mathrel {\rho } \mathbf {\hat{x}}$) iff the inequality $e(\mathbf {\hat{x}}) = {\downarrow }{\mathbf {\hat{x}}} \le \rho (\hat{x})$ holds, equivalently, iff the left diagram below commutes laxly:

The duals of $\hat{x}, \hat{x}_{i}$ are $\textbf{DL}$ morphisms $x, x_{i} :X \rightarrow 2$. Under duality and transposition the left diagram corresponds to the right diagram where $\nabla$ is the codiagonal given by $n$-fold conjunction, i.e. it sends $\bigotimes _{i=1}^{n} x_{i}$ to ${{\,\mathrm{\bigwedge }\,}}_{i=1}^{n}x_{i}$. Writing $F_{z} = z^{-1}(1)$ for the prime filter corresponding to a morphism $z \in \textbf{DL} (X, 2)$ the right diagram yields Goldblatt’s formula [16, p. 186] for the dual Priestley relation of an algebra h: we have $\hat{x} \mathrel {\rho } \mathbf {\hat{x}}$ iff $h[\prod _{i}F_{x_{i}}] \subseteq F_{x}$.

To express h in terms of $\rho$, it suffices to describe $h(\textbf{x})$ for a pure tensor $\textbf{x} \in (UX)^{\otimes n}$ by the universal property of the tensor product. We factor $\textbf{x} = \bigotimes _{i} x_{i} \cdot \nabla ^{-1} :U 2 \cong (U 2)^{\otimes n} \rightarrow (U X)^{\otimes n}$ to see that the element $h(\textbf{x})$ corresponds to the following morphism representing an element of the join-semilattice UX:

$$\begin{aligned} h \cdot \bigotimes _{i} x_{i} \cdot \nabla ^{-1} :U 2 \cong (U 2)^{\otimes n} \rightarrow (U X)^{\otimes n} \rightarrow U X. \end{aligned}$$

Its dual is the characteristic function

$$\begin{aligned} \hat{X} \xrightarrow {\rho } \mathbb {V}_{\!\downarrow }\hat{X}^{n} \xrightarrow {\mathbb {V}_{\!\downarrow }(\prod _{i} C_{i})} \mathbb {V}_{\!\downarrow }(\mathbb {V}_{\!\downarrow }1)^{n} \xrightarrow {\mathbb {V}_{\!\downarrow }\delta } \mathbb {V}_{\!\downarrow }\mathbb {V}_{\!\downarrow }1^{n} \xrightarrow {\bigcup } \mathbb {V}_{\!\downarrow }1^{n} \xrightarrow {\mathbb {V}_{\!\downarrow }\varDelta ^{-1}} \mathbb {V}_{\!\downarrow }1 = 2, \end{aligned}$$

where $C_{i}= \widehat{x_{i}^{+}}$ is the clopen upset of $\hat{X}$ dual to

$$\begin{aligned} x_{i} \in \textbf{JSL} (U 2, U X) \cong \textbf{DL} (FU 2, X) \cong \textbf{Priest} (\hat{X}, \mathbb {V}_{\!\downarrow }1) \cong \textbf{Priest} (\hat{X}, 2). \end{aligned}$$

This shows that $h(\textbf{x}) \in X \cong {{\,\mathrm{\textrm{Cl}}\,}}_{\uparrow }\hat{X}$ corresponds to the clopen upset

$$\begin{aligned} h(\textbf{x}) = \{a \in \hat{X} \mid \exists (b_{1}, \ldots , b_{n}) \in \rho (a) :\forall i :b_{i} \in C_{i} = \widehat{x_{i}^{+}} \} \in {{\,\mathrm{\textrm{Cl}}\,}}_{\uparrow }(\hat{X}), \end{aligned}$$

which is Goldblatt’s formula [16, p. 184] for the dual algebra of a relation $\rho$.

4.2 Partial Functions and Total Relations

As a further application of the adjoint framework we characterize those operators whose dual Priestley relation is a partial function or a total relation, respectively. We achieve this by considering two splittings of the adjunction (Proposition 3.6 and Remark 3.7). The tensor on all categories considered is the tensor product of their underlying join-semilattices.

First, split the adjunction into and , where $\textbf{DL} _{0}$ is the category of distributive lattices that are only bounded from below, and $P,P'$ are forgetful functors. The left adjoint $Q$ adds a fresh top element to a lattice in $\textbf{DL} _{0}$. The dual submonad $\hat{Q}\hat{P} \hookrightarrow \mathbb {V}_{\!\downarrow }$ on $\textbf{Priest}$ is given by

$$\begin{aligned} \hat{Q}\hat{P}\hat{D} \cong \widehat{QPD} \cong \textbf{DL} (QPD, 2) \cong \textbf{DL} _{0}(PD, P2). \end{aligned}$$

Every $f \in \textbf{DL} _{0}(PD, P2)$ either satisfies $f(1) = 1$, in which case $f \in \hat{D}$ is prime, or $f(1) = 0$ but then $f$ is the constant zero map $0! :PD \rightarrow P2$; note that $0!$ is clearly the bottom element in the pointwise ordering of $\textbf{DL} _{0}(PD, P2)$, so the monad $\hat{Q}\hat{P}$ just freely adds a bottom element. In particular, the dual category of $\textbf{DL} _{0}$ is readily seen to be equivalent to $\textbf{Priest} _{0}$, the category of Priestley spaces with a bottom element, and bottom-preserving continuous monotone maps. A continuous relation $\rho :X \rightarrow \hat{Q}\hat{P} \hat{X}$ is thus simply a partial continuous function.

Another splitting of the adjunction $F\dashv U$ is given by and , where $\textbf{JSL} _1$ is the category of join-semilattices with both a bottom and top element (which are preserved by homomorphisms). The right adjoints $R,R'$ are forgetful functors. The left adjoint L maps $J\in \textbf{JSL} _1$ to the distributive lattice $\mathcal {U}_{\textrm{fg}+}^{\circ }$ of non-empty finitely generated upsets of $J$, ordered by reverse inclusion. The submonad $\hat{L}\hat{R} \hookrightarrow \mathbb {V}_{\!\downarrow }$ thus maps a Priestley space $\hat{D}$ to

$$\begin{aligned} \hat{L}\hat{R}\hat{D} \cong \textbf{DL} (LR D, 2) \cong \textbf{JSL} _{1}(RD, R2) \cong {\mathbb {V}_{\!\downarrow }^+}\hat{D}, \end{aligned}$$

where $\mathbb {V}_{\!\downarrow }^+$ is the submonad of $\mathbb {V}_{\!\downarrow }$ taking non-empty closed downsets. Morphisms of type $X \rightarrow \mathbb {V}_{\!\downarrow }^+Y$ therefore are total Priestley relations. Proposition 3.6 thus yields the following result (the unary case is folklore, see e.g. [18, Lemma 4.6]):

Corollary 4.5

The dual Priestley relation of a U-operator (operator morphism, respectively) is a partial function iff the operator (operator morphism, respectively) preserves non-empty meets, and total iff it preserves $\top$.

5 Residuation Algebras

The abstract extended duality will now guide us in deriving a categorical duality between profinite ordered monoids and a full subcategory of residuation algebras which we call derivation algebras. This result is a non-trivial restriction of Gehrke’s duality [13, 14] between Priestley-topological algebras and residuation algebras. Our result is obtained by combining two ingredients: our framework for extended Stone duality from the previous sections and an isomorphism between residuation algebras and certain lattice coalgebras. The latter is first established for finite algebras via an operator on complete lattices we call tensor implication; extending it to locally finite algebras (Definition 5.22) then yields the desired duality with the category of profinite ordered monoids. To this end we introduce the notion of residuation morphism (Definition 5.8). The abstract extended duality then allows us to extend our results to relational morphisms of profinite ordered monoids and residuation algebras.

5.1 The Tensor Product of Distributive Lattices Revisited

Notation 5.1

By a lattice we always mean a bounded and distributive lattice, i.e. an object of $\textbf{DL}$. We often write $de$ for $d \wedge e$. The dual lattice of $D$ is denoted by $D^{\circ }$. The category of meet-semilattices (with a top element) is denoted $\textbf{MSL}$. Analogous to $\textbf{JSL}$ it has a tensor product $M \mathbin {{\boxtimes }}M'$ and is dual to the category of Stone meet-semilattices [19]. From now on we denote the forgetful functors from $\textbf{DL}$ to $\textbf{JSL}$ and $\textbf{MSL}$ by $U_{\vee }$ and $U_{\wedge }$, respectively. Sometimes we omit the forgetful functors $U_{\wedge }$ and $U_{\vee }$ for notational brevity and just write the respective tensor products of the underlying semilattices as $D \mathbin {{\otimes }}D'$ and $D \mathbin {{\boxtimes }}D'$.

Remark 5.2

The monad induced by the dual of $F_{\wedge } \dashv U_{\wedge }$ sends a Priestley space $X$ to its hyperspace ${\mathbb {V}_{\uparrow }} X$ of closed upsets [1]. The comonads of the adjunctions $F_{\wedge } \dashv U_{\wedge }$ and $F_{\vee } \dashv U_{\vee }$ are not isomorphic but conjugate: $F_{\wedge }U_{\wedge } \cong (F_{\vee }U_{\vee }(-)^{\circ })^{\circ }$. Their restrictions to the category of boolean algebras are isomorphic since their dual monads satisfy $\mathbb {V}_{\!\downarrow }= \mathbb {V}= \mathbb {V}_{\uparrow }$ – trivially so, as the order on their dual Priestley space is discrete. On the category of finite Priestley spaces, which are simply posets, $\mathbb {V}_{\!\downarrow }$ restricts to the downset monad, which further restricts to the finite powerset monad on the category of finite sets (i.e., discrete finite posets).

Remark 5.3

(Adjunctions on Lattices). By the adjoint functor theorem [25, Thm. V.6.1] a monotone function $f :D \rightarrow D'$ between complete lattices preserves all joins iff it has a right adjoint $f_{*} :D' \rightarrow D$, which is then given by $f_{*}(d') = {{\,\mathrm{\bigvee }\,}}_{f(d) \le d'} d$; dually, it preserves all meets iff it has a left adjoint $f^{*} :D' \rightarrow D$, given by $f^{*}(d') = {{\,\mathrm{\bigwedge }\,}}_{d' \le f(d)} d$. Finite lattices are complete, so every lattice homomorphism $f$ between finite lattices has a left and a right adjoint. The join-irreducibles $\mathcal {J} D$ of a finite lattice $D$ are precisely those elements $p\in D$ whose characteristic function $\chi _{p} :D \rightarrow 2$ (mapping $x \in D$ to $1$ iff $p \le x$) is a lattice morphism. The left adjoint of $\chi _{p}$, also denoted $p :2 \rightarrow D$, maps $1 \mapsto p$.

Lemma 5.4

(1):

The join- and meet-semilattice tensor products of distributive lattices $D, E$ are isomorphic, that is, there is an isomorphism $\omega :D \mathbin {{\otimes }}E \cong D \mathbin {{\boxtimes }}E$.

(2):

Adjunctions on lattices “compose horizontally”: Given adjunctions and on lattices, the following composites are adjoints:

Construction 5.5

For every finite lattice $D$ the map $x \mathbin {{\otimes }}(-) :D \rightarrow D \mathbin {{\otimes }}D$ preserves all joins, so it admits a right adjoint $x \multimap (-) :U_{\wedge }(D \mathbin {{\otimes }}D) \rightarrow U_{\wedge } D$ which we call tensor implication. By Remark 5.3, it is given by $x \multimap T = {{\,\mathrm{\bigvee }\,}}_{x \mathbin {{\otimes }}y \le T} y$. Analogously, we let denote the right adjoint of $(-) \mathbin {{\otimes }}x$.

Definition 5.6

A (boolean) residuation algebra consists of a (boolean) lattice $R \in \textbf{DL}$ equipped with $\textbf{MSL}$-morphisms $\setminus :R^{\circ } \mathbin {{\boxtimes }}R \rightarrow R$ and $\mathrel /:R \mathbin {{\boxtimes }}R^{\circ } \rightarrow R$, the left and right residual, satisfying the residuation property: $b \le a \setminus c \,\Longleftrightarrow \,a \le c \mathrel /b$. We call $R$ associative if it satisfies $x \setminus (z \mathrel /y) = (x \setminus z) \mathrel /y$ for all $x, y, z \in R$. A join-irreducible element $e \in \mathcal {J} R$ is a unit if it satisfies $e \setminus z = z = z \mathrel /e$.

Residuals may be thought of algebraic generalizations of language derivatives, but as the following examples indicate they are not limited to this interpretation.

Examples 5.7

(1):

Every distributive Heyting algebra is an associative residuation algebra with residuals $a \setminus c = a \rightarrow c$ and $c \mathrel /b = b \rightarrow c$.

(2):

Every boolean algebra $B$ is a non-associative residuation algebra with $x \setminus 1 = 1$ and $x \setminus z = \lnot x$ for $z \ne 1$. If $|B| > 1$ it does not have a unit.

(3):

The dual boolean algebra $\hat{X}$ of a continuous algebra $\cdot :X \times X \rightarrow X$ on a Stone space $X$ forms a residuation algebra: given clopens $A,C\subseteq X$, put

$$\begin{aligned} A \setminus C &= \{x\in X \mid \forall (a \in A) :a \cdot x \in C\},\\ C \mathrel /A &= \{x\in X \mid \forall (b \in B) :x \cdot b \in C\}. \end{aligned}$$

(4):

The regular languages ${{\,\mathrm{\textrm{Reg}}\,}}\varSigma$ over a finite alphabet $\varSigma$ form an associative boolean residuation algebra with residuals given by (extended) left and right derivatives: $K \setminus L = \{v \in \varSigma ^{*} \mid Kv \subseteq L\}$ and $L \mathrel /K = \{v \in \varSigma ^{*} \mid vK \subseteq L\}$. The singleton empty word $\{\varepsilon \}$ is a unit. This example is a special case of item (3) obtained by taking as Stone algebra the free profinite monoid $\widehat{\varSigma ^{*}}$.

We now introduce the notion of a residuation morphism between residuation algebras and also its relational generalization.

Definition 5.8

• (1) A lattice morphism $f :R \rightarrow S$ between unital residuation algebras is a (pure) residuation morphism if it satisfies the conditions

  

  The morphism $f$ is open if, additionally, it has a left adjoint. The category of unital residuation algebras with residuation morphisms is denoted $\textbf{Res}$.

• (2) A (lax) relational residuation morphism from a unital residuation algebra $R$ to a unital residuation algebra $S$ is a morphism $\rho \in \textbf{JSL} _{1}(R, S)$ satisfying

  $$\rho (x \setminus z) \le \rho (x) \setminus \rho (z) \quad {\text {and}} \quad e' \le \rho (e).$$

  Unital residuation algebras with relational residuation morphisms form a category $\textbf{RelRes}$.

We use the convention that for a subcategory $\textbf{C}$ of $\textbf{Res}$ or $\textbf{RelRes}$ we denote the full subcategory of $\textbf{C}$ with boolean carriers by $\textbf{BC}$.

Remark 5.9

Let us provide some intuition behind the choices made in Definition 5.8. Recall that a relational monoid morphism from a finite monoid $M$ to $N$ is a total relation $\rho :M \rightarrow \mathcal {P}N$ such that $\rho (x)\rho (y) \subseteq \rho (xy)$ and $1_{N} \in \rho (1_{M})$.

• (1) The notion of residuation morphism is derived from a result by Gehrke [14, Theorem 3.19], where it is shown to capture precisely the conditions satisfied by the duals of morphisms of binary Stone algebras.

• (2) We speak about relational morphisms of residuation algebras since for finite algebras these will dualize precisely to relational morphisms of finite monoids, which model inverses of surjective monoids homomorphisms [29, p. 38]: on finite monoids the inverse relation $e^{-1} :N \rightarrow \mathcal {P}M$ of a surjective homomorphism $e :M \twoheadrightarrow N$ is the right adjoint $e \dashv e^{-1}$ in the order-enriched category $\textbf{Rel}$ with sets as objects and relations as morphisms, i.e. as relations they satisfy $\textrm{id}\le e^{-1} \cdot e$ and $e \cdot e^{-1} \le 1$. Under duality the composition is reversed, so $e^{-1}$ dualizes to a left adjoint $\widehat{e^{-1}} \dashv \hat{e}$. As left adjoints between finite lattices are precisely the join-preserving functions this suggests the choice that relational morphisms of residuation algebras preserve finite joins (and not necessarily meets). Surjectivity of $e$ is equivalent to totality of $e^{-1}$, which by Corollary 4.5 is equivalent to $\widehat{e^{-1}}$ preserving the top element.

• (3) This is also the reasoning behind the naming for open residuation morphisms: if $e :M \twoheadrightarrow N$ is a continuous surjection between profinite monoids (that is, topological monoids in $\textbf{Stone}$), then $e^{-1} :N \rightarrow \mathbb {V}M$ is continuous precisely iff $e$ is an open map.

For open residuation morphisms the conditions (Back) and (Forth) can be combined into a much simpler condition. Over finite residuation algebras this is particularly convenient since every residuation morphism is open.

Lemma 5.10

Let $R, S$ be residuation algebras. A lattice morphism $f :R \rightarrow S$ is an open residuation morphism iff $f^{*}(e') = e$ and it satisfies the condition

Example 5.11

Let $\varSigma$, $\varDelta$ be finite alphabets. Every substitution $f_{0} :\varSigma \rightarrow \varDelta ^{*}$ can be extended to a monoid homomorphism $f :\varSigma ^{*} \rightarrow \varDelta ^{*}$, and for regular languages $L \in {{\,\mathrm{\textrm{Reg}}\,}}\varSigma$ and $K \in {{\,\mathrm{\textrm{Reg}}\,}}\varDelta$ both $f[L]$ and $f^{-1}[K]$ are also regular. Then $f^{-1} :{{\,\mathrm{\textrm{Reg}}\,}}\varDelta \rightarrow {{\,\mathrm{\textrm{Reg}}\,}}\varSigma$ is an open residuation morphism. Indeed, its left adjoint is $f[-]$, and we have $f[\{\varepsilon \}] = \{f(\varepsilon )\} = \{\varepsilon \}$ and

$$\begin{aligned} K \setminus f^{-1}[L] = \{w \mid K w \subseteq f^{-1}[L]\} = \{w \mid f[K]f(w) \subseteq L\} = f^{-1}(f[K] \setminus L). \end{aligned}$$

5.2 Finite Residuation Algebras

We will start by characterizing finite residuation algebras, and then generalize the results to locally finite residuation algebras This approach allows us to first introduce the key concepts and constructions of the duality on a finite level, and then extend them to more general structures by forming appropriate free completions. All results of this section apply more generally to structures with a complete and completely distributive lattice as carrier.

Construction 5.12

In a finite residuation algebra $R$ the partially applied residuals $(x \setminus -), (- \mathrel /y)$ have respective left adjoints $\mu (x,-) \dashv (x \setminus -)$ and $\mu (-, y) \dashv (- \mathrel /y)$ that can be combined, by the universal property of $\otimes$, into a $U_{\vee }$-algebra $\mu :U_{\vee }R \mathbin {{\otimes }}U_{\vee }R \rightarrow U_{\vee }R$ called multiplication. Every algebra $U_{\vee }D \mathbin {{\otimes }}U_{\vee } D \rightarrow U_{\vee }D$ on a finite lattice $D$ has a right adjoint $\gamma :U_{\wedge } D \rightarrow U_{\wedge }(D \mathbin {{\otimes }}D)$ that can, by using the isomorphism $\omega$ from Lemma 5.4, be extended to a $U_{\wedge }$-coalgebra

$$\begin{aligned} \hat{\gamma } = U_{\wedge } \omega \cdot \gamma :U_{\wedge } D \rightarrow U_{\wedge }(D \mathbin {{\otimes }}D) \cong U_{\wedge }(D \mathbin {{\boxtimes }}D) = U_{\wedge } D \mathbin {{\boxtimes }}U_{\wedge } D. \end{aligned}$$

Since $\gamma$ and $\hat{\gamma }$ are essentially the same function (differing only by the isomorphism $\omega$) we refer to both as comultiplication or coalgebra structure. Conversely, we obtain a $U_{\vee }$-algebra from a comultiplication $\gamma :U_{\wedge } D \rightarrow U_{\wedge }(D \mathbin {{\otimes }}D)$ by taking its left adjoint. In summary, each of $\mathrel /$, $\setminus$, $\mu$, $\gamma$ determine each other uniquely:

$$\begin{aligned} x \le z \mathrel /y \,\Longleftrightarrow \,y \le x \setminus z \,\Longleftrightarrow \,\mu (x \mathbin {{\otimes }}y) \le z \,\Longleftrightarrow \,x \mathbin {{\otimes }}y \le \gamma (z), \end{aligned}$$

Lemma 5.13

In a finite residuation algebra $R$ the residuals can be expressed via comultiplication $\gamma$ and tensor implication as $x \setminus z = x \multimap \gamma (z)$ and . Conversely, the comultiplication can be expressed via residuals as

$$\begin{aligned} \gamma (z) = {{\,\mathrm{\bigvee }\,}}_{x \in R} x \mathbin {{\otimes }}(x \setminus z) = {{\,\mathrm{\bigvee }\,}}_{p \in \mathcal {J}R} p \mathbin {{\otimes }}(p \setminus z). \end{aligned}$$

First we investigate when the comultiplication is a pure, i.e. lifts to a lattice morphism $R \rightarrow R + R$.

Lemma 5.14

For a finite residuation algebra $R$, the following are equivalent:

(1):

The comultiplication is pure, i.e., $\gamma (0) = 0$ and $\gamma (x \vee y) = \gamma (x) \vee \gamma (y)$.

(2):

For all $p \in \mathcal {J} R$ we have $p \setminus 0 = 0 = 0 \mathrel /p$, and the following equations hold:

$$ p \setminus (x \vee y) = p \setminus x \vee p \setminus y \qquad \text {and}\qquad (x \vee y) \mathrel /p = x \mathrel /p \vee y \mathrel /p. $$

(3):

For all $x, y \in R :\mu (x \mathbin {{\otimes }}y) = 0 \iff x = 0 \vee y = 0$, and $\mu [\mathcal {J}(R + R)] \subseteq \mathcal {J} R$.

Next we inspect how structural identities like (co-)associativity or unitality translate to the other operations. Note that while the statements are to be expected, the proof is non-trivial due to the complication introduced by the seemingly innocent isomorphism $\omega :R \mathbin {{\otimes }}R \cong R \mathbin {{\boxtimes }}R$. Recall that a coalgebra $c:U_{\wedge } R \rightarrow U_{\wedge } R \mathbin {{\boxtimes }}U_{\wedge } R$ is coassociative if $(c \mathbin {{\boxtimes }}\textrm{id}) \cdot c = (\textrm{id}\mathbin {{\boxtimes }}c) \cdot c$ and counital if it is equipped with a counit $\varepsilon \in \textbf{DL} (R, 2)$ such that $(\varepsilon \mathbin {{\boxtimes }}\textrm{id}) \cdot c = \textrm{id}= (\textrm{id}\mathbin {{\boxtimes }}\varepsilon ) \cdot c$.

Lemma 5.15

The following are equivalent for a finite residuation algebra $R$:

(1):

The comultiplication on $R$ is coassociative and has a counit.

(2):

The residuals are associative and $R$ has a unit.

(3):

The multiplication $\mu$ is associative and has a unit, i.e. a join-irreducible $e \in \mathcal {J} R$ satisfying $\mu (e \mathbin {{\otimes }}-) = \textrm{id}= \mu (- \mathbin {{\otimes }}e)$.

These lemmas suggest the following definitions.

Definition 5.16

• (1) A finite residuation algebra $R$ is pure if it satisfies (one of) the equivalent conditions of Lemma 5.14.

• (2) A finite residuation algebra $R$ is a finite derivation algebra if it is pure, associative and has a unit. The respective full subcategories of $\textbf{Res} _{\textrm{f}}$ and $\textbf{RelRes} _{\textrm{f}}$ are denoted by $\textbf{Der} _{\textrm{f}}$ and $\textbf{RelDer} _{\textrm{f}}$.

• (3) A (not necessarily finite) $U_{\wedge }$-coalgebra $\hat{\gamma } :U_{\wedge } C \rightarrow U_{\wedge }C \mathbin {{\boxtimes }}U_{\wedge } C$ is a $U_{\wedge }$-comonoid if its coassociative and counital, and a (lattice) comonoid if $\hat{\gamma }$ is pure.

In order to extend the correspondence of (finite) residuation algebras and $U_{\wedge }$-coalgebras to a categorical equivalence we introduce appropriate morphisms.

Definition 5.17

• (1) A pure morphism from a counital $U_{\wedge }$-coalgebra $(C, \hat{\gamma },\epsilon )$ to $(C', \hat{\gamma }',\epsilon ')$ is a lattice morphism $f :C \rightarrow D$ satisfying $(f \mathbin {{\boxtimes }}f) \cdot \hat{\gamma } = \hat{\gamma }' \cdot f$ and $\epsilon = \epsilon ' \cdot f$.

  

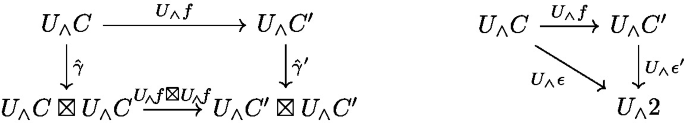
  The category of counital $U_{\wedge }$-coalgebras with pure morphisms is denoted by ${{\,\mathrm{\textbf{Coalg}}\,}}(U_{\wedge })$ and its full subcatgegory of $U_{\wedge }$-comonoids by $\textbf{Comon} (U_{\wedge })$, again with the full subcategory $\textbf{Comon}$ of comonoids.

• (2) Let $C$ and $C'$ be comonoids. A (lax) relational morphism from $C$ to $C'$ is a morphism $\rho \in \textbf{JSL} _{1}(C, C')$ satisfying $(\rho \mathbin {{\otimes }}\rho ) \cdot \gamma \le \gamma ' \cdot \rho \quad {\text {and}} \quad \epsilon \le \epsilon ' \cdot \rho$, i.e. the following diagrams in $\textbf{JSL}$ commute laxly:

  

  Comonoids with relational morphisms form a category $\textbf{RelComon}$.

Theorem 5.18

The following categories are isomorphic:

$$\begin{aligned} {{\,\mathrm{\textbf{Coalg}_{\textrm{f}}}\,}}(U_{\wedge }) \cong \textbf{Res} _{\textrm{f}}, \qquad \textbf{Comon} _{\textrm{f}} \cong \textbf{Der} _{\textrm{f}} \quad {\text {and}} \quad \textbf{RelComon} _{\textrm{f}} \cong \textbf{RelDer} _{\textrm{f}}. \end{aligned}$$

Proof

(Sketch). On objects the isomorphism swaps between residuals and comultiplication; the residual unit is left adjoint of the counit. The first isomorphism restricts to the second by Lemmas 5.14 and 5.15. On morphisms one proves that a lattice morphism $f :C \rightarrow C'$ is a pure coalgebra morphism iff it is an (open) residuation morphism, and if $C$ and $C'$ are comonoids, then $\rho \in \textbf{JSL} _{1}(C, C')$ is a relational comonoid morphism iff it is a relational residuation morphism.

From Theorem 5.18 we obtain the following dual characterization of finite ordered monoids; it restricts to the order-discrete setting of ordinary finite monoids and finite boolean derivation algebras.

Theorem 5.19

(1):

The category of finite ordered monoids is dually equivalent to the category of finite derivation algebras (or finite lattice comonoids):

$$\begin{aligned} \textbf{OrdMon} _{\textrm{f}} \simeq ^{\textrm{op}}\textbf{Comon} _{\textrm{f}} \cong \textbf{Der} _{\textrm{f}}. \end{aligned}$$

(2):

The category of finite ordered monoids with relational morphisms is dually equivalent to the category of finite derivation algebras (or finite lattice comonoids) with relational morphisms.

$$ \textbf{RelOrdMon} _{\textrm{f}} \simeq ^{\textrm{op}}\textbf{RelComon} _{\textrm{f}} \cong \textbf{RelDer} _{\textrm{f}}. $$

Proof

The first statement is a trivial extension of Theorem 5.18 by (finite) Priestley duality since finite ordered monoids dualize to finite lattice comonoids. For item (2) note that a relational ordered monoid morphism $(M, \cdot _{M}, 1_{M}) \rightarrow (N, \cdot _{N}, 1_{N})$ is a total relation $\rho :M \rightarrow \mathcal {D} N$ (where $\mathcal {D}$ is the downset monad) making the following diagrams commute laxly:

If we view $N$ as a finite Priestley space, then $\mathcal {D} N = \mathbb {V}_{\!\downarrow }N$, so the dual of $\rho$ under (order-enriched) extended duality is a relational morphism $\hat{\rho }^{-} \in \textbf{JSL} _{1}(\hat{N}, \hat{M})$ of finite lattice comonoids, or equivalently, a relational residuation morphism.

5.3 Locally Finite Residuation Algebras

The main complication in the generalization from finite to infinite structures comes from the reliance on adjoints, as these may not exist anymore on infinite lattices. The prime example of a residuation algebra in automata theory suggests a local translation between residuals and comultiplication:

Example 5.20

It is well-known that the boolean algebra ${{\,\mathrm{\textrm{Reg}}\,}}\varSigma$ of regular languages dualizes under Stone duality to the free profinite monoid $\widehat{\varSigma ^{*}}$ (see Pippenger [27]). The multiplication $\mu :\widehat{{\varSigma }^*} \times \widehat{{\varSigma }^*} \rightarrow \widehat{{\varSigma }^*}$ of profinite words dualizes under Stone duality to a comultiplication $\mu ^{-1} :{{\,\mathrm{\textrm{Reg}}\,}}\varSigma \rightarrow {{\,\mathrm{\textrm{Reg}}\,}}\varSigma + {{\,\mathrm{\textrm{Reg}}\,}}\varSigma$ on regular languages defined on $L \in {{\,\mathrm{\textrm{Reg}}\,}}\varSigma$ by

$$\begin{aligned} \mu ^{-1}(L) = {{\,\mathrm{\bigvee }\,}}_{[v] \in \textrm{Syn}_{L}} [v] \mathbin {{\otimes }}[v] \setminus L. \end{aligned}$$

(5.1)

Here $\textrm{Syn}_{L}$ is the syntactic monoid of L, whose elements are the equivalence classes of the equivalence relation on $\varSigma ^*$ defined by $v\equiv _L w$ iff v, w belong to the same residuals $K\setminus L \mathrel /M$. Gehrke [13, Thm. 15] has shown that, under Stone duality, $\textrm{Syn}_{L}$ dualizes to the residuation ideal generated by $L \in {{\,\mathrm{\textrm{Reg}}\,}}\varSigma$.

Definition 5.21

A residuation ideal of a residuation algebra $R$ is a sublattice $I \hookrightarrow R$ such that for all $z \in I$ and $x \in R$ one has $x \setminus z, z \mathrel /x \in R$. We denote the residuation ideal generated by a subset $X \subseteq R$ by $\setminus {X}/$.

Residuation ideals were used by Gehrke [14] to characterize quotients of Priestley topological algebras. Note that in the formula (5.1) for the comultiplication on regular languages it is crucial that the residuation ideal $\setminus {\{L\}}/$ generated by a single regular language $L$ is finite, as otherwise the join might not exist. This leads to the following restriction.

Definition 5.22

• (1) A residuation algebra $R$ is locally finite if every finite subset of $R$ is contained in a finite residuation ideal of $R$.

• (2) A $U_{\wedge }$-coalgebra $C$ is locally finite if every finite subset of $C$ is contained in a finite subcoalgebra of $C$. The category of locally finite comonoids is denoted $\textbf{Comon} _{\textrm{lf}}$.

Note that not every residuation algebra is locally finite, consider for example an infinite boolean algebra in Example 5.7(2).

Proposition 5.23

(1):

Every locally finite residuation algebra $R$ yields a locally finite $U_{\wedge }$-coalgebra $\gamma _{\setminus } :U_{\wedge } R \rightarrow U_{\wedge }(R \mathbin {{\otimes }}R)$ with comultiplication given by

$$ \gamma _{\setminus }(z) = (\iota _{A} \mathbin {{\otimes }}\iota _{A})(\gamma _{A}(z)) = {{\,\mathrm{\bigvee }\,}}_{x \in A} \iota _{A}(x) \mathbin {{\otimes }}\iota _{A}(x \setminus z) = {{\,\mathrm{\bigvee }\,}}_{p \in \mathcal {J} A} \iota _{A}(p) \mathbin {{\otimes }}\iota _{A}(p \setminus z) $$

for any finite residuation ideal $\iota _{A} :A \hookrightarrow R$ containing $z$ (here $\gamma _{A}$ is the comultiplication on $A$ as in Construction 5.12).

(2):

Every locally finite $U_{\wedge }$-coalgebra $(C, \gamma )$ yields any locally finite residuation algebra with the left residual given by $x \setminus _{\gamma } z = \iota _{A}(x \setminus _{A} z) = \iota _{A}(x \multimap \gamma (z) )$ for any finite subcoalgebra $\iota _{A} :A \hookrightarrow C$ containing $x, z$ (here $\setminus _{A}$ is the residual on $A$ as given by Construction 5.12). The residual has a canonical presentation as $x \setminus _{\gamma } z = \iota _{z}(\iota _{z}^{*}(x) \setminus z)$, where $\iota _{z} :\langle z \rangle \rightarrow C$ is the smallest (finite) subcoalgebra containing $z$. The right residual is defined analogously.

(3):

These translations are mutually inverse.

Proposition 5.23 shows that every locally finite residuation algebra carries a unique $U_{\wedge }$-coalgebra structure and vice versa. We may thus translate at will between the residuals and comultiplication as in the finite case and omit the subscripts. We extend Lemmas 5.14 and 5.15 to locally finite structures:

Lemma 5.24

Let $R$ be a locally finite residuation algebra.

(1):

Finite residuation ideals correspond to finite subcoalgebras.

(2):

The residuals are associative iff the comultiplication is coassociative.

(3):

The residuals have a unit iff the comultiplication is counital.

(4):

The comultiplication is pure iff every finite residuation ideal is pure (see Definition 5.16).

Remark 5.25

Lemma 5.24(4) characterizes locally finite residuation algebras with a pure comultiplication. By extended duality, their dual Priestley relation is functional. We note that Gehrke [14, Proposition 3.15] presented a necessary and sufficient condition for a general residuation algebra $R$ to have a functional dual relation, namely join-preservation at primes:

$$\begin{aligned} \forall F \in \textbf{DL} (R, 2) :\forall (a \in F), \forall (b, c \in R) :\exists a' \in F :a \setminus (b \vee c) \le (a' \setminus b) \vee (a' \setminus c). \end{aligned}$$

One can show that every locally finite residuation algebra satisfying Lemma 5.24(4) is join-preserving at primes.

Definition 5.26

A residuation algebra $R$ is a derivation algebra if it is locally finite, associative, unital and every finite residuation ideal $I$ is pure. The ensuing full subcategories of $\textbf{Res}$ and $\textbf{RelRes}$ are denoted $\textbf{Der}$ and $\textbf{RelDer}$.

Theorem 5.27

(1):

The category of locally finite residuation algebras and residuation morphisms is isomorphic to the category of locally finite unital $U_{\wedge }$-coalgebras and pure coalgebra morphisms.

(2):

The isomorphism restricts to the full subcategories of derivation algebras and locally finite comonoids.

(3):

The categories of derivation algebras and relational residuation morphisms and locally finite comonoids with relational morphisms are isomorphic.

Combining this characterization with our approach to extended Priestley duality we establish a duality between profinite ordered monoids and derivation algebras, and extend it to relational morphisms. Conceptually, this general duality is an extension of the finite duality $\textbf{OrdMon} _{\textrm{f}} \simeq ^{\textrm{op}}\textbf{Comon} _{\textrm{f}} \cong \textbf{Der} _{\textrm{f}}$ by forming suitable completions: Profinite ordered monoids are the Pro-completion (the free completion under cofiltered limits) of the category of finite ordered monoids; dually a routine verification establishes that lattice comonoids (and therefore also derivation algebras by Theorem 5.27(2)) form Ind-completions (free completions under directed colimits) of their respective subcategories of finite objects.

Proposition 5.28

The category of locally finite comonoids forms the Ind-completion of the category of finite comonoids:

$$\begin{aligned} \textbf{Comon} _{\textrm{lf}} \simeq {{\,\textrm{Ind}\,}}(\textbf{Comon} _{\textrm{f}}). \end{aligned}$$

We define a Priestley relational morphism between profinite ordered monoids $X, Y$ to be a Priestley relation $\rho :X \rightarrow \mathbb {V}_{\!\downarrow }Y$ such that $\rho (x) \rho (x') \subseteq \rho (xx')$ and $1_{N} \in \rho (1_{M})$.

Theorem 5.29

(1):

The category of derivation algebras is dually equivalent to the category of profinite ordered monoids:

$$ \textbf{Der} \cong \textbf{Comon} _{\textrm{lf}} \simeq ^{\textrm{op}}\textbf{ProfOrdMon}. $$

(2):

The category of derivation algebras and relational residuation morphisms is dually equivalent to the category of profinite ordered monoids and Priestley relational morphisms:

$$ \textbf{RelDer} \cong \textbf{RelComon} _{\textrm{lf}} \simeq ^{\textrm{op}}\textbf{RelProfOrdMon}. $$

Remark 5.30

• (1) Theorem 5.29 clearly restricts to profinite monoids with Stone relational morphisms and boolean derivation algebras. It is well-known that every Stone monoid is profinite (see e.g. [20]). So dually, every boolean comonoid is locally finite.

• (2) All results of Section 5 hold analogously for the extension of the “discrete” duality between posets (or sets) and algebraic completely distributive lattices (or completely atomic boolean algebras) along the free-forgetful adjunction between completely distributive lattices and complete join-semilattices. This yields a duality between the category of all (ordered) monoids and (completely distributive lattices) completely atomic boolean residuation algebras with open residuation morphisms. Moreover, this duality also can be extended to relational morphisms.

6 Conclusion and Future Work

We have presented an abstract approach to extending Stone-type dualities based on adjunctions between monoidal categories and instantiated it to recover and generalize extended Priestley duality. Guided by these foundations we have investigated residuation and derivation algebras and proved a duality between the latter and (ordered) profinite monoids, Moreover, we have extended this duality to relational morphisms.

Relational morphisms are an important tool in algebraic language theory, notably for charaterizing language operations algebraically. For instance, aperiodic relational morphisms are tightly connected to the concatenation product and the star operation on regular languages. In future work we intend to apply the new duality-theoretic results on relational morphisms to illuminate such connections, much in the spirit of the duality-theoretic persepective of Eilenberg’s Variety Theorem by Gehrke et. al. [15].

Another goal is to apply our abstract duality framework beyond classical Stone and Priestley dualities. Specifically, we aim to develop an extended duality theory for the recently developed nominal Stone duality [4], which would allow to generalize our present results on residuation algebras to the nominal setting and uncover new results about data languages.

A conceptually rather different dual characterization of the category of profinite monoids and continuous monoid morphisms in terms of semi-Galois categories has been provided by Uramoto [35]. Extending this result to relational morphisms, similar to our Theorem 5.29, is another interesting point for future work.