Abstract
Symmetry may seem like a self-evident property of an object – you know it when you see it – but for the study of crystallography a rigorous definition is required, so here goes: Symmetry is that property possessed by an object when some operation (translation, rotation, reflection, and/or inversion) leaves it indistinguishable from its original position. In other words, symmetry is a demonstration of the invariance of the object to the operation. Topics such as electronic bands, phonon dispersion, vibrational spectroscopy (e.g., Raman and IR), and the properties of crystalline materials generally require a good understanding of crystal symmetry.
There are no perfect symmetries, there is no pure randomness. Everything is an approximation of something else.
—Rick Delmonico
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Shubnikov fell victim to the Stalinist purges of the 1930s at the age of just 36.
- 2.
cos(a + b) = cos(a)cos(b) – sin(a)sin(b) and sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- 3.
The terms enantiomer and enantiomorph are used interchangeably. Both are derived from the Greek ἐναντίος (enantíos), meaning “opposite.” The terms enantiomer and chirality are mainly applied to molecules, whereas the term enantiomorph is preferred in crystallography.
- 4.
The notation was introduced in 1907 by German chemist Hermann Emil Fischer and is now obsolete for all molecules except sugars and amino acids. Working with glyceraldehyde, he named one variant D (from the Latin dextro, meaning “on the right”) and the other L (from the Latin laevo, meaning “on the left”). The modern notation would be R (from the Latin rectus, meaning “right”) and S (from the Latin sinister, meaning “left”).
- 5.
The designation is related to the position of the OH group (for sugars) or NH2 group (for amino acids) on the bottommost chiral centre when the molecule is drawn with the most oxidised carbon at the top.
- 6.
but not for lack of trying. The US company Richardson-Merrell requested approval on no fewer than six occasions but was refused each time because the company failed to provide clinical evidence to refute reports of patients who developed nerve damage in their limbs after long-term thalidomide use. The FDA finally approved the drug for some other uses in 1998.
- 7.
In a group containing elements a, b, c… elements a and b are conjugate if a = c−1bc. Every element is necessarily conjugate with itself (e.g., let c = E).
- 8.
“Spiegel” is German for “mirror.” These groups contain only an n-fold rotoreflection axis, where n must be even because when n is odd an n-fold rotoreflection axis is equivalent to a combination of an n-fold rotation axis and a perpendicular mirror plane: Sn = Cnh.
- 9.
These are sometimes referred to as reps, but the term irreps is much more widely accepted; therefore, to avoid confusion, reps will be used in reference to reducible representations, while irreps will be used for irreducible ones.
- 10.
Fans of Sudoku should love this!
- 11.
I cheated because I already knew what the character table looked like.
- 12.
In a group containing elements a, b, c… elements a and b are conjugate if a = c−1bc. Every element is necessarily conjugate with itself (e.g., let c = E).
- 13.
It is left to the reader to prove that \( {E}^{-1}{\upsigma}_{\mathrm{v}}E={C}_2^{-1}{\upsigma}_{\mathrm{v}}{C}_2={\upsigma}_{\mathrm{v}}\ne {\upsigma_v}^{\prime } \).
- 14.
An overtone band is the spectral band that occurs in a vibrational spectrum of a molecule when the molecule makes a transition from the ground state (v = 0) to the second excited state (v = 2), where v is the vibrational quantum number for the molecule. Overtone bands are multiples of the fundamental absorption frequency; that is, the first overtone is approximately twice the energy of the fundamental.
- 15.
I’m very impressed with you so far!
- 16.
The correct orientation of the site group symmetry elements can be easily inferred by placing an atom in a general position x,y,z and generating all the symmetry-related positions with crystal-simulation software.
Works Cited
G. Placzek, “Rayleigh-Streuung und Raman-Effekt,” in Handbuch der Radiologie, E. Marx, Ed., Leipzig, Akademische Ver-lagsgesellschaft M.B.H., 1934, p. 205–374.
“Application Note – The Raman Spectrum of Water,” StellarNet Inc., 14 August 2019. [Online]. Available: https://www.stellarnet.us/application-note-raman-spectrum-water/.
G. Behrens, L. Kuhn, R. Ubic and A. Heuer, “Raman spectra of vateritic calcium carbonate,” Spectroscopy Letters, vol. 28, no. 6, pp. 983–995, 1995.
W. G. Fately, F. R. Dollish, N. T. McDevitt and F. F. Bentley, Infrared and Raman Selection Rules for Molecular and Lattice Vibrations: The Correlation Method, New York: John Wiley and Sons, 1972.
G. Behrens, “The Martensitic Transformation in Zirconia, PhD Thesis, Case Western Reserve University,” 1993.
Author information
Authors and Affiliations
Review Questions
Review Questions
-
1.
Define the terms point group, abelian, holohedral, and enantiomorphic.
-
2.
Given the general position x,y,z, a mirror plane with a normal parallel to z would give rise to what symmetry-related position?
-
3.
Identify the point symmetry of the planar pattern shown below. Use a diagram on the image itself to illustrate the symmetry elements of this point group.
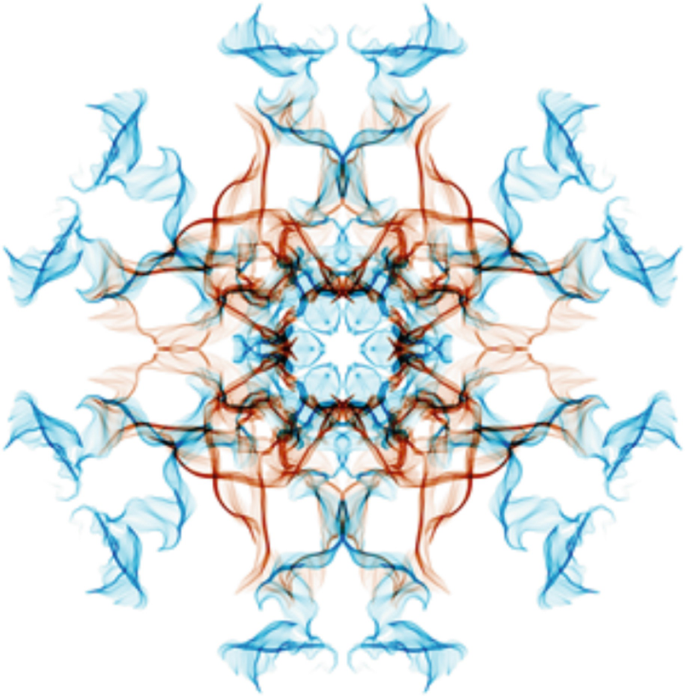
Calculate the coordinates of all of the general positions for this point group in an appropriate coordinate system.
-
4.
Draw objects in the 422 (D4) point group, placing all the correct symmetry elements in the appropriate places.
Calculate the coordinates for all the general positions.
Is there a centre of symmetry? How can you tell mathematically?
-
5.
What point group symmetry would result by adding an inversion centre to \( \overline{4}2\mathrm{m} \)?
-
6.
What point symmetry is formed by the outer radial daffodil petals shown below? What would the new point symmetry be if the central cone-shaped petal were also considered?

-
7.
Two unusual descriptions of point symmetry include 2m and 3/mm. What are the conventional notations? Draw the point groups, indicating both atomic positions and symmetry operations, and place the correct symmetry symbol in the centre.
-
8.
Draw a representation of 2/m point symmetry, including all the necessary symmetry elements and symmetry-related objects. Using this diagram, construct a multiplication table for this point group. Use either Schönflies or Hermann-Mauguin notation. Is this group abelian?
HINT: The order of the group is four.
-
9.
Draw a representation of 3m point symmetry, including all the necessary symmetry elements and symmetry-related objects, uniquely labeling all of the mirror symmetry elements present. Using this diagram, construct a multiplication table for this point group using the same labels. Use either Schönflies or Hermann-Mauguin notation. Is this group abelian?
HINT: The order of the group is six.
-
10.
Draw in all of the nontrivial proper rotation axes and/or mirror planes present within the planar pattern below. Outline the smallest primitive unit cell in the pattern. To what plane group does this pattern belong?

-
11.
State the point group that results if a centre of symmetry is added to the following 10 point groups: 1, 2, 3, 4, 6, 222, 422, 432, 23, and 32.
-
12.
In the image below:
Identify with the appropriate symbols all of the nontrivial proper rotation axes and reflection planes present.
Sketch in the smallest possible primitive unit cell.
To which planar system does this pattern belong? What is the plane group?

Rights and permissions
Copyright information
© 2024 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Ubic, R. (2024). Point Symmetry. In: Crystallography and Crystal Chemistry. Springer, Cham. https://doi.org/10.1007/978-3-031-49752-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-49752-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-49751-3
Online ISBN: 978-3-031-49752-0
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)





