Keywords

1 Introduction

When a diatomic molecule is exposed to intense light, the valence electron may tunnel from a higher potential (corresponding to an upfield atom) due to the suppressed internuclear barrier. This process is known as ionization enhancement and is a key mechanism in strong field ionization of molecules. Alternatively, the bound electron wave function can evolve adiabatically in the laser field, resulting in ionization from the downfield atom. We recently introduced a method for quantitatively retrieving the ratio of ionization events at the upfield and downfield atomic site in a diatomic molecule by comparing experimental data with quantum trajectory Monte Carlo simulations (QTMC) [1]. Our technique is based on the electron’s deflection in the asymmetric Coulomb potential of the molecule that is tilted against the laser polarization direction. This introduces an asymmetry in the final photoelectron momentum distribution, which depends on the ratio of electrons born at the upfield or downfield atom. We then applied this method to available experimental data from strong field ionization of a neutral N2 molecule with infrared laser light [2]. We found that although adiabatic evolution of the bound electron wave function (leading to increased downfield ionization) dominates for neutral molecules, nonadiabatic enhanced ionization still makes a significant contribution under typical experimental conditions, corresponding to the intermediate value γ ≈ 1, where γ is the Keldysh parameter.

The results described above rely on comparison of experimental data with semiclassical simulations. Below we detail Quantum Trajectory Monte Carlo simulations for modeling strong field ionization of diatomic molecules. Such simulations are valuable in interpreting strong field ionization experiments, where the Time Dependent Schrodinger Equation (TDSE) simulations become formidable even for a much simpler case of a helium atom [3]. The computational costs of TDSE scale unfavorably with wavelength, making semiclassical simulations, such as the ones presented in this paper, especially valuable for more complicated systems (such as molecules) or lower-frequency mid-infrared fields.

2 General Approach

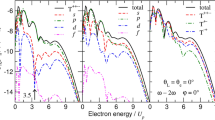
Below we present the methods behind Quantum Trajectory Monte Carlo (QTMC) simulation of molecules. These simulations arose from Classical Trajectory Monte Carlo (CTMC) simulations, with essential difference being that a phase is attached to each trajectory, accounting for quantum interference [4]. This becomes especially valuable for simulations of molecules, where trajectories coming from different parts of the molecule can interfere with each other (see Fig. 1).

Fig. 1
A simulation plot of V z versus V x for a strong field ionization of an N 2 molecule. Values decrease from the center to the periphery peaking at 7 to the power of 10 from (negative 1, 0.0) to (1, 0.0).

Results of Quantum Trajectory Monte Carlo Simulations (QTMC) after strong field ionization of an N2 molecule. The peak laser intensity is 1.3 × 1014 W/cm2 and wavelength is 800 nm, same as in [2]

Full size image

2.1 Details of QTMC Simulations

To understand the asymmetry observed in the experimental data, Quantum Trajectory Monte Carlo (QTMC) simulations were performed [5], where the corrections proposed in [6] and the phase depending on the atomic positions with respect to the polarization direction introduced in [7] were included. The peak intensity was set to I = 1.3 × 1014 W/cm2 and the wavelength is 800 nm, just as in the experiment [2]. As we want to compare our results directly to experimental results, assuming a constant intensity is not sufficient but we have to take into account that there is a spatial variation of the intensity in the focal volume. This intensity profile is commonly described by a Lorentzian along the laser beam axis, which for the sake of consistency with the nomenclature of cylindrical coordinates we will set to z for the following derivation, and by a Gaussian profile in ρ, the distance perpendicular to the beam axis [8].

Furthermore, in order to take into account that the shape of the molecular orbital changes the probability distribution of the initial transverse momentum, we modified the probability distribution by a pre-factor obtained in a partial Fourier transform [9], analogously to the way described in [10]. The molecular orbital that is needed for this method was computed in the STO-6G Gaussian basis with the restricted Hartree-Fock (RHF) method using the quantum chemistry package GAMESS [11]. In the basis set name, STO stands for ‘Slater Type Orbitals’ and 6G signifies that each atomic Slater-type orbital is represented by six Gaussian basis functions. The accuracy of the RHF/STO-6G calculation is supported by the fact that the ionization potential, computed according to Koopmans’ theorem [12] as minus the energy of the highest occupied molecular orbital, is 0.57 a.u. = 15.5 eV. This value is very close to the experimentally observed ionization potential of 15.6 eV.

The laser is polarized along the x-axis and is six cycles long under a cosine-squared-envelope. The ionization potential is chosen to be Ip = 15.6 eV [13]. Since we are in the intermediate nonadiabatic regime (γ = 0.9994), the nonadiabatic ionization theory of Li et al. [14] was used to describe the initial conditions at the tunnel exit. The Coulomb potential used during propagation is the same as the one described in the supplementary of [2] and in [7], where the positive charge that the molecule has after ionization is distributed equally between the two atomic centers.

One of the main challenges is that the tunneling barrier is not only modified by the laser field but also by the Coulomb potential from the other nucleus. Since the mutual distortion of the Coulomb wells is so weak at the tunnel exit that it is a good approximation to employ the atomic theory of Ref. [14] with the unshifted ionization potential of Ip = 15.6 eV to calculate the initial spatial conditions. Subsequently, as this theory assumes an atom placed at the origin, we merely shift this result by the central position of the respective atom the electron is born at.

Thus, we calculate the tunnel exits. In contrast, the tunnel width that mainly determines the tunneling probability is strongly affected by the internuclear Coulomb distortion and we cannot simply employ an atomic ionization theory that does not properly account for this effect when calculating the rates. Since solving this problem of the ratio of ionization from the up and downfield well is the aim of this work, we scan through different ionization ratios. This will lead to different degrees of asymmetry, which can then be compared to the asymmetry obtained from the experiment. To this end, we defined the ratio q of ionization from the two different sites as \( q=\frac{\# up-\# down}{\# up+\# down} \), where #up and #down are the number of electrons born upfield and downfield, respectively. The limits of q = −1 and q = +1 therefore correspond to the electrons being born exclusively downfield or upfield, respectively. Note that the two different atoms change being the up- and downfield atom several times during the pulse as the sign of the electric field changes.

A sample momentum distribution obtained in the described QTMC simulation is shown above.

2.2 Results

Sweeping over the ionization ratio in QTMC simulations, one can obtain a unique map of the ionization site ratio onto the asymmetry parameter. Locating the experimental asymmetry parameter on this theoretical map (see green dot in Fig. 2 below) allows to estimate the ratio at which the electrons were released from the up- and downfield well from the experimental data. The result indicates that ionization from the downfield well is favored in the studied system. Asymmetries like the one described here can be expected in any system that exhibits a notable asymmetry in the molecular potential with respect to the axis of polarization direction and thus to have a wide range of applications. The method presented in [1] stands out in that it tracks the ionization site for single ionization of neutral molecules, where the technique of analyzing Coulomb explosion, that has so far been used to track ionization sites in diatomic molecules, is not applicable.

Fig. 2
A fitted line graph plots a declining trend for a versus q. The experimental asymmetry is indicated at (negative 0.30, 0.0025), approximately.

Asymmetry in the electron momentum distribution (given by parameter “a” on the y-axis) as a function of the ratio of upfield vs. downfield ionization, given by “q” on the x-axis. The experimental asymmetry parameter (green dot) is extracted from the measurements published in [2]. In [1], the ratio q is extracted by comparing experimental data to QTMC simulations (points plotted with error bars). The experimental q = −0.379 obtained from this figure (see intersection of the vertical green line with the x-axis) corresponds to roughly two downfield electrons appearing for every upfield electron. The error bars account for the uncertainly in orientation of plus/minus 5 degrees

Full size image

As the asymmetry in the momentum distribution is due to the asymmetry in the Coulomb potential, this work also stands in line with those recent publications that highlight the importance of including the Coulomb effect as accurately as possible when theoretically describing holographic effects [15,16,17,18,19]. In particular, this study is a case in point for the strength of QTMC simulations over using SFA theories. As highest accuracy is required in terms of the Coulomb potential here, it is not sufficient to include the Coulomb potential perturbatively as it is, for example, done in Coulomb-corrected SFA theories [20, 21].

3 Conclusion and Outlook

Improvement of the theory presented here could be achieved by higher accuracy in the theoretical description of the diatomic model. For example, it is not clear whether it is a good approximation to distribute the ionic charge evenly to the two atomic centers after ionization. Even though the model of even charge distribution has been successfully applied in the theoretical interpretation of the very experimental data that are again used here, in the TDSE simulations [2] and the QTMC simulations in [7], a deeper study along these lines seems warranted, in particular if the theory is applied to other molecular systems.

Speaking of other systems, it seems important to emphasize that the theory presented can be applied to other molecules and laser parameters as well.

A larger bond length of the molecule would be expected to lead to a more pronounced asymmetry in the photoelectron momentum distribution, as long as the underlying assumptions of our model are satisfied. However, one should keep in mind that a larger bond length might change the whole underlying process, for example, of how the remaining positive charge is distributed to the ionic cores. Varying the bond length would be interesting in particular in that one might observe the transition from the electron being primarily born at the downfield atom to the electron being localized at the upfield well. Whereas dominant ionization from the downfield atom is expected in small molecules in which adiabatic adaption of the electron position plays a dominant role, as it was found to be the case for the N2 molecule presented in this chapter, the electron can be localized at the upfield well in larger molecules due to nonadiabatic effects that are crucial in the phenomenon of ionization enhancement (CREI).