Abstract
Scientists and practitioners increasingly rely on machine learning to model data and draw conclusions. Compared to statistical modeling approaches, machine learning makes fewer explicit assumptions about data structures, such as linearity. Consequently, the parameters of machine learning models usually cannot be easily related to the data generating process. To learn about the modeled relationships, partial dependence (PD) plots and permutation feature importance (PFI) are often used as interpretation methods. However, PD and PFI lack a theory that relates them to the data generating process. We formalize PD and PFI as statistical estimators of ground truth estimands rooted in the data generating process. We show that PD and PFI estimates deviate from this ground truth not only due to statistical biases, but also due to learner variance and Monte Carlo approximation errors. To account for these uncertainties in PD and PFI estimation, we propose the learner-PD and the learner-PFI based on model refits and propose corrected variance and confidence interval estimators.
C. Molnar, T. Freiesleben and G. König—Equal contribution.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- XAI
- Interpretable Machine Learning
- Permutation Feature Importance
- Partial Dependence Plot
- Statistical Inference
- Uncertainty Quantification
1 Introduction
Statistical models such as linear or logistic regression models are frequently used to learn about relationships in data. Assuming that a statistical model reflects the data generating process (DGP) well, we may interpret the model coefficients in place of the DGP and draw conclusions about the data. An important part of interpreting the coefficients is the quantification of their uncertainty via standard errors, which allows separation of random noise (non-significant coefficients) from real effects.
Increasingly, machine learning (ML) approaches – such as gradient-boosted trees, random forests or neural networks – are being used in science instead of or in addition to statistical models as they are able to learn highly-non linear relationships and interactions automatically. Applications range from modeling volunteer labor supply [4], mapping fish biomass [17], analyzing urban reservoirs [36], identifying disease-associated genetic variants [8], to inferring behavior from smartphone use [43]. However, in contrast to statistical models, machine learning approaches often lack a mapping between model parameters and properties of the DGP. This is problematic, since in scientific applications the model is only the means to an end: a better understanding of the DGP, in particular to learn what features are predictive of the target variable.
Interpretation methods [41] are a (partial) remedy to the lack of interpretable parameters of more complex models. Model-agnostic techniques, such as partial dependence (PD) plots [20] and permutation feature importance (PFI) [9, 18] can be applied to any ML model and are popular methods for describing the relationship between input features and model outcome on a global level. PD plots visualize the average effect that features have on the prediction, and PFI estimates how much each feature contributes to the model performance and therefore how relevant a feature is.
Scientists who want to use PD and PFI to draw conclusions about the DGP face a problem as these methods have been designed to describe the prediction function, but lack a theory linking them to the DGP. In particular, the uncertainty of PD and PFI with respect to the DGP is not quantified, making it hard for scientists to assess the extent to which it is justified to draw conclusions based on the PD and PFI.
Contributions. We are the first to treat PD and PFI as statistical estimators of ground truth properties in the DGP. We introduce two notions, model-PD/PFI and learner-PD/PFI, which allow to analyze the uncertainty due to Monte-Carlo integration and uncertainty due to the training data/process, respectively. We perform bias-variance decompositions and propose theorems of unbiasedness, standard estimators, and confidence intervals for both PD and PFI. In addition, we leverage a variance correction approach from model performance estimation [35] to adjust for variance underestimation due to sample dependency.
Structure. We start with a motivating example (Sect. 1.1) and a discussion of related work (Sect. 1.2). In the methods section (Sect. 2), we introduce PD and PFI formally, relate them to the DGP, and provide bias-variance decompositions, variance estimators and confidence intervals. In the simulation study in Sect. 3, we test our proposed methods in various settings and compare them to alternative approaches. In the application in Sect. 4, we revisit the motivating example to demonstrate how our confidence intervals for PD/PFI may help scientists to draw more justified conclusions about the DGP. Finally, we discuss the limitations of our work in Sect. 5.
1.1 Motivating Example
Imagine a researcher who wants to use machine learning methods and the publicly available UCI heart disease dataset [15] (\(n=918\)) not only to predict heart disease, but also to understand how the disease is associated with sociological and medical indicators.
To select the model class, she compares the performance w.r.t. the predicted probabilities of a logistic regression model, a decision tree (CART) [10], and a random forest classifier [9] using 5-fold cross validation measured by the Brier score on the dataset; the mean losses for the different models are 0.130 (logistic regression), 0.258 (tree), and 0.125 (random forest). Since the random forest outperforms the linear model and decision tree, she uses a random forest for further analysis; she fits the model on 60% of the data and uses the remaining 40% as test set.Footnote 1
To learn about the associations in the data, she applies the PD and PFI. To get interpretations that are true to the data and that avoid extrapolation, she employs conditional sampling based versions of PD and PFI (for a discussion of marginal versus conditional sampling, we refer to the literature [13, 19], Sect. 2.1, and Sect. 2.3). The conditional PD corresponds to the expected prediction and therefore indicates how the probability of having heart disease varies with the feature of interest [19]. Conditional feature importance quantifies the surplus contribution of each feature over the remaining features (and can be linked to conditional dependence with the prediction target [28, 45]).Footnote 2
The results (Fig. 1) match the researcher’s intuition. Many conditional PFI values are small, indicating that the features could be replaced with the remaining features. The most important features are the slope of the ECG segment (STSlope), the type of chest pain (ChestPainType), and cholesterol level (Cholesterol). Furthermore, the researcher is interested in the relationship between heart disease and age. Thus, she inspects the corresponding conditional PD plot. She observes that the probability of having chronic heart disease increases with age and that there is a small bump around the age of 55.
Although the researcher finds the results plausible, she is unsure whether her conclusions extend to the data generating process (DGP). Are features with nonzero feature importance actually relevant, or are the values nonzero by chance? Does the shape of the PDP really reflect the data? After all, various uncertainties could influence her result: The feature importance and conditional PD results vary when they are recomputed - even for the same model; and the random forest fit itself is a random variable as well.
Throughout this paper, we propose confidence intervals for partial dependence and feature importance values that take the uncertainties from the estimation of the interpretability method and the model fitting into account. We will return to this example in Sect. 4 and Fig. 6, where we show how our approach can help the researcher to evaluate the uncertainty in her estimates.
1.2 Related Work
PD: For models with inherent variance estimators (such as Bayesian additive regression trees) it is possible to construct model-based confidence intervals [11]. Moosbauer et al. [34] introduced a variance estimator for PD which is applicable to all probabilistic models that provide information on posterior (co)variance, such as Gaussian Processes (GPs). Furthermore, various applied articles contain computations of PD confidence bands [4, 16, 17, 22, 36, 37]. These approaches either quantify only the error due to Monte Carlo approximation or do not account for underestimation of the variance when covering learner variance. This demonstrates the need for a theoretical underpinning of this inferential tool for practical research.
PFI: Various proposals for confidence intervals and variance estimation exist. Many of them are specific to the random forest PFI [3, 26, 27], for which Altmann et al. [1] propose a test for null importance. There are also model-agnostic accounts that are more similar to our work [45,46,47], however, unlike these other proposals, we additionally correct for variance underestimation arising from resampling [35] and relate the estimators to the proposed ground truth PFI. An alternative approach for providing bounds on PFI is proposed by Fisher et al. [18] via Rashomon sets, which are sets of models with similar near-optimal prediction accuracy. Our approach differs since our bounds are relative to a fixed model or learning process, whereas Rashomon sets are defined exclusively by the model performance. Furthermore, alternative approaches of “model-free” inference have been introduced [38, 39, 48], which aim to infer properties of the data without an intermediary machine learning model.
2 Methods
In this section, we present our formal framework: We introduce notation and background on PD and PFI (Sect. 2.1); formulate PD and PFI as estimators of (proposed) ground truth estimands in the DGP (Sect. 2.3); apply bias and variance decompositions and separate different sources of uncertainty (Sect. 2.4); and propose variance estimators and confidence intervals for the model-PD/PFI (which only takes the variance from Monte-Carlo integration into account, see Sect. 2.5) and the learner-PD/PFI (which also takes learner variance into account, see Sect. 2.6).
2.1 Notation
We denote the joint distribution induced by the data generating process as \(\mathbb {P}_{XY}\), where X is a p-dimensional random variable and Y a 1-dimensional random variable. We consider the case where we aim to describe the true mapping from X to the target Y with \(f(X) = E[Y\mid X=x]\).Footnote 3 We denote a single random draw from the DGP with \(x^{(i)}\) and \(y^{(i)}\), and a dataset consisting of n draws \(\mathcal {D}_n\).
A machine learning model \(\hat{f}\) is a function (\(\hat{f}: \mathcal {X}\rightarrow \mathcal {Y}\)) that maps a vector x from the feature space \(\mathcal {X}\subseteq \mathbb {R}^p\) to a prediction \(\hat{y}\) (e.g. in \(\mathcal {Y}= \mathbb {R}\) for regression). The model \(\hat{f}\) is induced based on a dataset \(\mathcal {D}_{n}\), using a loss function \(L: \mathcal {Y}\times \mathbb {R}^p \rightarrow \mathbb {R}_0^+\). The model \(\hat{f}\) is induced by the learner algorithm \(I: \Delta \rightarrow \mathcal {H}\) that maps from the space of datasets \(\Delta \) to the function hypothesis space \(\mathcal {H}\). The learning process contains an essential source of randomness, namely the training data. Since the model \(\hat{f}\) is induced by the learner fed with data, it can be seen as a realization of a random variable \(F\) with distribution \(\mathbb {P}_{F}\). We assume that the model is evaluated with a risk function \(\mathcal {R}(\hat{f}) = \mathbb {E}_{XY} [L(Y, \hat{f}(X))] = \int L(y, \hat{f}(x)) d\mathbb {P}_{XY}\). The dataset \(\mathcal {D}_n\) is split into \(\mathcal {D}_{n_1}\) for model training and \(\mathcal {D}_{n_2}\) for evaluation. The empirical risk is estimated with \(\hat{\mathcal {R}}(\hat{f}_{\mathcal {D}_{n_2}, \lambda }) := \frac{1}{n_2} \sum _{i=1}^{n_2} L\left( y^{(i)},\hat{f}_{\mathcal {D}_{n_2}, \lambda }(x^{(i)})\right) \).
Many interpretation techniques require perturbing variables by resampling from marginal or conditional distributions. We use \(\phi \) to denote a sampler, which can formally be seen as a density function. A dataset drawn with a marginal sampler (denoted \(\phi _{marg}\)) follows \(P(X_j)\), and a dataset drawn with a conditional sampler (denoted \(\phi _{cond}\)) follows \(P(X_j|X_C)\). The choice of the sampler affects the interpretation of PD and PFI [2, 18, 32, 33, 45] and should depend on the modeler’s objective. Under certain conditions, the marginal sampler allows to estimate causal effects [49], but for correlated input features, the marginal sampler may create unrealistic data and the conditional sampler may be a better choice to draw inference [19] (see online Appendix A [31] for details).
2.2 Interpretation Techniques
Partial Dependence Plot. The PD of a feature set \(X_S\), \(S\subseteq \{1,\ldots ,p\}\) (usually \(\mid S \mid = 1\)) for a given \(x \in X_S\), a model \(\hat{f}\) and a sampler \(\phi : \mathcal {X}_S\rightarrow \lbrace \psi \mid \psi \) density on \(\mathcal {X}_C\rbrace \) is:
where \(\tilde{X}_C\) is a random variable distributed with density \(\phi (x)\), and C denote the indices of the remaining features so that \(S \cup C = \{1,\ldots , p\}\) and \(S \cap C = \emptyset \).
To estimate the PD for a specific function \(\hat{f}\) using Monte Carlo integration, we draw \(r\in \mathbb {N}\) samples for every \(x\in \mathcal {X}_S\) from \(\phi (x)\) and denote the corresponding dataset by \(B_{\phi (x)}=(\tilde{x}_C^{(i,x)})_{i=1,\dots ,r}\). The estimation is given by:
By partial dependence plot (PDP) we denote the graph that visualizes the PDP. The PDP consists of a line connecting the points \(\lbrace (x^{(g)}, \widehat{PD}_{S,\hat{f},\phi }(x^{(g)})\rbrace _{g=1}^G\), with G grid points that are usually equidistant or quantiles of \(\mathbb {P}_{X_S}\). See Fig. 1 for an example of a PDP.
For the marginal sampler, the PDP of a model \(\hat{f}\) visualizes the expected effect of a feature after marginalizing out the effects of all other features [20]. For the conditional sampler, the PDP is also called M-plot and visualizes the expected prediction given the features of interest, taking into account its associative dependencies with all other features [2, 20].
Permutation Feature Importance. The PFI of a feature set \(X_S\) (usually just one feature) for a model \(\hat{f}\) and a sampler \(\phi : \mathcal {X}_C\rightarrow \lbrace \psi \mid \psi \) density on \(\mathcal {X}_S\rbrace \) is defined by:
where \(\tilde{X}_S\) is a random variable distributed with density \(\phi (X_C) \sim P(X_S|X_C)\), and \(X_C\) are the remaining features \(\lbrace 1,\dots ,p\rbrace \setminus S\). To estimate the PFI for a specific function \(\hat{f}\) and a sampler \(\phi \) using Monte Carlo integration, we draw \(r\in \mathbb {N}\) samples for every datapoint \(x_C^{(i)}\in \mathcal {X}_C\) (\(x_C^{(i)}\) describes the feature values in C of the i-th instance in the evaluationFootnote 4 dataset \(D_{n_2}\)) from \(\phi (x_C^{(i)})\) and denote the corresponding datasets by \(B_{\phi (x_C^{(i)})}=(\tilde{x}_S^{(k,i)})_{k=1,\dots ,r}\). The estimation is given by:
We restrict PFI to losses that can be computed per instance.Footnote 5 See Fig. 1 for a PFI example.
If we resample the perturbed variables from the marginal distribution, the PFI of a model \(\hat{f}\) describes the change in loss if the feature values in \(X_S\) are randomly sampled from \(X_S\) i.e. the possible dependence to \(X_C\) and Y is broken (extrapolation) [9, 18]. If we sample \(X_S\) conditional on the remaining variables \(X_C\), PFI is also called the conditional PFI and may be interpreted as the additional importance of a feature given that we already know the other feature values [12, 25, 32, 45].
Indices. To avoid indices overhead and because PDP/PFI and their respective estimations are always relative to a fixed feature set S and sampler \(\phi \), we will abbreviate \(PD_{S,\hat{f},\phi }, \widehat{PD}_{S,\hat{f},\phi },PFI_{S,\hat{f},\phi }, \widehat{PFI}_{S,\hat{f},\phi }\) with \(PD_{\hat{f}}, \widehat{PD}_{\hat{f}},PFI_{\hat{f}}, \widehat{PFI}_{\hat{f}}\) respectively.
2.3 Relating the Model to the Data Generating Process
The goal of statistical inference is to gain knowledge about DGP properties via investigating model properties. For example, under certain assumptions, the coefficients of a generalized linear model (i.e. model properties) can be related to parameters of the respective conditional distribution defined by the DGP, such as conditional mean and covariance structure (i.e. DGP properties). Unfortunately, machine learning models such as random forests or neural networks lack such a mapping between learned model parameters and DGP properties. Interpretation methods such as PD and PFI provide external descriptors of how features affect the model predictions. However, PD and PFI are estimators that lack a counterpart estimand in the DGP.
We define the ground truth version of PD and PFI, we call them DGP-PD and the DGP-PFI, as the PD and PFI applied to the true function f instead of the trained model \(\hat{f}\):
Definition 1 (DGP-PD)
The DGP-PD is the PD applied to function \(f:\mathcal {X}\mapsto \mathcal {Y}\) of the DGP with sampler \(\phi : \mathcal {X}_S\rightarrow \lbrace \psi \mid \psi \) density on \(\mathcal {X}_C\rbrace \).
Definition 2 (DGP-PFI)
The DGP-PFI is the PFI applied to function \(f:\mathcal {X}\mapsto \mathcal {Y}\) of the DGP with sampler \(\phi : \mathcal {X}_C\rightarrow \lbrace \psi \mid \psi \) density on \(\mathcal {X}_S\rbrace \).
Note that the DGP-PD and DGP-PFI may not be well-defined for all possible samplers. The DGP \(f(x)=\mathbb {E}[Y\mid X=x]\) for instance is undefined for \(x\in \mathcal {X}\) with zero density (\(\psi _X(x)=0\)). For the marginal sampler, for instance, DGP-PD and DGP-PFI might not be defined if the input features show strong correlations [25]. Conditional samplers, on the other side, do not face this threat as they preserve dependencies between features and therefore do not create unrealistic inputs [2, 18, 32, 45].Footnote 6 However, under certain conditions, it can still be useful to also use other samplers than the conditional samplers to gain insight into the DGP. For example, under certain conditions, the marginal PDP allows to estimate causal effects [49] or recover relevant properties of linear DGPs [23].
Clearly, the function f is unknown in most applications, which makes it impossible to know the DGP-PD and DGP-PFI for these cases. However, Definitions 1 and 2 enable, at least in theory, to compare the PD/PFI of a model with the PD/PFI of the DGP in simulation studies and to research statistical biases. More importantly, the ground truth definitions of DGP-PD and DGP-PFI allow us to treat PD and PFI as statistical estimators of properties of the DGP.
In this work, we study PD and PFI as statistical estimators of the ground truth DPG-PD and DGP-PFI – including bias and variance decompositions – as well as confidence interval estimators. DGP-PD and DGP-PFI describe interesting properties of the DGP concerning the associational dependencies between the predictors and the target [19]; however, practitioners must decide whether these properties are relevant to answer their question or if different tools of model-analysis provide more interesting estimands.
2.4 Bias-Variance Decomposition
The definition of DGP-PD and DGP-PFI gives us a ground truth to which the PD and PFI of a model can be compared – at least in theory and simulation. The error of the estimation (mean squared error between estimator and estimand) can be decomposed into the systematic deviation from the true estimand (statistical bias) and the learner variance. PD and PFI are both expectations over the (usually unknown) joint distribution of the data. The expectations are therefore typically estimated from data using Monte Carlo integration, which adds another source of variation to the PFI and PD estimates. Figure 2 visualizes the chain of errors that stand between the estimand (DGP-PD, DGP-PFI) and the estimates (\(\widehat{PD}\), \(\widehat{PFI}\)).
For the PD, we compare the mean squared error (MSE) between the true DGP-PD (\(PD_{f}\) as defined in Eq. 1) with the theoretical PD of a model instance \(\hat{f}\) (\(PD_{\hat{f}}\)) at position x.
Here, \(F\) is the distribution of the trained models, which can be treated as a random variable. The bias-variance decomposition of the MSE of estimators is a well-known result [21]. For completeness, we provide a proof in online Appendix B [31]. Figure 3 visualizes bias and variance of a PD curve, and the variance due to Monte Carlo integration.
Similarly, the MSE of the theoretical PFI of a model (Eq. 3) can be decomposed into squared bias and variance. The proof can be found in online Appendix C [31].
The learner variance of PD/PFI stems from variance in the model fit, which depends on the training sample. When constructing confidence intervals, we must take into account the variance of PFI and PDP across model fits, and not just the error due to Monte Carlo integration. As we show in an application (Sect. 4), whether PD and PFI are based on a single model or are averaged across model refits can impact both the interpretation and especially the certainty of the interpretation. We therefore distinguish between model-PD/PFI and learner-PD/PFI, which are averaged over refitted models. Variance estimators for model-PD/PFI only account for variance due to Monte Carlo integration.
Illustration of bias, variance and Monte Carlo approximation for the PD with marginal sampling. Left: Various PDPs using different data for the Monte Carlo integration, but keeping the model fixed. Right: The green dashed line shows the DGP-PDP of a toy example. Each thin line is the PDP for the model fitted with a different sample, and the thick blue line is the average thereof. Deviations of the DGP-PDP from the expected PDP are due to bias. Deviations of the individual model-PDPs from the expected PDP are due to learner variance. (Color figure online)
2.5 Model-PD and Model-PFI
Here, we study the model-PD and the model-PFI, and provide variance and confidence interval estimators. With the terms model-PD and model-PFI, we refer to the original proposals for PD [20] and PFI [9, 18] for fixed models. Conditioning on a given model \(\hat{f}\) ignores the learner variance due to the learning process. Only the variance due to Monte Carlo integration can be considered in this case.
The model-PD estimator (Eq. (2)) is unbiased regarding the theoretical model-PD (Eq. (1)). Similarly, the estimated model-PFI (Eq. 4) is unbiased with respect to the theoretical model-PFI (Eq. 3). These findings rely on general properties of Monte Carlo integration, which state that Monte Carlo integration converges to the integral due to the law of large numbers. Proofs can be found in online Appendix D and F [31]. Moreover, under certain conditions, model-PD and model-PFI are unbiased estimators of the DGP-PD (Theorem 1) and DGP-PFI (Theorem 2), respectively.
To quantify the variance due to Monte Carlo integration and to construct confidence intervals, we calculate the variance across the sample. For the model-PD, the variance can be estimated with:
Similarly for the model-PFI, the variance can be estimated with:
where \(L^{(i)} = \frac{1}{r} \sum _{k=1}^{r} L(y^{(i)}, \hat{f}(\tilde{x}_S^{(k,i)},x^{(i)}_C)) - L(y^{(i)}, \hat{f}(x^{(i)}))\).
The model-PD and model-PFI are mean estimates of independent samples with estimated variance. As such, they can be modelled approximately with a t-distribution with \(r-1\) and \(n_2 - 1\) degrees of freedom, respectively. This allows us to construct point-wise confidence bands for the model-PD and confidence intervals for the model-PFI that capture the Monte Carlo integration uncertainty. We define point-wise \(1-\alpha \)-confidence bands around the estimated model-PD:
where \(t_{1-\tfrac{\alpha }{2}}\) is the \(1-\alpha /2\) quantile of the t-distribution with \(r - 1\) degrees of freedom. We proceed in the same manner for PFI but with \(n_2-1\) degrees of freedom:
Confidence intervals for model-PD and model-PFI ignore the learner variance. Therefore, the interpretation is limited to variance regarding the Monte Carlo integration, and we cannot generalize results to the DGP. The model-PD/PFI and their confidence bands/intervals are applicable when the focus is a fixed model.
2.6 Learner-PD and Learner-PFI
To account for the learner variance, we propose the learner-PD and the learner-PFI, which average the PD/PFI over m model fits \(\hat{f}_d\) with \(d \in \{1,\ldots ,m\}\). The models are produced by the same learning algorithm, but trained on different data samples, denoted by training sample indices \(B_d\) and the remaining test data \(B_{-d}\) so that \(B_d \cap B_{-d} = \emptyset \) and \(B_d \cup B_{-d} = \mathcal {D}_n\). The learner-variants are averages of the model-variants, where for each model-PD/PFI, the model is repeatedly “sampled” from the distribution of models \(F\).
The learner-PD is therefore the expected PD over the distribution of models generated by the learning process, i.e. \(\mathbb {E}_{F}[PD_{\hat{f}}(x)]\). We estimate the learner-PD with:
where \(\hat{f}_d\) is trained on sample indices \(B_d\) and the PD estimated with data \(B_{\phi (x),d}\) using a sampler \(\phi \) m-times.
Following the PD, the learner-PFI is the expected PFI over the distribution of models produced by the learner: \(\mathbb {E}_{F}[PFI_{\hat{f},\phi }]\). We propose the following estimator for the learner-PFI:
where losses \(L^{(i)}_{d} = L(y^{(i)}, \hat{f}_d(x^{(i)}))\) and \(\bar{\tilde{L}}^{(i)}_{d} = \frac{1}{r}\sum _{k=1}^{r} L(y^{(i)}, \hat{f}_d(\tilde{x}^{(k,i,d)}_S, x^{(i)}_C))\) are estimated with data \(B_{-d}\) and m-times sampled data \(B_{\phi (x),d}\) for a model trained on data \(B_d\). A similar estimator has been proposed by Janitza et al. [27] for random forests.
Bias of the Learner-PD. The learner-PD is an unbiased estimator of the expected PD over the distribution of models \(F\), since
The bias of the learner-PD regarding the DGP-PD is linked to the bias of the learner. If the learner is unbiased, the PDs are unbiased as well.
Theorem 1
Learner unbiasedness implies PD unbiasedness:
\(\mathbb {E}_{F}[\hat{f}(x)] = f(x) \implies \mathbb {E}_{F}[PD_{\hat{f}}(x)] = PD_{f}(x)\)
Proof Sketch 1
Applying Fubini’s Theorem allows us to switch the order of integrals. Further replacing \(\mathbb {E}_{F}[\hat{f}(x)]\) with f proves the unbiasedness. A full proof can be found in online Appendix E [31].
By learner bias, we refer to the expected deviation between the estimated \(\hat{f}\) and the true function f. Particularly interesting in this context is the inductive bias (i.e. the preference of one generalization over another) that is needed for learning ML models that generalize [30]. A wrong choice of inductive bias, such as searching models \(\hat{f}\) in a linear hypotheses class when f is non-linear, leads to deviations of the expected \(\hat{f}\) from f. But there are also other reasons why a bias of \(\hat{f}\) from f may occur, for example if using an insufficiently large sample of training data. We discuss the critical assumption of learner unbiasedness further in Sect. 5.
Bias of the Learner-PFI. The learner-PFI is unbiased regarding the expected learner-PFI over the distribution of models \(F\), since the learner-PFI is a simple mean estimate. However, unlike the learner-PD, learner unbiasedness does not generally imply unbiasedness of the learner-PFI regarding the DGP-PFI. This is generally only the case, if we use the conditional sampler.
Theorem 2
If the learner is unbiased with \(\mathbb {E}_{F}[\hat{f}]=f\) and the L2-loss is used, then the conditional model-PFI and conditional learner-PFI are unbiased estimators of the conditional DGP-PFI.
Proof Sketch 2
Both L and \(\tilde{L}\) can be decomposed into bias, variance, and irreducible error. Due to the subtraction, the irreducible error vanishes, and the differences of biases and variances remain. Model unbiasedness sets the bias terms to zero and variance becomes zero due to conditional sampling. The extended proof can be found in online Appendix G [31].
Intuitively, the model-PFI and learner-PFI should tend to have a negative bias and therefore underestimate the DGP-PFI. A model cannot use more information about the target than what is encoded in the DGP. However, as Theorem 3 shows, under specific conditions, the PFI using conditional sampling can be larger than the DGP-PFI.
Theorem 3
The difference between the conditional model-PFI and the conditional DGP-PFI is given by:
Proof Sketch 3
For the L2 loss, the expected loss of a model \(\hat{f}\) can be decomposed into the expected loss between \(\hat{f}\) and f and the expected variance of Y given X. Due to the subtraction, the latter term vanishes. The remainder can be simplified using that  and \(P(\tilde{X_S},X_C)=P(X_S,X_C)\) due to the conditional sampling. The extended proof can be found in online Appendix H [31].
and \(P(\tilde{X_S},X_C)=P(X_S,X_C)\) due to the conditional sampling. The extended proof can be found in online Appendix H [31].
However, for an overestimation of the conditional PFI to occur, the expected conditional variance of \(\hat{f}\) must be greater than the one of f. Moreover, \(\hat{f}\) and f must have a large expected conditional covariance, meaning that \(\hat{f}\) has learned something about f.
Variance Estimation. The learner-PD and learner-PFI vary not only due to learner variance (refitted models), but also due to using different samples each time for the Monte Carlo integration. Therefore, their variance estimates capture the entire modeling process. Consequently, learner-PD/PFI along with their variance estimators bring us closer to the DGP-PD/PFI, and only the systematic bias remains unknown.
We can estimate this point-wise variance of the learner-PD with:
And equivalently for the learner-PFI:
The correction term c depends on the data setting. In simulation settings that allow us to draw new training and test sets for each model, we can use \(c = 0\), yielding the standard variance estimators. In real world settings, we usually have a fixed dataset of size n, and models are refitted using resampling techniques. Consequently, data are shared by model refits, and variance estimators will underestimate the true variance [35]. To correct the variance estimate of the generalization error for bootstrapped or subsampled models, Nadeau and Bengio [35] suggested the correction term \(c = \frac{n_2}{n_1}\) (where \(n_2\) and \(n_1\) are sizes of test and training data). However, the correction remains a rough correction, relying on the strongly simplifying assumption that the correlation between model refits depends only on the number of shared observations in the respective training datasets and not on the specific observations that they share. While this assumption is usually wrong, we show in Sect. 3.1 that the correction term offers a vast improvement for variance estimation – compared to using no correction.
Confidence Bands and Intervals. Since the learner-PD and learner-PFI are means with estimated variance, we can use the t-distribution with \(m-1\) degrees of freedom to construct confidence bands/intervals, where m is the number of model fits. The point-wise confidence band for the learner-PD is:
where \(t_{1-\tfrac{\alpha }{2}}\) is the respective \(1-\alpha /2\) quantile of the t-distribution with \(m-1\) degrees of freedom. Equivalently, we propose a confidence interval for the learner-PFI:
Taking the learner variance into account can affect the interpretation, as we show in the application in Sect. 4. An additional advantage of the learner-PD and learner-PFI is that they make better use of the data, since a larger share of the data is employed as test data compared to only using a small holdout set.
3 Simulation Studies
In this Section, we study the coverage of the confidence intervals for the learner-PD/PFI on simulated examples (Sect. 3.1) and compare our proposed refitting-based variance estimation with model-based variance estimators (Sect. 3.2).
3.1 Confidence Interval Coverage Simulation
In simulations, we compared confidence interval performance between bootstrapping and subsampling, with and without variance correction. We simulated two DGPs: a linear DGP was defined as \(y = f(x) = x_1 - x_2 + \epsilon \) and a non-linear DGP as \(y = f(x) = x_1 - \sqrt{1 - x_2} + x_3 \cdot x_4 + (x_4/10)^2 + \epsilon \). All features were uniformly sampled from the unit interval [0; 1], and for both DGPs, we set \(\epsilon \sim N(0,1)\). We studied the two settings “simulation” and “real world” as described in Sect. 2.1. In both settings, we trained linear models (lm), regression trees (tree) and random forests (rf) each 15 times, and computed confidence intervals for the learner-PD and learner-PFI across the 15 refitted models. In the “simulation” setting, we sampled \(n \in \{100, 1000\}\) fresh data points for each model refit, where \(63.2\%\) of the data were used for training and the remaining \(36.8\%\) for PDP and PFI estimation.Footnote 7
In the “real world” setting, we sampled \(n \in \{100, 1000\}\) data points once per experiment, and generated \(15 \) training data sets using a bootstrap (sample size n with replacement, which yields \(0.632 \cdot n\) unique data points in expectation) or subsampling (sample size \(0.632 \cdot n\) without replacement). In both settings, the learner-PD and learner-PFI as well as their respective confidence intervals were computed over the \(15 \) retrained models. We repeated the experiment 10,000 times and counted how often the estimated confidence intervals covered the expected PD or PFI (\(\mathbb {E}_{F}[PD_{\hat{f}}]\) and \(\mathbb {E}_{F}[PFI_{\hat{f}}]\)) over the distribution of models \(F\).Footnote 8 These expected values were computed using 10,000 separate runs. The coverage estimates were averaged across features per scenario and for PD also across grid points (\(\{0.1, 0.3, 0.5, 0.7, 0.9\}\)) for all features.
Table 1 shows that in the “simulation” setting (“ideal”), we can recover confidence intervals using the standard variance estimation with the desired coverage probability. However, in the “real world” setting, the confidence intervals for both the learner-PD and learner-PFI are too narrow across all scenarios and both resampling strategies when the intervals are based on naive variance estimates. Some coverage probabilities are especially low, such as for linear models with 30%–40%.
The coverage probabilities drastically improve when the correction term is used (see Fig. 4a). However, in the simulated scenarios, these probabilities are still somewhat too narrow. For the linear model, the confidence intervals were the narrowest, with coverage probabilities of around 80%–90% for PD and 60%–80% for PFI across DGPs and sample sizes. The PD confidence bands were not heavily affected by increasing sample size n, but the PFI estimates became slightly narrower in most cases. In the case of decision trees, the adjusted confidence intervals were sometimes too large, especially for the adjusted bootstrap.
Except for trees on the non-linear DGP, the bootstrap outperformed subsampling in terms of coverage, i.e. the coverage was closer to the 95% level and rather erred on the side of “caution” with wider confidence intervals (see Fig. 4b). As recommended by Nadeau and Bengio [35], we used 15 refits. We additionally analyzed how the coverage and interval width changed by increasing refits from 2 to 30 and noticed that the coverage worsened with more refits while the width of the confidence intervals decreased. Increasing the number of refits incurs an inherent trade-off between interval width and coverage: The more refits are considered, the more accurate the learner-PFI and learner-PD become, and also the more certain the variance estimates become, scaling with 1/m. However, there is a limit to the information in the data, such that additional refits falsely reduce the variance estimate and the confidence intervals become too narrow. To refit the model 10–20 times seemed to be an acceptable trade-off between coverage and interval width, as demonstrated in Fig. 5. Below \({\sim }10\) refits, the confidence intervals were large and the mean PD/PFI estimates have a high variance. Above \({\sim }20\) refits, the widths no longer decreased substantially. The figures for the other scenarios can be found in online Appendix I [31].Footnote 9 With our simulation results, we could show that employing confidence intervals using the naive variance estimation (without correction) results in considerably too narrow intervals. While the simple correction term by Nadeau and Bengio [35] does not always provide the desired coverage probability, it is a vast improvement over the naive approach. We therefore recommend using the correction when computing confidence intervals for learner-PD and learner-PFI, as this is currently the best approach available. We also recommend refitting the model approximately 15 times. For more “cautious” confidence intervals, we recommend using confidence intervals based on resampling with replacement (bootstrap) over sampling without replacement (subsampling). However, besides wider confidence intervals, the bootstrap also requires additional attention when model-tuning with internal resampling is used; otherwise, data points may inadvertently be used in both training and validation datasets.
3.2 Comparison to Model-Based Approaches
While our methods based on model-refits provide confidence intervals for PD and PFI in a model-agnostic manner, it is also possible to exploit (co)variance estimates of probabilistic models to construct confidence intervals. Here, we will, for the case of PDFootnote 10, compare our approach with the model-based approach of Moosbauer et al. [34] applied to a Gaussian Process (GP) and a linear model (LM).Footnote 11 We find that our approach more reliably delivers better coverages that are closer to the \(1-\alpha \) confidence level; this can be explained by the fact that the model-based approach ignores the variance in Monte Carlo integration.
We consider the following simulation setting:
with \(X_j {\mathop {\sim }\limits ^{i.i.d.}} U(0,1)\) for all \(j \in \{1,...,5\}\). Given a DGP of the form \(y = f(x) + \epsilon \) the distribution of \(\epsilon \) is set to \(\epsilon \sim N(0, (0.2 \; \sigma (f(x)))^2)\).
We calculate the DGP-PD analytically. The experiments are performed 1000 times for \(n = 200\) and \(n = 1000\), where a random sample of \(n_{1} = 0.632 \cdot n\) is used to fit the models and the remaining \(n_{2} = 0.368 \cdot n\) observations are used to calculate the PD. Since model-based variance estimates for linear models can be derived analytically based on the variance of their coefficients, we additionally compare these estimates to our resampling-based approach (i.e. the learner-PD) for a correctly specified linear model. The model-based variance estimates can be calculated by one model fit per repetition. In contrast, we use 15 refits on subsampled data sets per repetition to compute the variance estimate for the resampling-based approach.Footnote 12 Footnote 13 We choose the grid points \(\{0.1, 0.3, 0.5, 0.7, 0.9\}\) and a confidence level of 0.95 to evaluate the mean and variance estimates of the PDs. Table 2 shows the results for both the model-based (mod) and the adjusted subsampling-based (subs) approach. While the subsampling-based approach shows almost perfect coverages for the different settings, the model-based approach is far off the nominal level with values around 0.35 for the correctly specified linear model. This gap can be explained by the MC integration variance which is not incorporated in the model-based approaches. Hence, if the MC error is relatively high compared to the model variance, coverages are bad. To illustrate this relationship, we calculated the average standard deviation of the MC integration variance estimator (see Eq. (5)) for the model-based approaches (see Table 2). Since the confidence bands of these approaches only cover the model variance, the confidence width is directly proportional to the model variance. If we compare the “MC se” column with the average widths of the model-based approach, it is observable that coverages are rather low (e.g., 0.34 for LM with \(n = 200\)) in the case where “MC se” divided by width is rather high (e.g., \(0.15/0.15 = 1\)) and vice versa.
Thus, if the main goal is to quantify both uncertainty sources inherent in the PD estimation and thus to receive reasonable coverages, the model-based approach cannot be recommended since only one of two sources of variability are covered by the estimates. Even for the linear model, which is commonly used for inferential purposes, the confidence bands for the PD estimates might be far too conservative as shown in Table 2. The subsampling-based variance estimates we proposed in this work however cover both the learner variance and the MC error and provide satisfying coverage values.
4 Application
We apply our proposed estimators to the motivational example from Sect. 1.1. We supposed that a researcher predicted chronic heart disease [15] (\(n=918\)) from sociological and medical indicators such as age, blood pressure and maximum heart rate. She fitted one random forest and estimated conditional PFI and conditional PDPs to interpret the result.
Instead of only computing the conditional PFI and conditional PDP for one model, we estimate the proposed conditional model-PFI and conditional learner-PFI along with the proposed confidence intervals. For the learner-based insights, we therefore refitted the model 15 times on resampled training sets.
Figure 6 shows model and learner based conditional PFI and conditional PDP with the corresponding confidence intervals (\(\alpha =0.05\)).
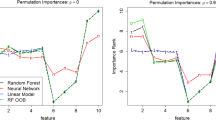
Learner-PFI and model-PFI disagree on the ordering of the features: they agree that slope of the ECG segment (STSlope) and the type of chest pain (ChestPainType) are the most important features; but learner-PFI ranks sex (Sex) and ST depression induced by exercise relative to rest (Oldpeak) next, while model-PFI ranks cholesterol (Cholesterol) second and resting state ECG (RestingECG) third. For both model-PFI and learner-PFI all except two confidence intervals include zero, namely STSlope and ChestPainType. The confidence intervals for model-PFI and learner-PFI indicate that both learner variance and the uncertainty stemming from the Monte Carlo integration are relatively high. The model-PFI cannot tell us to what extent the estimate varies due to learner variance; only the learner-PFI can quantify the learner variance.
Figure 6, bottom row, shows both the conditional model-PDP and the conditional learner-PDP for age (Age). Model-PDP and learner-PDP agree that individuals of higher age are more likely to have heart disease with a strong increase in prevalence around the age of 55. However, the confidence bands of the learner-PDP are wider than those of the model-PDP. Furthermore, the bump that can be observed in the model-PDP around the age of 50 is smoother in the learner PDP and should partly be attributed to uncertainties involved in model fitting. Neglecting the learner variance would mean being overconfident about the partial dependence curve. In particular, the Monte Carlo approximation error decreases with 1/n as the sample size n for PD and PFI estimation increases. Wrongly interpreted, this can lead to a false sense of confidence in the estimated effects and importance since only one model is considered and learner variance is ignored.
5 Discussion
We related the PD and the PFI to the DGP, proposed variance and confidence intervals, and discussed conditions for inference. Our derivations were motivated by taking an external view of the statistical inference process and postulating that there is a ground truth counterpart to PD/PFI in the DGP. To the best of our knowledge, statistical inference via model-agnostic interpretable machine learning is already used in practice, but under-explored in theory.
A critical assumption for inference of effects and importance using interpretable machine learning is the unbiasedness of the learner. The learner bias is difficult to test, and can be introduced by e.g. choice of model class, regularization, and feature selection. For example, regularization techniques such as LASSO introduce a small bias on purpose [44] to decrease learner variance and improve predictive performance. We must better understand how specific biases affect the prediction function and consequently PD and PFI estimates.
Another crucial limitation for inference of PD and PFI is the underestimation of variance due to data sharing between model refits. While we could show that a simple correction of the variance [35] vastly improves the coverage, a proper estimation of the variance remains an open issue. A promising approach relying on repeated nested cross validation to correctly estimate the variance was recently proposed by Bates et al. [6]. However, this approach is more computationally intensive by a factor of up to 1,000.
Furthermore, samplers are not readily available. Especially conditional sampling is a complex problem, and samplers must be trained using data. Training samplers even introduces another source of uncertainty to our estimates that we neglected in our work. It is difficult to separate this source of uncertainty from the uncertainty of the model learner, since trained samplers are correlated not only with each other, but possibly also with the trained models. We see integrating sampler uncertainty as an important step in providing reliable uncertainty estimates in practice, but we leave this to future work.
Statements and Declarations
Funding. This project is supported by the Bavarian State Ministry of Science and the Arts, the Bavarian Research Institute for Digital Transformation (bidt), the German Federal Ministry of Education and Research (BMBF) under Grant No. 01IS18036A, by the German Research Foundation (DFG) – Emmy Noether Grant 437611051 to MNW, and the Carl Zeiss Foundation (project on “Certification and Foundations of Safe Machine Learning Systems in Healthcare”). The authors of this work take full responsibilities for its content.
Availability of Data, Code, and Online Appendix. The data used in the application is openly available and referenced in this paper. The code for visualizations, simulations and the application is written in the R programming language [40] and is publicly available via https://github.com/gcskoenig/paper_inference_code. The online Appendix is available via [31].
Notes
- 1.
All code is publicly available as part of the supplementary material.
- 2.
Conditional interpretation methods require sampling from conditional distributions. She samples categorical variables using a log-loss optimal classifier, and samples continuous variables by predicting the conditional mean and resampling residuals (thereby assuming homoscedasticity). She fits a random forest once on the dataset for all sampling tasks. To model multivariate mixed distributions, she employs a sequential design [5, 7].
- 3.
This choice for f is motivated by the fact that the conditional expectation is the Bayes-optimal predictor for the L2 loss and for the log-loss optimal predictor in binary classification [24].
- 4.
- 5.
This excludes losses such as the area under the receiver operating characteristic curve (AUC).
- 6.
To illustrate the idea of unrealistic data points, think of two strongly correlated features such as the weight and height of a person. Not every combination of feature values is possible – a person with a weight of 4kg and a height of 2m is from a biological perspective inconceivable.
- 7.
We choose this training size (63.2%) to match the expected number of unique samples when using bootstrapping, which allows to compare bootstrapping and subsampling.
- 8.
The coverage does not refer to the DGP-PD/PFI, but rather to the expected learner-PD/PFI, as we studied the choices of resampling and correction for the learner variance.
- 9.
The CI coverage and width: for PD with n = 100 can be found in Figure I.1 and Figure I.2; for PD with n = 1000 can be found in Figure I.3 and Figure I.4; for PFI with n = 100 can be found in Figure I.5 and Figure I.6; for PFI with n = 1000 can be found in Figure I.7 and Figure I.8.
- 10.
We do not know of any application of Moosbauer et al.’s [34] approach to PFI of probabilistic models.
- 11.
- 12.
We use a marginal sampler for perturbations (since we assume uncorrelated features in all scenarios).
- 13.
We did not consider the bootstrapping approach in our experiments as we encountered numerical issues in the invertability of the covariance matrix (due to duplicated values introduced by bootstrap) [42].
References
Altmann, A., Toloşi, L., Sander, O., Lengauer, T.: Permutation importance: a corrected feature importance measure. Bioinformatics 26(10), 1340–1347 (2010)
Apley, D.W., Zhu, J.: Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc.: Ser. B (Stat. Methodol.) 82(4), 1059–1086 (2020)
Archer, K.J., Kimes, R.V.: Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 52(4), 2249–2260 (2008)
Bair, E., et al.: Multivariable modeling of phenotypic risk factors for first-onset TMD: the OPPERA prospective cohort study. J. Pain 14(12), T102–T115 (2013)
Bates, S., Candès, E., Janson, L., Wang, W.: Metropolized knockoff sampling. J. Am. Stat. Assoc. 116(535), 1413–1427 (2021)
Bates, S., Hastie, T., Tibshirani, R.: Cross-validation: what does it estimate and how well does it do it? J. Am. Stat. Assoc. 1–12 (2023)
Blesch, K., Watson, D.S., Wright, M.N.: Conditional feature importance for mixed data. AStA Adv. Stat. Anal. 1–20 (2023)
Boulesteix, A.L., Wright, M.N., Hoffmann, S., König, I.R.: Statistical learning approaches in the genetic epidemiology of complex diseases. Hum. Genet. 139(1), 73–84 (2020)
Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)
Breiman, L., Friedman, J., Stone, C.J., Olshen, R.: Classification and Regression Trees. CRC Press, Cambridge (1984)
Cafri, G., Bailey, B.A.: Understanding variable effects from black box prediction: quantifying effects in tree ensembles using partial dependence. J. Data Sci. 14(1), 67–95 (2016)
Candes, E., Fan, Y., Janson, L., Lv, J.: Panning for gold: ‘model-X’knockoffs for high dimensional controlled variable selection. J. R. Stat. Soc.: Ser. B (Stat. Methodol.) 80(3), 551–577 (2018)
Chen, H., Janizek, J.D., Lundberg, S., Lee, S.I.: True to the model or true to the data? arXiv preprint arXiv:2006.16234 (2020)
Chernozhukov, V., et al.: Double/debiased machine learning for treatment and structural parameters. Economet. J. 21(1), C1–C68 (2018)
Dua, D., Graff, C.: UCI machine learning repository (2017). http://archive.ics.uci.edu/ml
Emrich, E., Pierdzioch, C.: Public goods, private consumption, and human capital: using boosted regression trees to model volunteer labour supply. Rev. Econ./Jahrbuch für Wirtschaftswissenschaften 67(3) (2016)
Esselman, P.C., Stevenson, R.J., Lupi, F., Riseng, C.M., Wiley, M.J.: Landscape prediction and mapping of game fish biomass, an ecosystem service of Michigan rivers. North Am. J. Fish. Manag. 35(2), 302–320 (2015)
Fisher, A., Rudin, C., Dominici, F.: All models are wrong, but many are useful: learning a variable’s importance by studying an entire class of prediction models simultaneously. J. Mach. Learn. Res. 20(177), 1–81 (2019)
Freiesleben, T., König, G., Molnar, C., Tejero-Cantero, A.: Scientific inference with interpretable machine learning: analyzing models to learn about real-world phenomena. arXiv preprint arXiv:2206.05487 (2022)
Friedman, J.H.: Greedy function approximation: a gradient boosting machine. Ann. Stat. 1189–1232 (2001)
Geman, S., Bienenstock, E., Doursat, R.: Neural networks and the bias/variance dilemma. Neural Comput. 4(1), 1–58 (1992)
Grange, S.K., Carslaw, D.C.: Using meteorological normalisation to detect interventions in air quality time series. Sci. Total Environ. 653, 578–588 (2019)
Groemping, U.: Model-agnostic effects plots for interpreting machine learning models. Reports in Mathematics, Physics and Chemistry, Department II, Beuth University of Applied Sciences Berlin. Report 1/2020 (2020)
Hastie, T., Tibshirani, R., Friedman, J.H., Friedman, J.H.: The Elements of Statistical Learning: Data Mining, Inference, and Prediction, vol. 2. Springer, Heidelberg (2009)
Hooker, G., Mentch, L., Zhou, S.: Unrestricted permutation forces extrapolation: variable importance requires at least one more model, or there is no free variable importance. Stat. Comput. 31, 1–16 (2021)
Ishwaran, H., Lu, M.: Standard errors and confidence intervals for variable importance in random forest regression, classification, and survival. Stat. Med. 38(4), 558–582 (2019)
Janitza, S., Celik, E., Boulesteix, A.L.: A computationally fast variable importance test for random forests for high-dimensional data. Adv. Data Anal. Classif. 12(4), 885–915 (2018)
König, G., Molnar, C., Bischl, B., Grosse-Wentrup, M.: Relative feature importance. In: 2020 25th International Conference on Pattern Recognition (ICPR), pp. 9318–9325. IEEE (2021)
Zheng, W., van der Laan, M.J.: Cross-validated targeted minimum-loss-based estimation. In: Zheng, W., van der Laan, M.J. (eds.) Targeted Learning. SSS, pp. 459–474. Springer, New York (2011). https://doi.org/10.1007/978-1-4419-9782-1_27
Mitchell, T.M.: The need for biases in learning generalizations. Citeseer (1980)
Molnar, C., et al.: Online appendix for “Relating the Partial Dependence Plot and Permutation Feature Importance to the Data Generating Process” (2023). https://doi.org/10.6084/m9.figshare.23294945.v1
Molnar, C., König, G., Bischl, B., Casalicchio, G.: Model-agnostic feature importance and effects with dependent features: a conditional subgroup approach. Data Min. Knowl. Discov. 1–39 (2023)
Molnar, C., et al.: General pitfalls of model-agnostic interpretation methods for machine learning models. In: Holzinger, A., Goebel, R., Fong, R., Moon, T., Müller, K.R., Samek, W. (eds.) xxAI 2020. LNCS, vol. 13200, pp. 39–68. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-04083-2_4
Moosbauer, J., Herbinger, J., Casalicchio, G., Lindauer, M., Bischl, B.: Explaining hyperparameter optimization via partial dependence plots. In: Advances in Neural Information Processing Systems, vol. 34, pp. 2280–2291 (2021)
Nadeau, C., Bengio, Y.: Inference for the generalization error. Mach. Learn. 52(3), 239–281 (2003)
Obringer, R., Nateghi, R.: Predicting urban reservoir levels using statistical learning techniques. Sci. Rep. 8(1), 1–9 (2018)
Page, W.G., Wagenbrenner, N.S., Butler, B.W., Forthofer, J.M., Gibson, C.: An evaluation of NDFD weather forecasts for wildland fire behavior prediction. Weather Forecast. 33(1), 301–315 (2018)
Parr, T., Wilson, J.D.: A stratification approach to partial dependence for codependent variables. arXiv preprint arXiv:1907.06698 (2019)
Parr, T., Wilson, J.D., Hamrick, J.: Nonparametric feature impact and importance. arXiv preprint arXiv:2006.04750 (2020)
R Core Team: R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria (2018). https://www.R-project.org/
Ribeiro, M.T., Singh, S., Guestrin, C.: Model-agnostic interpretability of machine learning. ICML WHI 2016 (2016). arXiv preprint arXiv:1606.05386
Roustant, O., Ginsbourger, D., Deville, Y.: DiceKriging, DiceOptim: two R packages for the analysis of computer experiments by kriging-based metamodeling and optimization. J. Stat. Softw. 51(1), 1–55 (2012)
Stachl, C., et al.: Predicting personality from patterns of behavior collected with smartphones. Proc. Natl. Acad. Sci. 117(30), 17680–17687 (2020)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. Roy. Stat. Soc.: Ser. B (Methodol.) 58(1), 267–288 (1996)
Watson, D.S., Wright, M.N.: Testing conditional independence in supervised learning algorithms. Mach. Learn. 110, 2107–2129 (2021)
Williamson, B.D., Gilbert, P.B., Carone, M., Simon, N.: Nonparametric variable importance assessment using machine learning techniques. Biometrics (2019)
Williamson, B.D., Gilbert, P.B., Simon, N.R., Carone, M.: A general framework for inference on algorithm-agnostic variable importance. J. Am. Stat. Assoc. 1–14 (2021)
Zhang, L., Janson, L.: Floodgate: inference for model-free variable importance. arXiv preprint arXiv:2007.01283 (2020)
Zhao, Q., Hastie, T.: Causal interpretations of black-box models. J. Bus. Econ. Stat. 39(1), 272–281 (2021)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Molnar, C. et al. (2023). Relating the Partial Dependence Plot and Permutation Feature Importance to the Data Generating Process. In: Longo, L. (eds) Explainable Artificial Intelligence. xAI 2023. Communications in Computer and Information Science, vol 1901. Springer, Cham. https://doi.org/10.1007/978-3-031-44064-9_24
Download citation
DOI: https://doi.org/10.1007/978-3-031-44064-9_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-44063-2
Online ISBN: 978-3-031-44064-9
eBook Packages: Computer ScienceComputer Science (R0)