Keywords

1 Introduction and Related Work

Machine learning (ML) is on the verge of revolutionizing medical diagnosis, especially in imaging-based specialties such as PET. This new discipline is bringing a wealth of innovations to the analysis of large datasets in critical clinical studies like those focused on neurodegenerative diseases. In this article, we propose a set of ML-based regression models to reproduce [\(^{18}\)F]-FEPPA V\(_{\text {t}}\) values, which are a neuroinflammation hallmark, in a non-invasive way.

Neuroinflammation is a complex process involving the activation of immune cells within the central nervous system (CNS) in response to injury or infection [1]. While it is normal and essential for a neuroinflammation to occur in the brain as a response to previous triggers, it has been proven that an excessive or chronic inflammation may lead to the development and progression of neurodegenerative diseases such as Parkinson’s disease (PD) [2] and lead consequently to a loss of dopamine levels in the striatum region of the brain, more specifically in caudate and putamen regions.

Many factors contribute to this loss, including genetic factors [3], environmental factors [4], age [5], etc. Furthermore, several studies have shown that the activation of inflammatory pathways in the brain can contribute to the death of more dopamine neurons and amplify the motor symptoms of PD [6]. The inflammation in PD is actually characterized by the activation of particular glial cells in CNS, called microglia [7]. Recent studies have shown that a chronic activation of these cells can become harmful to the CNS [8]. Based on that, researchers have targeted neuroinflammation as a hallmark feature for PD’s disease, as well as for other neurodegenerative diseases such as Alzheimer’s disease [9], Huntington’s disease [10], etc. Tracking neuroinflammation can potentially provide valuable insights into the mechanisms underlying these diseases, in addition to an accurate and earlier detection and diagnosis, enabling earlier interventions and treatments [11]. PET uses a special scanner to detect radiation emitted by a small amount of radioactive substance called radiotracer or radiopharmaceutical, that has been injected into the body. The used radiotracer binds to markers of inflammation or other physiological processes that are associated with these diseases.

Researches have proved that measuring microglia activation can be performed through quantifying a protein called translocator 18 kDa protein (TSPO). The expression of TSPO is upregulated when microglia are activated in response to injury or other stimuli in the brain, hence the interest of researchers to develop TSPO radiotracers [12, 13]. [\(^{18}\)F]-FEPPA is one of the newest second generation TSPO PET radiotracer with greater affinity for its target. However, the quantification of its distribution in the brain cells requires the determination of a metabolite-corrected arterial input function (AIF), which is practically done through arterial cannulation. Although the risk related to arterial cannulation is low, it represents an invasive and logistically demanding procedure. Besides, the discomfort caused by this procedure often discourages subjects from participating in PET studies. Given these considerations, much studies have been carried out to obviate the need for arterial cannulation such as Population-Based Input Function (PBIF) [14,15,16,17] and Image Derived Input Function (IDIF) [18,19,20,21].

Recent studies have explored the use of machine learning (ML) approaches for estimating AIF [22,23,24]. While the use of these approaches has not been extensively investigated, recent studies have reported promising results. As the aforementioned methods, MLIF has different challenges to be addressed like the high dependency of its results on the quantity and quality of the available training data.

To the best of our knowledge, this is the first study to investigate the estimation of pharmacokinetic parameters directly from the given Time Activity Curves (TACs) of different brain regions and, hence, avoid any use of AIF. By using ML models, we were able to give an approximate value of V\(_{\text {t}}\), in a non-invasive way. Our results provide a novel perspective on PET images quantification.

Our paper addresses leveraging appropriate ML techniques to predict, in a non-invasive manner, the total volume of distribution (V\(_{\text {t}}\)) given the regional TACs. The data used in this study was acquired with [\(^{18}\)F]-FEPPA radiotracer. We organized our paper as follows: in the first section, we will give an overview of the dataset acquisition, the reference V\(_{\text {t}}\) estimation and the methods we used for Vt prediction. Next, we will discuss the results obtained from our ML models. In the conclusion, we will suggest some directions for future work.

2 Methods

In this section, we present details on features that have been used as input to our models, including data acquisition, region of interest (ROI) delineation, TACs generation, input function used in the quantification of PET data previously published in [25] and the genotype of the subjects included in the analysis. The training data contain relevant information about the biochemical transformations of the tracer in each of the brain regions and the genotype of the studied subject, as well as the correct response to the [\(^{18}\)F]-FEPPA V\(_{\text {t}}\).

2.1 Data Acquisition

Twenty four subjects with Parkinson’s Disease and twenty healthy controls underwent an [\(^{18}\)F]-FEPPA PET and magnetic resonance imaging scan. After radiotracer administration into the body of the patient and PET data acquisition, the collected PET raw data were reconstructed into images using ordered subset expectation maximization with point spread function (OSEM+PSF) reconstruction [26].

2.2 ROI-Based Time Activity Curve Generation

MRI images for all the subjects were acquired for co-registration with the corresponding PET images and the anatomical delineation of the 31 ROIs. The ROI template is transferred to the PET image space to extract the time activity curve for each ROI. The TACs are graphical representations of how radioactive tracers distribute and accumulate within tissues over time. In our study, dynamical series of images of [\(^{18}\)F]-FEPPA PET have been visually checked for head-motion and corrected using frame-by-frame realignment [25].

2.3 Input Function Measurement

AIF is determined during the PET scanning by gathering blood samples at discrete time points from the subject’s radial artery and measuring the concentration of the radioactive compound in every sample. Arterial blood was taken continuously at a rate 2.5 mL/min for the first 22.5 min after radioligand injection and the blood radioactivity levels were measured using an automatic blood sampling system (Model PBS-101 from Veenstra Instruments, Joure, The Netherlands). In addition, 4 to 8 ml manual arterial blood samples were obtained at 2.5, 7, 12, 15, 30, 45, 60, 90, and 120 min relative to time of injection. A bi-exponential function was used to fit the blood-to-plasma ratios. A Hill function was used to fit the percentage of unmetabolized radioligand. The dispersion effect was modeled as to the convolution with a monoexponential with dispersion coefficient of 16 s and corrected with iterative deconvolution [27].

2.4 Polymorphism Genotyping

The quantitative interpretations of [\(^{18}\)F]-FEPPA are impacted by the large inter-individual variability in binding affinity, which displays a trimodal distribution compatible with a co-dominant genetic trait [28]. Study of TSPO polymorphism explained the heterogeneity in binding potential by the difference in the affinity of the second-generation PET ligands for this protein. [\(^{18}\)F]-FEPPA radiotracers bind TSPO in brain tissue from different subjects in one of three ways: high-affinity binders, mixed affinity binders, and low-affinity binders (HABs, MABs and LABs). The transport rate of radiotracer is 1.5 to 2-fold higher in HABs than MABs and 4-fold higher in HABs than LABs. Since LABs are very rare, we limited our data collection to the two groups HABs and MABs only. More insights on TSPO polymorphism can be found in [29].

2.5 Kinetic Analysis

Kinetic modeling is a mathematical approach used in PET imaging to quantify the pharmacokinetics of a radiotracer in various tissues. In this study, we used the 2-compartmental model (2-TCM) [30] to fit our data. This model assumes that the radiotracer in the tissue compartment can be either specifically bound to the target receptor (specifically bound compartment) or it can be free (non-specifically bound compartment). The kinetics of tracer uptake have thus been modeled mathematically through differential equations describing the exchange rate of tracer concentrations among compartments in function of time as follows (1):

$$\begin{aligned} \frac{dC_1}{dt} = K_1 C_p(t) - (k_2 + k_3)C_1(t) + k_4 C_2(t) \end{aligned}$$
(1)
$$\begin{aligned} \frac{dC_2}{dt} = k_3C_1(t) - k_{4}C_2(t) \end{aligned}$$
(2)

where:

\(C_1\) is the tracer concentration in the non-displaceable compartment of the tissue (free and nonspecifically bound), \(C_p\) is the tracer concentration in the plasma also known as Arterial Input Function (AIF), \(C_2\) is the tracer concentration bound to the target receptors, \(K_1\) is the rate constant for transfer of tracer from plasma to the tissue, \(k_2\) is the rate constants for transfer of tracer from tissue to plasma, \(k_3\) and \(k_4\) are the rate constants for transfer of tracer from the non-displaceable compartment to the specific binding compartment of the tissue and vice versa, respectively. Knowing the tissue compartment comprises two different states of binding (non-displaceable + specific binding), the tissue concentration, \(C_t(t)\), is equal to the sum of the two states

$$\begin{aligned} C_t(t) = C_1(t) + C_2(t) \end{aligned}$$
(3)

Using the aforementioned differential equations, \(C_t(t)\) can be defined as follows:

$$\begin{aligned} \begin{gathered} C(t)=\frac{K_1}{b_2-b_1}\left[ \left( k_3+k_4-b_1\right) e^{-b_1 t}\right. \left. +\left( b_2-k_3-k_4\right) e^{-b_2 t}\right] \otimes C_p(t) \end{gathered} \end{aligned}$$
(4)

where \(b_1\) and \(b_2\) expressions are

(5)

and \(\otimes \) denotes the mathematical convolution. In this study, we have a particular interest in deriving quantitative information about the total volume of distribution of the radiotracer as this kinetic parameter reflects the overall density and distribution of the TSPO receptors in the brain. Precisely, V\(_{\text {t}}\) represents the ratio of the tracer amount in the target tissue at equilibrium to the amount of tracer in the plasma at the same time point. Mathematically, V\(_{\text {t}}\) can be expressed in function of model rate constants as follows:

$$\begin{aligned} V_t=K_1 / k_2\left( 1+k_3 / k_4\right) \end{aligned}$$
(6)

In TSPO studies, a higher V\(_{\text {t}}\) indicates a greater amount of tracer binding to the target protein, suggesting a higher level of neuroinflammation in the tissue [31].

2.6 Estimation of Reference Total Volume of Distribution

An estimate of V\(_{\text {t}}\) values was derived using the kinetic modeling tool of PMOD (https://www.pmod.com/web/). We utilized the blood TACs, plasma TACs, and regional TACs of the brain for each subject in our dataset to fit a reversible 2-TCM model, enabling us to estimate Vt values.

2.7 Total Volume of Distribution Prediction

After estimating the reference V\(_{\text {t}}\) values corresponding to each brain region and for each subject, we built our dataset by concatenating the TACs of different subjects. Initially, the TAC file of each subject contains the different intervals of scans, defined by the start and end time of the scan, and the corresponding radiotracer concentration at this interval, with respect to each brain region. On average, we have 31 ROIs for each subject. Then, we added to our dataset 3 categorical variables specifying the brain ROI, the genotype (HAB or MAB) and the health status (Healthy Control or Parkinson). For V\(_{\text {t}}\) prediction, a total of 44 subjects were included for the purpose of establishing predictive models using ML. Our predictive models are tree-based regression models, which use decision trees to predict continuous numerical values. The rationale behind choosing these approaches for our regression problem is their ability to handle the mixture of categorical and continuous variables as inputs, and to capture the non-linear relationships between variables. To find the optimal hyperparameters for our predictive models, a grid search approach was employed. Rather than dividing the available data into separate training and testing groups, 10-fold cross validation was utilized and the average performance was recorded.

2.8 Total Volume of Distribution Evaluation

To evaluate our models, the predicted V\(_{\text {t}}\) values were compared with the ones estimated by kinetic modeling and denoted as reference V\(_{\text {t}}\), for each region of interest, by the mean absolute error (MAE),

$$\begin{aligned} \begin{aligned} \textrm{MAE} = \frac{1}{n}\sum _{i=1}^{n}|Vt_i-\hat{Vt_i}| \\ \end{aligned} \end{aligned}$$
(7)

We also used Bland-Altman as a graphical method, to compare the predicted values of our ML models against the reference values, and asses the level of agreement between them. By plotting the difference between \(\hat{V_t}\) and \(V_t\) against their mean, it will help to identify any systematic bias between the two measurements, as well as the range of differences and outliers.

3 Results and Discussion

Results from comparisons between the reference and the predicted \(V_{t}\) in terms of MAE are summarized in Table 1. As shown in this table, all the tree models have predicted V\(_{\text {t}}\) with a mean absolute error ranging between 2.62 and 3, which is within an acceptable range of error for our particular problem, considering the median value of reference V\(_{\text {t}}\). These results indicate that our models are able to predict the target variable with reasonable accuracy and provide a good fit to the data. After evaluating the performance of the four tree-based models, we found that XGBoost outperformed the other models in terms of its evaluation metrics. It specifically achieved a lower MAE, equal to 2.62 compared to other models, indicating that it has a better overall performance and it can predict the target variable with greater precision. For this model, we investigated the relative importance of each feature in predicting the target variable. Based on the importance scores of XGBoost model, we can conclude that the tracer uptake concentration for the first 7 timepoints are the most influential features in making V\(_{\text {t}}\) predictions. In other words, these features are the most utilized by XGBoost in a split decision, while creating its decision trees.

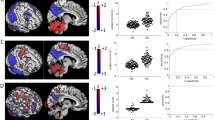
Table 1. Summary of Mean Absolute Error values for the selected machine learning models
Full size table

In order to provide a more comprehensive evaluation of the performance of XGBoost, we used the bland-altman plots as showed in Fig. 1. Central and outer dashed lines indicate mean value and mean ± 1.96 SD. It is important to mention that bland-altman is displaying the difference and average between the reference and predicted V\(_{\text {t}}\) for all the tissues of test data subjects. Figure 1 shows that the mean difference is 0 with a bias of 0.23 ± 2.82, among brain tissues, and 1.96 SD interval equal to −5.30 and +5.77, which is believed to be a tolerable result for a first attempt of predicting V\(_{\text {t}}\) directly from tracer uptake concentration in brain tissues. Furthermore, we can observe that the majority of the data points fell within the limits of agreement, reflecting an overall good agreement between the reference and predicted values of V\(_{\text {t}}\).

Fig. 1.
figure 1

Bland-Altman plots of predicted and reference total volume of distribution \(V_{t}\) using XGBoost model for all brain tissue regions.

Full size image

To further validate the results given by XGBoost, we investigated the ability of our model to highlight the genetic subgroup effects on TSPO binding. These effects have been previously explored in [25]. We are interested in reproducing these results, as we are analyzing the same dataset. In this part of our study, we will be focusing on putamen and caudate nucleus regions, as these regions are critically involved in the pathophysiology of Parkinson’s disease. Given the two possible studied genetic subgroups (HAB or MAB) and health status (HC or PD), we can distinguish between 4 groups as shown in Fig. 2. A total of 12 subjects were substracted from the initial data, 3 subjects from each group (HAB-HC, HAB-PD, MAB-HC and MAB-PD) to constitute the test data and we trained XGBoost model on the remaining data. The results showing the effect of genotype (MAB or HAB) on estimated V\(_{\text {t}}\) and predicted V\(_{\text {t}}\) for the caudate nucleus and putamen are illustrated in Fig. 2. This figure suggests that we can preserve the same effect of genotype revealed by the kinetic modeling estimated V\(_{\text {t}}\), with the exception of caudate V\(_{\text {t}}\) values of one group, which is the PD group. According to ML predicted V\(_{\text {t}}\), there is no significant difference in caudate V\(_{\text {t}}\) values within MAB-PD and HAB-PD, which is not the case for caudate V\(_{\text {t}}\) values, estimated using kinetic modeling. Still we have consistent findings for HC group in both putamen and caudate V\(_{\text {t}}\), and for PD group with regard to putamen V\(_{\text {t}}\) values, which can be considered as satisfactory results.

Fig. 2.
figure 2

Comparison of kinetic modeling estimated \(V_{t}\) and ML predicted \(V_{t}\) in the caudate nucleus and in the putamen, for different genetic subgroups. The two Asterisks in the plot indicate statistical difference between two groups.

Full size image

In Fig. 3, we conducted a paired t-test to determine if there were any significant differences between the reference and predicted values of V\(_{\text {t}}\). We found that predicted V\(_{\text {t}}\) are significantly different from reference V\(_{\text {t}}\) for MAB-PD and MAB-HC, respectively in the caudate nucleus and putamen regions. On the other hand, we have a good agreement between ML and kinetic modeling results for the remaining groups, in both regions, highlighting the consistency of our ML findings.

Fig. 3.
figure 3

Paired t-test showing differences of reference \(V_{t}\) and predicted \(V_{t}\) within subjects of the same subgroup, in both caudate nucleus and putamen tissues. The two Asterisks in the plot indicate statistical difference between two groups.

Full size image

In summary, conventional methods used for quantitative evaluation of PET imaging are achieved by means of kinetic modeling, based on compartmental and non-compartmental approaches. This requires an accurate measurement of IF as well as the application of complex kinetic modeling approaches depending on the used tracer. One of the limitations of compartment modeling is that these models use iterative fitting including IF to calculate the least squares between the measured data and the model data, which can lead to problems of overfitting and lack of reproducibility. In particular, an inappropriate IF often leads to imprecision of the assessed rates. In contrast, our proposed method, based on machine learning approaches and the [\(^{18}\)F]-FEPPA radiotracer dataset, provides a robust and reproducible solution. It is independent of the input function, representing a novelty in the quantitative analysis of PET.

4 Conclusion

In this paper, we investigated the feasibility of non-invasively estimating the V\(_{\text {t}}\) of [\(^{18}\)F]-FEPPA radiotracer, an indicator of neuroinflammation, using its activity concentration in brain tissue. We used several non-linear regression models to predict the [\(^{18}\)F]-FEPPA V\(_{\text {t}}\) in 31 brain regions of interest over 24 patients with Parkinson Disease and 20 healthy subjects. The XGBoost model showed the best results with a MAE of 2.6. Bland-Altman analysis results indicate that predicted V\(_{\text {t}}\) are in average very close to the reference with a bias of 0.23 2.82. We also found that significant main effect of genotype on [\(^{18}\)F]-FEPPA in both caudate and putamen have been preserved by predicted V\(_{\text {t}}\) values (p < 0.05) for the majority of groups. The results of paired t-test indicate that the difference between predicted and reference V\(_{\text {t}}\) is not statistically significant in 6 out of 8 groups. This study opens a new research direction in applying machine learning algorithms to provide a non-invasive and efficient tool to predict [\(^{18}\)F]-FEPPA V\(_{\text {t}}\) values, a hallmark of neuroinflammation that is believed to be a potential trigger for Parkinson’s disease development. As part of future work, our goal will be to develop predictive models to estimate the four pharmacokinetic parameters, namely K1, k2, k3, and k4. By accurately deriving these parameters, we aim to improve the estimation of the physiological parameters of the total volume of distribution V\(_{\text {t}}\) and the binding potential BP.