Abstract
In this paper we investigate the Curry-Howard correspondence for constructive modal logic in light of the gap between the proof equivalences enforced by the lambda calculi from the literature and by the recently defined winning strategies for this logic.
We define a new lambda-calculus for a minimal constructive modal logic by enriching the calculus from the literature with additional reduction rules and we prove normalization and confluence for our calculus. We then provide a typing system in the style of focused proof systems allowing us to provide a unique proof for each term in normal form, and we use this result to show a one-to-one correspondence between terms in normal form and winning innocent strategies.
The first author is supported by Villum Fonden, grant no. 50079. The second author is supported by the PRIN project RIPER (No. 20203FFYLK) The third author is supported by the US Air Force Office for Scientific Research under award number FA9550-21-1-0007.
You have full access to this open access chapter, Download conference paper PDF
Keywords
1 Introduction
Proof theory is the branch of mathematical logic whose aim is studying the properties of logical arguments (i.e., proofs) as well as the structure of proofs and their invariants. For this purpose, the most used representations of proofs are based on tree-like data structures inductively defined using inference rules of a proof system.Footnote 1 Natural deduction and sequent calculus are among the most used proof systems due to their intuitive representation. Both these proof systems were originally devised by Gentzen in order to prove the consistency of first-order arithmetic. Their versatility resulted in their employment for a wide variety of logics.
However, having formalisms able to represent proofs is not enough to define “what is a proof” since different derivations, or derivations in different proof systems, could represent the same abstract object. A notion of proof identity is therefore required to define a proof as a proper mathematical entity [19]. Such a notion of identity is provided by delineating the conditions under which two distinct formal representations of a proof represent the same logical argument. The definition of these conditions are often driven by semantic considerations (by performing specific transformations on two derivations, they can be transformed to the same object) or intuitive ones (two derivations only differ for the order in which the same rules are applied to the same formulas).
Natural deduction is often considered a satisfactory formalism since it allows to define a more canonical representation of proofs with respect to sequent calculus: sequent calculus derivations differing because of some rules permutations are represented (via a standard translation) by the same natural deduction derivation. Moreover, natural deduction provides a one-to-one correspondence between derivations and lambda-terms, called the Curry-Howard correspondence [49].
Constructive Modal Logic. Classical modal logics are obtained by extending classical logic with unary operators, called modalities, that qualify the truth of a judgment. The most used modalities are the \(\Box \) (called box) and its dual operator \(\Diamond \) (called diamond) which are usually interpreted as necessity and possibility. According to the interpretation of such modalities, modal logics find applications, for example, in knowledge representation [52], artificial intelligence [41] and the formal verification of computer programs [20, 37, 46]. The work of Fitch [22] initiated the investigation of the proof theory of modal logics extending intuitionistic logic, leading to numerous results on the topic [21, 27, 36, 40, 47].
In particular, the Curry-Howard correspondence has been extended to various constructive modal logics [7, 10, 17, 32, 33, 45]. Intuitionistic logic can be extended with modalities in different ways (for an overview see [48]): while in classical logic axioms involving only \(\Box \) provide also description of the behavior of \(\Diamond \), for intuitionistic logic this is no more the case since the duality of the two modalities does not hold anymore. This leads to different approaches. Constructive modal logics consider minimal sets of axioms to guarantee the definition of the behaviors of the \(\Box \) and \(\Diamond \) modalities. A second approach, referred to as intuitionistic modal logic, considers additional axioms in order to validate the Gödel-Gentzen translation [15]. In this work we consider a minimal fragment of the constructive modal logic CK only containing the implication \(\rightarrow \) and the modality \(\Box \). This fragment is enough to define types for a \(\lambda \)-calculus with a Let constructor [7] which can be interpreted as an explicit substitution and, for this reason, we more concisely denote by \( N \left[ M_1,\ldots M_n/x_1,\ldots ,x_n\right] _\blacksquare \) instead of \(\textsf{Let}\;M_1,\ldots M_n\;\textsf{be}\;x_1,\ldots ,x_n\;\textsf{in}\;N \).
Recent works on the the proof equivalence of constructive modal logics [6] expose a complexity gap between the proof equivalences induced by the natural deduction [10] and winning innocent strategies [5] for this logic. This discrepancy cannot be observed in intuitionistic propositional logic where there are one-to-one correspondences between natural deduction derivations, lambda terms and innocent winning strategies. In particular, in the logic CK we observe sequent calculus proofs which correspond to the same winning strategy but which cannot be represented by the same natural deduction derivation in the systems provided in [10, 32] (or equivalently corresponding to different modal \(\lambda \)-terms). By means of example, consider the terms \( x \left[ z/x\right] _\blacksquare \) and \( x \left[ z,w/x,y\right] _\blacksquare \) and their (unique) typing derivations shown in Fig. 1 (see Fig. 3 for the typing system).
Intuitively, the two terms \( x \left[ z/x\right] _\blacksquare \) and \( x \left[ z,w/x,y\right] _\blacksquare \) should be semantically equivalent since the explicit substitution of the variable y in the term x is vacuous. Said differently, if we explicit the substitution encoded by the constructor Let, both terms \( x \left[ z/x\right] _\blacksquare \) and \( x \left[ z,w/x,y\right] _\blacksquare \) should reduce to the term z.
In fact, this undesirable behavior disappear when considering the Winning Innocent Strategies for CK defined in [5]. In this syntax, both the above natural deduction derivations correspond to the same strategy below.

Contribution. In this paper we define a new modal \(\lambda \)-calculus for CK by considering additional rewriting rules that allow us to retrieve a one-to-one correspondence between terms in normal form and winning innocent strategies, that is, providing more canonical representatives for proofs with respect to natural deduction and modal \(\lambda \)-terms defined in the literature. From the technical point-of-view, we obtain this result by extending the operational semantics of the modal \(\lambda \)-calculus with the appropriate new reduction rules for the explicit substitution encoded by the Let, dealing with contraction and weakening operating on the variables bound by the Let. We call this set of rules the \(\kappa \)-reduction, which we show to be strongly normalizing using elementary combinatorial methods. In order to deal with the interaction of the \(\eta \)-reduction with \(\beta \)-reduction, we define a restricted \(\eta \)-reduction following an approach similar to the one used in [18, 31, 43]. We prove strong normalization and confluence for our new operational semantics.
After proving confluence and strong normalization for our modal \(\lambda \)-calculus, we provide a canonical typing system inspired by focused sequent calculi (see, e.g., [8]) providing a unique typing derivation for each term in normal form. We conclude by establishing a one-to-one correspondence between the winning strategies defined in [5] and proofs of this calculi, therefore with terms in normal form.
Related Work. To the best of our knowledge, the first paper proposing a Curry-Howard correspondence for the logic CK is [10]. In this work, the authors provide a natural deduction system for the logic CK by enriching the standard system for intuitionistic propositional logic with a generalized elimination rule capable of taking into account the behavior of the \(\Box \)-modality. At the level of lambda calculus, they enrich the syntax of terms by adding a new constructor Let defined as follows:

providing a notation which can be interpreted as an explicit substitution of the variable \(x_i\) with the term \(N_i\) for all occurrences of \(x_1 \ldots , x_n\) inside a term M. For this calculus, the authors only consider the usual \(\eta \) and \(\beta \) reductions plus the following reduction:

In [32] the author considers the usual \(\eta \) and \(\beta \) reduction with an the following additional \(\beta \)-reduction rule specifically designed to handle the explicit substitution construct.

In the same paper, the author provides a detailed proof of strong normalization and confluence for modal lambda terms with respect to the standard \(\eta \) and \(\beta \) reduction, plus this new \(\beta _2\) reduction. However, also this calculus does not manage to fix the aforementioned problem with canonicity.
An alternative natural deduction system (and \(\lambda \)-calculus) is proposed in [33], where the symmetry between elimination and introduction rules typical of natural deduction is restored. However, this result requires to define a sequent calculus where sequents have a more complex structure (dual-contexts), and lacks an in-depth study of the operational semantics because the \(\eta \)-expansion is not considered in the calculus.
Outline of the Paper. In Sect. 2 we recall the definition of the fragment of the logic CK we consider in this paper, as well as the main results on the proof theory for this logic, its natural deduction and lambda calculus. In Sect. 3 we define the modal \(\lambda \)-calculus we consider in this paper, proving its strong normalization and confluence properties. In Sect. 4 we provide a typing system in the style of focused sequent calculi, where we are able to narrow the proof search of the type assignment of our normal terms to a single derivation. In Sect. 5 we recall the definition of the game semantics for the logic we consider and we prove the one-to-one correspondence between terms in normal form and winning strategies.
For reason of space, we omit in the paper the proofs of those technical lemmas that are not particularly interesting (mostly by induction and case analysis). These proofs can be found in the extended version of this paper [4].
2 Preliminaries
In this section we recall the definition of the (fragment of the) constructive modal logic CK we consider in this paper, and we recall the definition and some terminology for modal \(\lambda \)-terms. We are interested in a minimal constructive modal logic whose formulas are defined from a countable set of propositional variables \(\mathcal {A}=\{a,b,c,\ldots \}\) using the following grammar:
We say that a formula is modality-free if it contains no occurrences of the modality \(\Box \). A formula is a \(\rightarrow \) -formula if it is of the form \(A\rightarrow B\). In the following we use Krivine’s convention [38] and write \((A_1, \ldots , A_n )\rightarrow C\) as a shortcut for \((A_1\rightarrow ( \cdots \rightarrow (A_n \rightarrow C)\cdots ))\) A sequent is an expression \(\varGamma \vdash C\) where \(\varGamma \) is a finite (possibly empty) list of formulas and C is a formula. If \(\varGamma =A_1,\ldots ,A_n\) and \(\sigma \) a permutation over \(\{1,\ldots , n\}\), then we may write \(\sigma (\varGamma )\) to denote \(A_{\sigma (1)},\ldots ,A_{\sigma (n)}\).
In this paper we consider the logic CK defined by extending the conjunction-free and disjunction-free fragment of intuitionistic propositional logic with the modality \(\Box \) whose behavior is defined by the necessitation rule and the axiom \(\mathsf K_1\) below.
The sequent calculus \(\textsf{SCK}\), whose rules are provided in Fig. 2, is a sound and complete proof system for the logic CK. This system have been extracted from the one presented in [39] and satisfies cut-elimination.
2.1 A Lambda Calculus for CK
The set of (untyped) modal \(\lambda \)-terms is defined inductively from a countable set of variables \(\mathcal V=\{x,y,\ldots \}\) using the following grammar:

modulo the standard \(\alpha \)-equivalence (denoted \(=_\alpha \), see [9]) and modulo the equivalence generated by the following permutations (for any \(\sigma \) permutation over the set \(\{1,\ldots , n\}\)) over the order of substitutions in the \(\left[ \cdot /\cdot \right] _\blacksquare \) constructor:

As usual, application associates to the left, and has higher precedence than abstraction. For example, \(\lambda xyz.xyz := \lambda x.(\lambda y.(\lambda z.((xy)z)))\). A modal \(\lambda \)-term is a (explicit) substitution if it is of the form
 , an application if of the form MN, and a \(\lambda \) -abstraction if of the form \(\lambda x.M\).
, an application if of the form MN, and a \(\lambda \) -abstraction if of the form \(\lambda x.M\).
The set of subterms of a term M (denoted \( \textsf{SUB}(M)\)) is defined as follows:

Its length \(|M|\) and its set of free variables \(\texttt {FV}(M)\) are defined as:

We denote \(|M|_{x}\) the number of the occurrences of the free variable x in a term M and we may write \(|M|_{x}=0\) if \(x\notin \texttt {FV}(M)\) and we say that a term M is linear in the variables \({x_1, \ldots , x_n}\) if \(|M|_{x_i}=1\) for all \(i\in \{1,\ldots , n\}\). We denote by \(M\left\{ N_1,\ldots , N_n/x_1,\ldots , x_n\right\} \) the result of the standard capture avoiding substitution of the occurrences of the variable \(x_1,\ldots , x_n\) in M with the term \(N_1,\ldots , N_n\) respectively (see, e.g., [50]).
A variable declaration is an expression x : A where x is a variable and A is a type, that is, a formula as defined in Equation (4). A (typing) context is a finite list \(\varGamma {:}{=}x_1: A_1,\ldots , x_n: A_n\) of distinct variable declarations. Given a context \(\varGamma = x_1 : A_1,\ldots , x_n : A_n\), we say that a variable x appears in \(\varGamma \) if \(x=x_i\) for a \(i\in \{1,\ldots , n\}\) and we denote by \(\varGamma , y : B\) the context \({ x_1 : A_1,\ldots , x_n : A_n,y: B}\) implicitly assuming that y does not appear in \(\varGamma \). A type assignment is an expression of the form \(\varGamma \vdash M : A\) where \(\varGamma \) is a context, M a modal \(\lambda \)-term and A a type.
Definition 1
Let \(\varGamma \vdash M : A\) be an type assignment. A typing derivation (or derivation for short) of \(\varGamma \vdash M : A\) in \(\textsf{ND}_{\textsf{CK}}\) is a finite tree of type assignment constructed using the rules in Fig. 3 in such a way it has root \(\varGamma \vdash M: A\) and each leaf is the conclusion of a \(\textsf{Id}\)-rule. A type assignment is derivable (in \(\textsf{ND}_{\textsf{CK}}\)) if there is a derivation with conclusion the given type assignment.
We denote by \(\varLambda \) (resp. by \(\varLambda ^\blacksquare \) and \(\varLambda ^\lambda \)) the set of modal \(\lambda \)-terms (resp. the set of substitutions and \(\lambda \)-abstractions in \(\varLambda \)) admitting a derivable type assignment in \(\textsf{ND}_{\textsf{CK}}\).
3 A New Modal Lambda Calculus
In this section we define a new modal lambda calculus by enriching the operational semantics of the previous calculi with additional reduction rules aiming at recovering canonicity, proving confluence and strong normalization properties.
To define our term rewriting rules, we require special care when they are applied in a proper sub-term. This is due to the fact that the explicit substitution encoded by \(\left[ \cdot /\cdot \right] _\blacksquare \) could capture free variables. For this reason, we introduce the notion of term with a hole as a term of the form \(\textbf{C}\left[ \circ \right] \) containing a single occurrence of a special variable \(\circ \). More precisely, the set \(\mathsf {CwH_{{}}}\) of terms with a hole and the two sets \(\mathsf {CwH_{{\eta _1}}}\) and \(\mathsf {CwH_{{\eta _2}}}\) of specific terms with a hole are defined by the following grammars:

We denote by \(\textbf{C}\left[ M\right] \) the term obtained by replacing the hole \(\circ \) in \(\textbf{C}\left[ \circ \right] \) with the term M. By means of example, if \(\textbf{C}\left[ \circ \right] =\circ \) then \(\textbf{C}\left[ M\right] =M\) and if \( \textbf{E}\left[ \circ \right] = (\lambda x.x N) \left[ \circ /x\right] _\blacksquare \) then \( \textbf{E}\left[ M\right] = (\lambda x.xN) \left[ M/x\right] _\blacksquare \). The reduction relations of our calculus are provided in Fig. 4, where the ground steps and the rules for extending them to specific contexts are provided.
Remark 1
The term constructor Let (i.e., \(\left[ \cdot /\cdot \right] _\blacksquare \) from Equation (2)) plays no role in the standard \(\eta \) and \(\beta \) reduction rules from the literature, where it behaves as a black-box during reduction. The inertness of this constructor with respect to normalization is indeed what makes the lambda calculus in [10, 32] unable to identify terms whose expected behavior is the same as, for example, the following pairs of terms:
Our operational semantics extends the one provided in [32]. The novelty of our approach is the definition of the \(\kappa \)-reduction and the restriction of the \(\eta \)-reduction. The former is needed to being able to identify modal \(\lambda \)-terms with the same expected computational meaning, as the ones in Eq. (5). The latter is carefully defined to avoid \(\eta \)-redexes that would make the reduction non-terminating, using a well-known technique in term rewriting theory (see, e.g., [31, 43]).
The need of these restrictions can be observed in the two following (unrestricted) \(\eta \)-reduction chains, which are both forbidden by our restricted rule from Fig. 4.

Moreover, our definition rules out interactions between the \(\eta \) and \(\beta \) reductions which could lead to infinite chains, as the ones shown below.

Definition 2
We define the following reduction relations:
For any \(\xi \in \{\beta ,\eta , \kappa , \beta \eta ,\beta \kappa , \beta \eta \kappa \}\), we denote by \( \rightsquigarrow ^+_{\xi }\) its transitive closure, by \( \rightsquigarrow ^=_{\xi } \) its reflexive closure, by \( \rightsquigarrow ^*_{\xi } \) its reflexive and transitive closure, and by \(\equiv _\xi \) the equivalence relation it enforces over terms, that is, its reflexive, symmetric and transitive closure. Given a term M, we denote by \( \textsf{nf}_{\xi } (M) \) the set of its \(\rightsquigarrow _{\xi }\) -normal form. A term M is strongly normalizable for \(\rightsquigarrow _{\xi } \) if it admits no infinite \(\rightsquigarrow _{\xi }\)-chains A reduction \(\rightsquigarrow _{\xi }\) is strongly normalizing if every term M is strongly normalizable for it. A reduction \( \rightsquigarrow _{\xi } \) is confluent if given \( M \rightsquigarrow ^*_{\xi } N_1 \) and \( M \rightsquigarrow ^*_{\xi } N_2 \) there exists a term N such that \( N_1 \rightsquigarrow ^*_{\xi } N \) and \( N_2 \rightsquigarrow ^*_{\xi } N\).
The substitution lemma and subject reduction theorem holds for the reduction \(\rightsquigarrow _{\beta \eta \kappa }\).
Lemma 1
[Substitution Lemma] Let \(\varGamma , x: B \vdash M: C\) and \(\varGamma \vdash N : B \) be derivable type assignments. Then \(\varGamma ,x:B\vdash M \left\{ N/ x\right\} : C\) is a derivable type assignment.
Theorem 1
Let \(\varGamma \vdash M: C\) be derivable. If \(M\rightsquigarrow _{\beta \eta \kappa }N\), then \(\varGamma \vdash N: C\).
Proof
Because of Lemma 1, it suffices to check the cases when M reduces to N in one ground step of \(\rightsquigarrow _{\beta \eta \kappa }\):
-
if \(M\rightsquigarrow _{\beta _{1}} N\), then \( M = (\lambda x . P)Q\) and \( N = P \left\{ Q/x\right\} \). The case where \( M \rightsquigarrow _{\beta _{2}} N \) uses a similar argument. The result follows the fact that if \(\varGamma , x: B \vdash M: C\) and \(\varGamma \vdash N : B \) are derivable type assignment, then \(\varGamma ,x:B\vdash M \left\{ N/ x\right\} :C\) by Lemma 1.
-
if \(M\rightsquigarrow _{\eta _{1}} N\), then \(C=A\rightarrow B\) and \(N=\lambda x.Mx\). The result follows by applying the rule \( \textsf{Abs}\). The case where \( M \rightsquigarrow _{\eta _{2}} N \) uses a similar argument;
-
if \(M\rightsquigarrow _{\kappa _{1}} N_1\), then
 such that x is not free in M, \(C=\Box B\), and
such that x is not free in M, \(C=\Box B\), and
 . Then there are derivations for \(\varGamma \vdash P_i:A_i\) for all \(i\in \{1,\ldots , n\}\) (for some \(A_i\)) and a derivation for \( x_1:A_1,\ldots ,x_k: A_k, x : A, x_{k+1}:A_{k+1}\ldots , x_n:A_n \vdash M' : B\). Therefore we have a derivation for \( x_1: A_1,\ldots , x_n: A_n \vdash M' : B\) since weakening is admissible (that is, whenever \(\varGamma ,x:A \vdash M : C\) is derivable and x does not occur free in M, then \(\varGamma \vdash M : C\) is also derivableFootnote 2. Then we have a derivation of \(\varGamma \vdash N: C\) with bottom-most rule a \(\mathsf {\Box \text {-}subst}\) with right-most premise \( x_1 : A_1,\ldots , x_n: A_n\vdash M' : B\). and a premise \(\varGamma \vdash P_i:A_i\) for each \(i\in \{1,\ldots , n\}\);
. Then there are derivations for \(\varGamma \vdash P_i:A_i\) for all \(i\in \{1,\ldots , n\}\) (for some \(A_i\)) and a derivation for \( x_1:A_1,\ldots ,x_k: A_k, x : A, x_{k+1}:A_{k+1}\ldots , x_n:A_n \vdash M' : B\). Therefore we have a derivation for \( x_1: A_1,\ldots , x_n: A_n \vdash M' : B\) since weakening is admissible (that is, whenever \(\varGamma ,x:A \vdash M : C\) is derivable and x does not occur free in M, then \(\varGamma \vdash M : C\) is also derivableFootnote 2. Then we have a derivation of \(\varGamma \vdash N: C\) with bottom-most rule a \(\mathsf {\Box \text {-}subst}\) with right-most premise \( x_1 : A_1,\ldots , x_n: A_n\vdash M' : B\). and a premise \(\varGamma \vdash P_i:A_i\) for each \(i\in \{1,\ldots , n\}\); -
if \(M\rightsquigarrow _{\kappa _{2}} N_1\), then we conclude similarly to the previous point since we have
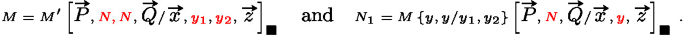
We can prove local confluence of \(\rightsquigarrow _{\beta \eta \kappa }\) by case analysis of the critical pairs using the following lemma.
Lemma 2
Let \(P,P'\) and Q modal \(\lambda \)-terms. If \( P \rightsquigarrow _{\beta \eta \kappa }P'\), then \(P\left\{ Q/x\right\} \rightsquigarrow _{\beta \eta \kappa }^*P'\left\{ Q/x\right\} \). Moreover, there is a \(N_Q\) such that \( Q \left\{ P/x\right\} \rightsquigarrow _{\beta \eta \kappa }^*N_Q\) and \( Q\left\{ P'/x\right\} \rightsquigarrow _{\beta \eta \kappa }^*N_Q\).
Proposition 1
The reduction \(\rightsquigarrow _{\beta \eta \kappa }\) is locally confluent.
Proof
We show that if there are M, \(N_1\) and \(N_2\) with \(N_1\ne N_2\) such that \( M \rightsquigarrow _{\beta \eta \kappa }N_1 \) and \( M \rightsquigarrow _{\beta \eta \kappa }N_2\), then there exists N such that \(N_1 \rightsquigarrow ^*_{\beta \eta \kappa } N \) and \( \rightsquigarrow ^*_{\beta \eta \kappa } N\). Without loss of generality we have the following cases:
-
1.
if \(M\rightsquigarrow _{\beta _{1}}N_1\) with \( M = (\lambda x . P) Q \) and \( N_1 = P \left\{ Q/x\right\} \), then \(N_2\) can only be obtained by applying \(\rightsquigarrow _{\beta \eta \kappa }\) the subterms P and Q of M. We conclude by Lemma 2;
-
2.
if \(M\rightsquigarrow _{\beta _{2}}N_1\) with
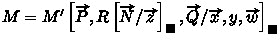 and with
and with
 , then \(N_2\) must be a term obtained by applying \(\rightsquigarrow _{\beta \eta \kappa }\) on R or on one of the terms in
, then \(N_2\) must be a term obtained by applying \(\rightsquigarrow _{\beta \eta \kappa }\) on R or on one of the terms in
 ,
,
 or
or
 . We conclude again by Lemma 2;
. We conclude again by Lemma 2; -
3.
if \(M\rightsquigarrow _{\eta _{1}} N_1\), then \( \varGamma \vdash M : A \rightarrow B \) and \( N_1 = \lambda x . M x\). Therefore, for any \(N_2\) such that \(M \rightsquigarrow _{\beta \eta \kappa }N_2\) we have that \(\varGamma \vdash N_2: A\rightarrow B\) (by subject reduction). Then
-
either \(N_2\) is not an abstraction and we conclude by letting \(N= \lambda x . N_2 x\).
-
otherwise \(N_2=\lambda y.M'\) and we conclude since \(N_1\rightsquigarrow _{\eta _{1}} \lambda x. N_2 x\rightsquigarrow _{\beta _{1}} N_2\).
-
-
4.
if \(M\rightsquigarrow _{\eta _{2}} N_1\) with \( \varGamma \vdash M : \Box A \) and \( N_1 = x \left[ M/x\right] _\blacksquare \), then we conclude with a similar argument with respect to the previous point by letting \(N= x \left[ N_2 /x\right] _\blacksquare \).
-
5.
if \(M\rightsquigarrow _{\kappa _{}}N_1\), then either
 , or
, or
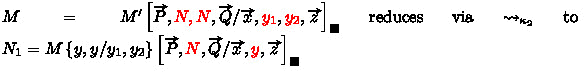 . In both cases we conclude with an argument similar to the one in Case (2).
. In both cases we conclude with an argument similar to the one in Case (2).
In order to prove the termination of \(\rightsquigarrow _{\beta \eta \kappa }\), we define the following measures.
Definition 3
Let M be a modal \(\lambda \)-term. We define the following multisets of derivable type assignments:

We then define \( \Vert M\Vert _\eta {:}{=} \Vert M\Vert _\eta ^1 + \Vert M\Vert _\eta ^2 \) with
We also define \( \Vert M\Vert _\kappa \) as the size of substitution subterms of M as follows:
Example 1
Intuitively, the measure \( \Vert \cdot \Vert _\eta \) does not take into account all the subterms of M, but only the ones on which we can apply the restricted \(\rightsquigarrow _{\eta _{}}\). For an example, consider the modal \(\lambda \)-term \(M = (\lambda z^{ a \rightarrow a }. z) y\) with \( \Vert M\Vert _\eta =3\) because all four subterms of M are of type a \(\rightarrow \)-formula, but the subterm \(\lambda z.z\) is an abstraction, therefore no \(\rightsquigarrow _{\eta _{}}\) can be applied on it. If \(M\rightsquigarrow _{\eta _{}}N\), because of the restrictions on \(\rightsquigarrow _{\eta _{}}\), we have that
-
either \(N = (\lambda z. z) (\lambda v . yv )\) with \( \Vert N\Vert _\eta =2\) because no \(\rightsquigarrow _{\eta _{}}\) can be applied to the subterms y and \(\lambda z.z\) (they occur on the left of an application) or \(\lambda v.yv\) (it is an abstraction), but only to the subterms z and the whole term N;
-
or \(N= \lambda v^a . ((\lambda z. z)y) v \) with \( \Vert N\Vert _\eta =2\) because \(\rightsquigarrow _{\eta _{}}\) can only be applied to the subterms z and y.
Lemma 3
Let M and N be modal \(\lambda \)-terms. If \( M \rightsquigarrow _{\eta _{}}N \), either \( \Vert N\Vert _\eta < \Vert M\Vert _\eta \) or there is \( N' \) such that \( N \rightsquigarrow _{\eta _{}}N' \) and \( \Vert N'\Vert _\eta < \Vert M\Vert _\eta \).
Lemma 4
The following commutations between \(\rightsquigarrow _{\beta _{}}\), \(\rightsquigarrow _{\eta _{}}\) and \(\rightsquigarrow _{\kappa _{}}\) hold:
-
if \(M\rightsquigarrow _{\kappa } N \rightsquigarrow _{\beta } N'\), then there is \( M' \) such that \(M\rightsquigarrow _{\beta } M'\) and \(M'\rightsquigarrow _{\kappa }^{*} N'\) ;
-
if \(M\rightsquigarrow _{\eta } N \rightsquigarrow _{\kappa } N'\), then there is \( M' \) such that \(M\rightsquigarrow _{\kappa } M'\) and \(M'\rightsquigarrow _{\eta }^{*} N'\) ;
-
if \(M\rightsquigarrow _{\beta } N \rightsquigarrow _{\eta } N'\), then there is \( M' \) such that \(M\rightsquigarrow _{\eta } M'\) and \(M'\rightsquigarrow _{\beta }^{*} N'\) .
Theorem 2
The reduction relation \(\rightsquigarrow _{\beta \eta \kappa }\) is strongly normalizing and confluent.
Proof
After Proposition 1, it suffices to prove that \(\rightsquigarrow _{\beta \eta \kappa }\) is strongly normalizing to conclude by Newman’s lemma that \(\rightsquigarrow _{\beta \eta \kappa }\) is also confluent.
To prove strong normalization we use the fact that the reductions \(\rightsquigarrow _{\beta _{}}\), \(\rightsquigarrow _{\eta _{}}\) and \(\rightsquigarrow _{\kappa _{}}\) are strongly normalizing: for \(\rightsquigarrow _{\beta _{}}\) the proof can be found in [32], for \(\rightsquigarrow _{\eta _{}}\) the proof is by induction on \( \Vert \cdot \Vert _\eta \) using Lemma 3, and for \(\rightsquigarrow _{\kappa _{}}\) it follows the fact that, by definition of \( \Vert \cdot \Vert _\kappa \), we have that \( \Vert M\Vert _\kappa > \Vert N\Vert _\kappa \) whenever \( M \rightsquigarrow _{\kappa _{}}N \). To conclude that \(\rightsquigarrow _{\beta \eta \kappa }\) also is strongly normalizing, the standard result (see, e.g., [50]) in rewriting theory ensuring that given two strongly normalizing reduction relations \(\rightsquigarrow _1\) and \(\rightsquigarrow _2 \) with \( \rightsquigarrow _1 \) confluent, if \( M \rightsquigarrow _2 N \) implies the existence of a reduction \(\textsf{nf}_1(M) \rightsquigarrow ^+_{2} \textsf{nf}_1 (N)\) for any M and N, , then \(\rightsquigarrow _1 \cup \rightsquigarrow _2\) is strongly normalizing. In our case, the fact that \( M \rightsquigarrow _2 N \) implies \(\textsf{nf}_1(M) \rightsquigarrow ^+_{2} \textsf{nf}_1 (N)\) is a corollary of Lemma 4.
Definition 4
The set \(\widehat{ \varLambda }\) is the set of modal \(\lambda \)-terms defined inductively as follows:
-
if x is a variable, \(T_1,\ldots , T_n\in \widehat{ \varLambda }\), and there are derivations for the types assignments \( \varGamma \vdash x : (A_1,\ldots , A_n) \rightarrow C\) with C atomic and \( \varGamma \vdash T_i: A_i\) for all \(i\in \{1,\ldots , n\}\), then \(xT_1\cdots T_n\in \widehat{ \varLambda }\). Variables are the special case with \(n=0\);
-
if \( T \in \widehat{ \varLambda }\) and there is a derivation of \( \varGamma , x : A \vdash T:C \), then \(\lambda x^A . T\in \widehat{ \varLambda }\);
-
if \(M\in \widehat{ \varLambda }\), \(\texttt {FV}(M)=\{x_1, \ldots , x_n\}\) and the type assignment \(x_1 : B_1, \dots , x_n : B_n \vdash M : C \) is derivable, and if there are n distinct terms \(T_1,\ldots ,T_n\in \varLambda \) of the shape \(T_i=y_iU_{i1}\cdots U_{ik_i}\) with \(U_{ij}\in \widehat{ \varLambda }\) for all \(i\in \{1,\ldots , n\}\) and \(j\in \{1,\ldots , k_i\}\), such that the type assignment \( \varGamma \vdash T_i:\Box B_i\) is derivable for all \(i\in \{1,\ldots , n\}\), then \( M \left[ T_1,\ldots ,T_n/x_1,\ldots ,x_n\right] _\blacksquare \in \widehat{ \varLambda }\).
Proposition 2
The set \(\widehat{ \varLambda }\) is the set of modal \(\lambda \)-terms in \(\beta \eta \kappa \)-normal form \( \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \).
Proof
By definition, every \(\widehat{ \varLambda }\subseteq \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \) is \(\rightsquigarrow _{\beta \eta \kappa }\)-normal. To prove the converse we proceed by induction on the structure of \( M \in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \):
-
if \( M = x\), then \(M\in \widehat{ \varLambda }\) by definition;
-
if \( M = \lambda x . M'\in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \), then also \( M' \in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \). By inductive hypothesis, this implies \( M' \in \widehat{ \varLambda }\). Therefore \( \lambda x . M' \in \widehat{ \varLambda }\);
-
if \( M = PQ \in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \), then both P and Q are in \( \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \) and there is a derivable type assignment \( \varGamma \vdash M : C\), and derivable type assignments \( \varGamma \vdash P : A \rightarrow C\) and \( \varGamma \vdash Q : A\). We have that no \(\rightsquigarrow _{\eta _{}}\)-rule can be applied to C because \(M\in \textsf{nf}_{\eta } (\varLambda ) \); thus C must be atomic. We know that P cannot be in \(\varLambda ^\lambda \) since \(M\in \textsf{nf}_{\beta } (\varLambda ) \) and P cannot be in \(\varLambda ^\blacksquare \) because \( \varGamma \vdash P : A\rightarrow C\) is derivable. Then by inductive hypothesis we have that \( P = x T_1, \dots T_n \) for some \(T_1,\ldots ,T_n\in \widehat{ \varLambda }\). We conclude that \( PQ \in \widehat{ \varLambda }\);
-
if \( M = P \left[ Q_1, \dots , Q_n/x_1, \dots , x_n\right] _\blacksquare \in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \), then there is a derivable type assignment \( x_1 : B_1, \dots , x_n : B_n \vdash P : C \) and derivable type assignments \(\varGamma \vdash Q_i:\Box B_i\) for all \(i\in \{1,\ldots , n\}\). Since \(M\in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \), then no \(\rightsquigarrow _{\beta \eta \kappa }\)-rule can be applied to M, nor to P; thus \(P\in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \). Similarly, since \(M\in \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \), then \(Q_i\notin \varLambda ^\blacksquare \) (otherwise we could apply \(\rightsquigarrow _{\beta _{}}^2\)), \(Q_i\in \textsf{nf}_{\beta \kappa } (\varLambda ) \) (since no \(\rightsquigarrow _{\beta \kappa }\)-rule can be applied to \( Q_i\)) and \(Q_i\) cannot be in \( \textsf{nf}_{\eta } (\varLambda ) \) (because \(Q_i:\Box B_i\) and otherwise \(\rightsquigarrow _{\eta _{}}\)-steps could be applied on M) for all \(i\in \{1,\ldots , n\}\). We conclude that \(M\in \widehat{ \varLambda }\).
4 A Canonical Type System for CK
In this section we present an alternative typing system for modal \(\lambda \)-terms where each term in \(\widehat{ \varLambda }\) admits exactly one typing derivation. The rules of this system (we call \(\mathsf {CK^F}\)) are provided in Fig. 5 and are conceived to reduce the non-determinism of the typing process, following the same approach used in designing focused sequent calculi [8, 12, 42]. Derivations and derivability in \(\mathsf {CK^F}\) are defined analogously to Definition 1, using rules in \(\mathsf {CK^F}\) instead of rules in \(\textsf{ND}_{\textsf{CK}}\). We remark that the structural rules of weakening and contraction are admissible in the system.
We can now prove a result of canonicity of \(\mathsf {CK^F}\) with respect to typing derivations of modal \(\lambda \)-terms in \( \textsf{nf}_{\beta \eta \kappa } (\varLambda ) \).
Theorem 3
Let \(T\in \widehat{ \varLambda }\) and \(\varGamma \vdash T:A\) be a derivable type assignment. Then there is a unique (up to \(\textsf{ex}\)-rules) derivation of \(\varGamma \vdash T : A\) in \(\mathsf {CK^F}\).
Proof
The proof of this theorem follows from the correspondence between the inductive definition of terms in \(\widehat{ \varLambda }\) (Definition 4) and the shape of the typing rules of \(\mathsf {CK^F}\). Details are provided the extended version of this paper [4].
5 Game Semantics for CK
In this section we recall definitions and results on the winning innocent strategies for the logic CK defined in [5]. For this purpose, we first recall the construction extending Hyland-Ong arenas [29, 44] for intuitionistic propositional formulas to represent formulas containing modalities, and then we recall the characterization of the winning innocent strategies representing proofs in CK. We conclude by proving the full-completeness result between for those strategies by showing a one-to-one correspondence between strategies for type assignments of terms in normal forms and their (unique) typing derivations in \(\mathsf {CK^F}\).
5.1 Arenas with Modalities
We recall the definition of arenas with modalities from [5] extending the encoding of arenas from [26, 30]. For this purpose, we assume the reader familiar with the definition of two-color directed graph (or 2-dag ’s for short), i.e., directed acyclic graphs with two disjoint sets of directed edges
 and
and
 (details can be found in [5, 26]).
(details can be found in [5, 26]).
Definition 5
The arena of a formula F is the 2-dag \(\left[ \!\left[ F\right] \!\right] \) with vertices are labeled by elements in \(\mathcal L=\mathcal A\cup \{\Box \}\) inductively defined as follows:

where \({}a\) and \(\Box \) denote the graphs consisting of a single vertex labeled by a and \(\Box \) respectively, and where the binary operation
 and
and
 on 2-dag’s are defined as follows:
on 2-dag’s are defined as follows:


The arena of a sequent \(A_1,\ldots ,A_n\vdash C\) is the arena \(\mathsf A\) of \(\left[ \!\left[ (A_1,\ldots ,A_n) \rightarrow C\right] \!\right] \).
Remark 2
By construction, an arena \(\mathcal G\) of a formula or a sequent \(\varGamma \vdash C\) always admits a unique non \(\Box \)-labeled vertex in
 , i.e., a unique vertex v with \(\ell (v) \ne \Box \) such that there is no \(w\in V_{\mathcal G}\) such that
, i.e., a unique vertex v with \(\ell (v) \ne \Box \) such that there is no \(w\in V_{\mathcal G}\) such that
 .
.
We draw 2-dag’s by representing a vertex v by its label \(\ell (v)\). If v and w are vertices of an 2-dag, then we draw if
 and if
and if
 . By means of example, consider the arena below.
. By means of example, consider the arena below.

Remark 3
All arenas of the form \(\left[ \!\left[ (A_{\sigma (1)},\ldots ,A_{\sigma (n)}) \rightarrow C\right] \!\right] \) have the same representation for any \(\sigma \) permutation over \(\{1,\ldots , n\}\). More in general, it can be shown that the arena of any two equivalent formulas modulo Currying \(A\rightarrow (B\rightarrow C)\sim B\rightarrow (A\rightarrow C)\) can be depicted by the same arena. However, whenever there may be ambiguity because of the presence of two vertices with the same label, we may represent the vertex \(v=((\cdots (v',i_1) \cdots ),i_n)\) (where \(i_1,\ldots , i_n\in \{0,1\}\)) by \(\ell (v)_{i_1, \ldots , i_n}\) instead of simply \(\ell (v)=\ell (v')\) (see Example 2).
Definition 6
Let \(\left[ \!\left[ F\right] \!\right] \) be an arena and v one of its vertices. The depth of v is the number
 of vertices in a
of vertices in a
 -path from v to a vertex in
-path from v to a vertex in
 Footnote 3. The address of v is defined as the unique sequence of modal vertices \(\textsf{add}({v})=m_1,\dots , m_h\) in \(V_{\left[ \!\left[ F\right] \!\right] }\) corresponding to the sequence of modalities in the path in the formula tree of F connecting the node of v to the root. If \(\textsf{add}({v})=m_1,\dots , m_h\), we denote by \(\textsf{add}^{k}({v})=m_k\) its \(k^{th}\) element and we call the height of v (denoted
Footnote 3. The address of v is defined as the unique sequence of modal vertices \(\textsf{add}({v})=m_1,\dots , m_h\) in \(V_{\left[ \!\left[ F\right] \!\right] }\) corresponding to the sequence of modalities in the path in the formula tree of F connecting the node of v to the root. If \(\textsf{add}({v})=m_1,\dots , m_h\), we denote by \(\textsf{add}^{k}({v})=m_k\) its \(k^{th}\) element and we call the height of v (denoted
 ) the number of elements in \(\textsf{add}({v})\).
) the number of elements in \(\textsf{add}({v})\).
Example 2
Below an alternative representation of its arena of the formula \(\big (a\rightarrow \Box (b\rightarrow (c\rightarrow \Box d))\big )\rightarrow \Box (e\rightarrow f)\) in Equation (8) where the ambiguity of the vertex representation is avoided by the use of indices, the corresponding formula-tree, and the complete list of the addresses of all vertices in this arena.

5.2 Games and Winning Innocent Strategies
In this subsection, we briefly recall the definitions of games and winning strategies from [5] required to make the paper self-contained. Note that differently from the previous works, we here include the additional information of the pointer function in the definition of views. This information is crucial for the results in Sect. 4 where we provide a one-to-one correspondence between our winning strategies and modal \(\lambda \)-terms.
Definition 7
Let \(\mathsf A\) be an arena. We call a move an occurrence of a vertex v of \(\mathsf A\) with \(\ell (v)\ne \Box \). The polarity of a move v is the parity of
 : a move is a \(\circ \) -move (resp. a \(\bullet \) -move) if
: a move is a \(\circ \) -move (resp. a \(\bullet \) -move) if
 is even (resp. odd).
is even (resp. odd).
A pointed sequence in \(\mathsf A\) is a pair \(\mathsf p=\langle \mathsf s_{}, f\rangle \) where \(\mathsf s_{}=\mathsf s_{0},\ldots , \mathsf s_{n}\) is a finite sequences of moves in \(\mathsf A\) and a pointer function \(f:\{1,\ldots , n\} \rightarrow \{0,\ldots , n-1\}\) such that \(f(i)<i \) and
 . The length of \(\mathsf p\) (denoted \(|\mathsf p|\)) is defined as the length of \(\mathsf s_{}\), that is, \(|\mathsf p|=n+1\). Note that we also use \(\epsilon \) to denote the empty pointed sequence \(\langle \epsilon ,\emptyset \rangle \).
. The length of \(\mathsf p\) (denoted \(|\mathsf p|\)) is defined as the length of \(\mathsf s_{}\), that is, \(|\mathsf p|=n+1\). Note that we also use \(\epsilon \) to denote the empty pointed sequence \(\langle \epsilon ,\emptyset \rangle \).
Remark 4
It follows by definition of view that the player \(\circ \) (resp. \(\bullet \)) can only play vertices whose
 is even (resp. odd). For this reason, for each \(v\in V_{\mathcal G}\) we write \(v^{\circ }\) (resp. \(v^{\bullet }\)) if the parity of
is even (resp. odd). For this reason, for each \(v\in V_{\mathcal G}\) we write \(v^{\circ }\) (resp. \(v^{\bullet }\)) if the parity of
 even (resp. odd).
even (resp. odd).
Note that the parity of a modality in the address of a move may not be the same as the parity of the move itself. By means of example, consider the vertex c in Example 2 which belongs in the scope of two modalities \(\Box _{011110}\) and \(\Box _{010}\) with odd parity.
Given two pointed sequences \(\mathsf p=\langle \mathsf s_{}, f\rangle \) and \(\mathsf p'= \langle \mathsf s_{}', f'\rangle \) in \(\mathsf A\), we write \(\mathsf p\sqsubseteq \mathsf p'\) whenever \(\mathsf s_{}\) is a prefix of \(\mathsf s_{}'\) (thus \(|\mathsf s_{}|\le |\mathsf s_{}'|\)) and \(f(i)=f'(i)\) for all \(i\in \{1,\ldots , |\mathsf p'|\}\) and we say that \(\mathsf p\) is a predecessor of \(\mathsf p'\) if \(\mathsf p\sqsubset \mathsf p'\) and \(|\mathsf p|=|\mathsf p'|-1\).
Definition 8
Let \(\mathsf A\) be an arena. A play on \(\mathsf A\) is a pointed sequence \(\mathsf p=\langle \mathsf s_{}, f\rangle \) such that, either \(\mathsf s_{}=\epsilon \), or \(\mathsf s_{i}\) and \(\mathsf s_{i+1}\) have opposite polarities for all \(i\in \{0,\ldots , |\mathsf p|-1\}\).
The game of \(\mathsf A\) (denoted \(\mathcal G_{\mathsf A}\)) is the set of prefix-closed sets of plays over \(\mathsf A\).
A view is a play \(\mathsf p=\langle \mathsf s_{}, f\rangle \) such that either \(\mathsf p=\epsilon \) or the following properties hold:

A winning innocent strategy (or \(\textsf{WIS}\) for short) for the game \(\mathcal G_{\mathsf A}\) is a finite non-empty prefix-closed set \(\mathcal S\) of views in \(\mathcal G_{\mathsf A}\) such that:

A view is maximal in \(\mathcal S\) if it is not prefix of any other view in \(\mathcal S\). \(\mathcal S\) is trivial if \(\mathcal S=\{\epsilon \}\). We say that \(\mathcal S\) is a \(\textsf{WIS}\) for a sequent \(A_1,\ldots , A_n \vdash C\) if \(\mathcal S\) is a \(\textsf{WIS}\) for \(\left[ \!\left[ A_1,\ldots , A_n \vdash C\right] \!\right] \).
The definition of \(\textsf{WIS}\) above is a reformulation of the one in the literature of game semantics for intuitionistic propositional logic [14, 26, 29]. In presence of modalities, this definition requires to be refined to guarantee the possibility of gather modalities in batches corresponding to the modalities introduced by a single application of the \(\textsf{K}^\Box \) (see Fig. 2). By means of example, consider the following arenas and their corresponding \(\textsf{WIS}\)s, which cannot represent valid proofs in CK because of the impossibility of applying rules handling the modalities in a correct way.
Example 3
Consider the formulas \(F_1=(\Box a)\rightarrow a\) and \(F_2=(\Box a \rightarrow \Box b) \rightarrow \Box (a \rightarrow b)\) and their arenas in Fig. 6. The set of views \(\mathcal S_1\) and \(\mathcal S_2\) are \(\textsf{WIS}\)s for \(F_1\) and \(F_2\) respectively. However, these formulas are not provable in \(\textsf{SCK}\) because the proof search fails (see Fig. 6). In particular, in the first case, no \(\textsf{K}^\Box \) can be applied because only there is a mismatch between the modalities on the left-hand side and on the right-hand side of the sequent; in the second case the problem is more subtle and, intuitively, is related to the fact that each \(\textsf{K}^\Box \) can remove only a single \(\Box ^{\circ }\) at a time, corresponding to the modality of the unique formula on the right-hand side of the sequent.
Therefore, in order to capture provability in CK, the notion of winning strategies has to be refined as follows.
Definition 9
Let \(\textsf{p}=(\mathsf s_{}, f)\) be a view in a strategy \(\mathcal S\) on an arena \(\mathsf A\), and let
 . We define the batched view of \(\textsf{p}\) as the
. We define the batched view of \(\textsf{p}\) as the
 matrix \(\mathcal F(\textsf{p})=\big ( \mathcal F(\textsf{p})_{0}, \dots , \mathcal F(\textsf{p})_{n}\big )\) with elements in \(V_{\mathcal G}\cup \{\epsilon \}\) such that the each column \(\mathcal F(\textsf{p})_{i}\) is defined as follows:
matrix \(\mathcal F(\textsf{p})=\big ( \mathcal F(\textsf{p})_{0}, \dots , \mathcal F(\textsf{p})_{n}\big )\) with elements in \(V_{\mathcal G}\cup \{\epsilon \}\) such that the each column \(\mathcal F(\textsf{p})_{i}\) is defined as follows:

We say that \(\textsf{p}\) is well-batched if \(|\textsf{add}({\mathsf s_{2k}})|=|\textsf{add}({\mathsf s_{2k+1}})|\) for every \(2k\in \{0,\ldots , |\mathsf p|-1\}\). Each well-batched view \(\textsf{p}\) induces an equivalence relation
 over \(V_{\mathcal G}\) generated by:
over \(V_{\mathcal G}\) generated by:

A \(\textsf{WIS}\) \(\mathcal S\) is linked if it contains only well-batched views and if for every \(\textsf{p}\in \mathcal S\) the
 -classes are of the shape \(\{v^{\bullet }_1, \dots , v^{\bullet }_n, w^{\circ }\}\).
-classes are of the shape \(\{v^{\bullet }_1, \dots , v^{\bullet }_n, w^{\circ }\}\).
A CK -winning innocent strategy (or \(\textsf{CK}\)-\(\textsf{WIS}\) for short) is a linked \(\textsf{WIS}\) \(\mathcal S\).Footnote 4
Example 4
Consider the arenas in Fig. 6. The batched view of the (unique) maximal views in \(\mathcal S_1\) and \(\mathcal S_2\) are \(\begin{pmatrix}\epsilon &{}\Box ^{\bullet }\\ a^{\circ }&{}a^{\bullet }\end{pmatrix}\) and \(\begin{pmatrix} \Box ^{\circ }_{10} &{} \Box ^{\bullet }_{010}&{}\Box ^{\circ }_{000}&{}\Box ^{\circ }_{10} \\ b^{\circ }&{} b^{\bullet } &{} a^{\circ } &{} a^{\bullet } \end{pmatrix}\) respectively. The first is not well-batched because \(a^{\circ }\) has height 0 while \(a^{\bullet }\) has height 1, while the second, even if well-batched, is not linked because the
 -class \(\{\Box ^{\circ }_{10} , \Box ^{\bullet }_{010},\Box ^{\circ }_{000} \}\) contains two \(\Box ^{\circ }\).
-class \(\{\Box ^{\circ }_{10} , \Box ^{\bullet }_{010},\Box ^{\circ }_{000} \}\) contains two \(\Box ^{\circ }\).
The definition of \(\textsf{CK}\)-\(\textsf{WIS}\)s allows us to obtain a full-completeness result with respect to CK which, together with the good compositionality properties of \(\textsf{CK}\)-\(\textsf{WIS}\)s shown in [5, 11], provides a full-complete denotational semantics for the logic CK. That is, every given \(\textsf{CK}\)-\(\textsf{WIS}\) is the encoding of a derivation in CK, and if a derivation \(\mathcal {D}\) reduces via cut-elimination to a derivation \(\mathcal {D}'\), then they are encoded by the same \(\textsf{CK}\)-\(\textsf{WIS}\).
Theorem 4
([5]). The set of \(\textsf{CK}\)-\(\textsf{WIS}\)s is a full-complete denotational model for CK.
5.3 Full Completeness for Modal Lambda Terms in Normal Form
We can prove the full completeness result using the type system \(\mathsf {CK^F}\) and relying on Theorem 3. For this purpose, we have to extend the definition of \(\alpha \)-equivalence from terms to type assignments in order to avoid technicality in our proofs, since in arenas we keep no track of variable names. For example, consider the \(\alpha \)-equivalent terms \(\lambda x.x\) and \(\lambda y.y\) whose derivation should be considered non-equivalent due to the fact that \(\alpha \)-equivalence does not extends to type assignments, therefore the two occurrence of the axiom rule with conclusion \(x:a\vdash x:a\) and \(y:a\vdash y:a\) should be considered distinct.Footnote 5
Definition 10
Let \(A_1,\ldots ,A_n\vdash C\) be a sequent. We define \(\varLambda (\varGamma \vdash C)\) as the set of terms M such that the typing derivation \(x_1:A_1,\ldots ,x_n:A_n\vdash M:C\) is derivable, that is,
If \(M,N \in \varLambda (\varGamma \vdash C)\), we define \(M =_{\alpha }^{\varGamma ;C}N \) as the smallest equivalence relation generated by the rule
 .
.
From now on, we consider derivations up the \(\alpha \)-equivalence defined above, that is, we consider derivations up to renaming of the variables occurring in a typing context.
Rules to construct a \(\textsf{CK}\)-\(\textsf{WIS}\) from a type derivation in \(\mathsf {CK^F}\). For reasons of readability, we assume there is an implicit map identifying the moves in the arenas of the type assignment in the premises with the moves in the arena of the type assignment in the conclusion. Note that \(c^{\circ }\) and \(c^{\bullet }\) are occurrences of the same atom c, but we have decorate them to improve readability.
Theorem 5
There is a one-to-one correspondence between terms in \(\widehat{ \varLambda }\cap \varLambda (\varGamma \vdash C)\) and \(\textsf{CK}\)-\(\textsf{WIS}\) for \(\varGamma \vdash C\).
Proof
Given a \(\textsf{CK}\)-\(\textsf{WIS}\) \(\mathcal S\) for \(\varGamma \vdash C\), we can define a (unique) typing derivation \(\mathcal {D}_\mathcal S\) in \(\mathsf {CK^F}\) of a term \(T_\mathcal S\in \widehat{ \varLambda }\cap \varLambda (\varGamma \vdash C)\) by induction on the lexicographic order over the pairs \((|\mathcal S|, |C|)\) reasoning on the inductive definition of \(\widehat{ \varLambda }\).
Similarly, given a type assignment \(\varGamma \vdash T: C\). for a \(T\in \widehat{ \varLambda }\), then, by Theorem 3, there is a (unique) derivation \(\mathcal {D}_T\) in \(\mathsf {CK^F}\). We define \(\mathcal S_T\) as the \(\textsf{CK}\)-\(\textsf{WIS}\) defined by induction on the number of rules in \(\mathcal {D}_T\) using the rules in Fig. 7. We conclude since we have that \(\mathcal S_{T_\mathcal S}=\mathcal S\) and \(T_{\mathcal S_T}=T\) by definition.
6 Conclusion
In this paper we introduced a new modal \(\lambda \)-calculus for the \(\Diamond \)-free fragment of the constructive modal logic CK (without conjunction or disjunction). This lambda calculus builds on the work in [32], by adding a restricted \(\eta \)-reduction as well as two new reduction rules dealing with the explicit substitution constructor used to model the modality \(\Box \). We proved normalization and confluence for this calculus and we provide a one-to-one correspondence between the set of terms in normal form and the set of winning strategies for the logic CK introduced in [5].
We foresee the possibility of extending the result presented in this paper to the entire disjunction-free fragment of CK, for which winning strategies are already defined in [5]. For this purpose, we should consider additional term constructors for terms whose type is a conjunction, as well as a new Let-like operator to model terms whose type is the modality \(\Diamond \)-formula similar to the one proposed in [10]. For this reason, in future works we plan to reformulate our lambda-calculus in the light of the novel line of research on calculi with explicit substitutions [1, 2, 34, 35]. This approach would allow us to simplify some of the technicalities and achieve a more elegant operational semantics. Another interesting prospective is to extend our approach to operational semantics to the Fitch-style modal \(\lambda \)-calculus studied in [53].
At the same time, we plan to make explicit that our game semantics provides a concrete model for the cartesian closed categories provided with a strong monoidal endofunctor [10, 33]. Indeed, categorical semantics of the calculus in [10] is modeled by means of cartesian closed categories equipped with a strong monoidal endofunctor taking into account the proof-theoretical behavior of the \(\Box \)-modality. We further conjecture that the syntactic category obtained via the quotient of modal terms modulo the relations we introduce in this paper is indeed a free cartesian closed category on a set of atoms with a strong monoidal endofunctor.
Notes
- 1.
It is worth noting that some proof systems (in the sense of [13]) allows to represent proofs using structures such as infinite trees (for non-well-founded proof systems, see, e.g., [16]), graphs (see proof nets [23, 24], combinatorial proofs [28] or proof diagrams [3]) or structures defined in a compositional way (see open deduction [25] and deep inference [51]).
- 2.
The admissibility of weakening is easily proven by induction on the size of a derivation.
- 3.
- 4.
We here provide a simpler definition of \(\textsf{CK}\)-\(\textsf{WIS}\)s w.r.t. the one in [5]. In fact, we are able here to simplify this definition because we are considering the \(\Diamond \)-free fragment of CK.
- 5.
Note that another possible way to deal with this problem is to label non-modal vertices of arenas by pairs of propositional atoms and variables instead of propositional variables only.
References
Accattoli, B.: Exponentials as substitutions and the cost of cut elimination in linear logic. In: Baier, C., Fisman, D. (eds.) LICS 2022: 37th Annual ACM/IEEE Symposium on Logic in Computer Science, Haifa, Israel, 2–5 August 2022, pp. 49:1–49:15. ACM (2022). https://doi.org/10.1145/3531130.3532445
Accattoli, B., Bonelli, E., Kesner, D., Lombardi, C.: A nonstandard standardization theorem. Association for Computing Machinery, New York (2014). https://doi.org/10.1145/2535838.2535886
Acclavio, M.: Proof diagrams for multiplicative linear logic: syntax and semantics. J. Autom. Reason. 63(4), 911–939 (2019). https://doi.org/10.1007/s10817-018-9466-4
Acclavio, M., Catta, D., Olimpieri, F.: Canonicity of proofs in constructive modal logic (extended version) (2023). https://doi.org/10.48550/arXiv.2304.05465
Acclavio, M., Catta, D., Straßburger, L.: Game semantics for constructive modal logic. In: Das, A., Negri, S. (eds.) TABLEAUX 2021. LNCS (LNAI), vol. 12842, pp. 428–445. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-86059-2_25
Acclavio, M., Straßburger, L.: Combinatorial proofs for constructive modal logic. In: Advances in Modal Logic 2022, Rennes, France (2022). https://hal.inria.fr/hal-03909538
Alechina, N., Mendler, M., de Paiva, V., Ritter, E.: Categorical and Kripke semantics for constructive S4 modal logic. In: Fribourg, L. (ed.) CSL 2001. LNCS, vol. 2142, pp. 292–307. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44802-0_21
Andreoli, J.M.: Focussing and proof construction. Ann. Pure Appl. Logic 107, 131–163 (2001)
Barendregt, H.P., Dekkers, W., Statman, R.: Lambda Calculus with Types. Perspectives in logic. Cambridge University Press, Cambridge (2013). http://www.cambridge.org/de/academic/subjects/mathematics/logic-categories-and-sets/lambda-calculus-types
Bellin, G., De Paiva, V., Ritter, E.: Extended Curry-Howard correspondence for a basic constructive modal logic. In: Proceedings of Methods for Modalities (2001)
Catta, D.: Les preuves vues comme des jeux et réciproquement: sémantique dialogique de langages naturel ou logiques. (Proofs as games and games as proofs: dialogical semantics of logical and natural languages). Ph.D. thesis, University of Montpellier, France (2021). https://tel.archives-ouvertes.fr/tel-03588308
Chaudhuri, K., Marin, S., Straßburger, L.: Modular focused proof systems for intuitionistic modal logics. In: Kesner, D., Pientka, B. (eds.) 1st International Conference on Formal Structures for Computation and Deduction, FSCD 2016, Porto, Portugal, 22–26 June 2016, LIPIcs, vol. 52, pp. 16:1–16:18. Leibniz-Zentrum fuer Informatik (2016)
Cook, S.A., Reckhow, R.A.: The relative efficiency of propositional proof systems. J. Symb. Logic 44(1), 36–50 (1979)
Danos, V., Herbelin, H., Regnier, L.: Game semantics & abstract machines. In: Proceedings, 11th Annual IEEE Symposium on Logic in Computer Science, New Brunswick, New Jersey, USA, 27–30 July 1996, pp. 394–405. IEEE Computer Society (1996). https://doi.org/10.1109/LICS.1996.561456
Das, A., Marin, S.: Brouwer meets kripke: constructivising modal logic. https://prooftheory.blog/2022/08/19/brouwer-meets-kripke-constructivising-modal-logic/. Accessed 19 Aug 2022
Das, A., Pous, D.: Non-wellfounded proof theory for (Kleene+action)(algebras+lattices). In: Computer Science Logic (CSL), Birmingham, United Kingdom (2018). https://doi.org/10.4230/LIPIcs.CSL.2018.19. https://hal.archives-ouvertes.fr/hal-01703942
Davies, R., Pfenning, F.: A modal analysis of staged computation. J. ACM 48(3), 555–604 (2001). https://doi.org/10.1145/382780.382785
Di Cosmo, R., Kesner, D.: Combining algebraic rewriting, extensional lambda calculi, and fixpoints. Theor. Comput. Sci. 169(2), 201–220 (1996). https://doi.org/10.1016/S0304-3975(96)00121-1
Došen, K.: Identity of proofs based on normalization and generality. Bull. Symb. Logic 9, 477–503 (2003)
Emerson, E.A., Clarke, E.M.: Using branching time temporal logic to synthesize synchronization skeletons. Sci. Comput. Program. 2(3), 241–266 (1982). https://doi.org/10.1016/0167-6423(83)90017-5
Fairtlough, M., Mendler, M.: Propositional lax logic. Inf. Comput. 137(1), 1–33 (1997)
Fitch, F.: Intuitionistic modal logic with quantifiers. Portugaliae Mathematica 7(2), 113–118 (1948)
Girard, J.Y.: Linear logic. Theor. Comput. Sci. 50, 1–102 (1987). https://doi.org/10.1016/0304-3975(87)90045-4
Girard, J.Y.: Proof-nets : the parallel syntax for proof-theory. In: Ursini, A., Agliano, P. (eds.) Logic and Algebra. Marcel Dekker, New York (1996)
Guglielmi, A., Gundersen, T., Parigot, M.: A proof calculus which reduces syntactic bureaucracy. In: Lynch, C. (ed.) Proceedings of the 21st International Conference on Rewriting Techniques and Applications, LIPIcs, vol. 6, pp. 135–150. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl (2010). https://doi.org/10.4230/LIPIcs.RTA.2010.135. http://drops.dagstuhl.de/opus/volltexte/2010/2649
Heijltjes, W., Hughes, D., Straßburger, L.: Intuitionistic proofs without syntax. In: LICS 2019–34th Annual ACM/IEEE Symposium on Logic in Computer Science, pp. 1–13. IEEE, Vancouver (2019). https://doi.org/10.1109/LICS.2019.8785827. https://hal.inria.fr/hal-02386878
Heilala, S., Pientka, B.: Bidirectional decision procedures for the intuitionistic propositional modal logic IS4. In: Pfenning, F. (ed.) CADE 2007. LNCS (LNAI), vol. 4603, pp. 116–131. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73595-3_9
Hughes, D.: Proofs Without Syntax. Ann. Math. 164(3), 1065–1076 (2006). https://doi.org/10.4007/annals.2006.164.1065
Hyland, J.M.E., Ong, C.L.: On full abstraction for PCF: i, ii, and III. Inf. Comput. 163(2), 285–408 (2000). https://doi.org/10.1006/inco.2000.2917
Hyland, J.M.E., Ong, C.H.L.: On full abstraction for PCF: I. Models, observables and the full abstraction problem, II. Dialogue games and innocent strategies, III. A fully abstract and universal game model. Inf. Comput. 163, 285–408 (2000)
Jay, C.B., Ghani, N.: The virtues of eta-expansion. J. Funct. Program. 5(2), 135–154 (1995). https://doi.org/10.1017/S0956796800001301
Kakutani, Y.: Call-by-name and call-by-value in normal modal logic. In: Shao, Z. (ed.) APLAS 2007. LNCS, vol. 4807, pp. 399–414. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76637-7_27
Kavvos, G.A.: Dual-context calculi for modal logic. Log. Methods Comput. Sci. 16(3) (2020). https://doi.org/10.23638/LMCS-16(3:10)2020
Kesner, D.: The theory of calculi with explicit substitutions revisited. In: Duparc, J., Henzinger, T.A. (eds.) CSL 2007. LNCS, vol. 4646, pp. 238–252. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74915-8_20
Kesner, D.: A theory of explicit substitutions with safe and full composition. Log. Methods Comput. Sci. 5(3) (2009). http://arxiv.org/abs/0905.2539
Kojima, K.: Semantical study of intuitionistic modal logics. Ph.D. thesis, Kyoto University (2012)
Kozen, D.: Results on the propositional mu-calculus. Theor. Comput. Sci. 27, 333–354 (1983). https://doi.org/10.1016/0304-3975(82)90125-6
Krivine, J.: Lambda-calculus, types and models. Ellis Horwood series in computers and their applications, Masson (1993)
Kuznets, R., Marin, S., Straßburger, L.: Justification logic for constructive modal logic. J. Appl. Logics IfCoLog J. Logics Appl. 8(8), 2313–2332 (2021). https://hal.inria.fr/hal-01614707
Mendler, M., Scheele, S.: Cut-free Gentzen calculus for multimodal CK. Inf. Comput. 209(12), 1465–1490 (2011)
Meyer, J.J., Veltmanw, F.: Intelligent agents and common sense reasoning. In: Blackburn, P., Van Benthem, J., Wolter, F. (eds.) Handbook of Modal Logic, Studies in Logic and Practical Reasoning, vol. 3, pp. 991–1029. Elsevier (2007). https://doi.org/10.1016/S1570-2464(07)80021-8. http://www.sciencedirect.com/science/article/pii/S1570246407800218
Miller, D., Volpe, M.: Focused labeled proof systems for modal logic. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 266–280. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_19
Mints, G.E.: Closed categories and the theory of proofs. J. Soviet Math. (1981). https://doi.org/10.1007/BF01404107
Murawski, A.S., Ong, C.-H.L.: Discreet games, light affine logic and PTIME computation. In: Clote, P.G., Schwichtenberg, H. (eds.) CSL 2000. LNCS, vol. 1862, pp. 427–441. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44622-2_29
Pfenning, F., Davies, R.: A judgmental reconstruction of modal logic. Math. Struct. Comput. Sci. 11(4), 511–540 (2001). https://doi.org/10.1017/S0960129501003322
Pnueli, A.: The temporal logic of programs. In: 18th Annual Symposium on Foundations of Computer Science, Providence, Rhode Island, USA, 31 October–1 November 1977, pp. 46–57. IEEE Computer Society (1977). https://doi.org/10.1109/SFCS.1977.32
Prawitz, D.: Natural Deduction: A Proof-Theoretical Study. Almquist and Wiksell (1965)
Simpson, A.: The Proof Theory and Semantics of Intuitionistic Modal Logic. Ph.D. thesis, University of Edinburgh (1994)
Sørensen, M.H., Urzyczyn, P.: Lectures on the Curry-Howard Isomorphism. Elsevier, Amsterdam (2006)
Terese: Term rewriting systems. Cambridge University Press (2003)
Tubella, A.A., Straßburger, L.: Introduction to Deep Inference (2019). https://hal.inria.fr/hal-02390267. lecture
Vakarelov, D.: Modal logics for knowledge representation systems. Theor. Comput. Sci. 90, 433–456 (1991)
Valliappan, N., Ruch, F., Tom’e Corti nas, C.: Normalization for fitch-style modal calculi. Proc. ACM Program. Lang. 6(ICFP), 772–798 (2022). https://doi.org/10.1145/3547649
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Acclavio, M., Catta, D., Olimpieri, F. (2023). Canonicity of Proofs in Constructive Modal Logic. In: Ramanayake, R., Urban, J. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2023. Lecture Notes in Computer Science(), vol 14278. Springer, Cham. https://doi.org/10.1007/978-3-031-43513-3_19
Download citation
DOI: https://doi.org/10.1007/978-3-031-43513-3_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43512-6
Online ISBN: 978-3-031-43513-3
eBook Packages: Computer ScienceComputer Science (R0)






 such that x is not free in M,
such that x is not free in M,  . Then there are derivations for
. Then there are derivations for 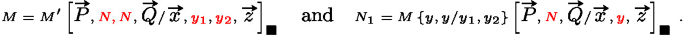
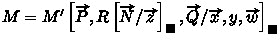 and with
and with
 , then
, then  ,
,
 or
or
 . We conclude again by Lemma
. We conclude again by Lemma  , or
, or
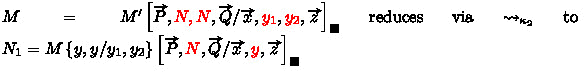 . In both cases we conclude with an argument similar to the one in Case (
. In both cases we conclude with an argument similar to the one in Case (


 -path from a vertex v to any vertex in
-path from a vertex v to any vertex in
 have the same length. Therefore the number
have the same length. Therefore the number
 is well-defined.
is well-defined.