Weak Supervision and Clustering-Based Sample Selection for Clinical Named Entity Recognition

Abstract

One of the central tasks of medical text analysis is to extract and structure meaningful information from plain-text clinical documents. Named Entity Recognition (NER) is a sub-task of information extraction that involves identifying predefined entities from unstructured free text. Notably, NER models require large amounts of human-labeled data to train, but human annotation is costly and laborious and often requires medical training. Here, we aim to overcome the shortage of manually annotated data by introducing a training scheme for NER models that uses an existing medical ontology to assign weak labels to entities and provides enhanced domain-specific model adaptation with in-domain continual pretraining. Due to limited human annotation resources, we develop a specific module to collect a more representative test dataset from the data lake than a random selection. To validate our framework, we invite clinicians to annotate the test set. In this way, we construct two Finnish medical NER datasets based on clinical records retrieved from a hospital’s data lake and evaluate the effectiveness of the proposed methods. The code is available at https://github.com/VRCMF/HAM-net.git.

1 Introduction

Although Electrical Health Records (EHR) are trending towards structured data, documentation in plain text remains popular in clinical work. As a result, text documents contain valuable information, which highlights the need for automatic information extraction and data structuring techniques for research and management purposes or to facilitate the clinician’s work. Electrical Health Records (EHR) are nowadays widely adopted by healthcare institutes and medical service providers. EHRs are created and maintained by healthcare service providers and consist of various information and data types related to patients’ healthcare. This includes narrative free-text reports, laboratory results, demographics, diagnosis codes, and images. During hospitalization, patients’ information is synchronically updated to the EHR system where clinicians can query the EHR system to obtain relevant medical information about patients. However, most clinical notes are in free-text format. Named Entity Recognition (NER) is a subtask of Natural Language Processing (NLP), aiming to detect and assign labels to pre-defined categories or concepts as they appear in the text, such as diseases, medicines, symptoms, anatomical structures, or procedures. NER is based on supervised learning. Thus, a substantial amount of training data consisting of input text and label sequences are required. To provide reliable token-level predictions, high-quality manually annotated data by clinical experts is necessary, which implies considerable human effort. Earlier, NER systems have been trained for different languages, such as for English text, such as n2c2¹, RadGraph [8], MalwareTextDB [14], and CoNLL2003 [18], and for smaller languages such as Finnish², but to our knowledge, no NER dataset for medical Finnish exists.

One solution to tackle the scarcity of manually labeled training data is to adopt distant supervision methods to generate labels for training samples based on external knowledge sources. In this framework, earlier approaches include, e.g., knowledge-based distant supervision, transfer learning from pretrained models, and dictionary-based methods, to name a few. For example, Zirikly et al. [25] and Wang et al. [22] leverage the transfer learning to project the label knowledge from resource-rich languages (English) into the low-resource one. Korkontzelos et al. [10] and Shang et al. [20] establish NER datasets based on in-domain dictionaries. It is necessary to generate entity-level supervision signals for training data and capitalize on domain-specific dictionaries and language knowledge.

We propose a novel NER framework called Hybrid Annotation Mechanism Network (HAM-net) to predict medical entities from clinical documents in an extremely low-resource scenario. We fuse a Finnish medical dictionary³ and a dependency parser for Finnish⁴ to enhance the annotation mechanism.

Considering the characteristics of medical-related NLP algorithms, we perform domain-specific continual pertaining (DCP) to resolve in-domain adaptation problems. Much research literature shows that language models suffer from performance degeneration on downstream tasks without taking in-domain adaptation into account [7, 9]. Currently, advanced language models, such as Bidirectional Encoder Representations from Transformers (BERT) [5] and Longformer [3], incorporate biomedical and clinical knowledge through pre-training on large-scale biomedical and clinical corpus [13]. We deploy domain-specific continual pretraining with the masked language modeling (MLM) objective on an enormous Finnish medical text from the data lake of the hospital. To endow our framework with better domain specification, we perform domain-specific continual pretraining to obtain domain-aware model parameters to initialize the NER model.

To validate the HAM-net in different medical documents, we retrieve patient clinical records from the data lake of the hospital and divide them into four text clusters based on frequent medical specialties to establish NER datasets. Also, we develop the Sample Selection Module (SSM) to choose the most informative data points as validation samples for better evaluation. The experiments show that the SSM is better than random selection, such that the validation samples generated by our module better represent the whole datasets.

Our contributions are illustrated in the following aspects:

• This paper proposes a novel framework to deal with the NER task in an extremely low-resource scenario, i.e., extract customized medical entities from clinical notes without human-annotated data.

• We integrate a Finnish medical dictionary and a Finnish language parsing pipeline to construct the Hybrid Annotation Mechanism (HAM) module for providing weakly labeled data.

• We design the Sample Selection Module (SSM) to select the representative samples for human annotation, which enables the reliable evaluation of our weakly supervised HAM-net and effectively reduces the annotation cost.

Fig. 1.

Overall architecture of HAM-net. The texts in patient clinical records from the hospital data lake are written in a low-resource language (Finnish).

2 Related Work

Medical NER detects medically meaningful entities in unstructured documents and classifies them into predefined labels, such as drug dosages, diseases, medical devices, and anatomical structures. Most early medical NER works utilize feature engineering techniques and machine learning algorithms to resolve medical NER tasks [17, 19, 21]. Deep learning-based NER approaches have recently achieved state-of-the-art (SOTA) performance across NER tasks because of the semantic composition and continuous real-valued vector representations through nonlinear processing provided by deep neural networks [12]. For example, in the clinical setting, Wu et al. [23] used the convolutional and recurrent neural networks to encode the input sentences while the sequential labels were generated by a task-specific layer, i.e., a classification layer.

Acquiring high-quality training data for deep learning models in the medical setting can be difficult because human annotation is labor-intensive and expensive. As a classical supervised learning task, the medical-named entity recognition task requires a substantial amount of entity-level supervision signal, e.g., anatomical structure and drug dosage, to learn the transformation function between input data and our desired targets from the training dataset. Two common weak supervision schemes, i.e., incomplete and inaccurate supervision, are extensively studied in research communities [24] to resolve the data scarcity problem. Incomplete supervision approaches select a small set of training samples from a dataset, and then human encoders assign labels to selected samples for training the model. Ferreira et al. [6] leverage active learning strategies to select the most informative samples on a clinical multi-label classification, i.e., international classification disease (ICS) coding task. Inaccurate supervision approaches generate weakly labeled data by assigning many training samples with supervision signals provided by outside resources, such as dictionaries, knowledge graphs, and databases. Nesterov et al. [16] leverage Medical Dictionary for Regulatory Activities (MedDRA), a subset of UMLS, to construct a knowledge base as annotation resources. The weakly labeled data generated by a rule-based model is fed into a BERT model to generate entity-level predictions.

3 Method

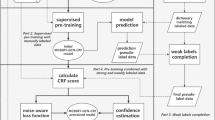
This section introduces our proposed framework, i.e., Hybrid Annotation Mechanism Network (HAM-net). It consists of a hybrid annotation mechanism (HAM) and a Sample Selection Module (SSM). The overall architecture of HAM-net is shown in Fig. 1. We retrieve Finnish patient clinical records from the hospital data lake and deploy our framework in a real-world scenario. Domain-specific Masked Language Modeling (MLM) is performed on a large-scale clinical corpus from the data lake to learn medical knowledge that provides the HAM-net with in-domain adaptation. The HAM automatically assigns weak labels to training samples. The SSM selects the most informative data points as validation samples, and doctors annotate the selected samples. The NER model uses weakly labeled data to train a model identifying and classifying entities into pre-defined labels.

Fig. 2.

Overall architecture of HAM-net. The patient clinical records from the hospital data lake are Finnish text. Annotation Dictionary is constructed based on the FinMesh ontology. Linguistic information, i.e., lemmatization and annotation mask, is derived from the Finnish neural parsing pipeline and human-defined rules. We leverage medical information from ontology and linguistic information to assign labels for given input entities.

3.1 Hybrid Annotation Mechanism

The Hybrid Annotation Mechanism (HAM) is divided into three steps as shown in Fig. 2, i.e., annotation dictionary construction, linguistic knowledge extraction, and weak label assignment. Firstly, we retrieve medical terms from the Finnish Medical Subject Heading (FinMesh) ontology and utilize parent-child relationships between subjects to establish hierarchical graphs. Each hierarchical graph consists of a root node and non-root nodes, which are used to construct a medical dictionary, i.e., the root node for the key and all non-root nodes for the terms. Based on clinicians’ suggestions, we merge “key-item” pairs in the medical dictionary to provide an annotation dictionary with six pre-defined labels. Secondly, we integrate linguistic knowledge of sequential input extracted by the Finnish neural parsing pipeline and human-defined rules to provide tokenized words, annotation masks, and lemmatization to facilitate the following entity-level annotation. Thirdly, we design a beam-mapping algorithm that assigns weak labels to entities for establishing NER training datasets.

Annotation Dictionary Construction. Assume a collection of medical subjects related to a top-level concept, e.g., kudokset (tissue), is denoted as $\mathcal {H}^{\prime }_i = \{h_i\}_{i=0}^{a+b+c+2}$, where a, b, and c represents each branch’s depth in a hierarchical tree. Each medical subject stores relevant information, including their parent and child subjects, medical concepts in different languages (Finnish, Swedish, and English), preferred labels, alternative concepts, and related subjects.

We define the hierarchical graph for the concept as $\mathcal {G}_h^i = (\mathcal {H}^{\prime }, \mathcal {E})$ where relevant medical subjects $\mathcal {H}^{\prime }$ are the graph’s vertices and $\mathcal {E}$ represents the edges or association rules of the hierarchical graph, i.e., parent-child relations between subjects. The edges are $\mathcal {E} \rightarrow \{\{h_i, h_j\}| h_i, h_j \in \mathcal {H}^{\prime }_i ~\text {and}~ i \ne j \}$ while the association rules of the hierarchical graph (refer to the Fig. 2) is defined as follows:

• $h_0 \rightarrow h_1 \rightarrow \cdots \rightarrow h_{a+2}$,

• $h_0 \rightarrow h_2 \rightarrow \cdots \rightarrow h_{a+b+2}$,

• $h_0 \rightarrow h_2 \rightarrow \cdots \rightarrow h_{a+b+c+2}$.

To construct a medical dictionary $\mathcal {M}_i$, we flatten the hierarchical graph $\mathcal {G}_h^i$ by pooling all vertices or subjects in the graph (except the top-level vertex $h_0$). Retrieved subjects are regarded as the dictionary’s terms, and the top-level vertex represents the dictionary’s key, so that the medical dictionary is denoted to $\textbf{M}_i(k_0) = \{h_i\}_{i=0}^{a+b+c+2}$. We regard the top-level vertex $h_0$ as a key of the medical dictionary $k_0$.

An annotation dictionary $A_j$ $(\text {where }j \in \{1, 2, \cdots , 6\})$ is provided by merging related hierarchical graphs based on clinicians’ suggestions, and the annotation dictionary is referred to as $A_j = \{\mathcal {M}_1(k_0^1), \mathcal {M}_2(k_0^2), \cdots , \mathcal {M}_m(k_0^m)\}$ where m is the number of related hierarchical graphs.

Annotation Masking and Lemmatization. Let X be a sentence with n tokens in a clinical document from the data lake. The sentence is denoted as $X = \{X_i\}_{i=1}^{n}$. The Finnish neural parser pipeline reads the sentence X and provides tokenized words ($X^o$), tokens’ lemmatization ($X^l$), part of speech (POS), morphological tags, and dependency parsing. Firstly, we provide an annotation mask ($X^m$) to avoid the label assignment over entities with no specific meaning, by leveraging the following pre-defined rules:

• Set $X^m_i$ as “False” if the POS of $X_i$ does not belong to [“NOUN”, “VERB”, “ADJ”, “ADV”].

• Set $X^m_i$ as “False” if the $X_i$ is a unit, e.g., “cm”, “kg”, “sec”, to name a few.

• Remove all Finnish stop words provided by stopwords-fi⁵.

Secondly, the pipeline lemmatizes the token $X_i$ and returns the original format of the token. The reason for extracting tokens’ lemmatization is that tokens in the clinical notes have different formats, such as past tense, plural, or misspellings, which might affect the string mapping during the entity-level annotation. Finally, the generated vectors, i.e., $X^o$, $X^l$, and $X^m$, align with the lengths of input sentence X to prevent dislocation mapping when the vectors participate in the following label assignment.

Weak Label Assignment. We develop an algorithm called beam mapping to assign weak labels to entities in the sentence. We adopt BIO scheme to define the entity boundaries. BIO stands for the beginning, inside, and outside of a textual segmentation. For example, NER systems assign [‘O’, ‘O’, ‘B-medical-condition’, ‘I-medical-condition’] for a given sequence [‘He’, ‘has’, ‘prostate’, ‘cancer’]. The algorithm iterates through all tokens in the sentence X and generates BIO scheme labels, i.e., a combination of tokens can be annotated, within the receptive windows Win containing a list of w position shifting, $\texttt {Win} \in [s_1, s_2, \cdots , s_w]$, where $s_w$ is a token at w position of a given sequence. For example, “prostate cancer” should be annotated as “B-Medical-condition” and “I-Medical-condition” rather than “B-Anatomical-structure” and “B-Medical-conditional” because it is plausible to treat the phrase “prostate cancer” as a unit instead of splitting them up.

Assume the beam mapping algorithm provides labels to tokens ranging from $X_i$ to $X_{i+s_j}$ where $j \in \{1, 2, \cdots , w\}$. Firstly, we check the $i_{th}$ element in the annotation mask $X^m$ and see whether $X^m_i$ is True because we directly assign “O” to the $X_i$ without executing the algorithm on the position i if the mask item is False. Secondly, a token mapping function generates the candidate labels on the lemmatizations of tokens $\{X_i^l\}_{i=i}^{i=i+s_j}$ by mapping each item in the annotation dictionary A to the lemmatizations. During the mapping, the algorithm selects candidates, i.e., terms in the annotation dictionary $A_j$, if the number of input tokens and lengths of each token equal the dictionary’s terms. We denote z selected candidates as $C = \{C_i\}_{i=1}^{z}$ and calculate Levenshtein distance between the input string and the candidate to estimate the similarity between two strings for choosing the most matched candidate. Merge the input list $\{X_i^l\}_{i=i}^{i=i+s_j}$ separated by the space character to provide the input string $S_{i:i+s_j}$. The Levenshtein distance between two strings (a and b) is shown as follows:

$$\begin{aligned} {\text {lev}}(a, b) = {\left\{ \begin{array}{ll} |a| &{}\text { if } |b| = 0, \\ |b| &{}\text { if } |a| = 0, \\ {\text {lev}}\big ({\text {tail}}(a),{\text {tail}}(b)\big ) &{}\text { if }a[0] = b[0]\\ 1+\min {\left\{ \begin{array}{ll} {\text {lev}}\big ({\text {tail}}(a), b\big ) \\ {\text {lev}}\big (a, {\text {tail}}(b)\big ) \\ {\text {lev}}\big ({\text {tail}}(a), {\text {tail}}(b)\big ) \\ \end{array}\right. }&\text {otherwise,} \end{array}\right. } \end{aligned}$$

(1)

where the ${\text {tail}}(.)$ is to retrieve all elements in a string except the first one. Thirdly, we get the best-matched terms for the tokens $\{X_i\}_{i=i}^{i=i+s_j}$ based on the distances. The weak labels $\{Y_i^\prime \}_{i=i}^{i=i+s_j}$ is provided by leveraging the indexes of the best candidates to look up the annotation dictionary A. The annotation rules for the BIO scheme are shown as follows:

• If the first label is empty, i.e., $Y_i^\prime = \text {``O''}$, we re-run the algorithm on the position $i+1$.

• If the first label is not empty, the weak labels $\{Y_i^\prime \}_{i=i}^{i=i+s_j}$ are:

  • The first element is the beginning of the text segment, $Y_i^\prime = \text {``B-lb''}$.

  • The rest elements are the inside of the text segment, $\{Y_i^\prime \}_{i=i+1}^{i=i+s_j} = \text {``I-lb''}$.

where “lb” is an arbitrary label from the annotation dictionary A. The weakly labeled data for the sentence X with n tokens can be represented as $\{(X_i, Y_i^\prime )\}_{i=1}^{n}$.

3.2 NER Backbone Network

We use the weakly labeled data provided by the HAM as input samples to train a NER model. Also, the weakly labeled data contains inherent label noise of distant supervision approaches, affecting predictions’ reliability. The noise stability property [2] shows that the noise will gradually attenuate when the noise propagates through a deep neural network. Therefore, a trained NER model, i.e., HAM-net, identifies and classifies entities into labels in a low-latency way. The label noise can be suppressed by the deep neural network or additional noise-suppressed approaches.

We leverage the word embedding technique to provide the word embedding matrix $\textbf{X}_i \in \mathbb {R}^{d_e \times n}$ of the $i_{th}$ sentence with n tokens. The input data is denoted as $\{(\textbf{X}_i, \textbf{Y}_i^\prime )\}_{i=1}^{N}$ where N is the total number of sentences and the $\textbf{Y}_{i}^\prime \in \mathbb {R}^{1 \times n}$ is to store the indexes of labels. We load the domain-specific model obtained with continual pretraining to initialize the encoder whose mapping function is denoted as $\mathcal {F}^\prime$(.). The vector $\textbf{X}_i$ is encoded as:

$$\begin{aligned} \mathbf {{Z}}_i^\prime = {\text {Softmax}}(\textbf{O}^\prime \mathcal {F}^\prime ({\textbf{X}_i})), \end{aligned}$$

(2)

where $\textbf{O}^\prime \in \mathbb {R}^{d_m \times d_h}$ is the weight matrix of the fully-connected layer and $d_m$ is the dimension of predefined label space. $\mathbf {{Z}}^\prime \in \mathbb {R}^{d_m \times n}$ represents the encoder’s output.

We also consider a CRF layer as the decoder of the NER model, denoted as $f(\textbf{Z}^\prime _i, j, \mathbf {{Y}}_{j-1}^\prime , \mathbf {{Y}}_{j}^\prime )$ where j is the position of the label to predict, $\mathbf {{Y}}_{j-1}^\prime$ represents the label for the $(j-1)_{th}$ token of the input sequence $\textbf{X}$, and $\mathbf {{Y}}_{j}^\prime$ is the label for the $j_{th}$ token of the input sequence $\textbf{X}$. The conditional probability vectors of the $i_{th}$ sentence is denoted as:

$$\begin{aligned} P(\mathbf {{Y}}_i^\prime | \textbf{Z}_i^\prime , \lambda )&= \frac{1}{G(\textbf{Z}^\prime )} \exp \sum _{j=1}^n \lambda _j f_j(\textbf{Z}^\prime _i, j, \mathbf {{Y}}_{i,j-1}^\prime , \mathbf {{Y}}_{i,j}^\prime )), \end{aligned}$$

(3)

$$\begin{aligned} G(\textbf{Z}^\prime )&= \exp \sum _{i=1}^N \sum _{j=1}^n \lambda _j f_j(\textbf{Z}'_i, j, \mathbf {{Y}}^\prime _{i,j-1}, \mathbf {{Y}}_{i,j}), \end{aligned}$$

(4)

where the $\lambda _j$ is the learn-able weight of $j_{th}$ CRF feature function. The $G(\textbf{Z}^\prime )$ represents the normalization factor of the CRF feature functions. The overall training loss of the HAM-net is:

$$\begin{aligned} \mathcal {L}(\textbf{Z}^\prime , \lambda , \textbf{Y}^\prime ) = \sum _{i=1}^{N} \log P(\mathbf {\textbf{Y}}_i^\prime | \textbf{X}'_i, \lambda ) - \sum _{j=1}^{m} \frac{\lambda ^2_j}{2\sigma ^2}, \end{aligned}$$

(5)

We train the model until convergence and use the Viterbi algorithm [11] to generate a label sequence for a new input sentence in the inference stage.

3.3 Sample Selection Module

To validate the effectiveness of our data annotation mechanism and NER model, we need the test set with a small set of samples annotated by clinicians. However, human annotation is expensive and labor-intensive, especially for doctors to assign entity-level labels to the test samples. To mitigate this problem, we developed the Sample Selection Module (SSM) to select samples that largely represent the datasets when constructing the test set. Compared with the random selection, the distributions of test samples provided by the SSM are closer to the distributions of each dataset. We provide the details about the SSM module as follows.

Note a set of g sentences $\phi \in \{\phi _1, \phi _2, \cdots , \phi _g\}$ from an arbitrary dataset. Firstly, we use the Finnish sentence transformer⁶ to embed sentences $\{\phi _i\}_{i=1}^{g}$ into vectors $\{\varPhi _i\}_{i=1}^{g}$, where the $i_{th}$ vector is $\varPhi _i \in \mathbb {R}^{1 \times d_s}$. The principal component analysis (PCA) [1] projects the high-dimension vector $\varPhi _i \in \mathbb {R}^{1 \times d_s}$ into a low-dimension vector $\hat{\varPhi }_i \in \mathbb {R}^{1 \times d_r}$ for dimensionality reduction while retraining the main patterns of the vectors. Secondly, we segment data points into different clusters by applying the Kmeans++ algorithm on the dimension-reduced vectors $\{\hat{\varPhi }_i\}_{i=1}^{g}$. For simplicity, we assume the vectors are in the same cluster, and the center point of the cluster is referred to as $\hat{\varPhi }_i^c \in \mathbb {R}^{1 \times d_r}$. Note that the center point might not be one of the vectors $\{\hat{\varPhi }_i\}_{i=1}^{g}$. The Euclidean distance between the center point $\hat{\varPhi }^c$ and the $i_{th}$ vector $\hat{\varPhi }_i$ is denoted as follows:

$$\begin{aligned} d(\hat{\varPhi }^c, \hat{\varPhi }_i) = \sqrt{\sum _{j=1}^{n}(\hat{\varPhi }^c[j] - \hat{\varPhi }_i[j])^2}, \end{aligned}$$

(6)

where $\hat{\varPhi }^c[j]$ is the $i_{th}$ element in the vector $\hat{\varPhi }^c$. We refer to the reciprocal of the normalized distances as the data sampling probabilities so that the sampling probability for the $i_{th}$ data point is denoted as:

$$\begin{aligned} p(i) = \frac{{\text {inv}}_p(i)}{\sum _{j=1}^{g} {\text {inv}}_p(j)}, ~~~~~~ {\text {inv}}_p(i) = \frac{1}{d(\hat{\varPhi }^c, \hat{\varPhi }_i)}. \end{aligned}$$

(7)

We sample the data point from the cluster with the probabilities p as a part of the test sample. After traversing all clusters, we obtain a collection of test samples that can better represent the whole dataset.

4 Experiments

4.1 Dataset

We conduct experiments on these two real-world datasets, namely medical radiology and medical surgery. We retrieve patient clinical records from the hospital’s data lake to build the basic medical corpus. Following the clinicians’ suggestions, we split the medical corpus into four text sets based on the medical specialties, i.e., “RTG (radiology reports)”, “KIR (surgery text)”, “SAD (radiotherapy documents)”, “OPER (procedures notes)”. The detailed specialty information can be found in the Kela - the Social Insurance Institution in Finland⁷. We combine the RTG and SAD sets into the medical radiology dataset, and the KIR and OPER sets into the medical surgery dataset. We only keep the main body of documents as a medical corpus for each clinical document and split some documents into sentences when constructing these two medical datasets. To better explore the model performance variation on different datasets, we truncate and maintain datasets at the same scale to eliminate the effect of data size.

Table 1. Numbers of weakly labeled entities based on four medical specialties. “B-X” and “I-X” represents the beginning and inside of a clinical term. To ensure anonymity, we represent values lower than 10 in the results as “<10”.

We leverage the SSM module and HAM scheme for each medical specialty to construct a human-annotated testing set and machine-annotated training set, respectively. We select 1000 sentences from both datasets based on the dataset sentence ratios, i.e., the number of sentences in each dataset over the number of sentences in all datasets. The number of sentences in different human-annotated datasets is 214 (KIR), 192 (RTG), 210 (SAD), and 192 (OPER). The rest of the sentences are used to construct the machine-annotated datasets by applying the HAM scheme mentioned in Sect. 3.1. Weakly labeled datasets generated by the HAM and clinician-annotated data are divided into training, validation, and test sets according to the predefined ratio, i.e., 7:2:1. For simplicity, we denote predefined NER labels as “Anatomical Structure (Stru)”, “Body Function and Measurement (Meas)”, “Medical Condition (Cond)”, “Medical Device (Devi)”, “Medical Procedure (Proc)”, and “Medication (Medi)”. Table 1 shows the statistical summary.

4.2 Baselines and Setup

We compare the three zero-shot baselines with different token classification layers and two variants of our proposed method. Three baselines are ZS-BERT (i.e., a Zero-Shot BERT-based model), ZS-BERT-LSR (i.e., Zero-Shot BERT with Label Smoothing Regularization), and ZS-BERT-CRF (i.e., Zero-Shot BERT with Conditional Random Field). We equip two token classification layers, i.e., softmax-based linear layers (Linear) and conditional random fields (CRF). The BERT model is pretrained over the collected corpus. All baselines are in the zero-shot setting and summarized as follows:

• ZS-BERT: A BERT model encodes input documents, and the linear layer decodes features into entity labels.

• $\text {ZS-BERT}_\text {LSR}$: Overall architecture is the same as the ZS-BERT, except the loss function is adjusted by the LSR.

• $\text {ZS-BERT}_\text {CRF}$: A CRF rather than a linear layer follows a BERT model to generate entity labels.

Accordingly, two variants of our proposed methods are HAM-Linear and HAM-LSR. HAM-Linear replaces the CRF layer of the HAM-net with a linear layer to generate token-level predictions; 2) HAM-LSR is the same as the HAM-Linear except for the model optimization part. The HAM-LSR leverages the label smoothing regularization (LSR) over the cross-entropy loss function.

We manually tune the hyper-parameter, select the best model evaluated on the validation set and report the results on the clinician-annotated test set. We use the base configuration of the BERT model to encode input sequences. The batch size is 1. The maximum length of the input is 512. We set the drop rate of all dropout layers as 0.03. The learning rate is $1e^{-5}$. We trained our neural network with mixed precision, i.e., FP16, to accelerate the training speed. We apply the early stopping strategy by monitoring the validation loss while the patience round is 5. The optimal PCA dimension for four datasets is ten, and the number of clusters is 2.

4.3 Main Results

To compare with baseline models, we report the model’s results on the precision, recall, and F1 scores. Table 2 reports the performance of all models.

Table 2. Experimental results, i.e., precision (P), recall (R) & F1 scores in %, on the medical surgery and medical radiology datasets.

Medical Surgery Dataset: Our model outperforms all baselines across evaluation metrics. The HAM achieved better scores compared with the best linear-decoding model, i.e., HAM-Linear. The HAM outperforms the HAM-LSR by 2.06, 0.72, and 0.68% points on precision, recall, and F1 scores.

Medical Radiology Dataset: Our model improves all evaluation scores on the medical radiology dataset. Compared with the HAM-Liner, the HAM improves the precision, recall, and F1 scores by 1.04, 0.13, and 0.69% points, respectively. The HAM also outperforms the HAM-LSR with 1.68, 1.00, and 1.27% points on all evaluation metrics.

4.4 The Effect of Sample Selection Module

We leverage Davies Bouldin scores [4] to find the optimal combination of the PCA projection dimension and clustering number. Figure 3 shows the distributions of Davies Bouldin scores with different PCA projection dimensions and clustering numbers on four datasets. From the figure, we can observe that cluster numbers largely affect the Davies Bouldin scores while the lower values indicating better clustering. Besides, we use different clustering algorithms, i.e., bisecting k-means and ward agglomerative clustering algorithm, to plot distributions of Davies Bouldin scores. The distributions show the same patterns as the k-means algorithm.

Fig. 3.

Davies Bouldin scores by different PCA projection dimensions and the number of clusters.

Table 3. Jensen-Shannon divergence between original label distributions and selected labels’ distribution provided by different selection methods.

To compare the random selection and SSM module, we exploit the Jensen-Shannon divergence [15] to measure the distribution distances between the full and selected datasets. Assume the distribution of the full dataset is P and the selected dataset is Q so that the Jenson-Shannon divergence is shown as follows:

$$\begin{aligned} \textrm{JSD}(P \parallel Q)= \frac{1}{2}D(P \parallel M)+\frac{1}{2}D(Q \parallel M). \end{aligned}$$

(8)

The SSM and random selection algorithms have been performed ten times and averaged across all results. Table 3 shows that the SSM significantly outperforms the random selection approach because the label distribution of the SSM is closer to the entire dataset.

4.5 The Effect of Continual Pretraining

We conduct an ablation experiment to study the effectiveness of domain-specific continual pretraining. Table 4 shows the results of the baselines and HAM with or without the domain-specific continual pretraining. We can observe that continual pretraining improves all scores on two medical NER datasets, validating that continual pretraining is important for the domain-specific application in this study.

Table 4. Comparison of the evaluation results of the model with or without the domain continual pertaining (DCP) on two medical NER datasets.

4.6 Discussion

One key limitation of this paper is that the experimental results of our model are not superior in terms of those evaluation scores. This is mainly because the training of our models uses weakly annotated labels. Automated annotated labels with distant supervision methods naturally cannot achieve superior performance over evaluation metrics in many cases. However, the proposed HAM method paves the way for training NER models without human-annotated data. In our experiments, we leverage the domain-specific continual pretraining to improve the model performance further. Developed NER systems requiring limited or zero supervision can be deployed to extremely low-resource scenarios, such as resource-restrained language and medical NLP applications. The medical NER task in extremely low-resource scenarios is very challenging. Future work can combine the proposed HAM and semi-supervised methods to build more reliable entity recognition systems. Our study used clinical notes in Finnish as a case study. However, our proposed method can be replicated in other languages. Taking English as an example, we can use the English MeSH as the ontology and the corresponding preprocessing techniques for English in our hybrid annotation mechanism to generate weakly supervised labels.

5 Conclusion

This paper developed a novel framework, Hybrid Annotation Mechanism Network (HAM-net), to extract entity-level medical information from the clinical text in an extremely low-resource scenario. We design the Hybrid Annotation Mechanism (HAM) to detect and classify entities in documents into predefined labels by utilizing the distant supervision signals from the Finnish medical subject headings. The weakly labeled data produced by the HAM module is further used to train a NER model based on contextualized representations and domain-specific continual pretraining. Due to the scarcity of annotated evaluation data, we developed the Sample Selection Module (SSM) to select the samples which can better represent the original datasets than the random selection approach. The proposed SSM method can effectively select more representative samples, thus reducing the annotation cost. The experimental results show that our framework can be adapted to train neural models and establish a strong baseline for future studies when there are no explicit supervision signals provided by human experts. And domain-specific continual pretraining can help to improve the performance of NER models trained with weakly annotated data.