Design of Additively Manufactured 3D Lattice Cores of Sandwich Panels

Abstract

This study analyzes 3D truss-based lattice cores in sandwich panels subjected to localized transversal loads using analytical methods. Compared to the common sandwich theories, the presented model may reveal stress concentrations induced by the localized loads. An advanced core design to reduce stress concentrations is provided by varying the core strut diameter through the thickness which leads to a graded core. A mass comparison between the homogeneous and the graded core shows that grading the core reduces the core weight by more than 20%. Based on finite element analysis, it can be demonstrated that the present model with a lowered modeling effort well captures the lattice strut stresses of the graded cores, particularly in load application regions.

1 Introduction

Outstanding mechanical properties offered by sandwich panels have encouraged engineers to use this kind of composite structures in lightweight applications [1,2,3]. Typically, sandwich panels consist of a low-density core enclosed by two high-strength face sheets. This three-layer design provides high bending stiffness with a relatively low structural mass. However, the sandwich core is vulnerable when localized transverse loads are applied [4, 5]. [6, 7] observed core failure near the load application region in sandwich structures during 3-point bending tests. Reinforcing the core using inserts may enhance the sandwich’s stiffness and strength, but it requires more material use and manufacturing processes [8, 9]. With additive manufacturing, novel approaches to reinforce sandwich cores are enabled since additive manufacturing has revolutionized the design of components and parts due to the flexibility offered by the layerwise manufacturing technology [10]. Thus, the core properties may be customized to fulfill local requirements. The resulting core is called a graded core, as the mechanical properties vary across the core. Using graded structures may significantly enhance the specific properties and the load carrying capacity of the sandwich and avoid over-dimensioned designs [11]. Recent studies considered lattice structures composed of periodic representative volume elements (RVE) as cores in sandwich panels to enhance the sandwich’s mechanical performance [12,13,14]. The design of these truss-like structures is derived from metallic atom crystals and offers high specific mechanical properties [15, 16]. [17] observed that layerwise graded lattices may exhibit higher energy absorption than homogeneous lattices. Since merely experimental and numerical methods are used to investigate these lattice structures, a novel analytical model to analyze graded 3D lattice cores is presented in this work. The analytical model allows an efficient analysis of strut-based cores with many RVEs, easy modeling and sufficiently precise calculation for pre-dimensioning and optimizing sandwich structures with lattice cores.

First, an RVE topology that satisfies the core design requirements is selected. An anisotropic homogeneous material with the corresponding elastic properties of the lattice on the macroscale is used to replace the lattice core and reduce the modeling effort. Thus, the lattice is homogenized. The lattice strut stresses are determined by dehomogenizing the core using the sandwich displacements. A higher-order sandwich theory is used to obtain the displacement in the considered sandwich. Due to the employed higher-order approach, stress concentrations near the load application regions are captured. To homogenize the stress distribution through the core thickness and achieve an even load distribution in the core, the lattice strut diameter and, thus, the core properties vary in a layerwise manner through the core thickness.

2 Model and Approach

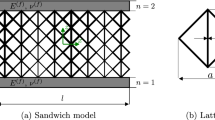
This work considers a sandwich panel subjected to a 3-point bending load. Due to the applied transversal force, normal bending stresses and transverse shear stresses occur in the face sheets and the core. Furthermore, normal transverse stresses are expected in the load application area. The sandwich face sheets mainly support the normal bending stresses since the core exhibits a relatively low stiffness. While the normal bending stresses decrease with lower core stiffness, the transverse normal stresses increase in the core. Besides supporting the transverse normal stress, the core transfers the transverse shear stresses in the sandwich. Therefore, a core material with a corresponding shear stiffness and vertical stiffness is required. Such core material properties are provided by face-centered cubic RVEs with vertical struts (F2CCZ), as shown in Fig. 1. The 45$^\circ$ inclined strut provides a high effective shear stiffness $G^*_{xz}$ in the xz-plane. The vertical strut reinforces this RVE in the z-direction and enhances the vertical stiffness $E^*_{zz}$. Thus, the F2CCZ RVE exhibits an orthotropic material behavior that can be described by nine indepndent elastic constants. The F2CCZ RVE can be characterized by the ratio between the RVE size a and the RVE strut diameter d, which is called aspect ratio a/d. Depending on the aspect ratio, the elastic properties and the density $\rho ^*$ of the RVE can be determined by

$$\begin{aligned}&\frac{E^{*}_{xx}}{E_s}=\frac{E^{*}_{yy}}{E_s}=0.51\, \left( \frac{a}{d}\right) ^{-2.17},&\frac{E^{*}_{zz}}{E_s}=1.37\, \left( \frac{a}{d}\right) ^{-2.21},\nonumber \\ {} \\&\frac{G^{*}_{xz}}{G_s}=0.57 \,\left( \frac{a}{d}\right) ^{-2.01},&\frac{\rho ^{*}}{\rho _s}=3.51 \,\left( \frac{a}{d}\right) ^{-1.88}, \nonumber \end{aligned}$$

(1)

where $E_s$ and $\rho _s$ are the strut material’s elastic stiffness and the density. Equation 1 is determined based on the analytical model presented by [18] and valid for aspect ratios $a/d>6$. This model assumes the lattice struts as beam elements made of isotropic elastic material and allows a precise calculation of the relative density. The relative density obtained by this model is not overestimated since the model considers the overlapping region between the lattice struts.

Fig. 1.

F2CCZ RVE topology

Figure 2a illustrates the considered sandwich with the F2CCZ lattice core. Depending on the F2CCZ RVE size a and the number of the RVEs in each spatial direction ($N_x,N_z, N_y$), the sandwich dimensions can be given by

$$\begin{aligned} l=N_x \times a, \,\,\,\,\,\, h^{\text {(c)}}=N_z \times a, \,\,\,\,\,\, t=N_y \times a, \end{aligned}$$

(2)

where l denotes the sandwich length, $h^{\text {(c)}}$ the core thickness, and t the sandwich depth. In Fig. 2b, the 3D model is reduced to a 2D model by assuming a plane strain state in the xz-plane ($\varepsilon _{yy}=0$). Furthermore, the face sheets are considered to be made of an isotropic material with the stiffness $E^{\text {(f)}}$ and the Poisson’s ratio $\nu ^{\text {(f)}}$. The sandwich total thickness h results from the sum of the core thickness $h^{\text {(c)}}$ and the face sheet thickness $h^{\text {(f)}}$ ($h=2h^{\text {(f)}}+h^{\text {(c)}}$). In addition to the global coordinate system xz at the midplane of the sandwich, each face sheet has a separate coordinate system $x_mz_m$ at the center of the layer, with m being the number of the face sheet. The considered core is modeled as a homogeneous material representing the mechanical properties of the lattice at the macroscale, which are determined by Eq. 1. Core decomposition into mathematical layers of equal thickness is performed to allow a variation of the core mechanical properties through the core thickness. Through the mathematical layers, merely the strut diameter of the RVEs is varied. Grading the strut diameter of the RVE affects a variation of the core stiffness through the core thickness. In this study, a symmetric graded core is intended as stress concentrations occur in the upper core half near the load application and in the bottom core half near the support points. To enable a symmetric core grading, at least four mathematical layers are required. The mathematical layers may involve several physical layers and have the corresponding mechanical properties of the physical lattice layers ($E_{xx,j}^{\text {(c)}},E_{zz,j}^{\text {(c)}},G_{xz,j}^{\text {(c)}},$ etc.), where j denotes the number of the mathematical layer ($j=[1,2,3,4]$). This modeling approach minimizes the number of degrees of freedom and reduces the modeling effort. Increasing the number of the mathematical layers may allow a smoother grading between the layers and offer more degrees of freedom while designing the core. However, the computational effort increases with each mathematical layer.

Fig. 2.

Considered sandwich model

In previous studies, it has been proven that first-order shear theory displacement presentations are suitable for describing the deformation behavior of the face sheets in sandwich panels. Therefore, each face sheet deformation is represented by the angular rotation $\psi ^{\text {(f)}}_{m}$ and the horizontal displacement $u^{\text {(f)}}_{0,m}$ and the vertical displacement $w^{\text {(f)}}_{0,m}$ of the face sheet’s mid-axis, where $m=1$ refers to the bottom face sheet and $m=2$ to the top face sheet. Thus, the displacement field can be represented as

$$\begin{aligned}&u^{\text {(f)}}_{m}(x,z)=u^{\text {(f)}}_{0,m}(x)+z\psi ^{\text {(f)}}_{m}(x),\text { and} \end{aligned}$$

(3)

$$\begin{aligned}&w^{\text {(f)}}_{m}(x,z)=w^{\text {(f)}}_{0,m}(x). \end{aligned}$$

(4)

Since the vertical displacements in these representations are functions of merely the x-coordinate, transverse strains $\varepsilon _{zz}$ cannot be considered in the face sheets. The horizontal strain $\varepsilon _{xx}$ and the shear strain $\gamma _{xz}$ are determined by the derivatives

$$\begin{aligned}&\varepsilon ^{\text {(f)}}_{xx,m}=\frac{\partial {u}^{\text {(f)}}_{0,m}(x)}{\partial x}+z\frac{\partial {\psi }^{\text {(f)}}_{m}(x)}{\partial x},\text { and} \end{aligned}$$

(5)

$$\begin{aligned}&\gamma _{xz,m}^{\text {(f)}}=\frac{\partial {w}^{\text {(f)}}_{0,m}(x)}{\partial x}+{\psi }^{\text {(f)}}_{m}(x). \end{aligned}$$

(6)

With the decomposition of the core into four mathematical layers, new degrees of freedom ($\tilde{u}_q^{\text {(c)}},\tilde{w}_q^{\text {(c)}}$) are used to describe the horizontal and vertical displacement along the interfaces between the mathematical layers, where q indicates the number of the interface ($q=[1,2,3,4,5]$). The displacement function in each mathematical layer is represented by a linear term that corresponds to the linear interpolation between the interface displacements. This displacement representation enables the determination of layerwise-constant transverse strain through the core thickness. Introducing new degrees of freedom ($\hat{u}_j^{\text {(c)}},\grave{u}_j^{\text {(c)}},\hat{w}_j^{\text {(c)}},\grave{w}_j^{\text {(c)}}$) with corresponding higher-order functions ($\hat{f}_j^{\text {(c)}}(z)$, $\grave{f}_j^{\text {(c)}}(z)$) in each mathematical layer allows capturing linear and cubic strain variation through the core thickness. The core displacement functions are given as

$$\begin{aligned} u_j^{\text {(c)}}(x,z)=\,&[(j-2)\tilde{u}_j^{\text {(c)}}(x)+(3-j)\tilde{u}_{j+1}^{\text {(c)}}(x)]+ \frac{4(\tilde{u}_{j+1}^{\text {(c)}}(x)-\tilde{u}_j^{\text {(c)}}(x))}{h^{\text {(c)}}}\,z \nonumber \\&+\hat{f}_j^{\text {(c)}}(z)\hat{u}_j^{\text {(c)}}(x)+\grave{f}_j^{\text {(c)}}(z)\grave{u}_j^{\text {(c)}}(x), \end{aligned}$$

(7)

$$\begin{aligned} w_j^{\text {(c)}}(x,z)=\,&[(j-2)\tilde{w}_j^{\text {(c)}}(x)+(3-j)\tilde{w}_{j+1}^{\text {(c)}}(x)]+ \frac{4(\tilde{w}_{j+1}^{\text {(c)}}(x)-\tilde{w}_j^{\text {(c)}}(x))}{h^{\text {(c)}}}\,z\nonumber \\&+\hat{f}_j^{\text {(c)}}(z)\hat{w}_j^{\text {(c)}}(x)+\grave{f}_j^{\text {(c)}}(z)\grave{w}_j^{\text {(c)}}(x). \end{aligned}$$

(8)

The shape functions $\hat{f}_j^{(\text {c})}(z),\grave{f}_j^{(\text {c})}(z)$ vanish at the interfaces to avoid displacement discontinuities

$$\begin{aligned} \hat{f}_j^{\text {(c)}}(z)=\,&-4(3-j)(2-j)-\frac{16(-2j+5)}{h^{\text {(c)}}}z-\frac{4^3}{{h^{\text {(c)}}}^2}z^2, \text {and} \end{aligned}$$

(9)

$$\begin{aligned} \grave{f}_j^{\text {(c)}}(z)=\,&\hat{f}_j^{\text {(c)}}(z)\,z . \end{aligned}$$

(10)

Differentiating the displacement functions in Eq. 7 and Eq. 8 yields the core strains in each core mathematical layer

$$\begin{aligned}&\varepsilon ^{\text {(c)}}_{xx,j}=\frac{\partial u_j^{\text {(c)}}}{\partial x},\end{aligned}$$

(11)

$$\begin{aligned}&\varepsilon ^{\text {(c)}}_{zz,j}=\frac{\partial w_j^{\text {(c)}}}{\partial z},\text { and}\end{aligned}$$

(12)

$$\begin{aligned}&\gamma ^{\text {(c)}}_{xz,j}=\frac{\partial u_j^{\text {(c)}}}{\partial z}+\frac{\partial w_j^{\text {(c)}}}{\partial x}. \end{aligned}$$

(13)

Derived from the generalized Hooke’s law and concerning the plane strain conditions, the constitutive law for the effective orthotropic core material core can be given as

$$\begin{aligned} \begin{bmatrix} \sigma ^{\text {(c)}}_{xx,j}\\ \\ \sigma ^{\text {(c)}}_{zz,j}\\ \\ \tau ^{\text {(c)}}_{xz,j} \end{bmatrix} \,=\, \begin{bmatrix} \frac{1-\nu ^{\text {(c)}}_{xy,j}\nu ^{\text {(c)}}_{yx,j}}{E^{\text {(c)}}_{xx,j}} &{} -\frac{\nu ^{\text {(c)}}_{xz,j}+\nu ^{\text {(c)}}_{xy,j}\nu ^{\text {(c)}}_{yz,j}}{E^{\text {(c)}}_{xx,j}} &{} 0\\ \\ -\frac{\nu ^{\text {(c)}}_{xz,j}+\nu ^{\text {(c)}}_{xy,j}\nu ^{\text {(c)}}_{yz,j}}{E^{\text {(c)}}_{xx,j}} &{}\frac{1-\nu ^{\text {(c)}}_{yz,j}\nu ^{\text {(c)}}_{zy,j}}{E^{\text {(c)}}_{zz,j}} &{} 0\\ \\ 0 &{} 0 &{}\frac{1}{G^{\text {(c)}}_{xz,j}}\\ \end{bmatrix}^{-1} \, \begin{bmatrix} \varepsilon ^{\text {(c)}}_{xx,j}\\ \\ \varepsilon ^{\text {(c)}}_{zz,j}\\ \\ \gamma ^{\text {(c)}}_{xz,j} \end{bmatrix}. \end{aligned}$$

(14)

The elastic constants may vary layerwise through the core thickness, resulting in a graded core design. The stresses in the isotropic face sheets are obtained from

$$\begin{aligned}&\sigma ^{\text {(f)}}_{xx,m} =\frac{E^{\text {(f)}}}{(1-{\nu ^{\text {(f)}}}^2)} \, \varepsilon ^{\text {(f)}}_{xx,m},\text { and}\end{aligned}$$

(15)

$$\begin{aligned}&\tau ^{\text {(f)}}_{xz,m} ={G^{\text {(f)}}} \gamma ^{\text {(f)}}_{xz,m}. \end{aligned}$$

(16)

The introduced degrees of freedom are unknown functions depending on the horizontal coordinate x. The principle of minimum potential energy is applied to determine these deformation functions in the considered load case. For this goal, the total potential energy $\varPi$ resulting from the sum of the inner strain energy $\varPi _i$ and the external potential energy $\varPi _e$ is required. Regarding the assumptions made, the total potential energy is determined by

$$\begin{aligned}&{\varPi }=\varPi ^{\text {(f)}}_{\text {i,1}}+\varPi ^{\text {(f)}}_{\text {i,2}}+\varPi ^{\text {(c)}}_{\text {i}}+\varPi _{\text {e}}, \end{aligned}$$

(17)

with

$$\begin{aligned}&\varPi ^{\text {(f)}}_{\text {i},m}=\frac{1}{2} \int _{-\frac{l}{2}}^{\frac{l}{2}}\int _{-\frac{h^{\text {(f)}}}{2}}^{\frac{h^{\text {(f)}}}{2}} \big ( \sigma ^{\text {(f)}}_{xx,m}\varepsilon ^{\text {(f)}}_{xx,m}+\tau ^{\text {(f)}}_{xz,m}\gamma ^{\text {(f)}}_{xz,m}\big ) \, \text {d}z\; \text {d}x\, \text {, and} \end{aligned}$$

(18)

$$\begin{aligned}&\varPi ^{\text {(c)}}_{\text {i}}=\frac{1}{2}\sum _{j=1}^{4} \int _{-\frac{l}{2}}^{\frac{l}{2}}\int _{\frac{-h^{\text {(c)}}}{2} +\frac{(j-1)h^{\text {(c)}}}{4}}^{\frac{-h^{\text {(c)}}}{2} +\frac{jh^{\text {(c)}}}{4}}( \sigma ^{\text {(c)}}_{zz,j}\varepsilon ^{\text {(c)}}_{zz,j} + \tau ^{\text {(c)}}_{xz,j} \gamma ^{\text {(c)}}_{xz,j}+\sigma ^{\text {(c)}}_{xx,j}\varepsilon ^{\text {(c)}}_{xx,j}) \, \text {d}z\; \text {d}x\,. \end{aligned}$$

(19)

The considered load case is illustrated in Fig. 3a. The applied force on the top face sheet at the mid of the top face sheet and the corresponding vertical displacement of the top face sheet leads to the following external energy formulation

$$\begin{aligned}&{\varPi _{\text {e}}}=\frac{-F}{t}w^{(\text {f})}_{0,2}(x=0). \end{aligned}$$

(20)

Fig. 3.

Boundary conditions and obtained lattice node displacements

The resulting equations from the condition $\delta \varPi =0$ represent a second-order differential equation system. The procedure for solving this equation system is presented in detail in [19]. Solving the corresponding equation system yields the unknown displacement functions of the sandwich and, thus, the displacement at the lattice nodes ($u^{(r)},w^{(r)}$), where r describes the RVE node number (Fig. 3b). However, the occurring stresses in the lattice struts are not obtained directly. Therefore, the homogenized core has to be dehomogenized by replacing it with the lattice on the mesoscale to determine these lattice strut stresses. The struts in the lattice on the mesoscale undergo a length change caused by the applied load. This length change can be expressed as a relationship between the displacements of the corresponding strut nodes. For this, the node displacements have to be transformed from the global coordinate system to the local coordinate system of the considered strut. The following equations describe the resulting length change of each strut within the F2CCZ RVE

$$\begin{aligned}&\varDelta l^{(1)}=(u^{(2)}-u^{(1)})\,\text {cos}(\pi /4)+(w^{(2)}-w^{(1)})\,\text {sin}(\pi /4),\nonumber \\&\varDelta l^{(2)}=(u^{(3)}-u^{(2)})\,\text {cos}(3\pi /4)+(w^{(3)}-w^{(2)})\,\text {sin}(3\pi /4),\\&\varDelta l^{(3)}=(u^{(4)}-u^{(3)})\,\text {cos}(5\pi /4)+(w^{(4)}-w^{(3)})\,\text {sin}(5\pi /4),\nonumber \end{aligned}$$

(21)

$$\begin{aligned}&\varDelta l^{(4)}=(u^{(1)}-u^{(4)})\,\text {cos}(-\pi /4)+(w^{(1)}-w^{(4)})\,\text {sin}(-\pi /4) \nonumber \\&\varDelta l^{(5)}=(w^{(3)}-w^{(1)}),\, \varDelta l^{(6)}=(w^{(5)}-w^{(1)})\,\text {sin}(\pi /4) \\&\varDelta l^{(7)}=(w^{(3)}-w^{(5)})\,\text {sin}(\pi /4).\nonumber \end{aligned}$$

(22)

Due to the symmetry, the change of the length in the struts 6 and 9, and the struts 6 and 7 are identical, i.e. $\varDelta l^{(6)}=\varDelta l^{(9)}$ and $\varDelta l^{(7)}=\varDelta l^{(8)}$. With the assumption that the nodes of the lattice do not transfer moments, the lattice strut stress is given by

$$\begin{aligned}&\sigma ^{(s)}=\frac{\varDelta l^{(s)}}{l^{(s)}}\,E^{(s)}, \end{aligned}$$

(23)

where the quantity s denotes the number of the strut within the F2CCZ RVE, as indicated in Fig. 3b.

3 Results

In this study, sandwich panels with a F2CCZ lattice core are analyzed. Two core types are compared: a homogeneous lattice core with a constant strut diameter (Fig. 4a), and a layerwise-graded lattice core with a variable strut diameter through the core thickness (Figure 4b). Since the cell size a does not vary through the thickness, changing the strut diameter leads to a varied aspect ratio and, thus, a varied stiffness and relative density. In the graded core, the strut diameter shows a symmetrical variation through the core thickness and affects a corresponding distribution of the effective core stiffness. The strut diameter within a mathematical layer remains constant. Each mathematical layer in the considered core includes four physical lattice layers, resulting in 16 physical layers ($N_z=16$). The graded core’s maximum strut diameter conforms to the homogeneous core’s strut diameter. The cell size a of the graded lattice and the homogeneous core are identical ($a=3$ mm). In the considered graded core, the ratio between the maximum transverse stiffness and minimum transverse stiffness is assumed to be (${E^{\text {(c)}}_{zz,\text {max}}}/{E^{\text {(c)}}_{zz,\text {min}}}=2$). The ratio between the maximum strut diameter and the minimum strut diameter of the graded core can be determined according to Eq. 1 by $d_{max}/d_{min}=\root 2.21 \of {2}$. Thus, the graded core has approx. 22% lower mass than the homogeneous core. Since both cores are composed of 16 physical layers, the core total thickness is 48 mm. Compared to the core thickness, the face sheets are thin and have a thickness of 2 mm. While the core consists of 176 RVEs along the sandwich length ($N_x=176$), merely one RVE is considered in the y-direction ($N_y=1$). The results generated by the derived model are compared to a FE solution obtained from a 3D analysis using the FE software ABAQUS. In the finite element analysis (FEA), quadratic 3D solid elements are used to mesh the face sheets, and beam elements represent the struts of the 3D lattice core. Additional to the boundary conditions presented in Fig. 4, no displacements in the depth direction are permitted in the FEA to fulfill the plane strain state conditions. Three paths along the core length are specified to assess the stresses in the core using the normalized strut stress $\overline{\sigma }^{(s)}=\sigma ^{(s)}/F$. The first path goes along the bottom core layer (highlighted in red in Fig. 4b), the second path along the mid core layer (blue), and the third one along the top core layer (green). Due to the symmetry, merely the struts of the left core half are analyzed. Furthermore, the stress variation through the core thickness at the load application position is evaluated.

Fig. 4.

2D view of the FE model with the corresponding boundary conditions

Figure 5 shows the stresses in the vertical struts through the thickness of the graded core (GC) and the homogeneous core (HC) at the load application position $x=0$. The occurring stresses in this area are mainly induced by the localized transverse loads. Thus, the struts there are under compression load. It can be demonstrated that the maximum stress occurs at the same position in the upper half of both cores and exhibits the same value. Due to the grading approach, the struts in the graded core show higher stresses in the mid core layers compared with the homogeneous core. However, the stresses there are below the maximum value. The stresses in the core bottom and top layers show similar distributions in both cores since these layers have the same strut diameter in the graded and homogeneous core. Moreover, it can be shown that the present model is in good agreement with FEA. The stress in the vertical struts along the pre-defined paths is illustrated in Fig. 6. For better visualization, merely the region beyond the load application and the support point is shown. Compared with the struts near the load application area, the struts are hardly loaded. Along these paths, the local effects caused by the transverse load subside. The stress distribution shows a compressive load in the upper core half and a tensile load in the bottom core half. No significant stresses are observed in the mid core layers. This distribution is because the vertical struts transfer the effective bending stress in the core, exhibiting a linear shape through the core thickness. Due to the relatively low stiffness of the core compared to the face sheet stiffness, the face sheets mainly support the normal bending stress, and the strut stresses induced by the sandwich bending are negligible compared to the strut stresses caused by the concentrated load. The stress along the bottom and top layer in the graded core presents a similar shape as in the homogeneous core. In the mid layer, a stress increase in the graded core is identified due to the smaller strut diameter in this layer.

Fig. 5.

Absolute normalized stresses in the vertical struts through the core thickness at $x=0$

The stress distribution along the core length in the inclined struts of the xz-plane is presented in Fig. 7. It can be seen that the inclined struts are higher loaded than the vertical struts beyond the stress concentration areas. While the stresses there show no variation along the mid layer, the stress in the top and bottom exhibits a linear distribution beyond the stress concentration areas. It can be observed that the stress in the inclined struts consists of two components. The constant effective shear stress causes the first stress component. The second stress component is induced by the sandwich bending and shows a linear increase with respect to the horizontal axis of the sandwich. Since the strut diameter of the bottom and top layers in both cores is identical, no stress changes along these layers caused by the core grading are identified. However, the strut diameter in the mid core layer shows a minimum value compared to the homogeneous core. Therefore, the struts in the graded core are higher loaded than in the homogeneous core. Although the inclined struts are higher stressed in the graded core, the stress there shows lower values than the maximum stress in the stress concentration area. Stresses in the inclined struts of the yz-plane are not presented as they support marginal stresses.

Fig. 6.

Normalized stresses in the vertical struts along the core length

Fig. 7.

Absolute normalized stresses in the inclined struts along the core length

Finally, the deflection of the top and bottom face sheets in the sandwiches with the homogeneous core and the graded core are compared, as illustrated in Fig. 8. A core compression is observed near the load application and the support points in both configurations. Core compression is the difference between the top face sheet deflection and the bottom face sheet displacement. Due to the employed grading approach, the sandwich with the graded core exhibits a higher deflection than the sandwich with the homogeneous core. In the sandwich with the graded core, the deflection increases by approx. 14% compared to the sandwich with the homogeneous core. Moreover, an increase in the core compression can be identified. However, the increase of the core compression and the sandwich deflection does not affect the strength of the core.

Fig. 8.

Deflection of the sandwich with a graded core (GC) and a homogeneous core (HC)

Based on the results obtained by the present model, it can be concluded that graded cores may significantly reduce the core mass without compromising the core strength. By using the selected grading approach, a mass reduction of 22% is achieved. The fabrication of layerwise graded lattices is enabled by additive manufacturing technologies, for instance, selective laser melting, as shown in [20]. Compared with results obtained from the FEA, the present model yields adequate stresses within one-tenth of the FEA computing time. Moreover, some new knowledge about the load distribution in strut-based lattice cores is acquired. With these gained acquirements about the load distribution across the strut-based lattice core, more suitable grading approaches may be applied to customize the strut diameter distribution in the core. This may be carried out within optimization loops to find an advanced core design. Sublayers may be introduced within the mathematical layers to enable a smoother strut diameter variation through the layers. Thus, the number of the sublayers conforms to the number of the core physical layers. If the strut diameter varies from physical layer to physical layer, each sublayer can be assigned a corresponding stiffness. This modeling yields good results without introducing additional displacement functions, as shown in [21]. While designing graded cores, the deflection of the sandwich must still be considered since the core stiffness declines with decreasing relative density. The increased deflection may be compensated, for instance, by grading the core along the horizontal axis of the sandwich.

4 Summary and Conclusion

This study introduced an analytical model to analyze graded strut-based lattice cores in sandwich panels. Compared to homogeneous cores, graded cores may minimize stress concentrations induced by localized loads without increasing the structural mass or reducing the core strength. Furthermore, the analytical model determines the strut stresses of the graded core using higher-order displacement representations. With the presented model, the core’s optimization and design procedure can be more efficiently performed since the derived model reduces the modeling and computation time by the factor 10. Compared with the homogeneous core, the graded core is advantageous as the graded core shows a reduced mass but the same strength. While designing graded cores in applications where the sandwich displacement may be critical, the total sandwich deflection should be considered since the core stiffness may decrease with strut diameter grading.