Keywords

1 Introduction

Loss of life and property may be caused by landslides in mountainous areas, particularly during or after prolonged periods of heavy rainfall. Understanding the factors that trigger and contribute to landslide occurrences and the subsequent debris transport distance is critical for landslide hazard assessment (Dai et al. 2003). Large residential communities are nevertheless frequently affected by the mass instability of soil slopes in regions of steep topography and experience prolonged hot and dry periods followed by extreme weather events (heavy rainfall, rainstorms). Although slope failures may originate because of human-induced factors such as slope-top loading or the removal of the toe of a natural slope for construction activities, numerous natural slopes become unstable simply because of the impact of rainwater penetrating the slope material layers (Collins Brian and Znidarcic 2004).

The interactions between landslide triggering and causative factors and the environment around them lead to the establishment and development of the landslide processes in the given area. Therefore, new insights into the prevention and mitigation of landslides may be gained through a better knowledge of the differences in landslide processes and the features of landslide movement (Yang et al. 2021). For this purpose, several studies on different landslide science aspects have been conducted, including case studies in numerous areas and their failure scenarios (Alimohammadlou et al. 2013).

This article presents the results of the slope stability analysis conducted in connection with a landslide event triggered by heavy rainfall in the Trung Chai commune, Sapa district, Vietnam. The stability of the analyzed slope was evaluated using finite element (FEM) and limit equilibrium (LEM) methods. By conducting deterministic and probabilistic analyses, this study determined the relationship between pore water pressure and the stability of the examined slope. In addition, the obtained relationship between the two primary landslide triggers (rainfall and seismic loading) is also a significant result of this study.

2 Study Area

Located in the northwest of Lao Cai Province, the Sapa district, which covers an area of 675.8 km2 and has an elevation of 150 m to more than 3000 m, is well-known as a famous tourist destination in Vietnam. In recent years, Sapa has experienced an increase in the frequency and magnitude of landslides due to rapid urbanization, construction, and agriculture. Most landslide incidents in the area were triggered by precipitation (Dang et al. 2018; Tien Bui et al. 2017).

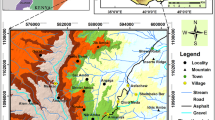
Trung Chai commune is located in the northeastern Sapa district, where the 4D national road connects Laocai city and the Sapa district. Trung Chai (14 landslides), Ta Van (16 landslides), and Ban Ho (27 landslides) are the three communes in Sapa that reported the highest number of landslides (Binh Van Duong et al. 2022). The combination of mountainous terrain and agricultural and construction activity has triggered numerous landslide events in this area. The sliding mass in this study (Fig. 1) was investigated during the construction of the Mong Sen Bridge, which connects the Sapa district and the Hanoi-Laocai expressway. This landslide event was triggered by a heavy rain event, which caused the displacement of slope materials and the formation of cracks on the surface of the sliding body.

Fig. 1
A digital elevation map of Trung Chai on the left presents the landslide area, rivers, and elevation from 581 to 2175 meters using different color shades. An inset map depicts the locations of Trung Chai and Hanoi. A satellite photo of the landslide area is on the right.

Location of landslide site

Full size image

3 Evaluation of Slope Stability for the Mong Sen Landslide

3.1 Methods

Both the factor of safety (FS) and the probability of failure (PF) are significant factors to determine when assessing slope stability. The quality of topographic and geotechnical data plays a critical role in establishing a simulation model of slope behavior to achieve highly accurate analysis results (Azizi et al. 2020). It is widely accepted that the ratio between the available shear strength (s) and the equilibrium shear stress (τ) (shear stress along the sliding surface required to maintain the stability of the slope) is defined as the factor of safety value (Duncan et al. 2014):

$$ FS=\frac{s}{\tau } $$
(1)

Slope stability is frequently quantified in geotechnical engineering using a factor of safety (FS) as the resulting value. Considered an indicator to define the likelihood of slope failures caused by a landslide, the FS value is used to predict the occurrence of landslide-related slope deformations (Fomenko et al. 2019; Fomenko and Zerkal 2017). By assuming that the values of all model input parameters are accurately known, the deterministic analysis produces a single value of FS. However, materials on slopes are frequently heterogeneous, with variations in spatial distribution and properties depending on the slope’s location and surrounding environment. Therefore, probabilistic analyses are especially helpful in slope stability studies because it allows the determination of the impact of uncertainty or variability in input parameters on the slope stability analysis results (Nagendran et al. 2019). Generally, statistical distributions can be assigned to the input parameters when conducting probabilistic analyses. Samples may be taken an unlimited number of times for each calculation, and combinations of these samples are used to determine the factor of safety (FS). The probability of failure (PF) for the slope may be defined as follows (Cami et al. 2021), according to the Eq. (2):

$$ PF\left(\%\right)=\frac{Number\ simulations\ with\ FS<1}{Total\ number\ of\ simulations} $$
(2)

In addition, a probabilistic analysis may also be conducted to determine the reliability index (RI), which is defined as the capacity of a system to perform necessary tasks under given circumstances for a predetermined amount of time (Wang and Constantino 2009). In a slope stability analysis, the safety of the slope is quantified by the reliability index based on the number of standard deviations that separate the best estimate of FS from the defined failure value of 1.0 (Christian John et al. 1994). Along with the factor of safety value, the reliability index determined in probabilistic analysis, which corresponds to the probability of failure, is also the indicator used to measure the stability of the slope. It has been determined that the greater the dependability index, the lower the probability of failure (Cheng and He 2020). Consequently, the definition of an acceptable level of safety, i.e., the highest failure probability value without structural collapse, is one of the most challenging aspects of reliability analysis. However, there are currently different proposals on this issue (Douglas J. Kamien 1997; Withiam et al. 1998). In geotechnical design, it is frequently required to have a reliability index value greater than 3.0 (i.e., PF equal to 0.001) to achieve performance that is better than “above average” (Abdulai and Sharifzadeh 2021).

3.2 Strength of Slope Materials

When conducting a slope stability analysis, the slope materials and their strength properties must be well-defined to improve the performance of the slope behavior model. In stability analysis models, the strength of slope materials may be determined using various failure criteria. In limit equilibrium analyses, the Mohr-Coulomb Failure Criterion and the Infinite Strength Failure Criterion were employed to determine the strength parameters of the upper soil and intact rock layers, respectively. Meanwhile, the Mohr-Coulomb Failure Criterion was used in the analyses that utilized the finite element method.

The soil samples were taken in the field survey during the dry and rainy seasons. Afterward, the physico-mechanical properties of the soil layer were determined using laboratory tests to provide input data for modeling. The direct shear test was conducted to determine the strength parameters of the Mohr-Coulomb criterion, including the friction angle and cohesion. The physico-mechanical properties of the soil layer are shown in Table 1.

Table 1 Parameters of soil layer
Full size table

For modeling the behavior of slopes in stability studies, the pore water pressure ratio (ru) has been widely used to describe the pore water pressure condition. As a result of the absence of PWP data in this study, the pore water pressure at any position may be best described using the pore water pressure ratio proposed by Bishop and Morgenstern (1960):

$$ {r}_u=\frac{u}{\gamma h} $$
(3)

where h denotes the depth of the point in the soil mass below the soil surface, and γ denotes the soil unit weight.

The general solutions are based on the assumption of a constant pore water pressure ratio (ru) throughout the cross-section, also known as a homogeneous pore water pressure distribution. However, the necessity for a single constant value is a significant drawback of the ru approach. The only circumstance in which the ru value is constant is when the piezometric line is at the ground surface, a scenario that occurs in nature relatively seldom.

In this study, the SLIDE model (Liao et al. 2010) was used to evaluate the variation in pore water pressure ratio based on rainfall data gathered during a heavy rainfall event from 22:00 h on May 30 to 24:00 h on May 31, 2020. At 15:00 h on May 31, the maximum ru value was 0.286. The relationship between pore water pressure ratio and rainfall intensity is shown in Fig. 2.

Fig. 2
A dual-axis graph plots rainfall intensity and r u versus time. The rainfall intensity bars follow an increasing-to-decreasing trend and are highest at (9, 27.5). The line of r u starts from (22, 0), increases to a peak at (15, 0.28), decreases, and ends at (16, 0.23). All data are estimated.

Relationship between rainfall intensity and ru

Full size image

3.3 Model Calibration

The models in this study were calibrated by comparing simulation results with actual slope failure data. Until recently, slope stability and risk assessments based on deformation analysis had been conducted by various geotechnical engineers. With the introduction of 3D methods into computations for slope stability, it has become possible to solve these problems (Bar et al. 2021). However, while performing slope stability assessments, various challenges remain unsolved. They are primarily due to uncertainties in the calculation of slope stability, such as inaccuracies in determining the strength parameters of the slope materials, the selection of methods for solving the problem, algorithms for optimizing the sliding surface (using GLE limit equilibrium methods), and inaccuracies in the establishment of the geometric model (Fig. 3).

Fig. 3
Two 3-D geometric models of land slopes. Both have 3 encircled areas on the sliding surface with values labeled on them. A, the values indicated are 1.414, 1.325, and 1.200. B, presents the values 1.409, 1.518, and 1.276.

Multimodal particle swarm optimization, Bishop’s method (a) and Spencer’s method (b)

Full size image

Despite minor inconsistencies between the calculation result and the actual data on the position of the landslide body, the authors considered the results produced using the Yanbu simplified method to be the most acceptable for evaluating landslide stability (Figs. 4 and 5).

Fig. 4
Two 3-D geometric models of land slopes. A, the stability of the slope is indicated using different color shades and has 2 overlapped circles on the sliding surface. B, the values indicated on the 3 color shaded regions are 1.222, 1.178, and 1.195. A colored circle is over the shaded regions.

The result of slope stability analysis using Slide3 in the dry season

Full size image
Fig. 5
Two 3-D geometric models of land slopes. A, the stability of the slope is indicated using different color shades and has two circles on them. B, the values indicated on the three color-shaded regions are 1.020, 0.954, and 0.967. A colored circle is drawn over the two regions.

The result of slope stability analysis using Slide3 at 10:00 h, May 31

Full size image

3.4 Results of the Slope Stability Analysis Using LEM

After configuring the Slide3 model’s input parameters, deterministic and probabilistic analyses were performed to determine the slope stability associated with changes in the pore water pressure caused by actual rainfall. These simulations were performed in the dry season and during periods of heavy rain, which increased the pore water pressure in the soil layer.

The analysis results indicated that the stability of the studied slope is maintained in the dry season. In simulations conducted during the dry season, the factor of safety (FS) value determined by probabilistic and deterministic analyses is 1.258 and 1.178, respectively. The probability of failure (PF) is 3.2%, which indicates that 3.2% of 1000 samples evaluated had a factor of safety value of less than 1 (Fig. 4).

The penetration of rainwater into the soil layer led to an increase in the pore water pressure ratio, which in turn resulted in a reduction in the slope stability or factor-of-safety value. The pore water pressure ratio increased from 0 in the absence of rain to 0.286 at 15:00 h on May 31. In probabilistic analysis, the FS value reduced from 1.258 to 0.901, whereas in deterministic analysis, it decreased from 1.178 to 0.895 (Table 2). When the pore water pressure ratio reached its maximum value, the probability of failure increased from 3.2% to 80.6%. In addition, the analysis results revealed that the studied slope became unstable around 10:00 h on May 31 when the FS value was less than one (Fig. 5).

Table 2 Results of slope stability analysis using LEM
Full size table

Figures 6 and 7 show the relationship between the variation of the FS and PF values and the change in the pore water pressure ratio of the soil layer on the slope, as determined by the probabilistic analysis conducted in Slide3. Simultaneously, the analysis results performed by Slide3 also indicated a relationship between the probability of failure (PF) and the reliability index (RI) (Fig. 8).

Fig. 6
A dual-axis graph plots r u and F S versus time step. The r u bars follow an increasing trend and it is the highest at (19, 0.29). The lines of F S underscore probabilistic and F S underscore deterministic follow a decreasing trend with a few fluctuations. All data are estimated.

Relationship between FS and ru by probabilistic and deterministic analysis in Slide3

Full size image
Fig. 7
A dual-axis graph plots r u and P F versus time step. The r u bars follow an increasing trend and the highest value is at (19, 0.29). The line of P F follows an increasing trend from (1, 2) to (19, 80). All data are estimated.

Relationship between PF and ru by probabilistic analysis in Slide3

Full size image
Fig. 8
A scatterplot of P F in percentage versus R I. The plots lie on a decreasing line from (negative 0.9, 80) to (1.85, 3). All data are estimated.

Relationship between PF and RI by probabilistic analysis in Slide3

Full size image

Meanwhile, a correlation between the factor of safety (FS) and the pore water pressure ratio was also determined using the deterministic analysis in Slide3 (Fig. 6). The higher the pore water pressure ratio in the soil layer, the lower the FS value and the higher the PF value.

Using the “section creator” function in Slide3, a cross-section was generated for stability analysis in Slide2 based on the three-dimensional slope analysis model in Slide3. Afterward, slope stability assessments utilizing the same precipitation scenario as in Slide3 were performed in Slide2.

The outcomes of slope stability simulations during the dry season (a) and at the failure time of slope (b) are shown in Fig. 9. The position of the sliding surface is in the middle of the examined slope, which is relatively compatible with the sliding surface position determined by Slide3 and the actual sliding mass position. According to the 2D analysis results, the slope is stable throughout the dry season, as shown by the factor of safety (FS) value of 1.164. The pore water pressure ratio has increased because of rainwater penetration into the soil layer, resulting in a decrease in the factor of safety value. As the pore water pressure ratio increased from 0 to 0.286, the FS value reduced from 1.164 to 0.902 (Fig. 10). In addition, the analysis performed in Slide2 indicated that the slope became unstable on May 31, around 10:00 h, when the ru value reached 0.144, which is equivalent to the simulation result in Slide3.

Fig. 9
Two 3-D models of a sloppy region. The values of the safety factor are indicated using different color shades with a color-coded scale on the bottom right of the model. A, an S F value of 1.164 is indicated for a region. B, an S F value of 0.986 is marked for a region.

The result of slope stability analysis using Slide2 in the dry season (a) and at 10:00 h, May 31 (b)

Full size image
Fig. 10
A dual-axis graph plots r u and F S versus time step. The r u bars follow an increasing trend and the highest value is at (19, 0.29). The line of F S follows a decreasing trend from (1, 1.18) to (19, 0.9). All data are estimated.

Relationship between FS and ru using Slide2

Full size image

Table 2 summarizes the stability analysis results for the examined slope at each analysis step. As a result, we have determined that the factor of safety and probability of failure are the functions of the pore water pressure ratio. As seen in Table 2 and graphs, an increase in pore water pressure reduces the factor of safety value and increases the probability of failure value. However, steps 17 and 18 of our research produced several unexpected results in Table 2. This issue can be explained as follows:

  1. 1)

    The pore water pressure ratio is used to characterize pore-water conditions in slope stability analyses. However, the necessity for a single constant value is a significant drawback of the ru method. It is well-known that the ru value is a constant only when the piezometric line is at the ground surface, which rarely occurs in nature. Therefore, it is not an ideal method to simulate actual groundwater conditions in all circumstances because the presence of any negative pore-water pressures is omitted when conducting simulations. Although the factor-of-safety results are acceptable, the analysis is based on the imperfect prediction of pore water pressure conditions.

  2. 2)

    These unexpected results may be caused by the sampling technique, the number of samples, the type of analysis, or the parameters used to set the sliding surface search method when performing simulations. However, increasing the number of analyzed samples and modifying the initial parameters will result in a considerable increase in analysis time and a significant increase in the demands on computational resources. Because the failure time of the slope has been determined, these anomalies have been accepted in this study.

Along with the factor of safety and probability of failure, the reliability index (RI) is a critical outcome for evaluating slope stability. The relationship between the probability of failure and the reliability index is shown in Fig. 8. As indicated by the computed maximum reliability index of 1.85 < 3, it is necessary to implement protection measures to prevent this slope from becoming unstable. In addition, the analysis results demonstrated that the analyzed slope becomes unstable rapidly under the impact of rainfall.

3.5 Results of the Slope Stability Analysis Using FEM

Using the same input parameters as limit equilibrium analyses, two- and three-dimensional slope stability evaluations were conducted using the finite element method. As indicated by three-dimensional analysis using RS3, the slope is stable in the dry season with a critical strength reduction factor (SRF) of 1.32 (Fig. 11a). The penetration of rainwater into the soil caused an increase in pore water pressure in the sliding mass on the examined slope, resulting in a decrease in the critical strength reduction factor. The SRF value decreased from 1.32 to 0.96, corresponding to the pore pressure ratio increasing from 0 to 0.286 (Table 3). Additionally, the analysis results indicated that the studied slope became unstable around 14:00 h on May 31, when the SRF reached 0.98 (Fig. 11b).

Fig. 11
Two 3-D geometric models of land slopes. The stability of the slope is indicated using different color shades. The values of critical S R F labeled on top of A and B are 1.32 and 0.98, respectively.

The result of the slope stability analysis using RS3 in the dry season (a) and at 14:00 h, May 31 (b)

Full size image
Table 3 Results of slope stability analysis using FEM
Full size table

An assessment result of the relationship between the critical strength reduction factor (SSR) as determined by the shear strength reduction method (SSR) integrated into RS3 and the pore water pressure ratio in the soil layer on the examined slope is shown in Fig. 12.

Fig. 12
A dual-axis graph plots r u and S R F versus time step. The r u bars follow an increasing trend and the highest value is at (19, 0.29). The line of S R F follows a decreasing trend from (1, 1.3) to (19, 0.98). All data are estimated.

Relationship between SRF and ru using RS3

Full size image

Generally, FS values determined by finite element analysis are higher than those calculated by limit equilibrium analysis. The FS values determined by RS3 are, on average, 1.06 times greater than those obtained by Slide3. The distribution of the instability zone predicted by finite element analysis corresponds to the results of limit equilibrium analysis.

For 2D slope stability analyses, the cross-section in RS2 was built up in the same way as in Slide2. The computed cross-sections were then set up using a uniform finite element mesh consisting of three-noded triangular elements. Simultaneously, this study investigated the influence of element mesh selection on the outcomes of stability analyses using meshes with 5000 (Fig. 13), 10,000 (Fig. 14), and 20,000 elements (Fig. 15). The SRF values obtained from the 5000 and 10,000 element meshes are higher than the SRF values obtained from RS3, whereas the SRF values obtained from the 20,000-element mesh are lower than those obtained from RS3. For simulations with grids of 5000 and 10,000 elements, the slope maintains a stable state with minimum strength reduction factors of 1.07 and 1.01, respectively. Meanwhile, the examined slope became unstable at about 14:00 h on May 31 when the strength reduction factor was 0.99, according to the stability analysis utilizing a 20,000-element mesh.

Fig. 13
Two 2-D geometric models of a land slope labeled A and B plot the total displacement values of 0.00 in most places. The highest values in A and B are at the center and towards the top of the sliding surface, which are 0.07 and 0.02, respectively.

The result of the stability analysis using RS2 in the dry season (a) and at 14:00 h, May 31 (b) (5000-element mesh)

Full size image
Fig. 14
Two 2-D geometric models of a land slope labeled A and B plot the total displacement values of 0.00 at most places, and the highest values are towards the top of the sliding surface. The highest values in A and B range from 0.04 to 0.05 and 0.01 to 0.02, respectively.

The result of the stability analysis using RS2 in the dry season (a) and at 14:00 h, May 31 (b) (10,000-element mesh)

Full size image
Fig. 15
Two 2-D geometric models of a land slope labeled A and B plot the total displacement values of 0.00 in most places. The highest values in A and B are on the top and from center to top of the sliding surface and their values are 0.04 and from 0.02 to 0.03, respectively.

The result of the stability analysis using RS2 in the dry season (a) and at 14:00 h, May 31 (b) (20,000-element mesh)

Full size image

Similar to RS3, the results of slope stability analysis by RS2 revealed the relationship between the strength reduction factor (SRF) and the pore water pressure ratio. Figure 16 shows the relationship between the strength reduction factor and the pore water pressure ratio using different element meshes. In addition, the relationship between the number of mesh elements and the strength reduction factor is shown in Fig. 17. As shown in the figures, the higher the number of mesh elements, the lower the calculated strength reduction factor.

Fig. 16
A dual-axis graph plots r u and S R F versus time step. The r u bars follow an increasing trend and the highest value is at (19, 0.29). The lines of 5000, 10000, and 20000 element meshes follow a decreasing trend. All data are estimated.

Relationship between SRF and ru using RS2

Full size image
Fig. 17
A multiline graph of strength reduction factor versus the 5000, 10000, and 20000 mesh elements plots 11 lines in a decreasing trend.

Relationship between SRF and element mesh

Full size image

When the slope is affected by precipitation, the shear strength decreases, and the weight of the soil mass increases, causing a reduction in SRF. In addition, a quasi-linear relationship between these two variables was also determined. The study indicated that the appropriate selection of a finite element mesh is a crucial factor that directly influences the simulation results and slope stability assessment. The slope stability analysis results for each step are detailed in Table 3.

3.6 Comparison of the Slope Stability Analysis Results Using LEM and FEM

All the results of calculating the change in FS values of the examined slope are shown in Fig. 18 to compare the difference in FS values between LEM and FEM stability analyses (Table 4).

Fig. 18
A multiline graph plots the factor of safety versus time step. 6 lines follow a decreasing trend, in which L E M underscore 3 D has a few fluctuations.

Results of stability analysis using FEM and LEM

Full size image
Table 4 Difference between FS values
Full size table

The study results revealed that the decreasing trend of the factor-of-safety graphs established by the two methods corresponds to the increase in the pore water pressure ratio. Nonetheless, analyses indicated that the finite element method yields greater FS values than those from the limit equilibrium method. In 3D simulations, the mean difference between the finite element method and the limit equilibrium method for calculating the FS values is only 6.03% (probabilistic) and 8.59% (deterministic). Meanwhile, in 2D analyses, the mean difference between the finite element method and the limit equilibrium method for the value of FS is 16.3 (5000-element mesh), 11.28 (10,000-element mesh), and 8.08% (20,000-element mesh), respectively. According to the simulation results, 3D analyses show a lower difference in FS values than 2D analyses. When comparing the outcomes of 2D and 3D finite element analyses, the mean difference in the FS values is 8.31 (5000-element mesh), 2.81 (10,000-element mesh), and −0.69% (20,000-element mesh), respectively. The simulation results revealed that 2D analysis with the 20,000-element grid provides the most comparable results to 3D analysis. The mean difference in the FS values between the 2D and 3D simulations using the limit equilibrium method is 2.78% (probabilistic) and 0.09% (deterministic). The FS values obtained from the 3D limit equilibrium analyses compared to the 2D analyses are consistent with the slope stability studies of numerous other authors.

3.7 Relationship Between Pore Water Pressure Ratio and Seismic Coefficient

Landslides may be triggered by a single earthquake in the Sapa area since the district is located in a seismically active zone of Vietnam. In addition, earthquakes that occur during rainy periods may increase the probability and scale of landslides, therefore increasing the potential damage. As a result, a relationship between pore water pressure and earthquake loading has been established in this study for examined sliding mass (Fig. 19). The area above the trendline indicates instability, whereas the area under this trendline indicates slope stability. When the ru value is high, as shown in Fig. 19, even a minor earthquake might cause slope failures. Destabilization of the studied slope might occur because of individual earthquakes with a seismic coefficient of approximately 0.08 or rainfall with a ru value of more than 0.19. When considering the combined effects of the two triggers, the equation shown in Fig. 19 may be employed. This relationship may be established for any natural or artificial slope in the study area to provide the most comprehensive evaluation of slope instability hazards.

Fig. 19
A scatterplot of pore water pressure ratio versus seismic coefficient. The plots lie on either side of a decreasing trend. The equations indicated on the graph are y = negative 2.6903 x + 0.2089 and R squared = 0.9777.

Relationship between pore water pressure ratio and seismic coefficient

Full size image

4 Conclusions

The slope stability assessment has a critical role, especially given the increasing development of urban areas in Vietnam’s mountainous provinces. The assessment quality has a significant impact on the selection of the worksite and the most suitable solutions for preventing slope failures. Based on the above idea, a slope stability analysis has been conducted for a landslide in Trung Chai commune, Sapa district, Lao Cai province.

The change in pore water pressure caused by rainfall was simulated using the pore water pressure ratio. Slope stability models may be established in two- and three-dimensions using input data obtained by field survey, including the digital elevation model of the sliding mass, the boundary between soil and rock layers, and their related physico-mechanical parameters. The Slide2, Slide3, and RS2, RS3 models were used to assess two-dimensional and three-dimensional slope stability utilizing the limit equilibrium and finite element methods, two of the most frequently employed methods in slope stability analysis. The variation in slope stability was investigated using probabilistic and deterministic analyses simultaneously. The study outcomes were utilized to establish correlations between slope stability (i.e., the factor of safety and probability of failure) and the change in PWP condition and to identify the slope failure moment. Comparing the 2D and 3D analysis results, the 2D FEM analyses provide a higher FS value than the 3D FEM analyses, whereas the 2D LEM analyses yield a lower FS value than the 3D LEM analyses. A comparison of the results between the FEM simulations and the LEM simulations reveals that the 2D and 3D FEM simulations provide higher FS values.

Despite some unexpected outcomes, the study investigated the behavior of slopes under the effect of precipitation and determined the moment of slope collapse. These results are consistent with the actual landslide occurrence, demonstrating the reliability of the simulation models. In Vietnam, the safety factor is currently the most significant parameter for evaluating slope stability. As a result, there is some subjective evaluation when studying slope stability, implying future risks. According to the research team, slope stability analysis reports should include additional values for the probability of failure and the reliability index. Additionally, it is necessary to establish a specific standard for the reliability index, which will be used to assess the probability of failure for various types of projects.