Compositional Probabilistic Model Checking with String Diagrams of MDPs

Abstract

We present a compositional model checking algorithm for Markov decision processes, in which they are composed in the categorical graphical language of string diagrams. The algorithm computes optimal expected rewards. Our theoretical development of the algorithm is supported by category theory, while what we call decomposition equalities for expected rewards act as a key enabler. Experimental evaluation demonstrates its performance advantages.

The authors are supported by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST. K.W. is supported by the JST grant No. JPMJFS2136.

1 Introduction

Probabilistic model checking is a topic that attracts both theoretical and practical interest. On the practical side, probabilistic system models can naturally accommodate uncertainties inherent in many real-world systems; moreover, probabilistic model checking can give quantitative answers, enabling more fine-grained assessment than qualitative verification. Model checking of Markov decision processes (MDPs)—the target problem of this paper—has additional practical values since it not only verifies a specification but also synthesizes an optimal control strategy. On the theoretical side, it is notable that probabilistic model checking has a number of efficient algorithms, despite the challenge that the problem involves continuous quantities (namely probabilities). See e.g. [1].

However, even those efficient algorithms can struggle when a model is enormous. Models can easily become enormous—the so-called state-space explosion problem—due to the growing complexity of modern verification targets. Models that exceed the memory size of a machine for verification are common.

Among possible countermeasures to state-space explosion, one with both mathematical blessings and a proven track record is compositionality. It takes as input a model with a compositional structure—where smaller component models are combined, sometimes with many layers—and processes the model in a divide-and-conquer manner. In particular, when there is repetition among components, compositional methods can exploit the repetition and reuse intermediate results, leading to a clear performance advantage.

Focusing our attention to MDP model checking, there have been many compositional methods proposed for various settings. One example is [14]: it studies probabilistic automata (they are only slightly different from MDPs) and in particular their parallel composition; the proposed method is a compositional framework, in an assume-guarantee style, based on multi-objective probabilistic model checking. Here, contracts among parallel components are not always automatically obtained. Another example is [11], where the so-called hierarchical model checking method for MDPs is introduced. It deals with sequential composition rather than parallel composition; assuming what can be called parametric homogeneity of components—they must be of the same shape while parameter values may vary—they present a model-checking algorithm that computes a guaranteed interval for the optimal expected reward.

In this work, inspired by these works and technically building on another recent work of ours [20], we present another compositional MDP model checking algorithm. We compose MDPs in string diagrams—a graphical language of category theory [15, Chap. XI] that has found applications in computer science [3, 8, 17]—that are more sequential than parallel. Our algorithm computes the optimal expected reward, unlike [11].

One key ingredient of the algorithm is the identification of compositionality as the preservation of algebraic structures; more specifically, we identify a compositional solution as a “homomorphisms” of suitable monoidal categories. This identification guided us in our development, explicating requirements of a desired compositional semantic domain (Sect. 2).

Another key ingredient is a couple of decomposition equalities for reachability probabilities, extended to expected rewards (Sect. 3). Those for reachability probabilities are well-known—one of them is Girard’s execution formula [7] in linear logic—but our extension to expected rewards seems new.

The last two key ingredients are combined in Sect. 4 to formulate a compositional solution. Here we benefit from general categorical constructions, namely the $\textrm{Int}$ construction [10] and change of base [5, 6].

We implemented the algorithm (it is called $\textrm{CompMDP}$) and present its experimental evaluation. Using the benchmarks inspired by real-world problems, we show that 1) $\textrm{CompMDP}$ can solve huge models in realistic time (e.g. $10^8$ positions, in 6–130 s); 2) compositionality does boost performance (in some ablation experiments); and 3) the choice of the degree of compositionality is important. The last is enabled in $\textrm{CompMDP}$ by the operator we call freeze.

Fig. 1.

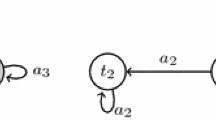
String diagrams of MDPs, an example (the Patrol benchmark in Sect. 5).

Fig. 2.

Sequential composition $\mathbin {;}$, sum $\oplus$, and loops of MDPs, illustrated.

Compositional Description of MDPs by String Diagrams. The calculus we use for composing MDPs is that of string diagrams. Figure 1 shows an example used in experiments. String diagrams offer two basic composition operations, sequential composition $\mathbin {;}$ and sum $\oplus$, illustrated in Fig. 2. The rearrangement of wires in $\mathcal {A}\oplus \mathcal {B}$ is for bundling up wires of the same direction. It is not essential.

We note that loops in MDPs can be described using these algebraic operations, as shown in Fig. 2. We extend MDPs with open ends so that they allow such composition; they are called open MDPs.

The formalism of string diagrams originates from category theory, specifically from the theory of monoidal categories (see e.g. [15, Chap. XI]). Capturing the mathematical essence of the algebraic structure of arrow composition $\circ$ and tensor product $\otimes$—they correspond to ;  and $\oplus$ in this work, respectively—monoidal categories and string diagrams have found their application in a wide variety of scientific disciplines, such as quantum field theory [12], quantum mechanics and computation [8], linguistics [17], signal flow diagrams [3], and so on.

Our reason for using string diagrams to compose MDPs is twofold. Firstly, string diagrams offer a rich metatheory—developed over the years together with its various applications—that we can readily exploit. Specifically, the theory covers functors, which are (structure-preserving) homomorphisms between monoidal categories. We introduce a solution functor $\mathcal {S}:\textbf{oMDP}\rightarrow \mathbb {S}$ from a category $\textbf{oMDP}$ of open MDPs to a semantic category $\mathbb {S}$ that consists of solutions. We show that the functor $\mathcal {S}$ preserves two composition operations, that is,

$$\begin{aligned} \mathcal {S}(\mathcal {A}\mathbin {;}\mathcal {B})= \mathcal {S}(\mathcal {A})\mathbin {;}\mathcal {S}(\mathcal {B}), \quad \mathcal {S}(\mathcal {A}\oplus \mathcal {B})= \mathcal {S}(\mathcal {A})\oplus \mathcal {S}(\mathcal {B}), \end{aligned}$$

(1)

where ;  and $\oplus$ on the right-hand sides are semantic composition operations on $\mathbb {S}$. The equalities (1) are nothing but compositionality: the solution of the whole (on the left) is computed from the solutions of its parts (on the right).

The second reason for using string diagrams is that they offer an expressive language for composing MDPs—one that enables an efficient description of a number of realistic system models—as we demonstrate with benchmarks in Sect. 5.

Granularity of Semantics: A Challenge Towards Compositionality Now the main technical challenge is the design of a semantic domain $\mathbb {S}$ (it is a category in our framework). We shall call it the challenge of granularity of semantics; it is encountered generally when one aims at compositional solutions.

• The coarsest candidate for $\mathbb {S}$ is the original semantic domain; it consists of solutions and nothing else. This coarsest candidate is not enough most of the time: when components are composed, they may interact with each other via a richer interface than mere solutions. (Consider a team of two people. Its performance is usually not the sum of each member’s, since there are other affecting factors such as work style, personal character, etc.)

• Therefore one would need to use a finer-grained semantic domain as $\mathbb {S}$, which, however, comes with a computational cost: in (1), one will have to carry around bigger data as intermediate solutions $\mathcal {S}(\mathcal {A})$ and $\mathcal {S}(\mathcal {B})$; their semantic composition will become more costly, too.

Therefore, in choosing $\mathbb {S}$, one should find the smallest enrichment¹ of the original semantic domain that addresses all relevant interactions between components and thus enables compositional solutions. This is a theoretical challenge.

In this work, following our recent work [20] that pursued a compositional solution of parity games, we use category theory as guidance in tackling the above challenge. Our goal is to obtain a solution functor $\mathcal {S}:\textbf{oMDP}\rightarrow \mathbb {S}$ that preserves suitable algebraic structures (see (1)); the specific notion of algebra of our interest is that of compact closed categories (compCC).

• The category $\textbf{oMDP}$ organizes open MDPs as a category. It is a compCC, and its algebraic operations are defined as in Fig. 2.

• For the solution functor $\mathcal {S}$ to be compositional, the semantic category $\mathbb {S}$ must itself be a compCC, that is, $\mathbb {S}$ has to be enriched so that the compCC operations ($\mathbin {;}$ and $\oplus$) are well-defined.

• Once such a semantic domain $\mathbb {S}$ is obtained, choosing $\mathcal {S}$ and showing that it preserves the algebraic operations are straightforward.

Specifically, we find that $\mathbb {S}$ must be enriched with reachability probabilities, in addition to the desired solutions (namely expected rewards), to be a compCC. This enrichment is based on the decomposition equalities we observe in Sect. 3.

After all, our semantic category $\mathbb {S}$ is as follows: 1) an object is a pair of natural numbers describing an interface (how many entrances and exits); 2) an arrow is a collection of “semantics,” collected over all possible (memoryless) schedulers $\tau$, which records the expected reward that the scheduler $\tau$ yields when it traverses from each entrance to each exit. The last “semantics” is enriched so that it records the reachability probability, too, for the sake of compositionality.

Related Work. Compositional model checking is studied e.g. in [4, 19, 20]. Besides, probabilistic model checking is an actively studied topic; see [1, Chap. 10] for a comprehensive account. We shall make a detailed comparison with the works [11, 14] that study compositional probabilistic model checking.

The work [14] introduces an assume-guarantee reasoning framework for parallel composition $\parallel$, as we already discussed. Parallel composition is out of our current scope; in fact, we believe that compositionality with respect to $\parallel$ requires a much bigger enrichment of a semantic domain $\mathbb {S}$ than mere reachability probabilities as in our work. The work [14] is remarkable in that its solution to this granularity problem—namely by assume-guarantee reasoning—is practically sensible (domain experts often have ideas about what contract to impose) and comes with automata-theoretic automation. That said, such contracts are not always automatically synthesized in [14], while our algorithm is fully automatic.

The work [11] is probably the closest to ours in the type of composition (sequential rather than parallel) and automation. However, the technical bases of the two works are quite different: theirs is the theory of parametric MDPs [18], which is why their emphasis is on parametrized components and interval solutions; ours is monoidal categories and some decomposition equalities (Sect. 3).

We note that the work [11] and ours are not strictly comparable. On the one hand, we do not need a crucial assumption in [11], namely that a locally optimal scheduler in each component is part of a globally optimal scheduler. The assumption limits the applicability of [11]—it practically forces each component to have only one exit. The assumption does not hold in our benchmarks Patrol and Wholesale (see Sect. 5). Our algorithm does not need the assumption since it collects the semantics of all relevant memoryless schedulers.

On the other hand, unlike [11], our algorithm is not parametric, so it cannot exploit the similarity of components if they only differ in parameter values. Note that the target problems are different, too (interval [11] vs. exact here).

Notations. For natural numbers m and n, we let $[m, n]{:}{=}\{m,m+1,\dotsc , n-1, n\}$; as a special case, we let $[m]{:}{=}\{1,2,\dotsc , m\}$ (we let $[0]=\emptyset$ by convention). The disjoint union of two sets X, Y is denoted by $X+Y$.

2 String Diagrams of MDPs

We introduce our calculus for composing MDPs, namely string diagrams of MDPs. Our formal definition is via their unidirectional and Markov chain (MC) restrictions. This apparent detour simplifies the theoretical development, allowing us to exploit the existing categorical infrastructure on (monoidal) categories.

2.1 Outline

We first make an overview of our technical development. Although we use some categorical terminologies, prior knowledge of them is not needed in this outline.

Fig. 3.

Categories of MDPs/MCs, semantic categories, and solution functors.

Figure 3 is an overview of relevant categories and functors. The verification targets—open MDPs—are arrows in the compact closed category (compCC) $\textbf{oMDP}$. The operations $\mathbin {;}, \oplus$ of compCCs compose MDPs, as shown in Fig. 2. Our semantic category is denoted by $\mathbb {S}$, and our goal is to define a solution functor $\textbf{oMDP}\rightarrow \mathbb {S}$ that is compositional. Mathematically, such a functor with the desired compositionality (cf. (1)) is called a compact closed functor.

Since its direct definition is tedious, our strategy is to obtain it from a unidirectional rightward framework $\mathcal {S}_{\textbf{r}}:\textbf{roMDP}\rightarrow \mathbb {S}_{\textbf{r}}$, which canonically induces the desired bidirectional framework via the celebrated $\textrm{Int}$ construction [10]. In particular, the category $\textbf{oMDP}$ is defined by $\textbf{oMDP}=\textrm{Int}(\textbf{roMDP})$; so are the semantic category and the solution functor ($\mathbb {S}=\textrm{Int}(\mathbb {S}_{\textbf{r}}), \mathcal {S}=\textrm{Int}(\mathcal {S}_{\textbf{r}})$).

Going this way, a complication that one would encounter in a direct definition of $\textbf{oMDP}$ (namely potential loops of transitions) is nicely taken care of by the $\textrm{Int}$ construction. Another benefit is that some natural equational axioms in $\textbf{oMDP}$—such as the associativity of sequential composition $\mathbin {;}$—follow automatically from those in $\textbf{roMDP}$, which are much easier to verify.

Mathematically, the unidirectional framework $\mathcal {S}_{\textbf{r}}:\textbf{roMDP}\rightarrow \mathbb {S}_{\textbf{r}}$ consists of traced symmetric monoidal categories (TSMCs) and traced symmetric monoidal functors; these are “algebras” of unidirectional graphs. The $\textrm{Int}$ construction turns TSMCs into compCCs, which are “algebras” of bidirectional graphs.

Yet another restriction is given by (rightward open) Markov chains (MCs). See the bottom row of Fig. 3. This MDP-to-MC restriction greatly simplifies our semantic development, freeing us from the bookkeeping of different schedulers. In fact, we can introduce (optimal memoryless) schedulers systematically by the categorical construction called change of base [5, 6]; this way we obtain the semantic category $\mathbb {S}_{\textbf{r}}$ from $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$.

(2)

2.2 Open MDPs

We first introduce open MDPs; they have open ends via which they compose. They come with a notion of arity—the numbers of open ends on their left and right, distinguishing leftward and rightward ones. For example, the one on the right is from (2, 1) to (1, 3).

Definition 2.1

(open MDP (oMDP)). Let A be a non-empty finite set, whose elements are called actions. An open MDP $\mathcal {A}$ (over the action set A) is the tuple $(\overline{m}^{},\overline{n}^{},Q, A,E,P,R)$ of the following data. We say that it is from $\overline{m}^{}$ to $\overline{n}^{}$.

• 1. $\overline{m}^{} = (m^{}_{\textbf{r}},\ m^{}_{\textbf{l}})$ and $\overline{n}^{} = (n^{}_{\textbf{r}},\ n^{}_{\textbf{l}})$ are pairs of natural numbers; they are called the left-arity and the right-arity, respectively. Moreover (see (2)), elements of $[m^{}_{\textbf{r}}+n^{}_{\textbf{l}}]$ are called entrances, and those of $[n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]$ are called exits.

• 2. Q is a finite set of positions.

• 3. $E:[m^{}_{\textbf{r}}+n^{}_{\textbf{l}}] \rightarrow Q + [n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]$ is an entry function, which maps each entrance to either a position (in Q) or an exit (in $[n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]$).

• 4. $P:Q\times A\times (Q + [n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]) \rightarrow {\mathbb R_{\ge 0} }$ determines transition probabilities, where we require $\sum _{s'\in Q+[n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]}P(s, a, s') \in \{0, 1\}$ for each $s\in Q$ and $a\in A$.

• 5. R is a reward function $R:Q\rightarrow {\mathbb R_{\ge 0} }$.

• 6. We impose the following “unique access to each exit” condition. Let ${{\,\textrm{exits}\,}}: ([m^{}_{\textbf{r}}+n^{}_{\textbf{l}}] + Q) \rightarrow \mathcal {P}([n^{}_{\textbf{r}}+m^{}_{\textbf{l}}])$ be the exit function that collects all immediately reachable exits, that is, 1) for each $s\in Q$, ${{\,\textrm{exits}\,}}(s) = \{ t \in [n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]\,|\,\exists a \in A. P(s,a,t) > 0 \}$, and 2) for each entrance $s \in [m^{}_{\textbf{r}}+n^{}_{\textbf{l}}]$, ${{\,\textrm{exits}\,}}(s) = \{E(s)\}$ if E(s) is an exit and ${{\,\textrm{exits}\,}}(s) = \emptyset$ otherwise.

  • For all $s,s' \in [m^{}_{\textbf{r}}+n^{}_{\textbf{l}}] + Q$, if ${{\,\textrm{exits}\,}}(s) \cap {{\,\textrm{exits}\,}}(s') \ne \emptyset$, then $s = s'$.

  • We further require that each exit is reached from an identical position by at most one action. That is, for each exit $t \in [n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]$, $s \in Q$, and $a,b \in A$, if both $P(s,a,t) > 0$ and $P(s,b,t) > 0$, then $a = b$.

Note that the unique access to each exit condition is for technical convenience; this can be easily enforced by adding an extra “access” position to an exit.

We define the semantics of open MDPs, which is essentially the standard semantics of MDPs given by expected cumulative rewards. In this paper, it suffices to consider memoryless schedulers (see Remark 2.1).

Definition 2.2

(path and scheduler). Let $\mathcal {A} = (\overline{m}^{},\overline{n}^{},Q, A, E,P,R)$ be an open MDP. A (finite) path $\pi ^{(i, j)}$ in $\mathcal {A}$ from an entrance $i\in [m^{}_{\textbf{r}}+n^{}_{\textbf{l}}]$ to an exit $j\in [n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]$ is a finite sequence $i, s_1,\dotsc , s_n, j$ such that $E(i) = s_1$ and for all $k \in [n]$, $s_k \in Q$. For each $k\in [n]$, $\pi ^{(i, j)}_k$ denotes $s_k$, and $\pi ^{(i, j)}_{n+1}$ denotes j. The set of all paths in $\mathcal {A}$ from i to j is denoted by $\textrm{Path}^{\mathcal {A}}(i, j)$.

A (memoryless) scheduler $\tau$ of $\mathcal {A}$ is a function $\tau :Q\rightarrow A$.

Remark 2.1

It is well-known (as hinted in [2]) that we can restrict to memoryless schedulers for optimal expected rewards, assuming that the MDP in question is almost surely terminating under any scheduler $(\dagger )$. We require the assumption $(\dagger )$ in our compositional framework, too, and it is true in all benchmarks in this paper. The assumption $(\dagger )$ must be checked only for the top-level (composed) MDP; $(\dagger )$ for its components can then be deduced.

Definition 2.3

(probability and reward of a path). Let $\mathcal {A} = (\overline{m}^{},\overline{n}^{},Q, A,E, P,R)$ be an open MDP, $\tau :Q\rightarrow A$ be a scheduler of $\mathcal {A}$, and $\pi ^{(i, j)}$ be a path in $\mathcal {A}$. The probability $\textrm{Pr}^{\mathcal {A}, \tau }(\pi ^{(i, j)} )$ of $\pi ^{(i, j)}$ under $\tau$ is $\textrm{Pr}^{\mathcal {A}, \tau }(\pi ^{(i, j)} ):=\textstyle \prod _{k=1}^n P\bigl (\,\pi ^{(i, j)}_k,\tau (\pi ^{(i, j)}_k),\pi ^{(i, j)}_{k+1}\,\bigr ).$ The reward $\textrm{Rw}^{\mathcal {A}}(\pi ^{(i, j)})$ along the path $\pi ^{(i, j)}$ is the sum of the position rewards, that is, $\textrm{Rw}^{\mathcal {A}}(\pi ^{(i, j)}) :=\sum _{k\in [n]} R(\pi ^{(i, j)}_k)$.

Our target problem on open MDPs is to compute the expected cumulative reward collected in a passage from a specified entrance i to a specified exit j. This is defined below, together with reachability probability, in the usual manner.

Definition 2.4

(reachability probability and expected (cumulative) reward of open MDPs). Let $\mathcal {A}$ be an open MDP and $\tau$ be a scheduler, as in Definition 2.2. Let i be an entrance and j be an exit.

The reachability probability $\textrm{RPr}^{\mathcal {A}, \tau }(i, j)$ from i to j, in $\mathcal {A}$ under $\tau$, is defined by $\textrm{RPr}^{\mathcal {A}, \tau }(i, j) :=\sum _{\pi ^{(i, j)}\in \textrm{Path}^{\mathcal {A}}(i, j)} \textrm{Pr}^{\mathcal {A}, \tau }(\pi ^{(i, j)})$.

The expected (cumulative) reward $\textrm{ERw}^{\mathcal {A},\tau }(i, j)$ from i to j, in $\mathcal {A}$ under $\tau$, is defined by $\textrm{ERw}^{\mathcal {A},\tau }(i, j):=\sum _{\pi ^{(i, j)}\in \textrm{Path}^{\mathcal {A}}(i, j)}\textrm{Pr}^{\mathcal {A}, \tau }(\pi ^{(i, j)})\cdot \textrm{Rw}^{\mathcal {A}}(\pi ^{(i, j)})$. Note that the infinite sum here always converges to a finite value; this is because there are only finitely many positions in $\mathcal {A}$. See e.g. [1].

Remark 2.2

In standard definitions such as Definition 2.4, it is common to either 1) assume $\textrm{RPr}^{\mathcal {A}, \tau }(i, j)=1$ for technical convenience [11], or 2) allow $\textrm{RPr}^{\mathcal {A}, \tau }(i, j)<1$, but in that case define $\textrm{ERw}^{\mathcal {A},\tau }(i, j):=\infty$ [1]. These definitions are not suited for our purpose (and for compositional model checking in general), since we take into account multiple exits, to each of which the reachability probability is typically $<1$, and we need non-$\infty$ expected rewards over those exits for compositionality. Note that our definition of expected reward is not conditional (unlike [1, Rem. 10.74]): when the reachability probability from i to j is small, it makes the expected reward small as well. Our notion of expected reward can be thought of as a “weighted sum” of rewards.

2.3 Rightward Open MDPs and Traced Monoidal String Diagrams

Following the outline (Sect. 2.1), in this section we focus on (unidirectional) rightward open MDPs and introduce the “algebra” $\textbf{roMDP}$ of them. The operations $\mathbin {;}, \oplus , \textrm{tr}$ of traced symmetric monoidal categories (TSMCs) compose rightward open MDPs in string diagrams.

Definition 2.5

(rightward open MDP (roMDP)). An open MDP $\mathcal {A} = (\overline{m}^{}, \overline{n}^{}, Q, A, E, P, R)$ is rightward if all its entrances are on the left and all its exits are on the right, that is, $\overline{m}^{} = (m^{}_{\textbf{r}}, 0^{}_{\textbf{l}})$ and $\overline{n}^{}= (n^{}_{\textbf{r}}, 0^{}_{\textbf{l}})$ for some $m^{}_{\textbf{r}}$ and $n^{}_{\textbf{r}}$. We write $\mathcal {A} = (m^{}_{\textbf{r}}, n^{}_{\textbf{r}}, Q, A, E, P, R)$, dropping 0 from the arities.

We say that a rightward open MDP $\mathcal {A}$ is from m to n, writing $\mathcal {A}:m\rightarrow n$, if it is from (m, 0) to (n, 0) as an open MDP.

We use an equivalence relation by roMDP isomorphism so that roMDPs satisfy TSMC axioms given in Sect. 2.4. See [21, Appendix A] for details.

We move on to introduce algebraic operations for composing rightward open MDPs. Two of them, namely sequential composition $\mathbin {;}$ and sum $\oplus$, look like Fig. 2 except that all wires are rightward. The other major operation is the trace operator $\textrm{tr}$ that realizes (unidirectional) loops, as illustrated in Fig. 4.

Fig. 4.

The trace operator.

Definition 2.6

(sequential composition $\mathbin {;}$ of roMDPs). Let $\mathcal {A}:m\rightarrow k$ and $\mathcal {B}:k\rightarrow n$ be rightward open MDPs with the same action set A and with matching arities. Their sequential composition $\mathcal {A} \mathbin {;}\mathcal {B}:m\rightarrow n$ is given by $\mathcal {A} \mathbin {;}\mathcal {B} :=\bigl (m, n, Q^{\mathcal {A}}+Q^{\mathcal {B}}, A, E^{\mathcal {A} \mathbin {;}\mathcal {B}}, P^{\mathcal {A} \mathbin {;}\mathcal {B}}, [R^{\mathcal {A}}, R^{\mathcal {B}}]\bigr )$, where

• $E^{\mathcal {A} \mathbin {;}\mathcal {B}}(i):=E^{\mathcal {A}}(i)$ if $E^{\mathcal {A}}(i) \in Q^{\mathcal {A}}$, and $E^{\mathcal {A} \mathbin {;}\mathcal {B}}(i):=E^{\mathcal {B}}(E^{\mathcal {A}}(i))$ otherwise (if the $\mathcal {A}$-entrance i goes to an $\mathcal {A}$-exit which is identified with a $\mathcal {B}$-entrance);

• the transition probabilities are defined in the following natural manner

  $$\begin{aligned} \begin{aligned} P^{\mathcal {A} \mathbin {;}\mathcal {B}}(s^{\mathcal {A}}, a, s')&:={\left\{ \begin{array}{ll} P^{\mathcal {A}}(s^{\mathcal {A}}, a, s') &{}\text {if}\, s' \in Q^{\mathcal {A}},\\ \sum \nolimits _{i \in [k]} P^{\mathcal {A}}(s^{\mathcal {A}}, a, i) \cdot \delta _{E^{\mathcal {B}}(i) = s'} &{}\text {otherwise (i.e.}\ s'\in Q^{\mathcal {B}}+[n]\text {),} \end{array}\right. }\\ P^{\mathcal {A} \mathbin {;}\mathcal {B}}(s^{\mathcal {B}}, a, s')&:={\left\{ \begin{array}{ll} P^{\mathcal {B}}(s^{\mathcal {B}}, a, s') &{}\text {if}\, s' \in Q^{\mathcal {B}} + [n],\\ 0 &{}\text {otherwise,} \end{array}\right. } \end{aligned} \end{aligned}$$

  where $\delta$ is a characteristic function (returning 1 if the condition is true);

• and $[R^{\mathcal {A}}, R^{\mathcal {B}}]:Q^{\mathcal {A}}+Q^{\mathcal {B}}\rightarrow {\mathbb R_{\ge 0} }$ combines $R^{\mathcal {A}}, R^{\mathcal {B}}$ by case distinction.

Defining sum $\oplus$ of roMDPs is straightforward, following Fig. 2. See [21, Appendix A] for details.

The trace operator $\textrm{tr}$ is primitive in the TSMC $\textbf{roMDP}$; it is crucial in defining bidirectional sequential composition shown in Fig. 2 (cf. Definition 2.9).

Definition 2.7

(the trace operator $\textrm{tr}^{}_{l;m,n}$ over roMDPs). Let $\mathcal {A}:l+m\rightarrow l+n$ be a rightward open MDP. The trace $\textrm{tr}^{}_{l;m,n}(\mathcal {A}):m\rightarrow n$ of $\mathcal {A}$ with respect to l is the roMDP $\textrm{tr}^{}_{l;m,n}(\mathcal {A}):=\bigl (m,n, Q^{\mathcal {A}},A,E,P,R^{\mathcal {A}}\bigr )$ (cf. Fig. 4), where

• The entry function E is defined naturally, using a sequence $i_{0},\dotsc , i_{k-1}$ of intermediate open ends (in $[l]$) until reaching a destination $i_{k}$.

  Precisely, we let $i_{0}:=i+l$ and $i_{j}=E^{\mathcal {A}}(i_{j-1})$ for each j. We let k to be the first index at which $i_{k}$ comes out of the loop, that is, 1) $i_{j}\in [l]$ for each $j\in [k-1]$, and 2) $i_{k}\in [l+1,l+n]+Q^{\mathcal {A}}$. Then we define E(i) by the following: $E(i):=i_{k}-l$ if $i_{k}\in [l+1,l+n]$; and $E(i):=i_{k}$ otherwise.

• The transition probabilities P are defined as follows. We let ${{\,\textrm{prec}\,}}(t)$ be the set of open ends in $[l]$—those which are in the loop—that eventually enter $\mathcal {A}$ at $t\in [l+1, n]+Q^{\mathcal {A}}$. Precisely, ${{\,\textrm{prec}\,}}(t) :=\{i\in [l]\mid \exists i_{0},\dotsc , i_{k}.\, i_{0}=i, i_{j+1} = E(i_j) \text {(for each j)}, i_{k}=t, i_{0},\dotsc , i_{k-1}\in [1,l], i_{k}\in [l+1, n]+Q^{\mathcal {A}} \}$. Using this,

  $$\begin{aligned} \begin{aligned} P(q, a, q')&\,{:=}{\left\{ \begin{array}{ll} P^{\mathcal {A}}(q, a, q'+l)+ \sum \nolimits _{i\in {{\,\textrm{prec}\,}}(q'+l) }P^{\mathcal {A}}(q, a, i) \text { if }q'\in [n], \\ P^{\mathcal {A}}(q, a, q') + \sum \nolimits _{i\in {{\,\textrm{prec}\,}}(q') }P^{\mathcal {A}}(q, a, i)\text { otherwise, i.e. if } q'\in Q^{\mathcal {A}}. \end{array}\right. } \end{aligned} \end{aligned}$$

Here $Q^{\mathcal {A}}$ and $[l]$ are assumed to be disjoint without loss of generality.

Remark 2.3

In string diagrams, it is common to annotate a wire with its type, such as $\overset{n}{\longrightarrow }$ for $\textrm{id}_{n}:n\rightarrow n$. It is also common to separate a wire for a sum type into wires of its component types, such as below on the left. Therefore the two diagrams below on the right designate the same mathematical entity. Note that, on its right-hand side, the type annotation 1 to each wire is omitted.

2.4 TSMC Equations Between roMDPs

Here we show that the three operations $\mathbin {;}, \oplus , \textrm{tr}$ on roMDPs satisfy the equational axioms of TSMCs [10], shown in Fig. 5. These equational axioms are not directly needed for compositional model checking. We nevertheless study them because 1) they validate some natural bookkeeping equivalences of roMDPs needed for their efficient handling, and 2) they act as a sanity check of the mathematical authenticity of our compositional framework. For example, the handling of open ends is subtle in Sect. 2.3—e.g. whether they should be positions or not—and the TSMC equational axioms led us to our current definitions.

Fig. 5.

The equational axioms of TSMCs, expressed for roMDPs, with some string diagram illustrations. Here we omit types of roMDPs; see [10] for details.

The TSMC axioms use some “positionless” roMDPs as wires, such as identities $\mathcal {I}_{m}$ (${\mathop {\text {---}\!\text {---}}\limits ^{m}}$ in string diagrams) and swaps $\mathcal {S}_{m, n}$ ($\times$). See [21, Appendix A] for details. The proof of the following is routine. For details, see [21, Appendix B].

Theorem 2.1

The three operations $\mathbin {;}, \oplus , \textrm{tr}$ on roMDPs, defined in Sect. 2.3, satisfy the equational axioms in Fig. 5 up-to isomorphisms (see [21, Appendix A] for details).    $\square$

Corollary 2.1

(a TSMC roMDP). Let $\textbf{roMDP}$ be the category whose objects are natural numbers and whose arrows are roMDPs over the action set A modulo isomorphisms. Then the operations $\mathbin {;},\oplus ,\textrm{tr},\mathcal {I},\mathcal {S}$ make $\textbf{roMDP}$ a traced symmetric monoidal category (TSMC).    $\square$

2.5 Open MDPs and “Compact Closed” String Diagrams

Following the outline in Sect. 2.1, we now introduce a bidirectional “compact closed” calculus of open MDPs (oMDPs), using the $\textrm{Int}$ construction [10] that turns TSMCs in general into compact closed categories (compCCs).

The following definition simply says $\textbf{oMDP}:=\textrm{Int}(\textbf{roMDP})$, although it uses concrete terms adapted to the current context.

Definition 2.8

(the category $\textbf{oMDP}$). The category $\textbf{oMDP}$ of open MDPs is defined as follows. Its objects are pairs $(m^{}_{\textbf{r}},m^{}_{\textbf{l}})$ of natural numbers. Its arrows are defined by rightward open MDPs as follows:

(3)

where the double lines mean “is the same thing as.”

The definition may not immediately justify its name: no open MDPs appear there; only roMDPs do. The point is that we identify the roMDP $\mathcal {A}$ in (3) with the oMDP $\varPsi (\mathcal {A})$ of the designated type, using “twists” in Fig. 6. See [21, Appendix A] for details.

We move on to describe algebraic operations for composing oMDPs. These operations come from the structure of $\textbf{oMDP}$ as a compCC; the latter, in turn, arises canonically from the $\textrm{Int}$ construction.

Definition 2.9

($\mathbin {;}$ of oMDPs). Let $\mathcal {A}:(m^{}_{\textbf{r}},m^{}_{\textbf{l}})\rightarrow (l^{}_{\textbf{r}},l^{}_{\textbf{l}})$ and $\mathcal {B}:(l^{}_{\textbf{r}},l^{}_{\textbf{l}})\rightarrow (n^{}_{\textbf{r}},n^{}_{\textbf{l}})$ be arrows in $\textbf{oMDP}$ with the same action set A. Their sequential composition $\mathcal {A}\mathbin {;}\mathcal {B}:(m^{}_{\textbf{r}},m^{}_{\textbf{l}})\rightarrow (n^{}_{\textbf{r}},n^{}_{\textbf{l}})$ is defined by the string diagram in Fig. 7, formulated in $\textbf{roMDP}$. Textually the definition is $\mathcal {A}\mathbin {;}\mathcal {B} :=\textrm{tr}^{}_{l^{}_{\textbf{l}};m^{}_{\textbf{r}} + n^{}_{\textbf{l}},n^{}_{\textbf{r}}+ m^{}_{\textbf{l}}}\big ((\mathcal {S}_{l^{}_{\textbf{l}}, m^{}_{\textbf{r}}}\oplus \mathcal {I}_{n^{}_{\textbf{l}}}) \mathbin {;}(\mathcal {A}\oplus \mathcal {I}_{n^{}_{\textbf{l}}}) \mathbin {;}(\mathcal {I}_{l^{}_{\textbf{r}}}\oplus \mathcal {S}_{m^{}_{\textbf{l}},n^{}_{\textbf{l}}}) \mathbin {;}(\mathcal {B}\oplus \mathcal {I}_{m^{}_{\textbf{l}}}) \mathbin {;}(\mathcal {S}_{n^{}_{\textbf{r}},l^{}_{\textbf{l}}}\oplus \mathcal {I}_{m^{}_{\textbf{l}}})\big )$.

Fig. 6.

Turning oMDPs to roMDPs, and vice versa, via twists.

Fig. 7.

String diagrams in $\textbf{roMDP}$ for $\mathcal {A}\mathbin {;}\mathcal {B}$, $\mathcal {A}\oplus \mathcal {B}$ in $\textbf{oMDP}$.

The definition of sum $\oplus$ of oMDPs is similarly shown in the string diagram in Fig. 7, formulated in $\textbf{roMDP}$. Definition of “wires” such as identities, swaps, units ($\subset$ in string diagrams) and counits ($\supset$) is easy, too.

Theorem 2.2

($\textbf{oMDP}$ is a compCC). The category $\textbf{oMDP}$ (Definition 2.8), equipped with the operations $\mathbin {;},\oplus$, is a compCC.    $\square$

3 Decomposition Equalities for Open Markov Chains

Here we exhibit some basic equalities that decompose the behavior of (rightward open) Markov chains. We start with such equalities on reachability probabilities (which are widely known) and extend them to equalities on expected rewards (which seem less known). Notably, the latter equalities involve not only expected rewards but also reachability probabilities.

Here we focus on rightward open Markov chains (roMCs), since the extension to richer settings is taken care of by categorical constructions. See Fig. 3.

Definition 3.1

(roMC). A rightward open Markov chain (roMC) $\mathcal {C}$ from m to n is an roMDP from m to n over the singleton action set $\{\star \}$.

For an roMC $\mathcal {C}$, its reachability probability $\textrm{RPr}^{\mathcal {C}}(i, j)$ and expected reward $\textrm{ERw}^{\mathcal {C}}(i, j)$ are defined as in Definition 2.4. The scheduler $\tau$ is omitted since it is unique.

Rightward open MCs, as a special case of roMDPs, form a TSMC (Corollary 2.1). It is denoted by $\textbf{roMC}$.

The following equalities are well-known, although they are not stated in terms of open MCs. Recall that $\textrm{RPr}^{\mathcal {C}}(i, k)$ is the probability of reaching the exit k from the entrance i in $\mathcal {C}$ (Definition 2.4). Recall also the definitions of $\mathcal {C}\mathbin {;}\mathcal {D}$ (Definition 2.6) and $\textrm{tr}^{}_{l;m,n}{}(\mathcal {E})$ (Definition 2.7), which are essentially as in Fig. 2 and Fig. 4.

Proposition 3.1

(decomposition equalities for $\textrm{RPr}$). Let $\mathcal {C}:m\rightarrow l$, $\mathcal {D}:l\rightarrow n$ and $\mathcal {E}:l+m\rightarrow l+n$ be roMCs. The following matrix equalities hold.

$$\begin{aligned}&\begin{array}{l} \bigl [\,\textrm{RPr}^{\mathcal {C} \mathbin {;}\mathcal {D}}(i, j)\,\bigr ]_{i\in [m],j\in [n]} \;=\; \bigl [\,\textrm{RPr}^{\mathcal {C}}(i, k)\,\bigr ]_{i\in [m],k\in [l]} \cdot \bigl [\,\textrm{RPr}^{\mathcal {D}}(k, j)\,\bigr ]_{k\in [l],j\in [n]}\ , \end{array} \end{aligned}$$

(4)

$$\begin{aligned}&\begin{array}{l} \bigl [\,\textrm{RPr}^{\textrm{tr}^{}_{l;m,n}{}(\mathcal {E})}(i, j) \,\bigr ]_{i\in [m],j\in [n]} \;=\; \bigl [\, \textrm{RPr}^{\mathcal {E}}(l+i, l+j) \,\bigr ]_{i\in [m],j\in [n]} + \textstyle \sum _{d\in {\mathbb N }} A\cdot B^{d} \cdot C. \end{array} \end{aligned}$$

(5)

Here $\bigl [\,\textrm{RPr}^{\mathcal {C} \mathbin {;}\mathcal {D}}(i, j)\,\bigr ]_{i\in [m],j\in [n]}$ denotes the $m\times n$ matrix with the designated components; other matrices are similar. The matrices A, B, C are given by $A:=\bigl [\, \textrm{RPr}^{\mathcal {E}}(l+i, k) \,\bigr ]_{i\in [m],k\in [l]}$, $B:=\bigl [\, \textrm{RPr}^{\mathcal {E}}(k, k') \,\bigr ]_{k\in [l],k'\in [l]}$, and $C:=\bigl [\, \textrm{RPr}^{\mathcal {E}}(k', l+j) \,\bigr ]_{k'\in [l],j\in [n]}$. In the last line, note that the matrix in the middle is the d-th power.

   $\square$

The first equality is easy, distinguishing cases on the intermediate open end k (mutually exclusive since MCs are rightward). The second says

which is intuitive. Here, the small circles in the diagram correspond to dead ends. It is known as Girard’s execution formula [7] in linear logic.

We now extend Prop. 3.1 to expected rewards $\textrm{ERw}^{\mathcal {C}}(i, j)$.

Proposition 3.2

(decomposition eq. for $\textrm{ERw}$). Let $\mathcal {C}:m\rightarrow l$, $\mathcal {D}:l\rightarrow n$ and $\mathcal {E}:l+m\rightarrow l+n$ be roMCs. The following equalities of matrices hold.

$$\begin{aligned}&\begin{array}{rl} \bigl [\,\textrm{ERw}^{\mathcal {C} \mathbin {;}\mathcal {D}}(i, j)\,\bigr ]_{ i\in [m] , j\in [n] } \;=\; &{}\bigl [\,\textrm{RPr}^{\mathcal {C}}(i, k)\,\bigr ]_{i\in [m],k\in [l]} \cdot \bigl [\,\textrm{ERw}^{\mathcal {D}}(k, j)\,\bigr ]_{k\in [l],j\in [n]} \\ &{}+ \bigl [\,\textrm{ERw}^{\mathcal {C}}(i, k)\,\bigr ]_{i\in [m],k\in [l]} \cdot \bigl [\,\textrm{RPr}^{\mathcal {D}}(k, j)\,\bigr ]_{k\in [l],j\in [n]}\ , \end{array} \end{aligned}$$

(6)

$$\begin{aligned}&\begin{array}{rl}&\bigl [\,\textrm{ERw}^{\textrm{tr}^{}_{l;m,n}{}(\mathcal {E})}(i, j) \,\bigr ]_{i\in [m],j\in [n]} \;=\; \bigl [\, \textrm{ERw}^{\mathcal {E}}(l+i, l+j) \,\bigr ]_{i\in [m],j\in [n]} + \textstyle \sum _{d\in {\mathbb N }} A\cdot B^{d}\cdot C. \end{array} \end{aligned}$$

(7)

Here A, B, C are the following $m \times 2$l$\,\times 2$l$\,\times 2$l$\,\times 2$l $\times n$ matrices.

$$\begin{aligned}&\begin{array}{ll} A &{}= \begin{pmatrix} \bigl [\, \textrm{RPr}^{\mathcal {E}}(l+i, k) \,\bigr ]_{i\in [m],k\in [l]} &{} \bigl [\, \textrm{ERw}^{\mathcal {E}}(l+i, k) \,\bigr ]_{i\in [m],k\in [l]} \\ \end{pmatrix}, \\ B &{}= \begin{pmatrix} \bigl [\, \textrm{RPr}^{\mathcal {E}}(k, k') \,\bigr ]_{k\in [l],k'\in [l]} &{} \bigl [\, \textrm{ERw}^{\mathcal {E}}(k, k') \,\bigr ]_{k\in [l],k'\in [l]} \\ \bigl [\, 0 \,\bigr ]_{k\in [l],k'\in [l]} &{} \bigl [\, \textrm{RPr}^{\mathcal {E}}(k, k') \,\bigr ]_{k\in [l],k'\in [l]} \end{pmatrix}, \\ C &{}= \begin{pmatrix} \bigl [\, \textrm{ERw}^{\mathcal {E}}(k', l+j) \,\bigr ]_{k'\in [l],j\in [n]}\\ \bigl [\, \textrm{RPr}^{\mathcal {E}}(k', l+j) \,\bigr ]_{k'\in [l],j\in [n]} \\ \end{pmatrix}. \end{array} \end{aligned}$$

   $\square$

Proposition 3.2 seems new, although proving them is not hard once the statements are given (see [21, Appendix C] for details). They enable one to compute the expected rewards of composite roMCs $\mathcal {C} \mathbin {;}\mathcal {D}$ and $\textrm{tr}^{}_{l;m,n}{\mathcal {E}}$ from those of component roMCs $\mathcal {C},\mathcal {D},\mathcal {E}$. They also signify the role of reachability probabilities in such computation, suggesting their use in the definition of semantic categories (cf. granularity of semantics in Sect. 1).

The last equalities in Propositions 3.1 and 3.2 involve infinite sums $\sum _{d\in {\mathbb N }}$, and one may wonder how to compute them. A key is their characterization as least fixed points via the Kleene theorem: the desired quantity on the left side ($\textrm{RPr}$ or $\textrm{ERw}$) is a solution of a suitable linear equation; see Proposition 3.3. With the given definitions, the proof of Propositions 3.1 and 3.2 is (lengthy but) routine work (see e.g. [1, Thm. 10.15]).

Proposition 3.3

(linear equation characterization for (5) and (7)). Let $\mathcal {E}:l+m\rightarrow l+n$ be an roMC, and $k\in [l+1,l+n]$ be a specified exit of $\mathcal {E}$. Consider the following linear equation on an unknown vector $[x_i]_{i\in [l+m]}$:

$$\begin{aligned} \bigl [\,x_i\,\bigr ]_{i\in [l+m]} = \bigl [\,\textrm{RPr}^{\mathcal {E}}(i, k)\,\bigr ]_{i\in [l+m]} + \bigl [\,\textrm{RPr}^{\mathcal {E}}(i, j)\,\bigr ]_{i\in [l+m], j\in [l]}\cdot \bigl [\,x_{j}\,\bigr ]_{j\in [l]}. \end{aligned}$$

(8)

Consider the least solution $[\tilde{x}_i]_{i\in [l+m]}$ of the equation. Then its part $[\tilde{x}_{i+l}]_{i\in [m]}$ is given by the vector $\big (\textrm{RPr}^{\textrm{tr}^{}_{l;m,n}{}(\mathcal {E})}(i, k-l)\big )_{i\in [m] }$ of suitable reachability probabilities.

Moreover, consider the following linear equation on an unknown $[y_i]_{i\in [l+m]}$:

$$\begin{aligned} \begin{aligned} \bigl [\,y_i\,\bigr ]_{i\in [l+m]} = \bigl [\,&\textrm{ERw}^{\mathcal {E}}(i, k)\,\bigr ]_{i\in [l+m]} + \bigl [\,\textrm{ERw}^{\mathcal {E}}(i, j)\,\bigr ]_{i\in [l+m], j\in [l]}\cdot \bigl [\,x_{j}\,\bigr ]_{j\in [l]}\\&+ \bigl [\,\textrm{RPr}^{\mathcal {E}}(i, j)\,\bigr ]_{i\in [l+m], j\in [l]}\cdot \bigl [\,y_{j}\,\bigr ]_{j\in [l]} , \end{aligned} \end{aligned}$$

(9)

where the unknown $[x_j]_{j\in [l]}$ is shared with (8). Consider the least solution $[\tilde{y}_i]_{i\in [l+m]}$ of the equation. Then its part $[\tilde{y}_{i+l}]_{i\in [m]}$ is given by the vector of suitable expected rewards, that is, $[\tilde{y}_{i+l}]_{i\in [m]} = \big (\textrm{ERw}^{\textrm{tr}^{}_{l;m,n}{}(\mathcal {E})}(i, k-l)\big )_{i\in [m] }$.

We can modify the linear Eqs. (8,9)—removing unreachable positions, specifically—so that they have unique solutions without changing the least ones. One can then solve these linear equations to compute the reachabilities and expected rewards in (5,7). This is a well-known technique for computing reachability probabilities [1, Thm. 10.19]; it is not hard to confirm the correctness of our current extension to expected rewards.

4 Semantic Categories and Solution Functors

We build on the decomposition equalities (Proposition 3.2) and define the semantic category $\mathbb {S}$ for compositional model checking. This is the main construct in our framework. Our definitions proceed in three steps, from roMCs to roMDPs to oMDPs (Fig. 3). The gaps between them are filled in using general constructions from category theory.

4.1 Semantic Category for Rightward Open MCs

We first define the semantic category $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ for roMCs (Fig. 3, bottom right).

Definition 4.1

(objects and arrows of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$). The category $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ has natural numbers m as objects. Its arrow $f:m \rightarrow n$ is given by an assignment, for each pair (i, j) of $i\in [m]$ and $j\in [n]$, of a pair $(p_{i,j}, r_{i,j})$ of nonnegative real numbers. There pairs $(p_{i,j}, r_{i,j})$ are subject to the following conditions.

• (Subnormality) $\sum _{j\in [n]}p_{i,j}\le 1$ for each $i\in [m]$.

• (Realizability) $p_{i,j}=0$ implies $r_{i,j}=0$.

Fig. 8.

An arrow $f:2\rightarrow 2$ in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$.

An illustration is in Fig. 8. For an object m, each $i\in [m]$ is identified with an open end, much like in $\textbf{roMC}$ and $\textbf{roMDP}$. For an arrow $f:m \rightarrow n$, the pair $f(i,j)=(p_{i,j}, r_{i,j})$ encodes a reachability probability and an expected reward, from an open end i to j; together they represent a possible roMC behavior.

We go on to define the algebraic operations of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ as a TSMC. While there is a categorical description of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ using a monad [16], we prefer a concrete definition here. See [21, Appendix D] for the categorical definition of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$.

Definition 4.2

(sequential composition $\mathbin {;}$ of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$). Let $f:m\rightarrow l$ and $g:l\rightarrow n$ be arrows in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$. Their sequential composition $f\mathbin {;}g:m\rightarrow n$ of f and g is defined as follows: letting $f(i, j) = (p^{f}_{i, j}, r^{f}_{i, j})$ and $g(i, j) = (p^{g}_{i, j}, r^{g}_{i, j})$, then $f\mathbin {;}g(i):=(p^{f\mathbin {;}g}_{i,j},r^{f\mathbin {;}g}_{i,j})_{j\in [n]}$ is given by

$$\begin{aligned} \bigl [\, p^{f\mathbin {;}g}_{i, j} \,\bigr ]_{i\in [m],j\in [n]} = \bigl [\,&p^{f}_{i, k}\,\bigr ]_{i\in [m],k\in [l]} \cdot \bigl [\,p^{g}_{k, j}\,\bigr ]_{k\in [l],j\in [n]}, \\ \bigl [\, r^{f\mathbin {;}g}_{i, j} \,\bigr ]_{i\in [m],j\in [n]} = \bigl [\,&p^{f}_{i, k}\,\bigr ]_{i\in [m],k\in [l]} \cdot \bigl [\,r^{g}_{k, j}\,\bigr ]_{k\in [l],j\in [n]}+ \bigl [\, r^{f}_{i, k}\,\bigr ]_{i\in [m],k\in [l]} \cdot \bigl [\,p^{g}_{k, j}\,\bigr ]_{k\in [l],j\in [n]} \end{aligned}$$

The sum $\oplus$ and the trace operator $\textrm{tr}$ of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ are defined similarly. To define and prove axioms of the trace operator (Fig. 5), we exploit the categorical theory of strong unique decomposition categories [9]. See [21, Appendix D].

Definition 4.3

($\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ as a TSMC). $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ is a TSMC, with its operations $\mathbin {;},\oplus ,\textrm{tr}$.

Once we expand the above definitions to concrete terms, it is evident that they mirror the decomposition equalities. Indeed, the sequential composition $\mathbin {;}$ mirrors the first equalities in Propositions 3.1 and 3.2. The same holds for the trace operator, too. Therefore, one can think of the above categorical development in Definition 4.2 and Definition 4.3 as a structured lifting of the (local) equalities in Propositions 3.1 and 3.2 to the (global) categorical structures, as shown in Fig. 3.

Once we found the semantic domain $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$, the following definition is easy.

Definition 4.4

($\mathcal {S}^{\textrm{MC}}_{\textbf{r}}$). The solution functor $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}:\textbf{roMC}\rightarrow \mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ is defined as follows. It carries an object m (a natural number) to the same m; it carries an arrow $\mathcal {C}:m\rightarrow n$ in $\textbf{roMC}$ to the arrow $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {C}):m\rightarrow n$ in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$, defined by

$$\begin{aligned} \mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {C})(i, j) :=\bigl (\,\textrm{RPr}^{\mathcal {C}}(i, j),\,\textrm{ERw}^{\mathcal {C}}(i, j)\,\bigr ), \end{aligned}$$

(10)

using reachability probabilities and expected rewards (Definition 2.4).

Theorem 4.1

($\mathcal {S}^{\textrm{MC}}_{\textbf{r}}$ is compositional). The correspondence $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}$, defined in (10), is a traced symmetric monoidal functor. That is, $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {C} \mathbin {;}\mathcal {D}) = \mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {C}) \mathbin {;}\mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {D})$, $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {C}\oplus \mathcal {D}) = \mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {C})\oplus \mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {D})$, and $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}( \textrm{tr}(\mathcal {E})) = \textrm{tr}(\mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\mathcal {E}))$. Here $\mathbin {;},\oplus ,\textrm{tr}$ on the left are from Sect. 2.3; those on the right are from Definition 4.3.    $\square$

4.2 Semantic Category of Rightward Open MDPs

We extend the theory in Sect. 4.1 from MCs to MDPs (Fig. 3). In particular, on the semantics side, we have to bundle up all possible behaviors of an MDP under different schedulers. We find that this is done systematically by change of base [5, 6]. We use the following notation for fixing scheduler $\tau$.

Definition 4.5

(roMC $\textrm{MC}(\mathcal {A}, \tau )$ induced by $\mathcal {A},\tau$). Let $\mathcal {A}:m\rightarrow n$ be a rightward open MDP and $\tau :Q^{\mathcal {A}}\rightarrow A$ be a memoryless scheduler. The rightward open MC $\textrm{MC}(\mathcal {A}, \tau )$ induced by $\mathcal {A}$ and $\tau$ is $(m,n,Q^{\mathcal {A}}, \{\star \},E^{A}, P^{\textrm{MC}(\mathcal {A}, \tau )},R^{\mathcal {A}})$, where for each $s\in Q$ and $t\in ([n^{}_{\textbf{r}}+m^{}_{\textbf{l}}]+Q)$, $P^{\textrm{MC}(\mathcal {A}, \tau )}(s, \star , t) :=P^{\mathcal {A}}(s, \tau (s), t)$.

Much like in Sect. 4.1, we first describe the semantic category $\mathbb {S}_{\textbf{r}}$ in concrete terms. We later use the categorical machinery to define its algebraic structure.

Definition 4.6

(objects and arrows of $\mathbb {S}_{\textbf{r}}$). The category $\mathbb {S}_{\textbf{r}}$ has natural numbers m as objects. Its arrow $F:m \rightarrow n$ is given by a set $\{f_{i}:m\rightarrow n \text { in} \mathbb {S}^{\textrm{MC}}_{\textbf{r}}\}_{i\in I}$ of arrows of the same type in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ (I is an arbitrary index set).

The above definition of arrows—collecting arrows in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$, each of which corresponds to the behavior of $\textrm{MC}(\mathcal {A}, \tau )$ for each $\tau$—follows from the change of base construction (specifically with the powerset functor $\mathcal {P}$ on the category $\textbf{Set}$ of sets). Its general theory gives sequential composition $\mathbin {;}$ for free (concretely described in Definition 4.7), together with equational axioms. See [21, Appendix D]. Sum $\oplus$ and trace $\textrm{tr}$ are not covered by general theory, but we can define them analogously to $\mathbin {;}$ in the current setting. Thus, for $\oplus$ and $\textrm{tr}$ as well, we are using change of base as an inspiration.

Here is a concrete description of algebraic operations. It applies the corresponding operation of $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ in the elementwise manner.

Definition 4.7

($\mathbin {;},\oplus ,\textrm{tr}$ in $\mathbb {S}_{\textbf{r}}$). Let $F:m\rightarrow l$, $G:l\rightarrow n$, $H:l+m\rightarrow l+n$ be arrows in $\mathbb {S}_{\textbf{r}}$. Their sequential composition $F\mathbin {;}G$ of F and G is given by $F\mathbin {;}G:=\{ f\mathbin {;}g\mid f\in F,\ g\in G\}$ where $f\mathbin {;}g$ is the sequential composition of f and g in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$. The trace $\textrm{tr}^{}_{l;m,n}(H):m\rightarrow n$ of H with respect to l is given by $\textrm{tr}^{}_{l;m,n}(H) :=\{ \textrm{tr}^{}_{l;m,n}(h) \mid h\in H\}$ where $\textrm{tr}^{}_{l;m,n}(h)$ is the trace of h with respect to l in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$.

Sum $\oplus$ in $\mathbb {S}_{\textbf{r}}$ is defined analogously, applying the operation in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ elementwise. See [21, Appendix A] for details.

Theorem 4.2

$\mathbb {S}_{\textbf{r}}$ is a TSMC.    $\square$

We now define a solution functor and prove its compositionality.

Definition 4.8

($\mathcal {S}_{\textbf{r}}$). The solution functor $\mathcal {S}_{\textbf{r}}:\textbf{roMDP}\rightarrow \mathbb {S}_{\textbf{r}}$ is defined as follows. It carries an object $m\in {\mathbb N }$ to m, and an arrow $\mathcal {A}:m\rightarrow n$ in $\textbf{roMDP}$ to $\mathcal {S}_{\textbf{r}}(\mathcal {A}):m\rightarrow n$ in $\mathbb {S}_{\textbf{r}}$. The latter is defined in the following elementwise manner, using $\mathcal {S}^{\textrm{MC}}_{\textbf{r}}$ in Definition 4.4.

$$\begin{aligned} \mathcal {S}_{\textbf{r}}(\mathcal {A}) \;:=\; \bigl \{ \mathcal {S}^{\textrm{MC}}_{\textbf{r}}(\textrm{MC}(\mathcal {A}, \tau ))\,\big |\, \tau :Q^{\mathcal {A}}\rightarrow A\text { a (memoryless) scheduler}\bigr \}. \end{aligned}$$

(11)

Theorem 4.3

(compositionality). The correspondence $\mathcal {S}_{\textbf{r}}:\textbf{roMDP}\rightarrow \mathbb {S}_{\textbf{r}}$ is a traced symmetric monoidal functor, preserving $\mathbin {;},\oplus ,\textrm{tr}$ as in Thm. 4.1.    $\square$

Remark 4.1

(memoryless schedulers). Our restriction to memoryless schedulers (cf. Definition 2.2) plays a crucial role in the proof of Theorem 4.3, specifically for the trace operator (i.e. loops, cf. Fig. 4). Intuitively, a memoryful scheduler for a loop may act differently in different iterations. Its technical consequence is that the elementwise definition of $\textrm{tr}$, as in Definition 4.7, no longer works for memoryful schedulers.

4.3 Semantic Category of MDPs

Finally, we extend from (unidirectional) roMDPs to (bidirectional) oMDPs (i.e. from the second to the first row in Fig. 3). The system-side construction is already presented in Sect. 2.5; the semantical side, described here, follows the same $\textrm{Int}$ construction [10]. The common intuition is that of twists, see Fig. 6.

Definition 4.9

(the semantic category $\mathbb {S}$). We define $\mathbb {S}=\textrm{Int}(\mathbb {S}_{\textbf{r}})$. Concretely, its objects are pairs $(m^{}_{\textbf{r}},m^{}_{\textbf{l}})$ of natural numbers. Its arrows are given by arrows of $\mathbb {S}_{\textbf{r}}$ as follows:

(12)

By general properties of $\textrm{Int}$, $\mathbb {S}$ is a compact closed category (compCC).

The $\textrm{Int}$ construction applies not only to categories but also to functors.

Definition 4.10

($\mathcal {S}$). The solution functor $\mathcal {S}:\textbf{oMDP}\rightarrow \mathbb {S}$ is defined by $\mathcal {S}=\textrm{Int}(\mathcal {S}_{\textbf{r}})$.

The following is our main theorem.

Theorem 4.4

(the solution $\mathcal {S}$ is compositional). The solution functor $\mathcal {S}:\textbf{oMDP}\rightarrow \mathbb {S}$ is a compact closed functor, preserving operations $\mathbin {;}, \oplus$ as in

$$\begin{aligned} \begin{array}{l} \mathcal {S}(\mathcal {A} \mathbin {;}\mathcal {B}) = \mathcal {S}(\mathcal {A}) \mathbin {;}\mathcal {S}(\mathcal {B}) ,\quad \mathcal {S}(\mathcal {A}\oplus \mathcal {B}) = \mathcal {S}(\mathcal {A})\oplus \mathcal {S}(\mathcal {B}) . \end{array}\qquad \square \end{aligned}$$

We can easily confirm, from Definitions 4.4 and 4.8, that $\mathcal {S}$ computes the solution we want. Given an open MDP $\mathcal {A}$, an entrance i and an exit j, $\mathcal {S}$ returns the set

$$\begin{aligned} \begin{array}{l} \bigl \{\,\bigl (\,\textrm{RPr}^{\textrm{MC}(\mathcal {A}, \tau )}(i, j),\,\textrm{ERw}^{\textrm{MC}(\mathcal {A}, \tau )}(i, j)\,\bigr ) \,\big |\, \tau \, \text {is a memoryless scheduler} \,\bigr \} \end{array} \end{aligned}$$

(13)

of pairs of a reachability probability and expected reward, under different schedulers, in a passage from i to j.

Remark 4.2

(synthesizing an optimal scheduler). The compositional solution functor $\mathcal {S}$ abstracts away schedulers and only records their results (see (13) where $\tau$ is not recorded). At the implementation level, we can explicitly record schedulers so that our compositional algorithm also synthesizes an optimal scheduler. We do not do so here for theoretical simplicity.

5 Implementation and Experiments

Meager Semantics. Since our problem is to compute optimal expected rewards, in our compositional algorithm, we can ignore those intermediate results which are totally subsumed by other results (i.e. those which come from clearly suboptimal schedulers). This notion of subsumption is formalized as an order $\le$ between parallel arrows in $\mathbb {S}^{\textrm{MC}}_{\textbf{r}}$ (cf. Definition 4.1): $(p_{i,j},r_{i,j})_{i,j} \le (p'_{i,j},r'_{i,j})_{i,j}$ if $p_{i,j}\le p'_{i,j}$ and $r_{i,j}\le r'_{i,j}$ for each i, j. Our implementation works with this meager semantics for better performance; specifically, it removes elements of $\mathcal {S}_{\textbf{r}}(\mathcal {A})$ in (11) that are subsumed by others. It is possible to formulate this meager semantics as categories and functors, compare it with the semantics in Sect. 4, and prove its correctness. We defer it to another venue for lack of space.

Implementation. We implemented the compositional solution functor $\mathcal {S}:\textbf{oMDP}\rightarrow \mathbb {S}$, using the meager semantics as discussed. This prototype implementation is in Python and called $\textrm{CompMDP}$.

$\textrm{CompMDP}$ takes a string diagram $\mathcal {A}$ of open MDPs as input; they are expressed in a textual format that uses operations $\mathbin {;},\oplus$ (such as the textual expression in Definition 2.9). Note that we are abusing notations here, identifying a string diagram of oMDPs and the composite oMDP $\mathcal {A}$ denoted by it.

Given such input $\mathcal {A}$, $\textrm{CompMDP}$ returns the arrow $\mathcal {S}(\mathcal {A})$, which is concretely given by pairs of a reachability probability and expected reward shown in (13) (we have suboptimal pairs removed, as discussed above). Since different pairs correspond to different schedulers, we choose a pair in which the expected reward is the greatest. This way we answer the optimal expected reward problem.

Freezing. In the input format of $\textrm{CompMDP}$, we have an additional freeze operator: any expression inside it is considered monolithic, and thus $\textrm{CompMDP}$ does not solve it compositionally. Those frozen oMDPs—i.e., those expressed by frozen expressions—are solved by PRISM [13] in our implementation.

Freezing allows us to choose how deep—in the sense of the nesting of string diagrams—we go compositional. For example, when a component oMDP $\mathcal {A}_{0}$ is small but has many loops, fully compositional model checking of $\mathcal {A}_{0}$ can be more expensive than (monolithic) PRISM. Freezing is useful in such situations.

We have found experimentally that the degree of freezing often should not be extremal (i.e. none or all). The optimal degree, which should be thus somewhere intermediate, is not known a priori.

However, there are not too many options (the number of layers in compositional model description), and freezing a half is recommended, both from our experience and for the purpose of binary search.

We require that a frozen oMDP should have a unique exit. Otherwise, an oMDP with a specified exit can have the reachability probability $<1$, in which case PRISM returns $\infty$ as the expected reward. The last is different from our definition of expected reward (Remark 2.2).

Research Questions. We posed the following questions.

• RQ1. Does the compositionality of $\textrm{CompMDP}$ help improve performance?

• RQ2. How much do we benefit from freezing, i.e., a feature that allows us to choose the degree of compositionality?

• RQ3. What is the absolute performance of $\textrm{CompMDP}$?

• RQ4. Does the formalism of string digrams accommodate real-world models, enabling their compositional model checking?

• RQ5. On which (compositional) models does $\textrm{CompMDP}$ work well?

Experiment Setting. We conducted experiments on Apple 2.3 GHz Dual-Core Intel Core i5 with 16 GB of RAM. We designed three benchmarks, called Patrol, Wholesale, and Packets, as string diagrams of MDPs. Patrol is sketched in Fig. 1; it has layers of tasks, rooms, floors, buildings and a neighborhood.

Wholesale is similar to Patrol, with four layers (item, dispatch, pipeline, wholesale), but their transition structures are more complex: they have more loops, and more actions are enabled in each position, compared to Patrol. The lowest-level component MDP is much larger, too: an item in Wholesale has 5000 positions, while a task in Patrol has a unique position.

Packets has two layers: the lower layer models a transmission of 100 packets with probabilistic failure. The upper layer is a sequence of copies of 2–5 variations of the lower layer—in total, we have 50 copies—modeling 50 batches of packets

For Patrol and Wholesale, we conducted experiments with varying degree of identification (DI); this can be seen as an ablation study. These benchmarks have identical copies of a component MDP in their string diagrams; high DI means that these copies are indeed expressed as multiple occurrences of the same variable, informing $\textrm{CompMDP}$ to reuse the intermediate solution. As DI goes lower, we introduce new variables for these copies and let them look different to $\textrm{CompMDP}$. Specifically, we have twice as many variables for DI-mid, and three (Patrol) or four (Wholesale) times as many for DI-low, as for DI-high.

For Packets, we conducted experiments with different degrees of freezing (FZ). FZ-none indicates no freezing, where our compositional algorithm digs all the way down to individual positions as component MDPs. FZ-all freezes everything, which means we simply used PRISM (no compositionality). FZ-int. (intermediate) freezes the lower of the two layers. Note that this includes the performance comparison between CompMDP and PRISM (i.e. FZ-all).

For Patrol and Wholesale, we also compared the performance of CompMDP and PRISM using their simple variations Patrol5 and Wholesale5. We did not use other variations (Patrol/Wholesale1–4) since the translation of the models to the PRISM format blowed up.

Table 1. Experimental results.

Results and Discussion. Table 1 summarizes the experiment results.

RQ1. A big advantage of compositional verification is that it can reuse intermediate results. This advantage is clearly observed in the ablation experiments with the benchmarks Patrol1–4 and Wholesale1–4: as the degree of reuse goes 1/2 and 1/3–1/4 (see above), the execution time grew inverse-proportionally. Moreover, with the benchmarks Packets1–4, Patrol5 and Wholesale5, we see that compositionality greatly improves performance, compared to PRISM (FZ-all). Overall, we can say that compositionality has clear performance advantages in probabilistic model checking.

RQ2. The Packets experiments show that controlling the degree of compositionality is important. Packet’s lower layer (frozen in FZ-int.) is a large and complex model, without a clear compositional structure; its fully compositional treatment turned out to be prohibitively expensive. The performance advantage of FZ-int. compared to PRISM (FZ-all) is encouraging. The Patrol5 and Wholesale5 experiments also show the advantage of compositionality.

RQ3. We find the absolute performance of $\textrm{CompMDP}$ quite satisfactory. The Patrol and Wholesale benchmarks are huge models, with so many positions that fitting their explicit state representation in memory is already nontrivial. $\textrm{CompMDP}$, exploiting their succinct presentation by string diagrams, successfully model-checked them in realistic time (6–130 s with DI-high).

RQ4. The experiments suggest that string diagrams are a practical modeling formalism, allowing faster solutions of realistic benchmarks. It seems likely that the formalism is more suited for task compositionality (where components are sub-tasks and they are sequentially composed with possible fallbacks and loops) rather than system compositionality (where components are sub-systems and they are parallelly composed).

RQ5. It seems that the number of locally optimal schedulers is an important factor: if there are many of them, then we have to record more in the intermediate solutions of the meager semantics. This number typically increases when more actions are available, as the comparison between Patrol and Wholesale.