Making $\textsf {IP}=\textsf {PSPACE}$ Practical: Efficient Interactive Protocols for BDD Algorithms

Abstract

We show that interactive protocols between a prover and a verifier, a well-known tool of complexity theory, can be used in practice to certify the correctness of automated reasoning tools.

Theoretically, interactive protocols exist for all $\textsf {PSPACE}$ problems. The verifier of a protocol checks the prover’s answer to a problem instance in probabilistic polynomial time, with polynomially many bits of communication, and with exponentially small probability of error. (The prover may need exponential time.) Existing interactive protocols are not used in practice because their provers use naive algorithms, inefficient even for small instances, that are incompatible with practical implementations of automated reasoning.

We bridge the gap between theory and practice by means of an interactive protocol whose prover uses BDDs. We consider the problem of counting the number of assignments to a QBF instance ($\#\text {CP}$), which has a natural BDD-based algorithm. We give an interactive protocol for $\#\text {CP}$ whose prover is implemented on top of an extended BDD library. The prover has only a linear overhead in computation time over the natural algorithm.

We have implemented our protocol in $\textsf {blic}$, a certifying tool for $\#\text {CP}$. Experiments on standard QBF benchmarks show that blic is competitive with state-of-the-art QBF-solvers. The run time of the verifier is negligible. While loss of absolute certainty can be concerning, the error probability in our experiments is at most $10^{-10}$ and reduces to $10^{-10k}$ by repeating the verification k times.

This work was supported by an ERC Advanced Grant (787367: PaVeS), by the Deutsche Forschungsgemeinschaft project 389792660 TRR 248—CPEC, and by the Research Training Network of the Deutsche Forschungsgemeinschaft (DFG) (378803395: ConVeY).

1 Introduction

Automated reasoning tools often underlie our assertions about the correctness of critical hardware and software components. In recent years, the scope and scalability of these techniques have grown significantly.

Automated reasoning tools are not immune to bugs. If we are to trust their verdict, it is important that they provide evidence of their correct behaviour. A substantial amount of research has gone into proof-producing automated reasoning tools [4, 14, 16, 22, 23]. These works define a notion of “correctness certificate” suitable for the reasoning problem at hand, and adapt the reasoning engine to produce independently checkable certificates. For example, SAT solvers produce either a satisfying assignment or a proof of unsatisfiability in some proof system, e.g. resolution (see [16] for a survey). Extending such certificates beyond boolean SAT is an active area of current research [3, 4, 18, 24, 29].

In the worst case, the size of certificates grows exponentially in the size of the input, even for boolean unsatisfiability (unless $\textsf{NP}$ $=$ $\textsf{coNP}$). If users have limited computational or communication resources, transferring and checking large certificates becomes a burden. Large certificates are not just a theoretical curiosity. In practice, resolution proofs for complex SAT problems may run to petabytes [15]. Ideally, we would prefer “small” certificates (polynomial in the size of the input) which can be checked independently in polynomial time.

The $\textsf {IP}=\textsf {PSPACE}$ theorem proves that certification with polynomial verification time is possible for any problem in $\textsf {PSPACE}$, provided one trades off absolute certainty for certainty with high probability [27]. The complexity class $\textsf {IP}$ consists of those languages for which there is a polynomial-round, complete and sound interactive protocol [1, 2, 13, 20]—a sequence of interactions between a (computationally unbounded) prover and a (computationally bounded) verifier after which the verifier decides whether the prover correctly performed a computation. The protocol is complete if, whenever an input belongs to the language, there is an honest prover who can convince a polynomial-time randomised verifier in a polynomial number of rounds. The protocol is sound if, whenever an input does not belong to the language, the Verifier will reject the input with high probability—no matter what certificates are provided to the Verifier. That is, a “Prover” cannot fool the certification process.

Since every language in $\textsf {PSPACE}$ has an interactive protocol, there are interactive protocols for UNSAT, QBF, counting QBF, safety verification of concurrent state machines, etc. Observe that the prover of a protocol may perform exponential time computations (which is unavoidable unless $\textsf{P}= \textsf {PSPACE}$), but the verifier only requires polynomial time in the original input.

If interactive protocols provide a foundation for small and efficiently verifiable certificates (at least for problems in $\textsf {PSPACE}$), why are they not in widespread practice? We believe the reason to be the following: for asymptotic complexity purposes, it suffices to use honest provers with best-case exponential complexity that naively enumerate all possibilities. Such provers are incompatible with automated reasoning tools, which use more sophisticated data structures and heuristics to scale to real-world examples. So we need to make practical algorithms for automated reasoning efficiently certifying. We call an algorithm efficiently certifying if, in addition to computing the output, it can execute the steps of an honest prover in an interactive protocol with only polynomial overhead over its running time.

In this paper, we show that algorithms using reduced ordered binary decision diagrams (henceforth called BDDs) [9] can be made efficiently certifying. We consider ${\#\text {CP}}$, the problem of computing the number of satisfying assignments of a circuit with partial evaluation (CP). Besides boolean nodes, a CP contains partial evaluation nodes (resp., ) that take a boolean predicate as input, say $\varphi$, and output the result of setting x to (resp., ) in $\varphi$. ${\#\text {CP}}$ generalises SAT, QBF, and counting SAT ($\#$SAT), and has a natural algorithm using BDDs: Compute BDDs for each node of the circuit in topological order, and count the accepting paths of the final BDD.

The theoretical part of the paper proceeds in two steps. First, we present CPCertify, a complete and sound interactive protocol for $\#\text {CP}$. CPCertify is similar to the SumCheck protocol [20]. It involves encoding boolean formulas as polynomials over a finite field. The prover is responsible for producing certain polynomials from the original circuit and evaluating them at points of the field chosen by the verifier. These polynomials are either multilinear (all exponents are at most 1) or quadratic (at most 2).

Second, we show that an honest prover in CPCertify can be implemented on top of a suitably extended BDD library. The run times of the certifying BDD algorithms are only a constant overhead over the computation time without certification—they depend linearly on the total number of nodes of the intermediate BDDs computed by the prover to solve the $\#\text {CP}$ instance. We use two key insights. The first is an encoding of multilinear polynomials as BDDs; we show that the intermediate BDDs represent all the multilinear polynomials a prover needs during the run of CPCertify. The second shows that the quadratic polynomials correspond to intermediate steps during the computation of the intermediate BDDs. We extend BDDs with additional “book-keeping” nodes that allow the prover to also compute the quadratic polynomials while solving the problem. So computing the polynomials required by CPCertify has zero additional cost; the only overhead is the cost of evaluating the polynomials at the field points chosen by the verifier.

We have implemented a certifying $\#\text {CP}$ solver based on our extended BDD library. Our experiments show that the solver is competitive with state-of-the-art non-certifying QBF solvers, and can outperform certifying QBF solvers based on BDDs. The number of bytes exchanged between the prover and the verifier are an order of magnitude smaller, and Verifier’s run time several orders of magnitude smaller, than current encodings of QBF proofs, while bounding the error probability to below $10^{-10}$. Thus, our results open the way for practically efficient, probabilistic certification of automated reasoning problems using interactive protocols.

Additional Related Work. Proof systems for SAT and QBF remain an active area of research—both in theoretical proof complexity and in practical tool development. Jussila, Sinz, and Biere [17, 28] showed how to extract extended resolution proofs from BDD operations. This is the basis for proof-producing SAT and QBF solvers based on BDDs [6,7,8]. As in our work, the proof uses intermediate nodes produced in the construction of the BDD operations. We focus on interactive certification instead of extended resolution proofs, which can be exponentially larger than the input formula.

Recently, Luo et al. [21] consider the problem of providing zero-knowledge proofs of unsatisfiability, a motivation similar but not equal to ours. Their techniques require the verifier to work in time polynomial in the proof, which can be exponentially bigger than the input formula. In contrast, the verifier of CPCertify runs in polynomial time in the input. Since any language in PSPACE has a zero knowledge proof [5], our protocol can in principle be made zero knowledge. Whether that system scales in practice is left for future work.

Full Version. Detailed proofs can be found in the full version of the paper [11].

2 Preliminaries

The Class $\textsf {IP}$. An interactive protocol between a Prover and a Verifier consists of a sequence of interactions in which a Verifier asks questions to a Prover, receives responses to the questions, and must ultimately decide if a common input x belongs to a language. The computational power of the Prover is unbounded but the Verifier is a randomised, polynomial-time algorithm.

Formally, let P, V denote (deterministic) Turing machines.

We say that $(r;m_1,...,m_{2k})$ is a k-round interaction, with $r,m_1,...,m_{2k}\in \{0,1\}^*$, if $m_{i+1}=V(r,m_1,...,m_i)$ for even i and $m_{i+1}=P(m_1,...,m_i)$ for odd i. We think of r as an additional sequence of bits given to Verifier V that is chosen randomly. The output ${\text {out}}(P, V)(x,r,k)$ is defined as $m_{2k}$, where $(r;m_1,...,m_{2k})$ is the unique k-round interaction with $m_1=x$.

A language L belongs to $\textsf {IP}$ if there are $V,P_H$ and polynomials $p_1,p_2,p_3$, s.t. $V(r,x,m_2,...,m_i)$ runs in time $p_1(\mathopen |x\mathclose |)$ for all $r,x,m_2,...,m_i$, and, for each x and an $r\in \{0,1\}^{p_2(\mathopen |x\mathclose |)}$ chosen uniformly at random:

• 1. (Completeness) $x\in L$ implies ${\text {out}}(P_H, V)(x,r,p_3(\mathopen |x\mathclose |)) = 1$ with probability 1, and

• 2. (Soundness) $x \notin L$ implies that for all P we have ${\text {out}}(P, V)(x,r,p_3(\mathopen |x\mathclose |)) = 1$ with probability at most $2^{-\mathopen |x\mathclose |}$.

Intuitively, in an interactive protocol, a computationally unbounded Prover interacts with a randomised polynomial-time Verifier for k rounds. In each round, Verifier sends probabilistic “challenges” to Prover, based on the input and the answers to prior challenges, and receives answers from Prover. At the end of k rounds, Verifier decides to accept or reject the input. The completeness property ensures that if the input belongs to the language L, then there is an “honest” Prover $P_H$ who can always convince Verifier that indeed $x\in L$. If the input does not belong to the language, then the soundness property ensures that Verifier rejects the input with high probability no matter how a (dishonest) Prover tries to convince them.

It is known that $\textsf {IP}= \textsf {PSPACE}$ [20, 27], that is, every language in $\textsf {PSPACE}$ has a polynomial-round interactive protocol. The proof exhibits an interactive protocol for the language QBF of true quantified boolean formulae; in particular, the honest Prover is a polynomial space, exponential time algorithm that uses a truth table representation of the formula to implement the protocol.

Polynomials. Interactive protocols make extensive use of polynomials over some prime finite field $\mathbb {F}$.

Let X be a finite set of variables. We use $x, y, z, \ldots$ for variables and $p, q, \ldots$ for polynomials. When we write a polynomial explicitly, we write it in brackets, e.g. $[3xy-z^2]$. We write $\textbf{1}$ and $\textbf{0}$ for the polynomials [1] and [0], respectively. We use the following operations on polynomials:

• Sum, difference, and product. Denoted $p+q$, $p-q$, $p \cdot q$, and defined as usual. For example, $[3xy-z^2]+[z^2+yz]=[3xy+yz]$ and $[x+y]\cdot [x-y]=[x^2-y^2]$.

• Partial evaluation. Denoted $\pi _{[{x :=a}]} \, p$, it returns the result of setting variable x to the field element a in the polynomial p, e.g. $\pi _{[{x :=5}]}[3xy-z^2]=[15y-z^2]$.

• Degree reduction. Denoted $\delta _x \, p$. It reduces the degree of x in all monomials of the polynomial to 1. For example, $\delta _x[x^3y+3x^2+7z^2]=[xy+3x+7z^2]$.

A (partial) assignment is a (partial) mapping $\sigma : X \rightarrow \mathbb {F}$. We write ${\mathrm {\Pi }}_{{\sigma }}\, p$ for $\pi _{[{x_1:=\sigma (x_1)}]}...\pi _{[{x_k:=\sigma (x_k)}]} \, p$, where $x_1,...,x_k$ are the variables for which $\sigma$ is defined. Additionally, we call $\sigma$ binary if $\sigma (x)\in \{0,1\}$ for each $x\in X$.

Binary and Multilinear Polynomials. A polynomial is multilinear in x if the degree of x in p is 0 or 1. A polynomial is multilinear if it is multilinear in all its variables. For example, $[xy-y^2]$ is multilinear in x but not in y, and $[3xy -2zy]$ is multilinear. A polynomial p is binary if ${\mathrm {\Pi }}_{{\sigma }}\, p \in \{\textbf{0},\textbf{1}\}$ for every binary assignment $\sigma$. Two polynomials p, q are binary equivalent, denoted $p\equiv _b q$, if ${\mathrm {\Pi }}_{{\sigma }}\, p={\mathrm {\Pi }}_{{\sigma }}\, q$ for every binary assignment $\sigma$. (Note that non-binary polynomials can be binary equivalent.)

3 Circuits with Partial Evaluation

We introduce circuits with partial evaluation (CP), a compact representation of quantified boolean formulae, and formulate #CP, the problem of counting the number of satisfying assignments of a $\text {CP}$. #CP generalises QBF, the satisfiability problem for quantified boolean formulas. Figure 1 shows an example of a CP. Informally, it is a directed acyclic graph whose nodes are labelled with variables, boolean operators, or partial evaluation operators $\pi _{[{x :=b}]}$. Intuitively, $\pi _{[{x :=b}]} \varphi$ sets the variable x to the truth value b in the formula $\varphi$. In this way, each node of a circuit stands for a boolean function, and the complete circuit stands for the boolean function of the root. Figure 1 shows the formulae represented by each node.

Definition 1

Let X denote a finite set of variables and $S\subseteq X$. A circuit with partial evaluation and variables in S (S-CP) has the form

• , , or x, where $x\in S$,

• $\lnot \varphi$, $\varphi \wedge \psi$, or $\varphi \vee \psi$, where $\varphi ,\psi$ are S-CPs, or

• $\pi _{[{y :=b}]} \, \varphi$, where $y\in X\setminus S$, , and $\varphi$ is an $(S\cup \{y\})$-CP.

The set of free variables of a S-CP $\varphi$ is ${\text {free}}(\varphi ):=S$. The children of a CP are inductively defined as follows: , , and x have no children; the children of $\varphi \wedge \psi$ and $\varphi \vee \psi$ are $\varphi$ and $\psi$; and the only child of $\lnot \varphi$ and $\pi _{[{y :=b}]}\, \varphi$ is $\varphi$. The set of descendants of $\varphi$ is the smallest set M containing $\varphi$ and all children of every element of M. The size of $\varphi$ is $\mathopen |\varphi \mathclose |:=\mathopen |M\mathclose |$.

Fig. 1.

A CP (Sect. 3), the boolean functions represented by each node (in boxes), and the arithmetisation of the formulae (Sect. 4.1).

We represent a CP $\varphi$ as a directed acyclic graph. The nodes of the graph are the descendants of $\varphi$. A CP $\varphi$ encodes a boolean predicate $P_\varphi$, which maps assignments to a truth value . It does so in the obvious manner, e.g., $P_x(\sigma ):=\sigma (x)$, $P_{\varphi \wedge \psi }(\sigma ):=P_\varphi (\sigma ) \wedge P_\psi (\sigma )$, etc. We use $\pi _{[{x :=b}]}$ as partial evaluation operator, so $P_{\pi _{[{x :=b}]}\varphi }(\sigma ):=P_\varphi (\sigma \cup \{x\mapsto b\})$. Intuitively, $\pi _{[{x :=b}]} \, \varphi$ replaces each occurrence of x in $\varphi$ by b. An assignment $\sigma$ satisfies $\varphi$ if . We define the macros

$$\begin{aligned} \forall _x\varphi&:= \pi _{[{x :=0}]} \, \varphi \wedge \pi _{[{x :=1}]} \, \varphi \\ \exists _x\varphi&:= \pi _{[{x :=0}]} \, \varphi \vee \pi _{[{x :=1}]} \, \varphi \end{aligned}$$

Figure 1 shows a $\text {CP}$ for the quantified boolean formula $\forall _y(\lnot x \vee (x \wedge y))$.

We consider the following problem:

Given a quantified boolean formula, we can use the macros for quantifiers to construct in linear time an equivalent CP, i.e., a CP with the same satisfying assignments. Similarly, #SAT instances can also be reduced to #CP.

Structure of the Rest of the Paper. In Sect. 4, we give an interactive protocol for #CP called CPCertify. In Sect. 5, we implement an honest Prover for CPCertify on top of an extended BDD-based algorithm for #CP. The prover runs in time polynomial in the size of the largest BDD for any of the subcircuits of the initial circuit. Together, these results yield our main result, Theorem 1, showing that any BDD-based algorithm can be modified to run an interactive protocol with small polynomial overhead. Finally, Sect. 6 presents empirical results.

4 An Interactive Protocol for #CP

In this section we describe an interactive protocol for #CP, following the SumCheck protocol of [20]. Section 4.1 introduces arithmetisation, a technique to transform #CP into an equivalent problem about polynomials. Section 4.2 shows how to transform #CP into an equivalent problem about evaluating polynomials of low degree. Finally, Sect. 4.3 presents an interactive protocol for this problem.

4.1 Arithmetisation

We define a mapping $[\![ {\cdot } ]\!]$ that assigns to each CP $\varphi$ a polynomial $[\![ {\varphi } ]\!]$ over the variables ${\text {free}}(\varphi )$, called the arithmetisation of $\varphi$:

• ; ; $[\![ {x} ]\!] := [x]$ for every $x \in X$; and $[\![ {\lnot \varphi } ]\!] := \textbf{1}- [\![ {\varphi } ]\!]$;

• $[\![ {\varphi \wedge \psi } ]\!] :=[\![ {\varphi } ]\!] \cdot [\![ {\psi } ]\!]$; and $[\![ {\varphi \vee \psi } ]\!] := [\![ {\varphi } ]\!]+ [\![ {\psi } ]\!]-[\![ {\varphi } ]\!]\cdot [\![ {\psi } ]\!]$;

• $[\![ {\pi _{[{x :=b}]} \, \varphi } ]\!]:=\pi _{[{x :=[\![ {b} ]\!]}]}[\![ {\varphi } ]\!]$, with $x\in {\text {free}}(\varphi )$, .

Figure 1 also shows the polynomials corresponding to the nodes of the CP.

Let $\mathbb {F}$ be a fixed prime finite field. Given an arbitrary truth assignment , let $\overline{\sigma } :X \rightarrow \mathbb {F}$ be the binary assignment given by $\overline{\sigma }(x) = 1$ if and $\overline{\sigma }(x) = 0$ if , where 0 and 1 denote the additive and multiplicative identities in $\mathbb {F}$. The mapping $[\![ {\cdot } ]\!]$ is defined to satisfy the following property, whose proof is immediate:

Proposition 1

Let $\varphi$ be an S-CP encoding some boolean predicate $P_\varphi$. Then $P_\varphi (\sigma ) = {\mathrm {\Pi }}_{{\overline{\sigma }}}\, [\![ {\varphi } ]\!]$ for every truth assignment $\sigma$ to S.

So, intuitively, the polynomial $[\![ {\varphi } ]\!]$ is a conservative extension of the predicate $P_\varphi$: It returns the same values for all binary assignments. Accordingly, in the rest of the paper we abuse language and write $\sigma$ instead of $\overline{\sigma }$ for the binary assignment corresponding to the truth assignment $\sigma$.

Observe that #CP can be reformulated as follows: given a CP $\varphi$, compute the number of binary assignments $\sigma$ s.t. ${\mathrm {\Pi }}_{{\sigma }}[\![ {\varphi } ]\!] = \textbf{1}$.

Fig. 2.

CPD and polynomials for the CP of Fig. 1.

4.2 Degree Reduction

Given a CP $\varphi$, its associated polynomial can have degree exponential in the height of $\varphi$. Since we are ultimately interested in evaluating polynomials over binary assignments, and since $x^2=x$ for $x\in {\{ 0,1 \}}$, we can convert polynomials to low degree without changing their behaviour on binary assignments.

For this, we use a degree-reduction operator $\delta _x$ for every variable x. The operator $\delta _x p$ reduces the exponent of all powers of x in p to 1. For example, $\delta _x [x^2y + 3 x y^2 - 2x^3 y^2+ 4] = [xy + 3x y^2 - 2xy^2 + 4]$. Observe that $\delta _x p\equiv _b p$. Instead of working on the input CP directly, we first convert it into a circuit with partial evaluation and degree reduction by inserting degree-reduction operators after binary operations. This ensures all intermediate polynomials obtained by arithmetisation have low degree.

Definition 2

A circuit with partial evaluation and degree reduction over the set S of variables (S-CPD) is defined in the same manner as an S-CP, extended as follows:

• if $\varphi$ is an S-CPD and $x\in S$, then $\delta _x\varphi$ is an S-CPD,

• $[\![ {\delta _x\varphi } ]\!]:=\delta _x[\![ {\varphi } ]\!]$, and

• $\varphi$ is the only child of $\delta _x\varphi$.

For an S-CPD $\varphi$ we define ${\text {free}}(\varphi )$, $\mathopen |\varphi \mathclose |$, children, descendants, and the graphical representation as for S-CPs.

We convert a CP $\varphi$ into a CPD ${\text {conv}}(\varphi )$ by adding a degree-reduction operator for each free variable before any binary operation.

Definition 3

Given a CP $\varphi$ with ${\text {free}}(\varphi )=\{x_1,...,x_k\}$, its associated CPD ${\text {conv}}(\varphi )$ is inductively defined as follows:

• , ,

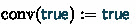• ${\text {conv}}(\lnot \psi ):=\lnot {\text {conv}}(\psi )$, ${\text {conv}}(\pi _{[{x :=b}]}\, \psi ):=\pi _{[{x :=b}]} \, {\text {conv}}(\psi )$, and

• ${\text {conv}}(\psi _1\circledast \psi _2):=\delta _{x_1}...\delta _{x_k}({\text {conv}}(\psi _1) \circledast {\text {conv}}(\psi _2))$, for $\circledast \in \{\vee ,\wedge \}$.

Figure 2 shows the CPD ${\text {conv}}(\varphi )$ for the CP $\varphi$ of Fig. 1, together with the polynomials corresponding to each node.

We collect some basic properties of CPDs:

Lemma 1

Let $\varphi$ be a CP.

• (a) $[\![ {{\text {conv}}(\varphi )} ]\!]$ is a binary multilinear polynomial and $[\![ {{\text {conv}}(\varphi )} ]\!]\equiv _b[\![ {\varphi } ]\!]$.

• (b) For every descendant $\psi$ of ${\text {conv}}(\varphi )$, $[\![ {\psi } ]\!]$ has maximum degree 2.

CPDs have another useful property. Recall that given a CP $\varphi$ we are interested in its number of satisfying assignments. The next lemma shows that this number can be computed by evaluating the polynomial $[\![ {{\text {conv}}(\varphi )} ]\!]$ on a single input.

Lemma 2

A CP $\varphi$ with n free variables has $m < \mathopen |\mathbb {F}\mathclose |$ satisfying assignments iff ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!]=m\cdot 2^{-n}$, where $\sigma$ is the assignment satisfying $\sigma (x) := 2^{-1}$ in the field $\mathbb {F}$ for every variable x.¹

4.3 CPCertify: An Interactive Protocol for #CP

We describe an interactive protocol, called CPCertify, for a CP $\varphi$ with n free variables. Let X denote the variables used in $\varphi$. Prover and Verifier fix a finite field with at least $m+1$ elements, where m is an upper bound on the number of assignments (e.g. $m=2^n$). Prover tries to convince the Verifier that ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!] = K$ for some $K \in \mathbb {F}$.

In the protocol, Verifier challenges Prover to compute polynomials of the form ${\mathrm {\Pi }}_{{\sigma }}([\![ {\psi } ]\!])$, where $\psi$ is a node of the CPD ${\text {conv}}(\varphi )$ and $\sigma :{\text {free}}(\psi )\rightarrow \mathbb {F}$ is a (non-binary!) assignment; we call the expression ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\psi )} ]\!]$ a challenge. Observe that all assignments are chosen by Verifier. Prover answers with some $k \in \mathbb {F}$. We call the expression ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\psi )} ]\!]=k$ a claim, or the answer to the challenge ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\psi )} ]\!]$.

CPCertify consists of an initialisation and a number of rounds, one for each descendant of ${\text {conv}}(\varphi )$. Rounds are executed in topological order, starting at the root, i.e. at ${\text {conv}}(\varphi )$ itself. The structure of a round for a node $\psi$ of ${\text {conv}}(\varphi )$ depends on whether $\psi$ is an internal node (including the root), or a leaf.

At each point, Verifier keeps track of a set $\mathcal {C}$ of claims that must be checked.

Initialisation. Verifier sends Prover the challenge ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!]$, where $\sigma (x) := 2^{-1}$ for every $x \in {\text {free}}(\varphi )$. Prover returns the claim ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!]=K$ for some $K \in \mathbb {F}$. (By Lemma 2, this amounts to claiming that $\varphi$ has $K \cdot 2^n$ satisfying assignments.) Verifier initialises $\mathcal {C}:=\{{\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!]=K\}$.

Round for an Internal Node. A round for an internal node $\psi$ runs as follows:

• (a) Verifier collects all claims $\{ {\mathrm {\Pi }}_{{\sigma _i}}[\![ {\psi } ]\!] = k_i\}_{i=1}^m$ in $\mathcal {C}$ relating to $\psi$, with assignments $\sigma _1,\ldots ,\sigma _m :{\text {free}}(\psi )\rightarrow \mathbb {F}$ and $k_1,...,k_m\in \mathbb {F}$. (Initially $\psi ={\text {conv}}(\varphi )$ and the only claim is ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!]=K$.)

• (b) If $m > 1$, Verifier interacts with Prover to compute a unique claim ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!] = k$ such that very likely² the claim is true only if all claims $\{{\mathrm {\Pi }}_{{\sigma _i}}[\![ {\psi } ]\!] = k_i\}_{i=1}^m$ are true. For this, Verifier sends a number of challenges, and checks that the answers are consistent with the prior claims. Based on these answers, Verifier then derives new claims. (See “Description of step (b)” below.)

• (c) Verifier interacts with Prover to compute a claim ${\mathrm {\Pi }}_{{\sigma '}}[\![ {\psi '} ]\!]=k'$ for each child $\psi '$ of $\psi$. This is similar to (b): if ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!] \ne k$, i.e. the unique claim from (b) does not hold, then very likely one of the resulting claims will be wrong. Depending on the type of $\psi$, the claims are computed based on the answers of Prover to challenges sent by Verifier. (See “Description of step (c)” below.)

• (d) In total, Verifier removed the claims $\{ {\mathrm {\Pi }}_{{\sigma _i}}[\![ {\psi } ]\!] = k_i\}_{i=1}^m$ from $\mathcal {C}$, and replaced them by one claim ${\mathrm {\Pi }}_{{\sigma '}}[\![ {\psi '} ]\!]=k'$ for each child $\psi '$ of $\psi$.

Observe that, since a node $\psi$ can be a child of several nodes, Verifier may collect multiple claims for $\psi$, one for each parent node.

Round for a Leaf. If $\psi$ is a leaf, then $\psi =x$ for a variable x, or . Verifier removes all claims $\{ {\mathrm {\Pi }}_{{\sigma _i}}[\![ {\psi } ]\!] = k_i\}_{i=1}^m$ from $\mathcal {C}$, computes the values $c_i:={\mathrm {\Pi }}_{{\sigma _i}}[\![ {\psi } ]\!]$, and rejects if $k_i\ne c_i$ for any i.

Observe that if all claims made by Prover about leaves are true, then very likely Prover’s initial claim is also true.

Description of Step (b). Let $\{ {\mathrm {\Pi }}_{{\sigma _i}}[\![ {\psi } ]\!] = k_i\}_{i=1}^m$ be the claims in $\mathcal {C}$ relating to node $\psi$. Verifier and Prover conduct step (b) as follows:

• (b.1) While there exists $x\in X$ s.t. $\sigma _1(x), \ldots ,\sigma _m(x)$ are not pairwise equal:

  • (b.1.1) For every $i\in \{1,...,m\}$, let $\sigma _i'$ denote the partial assignment which is undefined on x and otherwise matches $\sigma _i$. Verifier sends the challenges $\{{\mathrm {\Pi }}_{{\sigma '_i}}[\![ {\psi } ]\!]\}_{i=1}^m$ to Prover. Prover answers with claims $\{{\mathrm {\Pi }}_{{\sigma '_i}}[\![ {\psi } ]\!]=p_i\}_{i=1}^m$. Note that $p_1, \ldots , p_m$ are univariate polynomials with free variable x.

  • (b.1.2) Verifier checks whether $k_i=\pi _{[{x :=\sigma _i(x)}]} \, p_i$ holds for each i. If not, Verifier rejects. Otherwise, Verifier picks $r\in \mathbb {F}$ uniformly at random and updates $\sigma _i(x):=r$ and $k_i:=\pi _{[{x :=r}]}p_i$ for every $i\in \{1,...,m\}$.

• (b.2) If after exiting the loop the values $k_1,...,k_m$ are not pairwise equal, Verifier rejects. Otherwise (that is, if $k_1 =k_2 = \cdots =k_m)$, the set $\mathcal {C}$ now contains a unique claim ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!]=k$ relating to $\psi$.

Example 1

Consider the case in which $X = \{x\}$, and Prover has made two claims, ${\mathrm {\Pi }}_{{\sigma _1}}[\![ {\psi } ]\!] = k_1$ and ${\mathrm {\Pi }}_{{\sigma _2}}[\![ {\psi } ]\!] = k_2$ with $\sigma _1(x)=1$ and $\sigma _2(x)=2$. In step (b.1.1) we have $\sigma _1'=\sigma _2'$ (both are the empty assignment), and so Verifier sends the challenge $[\![ {\psi } ]\!]$ to Prover twice, who answers with claims $[\![ {\psi } ]\!]=p_1$ and $[\![ {\psi } ]\!]=p_2$. In step (b.1.2) Verifier checks that $p_1(1)=k_1$ and $p_2(2)=k_2$ hold, picks a random number r, and updates $\sigma _1(x):=\sigma _2(x):= r$ and $k_1:=p_1(r),k_2:=p_2(r)$. Now the condition of the while loop fails, so Verifier moves to (b.2) and checks $k_1=k_2$.

Description of Step (c). Let ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!] = k$ be the claim computed by Verifier in step (b). Verifier removes this claim from $\mathcal {C}$ and replaces it by claims about the children of $\psi$, depending on the structure of $\psi$:

• (c.1) If $\psi =\psi _1\circledast \psi _2$, for a $\circledast \in \{\vee ,\wedge \}$, then Verifier sends Prover challenges ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi _i} ]\!]$ for $i\in \{1,2\}$, and Prover sends claims ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi _i} ]\!]=k_i$ back. Verifier checks the consistency condition $k=\pi _{[{x :=k_1}]}\pi _{[{y :=k_2}]}[\![ {x\circledast y} ]\!]$, rejecting if it does not hold. If the condition holds, the claim ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi _i} ]\!]=k_i$ is added to $\mathcal {C}$, to be checked in the round for $\psi _i$.

• (c.2) If $\psi =\lnot \psi '$, then Verifier adds the claim ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi '} ]\!]=1-k$ to $\psi '$.

• (c.3) If $\psi =\pi _{[{x :=b}]} \, \psi '$, Verifier sets $\sigma ' := \sigma \cup \{x \mapsto b\}$ and adds the claim ${\mathrm {\Pi }}_{{\sigma '}}[\![ {\psi '} ]\!]=k$ to $\mathcal {C}$.

• (c.4) If $\psi =\delta _x\psi '$, then Verifier sends Prover the challenge ${\mathrm {\Pi }}_{{\sigma '}}[\![ {\psi '} ]\!]$, where $\sigma '$ denotes the partial assignment which is undefined on x and otherwise matches $\sigma$. Prover returns the claim $p:={\mathrm {\Pi }}_{{\sigma '}}[\![ {\psi '} ]\!]$. Observe that p is a univariate polynomial over x. Verifier checks the consistency condition $\pi _{[{x :=\sigma (x)}]}\delta _x \, p=k$, rejecting if it does not hold. If it holds, Verifier picks an $r\in \mathbb {F}$ uniformly at random, conducts the updates $\sigma (x):=r$ and $k:=\pi _{[{x :=r}]} \, p$, and adds ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi '} ]\!]=k$ to the set of claims about $\psi '$.

This concludes the description of the interactive protocol. We now show CPCertify is complete and sound.

Proposition 2

(CPCertify is complete and sound). Let $\varphi$ be a CP with n free variables. Let ${\mathrm {\Pi }}_{{\sigma }}[\![ {{\text {conv}}(\varphi )} ]\!]=K$ be the claim initially sent by Prover to Verifier. If the claim is true, then Prover has a strategy to make Verifier accept. If not, for every Prover, Verifier accepts with probability at most $4n\mathopen |\varphi \mathclose |/\mathopen |\mathbb {F}\mathclose |$.

If the original claim is correct, Prover can answer every challenge truthfully and all claims pass all of Verifier’s checks. So Verifier accepts. If the claim is not correct, we proceed round by round. We bound the probability that the Verifier is tricked in a single step to at most $2/\mathopen |\mathbb {F}\mathclose |$ using the Schwartz-Zippel Lemma. We then bound the number of such steps to $2n \mathopen |\varphi \mathclose |$ and use a union bound.

5 A BDD-Based Prover

We assume familiarity with reduced ordered binary decision diagrams (BDDs) [9]. We use BDDs over $X=\{x_1, \ldots , x_n\}$. We fix the variable order $x_1< x_{2}< \ldots < x_n$, i.e. the root node would decide based on the value of $x_n$.

Definition 4

BDDs are defined inductively as follows:

• and are BDDs of level 0;

• if $u\ne v$ are BDDs of level $\ell _u, \ell _v$ and $i > \ell _u, \ell _v$, then $\left\langle x_i, u, v \right\rangle$ is a BDD of level i;

• we identify $\left\langle x_i, u, u \right\rangle$ and u, for a BDD u of level $\ell _i$ and $i>\ell _u$.

The level of a BDD w is denoted $\ell (w)$. The set of descendants of w is the smallest set S with $w\in S$ and $u,v\in S$ for all $\left\langle x,u,v\right\rangle \in S$. The size $\mathopen |w\mathclose |$ of w is the number of its descendants.

The arithmetisation of a BDD w is the polynomial $[\![ {w} ]\!]$ defined as follows: , and $[\![ {\left\langle x,u,v\right\rangle } ]\!]:=[1-x]\cdot [\![ {u} ]\!]+[x]\cdot [\![ {v} ]\!]$.

Figure 3 shows a BDD for the boolean function $\varphi (x,y,z)=(x \wedge y \wedge \lnot z) \vee (\lnot x \wedge y \wedge z ) \vee (x \wedge \lnot y \wedge z)$ and the arithmetisation of each node.

BDDSolver: A BDD-based Algorithm for #CP. An instance $\varphi$ of #CP can be solved using BDDs. Starting at the leaves of $\varphi$, we iteratively compute a BDD for each node $\psi$ of the circuit encoding the boolean predicate $P_\psi$. At the end of this procedure we obtain a BDD for $P_\varphi$. The number of satisfying assignments of $\psi$ is the number of accepting paths of the BDD, which can be computed in linear time in the size of the BDD.

For a node $\psi = \psi _1 \circledast \psi _2$, given BDDs representing the predicates $P_{\varphi _1}$ and $P_{\varphi _2}$, we compute a BDD for the predicate $P_\varphi := P_{\varphi _1} \circledast P_{\varphi _2}$, using the ${\text {Apply}}_\circledast$ operator on BDDs. We name this algorithm for solving #CP “BDDSolver.”

Fig. 3.

A BDD and its arithmetisation. For $\left\langle x, u, v\right\rangle$, we denote the link from x to v with a solid edge and x to u with a dotted edge. We omit links to .

From BDDSolver to CPCertify. Our goal is to modify BDDSolver to play the role of an honest Prover in CPCertify with minimal overhead. In CPCertify, Prover repeatedly performs the same task: evaluate polynomials of the form ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!]$, where $\psi$ is a descendant of the CPD ${\text {conv}}(\varphi )$, and $\sigma$ assigns values to all free variables of $\psi$ except possibly one. Therefore, the polynomials have at most one free variable and, as we have seen, degree at most 2.

Before defining the concepts precisely, we give a brief overview of this section.

• First (Proposition 3), we show that BDDs correspond to binary multilinear polynomials. In particular, BDDs allow for efficient evaluation of the polynomial. As argued in Lemma 1(a), for every descendant $\psi$ of $\varphi$, the CPD ${\text {conv}}(\psi )$ (which is a descendant of ${\text {conv}}(\varphi )$) evaluates to a multilinear polynomial. In particular, Prover can use standard BDD algorithms to calculate the corresponding polynomials ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!]$ for all descendants $\psi$ of ${\text {conv}}(\varphi )$ that are neither binary operators nor degree reductions.

• Second (the rest of the section), we prove a surprising connection: the intermediate results obtained while executing the BDD algorithms (with slight adaptations) correspond precisely to the remaining descendants of ${\text {conv}}(\varphi )$.

The following proposition proves that BDDs represent exactly the binary multilinear polynomials.

Proposition 3

(a) For a BDD w, $[\![ {w} ]\!]$ is a binary multilinear polynomial. (b) For a binary multilinear polynomial p there is a unique BDD w s.t. $p =[\![ {w} ]\!]$.

Fig. 4.

A node of a CP ($\circledast$) gets a chain of degree reduction nodes in the associated CPD.

5.1 Extended BDDs

During the execution of CPCertify for a given CPD ${\text {conv}}(\varphi )$, Prover sends to Verifier claims of the form ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!]$, where $\psi$ is a descendant of ${\text {conv}}(\varphi )$, and $\sigma :X \rightarrow \mathbb {F}$ is a partial assignment. While all polynomials computed by CPCertify are binary, not all are multilinear: some polynomials have degree 2. For these polynomials, we introduce extended BDDs (eBDDs) and give eBDD-based algorithms for the following two tasks:

• 1. Compute an eBDD representing $[\![ {\psi } ]\!]$ for every node $\psi$ of ${\text {conv}}(\varphi )$.

• 2. Given an eBDD for $[\![ {\psi } ]\!]$ and a partial assignment $\sigma$, compute ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!]$.

Computing eBDDs for CPDs: Informal Introduction. Consider a CP $\varphi$ and its associated CPD ${\text {conv}}(\varphi )$. Each node of $\varphi$ induces a chain of nodes in ${\text {conv}}(\varphi )$, consisting of degree-reduction nodes $\delta _{x_1}, \ldots , \delta _{x_n}$, followed by the node itself (see Fig. 4). Given BDDs u and v for the children of the node in the CP, we can compute a BDD for the node itself using a well-known BDD algorithm ${\text {Apply}}_\circledast (u,v)$ parametric in the boolean operation $\circledast$ labelling the node [9]. Our goal is to transform ${\text {Apply}}_\circledast$ into an algorithm that computes eBDDs for all nodes in the chain, i.e. eBDDs for all the polynomials $p_0, p_1, \ldots , p_n$ of Fig. 4.

Roughly speaking, ${\text {Apply}}_\circledast (u, v)$ recursively computes BDDs $w_0 = {\text {Apply}}_\circledast (u_0, v_0)$ and $w_1 ={\text {Apply}}_\circledast (u_1, v_1)$, where $u_b$ and $v_b$ are the b-children of u and v, and then returns the BDD with $w_0$ and $w_1$ as 0- and 1-child, respectively.³

Most importantly, we modify ${\text {Apply}}_\circledast$ to run in breadth-first order. Figure 5 shows a graphical representation of a run of ${\text {Apply}}_\vee (u, v)$, where u and v are the two BDD nodes labelled by x. Square nodes represent pending calls to ${\text {Apply}}_\circledast$. Initially there is only one square call ${\text {Apply}}_\vee (u, v)$ (Fig. 5, top left). ${\text {Apply}}_\vee$ calls itself recursively for $u_0, v_0$ and $u_1, v_1$ (Fig. 5, top right). Each of the two calls splits again into two; however, the first three are identical (Fig. 5, bottom left), and so reduce to two. These two calls can now be resolved directly; they return nodes and , respectively. At this point, the children of ${\text {Apply}}_\circledast (u, v)$ become , and , which exists already as well (Fig. 5, bottom right).

We look at the diagrams of Fig. 5 not as a visualisation aid, but as graphs with two kinds of nodes: standard BDD nodes, represented as circles, and product nodes, represented as squares. We call them extended BDDs. Each node of an extended BDD is assigned a polynomial in the expected way: the polynomial $[\![ {u} ]\!]$ of a standard BDD node u with variable x is $x \cdot [\![ {u_1} ]\!] + (1-x) \cdot [\![ {u_0} ]\!]$, the polynomial $[\![ {v} ]\!]$ of a square $\wedge$-node v is $[\![ {v_0} ]\!] \cdot [\![ {v_1} ]\!]$, etc. In this way we assign to each eBDD a polynomial. In particular, we obtain the intermediate polynomials $p_0, p_1, p_2, p_3$ of the figure, one for each level in the recursion. In the rest of the section we show that these are precisely the polynomials $p_0, p_1, \ldots , p_n$ of Fig. 4.

Thus, in order to compute eBDDs for all nodes of a CPD ${\text {conv}}(\varphi )$, it suffices to compute BDDs for all nodes of the CP $\varphi$. Since we need to do this anyway to solve #CP, the polynomial certification does not incur any overhead.

Fig. 5.

Run of ${\text {Apply}}_\vee (u,v)$, but with recursive calls evaluated in breadth-first order. All missing edges go to node .

Extended BDDs. As for BDDs, we define eBDDs over $X=\{x_1, \ldots , x_n\}$ with the variable order $x_1<x_{2}<...<x_n$.

Definition 5

Let $\circledast$ be a binary boolean operator. The set of eBDDs (for $\circledast$) is inductively defined as follows:

• every BDD is also an eBDD of the same level;

• if u, v are BDDs (not eBDDs!), then $\left\langle u \circledast v\right\rangle$ is an eBDD of level l where $l:=\max \{\ell (u), \ell (v) \}$; we call eBDDs of this form product nodes;

• if $u\ne v$ are eBDDs and $i>\ell (u),\ell (v)$, then $\left\langle x_i, u, v\right\rangle$ is an eBDD of level i;

• we identify $\left\langle x_i, u, u\right\rangle$ and u for an eBDD u and $i>\ell (u)$.

The set of descendants of an eBDD w is the smallest set S with $w\in S$ and $u,v\in S$ for all $\left\langle u \circledast v\right\rangle , \left\langle x,u,v\right\rangle \in S$ The size of w is its number of descendants. For we identify $\left\langle u \circledast v\right\rangle$ with or according to the result of $\circledast$, e.g. , as . The arithmetisation of an eBDD for a boolean operator $\circledast \in \{\wedge , \vee \}$ is defined as for BDDs, with the extensions $[\![ {\left\langle u\wedge v\right\rangle } ]\!] = [\![ {u} ]\!]\cdot [\![ {v} ]\!]$ and $[\![ {\left\langle u\vee v\right\rangle } ]\!] = [\![ {u} ]\!]+[\![ {v} ]\!]-[\![ {u} ]\!]\cdot [\![ {v} ]\!]$.

Example 2

The diagrams in Fig. 5 are eBDDs for $\circledast := \vee$. Nodes of the form $\left\langle x, u, v\right\rangle$ and $\left\langle u \vee v\right\rangle$ are represented as circles and squares, respectively. Consider the top-left diagram. Abbreviating $x \oplus y := (x \wedge \lnot y) \vee (\lnot x \wedge y)$ we get $[\![ {{\text {Apply}}_\vee (u,v)} ]\!] = [\![ { (x \oplus y) \wedge (x \wedge y) } ]\!] = [\![ {x \oplus y} ]\!] \cdot [\![ {x \wedge y} ]\!] = (x (1 -y)+(1-x)\cdot y - xy(1-x)(1-y)) \cdot xy$, which is the polynomial $p_0$ shown in the figure.

Computing eBDDs for CPD s. Given a node of a CP corresponding to a binary operator $\circledast$, Prover has to compute polynomials $p_0,\, \delta _{x_1} p_0,\,\ldots ,\,\delta _{x_n}...\delta _{x_1} p_0$ corresponding to the nodes of the CPD shown on the right. We show that Prover can compute these polynomials by representing them as eBDDs. Table 1 describes an algorithm that gets as input an eBDD w of level n, and outputs a sequence $w_0,w_1,...,w_{n+1}$ of eBDDs such that $w_0=w$; $[\![ {w_{i+1}} ]\!]=\delta _{x_{n-i}}[\![ {w_{i}} ]\!]$ for every $0 \le i \le \ell (w)-1$; and $w_{n+1}$ is a BDD. Interpreted as sequence of eBDDs, Fig. 5 shows a run of this algorithm.

Notation. Given an eBDD w and eBDDs u, v such that $\ell (u) \ge \ell (v)$, we let w[u/v] denote the result of replacing u by v in w. For an eBDD $w=\left\langle x_i,w_0,w_1\right\rangle$ and $b\in \{0,1\}$ we define $\pi _{[{x_i:=b}]}w:=w_b$, and for $j>i$ we set $\pi _{[{x_j:=b}]}w:=w$. (Note that $[\![ {\pi _{[{x_j:=b}]}w} ]\!]=\pi _{[{x_j:=b}]}[\![ {w} ]\!]$ holds for any j where it is defined.)

Table 1. On the left: Algorithm computing eBDDs for the sequence $[\![ {w} ]\!]$, $\delta _{x_{n}} [\![ {w} ]\!]$, $\delta _{x_{n-1}} \delta _{x_{n}} [\![ {w} ]\!]$, $\ldots$, $\delta _{x_1} \cdots \delta _{x_{n}} [\![ {w} ]\!]$ of polynomials. On the right: Recursive algorithm to evaluate the polynomial represented by an eBDD at a given partial assignment. P(w) is a mapping used to memoize the polynomials returned by recursive calls.

Proposition 4

Let $\psi _1,\psi _2$ denote CPs and $u_1,u_2$ BDDs with $[\![ {u_i} ]\!]=[\![ {\psi _i} ]\!]$, $i\in \{1,2\}$. Let $w:=\left\langle u_1\circledast u_2\right\rangle$ denote an eBDD. Then $\textsc {ComputeEBDD}(w)$ satisfies $[\![ {w_0} ]\!]=[\![ {\psi _1\circledast \psi _2} ]\!]$ and $[\![ {w_{i+1}} ]\!]=\delta _{x_{n-i}}[\![ {w_{i}} ]\!]$ for every $0 \le i \le n-1$; moreover, $w_n$ is a BDD with $w_n={\text {Apply}}_\circledast (u_1,u_2)$. Finally, the algorithm runs in time $\mathcal {O}(T)$, where $T\in \mathcal {O}(\mathopen |u_1\mathclose |\cdot \mathopen |u_2\mathclose |)$ is the time taken by ${\text {Apply}}_\circledast (u_1,u_2)$.

Evaluating Polynomials Represented as eBDDs. Recall that Prover must evaluate expressions of the form ${\mathrm {\Pi }}_{{\sigma }}[\![ {\psi } ]\!]$ for some CPD $\psi$, where $\sigma$ assigns values to all variables of $\psi$ except for possibly one. We give an algorithm to evaluate arbitrary expressions ${\mathrm {\Pi }}_{{\sigma }}[\![ {w} ]\!]$, where w is an eBDD, and show that if there is at most one free variable then the algorithm takes linear time in the size of $\psi$. The algorithm is shown on the right of Table 1. It has the standard structure of BDD procedures: It recurs on the structure of the eBDD, memoizing the result of recursive calls so that the algorithm is called at most once with a given input.

Proposition 5

Let w denote an eBDD, $\sigma : X\rightarrow \mathbb {F}$ a partial assignment, and k the number of variables assigned by $\sigma$. Then EvaluateEBDD evaluates the polynomial ${\mathrm {\Pi }}_{{\sigma }}[\![ {w} ]\!]$ in time $\mathcal {O}\big (\!{\text {poly}}(2^{n-k})\cdot \mathopen |w\mathclose |\big )$.

5.2 Efficient Certification

In the CPCertify algorithm, Prover must (a) compute polynomials for all nodes of the CPD, and (b) evaluate them on assignments chosen by Verifier. In the last section we have seen that ComputeEBDD (for binary operations of the CP), combined with standard BDD algorithms (for all other operations), yields eBDDs representing all these polynomials—at no additional overhead, compared to a BDD-based implementation. This covers part (a). Regarding (b), recall that all polynomials computed in (a) have at most one variable. Therefore, using EvaluateEBDD we can evaluate a polynomial in linear time in the size of the eBDD representing it.

The Verifier CPCertify is implemented in a straightforward manner. As the algorithm runs in polynomial size w.r.t. the CP (and not the computed BDDs, which may be exponentially larger), incurring overhead is less of a concern.

Theorem 1

(Main Result). If BDDSolver solves an instance $\varphi$ of #CP with n variables in time T, with $T>n\mathopen |\varphi \mathclose |$, then

• (a) Prover computes eBDDs for all nodes of ${\text {conv}}(\varphi )$ in time $\mathcal {O}(T)$,

• (b) Prover responds to Verifier’s challenges in time $\mathcal {O}(nT)$, and

• (c) Verifier executes CPCertify in time $\mathcal {O}(n^2\mathopen |\varphi \mathclose |)$, with failure probability at most $4n\mathopen |\varphi \mathclose |/\mathopen |\mathbb {F}\mathclose |$.

As presented above, EvaluateEBDD incurs a factor-of-n overhead, as every node of the CPD must be evaluated. In our implementation, we use a caching strategy to reduce the complexity of Theorem 1(b) to $\mathcal {O}(T)$.

Note that the bounds above assume a uniform cost model. In particular, operations on BDD nodes and finite field arithmetic are assumed to be $\mathcal {O}(1)$. This is a reasonable assumption, as for a constant failure probability $\log \,\mathopen |\mathbb {F}\mathclose |\approx \log n$. Hence the finite field remains small. (It is possible to verify the number of assignments even if it exceeds $\mathopen |\mathbb {F}\mathclose |$, see below.)

5.3 Implementation Concerns

We list a number of points that are not described in detail in this paper, but need to be considered for an efficient implementation.

Finite Field Arithmetic. It is not necessary to use large finite fields. In particular, one can avoid the overhead of arbitrarily sized integers. For our implementation we fix the finite field $\mathbb {F}:=\mathbb {Z}_p$, with $p = 2^{61} -1$ (the largest Mersenne prime to fit in 64 bits).

Incremental eBDD Representation. Algorithm ComputeEBDD computes a sequence of eBDDs. These must not be stored explicitly, otherwise one incurs a space-overhead. Instead, we only store the last eBDD as well as the differences between each subsequent element of the sequence. To evaluate the eBDDs, we then revert to a previous state by applying the differences appropriately.

Evaluation Order. It simplifies the implementation if Prover only needs to evaluate nodes of the CPD in some (fixed) topological order. CPCertify can easily be adapted to guarantee this, by picking the next node appropriately in each iteration, and by evaluating only one child of a binary operator $\psi _1\circledast \psi _2$. The value of the other child can then be derived by solving a linear equation.

Efficient Evaluation. As stated in Theorem 1, using EvaluateEBDD Prover needs $\varOmega (nT)$ time to respond to Verifier’s challenges. In our implementation we instead use a caching strategy that reduces this time to $\mathcal {O}(T)$. Essentially, we exploit the special structure of ${\text {conv}}(\varphi )$: Verifier sends a sequence of challenges ${\mathrm {\Pi }}_{{\sigma _0}}\delta _{x_1}...\delta _{x_n}w, {\mathrm {\Pi }}_{{\sigma _1}}\delta _{x_2}...\delta _{x_n}w, ..., {\mathrm {\Pi }}_{{\sigma _n}}w$, where assignments $\sigma _i$ and $\sigma _{i+1}$ differ only in variables $x_i$ and $x_{i+1}$. The corresponding eBDDs likewise change only at levels i and $i+1$. We cache the linear coefficients of eBDD nodes that contribute to the arithmetisation of the root top-down, and the arithmetised values of nodes bottom up. As a result, only levels $i,i+1$ need to be updated.

Large Numbers of Assignments. If the number of satisfying assignments of a CP exceeds $\mathopen |\mathbb {F}\mathclose |$, Verifier would not be able to verify the count accurately. Instead of choosing $\mathopen |\mathbb {F}\mathclose |\ge 2^n$, which incurs a significant overhead, Verifier can query the precise number of assignments, and then choose $\mathopen |\mathbb {F}\mathclose |$ randomly. This introduces another possibility of failure, but (roughly speaking) it suffices to double $\log \,\mathopen |\mathbb {F}\mathclose |$ for the additional failure probability to match the existing one. Our implementation does not currently support this technique.

6 Evaluation

We have implemented an eBDD library, blic (BDD Library with Interactive Certification)⁴, that is a stand-in replacement for BDDs but additionally performs the role of Prover in the CPCertify protocol. We have also implemented a client that executes the protocol as Verifier. The eBDD library is about 900 lines of C++ code and the CPCertify protocol is about 400 lines. We have built a prototype certifying QBF solver in blic, totalling about 2600 lines of code. We aim to answer the following questions in our evaluation:

RQ1. :

Is a QBF solver with CPCertify-based certification competitive? If so, how high is the overhead of implementing CPCertify on top of the BDD operations?

RQ2. :

What is the amount of communication for Prover and Verifier in executing the CPCertify protocol, what is the time requirement for Verifier, and how do these numbers compare to proof sizes and proof checking times for certificates based on resolution and other proof systems?

RQ1: Performance of blic. We compare blic with CAQE, DepQBF, and PGBDDQ, three state-of-the-art QBF solvers. CAQE [10, 29] does not provide any certificates in its most recent version. DepQBF [12, 19] is a certifying QBF solver. PGBDDQ [7, 25] is an independent implementation of a BDD-based QBF solver. Both DepQBF and PGBDDQ provide specialised checkers for their certificates, though PGBDDQ can also proofs in standard QRAT format. Note that PGBDDQ is written in Python and generates proofs in an ASCII-based format, incurring overhead compared to the other tools.

Fig. 6.

(a) Time taken on instances (dashed lines are $y=100x$ and $y=0.01x$), (b) Cost of generating a certificate over computing the solution, (c) Time to verify the certificate, (d) Size of certificates

We take 172 QBF instances (all unsatisfiable) from the Crafted Instances track of the QBF Evaluation 2022.⁵ The Prenex CNF track of the QBF competition is not evaluated here. It features instances with a large number of variables. BDD-based solvers perform poorly under these circumstances without additional optimisations. Our overall goal is not to propose a new approach for solving QBF, but rather to certify a BDD-based approach, so we wanted to focus on cases where the existing BDD-based approaches are practical.

We ran each benchmark with a 10 min timeout; all tools other than CAQE were run with certificate production. All times were obtained on a machine with an Intel Xeon E7-8857 CPU and 1.58 TiB RAM⁶ running Linux. See the full version of the paper [11] for a detailed description. blic solved 96 out of 172 benchmarks, CAQE solved 98, DepQBF solved 87, and PGBDDQ solved 91. Figure 6(a) shows the run times of blic compared to the other tools. The plot indicates that blic is competitive on these instances, with a few cases, mostly from the Lonsing family of benchmarks, where blic is slower than DepQBF by an order of magnitude. Figure 6(b) shows the overhead of certification: for each benchmark (that finishes within a 10min timeout), we plot the ratio of the time to compute the answer to the time it takes to run Prover in CPCertify. The dotted regression line shows CPCertify has a 2.8$\times$ overhead over computing BDDs. For this set of examples, the error probability never exceeds $10^{-8.9}$ ($10^{-11.6}$ when Lonsing examples are excluded); running the verifier k times reduces it to $10^{-8.9k}$.

Table 2. Comparison of certificate generation, bytes exchanged between prover and verifier, and time taken to verify the certificate on a set of QBF benchmarks from [7]. “Solve time” is time taken to solve the instance and to generate a certificate (seconds), “Certificate” is the size of proof encoding for PGBDDQ, and bytes exchanged by CPCertify for blic, and “Verifier time” is time to verify the certificate (Verifier’s run time for blic and time taken by qchecker).

RQ2: Communication Cost of Certification and Verifier Time. We explore RQ2 by comparing the number of bytes exchanged between Prover and Verifier and the time needed for Verifier to execute CPCertify with the number of bytes in an QBF proof and the time required to verify the proof produced by DepQBF and PGBDDQ, for which we use QRPcheck [24, 26] and qchecker [7, 25], respectively. Note that the latter is written in Python.

We show that the overhead of certification is low. Figure 6(c) shows the run time of Verifier—this is generally negligible for blic, except for the Lonsing and KBKF families, which have a large number of variables, but very small BDDs. Figure 6(d) shows the total number of bytes exchanged between Prover and Verifier in blic against the size of the proofs generated by PGBDDQ and DepQBF. For large instances, the number of bytes exchanged in blic is significantly smaller than the size of the proofs. The exception are again the Lonsing and KBKNF families of instances. For both plots, the dotted line results from a log-linear regression.

In addition to the Crafted Instances, we compare against PGBDDQ on a challenging family of benchmarks used in the PGBDDQ paper (matching the parameters of [7, Table 3]); these are QBF encodings of a linear domino placing game.⁷ Our results are summarised in Table 2. The upper bound on Verifier error is $10^{-9.22}$. We show that blic outperforms PGBDDQ both in overall cost of computing the answer and the certificates as well as in the number of bytes communicated and the time used by Verifier.

Our results indicate that giving up absolute certainty through interactive protocols can lead to an order of magnitude smaller communication cost and several orders of magnitude smaller checking costs for the verifier.

7 Conclusion

We have presented a solver that combines BDDs with an interactive protocol. blic can be seen as a self-certifying BDD library able to certify the correctness of arbitrary sequences of BDD operations. In order to trust the result, a user must only trust the verifier (a straightforward program that poses challenges to the prover). We have shown that blic (including certification time) is competitive with other solvers, and Verifier’s time and error probabilities are negligible.

Our results show that $\textsf {IP}=\textsf {PSPACE}$ can become an important result not only in theory but also in the practice of automatic verification. From this perspective, our paper is a first step towards practical certification based on interactive protocols. While we have focused on BDDs, we can ask the more general question: which practical automated reasoning algorithms can be made efficiently certifying? For example, whether there is an interactive protocol and an efficient certifying version of modern SAT solving algorithms is an interesting open challenge.