A Flexible Toolchain for Symbolic Rabin Games under Fair and Stochastic Uncertainties

Abstract

We present a flexible and efficient toolchain to symbolically solve (standard) Rabin games, fair-adversarial Rabin games, and -player Rabin games. To our best knowledge, our tools are the first ones to be able to solve these problems. Furthermore, using these flexible game solvers as a back-end, we implemented a tool for computing correct-by-construction controllers for stochastic dynamical systems under LTL specifications. Our implementations use the recent theoretical result that all of these games can be solved using the same symbolic fixpoint algorithm but utilizing different, domain specific calculations of the involved predecessor operators. The main feature of our toolchain is the utilization of two programming abstractions: one to separate the symbolic fixpoint computations from the predecessor calculations, and another one to allow the integration of different BDD libraries as back-ends. In particular, we employ a multi-threaded execution of the fixpoint algorithm by using the multi-threaded BDD library Sylvan, which leads to enormous computational savings.

Authors ordered alphabetically. R. Majumdar and A.-K. Schmuck are partially supported by DFG project 389792660 TRR 248-CPEC. A.-K. Schmuck is additionally funded through DFG project (SCHM 3541/1-1). K. Mallik is supported by the ERC project ERC-2020-AdG 101020093. M. Rychlicki is supported by the EPSRC project EP/V00252X/1. S. Soudjani is supported by the following projects: EPSRC EP/V043676/1, EIC 101070802, and ERC 101089047.

1 Introduction

Piterman and Pnueli [17] derived the currently best known symbolic algorithm for solving two-player Rabin games over finite graphs with a theoretical complexity of $O(n^{k+1}k!)$ in time and space, where n is the number of states and k is the number of pairs in the winning condition. This work did not provide an implementation. In a series of papers [3, 4, 15, 16], Mallik et al. showed that this symbolic algorithm can be extended to solve different automated design questions for reactive hardware, software, and cyber-physical systems under fair or stochastic uncertainties. The main contribution of their work is to show that these extensions only require a very mild syntactic change of the Piterman-Pnueli fixed-point algorithm (with very little effect on its overall complexity) and domain-specific realizations of two types of predecessor operators used therein.

Using this insight, we present a toolchain for the efficient symbolic solution of different extensions of Rabin games. We have created three inter-connected libraries for solving different parts of the problem from different levels of abstraction. The first library, called Genie, offers a set of virtual classes to implement the fixpoint algorithm—abstractly, leaving open (i.e. virtual) the predecessor computation. Alongside, we created two other libraries, called FairSyn and Mascot-SDS, where FairSyn solves fair-adversarial [4] and -player Rabin games [3], while Mascot-SDS solves abstraction-based control problems [15, 16]. FairSyn and Mascot-SDS use the optimized fixpoint computation provided by Genie, with domain specific implementations of the predecessor operations.

The flexibility of our toolchain comes from two different programming abstractions in Genie. Firstly, Genie offers multiple high-level optimizations for solving the Rabin fixpoint, such as parallel execution (requires a thread-safe BDD library like Sylvan) and an acceleration technique [13], while abstracting away from the low-level implementations of the predecessor functions. As a result, any synthesis problem using the core Rabin fixpoint of Genie can use the optimizations without spending any extra implementation effort. We used these optimizations from FairSyn and Mascot-SDS, and achieved remarkable computational savings. Secondly, Genie offers easy portability of codes from one BDD library to another, which is important as different BDD libraries have different pros and cons, and the choice of the best library depends on the needs. We empirically showed how switching between the two BDD libraries Sylvan and CUDD impacts the performance of FairSyn and CUDD: overall, the Sylvan-based experiments were significantly faster, whereas the CUDD-based experiments consumed considerably lower amount of memory. Using the combined power of multi-threaded BDD operations using Sylvan and the optimizations offered by Genie, Mascot-SDS was between one and three orders of magnitude faster than the state-of-the-art tool in our experiments.

Comparison with Existing Tools: We are not aware of any available tool to directly solve (normal or stochastic) Rabin games symbolically. However, it is well-known how to translate stochastic Rabin games into (standard) Rabin games [5], and Rabin games into parity games, for which efficient solvers exist, e.g. oink [9]. Yet, efficient solutions of stochastic Rabin games via parity games are difficult to obtain, because: (i) the translation from a stochastic Rabin game to a Rabin game involves a quadratic blow-up, and the translation from a Rabin game to a parity game results in an exponential blow-up in the size of the game, (ii) symbolic fixpoint computations become cumbersome very fast for parity games, as the number of vertices and/or colors in the game graph increases, leading to high computation times in practice, and (iii) the only known algorithms capable of handling fair and stochastic uncertainties efficiently are all symbolic in nature, while most of the efficient parity game solvers are non-symbolic. Additionally, unlike the Rabin fixpoint, the nesting of the parity fixpoint does not enable parallel execution.

While it is well known that for normal parity games, computational tractability can be achieved by different non-symbolic algorithms, such as Zielonka’s algorithm [22], tangle learning [8] or strategy-improvement [19], implemented in oink [9], it is currently unclear if and how these algorithms allow for the efficient handling of fair or stochastic uncertainties. We are therefore unable to compare our toolchain to the translational workflow via parity games in a fair manner.

In the area of temporal logic control of stochastic systems, Mascot-SDS has two powerful features: (a) it can handle synthesis for the rich class of omega-regular (infinite-horizon) specifications, and (b) it provides both over- and under-approximations of the solution, thus enabling a quantitative refinement loop for improving the precision of the approximation. The features of Mascot-SDS is compared with other tools in the stochastic category of the recent ARCH competition (see the report [1] for the list of participating tools). As concluded in the report of the competition, other state-of-the-art tools in stochastic category are either limited to a fragment of $\omega$-regular specifications or do not provide any indication of the quality of the involved approximations. The only tool [10] that supports $\omega$-regular specifications uses a different alternate non-symbolic approach, against which Mascot-SDS fares significantly well in our experiments (see Sect. 4.2). Even if we leave stochasticity aside, our tool implements a new and orthogonal heuristic for multi-threaded computation of Rabin fixpoints, which is not considered by other controller synthesis tools [11].

2 Theoretical Background

We briefly state the synthesis problems our toolchain is solving. We follow the same (standard) notation for two-player game graphs, winning regions, strategies and $\mu$-calculus formulas, as in [4].

2.1 Solving Rabin Games Symbolically

Given a game graph $G=\left( V,V_0,V_1,E\right)$, a Rabin game is specified using a set of Rabin pairs $\mathcal {R}=\left\{ \left( Q_1,R_1,\right) ,\ldots ,\left( Q_k,R_k\right) \right\}$, with $Q_i,R_i\subseteq V$ for every $i\in [1;k]$, and $\varphi {:}{=}\bigvee _{i\in [1;k]} (\Diamond \Box \lnot R_i \wedge \Box \Diamond Q_i)$ being the Rabin acceptance condition. Piterman and Pnueli [17] showed that the winning region of a Rabin game can be computed using the $\mu$-calculus expression given in (2), where the set transformers $Cpre :2^{V} \rightarrow 2^{V}$ and $Apre :2^{V}\times 2^{V} \rightarrow 2^{V}$ are defined for every $S,T\subseteq V$ as:

$$\begin{aligned} Cpre (S) {:}{=}&\left\{ v\in V_0\mid \exists v'\in S\;.\; (v,v')\in E\right\} \nonumber \\&\quad \qquad \qquad \cup \left\{ v\in V_1\mid \forall v'\in V\;.\; (v,v')\in E \implies v'\in S\right\} ,\end{aligned}$$

(1a)

$$\begin{aligned} Apre (S,T) {:}{=}&Cpre (T). \end{aligned}$$

(1b)

Fair-Adversarial Rabin Games. A Rabin game is called fair-adversarial when there is an additional fairness assumption on a set of edges originating from $Player ~1$ vertices in G. Let $E^\ell \subseteq E \cap ( V_1\times V)$ be a given set of edges, called the live edges. Given $E^\ell$ and a Rabin winning condition $\varphi$, we say that $Player ~0$ wins the fair-adversarial Rabin game from a vertex v if $Player ~0$ wins the (normal) game for the modified winning condition $\varphi ^\ell {:}{=}\left( \bigwedge _{e=(v,v')\in E^\ell } (\Box \Diamond v \implies \Box \Diamond e) \right) \implies \varphi$. Based on the results of Banerjee et al. [4], fair-adversarial Rabin games can be solved via (2), by defining for every $S,T\subseteq V$

$$\begin{aligned} Cpre (S)&{:}{=}\left\{ v\in V_0\mid \exists v'\in S\;.\; (v,v')\in E\right\} \nonumber \\&\qquad \qquad \qquad \cup \left\{ v\in V_1\mid \forall v'\in V\;.\; (v,v')\in E \implies v'\in S\right\} ,\end{aligned}$$

(3a)

$$\begin{aligned} Apre (S,T)&{:}{=} Cpre (T)\cup \left\{ v\in Cpre (S)\cap V_1\mid \exists v'\in T\;.\; (v,v')\in E^\ell \right\} . \end{aligned}$$

(3b)

We see that (3) coincides with (1) if $E^\ell$ is empty.

-Player Rabin Games. A -player game is played on a game graph $\left( V,V_0,V_1,V_r,E\right)$, and the only difference from a 2-player game graph is the additional set of vertices $V_r$ which are called the random vertices. The sets $V_1$, $V_2$, and $V_r$ partition V. Based on the results of [3] -Player rabin games can be solved via (2) by defining for all $S,T\subseteq V$

$$\begin{aligned} Cpre (S)&{:}{=}\left\{ v\in V_0\mid \exists v'\in S\;.\; (v,v')\in E\right\} \nonumber \\&\quad \qquad \qquad \cup \left\{ v\in V_1\cup V_r\mid \forall v'\in V\;.\; (v,v')\in E \Rightarrow v'\in S\right\} ,\end{aligned}$$

(4a)

$$\begin{aligned} Apre (S,T)&{:}{=} Cpre (T)\cup \left\{ v\in Cpre (S)\cap V_r\mid \exists v'\in T\;.\; (v,v')\in E\right\} . \end{aligned}$$

(4b)

2.2 Computing Symbolic Controllers for Stochastic Dynamical Systems

A discrete-time stochastic dynamical system S is represented using a tuple $\left( X,U,W,f\right)$, where $X\subseteq \mathbb {R}^n$ is a continuous state space, U is a finite set of control inputs, $W \subset \mathbb {R}^n$ is a bounded set of disturbances, and $f:X\times U\rightarrow X$ is the nominal dynamics. If $x^k\in X$ and $u^k\in U$ are the state and control input of S at some time $k\in \mathbb {N}$, then the state at the next time step is given by:

$$\begin{aligned} x^{k+1} = f(x^k,u^k) + w^k, \end{aligned}$$

(5)

where $w^k$ is the disturbance at time k which is sampled from W using some (possibly unknown) distribution. Without loss of generality we assume that W is centered around the origin, which can be easily achieved by shifting f if needed. A path of S originating at $x^0\in X$ is an infinite sequence of states $x^0x^1\ldots$ for a given infinite sequence of control inputs $u^0u^1\ldots$, such that (5) is satisfied.

Let $\varphi$ be a given Rabin specification—called the control objective—defined using a finite set of predicates over X. For every controller $C:X\rightarrow U$, the domain of C, written $Dom (C)$, is the set of states from where the property $\varphi$ can be satisfied with probability 1. For a fixed $\varphi$, a controller $\hat{C}$ is called optimal if $Dom (\hat{C})$ contains the domain of every other controller C. The problem of computing such an optimal controller for the system in (5) is in general undecidable. Following [15], we compute an approximate solution instead.

This approximate solution is obtained by a discretization of the state space. For this, we assume that the state space X is a closed and bounded subset of the n-dimensional Euclidean space $\mathbb {R}^n$ for some $n>0$, and use the notation [[a, b)) to denote the set $\prod _{i\in [1; n]} [a_i,b_i)$. Now, consider a grid-based discretization $\widehat{X}$ of X, where $\widehat{X} = \left\{ [\![ a,b )\!) \mid a,b\in \mathbb {R}^n=X\right\}$. One of the key ingredients of our abstraction process is a function $\widehat{f}$ providing hyper-rectangular over-approximation of the one-step reachable set of the nominal dynamics f of the system S: for every grid element $\widehat{x}\in \widehat{X}$, we have $\widehat{f}(\widehat{x},u) = [\![ a',b')\!)\supseteq \left\{ x'\in X\mid \exists x\in \widehat{x}\;.\; x'=f(x,u)\right\}$. The function $\widehat{f}$ is known to be available for a wide class of commonly used forms of the function f, and in our implementation we assumed that f is mixed-monotone and $\widehat{f}$ is the so-called decomposition function (see standard literature for details [7]).

Given the over-approximation of the nominal dynamics obtained through $\widehat{f}$, we define, respectively, the over- and the under-approximation of the perturbed dynamics as $\overline{g}(\widehat{x},u) {:}{=}W\oplus \widehat{f}(\widehat{x},u)$ and $\underline{g}(\widehat{x},u) {:}{=}W\ominus (-\widehat{f}(\widehat{x},u))$, where $\oplus$ and $\ominus$ respectively denote the Minkowski sum and the Minkowski difference. Next, we transfer $\overline{g}$ and $\underline{g}$ to the abstract state space $\widehat{X}$ to obtain, respectively, the over- and the under-approximation in terms of the abstract transition function¹, i.e., $\overline{h}(\widehat{x},u) {:}{=}\left\{ \widehat{x}'\in \widehat{X}\mid \overline{g}(\widehat{x},u)\cap \widehat{x}'\ne \emptyset \right\}$ and $\underline{h}(\widehat{x},u) {:}{=}\left\{ \widehat{x}'\in \widehat{X}\mid \underline{g}(\widehat{x},u)\cap \widehat{x}' \ne \emptyset \right\}$. With $\overline{h}$ and $\underline{h}$ available, it was shown by Majumdar et al. [16] that the over-approximation of the optimal controller can be solved by using the fixpoint algorithm in (2), where the predecessor operators are defined for every $S,T\subseteq \widehat{X}$ as

$$\begin{aligned} Cpre (S)&{:}{=}\left\{ \widehat{x}\in \widehat{X}\mid \exists u\in U\;.\; \overline{h}(\widehat{x},u)\subseteq S\right\} \end{aligned}$$

(6a)

$$\begin{aligned} Apre (S,T)&{:}{=}\left\{ \widehat{x}\in \widehat{X}\mid \exists u\in U\;.\; \overline{h}(\widehat{x},u)\subseteq S\wedge \underline{h}(\widehat{x},u)\cap T\ne \emptyset \right\} . \end{aligned}$$

(6b)

3 Implementation Details

We develop three interconnected tools, Genie, FairSyn, and Mascot-SDS, which work in close harmony to implement efficient solvers for the solution of (2) with pre-operators defined via (3), (4) and (6), respectively. The tools use binary decision diagrams (BDD) to symbolically manipulate sets of vertices/states of the underlying system, and to manage the BDDs, we offer the flexibility to choose between two of the well-known existing BDD libraries, namely CUDD [20] and Sylvan [21]. The two libraries have their own merits: while CUDD has significantly lower memory footprint, Sylvan offers superior computation speed through multi-threaded BDD operations. Thus, the optimal choice of the library depends on the size of the problem, the computational time limit, and the memory budget, and through our implementation it is possible to choose one or the other by, in some cases, changing only a single line of code and, in the other cases, changing the value of just one flag. Moreover, we expect that integrating other BDD libraries having the same basic BDD operations in our tools will be easy and seamless—thanks to the programming abstraction offered by Genie. Such extensions will possibly bring more diverse set of computational strengths for solving the fundamental synthesis problems that we address.

Fig. 1.

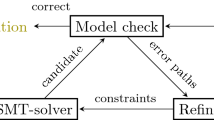
A schematic diagram of interaction among the three tools. Each block represents one class in the respective tool, and an arrow from class A to class B denotes that B depends on A. The dependency within each tool is shown using solid arrows, while the dependencies of Mascot-SDS and FairSyn on Genie is shown using dashed arrows.

The tools are primarily written using C++, with some small python scripts implementing parts of visualizations of outputs. The main classes of the three tools and their interactions are depicted in Fig. 1. We briefly describe the core functionalities of the tools in the following.

3.1 Genie

Genie implements the fixpoint algorithm (2) in the class BaseFixpoint through two layers of abstraction. One abstraction is through the virtual definitions of the $Cpre$ and $Apre$ operators, whose concrete implementations are provided in the front-end synthesis tools (in our case FairSyn and Mascot-SDS). Using this abstraction, we implemented two different optimizations for the efficient iterative computation of the Rabin fixpoint in (2)—independently from the actual implementations of the $Apre$ and $Cpre$ operators. The first optimization is a multi-threaded computation of the Rabin fixpoint, exploiting the fixpoint’s inherent parallel structure due to the independence among different sequences of $(p_1,p_2,\ldots )$ used to compute $\bigcup _{j=0}^k\mathcal {C}_{p_j}$. The second optimization is an accelerated computation of the Rabin fixpoint, achieved through bookkeeping of intermediate values of the BDD variables. The core of the acceleration procedure for general $\mu$-calculus fixpoints was proposed by Long et al. [13], and the details specific to the fixpoint in (2) can be found in the paper by Banerjee et al. [4].

The other abstraction in Genie is the set of virtually defined low-level BDD operations in the auxiliary class BaseUBDD, which enable us to easily switch between different off-the-shelf BDD libraries. The virtual BDD operations in BaseUBDD are concretely realized in the classes CuddUBDD and SylvanUBDD, which work as interfaces between, respectively, the CUDD and the Sylvan BDD libraries. Support for additional BDD libraries can be easily built by creating new interface classes. More details on the functionalities of Genie can be found in the longer version of this paper [14].

3.2 FairSyn

The core of FairSyn is written as a header-only library, which offers the infrastructure to solve (2) with pre-operators defined via (3) and (4). The main component of FairSyn is the class Fixpoint, which derives from the class BaseFixpoint from Genie, and implements the concrete definitions of $Cpre$ and $Apre$ in (3) and (4).

How to Use: For computing the winning region and the winning strategy in a fair-adversarial Rabin game (resp. a -player Rabin game) using FairSyn, one needs to write a program to create the game as a Fixpoint object. One possible way of constructing a Fixpoint object is through a synchronous product of a game graph (an object of class Arena) and a specification Rabin automaton (an object of class RabinAutomaton) with an input alphabet of sets of nodes of the Arena object. Following is a snippet:

where vars is a (possibly initially empty) set of integers which will contain the set of newly created BDD variables, nodes, sys_nodes, and env_nodes are, respectively, vectors of indices of various types of vertices, edges and live_edges are, respectively, vectors of the respective types of edges, inp_alphabet is a std::map object that maps input symbols of the Rabin automaton to the respective BDDs representing sets of nodes in the Arena, and filename is the name of the file in which the Rabin automaton is stored (using the standard HOA format [2]). The game is solved by calling Fp.Rabin, a member function of the Genie::BaseFixpoint class (see Sect. 3.1).

3.3 Mascot-SDS

The core of Mascot-SDS is also written as a header-only library. It is built on top of the well-known tool called SCOTS [18], with several classes of Mascot-SDS still retaining their original identities from SCOTS, owing to the close similarity of the basic uniform grid-based abstraction used in both tools. The main difference between the two tools is that Mascot-SDS synthesizes controllers for stochastic systems, while SCOTS synthesizes controllers for only non-stochastic systems.

The two main classes of Mascot-SDS are called SymbolicSet and SymbolicModel, which respectively model the abstract spaces obtained through uniform grid-based discretizations (like $\widehat{X}$ in Sect. 2.2) and the abstract transition relations ($\overline{h}$ and $\underline{h}$ in Sect. 2.2). The abstract transition relations are computed using an auxiliary class called SymbolicModelMonotonic (not shown in Fig. 1). Notice that we offer the flexibility to use both CUDD and Sylvan while creating objects from SymbolicSet and SymbolicModel. A Fixpoint object is a child of the class BaseFixpoint from Genie, which is created by taking a synchronous product between a SymbolicModel object and a RabinAutomaton object specifying the control objective given as user input. The class Fixpoint implements the concrete definitions of the $Cpre$ and $Apre$ operator according to (6).

How to Use: For ease of use, we have written a pair of tools called Synthesize and Simulate using the library of Mascot-SDS. Synthesize synthesizes controllers for stochastic dynamical systems whose nominal dynamics is mixed-monotone, and Simulate visualizes simulated closed-loop trajectories using the synthesized controller. The inputs to Synthesize include the dynamic model of the system and the control objective; the latter can be specified either in LTL or using a Rabin automaton. To use Synthesize, simply use the following syntax:

where the $\texttt {<input.cfg>}$ is an input configuration file containing all the inputs, and the $\texttt {<sylvan/cudd flag>}$ is either 1 or 0 depending on whether the parallel version using Sylvan is to be run or the sequential version using CUDD.

Some of the main ingredients in the input.cfg file are: (a) the description of the dynamical system’s variable spaces (like state space, input space, etc.) including their discretization parameters, (b) the file where the decomposition function of the nominal dynamics of the system is stored, (c) the absolute value of maximum disturbance, and (d) the specification either as an LTL formula or as the filename where a Rabin automaton is stored (in HOA format [2]). The decomposition function is required to be given as a C-compatible header file so that Synthesize can link to (use) this function at runtime (see the mascot-sds/examples/ directory for examples). When the specification is given as a Rabin automaton (over a labeling alphabet of the system states), the automaton needs to be stored in a file in the HOA format. Alternatively, an LTL specification can be given, along with a mapping between the atomic predicates and the states of the system. In that case Synthesize uses Owl [12] to convert the LTL specification to a Rabin automaton.

The output of Synthesize is a folder called data that contains pieces of the controller encoded in BDDs and stored in binary files as well as various metadata information stored in text files. These files can be processed by Simulate to visualize simulated closed-loop trajectories of the system. The usage of Simulate is similar to Synthesize:

where the input.cfg file should, in this case, contain information that are required to simulate the closed-loop, like simulation time steps, the python script that will plot the state space predicates (see the examples), etc.

4 Examples

We present experimental results, showcasing practical usability of our tools and comparing performances with the state of the art. All the experiments were run on a computer with Intel Xeon E7-8857 v2 48 core processor and 1.5 TB RAM.

4.1 Synthesizing Code-Aware Resource Mangers Using FairSyn

We consider a case study introduced by Chatterjee et al. [6]. In this example, there are two bounded FIFO queues, namely the broadcast and output queues, which interact among each other and transmit and receive data packets through a common network. The two queues are implemented using separate threads running on a single CPU. For this multi-threaded program, we consider the problem of synthesizing a code-aware resource manager, whose task is to grant different threads accesses to different shared synchronization resources (mutexes and counting semaphores). The specification is deadlock freedom across all threads at all time while assuming a fair scheduler (scheduling every thread always eventually) and fair progress in every thread (i.e., taking every existing execution branch always eventually). The resource-manager is code-aware, and has knowledge about the require and release characteristics of all threads for different resources. This enables us to avoid deadlocks more effectively than the case when the resource-manager does not have access to the code. Chatterjee et al. [6] showed that the synthesis problem (of the resource manager) can be reduced to the problem of computing the winning strategy in a -player game, which we solved using FairSyn.

Table 1 compares the computational resources for the CUDD and Sylvan-based implementations of FairSyn; more details can be found in our earlier work [4]. It can be observed that the Sylvan-based implementation is significantly faster, although it consumes much more memory.

Table 1. Performance of FairSyn; code-aware resource management benchmark.

4.2 Synthesizing Controllers for Stochastic Dynamical Systems Using Mascot-SDS

We use Mascot-SDS to synthesize controllers for two different applications.

A Bistable Switch. First, we compare our tool’s performance against the state-of-the-art tool called StochasticSynthesis (abbr. SS) [10] on a benchmark example that was proposed by the authors of SS. In this example, there is a 2-dimensional nonlinear bistable switch that is perturbed with bounded stochastic noise. There are two synthesis problems with two different control objectives: one, a safety objective, and, two, a Rabin objective with two Rabin pairs. The model of the system and the control objectives can be found in the original paper [10].

The tool SS uses graph theoretic techniques to solve the controller synthesis problem, which is an alternative approach that is substantially different from our symbolic fixpoint based technique. In Table 2, we summarize the performance of Mascot-SDS powered by CUDD and Sylvan, alongside the performance of SS. Both Mascot-SDS and SS compute controllers whose domains under-approximate the optimal controller domains. The second column of Table 2 shows a measure of the approximation error. For every comparable approximation error bound, both versions of Mascot-SDS significantly outperformed SS, both time and memory-wise. In fact, Mascot-SDS with Sylvan was at least an order of magnitude faster in all instances. This is particularly astonishing, since SS uses a sophisticated lazy abstraction refinement technique, whereas Mascot-SDS uses a plain uniform abstraction which is typically computationally expensive. This shows the immense potential of our toolchain; we plan to extend Mascot-SDS with lazy gridding, an orthogonal optimization, in a future release to make further computational savings. For Mascot-SDS itself, as expected, Sylvan was significantly faster than CUDD. On the other hand, though Sylvan used less memory than CUDD in the simpler setups (the ones with more error), the memory requirement of Sylvan quickly grew and surpassed that of CUDD for the more complicated setup.

Table 2. Performance comparison between Mascot-SDS and StochasticSynthesis (abbreviated as SS) [10] on the bistable switch. Col. 1 shows the specifications and the respective numbers of Rabin pairs, Col. 2 shows the approximation error ranges (smaller error means more intense computation), Col. 3, 4, and 5 Col. 6, 7, and 8 compare the peak memory footprint (as measured using the “time” command) for Mascot-SDS with CUDD, Mascot-SDS with Sylvan, and SS respectively. “TO” stands for timeout (5 h of cutoff time).

Table-Serving Robot. We consider the controller synthesis problem for a table-serving robot that needs to satisfy the following specification: $\Box \Diamond kitchen \wedge \Box \lnot obtsacle \wedge \left( \Box \Diamond request \leftrightarrow \Box \Diamond table \right)$, where $table$, $kitchen$, $obstacle$, and $request$ are predicates over the state space. The robot itself is modeled as the discrete-time abstraction of the standard 3-dimensional Dubins vehicle [15] with an additional (i.e., 4th) dimension that records if a $request$, which is controlled by the environment, is pending. In Table 3, we summarize the computational resources, and, in Fig. 2, we show a simulated closed-loop trajectory that was plotted using our tool Simulate. We observe that Sylvan was much faster, but CUDD consumed much less memory.

Table 3. Performance of Mascot-SDS with CUDD and Sylvan for the table-serving robot experiment.

Fig. 2.

Closed-loop trajectories for 100 time steps with $kitchen$ (green), $table$ (blue), and $obstacle$ (black). (Color figure online)