Abstract
The results of earlier investigations of the range theory of probability are displayed in a new context: the kinetic theory of gases in physics. The Second Law of thermodynamics is considered as a statement of probability. Boltzmann’s mathematical investigations are used as a starting point in the theory of gases. The presuppositions of this probabilistic theory are outlined: probabilities are already measured in terms of ranges. This application of the theory of probability is not a new or immature hypothesis in physics. The present account contradicts the notion that states which are less probable will transition to states which are more probable. The most probable state of a gas at rest is really an extraordinary number of different states. This account is consonant with Maxwell’s distribution for the speeds of molecules in a gas at rest (in an adiabatic flask).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Cf. Chap. 7, Section 3 on the meaning of such explanations.
- 2.
Incidentally, it may be shown that modern attempts to base a theory of matter solely on contact forces (and in place of the atomic theory, to base it on an assumption about paths of motion through a frictionless fluid which permeates space evenly) lead to the same consequences.
- 3.
Here I note that strictly speaking, this premise involves a bit of fiction; we cannot “leave the gas to itself”, that is, we cannot isolate it from all external influence. Rather, the actual situation is that it is in an equilibrium of temperature with its container. However, it is expedient to cling to that fiction temporarily, since the theory of this ideal case must be treated on its own merits, and so we may consider the gas to be contained in an adiabatic flask against which molecules may rebound with no loss of force.
- 4.
For those unfamiliar with the subject, I believe that the import of this statement is most readily rendered intelligible if I allude to its specific consequences: for example, that with contact between a warmer body and a colder one, heat always transfers from the former to the latter, but never the reverse. That is, it never happens that the warmer body becomes even warmer and the colder one colder. Further, it never happens that the kinetic energy – which is disarrayed and takes the form of heat – can be transformed into some directed motion in the form of translation or rotation (for bodies of finite dimensionality), and so forth.
- 5.
Boltzmann, L. (1877). Bemerkungen über einige Probleme der mechanischen Wärme-Theorie. Wiener Sitzungsberichte der kaiserlichen Akademie der Wissenschaften, mathematische-naturwissenschaftliche Classe, 75(2), p. 67.
- 6.
If one bears in mind that within certain general conditions the normal state is that state which is most probable given the total absence of all exact knowledge, and that there really always is such a lack with respect to the determinants of the tiniest particles, then the confident expectation of a general and enduring approximation to the normal state may be expressed as follows: that everywhere within a finite number of dimensions, just that variety of behavior is to be expected, which we assume for the current states of the smallest particles. In fact, this proposition represents the final result of all investigations involving probability in the field of molecular physics.
- 7.
I count a state as determined “by the value r1 with range \( {\varDelta}_{r_1} \)” if the value in question falls between r1 and \( {r}_1+{\varDelta}_{r_1} \).
- 8.
So for example, in the Wiener Sitzungsberichte etc. vol. 63(2), p. 400: “a value of function f, which is not further altered by the collisions of molecules, and consequently represents at least a possible type of distribution for states of molecules …”; also vol. 78(2), p. 41 and in many other places. [Boltzmann, L. (1871). Über das Wärmegleichgewicht zwischen mehratomigen Gasmolekülen. Wiener Sitzungsberichte der kaiserlichen Akademie der Wissenschaften, mathematisch-naturwissenschaftliche Classe, 63(2), 397–418. See also Boltzmann, L. (1909). Wissenschaftliche Abhandlungen, 2. Band. Leipzig: Barth (F. Hasenöhrl). Reissued 1969 – New York: Chelsea.]
- 9.
The probabilities which are to be assigned to individual molecules would not be independent of one another, just insofar as the location of each one excluded the possibility that another would occupy a position within an exceedingly small element of volume. That would not affect the result established here concerning the postulate about the size of the range. More importantly, this independence of the state of each individual molecule does not hold in connection with the constancy of the total kinetic energy present. This circumstance implies that the representation which we obtain for the probability of any state is in fact not strict in a formal sense, since the probability f has been assigned to each molecule, and all those probabilities are treated as independent. At most, these probabilities would be valid given infinitely many molecules. Hence it is easy to see that for a finite number of molecules, and considering the convention about probability for the conservation of energy (as given for example by Boltzmann in the second part of his article contained in volume 58 of the Wiener Sitzungsberichten), this is derived in just such a way as necessitated by the interpretation given here. It is known that the same result obtains once the number of molecules becomes very large, and those results do not depart significantly from the results one obtains by neglecting their dependence. For this reason, I believed I ought to restrict myself to the much simpler formulation given above. [Boltzmann, L. (1868). Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten. Wiener Sitzungsberichte der kaiserlichen Akademie der Wissenschaften, mathematisch-naturwissenschaftliche Classe, 58, 517–560.]
- 10.
One can make the meaning of this calculation more intuitive in the following way. If a point-mass continues straightforward in uniform motion, we can gauge the probability that at a certain point in time it may be found in a unit of space v, and its direction of motion may be found within the solid angle Δ, by the integral ∬dv dΔ. Then this integral remains constant, if we concentrate on the totality of states to which it may transition at any possible time. Then this represents the size of an original range. One sees this most easily for infinitely small ranges which are determined by two plane sections dF1 and dF2 which are perpendicular to the direction of motion, and by such a range of directions of motion where it would be possible to determine the direction of each point of the element dF1 by each point of dF2. As one sees at first glance, at the beginning of the time period in question, the operational range is given by dF1 multiplied by the solid angle which dF2 appears to have from the perspective of dF1. At the end of the time period, it is given by dF2 multiplied by the solid angle which dF1 appears to have from dF2; these two products are equal to one another. Without the influence of external forces, the range measured in this way is not changed by progressive motion. In the same way, by the ideal law of elastic impact, it is not changed by reflection against a solid wall (i.e., equality of angle of incidence and angle of reflection, and unaltered speed). If on the other hand, two bodies of comparable masses collide, then the operational range does change, since the distribution of speed does too.
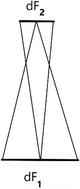
Then one may no longer make a satisfactory assignment of probability without considering speed; rather, the operational range must also span a certain range of speed. At first one might obtain values like ∭dν dΔ dc, where dc would be a derivative of speed. Let us call the ranges of two molecules specified in this way sa and \( {s}_a^{\prime } \) before the collision. After the collision let them be called sp und \( {s}_p^{\prime } \). Then further investigation shows that \( {s}_a\bullet {s}_a^{\prime } \) is not equal to \( {s}_p\bullet {s}_p^{\prime } \); rather these products vary in inverse proportion to the products of the kinetic energies before the collision, \( {c}_a^2\bullet {c}_a^{\prime^2} \) and after the collision, \( {c}_p^2\bullet {c}_p^{\prime^2} \). One of the requirements of the measurement of ranges – to respect originality – is then maintained in that one does not set the ranges of speeds to be proportional to the derivative dc, but rather proportional to that multiplied by a function f of speed, which is determined by the equation:
$$ {s}_a\bullet {s}_a^{\prime}\bullet f\left({c}_a\right)\bullet f\left({c}_a^{\prime}\right)={s}_p\bullet {s}_p^{\prime}\bullet f\left({c}_p\right)\bullet f\left({c}_p^{\prime}\right) $$or
$$ \frac{f\left({c}_a\right)\bullet f\left({c}_a^{\prime}\right)\ }{c_a^2\bullet {c}_a^{\prime^2}}=\frac{f\left({c}_p\right)\bullet f\left({c}_p^{\prime}\right)\ }{c_p^2\bullet {c}_p^{\prime^2}}. $$If we should call some operational ranges φ – which are ranges gauged by the magnitudes ∭dνdΔ f(c) dc – then it would always be that:
$$ {\varphi}_{(a)}\bullet {\varphi}_{(a)}^{\prime }={\varphi}_{(p)}\bullet {\varphi}_{(p)}^{\prime }. $$ - 11.
Boltzmann, L. (1878). Weitere Bemerkungen etc. Wiener Sitzungs-Berichte, 78(2), p. 44.
- 12.
By the way, the premise that was just advanced also leads to the conclusion that there could not be two different and continuous assignments of probability which satisfy the condition of constancy. That is, let us consider two infinitely small ranges s1 and s2, which represent correspondingly infinitely small and very closely neighbouring ranges, σ1 and σ2, at an earlier time. Then any assignment of probability must fulfill the condition that the probabilities attributed to both states s1 and s2 – let those probabilities be called φ(s1) and φ(s2) – must have the same ratio as σ1 to σ2. That ratio is uniquely determined, since σ1 and σ2 are extremely close as neighbours. Then it holds that: φ(s1) : φ(s2) = σ1 : σ2. And if ψ were to be a second probability function, then immediately the result follows that
$$ \varphi \left({s}_1\right):\varphi \left({s}_2\right)=\psi \left({s}_1\right):\psi \left({s}_2\right) $$or
$$ \frac{\varphi \left({s}_1\right)\ }{\psi \left({s}_1\right)} = \frac{\varphi \left({s}_2\right)\ }{\psi \left({s}_2\right)}, $$which means the two functions could only be distinguished by a constant factor. As is easy to see, whether continuity is here taken in its mathematical sense, or taken in the sense previously described (p. 51 in original; Chap. 3, Section 2), obviously will depend on the assumption one wants to make about the traceability of finitely different contemporary states to a few different earlier varieties of behavior (or for infinitely long periods of time, to infinitely few different earlier varieties). Here I restrict the postulate to the sense given previously, and hence once again I construe continuity in the non-mathematical sense.
- 13.
Boltzmann, L. (1878). Weitere Bemerkungen etc. Wiener Sitzungs-Berichte, 78(2), p. 45. [See also Boltzmann, L. (1909). Wissenschaftliche Abhandlungen, 2. Band. Leipzig: Barth (F. Hasenöhrl). Reissued 1969 – New York: Chelsea.]
- 14.
Boltzmann, L. (1880, 1881, 1881a). Zur Theorie der Gas-Reibung. Wiener Sitzungsberichte der kaiserlichen Akademie der Wissenschaften, 81(2), p. 117 and 84(2), pp. 40 & 1230.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Niall, K.K. (2023). Application of the Probability Calculus to Theoretical Physics. In: Johannes von Kries: Principles of the Probability Calculus. Studies in History and Philosophy of Science, vol 59. Springer, Cham. https://doi.org/10.1007/978-3-031-36506-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-36506-5_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-36505-8
Online ISBN: 978-3-031-36506-5
eBook Packages: HistoryHistory (R0)


