Keywords

1 Introduction

Microscopic self-propelled particles are naturally ubiquitous. Even a single drop of pond water may include thousands of tiny microbes swimming in fluids. Over the past two decades, researchers have extensively studied the dynamics of microswimmers [24] and artificially synthesized them using chemical and magnetic actuation [15]. Also, the microswimmers often produce structured and collective coherent behavior through non-local hydrodynamic interactions between individuals [9, 10, 33, 46]. The collective dynamics of hydrodynamically interacting active agents are called wet active matter, and the microswimmers are one of the major materials for computational and experimental research [3, 34].

The fluid dynamics around the microswimmer typically neglect inertia due to its microscopic size. Then, the fluid equations are linearized and simplified, while the swimmer problems usually contain moving and deforming boundaries. Resolving the hydrodynamic interactions is numerically expensive and a reduction of numerical costs are needed in modeling the collective dynamics of the microswimmers. A simplest model description of flow around a swimming cell is the Stokes dipole, called a pusher or puller, which depends on the direction of the flow obtained from a far-field extension of the flow around a microswimmer. Thus, the near-field hydrodynamics is not necessarily well captured, though such interactions are dominant in many collective dynamics. A prescribed flow model has been studied for active rods to prescribe the near-field flow [25, 32], and squirmers [22, 30, 31], whereas this excellent resolution requires extensive numerical resources.

Another approach to simplifying and coarse-graining the fluid flow is to use precise flow data. Ishimoto & Gaffney [19] used the data-driven coarse-graining representation of flow structure by superposition of regularised Stokeslets, based on digital microscopic images of experimentally-recorded swimming human sperm cells. With this method, they examined the sperm collective dynamics and demonstrated that finer details of flow structure may affect the population-level collective behaviors.

The primary aim of this study is to apply this methodology to the collective dynamics of swimming bacteria. This coherent turbulent-like behavior in a suspension of dense bacteria, which has been extensively studied and is known as bacterial turbulence, is characterized by vortices with sizes higher than the individual cells [2, 6]. Specifically, motivated by an experimental setup for a cell suspension in a narrow chamber or a liquid film [29, 37, 43], we focus on the collective dynamics of swimming cells in a plane under confinement. The assumption of in-plane swimming has been widely used for a simplification of the individual-based collective dynamics [6, 14, 22, 44]. Following these, we consider the quasi-two-dimensional system where cells’ movement and orientations are confined in a single plane but three-dimensional hydrodynamic cell-wall interactions are incorporated in addition to cell-cell interactions. The cell-wall hydrodynamic interactions are often subtle but can be attractive and repulsive depending on the swimming pattern [16, 28, 35, 36]. Our second aim is then to seek the hydrodynamic effects of the confinement on the collective behaviors.

More precisely, we will examine a multiscale simulation for a dense bacterial population in a two-dimensional plane, based on the regularized Stokeslet representation previously obtained from direct numerical simulation of flow around a single bacterium [21]. Similarly, considering the two parallel free-slip interfaces, we will demonstrate that geometrical confinement induces a different characteristic of the turbulent pattern. Bacteria swimming near a boundary disintegrate the chirality due to the rotlet dipole term [23] and we also explore the impact of these effects.

The remaining parts of the study are structured as follows: Section 2 summarizes the methodologies for a multiscale numerical simulation of microswimmer collective dynamics, Sect. 3 presents the simulation results and impacts of geometrical confinements, and Sect. 4 presents the summary and discussion.

2 Microswimmer Collective Dynamics with a Regularized Stokeslet Representation

2.1 Flow Representation

The study focuses on microswimmers whose surrounding fluid dynamics are governed by the Stokes equations of the low-Reynolds-number flow. We constructed a general solution using the linearity of the flow equations by superpositions of the fundamental solution, known as the Stokeslet, a flow induced by a point force. Indeed, superpositions of Stokeslets and higher-order Stokeslet multipoles approximate experimental flow data around biological microswimmers such as Volvox, Chlamydomonas, Euglena, and E. coli bacteria [7, 8, 11, 12, 38].

The regularized version of the Stokeslet has been extensively used for fast and convenient numerical computation, as Stokeslet and its multiples become singular at the point of force application [5]. The regularized Stokeslet contains an intrinsic width of force distribution as a regularized parameter, \(\epsilon \), although various types of regularization have been proposed [45]. The regularization for the external force application is made using a localized distribution function, \(\phi (\boldsymbol{r}, \epsilon )\), instead of the Dirac delta function. We use

$$\begin{aligned} \phi (\boldsymbol{r}, \epsilon )=\frac{15\epsilon ^4}{8\pi (r^2+\epsilon ^2)^{7/2}} , \end{aligned}$$
(1)

which becomes unity when integrating over a space. Here, \(r_i=(\boldsymbol{x}-\boldsymbol{x}_0)_i\) and \(r=|\boldsymbol{x}-\boldsymbol{x}_0|\) (\(i=1, 2, 3\)). The Stokeslet located at the position \(\boldsymbol{x}_0\) is given by

$$\begin{aligned} G^{\text {S}}_{ij}(\boldsymbol{x}; \epsilon )=\frac{(r^2+2\epsilon ^2)\delta _{ij}+r_ir_j}{(r^2+\epsilon ^2)^{3/2}} , \end{aligned}$$
(2)

where \(\delta _{ij}\) denotes the Kronecker delta. In this study, the Einstein summation convention is used only for the spatial indices. The flow by the regularized Stokeslet may be written based on linearity as \(u_i=G^{\text {S}}_{ij}f_j\). Another important Stokeslet singularity is the rotlet, which represents a flow induced by a point torque. We can obtain its regularized version by considering a localized torque. When we write this flow as \(u_i=G^\text {R}_{ij}m_j\), the regularized rotlet is given by

$$\begin{aligned} G^{\text {R}}_{ij}(\boldsymbol{x}; \epsilon )=\frac{2r^2+5\epsilon ^2}{(r^2+\epsilon ^2)^{5/2}}\epsilon _{ijk}r_k , \end{aligned}$$
(3)

where \(m_i\) denotes the torque and \(\epsilon _{ijk}\) indicates the Levi-Civita symbol.

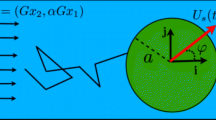
With the spatial parameter \(\epsilon \), a superposition of the regularized singularities excellently represents the near-field flow field around a shape-changing microswimmer, such as sperm [17, 18], and an elastic filament [4]. Ishimoto et al. [21] reported that the time-averaged flow including its near-field is well recapitulated by the superposition of the two regularized Stokeslets and two rotlets located near the centers of the cell body and flagellum, respectively, for a swimming bacterium. This physically intuitive representation was extracted from the direct computation of the Stokes equation around a single-flagellated bacterium via the boundary element method (Fig. 1). The two Stokeslets and rotlets, sharing its positions and directed along the flagellar axis, have the same magnitude but opposite signs to guarantee the force- and torque-balance relation. Also, its far-field counterpart, the force and torque doublet, failed to capture the near-field flow field (see [21]).

Fig. 1
figure 1

Figure reproduced from [21] with permission via the creative commons license, http://creativecommons.org/licenses/by/4.0

We obtained the flow fields around a single swimming bacterium from a the direct numerical computation using the boundary element method and b the superposition of the regularized Stokeslets and rotlets. The green dots represent the bacterial cell, and the white arrows show the streamline in the xy plane with the magnitude of the velocity fields shown by the differentiated color levels. The red curves represent three-dimensional (3D) streamlines, showing the 3D swirling flow due to the paired rotlets. The flagellum length is considered the unit of length.

Full size image

Subsequently, we made the system dimensionless by setting the flagellar length (\(\approx 10\mu \)m for E. coli) and flagellar rotation frequency (\(\approx 100\) Hz for E. coli) to be the units of length scale and time scale, respectively. For mass scale, we set the viscosity coefficient of the medium to unity.

In this study, we used the regularized representation as a model bacterium, as shown in Fig. 1. The flow field is expressed as

$$\begin{aligned} u_i(\boldsymbol{x},t)=\sum _{\text {g}}\sum _{\ell }G^{\text {g}}_{ij}(\boldsymbol{x},\boldsymbol{x}_0^{(\ell )}; \epsilon ^{(\text {g},\ell )})f^{(\text {g},\ell )}_j , \end{aligned}$$
(4)

where \(\ell =\{1, 2\}\), and the index \(\text {g}\in \{ \text {S}, \text {R}\}\) denotes the Stokeslet or the rotlet. The generalized force \(f_i^{\text {g}, \ell }\) therefore indicates the force when \(\text {g}=\text {S}\) and the torque when \(\text {g}=\text {R}\). Note that the positions of the Stokeslets and rotlets coincide and are denoted by \(\boldsymbol{x}_0^{(\ell )}\) and that force- and torque-balance relation is written as \(f^{(\text {g},1)}_j=-f^{(\text {g},2)}_j\). The parameters in Eq. (4) are provided in [21] and its accompanying supplementary material.

2.2 Modeling Interactions

Furthermore, we modeled the interactions between cells and simulated collective behavior. The explained methodologies follow multiscale modeling developed in [19]. Walker et al. [42] validated the numerical accuracy for quasi-two-dimensional swimming of paired sperm cells and compared the coarse-grained simulation study with the direct numerical simulation study via the boundary element method.

We consider N identical microswimmers whose surrounding flow field is represented as defined in Eq. (4). Furthermore, we assume that all swimmers move in a single plane (we set this as the xy plane) and denote the position and angle of each swimmer by \(\boldsymbol{X}^{(n)}\) and \(\theta ^{(n)}\), respectively, where we have introduced the swimmer label n (\(n=1, 2, \ldots , N)\). Also, we write its linear and angular velocities as

$$\begin{aligned} \frac{d\boldsymbol{X}^{(n)}}{dt}= & {} \boldsymbol{U}^{(n)}:=\boldsymbol{U}^{(n),\text {single}}+\boldsymbol{U}^{(n),\text {hyd}}+\boldsymbol{U}^{(n),\text {str}} \end{aligned}$$
(5)
$$\begin{aligned} \frac{d\theta ^{(n)}}{dt}= & {} \varOmega ^{(n)}:=\varOmega ^{(n),\text {hyd}}+\varOmega ^{(n),\text {str}} . \end{aligned}$$
(6)

The upper suffix ‘single’ denotes the individual swimming velocity in a free domain obtained from the boundary element calculation, noting that the angular velocity is zero due to the axisymmetric nature of the swimmer. The upper suffices for ‘hyd’ and ‘str’ denote the hydrodynamic and steric interactions between the cells, as explained below.

The velocity induced by the hydrodynamic interactions is typically complex as it depends not only on the relative configuration of the cells but also on the instantaneous cell shape. Alternatively, we introduced a closure relationship to approximate the hydrodynamic interactions based on the assumption that the collection of small spheres estimates the cell configuration. To elucidate this, we focused on a cell, labeled by n, and considered the flow field at the singularity point \(\boldsymbol{x}_0^{(n, \ell )}\) induced by surrounding cells. Using a simple superposition of the flow field, let us write this as follows:

$$\begin{aligned} u'_{i}(\boldsymbol{x}_0^{(n, \ell )}, t)=\sum _{n'=1, n'\ne n}^N \sum _{\text {g}, \ell } G^{\text {g}}_{ij}(\boldsymbol{x}_0^{(n, \ell )},\boldsymbol{x}_0^{(n', \ell ')};\epsilon ^{(n', \text {g}, \ell ')} ) f_j^{(\text {g},\ell )} . \end{aligned}$$
(7)

We considered this fluid field as the background flow for the nth cell and defined

$$\begin{aligned} \boldsymbol{u}_{\text {res}}^{(n,\ell )}=\boldsymbol{u}'(\boldsymbol{x}_0^{(n, \ell )})-\boldsymbol{U}^{(n),\text {hyd}}-\varOmega ^{(n),\text {hyd}}\boldsymbol{e}_z\times \boldsymbol{x}_{\text {rel}}^{(n,\ell )} . \end{aligned}$$
(8)

Here, the vector \(\boldsymbol{x}_{\text {rel}}\) represents the relative position to the cell centroid defined as

$$\begin{aligned} \boldsymbol{X}_c^{(n)}=\frac{\sum _{\ell }\boldsymbol{x}_0^{(n,\ell )}}{\sum _{\ell }1} , \end{aligned}$$
(9)

and its explicit form is given as

$$\begin{aligned} \boldsymbol{x}_{\text {rel}}^{(n,\ell )}=\boldsymbol{x}_0^{(n,\ell )}-\boldsymbol{X}_c^{(n)} . \end{aligned}$$
(10)

The closure equation to determine the hydrodynamic-induced velocities is given as

$$\begin{aligned} \sum _\ell \boldsymbol{u}_{\text {res}}^{(n,\ell )} = \sum _\ell \boldsymbol{x}_{\text {rel}}^{(n,\ell )} \times \boldsymbol{u}_{\text {res}}^{(n,\ell )} =\boldsymbol{0} , \end{aligned}$$
(11)

which may be interpreted by the force- and torque-balance equations once we assume that the cell consists of a set of arbitrarily small spherical particles. For the quasi-two-dimensional dynamics, we may directly derive the interaction velocities from the closure relations (11) as

$$\begin{aligned} \boldsymbol{U}^{(n),\text {hyd}}=\frac{\sum _{\ell }\boldsymbol{u}'(\boldsymbol{x}_0^{(n,\ell )})}{\sum _{\ell }1}~,~~ \varOmega ^{(n),\text {hyd}}=\frac{\sum _{\ell }{\boldsymbol{x}_\text {rel}}^{(n, \ell )}\times \boldsymbol{u}'(\boldsymbol{x}_0^{(n,\ell )})\cdot \boldsymbol{e}_z}{\sum _{\ell }|\boldsymbol{x}_{\text {rel}}^{(n, \ell )}|^2} . \end{aligned}$$
(12)

We further incorporate steric interactions between the cells to avoid cell-cell intersections. In this study, we assumed that the cells consist of four spheres along the cell body and flagellum. Also, the sphere radius is considered as a regularized parameter for the Stokeslet located in the cell body. The cell-cell steric repulsion acts as additional interaction velocities, which increase linearly to an intersecting distance between two spheres of different cells as a simple linear spring. We denote the additional velocity at a singularity point, \(\boldsymbol{x}_0^{(n,\ell )}\), by \(\boldsymbol{u}^{\text {str}}(\boldsymbol{x}_0^{(n,\ell )},t)\). The strength of the spring constant does not affect the study’s results once we set its size to be sufficiently large. Thus, the steric interaction then induces additional swimming velocities of cells, \(\boldsymbol{U}^{(n),\text {str}}\) and \(\boldsymbol{\varOmega }^{(n),\text {str}}\) in Eqs. (5) and (6), respectively. These are obtained by the same closure relation as Eq. (12) by replacing \(\boldsymbol{u}'\) with \(\boldsymbol{u}^{\text {str}}\).

2.3 Numerical Implementations

We considered the quasi-two-dimensional cell behavior in a rectangular box domain with a periodic boundary condition in the xy plane. Let \(L_x\), \(L_y\), and \(L_z\) be the lengths of the sides of the domain. We consider the horizontal domain sufficiently large compared with each cell size. Because of the horizontal periodic boundary condition, an infinite number of singularities needs to be summed up to represent the Stokeslet and other singularities that satisfy the boundary conditions. However, due to large domain size, the sub-leading terms are sufficiently small to be neglected in computing hydrodynamic interactions [19].

Additionally, we considered a quasi-two-dimensional domain confined by two parallel flat boundaries on which we imposed the free-slip boundary condition. The boundary conditions constitute an infinite sum of the image singularities used in standard singular Stokeslets and rotlets [26, 28]. This method of images is applicable even for regularized Stokeslets and rotlets. However, the regularized Stokeslet near a no-slip boundary, called the regularized Blakelet, contains the \(O(\epsilon )\) error [1, 41]. In this study, we summed up at most nine mirror images to validate the convergence of the infinite series. The free-slip parallel boundaries are appropriate in either oil-water or air-water interfaces, such as the microswimmer dynamics in a thin liquid film [27, 37]. However, they are known to be suitable for some microfluidic channel walls [13, 44].

Fig. 2
figure 2

Numerical simulation of bacterial collective behavior. a A snapshot of the population dynamics of cells interacting by steric repulsion only, indicating giant clusters of the cells. We used a red circle to illustrate each cell’s body and a blue rod to illustrate the flagellum. b A snapshot of the simulated population dynamics with the same parameter values and initial conditions but with hydrodynamic interactions. c The effective velocity vector field of the population, \(\boldsymbol{v}(\boldsymbol{x})\), at the time of b, is shown by blue arrows indicating the vortex structure characterizing the behavior of the bacterial turbulence

Full size image

We implemented the model equations presented in the previous sections using the Fortran program in [19]. Furthermore, we performed parallel computing within the cluster system in the Institute for Information Management and Communication (IIMC), Kyoto University.

3 Numerical Results

3.1 Quasi-Two-Dimensional Dynamics in a Free Space

Also, we considered the impacts of hydrodynamic interactions on collective behavior and examined whether our multiscale simulation can reproduce the dynamics of bacterial turbulence. Figure 2a, b shows snapshots of the numerical simulations of the bacterial dynamics with \(N=1500\) cells and the domain size being \(L_x=L_y=40\). However, we did not consider the vertical walls. In Fig. 2a, the hydrodynamic interactions, \(\boldsymbol{U}^{(n),\text {hyd}}\) and \(\boldsymbol{\varOmega }^{(n),\text {hyd}}\), were removed from the simulation, whereas these terms were considered in full simulation in Fig. 2b. We marked each cell body with a red circle and the flagellum as a blue rod.

Fig. 3
figure 3

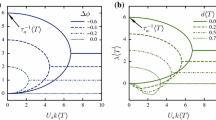
The equal-time velocity correlation function C as a function of relative distance, r in different confinement geometries with the system parameter values \(N=4000\) and \(L_x=L_y=40\). Colored map in the inset shows a snapshot of vorticity, \(\omega (x, y)\). The figure region corresponds to the size of the domain \(L_x=L_y=40\). The red and blue regions indicate positive and negative vortices, corresponding to the counter-clockwise and clockwise rotation, respectively. The cells move in the plane of \(z=0\) a with no external interfaces, b confined by two free-slip interfaces at \(z_{\text {bot}}=-0.2\) and \(z_{\text {top}}=0.2\), and c confined by two free-slip interfaces at \(z_{\text {top}}=-1.0\) and \(z_{\text {bot}}=1.0\)

Full size image

Despite the randomly distributed initial condition, cells tend to align with each other due to the elongated cell geometry and form several large clusters of cells (Fig. 2a) if the cells interact only by steric repulsion. Although the clusters may divide and merge, which is consistent with the past results that the steric interactions cause the motility-induced phase separation [40]. In contrast, the cell population disperses more uniformly (Fig. 2b) when the hydrodynamic interactions are incorporated. These temporal dynamics are considered spatial-temporal chaos. Furthermore, we computed the effective velocity fields \(\boldsymbol{v}(\boldsymbol{r}, t)\) from individual cell swimming. We observed that the large vortices with sizes larger than individual cells characterize the dynamics. Figure 2c presents the obtained velocity field plot that corresponds to the snapshot in Fig. 2b. Also, we used the equal-time velocity correlation function (VCF) to quantitatively evaluate the bacterial turbulence-like dynamics, as in [6]. The equal-time VCF is defined as

$$\begin{aligned} C(r)=\langle \boldsymbol{v}(\boldsymbol{x})\cdot \boldsymbol{v}(\boldsymbol{x}')\delta (r-|\boldsymbol{x}-\boldsymbol{x'}|) \rangle , \end{aligned}$$
(13)

where bracket \(\langle \cdots \rangle \) denotes the temporal average. The equal-time VCF for the hydrodynamically interacting bacterial cells possesses a zero around the distance \(r\approx 4\) and has a negative value until it decays to zero at the far field. Figure 3a shows the equal-time VCF for the parameter values with \(N=4000\) and \(L_x=L_y=40\) again in the absence of any external boundaries. The plots of the equal-time VCF are robust under the changes in system parameters, such as the number of cells and domain size. The simulation videos with higher cell density (\(N=4000, L_x=L_y=30\)) are available in the Supplemental Materials.

The first zero of the equal-time VCF is considered the characteristic length of the vortices. This value reads around \(40\mu \)m, which is consistent with experimental observations [6]. The effective vorticity fields are calculated by \(\boldsymbol{\omega }(\boldsymbol{x},t)=\nabla \times \boldsymbol{v}(\boldsymbol{x},t)\), and its z component, \(\omega =\boldsymbol{\omega }\cdot \boldsymbol{e}_z\) is plotted in the inset of Fig. 3a in the color contour, showing vortices with a characteristic length scale estimated by the equal-time VCF.

3.2 Quasi-Two-Dimensional Dynamics in Free-Slip Parallel Walls

We also studied the quasi-two-dimensional dynamics of bacterial cells confined in free-slip parallel boundaries. Let the plane of cell swimming be \(z=0\) and two free-slip interfaces be located at \(z=z_{\text {bot}}<0\) and \(z=z_{\text {top}}>0\).

As mentioned in the previous section, we computed equal-time VCF in different confined geometries, and the cases with \(N=4000\) and \(L_x=L_y=40\) are shown in Fig. 3b, c, with the simulation without external boundaries for comparison in Fig. 3a. Indistinguishable from the free-swimming case, the bacterial population exhibits turbulent-like behavior as observed in the snapshots of the effective vorticity field, \(\omega (x, y)\), as shown in the figure insets. Their swimming velocity is enhanced when they are confined.

The bacterial cells confined in a narrow chamber with \(z_{\text {bot}}=-0.2\) and \(z_{\text {top}}=0.2\) have a slightly larger vortex size characterized by the first zero of the equal-time VCF (Fig. 3b). When the chamber depth increases with the swimmer plane kept in the middle of the chamber, that is, \(z_{\text {bot}}=-z_{\text {top}}\), we observed that the rotlet-induced hydrodynamic boundary interactions vanished due to its symmetric geometrical configuration. The simulation results showed that the vortex size reaches its maximum when \(|z_{\text {bot}}|=z_{\text {top}}=1.0\) (Fig. 3c) and decreases with converging to the free-swimming case (Fig. 3a).

Fig. 4
figure 4

The equal-time velocity correlation function in different confinement geometries with snapshots of the vorticity field in the inset. Simulation parameters are the same as in Fig. 3 except for the boundary conditions. The cells move in the plane of \(z=0\) in the presence of a two free-slip interfaces at \(z_{\text {bot}}=-0.2\) and \(z_{\text {top}}=0.8\), b an infinite bottom free-slip interface at \(z_{\text {bot}}=-0.2\), and c an infinite bottom no-slip wall boundary at \(z_{\text {bot}}=-0.2\)

Full size image

We compared these results with the collective dynamics in changing the position of the top interface, keeping the bottom interface at \(z_{\text {bot}}=-0.2\). In asymmetric confinement, the rotlet hydrodynamic interactions lead to circling motion when the cell swims in isolation. However, such chiral individual cell motions are suppressed and not visible. The vortex size estimated by the equal-time VCF has the same tendency as the symmetric confinement and reaches a peak in the intermediate size of the two interfaces. Figure 4a shows the equal-time VCF plot with a snapshot of the vorticity field in the inset with \(z_{\text {bot}}=-0.2\) and \(z_{\text {top}}=0.8\).

The confinement condition approaches the half domain when the top interface is far apart. Figure 4b, c show the collective behavior in the presence of an infinite plane boundary on which we imposed the free-slip or no-slip boundary condition. The no-slip boundary is treated by the regularized Blakelet [1, 41]. With the different boundary conditions, the individual cell exhibits a circling motion with an opposite rotational direction. In the simulations, the circle radius was \(R \approx 2\) which agrees with the experimental results in E. coli bacterium [23]. Nevertheless, the collective behavior is almost the same as characterized by the similar vortex size, as shown in the figure. However, the swimming velocity is higher in the free-slip simulation.

4 Summary and Discussion

Subsequently, we report a multiscale simulation of the collective behavior of swimming bacteria moving in a plane using the regularized Stokeslet representation obtained from the direct numerical simulation of a single swimming cell. Considering the near-filed hydrodynamic and steric interactions, we reproduced the bacterial turbulence dynamics in a two-dimensional plane using the equal-time velocity correlation as an index to evaluate the turbulence structure.

We conducted further investigations on the impact of the cell-wall hydrodynamical interactions using the method of images to impose the two parallel free-slip interfaces. The simulation of the dynamics in the center plane between the two interfaces showed that the depth of the two interfaces affected the vortex-size characteristic. We considered the peak of the vortex size when the depth was of the same order as the individual cell size. Wensink et al. [43] suggested that the range of the hydrodynamical interactions can be changed in the presence of boundaries. With the two parallel interfaces, the flow around a single cell can stir regions. Thus, we can interpret an enhanced vortex as increased cell size.

We conducted simulation studies with an asymmetric vertical configuration of the two interfaces to consider the impact of the rotlet dipole term, which represents swirling flow due to the spinning of a bacterium and the flagellum. Though a dilute population of bacteria exhibited circling trajectories near a boundary, a dense population did not show such chiral behavior but almost homogeneous bacterial turbulence, implying that the rotlet dipole term is less important for the dynamics.

Recently, Qi et al. [31] considered a spheroidal squirmer with rotlet dipole contributions and its collective dynamics in a plane confined by a narrow chamber. Their study allows the swimmers to change their orientation in a small-angle range away from the swimming plane, although the translational motion is confined to a plane. Note that this is different from the current setting with the swimmer orientations also confined in the swimming plane. They reported that the presence of the rotlet dipole term affects the entire collective dynamics, which is different from the current observation. Further studies may consider extending the numerical methods used in this study to 3D motion. Furthermore, more complex geometrical confinements, such as doubly and triply confined chambers and obstacles and external flow fields [29, 44] are suggested for further studies.