Abstract
The Fujisaki-Okamoto (FO) transform (CRYPTO 1999 and JoC 2013) turns any weakly (i.e., IND-CPA) secure public-key encryption (PKE) scheme into a strongly (i.e., IND-CCA) secure key encapsulation method (KEM) in the random oracle model (ROM). Recently, the FO transform re-gained momentum as part of CRISTAL-Kyber, selected by the NIST as the PKE winner of the post-quantum cryptography standardization project.
Following Fischlin (ICALP 2005), we study the complete non-malleability of KEMs obtained via the FO transform. Intuitively, a KEM is completely non-malleable if no adversary can maul a given public key and ciphertext into a new public key and ciphertext encapsulating a related key for the underlying blockcipher.
On the negative side, we find that KEMs derived via FO are not completely non-malleable in general. On the positive side, we show that complete non-malleability holds in the ROM by assuming the underlying PKE scheme meets an additional property, or by a slight tweak of the transformation.
M. Salvino—The work was carried out whilst the author was a student at Sapienza University of Rome, Rome, IT.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
He also proves that the original version of RSA-OAEP, as well as the Cramer-Shoup PKE [8], is not completely non-malleable.
- 2.
Each of \(\textsf{U}\) and \(\textsf{U}_m\) also comes in 2 variants, but the difference is irrelevant for what follows.
References
Barbosa, M., Farshim, P.: Relations among notions of complete non-malleability: Indistinguishability characterisation and efficient construction without random oracles. In: Steinfeld, R., Hawkes, P. (eds.) ACISP (2010)
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th Annual Symposium on Foundations of Computer Science, FOCS 1997, Miami Beach, Florida, USA, 19–22 October 1997, pp. 394–403. IEEE Computer Society (1997)
Bellare, M., Desai, A., Pointcheval, D., Rogaway, P.: Relations among notions of security for public-key encryption schemes. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 26–45. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055718
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 531–545. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_41
Bellare, M., Namprempre, C.: Authenticated encryption: relations among notions and analysis of the generic composition paradigm. J. Cryptol. 21(4), 469–491 (2008)
Bellare, M., Sahai, A.: Non-malleable encryption: equivalence between two notions, and an indistinguishability-based characterization. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 519–536. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_33
Boldyreva, A., Fischlin, M.: Analysis of random oracle instantiation scenarios for OAEP and other practical schemes. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 412–429. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_25
Cramer, R., Shoup, V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 13–25. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055717
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: Koutsougeras, C., Vitter, J.S. (eds.) Proceedings of the 23rd Annual ACM Symposium on Theory of Computing, 5–8 May 1991, New Orleans, Louisiana, USA, pp. 542–552. ACM (1991)
Duman, J., Hövelmanns, K., Kiltz, E., Lyubashevsky, V., Seiler, G.: Faster lattice-based kems via a generic Fujisaki-Okamoto transform using prefix hashing. In: Kim, Y., Kim, J., Vigna, G., Shi, E. (eds.) CCS ’21: 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, Republic of Korea, 15–19 November 2021, pp. 2722–2737. ACM (2021)
Faust, S., Kohlweiss, M., Marson, G.A., Venturi, D.: On the non-malleability of the fiat-Shamir transform. In: Galbraith, S., Nandi, M. (eds.) INDOCRYPT 2012. LNCS, vol. 7668, pp. 60–79. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34931-7_5
Fischlin, M.: Completely non-malleable schemes. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 779–790. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_63
Friolo, D., Salvino, M., Venturi, D.: On the complete non-malleability of the Fujisaki-Okamoto transform. Cryptology ePrint Archive, Paper 2022/1654 (2022). https://eprint.iacr.org/2022/1654
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 537–554. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_34
Hofheinz, D., Hövelmanns, K., Kiltz, E.: A modular analysis of the Fujisaki-Okamoto transformation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 341–371. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_12
Libert, B., Yung, M.: Efficient completely non-malleable public key encryption. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6198, pp. 127–139. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14165-2_12
Nagao, W., Manabe, Y., Okamoto, T.: On the equivalence of several security notions of key encapsulation mechanism. IACR Cryptology ePrint Archive, p. 268 (2006). https://eprint.iacr.org/2006/268
NIST: Nist announces first four quantum-resistant cryptographic algorithms (2022). https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms
Pass, R., Shelat, A., Vaikuntanathan, V.: Relations among notions of non-malleability for encryption. In: Kurosawa, K. (ed.) ASIACRYPT, vol. 4833, pp. 519–535 (2007)
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_35
Sepahi, R., Steinfeld, R., Pieprzyk, J.: Lattice-based completely non-malleable PKE in the standard model (poster). In: Parampalli, U., Hawkes, P. (eds.) ACISP 2011. LNCS, vol. 6812, pp. 407–411. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22497-3_26
Sepahi, R., Steinfeld, R., Pieprzyk, J.: Lattice-based completely non-malleable public-key encryption in the standard model. Des. Codes Cryptogr. 71(2), 293–313 (2014)
Ventre, C., Visconti, I.: Completely non-malleable encryption revisited. In: Cramer, R. (ed.) PKC 2008. LNCS, vol. 4939, pp. 65–84. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78440-1_5
Acknowledgements
We thank all the anonymous reviewer for their insightful comments. The work of the first and third authors is partially supported by project SERICS (PE00000014) under the NRRP MUR program funded by the EU - NGEU and by Sapienza University under the project SPECTRA.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
A Supporting Proofs
A Supporting Proofs
1.1 A.1 Proof of Theorem 1
Proof
The intuition behind the proof is to define the scheme \(\varPi '\) in such a way that the adversary can leverage its structure to succeed in the NM-ATK* experiment. In particular, we define \(\varPi '\) in the following way:

We can clearly see that \(\varPi '\) is not NM-ATK* secure. Indeed, an efficient adversary \({\textsf{A}}\) receiving a public key \(\textsf{pk}\), the challenge ciphertext \(c\) and an encapsulation key \(\textsf{K}\) (either the real or the fake one), just have to flip the last bit of \(\textsf{pk}\) denoted \(\textsf{pk}' := \textsf{pk}||\bar{b}\), a relation \(R\) and the challenge ciphertext \(c\). In this case, \({\textsf{A}}\) will always succeeds in breaking NM-ATK* security of \(\varPi '\). However, \(\varPi '\) is still NM-ATK secure. Indeed, this is true because the adversary has to break NM-ATK security of \(\varPi '\) under the key \(\textsf{pk}\), but for how \(\varPi ^{'}\) is defined, this is equivalent to break NM-ATK security of \(\varPi \). If an adversary is able to break NM-ATK security of \(\varPi '\), then he can also break NM-ATK security of \(\varPi \), and this represent a contradiction to our assumption that \(\varPi \) is NM-ATK secure. \(\square \)
1.2 A.2 Proof of Theorem 3
Proof
The sequence of games and the consequential differences in the oracles are described in Fig. 4.
Sequence of games needed to prove Theorem 3 and the consequential modifications of the oracles.
The proofs that \(\textsf{KEM}^{nm\text {-}cca2*}_{\tilde{\varPi }_1^{\bot }, {\textsf{B}}}(\lambda ) \equiv \textbf{G}_{0}^{{\textsf{B}}}(\lambda )\), \(\textbf{G}_0^{\textsf{B}}(\lambda ) \equiv \textbf{G}_1^{\textsf{B}}(\lambda )\), and that \(\textbf{G}_2^{\textsf{B}}(\lambda )\approx _{c}\textbf{G}_3^{\textsf{B}}(\lambda )\) are identical to Lemma 1, 2 and 4 respectively.
Lemma 6
\(\textbf{G}_1^{\textsf{B}}(\lambda ) \approx _c \textbf{G}_2^{\textsf{B}}(\lambda )\).
Proof
The proof is identical to Lemma 3, except that now we do not use public key uniqueness of the underlying PKE scheme to argue that the \(\textbf{G}_1\) and \(\textbf{G}_2\) are identically distributed conditioned to the fact that the event \({\textsf{QUERY}}\) does not happen. In this case, the adversary can try to distinguish between \(\textbf{G}_1\) and \(\textbf{G}_2\) by guessing the plaintext \(m^*\) of \(c^*\), calculate \(\textsf{K}':=\textsf{H}(m^*,c^*,\textsf{pk}^*)\) and then check whether \(\textsf{K}'\) is equal to \(\textsf{K}^*\) or not. However, this coincides with the \({\textsf{QUERY}}\) event. Alternatively, the adversary might try to distinguish making \(\textbf{G}_1\) always output 1, i.e. \({\textsf{B}}\) tries to come up with a tuple \((\textsf{pk}',R,c')\) for which the relation \(R(\textsf{K}',\textsf{K}^*,\textsf{pk}',\textsf{pk}^*,c')\) holds for a key \(\textsf{K}^*\) encapsulated by \(c^*\) under \(\textsf{pk}'\) (as in \(\textbf{G}_1\)), but does not hold when such key is randomly chosen (as in \(\textbf{G}_2\)). However, for the random oracle assumption, since \(\textsf{pk}'\) is part of the input of \(\textsf{H}\), the key \(\textsf{K}':=\textsf{H}(m^*,c^*,\textsf{pk}')\) will be independent from \(\textsf{K}^*:=\textsf{H}(m^*,c^*,\textsf{pk}^*)\). Thus, the distribution of \(\textbf{G}_1\) and \(\textbf{G}_2\) is identical when \({\textsf{QUERY}}\) is not triggered.
As in Lemma 3, to estimate \(\text{ Pr }\left[ {\textsf{QUERY}}\right] \) we construct an efficient adversary \({\textsf{A}}\) breaking OW-PCVA of \(\textsf{PKE}_{1}\) when \({\textsf{QUERY}}\) occurs. We define \({\textsf{A}}\) in Fig. 5.
Notice that \({\textsf{A}}\) perfectly simulates \(\textbf{G}_1\). Indeed, the occurrence of \({\textsf{QUERY}}\) implies that \({\textsf{B}}\) has queried \(\textsf{H}\) about \((m,c,\textsf{pk})\), in which \((m,c,\textsf{pk}) \in \mathcal {L}_{H}\) for \(m= m^*\), \(c=c^*\) and \(\textsf{pk}=\textsf{pk}^*\). \({\textsf{A}}\) then returns \(m= m^*\). Since such event coincides with \({\textsf{QUERY}}\), we get that the probability of \({\textsf{B}}\) of triggering \({\textsf{QUERY}}\) coincides with the probability of \({\textsf{A}}\) in winning the OW-PCVA experiment, i.e. \(\text{ Pr }\left[ {\textsf{QUERY}}\right] = \text{ Pr }\left[ \textsf{PKE}_{\varPi _{1}, {\textsf{A}}}^{ow\text {-}pcva}(\lambda )\right] \le \textsf{negl}(\lambda ).\) \(\square \)
Lemma 7
\(\textbf{G}_3^{\textsf{B}}(\lambda ) \equiv \textsf{KEM}_{\tilde{\varPi }_1,{\textsf{B}},\S }^{nm\text {-}cca2*}(\lambda ).\)
Proof
Since \(\textbf{G}_{3}\) is similar to \(\textbf{G}_{0}\), with the only difference that the encapsulation key \(\textsf{K}^*\) is uniform it is independent from the one obtained by querying \(\textsf{H}\), for the same considerations that we did for \(\textbf{G}_{0}\), it holds that the two distributions are identically distributed. \(\square \)
Combining the above lemmas, we get that \(\textsf{KEM}_{\tilde{\varPi }_1^{\bot }, {\textsf{B}}}^{nm\text {-}cca2*}(\lambda )\approx _{c}\textsf{KEM}_{\tilde{\varPi }_1^{\bot }, {\textsf{B}},\$}^{nm\text {-}cca2*}(\lambda )\). \(\square \)
1.3 A.3 Proof of Theorem 4
Proof
Let us assume that there exists a PPT adversary \({\textsf{A}}\) that breaks NM-ATK* security of \(\varPi '\) with non-negligible probability, then we can build an efficient distinguisher \({\textsf{D}}\) that breaks NM-ATK* security of \(\varPi \). The intuition behind the proof is that \({\textsf{D}}\) will choose a distribution over the message space in such a way that only two messages, say \(\textsf{K}\) and \(\textsf{K}'\), can be sampled by the the challenger playing NM-ATK* of the PKE scheme \(\varPi \). In particular, \({\textsf{D}}\) does the following:
-
1.
Takes as input a public key \(\textsf{pk}\) and chooses a message distribution \(\mathcal {M}\) from which only two messages can be chosen, which we call \(\textsf{K}\) and \(\textsf{K}'\).
-
2.
Takes as input a challenge ciphertext \(c\) which is either an encryption of \(\textsf{K}\) under \(\textsf{pk}\) or an encryption of \(\textsf{K}'\) under \(\textsf{pk}\).
-
3.
Run \({\textsf{A}}(\textsf{pk}, c, \textsf{K})\). When \({\textsf{A}}\) asks a decapsulation-oracle query for a ciphertext \(\hat{c}\) do the following:
-
(a)
Query the decryption oracle \(\textsf{Dec}(\textsf{sk}^*,\cdot )\) about \(\hat{c}\) to obtain a key \(\hat{\textsf{K}}\).
-
(b)
Return \(\hat{\textsf{K}}\) to \({\textsf{A}}\).
-
(a)
-
4.
When \({\textsf{A}}\) returns \((\textsf{pk}', R, c')\), return \((\textsf{pk}', R, c')\) as well.
Let us analyze the behavior of \({\textsf{D}}\). First, notice that, independently from \(c\), \({\textsf{D}}\) will always send the tuple \((\textsf{pk}, c, \textsf{K})\) to \({\textsf{A}}\). Recall also that the message space of \(c\) is restricted to messages \(\textsf{K}\) and \(\textsf{K}'\). In particular, when \(c\) is an encryption of \(\textsf{K}\) under \(\textsf{pk}\), \({\textsf{D}}\) the view of \({\textsf{A}}\) when run as a subroutine of \({\textsf{D}}\) is identically distributed to its view in \(\textsf{KEM}^{nm\text {-}atk*}_{\varPi ', {\textsf{A}}}(\lambda )\). When \(c\) is an encryption of \(\textsf{K}'\) under \(\textsf{pk}\), since \(\textsf{K}'\) is uniform and independent from \(\textsf{K}\), the view of \({\textsf{A}}\) when run as a subroutine of \({\textsf{D}}\) is distributed identically to its view in \(\textsf{KEM}^{nm\text {-}atk*}_{\varPi ', {\textsf{A}}, \$}(\lambda )\). To summarize, the probability that \({\textsf{D}}\) distinguishes between \(\textsf{PKE}^{nm\text {-}atk*}_{\varPi , {\textsf{D}}}(\lambda )\) and \(\textsf{PKE}^{nm\text {-}atk*}_{\varPi , {\textsf{D}}, \$}(\lambda )\) is the same of \({\textsf{A}}\) distinguishing between \(\textsf{KEM}^{nm\text {-}atk*}_{\varPi ', {\textsf{A}}, \$}(\lambda )\) and \(\textsf{KEM}^{nm\text {-}atk*}_{\varPi ', {\textsf{A}}, \$}(\lambda )\), that we assumed to be non-negligible. \(\square \)
1.4 A.4 Proof of Theorem 5
Proof
Correctness of the obtained PKE follows from the \(\epsilon \)-correctness of the underlying KEM and SKE schemes. The idea behind the proof is that, given the challenge ciphertext \(c^*=(c^*_1,c^*_2)\), we can use NM-ATK* security of \(\varPi ^{kem}\) to decouple the key encapsulated in \(c^*_1\) from the key used in \(c^*_2\) to encrypt the message with the underlying SKE scheme \(\varPi ^{ske}\). At this point, since the encapsulated key is randomly chosen and independent from the encryption key, it is not possible to for \({\textsf{A}}\) to distinguish between a correct encryption (i.e., where the encapsulated key and the encryption key are the same) and an encryption where the key encapsulated in \(c^*\) is randomly chosen and independent from the one used to encrypt \(c^*_2\). This holds even if \({\textsf{A}}\) is allowed to maul \(\textsf{pk}^*\) into some related public key \(\textsf{pk}'\). The next step is to use the NM-ATK security of \(\varPi ^{ske}\) to decouple \(m^*\) from the relation \(R\), i.e. given a ciphertext \(c^*_2\) encrypting \(m^*\), it is infeasible for an adversary to distinguish between the experiment where the relation \(R\) was checked by using either \(m^*\) or \(\tilde{m}\). Finally, NM-ATK* security of \(\varPi ^{kem}\) can be used to re-join together the key encapsulated in \(c^*_1\) with the key used to encrypt \(m\) in \(c^*_2\). Let \({\textsf{A}}= {\textsf{A}}^{hy}\), the sequence of games is described in Fig. 6. The part of the proof required for a specific flavour of NM-ATK* will be highligthed with a tag [NM-ATK*].
Sequence of games needed to prove Theorem 5.
Lemma 8
\(\textbf{G}_0(\lambda )\approx _{c}\textbf{G}_1(\lambda )\).
Proof
Let us assume that \({\textsf{A}}^{hy}\) can distinguish between \(\textbf{G}_0\) and \(\textbf{G}_1\) with non-negligible probability. We can construct an adversary \({\textsf{A}}^{nm}\) breaking NM-ATK* security of \(\varPi ^{kem}\). \({\textsf{A}}^{nm}\) behaves as follows:
-
1.
Take as input a public key \(\textsf{pk}^*\), a ciphertext \(c\) and a key \(\hat{\textsf{K}}\), where either \(\hat{\textsf{K}} = \textsf{K}^*\) (the key encapsulated in c) or
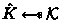 .
. -
2.
Run \({\textsf{A}}^{hy}(\textsf{pk}^*)\).
[NM-CCA*1/NM-CCA2*] When \({\textsf{A}}^{hy}\) asks a decryption-oracle query about a ciphertext \((c_{1}, c_{2})\) query \(\textsf{Decaps}(\textsf{sk}^*,\cdot )\) about \(c_{1}\) to obtain a key \(\textsf{K}'\) and return \(m:= \textsf{Dec}(\textsf{K}',c_{2})\).
When \({\textsf{A}}^{hy}\) outputs a message distribution \(\mathcal {M}\), take a uniform message
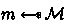 , compute
, compute  and return \(c^*=(c, c')\) to \({\textsf{A}}^{hy}\).
and return \(c^*=(c, c')\) to \({\textsf{A}}^{hy}\). -
3.
[NM-CCA2*] When \({\textsf{A}}^{hy}\) asks a decryption-oracle query about a ciphertext \((c_{1}, c_{2})\) do the following:
-
if \(c_{1} = c\) and \(c_{2} = c'\) then return \(m := \bot \) (i.e. the query is not admissible).
-
if \(c_{1} = c\) and \(c_{2} \ne c'\) then return \(m:= \textsf{Dec}(\hat{\textsf{K}},c_{2})\).
-
else, query \(\textsf{Decaps}^{(c^*)}(\textsf{sk}^*,\cdot )\) about \(c_{1}\) to obtain a key \(\textsf{K}'\) and return \(m:= \textsf{Dec}(\textsf{K}',c_{2})\).
-
-
4.
When \({\textsf{A}}^{hy}\) outputs \((\textsf{pk}, R, (c_{1}, c_{2}))\), output \((\textsf{pk}, R', c_{1})\), where \(R'(\cdot ,\cdot ,\textsf{pk},\textsf{pk}^*,c)=R(\cdot ,\cdot ,\textsf{pk},\textsf{pk}^*,c)\).
Notice that, since the only difference between \(\textbf{G}_0\) and \(\textbf{G}_1\) is that in \(\textbf{G}_1\) the key is chosen at random, the only hope for he adversary \({\textsf{A}}^{hyb}\) to distinguish between the two hybrids is by finding a relation holding between \(\textsf{pk}\), \(\textsf{pk}^*\), and \(c\) that is satisfied in \(\textbf{G}_0\) but not in \(\textbf{G}_1\) (or vice-versa). Hence, \(R'(\cdot ,\cdot ,\textsf{pk},\textsf{pk}^*,c)=R(\cdot ,\cdot ,\textsf{pk},\textsf{pk}^*,c)\) is indeed a suitable relation for \({\textsf{A}}^{nm}\). When \(\hat{\textsf{K}}\) taken as input by \({\textsf{A}}^{nm}\) is \(\textsf{K}^*\), then \({\textsf{A}}^{nm}\) perfectly simulates \(\textbf{G}_0\). When \(\hat{\textsf{K}}\) taken as input by \({\textsf{A}}^{nm}\) is randomly chosen, \({\textsf{A}}^{nm}\) perfectly simulates \(\textbf{G}_1\). If \({\textsf{A}}^{hy}\) distinguishes between \(\textbf{G}_0\) and \(\textbf{G}_1\) with non-negligible probability, then \({\textsf{A}}^{nm}\) breaks NM-ATK* security of the underlying KEM scheme with non-negligible probability. This leads to a contradiction. \(\square \)
Lemma 9
\(\textbf{G}_1(\lambda )\approx _{c}\textbf{G}_2(\lambda )\).
Proof
Let us assume that \({\textsf{A}}^{hy}\) can distinguish between \(\textbf{G}_1\) and \(\textbf{G}_2\) with non-negligible probability, we construct an adversary \({\textsf{A}}^{atk}\) breaking NM-ATK security of \(\varPi ^{ske}\). \({\textsf{A}}^{atk}\) behaves as follows:
-
1.
Receive as input a key \(\textsf{K}\).
-
2.
Generate a pair
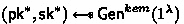 .
. -
3.
Run \({\textsf{A}}^{hy}(\textsf{pk}^*)\).
[NM-CCA*1/NM-CCA2*] When \({\textsf{A}}^{hy}\) asks a decryption-oracle query about a ciphertext \((c_{1}, c_{2})\), query the decryption oracle \(\textsf{Dec}(\hat{\textsf{K}},\cdot )\) of the NM-CCA experiment about \(c_{2}\) to obtain a message \(m\).
-
4.
When \({\textsf{A}}^{hy}\) outputs a message distribution \(\mathcal {M}\), output \(\mathcal {M}\) to the challenger.
-
5.
When receiving a ciphertext \(c'\) from the challenger, compute
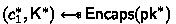 , and output \((c_1^*,c')\) to \({\textsf{A}}^{hy}\).
, and output \((c_1^*,c')\) to \({\textsf{A}}^{hy}\). -
6.
[NM-CCA2*] When \({\textsf{A}}^{hy}\) asks a decryption-oracle query about a ciphertext \((c_{1}, c_{2})\) do the following:
-
if \(c_{1} = c_1^*\) and \(c_{2} = c'\) then return \(m := \bot \) (i.e. the query is not admissible).
-
else, query \(\textsf{Dec}^{(c')}(\hat{\textsf{K}},\cdot )\) about \(c_{2}\) to obtain \(m:= \textsf{Dec}(\textsf{K}',c_{2})\). Then, outputs \(m\) to \({\textsf{A}}^{hyb}\).
-
-
7.
When \({\textsf{A}}^{hy}\) outputs \((\textsf{pk}, R, (c_{1}, c_{2}))\), \({\textsf{A}}^{atk}\) output \((R',c_2)\) to the challenger, where \(R'(m_0,m_1)=R(m_0,m_1,\cdot ,\cdot ,\cdot )\). The challenger either checks \(R'(m,m^*)=1\) where \(m^*:=\textsf{Dec}(\hat{\textsf{K}},c')\) if \({\textsf{A}}^{atk}\) is in \(\textsf{SKE}^{nm\text {-}atk}_{\varPi ^{ske},{\textsf{A}}^{atk}}\) or checks if \(R'(m,\tilde{m})=1\) if \(\tilde{m}\) is an randomly chosen message independent from \(c^*\). Note that the only difference between \(\textbf{G}_1\) and \(\textbf{G}_2\) is that the game checks that \(m^*\) given as an input to \(R\) is encrypted in \(c^*_2\), whereas in \(\textbf{G}_2\) the relation \(R\) takes as an input a random \(\tilde{m}\). Thus, the only hope for \({\textsf{A}}^{hyb}\) in distinguishing between the two hybrids is by finding a relation holding between \(m\) and \(m^*\) but not between \(m\) and \(\tilde{m}\) (or vince-versa). Thus, we are allowed to cast \(R'(m_0,m_1)\) as \(R(m_0,m_1,\cdot ,\cdot ,\cdot )\). When the relation \(R\) takes \(m^*\) in input, then \({\textsf{A}}^{atk}\) perfectly simulates \(\textbf{G}_1\). When the relation \(R\) takes a random \(\tilde{m}\) in input, \({\textsf{A}}^{atk}\) perfectly simulates \(\textbf{G}_2\).
If \({\textsf{A}}^{hy}\) distinguishes between \(\textbf{G}_1\) and \(\textbf{G}_2\) with non-negligible probability, then \({\textsf{A}}^{atk}\) breaks NM-ATK security of the underlying SKE scheme with non-negligible probability. This leads to a contradiction. \(\square \)
Lemma 10
\(\textbf{G}_2^{{\textsf{A}}}(\lambda )\approx _{c}\textbf{G}_3^{{\textsf{A}}}(\lambda )\)
Proof
Let us assume that \({\textsf{A}}^{hy}\) can distinguish between \(\textbf{G}_2\) and \(\textbf{G}_3\) with non-negligible probability, we construct an adversary \({\textsf{A}}^{nm}\) breaking NM-ATK* security of \(\varPi ^{kem}\). \({\textsf{A}}^{nm}\) behaves as follows:
-
1.
Takes as input a public key \(\textsf{pk}^*\), a ciphertext \(c\) and a key \(\hat{\textsf{K}}\), where either \(\hat{\textsf{K}} = \textsf{K}^*\) (the key encapsulated in c) or
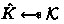 .
. -
2.
Run \({\textsf{A}}^{hy}(\textsf{pk}^*)\).
[NM-CCA*1/NM-CCA2*] When \({\textsf{A}}^{hy}\) asks a decryption-oracle query about a ciphertext \((c_{1}, c_{2})\) query \(\textsf{Decaps}(\textsf{sk}^*,\cdot )\) about \(c_{1}\) to obtain a key \(\textsf{K}'\) and return \(m:= \textsf{Dec}(\textsf{K}',c_{2})\).
-
3.
When \({\textsf{A}}^{hy}\) outputs a message distribution \(\mathcal {M}\), take two uniform messages
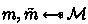 , compute
, compute 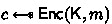 and return \(c^*=(c, c')\) to \({\textsf{A}}^{hy}\).
and return \(c^*=(c, c')\) to \({\textsf{A}}^{hy}\). -
4.
[NM-CCA2*] When \({\textsf{A}}^{hy}\) asks a decryption-oracle query about a ciphertext \((c_{1}, c_{2})\) do the following:
-
if \(c_{1} = c\) and \(c_{2} = c'\) then return \(m := \bot \) (i.e. the query is not admissible).
-
if \(c_{1} = c\) and \(c_{2} \ne c'\) then return \(m:= \textsf{Dec}(\hat{\textsf{K}},c_{2})\).
-
else, query \(\textsf{Decaps}^{(c^*)}(\textsf{sk}^*,\cdot )\) about \(c_{1}\) to obtain a key \(\textsf{K}'\) and return \(m:= \textsf{Dec}(\textsf{K}',c_{2})\).
-
-
5.
When \({\textsf{A}}^{hy}\) outputs \((\textsf{pk}, R, (c_{1}, c_{2}))\), output \((\textsf{pk}, R', c_{1})\), where \(R'(\cdot ,\cdot ,\textsf{pk},\textsf{pk}^*,c)=R(\cdot ,\cdot ,\textsf{pk},\textsf{pk}^*,c)\).
Notice that, since the only difference between \(\textbf{G}_2\) and \(\textbf{G}_3\) is that in \(\textbf{G}_2\) the key is chosen at random, the only hope for he adversary \({\textsf{A}}^{hyb}\) to distinguish between the two hybrids is by finding a relation holding between \(\textsf{pk}\), \(\textsf{pk}^*\), and \(c\) that is satisfied in \(\textbf{G}_2\) but not in \(\textbf{G}_3\) (or vice-versa). Hence, \(R'\) is a suitable relation for \({\textsf{A}}^{nm}\). When the kehy \(\hat{\textsf{K}}\) taken as input by \({\textsf{A}}^{nm}\) is randomly chosen, it perfectly simulates \(\textbf{G}_2\). When the key \(\hat{\textsf{K}}\) taken as input by \({\textsf{A}}^{nm}\) is \(\textsf{K}^*\), then \({\textsf{A}}^{nm}\) perfectly simulates \(\textbf{G}_3\). If \({\textsf{A}}^{hy}\) distinguishes between \(\textbf{G}_2\) and \(\textbf{G}_3\) with non-negligible probability, then \({\textsf{A}}^{nm}\) breaks NM-ATK* security of the underlying KEM scheme with non-negligible probability. This leads to a contradiction. \(\square \)
It is easy to see that \(\textbf{G}_0^{\textsf{A}}(\lambda )\equiv \textsf{PKE}^{nm\text {-}atk*}_{\varPi ^{hy},{\textsf{A}}}(\lambda )\) and that \(\textbf{G}_3^{\textsf{A}}(\lambda )\equiv \textsf{PKE}^{nm\text {-}atk*}_{\varPi ^{hy},{\textsf{A}},\$}(\lambda )\). by combining the above lemmas, we have that \(\textsf{PKE}^{nm\text {-}atk*}_{\varPi ^{hy},{\textsf{A}}}(\lambda ) \approx _{c}\textsf{PKE}^{nm\text {-}atk*}_{\varPi ^{hy},{\textsf{A}},\$}(\lambda ).\) \(\square \)
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Friolo, D., Salvino, M., Venturi, D. (2023). On the Complete Non-malleability of the Fujisaki-Okamoto Transform. In: Tibouchi, M., Wang, X. (eds) Applied Cryptography and Network Security. ACNS 2023. Lecture Notes in Computer Science, vol 13906. Springer, Cham. https://doi.org/10.1007/978-3-031-33491-7_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-33491-7_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-33490-0
Online ISBN: 978-3-031-33491-7
eBook Packages: Computer ScienceComputer Science (R0)








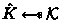 .
.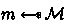 , compute
, compute  and return
and return 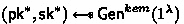 .
.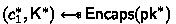 , and output
, and output 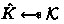 .
.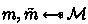 , compute
, compute 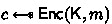 and return
and return