Abstract
This chapter provides an overview of different conceptualizations of student engagement with mathematical ideas in studies that occur in mathematics classrooms and teaching experiment environments, and the types of quality student mathematics learning activities that result in desired learning outcomes. Over the last three decades, mathematics curriculum initiatives have called for the development of student behaviors and dispositions (i.e., mathematical competencies, processes, proficiencies, and practices) that actively engage all students in knowing and doing mathematics. According to Medley (1987), it is axiomatic that all learning depends on the activity of the learner. One of the main purposes of teaching is to provide students with effective and equitable experiences that will result in successful learner outcomes. Given the complexity of studying student engagement with learning activities, including the “constraint-support system” (Kaput in Handbook of research on mathematics teaching and learning, Macmillan, 1992) of technology-based mathematics activities, and the persistent challenges of conducting research in mathematics classrooms, this chapter describes the evolution of research examining student learning experiences through the lens of multiple theoretical perspectives that provide explanations relevant to how and why student behaviors and dispositions develop in the way they do within different learning environments.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Process standards
- Mathematical proficiency
- Standards for mathematical practice
- Mathematical competencies
- Student engagement
- Productive disposition
- Productive struggle
- Productive failure
- Teaching experiments
- Technology in mathematics education
1 Introduction
In the late 1980s, to understand “good” teachers and improve teaching practices, Medley (1987) reviewed prior research on teaching and teacher education and identified 10 different variables that were studied to determine effective teaching (Introduction, this volume). Using a chain of effects of presage-process–product research, he reviewed studies that focused on measuring teaching and student behaviors that resulted in desired student learning outcomes. Further, he identified six of the 10 variables (Types A—F) as “online variables” (p. 105) that were in direct control of the teacher and these variables could be studied individually or in relationships between two or more variables. Using Manizade et al.’s (2019) adaptation of Medley’s work for mathematics education (Introduction, this volume), this chapter describes an analysis and review of the literature relevant to the Type B variable, student engagement in mathematics learning activities, over the last three decades. According to Medley, student learning activities are defined in the following way:
Pupil learning activities occur in the classroom. The principal means by which teaching can affect learning outcomes is through its influence on pupil behaviors in the classroom. The function of teaching is to provide pupils with experiences that will result in desired outcomes. It is axiomatic that all learning depends on the activity of the learner. (p. 105)
As mathematics education researchers, we are interested in examining relationships between how students engage in or approach student learning activities (Type B) that result in the successful achievement of desired student learning outcomes (Type A). It is the teacher practices in classrooms (Type C) that are needed to facilitate effective and equitable student interactions with learning activities in which students develop mathematical content knowledge and engage in the process of doing mathematics.
Yet, what are the characteristics of student engagement in learning activities that promote the development of content knowledge? What behaviors do students actively engage in while learning mathematics that reflect what it means to know and do mathematics? Can these learning activities be generalized across diverse K-12 classrooms, including settings that use a wide range of technological tools that support a “synergistic relationship” between technical and conceptual dimensions of mathematical activity (Zbiek et al., 2007)? How do teachers facilitate and enhance students’ experiences while learning mathematics? One way to address these questions is to consider a review since Medley’s work of how the global mathematics education community has described constructs that further explore students’ development of mathematics content knowledge and engagement in learning activities while doing mathematics.
A historical review of reform-based mathematics curriculum initiatives provides insight into visions of various student learning activities, including the use of technology, which impact how students engage in knowing and doing mathematics (Sect. 2). To address the many names for these activities, I use Kobett and Karp’s (2020, p. 40) terminology of behaviors and dispositions (i.e., proficiencies, processes, practices, competencies, and habits of mind) to identify the multiple and intersecting student experiences that are relevant to how students develop and show evidence of their mathematical thinking. Section 3 articulates multiple theoretical perspectives that capture how the process of student learning occurs in different learning environments. This is followed by studies relevant to student engagement in making sense of mathematics (problem-solving behaviors) and perseverance (productive dispositions) that are often linked to instructional practices to support desired learning outcomes (Sect. 4). For some studies, Medley’s methodology concerns are addressed related to the quality and effectiveness of research. Lastly, a discussion of findings is presented and implications for future mathematics education research in the area of student mathematics learning activities and active student engagement in knowing and doing mathematics (Sect. 5).
2 Student Mathematics Learning Activities: An Overview
Over the past several decades, early reform initiatives in the United States [U.S.] (National Council of Teachers of Mathematics [NCTM], 1980, 1989, 1991, 1995, 2000; National Research Council [NRC], 2001) and other countries, such as Denmark, New Zealand, and Australia (Davidson et al., 2019; Hipkins, 2018; McDowell & Hipkins, 2018; Niss, 2003) have promoted new curricula frameworks to develop mathematics content knowledge and learning activities to improve student mathematics achievement. The organization of curriculum centered on content at different grade bands with some consideration of behaviors needed to engage students in learning mathematics. Student mathematics learning activities are a set of behaviors and dispositions students engage in to achieve learning goals that reflect an in-depth understanding of mathematics. From the last three decades, this overview documents a shift toward a focus on student thinking needed to build a conceptual understanding of mathematics and identifying how students should experience solving mathematical tasks. A review of reform initiatives shows an evolution of specificity of learner activities envisioned to meet high-quality curriculum goals that support students’ learning of mathematics with understanding.
Beginning in the mid-1970s and into the decade of the 1980s, school curriculum reform focused on accountability and measurable standards that demonstrated students’ achievement in mathematics (Cuban, 1992; Pink, 1989). Teacher certification standards and higher student graduation requirements were raised in the hopes of improving the teaching and learning of mathematics. The 1983 publication, A Nation at Risk (National Commission, 1983) reported the failure of the U.S. school system with the decline of student test scores and achievement levels. Students lacked mathematical competence and they were unable to problem solve. At the same time, the business community became aware of a shrinking supply of skilled workers causing them to become involved in public school reform (Cuban, 1992; Martin, 1989; Sola, 1989). According to Martin (1989), businesses supported education initiatives because of the potential of providing skilled workers, including those able to work with the emergence of technology. Yet, the need for accountability prompted a return to teaching basic skills and the measurement of student behavioral objectives (i.e., achievement of performance goals) where students completed rote procedures and computations that could be easily measured.
During the decades of the 1970s and 1980s, what appeared to be missing was a focus on measuring student achievement of learning goals (Smith & Sherin, 2019). Moving beyond equating knowing mathematics as successfully completing procedures, researchers needed to show evidence of what students “understood” about specific mathematics content as a result of engaging in learning experiences in the classroom. In response to the needs of the discipline and society for the 1980s, NCTM published the Agenda for Action (1980), which recommended future directions for improving the teaching and learning of mathematics. Based on reports of low mathematics performance, the student behavior of problem solving became central for engaging students in a mathematics learning activity and has remained a primary focus in curriculum initiatives over the last three decades.
In the 1990s, the NCTM trilogy of U.S. Standards reform initiatives (1989, 1991, 1995) provided a vision for the organization of school mathematics curriculum and evaluation, teaching, and assessment. The sets of standards described the nature of mathematics with an emphasis on students developing a conceptual understanding of mathematics rather than an acquisition of procedural knowledge, skills, and facts. Based on interpretations of Piaget’s (1970) and Vygotsky’s (1981) work, constructivist and social constructivist theories of learning supported a new vision of students constructing knowledge individually or collaboratively, rather than passively receiving knowledge. Mathematics represented a dynamic, changing discipline rather than a static body of knowledge. However, it is critical to state that the early sets of NCTM standards represented “statements of values” and that underlying assumptions about the teaching and learning of mathematics “were not well anchored in either research or theory” (Kilpatrick, 2003, p. 1). Likewise, Lesh et al.'s (2020) recent review of learning theories in mathematics education found that the early “NCTM Standards themselves were not based on any research per se, but simply an envisioning of what mathematics education in classrooms (i.e., in practice) might look like and what the appropriate content might look like, keeping the learner in mind” (p. 862). One of the issues relevant to a lack of research may be attributed to transitioning from past theories and methods of measuring procedural, student performance goals to a vision of measuring conceptual, student learning goals often showed little, if any, research related to new ways of teaching and learning. This is because the sets of standards had not been implemented in many mathematics classrooms. Moreover, although the curriculum initiatives promoted mathematics content learning goals and engagement in student mathematical learning activities (i.e., behaviors and dispositions), teaching practices (Type C) that support student learning with understanding were missing.
In response to a lack of research and explicitly connected to an updated version of U.S. standards (NCTM, 2000), Kilpatrick (2003) asserted that a companion publication (NCTM, 2003) synthesized a review of the literature that informed the vision of school mathematics in the 1990s and 2000. In this publication, Sfard reviewed learning theory research and identified ten mathematical learner needs that were reflected in the curriculum changes of the NCTM standards. For example, she identified learners as having a “need for meaning and the need to understand ourselves and the world around us have come to be recognized as the basic driving force behind all our intellectual activities” (p. 356). Bringing the needs of learners to the forefront, researchers raised new questions about how to measure student behaviors and dispositions that provide detailed explanations of students’ need for “meaning” while learning mathematics with understanding and what does this look like in mathematics classrooms.
Recognizing the ever-present dilemma of balancing the needs of mathematics (discipline theory) and the needs of the learner (psychological theory) in the organization of curriculum, Sfard asserted: “In our attempts to improve the learning of mathematics, we will always remain torn between two concerns: Our concern about the learner and our concern about the quality of the mathematics being learned” (p. 386). When one of these theories controls too much of the school mathematics curriculum, then disruption occurs within the entire curriculum. Over the last three decades and across different countries, the challenge of this dilemma has continued to be addressed with frameworks of curriculum initiatives that identify content knowledge students should know and processes students need to engage in while doing mathematics. Reviewing the relevant literature, a number of terms and documents pertaining to student behaviors and dispositions will appear in this section and be discussed further throughout the chapter. Brief, capsule definitions of these terms and documents are included in the Appendix. The goal of the following subsections is to identify and compare student mathematics learning activities (Type B) that have evolved with students becoming knowers and doers of mathematics.
2.1 Mathematical Processes
After much debate related to the dilemma Sfard (2003) articulated about balancing the needs of both the discipline and learners, the U.S. Principles and Standards of School Mathematics (NCTM, 2000) expanded the vision of mathematics education to include a more deliberate focus on school curriculum organized around the framework of process standards to promote learning activities students should engage in while doing mathematics. Rather than describe performance goals of doing procedures, the processes defined what mathematicians might do and say when problem solving. The process standards recommended providing all students opportunities to learn mathematics through engagement in five overlapping processes: problem solving, communication, representation, making connections, and reasoning and proof (NCTM, 2000). Problem solving is the primary action of mathematics activity and it has always been recommended as way to know and do mathematics (NCTM, 1980). The learning activity of reasoning develops through problem solving. Compared to an earlier set of process standards (NCTM, 1989), representation was added to the original four processes as a way to engage students in making their mathematical thinking explicit. To support students’ development of mathematical reasoning and proof, Huinker (2015) extended Lesh et al. (1987) modes of representation: contextual, physical, visual, verbal, and symbolic, with an explicit focus on students building representational competence from which mathematical connections are made “between” and “within” representations. In Sect. 2.5, Zbeik et al. (2007) use an equivalent term of representation fluency as a construct to describe students’ access and engagement with multiple representations in technological environments. The process standards inform ways students could participate while engaged in knowing and doing mathematics.
2.2 Mathematical Competencies
At the same time, in 2000, the Denmark Ministry of Education created a national committee to examine ways to improve mathematics teaching and learning. Their work resulted in the Mathematical Competencies and Learning of Mathematics: The Danish KOM Project (Niss, 2003). In this report, mathematical competence was defined as having “the ability to understand, judge, do, and use mathematics in a variety of intra- and extra-mathematical contexts and situations in which mathematics plays or could play a role” (p. 7). The project identified eight mathematical competencies that demonstrated evidence of students’ “mental or physical processes, activities, and behaviors” (p. 9). The competencies extended NCTM’s process standards and included: thinking mathematically, posing and solving mathematical problems, modeling mathematically, reasoning mathematically, representing mathematical entities, handling mathematical symbols and formalisms, communicating in, with, and about mathematics, and making use of aids and tools (including instructional technology) (Niss, 2003). This framework of mathematical competencies is relevant to Manizade et al.’s (2019) adaptation of Medley’s Type B variable as they identify learning experiences students should engage in to develop a deep understanding of mathematics articulated in high-quality curriculum goals.
In a similar vein focused on identifying mathematical competencies, the Program for International Student Assessment [PISA] (PISA, 2021) measures to what extent 15-year-olds use their many years of building mathematical knowledge to solve real-world problems. In students’ lives outside of school, they need to solve problems that often demand the use and integration of multiple mathematical topics, rather than only knowing how to use a single procedure learned in a mathematics lesson. PISA assesses different mathematical competencies that gauge students’ mathematical literacy; that is, “an individual’s capacity to reason mathematically and to formulate, employ, and interpret mathematics to solve problems in a variety of real-world contexts” (PISA, 2021). The PISA mathematical literacy framework lists multiple competencies under each of three clusters: reproduction, connections, and reflection. As a research fellow at the Australian Council for Educational Research (ACER) at the beginning of the last decade, Turner (2010) reviewed research analyzing PISA mathematics test items. To be successful in solving contextual problems, he found that students needed to activate prior mathematical knowledge. Further, he reported students’ difficulty in problem solving when they needed to activate more rather than fewer mathematics competencies. Similar to Denmark’s competencies, the PISA competencies included the following: communication, mathematising, representation, reasoning and argument, strategic thinking, and using symbolic, formal, and technical language and operations. Turner argued for teacher activities (Type C) in which they increased a focus on these competencies (Type B) to engage students in developing mathematical literacy.
Over the last two decades, a Ministry of Education-funded project, Competencies in New Zealand Curriculum (NZC) (McDowall & Hipkins, 2018; Hipkins, 2018), described an evolution and research base of key competencies for student learning in general and eight content learning areas for the twenty-first century. Connected to a PISA framework, a construct of competencies originated from an Organization for Economic Development (OECD) Definition and Selection Competencies (DeSeCo) Project which produced a framework to guide the development of PISA assessments (Hipkins, 2018). For the NZC, each learning area described “what they [students] will come to know and do” (Ministry of Education, 2015, p. 37) and identified five key competencies: thinking, relating to others, using language, symbols, and text, managing self, and participating/contributing. According to the Ministry of Education (2020), “Key competencies matter because they support dispositions that will enable young people to learn well now, and to go on learning throughout their lives… Dispositions mean learners are ready (i.e., being motivated to use particular knowledge, skills, and values to achieve the task at hand), willing (i.e., recognizing when it is relevant to draw on these), and able (i.e., knowing how to do so appropriately).” Similar to the framework of proficiency strands (NRC, 2001) and Kobett and Karp’s explicit inclusion of “disposition” when describing students’ knowing and doing mathematics, the NZC recognized the critical role of dispositions needed for current and future student learning. In mathematics and statistics, “students explore relationships in quantities, space, and data and learn to express relationships in ways that help them to make sense of the world around them” (p. 17). When examining mathematical connections to four of the key competencies: thinking, relating to others, using language, symbols, and text, and participating and contributing, the NZC stated: “Students develop the ability to think creatively, critically, strategically and logically… They learn to create models and predict outcomes, to conjecture, to justify and verify, and to seek patterns and generalizations… [there is] a broad range of practical applications in everyday life, in other learning areas, and in workplaces” (p. 26). Within the NZC, three interrelated strands of eight levels of achievement objectives are identified: number and algebra, geometry and measurement, and statistics. Each level begins with this statement: “In a range of meaningful contexts, students will be engaged in thinking mathematically and statistically. They will solve problems and model situations that require them to:” (Ministry of Education, 2014). Similar to other frameworks of competencies described previously, there is a focus on students engaged in thinking, meaningful contexts, knowing, doing, and dispositions.
McDowall and Hipkins’ (2018) review of large systematic studies that examined competencies in the NZC resulted in emergent themes that defined “four phases in the ways that key competencies have been understood and enacted in the overall school curriculum” (p. 2). Between 2006 and 2018, these phases provided a “trajectory of change” when considering the nature of student learning and how to weave the competencies into the curriculum. As an example, although there was overlap between the phases, in phase two (i.e., 2007–2011), “relationships between key competencies and ideas about learning to learn (an NZC principle) and lifelong learning (a part of the NZC vision)” (p. 7) came to the forefront. Research examined how the NZC was implemented across multiple schools and what barriers existed. A shift occurred in phase three (i.e., 2011–2014) with a recognition of a need for the “weaving of key competencies and learning area content” (p. 9); that is, relationships were examined between competencies and desired discipline-specific learning outcomes (Type A).
Moreover, “students’ opportunities to develop their key competencies were closely tied to the pedagogy used by the teacher” (p. 9) (Type B and C variables). To engage students in learning activities, they needed tasks where they took “meaningful action in real-world contexts” (p. 10) and other pedagogical approaches included critical inquiry and experimental learning. To investigate phase four studies, which are ongoing, McDowall and Hipkins (2018) reported: (1) “Students should actively use and build knowledge, as opposed to just being consumers of knowledge produced by others;” (2) “There should be opportunities for students to collaborate in more demanding ways than simply group work;” and (3) “The diverse life experiences and ways of being that students bring to learning are seen as a resource for learning rather than a problem to be managed” (p. 12). Looking ahead to future research, Hipkins et al. (2018) examined the OECD 2030 Learning Framework (p. 2) and its alignment and implications for the NZC. As in the past, the 2030 framework identifies a focus on knowledge, skills, attitudes, and values leading to competencies for individual and societal well-being. The OECD framework development is a collaborative, international project and a work-in-progress. It is intended to update the DeSeCo framework for PISA assessments and provide a pathway for future research connecting student learning activities, teacher activities, and student learning outcomes (Type A, B, and C variables, Introduction, this volume).
2.3 Mathematical Proficiency
In the same time period as the updated NCTM (2000) process standards, the National Research Council’s [NRC] Mathematics Learning Study Committee published Adding It Up: Helping Children Learn Mathematics (2001) to identify how students attain mathematical proficiency through cognitive and affective engagement within these five strands: conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition. By including the last strand, productive disposition, the NRC committee asserted the value of beliefs, attitudes, and emotions and their affective impact on students’ engagement in learning mathematics. According to NRC, conceptual understanding is defined as the “comprehension of mathematical concepts, operations, and relationships” and productive disposition is the “habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy” (p. 116). Making connections to the strands, Kobett and Karp (2020) mapped each proficiency to examples of what students’ strength behaviors look like in a classroom setting. For conceptual understanding, they included a student question, “Why do we call some numbers square numbers? Why do we call some numbers cube numbers?” and explained: “When students make a comment that something doesn’t make sense to them, that is an indication that they desire mathematics should be a sense-making activity” (p. 42). Not only was this student engaged in making sense of the meaning of different types of numbers, the student asked why questions to develop reasoning about the structure of numbers.
In Australia, the national curriculum standards identified mathematical reasoning as both a process that demonstrates mathematical thinking and a strategy for learning mathematics (Davidson et al., 2019). According to the Australian Curriculum and Assessment Reporting Authority (ACARA, 2017), reasoning is one of the four proficiency strands students engage in when “thinking and doing of mathematics.” In other words, the process of reasoning provides insight into students’ mathematical thinking and their engagement in student learning activities. The other three proficiency strands are understanding, fluency, and problem-solving. The four Australian proficiency strands “describe the actions in which students can engage when learning and using the content” (ACARA, 2017). Thus, the proficiency strands suggest a call for research that examines students’ mathematical thinking when developing content knowledge (learning) and engagement in doing mathematics (using the content).
2.4 Standards for Mathematical Practice
In 2010, the U.S. created the national Common Core State Standards for Mathematics (CCSSM) (National Governors Association [NGA] Center for Best Practices and Council of Chief State School Officers [CCSSO], 2010), which included specific mathematical competencies for students called the Standards for Mathematical Practice (SMP). Many of the same international mathematical behaviors identified previously were stated: (1) make sense of problems and persevere in solving them, (2) reason abstractly and quantitatively, (3) construct viable arguments and critique the reasoning of others, (4) model with mathematics, (5) use appropriate tools strategically, (6) attend to precision, (7) look for and make use of structure, and (8) look for and express regularity in repeated reasoning. For the U.S., the CCSSM continued an evolution of reform visions stated in earlier initiatives and by other international researchers (Bostic & Sondergeld, 2015; Hipkins, 2018; Keazer & Jung, 2020; Kobett & Karp, 2020; Koestler et al., 2013; McDowall & Hipkins, 2018; NRC, 2001; Sanchez et al., 2015; Sfard, 2003; Turner, 2010). One purpose for creating the CCSSM was to provide consistency across the U.S. in K-12 grade-level curriculum standards rather than each state having different standards. The eight SMP described how students should engage in mathematics learning activities to become “doers of mathematics” (Kobett & Karp, 2020, p. 40).
In summary, when reviewing the aforementioned frameworks of curriculum initiatives, there is a shift toward making explicit how students should experience doing mathematics while making sense of their developing mathematical content knowledge. To demonstrate the evolution of student learning activities across different reform initiatives, a few mathematics educators have compared behaviors and dispositions found in the documents. Kobert and Karp described connections between the mathematical proficiency strands and SMP. If researchers use Manizade et al.’s (2019) framework (Introduction, this volume) for examining relationships between classroom Type C and B variables (i.e., teacher-student activities), studies could address Kobert and Karp’s challenge: “We want teachers to think about how their students respond to and interact with mathematics learning via each of these components and that, in doing so, they listen for whispers of their students’ previously undetected strengths” (p. 41). What research exists that documents how students engage in learning activities portrayed in frameworks of curriculum initiatives to develop a deep understanding of mathematics and how do teachers listen and respond to their students? Recently, Lesh et al. (2020) argued: “The mathematics education community still does not know how to operationally define measurable conceptions of almost any of the higher-level understandings or abilities that the CCSC Standards refers to as mathematical practices” (p. 863). In essence, when working with the complexity of studying the nature of students’ mathematical learning with understanding and student engagement in a range of mathematical practices (i.e., behaviors and dispositions), do studies exist for the knowledge base that provide evidence of measures to define effective and equitable student experiences with learning activities in mathematics classrooms, including technology-based environments?
A potential line of research could take advantage of Koestler et al.’s and Kobett and Karp’s alignment between the NCTM process standards and the Common Core standards of mathematical practice. These authors presented classroom vignettes for each SMP to illustrate how students engaged in doing these learning activities. Specifically, the problem-solving process standard was connected to all eight SMP. This suggests if researchers focused on students’ engagement with the first SMP, make sense of problems and persevere in solving them, there is a strong possibility that students will be engaged in the other “higher-level” practices. Given that similar practices are articulated across international frameworks of curriculum initiatives, research is warranted to provide evidence of students’ engagement in problem-solving behaviors (i.e., making sense of mathematics) and productive dispositions (i.e., perseverance).
2.5 Cognitive Technological Tools and Student Mathematics Learning Activities
In the Second Handbook of Research on Mathematics Teaching and Learning, Zbiek et al. (2007) articulated a perspective of multiple constructs researchers should use to examine students’ mathematical understanding while engaged in technology-based learning activities. Reviewing earlier research, the authors used the term cognitive technological (CT) tools to represent a wide variety of technologies that reflect a technical dimension, conceptual dimension, and a “synergistic relationship” among these two dimensions. Focusing on the technical dimension, CT tools “must allow the user the means to take actions on mathematical objects or representations of these objects” (p. 1171). Examining the conceptual dimension, CT tools provide “reactive visual feedback” as “observable evidence of the consequences of the user’s actions” (p. 1171). Zbiek et al. cautioned researchers against the study of mathematics teaching and learning in technological settings using only one dimension. This is attributed to the fact that student learning activities may include technical actions, such as solving equations and graphing, and simultaneously these actions are informed by students’ conceptual understanding and reasoning, such as conjecturing, finding patterns, and generalizing. Similarly, in the recent Compendium for Research in Mathematics Education, Roschelle et al. (2017) described a change in technology media over the last two decades from static to dynamic representations whereby students learn mathematics with understanding over time. Roschelle et al. identified dynamism as a new construct that incorporates a “time dimension” for students making sense of mathematics through dynamic representations. Specifically, they asked: “How is a mathematical representation being connected to a student’s experience of time to advance understanding of mathematical relationships?” (p. 863). To support students’ learning of difficult mathematical topics, Roschelle et al. used the “design of dynamic representations to enable new means of access [for students] to the topic” (p. 865). In Sect. 3, two of the emerging theoretical perspectives are grounded in conceptual studies (Hackenburg, 2010; Simon et al., 2016, 2018) whereby students use the dynamism of computer microworlds to support research focused on the interrelationship between technical and conceptual dimensions.
When students engage in doing technology-based mathematics learning activities, they may set goals and search to find appropriate CT tools that are needed to solve a mathematical task. Dependent upon the cognitive demand of a task, students can set different types of goals (i.e., performance or learning) which results in students exhibiting different types of behaviors. When using these CT tools, Zbiek et al. (2007) identified two types of activities students engage in when solving tasks: exploratory and expressive (p. 1180). Building on mathematical modeling research (Bliss & Ogborn, 1989), students engaged in doing exploratory activities will follow teacher instructions to use specific CT tools and procedures. On the other hand, expressive activities allow students to select their own CT tools and make their own decisions on how they will solve a technology-based task. Mathematics curricula often include “explorations” for students to engage with different learning activities and dependent upon how much teacher direction (Type C) is given, elements of both exploratory and expressive activity can be observed. Examining how students engage in doing mathematics through these two forms of activity will often result in different student learning outcomes (Type A). As an example of expressive activity, Zbiek et al. described the role of “play” in learning where students were allowed the freedom of unstructured play and time to try a range of different actions with CT tools to determine what was possible or not possible as they viewed the results of their actions. Students engaged individually or with partners and eagerly called out what they observed in a technological setting. However, the conundrum of the “play paradox” (Hoyles & Noss, 1992) comes to the forefront, where many CT tools offer students such a wide range of processes for solving problems, that they may never encounter the mathematical content a teacher intended or what the designers of a technology-based activity planned. Zbiek et al. offered mixed research results on the productive use of unstructured, expressive play versus structured, exploratory play to engage students in learning and doing mathematics.
Moreover, in a technological setting, researchers have examined both types of activity (i.e., exploratory or expressive) that students engaged in and made observations of students’ corresponding behaviors which “lead to insights about the appropriateness of their use of those tools and about their understanding of mathematics” (Zbiek et al., 2007, p. 1184). Specifically, inferences about students’ mathematical thinking were supported by students’ actions with CT tools, which in turn, reflected students’ mental actions. To categorize student behaviors, Zbiek et al. introduced the construct of work method which draws upon the research of Guin and Trouche (1999) and Trouche (2005). In a 1999 study of 17- to 18-year-old students’ engagement with mathematical tasks that included an option to use symbolic calculators, Guin and Trouche reported five different student work methods: random, mechanical, resourceful, rational, and theoretical. As an example, students using a random work method would search using trial and error to find a CT tool action that would give any answer (i.e., correct or incorrect) for a mathematical task. Yet, students’ engagement in a random process of finding any result often provided evidence of students missing the mathematical analysis of a problem. In other words, students accepted the results without any reflection related to the underlying mathematics which hindered their ability to achieve mathematical learning goals.
Revisiting the development of frameworks for mathematics curricula designed for student engagement with learning activities, some researchers (Sandoval et al., 2000 and Hong & Thomas, 2002 as cited in Zbiek et al., 2007) have identified the construct of representational fluency as a lens to study students’ learning by noticing how and why students interact and make sense of multiple representations of the same mathematics entity. How might students think differently about possible models and strategies for problem solving in a technological environment that provides quick access to multiple representations? Also, how could the selection of mathematics content go beyond traditional school mathematics due to the potential capabilities of CT tools? Consistent with other researchers, Zbiek et al. described representational fluency as “the ability to translate across representations, the ability to draw meaning about a mathematical entity from different representations of that mathematical entity, and the ability to generalize across different representations” (p. 1192). Access to technology can provide learners with opportunities to use different actions to ‘try out’ multiple representations and make sense of expected or unexpected results. As students reflect on their actions and begin to understand the meaning of each representation, they have an opportunity to develop representational fluency which could lead to a deep understanding of mathematical concepts.
Taken together, addressing research studies examining student engagement in learning activities (Type B) portrayed in frameworks of curriculum initiatives, including technological environments, provides insight relevant to both cognitive and affective aspects of student learners as they become knowers and doers of mathematics. To address Lesh et al.’s (2020) concerns, researchers can ask: How have we transitioned from measuring student learning for lower-level procedural outcomes toward analyzing student learning associated with desired higher-level thinking student outcomes (Type A)? One way researchers may respond is to consider a review since Medley’s work of important constructs that interpret existing research and target new areas of research with a focus on the complexity of the learning and teaching process; that is, the interrelationships between teachers, students, mathematical activities, curriculum content, and the added effect of technology. In the next section, three theoretical perspectives provide explanations relevant to how and why student behaviors and dispositions develop in the way they do within different learning environments.
3 Theoretical Perspectives
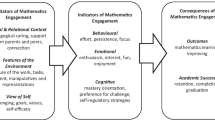
Within a framework for research relevant to study student behaviors and dispositions, questions can be raised that warrant further investigation about how and why students engage in learning activities. What kinds of interactions provide students with learning opportunities to develop mathematical knowledge with understanding and do mathematics? Are there patterns in how students become “knowers and doers of mathematics” or is it idiosyncratic for individual students? Middleton et al.'s (2017) recent review of engagement research articulates the complexity of studying the phenomenon of student engagement while learning and doing mathematics. They reported four individual and overlapping components of engagement: behavioral, cognitive, affective, and social. There are research challenges in providing explanations that attend to the four different components of engagement in learning activities to move our understanding of students’ mathematical thinking forward. Jansen (2020) elaborated and defined engagement with mathematics as “an interactive relationship students have with the subject matter, as manifested in the moment through expressions of behavior and experiences of emotion and cognitive activity, and is constructed through opportunities to do mathematics” (p. 273). To advance research relevant to student learning activities, researchers could consider Jansen’s recent focus on cognitive and social aspects of behaviors “in the moment” to provide evidence of what engagement might look like for students building mathematical content knowledge. In Siedal and Shavelon’s (2007) meta-analysis of studies of teaching effectiveness related to student learning during the period 1995 to 2004, they articulated the role of student learning activities needed to build understanding:
We assumed that learning is a set of constructive processes in which the individual student (alone or socially) builds, activates, elaborates, and organizes knowledge structures. These processes are internal to the student and can be facilitated and fostered by components of teaching. Moreover, we assumed that higher order learning and a deep understanding of learning content is based on the quality of knowledge building and, thus, on the execution of learning activities. Learning activities should evoke both basic information processing and domain-specific processing. Consequently, we assumed the area of executing learning activities to be most proximal to knowledge building. (p. 462)
Relevant to Manizade et al.’s (2019) framework of examining relationships between variables to determine “good” teaching (Introduction, this volume), Siedal and Shavelson’s meta-analysis reported constructivist and social constructivist paradigms of knowing in studies that made connections between students’ execution of student mathematics learning activities (Type B), desirable student learning outcomes (Type A), and interactive teaching behaviors (Type C). Different theories of learning hypothesize frameworks centered on student engagement in mathematical learning activities and consequential desired student learning outcomes. As researchers interpret particular aspects of the learning process, it is framed by their own construction of theories to explain what they notice in students’ behaviors and dispositions.
In this section, I describe three theoretical perspectives that provide explanations of student engagement in learning activities which are needed to develop mathematical content knowledge with understanding and engage in processes envisioned in frameworks of curriculum initiatives over the last three decades. Departing from describing student learning activities in mathematics classrooms, two researchers’ conceptualizations of learning are examined through individual dyads and one-on-one teaching experiments using technology-based problems (Hackenberg, 2010; Simon et al., 2016, 2018; Tzur, 1999; Tzur & Simon, 2004). According to Tzur (2004), teaching experiments allow a teacher-researcher to present tasks, use ongoing analysis of students’ current cognitive constructs, and design more tasks that promote students’ engagement in constructing higher-level mathematical thinking. On the other hand, consistent with Medley’s call for research in classroom settings, Liljedahl (2016) studied connections between teaching practices and student engagement in learning activities in mathematics classrooms (Type CB research).
3.1 Developing Schemes: Progressive Coordination of Actions
Hackenberg’s (2010) model of students’ reversible multiplicative schemes is an important contribution to the evolution of research on students’ engagement in mathematics learning activities. Synthesizing prior studies of students’ development of fraction knowledge (Steffe, 1994; Tzur, 1995, 1999, 2004), Hackenberg identified three areas of research that informed key theoretical constructs for her study: (a) building on students’ prior knowledge and everyday experiences with fractions; (b) student learning activities for fraction knowledge—partitioning and unitizing; and (c) three of Kieren’s (1980) five subconstructs of fractions—quotients, operators, and measures of length. Further, she studied the process of reversibility in developing multiplicative relationships. Solving a problem with a sequence of actions in one direction is not easily decomposed to reorganize a scheme in the other direction. Before reporting on the results of Hackenberg’s study, her interpretation of scheme theory is described to explain one theory about how learners develop mathematical knowledge. Similar to Medley’s review, she drew upon theories of Piaget and Vygotsky to explain how students learn mathematics.
Hackenberg defined mathematical learning “as a process in which people make accommodations in schemes in ongoing interaction with their experiential world” (p. 385). According to von Glasersfeld’s (1989) interpretation of Piaget’s theories, a scheme consists of three parts: (a) an individual recognizes a situation or experience from a previous situation, (b) engagement in an activity associated with this situation, and (c) expecting the same result or outcome experienced when previously engaged in the activity. When examining fraction knowledge that is needed to develop multiplicative schemes, learners engage in activities, such as partitioning, dis-embedding, iterating, and splitting (see Steffe & Olive, 2010; Tzur, 1995, 1999, 2004 for details of these operations). A perturbation occurs when a learner’s current schemes no longer appear useful because they do not fit past learning experiences. To eliminate perturbations, schemes either remain stable, or become modified contingent upon a learner’s actions and reflections. For Hackenberg, a perturbation explains any reorganization of a learner’s existing schemes. Through repeated experiences, a process of reflective abstraction internalizes knowledge based upon the entire cycle of perturbation, action, and reflection. If a learner coordinates a scheme successfully using accommodation and does not need to physically act on parts of a task while describing his or her reasoning, an anticipatory scheme is constructed.
Hackenberg’s research design allowed her to engage four sixth-grade students in problems to facilitate each learner’s construction of anticipatory fraction schemes for reversible multiplicative relationships. Data collection consisted of videotaped episodes with cameras focused on interactions between a pair of students and researcher, and a recording of students’ computer or written work. Students used the JavaBars computer program (Biddlecomb & Olive, 2000) to facilitate a meaningful interpretation of the fraction construct of measure as length. Olive (1994) stated that microworlds are “tools for the teacher/researchers to construct situations in which they can use their emerging models of the children’s mathematics” (p. 71).
Using retrospective analysis of the video files, Hackenberg examined each student’s cognitive structures and how schemes changed over time. She reported that students constructed schemes to solve tasks when a fraction relationship existed between known and unknown quantities. One pair of students demonstrated use of fraction anticipatory schemes. Only one of the four students also engaged in reversible schemes when constructing reciprocal relationships. Hackenberg found that students’ construction of anticipatory schemes for multiplicative relationships required a coordination of three levels of units prior to engaging in an activity. Teaching experiments using technology-based problems offer an environment where researchers can examine students’ engagement in exploratory or expressive activities (Zbiek et al., 2007). Further, researchers could study how these two activities in technological settings are related to scheme theory to provide an explanation of student actions and reflections when they are building mathematical content knowledge and doing mathematics.
3.2 Learning Through Activity: Progressive Coordination of Mathematical Concepts
In a similar vein, building upon Piaget’s (1980) theoretical construct of reflective abstraction, Learning Through Activity [LTA] (Simon et al., 2016, 2018) is a research model that examines how learners engage in learning activities to develop mathematical concepts. In an evolution of research on student learning activities, prior LTA research from the past 10 years provided insight for an emerging integrated theory relevant to students’ conceptual learning and instructional design. Using Manizade et al.’s (2019) framework, the LTA research model potentially informs future research making connections between Type D, C, B, and A variables (Introduction, this volume). Specifically, the LTA model seeks to answer this question: “How do humans learn mathematical concepts, and how can instruction be designed to enlist these learning processes in service of learning particular mathematical concepts?” (Simon et al., 2018, p. 96). Further, what is the process that engages a learner to move forward from constructing one concept to a higher-level concept in a learner’s network of knowledge for different mathematical concepts? And how can this learning process be promoted?
To study these questions, Simon et al. (2018) proposed an elaboration of the construct of reflective abstraction with two refinements: Focusing on new concepts developed from prior concepts rather than using schemes, and a shift away from earlier work of abstractions attributed to a reflection of activity-effect relationships (Simon et al., 2004). The authors asserted that perturbations do not provide evidence of how learning occurs and scheme theory does not explain what a learner “attends to” in order to achieve a learning goal. Moreover, they no longer viewed reflective abstraction as a chronological sequence of actions for developing a new concept, but a construction of higher-level concepts based on lower-level actions. Balancing the needs of mathematics and a learner, Simon et al. (2018) described developing concepts as a “bi-directional” process; “that is, how one explains conceptual learning is dependent on the nature of a concept, and the nature of a concept is, in part, determined by the process through which it is constructed” (p. 98). A concept consists of a goal (e.g., solve a task) and an action a learner takes to achieve the goal. When engaged in mathematical activity, learning may not occur if there are no prior actions (i.e., mental activities) a learner can access. In LTA’s model, actions are considered components of concepts, which transforms the construct of reflective abstraction from a coordination of actions to a coordination of existing concepts (Simon et al., 2016). Student learning activities provide opportunities for learners to construct mathematical concepts if they are aware of a sequence of available mental actions they have already constructed.
As an example of progressive coordination of concepts, Simon et al. (2018) analyzed the 5-year Measurement Approach to Rational Number (MARN) Project data. Similar to Hackenberg’s (2010) study, the same program, JavaBars, was used to facilitate students’ construction of fraction and multiplicative concepts. A teacher-researcher interacted one-on-one with a student to avoid the influence of others’ thinking that is often encouraged in classroom settings. The task sequence research design included: “(1) Assess the relevant understanding of the learner; (2) Specify the learning goal (intended abstraction); (3) Identify an activity or activity sequence that the learner already has available that could be the basis for the new abstraction; and (4) Design a sequence of tasks that is likely to bring forth the learners’ use of this activity and lead to the intended abstraction” (Simon et al., 2016, p. 67). When students engaged in carefully designed tasks intended to promote conceptual learning, individual learning processes illustrated “in the moment” thinking and student focus while solving the task.
Building on Tzur and Simon’s (2004) hypothesis that two stages, participatory and anticipation, are necessary to develop mathematical concepts, LTA researchers (Simon et al., 2016, 2018) proposed that an initial reflective abstraction is only the first of two stages for building a mathematical concept. For the first, participatory stage, a learner engages in an activity and uses existing concepts to begin to develop new mathematical knowledge. The analyses of MARN data provided evidence that learners may not be able to use their initial abstraction (concept) created one day for a similar task the following day. Only when a learner could call upon an earlier abstraction (concept) in different contexts, LTA researchers identified this second stage as anticipatory. Simon et al. (2018) reported that a fourth-grade student coordinated pairs of actions when determining a composite fraction amount of a whole number quantity. Higher-level conceptual knowledge was built upon prior existing knowledge. The two-stage distinction represents a new aspect of research when analyzing qualitative data of student engagement in learning activities. Still, LTA researchers point out that future research is needed to provide a more detailed explanation of how teachers can promote a transition from students’ participatory stage to an anticipatory stage for developing conceptual knowledge. What is the role of teacher activities (Type C) to facilitate this transition of students engaged in knowing and doing mathematics (Type B)?
To inform data analysis and instructional design, LTA researchers (Simon et al., 2016, 2018) also continued to study the development of a reversible concept Hackenberg (2010) and other researchers (Steffe, 1994; Tzur, 2004) have examined as a necessary part of conceptual learning. A student may construct a reversible concept when he or she does not need to engage in lower-level actions where the original concept was developed. Using the context of Cognitively Guided Instruction (CGI) research-based addition and subtraction tasks (Carpenter et al., 2015), LTA researchers built a typology of reversibility for six potential tasks (see Simon et al., 2016, 2018 for details of reversible concepts). Consistent with Hackenberg’s (2010) findings for reversibility, Simon et al. (2018) reported that a learner may have an original concept and not easily construct reversible concepts. The typology of reversibility has informed these researchers’ decisions related to the design of instructional tasks used during the LTA teaching episodes.
Overall, LTA’s theoretical perspective focuses on explaining the process of building conceptual knowledge through students’ engagement in learning activities as a progressive coordination of mathematical concepts. Using ongoing data analyses, individual tasks and sequences of tasks are modified dependent upon a learner’s progress. If no new concept is developed, more of the same or different experiences are needed to facilitate student reflection and a new abstraction. A challenge for researchers is to reflect upon ways to apply LTA’s theory beyond individual students engaged in teaching experiment settings and implemented in whole-classroom settings. To this end, in the next section, I provide an example of student construction of mathematical knowledge and engagement in learning activities in the context of classrooms.
3.3 The AHA! Experience: Proxies of Student Engagement
Medley (1987) recommended five different types of future research needed to inform effective teaching practices, with two types focused on student learning activities in classroom settings: Type BA, “research relates learning outcomes to pupil learning experiences” and Type CB, “research relates interactive teacher behavior to pupil learning activities” (p. 110). For Type CB relationships, Medley posed the following two questions for researchers to examine: “The teacher whose pupils have the best learning experiences in school (Type B)? The teacher whose classroom behavior conforms most closely to some conception of ‘best’ practice (Type C)?” (p. 106). Using Manizade et al.’s (2019) framework (Introduction, this volume), studies are needed that focus on student–teacher interactions between student learning activities and interactive teacher behaviors that engage students in becoming knowers and doers of mathematics.
As an example of Type CB research which evolved from 10 years of earlier research in Canada, Liljedahl (2016) proposed nine elements of critical teaching practices that are needed for teachers to orchestrate and sustain student thinking in mathematics classrooms. Moreover, he identified student proxies of engagement to describe and measure the effectiveness of the nine elements of teaching practices to facilitate student learning. In many of his classroom observations, he reported how teachers implicitly assumed “that the students either could not or would not think” (p. 362). This may be related to established classroom norms that supported learning in traditional ways which hindered students’ ability to engage in thinking and problem-solving behaviors recommended by reform curriculum initiatives.
Liledahl argued for a transition moving away from a non-thinking toward a thinking classroom; that is, “a space that is inhabited by thinking individuals as well as individuals thinking collectively, learning together and constructing knowledge and understanding through activity and discussion” (p. 362). Consistent with other researchers’ (Cobb, 1994; Cobb et al., 1992) calls for the coordination of Piaget’s (1970) constructivist and Vygotsky’s (1981) sociocultural perspectives, Liljedahl assumed that knowledge is constructed both individually and collectively, during social interactions with others while engaged in doing mathematical activities. For Cobb (1994), these two complementary perspectives address how theories of learning emerge; that is, “the sociocultural perspective gives rise to theories of the conditions for the possibility of learning, whereas theories developed from the constructivist perspective focus on both what students learn and the processes by which they do so” (p. 18). As described earlier, Hackenberg’s and Simon et al.’s research approach of teaching experiments provided explanations for the process of student learning outside mathematics classrooms.
To inform Liljedah’s (2016) study of teaching and learning practices in secondary mathematics classrooms, it is useful to review his perspective on the process of mathematical learning “in the moment” during group work and individual problem solving. In 2005, experiences in his mathematics course for prospective elementary school teachers (PTs) affected their thinking about teaching and learning mathematics. An AHA! experience occurred when “a problem has just been solved, or a new piece of mathematics has been found, and it has happened in a flash of insight, in a moment of illumination” (Liljedahl, 2005, p. 219). If a student was “stuck” working on a problem, but experienced an AHA! moment, she or he became “unstuck” and continued to make progress. Liljedahl studied the learning process of how this sudden insight or AHA! experience happened and how it affected the PTs’ ability to make sense of problems and persevere. Some PTs often identify themselves as failures in mathematics based on a lack of successful learning experiences and they exhibit high math anxiety in mathematics courses. Given the vision of mathematics curriculum initiatives for learners to develop a deep understanding of mathematics, a potential increase in the intensity of affective responses may result in promoting more negative attitudes when compared to learning routine procedures. Liljedahl’s conceptual framework included attention to the affective domain for learning mathematics; that is, examining the constructs of beliefs, attitudes, and emotions (McLeod, 1992). Beliefs reflect low levels of affective involvement, are relatively stable, and develop over a long period of time. According to McLeod, attitude “refers to affective responses that involve positive or negative feelings of moderate intensity and reasonable stability” (p. 581). By contrast, the emotional aspects of learning are unstable and connect more to “in the moment” feelings that are “fleeting” (McLeod, 1992).
To study the process of how learning occurs when students experience insight during an AHA! experience, Liljedahl (2005) examined how “moments of illumination” were related to positive emotions and how they changed PTs beliefs and attitudes about doing mathematics. For an assignment, PTs wrote about an AHA! experience while problem solving. Analyzing responses, Liljedahl reported four affective themes: anxiety, pleasure, change in beliefs, and change in attitudes. He found that repeated positive emotional AHA! experiences produced positive beliefs and attitudes about mathematics and students’ abilities to do mathematics. As an example, one PT wrote: “AHA moments are those great moments of deeper understanding and clarification of problems where incorrect or incomplete understanding is overcome. These moments inspire us and encourage us to keep going despite the frustration and anxiety that often tends to overwhelm us in times of difficulty when attempting to solve a problem” (p. 231). Engaged in making sense of mathematics, this PT became aware of her need to persevere, as moments of insight can lead to an understanding of mathematics. Liljedahl hypothesized two explanations for a high degree of change in the affective domain: “Positive emotion that is achieved during an AHA! experience is much more powerful than the emotions that are achieved through non-illuminated problem solving” and “Having solved something challenging, or understood something difficult, besides being a great accomplishment is also a measure of what is possible” (p. 231). AHA! experiences promoted changes in PTs’ behaviors and dispositions; that is, engagement in student learning activities of problem solving and perseverance.
Liljedahl (2016) extended his work and investigated engagement of secondary mathematics students who worked together in small groups of two to four to solve problem-solving tasks. He studied the interaction between Type B and C variables by examining the effect of different teaching practices and how students engaged in problem solving. To inform his observations, he used Mason’s (2002) framework of noticing; that is, “Noticing refers to the act of focusing attention and making sense of situational features in a visually complex world” (Jacobs & Spangler, 2017, p. 771). From data analysis, he proposed nine elements of effective mathematics teaching practices for building and sustaining a thinking classroom (see Liljedahl, 2016; for list/analysis of practices). Using an iterative design-based research approach, each element provided opportunities for teaching practices to be refined or dropped, depending on how students engaged in mathematical thinking while problem solving. Still, Liljedahl reported that it was challenging for teachers and students to shift from traditional, familiar classroom norms. To resolve this issue, he used a “contrarian” approach in which an ineffective practice was changed to the exact opposite and then implemented in mathematics classrooms.
Liljedahl measured the effectiveness of teaching practices by studying “proxies of engagement—observable and measurable (either qualitatively or quantitatively) student behaviors” (p. 366). He referred to these behaviors as “proxies” because he did not have direct access to student thinking and he could not tell if the mathematical thinking was an individual construction, or, collective thinking due to interactions with others. He reported eight student behaviors and dispositions: (1) time to task, (2) time to first mathematical notation, (3) eagerness to start, (4) discussion, (5) participation, (6) persistence, (7) non-linearity of work, and (8) knowledge mobility. As described in Sect. 2, linkages can be made between Liljedahl’s student engagement in learning activities (Type B) and those listed in various frameworks of curriculum initiatives. In response to Lesh et al.’s (2020) concerns of the need for “measures” of higher-level student understanding, Liljedahl provided a framework of student behaviors and dispositions that could be used in future studies to provide evidence of the effects of students’ engagement in learning activities while building content knowledge and doing mathematics.
Moreover, Middleton et al. (2017) reported researchers studying student engagement experiences often approach their studies using a lens of an observational study. Also, interview data can provide more detailed insights on the observed behaviors. For his 2016 study, Liljedahl conducted follow-up interviews to confirm teachers’ interpretation of student behaviors. Similar to other research perspectives focused on how student mathematical learning occurs and described in this section, Liljedahl asserted that we need “to honor the activities of a thinking classroom through a focus on the processes of learning more so than the products and it needs to include both group work and individual work” (p. 382). That is, as Medley (1987) recommended for the future evolution of research for teaching, there is a need to focus on the interplay between elements of teaching practices and student engagement in learning activities (Type B and C variables) rather than examining only student learning outcomes (Type A).
In summary, the last three decades of frameworks of mathematics curriculum initiatives impacted researchers’ approaches to studying the needs of the learner and needs of the discipline for effective mathematics teaching and learning. The complexity of studying student engagement in higher-level thinking with understanding has called for an examination of student learning activities through a lens of various theoretical perspectives that provide explanations relevant to how and why student behaviors and dispositions develop in the way they do. Given the different perspectives relevant to students’ development of mathematical thinking with understanding and doing mathematics, theories have emerged in particular settings using teaching experiments in technological settings and mathematics classroom environments. As students become knowers and doers of mathematics, Chan and Clark (2017) address the difficulty in conducting valid and reliable research studies of student learning in classroom settings, as there is a “tension between the need for control in an experimental environment and the freedom needed for the participants to interact and behave as they would in a naturalistic classroom setting remains a challenge in the design of research studies investigating student learning in social settings” (p. 954).
Nevertheless, different theoretical perspectives allow researchers to gain insight into potential refinements in the conceptualization or design of studies that examine student learning activities and active student engagement within diverse individual and whole-class settings, including CT tool environments. This could result in unique insights emerging from studies making explicit connections between Type A, B, and C variable relationships. The next section characterizes a selection of studies of student mathematics learning activities identified earlier in Sect. 2 that encompass most behaviors and dispositions into two main activities: (1) making sense of mathematics (i.e., problem-solving) and (2) perseverance in doing mathematics: productive disposition, productive struggle, and productive failure. Taken together, the studies extend the mathematics education knowledge base of the effects of student learning activities when students engage in developing mathematics knowledge with understanding and doing mathematics. Each study includes a brief description of methodology to address Medley’s (1987) quality concerns related to conceptualization, instrumentation, design, and statistical analysis.
4 Making Sense and Perseverance Involved in Learning Mathematics Knowledge
4.1 Problem Solving
Mathematicians, mathematics educators, and teachers have described the problem-solving process in multiple ways (Schoenfeld, 1992) which has led to the development of research agendas focused on examining student behaviors supporting the development of mathematical knowledge (Lesh & Zawojewski, 2007; Schoenfeld, 1992; Schoenfeld & the Teaching for Robust Understanding [TRU] project, 2016). According to Santos-Trigo’s (2020) recent review of mathematics education research literature, problem solving is defined as “the systematic study of what the process of formulating and solving problems entails and the ways to structure problem-solving approaches to learn mathematics” (p. 687). Over the last three decades, studying the behaviors and dispositions of student engagement in problem solving has continued to be a research priority with an emphasis on detailed accounts of teacher expectations for problem solving and student interactions in mathematics classrooms. This is attributed to the shift of focus on teachers understanding students’ mathematical thinking “in the moment” and making connections between Type B and C variables (Manizade et al., 2019). Lesh and Zawojewski (2007) described students’ engagement in problem solving as using “several iterative cycles of expressing, testing and revising mathematical interpretations—and of sorting out, integrating, modifying, revising, or refining clusters of mathematical concepts from various topics within and beyond mathematics” (p. 782). As described earlier, teaching experiment methodology (Hackenberg, 2010; Simon et al., 2016, 2018) has provided an opportunity for researchers to examine students’ thinking “in the moment” and explain how students develop mathematical conceptual understanding.
An emerging field of research is investigating student learning activities (see Sect. 2) identified in the Common Core standards of mathematical practice [SMP] (Bostic & Sondergeld, 2015; Gilbert, 2014; Sanchez et al., 2015) and similar mathematical competencies (Hipkins, 2018; McDowell & Hipkins, 2018; Niss, 2003; NRC, 2001; Turner, 2010) that focus on students’ sense-making and extends Polya’s (2004) problem-solving research. A new term of mathematical sense-making defines the needs of a learner when engaged in problem solving as a critical component of what it means for students to know and do mathematics. A limited number of qualitative studies (Bostic & Sondergeld, 2015; Kapur, 2014; Warshauer, 2015) have examined research questions focused on students’ problem-solving experiences in mathematics classrooms. Although the term problem solving is not explicitly stated in the SMP, the meaning is implicit and places a priority on problem solving as students “make sense” of mathematical content.
The literature revealed various teacher interpretations (Type C) of student problem-solving behaviors (Type B) as envisioned in frameworks of mathematics curriculum initiatives. In an exploratory study, Keazer and Jung (2020) designed a survey for 71 PTs in which they responded to questions about student mathematics learning activities. For example, PTs read a paragraph description of the first SMP and were asked to think about their future teaching when responding: “Which aspect of SMP1 do you think will be most difficult for you to develop in your students? Why?” (p. 82). Separate statements of the SMP1 description were matched alongside PT responses that described anticipated difficulties when engaging students in these behaviors and dispositions. The PTs selected: They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt, with the highest frequency as the most difficult learning activity to develop; the second highest activity was: Mathematically proficient students check their answers to problems using a different method, and they continually ask themselves, ‘Does this make sense?’ Encouraging their future students to plan, use more than one strategy, and reflect on the problem-solving process as “making sense” did not appear to be a strength. Close to one-third of the PTs shared that they themselves struggled with some of the expected learning goals of SMP1. Consequently, it was a major challenge for many PTs to anticipate how they would engage students in learning activities (Type B) in their future mathematics classrooms.
Keazer and Jung’s findings led to their design of a conceptual framework matching student behaviors and dispositions articulated in the SMP1 sentences to Polya’s (2004) four problem-solving phases. Citing the research of Schoenfeld and the TRU project (2016) with a focus on the cognitive demand of tasks dimension, they proposed using the SMP1-Polya framework to facilitate prospective and practicing teachers’ understanding of different levels of sense making (i.e., problem solving). According to Keazer and Jung, “SMP1 aligns with level 3 sense making, in which the teacher supports students in mathematical exploration and productive struggle that results in understanding and engagement in mathematical practices” (p. 88). Making connections explicit between sections of SMP1 sentences and Polya’s problem-solving phases could provide an entry point for supporting teachers’ understanding of student engagement in problem-solving experiences. With the high frequency of two SMP1 statements in the PTs responses, the student behaviors of Polya’s second phase, devise a plan, and fourth phase, look back, continued to show the need to engage students in problem solving or making sense of mathematics to develop a progression of understanding mathematical concepts. For researchers interested in understanding different levels of students’ sense making that supports participatory and anticipatory conceptual development, problem-solving activities may provide an opportunity to examine LTA’s theory of progression of concepts (Simon et al., 2016, 2018) beyond individual students to small- and whole-group work methods in mathematics classrooms.
4.2 Productive Disposition
Building upon Liljedahl’s (2016) theoretical perspective that includes affective factors of learner engagement, recent studies are focusing on student “perseverance” in solving problems. As described earlier, the NRC (2001) defined an affective strand of productive disposition as viewing “mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy” (p. 116). Gilbert (2014) broadened the meaning of productive disposition to include learning activities in which students are “making sense of problems and persevering in solving them” and linkages to motivational theory. Observing students actively engaged in doing mathematics, researchers could ask: What do strengths-based learners look like when they exhibit the characteristics of a productive disposition in mathematics classrooms? According to Kobett and Karp (2020), “They are just curious and fascinated. They work diligently, even when faced with obstacles. They try again when stymied. They understand that learning mathematics can be hard work and they will, therefore, often continue to work well after their peers have given up” (p. 43). For further investigation, how might researchers study and measure these characteristics of students displaying productive disposition?
As an example, in October 2005, Gilbert (2014) surveyed a sample of 140 prealgebra students who volunteered to participate from two California middle schools. She hypothesized a relationship between productive disposition (Type B) and an achievement-related (Type A) variables. Specifically, she studied a relationship between students’ abilities to attend to precision when they critiqued another student’s work. To examine student learning activities, Gilbert stated, “The behaviors required to demonstrate these SMP thus relate to psychological constructs that go beyond ability beliefs (e.g., efficacy) and utility value (i.e., usefulness of mathematics)” (p. 340). First, students responded to survey questions that measured motivational constructs associated with productive disposition, such as, “My main goal in math is to learn as much as I can” (mastery-approach goal) (p. 342). Second, students completed an assessment item which measured their ability to add fractions with unlike denominators. Third, using an open-ended question, students were given a student’s incorrect work, ½ + ¾ = 4/6, and asked to write an explanation to the student indicating why the answer was right or wrong.
Gilbert reported using reliability and factor analyses with an examination of correlations that documented the subscales measured distinct constructs of productive disposition. She found that 44% of the students responded with a more precise critique of a student’s incorrect strategy by engaging longer and suggested at least two steps to correct the student’s work. Also, a multivariate analysis of variance supported the hypothesis that students who responded with a more precise critique of a peer’s work reported a higher productive disposition than students who responded with a basic critique. Two motivation constructs: (1) productive disposition and (2) mastery approach goals and negative emotions, showed statistically significant differences between the two groups. Based on survey responses, more precise critique students reported higher mastery-approach goals and less frequent negative emotions compared to basic critique students. The results of this study suggest more research is needed to focus on NCTM’s (2014) effective teaching practices (Type C), including “building procedural fluency from conceptual understanding” (Type B, mastery-approach goals), where the procedure of adding fractions is built upon a foundation of conceptual understanding. Using multiple representations of fractions, students could be provided with opportunities to make connections between concepts and procedures situated in a classroom where meaningful mathematics discourse occurs.
4.3 Productive Struggle
Beginning elementary school teachers often say that students should not “struggle” or be confused in learning mathematics and if they do struggle, a teacher may restate the same strategy for students to follow. Keazer and Jung (2020) reported a few PTs stated they needed to “show and tell” (Type C) all possible strategies to students rather than engage them in productive struggle. However, researchers have reported the positive effects of productive struggle whereby the act of struggling is crucial for students learning mathematics with understanding (Hiebert & Grouws, 2007; Keazer & Jung, 2020; NCTM, 2014; Schoenfeld & TRU, 2016; Warshauer, 2015). Hiebert and Grouws (2007) defined productive struggle as a student learning behavior that promotes students making sense of mathematics and is necessary to develop conceptual understanding. In a similar manner, Dingham et al. (2019) identified productive struggle as “intellectual effort students expend to make sense of mathematical concepts that are challenging but fall within the students’ reasoning capabilities” (p. 91). Schoenfeld and the TRU project (2016) identified five dimensions of mathematics learning activities that were necessary to ensure that classroom environments supported students as “powerful thinkers.” In response to the needs of the discipline, one dimension focused on the cognitive demand of tasks in “which students have opportunities to grapple with and make sense of important disciplinary ideas and their use. Students learn best when they are challenged… The level of challenge should be conducive to what has been called productive struggle” (p. 1). Similar to behaviors and dispositions described in Sect. 2, productive struggle engages students in perseverance when solving challenging problems. Schoenfeld and the TRU project (2016) reported teachers categorized at the highest level supported “students in productive struggle in building understandings and engaging in mathematical practices” (p. 24). Likewise, NCTM (2014) explicitly addressed the need for teachers to engage students in productive struggle: “Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and support to engage in productive struggle as they grapple with mathematical ideas and relationships” (p. 48).
Warshauer (2015) studied what different types of student struggle looked like in six U.S. middle school mathematics classrooms and how teachers responded to their students’ struggles (Type CB research). His conceptual framework centered on the “process of struggling to make sense” (p. 378) for a deep understanding of mathematics, the relationship between the students’ struggles and the types of mathematical tasks explored, and the dynamic, social nature of interaction when teachers responded as helping or hindering student learning. Given the complexity of studying student–teacher and student–student interactions, he conducted embedded case study methodology (Yin, 2009) using instructional episodes. Multiple sources of data allowed for triangulation of the data to establish dependability, confirmability, and transferability when he reported findings of the study.
Warshauer developed a productive struggle framework for reporting the frequency of four different types of student behavior of struggle: get started, carry out a process, uncertainty in explaining and sense-making, and express misconception and errors (Type B). As an example, “confusion about what the task was asking” or a “gesture of uncertainty or resignation” (p. 385) described students struggling at the beginning of the problem-solving process. It should be noted that there is a parallel alignment in some of his framework categories to Polya’s (2004) four phases of problem solving; that is, “get started” with Polya’s first phase and “carry out the process” with the third phase. Similar to Keazer and Jung’s (2020) study, connecting student struggles to some of Polya’s problem-solving phases could provide researchers with a new lens for analyzing students’ sense-making through existing problem-solving literature.
For student–student interactions, Warshauer reported students’ “uncertainty in explaining and sense-making” when their explanations lacked clarity and did not make sense to other students, or they struggled with appropriate responses. He found evidence of proportional reasoning misconceptions such as using additive rather than multiplicative thinking for the meaning of ratios. For teacher-student interactions, Warshauer reported the frequency of four different types of teacher responses to student struggles: telling, directed guidance, probing guidance, and affordance (Type C). The first two types of responses did not engage students in productively understanding the concept of proportional reasoning. As might be anticipated, a telling response often enabled a student to move beyond being stuck, but used a teacher’s thinking rather than student thinking. Often, a procedure was stated for a student to follow which resulted in lowering a problem’s level of cognitive demand. Both the last two types of teacher responses supported students’ thinking without lowering the level of cognitive demand.
Warshauer identified three outcomes of student struggles: productive, productive at a lower level, and unproductive. Productive interactions included: “(1) maintained the intended goals and cognitive demand of the task; (2) supported students’ thinking by acknowledging effort and mathematical understanding and (3) enabled students to move forward in the task execution through student actions” (p. 390). He reported 42% of student struggles met all three criteria, 40% of the interactions only used the second criteria, and 18% of struggles were unproductive. For unproductive struggles, students were not “making progress toward the goals of the task; reached a solution but a task that had been transformed to a procedural one that significantly reduced the task’s intended cognitive demand; or if the students simply stopped trying” (p. 391). In essence, teachers balanced how much they pressed students to persevere based on students’ levels of tolerance for frustration at different levels of cognitive demand. Productive struggle depended on keeping tasks at higher cognitive-demand levels, supporting students’ perseverance, and teachers who provided guidance and affordance. These results promote the future use of a productive struggle framework as a tool for researchers examining students’ productive struggles (Type B) and teacher-student interactions (Type BC research).
4.4 Productive Failure
Research on examining students’ productive struggle when attempting to make sense of mathematics content and persevere in solving problems, is related to engagement in another Type B variable: productive failure (Kapur, 2010, 2014; Simpson & Maltese, 2017). Failure can be defined in many ways, such as, giving up or stopping engagement in an activity, not reaching the intended goal, or incorrect problem solutions. Further, failure can bring to the forefront negative connotations such as “negative emotional states (e.g., fear, anxiety, depression), low perceptions of self, diminished sense of belonging, less academic risk taking, and avoidant behaviors” (Simpson & Maltese, 2017, p. 223). These negative behaviors and dispositions suggest that failure may decrease students’ desire or ability to continue to problem solve. Still, what might happen if we view failure as a “necessary and sufficient condition” for students’ engagement in learning activities? In what ways might students’ metacognitive analysis of their problem-solving process while stuck on a problem make errors explicit, or, how may critiquing their peers’ use of models and strategies support learning? According to the Partnership for 21st Century Learning (2019), creativity and innovation are enhanced through failure; that is, persistent attempts are part of innovative practices marked by “a long-term, cyclical process of small successes and frequent mistakes” (p. 4). How might this process of success and failure be part of learning activities?
Simpson and Maltese (2017) studied the role of failure in the development of science, technology, engineering, or mathematics (STEM) professionals. They interviewed 99 STEM professionals about their experiences in entering and pursuing a STEM-related career. Using life history interviews, they focused on how participants’ failure shaped: outlooks connected to failure, career trajectories within STEM fields, and provision of additional skills. They reported about one-fifth of the professionals described failure as a positive experience. However, when using a follow-up survey and asked if “the term failure was an accurate representation or label of their experiences, 67% disagreed and claimed words and phrases such as inadaptability, setback, unsuccessful, not living up to expected outcomes, defeat, and learning opportunity as more suitable” (p. 228). Rather than considering failure as an end to becoming a STEM-related professional, they reported two-thirds of respondents saw failure as a minor setback that motivated them to move past difficulties in coursework or professional projects. Also, they described the trait of “persistence” as the most “important quality to possess when experiencing instances of failure” (p. 233). As described earlier, perseverance is a productive student mathematics learning activity envisioned by curriculum initiatives over the last three decades.
In a study of ninth-grade students who lived in the national capital region of India, Kapur (2014) proposed that engaging students in problem solving which initially resulted in productive failure would ensure “correct conceptual knowledge and mathematical procedures over faulty ones” (p. 1009). For Kapur, the term productive failure meant that students’ initial individual problem-solving attempts were unsuccessful in finding correct solutions, and became productive when supported with appropriate mathematics classroom instruction. Similar to productive behaviors researched over the last decade, Kapur hypothesized relationships between individual student failure (Type B), sequence of teaching phases (Type C), and student outcomes (Type A). For Kapur’s (2014) study, in one classroom, students first participated in a problem-solving (PS) phase for standard deviation (SD) problems that was followed by a direct instruction (DI) phase. In the comparison classroom, the same teacher first taught students using DI followed by a PS phase. During the PS phase, students solved a SD practical problem individually and the teacher encouraged them to use multiple strategies and find as many solutions as possible. For the more traditional DI phase, the teacher showed four examples of SD problems, gave time for individual student practice, and provided student feedback related to common SD misconceptions.
Similar to Gilbert’s (2014) study, Kapur examined aspects of both cognitive and affective behaviors and dispositions using surveys and mathematics content knowledge measures. He designed four instruments to measure students’ learning of SD concepts and procedures. These included a pre- and post-test of SD knowledge and survey questions relevant to engagement and mental effort. Kapur reported that the class of students who began instruction with a PS phase provided an average of six different solutions to a SD practical problem. The number of solutions served as a “proxy” measure of students’ prior knowledge activation. By comparison, the other class of students beginning with DI, only demonstrated an average of three different solutions.
Examining affective behaviors and dispositions, data collected from survey questions provided evidence of significantly greater mental effort of productive failure students (PS phase first) compared to DI students (PS phase second) during both phases of instruction. Yet, Kapur found no significant difference between the two sequences of instruction on math ability or prior SD knowledge. Analyzing posttest data and the two different sequences of instruction, Kapur reported “significant multivariate main effects only of math ability and condition” (p. 1013). Although there was no significant difference between students’ procedural knowledge in either classroom, students engaged in the PS phase first, significantly outperformed students receiving the DI phase first on posttest conceptual understanding and transfer items. No significant correlations appeared in the data for students beginning with DI.
Kapur’s research supports a learner’s perspective that is relevant to NCTM’s (2014) teaching practices whereby teachers provide students time to think, make conjectures, and use their own strategies while problem solving: “Effective teaching of mathematics engages students in solving and discussing tasks that promote mathematical reasoning and problem solving and allow multiple entry points and varied solution strategies” (p. 17). Kapur’s study provides specificity for this teaching practice (Type C) by supporting engagement in student learner activities (Type B) that may include productive failure first at the beginning of a lesson. After experiencing a PS phase followed by more instruction, students engaged in more mental effort and demonstrated more conceptual understanding than students who experienced DI (teaching as telling) at the beginning of a lesson. Thus, it appeared that productive failure provided students with an opportunity to learn from their own failed solutions and they were ready to engage in classroom-based instruction with a focus on important mathematical ideas relevant to SD. For teachers who believe it takes too much time to allow students to think and engage individually in the PS process, Kapur found that “time on task, the number of problems solved, and materials for each of the phases were identical in both [classes]” (p. 1010).
5 Discussion of Findings and Future Implications
What can be learned from this selected analysis and review of student mathematics learning activities that actively engage students in knowing and doing mathematics? How has research evolved over the last three decades to support students’ development of mathematical content knowledge and engagement in processes (i.e., behaviors and dispositions) that have been identified in multiple frameworks of international mathematics curriculum initiatives? How has the increased availability of CT tools for students enhanced researchers’ observations and inferences of students’ thinking, including technologies to advance research methodologies? What theoretical perspectives have researchers refined for examining the nature of students’ construction of mathematical content knowledge with understanding to provide explanations relevant to how and why student behaviors and dispositions develop in the way they do within different learning environments? Lastly, how has this chapter informed future research needed to advance our understanding of student learning activities?
To address these questions, this chapter’s review and analysis of three decades of research highlight the contributions of selected studies related to understanding the nature of student mathematics learning activities and the resulting impact on students’ knowing and doing mathematics. The findings offer insights for researchers, curriculum designers, administrators, teachers, parents, students, and other stakeholders involved in mathematics teaching and learning, situated in both non-technological and technological environments. First, a major theme in this chapter of studies of student learning activities was researchers’ increased focus on reviewing multiple characterizations of mathematical behaviors and dispositions to refine competency frameworks to study how students actively engage in the processes of learning mathematics. An evolution of similar and interrelated learning activities from different countries provided details about what processes to study and how to analyze the effect of students’ learning experiences, including two main learning activities of making sense of mathematical knowledge and perseverance in doing mathematics. At the beginning of the twenty-first century, Sfard (2003) asserted that learning activities should “engage students in what may count as an authentic activity of mathematizing rather than in learning ready-made mathematical facts” (p. 354). There has been growth in researchers’ understanding of what constructs to study related to student mathematics learning activities (Type B) and various theoretical perspectives that provide explanations of students’ engagement in knowing and doing mathematics.
Although Kobert and Karp (2020) created an alignment of student behaviors and dispositions between the five strands of mathematical proficiency (NRC, 2001) and the eight standards of mathematical practice (NGA Center for Best Practices and CCSSO, 2010), few studies have focused on this alignment and what can be learned to inform our understanding of student engagement in learning activities. Researchers could further examine the relationships among these multiple frameworks in curriculum initiatives and the impact of using different (albeit similar) frameworks (see Sect. 2) to examine students’ active engagement in learning mathematics. What is the same and what is different in using these identified mathematical behaviors and dispositions to investigate students’ knowing and doing mathematics? As another example, how might researchers take advantage of Koestler et al.’s (2013) and Kobett and Karp’s alignment between the process standards (NCTM, 2000) and standards of mathematical practice (NGA Center for Best Practices and CCSSO, 2010)? What insights might emerge when researchers “synergize” these two frameworks together to inform research studies about students’ engagement in mathematics learning activities? To respond to engaging students in an “authentic activity of mathematizing” that mathematicians display when they know and do mathematics (see Sect. 2), researchers could build upon a rich tradition of studying students’ problem-solving behaviors (e.g., Polya’s problem-solving phases) with a further examination of critical connections between frameworks and conceptualizations of higher-level mathematical processes. Further, research could focus on at least three of Liljedahl’s (2016) proxies of student engagement (i.e., discussion, participation, and persistence) to examine and explain students’ perseverance while problem solving, both individually and in groups, to make inferences about students’ mathematical thinking.
Second, research over the past three decades has extended our understanding of how and why the process of student engagement in learning and doing mathematics occurs in different learning environments. Using teaching experiment methodology, a small number of studies have articulated emerging theoretical perspectives that focused on analyzing students’ development of mathematical concepts in technological settings outside the classroom (Hackenberg, 2010; Simon et al., 2016, 2018). From these studies, observations and analyses documented how students engaged in a sequence of learning activities using CT tools that were intended to promote students’ reflective abstraction and reversible thinking for rational number concepts. How might a similar cycle of students’ engagement in learning activities including CT tools and coupled with researchers’ noticing and analyses provide a research pathway to further our understanding and infer students’ mathematical thinking for reversible thinking in different conceptual areas? Simon et al. (2018) proposed that researchers could positively contribute to addressing unsuccessful mathematics instruction for specific conceptual areas (e.g., fractions, ratios, proportions, and other) through implementing the LTA research model.
One result of the last decade of research, Simon et al. (2018) refined an earlier theoretical framework of scheme theory and moved research forward with a better understanding of the constructs of student learning to create the LTA theory which resulted in analyzing students’ progressive development of concepts. In what ways could researchers use the LTA research model of task sequence design and analyses to investigate students’ engagement in mathematical processes that focus on a progressive concept development and lead to intended abstractions in non-technological environments? Further studies of students’ learning with understanding in different areas of mathematics could provide more useful explanations as to how and why students’ knowledge changes or does not change “over time” or “in the moment.” Moreover, if researchers look beyond using teaching experiment methodology, what can be gleaned from the LTA approach to investigate small- and whole-group student engagement in knowing and doing mathematics in classrooms? In particular, findings from Liljedahl’s (2005, 2016) studies should be explored using his new conceptual framework to measure and expand our understanding of a relationship between mathematics teaching practices and student learning activities (Type CB research) that seems necessary to build and sustain thinking classrooms. Furthermore, the past two decades of research studies about student mathematics learning activities has shown an increased focus of examining the interrelationships between Type B and C variables (Keazer & Jung, 2020; Schoenfeld & TRU, 2016; Warshauer, 2015) to inform our understanding of the effects of students’ engagement in learning activities. Yet, more studies are needed to explore research questions about relationships among Type B and A variables (Gilbert, 2014) and Type A, B, and C variables (Kapur, 2014) to improve student learning outcomes (Type A).
A third finding of this chapter is the identification of some of the important constructs (e.g., expressive activity, exploratory activity, representational fluency, and others) that are needed to inform research related to technology-based mathematics teaching and learning (Zbiek et al, 2007). These constructs should be further explored to refine our current understanding of links between student engagement in the processes (i.e., behaviors and dispositions) of learning mathematics and students’ use of CT tools. As an example of future research for studying “promising variables” with student-tool relationships, Zbiek et al. proposed: “Students’ dragging behavior [with CT tools] could be viewed as an intervening variable between the mathematical activity and student achievement” (p. 1201). In other words, using Manizade et al.’s (2019) framework for examining relationships between Type B and A variables (Introduction, this volume), researchers should investigate the potential of a new “intervening variable” between two adjacent variables in the adaptation of Medley’s (1987) work that could provide evidence of how students engage in learning and doing mathematics in technological settings.
Given the documentation of some unproductive student work methods, Zbiek et al. call for “research that identifies constructs that are associated with the development of judicious use [italics added] of technology” (p. 1186); that is, examining teacher activities (Type C) which facilitate students being aware of their need to focus on the mathematics content of a task and use productive work methods (Type B). Researcher observations of successful and unsuccessful student behaviors when using CT tools may provide insight into how the successful use of technology can be sustained and ways to change unsuccessful student behaviors.
Further questions that warrant researchers’ investigation of students’ mathematical learning and engagement with technology-based activities include: If students encounter an unexpected result with one representation (using CT tools), do they stay with that representation, or switch to another representation that provides more insight as a way to solve a given task? What is the role of teacher activities (Type C) in engaging students in their development of representational fluency? As described in Sect. 2, access to technology introduces the “play paradox” where unstructured, expressive activity can enable some students to avoid the intended mathematical content of an activity. How might studies of understanding students’ development of representational fluency provide evidence of the effect of exploratory activity and expressive activity in technological settings? Zbiek et al. advocate for studies of “how the representational fluency of a group relates to the representational fluency of individuals in the group” (p. 1194). Also, is there a relationship between the construct of representational fluency and student work methods (Zbiek et al.)? Within technological environments, researchers should consider many of these questions and examine relationships between Type A, B, and C variables to inform the knowledge base of student mathematics learning activities.
Fourth, reviewing different conceptualizations of student engagement in mathematics learning activities focused on not only identifying behaviors and dispositions that actively engage students in knowing and doing mathematics in existing studies but also to suggest new directions in building the knowledge base related to student mathematics learning activities. A clear trend of this chapter’s selected review of studies about student learning activities focused on how and why students make sense of mathematics “in the moment” and perseverance to know and do mathematics “over time.” Whether using teaching experiments or classroom settings, researchers investigated and explained students’ engagement in learning mathematics with understanding and doing mathematics. As an example, Liljedahl’s (2005) study of PTs’ problem-solving activities and their “AHA! moments of illumination” promoted positive changes in their mathematical understanding (i.e., cognitive construct) and productive dispositions (i.e., affective construct). Complementary relationships between cognitive and affective constructs of students’ mathematical learning experiences could inform future research design for individual studies or sets of related studies. Moreover, studies with an increased focus of examining interrelationships between Type B and C variables provided evidence of how teachers responded to individual students’ use of or lack of problem-solving strategies and informed their decision-making on next steps in a lesson or sequence of lessons (see Sects. 3 and 4).
To advance our current understanding of mathematics teaching and learning, there is a continued need to review and extend the knowledge base related to the development of student behaviors and dispositions that actively engage all students in knowing and doing mathematics. One way to move the knowledge base forward is a consideration of the results of the past decade with an increasing availability of wide-ranging technological methodologies that can provide data about students’ engagement in mathematics learning activities to both teachers and researchers (Type CB research). To address the gap between research and practice for understanding and improving students’ mathematical learning experiences, Cai et al. (2018) proposed the collection, analysis, and use of “continuous data on the learning experiences of each student” (p. 363) to facilitate researchers’ understanding of explicit connections between teaching practices (Type C) and student learning activities (Type B). Yet, questions need to be considered if technological and methodological tools exist without overwhelming both researchers and teachers with too many data? According to Cai et al. (2018), the “capacity to capture, process, and store comprehensive cognitive and noncognitive data longitudinally for every student either already exists or is on the near horizon” (p. 364). Two years later, Cai et al. (2020) described current digital tools for collecting and managing student data but acknowledged that technological tools that could be used “during [classroom] lessons to monitor small-group discussion, analyze student work, and even gauge students’ affect” (p. 392) are still under development. Still, examining the future potential of technology to access student mathematical thinking for each student in the next decade, Cai et al. (2018) have proposed a framework for collecting, analyzing, and using data on students’ mathematical experiences that uses a three-part time frame: (1) in the moment, (2) short term, and (3) long term (p. 366). In addition, both cognitive and noncognitive learning experiences, such as “students unexpected responses” and “students’ engagement with tasks” are identified and have been reported in prior studies of student mathematics learning activities (see Cai et al., 2018, for further framework details). Future research is needed to ground this framework in the data across multiple diverse settings.
Notwithstanding and looking to the next decade, Bartell et al. (2017) asserted that the “CCSSM, with its implicit political and economic goals and its lack of explicit attention to race, gender, class, and so forth, is not framed to support equity” (p. 9). Consequently, Bartell et al. designed a framework to connect research-based equitable mathematical teaching practices (Type C) with all the SMP (Type B) to explicitly address issues of equity. Making connections, they identified nine core teaching practices described in the chapter on culture, race, and power in the Second Handbook of Research on Mathematics Teaching (Diversity in Mathematics Education , 2007) and more recent research (see Bartell et al., 2017, for details of the practices). As an emerging field of research, their framework offers existing and new research connections between student mathematics learning activities and equitable mathematical teaching practices (Type BC research). Each part of the framework provides multiple entry points for research supporting what it means for students to actively engage in effective and equitable mathematical learning activities. Students’ engagement in mathematical behaviors and dispositions needs to be studied in particular contexts and situations to inform and extend the knowledge base of what works and does not work for all students to become knowers and doers of mathematics.
References
Australian Curriculum Assessment and Reporting Authority. (2017). The Australian curriculum: Mathematics: Key ideas. https://www.australiancurriculum.edu.au/f-10curriculum/mathematics/key-ideas/.
Bartell, T., Wager, A., Edwards, A., Battey, D., Foote, M., & Spencer, J. (2017). Toward a framework for research linking equitable teaching with the standards for mathematical practice. Journal for Research in Mathematics Education, 48(1), 7–28.
Biddlecomb, B. D. (1994). Theory-based development of computer microworlds. Journal of Research in Childhood and Education, 8(2), 87–98.
Biddlecomb, B., & Olive, J. (2000). JavaBars [computer software]. http://math.coe.uga.edu/olive/welcome.html.
Bliss, J., & Ogborn, J. (1989). Tools for exploratory learning. Journal of Computer-Assisted Learning, 5, 37–50.
Bostic, J. D., & Sondergeld, T. A. (2015). Measuring sixth-grade students’ problem solving: Validating an instrument addressing the mathematics common core. School Science and Mathematics, 115(6), 281–291.
Cai, J., Morris, A., Hohensee, C., Hwang, S., Robison, V., & Hiebert, J. (2018). Using data to understand and improving students’ learning: Empowering teachers and researchers through building and using a knowledge base. Journal for Research in Mathematics Education, 49(4), 362–372. https://doi.org/10.5951/jresematheduc.49.4.0362
Cai, J., Morris, A., Hohensee, C., Hwang, S., Robison, V., Cirillo, M., Kramer, S. L., & Hiebert, J. (2020). Improving the impact of research on practice: Capitalizing on technological advances for research. Journal for Research in Mathematics Education, 51(5), 518–529. https://www.jstor.org/stable/10.5951/jresematheduc-2020-0165.
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (2015). Children’s mathematics: Cognitively guided instruction (2nd ed.). Heineman.
Chan, M. C. E., & Clarke, D. (2017). Structured affordances in the use of open-ended tasks to facilitate collaborative problem solving. ZDM Mathematics Education, 49, 951–963. https://doi.org/10.1007/s11858-017-0876-2
Cobb, P. (1994). Where is the mind? Constructivist and sociocultural perspectives on mathematical development. Educational Researcher, 22, 3–29.
Cobb, P., Yackel, E., & Wood, T. (1992). A constructivist alternative to the representational view of mind in mathematics education. Journal for Research in Mathematics Education, 23, 2–33.
Cuban, L. (1992). The corporate myth of reforming public schools. Phi Delta Kappan, 73(1), 37–82.
Davidson, A., Herbert, S., & Bragg, L. A. (2019). Supporting elementary teachers’ planning and assessing of mathematical reasoning. International Journal of Science and Mathematics Education, 17(6), 1151–1171. https://doi.org/10.1007/s10763-018-9904-0
Dingham, S. W., Kent, L. B., McComas, K. K., & Orona, C. C. (2019). The language of mathematics education: An expanded glossary of key terms and concepts in mathematics teaching and learning. Koninklijke Brill NV. https://doi.org/10.1163/9789004412651.
Diversity in Mathematics Education. (2007). Culture, race, power, and mathematics education. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 405–434). Information Age Publishing.
Gilbert, M. (2014). Using productive disposition to differentiate between students’ level of precision when critiquing a peer’s work. School Science and Mathematics, 114(7), 339–348. https://doi.org/10.1111/ssm.12086
Guin, D., & Trouche, L. (1999). The complex process of coverting tools into mathematical instruments: The case of calculators. International Journal of Computers for Mathematical Learning, 3, 195–227.
Hackenberg, A. J. (2010). Students’ reasoning with reversible multiplicative relationships. Cognition and Instruction, 28(4), 383–432. https://doi.org/10.1080/07370008.2010.511565
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 371–404). Information Age Publishing.
Hipkins, R. (2018). How the key concepts were developed: The evidence base. New Zealand Council for Educational Research.
Hipkins, R., McDowall, S., & Wood, B. (2018). How key competencies are treated in the OECD ‘2030’ framework: Implications for the New Zealand curriculum. New Zealand Council for Educational Research.
Hong, Y. Y., & Thomas, M. O. J. (2002). Representational versatility and linear algebraic equations. Proceedings of the international conference on computers in education (vol. 2, pp. 1002–1006). ICCE.
Hoyles, C., & Noss, R. (1992). A pedagogy for mathematical microworlds. Educational Studies in Mathematics, 23(1), 31–57.
Huinker, D. (2015). Representational competence: A renewed focus for classroom practice in mathematics. Wisconsin Teacher of Mathematics, 67(2), 4–8.
Jacobs, V. R., & Spangler, D. A. (2017). Research on core practices in K-12 mathematics teaching. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 766–792). NCTM.
Jansen, A. (2020). Engagement with mathematics. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 273–276). Springer International Publishing.
Kapur, M. (2010). Productive failure in mathematical problem solving. Instructional Science, 38(6), 523–550.
Kapur, M. (2014). Productive failure in learning math. Cognitive Science, 38, 1008–1022. https://doi.org/10.1111/cogs.12107
Kaput, J. J. (1992). Technology and mathematics education. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 515–556). Macmillan.
Keazer, L. M., & Jung, H. (2020). Prospective teachers anticipate challenges fostering the mathematical practice of making sense. School Science and Mathematics, 120, 79–89. https://doi.org/10.1111/ssm.12390
Kieren, T. E. (1980). The rational number construct-its elements and mechanisms. In T. E. Kieren (Ed.), Recent research on number learning (pp. 125–150). Columbus.
Kilpatrick, J. (2003). Introduction. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 1–4 ). NCTM.
Kobett, B. M., & Karp, K. S. (2020). Strength-based teaching and learning in mathematics: Five teaching turnarounds for grades k-6. NCTM.
Koestler, C., Felton, M., Bieda, K., & Otten, S. (2013). Connecting the NCTM process standards and the CCSSM practices. NCTM.
Lesh, R., Post, T., & Behr, M. (1987). Representations and translations among representations in mathematics learning and problem solving. In C. Janvier (Ed.), Problems of representation in the teaching and learning mathematics (pp. 33–40). Erlbaum.
Lesh, R., & Zawojewski, J. (2007). Problem solving and modeling. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 763–804). Information Age Publishing.
Lesh, R. A., Sriraman, B., & English, L. (2020). Theories of learning mathematics. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 861–869). Springer International Publishing.
Liljedahl, P. G. (2005). Mathematical discovery and affect: The effect of AHA! experiences on undergraduate mathematics students. International Journal of Mathematical Education in Science and Technology, 36(2–3), 219–236. https://doi.org/10.1080/00207390412331316997
Liljedahl, P. (2016). Building thinking classrooms: Conditions for problem-solving. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and Solving Mathematical Problems (pp. 361–386). Springer International Publishing. https://doi.org/10.1007/978-3-319-28023-3_21.
Manizade, A., & Ribeiro, M., Makonye, J. P., Mellone, M., & Jakobsen, A. (2019). International perspectives on evolution of research on teaching mathematics. In M. Graven, H. Venkat, A. Essien & P. Vale (Eds.). Proceedings of the 43rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 179–180). PME.
Martin, D. T. (1989). A critique of the concept of work and education in the school reform reports. In C. M. Shea, E. Kahana, & P. Sola (Eds.), The new servants of power: A critique of the 1980s school reform movement (pp. 39–56). Greenwood Press.
Mason, J. (2002). Researching your own practice: The discipline of noticing. Routledge.
McDowell, S., & Hipkins, R. (2018). How the key concepts developed over time: Insights from the research. New Zealand Council for Educational Research. https://www.nzcer.org.nz/research/publications/key-competencies-insights.
McLeod, D. B. (1992). Research on affect in mathematics education: A reconceptualization. In D. Grouws (Ed.), Handbook of research in mathematics teaching and learning (pp. 575–596). MacMillan.
Medley, D. M. (1987). Evolution of research on teaching. In M. J. Dunkin (Ed.), The international encyclopedia of teaching and teacher education (pp. 105–113). Pergamon Press.
Middleton, J., Jansen, A., & Goldin, G. A. (2017). The complexities of mathematical engagement: Motivation, affect, and social interactions. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 667–699). NCTM.
Ministry of Education (2014). The New Zealand curriculum online: Mathematics and statistics. Author. https://nzcurriculum.tki.org.nz/The-New-Zealand-Curriculum/Mathematics-and-statistics/Achievement-objectives#collapsible1.
Ministry of Education. (2015). The New Zealand curriculum. Author. https://www.education.govt.nz/.
Ministry of Education. (2020). The New Zealand curriculum online: Key competencies. Author. https://nzcurriculum.tki.org.nz/Key-competencies#collapsible2.
National Council of Teachers of Mathematics. (1980). An agenda for action. Author.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Author.
National Council of Teachers of Mathematics. (1991). Professional standards for school mathematics. Author.
National Council of Teachers of Mathematics. (1995). Assessment standards for school mathematics. Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Author.
National Council of Teachers of Mathematics. (2003). A research companion to principles and standards for school mathematics. Author.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Author.
National Commission on Excellence in Education. (1983). A nation at risk: The imperative for educational reform. Government Printing Office.
National Governors Association Center for Best Practices and Council of Chief State School Officers. (2010). Common core state standards for mathematics. Author. http://www.corestandards.org/Math/Practice.
National Research Council. (2001). Adding it up: Helping children learn mathematics. In J. Kilpatick, J. Swafford, & B. Findell (Eds.), Mathematics learning study committee, center for education, division of behavioral and social sciences and education. National Academy Press.
Niss, M. (2003) Mathematical competencies and the learning of mathematics: The Danish KOM project. In A. Gagatsis and S. Papastavridis (Eds.), 3rd Mediterranean conference on mathematical education—Athens, Hellas, 3–5 Jan 2003 (pp. 116–124). Hellenic Mathematical Society. http://www.math.chalmers.se/Math/Grundutb/CTH/mve375/1213/docs/KOMkompetenser.pdf.
Olive, J. (1994). Children’s construction of fractions using tools for interactive mathematical activity (TIMA) microworlds. In D. Kirshner (Ed.), Proceedings of the sixteenth annual meeting of the North American chapter of the international group for the psychology of mathematics education (p. 71). Louisiana State University.
Partnership for 21st Century Learning (2019). Framework for 21st century definitions (p. 21). http://static.battelleforkids.org/documents/p21/P21_Framework_DefinitionsBFK.pdf.
Piaget, J. (1970). Genetic epistemology. Norton & Norton.
Piaget, J. (1980). Adaptation and intelligence: Organic selection and phenocopy. University of Chicago Press.
Pink, W. T. (1989). The new equity: Competing visions. In C. M. Shea, E. Kahana, & P. Sola (Eds.), The new servants of power: A critique of the 1980s school reform movement (pp. 123–136). Greenwood Press.
Polya, G. (2004). How to solve it: A new aspect of mathematical method. Princeton University Press.
Program for International Student Assessment. (2021). PISA 2021 mathematics framework. https://pisa2021-maths.oecd.org/#Twenty-First-Century-Skills.
Roschelle, J., Noss, R., Blikstein, P., & Jackiw, N. (2017). Technology for learning mathematics. In J. Cai (Ed.), Compendium for research in mathematics education (pp. 853–875). NCTM.
Sanchez, W. B., Lischka, A. E., Edenfield, K. W., & Gammill, R. (2015). An emergent framework: Views of mathematical processes. School Science and Mathematics, 115(2), 88–99.
Sandoval, W. A., Bell, P., Coleman, E., Enyedy, N., & Suthers, D. (2000). Designing knowledge representations for epistemic practices in science learning. Paper presented at the annual meeting of the American Educational Research Association.
Santos-Trigo, M. (2020). Problem solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 686–693). Springer International Publishing.
Schoenfeld, A. H. (1985). Mathematical problem solving. Academic Press.
Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. Grouws (Ed.), Handbook of research in mathematics teaching and learning (pp. 334–370). MacMillan.
Schoenfeld, A. H., & The Teaching for Robust Understanding Project. (2016). An introduction to the teaching for robust understanding (TRU) framework. Graduate School of Education. http://map.mathshell.org/trumath.php.
Sfard, A. (2003). Balancing the unbalanceable: The NCTM Standards in light of theories of learning mathematics. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 353–392). NCTM.
Siedel, T., & Shavelson, R. J. (2007). Teaching effectiveness research in the past decade: The role of theory and research design in disentangling meta-analysis results. Review of Educational Research, 77(4), 454–499. https://doi.org/10.3102/0034654307310317.
Simon, M. A., Placa, N., & Avitzur, A. (2016). Participatory and anticipatory stages of mathematical concept learning: Further empirical and theoretical development. Journal for Research in Mathematics Education, 47(1), 63–93.
Simon, M. A., Tzur, R., Heinz, K., & Kinzel, M. (2004). Explicating a mechanism for conceptual learning: Elaborating the construct of reflective abstraction. Journal for Research in Mathematics Education, 35(5), 305–329. https://doi.org/10.2307/30034818
Simon, M. A., Kara, M., Placa, N., & Avitzur, A. (2018). Towards an integrated theory of mathematics conceptual learning and instructional design: The Learning through activity theoretical framework. Journal of Mathematical Behavior, 52, 95–112. https://doi.org/10.1016/j.jmathb.2018.04.002
Simpson, A., & Maltese, A. (2017). “Failure is a major component of learning anything”: The role of failure in the development of STEM professionals. Journal of Science Education and Technology, 26, 223–237. https://doi.org/10.1007/s10956-016-9674-9
Smith, M., & Sherin, M. G. (2019). The five practices in practice: Successfully orchestrating mathematics discussions in your middle school classroom. Corwin.
Sola, P. (1989). The corporate community on the ideal business-school alliance: A historical and ethical critique. In C. M. Shea, E. Kahana, & P. Sola (Eds.), The new servants of power: A critique of the 1980s school reform movement (pp. 75–86). Greenwood Press.
Steffe, L. P. (1994). Children’s multiplying schemes. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 3–39). State University of New York Press.
Steffe, L. P., & Olive, J. (2010). Children’s fractional knowledge. Tools for interactive mathematical activity (TIMA). [Computer program]. (1994). University of Georgia.
Trouche, L. (2005). An instrumental approach to mathematics learning in symbolic calculator environments. In D. Guin, K. Ruthven, & L. Trouche (Eds.), The didactical challenge of symbolic calculators: Turning a computational device into a mathematical instrument (pp. 137–162). Springer International Publishing.
Turner, R. (2010). Exploring mathematical competencies. Research Developments, 24(24). https://research.acer.edu.au/resdev/vol24/iss24/5.
Tzur, R. (1995). Interaction and children’s fraction learning (Doctoral dissertation). Available from ProQuest Dissertations and Theses database (UMI No. 9604082).
Tzur, R. (1999). An integrated study of children’s construction of improper fractions and the teacher’s role in promoting that learning. Journal for Research in Mathematics Education, 30(4), 390–416.
Tzur, R. (2004). Teacher and students’ joint production of a reversible fraction conception. Journal of Mathematical Behavior, 23, 93–114. https://doi.org/10.1016/j.jmathb.2003.12.006
Tzur, R., & Simon, M. A. (2004). Distinguishing two stages of mathematics conceptual learning. International Journal of Science and Mathematics Education, 2(2), 287–304. https://doi.org/10.1007/s10763-004-7479-4
Vygotsky, L. S. (1981). The genesis of higher mental functions. In J. V. Wertsch (Ed.), The concept of activity in soviet psychology (pp. 144–188). M. E. Sharpe.
Warshauer, H. K. (2015). Productive struggle in middle school mathematics classrooms. Journal of Mathematics Teacher Education, 17(4), 375–399. https://doi.org/10.1007/s10857-014-9286-3
Yin, R. K. (2009). Case study research design and methods (Vol. 5). Sage.
Zbiek, R. M., Heid, M. K., Blume, G. W., & Dick, T. P. (2007). Research on technology in mathematics education. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 1169–1207). Information Age Publishing.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Brief, Capsule Definitions of Terms and Documents for Chapter 6
Brief, Capsule Definitions of Terms and Documents for Chapter 6
-
Assessment, curriculum and evaluation, and professional standards for school mathematics: A trilogy of documents that provided a vision for the organization of curriculum reform in the U.S. in the 1990s (National Council of Teachers of Mathematics [NCTM], 1989, 1991, 1995).
-
Behaviors and dispositions: Identification of student experiences, such as, proficiencies, processes, practices, competencies, and habits of mind (Kobett & Karp, 2020, p. 40) that demonstrate how students develop and show evidence of their mathematical thinking.
-
Cognitive technological (CT) tools: Consists of tools that support a “synergistic relationship” between technical and conceptual dimensions of mathematical activity in technological environments (Zbiek, Heid, Blume, & Dick, 2007).
-
Competencies: Frameworks for knowing and doing mathematics, such as, (1) Denmark’s (2003) mathematical competencies that provided evidence of students’ “mental or physical processes, activities, and behaviors” (p. 9); (2) Program for International Student Assessment [PISA] (PISA, 2021) assessed mathematical competencies as “an individual’s capacity to reason mathematically and to formulate, employ, and interpret mathematics to solve problems in a variety of real-world contexts” (PISA, 2021); and (3) Identified in the New Zealand Curriculum (NZC), competencies “that describe what they [students] will come to know and do” (Ministry of Education, 2015, p. 37).
-
Conceptual understanding: Student learning is defined as the “comprehension of mathematical concepts, operations, and relationships” (National Research Council [NRC], 2001, p. 116).
-
Direct instruction (DI): Traditional, instructional methods where students watch, listen, and take notes about problems that teachers provide procedures and solutions for students to follow and use (Kapur, 2014).
-
Learning goals: Focus on student “understanding” where students build knowledge; “Explicitly state what students will understand about mathematics as a result of engaging in a particular lesson” (Smith & Sherin, 2019, p. 14).
-
Learning through activity[LTA]: A research model that examines how learners actively engage in learning activities through a progressive coordination of mathematical concepts (Simon, Kara, Placa, & Avitzur, 2018; Simon, Placa, & Avitzur, 2016).
-
Mathematical sense-making: Student engagement in processes, such as problem solving, to learn mathematics with understanding; one aspect of what it means to know and do mathematics.
-
National Governors Association [NGA] Center for Best Practices & Council of Chief State School Officers [CCSSO]: Authors of the U.S. Common Core State Standards for Mathematics (CCSSM), 2010.
-
Organization for Economic Development (OECD) Definition and Selection Competencies (DeSeCo) Project: Created a framework to guide the development of PISA assessments.
-
Performance goals: Focus on the end result or product of students’ engagement in learning mathematics: “What students will be able to do as a result in engaging in a lesson” (Smith & Sherin, 2019, p. 14).
-
Principles and standards for school mathematics: Updated U.S. document that provides a vision for curriculum reform at the beginning of the twenty-first century (NCTM, 2000).
-
Problem-solving: Defined as “the systematic study of what the process of formulating and solving problems entails and the ways to structure problem-solving approaches to learn mathematics” (Santos-Trigo, 2020, p. 687).
-
Process standards: Five processes that define what mathematicians might do and say when engaged in doing mathematics: Problem solving, communication, representation, making connections, and reasoning and proof (NCTM, 2000).
-
Productive disposition: An affective construct defined as learners having an “habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy” (NRC, 2001, p. 116).
-
Productive failure: Students’ initial problem-solving attempts are unsuccessful and became productive when supported with appropriate mathematics classroom instruction (Kapur, 2014).
-
Productive struggle: A student learning behavior that promotes learners making sense of mathematics and is necessary to develop conceptual understanding (Hiebert & Grouws, 2007); “Intellectual effort students expend to make sense of mathematical concepts that are challenging but fall within the students’ reasoning capabilities” (Dingman, Kent, McComas, & Orona, 2019, p. 91)
-
Proficiencies: Frameworks for students’ engagement while learning mathematics, such as, (a) Cognitive and affective proficiencies for five strands: conceptual understanding, procedural fluency, strategic competence, adaptive reasoning, and productive disposition (NRC, 2001); and (b) Reasoning as one of the four proficiency strands students engage inwhen “thinking and doing of mathematics” (Australia Curriculum and Assessment Reporting Authority [ACARA], 2017).
-
Prospective elementary school teachers (PTs) and AHA! Experience: Students engage in problem solving and experience how “a problem has just been solved, or a new piece of mathematics has been found, and it has happened in a flash of insight, in a moment of illumination” (Liljedahl, 2005, p. 219).
-
Representational fluency: Within or outside technological environments, “The ability to translate across representations, the ability to draw meaning about a mathematical entity from different representations of that mathematical entity, and the ability to generalize across different representations” (Zbiek et al., 2007, p. 1192).
-
Research for principles and standards for school mathematics: Research literature that informed the U.S. vision of school mathematics in the 1990s and 2000 (NCTM, 2003).
-
Scheme: A cycle of perturbation, action, and reflection in which an individual anticipates, acts and mentally prepares, and assesses the outcome of his or her actions (Hackenberg, 2010; Steffe, 1994; von Glasersfeld, 1995)
-
Standards for Mathematical practice (SMP): Eight mathematical competencies identified as a national Common Core State Standards for Mathematics (CCSSM) in the U.S., 2010.
-
Student learning activities: “In the classroom… All learning depends on the activity of the learner” (Medley, 1987, p. 105).
-
Student engagement: Defined as “an interactive relationship students have with the subject matter, as manifested in the moment through expressions of behavior and experiences of emotion and cognitive activity, and is constructed through opportunities to do mathematics” (Jansen, 2020, p. 273).
-
Teaching for robust understanding [TRU] project: Framework of five dimensions of classroom activity that supports professional development (PD) to engage teachers in creating a classroom student learning environment that facilitates the development of powerful thinkers (Schoenfeld & the TRU project, 2016).
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Timmerman, M.A. (2023). Student Mathematics Learning Activities. In: Manizade, A., Buchholtz, N., Beswick, K. (eds) The Evolution of Research on Teaching Mathematics. Mathematics Education in the Digital Era, vol 22. Springer, Cham. https://doi.org/10.1007/978-3-031-31193-2_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-31193-2_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-31192-5
Online ISBN: 978-3-031-31193-2
eBook Packages: EducationEducation (R0)