Keywords

1 Introduction

In this chapter, we focus on research in mathematics teaching such as mathematics teacher planning, assessment, and other teacher-related activities when students are not present (“pre- and post-active”; Type D). These are the types of activities that mathematics teachers do to promote student learning while no students are present; in other words, this chapter focuses on the invisible part of teaching mathematics. These activities are important means by which the teacher exercises control over their teaching and are also the main way that a teacher’s professional knowledge, competencies, skills, and beliefs (Type E; see Fig. 3 in Chap. 1, this volume) impact the process of teaching mathematics. Type E is necessary but not sufficient for producing quality student–teacher interactions in the mathematics classroom (e.g., Sullivan et al., 2009). Enactment of the teaching practice interactively with students is a direct result of teachers’ pre- and post-active (Type D) actions. Type D, therefore, determines how well the teacher performs the main interactive function of teaching mathematics (Type C) and how successfully the teacher accomplishes the purpose of teaching. Our perspective is premised on the belief that theory drives teaching practice, and, in this chapter, we demonstrate how that connection functions in relation to teacher’s pre- and post-active  actions (Type D).

The chapter includes a discussion of how teachers relate the problems they encounter in the practice of teaching mathematics to their professional knowledge, competencies, skills, and beliefs in deploying their available resources and their own abilities. Teachers’ subjective decision-making is based on the Type E elements that they possess, and the configuration of a teacher’s Type E elements “stabilizes [the teacher’s] world” (Žižek, 2012, p. 367, as cited in Brown, 2016, p. 86) through their subjective, decision-making process. This decision-making process could be based, for instance, on the most recent professional development presentation that they attended and ideas that they bought into, or on a conference presentation that their principal attended and practices subsequently imposed on the teachers. In either case, and even without having attended a recent conference, teachers’ choices and objectified beliefs are a product of the constraints within which they are working (Ingram & Clay, 2000). Thus, their decision-making process produces observable pre-post classroom actions that are the focus of this chapter. We also address the ways in which cultural and digital contexts affect Type D. Additionally, we discuss the theoretical and methodological challenges associated with conceptualization of the Type D domain, instrumentation, and research design.

1.1 Statement of the Problem

It is important to study Type D because teacher planning, which includes introducing key ideas, selecting associated tasks, and creating assessments to measure student understanding, has a great effect on the learning opportunities for students (Akyuz et al., 2013; Sullivan et al., 2009). It provides for targeted understanding of the lesson content, managing classroom transitions, and allows for a focus on classroom processes (Clark & Yinger, 1987). This applies not only to daily lesson plans, but also to unit plans that cover a range of related topics (Roche et al., 2014). McAlpine et al. (2006) specifically called for more research on the ways in which teachers think and the connection between teachers’ thinking and its influence on their teaching actions. This connection is hypothesized to be particularly useful in studying the relationship between teachers’ “theories-in-use” and teachers’ thinking (Kane et al., 2002; McAlpine et al., 2006). Sullivan et al. (2009) called for more professional development to improve teachers’ abilities to take a mathematical task and convert it into a “meaningful learning experience” (p. 85), noting that Type E was necessary but not sufficient for this conversion. Thus, regardless of a teacher’s perspective on teaching mathematics as described by the theoretical framework that we present in this chapter (see Fig. 1), research on improving Type D is important because it contains the potential for improving the quality of mathematics instruction (Lewis et al., 2013).

Fig. 1
A flow diagram defines the perspective on planning and teaching mathematics. Some of the theories are situated learning theory, behaviorism, and structuralism. Corresponding goals, planning, and classroom interaction result in reflection, anticipation, and assessment which help in planning.

Epistemological perspectives on teachers’ Type D

Full size image

Depending on the importance the teacher assigns to planning, the outcomes of planning manifest in different ways through the observable and enacted lesson. Zazkis et al. (2009) compared Japanese teachers’ planning—which was focused on the process of student learning and discovery of concepts—and American teachers’ planning—which was focused on specific content outcomes. They found that the ways in which teachers talked about the professional act of planning varied greatly between the two groups and differences aligned with the observable outcome of the written lesson plan and its enactment. If teachers think of planning as a high-level professional task that is an important part of the act of teaching, then the produced written plan and its enactment lead to different types of teaching than is the case for a teacher who does not think of planning as having a central role in their practice (Zazkis et al., 2009). Designing lesson plans that incorporate teachers’ goals and are focused on “students’ anticipated learning” (Akyuz et al., 2013, p. 94) has been the focus of key reform-based documents, including Adding It Up (Kilpatrick et al., 2001). Further, Hiebert et al. (2003) emphasized the importance of developing teachers’ Type D: “[T]eachers need to design lessons with clear goals in mind, monitor their implementation, collect feedback, and interpret the feedback in order to revise and improve future practice” (p. 206).

Regardless of the knowledge, competencies, skills, and beliefs that teachers develop in their teacher preparation programs, they often go back to the way they were taught when faced with the challenges of the everyday classroom: “People learn to teach, in part, by growing up in a culture—by serving as passive apprentices for 12 years or more when they themselves were students. When they face the real challenges of the classroom, they often abandon new practices and revert to the teaching methods their teachers used” (Hiebert et al., 2003, p. 201). It becomes extremely important therefore to develop teachers’ abilities to plan quality mathematics lessons with specific goals in mind, and to use student data to make decisions about subsequent planning and instruction. As McAlpine et al. (2006) suggested, we need to develop a “language” (p. 129) for talking about teachers’ Type D activity to fully realize it as a domain of mathematics education research. To develop this necessary “language” for Type D research, we propose the conceptual framework in Fig. 1 for discussing literature related to Type D. We subscribe to Akyuz et al.’s (2013) definition of Type D, that cyclically relates preparation (pre-active) to reflection, anticipation, assessment, and revision (post-active). In their model relating these variables, reflection, anticipation, and assessment interrelate laterally with each other, all of which then inform revision. Revision, then, cycles back to preparation as the pre-active variable.

The chapter can be thought of as broken into three main themes. In the first theme, we situate our current work: we discuss the connection between Type D and Type E (knowledge, competencies, skills, and beliefs), followed by a discussion of the goals of Type D broadly. The second theme constitutes the bulk of the chapter: we discuss each of the epistemological perspectives in Fig. 1, including a definition, goals of teaching, and examples from the literature. The third theme provides commentary on the first two themes: we discuss pros and cons of each perspective, followed by a commentary on the relationship of each perspective to cultural contexts, and we conclude with a brief discussion of the implications of each perspective on the task of lesson planning. We close by noting implications for future directions of research as a result of the intervention we offer in the present chapter.

2 The Connection of Type D to Knowledge, Competencies, Skills, and Beliefs

Teachers’ knowledge, competencies, skills, and beliefs (Type E) are connected to the way they plan their mathematics instruction and influences their decision-making, evidenced in the ways they implement their lessons. In some cases, this connection is conscious, and in other cases, it is unconscious. There are various factors that can affect teachers’ lesson planning and instruction, including their beliefs about the nature of mathematics, such as whether they hold an instrumental, Platonist, or problem-solving view (Beswick, 2005; Ernest, 1989); learning theories; and the pedagogical practices and approaches in which they have been trained. Most importantly, teachers can use combinations of these factors to produce and implement a lesson, and to assess students.

Kilpatrick et al. (2001), for example, discussed the connection between Types C, D, E, and F—what they call teaching for mathematical proficiency—with the following components:

  1. (1)

    conceptual understanding of the core knowledge required in the practice of teaching;

  2. (2)

    fluency in carrying out basic instructional routines;

  3. (3)

    strategic competence in planning effective instruction and solving problems that arise during instruction;

  4. (4)

    adaptive reasoning in justifying and explaining one’s instructional practices and in reflecting on those practices so as to improve them; and

  5. (5)

    productive disposition towards mathematics, teaching, learning, and the improvement of practice.

    (Kilpatrick et al., 2001, p. 380)

We align components (1) and (2) with Type E; component (3) with Types D and C; component (4) with Type D; and component (5) with Type F.

While theories may influence teachers consciously and unconsciously, typically once they are with their students, they operate (and make pedagogical—and specifically, planning—decisions and choices) in a way that strives for synchronicity and harmony between their previous experiences of successes in teaching; their knowledge, competencies, and skills; their unique mixes of students and content for each of their course preparations; and the institutional constraints within which they are working (cf. Ingram & Clay, 2000). While a theory of learning may influence these decisions and choices, it wouldn’t necessarily have to “inform” them per se. For example, if a teacher has attended a “project-based learning” workshop, they may be motivated to try some of the techniques or lessons they were exposed to, but they are likely to do so as an adaptation of their existing lesson-planning practices. Regardless of the reasons behind specific instances of decision-making that are evident in their lesson planning, assessment, or instruction, we focus on the teachers’ objectified beliefs—that is, observable behaviors—that ostensibly have been chosen because they stabilize the teacher’s world. The focus of this chapter is not, then, on the “why” of the decision-making processes, but rather on “how” it manifests in the observable research components of Type D.

In science education, researchers (e.g., Carlson et al., 2019) have reconceptualized teachers’ knowledge to include Enacted Pedagogical Content Knowledge (ePCK) and Personal Pedagogical Content Knowledge (pPCK), both of which include knowledge associated with Type D, namely, planning and reflection. These researchers defined ePCK as knowledge for planning and reflection that is situated within the school, classroom, and individual students’ interactional contexts (cf. Ingram & Clay, 2000) with the teacher and the teacher’s subject matter knowledge and discipline-related skills. Personal PCK includes the PCK influences that have occurred over the teacher’s life, experiences, and interactions with other professionals (e.g., fellow teachers, researchers, coursework, professional development, reading journal articles) that have accumulated to shape and inform their ePCK. In other words, pPCK builds over time and experience to increase the sophistication with which they deploy their knowledge in thinking about, planning, and reflecting on their lessons. Additionally, ePCK is a subset of pPCK, meaning that the enacted—viz. observable—knowledge of a teacher is contained within their set of personal PCK, indicating that observable Type D can be conceived as objectification of personal knowledge and epistemological commitments. Thus, utilizing epistemological frameworks facilitates insight when studying teachers’ Type D. When conceptualized in this way, the teacher’s pPCK is a privately held knowledge that is unique to the teacher, whereas ePCK is the mode of the teacher’s knowledge with which the students most directly interact. The connection between ePCK and pPCK reveals that teachers’ epistemological commitments, knowledge about how students learn mathematics, and corresponding knowledge about how best to teach mathematics interrelate both at a micro-level (e.g., planning a particular lesson) and a macro-level (e.g., shaped over their lives, experiences, and professional formation). It is pertinent, therefore, for mathematics education researchers to consider how the objectifications of this knowledge—as Type D observable behaviors in the form of decisions and choices—shape their teaching. As we explore in this chapter, some epistemological commitments have been explored apropos of Type D whilst others warrant further investigation by researchers.

3 Goals of Pre- and Post-active Teacher Activities

The purpose of this chapter is to focus on the decisions and choices teachers make while students are not present. Ultimately, these decisions and choices—regardless of any espoused epistemology or pedagogy—directly impact their lesson plans, which become the basis for what they subsequently enact in the classroom. Tricoglus (2007) explored planning and collaboration amongst mathematics teachers, revealing that teachers’ development of tasks and lesson plans involves cyclical thinking as they become more knowledgeable about them. The study highlighted three types of thinking that teachers engaged in when planning: deliberative thinking, which is the considered thought that generates ideas and future plans; interpretive thinking, which is the part in the process where decisions are made and problems are managed; and metacognition, which is evaluative, reflective thinking. These three types of thinking are the basis for teachers’ decisions and choices about the tasks and lesson plans they create, and are informed by their perspectives on teaching and learning mathematics. As teachers think about their beliefs and knowledge in this cyclical process, they formulate goals for their teaching as well as actions they intend to take to reach them (Aguirre & Speer, 2000; Akyuz et al., 2013; Schoenfeld, 1998).

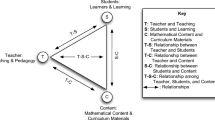
In Fig. 1, we provide a framework emergent from the literature presenting eight categories that researchers have used when describing lesson planning and mathematics instruction. These eight categories are not strictly types of learning theories but rather the perspectives that researchers have characterized teachers as appearing to be enacting, through their decisions and choice-making, to represent observable and objectified beliefs, knowledge, competencies, and skills (Type E). The aim of Type D is to articulate “the learning goals for the lesson, and the hypotheses that link planned instructional activities with expected learning outcomes” (Hiebert et al., 2003, pp. 207–208). Importantly, the focus of the teaching can be either on the goal of the lesson, or on the activities included in the lesson, regardless of the perspective the teacher adopts. When the focus is on the goal of the lesson, the teacher is likely to consider common student challenges with respect to the mathematical concepts taught, typical questions or difficulties students might experience based on their developmental levels, as well as ways to address those challenges and difficulties (West & Staub, 2003). However, if the focus is on the activity itself, then it is less likely that teachers will think of students’ conceptual development of the mathematics. Instead, the focus lands on the “how to”: lessons can become more prescribed and rigid, which potentially allows for missed opportunities when teachable moments arise (e.g., Akyuz et al., 2013).

Regardless of teachers’ theoretical frameworks or beliefs about teaching mathematics or the nature of mathematics, all teachers operate within institutional, economic, cultural, familial, and logistical constraints (Ingram & Clay, 2000). Thus, the goals adopted by teachers for their teaching can be diverse, encompassing achieving high standardized test scores, developing interest in mathematics in their students, preparing students for futures of entering the workforce or college, meeting curricular demands of the administration, communicating ideas about mathematics, enabling students to solve a given problem multiple ways or to see the connection between different mathematical ideas, and describing patterns students might see in the world using mathematics. These are different performance or learning goals, and while not mutually exclusive, they cannot all be goals for a single lesson. The teacher will consciously and unconsciously use goals to formulate the actions they take when planning a lesson or assessing student work. For example, if a teacher’s goal is for the students to be able to talk to each other about the mathematics, then the lesson planning decisions will be very different from what they would be if the goal was for students to be able to replicate the process presented by the teacher in instruction.

Despite the many challenges, the teacher must know how to create and carry out their plan and, most importantly, how to be flexible with their plan in changing classroom circumstances (Akyuz et al., 2013). A teacher will be faced with goals from other sources such as department chairs, parents, principals, school boards, state departments of education, co-workers, and so forth. Each of these sources has an interest in what the teacher is doing in the classroom. The goals produced by these parties and subsequently imposed on the teacher, whether directly or indirectly, exist in addition to the teacher’s own goals. The best-case scenario is that the teacher’s goals and the goals of these other sources are in harmony. However, if that is not the case, and the teacher has the job of synthesizing disparate goals from various sources, the result will be that the teacher’s goals—as objectified beliefs, observed through their lesson planning process—become a product of stabilizing the reality of their world and being.

4 Theoretical Perspectives for Teaching Mathematics that Are Present in Type D

In this section, we discuss and define each of the perspectives in Fig. 1, the goals for teaching associated with each, and provide some examples from the literature. The literature surveyed was selected for the representativeness each article provided for illustrating each of the epistemological perspectives in Fig. 1 apropos of Type D. An EBSCOhost search of the electronic library system of a major research university in the United States with keywords related to Type D was performed. We operated with three inclusion criteria: (1) Western context (US, Europe, Australia, New Zealand, etc.) for either the author or study setting; (2) articles written between 2000 and the present; and (3) articles must be about mathematics education specifically. Literature by a Western author performing a study in a non-Western context was also excluded. We then manually accessed each article to screen to relevance. Articles in which the primary focus was not on Type D were excluded. On reviewing the included literature, we noticed the emergence of eight epistemological themes with respect to the way the articles were situating and discussing Type D. We organized the literature into these eight themes, as seen in Fig. 1.

In each of the examples discussed, some researchers explicitly cited a theoretical perspective from Fig. 1, and in others, our characterization of a study as having employed a particular epistemological perspective is based on our interpretation of the researchers’ work. The examples given are in no way exhaustive but rather serve to demonstrate each particular perspective in recent literature. While we acknowledge that cultural context is of great importance in understanding Type D, we only considered research from the Western context in the survey of literature that follows. A more complete discussion of the cultural context of the eight epistemological perspectives is included later in the chapter.

4.1 Situated Learning Theory as Perspective

4.1.1 Definition

Situated learning theory (SLT), originally developed in the work of Lave and Wenger (Lave & Wenger, 1991; Wenger, 1998), represented a departure from other learning theories in existence in the 1990s by situating knowledge in the community rather than in individuals. The tonality shift here from individuals to communities is important to distinguish situated learning theory from other sociocultural theories of learning: epistemology itself is exclusively located in the community, entirely “decentered” (Lave & Wenger, 1991, p. 86) from the individual, and exists as a historical function of time including the future. This perspective differs from social constructivism because situated learning theory does not posit any individual possession of knowledge. Instead, knowledge is experienced and participated in rather than possessing deterministic ontology, because at any point in time it is not possible to capture the community’s learning as such. An individual person’s role in this epistemology exists in their emergent formation of an identity as a member of that community.

A useful metaphor for conceptualizing SLT is apprenticeship (Lave & Wenger, 1991). The apprentice first must initiate a connection to one of the community members, an act that expresses the aspiring apprentice’s desire to participate in the community. The apprentice then trains under the tutelage of one of the experts in the community. The community discourse proceeds through interactions between oldtimers and newcomers (Lave & Wenger, 1991). Oldtimers are established members of the community who have participated in the community and its activities for a long time. Newcomers are novices and just beginning their apprenticeship journey into the community. Through this process, the apprentice—over time—becomes an expert and an oldtimer in their own right, thus bringing in new apprentices and repeating the cycle. If a student—a newcomer—desires to become a member of a community, they must initiate an apprenticeship with an expert, and spend the substantial amount of time required performing the labor and activities of the community to become an expert theirself. If one were to ask either the oldtimer or the newcomer when—exactly—they had learned to become a central member of the community or an expert, their answer would involve their entire career, perhaps with one or two critical moments when their status as an expert was validated by other member(s) of the community. Traditionally, university mathematics departments function in this way, where students are immersed in the practices of the mathematics community under the apprenticeship of their professors (experts). However, if a mathematics teacher does not think like a mathematician, they are unlikely to train their newcomers to think as mathematicians. In this case, instead of raising up newcomers as experts (mathematics doers as people who are able to perform “doing mathematics” tasks; see Stein et al., 2000, p. 16), they will raise people who can act mathematically by producing a memorized sequence of procedures, a devolvement that more closely resembles behaviorism.

4.1.2 Goals of Teaching

For the teacher taking the perspective of SLT, the goal of their teaching is to build and operate a model of apprenticeship and legitimate peripheral participation (LPP)—the novice participation of newcomers who are not yet central to the community nor close to its experts—in the classroom. “[T]he important point concerning learning [in SLT] is one of access to practice as resource for learning, rather than to instruction. Issues of motivation, identity, and language deserve further discussion” (Lave & Wenger, 1991, p. 80). The teacher acts as the expert—the oldtimer—who is responsible for enabling the students—the newcomers—to engage in LPP into the community of mathematics. Of course, the teacher cannot expect that all their students will become professional mathematicians in the future, but that is not the purpose of the students’ LPP. Rather, the students’ LPP in the community of mathematics represents their experience of mathematics “learning”—that is, the experience of the peripheral participation is homologous to the content being learned. In other words, the content of knowledge-learning is conceived as the process of becoming a certain type of person in the mathematics classroom. There is a critical bifurcation that must be at the forefront of the teacher’s mind, and that will determine whether the students’ LPP is indeed located within the landscape of the community of mathematics, or if it is located within the (nominal) community of public-school actors, wherein the focus is more closely aligned with following a perfect sequence of steps as with the behaviorist approach. If the former has been achieved in the teacher’s mindset, then the teacher is prepared to enact teaching from the SLT perspective. In practice, this may involve modeling for students the correct mathematical language (Morgan et al., 2014; cf. Pimm, 2014) and discourse patterns, how to solve problems and practice communicating their thinking (Sfard, 2008), and the rigor needed to perform mathematical labor in the normative cadence and standards of the community (Herbel-Eisenmann et al., 2015).

The SLT perspective is different from the behaviorist perspective in that the latter is concerned with student outcomes on assessments. In the latter, knowledge outcomes are outcomes in and for themselves, rather than being related to a process of becoming a certain type of person who has a sense of belonging in the mathematics community. In SLT, the product of LPP is that students develop a mathematical identity that affords them membership in the mathematics community—even if at a very surface level—because they have been trained to act and think like mathematicians, so in situations where mathematics is at the fore, their mathematical identity acts as a membership card for that situation. When using technology in the mathematics classroom from the SLT approach, teachers use educational technology to propose and provide opportunities to solve complex problems that students would not be able to solve without technology, instead of using technology as a black-box where mathematical reasoning is not required in order for learners and teachers to produce a correct answer (Gueudet & Pepin, this volume; Goos et al., 2000; Leung & Bolite-Frank, 2015; Straesser, 2002).

4.1.3 Examples from the Literature

Sfard (2008) has contributed greatly to the development of SLT as a perspective in mathematics education. One of the key notions developed by Sfard was that of commognition, which is a neologism of “communication” and “cognition.” The notion of commognition emphasizes that “cognitive processes and interpersonal communication are … different manifestations of basically the same phenomenon” (Sfard, 2008, p. 83), thus showing that the psychological aspect of other perspectives in Fig. 1 are homologous to the acts of LPP in the SLT perspective. Her theoretical work has led other scholars such as Krummheuer (2011) to develop empirical representations of what it looks like to see LPP occurring in a mathematics classroom between teachers and students. Pertinent for this chapter is the way in which teachers plan their interaction with students. The SLT teacher will have planned for things like “eavesdropping” during active learning student activities, to qualify the students’ participation in the activity and help students maintain the desired direction of their LPP, presumably towards the “doing mathematics” of the mathematical topic of the planned lesson. The SLT teacher would anticipate during the planning process key observable behaviors of the students, qualified through the characteristics of “doing mathematics” for the mathematical topic of the lesson. This is similar to the “key questions” that are typically taught to future teachers as a lesson planning tactic (Atkin & Karplus, 1962). The work of Sfard, Krummheuer, and others elucidate the dangers of assuming that cognition and participation are separate phenomena: psychological phenomena do not occur without the environment, culture, history, and materiality of people in community with each other. Thus, in SLT, the “psychology”—if it can indeed be called that—of mathematics teaching and learning is precisely homologous to the participation of teachers and students in the LPP dyad of oldtimers and newcomers.

Dawkins and Weber (2017) described the process of teaching students how to prove in an undergraduate mathematics class. They seemed to herald the time-honored mathematical practice of developing a proof argument as an enculturation mechanism into the enlightened learning state that is ostensibly desired for all students of mathematics. While Dawkins and Weber’s article deals with undergraduate mathematics, their critique directly translates to K-12 mathematics by aligning with the “doing mathematics” (Stein et al., 2000, p. 16) level of activity as described in curriculum standards such as those from the National Council of Teachers of Mathematics. In teacher preparation programs across the US (from which context we are writing the present chapter), pre-service teachers are trained to design and implement tasks that point towards an end-goal of being at the “doing mathematics” level. Indeed, the obsession with “doing mathematics” led Baldino and Cabral (2021) to question the qualifications applied by the teachers to the students who are ostensibly attempting to “do mathematics” in the classroom. Is the students’ effort (i.e., labor) good enough to be considered “doing mathematics?” This qualification is for the teacher to decide, and in thus deciding, excludes knowledge from students who are not laboring in the intended way, that is, in the way that a mathematician would be. This judgement differential crystallizes the hidden dimension of the teacher’s exercise of power in the SLT learning environment: that it is not clear who the “mathematicians” are, nor is it clear what their practice might be or not be.

4.2 Behaviorism as Perspective

4.2.1 Definition

Behaviorism as an approach for teaching mathematics originated in classical psychology (e.g., Bloom, 1956; Gagne et al., 1993; Skinner, 1938; Thorndike, 1898, 1905). In mathematics classrooms, the goal of the behaviorist is to elicit a desired response when a given stimulus is presented and to make undesired responses less likely based on consequences (see Freudenthal, 1978). This relationship between consequences and behaviors is called conditioning. Many behaviorists take the stance that students are “born as blank slates,” and thus without mathematics, and that by learning the desired behaviors, acquire mathematical knowledge. The learning of mathematics is thus largely the result of the classroom environment being structured with the behavior–consequence doublet at its fore. In the current educational environment, behaviorism is still widely used if we look at the software and programs being utilized by teachers and schools, where students are given games to play that are focused on efficient achievement of low-level skills rather than engaging in conceptual understanding of higher-order tasks (e.g., Reflex Math software). Another example is when technology is used as a master (Geiger, 2005; Goos et al., 2000; Martinovic & Manizade, 2014), meaning that the technology knows the mathematics and the student believes or takes-for-granted any output produced by the software—lacking knowledge, competencies, and skills to engage his or her mathematical thinking to evaluate the outcome produced by the technology.

4.2.2 Goals of Teaching

The goal of the behaviorist approach is to create a perfect sequence of steps when teaching a mathematical topic that can be taught to a student procedurally with an expectation that the student will be able to repeat this sequence to produce the desired outcome. The main goal is to master the procedure and produce a desired outcome rather than examine the idea, construct new meaning, or make connections to other ideas within mathematics.

Psychology has historically described two types of behaviorism—classical conditioning and operant conditioning (Ormrod, 2020). The operant paradigm is more widely used in mathematics education settings, such as by pairing a reward with a desired behavior such as correctly answering mathematics problems. The goal of operant conditioning is to change current behavior towards the desired behavior by incentivizing with rewards. In the case of mathematics education, the desired behavior becomes the ability to correctly replicate procedures on tasks, and contrasts with a student’s own mathematical thinking because the student is being rewarded for replicating the steps as prescribed by the teacher rather for exercising creative agency over their own mathematics. The result of this, in the classroom, is that mathematics procedures are reproduced in students with high efficacy and efficiency; it is easy for the teacher to see that her students are performing the mathematics in the desired way and that the entire class is making progress. This is useful in training students to be prepared for standardized tests. Thus, the goals of the behaviorist teacher are to create a classroom environment that focuses on the desired behaviors as propagated by the teacher, along with a culture of expecting rewards for those desired behaviors. In this way, the behaviorist teacher’s goals are more focused on conditioning the behavior (e.g., reproducing a procedure) rather than understanding the mathematical concepts involved in the procedure.

4.2.3 Examples from the Literature

Kilpatrick et al. (2001) described vignettes of teachers’ planning and subsequent lesson enactment that follow the behaviorist perspective. In one example, Mr. Angelo (pseudonym) planned a lesson on multiplication by selecting only examples that would make it “likely that all students [would] be able to produce correct answers” (p. 329), as long as they memorized the presented rule. Despite these researchers’ elucidation of this early in the twenty-first century, more recent research has continued to detect the same behaviorist phenomena in mathematics classrooms.

Amador and Lamberg (2013) found that veteran teachers were guided by a behaviorist orientation towards their lesson planning, whereas novice teachers were not—the latter tended towards cognitive learning theory instead, which will be discussed in the next section. For the veteran teachers, lesson planning was guided by what Amador and Lamberg characterized as a testing trajectory, borrowing the term and structural diagram from Simon’s (1995) work on Hypothetical Learning Trajectories (HLTs). In the testing trajectory, lesson plans were reverse engineered to produce a desired behavior in the students: that they could read, understand, and answer test questions correctly. In this type of lesson planning, the veteran teachers objectified four types of professional knowledge: (1) their knowledge about the test content and structure; (2) their beliefs about how to best prepare for a test; (3) their knowledge about how students achieve apropos of specific mathematics content, i.e., anticipating student misconceptions; and (4) their knowledge about how classroom activities and representations directly support test preparation and align with test questions, i.e., as opposed to concept development. Interestingly, one of the veteran teachers in the study also described her beliefs about the nature of mathematics as being inherently procedural.

Also straddling the line between the behaviorist and cognitive learning theory perspectives, Chizhik and Chizhik (2016) issued a call to the field to reject behaviorism in favor of cognitive learning theory—the latter will be discussed in the next section. Chizhik and Chizhik embraced the cognitivism of Vygotsky (1986) and the cognitive learning theorists as a retort to the behaviorist legacy that has overshadowed teacher preparation curricula on lesson planning since Tyler’s (1949) foundational text on curriculum and instruction. At the time of publication of Tyler’s work, the education field was primarily influenced by behavioral psychology, a focus that has since shifted—at least in other areas of educational research—to cognitive psychology. Chizhik and Chizhik (2016) argued that research on lesson planning has not similarly updated to the cognitive perspective, remaining “stuck” in the behavioral psychology of 70 years ago.

Technology-influenced Return to Behaviorism. The advent of technology in mathematics classrooms presents the danger of a return to the behaviorist approach for teaching mathematics, by focusing on rote memorization and practice of skills that are not based on student cognition of the mathematics presented through the technology. When used in this way, some technology functions as a novel way to keep students occupied with activity during class and makes it easy for teachers to monitor student completion of work—i.e., students successfully performing a desired behavior such as answering questions correctly—rather than students’ development of the mathematical concepts. The operant reward is the two-fold novelty of the use of technology in and for itself, as well as the novelty of “winning” games or completing the puzzle correctly. In this way, the mathematics is secondary to the game’s or puzzle’s architecture, and thus the reward is not mathematical in nature.

During the COVID pandemic, school systems across the world were forced to transition to a virtual learning environment to protect the health and safety of students. They utilized various educational platforms and software (e.g., Mathletics, Reflex Math, and Sumdog). These Online Mathematics Instructional Program (OMPI) platforms use the behaviorist approach for teaching mathematics to motivate students (Darragh, 2021; Jablonka, 2017). As a result, opportunities for collaboration, problem solving, and using contextual mathematics were no longer present but were replaced by the development of superficial mathematical skills (Darragh, 2021).

We do not suggest that all technology is inherently slanted towards the behaviorist approach for teaching mathematics, but we do suggest that technology can be and often is used in that way (Parkhurst et al., 2010). In the institutionalized context of schooling, adopting any educational technology or platform is tied to teachers’ goals for teaching mathematics and their goals for students’ learning. Widely used dynamic platforms and software such as GeoGebra or Desmos can be pedagogically utilized in a way that is explicitly counter to the return to behaviorism (Edwards and Jones, 2006; Hohenwarter et al., 2008; Verhoef et al., 2015). The ways teachers use technologies present evidence of the perspective for teaching mathematics they enact, as described in the framework we present in this chapter. More research is warranted to explore gaps between the potential of technology and the actual uses of technology in schools, a need that is compounded by the fast-paced evolution of technologies that are available and adopted by schools (Moore, 2020).

4.3 Cognitive Learning Theory as Perspective

4.3.1 Definition

Psychology is also the origin of cognitive learning theory (CLT) as a perspective informing what happens in mathematics classrooms, although innovations such as those of Piaget (1970a, 1970b) changed the perspective from a focus on behaviors to a focus on cognitive development. This perspective includes radical constructivism, which conceptualizes knowledge as the product of cognitive processes that construct or form individualized understandings of concepts. Cognitive learning theory strictly focuses on matching learning opportunities in mathematics with learners’ natural cognitive abilities and processes. The major departure of cognitive learning theory from behaviorism was encapsulated in the development of the notion of mental representations and associations. Mental representations and associations describe the ways in which students “build up their picture of the world piece by piece” (von Glasersfeld & Steffe, 1991, p. 92); thus, knowledge is not conceived of as a “commodity that can be transferred from a teacher to a learner” (p. 93). Mental representations and associations are not necessarily in exact correspondence with observable behaviors; that is, observable behavior does not necessarily capture the entirety of what a student knows. The student has mental representations and associations, what Piaget (1970a, 1970b) called structures, that may or may not be reflected in their behavior. Behaviors are separate from these structures. Thus, a pedagogical approach that merely focuses on behaviors falls short of accurately designing for and assessing the goals and products of teaching.

4.3.2 Goals of Teaching

Cognitive learning theory focuses on students’ development in thinking and provides learning opportunities that match the progression of this development. Unlike the behaviorist perspective where the focus is on the outcome of learning, cognitive learning theory focuses on enhancing the process of conceptual development through learning experiences. The goal of the teacher is to take an active role in helping students to make connections among their ideas, thus progressing from a simple conception of a topic towards a more complex one.

Freudenthal (1973, 1991) and Gravemeijer (2004) described the process of guided reinvention, wherein the teacher pre-actively conducts “a thought experiment to envision a learning route the class might invent itself” (Stephan et al., 2014, p. 39) to mimic the evolution of mathematical concepts over decades or centuries. As a result, the teacher intentionally creates opportunities for students to explore and develop their own meanings of mathematics and mathematical concepts over the course of planned lesson units. The planned lesson units, which are teachers’ Type D, act as the guide for students’ reinvention of concepts and personal construction of meaning about those concepts: “[T]he learning route is designed so that the concepts emerge as students engage in the instructional sequence. It is in this sense that we say that students ‘reinvent’ mathematics” (Stephan et al., 2014, p. 39). In addition, the CLT teacher can only plan for what students might do, not what they will do—and for that matter, what students’ constructed mathematical concepts and meanings might be as a result of their teaching.

Guided reinvention is pedagogically operationalized through work of radical constructivists Simon and colleagues (e.g., 1995, 2018). They developed the Learning Through Activity (LTA; Simon et al., 2018) framework based on the assumption that teachers can promote abstraction with engineered sequences of tasks. The framework extends from the teacher’s pre-active engineering and sequencing of tasks all the way through students’ abstraction of concepts. The engineering and sequencing portion of the framework is Type D; the task actively presented to students is Type C; the reflective abstraction is Type B; and the concept as the product of students’ abstraction is Type A. Thus, the CLT teacher’s Type D consists chiefly of task engineering and sequencing for the intended conceptual development trajectory: “If a concept is a result of reflective abstraction, that is an abstraction derived from activity, then it should be possible to engineer a sequence of tasks that elicits appropriate activity that promotes abstraction from that activity” (Simon et al., 2018, p. 103).

4.3.3 Examples from the Literature

Stephan et al. (2014) presented a cogent description of guided reinvention planning and teaching through a case study of 7th grade teachers who designed an instructional sequence of tasks intended to guide students in reinventing the rules of positive and negative integers, and integer operations. The task sequence started with a realistic context of financial transactions (e.g., net worth, assets, and debts) symbolized by integers and signs. The sequence progressed towards a purely abstract symbolization of signed integers and their operations, so that students through this process would explore and reinvent the meaning of these concepts for themselves.

Amador and Lamberg (2013) studied the ways in which teachers designed learning trajectories and planned corresponding lessons within the institutional constraints of the school, such as testing. They conceptualized the study using CLT in order to investigate how teachers addressed the high-stakes nature of standardized testing apropos of the daily work of teaching, and how the task of preparing students for such tests might be different for different teachers. In order to do this, they theorized an analog to the HLT called a testing trajectory where preparation for the testing environment was the driver for decision-making in the planning and teaching process. Four teachers were interviewed—three veteran teachers and one novice, first-year teacher. The three veteran teachers’ planning was guided by the testing trajectory whereas the novice teacher’s planning was guided by conceptual development in the form of an HLT. That is, the veteran teachers worked backwards from the known parameters and format of the testing environment in order to theorize a hypothetical trajectory for preparing students to answer test questions whereas the novice teacher worked backwards from the mathematics conceptual goal in order to theorize a hypothetical learning trajectory for students’ development of that concept. The direct link to this conceptual outcome was not implicated in the testing environment for the novice teacher. We identify the novice teacher as having taken the CLT perspective whereas the veteran teachers were effectively acting as behaviorists.

Chizhik and Chizhik (2016) issued a call to embrace CLT in lesson planning in tandem with a rejection of behaviorism. They note that, historically in teacher education, the texts being used in teacher preparation programs (TPPs) trace their origins to the behavioral psychology of Tyler (1949). Despite the field of education having since moved away (since the 1970s and 1980s; e.g., Vygotsky, 1986) from behaviorism in its predominant theoretical stance, TPP curricula on lesson planning have not consistently made the same update. This could potentially lead to the divide in teacher planning practices observed by Amador and Lamberg (2013). Chizhik and Chizhik (2016) argued for a reformulation of the lesson planning TPP curriculum to involve the following major components: (1) reconceptualize learning objectives by theorizing a CLT-based version of Bloom’s Taxonomy; and (2) reconceptualize instruction to maximize student engagement, sharing of ideas and thinking, and (3) meaningful teacher feedback, with these three components being the major drivers towards students’ success on tests.

Fernandez and Cannon (2005) conducted a case study comparison of Japanese and US teachers’ lesson planning habits. They found that the two groups of teachers conceptualized the task of lesson planning in very different ways. The Japanese teachers’ views of the task of lesson planning centered on conceptualizing students as active participants in the learning process and prioritized students’ development of positive attitudes towards learning mathematics. The US teachers’ views of the task of lesson planning, conversely, centered on conceptualizing themselves as effective teachers of the content. While the US teachers were concerned with student engagement, they grouped it under the characteristics of being an effective teacher. Thus, the difference in the two cultural paradigms of the teachers in the study meant that the purpose of their lesson planning manifested in very different ways. The US teachers planned with their own performance in mind, whereas the Japanese teachers planned with their student’s cognition and affect in mind. In both cases, CLT could be implicated, but it is certainly more evident in the Japanese teachers’ privileging of the students’ position in the CLT paradigm. In both cases, CLT could be implicated because of the focus on trajectorial development of the mathematical content through the planned lesson.

Lewis et al. (2009) contributed a theoretical model that combined elements of CLT and SLT for the purpose of application to Lesson Study (LS), a pedagogical approach to analysis of, reflection on, and refinement of lesson plans typically done in groups of teachers. In their model, they synthesized elements of both theories in various stages of LS, with the aim of theorizing how lesson improvement materializes from the LS process. The model connects CLT with these aspects of LS: (1) building understanding of the content area as well as students’ and colleagues’ thinking about it; (2) studying the standards, curriculum, and existing lesson plans to decide on building blocks for the conceptual development of the target lesson; (3) writing down lesson plan ideas that elucidate goals for student thinking—and student learning differences—to make them visible to colleagues; (4) observe a colleague teach a version of the lesson, paying attention to links between students’ thinking and lesson design apropos of learning goals; and (5) noting instructional practices that should be improved to support the learning goals of the lesson. Other aspects of the model focused more on SLT, such as collaboration amongst colleagues and sharing ownership of the LS process. By theorizing the LS process through the CLT perspective, Lewis and colleagues offered a more cogent description of the work of Simon et al. (2018) with specific regard to the task of lesson study and planning.

Finally, Sullivan et al. (2013, 2015) have used CLT to research lesson planning. In their work, they connect Type D to Type C, with the distinction being that in Type D, the focus is on helping teachers identify important mathematical ideas that are fundamental for teaching a topic, whereas in Type C, they suggest that by improving teachers’ knowledge of mathematics through collaborative planning, their ability to plan for a given mathematical objective will improve. In their 2013 paper, they described the ways in which teachers use the Australian national curriculum documents during planning. They found that many teachers assume agency over planning decisions when reading and interpreting curriculum documents and execute those decisions with resolve. Thus, they claimed that authors of curriculum document should construct such documents with explicit focus on inspiring teachers’ decision agency in enacting the national curriculum standards. In short, Sullivan et al. (2013) argued that external actors in the school context (such as administrators, curriculum developers, etc.) should focus on unlocking teachers’ planning agency potential rather than attempting to structure or restrict it, and that collaborative planning should be ritualized in schools. In this process, the teachers in the 2013 study took up agential decision-making about their planning through a process of reading the curriculum documents. Sullivan et al. (2015) closely tied this work to the CLT perspective, by focusing on the teachers’ engagement with lesson planning practices that match students’ cognitive process (assumedly along an HLT or similar trajectory) with the difficulty of struggle in the lesson’s sequencing. In this way, teachers use CLT to reduce negative student experiences with the HLT and improve the lesson without reducing the cognitive demand—a crucial component of a successful application of CLT—of the lesson’s tasks.

Sullivan et al. (2015) necessarily leads us to a discussion of the productive struggle and productive failure literature. This contrasts with the didactic perspective on teaching mathematics wherein the teacher “must produce a recontextualization and a repersonalization of the knowledge. It must become the student’s knowledge” (Brousseau, 2002, p. 23, emphasis in original). The term productive struggle is defined as a necessary student learning behavior for building conceptual understanding and for promoting students’ sense making (Heibert & Grouws, 2007). Other researchers describe the goal of a CLT teacher as to teach for the robust understanding of mathematics by supporting students in productive struggle while building understandings through actively engaging in mathematical practices (Schoenfeld, 2014; Schoenfeld & TRU Project, 2016). The TRU project team describes five dimensions of powerful classrooms: (1) mathematics; (2) cognitive demand; (3) equitable access to content; (4) agency, ownership, and identity; and (5) formative assessment (Schoenfeld & TRU Project, 2016). They stress the importance of focusing on these dimensions during the lesson planning and reflection process (Type D). In addition, researchers encourage teachers to plan for students’ productive failures as a necessary inseparable and cyclical portion of mathematics problem solving and learning (Kapur, 2010, 2014; Simpson & Maltese, 2017). Warshauer et al. (2021) highlight the importance of preservice mathematics teachers learning to identify strategies and practices that can be used for planning and supporting productive struggle in the classroom.

4.4 Social Constructivism as Perspective

4.4.1 Definition

In social constructivism (SC), which is based on the work of Vygotsky (1960), the classroom community constructs knowledge and understanding as a cultural product of students’ learning experience. In the SC mathematics classroom, the shared nature of the knowledge is distinct from the cognitive learning theory perspective, because the personally held mathematical knowledge of an individual student is a reflection of the community’s construction of that knowledge rather than a personal product of construction of mental representations. The social constructivism perspective was further developed in varying ways by teams of scholars, including but not limited to the work of Bishop (acculturation; 1988), Resnick (socializing; 1988), and Cobb and Yackel (emergent perspective; 1996). Acculturation is induction of students into a foreign or alien culture (e.g., the mathematics classroom). In the culture of the mathematics classroom, this process includes interacting with others to perform the activities of counting, locating, measuring, designing, playing, and explaining (Bishop, 1988) to develop mathematical knowledge. Socializing refers to social constructivism over time, where “personal habits and traits are shaped through participation in social interactions with particular demand and reward characteristics,” with the goal of the student “gradually tak[ing] on the characteristics of [the teacher]” (Resnick, 1988, p. 12). In the emergent perspective (Cobb & Yackel, 1996), cognitive and social perspectives work in parallel, with the teacher simultaneously interpreting students’ cognition (e.g., beliefs about self and others, the nature of mathematics, conceptions of mathematical ideas) and students’ social interactions (e.g., classroom norms, mathematical norms, and mathematical practices).

4.4.2 Goals of Teaching

The goal of the SC teacher is to involve students in a community discourse about mathematics through teaching that is focused on classroom discussion. The discourse promoted by the teacher is guided by the relevant mathematical tasks and investigations, with the teacher being the instrument of enculturation into the mathematizing culture; the students meanwhile are the ones being acculturated (Bishop, 1988). By encouraging students to form new understandings of mathematics using their interpretations of prior mathematical knowledge, the teacher aims to empower students to contribute to the reconstruction—instead of reproduction—of new mathematical knowledge. In other words, SC teacher’s goal is to provide students with opportunities to develop subjective knowledge that must be constructed and validated through and within sociocultural interactions so that the subjective knowledge may become objective knowledge of the group.

4.4.3 Examples from the Literature

Purdum-Cassidy et al. (2015) used social constructivism in their study of the way in which teachers plan for questioning (e.g., key questions on a lesson plan) in elementary mathematics classes. In their Vygotskian framing, they noted how “conceptual knowledge first occurs between learners … and then moves within the learner” (p. 81). Social constructivism thus positions the teacher’s key point of access—apropos their potential for impacting student learning outcomes—as that of influencing what happens between students in the classroom. The intrapsychological impacts that occur consequently are left to each student’s own psyches for the purposes of meaning-making. The teacher should thus be primarily concerned with impacting the social construction of knowledge. In their study, Purdum-Cassidy and colleagues focused on the role of questioning (their own plans for key questions) and the role of interpreting and answering students’ questions during the lesson—overall what is generally called discourse in the mathematics education literature. In particular, they note how pre-service elementary teachers struggle to plan for and write key questions when planning a lesson. As an intervention, these researchers investigated the possibilities of children’s books that have mathematical topics in helping teachers plan for mathematical questioning in their lessons. Since children’s literature is discursively organized (viz. into the format of a story), the same structure can be ported over into the structuring of questions qua discourse. Such discursively structured questioning prompts the classroom community to socially construct knowledge—vis-à-vis questioning and discourse—that is then internally reified for each student.

Sullivan et al. (2015) investigated the connection between professional development and teachers’ abilities to plan for scaffolding challenging mathematics tasks. In their study, they investigated how teachers exposed to challenging tasks that require student collaboration (such as inquiry tasks). Such tasks were initially uncomfortable for teachers to use, but once they had been supported by professional development, teachers felt confident in planning for such tasks and were more likely to seek out more inquiry tasks. This finding indicates that teachers are often hesitant to engage in the SC perspective when planning for and enacting mathematics lessons, but that this hesitation can be alleviated through the use of directed training on the approach.

4.5 Structuralism as Perspective

4.5.1 Definition

The structuralist approach originates from both mathematics and psychology. Dienes (1960) emphasized the importance of children learning through the use of manipulatives (e.g., Gningue, 2016); however, classic examples of the structuralist approach can be found in every branch of mathematics. For instance, the Poincaré and Beltrami-Klein models for describing hyperbolic geometry are used to help learners develop fundamental understanding of hyperbolic space that is challenging to visualize otherwise. The focus of the structuralist perspective is on the structures and theories that underlie the mathematics presented. This perspective is often conflated with the constructivist approaches for teaching mathematics. It overlaps with radical constructivism in that there is a focus on theories of cognitive development and students’ concept formation of a specific mathematical idea. However, the structuralist approach differs in that the focus is on discovering the structures that are introduced to students by the teacher, who is using those structures as a framework around which mathematical understanding can be developed, rather than constructing them. An example in K-12 teaching is the use of AlgeBlocks to visually demonstrate multiplication of polynomials, a mathematical process that would otherwise be only abstract and symbolic (de Walle et al., 2017). The difference, thus, is that the structuralist perspective is focused on discovering the existing mathematical structure of polynomial multiplication, a structure that is already there. Conversely, the constructivist perspective does not conceive of an existing structure that the student must reach through their mathematical activity, but rather, is exploring to construct their own concepts from scratch. The structuralist, therefore, can talk about misconceptions and misunderstandings when a student’s understanding is incongruent with the relevant structure, whereas constructivists do not use that term since the student’s concept is its own referent.

4.5.2 Goals of Teaching

The goal of the structuralist teacher is to guide students in discovering a mathematical structure, through the use of exemplary and sequenced tasks, each of which draws particular attention to some limit-case aspect of the structure. As already mentioned, one of the characteristics of the structuralist approach is an emphasis on the use of manipulatives. The manipulatives allow the student to experience an embodiment of the mathematical structure during their discovery process. Additionally, there is a spiral design in the curriculum that allows for revisiting key mathematical structures in a cycle, delving into them more deeply each time.

A relevant metaphor here is the way in which a house is built: the cornerstones of the foundation must be located first, followed by the joists in the floors and beams in the walls, and it is not until this skeleton is truly discovered from behind the plaster walls (the general case examples), that the house’s structure could be said to be truly discovered. Thus, the structuralist teacher must first check their own understanding of the structure against the mathematical community and literature, and then locate exemplary cases of problems that will illuminate the cornerstones, beams, and joists of the structure. These must be carefully sequenced so that the student will follow the same path in discovering the hierarchy of the structure; for example, it would make no sense to study the roof trusses without first having discovered where the studs in the walls are. This identification and sequencing of exemplary tasks then leads students to develop a more general understanding of the structure as the teacher generalizes these exemplary cases. In practice, this typically follows the arc of beginning with manipulatives, then moving to a pictorial representation of the manipulatives (i.e., drawings), then associating the drawings with abstract symbols or ideas, and finally removing the manipulatives altogether so that the abstract symbols represent the structure itself in the student’s mind.

In the structuralist approach, models and manipulatives are used to help students discover mathematical structures, but none of the models are robust enough to be applicable in every case or to demonstrate every attribute of the mathematical structure’s complexity. The teacher, therefore, uses manipulatives to help students discover a particular aspect or develop understanding of a particular example. These particulars can then be used to develop understanding of the mathematical structure more generally.

Mathematics education literature on multiple representations exemplify the practical use of the structuralist approach in mathematics classrooms. Researchers discuss the importance of using multiple representations and developing fluency in flexibly moving between them, such as visual, pictorial, graphical, numeric, and algebraic (e.g., Ainsworth, 2006; Deliyanni et al., 2016; Goldin, 2002; Goldin & Shteingold, 2001; Mitchell et al., 2014; Stylianou, 2010). Manipulatives can be used as a tool for making and presenting representations and can either be virtual (on computers) or physical. Planning for these types of lessons thus includes envisioning tasks with different representation in sequence from concrete to abstract, and tasks that promote the students’ movement between the multiple representations’ uses. Illustrations of classroom implications of the structuralist approach to Type D can be found in mathematics educators’ works designed for training pre-service teachers (e.g., Beckmann, 2022; Kilpatrick et al., 2001; Van de Walle, 2017).

4.5.3 Examples from the Literature

Pierce and Stacey (2009) discussed the use of graphing calculators in a structuralist classroom. In their study, they emphasized the importance of four aspects of lesson planning for the use of technology within the structuralist approach: (1) focusing on the main goal of the lesson and thoughtfully selecting multiple representations that directly support the goal; (2) identify, for each representation, a specific purpose aligned with student engagement; (3) “establish naming protocols for variables” (p. 231) so that students can translate variables across technologies and representations easily; and (4) reducing any excessive cognitive demand so that technology does not distract or detract from the lesson goal and students’ engagement with the intended mathematics. These researchers argued that technology allows the teacher to support the goals of the lesson as identified by the teacher during lesson planning. Depending on the goals for the lesson, the structuralist teacher might need to restrict the strategies that emerge during the discussion or restrict the representations being used, or plan for the reduction of distractions due to the technology (Pierce & Stacey, 2009).

In their study of the low-performing middle school mathematics classrooms, Panasuk and Todd (2005) present a conceptual framework within a structuralist approach for teaching mathematics that guided the development of the instrument titled Lesson Plan Evaluation Rubric (LPER) for the assessment of mathematics teachers’ lesson planning process. The researchers also described a four stages of lesson planning (FSLP) strategy comprising: (1) planning of objectives, formulated in terms of students’ observable behavior; (2) design of homework, that matches the lesson’s objectives; (3) inclusion of developmental activities that reflect the lesson’s objectives and advance students’ development and learning; and (4) planning mental mathematics that include activities to stimulate students’ prior knowledge, and prepare students for the acquisition of new concepts. The FSLP strategy focuses on the development of lessons involving multiple representations such as visual representations (diagrams, pictures, graphs, tables), verbal representations (words), and symbolic representations (variables, expressions, operations, equations) to address students’ misconceptions and assess students’ progress toward meeting learning objectives. Moreover, the strategy produced lessons that were comprehensive and coherent by emphasizing alignment between homework, classroom activities, and mental mathematics. The researchers claimed that to incorporate FSLP effectively, lesson plans must be flexible yet logical in their design to accommodate the distinctive needs of each student. Furthermore, this strategy encourages teachers to continuously adjust and adapt to achieve the desired learning outcomes. In addition, this strategy is compatible with Gueudet and Pepin’s (this volume) concept of coherence-in-use, which they define as the degree to which there is coherence within teachers’ (enacted) propositions to their students, after teachers have consulted various curricular materials.

Harbour et al. (2016) described a process of structuralist lesson planning, that included beginning with a diagnostic interview to determine a student’s existing understanding of a concept, and then comparing that understanding with a standards-informed intended goal for the student’s understanding as a result of the lesson. The teacher then, based on this gap, takes four considerations into their lesson planning: (1) plan the lesson to utilize instructional strategies that explicitly focus on students’ conceptual understanding of the topic; (2) plan explicit scaffolding and feedback opportunities into the lesson; (3) plan for student think-alouds and teacher think-alouds; and (4) plan for the use of concrete materials, visual representations, and numeric representations.

4.6 Problem Solving as Perspective

4.6.1 Definition

Problem solving as an instructional approach in mathematics classrooms is a type of teaching that focuses on developing students’ problem-solving skills and abilities to persist when faced with problems with which they have no experience, rather than practicing skills that they have already previously learned (e.g., from prior instruction). The focus is on both the mathematical content and the process, with the intention to produce and interpret different approaches and strategies for solving the same problem. This approach—based on the theoretical framework developed by Polya (1945/2015) in How to Solve It—originated in the 1980s with the Cockcroft Report, Mathematics Counts (UK), and NCTM’s Agenda for Action, all of which called for problem solving and investigations to be included in mathematics teaching. Schoenfeld (1983) has argued that studying problem solving requires the consideration of different and distinct domains of behavior and knowledge—knowledge resources, control, beliefs, heuristics, and practices—rather than purely relying on cognitive psychology.

4.6.2 Goals of Teaching

The goal of the teacher in a classroom that focuses on problem solving as an instructional approach is to create a thinking classroom (Liljedahl, 2019; Liljedahl et al., 2016) in which students are given tasks that encourage thinking. This is the kind of task or activity that does not focus on precise application of a known procedure, implementation of a taught algorithm, or the smooth execution of a formula. In other words, problem solving is a messy, non-linear, and idiosyncratic process (Liljedahl, 2020). Problem solving strategies include—but are not limited to—guess-and-check, making lists or tables, looking for patterns, working backwards, making a model, drawing a picture, and trying a simpler problem first. The goal of the teacher is to encourage students to analyze each problem for what is given and what constraints are present, to highlight the relationships between variables, and to explicate the goals of solving the problem. The teacher creates opportunities for students to explain the meaning of the problem, as well as to ask reflective questions such as “I wonder…” and “Does this make sense?” (Common Core State Standards Initiative, 2010; Kobett & Karp, 2020; Timmerman, this volume).

4.6.3 Examples from the Literature

Liljedahl (2020) listed the practices teachers have to consider when planning for lessons in a thinking mathematics classroom. The list comprises 14 general categories of practice that all teachers adhere to in some shape or form: (1) What are the types of tasks we use; (2) How we form collaborative groups; (3) Where students work; (4) How we arrange the furniture; (5) How we answer questions; (6) When, where, and how we give tasks; (7) What homework looks like; (8) How we foster student autonomy; (9) How we use hints and extensions to further understanding; (10) How we consolidate a lesson; (11) How students take notes; (12) What we choose to evaluate; (13) How we use formative assessment; and (14) How we grade.

As a case example of this approach to Type D, Lilejdahl (2015) studied teachers’ planning for problem solving in numeracy lessons. He investigated how a group of mathematics teachers engaged in lesson planning from the problem solving perspective over the course of six months, discussing their challenges with each other whilst shifting their goals for the lesson from a more traditional focus on students’ knowledge to a focus on planning for students’ quality of participation in the problem solving tasks. Through this shift in focus, the teachers began to plan for students’ quality of engagement with the tasks—i.e., through the act of problem solving—rather than on designing lessons to transmit and assess a quantity of knowledge. This shift in focus was characterized by teachers’ embrace of open-ended, complex problems with multiple parameters that required students to engage in thinking critically about the problem and the parameters within which they would be expected to solve the problem, in other words, the boundaries that circumscribed the problem. By focusing on the problem and its particularities, teachers’ Type D assumed a different form than would have been required for more traditional, knowledge-based lesson planning. In particular, Liljedahl (2015) found that teachers who aimed at problem solving Type D focused on how to design the task with problem solving as its goal rather than students’ knowledge outcomes.

Another example can be found in Zazkis et al.’s (2009) theorization of the impasse of teacher educators who teach their students to plan lessons comprehensively (i.e., with knowledge and outcome goals) thereby restricting the aims of mathematics education to those captured in curriculum documents. In the article, they juxtapose “planning teaching” (i.e., planning for knowledge and content goals) versus “teaching planning” (i.e., planning for students’ engagement in problem solving). By utilizing the practice of lesson plays, the authors theorized how planning for problem solving incorporates consideration of the “contingencies of teaching” (John, 2006, p. 487, as cited in Zazkis et al., 2009). With a shifted focus on problem solving instead of knowledge goals, “planning for teaching” instead of “teaching how to plan" prioritizes the playfulness and student activities of problem solving. These activities are captured in Liljedahl’s (2020) list of characteristics in aligning the teachers’ and students’ actions as “artifacts of the [lesson] planning structure” (Zazkis et al., 2009, p. 43), such as teachers’ responses to students’ unexpected progression through the problem solving nature of the lesson—or in other words, alignment of teachers’ planning for the teaching of their students as opposed to teachers’ planning of the lesson itself as an artifact.

4.7 Culturally Relevant Pedagogy as Perspective

4.7.1 Definition

Culturally relevant pedagogy (CRP; Gay, 2010, 2018; Jett, 2013; Ladson-Billings, 2014) as a teaching perspective emerged out of the Realistic Mathematics Education movement (RME; viz. Freudenthal, 1991) in response to the rise of post-colonial studies in education. CRP is one way of addressing the RME heuristic that mathematics be contextualized to students’ cultures. As Makonye (2020) noted, the imperative of CRP and contextualized mathematics is evidenced by the high rates of failure seen in school mathematics amongst marginalized populations, many of which are the modern product of colonialist efforts. CRP directly problematizes the Western, colonialist notion that mathematics is objective, and that it is not value-laden by a culture (viz. Bishop, 1988). The erroneous belief that mathematics is in fact objective leads to what is experienced in modernity as the perceived universality of mathematics, and moreover, the “truth” of mathematics. Not only is this problematic for students’ learning of mathematics, but also for mathematics teachers’ training, because the training experiences of mathematics teachers predicate the beliefs they will have about mathematics, and subsequently will affect the ways in which they will be conditioned to enact their training in a classroom with students. Because of this, the issue of CRP has just as many implications for teaching as it does for learning.

CRP is based on the assumptions that cultural groups engage in behavior that is based in mathematics or mathematical elements, and that knowledge is produced through and by culture and history. Thus, mathematical thinking must be consistent with the cultural context of the students. For example, enacting CRP teaching of students in a majority Black inner-city school in the US might consist of instruction that focuses on the origin of mathematical concepts within that culture and word problems or projects about mathematics within the Black culture and history of that city.

Additionally, ethnomathematics has been a well-known research topic in mathematics teaching since D’Ambrosio (1985) introduced the term. (Also, for a discussion of how ethnomathematics implicates ethical responsibilities, such as through the use of technology, see D'Ambrosio, 1999). He defined ethnomathematics as “the mathematics which is practiced among identifiable cultural groups, such as national-tribal societies, labor groups, children of a certain age bracket, professional classes, and so on” (D'Ambrosio, 1985, p. 45, our emphasis). Thus, D’Ambrosio argued that ethnomathematics is conceptualized in contrast to the school mathematics which has the aim of maintaining and reproducing economic and social structures, “reminiscent of that given to the aristocracy when a good training in mathematics was essential for preparing the elite (as advocated by Plato), and at the same time allows this elite to assume effective management of the productive sector” (p. 45). Because of this distinction, we characterize CRP as owing its intellectual heritage to ethnomathematics but is markedly separate from it in terms of its degree of institutionalization and purpose. Ethnomathematics is not concerned with the teaching of mathematics in institutionalized settings, like schools. In fact, scholars (e.g., Pais, 2011) have revealed a growing misuse of ethnomathematical research, wherein the economic and cultural reality of the identifiable cultural group is removed from the ethnomathematics in the act of institutionalizing it.

4.7.2 Goals of Teaching

CRP teaching can be characterized by mathematics content that is explicitly situated within a contextual frame unique to the culture of the students being taught. Instead of focusing on the arbitrary nature of traditional mathematical structures, CRP bases mathematics in cultural activities and knowledge most relevant to the students. By doing so, teachers empower their students and present mathematics as intimately relevant to their students’ cultural lives instead of being abstract and formalist, thus giving mathematics a useful application for all students within the cultural context. As a result, for the CRP teacher, mathematics teaching includes explication of the value-laden nature of the mathematical concepts being taught, as well as adopting a perspective that their work as a teacher is to enculturate students into the culture of mathematics—whether that culture be Western and normative or Indigenous and marginal. This can, in many cases, lead to a conflict between the culture of the CRP teacher and the culture within which the mathematics is being contextualized (Bishop, 1988). Thus, teachers must be proficient in not only their content and professionally situated knowledge of mathematics, but also in the cultural history and practices of the students whom they are teaching. As a result, traditional curriculum materials must be supplemented or redesigned to support CRP instructional efforts. In this process, the CRP teacher must be careful not to essentialize students’ culture (McCarty & Lee, 2014).

4.7.3 Examples from the Literature

An example of CRP teaching can be seen in American Indian and Indigenous studies, such as those conducted by Ruef et al. (2020), who studied how mathematical concepts are represented in the Ichishkíin language of the Yakima culture. In the article, the authors weave together a complex theoretical perspective to frame their work in a comprehensive framework of theory. In their analysis, they establish the fact that mathematics is culturally situated in the western/American context which is markedly different than for the Yakima people. One of the stories they described from the interview data (with a Yakima Elder) is that the word for “fraction” comes from the same root word in their native language for the process that happened when the White European settlers broke apart their nation by giving them the “choice” of either complete genocide or surrender of lands. The native language of the tribe uses this term for “broken” when they are talking about fractions. This shows how subtle the cultural situatedness of mathematics can be, and that researchers from dominant social groups are unable to fully grasp the concept of the differences in lived experience of other peoples’ mathematics. Through the CRP perspective, implications for teachers’ Type D “are not subtle” (Ruef et al., 2020, p. 316): mathematics can function as a form of White supremacy qua White knowledge production. Thus, the CRP teacher understands the culture of the students they teach, allowing them to plan lessons and assess student learning within that cultural frame. As Ruef et al. (2020) concluded, the work of planning for mathematics lessons and assessing student work—informed by CRP—is built around the concomitance of students’ cultural language and mathematical concepts so that students and teachers are connected through the place and time in which they are engaged in mathematics learning. The Alliance of Indigenous Math Circles (www.aimathcircles.org) offers resources for teachers interested in planning CRP mathematics lessons in the Indigenous American Indian context.

Jett (2013) wrote about the context of working in pre-service mathematics teacher university courses so that the content and methods taught are of racial relevance to his students. Failure to conceptualize mathematics teacher education through a lens of cultural relevance is, for Jett, an act of fracturing the identities of pre-service mathematics teachers as they are learning to plan and implement lessons. Culturally responsive pedagogy, thus, becomes a key driver in the ways that pre-service mathematics teachers are taught to plan lessons because, as Ladson-Billings (2009) said, CRP “empowers students intellectually, socially, emotionally, and politically, by using cultural referents to impart knowledge, skills, and attitudes” (p. 20). Without CRP training in teacher education, future mathematics teachers are not equipped to plan CRP lessons of their own. An example of this can see in a study by Makonye (2020), who illustrated the consequences of teaching mathematics outside of students’ cultural contexts. Makonye gave the example of interest in the banking system and how it is irrelevant or unrelatable to students in South Africa, because requesting interest for any money loaned is considered immoral. When being taught about the application of interest and related mathematical concepts, South African students face challenges because the applications are based on a culturally irrelevant phenomenon and thus the mathematical concept’s universality fails (Makonye, 2020).

Skovsmose (2021) offers additional implications for CRP in the planning of mathematics lessons, namely that situations of crisis can serve as bases of lesson plans. As a human race, there are universally shared experiences (e.g., pandemic) that create cultural cohesion constitutive of “cultural relevance” for all students in a classroom. For example, a teacher could use mathematics to teach a lesson on a crisis or a critical situation such as COVID-19 to which all students could culturally relate; the cultural context of COVID-19 is primary to all people because they have all experienced it. From a CRP perspective, COVID-19 is a cultural phenomenon and thus can be used to create and/or illustrate how the relevance of the mathematical activity can be presented pedagogically within a cultural group.

4.8 Project and Problem-Based Learning as Perspective

4.8.1 Definition

Project and Problem-Based Learning (PBL) is a perspective for teaching mathematics that is based on the assumption that mathematical knowledge has to be presented in the real-world contexts of students’ environment. The environment provides meaning to the mathematics or contexts out of which new knowledge can be drawn. An example of this approach can be found in works that use nature as a context to teach mathematics concepts (e.g., Adam, 2003/2006; Toni, 2021). On the one hand, by exploring problems in the environment students are prompted to discover mathematical concepts. On the other hand, the abstract structures of mathematics can be imposed on an environmental or contextual situation, allowing the situation or context to be reinterpreted using mathematical concepts. The PBL teacher views mathematics as inseparable from the environment or context in which it exists or originates. In other words, every mathematical topic is presented within its context: the context itself is the source of inspiration and motivation for students’ interest in the mathematics, as well as the starting point for developing new mathematical knowledge. This means that the teacher is not there to impose notions onto the child, but rather, to select the influences (also see Dewey, 1897).

Based on an extensive review on PBL literature, Merritt et al. (2017) found that different definitions existed. Most relevant for the mathematics education community are the functional/curriculum design, constructivist, and conceptual change definitions. Based on their analysis, we align the functional/curriculum design definition with the inquiry-based learning literature, the constructivist definition with the cognitive learning theory perspective discussed in the present chapter, and the conceptual change definition with the structuralist perspective also discussed in the present chapter. We conjecture that teachers who participate in educational experiences to learn about PBL—such as professional development events—accept PBL as a novel pedagogical tool without explicit reference to one of the three aforementioned definitions. Rather, when they return to their classroom and choose to plan lessons from their newly learned PBL perspective, they retroactively assign epistemological meaning to the lesson based on their other beliefs about mathematics teaching and learning; these beliefs then become objectified through the planning, enactment, and assessment of the PBL lesson. More research is needed in this area.

4.8.2 Goals of Teaching

The goal of PBL is for individual learners to construct mathematical concepts from the context familiar to them. The teacher uses real-world contexts as a source of inspiration, abstraction, meaning, and motivation for learning mathematics. As a result, the goal of teaching mathematics from this perspective is that students understand the mathematical concepts as intimately emergent from the context and environment itself. Thus, the student learns the structure of the environment as a mathematical structure along with learning the mathematical concepts. A characteristic of this approach apropos of pedagogy is the implementation of collaborative group projects that often utilize statistical analyses, mathematical modeling, and exploratory activities (Capraro et al., 2013; Lee, 2018).

4.8.3 Examples from the Literature

Literature on PBL related to Type D has come from the STEM Education, Engineering Education, and Science Education fields (e.g., Cheaney & Ingebritsen, 2005; Miller & Krajcik, 2019; Mills & Treagust, 2003). For example, Miller and Krajcik (2019) reported on a four-year action research project they did in their own classes in teacher education, on how best to align science teacher preparation with the goals of PBL as outlined in official curriculum documents such as the Next Generation Science Standards (NGSS; NGSS Lead State Partners, 2013). They highlighted the connection between the goals of PBL and developing students’ knowledge-in-use (see Pellegrino & Hilton, 2012), which is the “capacity that learners need to apply knowledge to make decisions and solve problems, and to evaluate when and how to get more information when necessary” (Miller & Krajcik, 2019, p. 1). Miller and Krajcik (2019) elucidated that planning for PBL lessons means planning for the creation of a specific type of learning environment: a “sense-making and knowledge generating environment” (p. 5) that is designed to pique students’ interest about natural phenomena or situations in the real world through the pursuit of questions about the world. As such, the teacher creating the PBL environment must establish driving questions to guide: (1) the lesson; (2) the development of the students’ knowledge-in-use; and (3) the development of artifacts (concrete representations) as the results of the PBL investigation. Specific instances of Type D in Miller and Krajcik's (2019)  process include: (1) planning for driving questions “about a problem to be solved or experience to be explained that promote wonderment about the world” (p. 6); (2) including students’ participation in scientific practices in the lesson plan; (3) planning for students’ exploration of the driving questions through “collaborative sensemaking activities” (p. 6) that are designed to engage “in shared knowledge building” (p. 6); (4) planning for scaffolding the development of students’ knowledge-in-use through the use of discursive pedagogical tools; and (5) assessing the artifacts students produce as a result of the PBL lesson for the extent to which they “scientifically address the driving questions with increasing sophistication” (p. 6).

Conversely, the mathematics education literature on PBL focuses primarily on students’ conceptual understanding of mathematics and/or beliefs about and attitudes towards mathematics as a result of having participated in a PBL lesson (e.g., Knezek & Christiansen, 2020; Merritt et al., 2017). Merritt et al. (2017) found that all the studies in mathematics and science PBL that they reviewed were concerned with students’ knowledge, achievement, and affectual outcomes. The literature on PBL and its Type D implications are relevant to mathematics teaching and teacher education as well. Considering the growing interest in PBL and the larger increase in focus on STEM education, this gap in the literature needs to be addressed in order to better understand how the mathematics teacher who wishes to implement PBL lessons plans for and assesses the impacts of those lessons.

5 Pros and Cons for Each Perspective

Each aforementioned instructional approach for teaching mathematics has advantages and difficulties associated with it. Planning based on each instructional approach therefore presents unique challenges. We survey these briefly, not exhaustively, in this section.

From the Situated Learning Theory (SLT) perspective, the goal of the teacher is to develop a students’ sense of belonging in the mathematics community (e.g., using correct mathematical language and discourse patterns, solving problems, and practicing communication of their thinking, and doing mathematics). The knowledge is situated in the mathematics community rather than an individual and the students are treated as a newcomer apprentices in the community where the oldtimers—mathematics teachers—engage in doing mathematics as the leaders of the mathematical community. The challenge with this approach is the time needed to develop mathematical community and the norms associated with it, including the teacher’s identity as a member of the community—a practicing mathematician—and the students’ identities as legitimate participants in the community’s periphery. Knowledge is conceived of as identity development and belonging, either as newcomers or oldtimers, in the community. This is challenging to plan for with a diverse and/or large classroom of students and institutional constraints that may not afford it or value such educational goals. An additional challenge is that the teacher needs to make the distinction between whether the students’ mathematical labor is sufficient to support their apprenticeship contra epistemic exclusion, and to be clear about what “doing mathematics” might look like. The SLT teacher will also need to continuously reflect on their own understanding of what it means to “do mathematics,” as such an inference can be rather opaque, and thus the SLT teacher needs to consider the material labor of their students as well: “To compensate for epistemic exclusion, we seek to develop a reliable way to evaluate the effort to understand mathematics” (Baldino & Cabral, 2021, p. 280, emphasis in original). In our words, this effort represents students’ legitimate peripheral participation and desire to become an oldtimer.

The Behaviorist classroom—where the focus of mathematics teaching is on showing students how to reproduce a perfect sequence of steps when solving a mathematical problem, and where the goal is on producing correct answers rather than understanding the meaning behind the mathematical concepts—works well when developing procedural fluency of mathematical concepts and ideas that have low cognitive demand (e.g., skill/drill activities and technology-related tasks designed to improve fluency). However, when addressing mathematical concepts with a high cognitive demand or that require critical thinking, this perspective is not appropriate for mathematics planning and teaching.

In the Cognitive Learning Theory (CLT) classroom, mathematics teachers plan lessons that allow space for learners to develop their own structures and construct their own meanings for mathematics. This requires additional time for mathematics instruction and there is a danger that a lesson can become a set of unrelated activities and lose its focus with respect to the students’ construction of the lesson’s mathematical aim. To avoid this, the CLT teacher plays an active role in aligning lesson plans with hypothetical learning trajectories, addressing individual student’s needs throughout the construction process, and assisting learners in making connections between big mathematical ideas.

In the Social Constructivist (SC) mathematics classroom, teachers plan for mathematics learning where students develop their objective knowledge of mathematics concepts through a collaborative classroom discourse during which their subjective knowledge is examined, dissected, and confirmed by the group. Thus, any knowledge production is jointly owned by the classroom community. A challenge with SC planning is that the mathematics teacher has to be knowledgeable of various mathematical approaches for a given problem, attitudes in the mathematical community, and the processes of developing new mathematical knowledge between people.

In the Structuralist classroom, mathematics teachers plan to use various mathematical models that help students to simplify and reveal abstract mathematical structures. Each model used (e.g., AlgeBlocks, Geostrips) has limitations and therefore cannot be used as the sole source of explanation. The emphasis is on a student discovering underlying structures presented by the teacher instead of exploring and constructing their own mathematical structures (as in CLT). A difficulty with planning in the structuralist classroom is that teachers have to be knowledgeable about various appropriate models for each topic taught, the strengths and limitations of each model, and appropriate supplementary instructional tools and strategies needed for comprehensive understanding of essential mathematics.

In the Problem Solving (PS) classroom, the focus is on multiple strategies for solving a given problem and being able to make connections to other strategies or other problems, rather than the content understanding that results from it. PS has the advantage of engaging students in mathematics making and creating new knowledge through the experience of dealing with unfamiliar situations as opposed to receiving knowledge through direct instruction from a teacher. It differs from radical constructivism in that it does not focus on the concepts that are constructed by students but rather focuses on the analytic schemes, critical thinking processes, and intuitions they develop for solving posed problems. A difficulty in this approach is that it often is misaligned with institutional goals for mathematics teaching—such as standardized testing of content knowledge—so that planning for PS lessons results in planning for student outcomes that are often not represented in curriculum documents.

The Culturally Relevant Pedagogy (CRP) approach can lead to the development of students’ critical consciousness of social structures and inequities, as well as centering mathematics in the cultural practices and realities most familiar to students. This has the potential to reinvigorate students’ cultures with mathematical meaning and—further—to position students’ lived cultural experiences as mathematical experiences. The difficulty with CRP planning and teaching is that the teacher must be an expert not only in the mathematics content taught, but also in the culture/s of their students. Thus, curriculum materials must be tailored to provide mathematical content within the cultural context.

In the Problem- and Project-Based Learning (PBL) classroom, teachers plan mathematical activities within real-world contexts, so the meaning assigned to mathematical knowledge is contextualized in the real-world situations used to teach the mathematical concepts. A PBL lesson typically includes an open-ended problem to which students attempt to develop a solution. Planning for such lessons requires teachers to have comprehensive knowledge about mathematics in real-world situations, as well as the pedagogical knowledge to translate this contextualized mathematics into planned activities and assessment strategies. Another issue with this approach, similarly to CLT, is that students construct their own understanding of mathematical concepts and solutions to problems, without any guarantee that those concepts or solutions will be in complete agreement with lesson objectives, institutional and curriculum documents, or community norms. Thus, planning for a PBL lesson means incorporating additional teacher guidance (to help students in their problem-solving process) into the lesson plan.

As we have shown, each perspective for planning and teaching mathematics has certain benefits and drawbacks, and each is not appropriate for every lesson. Developing teachers’ Type D means developing their ability to operationalize the different perspectives we present in this chapter as well as the ability to differentiate goals for mathematics lessons and identify the most appropriate type of epistemological commitment to support the teaching of different mathematics topics. Furthermore, developing teachers’ Type D means developing self-awareness of one’s a priori epistemological commitments about the teaching and learning of mathematics, and how these commitments may help or detract from planning and teaching a particular mathematics lesson.

6 The Epistemological Perspectives in Different Cultural Contexts

Culture is a foundationally structuring element of human experience and the social link between people. None of the eight epistemological perspectives are immune from this, because it is these perspectives that describe what teachers actually do when planning for and reflecting on their teaching work in the classroom. In the case of SLT, apprenticeship may take very different forms in different cultural settings, such as schooling and as apprenticeship outside of formal schooling. In the case of behaviorism, the paradigm itself is value-laden in a unique way that may socio-politically charge any attempts to stray from it; consider a cultural setting where teachers are seen as the holders of knowledge and wherein students are expected to replicate exactly what the teacher tells them to do rather than discursively engage it. In the case of CLT, there may be cultural and institutional commitments that position CLT as a proposition outside of the role of school. In the case of SC, as with SLT, there may be an issue with implementing an SC agenda where discourse between students and teachers—and between students and each other—is not culturally privileged. In the case of structuralism, manipulatives are expensive, and not even in the wealthiest of Western countries are manipulates available in every classroom of every school. In the case of PS, again, this perspective is value-laden—why solve a single problem multiple ways if the economic situation in the context calls only for one solution? In the case of CRP, cultural context is central. However, consider the situation where a wealthy, White, suburban school is attempting to deploy CRP without any input from minority populations, leading inevitably to perversion of its theoretical principles; critical educators are crucial for CRP’s deployment. And finally, in the case of PBL, like structuralism, classroom materials and resources are required, as well as time and institutional flexibility regarding expectations of student outcomes within prescribed timelines and alignment with state warranties (e.g., government testing). We avow all of these cultural conditions as crucial to the employment of the eight epistemological paradigms in Fig. 1 but the purpose of this chapter was to survey the status of literature and knowledge regarding Type D in the recent Western context. The constraints listed are just some of the myriad constraints under which every teacher works (Ingram & Clay, 2000), and we leave it as an intellectual challenge to the reader to envision what implications these cultural considerations may have when considering Type D.

7 Implications for Lesson Planning

There are three additional implications related to Type D that teachers must consider when planning: the layout of the learning space, instrumentation related to lesson planning, and student assessment. We survey these briefly in this section.

7.1 Layout of the Learning Space

The layout of the room, the way the physical space is prepared, the way the board is organized, and the students’ access to manipulatives and technology are all key aspects of lesson planning. For example, the Instructional Quality Assessment (IQA; Boston & Smith, 2009; Boston & Wilhelm, 2017) lesson observation rubric includes a section that requires a description of the physical classroom layout, as well as a section about the potential of the task. Liljedahl (2020) emphasized the importance of the space/physical layout in creating thinking classrooms, noting that the physical layout of the room must correlate with and support the goals of the lesson. Considering the different perspectives on planning and teaching lessons presented in this chapter, the corresponding layouts that teachers plan for each approach must be coherent with the teacher’s epistemological commitments, the goals of the lesson, and their corresponding intended experiences for students.

7.2 Instrumentation Related to Lesson Planning

There are various instruments for evaluating the quality of lesson plans. These include but are not limited to the Guide to Core Issues in Mathematics Lesson Design (West & Staub, 2003) based on their Framework for Lesson Design and Analysis, the IQA Lesson Plan Rubric (Boston & Smith, 2009; Boston & Wilhelm, 2017), the Lesson Plan Evaluation Rubric (Panasuk et al., 2005), the Observation and Reflection Guide for a Mathematics Lesson (Grant et al., 2009), the Thinking Through a Lesson Protocol (Smith et al., 2008), and the 5E Lesson Plan Format (Goldston et al., 2010) which originated in science education. While these tools have been invaluable over the past two decades, lesson plan evaluation practice is lagging in research because it does not account for various the theoretical perspectives that we have described in this chapter. Indeed, Chizhik and Chizhik (2016) claimed that research on lesson planning is “stuck” in the behaviorist perspective. Furthermore, Medley (1987) argued that in order to conduct quality research, the issues of conceptualization, instrumentation, and design have to be addressed; thus, it is important to advance the design of instrumentation for lesson planning that does not discriminate against any particular theoretical perspective in which it is based. Without quality lesson planning, there cannot be quality instruction in mathematics classrooms.

7.3 Student Assessment

Analyzing student assessment is an integral part of teachers’ reflection on their pre- and post-classroom activities. Research related to student assessment is discussed in depth by Radišić (this volume). The advent of educational technology and online teaching has brought with it changes to student assessment. In virtual and physical mathematics classrooms, teachers use “technology as a servant” to serve as an assessment tool (Gueudet & Pepin, this volume; Geiger, 2005; Goos et al., 2000; Martinovic & Manizade, 2014). These considerations and more are discussed by Gueudet and Pepin (this volume). Due to space limitations, we will not expand on issues related to research on student assessment in this chapter.

8 Conclusion and Future Directions of Research

Teacher preparation and development programs provide “experiences designed to increase mathematics teachers’ range of competencies” (Type J). They have been conceptualized in our adaptation of Medley’s (1987) presage-process-product approach to understanding the inter-relationship of the variables that impact student learning outcomes as intervening between pre-existing mathematics teacher characteristics (Type F), and the competencies, knowledge, and skills (Type E) that teachers bring to the preactive tasks of teaching (Type D). Among Type E variables, there is arguably a dual focus in mathematics teacher education and development programs on teachers’ knowledge and dispositions on the one hand, and on observable classroom competence on the other. This is evident in the oft-lamented gap between theory and practice noted by Dewey (1904) and identified by Korthagen (2017) as the central problem of teacher education and development throughout the twentieth century. According to Charalambous and Delaney (2020), practice is used in the mathematics education literature in at least four different ways: to distinguish between having an idea and enacting it; as something that is repeated with a view to improving performance; to describe the practice of teaching as having taken on the identity of a teacher; and, to describe classroom activities that are done habitually. While not excluding practices that occur in preparation for or following classroom activity, in each case the emphasis is on the teachers’ actions in classrooms with students. That is, efforts to address the theory–practice gap in teacher education and development can been seen as an attempt to link Type E variables (mathematics teacher knowledge, competencies, skills, and beliefs) directly to Type C variables (interactive mathematics teacher activities that occur in the presence of students) with insufficient attention to Type D variables such as planning.

The approach taken in this chapter to the pre- and post-active actions of teaching foregrounds the importance of the teachers’ theoretical perspectives in determining the goals they have for teaching and hence the kinds of activities that they plan to use in their teaching, as well as the ways in which they reflect on and self-assess their teaching. We argue that teachers’ pre-active competencies such as lesson and unit planning—not simply as a technical skill or means of ensuring that novice teachers have “thought through” what they will do in their interactions with students, but as a theoretically driven bridge between teaching knowledge (typically characterized as theory) and practice—has the potential to address the traditionally perceived theory–practice gap. One way in which such an approach might manifest is in taking a step back from lesson planning proformas and the like that specify such things as how to formulate the objectives of a lesson—to first reflect on the over-arching goals of one’s mathematics teaching and its theoretical underpinnings. It should, thereby, be possible to trace a coherent theoretical perspective along the chain from Type E to Type D to Type C variables, influenced and constrained by Type J and Type I variables.

In conclusion, we found that some theoretical perspectives with respect to Type D have been researched well (such as CLT) while others (such as SLT and PBL) have not. With the current impetus of reform in the digital era of mathematics education, we believe these under-researched perspectives warrant further research with respect to Type D to investigate their potential for improving teachers’ practice of lesson planning, assessment, and reflection. Elevating planning from a technical skill to a theoretically informed aspect of mathematics teaching would likely motivate further research on the topic as called for by Kilpatrick et al. (2001) who suggested that more research needs to be done on teacher planning, specifically, “What do teachers read when planning?”, “How do they interpret and use what they read?”, “And how do those uses affect their teaching?” (p. 337). The answers to each of these questions depend upon the theoretical perspective through which the teacher views the goals of their mathematics teaching. Consistent with this, our consideration of examples from the literature of each of the epistemological perspectives we identified in Fig. 1 highlight the scope of and need for mathematics education researchers to be more explicit in relation to the theoretical perspectives that underpin their own thinking and the studies on which they report.