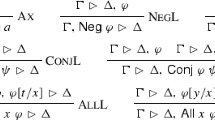A Logical Framework with Higher-Order Rational (Circular) Terms

Abstract

Logical frameworks provide natural and direct ways of specifying and reasoning within deductive systems. The logical framework LF and subsequent developments focus on finitary proof systems, making the formalization of circular proof systems in such logical frameworks a cumbersome and awkward task. To address this issue, we propose $\text {CoLF}$, a conservative extension of LF with higher-order rational terms and mixed inductive and coinductive definitions. In this framework, two terms are equal if they unfold to the same infinite regular Böhm tree. Both term equality and type checking are decidable in $\text {CoLF}$. We illustrate the elegance and expressive power of the framework with several small case studies.

1 Introduction

A logical framework provides a uniform way of formalizing and mechanically checking derivations for a variety of deductive systems common in the definitions of logics and programming languages. In this paper we propose a conservative extension of the logical framework LF [18] to support direct representations of rational (circular) terms and deductions.

The main methodology of a logical framework is to establish a bijective correspondence between derivations of a judgment in the object logic and canonical terms of a type in the framework. In this way, proof checking in the object logic is reduced to type checking in the framework. One notable feature of LF is the use of abstract binding trees, where substitution in the object logic can be encoded as substitution in the framework, leading to elegant encodings. On the other hand, encodings of rational terms, circular derivations, and their equality relations are rather cumbersome. We therefore propose the logical framework $\text {CoLF}$ as a conservative extension of LF in which both circular syntactic objects and derivations in an object logic can be elegantly represented as higher-order rational dependently typed terms. This makes $\text {CoLF}$ a uniform framework for formalizing proof systems on cyclic structures. We prove the decidability of type checking and soundness of equality checking of higher-order rational terms.

While CoLF allows formalization of circular derivations, proofs by coinduction about such circular encodings can only be represented as relations in CoLF, mirroring a similar limitation of LF regarding induction. In future work, we plan to extend CoLF to support checking of meta-theoretic properties of encodings analogous to the way Twelf [27] can check properties of encodings in LF.

The main contributions of this paper are:

• The type theory of a logical framework with higher-order rational terms. The theory allows natural and adequate representations of circular objects and circular derivations (Section 3).

• A decidable trace condition for ensuring the validity of circular terms and derivations arising from mixed inductive and coinductive definitions (Section 3.3).

• A sound and complete algorithm to decide the equality of two higher-order rational terms (Section 3.5).

• A proof of decidability of type-checking in the framework (Section 3.7).

• Case studies of encoding subtyping derivations of recursive types (Section 4).

An extended version of this paper, available at https://arxiv.org/abs/2210.06663, has an appendix that contains additional materials. We have implemented $\text {CoLF}$ in OCaml and the implementation can be accessed at https://www.andrew.cmu.edu/user/zhiboc/colf.html. An additional case study of the meta-encoding the term model of CoLF in CoLF is presented in Appendix J of the extended version.

2 Mixed Inductive and Coinductive Definitions

We motivate our design through simple examples of natural numbers, conatural numbers, and finitely padded streams. The examples serve to illustrate the idea of coinductive interpretations, and they do not involve dependent types or higher-order terms. More complex examples will be introduced later in the case studies (Section 4).

Natural Numbers. The set of natural numbers is inductively generated by zero and successor. In a logical framework such as LF, one would encode natural numbers as the signature consisting of the first three lines in the top left part of Fig. 1.

The type theory ensures that canonical terms of the type ${{\mathtt {{nat}}}}$ are in one-to-one correspondence with the natural numbers. Specifically the infinite stack of successors ${{\mathtt {{succ\, (succ\, (succ\, \dots ))}}}}$ is not a valid term of type ${{\mathtt {{nat}}}}$. Therefore, the circular term w1 is not a valid term.

Conatural Numbers. We may naturally specify that a type admits a coinductive interpretation by introducing a new syntactic kind ${\textsf{cotype}}$. The kind ${\textsf{cotype}}$ behaves just like the kind ${\textsf{type}}$ except that now the terms under ${\textsf{cotype}}$ are allowed to be circular. A slightly adapted signature would encode the set of conatural numbers, shown as the first three lines in the bottom left part of Fig. 1.

Fig. 1.

Signatures and Examples for Section 2

Because ${{\mathtt {{conat}}}}$ is a coinductive type, the canonical forms of type ${{\mathtt {{conat}}}}$ includes ${{\mathtt {{cosucc}}}}^n \, {{\mathtt {{cozero}}}}$ for all n and the infinite stack of ${{\mathtt {{cosucc}}}}$, which is in one to one correspondence with the set of conatural numbers. Specifically, the infinite stack of cosucc, may be represented by the valid circular term w2 as in Fig. 1. The equality of terms in CoLF is the equality of the infinite trees generated by unfolding the terms, which corresponds to a bisimulation between circular terms. For example, an alternative representation of the infinite stack of cosucc is the term w3, and CoLF will treat w2 and w3 as equal terms, as shown by the last three lines in the bottom left part of Fig. 1. The terms w2 and w3 are proved equal by reflexivity. On the other hand, a formulation of conats in LF would involve an explicit constructor, e.g. mu : (conat -> conat) -> conat. The encoding of equality is now complicated and one needs to work with an explicit equality judgment whenever a conat is used. Functions defined by coinduction (e.g., bisimulation in Appendix K of the extended version) need to be encoded as relations in CoLF.

2.1 Finitely Padded Rational Streams

As an example of mixed inductive and coinductive definition, we consider rational streams of natural numbers with finite paddings in between. These streams are special instances of left-fair streams [5]. We define streams coinductively and define paddings inductively, such that there are infinitely many numbers in the stream but only finitely many paddings between numbers, shown in the signature consisting of first five lines in the right column of Fig. 1. For example, the term s1 in Fig. 1 represents a stream of natural number 1’s with two paddings in between. Because padding is a type, the term p2 is not valid, as it is essentially an infinite stack of pad constructors. Definitions in a CoLF signature can refer to each other. Thus, the terms s3 and s4 denote the same padded stream, and the terms p6, p7 and p2 denote the same invalid stream consisting of purely paddings.

Priorities. To ensure the adequacy of representation, types of kind ${\textsf{cotype}}$ admit circular terms while types of kind ${\textsf{type}}$ admit only finitary terms. It is obvious that the circular term w1 is not a valid term of type nat due to the presence of an infinite stack of inductive constructors, and the circular term w2 is a valid term of type conat because it is a stack of coinductive constructors. However, when we have both inductive and coinductive types, it is unclear whether a circular term (e.g. s1) is valid. Historically, priorities are used to resolve this ambiguity [11]. A priority is assigned to each inductive or coinductive type, and constructors inherit priorities from their types. Constructors with the highest priority types are then viewed as primary. In CoLF, priorities are determined by the order of their declarations. Type families declared later have higher priorities than those declared earlier. In this way, the type pstream has higher priority than the type padding. Constructor cocons inherits the priority of pstream, and the term s1 is viewed as an infinite stack of cocons and is thus valid. Similarly, terms s3 and s4 are also valid. If we switch the order of declaration of padding and pstream (thereby switching their priorities), then terms s1, s3, and s4 are no longer valid.

3 The Type Theory

We formulate the type theory of $\text {CoLF}$, a dependent type theory with higher-order rational terms and decidable type checking. The higher-order rational terms correspond to $\bot$-free regular Böhm trees [21] and have decidable equality.

3.1 Higher-Order Rational Terms

When we consider first order terms (terms without $\lambda$-binders), the rational terms are terms with only finitely many distinct subterms, and thus their equality is decidable. We translate this intuition to the higher-order setting. The higher-order rational terms are those with finitely many subterms up to renaming of free and bound variables. We give several examples of rational and non-rational terms using the signatures in Section 2.

• 1. The term w2 in Fig. 1 is a first-order rational term.

• 2. A stream counting up from zero ${{\mathbf {{up}}}}_0 = {\mathsf {{cocons}}}\, {\mathsf {{zero}}}\, ({\mathsf {{next}}}\, ({\mathsf {{cocons}}}\, ({\mathsf {{succ}}}\, {\mathsf {{zero}}})\, ({\mathsf {{next}}}\, (\dots ))))$ is a first-order term that is not rational.

• 3. A stream that repeats its argument ${{\mathbf {{R_2}}}} = \lambda x.\, {\mathsf {{cocons}}}\, x\, ({\mathsf {{next}}}\, ({{\mathbf {{R_2}}}}\, x))$ is a higher-order rational term.

• 4. A stream that counts up from a given number ${{\mathbf {{up}}}} = \lambda x.\, {\mathsf {{cocons}}}\, x\, ({\mathsf {{next}}}\, ({{\mathbf {{up}}}}\, ({\mathsf {{succ}}}\, x)))$ is not a rational higher-order term.

In the definitions above, bolded symbols on the left of the equality signs are called recursion constants. It is crucial that in higher-order rational terms, all arguments to recursion constants are bound variables and not other kinds of terms. We call this restriction the prepattern restriction as it is similar to Miller’s pattern restriction [24] except that we allow repetition of arguments. The prepattern restriction marks the key difference between the higher-order rational term ${{\mathbf {{R_2}}}}$ and the infinitary term ${{\mathbf {{up}}}}$. The term ${{\mathbf {{up}}}}$ is not rational because the argument to ${{\mathbf {{up}}}}$ is ${\mathsf {{succ}}}\, x$, which is not a bound variable.

3.2 Syntax

We build subsequent developments on canonical LF [19], a formulation of the LF type theory where terms are always in their canonical form. Canonical forms do not contain $\beta$-redexes and are fully $\eta$-expanded with respect to their typing, supporting bijective correspondences between object logic derivations and the terms of the framework. One drawback of this presentation is that canonical terms are not closed under syntactic substitutions, and the technique of hereditary substitution addresses this problem [29].

The syntax of the theory follows the grammar shown in Fig. 2. We use the standard notion of spines. For example, a term $x\, M_1\, M_2\, M_3$ will be written as $x \cdot (M_1; M_2; M_3)$ where x is the head and $M_1; M_2; M_3$ is the spine. To express rational terms, we add recursive definitions of the form $r : A = M$ to the signature, where M must be contractive (judgment M ${\textsf{contra}}$) in that the head of M must be a constant or a variable. Recursive definitions look like notational definitions [26], but their semantics are very different. Recursive definitions are interpreted recursively in that the definition M may mention the recursion constant r, and other recursion constants including those defined later in the signature, while notational definitions in LF [26] cannot be recursive. Recursion constants are treated specially as a syntactic entity that is different from variables or constructors (nonrecursive constants). To ensure the conservativity over LF, we further require all definitions in $\varSigma$ to be linearly ordered. That is, only in the body of a recursive definition can we “forward reference”, and we can only forward reference other recursion constants. All other declarations must strictly refer to names that have been defined previously. We write $\lambda \overline{x}$ and $\overline{M}$ to mean a sequence of $\lambda$-abstractions and a sequence of terms respectively. We write x, y, z for variables, c, d for term constants (also called constructors), a for type family constants, and $r, r', r''$ for recursion constants.

To enforce the prepattern restriction, we use a technical device called prepattern $\varPi$-abstractions, and associated notion of prepattern variables and prepattern spines. Prepattern $\varPi$-abstractions are written as $\varPi x \mathrel {\hat{:}}A_2.\, A_1$, and x will be a prepattern variable (written $x\mathrel {\hat{:}}A_2$) in $A_1$. Moreover, in $A_1$, if y is a variable of a prepattern type $\varPi w \mathrel {\hat{:}}A_2. B$, then the prepattern application of y to x will be realized as the head y followed by a prepattern spine ([x]), written $y\cdot ([x])$. The semantics is that prepattern variables may only be substituted by other prepattern variables, while ordinary variables can be substituted by arbitrary terms (which include other prepattern variables). In a well-typed signature, if $r : A = M$ is a recursion declaration, then A consists of purely prepattern $\varPi$-abstractions (judgment $A {\textsf{prepat}}$) and for all $r \cdot S$ in the signature, S consists of purely prepattern applications and is thus called a prepattern spine (judgment $S {\textsf{prepat}}$). The prepattern variables are similar to those introduced by the $\nabla$-operator [25], which models the concept of fresh names, but here in a dependently typed setting, types may depend on prepattern variables.

Fig. 2.

The Syntax for $\text {CoLF}$

In an actual implementation, the usages of prepattern types may impose additional burdens on the programmer. As a remedy, the implementation could infer which variables are prepattern variables based on whether they appear as arguments to recursion constants and propagate such information.

3.3 Trace Condition

In a signature $\varSigma$, we say that a type A is inductive if $A = \varPi x_1\dots \varPi x_n:A_n. a\cdot S$ and $a : \varPi y_1 \dots \varPi y_m : B_m.\, {\textsf{type}}$, and a type A coinductive if $A = \varPi x_1\dots \varPi x_n:A_n. a\cdot S$ and $a : \varPi y_1 \dots \varPi y_m : B_m.\, {\textsf{cotype}}$. A constructor c is inductive if $c : A \in \varSigma$ and A is inductive, and c is coinductive if $c : A \in \varSigma$ and A is coinductive.

The validity of the terms is enforced through a trace condition [8, 17] on cycles. A trace is a sequence of constructor constants or variables, where each constructor or variable is a child of the previous one. A trace from a recursion constant r to itself is a sequence starting with the head of the definition of r and ending with the parent of an occurrence of r. In Fig. 1, a trace from p2 to itself is $[{{\mathtt {{pad}}}}]$, and a trace from s1 to itself is $[{{\mathtt {{cocons}}}}, {{\mathtt {{pad}}}}, {{\mathtt {{pad}}}}, {{\mathtt {{next}}}}]$. Traces cross into definitions of recursion constants. Thus, a trace from p6 to itself is $[{{\mathtt {{pad}}}}, {{\mathtt {{pad}}}}]$, which is also a trace from p7 to itself. A trace from s4 to itself is $[{{\mathtt {{cocons}}}}, {{\mathtt {{next}}}}]$, and a trace from p5 to itself is $[{{\mathtt {{next}}}}, {{\mathtt {{cocons}}}}]$. If $r = \lambda x. f\, (r\, x)\, (g\, (r\, x))$ (more precisely $r = \lambda x.\, f\cdot (r\cdot ([x]); g\cdot (r \cdot ([x])))$), then there are two traces from r to itself, i.e., [f] and [f, g].

A higher-order rational term M is trace-valid if for all recursion constants r in M, each trace from r to itself contains a coinductive constructor, and that coinductive constructor has the highest priority among all constructors on that trace. To ensure trace validity, it is sufficient to check in a recursive definition, all occurrences of recursion constants are guarded by some coinductive constructor of the highest priority. The guardedness condition (judgment $\vdash _\varSigma r \rtimes {}M$) means that occurrences of r in M are guarded by some coinductive constructor of the highest priority, and the condition is decidable. In a well-typed signature $\varSigma$, if $r : A= M \in \varSigma$, then $\vdash _\varSigma r\rtimes {}M$. A detailed algorithm for checking trace-validity is presented in Appendix B.2 of the extended version. The reader may check guardedness for all valid terms in Fig. 1.

3.4 Hereditary Substitution

Hereditary substitution [19, 29] provides a method of substituting one canonical term into another and still get a canonical term as the output by performing type-based normalization. This technique simplifies the definition of the term equality in the original LF [18, 20] by separating the term equality and normalization from type checking. We extend the definition of hereditary substitution to account for recursion constants. Hereditary substitution is a partial operation on terms. When input term is not well-typed or prepattern restriction is not respected, the output may be undefined.

Hereditary substitution takes as an extra argument the simple type of the term being substituted by. The simple type $\tau$ is inductively generated by the following grammar.

$$\begin{aligned} \tau :\,\!:= * \mid \tau _1 \rightarrow \tau _2 \end{aligned}$$

We write ${{A}^o}$ for the simple type that results from erasing dependencies in A. We write $[N/x]^\tau M$ for hereditarily substituting N for free ordinary variable x in M. The definition proceeds by induction on $\tau$ and the structure of M. For prepattern variables, since they may only stand for other prepattern variables, we use a notion of renaming substitution. The renaming substitution $\llbracket {y/x} \rrbracket$ $M$ renames a prepattern variable or an ordinary variable x to prepattern variable y in M. Both substitutions naturally extend to other syntactic kinds. Hereditary substitution relies on renaming substitution when reducing prepattern applications. Because of the prepattern restriction, recursion constants are only applied to prepattern variables in a well-formed signature, and we never substitute into a recursive definition. Let $\sigma$ be a simultaneous renaming substitution, a notion generalized from renaming substitutions, we write $\llbracket {\sigma } \rrbracket$ $M$ for carrying out substitution $\sigma$ on M.

The definition for hereditary substitution is shown in Fig. 3. Appendix A of the extended version contains other straightforward cases of the definition. We note that prepattern $\varPi$-types erase to a base type $*$ because we may only apply terms of prepattern $\varPi$-types to prepattern variables, and thus the structure of the argument term does not matter.

Fig. 3.

Hereditary Substitutions

3.5 Term Equality

The equality checking of circular terms is carried out by iteratively unfolding recursive definitions [1, 6, 14, 23]. The algorithm here is a slight adaptation of the equality algorithm for regular Böhm trees by Huet [21], tailored to the specific case of $\text {CoLF}$’s canonical term syntax. We emphasize that the equality algorithm can treat terms that are not trace-valid or well-typed, and is thus decoupled from validity checking and type checking. The algorithm itself checks for the prepattern restriction on recursion constants and contractiveness condition on recursive definitions. These checks are essential to ensure termination in the presence of forward referencing inside recursive definitions.

We define the judgment $\varDelta ; \varTheta \vdash _\varSigma M = M'$ to mean M and $M'$, with free variables from $\varTheta$, are equal under the assumptions $\varDelta$, with consideration of recursive definitions in $\varSigma$. The variable list $\varTheta$ is similar to $\varGamma$ except it doesn’t have the types for the variables. It is merely a list of pairwise distinct variables. Similarly, we define the judgment $\varDelta ; \varTheta \vdash _\varSigma S = S'$ to mean spines S and $S'$ are element-wise equal. Equalities in $\varDelta$ will be of the form $({\varTheta }\vdash {M}={M'})$ where $\varTheta$ holds free variables of M and $M'$. We write $\varTheta \vdash M$ to mean that $FV(M) \subseteq \varTheta$. We define simultaneous variable renaming, that $\sigma$ is a variable renaming from $\varTheta '$ to $\varTheta$, written $\varTheta \vdash \sigma : \varTheta '$ to mean that if $\varTheta ' \vdash M$, then $\varTheta \vdash \llbracket {\sigma } \rrbracket {M}$. For instance, if we have $x \vdash \llbracket {x/y, x/z} \rrbracket : y, z$ and $y, z \vdash y \cdot [{z}]$, then $x \vdash \llbracket {x/y, x/z} \rrbracket (y \cdot [{z}])$, i.e., $x \vdash x \cdot [{x}]$. The rules for the judgments are presented in Fig. 4. Recall that M is contractive ($M\,{\textsf{contra}}$) if the head of M is not a recursion constant.

An Example. Assume the signature in Section 2.1, and consider a stream generator that repeats its arguments. The stream may be represented by terms r1 and r2 below. Note that in the concrete syntax, square brackets represent $\lambda$-abstractions.

Because r1 is a recursion constant, its type is a prepattern-$\varPi$ type, and this restriction is respected in the body as x is a prepattern variable.

Fig. 4.

Equality Checking

We want to show that r1 and r2 are equal in the framework. Let $\varSigma$ be the signature of Section 2.1 plus the definitions for r1 and r2. We illustrate the process of checking that $;\vdash _{\varSigma } \lambda x.\, {{\mathtt {{r1}}}} \cdot ([{x}]) = \lambda x.\, {{\mathtt {{r2}}}} \cdot ([{x}])$ as a search procedure for a derivation of this judgment, where initially both $\varDelta$ and $\varTheta$ are empty.

Immediately after rule (6) we encounter $; x \vdash _{\varSigma } {{\mathtt {{r1}}}} \cdot ([{x}]) = {{\mathtt {{r2}}}}\cdot ( [{x}])$, we memoize this equality by storing ${({x}\vdash {{{\mathtt {{r1}}}} \cdot ([{x}])}={{{\mathtt {{r2}}}}\cdot ( [{x}])})}$ in $\varDelta$ as in rule (2), and unfold the left-hand side. Then we proceed with the judgment.

$$ {({x}\vdash {{{\mathtt {{r1}}}} \cdot ([{x}])}={{{\mathtt {{r2}}}}\cdot ( [{x}])})} ; x \vdash _\varSigma {{\mathtt {{cocons}}}} \cdot (x; {{\mathtt {{next}}}} \cdot ({{\mathtt {{r1}}}} \cdot ( [{x}]))) = {{\mathtt {{r2}}}} \cdot ([{x}]) $$

We then use rule (3) to unfold the right-hand side and store then current equation in the context. Then after several structural rules, we have

$$\begin{aligned} {({x}\vdash {{{\mathtt {{r1}}}} \cdot ([{x}])}={{{\mathtt {{r2}}}}\cdot ( [{x}])})}, \dots ; x \vdash _\varSigma {{\mathtt {{r1}}}} \cdot ( [{x}]) = {{\mathtt {{cocons}}}}\cdot (x; {{\mathtt {{next}}}}\cdot ({{\mathtt {{r2}}}} \cdot ([{x}]))) \end{aligned}$$

At this point, rule (2) applies. We add the current equation to the context and unfold the left recursive definition. Then after several structural rules, we encounter the following judgment.

$$ {({x}\vdash {{{\mathtt {{r1}}}} \cdot ([{x}])}={{{\mathtt {{r2}}}}\cdot ( [{x}])})} , \dots ; x \vdash _\varSigma {{\mathtt {{r1}}}} \cdot ( [{x}]) = {{\mathtt {{r2}}}} \cdot ([{x}])$$

Now we can close the derivation with rule (1) using identity substitution.

Decidability. Huet [21] has proved the termination, soundness, and completeness in the case of untyped regular Böhm trees. Our proof shares the essential idea with their proof. The termination relies on the fact that terms only admit finitely many subterms modulo renaming of both free and bound variables, and only subterms will appear in $\varDelta$. The soundness and completeness are proved with respect to the infinite Böhm tree [4] generated by unfolding the terms indefinitely, which again corresponds to a bisimulation between terms.

Theorem 1 (Decidability of Term Equality)

It is decidable whether $\varDelta ; \varTheta \vdash _\varSigma M = M'$ for any rational term M and $M'$.

Proof

We first show that there is a limit on the number of equations in $\varDelta$. Then the termination follows the lexicographic order of the assumption capacity (difference between current number of assumptions in $\varDelta$ and the maximum), and the structure of the terms under comparison. It is obvious that rules (4)(5)(6) decompose the structure of the terms and rules (2)(3) reduce assumption capacity. It remains to show that the size of $\varDelta$ has a limit.

The prepattern conditions on rules (2)(3) ensure that the expansion of recursive definitions will only involve renaming substitutions, and thus the resulting term will be an $\alpha$-renaming of the underlying definition. No structurally new terms will be produced as a result of renaming substitution in rules (2)(3). We construct a finite set of all possible terms that could be added to the context. Each term is of finite depth and breadth limited by the existing constructs in the signature, and consists of finitely many constants, variables, and recursion constants. The constants and recursion constants are limited to those already presented in the signature. Although there are infinitely many variables, there are finitely many terms of bounded depth and width that are distinct modulo renaming of both bound and free variables. Thus, the set of terms that can appear as an element of $\varDelta$ is finite, modulo renaming of free variables. The estimate of a rough upper bound can be found in Appendix D of the extended version.

We specify the infinite unfolding by specifying its unfolding to a Böhm tree of depth k, which is a finite approximation to the infinite Böhm tree, for each $k \in \mathbb {N}$. Then the infinite Böhm tree is limit of all its finite approximations. We use the judgment $\exp _{({k})}(M)=_{({k})}M'$ to denote the expansion of a higher-order rational term M to a Böhm tree $M'$ of depth k, and use the judgment $\exp (N) = N'$ to express that the higher-order rational term M expands to infinite Böhm tree $N'$. We also enrich the syntax of Böhm trees with prepattern variables. The full set of expansion rules can be found in Appendix E of the extended version. All cases are structural except for the following case when we expand a recursion constant, where we look up the definition of the recursion constant and plug in the arguments.

$$ \exp _{({k+1})}( r \cdot S) = _{({k+1})} \exp _{({k+1})}(S \rhd ^{A^o} M) \text { if }r : A = M \in \varSigma \text { and }S \ {\textsf{prepat}}$$

Lemma 1 (Expansion Commutes with Hereditary Substitution)

For all k, $\tau$, M and N, $\exp _{({k})}([N/x]^\tau M) =_{({k})} [\exp _{({k})}(N)/x]^\tau (\exp _{({k})} (M))$ if defined.

Proof

Directly by lexicographic induction on k and the structure of M.

Theorem 2 (Soundness of Term Equality)

If $\cdot ; \varTheta \vdash M = M'$, then $\exp _{({k})}(M) =_{({k})} \exp _{({k})}(M')$ for all k.

Proof

By lexicographic induction on the depth k and the derivation $\varDelta ; \varTheta \vdash M = M'$. The case for the rule (1) is immediate by applying renaming substitutions at the closure rule. The cases for rules (2)(3) follow from the commutation lemma. The cases for rules (4)(5)(6) follow from the definition of $\exp$.

Theorem 3 (Completeness of Term Equality)

For rational terms M and $M'$, with free variables from $\varTheta$, if $\exp (M) = \exp (M')$, then $\cdot ; \varTheta \vdash M = M'$.

Proof

The equality algorithm is syntax-directed. We construct the derivation of $\cdot ; \varTheta \vdash M = M'$ by syntax-directed proof search following the structure of M. Every trace of $\exp (M)$ and $\exp (M')$ corresponds to a trace in the derivation of $\cdot ; \varTheta \vdash M = M'$. If $\exp (M) = \exp (M')$, then two terms are equal on every trace, and there will be exactly one rule that applies at every point in the construction of the equality derivation. Termination is assured by Theorem 1.

3.6 Type Checking Rules

For type checking, we define the judgments in Fig. 5 by simultaneous induction. Because recursion constants may be forward referenced, we need to have access to later declarations that have not been checked during the checking of earlier declarations. In order to ensure the otherwise linear order of the declarations, the type checking judgments are parametrized by a pair of signatures ${\varXi ; \varSigma }$, where $\varXi$ is the local signature that contains type-checked declarations before the current declaration and $\varSigma$ is the global signature that contains full signatures, including declarations that have not been checked. In particular, recursion constants available for forward-referencing will be in $\varSigma$ but not $\varXi$. The type equality judgments $\varGamma \vdash _\varSigma A_1 = A_2$, $\varGamma \vdash _\varSigma P_1 = P_2$ only need to read recursive definitions from the global signature, and do not need to access the local signature.

Fig. 5.

Type Checking Judgments

A selection of type checking rules that are essential are presented in Fig. 6. The rest of the rules can be found in Appendix F of the extended version. To ensure the correct type checking order, i.e., the body of a recursive definition is checked after the types of all recursion constants within are checked, we defer checking the body of all recursive definitions to the end. This approach is viable because the term equality algorithm soundly terminates even when the recursive definition is not well-typed. For instance, if the signature $\varSigma = c_1 : A_1, c_2 : A_2, r_1 : A_3 = M_1, c_3 : A_4, r_2 : A_5 = M_2$, then the order of checking is $A_1, A_2, A_3, A_4, A_5, M_1, M_2$. This order is expressed in the type checking rules by an annotation on specific premise of the rules. The annotation $[{ \vdash _{{\varXi ; \varSigma }} M \Leftarrow A }]^{{\mathsf {{1:deferred}}}}$ means that this judgment is to be checked after all the typing judgments have been checked. That is, when we check this premise, we have checked that $\vdash _\varSigma \varSigma \mathrel {{\textsf{sig}}}$. Because of the deferred checking of recursive definitions, the judgment $\vdash _\varSigma \varXi \mathrel {{\textsf{sig}}}$ does not require the body of recursion declarations in $\varXi$ to be well-typed. However, the categorical judgment $\varSigma \mathrel {{\textsf{sig}}}$ requires the body of every recursion declaration to be well-typed.

To enforce the restriction that forward references only happen in a recursive definition, the annotation $[\text {or }r : A = M \in \varSigma ] ^ {{\mathsf {{2:definitions}}}}$ means that forward reference only occurs during the checking of recursive definitions (which are deferred) and nowhere else.

Fig. 6.

Type Checking Rules (Condensed Selection)

3.7 Metatheorems

We state some properties about hereditary substitution and type checking.

Theorem 4 (Hereditary Substitution Respects Typing)

Given a checked signature $\varSigma$ where $\varSigma \mathrel {{\textsf{sig}}}$, if $\varGamma \vdash _{\varXi ; \varSigma }N \Leftarrow A$ and $\varGamma , x : A, \varGamma ' \vdash M \Leftarrow B$, then $\varGamma , [N/x]^{{A}^o}\varGamma '\vdash _{\varXi ; \varSigma }[N/x]^{A^o} M \Leftarrow [N/x]^{A^o}B$.

Proof

By induction on the second derivation, with similar theorems for other judgment forms. This proof is similar to those in [19, 29]. Because of the prepattern restriction, hereditary substitutions do not occur inside recursive definitions and is thus similar to hereditary substitutions in LF.

Theorem 5 (Decidability of Type Checking)

All typing judgments are algorithmically decidable.

Proof

The type checking judgment is syntax directed. Hereditary substitutions are defined by induction on the erased simple types and always terminate. Equality of types ultimately reduces to equality of terms, and we have proved its termination in Section 3.5.

4 Encoding Subtyping Systems for Recursive Types

In the presentation of case studies, we use the concrete syntax of our implementation, following Twelf [27]. The prepattern annotations are omitted. The full convention can be found in Appendix G of the extended version. Representations of circular derivations involve dependent usages of ${\textsf{cotype}}$’s.

4.1 Encoding a Classical Subtyping System

We present a mixed inductive and coinductive definition of subtyping using Danielsson and Altenkirch’s [14] subtyping system. The systems concern the subtyping of types given by the following grammar.

(1)

The subtyping judgment is defined by five axioms and two rules, The axioms are

• 1. $\bot \le \tau$ (${\mathsf {{bot}}}$)

• 2. $\tau \le \top$(${\mathsf {{top}}}$)

• 3. $\mu X.\tau _1\rightarrow \tau _2 \le [\mu X.\tau _1 \rightarrow \tau _2/X](\tau _1\rightarrow \tau _2)$ (${\mathsf {{unfold}}}$)

• 4. $[\mu X.\tau _1\rightarrow \tau _2/X](\tau _1\rightarrow \tau _2) \le \mu X.\tau _1\rightarrow \tau _2$ (${\mathsf {{fold}}}$)

• 5. $\tau \le \tau$ (${\mathsf {{refl}}}$)

And the rules are shown below, where ${\mathsf {{arr}}}$ is coinductive and is written using a double horizontal line, and ${\mathsf {{trans}}}$ is inductive. The validity condition of mixed induction and coinduction entails that a derivation consisting purely of ${\mathsf {{trans}}}$ rules is not valid.

Danielsson and Altenkirch defined the rules using Agda’s mixed inductive and coinductive datatype (shown in Appendix H of the extended version) and the encoding in $\text {CoLF}$ is shown in Fig. 7. The curly brackets indicate explicit $\varPi$-abstractions and the free capitalized variables are implicit $\varPi$-abstracted. We note that the mixed inductive and coinductive nature of the subtyping rules reflected in $\text {CoLF}$ as two predicates, the inductive subtp and the coinductive subtpinf, and the latter has a higher priority. Clauses defining one predicate refer to the other predicate as a premise, e.g. subtp/arr and inf/arr. Let $\ulcorner {-}\urcorner$ denote the encoding relation, and we have .

Fig. 7.

An Encoding of Subtyping in $\text {CoLF}$

Theorem 6 (Adequacy of Encoding)

• 1. There is a compositional bijection between recursive types and valid canonical terms of type tp

• 2. For types $\sigma$ and $\tau$, there is a compositional bijection between valid cyclic subtyping derivations of $\sigma \le \tau$, and valid canonical terms of type subtp $\ulcorner {\sigma }\urcorner \, \ulcorner {\tau }\urcorner$.

Proof

• 1. Directly by induction on the structure of recursive types in the forward direction, and by induction on the structure of the typing derivation in the reverse direction.

• 2. By induction on the syntax of the circular derivations in the forward direction, and by induction on the syntax of the higher-order rational terms in the reverse direction. Note that cycles in the circular derivations correspond directly to occurrences of recursion constants. The validity condition of mixed induction and coinduction coincides with CoLF validity.

We give an example of the subtyping derivation of . Let and .

Here is the encoding in $\text {CoLF}$:

We note that the circular definition is valid by the presence of the constructor inf/arr along the trace from s_sub_t to itself. The presence of the coinductive ${\mathsf {{arr}}}$ rule is the validity condition of mixed inductive and coinductive definitions.

There are two key differences between a $\text {CoLF}$ encoding and an Agda encoding. First, in Agda one needs to use explicit names for $\mu$-bound variables or de Bruijn indices, while in CoLF one uses abstract binding trees. Second, Agda does not have built-in coinductive equality but CoLF has built-in equality. In Agda, the one step of unfolding s_sub_t is not equal to s_sub_t, but in $\text {CoLF}$, they are equal.

4.2 Encoding a Polarized Circular Subtyping System for Equirecursive Types

We present an encoding of a variant Lakhani et al.’s polarized subtyping system [22] into $\text {CoLF}$. The system is circular. Due to space constraints, we only present the encoding for the positive types fragment and their emptiness derivations. This is an important part in the subtyping system because an empty type is a subtype of any other type. The full encoding of the polarized subtyping system can be found in Appendix I of the extended version.

Encoding of Positive Equirecursive Types. The equirecursive nature is captured by a signature $\varSigma$ providing recursive definitions for type names $t^+$.

$$\begin{aligned} \begin{aligned}&\tau ^+, \sigma ^+ :\,\!:= t_1^+ \otimes t_2^+ \mid \textbf{1} \mid t_1^+ \oplus t_2^+ \mid \textbf{0} \\&\varSigma :\,\!:= \cdot \mid \varSigma , t^+ = \tau ^+ \\ \end{aligned} \end{aligned}$$

Equirecursive types are directly encoded as recursion constants in the system, and the framework automatically provides equirecursive type equality checking. Because equirecursive types are circular, positive types are encoded as ${\textsf{cotype}}$.

Theorem 7 (Adequacy of Type Encoding)

There is a bijection between circular types defined in an object signature for the positive types fragment and canonical forms of the postp in $\text {CoLF}$.

Proof

By induction on the syntax in both directions.

Encoding of the Emptiness Judgment. The emptiness judgment $t {\mathsf {{empty}}}$ is defined by the following rules. We stress that these rules are to be interpreted coinductively.

In $\text {CoLF}$, the rules are encoded as follows. The coinductive nature is reflected by the typing of empty : postp -> cotype, which postulates that the predicate empty is to be interpreted coinductively.

Theorem 8 (Adequacy of Encoding)

There is a bijection between the circular derivations of $t {\mathsf {{empty}}}$ and the canonical forms of the type $\mathtt {empty\,\ulcorner {t}\urcorner }$.

Proof

By induction on the syntax of the circular derivation in both directions.

As an example, we may show that the type t, where $t = \textbf{1} \otimes t$, is empty by the following circular derivation.

This derivation can be encoded as follows.

The reader is advised to take a look at Appendix I.3 of the extended version for two simple yet elegant examples of subtyping derivations.

5 Related Work

Cyclic $\lambda$-Calculus and Circular Terms. Ariola and Blom [2], and Ariola and Klop [3] studied the confluence property of reduction of cyclic $\lambda$-calculus. Their calculus differs from CoLF in several aspects. Their calculus is designed to capture reasoning principles of recursive functions and thus has a general recursive let structure that can be attached to terms at any levels. Terms are equated up to infinite Lévy-Longo trees (with decidable equality), but equality as Böhm trees is not decidable. CoLF is designed for circular terms and circular derivations, and all recursive definitions occur at the top level. Terms are equated up to infinite Böhm trees and the equality is decidable. Our equality algorithm is adapted from Huet’algorithm for the regular Böhm trees [21]. Equality on first-order terms has been studied both in its own respect [16] and in the context of subtyping for recursive types [1, 6, 14, 23]. Our algorithm when applied to first-order terms is “the same”. Courcelle [13] and Djelloul et al. [15] have studied the properties of first-order circular terms. Simon [28] designed a coinductive logic programming language based on the first-order circular terms. Contrary to $\text {CoLF}$, there are no mutual dependencies between inductive and coinductive predicates in Simon’s language.

Logical Frameworks. Harper et al. [18] designed the logical framework LF, which this work extends upon. Pfenning et al. later adds notational definitions [26]. The method of hereditary substitution was developed as part of the research on linear and concurrent logical frameworks [9, 10, 29]. Harper and Licata demonstrated the method in formalizing the metatheory of simply typed $\lambda$-calculus [19]. In his master’s thesis, Chen has investigated a mixed inductive and coinductive logical framework with an infinite stack of priorities but only in the context of a first-order type theory [12].

Mixed Induction and Coinduction and Circular Proof Systems. The equality and subtyping systems of recursive types [1, 6, 14, 22, 23] have traditionally recognized coinduction and more recently mixed induction and coinduction as an underlying framework. Fortier and Santocanale [17] devised a circular proof system for propositional linear sequent calculus with mixed inductive and coinductive predicates. This system together with Charatonik et al.’s Horn $\mu$-calculus [11] motivated the validity condition of CoLF. Brotherston and Simpson devised an infinitary and a circular proof system as methods of carrying out induction [7, 8]. Due to the complexity of their validity condition, the encoding of Brotherston and Simpson’s system in full generality and Fortier and Santocanale’s system is currently not immediate and is considered in ongoing work.

6 Conclusion

We have presented the type theory of a novel logical framework with higher-order rational terms, that admit coinductive and mixed inductive and coinductive interpretations. We have proposed the prepattern variables and prepattern $\varPi$-types to give a type-theoretic formulation of regular Böhm trees. Circular objects and derivations are represented as higher-order rational terms, as demonstrated in the case study of the subtyping deductive systems for recursive types.

We once again highlight the methodology of logical frameworks and what $\text {CoLF}$ accomplishes. Logical frameworks internalize equalities that are present in the term model for an object logic. LF [18] internalizes $\alpha \beta \eta$-equivalence of the dependently typed $\lambda$-calculus. Within LF, one is not able to write a specification that distinguishes two terms that are $\alpha$ or $\beta$-equivalent, because those two corresponding derivations are identical in the object logic. Similarly, the concurrent logical framework CLF [29] internalizes equalities of concurrent processes that only differ in the order of independent events. The logical framework $\text {CoLF}$ internalizes the equality of circular derivations. Using $\text {CoLF}$, one cannot write a specification that distinguishes between two different finitary representations of the same circular proof. It is this property that makes $\text {CoLF}$ a more suitable framework for encoding circular derivations than existing finitary frameworks.