Compositional Learning for Interleaving Parallel Automata

Abstract

Active automata learning has been a successful technique to learn the behaviour of state-based systems by interacting with them through queries. In this paper, we develop a compositional algorithm for active automata learning in which systems comprising interleaving parallel components are learned compositionally. Our algorithm automatically learns the structure of systems while learning the behaviour of the components. We prove that our approach is sound and that it learns a maximal set of interleaving parallel components. We empirically evaluate the effectiveness of our approach and show that our approach requires significantly fewer numbers of input symbols and resets while learning systems. Our empirical evaluation is based on a large number of subject systems obtained from a case study in the automotive domain.

1 Introduction

Active automata learning has been successfully used to learn models of complex industrial systems such as communication- and security protocols [11], biometric passports [2], smart cards [1], large-scale printing machines [33], and lithography machines for integrated circuits [15, 32]; we refer to the recent survey by Howar and Steffen on the practical applications of active automata learning [16]. Throughout these applications of automata learning, scalability issues have been pointed out [15, 32]. It has also been suggested that compositional learning, i.e., learning a system through learning its components, is a promising approach to tame the complexity of learning [10, 12].

Some early attempts have been recently made in learning structured models of systems [10, 27] (we refer to the Related Work for an in-depth analysis). For example, the approach proposed by al-Duhaiby and Groote [10] decomposes the learning process into learning its parallel components; however, it relies on a deep knowledge of the system under learning, and the intricate interaction of the various actions being learned. In this paper, we propose an approach based on Dana Angluin’s celebrated L$^*$ algorithm [6], to learn the components of a system featuring an interleaving parallel composition. Our approach, called CL$^*$, does not assume any pre-knowledge of the structure and the alphabet of these components; instead, we learn this information automatically and on-the-fly, while providing a rigorous guarantee of the learned information. This is particularly relevant in the context of legacy and black-box systems where architectural discovery is challenging [8, 22].

Fig. 1.

(a) Initial system with two concurrent FSMs (b) Partition the input alphabet to 4 elements and learn each component individually (c) Use the counter-example ab to merge two components

The gist of our approach is to learn the System Under Learning (SUL) in separate components with disjoint alphabets. We start with a partition comprising only singleton sets. The interleaving parallel composition of the components gives us the total behavior of the system. We pass the result to the teacher, and by exploiting the counter-examples returned, we iteratively merge the alphabet of the individual components.

Example.  Figure 1(a) shows an example of two parallel Finite State Machines (FSMs) over the input alphabet $\{a,b,c,d\}$ and output alphabet $\{0,1\}$. We start by partitioning the alphabet into disjoint singleton sets of elements. The parallel composition of the 4 learned FSMs of Figure 1(b) does not comply with the original system, and the teacher may return the counter-example ab. The string ab generates the output sequence 10 in (a) but the output sequence in (b) is 11. The counter-example suggests to merge the sets $\{a\}$ and $\{b\}$ and restart the learning process which leads to the FSMs in Figure 1(c). One further merging step results in learning the original system. We provide a theoretical proof of correctness of this compositional construction, meaning that it is guaranteed to construct a correct system.

To study the effectiveness of our approach in practice, we designed an empirical experiment to investigate the following two research questions:

• RQ1 Does CL$^*$ require fewer resets, compared to L$^*$?

• RQ2 Does CL$^*$ require fewer input symbols, compared to L$^*$?

Our research questions are motivated by the following facts: 1) Resets are a major contributing factor in learning practical systems as they are immensely time- and resource consuming [31]. Hence, reducing the number of resets can have a significant impact in the learning process. 2) The total number of symbols used in interacting with the system under learning provides us with a total measure of cost for the learning process and hence, reducing the total cost is a fair indicator of improved efficiency [9, 36].

To answer these questions, we use a benchmark based an industrial automotive system. We design a number of experiments on learning various combinations of components in this system, gather empirical data, and analyse them through statistical hypothesis testing. Our results indicate that our compositional approach significantly improves the efficiency of learning compared to the monolithic L$^*$ learning algorithm. The implementation of the algorithm, experiments, and their results can be found on-line in our lab package [23] (https://github.com/faezeh-lbf/CL-Star).

The remainder of this paper is organised as follows. In Section 2, we review the related work and position our research with respect to the state of the art. In Section 3, we present the preliminary definitions that are used throughout the rest of the paper. In Section 4, we present our algorithm and its proof of correctness and termination. We evaluate our algorithm on a benchmark from the automotive domain in Section 5. We conclude the paper and present the directions of our ongoing and future research in Section 6.

2 Related Work

Active automata learning is a technique used to find the underlying model of a black box system by posing queries and building a hypothesis in an iterative manner. There is substantial early work in this domain, e.g., under the name system identification or grammar inference; we refer to the accessible introduction by Vaandrager [36] for more information. A seminal work in this domain is the L$^*$ algorithm by Dana Angluin [6], which comes with theoretical complexity bounds for the learning process using a representation called the “Minimally Adequate Teacher” (MAT).

MAT hypothesises a teacher that is capable of responding to membership queries (MQs) and equivalence queries (EQs); the former checks the outcome of a sequence of inputs (e.g., with their respective outputs, or with their membership in the language of the automaton) and the latter checks whether a hypothesised automaton is equivalent to the system under learning. Our work replaces a single MAT with multiple MATs that can potentially run in parallel and learn different components of the black-box system automatically.

Learning structured systems and in particular, compositional learning of parallel systems has been studied recently in the literature. Moerman [27] proposes an algorithm to learn parallel interleaving Moore machines. Our algorithm differs from Moerman’s algorithm in that in the parallel composition of Moore machines, the output of each individual component is explicitly specified, because the output of the system is specified as a tuple of the outputs of its components. In other words, the underlying structure is immediately exposed by considering the type of outputs produced by the system under learning. However, in our approach, we need to identify the components and assign outputs to them on-the-fly since the decomposition is not explicit in parallel composition. Al-Duhaiby and Groote [10] learn parallel labelled transitions systems with the possibility of synchronisation among them. In order to develop their algorithm, they assume a priori knowledge of mutual dependencies among actions in terms of a confluence relation. This type of information is difficult to obtain and the domain knowledge in this regard may be error prone. Particularly for legacy and large black-box systems (e.g., binary code), architectural discovery has proven challenging [8, 22]. We address this challenge and go beyond the existing approaches by learning about confluence of actions on-the-fly through observing the minimal counter-examples generated by the MAT(s).

Frohme and Steffen [12] introduce a compositional learning approach for Systems of Procedural Automata [13]; these are collections of DFAs that may “call” each, akin to the way non-terminals may be used in defining other non-terminals in a grammar. Their approach is essentially different from ours in that the calls across automata are assumed to be observable and hence the general structure is assumed to be known; in our approach, we learn the structure by observing implicit dependencies among the learned automata through analysing counter-examples. Also their approach is aimed at a richer and more expressive type of systems, namely pushdown systems, which justifies the requirement for additional information.

L$^*$ has been improved significantly in the past few years; the major improvements upon L$^*$ can be broadly categorised into three categories: 1) improving the data structures used to store and retrieve the learned information [19, 21, 31, 37]; 2) improving the way counter-examples are processed in refining the hypothesis [3, 17, 28, 31]; 3) learning more expressive models, such as register- [14, 18] and timed automata [5, 34]. This third category of improvements is orthogonal to our contribution and extension of our approach can be considered in those contexts as well.

Two notable recent improvements, in the first two categories, are L$^\#$ [37] and L$^\lambda$ [17], respectively. L$^\#$ uses the notion of apartness to organise and maintain a tree-shaped data-structure about the learned automaton. L$^\lambda$ uses a search-based method to incorporate the information about the counter-example into the learned hypothesis. The improvements brought about by L$^\lambda$ can be readily incorporated into our approach, particularly since our approach relies on finding minimal counter-examples. Integrating our approach into L$^\#$ requires a more careful consideration of maintaining and composing tree-shaped data structures when detecting dependencies. We expect that both of these combinations will further improve the efficiency of our proposed method.

3 Preliminaries

In this section, we review the basic notions used throughout the remainder of the paper. We start by formalising the notion of a finite state machine, which is the underlying model of the system under learning and move on to parallel composition and decomposition (called projection) as well as the concept of (in)dependent actions, which are essential in identifying the parallel components. Finally, we conclude this section by recalling the basic concepts of active automata learning and the L$^*$ algorithm.

3.1 Finite State Machines (FSMs)

Finite state machines (also called Mealy machines), defined below, are straightforward generalisations of finite automata in which the transitions produce outputs (rather than only indicating acceptance or non-acceptance):

Definition 1

(Finite State Machine) A Finite State Machine (FSM) M is a sixtuple $(S, s_0, I, O, \delta , \lambda )$ where :

• S is a finite set of internal states,

• $s_0 \in S$ is the initial state,

• I is a set of actions, representing the input alphabet,

• O is the set of outputs,

• $\delta : S \times I \rightarrow S$ is a total state transition function,

• $\lambda : S \times I \rightarrow O$ is a total output function.

An FSM starts in the initial state $s_0$ and accepts a word (a sequence of actions of its input alphabet) in order to produce an equally-sized sequence of outputs. State transition- $\delta$ and output function $\lambda$ determine the next state and the output of an FSM upon receiving a single input. For each $s, s' \in S$, $i \in I$, and $o \in O$, we write when $\delta (s, i) = s'$ and $\lambda (s, i) = o$.

State transitions are extended inductively from a single input $i \in I$, to a sequence of inputs $w \in I^*$, i.e., we define $\delta (s, \epsilon )= s$ and $\lambda (s,\epsilon ) = \epsilon$ where $\epsilon$ is the empty sequence; and for $s \in S, w \in I^*$, and $a \in I$, we have $\delta (s, w a)=\delta (\delta (s, wa), a)$ and $\lambda (s, w a) = \lambda (s,w) \lambda (\delta (s, w),a)$, where juxtaposition of sequences denotes concatenation. For the sake of conciseness, we write $\delta (w)$ and $\lambda (w)$ instead of $\delta (s_0, w)$ and $\lambda (s_0,w)$.

In much of the literature in active learning, the system under learning is assumed to be complete and deterministic and we follow this common assumption in Definition 1 by requiring the state transition and output relations to be total functions. While the determinism assumption is essential for our forthcoming results to hold, we expect that the existing recipes for learning non-deterministic state machines can be made compositional using a similar approach as ours.

3.2 (De)Composing FSMs

Our aim is to produce a compositional learning algorithm for systems composed of interleaving parallel components, defined below. Due to the interleaving nature of parallel composition and determinism of the system under learning, the alphabets of these components are assumed to be disjoint.

Definition 2

(Interleaving Parallel Composition) For two FSMs $M_i = (S_i, s_{0_i}, I_i, O_i, \delta _i, \lambda _i)$, with $i \in \{0,1\}$, where $I_0 \cap I_1 = \emptyset$, the interleaving parallel composition of $M_0$ and $M_1$, denoted by $M_0 ~||~ M_1$, is an FSM defined as

$$(S_0 \times S_1,(s_{0_0},s_{0_1}), I_0 \cup I_1, O_0 \cup O_1, \delta , \lambda ) $$

where $\delta$ and $\lambda$ are defined by

$$ \delta ((s_0,s_1),a)=\left\{ \begin{array}{ll} (\delta _0(s_0,a),s_1)&{}\text {if }a\in I_0,\\ (s_0,\delta _1(s_1,a))&{}\text {otherwise, and}\\ \end{array}\right.\quad \lambda ((s_0,s_1),a)=\left\{ \begin{array}{ll} \lambda _0(s_0,a)&{}\text {if }a\in I_0,\\ \lambda _1(s_1,a)&{}\text {otherwise.}\\ \end{array}\right. $$

For $s_0 \in S_0$, $s_1 \in S_1$, and $a \in I_0 \cup I_1$

Next, we define the notions of projections for FSMs and for words; these notions are further used in the notion of (in)dependence and eventually in our proof of correctness to establish that the composed system has the same behaviour as the composition of the learned components.

Definition 3

(Projection of an FSM) The projection of an FSM $M = (S, s_0, I, O, \delta , \lambda )$ on a set of inputs $I' \subseteq I$ denoted by $P(M, I')$, is an FSM $(S, s_0, I', O', \delta ', \lambda ')$, where

• $\delta '(s,a) = \delta (s,a)$ for $a \in I'$,

• $\lambda '(s,a) = \lambda (s,a)$ for $a \in I'$, and

• $O' = \{o \in O ~|~ \exists a \in I'.~\exists s \in S. ~ \lambda (s, a)= o\}$.

Definition 4

(Projection of a word) The projection of a word $w \in I^*$ on a set of inputs $I' \subseteq I$, denoted by $P_{I'}(w)$, is inductively defined as follows:

$$ \begin{array}{lcl} P_{I'}(\epsilon ) &{}:=&{} \epsilon , \\ P_{I'}(a u) &{} :=&{} \left\{ \begin{array}{ll} a P_{I'}(u) &{} \text{ if } a \in {I'}, \\ P_{I'}(u) &{} \text {otherwise}. \end{array} \right. \end{array} $$

Definition 5

(Projection of an output sequence) The projection of the output sequence $w = o_1 \dots o_n$ with respect to an equally-sized sequence of inputs $v = i_1, \dots , i_n \in I^*$ and a subset of inputs $I' \subseteq I$, denoted by $P_{I'}(w,v)$, is defined as follows:

$$ \begin{array}{lcl} P_{I'}(\epsilon , \epsilon ):=\epsilon ,\\ P_{I'}(o w,a v):= \left\{ \begin{array}{ll} o P_{I'}(w,v)&{}\text {if }a\in I',\\ P_{I'}(w,v)&{}\text {otherwise.} \end{array}\right. \end{array} $$

Definition 6

((In)Dependent Actions) Consider an FSM M with a set of inputs I. The subsets $I_0,$ $\ldots ,$ $I_n \subseteq I$ form an independent partition of I when for any $u \in I^*$, $\lambda _{P(M, I_0) || \ldots || P(M, I_n)} (u) = \lambda _M (u)$. Two inputs $i_0, i_1 \in I$ are independent when they belong to two distinct subsets of an independent partition. Two input actions are dependent, when they are not independent.

Example. The partition $\big \{\{a\},\{b\},\{c,d\}\big \}$ in Figure 1(a) is not an independent partition because $\lambda _M(ab)=10$ but $\lambda _{P(M,\{a\})||P(M,\{b\})||P(M,\{c,d\})}(ab)=11$.

It immediately follows from Definition 6 and associativity of parallel composition (with respect to trace equivalence) that any coarser partitioning based on an independent partition is also an independent partitioning; this is formalised in the following corollary.

Corollary 1

By combining two or more sets of an independent partition, the resulting partition remains independent.

Moreover, it holds that any smaller subset of an independent partitioning is also an independent partitioning of the original state machine projected on the alphabet of the smaller subset, as specified and proven below.

Lemma 1

Consider an independent partition $I_0, \dots , I_n$ of inputs I for an FSM M; then for $K\subseteq \{0,\dots ,n\}$, $\{I_i \mid i \in K\}$ is an independent partition for $P(M, \bigcup _{i \in K}( I_i))$.

Proof

Consider any subset $K\subseteq \{0,\dots ,n\}$ and $\{I_i \mid i \in K\}$ and consider any input sequence $u \in (\bigcup _{i \in K} I_i)^*$. Since u does not contain a symbol that is in any $I_j$ for $j \notin K$, we have that $\lambda _{||_{i \in K} P(M, I_i)} (u) = \lambda _{P(M, I_0) || \ldots || P(M, I_n)} (u)$. Since $I_0,\ldots ,I_n$ are independent, it follows likewise that $\lambda _{P(M, I_0) || \ldots || P(M, I_n)} (u) = \lambda _M (u)$. Using again that u has no symbol in any $I_j$ for $j\notin K$, we know that $\lambda _M (u)=\lambda _{P(M, \bigcup _{i \in K}( I_i))}(u)$. Hence, $\lambda _{||_{i \in K} P(M, I_i)} (u)= \lambda _{P(M, \bigcup _{i \in K}( I_i))} (u)$, which was to be shown.

   $\blacksquare$

Lemma 2

For any independent partition $I_0, \dots , I_n \subseteq I$, $w \in I^*$ and $0\le i\le n$, and state s it holds that $P_{I_i}(\lambda _M(s,w),w) = \lambda _{P(M, I_i)} (s, P_{I_i}(w))$.

Proof

The proof uses induction on the length of w. Instead of proving the thesis, we prove the following stronger statement, which is possible because M can be viewed as the parallel construction of independent components.

$$ P_{I_i}(\lambda _M((s_0,\ldots s_n),w),w) = \lambda _{P(M, I_i)} ((s'_0,\ldots ,s'_n),P_{I_i}(w))\text { with }s_i=s'_i. $$

Note that the lemma directly follows from this. Below we write $\vec {s}$ for $s_0,\ldots ,s_n$, and likewise for $\vec {s}'$ and $\vec {s}''$.

The base case ($|w|=0$) holds trivially as $w=\epsilon$. For the induction step we assume that the induction hypothesis holds for $|w|=k$ and we show that it holds for $w'=a w$ for arbitrary $a\in I$.

We first consider the case where $a \notin I_i$. We derive

$$\begin{aligned} P_{I_i}(\lambda _M(\vec {s}, a w),a w)&= P_{I_i}(\lambda _M(\vec {s},a)\lambda _M(\delta (\vec {s},a), w),a w){} & {} \text {Definition~1}\\&= P_{I_i}(\lambda _M(\delta (\vec {s},a),w),w){} & {} \text {Definition~5.}\\&= \lambda _{P(M, I_i)}(\vec {s}',P_{I_i}(w)){} & {} \text {Induction hypothesis}. \\&=\lambda _{P(M, I_i)} (\vec {s}'', P_{I_i}(a w)){} & {} \text {Definition~4}. \end{aligned}$$

By construction the i-th state in $\delta (\vec {s},a)$ is equal to $s_i$ as $a\notin I_i$. Hence, using the induction hypothesis, $\vec {s}_i'=s_i$. By definition $\vec {s}'=\delta (\vec {s}'',a)$ and hence, $\vec {s}_i''=\vec {s}_i'=\vec {s}_i$ as we had to show.

The other case we must consider is $a \in I_i$. Again the derivation is straightforward.

$$\begin{aligned} P_{I_i}(\lambda _M(\vec {s}, a w),a w)&= P_{I_i}(\lambda _M(\vec {s},a)\lambda _M(\delta (\vec {s},a), w),a w){} & {} \text {Definition~1}\\&= \lambda _M(\vec {s},a) P_{I_i}(\lambda _M(\delta (\vec {s},a),w),w){} & {} \text {Definition~5.}\\&= \lambda _M(\vec {s}',a) \lambda _{P(M, I_i)}(\delta (\vec {s}',a),P_{I_i}(w)){} & {} \text {Induction hypothesis}. \\&=\lambda _{P(M, I_i)} (\vec {s}, P_{I_i}(a w)){} & {} \text {Definition~4}. \end{aligned}$$

Using the induction hypothesis it follows that $s_i=s'_i$, which concludes the proof.    $\blacksquare$

3.3 Model Learning

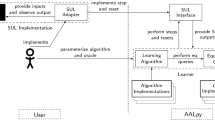
Active model learning, introduced by Dana Angluin, was originally designed to formulate a hypothesis $\mathcal {H}$ about the behavior of a System Under Learning (SUL) as an FSM. Model learning is often described in terms of the Minimally Adequate Teacher (MAT). In the MAT framework, there are two phases: (i) hypothesis construction, where a learning algorithm poses Membership Queries (MQ) to gain knowledge about the SUL using reset operations and input sequences; and (ii) hypothesis validation, where based on the model learned so far, the learner proposes a hypothesis $\mathcal {H}$ about the “language” of the SUL and asks Equivalence Queries (EQ) to test it. The results of the queries are organised in an observation table. The table is iteratively refined and is used to formulate $\mathcal {H}$.

Definition 7

(Observation Table) An observation table is a triple (S, E, T), where $S \subseteq I^*$ is a prefix-closed set of input strings (i.e., prefixes); $E \subseteq I^+$ is a suffix-closed set of input strings (i.e., suffixes); and T is a table where rows are labeled by elements from $S \cup (S.I)$, columns are labeled by elements from E, such that for all $\textit{pre} \in S \cup (S.I)$ and $\textit{suf} \in E$, $T (\textit{pre}, \textit{suf} )$ is the SUL’s output suffix of size $|\textit{suf}|$ for the input sequence $\textit{pre}.\textit{suf}$.

The L$^*$ algorithm initially starts with S only containing the empty word $\epsilon$, and E equals set of inputs alphabet I. Two crucial properties of the observation table, closedness and consistency, defined below, allow for the construction of a hypothesis.

Definition 8

(Closedness Property) An observation table is closed iff for all $w \in S.I$ there is a $w' \in S$ that for all $\textit{suf} \in E$, $T(w, \textit{suf}) = T(w', \textit{suf})$ holds.

Definition 9

(Consistency Property) An observation table is consistent iff for all $\textit{pre}_1, \textit{pre}_2 \in S$, if for all $\textit{suf} \in E$, $T(\textit{pre}_1, \textit{suf}) = T(\textit{pre}_2, \textit{suf})$, it holds that $T(\textit{pre}_1.\alpha , \textit{suf} ) = T(\textit{pre}_2.\alpha , \textit{suf})$ for all $\alpha \in I, \textit{suf} \in E$.

MQs are posed until these two properties hold, and once they do, a hypothesis $\mathcal {H}$ is formulated. After formulating $\mathcal {H}$, L$^*$ works under the assumption that an EQ can return either a counter-example (CE) exposing the non-conformance, or yes, if $\mathcal {H}$ is indeed equivalent to the SUL. When a $\texttt{CE}$ is found, a $\texttt{CE}$ processing method adds prefixes and/or suffixes to the observation table and hence refines $\mathcal {H}$. The aforementioned steps are repeated until EQ confirms that $\mathcal {H}$ and SUL are the same. In between MQs, we often need to bring the FSM back to a known state; this is done through reset operations, which are one of our metrics for measuring the efficiency of the algorithm. EQs are posed by running a large number of test-cases and hence they are (two- to three) orders of magnitude larger than MQs. These test cases are generated through a random-walk of the graph or through a deterministic algorithm that tests all states and transitions for a given fault model. Two examples of deterministic test-case generation algorithms are the W- and WP-method [7]. It appears from recent empirical evaluations that for realistic systems deterministic equivalence queries are not efficient [4].

Since we are going to be learning the system in terms of components with disjoint alphabets, we define the following projection operator that removes all the transitions that are not in the projected alphabet. Our compositional learning algorithm basically learns a black-box with respect to its projection on the actions available in each purported component.

Definition 10

( ) Given an SUL $M=(S, s_0, I, O, \delta , \lambda )$ and $I' \subset I$, $L^*(M,I')$ returns $P(M, I')$ by running algorithm L$^*$ with projected alphabet $I'$ on M.

4 Compositional Active Learning

In this section, we present an algorithm that learns the SUL in separate components and uses the interleaving parallel composition of the learned components to reach the total behavior of the system. Each component has an input alphabet $I_i$, which is disjoint from the alphabet of all the other components. The set of the input alphabets of components $I^F = \{I_1, \, \dots , \, I_{n}\}$ is a partition of the total system’s input alphabet. The main idea is to find an independent partitioning $I^F$. To reach such a partitioning, we start with a partition with singleton sets and iteratively merge those sets that are found to be dependent on each other. Then for $I_i \in I^F$, we learn the SUL with the projected alphabet $I_i$, and compute the product of the obtained components with interleaving parallel composition. The result is equivalent to the SUL if $I^F$ is an independent partition.

Definition 11

(LearnInParts) The $\textit{LearnInParts}$ function gets $M=(S, s_0, I, O, \delta , \lambda )$ and the partition $I^F=\{I_1, \, \dots , \, I_{n}\}$ of I and returns the interleaving parallel composition of the learned components.

$$ \textit{LearnInParts}(M, I^F) = L^*(M, I_1) \, ~|| \, \dots ||~ L^*(M, I_n). $$

Definition 12

(Composition) Given a partition $I^F = \{I_1, \, \dots , \, I_{n}\}$ and $D \subseteq \{1, \dots , n\}$, the $\textit{Composition}$ of $I^F$ over D merges all the $I_i$ ($i \in D$) in $I^F$.

$$ Composition(I^F, D) = (I^F \setminus \{I_i| i \in D\} ) \cup \big \{ \bigcup _{i \in D} I_i \big \}. $$

Example. If $I^F = \{\{a\},\{b\},\{c\}, \{d\}\}$ and $D=\{1,3,4\}$, then $Composition(I^F, D) = \{\{a,c,d\},\{b\}\}$.

Definition 13

(InvolvedSets) The function $\textit{InvolvedSets}$ gets a counter-example $\texttt{CE}$ and a partition $I^F = \{I_1, \, \dots , \, I_{n}\}$ and returns indices of the sets in $I^F$ that contains at least one character of $\texttt{CE}$:

$$ InvolvedSets (\texttt{CE}, I^F) = \{j ~ | ~ I_j \in I^F, ~ \exists i ~ \texttt{CE}[i] \in I_j \}, $$

where the $i^{th}$ character of $\texttt{CE}$ is denoted by by $\texttt{CE}[i]$.

The function $\textit{InvolvedSets}$ allows us to detect some dependent sets by using a minimal counter-example since all actions in the counter-example are dependent, as we prove in Theorem 2.

Algorithm 1 shows the pseudo-code of the compositional learning algorithm. Initially the algorithm is called with the singleton partitioning $I^F$ of the alphabet I and the SUL M, i.e., if the input alphabet is $I = \{a_1, a_2, \ldots , a_n\}$, then the initial partition of the alphabet will be $I^F = \{\{a_1\}, \{a_2\}, \ldots , \{a_n\}\}$. The $\textit{LearnInParts}$ method on line 2 learns each of the components given the corresponding alphabet set using the algorithm L$^*$ and returns the interleaving parallel composition of the learned components. If the oracle (MAT) returns yes for the equivalence query regarding hypothesis $\mathcal {H}$, the algorithm terminates and returns $\mathcal {H}$. Otherwise an(other) iteration of the loop is performed. The $\textit{InvolvedSets}$ method in line 6 extracts the dependent sets from the counter-example returned by the oracle; subsequently, $\textit{Composition}$ merges those sets into one. The $\textit{LearnInParts}$ method in line 8 is run again and the loop continues until the correct hypothesis is learned. We assume that the oracle always returns a minimal counter-example; this assumption is used in the proof of soundness (Theorem 2).

4.1 Termination Analysis

To prove the termination of our algorithm, we start with the following lemma which indicates how the counter-example is used to merge the partitions.

Lemma 3

Let $I^F = \{I_1,\dots ,I_m\}$ be a partition of the system’s input alphabet. If the teacher responds with a counter-example $\texttt{CE}$, then there are at least two actions $u \in I_i, v \in I_j$ in $\texttt{CE}$ such that $I_i \ne I_j ~ \wedge ~ I_i, I_j \in I^F$.

Proof

We prove this by contradiction. Suppose $\texttt{CE}$ consists of actions that all belong to $I_i$. Let $C_i = L^*(M, I_i)$ with output function $\lambda _{C_i}$. Since the output of L$^*$ is always the correctly learned FSM of the SUL, $\lambda _M(\texttt{CE})=\lambda _{C_i}(\texttt{CE})$. Also, since $C_i$ is a component of $\mathcal {H}$ produced by $\underline{LearnInParts}$, $\lambda _{\mathcal {H}}(\texttt{CE})=\lambda _{C_i}(\texttt{CE})$ based on Definition 2. This means $\texttt{CE}$ can not be a counter-example.    $\blacksquare$

The next lemma uses Lemma 3 to show how counter-examples will ensure progress in the algorithm, eventually guaranteeing termination.

Lemma 4

At each round of the algorithm CL$^*$, $|I^F|$ decreases by at least 1.

Proof

By Lemma 3, at each round of the algorithm, at least two dependent sets are found by InvolvedSets, and the algorithm merges these dependent sets into a single set. Thus the size of the partition decrements by at least one; hence, the lemma follows.    $\blacksquare$

Now we have the necessary ingredients to prove termination below.

Theorem 1

The Compositional Learning Algorithm terminates.

Proof

Assume, towards contradiction, that the algorithm does not terminate. Let I be the alphabet, an $I^F_k$ be the partition of I after the $k^{th}$ round of the algorithm. By Lemma 4, after at least $k = |I|-1$ rounds, $|I^F_k| = 1$. Also by the assumption, the algorithm has not terminated at round k. Since $I^F_k = I$, the algorithm reduces to algorithm L$^*$ which terminates. Hence, the contradiction.    $\blacksquare$

We prove next that every time we merge two partitions, there is a sound reason (i.e., dependency of actions) for it.

Theorem 2

Let $\texttt{CE}$ be the minimal counter-example returned by the oracle at round k of the algorithm and $I^F = \{I_1,\dots , I_n\}$ the partition of the alphabet at the same round. Then, all actions in $\texttt{CE}$ are dependent.

Proof

Let $\texttt{CE} = wa$, $w \in I^*$ and $a \in I$, and $d = \{d_1, \dots , d_m\}$ be an independent partition for the SUL M. Assume some actions in w are independent from a (proof by contradiction). Let $d_k$ be the set in d that includes a. The set $I \setminus d_k$ contains all the independent actions from a. For M, we define $O_M = P_{d_k}(\lambda _M(wa))$; according to Lemma 2, $O_M = \lambda _{P(M, d_k)}(P_{d_k}(wa))$. The algorithm makes the hypothesis $\mathcal {H} = P(M, I_1)|| \dots || P(M, I_n)$ at the current round k. Since $d_k$ is the union of a subset of $I^F$ (algorithm has not terminated yet), $O_{\mathcal {H}} = P_{d_k}(\lambda _{\mathcal {H}}(wa)) = \lambda _{P(\mathcal {H}, d_k)}(P_{d_k}(wa))$. If $O_{\mathcal {H}} \ne O_M$, then $P_{d_k}(wa)$ is a smaller counter-example than wa, which is a contradiction. Otherwise if $O_{\mathcal {H}} = O_M$, given that wa is a counter-example, $P_{I \setminus d_k}(\lambda _M(wa)) \ne P_{I \setminus d_k}(\lambda _{\mathcal {H}}(wa))$; if so, $P_{I \setminus d_k}(wa)$ is a smaller counter-example, hence the contradiction.    $\blacksquare$

By Theorems 2 and 1, we have shown that the algorithm detects the independent action sets and eventually terminates. The next theorem is formulated to show that it terminates as soon as all dependent action sets have been detected.

Theorem 3

Let $I^F = \{I_1, \dots , I_n\}$ be an independent partition of the alphabet at round k. The algorithm terminates in this round.

Proof

We prove this by contradiction. Assume that the algorithm does not terminate, and $\texttt{CE}$ is the minimal counter-example returned by the oracle. By theorem 2, $\underline{InvolvedSets}$ returns two or more dependent sets from $I^F$. Since all the elements in $I^F$ are pairwise independent, we confront the contradiction.    $\blacksquare$

4.2 Processing Counter-examples

As mentioned in Theorem 2, we require all the actions in a minimal counter-example returned by the oracle to be dependent. However, most equivalence checking methods do not find the minimal counter-example. For a non-minimal counter-example, we define a process called “distillation”, which asks a number of extra queries to find the dependent actions. It iteratively gets a subset of $\textit{InvolvedSets}$($\texttt{CE}$, $I^F$) in the order of their sizes and merges its members together, producing a set M. The algorithm introduces $P_M(\texttt{CE})$ as output if it is a counter-example.

Suppose $\texttt{CE}$ is the counter-example returned by the oracle at round k of the algorithm, and $I^F$ is the alphabet partition at that round. To distill two or more dependent sets from $\texttt{CE}$, we follow Algorithm 2. The function $\textit{CutCE}$ on line 2 takes a counter-example $\texttt{CE}$ and returns the smallest prefix of $\texttt{CE}$, which is also a counter-example (i.e., the SUL and the hypothesis model produce different outputs for it). Then, iteratively, it gets a subset of $\textit{InvolvedSets}$($\texttt{CE}$, $I^F$) in the order of their sizes and merges its members together, producing set M. The algorithm returns $P_M(\texttt{CE})$ as output if it is a counter-example.

The cost of CE-distillation algorithms is exponential in terms of the size of $\texttt{CE}$ in the worst case. However, in the results section, we show that in practice, the cost of this part is not very significant compared to the total cost of learning.

Theorem 4

All actions in the output of the CE distillation algorithm are dependent.

The proof is omitted as it is similar to the proof of Theorem 2.

5 Empirical Evaluation

In this section, we present the design and the results of the experiments carried out to evaluate our approach, in order to answer the following research questions:

• RQ1 Does CL$^*$ require fewer resets, compared to L$^*$?

• RQ2 Does CL$^*$ require fewer input symbols, compared to L$^*$?

As stated in Section 1, these two research questions measure the efficiency of a learning method in a machine-independent manner: the number of input symbols summarises the total cost of a learning campaign, while the number of resets summarises one of its most costly parts. Note that although active learning processes are structured in terms of queries, the queries used in the processes have vastly different lengths and it has been observed earlier that the total number of input symbols is a more accurate metric for comparison of learning algorithms than the number queries [36].

5.1 Subject Systems

A meaningful benchmark for our method should feature systems of various state sizes and various numbers of parallel components and with a non-trivial structure that may require multiple learning rounds. Also, we would like to have realistic systems, so that our comparisons have meaningful practical implications.

To this end, we choose the Body Comfort System (BCS) [25], which is an automotive software product line (SPL) of a Volkswagen Golf model. This SPL has 27 components, each representing a feature that provides specific functionality. The transition system of each component is provided in a detailed technical report [24]. We use the finite state machines of the components constructed from the transition system representations in [35] and compose several random samples utilising the interleaving parallel composition (Definition 2) to build the product FSMs. We automatically constructed 100 FSMs consisting of a minimum of two and a maximum of nine components in this case study. The maximum number is chosen due the performance limits of L$^*$; beyond this limit, our learning campaign for L$^*$ could take more than four hours. All experiments were conducted on a computer with an Intel^® Core^™ M-5Y10c CPU and and 8GB of physical memory running Ubuntu version 20 and LearnLib version 0.16.0. Our subject systems have a minimum of 300 states and a maximum of 3840 states, and their average number of states is 1278.2 with a standard deviation of 847. We started the calculation of the metrics for subject systems of at least 300 states, since for small subject systems, the advantage of compositional learning is not significant.

5.2 Experiment Design

To answer the research questions, we implemented the compositional learning algorithm on top of the LearnLib framework [30]. This implementation uses the equivalence oracle in two places; to learn projections in the $\textit{LearnInParts}$ function and to check the hypothesis/SUL equivalence. The performance of the algorithm significantly relies on the type of equivalence queries used by the underlying L$^*$ algorithm. We experimented with a number of equivalence methods and settled upon using random walks; when using deterministic algorithms such as the WP- and the WP-method, for large systems, the cost of equivalence queries becomes prohibitively high and obscures any gain obtained from compositionality. To ensure that our results are sound, we have carried out similar experiments by using an additional deterministic equivalence query at the end of the learning campaign, when the last random equivalence query does not return any counter-example. This additional step verifies our comparisons when an assurance about the accuracy of the learning process is required. More details about these additional experiments can be found in our public lab package [23] (https://github.com/faezeh-lbf/CL-Star).

We enabled caching, since caching significantly reduces repetitive queries. We repeat each learning process three times, comparing the number of resets and input symbols for L$^*$ and CL$^*$.

In addition to reporting the median metrics, their standard deviations, and the relative percentage of improvements, we use the statistical T-test to answer the research questions with statistical confidence and report the p-values. We analyse the distribution of the results and establish their normality using K-tests. We use the SciPy [20] library of Python to perform statistical analysis and Seaborn [38] for visualising the results.

5.3 Results

Table 1. Comparing the total number of input symbols in the CL$^*$ and L$^*$ methods

Table 2. Comparing the total number of resets in the CL$^*$ and L$^*$ methods

In this section, we first present the results of our experiments and use them to answer our research questions. Then we show how the number of components in an FSM affects the efficiency of our algorithm. Finally, we discuss threats to the validity of our empirical results.

Fig. 2.

The total number of input symbols and resets in the CL$^*$ and L$^*$ methods

We cluster the benchmark into eight categories based on the FSM’s number of states and illustrate the distribution of input symbols and resets for each cluster in Figure 2. In this figure, the CL$^*$ and L$^*$ methods are compared based on the metrics mentioned. The scale of the x-axis (the value of metrics) is logarithmic.

Tables 1 and 2 summarise the results of our experiments. For each category, we calculate the median and standard deviation of our metrics (the number of input symbols and resets) both for L$^*$ and CL$^*$. The metric “progress percentage" is defined to measure the improvement brought about by compositional learning (compared to L$^*$). For each metric, the progress percentage is calculated as $(1- \frac{p}{q}) *100$, where p and q are the value of that metric in CL$^*$ and L$^*$, respectively. A positive progress percentage in a metric shows that the CL$^*$ is more efficient in terms of that metric. To measure the statistical significance, we used the one-sided paired sample T-test to check if there was a significant difference ($p < 0.05$) between the metrics in the two algorithms.

Both Tables 1 and 2 indicate major improvements, particularly for large systems, in terms of the total number of input symbols and resets, respectively. Compositional learning reduces the number of symbols up to 70.80 percent and the number of resets up to 95.83 percent. The statistical tests also confirm this observations and the p-values obtained from the tests are in all cases very low; in case of the number of input symbols the p-values range from $10^{-2}$ to $10^{-12}$, while for resets they range from $10^{-6}$ to $10^{-43}$, which are well-below the usual statistical p-values (0.05) and represent a very high statistical significance.

Fig. 3.

The diagrams of improvement brought about by compositional learning vs. size of the SUL in terms of number states (left) and components (right).

Fig. 4.

The effect of FSM sizes in terms of the number of components and states on the total number of input symbols.

The plots in Figure 3 visualise the improvements brought about by compositional learning. This plot demonstrates that the saving due to compositional learning increases as the number of components in SULs increases. We further analysed the trends of our measured metrics in terms of the number of states and the number of parallel components. These trends are depicted for the total number of input symbols in Figure 4 and for the number of resets in Figure 5, respectively. These figures indicate that the increase of both metrics with the number of states is more moderate for the compositional learning approach, i.e., compositional learning is more scalable. More importantly, the right-hand-side of both figures signifies the effect of compositional learning when the number of parallel components increases while the number of states remains fixed.

Figure 6 shows the effect of the number of components on the total number of input symbols for a fixed state-space size for algorithms L$^*$ and CL$^*$. In this plot, as the number of components increases, the corresponding dot will become darker and larger. According to this figure, the learning cost is lower for SULs with more components in both L$^*$ and CL$^*$. Still, for CL$^*$ (the right side), the cost of learning SULs with more components is significantly lower because we structurally learn these components essentially independently.

Fig. 5.

The effect of the size of FSMs in terms of the number of components and states on the total number of required input resets.

Fig. 6.

The relation between the total number of symbols and the number of states and components for the algorithms L$^*$ (left) and CL$^*$ (right).

As mentioned in Section 4.2, the cost of the CE distillation process can increase exponentially in the size of the counter-example. However, in practice, it seems to be much more tractable. To evaluate this, we count the number of input symbols required by the CE distillation process to learn each SUL. The median value of this metric is 1961 input symbols, which is insignificant compared the total cost of learning. In fact, the cost of CE distillation process for each group in Table 1 is between 0.037 and 0.12 percent of the total learning cost; the reported total learning cost (total number of input symbols) includes the cost of CE distillation.

5.4 Threats to Validity

In this section, we summarise the major threats to the validity of our empirical conclusions. First, we analyse the threats to conclusion validity, i.e., whether the empirical conclusions necessarily follow from the experiments carried out. Then, we discuss the threats to external validity concerning the generalisation of our results to other systems.

We mitigated conclusion validity threats by using statistical tests to ensure that our observations (both in terms of improvement percentages in Tables 1 and 2 and the visual observations in Figures 2) do represent a statistically significant improvement. We opt for one-sided paired sample T-tests in order to minimise the threats to conclusion validity. We only conclude that the CL$^*$ is more efficient than the L$^*$ when there is a meaningful difference ($p < 0.05$) between the results of L$^*$ and CL$^*$. To make sure that the chosen statistical test is applicable, we analysed the distribution of the data first.

We mitigated the risk of conclusion validity by using subject systems that are based on practical systems rather than using randomly generated FSMs. However, further research is needed to analyse the performance of our approach based on other benchmarks from other domains. We also mitigated the effect of using random equivalence queries by repeating the experiments with a final deterministic query.

6 Conclusions

In this paper, we presented a compositional learning method based on Angluin’s algorithm L$^*$ that detects and independently learns interleaving parallel components of the system under learning. We proved that our algorithm, called CL$^*$, is correct and we empirically showed that it causes significant gains in the number of input symbols and the number of resets in a learning campaign. The gain is significantly increased with the number of parallel components.

Our algorithm is naturally amenable to parallelisation and developing a parallel implementation is a natural next step. A more thorough investigation of counter-example processing in order to efficiently find a minimal counter-example is an area of further research, particularly, in the light of the recent results in this area [13]. Finding a trade-off between using deterministic and random (or mutation-based) equivalence queries is another area of future research. We would also like to investigate the possibility of developing equivalence queries that take the structure of the systems into account: we have observed that much of the effort in the final equivalence query (on the composed system) is redundant and the final equivalence query can be made much more efficient by only considering the dependencies among purportedly independent partitions. Finally, extending our notion of parallel composition to allow for a possible synchronisation of components is another direction of future work; we believe inspirations from concurrency theory and in particular, Milner and Moller’s prime decomposition theorem [26] may prove effective in this regard. Independently from our work, Neele and Sammartino [29] proposed an approach to learn synchronous parallel composition, under the assumption of knowing the alphabets of the components. This is a promising approach to incorporate synchronous parallel composition into our framework.