Abstract
We introduce the global conflict graph of DQCNFs (dependency quantified conjunctive normal forms), recording clashes between clauses on such universal variables on which all existential variables depend (called “global variables”). The biclique covers of this graph correspond to the eligible clause-slices of the DQCNF which consider only the global variables. We show that all such slices yield satisfiability-equivalent variations. This opens the possibility to realise this slice using as few global variables as possible. We give basic theoretical results and first supporting experimental data.
O. Kullmann—Supported by EPSRC grant EP/S015523/1.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- QBF solving
- DQBF
- 2QCNF
- biclique cover problem
- conflict graph
- preprocessing
- Horn clause-sets
- minimal unsatisfiability
1 Introduction
The last two decades have seen enormous progress in quantified Boolean formula (QBF) theory and technology, as witnessed by the Handbook chapters [2, 14]. Core areas are preprocessing techniques, result validation of the solvers, strategy extraction, and theoretical lower bounds. There are many applications in the areas of artificial intelligence, planning, two player gaming and synthesis; see the overview [25]. This progress is complemented by the annual QBF competition called QBFEval (see [21]). A special class of QBF, 2QBF, is used to model problems with simple quantifier structure (see [1, 24] for basic references). In the other direction, the more expressive logic DQBF has also seen recent progress in this decade; see for example [3, 12, 13, 26]. Here solving techniques from SAT and QBFs are generalised, including preprocessing, strategy extraction and circuit synthesis. We remind at the central complexity classes covered here: SAT is NP-complete, 2QBF is \(\varPi _2^P\)-complete, QBF is PSPACE-complete, and DQBF is NEXPTIME-complete. In our paper we rely on the CNF-structure, and thus we will use 2QCNF instead of 2QBF, and DQCNF instead of DQBF.
In our paper we present a new, at first sight astonishing, but essentially simple theoretical insight into general DQCNFs, which enables transformations of problem instances, maintaining satisfiability-equivalence. We consider “global variables”, universal variables on which every existential variable depends, and the corresponding “slice” of the CNF (the parts of the clauses using these variables). The main insight is that we can replace this global slice by any other global slice (using completely different variables and clauses), with the only condition that the conflict (clashing) patterns between global literals need to be maintained. These conflict patterns can be represented by bicliques in graphs, with one biclique corresponding to one variable with its positive and negative occurrences, establishing the two sides of the biclique (where all vertices from the two sides are connected). In this way the tools of the theory of biclique (edge) covers (and also biclique partitions) of graphs can be used to find “better” global slices. A natural first metric for “better” is to use fewer bicliques, and the corresponding decision problem, whether a graph has a biclique cover using at most a given number of bicliques, is the NP-complete Problem GT18 in the classical book [11]. The smallest number of bicliques needed to cover a graph is called the biclique cover number, or also the bipartite dimension. In our context there is a very natural alternative point of view of biclique-covers/partitions, namely representing bicliques by boolean variables in CNFs, and then instead of a biclique-cover we just have a CNF realising the graph, which means its conflict graph is the given graph; now “fewer bicliques” means “fewer variables”. This has apparently been first explored in [10, 18]. The potential applications of this new transformation (changing the global slice) are in preprocessing for solving, and also the proof complexity aspect seems very interesting — how much do such changes affect the complexity of the formula?
We now run through a simple example, which shows the main topic of the paper in a nutshell: Using graph theory connected to CNFs to lower the number of (certain) universal variables in a DQCNF.
1.1 Using fewer universal variables
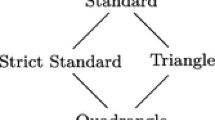
Consider the DQCNF \(\boldsymbol{F}\) with four universal and two existential variables
where \(F := (y_1 \vee x_2 \vee x_3) \wedge (\lnot y_1 \vee x_1 \vee \lnot x_2) \wedge (\lnot y_2 \vee \lnot x_1 \vee \lnot x_2 \vee \lnot x_3 \vee x_4) \wedge (y_2 \vee \lnot x_4)\). The universal variables of \(\boldsymbol{F}\) are \(x_1,x_2,x_3, x_4\), the existential variables are \(y_1, y_2\), with their dependencies shown in brackets. \(\boldsymbol{F}\) has a solution: \(y_1 = \lnot x_2\), \(y_2 = x_4\) (which makes all clauses tautologies). A central concept for this paper is that of a global variable, which is a universal variable such that all existential variables depend on it. The global variables of \(\boldsymbol{F}\) are \(x_1, x_2, x_3\). The sub-clauses given by the global variables yield the global slice, which is denoted by \({{\,\textrm{gsl}\,}}(\boldsymbol{F})\) (switching from logical to clause-notation — the global slice is just a CNF-clause-set):
The second central concept of this paper is the global conflict graph \({{\,\textrm{gcg}\,}}(\boldsymbol{F})\), which is the conflict graph of the global slice: the clauses are the vertices, and an edge connects clauses iff they have clashing literals:

Note that indeed we have a graph, and there is only one edge between \(\{ x_2, x_3 \}\) and \(\{ \overline{x_1}, \overline{x_2}, \overline{x_3} \}\) (not two). Now the basic insight of our paper (Corollary 2) is:
Any clause-set realising the conflict-graph
can be used instead of the (given) global slice.
Here by “realising” we just mean that the clause-set has the given conflict-graph. In our case, the triangle can be realised with just two variables \(x_1, x_2\), yielding

This triangle-realisation is Horn, minimally unsatisfiable, with one clause more than variables (we will show that this is always available). We obtain the new DQCNF \(\boldsymbol{F}'\) (which is satisfiability-equivalent to \(\boldsymbol{F}\), also shown for comparison):

where a solution now is \(y_1 = \lnot x_1\), \(y_2 = x_4\). In general we are aiming at reducing the number of global variables, by using a smaller CNF-realisation of the global conflict graph. Since minimising the number of global variables is NP-hard, for this first study we only consider fixed predetermined replacement-schemes.
1.2 Overview
In Section 2 we present basic definitions related to logic and graph theory. Especially the conflict graph of clause-sets is given in Definition 1, and in Subsection 2.2 we discuss biclique-covers/partitions, and how they relate to conflict graphs (Lemma 1). Section 3 then discusses the semantics of global variables in DQCNFs. Theorem 1 spells out the basic fact that global variables can be expanded (they can be eliminated by considering all assignments to them), and that the results are captured by independent (clash-free) sets of the global conflict graph. In Definition 7 we make precise what it means that one DQCNF is obtained from another one by replacing the global slice with an equivalent one, namely having the same global conflict graph, and being the same after removal of the global slices. Corollary 2 then says that such DQCNFs are satisfiability-equivalent.
In Section 4 we study the most basic realisations, “precise” and “imprecise” ones, the former realising precisely the number of given parallel edges in a given multigraph. We start in Subsection 4.1 by using “full clause-sets”, which are clause-sets where all clauses contain the same variables. So these are (imprecise) realisations of complete graphs, and indeed contain optimal ones (always w.r.t. the number of variables). In Subsection 4.2 we consider the trivial realisations, where every clash is realised by one new variable with one positive and one negative occurrence. A new perspective on basic realisations by “singular variables”, which occur in one sign only once, is then presented in Subsection 4.3. In Lemma 2 we give a simple generation process for the class of Horn minimally unsatisfiable clause-sets (HMUs), and, exploiting this, in Theorem 2 we show that every graph has a precise realisation by HMUs, computable in linear time. In Corollary 4 we obtain that every DQCNF with m clauses can be transformed in linear time into a satisfiability-equivalent one with only the global slice changed, so that now there are at most \(m-1\) global variables, using for each connected component of the global conflict graph a (variable-disjoint) HMU.
We now come to the experimental part of the paper. In Section 5 we present the first instance of a general scheme for generating 2QCNF, which are DQCNFs of the form \(\forall X \exists Y : F\), where X is the set of global variables, and Y the set of existential variables. The general scheme starts with a graph G with m vertices, and chooses some realisation F of G. One chooses the number \(C \ge 1\) of connected components of the (overall) global conflict graph, consisting of C vertex-disjoint copies of G, realised by C variable-disjoint copies of F. This yields altogether \(C \cdot m\) clauses. On these Cm clauses finally the existential slice is created, with n variables, which makes altogether three parameters (C, m, n). For the graphs G we choose complete graphs, and for the realisations the trivial realisation, the (unique) HMU realisation, and the (optimum) log (full) realisation, considering only powers of two: \(m = 2^p\). Finally for the existential slice we create random 3-CNFs. The basic question we want to explore is Hypothesis SIB: is using fewer global variables better for solving? We run two leading solvers on a selection of benchmark sets, which is presented in Section 6; see [19] for the benchmarks. To a large extend SIB is validated; we found only one parameter triple where the HMU-realisation could have some edge over the log-realisation, and present the finding. We conclude in Section 7 with future research directions.
2 Preliminaries
2.1 Logic
We have an infinite set of variables to start with; these variables can be used as universal or existential (boolean) variables in DQCNFs (see below), or just as plain (boolean) variables in clause-sets. We usually write v for a variable, using x for literals, with \(\overline{x}\) the complement of a literal (“negation”). A clause C is a (finite) set of literals not containing clashing literals, that is, there is no \(x \in C\) with \(\overline{x} \in C\). Using \(\overline{L} := \{ \overline{x} : x \in L \}\) for a set L of literals, clash-freeness of clauses C means the condition \(C \cap \overline{C} = \emptyset \). A clause-set F is a finite set of clauses. We use \({{\,\textrm{var}\,}}(x)\) for the underlying variable of a literal x, \({{\,\textrm{var}\,}}(C) := \{ {{\,\textrm{var}\,}}(x) : x \in C \}\) for the set of variables occurring (positively or negatively) in a clause C, and \({{\,\textrm{var}\,}}(F) := \bigcup _{C \in F} {{\,\textrm{var}\,}}(C)\) for the set of variables occurring in F. As measures for clause-sets F we use (taking values in \(\mathbb {N}_0= \{ x \in \mathbb {Z}: x \ge 0 \}\)):
-
1.
\(n(F) := |{{\,\textrm{var}\,}}(F) | \in \mathbb {N}_0\) for the number of variables in F;
-
2.
\(c(F) := |F | \in \mathbb {N}_0\) for the number of clauses in F;
-
3.
\(\delta (F) := c(F) - n(F) \in \mathbb {Z}\) for the deficiency of F.
Since in general we can not avoid having clauses with multiplicity, and we want to name clauses, we also use labelled clause-sets, which are pairs (L, F), where L is the (finite) set of (clause-)labels, and F is a map with domain L, mapping every label \(l \in L\) to a clause F(l). An ordinary clause-set F is converted into a labelled clause-set by using F as the label-set, and using the identity on F as clause-map. A DQCNF is a 4-tuple \(\boldsymbol{F} = (A,E,F,D)\), where
-
A, E are disjoint sets of variables, the universal and the existential variables;
-
F is a clause-set over \(A \cup E\) (i.e., using literals with variables from A or E);
-
D maps every existential variable v to \(D(v) \subseteq A\) (the set of universal variables on which v depends; boolean variables have \(D(v) = \emptyset \)).
A satisfying (total) assignment of \(\boldsymbol{F}\) is a map \(\varPhi \) with domain E, where \(\varPhi (v)\) is a boolean function over the variables D(v), such that F after substitution via \(\varPhi \) becomes a tautology (over A), where F is understood as a CNF (a conjunction of clauses, where a clause is a disjunction of literals). A DQCNF \(\boldsymbol{F}\) is satisfiable if it has a satisfying assignment, otherwise \(\boldsymbol{F}\) is unsatisfiable. Two DQCNFs are satisfiability-equivalent if either both are satisfiable or both are unsatisfiable.
2.2 Graphs
We use \(\left( {\begin{array}{c}V\\ 2\end{array}}\right) \) to denote the set of 2-element subsets of a set V. A graph is a pair (V, E), with V the (finite) vertex-set, and \(E \subseteq \left( {\begin{array}{c}V\\ 2\end{array}}\right) \) the edge-set (undirected, no parallel edges or (self-)loops). More generally, a multigraph is a pair (V, E), with V as before, while \(E: \left( {\begin{array}{c}V\\ 2\end{array}}\right) \rightarrow \mathbb {N}_0\) maps every potential edge to its multiplicity (a natural number \(\ge 0\)). An ordinary graph is converted into a multigraph by using the characteristic function of the edge-set. In the other direction, the underlying graph of a multigraph (V, E) has the edge \(\{ v,w \}\) iff \(E(\{ v,w \}) \ge 1\). We use V(G) for the vertex-set of a (multi)graph G, and E(G) for the edge-set of a graph G resp. for the edge-function of a multigraph G. An independent set \(I \subseteq V(G)\) of a (multi)graph G has no edge \(e \in E(G)\) with \(e \subseteq I\) (resp. \(E(G)(e) \subseteq I\)). For the number of vertices we use \(|V(G) | \in \mathbb {N}_0\), while for the number of edges we use \(|E(G) | \in \mathbb {N}_0\), which for a multigraph G is defined as \(|E(G) | := \sum _{e \in \left( {\begin{array}{c}V(G)\\ 2\end{array}}\right) } E(G)(e)\), that is, as the sum of edge-multiplicities. \(K_n\) is the complete graph with \(n \in \mathbb {N}_0\) vertices, that is, \(V(K_n) = \{ 1, \dots , n \}\) and \(E(G) = \left( {\begin{array}{c}V(G)\\ 2\end{array}}\right) \) (thus \(|E(K_n) | = \frac{1}{2} n (n-1)\)).
Definition 1
Consider a labelled clause-set (L, F). The conflict multigraph \({{\,\textrm{cmg}\,}}(F)\) is the multigraph with vertex-set L, where the multiplicity of an edge \(\{ a,b \}\) (for labels \(a, b \in L\)) is \(|F(a) \cap \overline{F(b)} |\), that is, the number of clashing literals between the clauses of a and b. The conflict graph \({{\,\textrm{cg}\,}}(F)\) is the underlying graph of \({{\,\textrm{cmg}\,}}(F)\). A labelled clause-set (L, F) precisely-realises a multigraph G, if \({{\,\textrm{cmg}\,}}(L,F) = G\), and realises a graph G, if \({{\,\textrm{cg}\,}}(L,F) = G\).
We write “precisely-realise” instead of “precisely realise” to avoid grammatical ambiguity (as in “that precisely realises what I want”).
A biclique in a multigraph G is a pair (A, B) of disjoint vertex sets \(A, B \subseteq V(G)\), such that all \(a \in A\) are adjacent with all \(b \in B\). The corresponding characteristic function maps exactly the edges \(\{ a,b \}\) to 1 (all other edges to zero). A biclique partition of G is a family \(((A_i,B_i))_{i \in I}\) of bicliques in G, such that the sum of characteristic functions equals the edge-function of G, while for a biclique cover of G that sum needs to be equal zero exactly for the non-edges. For graphs G a biclique represents the corresponding set of edges of G, and a biclique partition yields a partitioning of the edge-set, while a biclique cover has as its union the edge-set. For (multi)graphs G by \(\mathbf {{{\,\textrm{bcp}\,}}(G)} \in \mathbb {N}_0\) resp. \(\mathbf {{{\,\textrm{bcc}\,}}(G)} \in \mathbb {N}_0\) the minimum number of bicliques in a biclique partition resp. cover of G is denoted. For an overview on the complexity of computing \({{\,\textrm{bcp}\,}}(G)\) and \({{\,\textrm{bcc}\,}}(G)\) see [4, 7, 9]. That boolean clause-sets yield a natural environment for biclique partitions (and covers) was apparently first realised in [18]:
Lemma 1
For a multigraph G the biclique partitions resp. biclique covers correspond, up to handling of degenerations, to precise-realisation resp. realisations of G by labelled clause-sets (Definition 1), with the bicliques corresponding to the variables and their positive and negative occurrences. \({{\,\textrm{bcp}\,}}(G)\) is the minimal number of variables in a precise-realisation of G, while \({{\,\textrm{bcc}\,}}(G)\) is the minimal number of variables in a realisation of G.
We are mostly interested in (imprecise-)realisations, since we are interested in using realisations F with as few variables as possible (i.e., minimising n(F), which is equivalent to maximising \(\delta (F)\)). However also precise-realisations can be of interest, since they are smaller in regards to the number of literal occurrences.
With the example from Subsection 1.1 we have already seen two different realisations of the triangle \(K_3\) (thus using the label-set \(\{ 1,2,3 \}\)), namely first using three variables in \(\big \{ \, 1\mapsto \{ x_2, x_3 \}, 2\mapsto \{ x_1, \overline{x_2} \}, 3\mapsto \{ \overline{x_1}, \overline{x_2}, \overline{x_3} \} \, \big \}\), corresponding to the biclique cover by the three bicliques \((\{ 2 \},\{ 3 \}), (\{ 1 \},\{ 2,3 \}), (\{ 1 \},\{ 3 \})\), and second using two variables in \(\big \{ \, 1\mapsto \{ x_1 \}, 2\mapsto \{ \overline{x_1}, x_2 \}, 3\mapsto \{ \overline{x_1}, \overline{x_2} \} \, \big \}\), corresponding to the biclique cover by the two bicliques \((\{ 1 \},\{ 2,3 \}), (\{ 2 \},\{ 3 \})\). The latter is a precise-realisation (the cover is a partition).
3 The global conflict graph
We now study the simplest type of universal variables of a DQCNF, called “global variables”, which are the variables every existential variable depends on. In the final result, Corollary 2, we will see that concerning satisfiability (at all), all what matters about global variables is the clashes they create between the clauses.
Definition 2
A global variable of a DQCNF \(\boldsymbol{F} = (A,E,F,D)\) is a universal variable, such that every existential variable depends on it. We denote the set of all global variables by \({{\,\textrm{gvar}\,}}(\boldsymbol{F}) := \{ v \in A : \forall \, w \in E : v \in D(w) \}\).
We note that the notion of a global variable does not depend on the clauses. A DQCNF might not have any global variable. For a 2QCNF the global variables are all the universal variables, i.e., \({{\,\textrm{gvar}\,}}(A,E,F,D) = A\) (that is indeed the definition of 2QCNF). In order to access the clause-parts with global literals, we consider a DQCNF as “sliced up” by their variable-sets, for example for a QCNF \(\exists X \forall Y \exists Z : F\) we have three natural slices, for X, Y, Z.
Definition 3
For a DQCNF \(\boldsymbol{F} = (A,E,F,D)\) and some set \(V \subseteq A \cup E\) of variables, the V -slice is the labelled clause-set \((F, F_V)\) (using the clauses of F as labels), such that the clause of label \(C \in F\) is \(F_V(C) := C[V] := \{ x \in C : {{\,\textrm{var}\,}}(x) \in V \}\). The global slice of \(\boldsymbol{F}\) is the \({{\,\textrm{gvar}\,}}(\boldsymbol{F})\)-slice, denoted by \(\mathbf {{{\,\textrm{gsl}\,}}(\boldsymbol{F})}\).
Combining Definition 1, 2, and 3, we obtain the “global conflict graph” as the conflict graph of the global slice:
Definition 4
For a DQCNF \(\boldsymbol{F} = (A,E,F,D)\) the global conflict graph resp. multigraph is \(\mathbf {{{\,\textrm{gcg}\,}}(\boldsymbol{F})} := {{\,\textrm{cg}\,}}({{\,\textrm{gsl}\,}}(\boldsymbol{F}))\) resp. \(\mathbf {{{\,\textrm{gcmg}\,}}(\boldsymbol{F})} := {{\,\textrm{cmg}\,}}({{\,\textrm{gsl}\,}}(\boldsymbol{F}))\).
The vertices of the global conflict (multi)graph are the clauses, with the edges corresponding to clashes between literals over global variables. Note that the realisations of the global conflict graph are the same as the realisations of the global conflict multigraph (for realisations, multiplicities of edges are irrelevant).
We need the ability to remove the global variables (obtaining another DQCNF), for which we introduce the following notation:
Definition 5
For a DQCNF \(\boldsymbol{F} = (A,E,F,D)\) let \(V := {{\,\textrm{gvar}\,}}(\boldsymbol{F})\) be the set of global variables, while \(V' := (A \cup E) \setminus V\) is the set of other variables. We define
with “m” for “minus”, which is the DQCNF obtained by removing the global variables from its universal variables (removing all literals with underlying global variable). Here \(C - V := C[V']\) (removing all literals with variables from V).
The semantic contribution of global variables is captured by the global-clash-free sub-clause-sets and their related sub-DQCNFs:
Definition 6
Consider a DQCNF \(\boldsymbol{F} = (A,E,F,D)\). A globally-independent sub-clause-set of \(\boldsymbol{F}\) is a clause-set \(F' \subseteq F\) which is an independent subset of \({{\,\textrm{gcg}\,}}(F)\) (that is, the global variables of F are all pure variables, appearing only in one sign, in \(F'\)). A globally-independent sub-DQCNF is some \({{\,\textrm{mgvar}\,}}(A,E,F',D)\) for some globally-independent sub-clause-set \(F'\). Speaking of maximal globally-independent, we restrict the \(F' \subseteq F\) to maximal independent subsets of \({{\,\textrm{gcg}\,}}(F)\). The set of all maximally globally-independent sub-DQCNFs is denoted by \({{\,\textrm{gind}\,}}(\boldsymbol{F})\), and two DQCNF’s \(\boldsymbol{F}, \boldsymbol{F}'\) are called gind-equivalent if \({{\,\textrm{gind}\,}}(\boldsymbol{F}) = {{\,\textrm{gind}\,}}(\boldsymbol{F}')\).
We note that two gind-equivalent DQCNFs have the same existential variables, and that gind-equivalence is indeed an equivalence relation. We now come in Theorem 1 to the basic observation about the role played by global literals (literals whose underlying variables are global). Most basic is the insight that global variables are exactly the variables which always allow reducing the problem by substituting all possible truth values, which we illustrate by a simple example:
Example 1
Let \(A := \{ a \}\), \(E := \{ x \}\), \(F := \{ \{ a, \overline{x} \}, \{ \overline{a}, x \} \}\), \(D_1 := (x \mapsto A)\), \(D_2 := (x \mapsto \emptyset )\), and finally \(\boldsymbol{F}_i := (A,E,F,D_i)\) for \(i =1,2\). Less formally, we have two QCNFs: \(\boldsymbol{F}_1 \triangleq \forall a \exists x : F\) and \(\boldsymbol{F}_2 \triangleq \exists x \forall a : F\), where \(F \triangleq a \leftrightarrow x\). Obviously \(\boldsymbol{F}_1\) is satisfiable, with the unique solution \(x \triangleq a\), while \(\boldsymbol{F}_2\) is unsatisfiable.
We have \({{\,\textrm{gvar}\,}}(\boldsymbol{F}_1) = \{ a \}\), while \({{\,\textrm{gvar}\,}}(\boldsymbol{F}_2) = \emptyset \). Substituting \(a \mapsto 0\) into \(\boldsymbol{F}_1\) or \(\boldsymbol{F}_2\) yields in both cases the DQCNF \(\boldsymbol{G}_0 = \exists x : \lnot x\), while \(a \mapsto 1\) yields \(\boldsymbol{G}_1 = \exists x : x\). \(\boldsymbol{G}_\varepsilon \) has the unique solution \(x \triangleq \varepsilon \) for \(\varepsilon \in \{ 0,1 \}\). For \(\boldsymbol{F}_1\) we are then able to get a solution for x, since x depends on a, and thus we can select the appropriate solution from \(\boldsymbol{G}_\varepsilon \), depending on the value \(\varepsilon \). While x does not depend on a in \(\boldsymbol{F}_2\), and thus we could only lift the solutions from \(\boldsymbol{G}_{0,1}\) to \(\boldsymbol{F}_2\) if they would be the same in both cases.
The vertices of the global conflict graphs of \(\boldsymbol{F}_1, \boldsymbol{F}_2\) are the two clauses, which in \(\boldsymbol{F}_1\) are connected by an edge, while in \(\boldsymbol{F}_2\) they are isolated. So \({{\,\textrm{gind}\,}}(\boldsymbol{F}_1) \triangleq \{ \exists x : \lnot x, \exists x : x \}\), while \({{\,\textrm{gind}\,}}(\boldsymbol{F}_2) = \{ \boldsymbol{F}_2 \}\).
Theorem 1
A DQCNF \(\boldsymbol{F} = (A,E,F,D)\) is unsatisfiable iff there is some unsatisfiable maximal globally-independent sub-DQCNF of \(\boldsymbol{F}\).
Proof
We show the equivalent statement: \(\boldsymbol{F}\) is satisfiable iff all maximal globally-independent sub-DQCNFs are satisfiable.
Let \(V := {{\,\textrm{gvar}\,}}(\boldsymbol{F})\). \(\boldsymbol{F}\) is satisfiable iff for all boolean total assignments \(\varphi : V \rightarrow \{ 0,1 \}\), after substitution of \(\varphi \) into \(\boldsymbol{F}\), the resulting DQCNF \(\varphi * \boldsymbol{F} := (A \setminus V, E, \varphi * F, (D(v) \setminus V)_{v \in E})\) is satisfiable, where \(\varphi * F\) is the usual application of a partial assignment to a clause-set (removing all satisfied clauses, and removing the falsified literals from the remaining clauses): The direction from left to right holds for all partial assignments to universal variables, while the direction from right to left uses that the variables in V are global, and thus the boolean functions used in a satisfying assignment of a DQCNF can be made dependent on them. Now the clauses of \(\varphi * F\) come from an independent subset of \({{\,\textrm{gcg}\,}}(\boldsymbol{F})\), since an edge, that is a clash, would cause one of the two clauses involved to be satisfied. And for every maximal independent subset \(F'\) we can find \(\varphi : V \rightarrow \{ 0,1 \}\) satisfying exactly all clauses in \(F \setminus F'\), by setting all global literals occurring in \(F'\) to 1. Thus the maximal independent \(F' \subseteq F\) cover exactly the relevant (maximal) cases of \(\varphi * \boldsymbol{F}\), which shows the assertion. \(\square \)
Thus \(\boldsymbol{F}\) is unsatisfiable iff \({{\,\textrm{gind}\,}}(\boldsymbol{F})\) contains an unsatisfiable element:
Corollary 1
Gind-equivalence implies sat-equivalence, that is, if for DQCNF \(\boldsymbol{F}, \boldsymbol{F}'\) holds \({{\,\textrm{gind}\,}}(\boldsymbol{F}) = {{\,\textrm{gind}\,}}(\boldsymbol{F}')\), then \(\boldsymbol{F}\) is satisfiable iff \(\boldsymbol{F}'\) is satisfiable.
A sufficient condition for \(\boldsymbol{F}, \boldsymbol{F}'\) being gind-equivalent is that \(\boldsymbol{F}'\) is obtained from \(\boldsymbol{F}\) by replacing the global slice in such a way that the global conflict graph is maintained. The precise concept is captured by “global-conflict-graph-equivalence”:
Definition 7
Two DQCNFs \(\boldsymbol{F} = (A,E,F,D)\), \(\boldsymbol{F}' = (A',E',F',D')\) are gcg-equivalent if the following conditions hold:
-
1.
\({{\,\textrm{mgvar}\,}}(\boldsymbol{F}) = {{\,\textrm{mgvar}\,}}(\boldsymbol{F}')\).
-
2.
There is a bijection \(\sigma : F \rightarrow F'\), which is an isomorphism from \({{\,\textrm{gcg}\,}}(\boldsymbol{F})\) to \({{\,\textrm{gcg}\,}}(\boldsymbol{F}')\), such that for all \(C \in F\) we have \(C - {{\,\textrm{gvar}\,}}(\boldsymbol{F}) = \sigma (C) - {{\,\textrm{gvar}\,}}(\boldsymbol{F}')\).
The first condition of Definition 7 says that after removal of the global variables, we have exactly the same DQCNFs, while the second condition says that the global literals inserted into the clauses of \({{\,\textrm{mgvar}\,}}(\boldsymbol{F}) = {{\,\textrm{mgvar}\,}}(\boldsymbol{F}')\) yield exactly the same conflict-pattern (and thus the same independent subsets).
Corollary 2
Gcg-equivalence implies gind-equivalence. Thus two gcg-equivalent DQCNFs are sat-equivalent.
In the following Section 4 we will consider the problem of constructing gcg-equivalences. This is just a study of graphs G and their (CNF-)realisations, since all what matters here is the global slice of a DQCNF, which is just a boolean CNF. Furthermore we only need to consider connected graphs, since every connected component of G can be handled separately.
4 Realisations
We now introduce the three most basic classes of realisations of multigraphs:
-
1.
In Subsection 4.1 we consider clause-sets, where all clauses contain the same variables (“full clause-sets”). These realisations realise exactly complete graphs (all vertices connected to each other), and they contain the optimum realisation (always w.r.t. the number of variables), which we call log-realisations (of complete graphs).
-
2.
In Subsection 4.2 we consider realisations, which as biclique-partitions/covers only contain bicliques which are single edges. In this way every multigraph is (trivially) precisely-realised, and we speak of trivial realisations.
-
3.
In Subsection 4.3 we consider more generally realisations, which correspond to biclique-partitions/covers containing only claws (connecting one vertex with many). Here we get better bounds, and it is known that every connected graph with m vertices allows such a precise-realisations with \(m-1\) variables. Looking closer, one sees that these realisations actually encode unit-clause propagation, and thus the underlying class of clause-sets is the class of minimally unsatisfiable Horn clause-sets (which are special cases of MUs of deficiency 1). We call these realisations HMU-realisations.
These three representation-classes are based on three classes of clause-sets:
Definition 8
For a clause-set F we introduce the following special cases of variables \(v \in {{\,\textrm{var}\,}}(F)\):
-
1.
v is full if every clause contains v (positively or negatively);
-
2.
v is 1-singular if it occurs in both signs exactly once;
-
3.
v is singular if it occurs in both signs, and in one sign exactly once.
A clause-set having only full resp. 1-singular resp. singular variables is a full resp. totally 1-singular resp. totally singular clause-set.
4.1 Full clause-sets
Any full clause-set F realises the complete graph \(K_{c(F)}\) with c(F) many vertices. Indeed the realisations of the complete graphs are exactly the hitting clause-sets (any two clauses clash; as DNFs also known as orthogonal or disjoint DNFs), and we will see in Corollary 5 another class of hitting clause-sets. For a complete graph \(K_m\) with \(m \in \mathbb {N}\) vertices, it is well-known ([8]) that \({{\,\textrm{bcc}\,}}(K_m) = \lceil \lg (m) \rceil \), where \(\lg (m)\) is the binary logarithm of m. Such optimal realisations F are obtained from the canonical (full) clause-set with \(n := \lceil \lg (m) \rceil \) many variables and \(2^n\) clauses by selecting any m clauses.
In contrast to this we have the Theorem of Graham-Pollak ([15]), which states \({{\,\textrm{bcp}\,}}(K_m) = m-1\). Thus there exists a precise-realisation of \(K_m\) with deficiency 1 (which is optimal among precise-realisations), and in the already mentioned Corollary 5 we will see an example for that (the simplest example). More generally, in Subsection 4.2 we will indeed see that every nonempty connected graph has a minimally unsatisfiable precise-realisation F with \(\delta (F) = 1\). We note that the above optimal logarithmic realisations by full clause-sets are minimally unsatisfiable iff m is a power of two (otherwise they are satisfiable); this could be repaired by removal of literal occurrences for the non-powers of two, but we have to leave this refinement to future work, and in this paper we only consider the cases \(m = 2^n\).
4.2 Totally 1-singular clause-sets
Obviously, every multigraph G can be precisely-realised by a totally 1-singular clause-set F with \(n(F) = |E(G) |\). For a connected G, these precise-realisations are minimally unsatisfiable iff G is a tree; these are exactly the marginal minimally unsatisfiable clause-sets of deficiency 1 (see Corollary 6). Otherwise they are satisfiable.
4.3 Totally singular MUs
It is well-known that every connected graph G with \(m := |E(G) | \ge 1\) vertices has a claw-decomposition with \(m-1\) claws, and thus \({{\,\textrm{bcp}\,}}(G) \le m-1\). Here a “claw” is a special biclique, with one side having exactly one vertex. The proof uses a elimination-sequence \(v_1, \dots , v_{m-1}\) of G, which removes one vertex after the other (including incident edges) such that always a (nonempty) connected graph is maintained. That is, \(G_0 := G\), while \(G_i := G_{i-1} - v_i\) for \(i = 0, \dots , m-1\): the defining property of “elimination-sequence” is that each \(G_i\) is connected (and nonempty — eliminating the last vertex would yield a superfluous claw, with one side being empty). Here for a graph G and a vertex \(v \in V(G)\) we define \(G - v := (V(G) \setminus \{ v \}, \{ e \in E(G) : v \notin e \})\).
The existence of an elimination-sequence, and computing it in linear time in the size of the graph, can be accomplished as follows (this is well-known, see e.g. [6, Proposition 1.4.1], but for completeness we discuss it here):
-
(a)
an elimination-sequence for a spanning tree of G (which can be computed in linear time) is an elimination-sequence for G;
-
(b)
an elimination-sequence for a tree is a sequence removing one leaf after the other (these are the vertices of degree 1, that is, having exactly one neighbour); by a procedure similar to unit-clause propagation this can be accomplished in linear time as well.
A claw in a biclique-partition is a singular variable in the corresponding realisation. Thus we obtain that G has a totally singular realisation F with \(m-1\) variables (and m clauses, thus of deficiency 1). Now indeed the F constructed in this way are exactly the minimally unsatisfiable Horn clause-sets, and this correspondence, based on unit-clause propagation, we discuss in this subsection.
It is useful to introduce the following three classes of clause-sets:
-
\(\mathcal{M}\mathcal{U}\) is the class of all minimally unsatisfiable clause-sets, that is, all unsatisfiable clause-sets F such that \(F \setminus \{ C \}\) is satisfiable for all \(C \in F\).
-
\(\mathcal{H}\mathcal{O}\) is the class of all Horn clause-sets, defined by the property that every clause contains at most one positive literal (i.e., all F such that for all \(C \in F\) holds \(|C \cap {{\,\textrm{var}\,}}(C) | \le 1\)).
-
\(\mathcal {HMU}:= \mathcal{H}\mathcal{O}\cap \mathcal{M}\mathcal{U}\) are the minimally unsatisfiable Horn clause-sets.
For a general overview on minimally unsatisfiable formulas see [17], while [5, Corollary 10] seems the first source for the fact that HMUs have deficiency 1.
Lemma 2
The class \(\mathcal {HMU}\) is generated by the following process (each step called a singular positive unit-extension):
-
1.
Start with \(\{ \bot \}\).
-
2.
For some F already created, choose a variable \(v \notin {{\,\textrm{var}\,}}(F)\) and some \(\emptyset \not = F_0 \subseteq F\), and create a new clause-set \(F' := \{ \{ v \} \} \cup (F \setminus F_0) \cup \{ C \cup \{ \overline{v} \} : C \in F_0 \}\) (that is, add the unit-clause \(\{ v \}\), and add the literal \(\overline{v}\) to the clauses of \(F_0\)).
Proof
It is easy to see that all generated clause-sets are elements of \(\mathcal {HMU}\). It remains to show that all \(F \in \mathcal {HMU}\) can be generated; we show this by induction on n(F). For \(n(F) = 0\) we have \(F = \{ \bot \}\), which is the base case of the generation process. So assume \(n(F) > 0\). F must contain a positive unit-clause \(\{ v \}\) (otherwise every clause would contain a negative literal, due to the Horn-property, and then setting all literals to 0 would be a satisfying assignment). Due to F being minimally unsatisfiable, there is no other clause than \(\{ v \}\) containing the positive literal v. Now setting v to 1 produces \(F' \in \mathcal {HMU}\), where we can apply the induction hypothesis to \(F'\), and from \(F'\) by one step of singular positive unit-extension with v we obtain F. \(\square \)
The following four properties of HMUs follow all easily from the generation process of Lemma 2 by induction:
Corollary 3
Clause-sets \(F \in \mathcal {HMU}\) have the following properties:
-
1.
F is totally singular (indeed for every variable the positive literal occurs exactly once).
-
2.
The number n(F) of variables equals the number of singular unit-extensions applied, while \(c(F) = n(F) + 1\). Thus F has deficiency 1 (\(\delta (F) = 1\)).
-
3.
F has exactly one negative clause.
-
4.
The conflict multigraph of F is a graph (at most one conflict between clauses).
So HMUs precisely-realise nonempty connected graphs, and indeed they realise exactly those:
Theorem 2
For every connected nonempty (finite) graph G one can construct in linear time (in the length of G, i.e., in \(|V(G) | + |E(G) |\)) an HMU precisely-realising G.
Proof
For G compute an elimination-sequence \(v_1, \dots , v_{m-1}\) as explained at the beginning of the subsection, and use these vertices as variables for the generation process according to Lemma 2, where \(F_0\) is the set of neighbours. \(\square \)
The novelty of Theorem 2 from the graph-theoretical perspective lies in relating biclique partitions by claws with realisations by HMUs (note that realisation by any totally singular clause-set of deficiency 1 is trivial). The restriction to graphs (without parallel edges) is natural here, since our main interest is in imprecise-realisations (using as few variables as possible). A related result here for precise-realisations of multigraphs is given in [27], where it is shown (in graph-theoretical language), that for every graph G the multigraph \(G'\) with \(V(G) = V(G')\), which has as many edges between vertices as is given by their distance in G, has a precise-realisation F with \(\delta (F) \ge 1\); such an F yields a so-called “addressing” of G.
Corollary 4
For each DQCNF \(\boldsymbol{F}\) there is a gcg-equivalent \(\boldsymbol{F}'\) such that the global slice of \(\boldsymbol{F}'\) is a variable-disjoint union of HMUs.
Recall that a “hitting clause-set” is a clause-set F such that every two (different) clauses clash; full clause-sets are a special case. In other words, hitting clause-sets are exactly the realisations of complete graphs.
Corollary 5
The hitting HMUs are exactly those where for each singular unit-extension step \(F_0 = F\) holds. For every \(n \in \mathbb {N}_0\) there is up to isomorphism exactly one such clause-set, called \(S_n\), with \(n(S_n) = n\).
Corollary 6
The totally 1-singular HMUs are exactly those where for each singular unit-extension step \(|F_0 | = 1\) holds; they precisely-realise exactly all trees.
5 A basic generator
The main target of this first experimental evaluation is the validation or refutation of the Hypothesis SIB: “Small Is Better” — the smaller the number of variables in the realisation, the easier to solve.
First, to generate test-instances, we take the simplest approach for our generator, focusing on generating 2QCNFs. For 2QCNFs, the global variables are all the universal variables (for more information, see Section 3), and thus the universal slice is the same as the global slice. The following is an example of 2QCNF in the standard QDIMACS form, with 6 variables and 4 clauses:

For the presentation, existential literals precede the universal literals, using a separator "|". The existential slice is \(\{ \{ -1, -3, 4 \}, \{ -1, -2, 3 \}, \{ 1,-2, 5 \}, \{ 1, 3, -4 \} \}\), while the universal (global) slice is \(\{ \{ 5 \}, \{ -5 \}, \{ 6 \}, \{ -6 \} \}\). In Section 3 we considered the case of connected graphs. Real world instances have indeed a large number of connected (global) components, and so we are using \(C \in \mathbb {N}\) many components. Altogether the parameters (C, p, n) specify the generated 2QCNF, where \(p \in \mathbb {N}\) is the (binary log of the) number of vertices in a component, and \(n \in \mathbb {N}\) is the total number of existential variables.
For the component-conflict-graph of the universal slice, we use the complete graph with \(m := 2^p\) vertices (clauses), and \(q := \frac{1}{2} m (m - 1)\) edges — this is the simplest case where we have an exponential separation between the optimum realisation and the HMU-realisation. So the total number of generated clauses is \(C \cdot m\). In the above QDIMACS we have \(C=2\) and \(p=1\) (the smallest value to obtain a proper 2QCNF), thus \(q = 1\). For the existential slice we choose a random 3-CNF with n variables and \(C \cdot m\) clauses; note that components of the conflict graph do not play any role here. We use the three realisation from Section 4 (for each component, with m clauses):
-
Trivial: q variables (Subsection 4.2; all clauses have length \(m-1\)).
-
HMU: \(m-1\) variables (\(S_{m-1}\) from Corollary 5; clause-lengths \(1, \dots , m-1\)).
-
Log: a full clause-set with p variables (Subsection 4.1).
Example 2
Below we display a generated 2QCNF for all three realisations, with \((C, p, n) = (2, 2, 4)\). Thus \(m = 2^2 = 4\) clauses per component, making \(2 \cdot 4 = 8\) clauses in total. The existential slice is a uniform random 3-CNF with 4 variables and 8 clauses. For each component, the trivial realisation uses \(q = \frac{1}{2} \cdot 4 \cdot 3 = 6\) variables, HMU uses 3 variables, and log uses 2 variables. Leftmost is the trivial realisation, then the HMU realisation, and finally the logarithmic realisation:

6 Experimental results
We use two top-performing 2QCNF solvers, DepQBF [20] and CADET [23], based on the QBFEVAL 2020 competition results [22]. In order to avoid the known high variability on satisfiable instances, for this first experimental evaluation we only considered unsatisfiable instances (throwing away satisfiable instances). Recall that we use parameter values (C, p, n) according to Section 5. For each parameter value, we generated 1000 instances and report the results only on the unsatisfiable instances. In general we tried to select values such that the created benchmarks are of medium hardness, around at most one hour, considering all three realisations (trivial, HMU, logarithmic). Now it turned out that the trivial realisation caused mostly very hard instances, and so our selection process focuses on HMU and logarithmic realisations. We found in general Hypothesis SIB (“small is better”) well validated: On all parameters considered, both solvers solved more instances with the logarithmic realisation and had a better average runtime than with the HMU-realisation. All the experiments were conducted on Intel(R) Xeon(R) E5-2620 v4 @ 2.10GHz CPUs with a time limit of \(3600\mathrm s\) and memory limit of 8 GB per instance. Memory usage for instance generation and solving processes of generated benchmarks was minimal (\(< 1\) GB). The summary of the results is as follows, using rounded runtimes:

The solver column labelled with “D” refers to DepQBF, while “C” is CADET. The mean and median consider only instances solved by the corresponding solver. For example for Row 1D, the HMU-mean 280 as well as the HMU-median 82 relates only to the runtimes on the 978 HMU-instances solved by DepQBF.
The table shows that the Hypothesis SIB is mostly validated for the \(2 \cdot 6 = 12\) rows (only comparing HMU and log now). First there are 6 fully conforming rows, namely 1DC, 2D, 3D, 5D, and 6C, where more instances were solved for the log-realisation, and this also with better mean and median times. Then there are 4 mostly conforming rows 2C, 3C, 4D, and 5C, where we have also clearly more solved log-realisations, while mean or median could be better for HMU, but only for a small number of instances. This leaves two exceptional rows: 4C and 6D. We need to leave 4C for more extensive experimentation: these instances were very hard for CADET, and the number of solved instances is too small for a statistical analysis. For the 6D instances with \((C,p,n) = (14,4,11)\), the median solving time for the HMU realisation is better (\(92 \mathrm s\) versus \(172 \mathrm s\)), and it solves nearly as many instances as the logarithmic realisation. However, the average solving time for the HMU realisation is worse than for the logarithmic realisation (\(301 \mathrm s\) versus \(294 \mathrm s\); timeouts are not included in these averages). This warrants further investigation, and the density plot (the second plot shows times \(\le 1000 \mathrm s\) only) can provide additional insight:
The mean values shown in the plots now include the \(3600 \mathrm s\) timeout, which for HMU increases the mean to \(397 \mathrm s\). The second plot, which shows times \(\le 1000 \mathrm s\), reveals that the HMU realisation solves several instances faster than the logarithmic realisation, but its performance deteriorates over time, with fewer and fewer instances solved. The first plot, which shows the overall picture, shows a spike for the HMU realisation at times \(\le 3600 \mathrm s\) at the tail end, indicating that 29 instances timed out (while the logarithmic realisation solved all instances). When the timeout is increased from \(3600 \mathrm s\) to \(18000 \mathrm s\), the mean of the HMU realisation increases to \(445 \mathrm s\).
On these instances we could devise a portfolio strategy in which both HMU and logarithmic realisation instances run in parallel, while aborting HMU realisation relatively quickly — in this way one could achieve a faster average solving time overall. While this parameter triple is interesting, more investigation is required to understand the precise causes of this behaviour.
7 Conclusion and Outlook
We have introduced the global conflict graph of DQCNFs, which represents the clashes (conflicts) between global literals; for 2QCNFs the global literals are just the universal literals. We have shown that the corresponding global slice can be replaced by anything else which just reproduces the conflict graph. We then switched to investigating (CNF-)realisations of arbitrary graphs, concentrating on the three most basic classes, given by full clause-sets (complete graphs only), by variables occurring only twice, and by HMUs (Horn minimally unsatisfiable clause-sets). For the latter we showed that they can realise everything, and thus yield the upper bound \(m-k\) on the number of global variables needed for any DQCNF with m clauses and k connected components of the conflict graph; such a transformation can be computed in linear time. We created then families of 2QCNF instances, with a relatively small number of connected components, and consisting of small complete graphs; together with any of the three basic realisations (full-log, trivial, HMU) this creates the universal slice, while the existential slice is given by a random 3-CNF. We investigated whether indeed in this setting fewer universal variables mean easier solving, and found that in general well supported. There are many future avenues for research and practice:
-
1.
In a forthcoming paper we investigate the global conflict graph of real-world instances — when and how we can simplify the global slice (using several metrics), and what effect this has on solving time (for satisfiable and unsatisfiable instances). For the minimisation of the number of variables, naturally SAT-solving is employed.
-
2.
The instances created for this first experimental evaluation can be generalised by a general DQCNF generator, which takes as input-parameters (a) graph families for the global conflict graphs, (b) realisation strategies to produce the global slice, and (c) some generator to create the DQCNF minus the global slice.
-
3.
Especially interesting should be classes where an exponential separation between the best and an HMU-realisation exists. We have seen the example of complete graphs; a more complex class are the grid graphs ([16]).
Of course, insights into the behaviour of solvers is an important goal here.
On the theory side, a fundamental question here is to investigate which restricted classes of global conflict graphs still yield completeness for the respective complexity classes. Finally it seems natural to conjecture that allowing arbitrary transformations of the global slice can have a huge influence on various complexity issues, like proof-length in various calculi, and the complexities of strategy extraction.
References
Valeriy Balabanov, Jie-Hong Roland Jiang, Christoph Scholl, Alan Mishchenko, and Robert K. Brayton. 2QBF: Challenges and solutions. In Nadia Creignou and Daniel Le Berre, editors, Theory and Applications of Satisfiability Testing - SAT 2016 - 19th International Conference, Bordeaux, France, July 5-8, 2016, Proceedings, volume 9710 of Lecture Notes in Computer Science, pages 453–469. Springer, 2016. URL: https://doi.org/10.1007/978-3-319-40970-2_28, https://doi.org/10.1007/978-3-319-40970-2_28.
Olaf Beyersdorff, Mikolás Janota, Florian Lonsing, and Martina Seidl. Quantified Boolean Formulas. In Armin Biere, Marijn Heule, Hans van Maaren, and Toby Walsh, editors, Handbook of Satisfiability - Second Edition, volume 336 of Frontiers in Artificial Intelligence and Applications, pages 1177–1221. IOS Press, 2021. https://doi.org/10.3233/FAIA201015.
Joshua Blinkhorn, Tomás Peitl, and Friedrich Slivovsky. Davis and Putnam meet Henkin: Solving DQBF with resolution. In Chu-Min Li and Felip Manyà, editors, Theory and Applications of Satisfiability Testing - SAT 2021 - 24th International Conference, Barcelona, Spain, July 5-9, 2021, Proceedings, volume 12831 of Lecture Notes in Computer Science, pages 30–46. Springer, 2021. https://doi.org/10.1007/978-3-030-80223-3_4.
Sunil Chandran, Davis Issac, and Andreas Karrenbauer. On the Parameterized Complexity of Biclique Cover and Partition. In Jiong Guo and Danny Hermelin, editors, 11th International Symposium on Parameterized and Exact Computation (IPEC 2016), volume 63 of Leibniz International Proceedings in Informatics (LIPIcs), pages 11:1–11:13. Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2017. https://doi.org/10.4230/LIPIcs.IPEC.2016.11.
Gennady Davydov, Inna Davydova, and Hans Kleine Büning. An efficient algorithm for the minimal unsatisfiability problem for a subclass of CNF. Annals of Mathematics and Artificial Intelligence, 23(3-4):229–245, 1998. https://doi.org/10.1023/A:1018924526592.
Reinhard Diestel. Graph Theory, volume 173 of Graduate Texts in Mathematics. Springer, New York, second edition, 2000. ISBN 0-387-98976-5. URL: http://www.esi2.us.es/~mbilbao/pdffiles/DiestelGT.pdf.
Alessandro Epasto and Eli Upfal. Efficient approximation for restricted biclique cover problems. Algorithms, 11(6):84, June 2018. https://doi.org/10.3390/a11060084.
Peter C. Fishburn and Peter L. Hammer. Bipartite dimensions and bipartite degrees of graphs. Discrete Mathematics, 160(1):127–148, 1996. https://doi.org/10.1016/0012-365X(95)00154-O.
Herbert Fleischner, Egbert Mujuni, Daniël Paulusma, and Stefan Szeider. Covering graphs with few complete bipartite subgraphs. Theoretical Computer Science, 410:2045–2053, 2009. https://doi.org/10.1016/j.tcs.2008.12.059.
Nicola Galesi and Oliver Kullmann. Polynomial time SAT decision, hypergraph transversals and the hermitian rank. In Holger H. Hoos and David G. Mitchell, editors, Theory and Applications of Satisfiability Testing 2004, volume 3542 of Lecture Notes in Computer Science, pages 89–104, Berlin, 2005. Springer. https://doi.org/10.1007/11527695_8.
Michael R. Garey and David S. Johnson. Computers and Intractability / A Guide to the Theory of NP-Completeness. W.H. Freeman and Company, 1979.
Aile Ge-Ernst, Christoph Scholl, and Ralf Wimmer. Localizing quantifiers for DQBF. In Clark W. Barrett and Jin Yang, editors, 2019 Formal Methods in Computer Aided Design, FMCAD 2019, San Jose, CA, USA, October 22-25, 2019, pages 184–192. IEEE, 2019. https://doi.org/10.23919/FMCAD.2019.8894269.
Karina Gitina, Ralf Wimmer, Sven Reimer, Matthias Sauer, Christoph Scholl, and Bernd Becker. Solving DQBF through quantifier elimination. In Wolfgang Nebel and David Atienza, editors, Proceedings of the 2015 Design, Automation & Test in Europe Conference & Exhibition, DATE 2015, Grenoble, France, March 9-13, 2015, pages 1617–1622. ACM, 2015. URL: http://dl.acm.org/citation.cfm?id=2757188.
Enrico Giunchiglia, Paolo Marin, and Massimo Narizzano. Reasoning with Quantified Boolean Formulas. In Armin Biere, Marijn Heule, Hans van Maaren, and Toby Walsh, editors, Handbook of Satisfiability - Second Edition, volume 336 of Frontiers in Artificial Intelligence and Applications, pages 1157–1176. IOS Press, 2021. https://doi.org/10.3233/FAIA201014.
Ronald L. Graham and H.O. Pollak. On the addressing problem for loop switching. Bell System Technical Journal, 50(8):2495–2519, 1971. https://doi.org/10.1002/j.1538-7305.1971.tb02618.x.
Krystal Guo, Tony Huynh, and Marco Macchia. The biclique covering number of grids. The Electronic Journal of Combinatorics, 26(4):P4.27, 2019. URL:https://www.combinatorics.org/ojs/index.php/eljc/article/view/v26i4p27/pdf.
Hans Kleine Büning and Oliver Kullmann. Minimal unsatisfiability and autarkies. In Armin Biere, Marijn J.H. Heule, Hans van Maaren, and Toby Walsh, editors, Handbook of Satisfiability, volume 185 of Frontiers in Artificial Intelligence and Applications, chapter 11, pages 339–401. IOS Press, February 2009. https://doi.org/10.3233/978-1-58603-929-5-339.
Oliver Kullmann. The combinatorics of conflicts between clauses. In Enrico Giunchiglia and Armando Tacchella, editors, Theory and Applications of Satisfiability Testing 2003, volume 2919 of Lecture Notes in Computer Science, pages 426–440, Berlin, 2004. Springer. https://doi.org/10.1007/978-3-540-24605-3_32.
Oliver Kullmann and Ankit Shukla. TransformingQBFusingBicliqueCovers_Tacas2022, January 2023. GitHub repository. URL: https://github.com/OKullmann/TransformingQBFusingBicliqueCovers_Tacas2022.
Florian Lonsing and Uwe Egly. Depqbf 6.0: A search-based QBF solver beyond traditional QCDCL. In Leonardo de Moura, editor, Automated Deduction - CADE 26 - 26th International Conference on Automated Deduction, Gothenburg, Sweden, August 6-11, 2017, Proceedings, volume 10395 of Lecture Notes in Computer Science, pages 371–384. Springer, 2017. https://doi.org/10.1007/978-3-319-63046-5_23.
Luca Pulina and Martina Seidl. The 2016 and 2017 QBF solvers evaluations (qbfeval’16 and qbfeval’17). Artif. Intell., 274:224–248, 2019. https://doi.org/10.1016/j.artint.2019.04.002.
Luca Pulina, Martina Seidl, and Ankit Shukla. QBFeval’18–competitive evaluation of QBF solvers, 2018.
Markus N. Rabe and Sanjit A. Seshia. Incremental determinization. In Nadia Creignou and Daniel Le Berre, editors, Theory and Applications of Satisfiability Testing - SAT 2016 - 19th International Conference, Bordeaux, France, July 5-8, 2016, Proceedings, volume 9710 of Lecture Notes in Computer Science, pages 375–392. Springer, 2016. https://doi.org/10.1007/978-3-319-40970-2_23.
Markus N. Rabe, Leander Tentrup, Cameron Rasmussen, and Sanjit A. Seshia. Understanding and extending incremental determinization for 2QBF.In Hana Chockler and Georg Weissenbacher, editors, Computer Aided Verification - 30th International Conference, CAV 2018, Held as Part of the Federated Logic Conference, FloC 2018, Oxford, UK, July 14-17, 2018, Proceedings, Part II, volume 10982 of Lecture Notes in Computer Science, pages 256–274. Springer, 2018.https://doi.org/10.1007/978-3-319-96142-2_17.
Ankit Shukla, Armin Biere, Luca Pulina, and Martina Seidl. A survey on applications of Quantified boolean formulas. In 31st IEEE International Conference on Tools with Artificial Intelligence, ICTAI 2019, Portland, OR, USA, November 4-6, 2019, pages 78–84. IEEE, 2019. https://doi.org/10.1109/ICTAI.2019.00020.
Leander Tentrup and Markus N. Rabe. Clausal abstraction for DQBF. In Mikolás Janota and Inês Lynce, editors, Theory and Applications of Satisfiability Testing - SAT 2019 - 22nd International Conference, SAT 2019, Lisbon, Portugal, July 9-12, 2019, Proceedings, volume 11628 of Lecture Notes in Computer Science, pages 388–405. Springer, 2019. https://doi.org/10.1007/978-3-030-24258-9_27.
Peter M. Winkler. Proof of the squashed cube conjecture. Combinatorica, 3(1):135–139, 1983. https://doi.org/10.1007/BF02579350.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Kullmann, O., Shukla, A. (2023). Transforming Quantified Boolean Formulas Using Biclique Covers. In: Sankaranarayanan, S., Sharygina, N. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2023. Lecture Notes in Computer Science, vol 13994. Springer, Cham. https://doi.org/10.1007/978-3-031-30820-8_23
Download citation
DOI: https://doi.org/10.1007/978-3-031-30820-8_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30819-2
Online ISBN: 978-3-031-30820-8
eBook Packages: Computer ScienceComputer Science (R0)