Keywords

figure a
figure b

1 Introduction

Formal property verification (FPV) plays an essential role in hardware verification. Symbolic simulation is one of the model checking techniques used for FPV. It explores all paths of the design circuit simultaneously with symbolic values to work around the state explosion problem [6].

In this paper, we present WASIM, a word-level abstract symbolic simulation framework with customizable abstraction/refinement functions. In the practice of hardware formal verification, we consider the guidance from human verification engineers as the key to scaling formal techniques up for industrial-size designs. Therefore, in WASIM, we emphasize easy user-interaction that allows engineers to freely control the simulation process and plug-in their own design-specific abstraction functions. WASIM can also ensure its trustworthiness through a certificate (an inductive invariant) constructed from the traces of symbolic simulation.

Fig. 1.
figure 1

Workflow of WASIM

Full size image

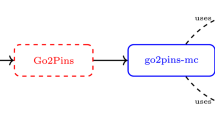
Figure 1 demonstrates the workflow of WASIM. We highlight some of its features below:

  1. 1.

    WASIM has a full support for synthesizable Verilog through the integration with Yosys [17].

  2. 2.

    WASIM provides a set of Python API for rich user interactions.

  3. 3.

    WASIM performs symbolic simulation at the word level. It supports customizable abstraction refinement functions and has built-in state simplification functions to scale up for larger designs.

  4. 4.

    Users may freely extract symbolic state representations for various use cases (e.g., formal property verification).

The remainder of this paper is organized as follows. The next section demonstrates the functionalities of WASIM, followed by a short presentation of user interface in Sect. 3. Sect. 4 reports the results on case studies. Sect. 5 discusses related work. Finally, Sect. 6 concludes the paper.

2 WASIM Functionalities

The WASIM framework is built on top of PySMT [11], a unified interface for multiple SMT solvers. The functionalities are described below.

2.1 Input Processing.

The input Verilog circuits are initially processed by the open-source synthesis suite Yosys and transformed into the Btor2 format [15], an efficient word-level representation for a state transition system (STS). WASIM consumes Btor2 with a parser modified from CoSA (CoreIR Symbolic Analyzer) [14].

2.2 Representing Simulation States using SMT formulas.

The state in WASIM is represented using SMT formulas, with one for each state variable assignment. There are also assumptions (SMT formulas) associated with each state. The assumptions capture the additional constraints on a symbolic trace, for example, certain input combinations will never happen. The state is reachable (realizable) if all assumptions are satisfiable. The state representation may also include undetermined values (‘X’ values). We keep a special set of SMT variables to represent the ‘X’ values.

2.3 Symbolic Simulation.

Symbolic simulation is mainly achieved through substitution. Variables in the transition function of an STS are substituted by variable assignments from the previous cycle. Unassigned input or unknown state variables are replaced by ‘X’ values. WASIM can explore either the state in the next one cycle (single-step simulation) or traverse a set of states until no new (abstract) states are found (multi-step simulation). Expression simplification and abstraction are used in WASIM to reduce the size of the state representation.

2.4 Expression Simplification.

Expression simplification reduces the size of an SMT formula in the state representation through the combination of various techniques. The built-in rewriting functionality in SMT solvers serves as the ‘X’-agnostic simplification step. After this first step, WASIM proceeds with ‘X’-aware simplification that checks if any ‘X’ value can be reduced given the state assumptions. For example, an ‘X’ is reducible if it resides in the unreachable branch of an ITE (if-then-else) operator. WASIM traverses the abstract syntax tree of SMT expressions and heuristically guess-and-check reducible ‘X’ values. When confirmed, WASIM further rewrites the expression to syntactically eliminate the ‘X’ values. We design several patterns for common rewriting. For the most general case, WASIM will fall back to query the CVC5 [2] SyGuS solver [1] to synthesize a new expression without ‘X’.

2.5 Abstraction Refinement.

We allow users to define abstraction functions that map a concrete state into an abstract domain. A simple example of such abstraction is to leave out certain registers in the symbolic state representation by replacing them with ‘X’ values. The abstraction could be design-specific — engineers familiar with the hardware microarchitecture may have better ideas on which registers to omit. Therefore, we give such freedom to the WASIM users and allow them to specify their own abstraction functions. Abstraction is also essential to the efficient state traversal because it is almost impossible to traverse the concrete state space of a large hardware design. When it is hard to pre-determine the best abstraction function, users can specify a refinement function and perform dynamic abstraction-refinement during symbolic simulation. An example of abstraction refinement function is demonstrated below in Sect. 3.2

3 User Interface

WASIM provides a Python interface to control the simulation, apply abstraction or refinement and manipulate the symbolic expressions in state representations.

3.1 Simulation Process Control.

WASIM provides a single-step simulation function sim_one_step for forward symbolic simulation of one clock cycle. Users can perform bounded-step simulation by using the function in a range-based loop.

On the other hand, there is often the need for unbounded simulation. WASIM provides an unbounded simulation function traverse_all_states. As its name suggests, this function instructs the simulator to search for all symbolic states that are reachable from the current state. Users may optionally provide a termination condition and the simulator will only search for reachable states before the condition becomes true. This is useful, for example, when searching for all symbolic states when an instruction is stalled in a certain pipeline stage.

3.2 Customizable Abstraction/Refinement Function.

Users may provide a callable Python object as the abstraction/refinement function. The abstraction function should transfer one symbolic state to its counterpart in the abstract domain, while the refinement function returns a list of states.

Here we give an example of user-specified dynamic abstraction refinement during symbolic simulation. In microprocessor verification, we can use symbolic simulation to check that the arithmetic processing pipeline is functionally correct by computing the output symbolic state from symbolic pipeline inputs. There are external signals coming into the pipeline that only affect latency rather than the arithmetic function. Abstraction can be applied to omit all external signals, however, the final abstract symbolic state might become too coarse. A refinement function can lazily bring back the external signals and branch the execution based on certain signal combinations, until the final symbolic states are sufficiently accurate to check for functional correctness. This example will require the simulator to have a pluggable interface for abstraction/refinement functions.

3.3 Symbolic State Extraction and Manipulation.

In order to use the result of symbolic simulation, WASIM allows users to freely extract and manipulate the symbolic expressions in a state representation. Simulation traces are available as Python lists. Users can collect all states in any simulation step and obtain the expressions of arbitrary state variable assignment. By checking the satisfiability of the conjunction of all variable assignments, the assumptions, and the negated property, users can check for property violations on a symbolic state. WASIM can also evaluate arbitrary functions over state variables given the variable assignment. This is useful to compute the symbolic value of wires in Verilog. Finally, users may re-assign an intermediate state and restart the simulation from that point.

Symbolic state extraction and manipulation enable two use cases: formal property verification and inductive invariant construction. Users can achieve formal property verification by checking the violation of properties on all abstract simulation states extracted from symbolic state traversal. Fragments of expressions in symbolic states are also helpful in the construction of inductive invariants, which could serve as the certificate for the abstract state traversal. For example,

$$\begin{aligned} \left( sv_1 =\ expr_1 \right) \wedge \left( sv_2 =\ expr_2 \right) \wedge ... \end{aligned}$$

indicates that the STS resides in one (abstract) symbolic state where \(sv_1, sv_2, ...\) are the state variables, and \(expr_1, expr_2, ...\) are the symbolic expressions in state representation. By taking the disjunction of all such formulas of all reachable abstract symbolic states, we cover the whole abstract state space and therefore, the disjunction will constitute an inductive invariant for this STS. To certify a specific safety property is valid, one can build from this inductive invariant with additional expression fragments to create a safe inductive invariant.

4 Case Studies

We demonstrate the usage of WASIM with two verification case studies on pipelined hardware designs. The design statistics are shown in Table 1, including the number of state bits and logic gates.

Designs under verification. The first design is a simple arithmetic pipeline with two variants implemented with or without external stall signals. They share the same datapath that performs a multiply-accumulate (MAC) operation. The second design is a simple 3-stage pipeline that resembles the backend of a processor core. It contains data forwarding logic and the control logic to handle external stall signals. Verification in this case study checks if these hardware designs are implemented with the correct functions. Despite the relatively small size, some are already nontrivial for a symbolic model checker.

Users’ input. For simple MAC without stall signals, users only need to provide a simulation script with bounded simulation steps. For all other designs, certain stages may be stalled by external signals for a period of time. The simulation script instructs the simulator to case-split based on the value of external stall signals and symbolically explore all stalled states in each step. The abstraction function only keeps the concrete representation in the downstream of the stalled stage, therefore, there are only a small number of stalled states in the abstract domain. Finally, users may check the given properties are valid on every symbolic path and the symbolic expressions in the state representations are used to construct parts of inductive invariants. The inductive invariants are further checked to ensure the correctness of simulation process given the user-provided abstraction functions.

Results of the experiment. In the experiments, we compare with the IC3/PDR symbolic model checking method implemented in Berkeley-ABC. The last three columns in Table 1 are the time of symbolic simulation, the time of checking functional properties on all traces and the time for checking the validity of inductive invariants. Results show that for the 3-stage-pipe-* problems, with proper guidance from a human verification engineer, symbolic simulation can outperform autonomous model checking with order-of-magnitude speed-up. The results are obtained on a server running Ubuntu 20.04 with a 2.9 GHz Intel Xeon(R) Platinum 8375C CPU and 128G RAM.

Table 1. Experimental Results
Full size table

5 Related Works

Apart from WASIM, VossII [16] is another tool for hardware symbolic simulation which implements the symbolic trajectory evaluation (STE) method [12, 13]. VossII is mainly on the bit level using binary decision diagrams (BDDs) as the state representation. Several extensions to the original STE method have been proposed so far. For example, generalized STE (GSTE) enables unbounded property verification using assertion graphs [18], and the word-level STE (WSTE) achieves a higher level of abstraction with word-level variables in bit-fields [7]. These extensions are typically only available in a commercial STE implementation. Moreover, users must be fluent in a domain-specific functional programming language named fl in order to use VossII.

On the other hand, tools based on symbolic model checking are broadly available for hardware formal verification, for example, Berkeley-ABC [5], which is a powerful open-source tool implementing a collection of various model checking algorithms [3, 4, 8]. Unlike symbolic simulation, symbolic model checking runs autonomously to prove or falsify given properties without user interactions. However, without proper human guidance, model checking tools may suffer more from the scalability problem.

6 Conclusions

In this paper, we present the design and usage of WASIM, a word-level abstract symbolic simulation framework. WASIM is featured with a Python user interface and pluggable abstraction/refinement functions to facilitate human verification engineers to bring in their insights to better scale formal methods for hardware designs. Applications of WASIM include formal property verification and inductive invariant generation. Our case studies show that this strategy can be helpful for some problems that are hard for autonomous model checking.