Fast and Correct Gradient-Based Optimisation for Probabilistic Programming via Smoothing

Abstract

We study the foundations of variational inference, which frames posterior inference as an optimisation problem, for probabilistic programming. The dominant approach for optimisation in practice is stochastic gradient descent. In particular, a variant using the so-called reparameterisation gradient estimator exhibits fast convergence in a traditional statistics setting. Unfortunately, discontinuities, which are readily expressible in programming languages, can compromise the correctness of this approach. We consider a simple (higher-order, probabilistic) programming language with conditionals, and we endow our language with both a measurable and a smoothed (approximate) value semantics. We present type systems which establish technical pre-conditions. Thus we can prove stochastic gradient descent with the reparameterisation gradient estimator to be correct when applied to the smoothed problem. Besides, we can solve the original problem up to any error tolerance by choosing an accuracy coefficient suitably. Empirically we demonstrate that our approach has a similar convergence as a key competitor, but is simpler, faster, and attains orders of magnitude reduction in work-normalised variance.

1 Introduction

Probabilistic programming is a programming paradigm which has the vision to make statistical methods, in particular Bayesian inference, accessible to a wide audience. This is achieved by a separation of concerns: the domain experts wishing to gain statistical insights focus on modelling, whilst the inference is performed automatically. (In some recent systems [4, 9] users can improve efficiency by writing their own inference code.)

In essence, probabilistic programming languages extend more traditional programming languages with constructs such as $\textbf{score}$ or $\textbf{observe}$ (as well as $\textbf{sample}\,$) to define the prior $p(\textbf{z})$ and likelihood $p({\textbf{x}}\mid \textbf{z})$. The task of inference is to derive the posterior $p(\textbf{z}\mid {\textbf{x}})$, which is in principle governed by Bayes’ law yet usually intractable.

Whilst the paradigm was originally conceived in the context of statistics and Bayesian machine learning, probabilistic programming has in recent years proven to be a very fruitful subject for the programming language community. Researchers have made significant theoretical contributions such as underpinning languages with rigorous (categorical) semantics [10, 12, 15, 34, 35, 37] and investigating the correctness of inference algorithms [7, 16, 22]. The latter were mostly designed in the context of “traditional” statistics and features such as conditionals, which are ubiquitous in programming, pose a major challenge for correctness.

Inference algorithms broadly fall into two categories: Markov chain Monte Carlo (MCMC), which yields a sequence of samples asymptotically approaching the true posterior, and variational inference.

Variational Inference. In the variational inference approach to Bayesian statistics [5, 6, 30, 40], the problem of approximating difficult-to-compute posterior probability distributions is transformed to an optimisation problem. The idea is to approximate the posterior probability $p(\textbf{z}\mid {\textbf{x}})$ using a family of “simpler” densities $q_{\boldsymbol{\theta }}(\textbf{z})$ over the latent variables $\textbf{z}$, parameterised by ${\boldsymbol{\theta }}$. The optimisation problem is then to find the parameter ${\boldsymbol{\theta }}^*$ such that $q_{{\boldsymbol{\theta }}^*}(\textbf{z})$ is “closest” to the true posterior $p(\textbf{z}\mid {\textbf{x}})$. Since the variational family may not contain the true posterior, $q_{{\boldsymbol{\theta }}^*}$ is an approximation in general. In practice, variational inference has proven to yield good approximations much faster than MCMC.

Formally, the idea is captured by minimising the KL-divergence [5, 30] between the variational approximation and the true posterior. This is equivalent to maximising the ELBO function, which only depends on the joint distribution $p({\textbf{x}},\textbf{z})$ and not the posterior, which we seek to infer after all:

$$\begin{aligned} \textrm{ELBO}_{\boldsymbol{\theta }}{:}{=}\mathbb {E}_{\textbf{z}\sim q_{\boldsymbol{\theta }}{(\textbf{z})}}[\log p({\textbf{x}},\textbf{z})-\log q_{\boldsymbol{\theta }}(\textbf{z})] \end{aligned}$$

(1)

Gradient Based Optimisation. In practice, variants of Stochastic Gradient Descent (SGD) are frequently employed to solve optimisation problems of the following form: $\text {argmin}_{\boldsymbol{\theta }}\,\mathbb {E}_{\textbf{s}\sim q{(\textbf{s})}}[f({\boldsymbol{\theta }},\textbf{s})]$. In its simplest version, SGD follows Monte Carlo estimates of the gradient in each step:

$$\begin{aligned} {\boldsymbol{\theta }}_{k+1}&{:}{=}{\boldsymbol{\theta }}_k-\gamma _k\cdot \underbrace{\frac{1}{N}\sum _{i=1}^N\nabla _\theta f\left( {\boldsymbol{\theta }}_k,\textbf{s}_k^{(i)}\right) }_{\text {gradient estimator}} \end{aligned}$$

where $\textbf{s}_k^{(i)}\sim q\left( \textbf{s}_k^{(i)}\right)$ and $\gamma _k$ is the step size.

For the correctness of SGD it is crucial that the estimation of the gradient is unbiased, i.e. correct in expectation:

$$\begin{aligned} \mathbb {E}_{\textbf{s}^{(1)},\ldots ,\textbf{s}^{(N)}\sim q}\left[ \frac{1}{N}\sum _{i=1}^N\nabla _\theta f\left( {\boldsymbol{\theta }},\textbf{s}^{(i)}\right) \right] =\nabla _\theta \mathbb {E}_{\textbf{s}\sim q{(\textbf{s})}}[f({\boldsymbol{\theta }},\textbf{s})] \end{aligned}$$

This property, which is about commuting differentiation and integration, can be established by the dominated convergence theorem [21, Theorem 6.28].

Note that we cannot directly estimate the gradient of the ELBO in Eq. (1) with Monte Carlo because the distribution w.r.t. which the expectation is taken also depends on the parameters. However, the so-called log-derivative trick can be used to derive an unbiased estimate, which is known as the Score or REINFORCE estimator [27, 28, 31, 38].

Reparameterisation Gradient. Whilst the score estimator has the virtue of being very widely applicable, it unfortunately suffers from high variance, which can cause SGD to yield very poor results¹.

The reparameterisation gradient estimator—the dominant approach in variational inference—reparameterises the latent variable $\textbf{z}$ in terms of a base random variable $\textbf{s}$ (viewed as the entropy source) via a diffeomorphic transformation ${\boldsymbol{\phi }}_{\boldsymbol{\theta }}$, such as a location-scale transformation or cumulative distribution function. For example, if the distribution of the latent variable z is a Gaussian $\mathcal {N}(z \mid \mu , \sigma ^2)$ with parameters ${\boldsymbol{\theta }}= \{\mu ,\sigma \}$ then the location-scale transformation using the standard normal as the base distribution gives rise to the reparameterisation

$$\begin{aligned} z \sim \mathcal N(z \mid \mu , \sigma ^2) \iff z = \phi _{\mu ,\sigma }(s), \quad s \sim \mathcal N(0,1). \end{aligned}$$

(2)

where $\phi _{\mu ,\sigma }(s){:}{=}s\cdot \sigma +\mu$. The key advantage of this setup (often called “reparameterisation trick” [20, 32, 36]) is that we have removed the dependency on ${\boldsymbol{\theta }}$ from the distribution w.r.t. which the expectation is taken. Therefore, we can now differentiate (by backpropagation) with respect to the parameters ${\boldsymbol{\theta }}$ of the variational distributions using Monte Carlo simulation with draws from the base distribution $\textbf{s}$. Thus, succinctly, we have

$$\begin{aligned} \nabla _{\boldsymbol{\theta }}\,\mathbb {E}_{\textbf{z}\sim q_{\boldsymbol{\theta }}(\textbf{z})}[f({\boldsymbol{\theta }},\textbf{z})] = \nabla _{\boldsymbol{\theta }}\,\mathbb {E}_{\textbf{s}\sim q(\textbf{s})}[f({\boldsymbol{\theta }},{\boldsymbol{\phi }}_{\boldsymbol{\theta }}(\textbf{s}))]&= \mathbb {E}_{\textbf{s}\sim q(\textbf{s})}[\nabla _{\boldsymbol{\theta }}\, f({\boldsymbol{\theta }},{\boldsymbol{\phi }}_{\boldsymbol{\theta }}(\textbf{s}))] \end{aligned}$$

The main benefit of the reparameterisation gradient estimator is that it has a significantly lower variance than the score estimator, resulting in faster convergence.

Bias of the Reparameterisation Gradient. Unfortunately, the reparameterisation gradient estimator is biased for non-differentiable models [23], which are readily expressible in programming languages with conditionals:

Example 1

The counterexample in [23, Proposition 2], where the objective function is the ELBO for a non-differentiable model, can be simplified to

$$\begin{aligned} f(\theta ,s)&= -0.5\cdot \theta ^2+ {\left\{ \begin{array}{ll} 0&{}\text {if }s+\theta <0\\ 1&{}\text {otherwise}\end{array}\right. } \end{aligned}$$

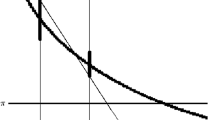
Observe that (see Fig. 1a):

$$ \nabla _\theta \,\mathbb {E}_{s\sim \mathcal N(0,1)}\left[ f(\theta ,s)\right] = -\theta +\mathcal N(-\theta \mid 0,1) \ne -\theta = \mathbb {E}_{s\sim \mathcal N(0,1)}\left[ \nabla _\theta f(\theta ,s)\right] $$

Crucially this may compromise convergence to critical points or maximisers: even if we can find a point where the gradient estimator vanishes, it may not be a critical point (let alone optimum) of the original optimisation problem (cf. Fig. 1b)

Fig. 1.

Bias of the reparameterisation gradient estimator for Example 1.

Informal Approach

As our starting point we take a variant of the simply typed lambda calculus with reals, conditionals and a sampling construct. We abstract the optimisation of the ELBO to the following generic optimisation problem

$$\begin{aligned} \text {argmin}_{\boldsymbol{\theta }}\,\mathbb {E}_{\textbf{s}\sim \mathcal D}[\llbracket M\rrbracket ({\boldsymbol{\theta }},\textbf{s})] \end{aligned}$$

(3)

where $\llbracket M\rrbracket$ is the value function [7, 26] of a program M and $\mathcal D$ is independent of the parameters ${\boldsymbol{\theta }}$ and it is determined by the distributions from which M samples. Owing to the presence of conditionals, the function $\llbracket M\rrbracket$ may not be continuous, let alone differentiable.

Fig. 2.

(Logistic) sigmoid function $\sigma _\eta$ (dotted: $\eta =\frac{1}{3}$, dashed: $\eta =\frac{1}{15}$) and the Heaviside step function (red, solid).

Example 1 can be expressed as

$$\begin{aligned} (\lambda {z}{.}-0.5\cdot \theta ^2+(\textbf{if }\,z <0\,\textbf{ then }\,0\,\textbf{ else }\,1))\,(\textbf{sample}\,_\mathcal N+\theta ) \end{aligned}$$

Our approach is based on a denotational semantics $\llbracket (-)\rrbracket _{\eta }$ (for accuracy coefficient $\eta > 0$) of programs in the (new) cartesian closed category $\textbf{VectFr}$, which generalises smooth manifolds and extends Frölicher spaces (see e.g. [13, 33]) with a vector space structure.

Intuitively, we replace the Heaviside step-function usually arising in the interpretation of conditionals by smooth approximations. In particular, we interpret the conditional of Example 1 as

$$\begin{aligned}\begin{gathered} \llbracket \textbf{if }\,s+\theta <0\,\textbf{ then }\,\underline{0}\,\textbf{ else }\,\underline{1}\rrbracket _{\eta }(\theta ,s){:}{=}\sigma _\eta (s+\theta ) \end{gathered}\end{aligned}$$

where $\sigma _\eta$ is a smooth function. For instance we can choose $\sigma _\eta (x){:}{=}\sigma (\frac{x}{\eta })$ where $\sigma (x) {:}{=}\frac{1}{1+\exp (-x)}$ is the (logistic) sigmoid function (cf. Fig. 2). Thus, the program M is interpreted by a smooth function $\llbracket M\rrbracket _{\eta }$, for which the reparameterisation gradient may be estimated unbiasedly. Therefore, we apply stochastic gradient descent on the smoothed program.

Contributions

The high-level contribution of this paper is laying a theoretical foundation for correct yet efficient (variational) inference for probabilistic programming. We employ a smoothed interpretation of programs to obtain unbiased (reparameterisation) gradient estimators and establish technical pre-conditions by type systems. In more detail:

• 1. We present a simple (higher-order) programming language with conditionals. We employ trace types to capture precisely the samples drawn in a fully eager call-by-value evaluation strategy.

• 2. We endow our language with both a (measurable) denotational value semantics and a smoothed (hence approximate) value semantics. For the latter we furnish a categorical model based on Frölicher spaces.

• 3. We develop type systems enforcing vital technical pre-conditions: unbiasedness of the reparameterisation gradient estimator and the correctness of stochastic gradient descent, as well as the uniform convergence of the smoothing to the original problem. Thus, our smoothing approach in principle yields correct solutions up to arbitrary error tolerances.

• 4. We conduct an empirical evaluation demonstrating that our approach exhibits a similar convergence to an unbiased correction of the reparameterised gradient estimator by [23] – our main baseline. However our estimator is simpler and more efficient: it is faster and attains orders of magnitude reduction in work-normalised variance.

Outline. In the next section we introduce a simple higher-order probabilistic programming language, its denotational value semantics and operational semantics; Optimisation Problem 1 is then stated. Section 3 is devoted to a smoothed denotational value semantics, and we state the Smooth Optimisation Problem 2. In Section 4 and 5 we develop annotation based type systems enforcing the correctness of SGD and the convergence of the smoothing, respectively. Related work is briefly discussed in Section 6 before we present the results of our empirical evaluation in Section 7. We conclude in Section 8 and discuss future directions.

Notation. We use the following conventions: bold font for vectors and lists, $\mathbin {++}$ for concatenation of lists, $\nabla _{\boldsymbol{\theta }}$ for gradients (w.r.t. ${\boldsymbol{\theta }}$),$[\phi ]$ for the Iverson bracket of a predicate $\phi$ and calligraphic font for distributions, in particular $\mathcal N$ for normal distributions. Besides, we highlight noteworthy items using .

2 A Simple Programming Language

In this section, we introduce our programming language, which is the simply-typed lambda calculus with reals, augmented with conditionals and sampling from continuous distributions.

2.1 Syntax

The raw terms of the programming language are defined by the grammar:

$$\begin{aligned} M::= x&\mid \theta _i\mid \underline{r}\mid \underline{+}\mid \underline{\cdot }\mid \underline{-}\mid \underline{{}^{-1}}\mid \underline{\exp }\mid \underline{\log }\\&\mid \textbf{if }\,M <0\,\textbf{ then }\,M\,\textbf{ else }\,M\mid \textbf{sample}\,_\mathcal D\mid \lambda {x}{.}\, M\mid M\,M \end{aligned}$$

where x and $\theta _i$ respectively range over (denumerable collections of) variables and parameters, $r \in \mathbb R$, and $\mathcal D$ is a probability distribution over $\mathbb R$ (potentially with a support which is a strict subset of $\mathbb R$). As is customary we use infix, postfix and prefix notation: $M\mathbin {\underline{+}}N$ (addition), $M\mathbin {\underline{\cdot }}N$ (multiplication), $M\underline{{}^{-1}}$ (inverse), and $\underline{-}M$ (numeric negation). We frequently omit the underline to reduce clutter.

Example 2

(Encoding the ELBO for Variational Inference). We consider the example used by [23] in their Prop. 2 to prove the biasedness of the reparameterisation gradient. (In Example 1 we discussed a simplified version thereof.) The density is

$$\begin{aligned} p(z)&{:}{=}\mathcal N(z\mid 0,1)\cdot {\left\{ \begin{array}{ll} \mathcal N(0\mid -2,1)&{}\text {if }z<0\\ \mathcal N(0\mid 5,1)&{}\text {otherwise}\end{array}\right. } \end{aligned}$$

and they use a variational family with density $q_\theta (z){:}{=}\mathcal N(z\mid \theta ,1)$, which is reparameterised using a standard normal noise distribution and transformation $s\mapsto s+\theta$.

First, we define an auxiliary term for the pdf of normals with mean m and standard derivation s:

$$\begin{aligned} N\equiv \lambda x,m,s{.}\, \big (\underline{\sqrt{2\pi }}\cdot s\big )^{-1}\cdot \underline{\exp }\,\Big (\underline{-0.5}\cdot \big ((x+(-m))\cdot s^{-1}\big )^2\Big ) \end{aligned}$$

Then, we can define

$$\begin{aligned} M&\equiv \big (\lambda {z}{.}\, \underbrace{\underline{\log }\,(N\,z\,\underline{0}\,\underline{1})+(\textbf{if }\,z <0\,\textbf{ then }\,\underline{\log }\,(N\,\underline{0}\,\underline{(-2)}\,{\underline{1}})\,\textbf{ else }\,\underline{\log }\,(N\,\underline{0}\,\underline{5}\,\underline{1}))}_{\log p}-\\&\qquad \qquad \qquad \qquad \qquad \qquad \underbrace{\underline{\log }\,(N\,z\,\theta \,\underline{1})}_{\log q_\theta }\big ) \,\big (\textbf{sample}\,_\mathcal N+\theta \big ) \end{aligned}$$

2.2 A Basic Trace-Based Type System

Types are generated from base types ($R$ and $R_{>0}$, the reals and positive reals) and trace types (typically $\varSigma$, which is a finite list of probability distributions) as well as by a trace-based function space constructor of the form $\tau \bullet \varSigma \rightarrow \tau '$. Formally types are defined by the following grammar:

where $\mathcal D_i$ are probability distributions. Intuitively a trace type is a description of the space of execution traces of a probabilistic program. Using trace types, a distinctive feature of our type system is that a program’s type precisely characterises the space of its possible execution traces [24]. We use list concatenation notation $\mathbin {++}$ for trace types, and the shorthand $\tau _1\rightarrow \tau _2$ for function types of the form $\tau _1\bullet []\rightarrow \tau _2$. Intuitively, a term has type $\tau \bullet \varSigma \rightarrow \tau '$ if, when given a value of type $\tau$, it reduces to a value of type $\tau '$ using all the samples in $\varSigma$.

Dual context typing judgements of the form, $\varGamma \mid \varSigma \vdash M:\tau$, are defined in Fig. 3b, where $\varGamma = x_1:\tau _1, \cdots , x_n:\tau _n, \theta _1 : \tau _1', \cdots , \theta _m : \tau _m'$ is a finite map describing a set of variable-type and parameter-type bindings; and the trace type $\varSigma$ precisely captures the distributions from which samples are drawn in a (fully eager) call-by-value evaluation of the term M.

The subtyping of types, as defined in Fig. 3a, is essentially standard; for contexts, we define $\varGamma \sqsubseteq \varGamma '$ if for every $x:\tau$ in $\varGamma$ there exists $x:\tau '$ in $\varGamma '$ such that $\tau '\sqsubseteq \tau$.

Trace types are unique [18]:

Lemma 1

If $\varGamma \mid \varSigma \vdash M:\tau$ and $\varGamma \mid \varSigma '\vdash M:\tau '$ then $\varSigma =\varSigma '$.

A term has safe type $\sigma$ if it does not contain $\textbf{sample}\,_\mathcal D$ or $\sigma$ is a base type. Thus, perhaps slightly confusingly, we have ${} \mid [\mathcal D]\vdash \textbf{sample}\,_\mathcal D:R$, and $R$ is considered a safe type. Note that we use the metavariable $\sigma$ to denote safe types.

Conditionals. The branches of conditionals must have a safe type. Otherwise it would not be clear how to type terms such as

$$\begin{aligned} M&\equiv \textbf{if }\,x <0\,\textbf{ then }\,(\lambda {x}{.}\, \textbf{sample}\,_\mathcal N)\,\textbf{ else }\,(\lambda {x}{.}\, \textbf{sample}\,_\mathcal E+\textbf{sample}\,_\mathcal E)\\ N&\equiv (\lambda {f}{.}\, f\,(f\,\textbf{sample}\,_\mathcal N))\,M \end{aligned}$$

because the branches draw a different number of samples from different distributions, and have types $R\bullet [\mathcal N]\rightarrow R$ and $R\bullet [\mathcal E,\mathcal E]\rightarrow R$, respectively. However, for $M'\equiv \textbf{if }\,x <0\,\textbf{ then }\,\textbf{sample}\,_\mathcal N\,\textbf{ else }\,\textbf{sample}\,_\mathcal E+\textbf{sample}\,_\mathcal E$ we can (safely) type

$$\begin{aligned} x:R\mid [\mathcal N,\mathcal E,\mathcal E]&\vdash M':R\\ \mid []&\vdash \lambda {x}{.}\, M':R\bullet [\mathcal N,\mathcal E,\mathcal E]\rightarrow R\\ \mid [\mathcal N,\mathcal N,\mathcal E,\mathcal E,\mathcal N,\mathcal E,\mathcal E]&\vdash (\lambda {f}{.}\, f\,(f\,\textbf{sample}\,_\mathcal N))\,(\lambda {x}{.}\, M'):R\end{aligned}$$

Fig. 3.

A Basic Trace-based Type System

Example 3

Consider the following terms:

$$\begin{aligned} L&\equiv \lambda {x}{.}\,\textbf{sample}\,_\mathcal N+\textbf{sample}\,_\mathcal N\\ M&\equiv \textbf{if }\,x <0\,\textbf{ then }\,(\lambda {y}{.}\, y+y)\,\textbf{sample}\,_\mathcal N\,\textbf{ else }\,(\textbf{sample}\,_\mathcal N+\textbf{sample}\,_\mathcal N) \end{aligned}$$

We can derive the following typing judgements:

$$\begin{aligned} \mid []&\vdash L:R_{>0}\bullet [\mathcal N,\mathcal N]\rightarrow R\\ x : R_{>0}\mid [\mathcal N,\mathcal N,\mathcal N]&\vdash M:R\\ \mid []&\vdash \lambda {x}{.}\, M:R_{>0}\bullet [\mathcal N,\mathcal N,\mathcal N]\rightarrow R\\ \mid [\mathcal N,\mathcal N,\mathcal N,\mathcal N]&\vdash (\lambda {x}{.}\, M)\,\textbf{sample}\,_\mathcal N:R\\ {} \mid [\mathcal N, \mathcal N]&\vdash (\lambda {f}{.}\, f \, (f \, 0))\,(\lambda {x}{.}\, \textbf{sample}\,_\mathcal N) : R\end{aligned}$$

Note that $\textbf{if }\,x <0\,\textbf{ then }\,(\lambda {x}{.}\,\textbf{sample}\,_\mathcal N)\,\textbf{ else }\,(\lambda {x}{.}\, x)$ is not typable.

2.3 Denotational Value Semantics

Next, we endow our language with a (measurable) value semantics. It is well-known that the category of measurable spaces and measurable functions is not cartesian-closed [1], which means that there is no interpretation of the lambda calculus as measurable functions. These difficulties led [14] to develop the category $\textbf{QBS}$ of quasi-Borel spaces. Notably, morphisms can be combined piecewisely, which we need for conditionals.

We interpret our programming language in the category $\textbf{QBS}$ of quasi-Borel spaces. Types are interpreted as follows:

$$ \begin{array}{c} \llbracket R\rrbracket {:}{=}(\mathbb R, M_\mathbb R) \qquad \llbracket R_{>0}\rrbracket {:}{=}(\mathbb R_{>0}, M_{\mathbb R_{>0}}) \qquad \llbracket [\mathcal D_1,\ldots ,\mathcal D_n]\rrbracket {:}{=}(\mathbb R, M_\mathbb R)^n\\ \llbracket \tau _1\bullet \varSigma \rightarrow \tau _2\rrbracket {:}{=}\llbracket \tau _1\rrbracket \times \llbracket \varSigma \rrbracket \Rightarrow \llbracket \tau _2\rrbracket \end{array} $$

where $M_\mathbb R$ is the set of measurable functions $\mathbb R\rightarrow \mathbb R$; similarly for $M_{\mathbb R_{>0}}$. (As for trace types, we use list notation (and list concatenation) for traces.)

We first define a handy helper function for interpreting application. For $f:\llbracket \varGamma \rrbracket \times \mathbb R^{n_1}\Rightarrow \llbracket \tau _1\bullet \varSigma _3\rightarrow \tau _2\rrbracket$ and $g:\llbracket \varGamma \rrbracket \times \mathbb R^{n_2}\Rightarrow \llbracket \tau _1\rrbracket$ define

$$\begin{aligned} f\mathbin {@}g:\llbracket \varGamma \rrbracket \times \mathbb R^{n_1+n_2+|\varSigma _3|}&\Rightarrow \llbracket \tau _2\rrbracket \\ (\gamma ,\textbf{s}_1\mathbin {++}\textbf{s}_2\mathbin {++}\textbf{s}_3)&\mapsto f(\gamma ,\textbf{s}_1)(g(\gamma ,\textbf{s}_2),\textbf{s}_3)&\textbf{s}_1\in \mathbb R^{n_1},\textbf{s}_2\in \mathbb R^{n_2},\textbf{s}_3\in \mathbb R^{|\varSigma _3|} \end{aligned}$$

We interpret terms-in-context, $\llbracket \varGamma \mid \varSigma \vdash M:\tau \rrbracket :\llbracket \varGamma \rrbracket \times \llbracket \varSigma \rrbracket \rightarrow \llbracket \tau \rrbracket$, as follows:

It is not difficult to see that this interpretation of terms-in-context is well-defined and total. For the conditional clause, we may assume that the trace type and the trace are presented as partitions $\varSigma _1 \mathbin {++}\varSigma _2 \mathbin {++}\varSigma _3$ and $\textbf{s}_1 \mathbin {++}\textbf{s}_2 \mathbin {++}\textbf{s}_3$ respectively. This is justified because it follows from the judgement $\varGamma \mid \varSigma _1\mathbin {++}\varSigma _2\mathbin {++}\varSigma _3\vdash \textbf{if }\,L <0\,\textbf{ then }\,M\,\textbf{ else }\,N:\tau$ that $\varGamma \mid \varSigma _1 \vdash L : R$, $\varGamma \mid \varSigma _2 \vdash M : \sigma$ and $\varGamma \mid \varSigma _3 \vdash N : \sigma$ are provable; and we know that each of $\varSigma _1, \varSigma _2$ and $\varSigma _3$ is unique, thanks to Lemma 1; their respective lengths then determine the partition $\textbf{s}_1 \mathbin {++}\textbf{s}_2 \mathbin {++}\textbf{s}_3$. Similarly for the application clause, the components $\varSigma _1$ and $\varSigma _2$ are determined by Lemma 1, and $\varSigma _3$ by the type of M.

2.4 Relation to Operational Semantics

We can also endow our language with a big-step CBV sampling-based semantics similar to [7, 26], as defined in [18, Fig. 6]. We write $M\Downarrow _w^\textbf{sV}$ to mean that M reduces to value V, which is a real constant or an abstraction, using the execution trace $\textbf{s}$ and accumulating weight w.

Based on this, we can define the value- and weight-functions:

$$\begin{aligned} {{\,\textrm{value}\,}}_M(\textbf{s})&{:}{=}{\left\{ \begin{array}{ll} V&{}\text {if }M\Downarrow ^\textbf{s}_w V\\ \textrm{undef}&{}\text {otherwise}\end{array}\right. }&{{\,\textrm{weight}\,}}_M(\textbf{s})&{:}{=}{\left\{ \begin{array}{ll} w&{}\text {if }M\Downarrow ^\textbf{s}_w V\\ 0&{}\text {otherwise}\end{array}\right. } \end{aligned}$$

Our semantics is a bit non-standard in that for conditionals we evaluate both branches eagerly. The technical advantage is that for every (closed) term-in-context, ${} \mid [\mathcal D_1, \cdots , \mathcal D_n] \vdash M : \iota$, M reduces to a (unique) value using exactly the traces of the length encoded in the typing, i.e., n.

So in this sense, the operational semantics is “total”: there is no divergence. Notice that there is no partiality caused by partial primitives such as 1/x, thanks to the typing.

Moreover there is a simple connection to our denotational value semantics:

Proposition 1

Let ${} \mid [\mathcal D_1,\ldots ,\mathcal D_n]\vdash M:\iota$. Then

• 1. ${{\,\textrm{dom}\,}}({{\,\textrm{value}\,}}_M)=\mathbb R^n$

• 2. $\underline{\llbracket M\rrbracket }={{\,\textrm{value}\,}}_M$

• 3. ${{\,\textrm{weight}\,}}_M(\textbf{s})=\prod _{j=1}^n\textrm{pdf}_{\mathcal D_j}(s_j)$

2.5 Problem Statement

We are finally ready to formally state our optimisation problem:

Problem 1

Optimisation

Given: term-in-context, $\theta _1 : \iota _1, \cdots , \theta _m : \iota _m \mid [\mathcal D_1,\ldots ,\mathcal D_n]\vdash M:R$

Find: $\text {argmin}_{\boldsymbol{\theta }}\ \mathbb {E}_{s_1\sim \mathcal D_1,\ldots ,s_n\sim \mathcal D_n}\left[ \llbracket M\rrbracket ({\boldsymbol{\theta }},\textbf{s})\right]$

3 Smoothed Denotational Value Semantics

Now we turn to our smoothed denotational value semantics, which we use to avoid the bias in the reparameterisation gradient estimator. It is parameterised by a family of smooth functions $\sigma _\eta :\mathbb R\rightarrow [0,1]$. Intuitively, we replace the Heaviside step-function arising in the interpretation of conditionals by smooth approximations (cf. Fig. 2). In particular, conditionals $\textbf{if }\,z <0\,\textbf{ then }\,\underline{0}\,\textbf{ else }\,\underline{1}$ are interpreted as $z\mapsto \sigma _\eta (z)$ rather than $[z\ge 0]$ (using Iverson brackets).

Our primary example is $\sigma _\eta (x){:}{=}\sigma (\frac{x}{\eta })$, where $\sigma$ is the (logistic) sigmoid $\sigma (x){:}{=}\frac{1}{1+\exp (-x)}$, see Fig. 2. Whilst at this stage no further properties other than smoothness are required, we will later need to restrict $\sigma _\eta$ to have good properties, in particular to convergence to the Heaviside step function.

As a categorical model we propose vector Frölicher spaces $\textbf{VectFr}$, which (to our knowledge) is a new construction, affording a simple and direct interpretation of the smoothed conditionals.

3.1 Frölicher Spaces

We recall the definition of Frölicher spaces, which generalise smooth spaces²: A Frölicher space is a triple $(X,\mathcal C_X,\mathcal F_X)$ where X is a set, $\mathcal C_X\subseteq \textbf{Set}(\mathbb R,X)$ is a set of curves and $\mathcal F_X\subseteq \textbf{Set}(X,\mathbb R)$ is a set of functionals. satisfying

• 1. if $c\in \mathcal C_X$ and $f\in \mathcal F_X$ then $f\circ c\in C^\infty (\mathbb R,\mathbb R)$

• 2. if $c:\mathbb R\rightarrow X$ such that for all $f\in \mathcal F_X$, $f\circ c\in C^\infty (\mathbb R,\mathbb R)$ then $c\in \mathcal C_X$

• 3. if $f:X\rightarrow \mathbb R$ such that for all $c\in \mathcal C_X$, $f \circ c\in C^\infty (\mathbb R,\mathbb R)$ then $f\in \mathcal F_X$.

A morphism between Frölicher spaces $(X,\mathcal C_X,\mathcal F_X)$ and $(Y,\mathcal C_Y,\mathcal F_Y)$ is a map $\phi :X\rightarrow Y$ satisfying $f\circ \phi \circ c\in C^\infty (\mathbb R,\mathbb R)$ for all $f\in \mathcal F_Y$ and $c\in \mathcal C_X$.

Frölicher spaces and their morphisms constitute a category $\textbf{Fr}$, which is well-known to be cartesian closed [13, 33].

3.2 Vector Frölicher Spaces

To interpret our programming language smoothly we would like to interpret conditionals as $\sigma _\eta$-weighted convex combinations of its branches:

$$\begin{aligned}&\llbracket \textbf{if }\,L <0\,\textbf{ then }\,M\,\textbf{ else }\,N\rrbracket _{\eta }(\gamma ,\textbf{s}_1\mathbin {++}\textbf{s}_2\mathbin {++}\textbf{s}_3)\, {:}{=}\nonumber \\&\qquad \qquad \quad \sigma _\eta (-\llbracket L\rrbracket _{\eta }(\gamma ,\textbf{s}_1))\cdot \llbracket M\rrbracket _{\eta }(\gamma ,\textbf{s}_2)+\sigma _\eta (\llbracket L\rrbracket _{\eta }(\gamma ,\textbf{s}_1))\cdot \llbracket N\rrbracket _{\eta }(\gamma ,\textbf{s}_3) \end{aligned}$$

(4)

By what we have discussed so far, this only makes sense if the branches have ground type because Frölicher spaces are not equipped with a vector space structure but we take weighted combinations of morphisms. In particular if $\phi _1,\phi _2:X\rightarrow Y$ and $\alpha :X\rightarrow \mathbb R$ are morphisms then $\alpha \, \phi _1+\phi _2$ ought to be a morphism too. Therefore, we enrich Frölicher spaces with an additional vector space structure:

Definition 1

An $\mathbb R$-vector Frölicher space is a Frölicher space $(X,\mathcal C_X,\mathcal F_X)$ such that X is an $\mathbb R$-vector space and whenever $c,c'\in \mathcal C_X$ and $\alpha \in C^\infty (\mathbb R,\mathbb R)$ then $\alpha \, c+c'\in \mathcal C_X$ (defined pointwise).

A morphism between $\mathbb R$-vector Frölicher spaces is a morphism between Frölicher spaces, i.e. $\phi :(X,\mathcal C_X,\mathcal F_X)\rightarrow (Y,\mathcal C_Y,\mathcal F_Y)$ is a morphism if for all $c\in \mathcal C_X$ and $f\in \mathcal F_Y$, $f\circ \phi \circ c\in C^\infty (\mathbb R,\mathbb R)$.

$\mathbb R$-vector Frölicher space and their morphisms constitute a category $\textbf{VectFr}$. There is an evident forgetful functor fully faithfully embedding $\textbf{VectFr}$ in $\textbf{Fr}$. Note that the above restriction is a bit stronger than requiring that $\mathcal C_X$ is also a vector space. ($\alpha$ is not necessarily a constant.) The main benefit is the following, which is crucial for the interpretation of conditionals as in Eq. (4):

Lemma 2

If $\phi _1,\phi _2\in \textbf{VectFr}(X,Y)$ and $\alpha \in \textbf{VectFr}(X,\mathbb R)$ then $\alpha \, \phi _1+\phi _2\in \textbf{VectFr}(X,Y)$ (defined pointwisely).

Proof

Suppose $c\in \mathcal C_X$ and $f\in \mathcal F_Y$. Then $(\alpha _1 \, \phi _1+\phi _2)\circ c=(\alpha \circ c)\cdot (\phi _1\circ c)+(\phi _2\circ c)\in \mathcal C_Y$ (defined pointwisely) and the claim follows.

Similarly as for Frölicher spaces, if X is an $\mathbb R$-vector space then any $\mathcal C\subseteq \textbf{Set}(X,\mathbb R)$ generates a $\mathbb R$-vector Frölicher space $(X,\mathcal C_X,\mathcal F_X)$, where

$$\begin{aligned} \mathcal F_X&{:}{=}\{f:X\rightarrow \mathbb R\mid \forall c\in \mathcal {C}{.}\, f\circ c\in C^\infty (\mathbb R,\mathbb R)\}\\ \widetilde{\mathcal C}_X&{:}{=}\{c:\mathbb R\rightarrow X\mid \forall f\in \mathcal {F}_X{.}\, f\circ c\in C^\infty (\mathbb R,\mathbb R)\}\\ \mathcal C_X&{:}{=}\left\{ \sum _{i=1}^n\alpha _i \, c_i\mid n\in \mathbb N,\forall i\le n{.}\, \alpha _i\in C^\infty (\mathbb R,\mathbb R), c_i\in \widetilde{\mathcal C}_X\right\} \end{aligned}$$

Having modified the notion of Frölicher spaces generated by a set of curves, the proof for cartesian closure carries over [18] and we conclude:

Proposition 2

$\textbf{VectFr}$ is cartesian closed.

3.3 Smoothed Interpretation

We have now discussed all ingredients to interpret our language (smoothly) in the cartesian closed category $\textbf{VectFr}$. We call $\llbracket M\rrbracket _{\eta }$ the $\eta$-smoothing of $\llbracket M\rrbracket$ (or of M, by abuse of language). The interpretation is mostly standard and follows Section 2.3, except for the case for conditionals. The latter is given by Eq. (4), for which the additional vector space structure is required.

Finally, we can phrase a smoothed version of our Optimisation Problem 1:

Problem 2

$\eta$-Smoothed Optimisation

Given: term-in-context, $\theta _1 : \iota _1, \cdots , \theta _m : \iota _m \mid [\mathcal D_1,\ldots ,\mathcal D_n]\vdash M:R$, and accuracy coefficient $\eta >0$

Find: $\text {argmin}_{\boldsymbol{\theta }}\ \mathbb {E}_{s_1\sim \mathcal D_1,\ldots ,s_n\sim \mathcal D_n}\left[ \llbracket M\rrbracket _{\eta }({\boldsymbol{\theta }},\textbf{s})\right]$

4 Correctness of SGD for Smoothed Problem and Unbiasedness of the Reparameterisation Gradient

Next, we apply stochastic gradient descent (SGD) with the reparameterisation gradient estimator to the smoothed problem (for the batch size $N=1$):

$$\begin{aligned} {\boldsymbol{\theta }}_{k+1}&{:}{=}{\boldsymbol{\theta }}_k-\gamma _k\cdot \nabla _\theta \llbracket M\rrbracket _{\eta }\left( {\boldsymbol{\theta }}_k,\textbf{s}_k\right)&\textbf{s}_k\sim \mathbf {\mathcal D}\end{aligned}$$

(5)

where ${\boldsymbol{\theta }}\mid [\textbf{s}\sim \mathbf {\mathcal D}]\vdash M:R$ (slightly abusing notation in the trace type).

A classical choice for the step-size sequence is $\gamma _k\in \varTheta (1/k)$, which satisfies the so-called Robbins-Monro criterion:

$$\begin{aligned} \sum _{k\in \mathbb N}\gamma _k&=\infty&\sum _{k\in \mathbb N}\gamma ^2_k&<\infty \end{aligned}$$

(6)

In this section we wish to establish the correctness of the SGD procedure applied to the smoothing Eq. (5).

4.1 Desiderata

First, we ought to take a step back and observe that the optimisation problems we are trying to solve can be ill-defined due to a failure of integrability: take $M\equiv (\lambda {x}{.} \underline{\exp }\,(x\mathbin {\underline{\cdot }}x))\,\textbf{sample}\,_\mathcal N$: we have $\mathbb {E}_{z\sim \mathcal N}[\llbracket M\rrbracket (z)]=\infty$, independently of parameters. Therefore, we aim to guarantee:

• (SGD0) The optimisation problems (both smoothed and unsmoothed) are well-defined.

Since $\mathbb {E}[\llbracket M\rrbracket _{\eta }({\boldsymbol{\theta }},\textbf{s})]$ (and $\mathbb {E}[\llbracket M\rrbracket ({\boldsymbol{\theta }},\textbf{s})]$) may not be a convex function in the parameters ${\boldsymbol{\theta }}$, we cannot hope to always find global optima. We seek instead stationary points, where the gradient w.r.t. the parameters ${\boldsymbol{\theta }}$ vanishes. The following results (whose proof is standard) provide sufficient conditions for the convergence of SGD to stationary points (see e.g. [3] or [2, Chapter 2]):

Proposition 3

(Convergence). Suppose $(\gamma _k)_{k\in \mathbb N}$ satisfies the Robbins-Monro criterion Eq. (6) and $g({\boldsymbol{\theta }}){:}{=}\mathbb {E}_{\textbf{s}}[f({\boldsymbol{\theta }},\textbf{s})]$ is well-defined. If ${\boldsymbol{\varTheta }}\subseteq \mathbb R^m$ satisfies

• (SGD1) Unbiasedness: $\nabla _{\boldsymbol{\theta }}g({\boldsymbol{\theta }})=\mathbb {E}_\textbf{s}[\nabla _{\boldsymbol{\theta }}f({\boldsymbol{\theta }},\textbf{s})]$ for all ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$

• (SGD2) g is L-Lipschitz smooth on ${\boldsymbol{\varTheta }}$ for some $L>0$:

  $$ \Vert \nabla _{\boldsymbol{\theta }}g({\boldsymbol{\theta }})-\nabla _{\boldsymbol{\theta }}g({\boldsymbol{\theta }}')\Vert \le L\cdot \Vert {\boldsymbol{\theta }}-{\boldsymbol{\theta }}'\Vert \qquad \text {for all }{\boldsymbol{\theta }},{\boldsymbol{\theta }}'\in {\boldsymbol{\varTheta }}$$

• (SGD3) Bounded Variance: $\sup _{{\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}}\mathbb {E}_{\textbf{s}}[\Vert \nabla _{\boldsymbol{\theta }}f({\boldsymbol{\theta }},\textbf{s})\Vert ^2]<\infty$

then $\inf _{i\in \mathbb N}\mathbb {E}[\Vert \nabla g({\boldsymbol{\theta }}_i)\Vert ^2]=0$ or ${\boldsymbol{\theta }}_i\not \in {\boldsymbol{\varTheta }}$ for some $i\in \mathbb N$.

Unbiasedness (SGD1) requires commuting differentiation and integration. The validity of this operation can be established by the dominated convergence theorem [21, Theorem 6.28], see [18]. To be applicable the partial derivatives of f w.r.t. the parameters need to be dominated uniformly by an integrable function. Formally:

Definition 2

Let $f:{\boldsymbol{\varTheta }}\times \mathbb R^n\rightarrow \mathbb R$ and $g:\mathbb R^n\rightarrow \mathbb R$. We say that g uniformly dominates f if for all $({\boldsymbol{\theta }},\textbf{s})\in {\boldsymbol{\varTheta }}\times \mathbb R^n$, $|f({\boldsymbol{\theta }},\textbf{s})|\le g(\textbf{s})$.

Also note that for Lipschitz smoothness (SGD2) it suffices to uniformly bound the second-order partial derivatives.

In the remainder of this section we present two type systems which restrict the language to guarantee properties (SGD0) to (SGD3).

4.2 Piecewise Polynomials and Distributions with Finite Moments

As a first illustrative step we consider a type system $\vdash _{\textrm{poly}}$, which restricts terms to (piecewise) polynomials, and distributions with finite moments. Recall that a distribution $\mathcal D$ has (all) finite moments if for all $p\in \mathbb N$, $\mathbb {E}_{s\sim \mathcal D}[|s|^p]<\infty$. Distributions with finite moments include the following commonly used distributions: normal, exponential, logistic and gamma distributions. A non-example is the Cauchy distribution, which famously does not even have an expectation.

Definition 3

For a distribution $\mathcal D$ with finite moments, $f:\mathbb R^n\rightarrow \mathbb R$ has (all) finite moments if for all $p\in \mathbb N$, $\mathbb {E}_{\textbf{s}\sim \mathcal D}[|f(\textbf{s})|^p]<\infty$.

Functions with finite moments have good closure properties:

Lemma 3

If $f,g:\mathbb R^n\rightarrow \mathbb R$ have (all) finite moments so do $-f,f+g,f\cdot g$.

In particular, if a distribution has finite moments then polynomials do, too. Consequently, intuitively, it is sufficient to simply (the details are explicitly spelled out in [18]):

• 1. require that the distributions $\mathcal D$ in the sample rule have finite moments:

  

• 2. remove the rules for $\underline{{}^{-1}}$, $\underline{\exp }$ and $\underline{\log }$ from the type system $\vdash _{\textrm{poly}}$.

Type Soundness I: Well-Definedness. Henceforth, we fix parameters $\theta _1:\iota _1,\ldots ,\theta _m:\iota _m$. Intuitively, it is pretty obvious that $\llbracket M\rrbracket$ is a piecewise polynomial whenever ${\boldsymbol{\theta }}\mid \varSigma \vdash _{\textrm{poly}}M:\iota$. Nonetheless, we prove the property formally to illustrate our proof technique, a variant of logical relations, employed throughout the rest of the paper.

We define a slightly stronger logical predicate $\mathcal P^{(n)}_\tau$ on ${\boldsymbol{\varTheta }}\times \mathbb R^n\rightarrow \llbracket \tau \rrbracket$, which allows us to obtain a uniform upper bound:

• 1. $f\in \mathcal P^{(n)}_\iota$ if f is uniformly dominated by a function with finite moments

• 2. $f\in \mathcal P^{(n)}_{\tau _1\bullet \varSigma _3\rightarrow \tau _2}$ if for all $n_2\in \mathbb N$ and $g\in \mathcal P^{(n+n_2)}_{\tau _1}$, $f\mathbin {\odot }g\in \mathcal P^{(n+n_2+|\varSigma _3|)}_{\tau _2}$

where for $f:{\boldsymbol{\varTheta }}\times \mathbb R^{n_1}\rightarrow \llbracket \tau _1\bullet \varSigma _3\rightarrow \tau _2\rrbracket$ and $g:{\boldsymbol{\varTheta }}\times \mathbb R^{n_1+n_2}\rightarrow \llbracket \tau _1\rrbracket$ we define

$$\begin{aligned}&f\mathbin {\odot }g:{\boldsymbol{\varTheta }}\times \mathbb R^{n_1+n_2+|\varSigma _3|}&\rightarrow \tau _2\\&\qquad \quad ({\boldsymbol{\theta }},\textbf{s}_1\mathbin {++}\textbf{s}_2\mathbin {++}\textbf{s}_3)&\mapsto f({\boldsymbol{\theta }},\textbf{s}_1)(g({\boldsymbol{\theta }},\textbf{s}_1\mathbin {++}\textbf{s}_2),\textbf{s}_3) \end{aligned}$$

Intuitively, g may depend on the samples in $\textbf{s}_2$ (in addition to $\textbf{s}_1$) and the function application may consume further samples $\textbf{s}_3$ (as determined by the trace type $\varSigma _3$). By induction on safe types we prove the following result, which is important for conditionals:

Lemma 4

If $f\in \mathcal P^{(n)}_\iota$ and $g,h\in \mathcal P^{(n)}_\sigma$ then $[f(-)<0]\mathbin {\cdot }g+[f(-)\ge 0]\mathbin {\cdot }h\in \mathcal P^{(n)}_\sigma$.

Proof

For base types it follows from Lemma 3. Hence, suppose $\sigma$ has the form $\sigma _1\bullet []\rightarrow \sigma _2$. Let $n_2\in \mathbb N$ and $x\in \mathcal P_{\sigma _1}^{n+n_2}$. By definition, $(g\mathbin {\odot }x),(h\mathbin {\odot }x)\in \mathcal P_{\sigma _2}^{(n+n_2)}$. Let $\widehat{f}$ be the extension (ignoring the additional samples) of f to ${\boldsymbol{\varTheta }}\times \mathbb R^{n+n_2}\rightarrow \mathbb R$. It is easy to see that also $\widehat{f}\in \mathcal P_\iota ^{(n+n_2)}$ By the inductive hypothesis,

$$\begin{aligned}{}[\widehat{f}(-)<0]\cdot (g\mathbin {\odot }x)+[\widehat{f}(-)\ge 0]\cdot (h\mathbin {\odot }x)\in \mathcal P^{(n+n_2)}_{\sigma _2} \end{aligned}$$

Finally, by definition,

$$\begin{aligned} ([f(-)<0]\cdot g+[f(-)\ge 0]\cdot h)\mathbin {\odot }x=[\widehat{f}(-)<0]\cdot (g\mathbin {\odot }x)+[\widehat{f}(-)\ge 0]\cdot (h\mathbin {\odot }x) \end{aligned}$$

Assumption 1

We assume that ${\boldsymbol{\varTheta }}\subseteq \llbracket \iota _1\rrbracket \times \cdots \times \llbracket \iota _m\rrbracket$ is compact.

Lemma 5

(Fundamental). If ${\boldsymbol{\theta }},x_1:\tau _1,\ldots ,x_\ell :\tau _\ell \mid \varSigma \vdash _{\textrm{poly}}M:\tau$, $n\in \mathbb N$, $\xi _1\in \mathcal P^{(n)}_{\tau _1},\ldots ,\xi _\ell \in \mathcal P^{(n)}_{\tau _\ell }$ then $\llbracket M\rrbracket \mathbin {*}\langle \xi _1,\ldots ,\xi _\ell \rangle \in \mathcal P^{(n+|\varSigma |)}_{\tau }$, where

$$\begin{aligned} \llbracket M\rrbracket \mathbin {*}\langle \xi _1,\ldots ,\xi _\ell \rangle :{\boldsymbol{\varTheta }}\times \mathbb R^{n+|\varSigma |}&\rightarrow \llbracket \tau \rrbracket \\ ({\boldsymbol{\theta }},\textbf{s}\mathbin {++}\textbf{s}')&\mapsto \llbracket M\rrbracket (({\boldsymbol{\theta }}, \xi _1({\boldsymbol{\theta }},\textbf{s}),\ldots ,\xi _\ell ({\boldsymbol{\theta }},\textbf{s})),\textbf{s}') \end{aligned}$$

It is worth noting that, in contrast to more standard fundamental lemmas, here we need to capture the dependency of the free variables on some number n of further samples. E.g. in the context of $(\lambda {x}{.}\, x)\,\textbf{sample}\,_\mathcal N$ the subterm x depends on a sample although this is not apparent if we consider x in isolation.

Lemma 5 is proven by structural induction [18]. The most interesting cases include: parameters, primitive operations and conditionals. In the case for parameters we exploit the compactness of ${\boldsymbol{\varTheta }}$ (Assumption 1). For primitive operations we note that as a consequence of Lemma 3 each $\mathcal P_{\iota }^{(n)}$ is closed under negation³, addition and multiplication. Finally, for conditionals we exploit Lemma 3.

Type Soundness II: Correctness of SGD. Next, we address the integrability for the smoothed problem as well as (SGD1) to (SGD3). We establish that not only $\llbracket M\rrbracket _{\eta }$ but also its partial derivatives up to order 2 are uniformly dominated by functions with finite moments. For this to possibly hold we require:

Assumption 2

For every $\eta >0$,

$$\begin{aligned} \sup _{x\in \mathbb R}|\sigma _\eta (x)|&<\infty&\sup _{x\in \mathbb R}|\sigma _\eta '(x)|&<\infty&\sup _{x\in \mathbb R}|\sigma _\eta ''(x)|&<\infty \end{aligned}$$

Note that, for example, the logistic sigmoid satisfies Assumption 2.

We can then prove a fundamental lemma similar to Lemma 5, mutatis mutandis, using a logical predicate in $\textbf{VectFr}$. We stipulate $f\in \mathcal Q^{(n)}_{\iota }$ if its partial derivatives up to order 2 are uniformly dominated by a function with finite moments. In addition to Lemma 3 we exploit standard rules for differentiation (such as the sum, product and chain rule) as well as Assumption 2. We conclude:

Proposition 4

If ${\boldsymbol{\theta }}\mid \varSigma \vdash _{\textrm{poly}}M:R$ then the partial derivatives up to order 2 of $\llbracket M\rrbracket _{\eta }$ are uniformly dominated by a function with all finite moments.

Consequently, the Smoothed Optimisation Problem 2 is not only well-defined but, by the dominated convergence theorem [21, Theorem 6.28], the reparameterisation gradient estimator is unbiased. Furthermore, (SGD1) to (SGD3) are satisfied and SGD is correct.

Discussion. The type system $\vdash _{\textrm{poly}}$ is simple yet guarantees correctness of SGD. However, it is somewhat restrictive; in particular, it does not allow the expression of many ELBOs arising in variational inference directly as they often have the form of logarithms of exponential terms (cf. Example 2).

4.3 A Generic Type System with Annotations

Next, we present a generic type system with annotations. In Section 4.4 we give an instantiation to make $\vdash _{\textrm{poly}}$ more permissible and in Section 5 we turn towards a different property: the uniform convergence of the smoothings.

Typing judgements have the form $\varGamma \mid \varSigma \vdash _?M:\tau$, where “?” indicates the property we aim to establish, and we annotate base types. Thus, types are generated from

Annotations are drawn from a set and may possibly restricted for safe types. Secondly, the trace types are now annotated with variables, typically $\varSigma = [s_1\sim \mathcal D_1,\ldots ,s_n\sim \mathcal D_n]$ where the variables $s_j$ are pairwise distinct.

For the subtyping relation we can constrain the annotations at the base type level [18]; the extension to higher types is accomplished as before.

The typing rules have the same form but they are extended with the annotations on base types and side conditions possibly constraining them. For example, the rules for addition, exponentiation and sampling are modified as follows:

The rules for subtyping, variables, abstractions and applications do not need to be changed at all but they use annotated types instead of the types of Section 2.2.

The full type system is presented in [18].

Table 1. Overview of type systems in this paper.

$\vdash _{\textrm{poly}}$ can be considered a special case of $\vdash _?$ whereby we use the singleton $*$ as annotations, a contradictory side condition (such as $\textrm{false}$) for the undesired primitives $\underline{{}^{-1}}$, $\underline{\exp }$ and $\underline{\log }$, and use the side condition “$\mathcal D$ has finite moments” for sample as above.

Table 1 provides an overview of the type systems of this paper and their purpose. $\vdash _?$ and its instantiations refine the basic type system of Section 2.2 in the sense that if a term-in-context is provable in the annotated type system, then its erasure (i.e. erasure of the annotations of base types and distributions) is provable in the basic type system. This is straightforward to check.

4.4 A More Permissible Type System

In this section we discuss another instantiation, $\vdash _{\textrm{SGD}}$, of the generic type system system to guarantee (SGD0) to (SGD3), which is more permissible than $\vdash _{\textrm{poly}}$. In particular, we would like to support Example 2, which uses logarithms and densities involving exponentials. Intuitively, we need to ensure that subterms involving $\underline{\exp }$ are “neutralised” by a corresponding $\underline{\log }$. To achieve this we annotate base types with 0 or 1, ordered discretely. 0 is the only annotation for safe base types and can be thought of as “integrable”; 1 denotes “needs to be passed through log”. More precisely, we constrain the typing rules such that if ${\boldsymbol{\theta }}\mid \varSigma \vdash _{\textrm{SGD}}M:\iota ^{(e)}$ then⁴ $\log ^e\circ \llbracket M\rrbracket$ and the partial derivatives of $\log ^e\circ \llbracket M\rrbracket _{\eta }$ up to order 2 are uniformly dominated by a function with finite moments.

We subtype base types as follows: $\iota _1^{(e_1)}\sqsubseteq _{\textrm{SGD}}\iota _2^{(e_2)}$ if $\iota _1\sqsubseteq \iota _2$ (as defined in Fig. 3a) and $e_1=e_2$, or $\iota _1=R_{>0}=\iota _2$ and $e_1\le e_2$. The second disjunct may come as a surprise but we ensure that terms of type $R_{>0}^{(0)}$ cannot depend on samples at all.

Fig. 4.

Excerpt of the typing rules (cf. [18]) for the correctness of SGD.

In Fig. 4 we list the most important rules; we relegate the full type system to [18]. $\underline{\exp }$ and $\underline{\log }$ increase and decrease the annotation respectively. The rules for the primitive operations and conditionals are motivated by the closure properties of Lemma 3 and the elementary fact that $\log \circ (f\cdot g)=(\log \circ f)+(\log \circ g)$ and $\log \circ (f^{-1})=-\log \circ f$ for $f,g:{\boldsymbol{\varTheta }}\times \mathbb R^n\rightarrow \mathbb R$.

Example 4

$\theta :R_{>0}^{(0)}\mid [\mathcal N,\mathcal N]\vdash _{\textrm{SGD}}\underline{\log }\,(\theta ^{-1}\cdot \underline{\exp }\,(\textbf{sample}\,_\mathcal N))+\textbf{sample}\,_\mathcal N:R^{(0)}$

Note that the branches of conditionals need to have safe type, which rules out branches with type $R^{(1)}$. This is because logarithms do not behave nicely when composed with addition as used in the smoothed interpretation of conditionals.

Besides, observe that in the rules for logarithm and inverses $e=0$ is allowed, which may come as a surprise⁵. This is e.g. necessary for the typability of the variational inference Example 2:

Example 5

(Typing for Variational Inference). It holds $\mid []\vdash N:R^{(0)}\rightarrow R^{(0)}\rightarrow R_{>0}^{(0)}\rightarrow R_{>0}^{(1)}$ and $\theta :R^{(0)}\mid [s_1\sim \mathcal N]\vdash M:R^{(0)}$.

Type Soundness. To formally establish type soundness, we can use a logical predicate, which is very similar to the one in Section 4.2 (N.B. the additional Item 2): in particular $f\in \mathcal Q^{(n)}_{\iota ^{(e)}}$ if

• 1. partial derivatives of $\log ^e\circ f$ up to order 2 are uniformly dominated by a function with finite moments

• 2. if $\iota ^{(e)}$ is $R_{>0}^{(0)}$ then f is dominated by a positive constant function

Using this and a similar logical predicate for $\llbracket (-)\rrbracket$ we can show:

Proposition 5

If $\theta _1:\iota ^{(0)},\ldots ,\theta _m:\iota _m^{(0)}\mid \varSigma \vdash _{\textrm{SGD}}M:\iota ^{(0)}$ then

• 1. all distributions in $\varSigma$ have finite moments

• 2. $\llbracket M\rrbracket$ and for each $\eta >0$ the partial derivatives up to order 2 of $\llbracket M\rrbracket _{\eta }$ are uniformly dominated by a function with finite moments.

Consequently, again the Smoothed Optimisation Problem 2 is not only well-defined but by the dominated convergence theorem, the reparameterisation gradient estimator is unbiased. Furthermore, (SGD1) to (SGD3) are satisfied and SGD is correct.

5 Uniform Convergence

In the preceding section we have shown that SGD with the reparameterisation gradient can be employed to correctly (in the sense of Proposition 3) solve the Smoothed Optimisation Problem 2 for any fixed accuracy coefficient. However, a priori, it is not clear how a solution of the Smoothed Problem 2 can help to solve the original Problem 1.

The following illustrates the potential for significant discrepancies:

Example 6

Consider $M\equiv \textbf{if }\,0 <0\,\textbf{ then }\,\theta \cdot \theta +\underline{1}\,\textbf{ else }\,(\theta -\underline{1})\cdot (\theta -\underline{1})$. Notice that the global minimum and the only stationary point of $\llbracket M\rrbracket _{\eta }$ is at $\theta =\frac{1}{2}$ regardless of $\eta >0$, where $\llbracket M\rrbracket _{\eta }(\frac{1}{2})=\frac{3}{4}$. On the other hand $\llbracket M\rrbracket (\frac{1}{2})=\frac{1}{4}$ and the global minimum of $\llbracket M\rrbracket$ is at $\theta =1$.

In this section we investigate under which conditions the smoothed objective function converges to the original objective function uniformly in ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$:

• (Unif) $\mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}\left[ \llbracket M\rrbracket _{\eta }({\boldsymbol{\theta }},\textbf{s})\right] \xrightarrow {\text {unif.}}\mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}\left[ \llbracket M\rrbracket ({\boldsymbol{\theta }},\textbf{s})\right]$ as $\eta \searrow 0$ for ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$

We design a type system guaranteeing this.

The practical significance of uniform convergence is that before running SGD, for every error tolerance $\epsilon >0$ we can find an accuracy coefficient $\eta >0$ such that the difference between the smoothed and original objective function does not exceed $\epsilon$, in particular for ${\boldsymbol{\theta }}^*$ delivered by the SGD run for the $\eta$-smoothed problem.

Discussion of Restrictions. To rule out the pathology of Example 6 we require that guards are non-0 almost everywhere.

Furthermore, as a consequence of the uniform limit theorem [29], (Unif) can only possibly hold if the expectation $\mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}\left[ \llbracket M\rrbracket ({\boldsymbol{\theta }},\textbf{s})\right]$ is continuous (as a function of the parameters ${\boldsymbol{\theta }}$). For a straightforward counterexample take $M\equiv \textbf{if }\,\theta <0\,\textbf{ then }\,\underline{0}\,\textbf{ else }\,\underline{1}$, we have $\mathbb {E}_{\textbf{s}}[\llbracket M\rrbracket (\theta )]=[\theta \ge 0]$ which is discontinuous, let alone differentiable, at $\theta = 0$. Our approach is to require that guards do not depend directly on parameters but they may do so, indirectly, via a diffeomorphic⁶ reparameterisation transform; see Example 8. We call such guards safe.

In summary, our aim, intuitively, is to ensure that guards are the composition of a diffeomorphic transformation of the random samples (potentially depending on parameters) and a function which does not vanish almost everywhere.

5.1 Type System for Guard Safety

In order to enforce this requirement and to make the transformation more explicit, we introduce syntactic sugar, $\textbf{transform}\,\textbf{sample}\,_{\mathcal D}\,\textbf{ by }\,T$, for applications of the form $T\,\textbf{sample}\,_\mathcal D$.

Example 7

As expressed in Eq. (2), we can obtain samples from $\mathcal N(\mu ,\sigma ^2)$ via $\textbf{transform}\,\textbf{sample}\,_{\mathcal N}\,\textbf{ by }\,(\lambda {s}{.}\, s\cdot \sigma +\mu )$, which is syntactic sugar for the term $(\lambda {s}{.}\, s\cdot \sigma +\mu )\,\textbf{sample}\,_\mathcal N$.

We propose another instance of the generic type system of Section 4.3, $\vdash _{\textrm{unif}}$, where we annotate base types by $\alpha =(g,\varDelta )$, where $g\in \{\textbf{f},\textbf{t}\}$ denotes whether we seek to establish guard safety and $\varDelta$ is a finite set of $s_j$ capturing possible dependencies on samples. We subtype base types as follows: $\iota _1^{(g_1,\varDelta _1)}\sqsubseteq _{\textrm{unif}}\iota _2^{(g_2,\varDelta _2)}$ if $\iota _1\sqsubseteq \iota _2$ (as defined in Fig. 3a), $\varDelta _1\subseteq \varDelta _2$ and $g_1\preceq g_2$, where $\textbf{t}\preceq \textbf{f}$. This is motivated by the intuition that we can always drop⁷ guard safety and add more dependencies.

The rule for conditionals ensures that only safe guards are used. The unary operations preserve variable dependencies and guard safety. Parameters and constants are not guard safe and depend on no samples (see [18] for the full type system):

A term ${\boldsymbol{\theta }}\mid []\vdash _{\textrm{unif}}T:R^{\alpha }\rightarrow R^{\alpha }$ is diffeomorphic if $\llbracket T\rrbracket ({\boldsymbol{\theta }},[])=\llbracket T\rrbracket _{\eta }({\boldsymbol{\theta }},[]) :\mathbb R\rightarrow \mathbb R$ is a diffeomorphism for each ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$, i.e. differentiable and bijective with differentiable inverse.

First, we can express affine transformations, in particular, the location-scale transformations as in Example 7:

Example 8

(Location-Scale Transformation). The term-in-context

$$ \sigma :R_{>0}^{(\textbf{f},\emptyset )},\mu :R^{(\textbf{f},\emptyset )} \mid [] \vdash \lambda {s}{.}\,\sigma \cdot s +\mu :R^{(\textbf{f},\{s_1\})} \rightarrow R^{(\textbf{f},\{s_1\})} $$

is diffeomorphic. (However for it is not because it admits $\sigma =0$.) Hence, the reparameterisation transform

$$ G \equiv \sigma :R_{>0}^{(\textbf{f},\emptyset )},\mu :R^{(\textbf{f},\emptyset )} \mid [s_1 : \mathcal D] \vdash \textbf{transform}\,\textbf{sample}\,_{\mathcal D}\,\textbf{ by }\,(\lambda s. s\cdot \sigma + \mu ) : R^{(\textbf{t},\{ s_1 \})} $$

which has g-flag $\textbf{t}$, is admissible as a guard term. Notice that G depends on the parameters, $\sigma$ and $\mu$, indirectly through a diffeomorphism, which is permitted by the type system.

If guard safety is sought to be established for the binary operations, we require that operands do not share dependencies on samples:

This is designed to address:

Example 9

(Non-Constant Guards). We have ${}\mid [] \vdash (\lambda x . x + (- x)) : R^{(\textbf{f},\{s_1\})} \rightarrow R^{(\textbf{f},\{s_1\})},$ noting that we must use $g = \textbf{f}$ for the $\underline{+}$ rule; and because $R^{(\textbf{t},\{s_j\})} \sqsubseteq _{\textrm{unif}} R^{(\textbf{f},\{s_j\})}$, we have

$$ {}\mid [] \vdash (\lambda x . x + (\underline{-}x)) : R^{(\textbf{t},\{s_1\})} \rightarrow R^{(\textbf{f},\{s_1\})} . $$

Now $\textbf{transform}\,\textbf{sample}\,_{\mathcal D}\,\textbf{ by }\,(\lambda y. y)$ has type $R^{(\textbf{t},\{s_1\})}$ with the g-flag necessarily set to $\textbf{t}$; and so the term

$$ M \equiv \big (\lambda x. x+(- x)\big ) \, \textbf{transform}\,\textbf{sample}\,_{\mathcal D}\,\textbf{ by }\,(\lambda y. y) $$

which denotes 0, has type $R^{(\textbf{f},\{s_1\})}$, but not $R^{(\textbf{t},\{s_1\})}$. It follows that M cannot be used in guards (notice the side condition of the rule for conditional), which is as desired: recall Example 6. Similarly consider the term

$$\begin{aligned} N&\equiv \big (\lambda x. (\lambda y \, z . \textbf{if }\,y + (- z) <0\,\textbf{ then }\,M_1\,\textbf{ else }\,M_2 ) \, x \, x \big ) \nonumber \\&\qquad \qquad \qquad \qquad \, (\textbf{transform}\,\textbf{sample}\,_{\mathcal D}\,\textbf{ by }\,(\lambda y. y)) \end{aligned}$$

(7)

When evaluated, the term ${y + (- z)}$ in the guard has denotation 0. For the same reason as above, the term N is not refinement typable.

The type system is however incomplete, in the sense that there are terms-in-context that satisfy the property (Unif) but which are not typable.

Example 10

(Incompleteness). The following term-in-context denotes the “identity”:

$$ {}\mid [] \vdash (\lambda x . (\underline{2} \cdot x) + (- x)) : R^{(\textbf{t},\{s_1\})} \rightarrow R^{(\textbf{f},\{s_1\})} $$

but it does not have type $R^{(\textbf{t},\{s_1\})} \rightarrow R^{(\textbf{t},\{s_1\})}$. Then, using the same reasoning as Example 9, the term

$$ G \equiv (\lambda x. (\underline{2} \cdot x) + (- x)) \, (\textbf{transform}\,\textbf{sample}\,_{\mathcal D}\,\textbf{ by }\,(\lambda y. y)) $$

has type $R^{(\textbf{f},\{s_1\})}$, but not $R^{(\textbf{t},\{s_1\})}$, and so $\textbf{if }\,G <0\,\textbf{ then }\,\underline{0}\,\textbf{ else }\,\underline{1}$ is not typable, even though G can safely be used in guards.

5.2 Type Soundness

Henceforth, we fix parameters $\theta _1:\iota ^{(\textbf{f},\emptyset )}_1,\ldots ,\theta _m:\iota ^{(\textbf{f},\emptyset )}_m$.

Now, we address how to show property (Unif), i.e. that for ${\boldsymbol{\theta }}\mid \varSigma \vdash _{\textrm{unif}}M:\iota ^{(g,\varDelta )}$, the $\eta$-smoothed $\mathbb {E}[\llbracket M\rrbracket _{\eta }({\boldsymbol{\theta }},\textbf{s})]$ converges uniformly for ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$ as $\eta \searrow 0$. For this to hold we clearly need to require that $\sigma _\eta$ has good (uniform) convergence properties (as far as the unavoidable discontinuity at 0 allows for):

Assumption 3

For every $\delta >0$, $\sigma _\eta \xrightarrow {\text {unif.}}[(-)>0]$ on $(-\infty ,-\delta )\cup (\delta ,\infty )$.

Observe that in general even if M is typable $\llbracket M\rrbracket _{\eta }$ does not converge uniformly in both ${\boldsymbol{\theta }}$ and $\textbf{s}$ because $\llbracket M\rrbracket$ may still be discontinuous in $\textbf{s}$:

Example 11

For $M\equiv \textbf{if }\,(\textbf{transform}\,\textbf{sample}\,_{\mathcal N}\,\textbf{ by }\,(\lambda {s}{.}\, s+\theta )) <0\,\textbf{ then }\,\underline{0}\,\textbf{ else }\,\underline{1}$, $\llbracket M\rrbracket (\theta ,s)=[s+\theta \ge 0]$, which is discontinuous, and $\llbracket M\rrbracket _{\eta }(\theta ,s)=\sigma _\eta (s+\theta )$.

However, if ${\boldsymbol{\theta }}\mid \varSigma \vdash M:\iota ^{(g,\varDelta )}$ then $\llbracket M\rrbracket _{\eta }$ does converge to $\llbracket M\rrbracket$ uniformly almost uniformly, i.e., uniformly in ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$ and almost uniformly in $\textbf{s}\in \mathbb R^n$. Formally, we define:

Definition 4

Let $f,f_\eta :{\boldsymbol{\varTheta }}\times \mathbb R^n\rightarrow \mathbb R$, $\mu$ be a measure on $\mathbb R^n$. We say that $f_\eta$ converges uniformly almost uniformly to f (notation: $f_\eta \xrightarrow {\text {u.a.u.}}f$) if there exist sequences $(\delta _k)_{k\in \mathbb N}$, $(\epsilon _k)_{k\in \mathbb N}$ and $(\eta _k)_{k\in \mathbb N}$ such that $\lim _{k \rightarrow \infty }\delta _k=0=\lim _{k \rightarrow \infty }\epsilon _k$; and for every $k\in \mathbb N$ and ${\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}$ there exists $U\subseteq \mathbb R^n$ such that

• 1. $\mu (U)<\delta _k$ and

• 2. for every $0<\eta <\eta _k$ and $\textbf{s}\in \mathbb R^n\setminus U$, $|f_\eta ({\boldsymbol{\theta }},\textbf{s})-f({\boldsymbol{\theta }},\textbf{s})|<\epsilon _k$.

If $f,f_\eta$ are independent of ${\boldsymbol{\theta }}$ this notion coincides with standard almost uniform convergence. For M from Example 11 $\llbracket M\rrbracket _{\eta }\xrightarrow {\text {u.a.u.}}\llbracket M\rrbracket$ holds although uniform convergence fails.

However, uniform almost uniform convergence entails uniform convergence of expectations:

Lemma 6

Let $f,f_\eta :{\boldsymbol{\varTheta }}\times \mathbb R^n\rightarrow \mathbb R$ have finite moments.

If $f_\eta \xrightarrow {\text {u.a.u.}}f$ then $\mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}[f_\eta ({\boldsymbol{\theta }},\textbf{s})]\xrightarrow {\text {unif.}}\mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}[f({\boldsymbol{\theta }},\textbf{s})]$.

As a consequence, it suffices to establish $\llbracket M\rrbracket _{\eta }\xrightarrow {\text {u.a.u.}}\llbracket M\rrbracket$. We achieve this by positing an infinitary logical relation between sequences of morphisms in $\textbf{VectFr}$ (corresponding to the smoothings) and morphisms in $\textbf{QBS}$ (corresponding to the measurable standard semantics). We then prove a fundamental lemma (details are in [18]). Not surprisingly the case for conditionals is most interesting. This makes use of Assumption 3 and exploits that guards, for which the typing rules assert the guard safety flag to be $\textbf{t}$, can only be 0 at sets of measure 0. We conclude:

Theorem 1

If $\theta _1:\iota ^{(\textbf{f},\emptyset )}_1,\ldots ,\theta _m:\iota ^{(\textbf{f},\emptyset )}_m\mid \varSigma \vdash _{\textrm{unif}}M:R^{(g,\varDelta )}$ then $\llbracket M\rrbracket _{\eta }\xrightarrow {\text {u.a.u.}}\llbracket M\rrbracket$. In particular, if $\llbracket M\rrbracket _{\eta }$ and $\llbracket M\rrbracket$ also have finite moments then

$$\begin{aligned} \mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}[\llbracket M\rrbracket _{\eta }({\boldsymbol{\theta }},\textbf{s})]&\xrightarrow {\text {unif.}}\mathbb {E}_{\textbf{s}\sim \mathbf {\mathcal D}}[\llbracket M\rrbracket ({\boldsymbol{\theta }},\textbf{s})]&\text { as } \eta \searrow 0\text { for }{\boldsymbol{\theta }}\in {\boldsymbol{\varTheta }}\end{aligned}$$

We finally note that $\vdash _{\textrm{unif}}$ can be made more permissible by adding syntactic sugar for a-fold (for $a\in \mathbb N_{>0}$) addition $\underline{a\,\cdot }\,M\equiv M\mathbin {\underline{+}}\cdots \mathbin {\underline{+}}M$ and multiplication $M\underline{{}^a}\equiv M\mathbin {\underline{\cdot }}\cdots \mathbin {\underline{\cdot }}M$. This admits more terms as guards, but safely [18].

6 Related Work

[23] is both the starting point for our work and the most natural source for comparison. They correct the (biased) reparameterisation gradient estimator for non-differentiable models by additional non-trivial boundary terms. They present an efficient method for affine guards only. Besides, they are not concerned with the convergence of gradient-based optimisation procedures; nor do they discuss how assumptions they make may be manifested in a programming language.

In the context of the reparameterisation gradient, [25] and [17] relax discrete random variables in a continuous way, effectively dealing with a specific class of discontinuous models. [39] use a similar smoothing for discontinuous optimisation but they do not consider a full programming language.

Motivated by guaranteeing absolute continuity (which is a necessary but not sufficient criterion for the correctness of e.g. variational inference), [24] use an approach similar to our trace types to track the samples which are drawn. They do not support standard conditionals but their “work-around” is also eager in the sense of combining the traces of both branches. Besides, they do not support a full higher-order language, in which higher-order terms can draw samples. Thus, they do not need to consider function types tracking the samples drawn during evaluation.

7 Empirical Evaluation

We evaluate our smoothed gradient estimator (Smooth) against the biased reparameterisation estimator (Reparam), the unbiased correction of it (LYY18) due to [23], and the unbiased (Score) estimator [27, 31, 38]. The experimental setup is based on that of [23]. The implementation is written in Python, using automatic differentiation (provided by the jax library) to implement each of the above estimators for an arbitrary probabilistic program. For each estimator and model, we used the Adam [19] optimiser for 10, 000 iterations using a learning rate of 0.001, with the exception of xornet for which we used 0.01. The initial model parameters ${\boldsymbol{\theta }}_0$ were fixed for each model across all runs. In each iteration, we used $N=16$ Monte Carlo samples from the gradient estimator. For the Lyy18 estimator, a single subsample for the boundary term was used in each estimate. For our smoothed estimator we use accuracy coefficients $\eta \in \{0.1,0.15,0.2\}$. Further details are discussed in [18, Appendix E.1].

Compilation for First-Order Programs. All our benchmarks are first-order. We compile a potentially discontinuous program to a smooth program (parameterised by $\sigma _\eta$) using the compatible closure of

$$\begin{aligned} \textbf{if }\,L <0\,\textbf{ then }\,M\,\textbf{ else }\,N\rightsquigarrow (\lambda {w}{.}\, \sigma _\eta (-w)\cdot M+\sigma _\eta (w)\cdot N)\,L \end{aligned}$$

Note that the size only increases linearly and that we avoid of an exponential blow-up by using abstractions rather than duplicating the guard L.

Models. We include the models from [23], an example from differential privacy [11] and a neural network for which our main competitor, the estimator of [23], is not applicable (see [18, Appendix E.2] for more details).

Fig. 5.

ELBO trajectories for each model. A single colour is used for each estimator and the accuracy coefficient $\eta =0.1,0.15,0.2$ for Smooth is represented by dashed, solid and dotted lines respectively.

Analysis of Results

We plot the ELBO trajectories in Fig. 5 and include data on the computational cost and work-normalised variance [8] in [18, Table 2]. (Variances can be improved in a routine fashion by e.g. taking more samples.)

The ELBO graph for the temperature model in Fig. 5a and the cheating model in Fig. 5d shows that the Reparam estimator is biased, converging to suboptimal values when compared to the Smooth and Lyy18 estimators. For temperature we can also see from the graph and the data in [18, Table 2a] that the Score estimator exhibits extremely high variance, and does not converge.

Finally, the xornet model shows the difficulty of training step-function based neural nets. The Lyy18 estimator is not applicable here since there are non-affine conditionals. In Fig. 5e, the Reparam estimator makes no progress while other estimators manage to converge to close to 0 ELBO, showing that they learn a network that correctly classifies all points. In particular, the Smooth estimator converges the quickest.

Summa summarum, the results reveal where the Reparam estimator is biased and that the Smooth estimator does not have the same limitation. Where the Lyy18 estimator is defined, they converge to roughly the same objective value. Our smoothing approach is generalisable to more complex models such as neural networks with non-linear boundaries, as well as simpler and cheaper (there is no need to compute a correction term). Besides, our estimator has consistently significantly lower work-normalised variance, up to 3 orders of magnitude.

8 Conclusion and Future Directions

We have discussed a simple probabilistic programming language to formalise an optimisation problem arising e.g. in variational inference for probabilistic programming. We have endowed our language with a denotational (measurable) value semantics and a smoothed approximation of potentially discontinuous programs, which is parameterised by an accuracy coefficient. We have proposed type systems to guarantee pleasing properties in the context of the optimisation problem: For a fixed accuracy coefficient, stochastic gradient descent converges to stationary points even with the reparameterisation gradient (which is unbiased). Besides, the smoothed objective function converges uniformly to the true objective as the accuracy is improved.

Our type systems can be used to independently check these two properties to obtain partial theoretical guarantees even if one of the systems suffers from incompleteness. We also stress that SGD and the smoothed unbiased gradient estimator can even be applied to programs which are not typable.

Experiments with our prototype implementation confirm the benefits of reduced variance and unbiasedness. Compared to the unbiased correction of the reparameterised gradient estimator due to [23], our estimator has a similar convergence, but is simpler, faster, and attains orders of magnitude (2 to 3,000 x) reduction in work-normalised variance.

Future Directions. A natural avenue for future research is to make the language and type systems more complete, i.e. to support more well-behaved programs, in particular programs involving recursion.

Furthermore, the choice of accuracy coefficients leaves room for further investigations. We anticipate it could be fruitful not to fix an accuracy coefficient upfront but to gradually enhance it during the optimisation either via a pre-determined schedule (dependent on structural properties of the program), or adaptively.