Abstract
We study increasingly expressive type systems, from \(F^\mu \)—an extension of the polymorphic lambda calculus with equirecursive types—to \(F^{\mu ;}_\omega \)—the higher-order polymorphic lambda calculus with equirecursive types and context-free session types. Type equivalence is given by a standard bisimulation defined over a novel labelled transition system for types. Our system subsumes the contractive fragment of \(F^\mu _\omega \) as studied in the literature. Decidability results for type equivalence of the various type languages are obtained from the translation of types into objects of an appropriate computational model: finite-state automata, simple grammars and deterministic pushdown automata. We show that type equivalence is decidable for a significant fragment of the type language. We further propose a message-passing, concurrent functional language equipped with the expressive type language and show that it enjoys preservation and absence of runtime errors for typable processes.
Support for this research was provided by the Fundação para a Ciência e a Tecnologia through project SafeSessions, ref. PTDC/CCI-COM/6453/2020, and by the LASIGE Research Unit, ref. UIDB/00408/2020 and ref. UIDP/00408/2020. A full version is available on arXiv [20].
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Extensions of the \(\lambda \)-calculus to include increasingly sophisticated type structures have been extensively studied and have led to systems whose importance is widely recognized: System F [60], System \(F^{\mu }\) [30], System \(F_{\omega }\) [36], System \(F^{\mu }_\omega \) [14]. Ideally, we would like to combine a wishlist of type structures and get a super-powerful system with vast expressiveness. However, the expressiveness of types is naturally limited by the universe where they are supposed to live: programming languages. Expressive type systems pose challenges to compilers that other (less expressive) types do not even reveal; one such example is type equivalence checking.
System F can be enriched with different type constructors for specifying communication protocols. We analyse the impact of combinations of such constructors on the type equivalence problem. In order to do so, we extend System F with session types [42, 43, 67]. Session types provide for detailed protocol specifications in the form of types. Traditional recursive session types are limited to tail recursion, thus failing to capture all protocols whose traces cannot be characterized by regular languages. Context-free session types overcome this limitation by extending types with a notion of sequential composition,
 [2, 68]. The set of types together with the
[2, 68]. The set of types together with the
 binary operation constitutes a monoid, for which a new type,
binary operation constitutes a monoid, for which a new type,
 , acts as the neutral element and
, acts as the neutral element and
 acts as an absorbing element.
acts as an absorbing element.
The regular recursive type
 describes an integer stream as seen from the point of view of the consumer. It offers a choice between
describes an integer stream as seen from the point of view of the consumer. It offers a choice between
 —after which the channel must be closed (as witnessed by type
—after which the channel must be closed (as witnessed by type
 )—and
)—and
 —after which an integer value must be received, followed by the rest of the stream. Types are categorised by kinds, so that we know that the recursion variable
—after which an integer value must be received, followed by the rest of the stream. Types are categorised by kinds, so that we know that the recursion variable
 is of kind session—denoted by
is of kind session—denoted by
 —and, thus, can be used with semicolon. Instead, we might want to write a type with a more context-free flavour. The type
—and, thus, can be used with semicolon. Instead, we might want to write a type with a more context-free flavour. The type
 describes a protocol for the type-safe streaming of integer trees on channels. The continuation to the
describes a protocol for the type-safe streaming of integer trees on channels. The continuation to the
 option is
option is
 , where no communication occurs but the channel is still open for further composition. The continuation to the
, where no communication occurs but the channel is still open for further composition. The continuation to the
 choice receives a left subtree, an integer at the root and a right subtree. In either case, once the whole tree is received, the channel must be closed, as witnessed by the final
choice receives a left subtree, an integer at the root and a right subtree. In either case, once the whole tree is received, the channel must be closed, as witnessed by the final
 . Beyond first-order context-free session types (where only basic types are exchanged) [2, 68] we may be interested in higher-order session types capable of exchanging values of complex types [19]. A goal of this paper is the integration of higher-order context-free session types into system \(F^{\mu }_\omega \). We want to be able to abstract the type that is received on a tree channel, which is now possible by writing
. Beyond first-order context-free session types (where only basic types are exchanged) [2, 68] we may be interested in higher-order session types capable of exchanging values of complex types [19]. A goal of this paper is the integration of higher-order context-free session types into system \(F^{\mu }_\omega \). We want to be able to abstract the type that is received on a tree channel, which is now possible by writing
 , where
, where
 is the kind of functional types.
is the kind of functional types.
A form of abstraction over session types with general recursion was proposed by Das et al. [24, 25] via (nested) parametric polymorphism. In the notation of Das et al., we can write a type equation for abstracting the type being received on a stream channel
 . Using abstractions, we can write
. Using abstractions, we can write
 as a function of its parameter
as a function of its parameter
 ,
,

 ; alternatively, we can use the
; alternatively, we can use the
 -operator to rewrite the
-operator to rewrite the
 type as
type as
 Das et al. proved that parametrized type definitions over regular session types are strictly more expressive than context-free session types. To some extent, this analogy guides our approach: if adding abstraction (via parametric polymorphism) to regular types leads to nested types, what exactly does it mean to add abstraction (via a type-level \(\lambda \)-operator) to context-free types? Throughout this paper we analyse several increments to System \(F^\mu \) that culminate in adding \(\lambda \)-abstraction to context-free session types.
Das et al. proved that parametrized type definitions over regular session types are strictly more expressive than context-free session types. To some extent, this analogy guides our approach: if adding abstraction (via parametric polymorphism) to regular types leads to nested types, what exactly does it mean to add abstraction (via a type-level \(\lambda \)-operator) to context-free types? Throughout this paper we analyse several increments to System \(F^\mu \) that culminate in adding \(\lambda \)-abstraction to context-free session types.
One of our focuses is necessarily the analysis of the type equivalence problem. The uncertainty about the decidability of this problem over recursive parametric types goes back to the 1970s [16, 63]. Although the type equivalence problem for parametric (nested) session types and context-free session types is decidable, that for the combination of abstractions over context-free types may no longer be. In fact, this analysis constitutes an interesting journey towards a better understanding of the role of higher-order polymorphic recursion in presence of sequential composition, as well as the gains (and losses) resulting from combining abstraction with arbitrary (rather than tail) recursion.
Ultimately, decidability is not a sufficiently valuable measure regarding a type system’s practicality. We look for type systems that may be incorporated into compilers. For that reason, we are interested in algorithms for type equivalence checking. Equivalence in \(F^{\mu }_\omega \) alone is already at least as hard as equivalence of deterministic pushdown automata. If we restrict recursion to the monomorphic case (requiring recursion variables to denote proper types, that is of kind
 or
or
 , collectively denoted by
, collectively denoted by
 ) we lower the complexity of type equivalence to that of equivalence for finite-state automata. The extension with context-free session types is slightly more complex. In order to obtain “good” algorithms, we restrict the recursion to the monomorphic case, arriving at classes \(F^{\mu _*}_\omega , F^{\mu _*;}_\omega \). Now the type equality problem for \(F^{\mu _*;}_\omega \) translates to the equivalence problem for simple grammars, which is still decidable [4, 33]. Since \(F^{\mu _*;}_\omega \) subsumes \(F^{\mu _*}_\omega \), our proof of the decidability of type equivalence serves as an alternative to that of Cai et al. [14] (restricted to contractive types).
) we lower the complexity of type equivalence to that of equivalence for finite-state automata. The extension with context-free session types is slightly more complex. In order to obtain “good” algorithms, we restrict the recursion to the monomorphic case, arriving at classes \(F^{\mu _*}_\omega , F^{\mu _*;}_\omega \). Now the type equality problem for \(F^{\mu _*;}_\omega \) translates to the equivalence problem for simple grammars, which is still decidable [4, 33]. Since \(F^{\mu _*;}_\omega \) subsumes \(F^{\mu _*}_\omega \), our proof of the decidability of type equivalence serves as an alternative to that of Cai et al. [14] (restricted to contractive types).
Higher-order polymorphism allows for the definition of type operators and the internalisation of various (session-type) constructs that would otherwise be offered as built-in constructors. In this way, we are able to internalise basic session-type constructors such as sequential composition
 and the
and the
 type operator (which reverses the direction of communication between parties). Duality is often treated as an external macro. Gay et al. [34] explore different ways of handling the dual operator, all in a monomorphic setting. In the presence of polymorphism the dual operator cannot be fully eliminated without introducing co-variables. Internalisation offers a much cleaner solution.
type operator (which reverses the direction of communication between parties). Duality is often treated as an external macro. Gay et al. [34] explore different ways of handling the dual operator, all in a monomorphic setting. In the presence of polymorphism the dual operator cannot be fully eliminated without introducing co-variables. Internalisation offers a much cleaner solution.
Due to the presence of sequential composition, regular trees are not a powerful enough model for representing types (
 in Section 2 is an example). The main technical challenge when combining System \(F^{\mu }_\omega \) and context-free session types is making sure that the resulting model can still be represented by simple grammars, so that type equivalence may be decided by a practical algorithm. The difficulties arise with renaming bound variables. For infinite types, both renaming with fresh variables and using de Bruijn indices may create an infinite number of distinct variables, which makes the construction of a simple grammar simply impossible. For example, take the type
in Section 2 is an example). The main technical challenge when combining System \(F^{\mu }_\omega \) and context-free session types is making sure that the resulting model can still be represented by simple grammars, so that type equivalence may be decided by a practical algorithm. The difficulties arise with renaming bound variables. For infinite types, both renaming with fresh variables and using de Bruijn indices may create an infinite number of distinct variables, which makes the construction of a simple grammar simply impossible. For example, take the type
 , which stands for the infinite type
, which stands for the infinite type
 Renaming this type using a fresh variable at each step would result in a type of the form
Renaming this type using a fresh variable at each step would result in a type of the form
 , requiring infinitely many variables. Similarly, de Bruijn indices [27] yield a type of the form
, requiring infinitely many variables. Similarly, de Bruijn indices [27] yield a type of the form
 that requires an infinite number of natural indices. We thus introduce minimal renaming that uses the least amount of variable names as possible (cf. Gauthier and Pottier [30]). This ensures that only finitely many terminal symbols are necessary, allowing for translating types into simple grammars.
that requires an infinite number of natural indices. We thus introduce minimal renaming that uses the least amount of variable names as possible (cf. Gauthier and Pottier [30]). This ensures that only finitely many terminal symbols are necessary, allowing for translating types into simple grammars.
Type languages live in term languages and we propose a term language to consume \(F^{\mu ;}_\omega \) types. Based on Almeida et al. [2], we introduce a message-passing concurrent programming language. Type checking is decidable if type equivalence is, and it is, in particular, for \(F^{\mu _*;}_\omega \).
The main contributions of this paper are as follows.
-
The integration of (higher-order) context-free session types into system \(F^{\mu }_\omega \), dubbed \(F^{\mu ;}_\omega \).
-
A semantic definition of type equivalence via a labelled transition system.
-
The identification of a suitable fragment of System \(F^{\mu ;}_\omega \) for which type equivalence is reduced to the bisimilarity of simple grammars.
-
A proof that type equivalence on the full System \(F^{\mu ;}_\omega \) is at least as hard as bisimilarity of deterministic pushdown automata.
-
The first internalisation of the
 type operator in a type language.
type operator in a type language. -
A term language to consume \(F^{\mu ;}_\omega \) types and an accompanying metatheory.
The type system presented in the paper combines three constructions: sequential composition of session types, higher-order kinds via type-level abstraction and application, and higher-order recursion. Prior to our work there is the system by Almeida et al. [4] which incorporates sequential composition and (first-order) recursion, but no higher-order kinds. There is also the system by Cai et al. [14] which incorporates higher-order kinds and higher-order recursion, but no sequential composition. Our system is the first to incorporate all three constructions. Although some of the results are incremental and generalize results from the literature, the main technical challenge is understanding the border past which they do not hold anymore. For example, “just” including higher-order kinds into the system by Almeida et al. does not work, since we need to pay close attention to variable names, making sure that type equivalence is invariant with respect to alpha-conversion (renaming of bound variables). This called for a novel notion of renaming, inspired by Gauthier and Pottier [30]. Similarly, “just” including sequential composition into the system of Cai et al. does not work, since finite-state automata (or regular trees) are not enough to capture the expressive power of the new type system, even when restricted to first-order recursion. This required us to look at the more expressive framework of simple grammars, and introduce a translation from types to words of a simple grammar.
The rest of the paper is organised as follows. The next section motivates the type language and introduces the term language with an example. Section 3 introduces System \(F^{\mu ;}_\omega \), Section 4 discusses type equivalence and Section 5 shows that type equivalence is decidable for a fragment of the type language. Section 6 presents the term language and its metatheory. Section 7 discusses related work and Section 8 concludes the paper with pointers for future work. Proofs for the main results can be found in a technical report on arXiv [20].
2 Motivation
Our goal is to study type systems that combine equirecursion, higher-order polymorphism, and higher-order context-free session types, while incorporating these in programming languages.
Extensions of System F. Figure 1 motivates the construction by proposing six different type languages, culminating with \(F^{\mu ;}_\omega \). The initial system, \(F^{\mu }\), includes well-known basic type operators [57]: functions
 , records
, records
 and variants
and variants
 . Type
. Type
 is short for
is short for
 , the empty record; we can imagine that
, the empty record; we can imagine that
 stands in place of an arbitrary scalar type such as
stands in place of an arbitrary scalar type such as
 and
and
 . We also include variable names
. We also include variable names
 , type quantification
, type quantification
 and recursion
and recursion
 . To control type formation, all variable bindings must be kinded with some kind
. To control type formation, all variable bindings must be kinded with some kind
 , even if for the initial system, \(F^{\mu }\), we only use the functional kind
, even if for the initial system, \(F^{\mu }\), we only use the functional kind
 .
.
We then build on \(F^{\mu }\) by considering (regular, tail recursive) session types; we represent the resulting system by \(F^{\mu \cdot }\). For example
 is a type for a channel endpoint that receives an integer, sends a boolean, and terminates. At this point we introduce a kind
is a type for a channel endpoint that receives an integer, sends a boolean, and terminates. At this point we introduce a kind
 of session types to restrict the ways in which we can combine session and functional types together. For example, a well-formed type
of session types to restrict the ways in which we can combine session and functional types together. For example, a well-formed type
 is of kind
is of kind
 and requires
and requires
 to be also of kind
to be also of kind
 (whereas
(whereas
 can be of kind
can be of kind
 , that is
, that is
 or
or
 ). An example of an infinite session type is
). An example of an infinite session type is
 that endlessly outputs integer values. For a more elaborate example consider the type
that endlessly outputs integer values. For a more elaborate example consider the type
 that specifies a channel endpoint for receiving a (finite or infinite) stream of integer values. Communication ends after choice
that specifies a channel endpoint for receiving a (finite or infinite) stream of integer values. Communication ends after choice
 is selected.
is selected.
The next step of our construction takes us to context-free session types; the resulting system is denoted by \(F^{\mu ;}\). We introduce a new construct for sequential composition
 , and a new type
, and a new type
 , acting as the neutral element of sequential composition [68]. The message constructors are now unary (
, acting as the neutral element of sequential composition [68]. The message constructors are now unary (
 and
and
 ) rather than binary. In System \(F^{\mu ;}\) we distinguish between the traditional
) rather than binary. In System \(F^{\mu ;}\) we distinguish between the traditional
 type and the
type and the
 type. These types have different behaviours:
type. These types have different behaviours:
 terminates a channel, while
terminates a channel, while
 allows for further communication. Type equality is more subtle for context-free session types, because of the monoidal semantics of sequential composition. It is derivable from the following axioms:
allows for further communication. Type equality is more subtle for context-free session types, because of the monoidal semantics of sequential composition. It is derivable from the following axioms:

Although the syntax of \(F^{\mu \cdot }\) is not formally included in the syntax of \(F^{\mu ;}\), we can embed recursive session types into context-free session types by mapping
 into
into
 . It is well-known that context-free session types allow for higher computational expressivity: while \(F^{\mu }\) and \(F^{\mu \cdot }\) can be represented via finite-state automata, \(F^{\mu ;}\) can only be represented with simple grammars [4, 33].
. It is well-known that context-free session types allow for higher computational expressivity: while \(F^{\mu }\) and \(F^{\mu \cdot }\) can be represented via finite-state automata, \(F^{\mu ;}\) can only be represented with simple grammars [4, 33].
To finalise our construction, we include type abstraction
 and type application
and type application
 . Again, type abstraction binds a variable which must be kinded. Kinds can now be of higher-order
. Again, type abstraction binds a variable which must be kinded. Kinds can now be of higher-order
 . For each of the three systems \(F^{\mu }\), \(F^{\mu \cdot }\), \(F^{\mu ;}\) we arrive at a higher-order version, respectively \(F^{\mu }_\omega \), \(F^{\mu \cdot }_\omega \), \(F^{\mu ;}_\omega \) (all of which we represent as \(F^{M}_\omega \)). In System \(F^{\mu \cdot }_\omega \), for example, we can specify channels for receiving (finite or infinite) sequences of values of arbitrary (but fixed) types,
. For each of the three systems \(F^{\mu }\), \(F^{\mu \cdot }\), \(F^{\mu ;}\) we arrive at a higher-order version, respectively \(F^{\mu }_\omega \), \(F^{\mu \cdot }_\omega \), \(F^{\mu ;}_\omega \) (all of which we represent as \(F^{M}_\omega \)). In System \(F^{\mu \cdot }_\omega \), for example, we can specify channels for receiving (finite or infinite) sequences of values of arbitrary (but fixed) types,

where
 can be instantiated with the desired type; in particular,
can be instantiated with the desired type; in particular,
 would be equivalent to the aforementioned
would be equivalent to the aforementioned
 .
.
It turns out that the expressive power of general higher-order systems \(F^{M}_\omega \) is too large for practical purposes. Even the simplest case \(F^{\mu }_\omega \) is at least as expressive as deterministic pushdown automata (or equivalently, first-order grammars), for which known equivalence algorithms are notoriously impractical. By impractical we mean that, although there exists a proof of decidability (due to Sénizergues [61], later improved by Stirling and Jancar [46, 65]), the underlying algorithm is rather complex. To the best of our knowledge, there is no practical implementation of an algorithm to decide the equivalence of deterministic pushdown automata. This is essentially due to polymorphic recursion, which can be encoded by a higher-order \(\mu \)-operator (we provide an example at the end of Section 5). Therefore, it makes sense to restrict the kind
 of the recursion operator
of the recursion operator
 . We use the notation \(\mu _*\) to mean the subclass of types written using only
. We use the notation \(\mu _*\) to mean the subclass of types written using only
 -kinded recursion, i.e.,
-kinded recursion, i.e.,
 or
or
 .
.
Figure 2 summarizes the main relations between the classes of types in our paper. Firstly, we obtain a lattice where the expressive power increases as we travel down (from functional to session to context-free session types) and right (from simple polymorphism to higher-order polymorphism with monomorphic recursion to arbitrary recursion). Four of the classes can be represented using finite-state automata (up to \(F^{\mu _*\cdot }_\omega \)). By including sequential composition (\(F^{\mu ;}\) and \(F^{\mu _*;}_\omega \)) we are still able to represent types using simple grammars. Once we allow for arbitrary recursion, the expressiveness of our model requires the computational power of deterministic pushdown automata.
Programming with \(F^{\mu ;}_\omega \). We now turn our attention to the term language, a message passing, concurrent functional language, equipped with context-free session types. Start with a stream of values of type a. Such a stream, when seen from the side of the reader, offers two choices: Done and More. In the former case the interaction is over; in the latter the reader reads a value of type a, as in ?a, and recurses. This is the stream type we have seen before only that, rather than closing the channel endpoint (with type
 ), it terminates with type
), it terminates with type
 , so that it may be sequentially composed with other types. In this informal introduction to the term language we omit the kinds of type variables.
, so that it may be sequentially composed with other types. In this informal introduction to the term language we omit the kinds of type variables.

A fold channel, as seen from the side of the folder, is a type of the following form. We assume that application binds tighter than semicolon, that is, type
 is interpreted as
is interpreted as
 .
.

Consumers of this type first receive the folding function, then the starting element, then the elements to fold in the form of a stream, and finally output the result of the fold. The type terminates with
 for we do not expect type Fold to be further composed. Compare Fold with the type for a conventional functional left fold:
for we do not expect type Fold to be further composed. Compare Fold with the type for a conventional functional left fold:
 .
.
We now develop a function that consumes a Fold channel. Syntax
 is for the inverse function application with low priority, that is
is for the inverse function application with low priority, that is
 . Recall that
. Recall that
 is an alternative notation for the empty record type, {}.
is an alternative notation for the empty record type, {}.

Function foldServer consumes the initial part of the channel and passes the rest of the channel to the recursive function foldS that consumes the whole stream while accumulating the fold value. In the end, when branch Done is selected, the fold value is written on the channel and the channel closed. In general, the channel operators—
 ,
,
 ,
,
 —return the same channel in the form of a new identifier. It is customary to reuse the identifier name—c in the example, as in
—return the same channel in the form of a new identifier. It is customary to reuse the identifier name—c in the example, as in
 —since it denotes the same channel. Syntax
—since it denotes the same channel. Syntax
 hides the continuation channel. The case for the external choice—
hides the continuation channel. The case for the external choice—
 —also returns the continuation (in each branch) so that interaction on the channel endpoint may proceed.
—also returns the continuation (in each branch) so that interaction on the channel endpoint may proceed.
We may now write different clients for the foldServer. Examples include a client that generates a stream from a pair of integer values (denoting an interval); another that generates the stream from a list of values; and yet another that generates the stream from a binary tree. We propose a further client. Consider the type of a channel that exchanges trees in a serialized format [68]. Its polymorphic version, as seen from the point of view of the reader, is as follows:

We transform trees as we read from tree channels into streams. Function flatten receives a tree channel and a stream channel (as seen from the point of view of the writer, hence the
 ) and returns the unused part of the latter.
) and returns the unused part of the latter.

We are now in a position to write a client that checks whether all values in a tree channel are positive.

The client sends a function and the starting value on the fold channel. Then, it flattens the given tree t, receives the folded value and closes the channel. Syntax
 is for term-level type application. We mean to flatten a tree of
is for term-level type application. We mean to flatten a tree of
 values on a stream channel whose continuation is of type
values on a stream channel whose continuation is of type
 . The continuation channel is bound to
. The continuation channel is bound to
 so that we may further receive the fold value and thereupon close the channel. Syntax
so that we may further receive the fold value and thereupon close the channel. Syntax
 is for sequential composition and abbreviates
is for sequential composition and abbreviates
 given that {}, the
given that {}, the
 value, is linear and hence must be consumed.
value, is linear and hence must be consumed.
Finally, a simple application creates a new
 channel, passing one end to a thread that produces a tree channel. Function
channel, passing one end to a thread that produces a tree channel. Function
 creates a channel and returns its two ends. It then creates a
creates a channel and returns its two ends. It then creates a
 channel, distributes one end to a thread foldServer and the other to function allPositive. The
channel, distributes one end to a thread foldServer and the other to function allPositive. The
 primitive receives a suspended computation (a thunk, of the form
primitive receives a suspended computation (a thunk, of the form
 ) and creates a new thread that runs in parallel with that from where the
) and creates a new thread that runs in parallel with that from where the
 was issued.
was issued.

3 Kinds and Types
This section introduces in detail System \(F^{\mu ;}_\omega \), an extension of System \(F^{\mu }_\omega \) incorporating higher-order context-free session types. The syntax of types is presented in Fig. 3. A type is either a constant
 (as in Fig. 4), a type variable
(as in Fig. 4), a type variable
 , an abstraction
, an abstraction
 or an application
or an application
 . Besides incorporating the standard session type constructors as constants, system \(F^{\mu ;}_\omega \) also includes
. Besides incorporating the standard session type constructors as constants, system \(F^{\mu ;}_\omega \) also includes
 as a constant for a type operator mapping a session type to its dual. Note also that
as a constant for a type operator mapping a session type to its dual. Note also that
 is syntactic sugar for
is syntactic sugar for
 . Analogously,
. Analogously,
 abbreviates
abbreviates
 . This simplifies our analysis as lambda abstraction becomes the only binding operator.
. This simplifies our analysis as lambda abstraction becomes the only binding operator.
A distinction between session and functional types is made resorting to kinds
 and
and
 , respectively. These are the kinds of proper types,
, respectively. These are the kinds of proper types,
 ; we use the symbol
; we use the symbol
 to represent either the kind of a proper type or that of a type operator, of the form
to represent either the kind of a proper type or that of a type operator, of the form
 . A kinding context \(\varDelta \) stores kinds for type variables using bindings of the form
. A kinding context \(\varDelta \) stores kinds for type variables using bindings of the form
 . Notation
. Notation
 denotes the update of kinding context \(\varDelta \), defined as
denotes the update of kinding context \(\varDelta \), defined as
 and
and
 when
when
 .
.
To define type formation, we require a few notions. Firstly comes the notion of renaming, adapted from Gauthier and Pottier [30] and presented in Fig. 5. Renaming essentially replaces a type
 by a minimal alpha-conversion of
by a minimal alpha-conversion of
 . By alpha-conversion we mean that
. By alpha-conversion we mean that
 renames bound variables in
renames bound variables in
 . By “minimal” we mean that each bound variable is renamed to its lowest possible value. We assume at our disposal a countable well-ordered set of type variables
. By “minimal” we mean that each bound variable is renamed to its lowest possible value. We assume at our disposal a countable well-ordered set of type variables
 . In
. In
 , parameter S is a set containing type variables unavailable for renaming; in the outset of the renaming process S is the empty set, since all variables are available. In that case the subscript S is often omitted. The case for lambda abstraction renames the bound variable by the smallest variable not in the set
, parameter S is a set containing type variables unavailable for renaming; in the outset of the renaming process S is the empty set, since all variables are available. In that case the subscript S is often omitted. The case for lambda abstraction renames the bound variable by the smallest variable not in the set
 , which we denote by
, which we denote by
 .
.
Renaming is what allows us to check whether type abstractions
 ,
,
 are equivalent. For the types to be equivalent, both bound variables
are equivalent. For the types to be equivalent, both bound variables
 and
and
 ought to be renamed to the same variable
ought to be renamed to the same variable
 . In summary, renaming provides a syntax-guided approach to the equivalence of lambda-abstractions, where the names of bound variables should not matter. Our notion of type equivalence preserves alpha-conversions up to renaming: if
. In summary, renaming provides a syntax-guided approach to the equivalence of lambda-abstractions, where the names of bound variables should not matter. Our notion of type equivalence preserves alpha-conversions up to renaming: if
 and
and
 only differ on bound variables, then
only differ on bound variables, then
 and in particular
and in particular
 . We will come back to this point after we define type equivalence in Section 4.
. We will come back to this point after we define type equivalence in Section 4.
We can easily see that renaming uses the minimum amount of variable names possible; for example,
 . Notice how both bound variables
. Notice how both bound variables
 and
and
 are renamed to
are renamed to
 , the first variable available for replacement. Also, renaming blatantly violates the Barendregt’s variable convention [9] used in so many works; for example
, the first variable available for replacement. Also, renaming blatantly violates the Barendregt’s variable convention [9] used in so many works; for example
 , where variable
, where variable
 is both free and bound in the resulting type. Even if renaming violates the variable convention, substitution can still be performed without resorting to the “on-the-fly” renaming of Curry and Feys [21, 40]. When
is both free and bound in the resulting type. Even if renaming violates the variable convention, substitution can still be performed without resorting to the “on-the-fly” renaming of Curry and Feys [21, 40]. When
 , we have that
, we have that

Then, we have
 since the renaming rule for application guarantees that
since the renaming rule for application guarantees that
 . Otherwise if
. Otherwise if
 , we have
, we have
 . This justifies the inclusion of set S in the renaming process. From now on, we assume that all types have gone through the renaming process.
. This justifies the inclusion of set S in the renaming process. From now on, we assume that all types have gone through the renaming process.
Next comes the notion of type reduction (Fig. 6). Apart from beta reduction (rule R-\(\beta \)), the definition provides for sequential composition, for unfolding recursive types and for reducing
 types. Note that renaming is further invoked in rule R-\(\beta \) for beta reduction does not preserve renaming: consider the renamed type
types. Note that renaming is further invoked in rule R-\(\beta \) for beta reduction does not preserve renaming: consider the renamed type
 . The type resulting from the substitution
. The type resulting from the substitution
 is
is
 which is not renamed and, therefore, not equivalent to
which is not renamed and, therefore, not equivalent to
 according to our rules in Section 4. Thanks to our modified rule R-\(\beta \), we preserve renaming under reductions: if
according to our rules in Section 4. Thanks to our modified rule R-\(\beta \), we preserve renaming under reductions: if
 and
and
 then
then
 .
.
We also need the notion of weak head normal form borrowed from the lambda calculus [9, 10]. We say that a type
 is in weak head normal form,
is in weak head normal form,
 , if it is irreducible, i.e.,
, if it is irreducible, i.e.,
 . Although this is a negative definition, in the technical report we provide an equivalent, rule-based characterisation of weak head normal form types, which can be used in a compiler as well as in our proofs. We say that type
. Although this is a negative definition, in the technical report we provide an equivalent, rule-based characterisation of weak head normal form types, which can be used in a compiler as well as in our proofs. We say that type
 normalises to type
normalises to type
 , written
, written
 , if
, if
 and
and
 is reached from
is reached from
 in a finite number of reduction steps (note that any term which is already whnf normalises to itself). We write
in a finite number of reduction steps (note that any term which is already whnf normalises to itself). We write
 to denote that
to denote that
 for some
for some
 .
.
For example, suppose we want to normalise the type
 , where
, where
 is the type
is the type
 . By computing all reductions from
. By computing all reductions from
 , we obtain
, we obtain
 for which we conclude that
for which we conclude that
 . Similarly, we can reason that
. Similarly, we can reason that
 ,
,
 and
and
 are all examples of non-normalising expressions.
are all examples of non-normalising expressions.
Equipped with normalisation, we can introduce type formation, which we do via the rules in Fig. 7. Rule K-Const introduces constants as types whose kinds match those of Fig. 4. Rule K-Var reads the kind of a type variable from context \(\varDelta \). An abstraction
 is a well-formed type with kind
is a well-formed type with kind
 if
if
 is well formed in context \(\varDelta \) updated with entry
is well formed in context \(\varDelta \) updated with entry
 (rule K-TAbs). The update is necessary since we are dealing with renamed types and the same type variable may appear with different kinds in nested abstractions.
(rule K-TAbs). The update is necessary since we are dealing with renamed types and the same type variable may appear with different kinds in nested abstractions.
It is not until we reach rule K-TApp that we find a proviso about the normalisation of a type. This is standard and analogous to a condition on contractivity. The goal is to eliminate types that reduce indefinitely without reaching a whnf.
Theorem 1
Let
 .
.
-
Preservation. If
 , then
, then
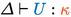 .
. -
Confluence. If
 and
and
 , then
, then
 and
and
 .
. -
Weak normalisation.
 for some
for some
 . Furthermore, if
. Furthermore, if
 , then
, then
 .
.
We finally arrive at the main decidability result in this section. In its proof, we make use of the fact that recursion is restricted to kind
 to limit the possible subexpressions of the form
to limit the possible subexpressions of the form
 that might appear in the normalisation of
that might appear in the normalisation of
 .
.
Theorem 2 (Decidability of type formation)
 is decidable for types in \(F^{\mu _*;}_\omega \).
is decidable for types in \(F^{\mu _*;}_\omega \).
4 Type equivalence
This section introduces type bisimulation as our notion of type equivalence. We define a labelled transition system (LTS) on the space of all types and write
 to denote that
to denote that
 has a transition by label
has a transition by label
 to
to
 . The grammar for labels and the LTS rules are in Fig. 8.
. The grammar for labels and the LTS rules are in Fig. 8.
If
 is not in weak head normal form, then we must normalise it to some type
is not in weak head normal form, then we must normalise it to some type
 , so that
, so that
 has the same transitions as
has the same transitions as
 (rule L-Red). Otherwise if
(rule L-Red). Otherwise if
 , then the transitions of
, then the transitions of
 can be immediately derived by looking at the corresponding rule for
can be immediately derived by looking at the corresponding rule for
 as follows. If
as follows. If
 is a variable, use rule L-Var1 (with \(m=0\)). If
is a variable, use rule L-Var1 (with \(m=0\)). If
 is a constant (other than
is a constant (other than
 ), use rule L-Const. Note that if
), use rule L-Const. Note that if
 is a lone
is a lone
 , then it has no transitions. If
, then it has no transitions. If
 is an abstraction, use rule L-Abs.
is an abstraction, use rule L-Abs.
If
 is an application, then we need to look inside the head. We write
is an application, then we need to look inside the head. We write
 as
as
 with \(m\ge 1\) where
with \(m\ge 1\) where
 is not an application, and look at
is not an application, and look at
 . If
. If
 is a variable, use rules L-Var1 and L-Var2. If
is a variable, use rules L-Var1 and L-Var2. If
 is one of the constants
is one of the constants
 ,
,
 ,
,
 or
or
 , use rule L-ConstApp. Note that
, use rule L-ConstApp. Note that
 is neither an abstraction nor
is neither an abstraction nor
 , since
, since
 is in weak head normal form. If
is in weak head normal form. If
 is
is
 , we use rules L-Msg1 and L-Msg2. If
, we use rules L-Msg1 and L-Msg2. If
 is
is
 , then the only way for
, then the only way for
 to be well-formed and in weak head normal form is if \(m=1\) and
to be well-formed and in weak head normal form is if \(m=1\) and
 is
is
 or
or
 , in which case we use rules L-DualVar1 and L-DualVar2.
, in which case we use rules L-DualVar1 and L-DualVar2.
If
 is
is
 , we require an additional case analysis on
, we require an additional case analysis on
 . If \(m=1\), use rule L-Seq1. Otherwise \(m=2\) due to kinding. If
. If \(m=1\), use rule L-Seq1. Otherwise \(m=2\) due to kinding. If
 is a variable, use rule L-VarSeq1 (with \(m=0\)). If
is a variable, use rule L-VarSeq1 (with \(m=0\)). If
 is a constant, then it must be of kind
is a constant, then it must be of kind
 .
.
 cannot be
cannot be
 , because
, because
 is in weak normal form, so it must be
is in weak normal form, so it must be
 , in which case we use rule L-EndSeq (
, in which case we use rule L-EndSeq (
 is an absorbing element, so
is an absorbing element, so
 simply makes a transition to
simply makes a transition to
 without executing
without executing
 ). If
). If
 is
is
 . Note that
. Note that
 cannot be an abstraction due to kinding.
cannot be an abstraction due to kinding.
If
 is an application, then again we write
is an application, then again we write
 as
as
 with \(n\ge 1\) where the head
with \(n\ge 1\) where the head
 is not an application, and look at
is not an application, and look at
 . If
. If
 is a variable, use rules L-VarSeq1 and L-VarSeq2. If
is a variable, use rules L-VarSeq1 and L-VarSeq2. If
 is a constant, it must be one of
is a constant, it must be one of
 ,
,
 ,
,
 ,
,
 or
or
 due to kinding. If
due to kinding. If
 is
is
 , use rules L-MsgSeq1 and L-MsgSeq2. If
, use rules L-MsgSeq1 and L-MsgSeq2. If
 is
is
 , use rule L-ChoiceSeq. If
, use rule L-ChoiceSeq. If
 is
is
 , the only way for
, the only way for
 to be well-formed and in weak head normal form is if \(n=1\) and
to be well-formed and in weak head normal form is if \(n=1\) and
 is
is
 or
or
 , in which case we use rules L-DualSeq1 and L-DualSeq2. Note that
, in which case we use rules L-DualSeq1 and L-DualSeq2. Note that
 cannot be
cannot be
 ,
,
 or an abstraction, since
or an abstraction, since
 is in weak normal form.
is in weak normal form.
Let us clarify our LTS rules with an example. Consider the following type
 and call it
and call it
 .
.
 is a type abstraction (on type variable
is a type abstraction (on type variable
 ), of kind
), of kind
 . It specifies a channel alternating between: offer a choice and output a value of type
. It specifies a channel alternating between: offer a choice and output a value of type
 ; or select a choice and input a value of type
; or select a choice and input a value of type
 . The polarity is swapped thanks to the application of constant
. The polarity is swapped thanks to the application of constant
 to the recursion variable
to the recursion variable
 . To construct the (fragment of the) LTS generated by this type, let us first desugar
. To construct the (fragment of the) LTS generated by this type, let us first desugar
 into
into
 where
where
 is the type
is the type
 . Notice that
. Notice that
 normalises to
normalises to
 . The LTS for the example is sketched in Fig. 9. In this case, only finitely many types appear. However, more elaborate examples involving sequential composition or higher-order recursion may lead to an infinite graph of transitions.
. The LTS for the example is sketched in Fig. 9. In this case, only finitely many types appear. However, more elaborate examples involving sequential composition or higher-order recursion may lead to an infinite graph of transitions.
Given the LTS rules, we can define, in the standard way, a notion of bisimulation. A binary relation R on types is called a bisimulation if, for every
 and every transition label
and every transition label
 :
:
-
1.
if
 , then there exists
, then there exists
 s.t.
s.t.
 and
and
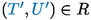 ;
; -
2.
if
 , then there exists
, then there exists
 s.t.
s.t.
 and
and
 .
.
We say that types
 and
and
 are bisimilar, written
are bisimilar, written
 , if there exists a bisimulation R such that
, if there exists a bisimulation R such that
 .
.
Intuitively, a notion of type equivalence must preserve and reflect the syntax of type constructors: for example, a type
 is equivalent to a type
is equivalent to a type
 iff
iff
 ,
,
 are equivalent and
are equivalent and
 ,
,
 are equivalent. Using the bisimulation technique, we achieve this by considering a labelled transition system on types:
are equivalent. Using the bisimulation technique, we achieve this by considering a labelled transition system on types:
 has a transition labelled
has a transition labelled
 to
to
 and a transition labelled
and a transition labelled
 to
to
 . In this way,
. In this way,
 can only be equivalent to another type which has two transitions with those same labels. For each of the type constructors (
can only be equivalent to another type which has two transitions with those same labels. For each of the type constructors (
 ,
,
 ,
,
 ,
,
 ,
,
 , and so on) we have suitable transition rules. Moreover, a type sometimes needs to be reduced before a type constructor is found at the root of the syntax tree. If
, and so on) we have suitable transition rules. Moreover, a type sometimes needs to be reduced before a type constructor is found at the root of the syntax tree. If
 normalizes to
normalizes to
 , then we expect
, then we expect
 and
and
 to be bisimilar, which is achieved thanks to rule L-Red. This handles the various reductions: beta-reductions arising from lambda-abstraction and applications (e.g.,
to be bisimilar, which is achieved thanks to rule L-Red. This handles the various reductions: beta-reductions arising from lambda-abstraction and applications (e.g.,
 reduces to
reduces to
 ), reductions arising from the monoidal structure of sequential composition (e.g.,
), reductions arising from the monoidal structure of sequential composition (e.g.,
 reduces to
reduces to
 ), reductions arising from the internalisation of duality as a type constructor (e.g.,
), reductions arising from the internalisation of duality as a type constructor (e.g.,
 reduces to
reduces to
 ) and reductions arising from the recursion (e.g.,
) and reductions arising from the recursion (e.g.,
 reduces to
reduces to
 ).
).
Our notion of type equivalence enjoys natural properties and behaves as expected with respect to the notions of reduction, normalisation and kinding from Section 3. We can derive rules for type equivalence, that could be used to define another coinductive notion of equivalence, via effective syntax-directed rules. We can show that type equivalence is preserved under renaming, reduction and normalisation. We can also show that the axioms for sequential composition in the introduction (1) are derivable from our notion of bisimulation. These additional results are presented in the technical report [20].
5 Decidability of type equivalence
This section presents results on decidability of type equivalence. Our approach consists in translating types to objects in some computational model. We look at finite-state automata (for types in \(F^{\mu }\), \(F^{\mu _*}_\omega \), \(F^{\mu \cdot }\), and \(F^{\mu _*\cdot }_\omega \)), simple grammars (for types in \(F^{\mu ;}\) and \(F^{\mu _*;}_\omega \)) and deterministic pushdown automata (for types in \(F^{\mu }_\omega \), \(F^{\mu \cdot }_\omega \) and \(F^{\mu ;}_\omega \)).
We say that a grammar in Greibach normal form is a tuple
 where: \(\mathcal T \) is a set of terminal symbols, denoted by
where: \(\mathcal T \) is a set of terminal symbols, denoted by
 ; \(\mathcal N \) is a set of nonterminal symbols, denoted by
; \(\mathcal N \) is a set of nonterminal symbols, denoted by
 ;
;
 is the starting word; and \(\mathcal R \subseteq \mathcal N \times \mathcal T \times \mathcal N ^*\) is a set of productions. A grammar is said to be simple if, for every nonterminal
is the starting word; and \(\mathcal R \subseteq \mathcal N \times \mathcal T \times \mathcal N ^*\) is a set of productions. A grammar is said to be simple if, for every nonterminal
 and every terminal
and every terminal
 , there is at most one production
, there is at most one production
 [51].
[51].
Greek letters
 and
and
 denote (possibly empty) words of nonterminal symbols. Productions are written as
denote (possibly empty) words of nonterminal symbols. Productions are written as
 . We define a notion of bisimulation for grammars via a labelled transition system. The system comprises a set of states \(\mathcal N ^*\) corresponding to words of nonterminal symbols. For each production
. We define a notion of bisimulation for grammars via a labelled transition system. The system comprises a set of states \(\mathcal N ^*\) corresponding to words of nonterminal symbols. For each production
 and each word of nonterminal symbols
and each word of nonterminal symbols
 , we have a labelled transition
, we have a labelled transition
 . We let \(\approx \) denote the bisimulation relation for grammars (the definition is similar to that in Section 4).
. We let \(\approx \) denote the bisimulation relation for grammars (the definition is similar to that in Section 4).
For the moment we focus on the class \(F^{\mu _*;}_\omega \) and we explain how to convert a type
 into a simple grammar
into a simple grammar
 . The conversion is based on a function
. The conversion is based on a function
 that maps each type
that maps each type
 into a word of nonterminal symbols, while introducing fresh nonterminals and productions. In our construction, following the approach by Costa et al. [19], we use a nonterminal symbol with no productions, denoted by
into a word of nonterminal symbols, while introducing fresh nonterminals and productions. In our construction, following the approach by Costa et al. [19], we use a nonterminal symbol with no productions, denoted by
 , in order to separate the two descendants of a send/receive operation such as
, in order to separate the two descendants of a send/receive operation such as
 . The sequence of nonterminal symbols
. The sequence of nonterminal symbols
 is defined as follows. First consider the cases in which
is defined as follows. First consider the cases in which
 .
.
-
For any \(m\ge 0\):
 for
for
 a fresh nonterminal symbol with a production
a fresh nonterminal symbol with a production
 as well as
as well as
 for each \(1\le j\le m\).
for each \(1\le j\le m\). -
 .
. -
 for
for
 a fresh symbol with a single production
a fresh symbol with a single production
 .
. -
for any
 :
:
 for
for
 a fresh nonterminal symbol with a single production
a fresh nonterminal symbol with a single production
 .
. -
 for
for
 a fresh symbol with a production
a fresh symbol with a production
 .
. -
for any \(m\ge 1\) and for
 one of
one of
 ,
,
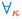 ,
,
 ,
,
 :
:
 for a fresh nonterminal
for a fresh nonterminal
 with a production
with a production
 for each \(1\le j\le m\).
for each \(1\le j\le m\). -
 for
for
 fresh with productions
fresh with productions
 and
and
 .
. -
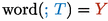 for
for
 a fresh symbol with a production
a fresh symbol with a production
 .
. -
 .
. -
 for
for
 a fresh symbol with productions
a fresh symbol with productions
 and
and
 .
.
Finally, let us handle the cases where
 is not in weak head normal form.
is not in weak head normal form.
-
If
 , then
, then
 .
. -
Otherwise if
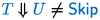 , then
, then
 for
for
 a fresh nonterminal symbol. Let
a fresh nonterminal symbol. Let
 . Then
. Then
 has a production
has a production
 for each production
for each production
 .
.
In the above construction, we create fresh symbols each time we encounter a weak head normal form other than
 . In other words,
. In other words,
 is the set containing
is the set containing
 and all nonterminals
and all nonterminals
 created during the computation of
created during the computation of
 . Another key insight is that the sequential composition of types is translated into a concatenation of words:
. Another key insight is that the sequential composition of types is translated into a concatenation of words:
 . This allows our construction to terminate: even if the transitions lead to infinitely many types, they are split on the sequential composition operator, and so we only need to consider finitely many subexpressions.
. This allows our construction to terminate: even if the transitions lead to infinitely many types, they are split on the sequential composition operator, and so we only need to consider finitely many subexpressions.
For the last case in our construction to be well-defined, i.e., when
 , we require
, we require
 to be non-empty. Indeed, if
to be non-empty. Indeed, if
 , then we can observe (by inspecting all cases) that
, then we can observe (by inspecting all cases) that
 iff
iff
 . We also need to argue that the construction of
. We also need to argue that the construction of
 eventually terminates. For this, we keep track of all types visited during the construction, and we only add a fresh nonterminal
eventually terminates. For this, we keep track of all types visited during the construction, and we only add a fresh nonterminal
 to our grammar if the type visited is syntactically different from all types visited so far. Therefore, we reuse the same symbol
to our grammar if the type visited is syntactically different from all types visited so far. Therefore, we reuse the same symbol
 with the same productions each time we revisit a type. With all these observations, we get the following result.
with the same productions each time we revisit a type. With all these observations, we get the following result.
Lemma 1
Suppose that
 . Then the construction of
. Then the construction of
 terminates producing a simple grammar.
terminates producing a simple grammar.
We illustrate the above construction with the polymorphic tree exchanging example from Section 2,

that is written in \(F^{\mu _*;}_\omega \) as
 For ease of notation, in this example we write
For ease of notation, in this example we write
 as shorthand for
as shorthand for
 . Since
. Since
 is in weak head normal form,
is in weak head normal form,
 returns a fresh symbol, which we call
returns a fresh symbol, which we call
 . We also have a production
. We also have a production
 , where
, where
 is the type
is the type
 . Since
. Since
 is not in whnf, we must normalise it, to get
is not in whnf, we must normalise it, to get
 . Therefore
. Therefore
 returns a fresh symbol, which we call
returns a fresh symbol, which we call
 . To obtain the transitions of
. To obtain the transitions of
 , we must first compute
, we must first compute
 , which is a fresh symbol
, which is a fresh symbol
 with transitions
with transitions
 and
and
 . Thus we also get
. Thus we also get
 and
and
 .
.
We have
 , but we still need to compute
, but we still need to compute
 . This type normalises to
. This type normalises to
 since
since
 . Thus
. Thus
 is a fresh symbol
is a fresh symbol
 . To obtain the productions of
. To obtain the productions of
 we must compute
we must compute
 . At this point we already have
. At this point we already have
 and
and
 . We still need to compute
. We still need to compute
 , which is a fresh symbol
, which is a fresh symbol
 with productions
with productions
 and
and
 . In turn,
. In turn,
 is a fresh symbol
is a fresh symbol
 with a production
with a production
 . Finally, we get
. Finally, we get
 , which means we can write the productions for
, which means we can write the productions for
 :
:
 and
and
 .
.
Putting all this together, we can finally obtain the simple grammar:

Next, we argue that type equivalence (i.e., bisimilarity on types) corresponds to bisimilarity on the corresponding grammars. This is achieved by the following lemma, that asserts that the LTS of a type and the LTS of the corresponding word of nonterminals have exactly the same transitions.
Lemma 2 (Full abstraction)
Let
 and
and
 the corresponding simple grammar. Suppose also that
the corresponding simple grammar. Suppose also that
 .
.
-
1.
If
 then there exists
then there exists
 such that
such that
 and
and
 .
. -
2.
If
 then there exists
then there exists
 such that
such that
 and
and
 .
.
As a consequence of the above result, we get soundness and completeness of the bisimilarity
 with respect to the bisimilarity
with respect to the bisimilarity
 . Indeed by Lemma 2, any sequence of transitions starting from
. Indeed by Lemma 2, any sequence of transitions starting from
 can be matched by a sequence of transitions starting from
can be matched by a sequence of transitions starting from
 ; and similarly for
; and similarly for
 . Thus
. Thus
 iff
iff
 .
.
Theorem 3
The type equivalence problem is decidable for types in \(F^{\mu _*;}_\omega \).
For the remainder of this section, we look at the other classes of types in Fig. 2 and examine the computation models they correspond to. Since class \(F^{\mu ;}\) is contained in \(F^{\mu _*;}_\omega \), we can express types without \(\lambda \)-abstractions with simple grammars as well. In this way we recover previous results in the literature [4, 19].
Let us now look at the class \(F^{\mu _*\cdot }_\omega \). In this class we do not have
 nor sequential composition and message operators are binary (
nor sequential composition and message operators are binary (
 ) rather than unary. Since we do not have sequential composition, there is no need to consider words of nonterminals, and instead it suffices to translate types into single symbols, i.e., states in an automaton. Moreover, since there is no recursion beyond
) rather than unary. Since we do not have sequential composition, there is no need to consider words of nonterminals, and instead it suffices to translate types into single symbols, i.e., states in an automaton. Moreover, since there is no recursion beyond
 , only finitely many types can be reached from a given
, only finitely many types can be reached from a given
 . We can thus adapt our construction as follows for \(F^{\mu _*\cdot }_\omega \). In the definition of the LTS (Fig. 8):
. We can thus adapt our construction as follows for \(F^{\mu _*\cdot }_\omega \). In the definition of the LTS (Fig. 8):
-
discard all rules involving sequential composition;
-
discard rules L-Var1 for \(m>0\) and L-DualVar2 (they were only needed to distinguish types in sequential composition);
-
discard case
 in rule L-Const (so that
in rule L-Const (so that
 no longer has transitions);
no longer has transitions); -
replace
 with
with
 on the right-hand side of rules L-Var1 with \(m=0\) and L-Const;
on the right-hand side of rules L-Var1 with \(m=0\) and L-Const; -
discard rules L-Msg1 and L-Msg2 and treat
 like the other constants in rule L-ConstApp.
like the other constants in rule L-ConstApp.
Also replace the construction of
 into a construction of
into a construction of
 , associating to each type
, associating to each type
 a state in a finite-state automata. For each transition
a state in a finite-state automata. For each transition
 we have the corresponding transition
we have the corresponding transition
 . Notice that the resulting automata is deterministic since the original LTS is also deterministic (for each type
. Notice that the resulting automata is deterministic since the original LTS is also deterministic (for each type
 and label
and label
 , there is at most one transition
, there is at most one transition
 ). Since bisimilarity of deterministic finite-state automata can be decided in polynomial time [44], we get the following results.
). Since bisimilarity of deterministic finite-state automata can be decided in polynomial time [44], we get the following results.
Theorem 4
-
1.
To each type
 in \(F^{\mu _*\cdot }_\omega \) we can associate a finite-state automata corresponding to the (fragment of the) LTS generated by
in \(F^{\mu _*\cdot }_\omega \) we can associate a finite-state automata corresponding to the (fragment of the) LTS generated by
 .
. -
2.
The type equivalence problem is polynomial-time decidable for types in \(F^{\mu _*\cdot }_\omega \).
Clearly, Theorem 4 applies to the subclasses of \(F^{\mu _*\cdot }_\omega \): \(F^{\mu }\), \(F^{\mu \cdot }\) and \(F^{\mu _*}_\omega \). In this way we recover previous results in the literature [14, 19, 33].
Finally, we consider the classes \(F^{\mu }_\omega \), \(F^{\mu \cdot }_\omega \) and \(F^{\mu ;}_\omega \) involving arbitrarily-kinded recursion. We shall show that these classes are already powerful enough to simulate deterministic pushdown automata; hence, the type equivalence problem becomes impractical (i.e., no practical implementation of an algorithm is known). We only focus on the simplest case \(F^{\mu }_\omega \), as the others two classes are even more expressive. Instead of looking at deterministic pushdown automata, we look at deterministic first-order grammars, which constitute an equivalent model of computation [46]. This choice simplifies our construction. We say that a first-order grammar is a tuple
 where:
where:
-
\(\mathcal X \) is a set of variables
 ; \(\mathcal T \) is a set of terminal symbols
; \(\mathcal T \) is a set of terminal symbols
 ; \(\mathcal N \) is a set of nonterminal symbols
; \(\mathcal N \) is a set of nonterminal symbols
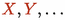
-
each nonterminal
 has an arity
has an arity
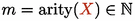 .
. -
the set \(\mathcal E \) of expressions over \(\mathcal X \), \(\mathcal N \) is inductively defined by two rules: any variable
 is an expression; if
is an expression; if
 and
and
 are expressions, then so is
are expressions, then so is
 . Whenever \(m=0\),
. Whenever \(m=0\),
 is called a constant.
is called a constant. -
 is an expression over \(\mathcal N \), called the initial expression.
is an expression over \(\mathcal N \), called the initial expression. -
\(\mathcal R \) is a set of productions. Each production is a triple
 , written as
, written as
 , where
, where
 and the variables in
and the variables in
 must be taken from
must be taken from
 .
.
A first-order grammar is deterministic if, for every
 and
and
 , there is at most one production
, there is at most one production
 .
.
Just as a simple grammar defines an LTS over words of nonterminals, a first-order grammar defines an LTS over the set \(\mathcal E _0\) of closed expressions. For each production
 we have the labelled transition
we have the labelled transition
 .
.
Let
 denote bisimilarity over closed expressions according to a first-order grammar. We now present a fully abstract (i.e., preserving bisimilarity) translation of a deterministic first-order grammar into a type in \(F^{\mu }_\omega \). Each grammar variable
denote bisimilarity over closed expressions according to a first-order grammar. We now present a fully abstract (i.e., preserving bisimilarity) translation of a deterministic first-order grammar into a type in \(F^{\mu }_\omega \). Each grammar variable
 has a corresponding type variable
has a corresponding type variable
 (of kind
(of kind
 ). An expression
). An expression
 is represented as a type application
is represented as a type application
 . If
. If
 has arity m and the productions
has arity m and the productions
 for a range of j, then we write the equation specifying
for a range of j, then we write the equation specifying
 as a record (since the first-order grammar is deterministic, all record labels are distinct, and thus the right-hand side on the equation specifying
as a record (since the first-order grammar is deterministic, all record labels are distinct, and thus the right-hand side on the equation specifying
 is well-formed).
is well-formed).

This gives rise to a system of equations
 , one for each nonterminal
, one for each nonterminal
 , where the nonterminals may appear in the right-hand sides
, where the nonterminals may appear in the right-hand sides
 . Finally, given an initial expression
. Finally, given an initial expression
 , it is standard how to convert it into a \(\mu \)-type using the system above.
, it is standard how to convert it into a \(\mu \)-type using the system above.
Using the above translation, we are able to simulate a transition
 of the first-order grammar as a transition
of the first-order grammar as a transition
 on the corresponding types. Therefore, the translation is fully abstract and we get the following result.
on the corresponding types. Therefore, the translation is fully abstract and we get the following result.
Theorem 5
Let
 and
and
 be closed expressions on a first-order grammar and
be closed expressions on a first-order grammar and
 the corresponding types. Then
the corresponding types. Then
 iff
iff
 .
.
Let us work on an example to better understand the above translation. Consider the language \(L_3 = \{\ell ^nar^na \mid n\ge 0\} \cup \{\ell ^nbr^nb \mid n\ge 0\}\) over the alphabet \(\{a,b,\ell ,r\}\). \(L_3\) is a typical example of a language that cannot be described with a simple grammar, but can be accepted by a deterministic pushdown automaton [51]. Consider the first-order grammar with nonterminals
 , initial expression
, initial expression
 , and productions
, and productions

Note that
 is a constant without productions. It is easy to see that the traces of this first-order grammar correspond exactly to the words in \(L_3\). By following the steps in the above translation, we arrive at the system of equations
is a constant without productions. It is easy to see that the traces of this first-order grammar correspond exactly to the words in \(L_3\). By following the steps in the above translation, we arrive at the system of equations

Therefore, the initial expression
 becomes the type
becomes the type

whose transitions simulate the transitions of the first-order grammar.
6 The term language and its metatheory
This section briefly introduces a concurrent functional language equipped with \(F^{\mu _*;}_\omega \) types, together with its metatheory. The results mostly follow from those in the literature, although explicit recursion at the term level and the unrestricted bindings in typing contexts are somewhat new in session types. The complete set of rules is to be found in the technical report [20].
The syntax of terms and processes is defined by the grammar in Fig. 10. The same figure introduces types for the constants. The term language is essentially the polymorphic lambda calculus with support for session operators, formulated as in Almeida et al. and Cai et al. [2, 14]. From System F it comprises terms and type abstractions, records and variants, including constructors and destructors in each case. The support for session operations and concurrency includes channel creation (
 ), the different channel operations (
), the different channel operations (
 ,
,
 ,
,
 ,
,
 and
and
 ) and thread creation (
) and thread creation (
 ). We program at the term level and use processes only for the runtime. Processes include terms as threads, parallel composition and channel creation, all inspired in the pi-calculus with double binders [73].
). We program at the term level and use processes only for the runtime. Processes include terms as threads, parallel composition and channel creation, all inspired in the pi-calculus with double binders [73].
Process typing and an excerpt of term typing is in Fig. 11. A judgement of the form
 records the fact that term
records the fact that term
 has type
has type
 under contexts \(\varDelta \) (recording kinds for type variables) and \(\varGamma \) (recording types for term variables). The judgement for processes,
under contexts \(\varDelta \) (recording kinds for type variables) and \(\varGamma \) (recording types for term variables). The judgement for processes,
 , says that
, says that
 is well-typed under context \(\varGamma \). It simplifies that for terms, since processes feature no free type variables and are assigned no particular type. Once again, the rules are adapted from the two above cited works. The difference to Cai et al. is that we work in a linear setting and hence axioms (T-Const and T-Var) work on an empty context, and most of the other rules must split the context accordingly. Rule T-TAbs simplifies that of Cai et al.; we can easily show that both rules are interchangeable. We support exponentials [37] for recursive functions, so that one may write functions that feature more than one recursive call (good for consuming binary trees, for example) and branches that do not use the recursive function (for code that is supposed to terminate). Towards this end, we add an unrestricted binding
is well-typed under context \(\varGamma \). It simplifies that for terms, since processes feature no free type variables and are assigned no particular type. Once again, the rules are adapted from the two above cited works. The difference to Cai et al. is that we work in a linear setting and hence axioms (T-Const and T-Var) work on an empty context, and most of the other rules must split the context accordingly. Rule T-TAbs simplifies that of Cai et al.; we can easily show that both rules are interchangeable. We support exponentials [37] for recursive functions, so that one may write functions that feature more than one recursive call (good for consuming binary trees, for example) and branches that do not use the recursive function (for code that is supposed to terminate). Towards this end, we add an unrestricted binding
 in term variable contexts, an explicit rule for
in term variable contexts, an explicit rule for
 (as opposed to making
(as opposed to making
 a constant as in Cai et al. [14]) and substructural rules for unrestricted bindings (T-Dereliction, T-Weakening and T-Contraction).
a constant as in Cai et al. [14]) and substructural rules for unrestricted bindings (T-Dereliction, T-Weakening and T-Contraction).
Thanks to the power of System F, most of the session and concurrency operators are expressed as constants. For example,
 receives a session type
receives a session type
 with
with
 , the payload of the message, an arbitrary type and
, the payload of the message, an arbitrary type and
 , the continuation, a session type, and returns a pair of the value received and the continuation channel. As usual
, the continuation, a session type, and returns a pair of the value received and the continuation channel. As usual
 abbreviates the type
abbreviates the type
 . The exception is the external choice (T-Match) which can not be captured by a type (similarly to T-Case) and hence requires a dedicated typing rule.
. The exception is the external choice (T-Match) which can not be captured by a type (similarly to T-Case) and hence requires a dedicated typing rule.
Process reduction is in Fig. 12. Following Milner [55] we factor out processes by means of a structural congruence relation that accounts for the associative and commutative nature of parallel composition, scope extrusion and exchanging the order of channel bindings. We now address the metatheory of our language, starting with preservation for both terms and processes.
Theorem 6 (Preservation)
-
1.
If
 and
and
 , then
, then
 .
. -
2.
If
 and
and
 , then
, then
 .
. -
3.
If
 and
and
 , then
, then
 .
.
Progress for the term language is assured only when the typing context contains channel endpoints only. When \(\varDelta \) is understood from the context we write
 to mean that \(\varGamma \) contains only types of kind
to mean that \(\varGamma \) contains only types of kind
 , that is
, that is
 for all types
for all types
 in \(\varGamma \). Well typed terms are values, or else they may reduce or are ready to reduce at the process level. Reduction in the case of session operations—
in \(\varGamma \). Well typed terms are values, or else they may reduce or are ready to reduce at the process level. Reduction in the case of session operations—
 ,
,
 ,
,
 ,
,
 ,
,
 —is pending a matching counterpart.
—is pending a matching counterpart.
Theorem 7 (Progress for the term language)
If
 , then
, then
 is a value,
is a value,
 reduces, or
reduces, or
 is stuck in one of the following forms:
is stuck in one of the following forms:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 , or
, or
 .
.
In order to state our result on the absence of runtime errors we need a few notions on the structure of terms and processes; here we follow Almeida et al. [2]. The subject of an expression
 , denoted by
, denoted by
 , is
, is
 in the following cases.
in the following cases.

Two terms
 and
and
 agree on channel
agree on channel
 , notation
, notation
 , in the following cases (symmetric forms omitted).
, in the following cases (symmetric forms omitted).

A closed process is a runtime error if it is structurally congruent to some process that contains a subexpression or subprocess of one of the following forms.
-
1.
 where
where
 is not a
is not a
 or a
or a
 and
and
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ;
; -
2.
 where
where
 in not a
in not a
 and
and
 ,
,
 ,
,
 ,
,
 ,
,
 ;
; -
3.
 and
and
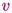 is not of the form
is not of the form
 ;
; -
4.
 and
and
 or
or
 with \(j \notin I\);
with \(j \notin I\); -
5.
 or
or
 or
or
 or
or
 or
or
 and
and
 is not an endpoint
is not an endpoint
 ;
; -
6.
 and
and
 ;
; -
7.
 and
and
 ,
,
 ,
,
 .
.
The four cases are standard to system F with records and variants. The support for session types and concurrency in the first two cases (term and type application) are derived from the types of values for such operators (Fig. 10). Item 5 addresses session operators applied to non endpoints. Item 6 is for two concurrent session operators on the same channel end. Finally, Item 7 is for mismatches on two session operations on two endpoints for the same channel.
Theorem 8 (Safety)
If
 , then
, then
 is not a runtime error.
is not a runtime error.
An algorithmic typing system can be easily extracted from the declarative system for terms in Fig. 11 via a bidirectional type system, formulated along the lines of Almeida et al. [2].
7 Related Work
Equirecursion in system F. In first investigations on equirecursive types, the notion of type equivalence is often formulated in a coinductive fashion [5, 11, 18, 29, 38]. Two types are equivalent if they unroll into the same infinite tree. Whenever this unrolling is the only type-level computation, such trees are regular, enabling efficient decision procedures. Some authors have studied equirecursion together with other notions of type-level computation. Solomon considers parameterized type definitions, which correspond to higher-order kinds [63]. These implicitly correspond to \(\lambda \)-terms, since reduction occurs as types are allowed to call other types. Some authors consider equirecursion in system \(F_\omega \), with weaker or stronger notions of equality [1, 12, 14, 41]. Regarding equirecursion in system F, the model of Cai et al. [14] is the closest to ours, and indeed our results up to \(F^{\mu _*\cdot }_\omega \) can be seen as a generalisation of theirs. However, Cai et al. depart from the usual setting by allowing non-contractive types (which most authors forbid, including this work), requiring a sort of infinitary lambda calculus. Moreover, this work further extends additional equivalence properties by including session types with their distinctive semantics, such as sequential composition and duality.
Session type systems. Session types were introduced in the 90s by Honda et al. [42, 43, 67]. Equirecursion was the first approach used to construct infinite session types, which often allows type equality to be interpreted according to a coinductive notion of bisimulation [52]. In this vein, Keizer et al. [48] utilize coalgebras to represent session types. Since the inception of session types, there has been an interest in extending the theory to nonregular protocols [58, 59, 66]. Context-free session types emerged as a natural extension, as it still allowed for practical type equality algorithms [3, 4, 19, 28, 56, 68]. Other approaches that go beyond regular session types include nested session types [24] as well as 1-counter, pushdown and 2-counter session types [33]. However, the more expressive notions are not amenable to practical type equivalence algorithms, just like the higher-order types present in our system \(F^{\mu }_\omega \). Polymorphism in session types has also been a topic of interest, with or without recursion [15, 22, 23, 31, 39].
Dual type operator. This work is, to the best of our knowledge, the first that internalises duality as a type constructor. Other settings, such as the language Alms [72], consider duality for session types as a user-definable, not built in, type function. Our
 is a type operator, not a type function. The difference is that a type function involves a type-level computation, which converges to a type written without dual. For example, in Alms we would have
is a type operator, not a type function. The difference is that a type function involves a type-level computation, which converges to a type written without dual. For example, in Alms we would have
 (as a type-level computation), both sides being the same type. In our setting,
(as a type-level computation), both sides being the same type. In our setting,
 is a type on its own, which happens to be equivalent to
is a type on its own, which happens to be equivalent to
 . At the same time, our setting allows for types such as
. At the same time, our setting allows for types such as
 , or
, or
 , which do not reduce.
, which do not reduce.
Type equivalence algorithms. Algorithms for deciding the equivalence of types must inherently be related to the computational power of the corresponding type system. This has been used implicitly or explicitly to obtain decidability results. As already explained, if equirecursion is the only type-level computation, types can be represented as finite-state automata (or equivalently, infinite regular trees). Although some exponential time algorithms were first proposed [32], it has been established that the problem can be solved in quadratic time [53], which is to be expected as it matches the corresponding problem of bisimulation of finite-state automata [44]; see also Pierce [57].
The next ‘simplest’ model of computation is that of simple grammars, which intuitively correspond to deterministic pushdown automata with a single state [33]. Almeida et al. [4] provided a practical algorithm for checking the bisimilarity of simple grammars. By dropping the determinism assumption, we arrive at Greibach normal form grammars, which are equivalent to basic process algebras [6, 7]. Bisimilarity algorithms have been studied extensively in this setting [13, 17, 47, 49]; presently it is known that the complexity of the problem lies between EXPTIME and 2-EXPTIME, which does not exclude the possibility of a polynomial time algorithm for the simpler model of simple grammars.
In this paper we present a reduction from first-order grammars to \(F^{\mu }_\omega \)-types, showing that the more expressive type systems (\(F^{\mu }_\omega \), presented here and in Cai et al. [14], as well as its extensions) are at least as powerful as deterministic pushdown automata. As far as we know, the closest result to ours is by Solomon [63], which shows conversions between a universe of “context-free types” and deterministic context-free languages. The universe of types studied by Solomon is different from \(F^{\mu }_\omega \). With some work we could prove that Solomon’s types can be embedded into \(F^{\mu }_\omega \), which would entail our result as a corollary. However, it is easier and simpler to prove directly the reduction as we did.
The equivalence problem for deterministic pushdown automata was a notorious open problem for a long time, until Sénizergues showed it to be decidable [61, 62]. Since his proof, many authors have tried to refine the result in an attempt to arrive at an implementable algorithm [46, 64, 65].
Concurrent term languages. The usefulness of a type system is directly related to its capability to be used in a programming language. Type systems such as the ones discussed in this work lend themselves quite readily to functional term languages [45]. For session types, existing term languages are either inspired in the pi calculus [26, 69, 73] or in the lambda calculus [35, 54, 70], or even the two [71]. The system presented in this paper is linear, meaning that resources must be used exactly once [50, 74]. Some authors go beyond linearity by considering unrestricted type qualifiers [48, 73] or manifest sharing [8].
8 Conclusion and future work
This paper introduces an extension of system F which includes equirecursion, lambda abstractions, and context-free session types. We present type equivalence algorithms, and a term language and its metatheory. Although we have defined a rather general system, it turns out that for practical purposes one must restrict recursion to
 , that is, to type-level monomorphic recursion. In any case, the main system \(F^{\mu _*;}_\omega \) is a non-trivial extension of (the contractive fragment of) \(F^{\mu _*}_\omega \) (studied by Cai et al. [14]) as well as \(F^{\mu ;}\) (studied by Almeida et al. [19]).
, that is, to type-level monomorphic recursion. In any case, the main system \(F^{\mu _*;}_\omega \) is a non-trivial extension of (the contractive fragment of) \(F^{\mu _*}_\omega \) (studied by Cai et al. [14]) as well as \(F^{\mu ;}\) (studied by Almeida et al. [19]).
We have only considered polymorphic types of a functional nature: type
 must always be of kind
must always be of kind
 . It is worth investigating polymorphism over session types, as it would allow further additional behaviour. For example, we could be interested in streaming values of heterogeneous nature, as in type
. It is worth investigating polymorphism over session types, as it would allow further additional behaviour. For example, we could be interested in streaming values of heterogeneous nature, as in type
 . It is however unclear whether this extension would still allow a translation into a simple grammar.
. It is however unclear whether this extension would still allow a translation into a simple grammar.
We proved that the type equivalence problem for systems \(F^{\mu }_\omega \), \(F^{\mu \cdot }_\omega \), \(F^{\mu ;}_\omega \) is at least as hard as a non-efficiently-decidable problem. We conjecture that these systems have the same power as deterministic pushdown automata (and hence, admit decidable type equivalence), but we do not have a construction to prove this result. In any case, our proof that the type equivalence problem is at least as hard as the bisimilarity of deterministic pushdown automata is enough to justify focus on the significant fragment with restricted recursion.
We study either full recursion (for theoretical results) or recursion limited to kind
 (for algorithmic results). It would be interesting to study in-between kinds of recursion; the next natural example is
(for algorithmic results). It would be interesting to study in-between kinds of recursion; the next natural example is
 . What model of computation would we arrive at if we consider types written with this recursion operator? We conjecture that types \(F^{\mu }_\omega \) and \(F^{\mu \cdot }_\omega \), when restricted to recursion of kind
. What model of computation would we arrive at if we consider types written with this recursion operator? We conjecture that types \(F^{\mu }_\omega \) and \(F^{\mu \cdot }_\omega \), when restricted to recursion of kind
 , would still be expressible as simple grammars, whereas such a restriction in the more powerful \(F^{\mu ;}_\omega \) would take us beyond this model, but perhaps without reaching the expressivity of deterministic pushdown automata.
, would still be expressible as simple grammars, whereas such a restriction in the more powerful \(F^{\mu ;}_\omega \) would take us beyond this model, but perhaps without reaching the expressivity of deterministic pushdown automata.
References
Abel, A.: Type-based termination: a polymorphic lambda-calculus with sized higher-order types. Ph.D. thesis, Ludwig Maximilians University Munich (2007), https://d-nb.info/984765581
Almeida, B., Mordido, A., Thiemann, P., Vasconcelos, V.T.: Polymorphic lambda calculus with context-free session types. Inf. Comput. 289(Part), 104948 (2022). https://doi.org/10.1016/j.ic.2022.104948
Almeida, B., Mordido, A., Vasconcelos, V.T.: FreeST: Context-free session types in a functional language. In: PLACES. EPTCS, vol. 291, pp. 12–23 (2019). https://doi.org/10.4204/EPTCS.291.2
Almeida, B., Mordido, A., Vasconcelos, V.T.: Deciding the bisimilarity of context-free session types. In: TACAS. LNCS, vol. 12079, pp. 39–56. Springer (2020). https://doi.org/10.1007/978-3-030-45237-7_3
Amadio, R.M., Cardelli, L.: Subtyping recursive types. In: POPL. pp. 104–118. ACM Press (1991). https://doi.org/10.1145/99583.99600
Baeten, J.C.M., Bergstra, J.A., Klop, J.W.: Decidability of bisimulation equivalence for processes generating context-free languages. In: PARLE. LNCS, vol. 259, pp. 94–111. Springer (1987). https://doi.org/10.1007/3-540-17945-3_5
Baeten, J.C.M., Bergstra, J.A., Klop, J.W.: Decidability of bisimulation equivalence for processes generating context-free languages. J. ACM 40(3), 653–682 (1993). https://doi.org/10.1145/174130.174141
Balzer, S., Pfenning, F.: Manifest sharing with session types. Proc. ACM Program. Lang. 1(ICFP), 37:1–37:29 (2017). https://doi.org/10.1145/3110281
Barendregt, H.P.: The lambda calculus - its syntax and semantics, Studies in logic and the foundations of mathematics, vol. 103. North-Holland (1985)
Barendregt, H.P.: The type free lambda calculus. In: Studies in Logic and the Foundations of Mathematics, vol. 90, pp. 1091–1132. Elsevier (1977)
Brandt, M., Henglein, F.: Coinductive axiomatization of recursive type equality and subtyping. Fundam. Informaticae 33(4), 309–338 (1998). https://doi.org/10.3233/FI-1998-33401
Bruce, K.B., Cardelli, L., Pierce, B.C.: Comparing object encodings. In: TACS. LNCS, vol. 1281, pp. 415–438. Springer (1997). https://doi.org/10.1007/BFb0014561
Burkart, O., Caucal, D., Steffen, B.: An elementary bisimulation decision procedure for arbitrary context-free processes. In: MFCS. LNCS, vol. 969, pp. 423–433. Springer (1995). https://doi.org/10.1007/3-540-60246-1_148
Cai, Y., Giarrusso, P.G., Ostermann, K.: System F-omega with equirecursive types for datatype-generic programming. In: POPL. pp. 30–43. ACM (2016). https://doi.org/10.1145/2837614.2837660
Caires, L., Pérez, J.A., Pfenning, F., Toninho, B.: Behavioral polymorphism and parametricity in session-based communication. In: ESOP. LNCS, vol. 7792, pp. 330–349. Springer (2013). https://doi.org/10.1007/978-3-642-37036-6_19
Cardelli, L., Wegner, P.: On understanding types, data abstraction, and polymorphism. ACM Comput. Surv. 17(4), 471–522 (1985). https://doi.org/10.1145/6041.6042
Christensen, S., Hüttel, H., Stirling, C.: Bisimulation equivalence is decidable for all context-free processes. Inf. Comput. 121(2), 143–148 (1995). https://doi.org/10.1006/inco.1995.1129
Colazzo, D., Ghelli, G.: Subtyping recursive types in kernel Fun. In: LICS. pp. 137–146. IEEE Computer Society (1999). https://doi.org/10.1109/LICS.1999.782605
Costa, D., Mordido, A., Poças, D., Vasconcelos, V.T.: Higher-order context-free session types in system F. In: PLACES. EPTCS, vol. 356, pp. 24–35 (2022). https://doi.org/10.4204/EPTCS.356.3
Costa, D., Mordido, A., Poças, D., Vasconcelos, V.T.: System \(F^{\mu }_{\omega }\) with context-free session types. CoRR abs/2301.08659 (2023), http://arxiv.org/abs/2301.08659
Curry, H.H., Feys, R., Craig, W. (eds.): Combinatory Logic, Volume I. North-Holland (1958)
Dardha, O.: Recursive session types revisited. In: BEAT. EPTCS, vol. 162, pp. 27–34 (2014). https://doi.org/10.4204/EPTCS.162.4
Dardha, O., Giachino, E., Sangiorgi, D.: Session types revisited. Inf. Comput. 256, 253–286 (2017). https://doi.org/10.1016/j.ic.2017.06.002
Das, A., DeYoung, H., Mordido, A., Pfenning, F.: Nested session types. In: ESOP. LNCS, vol. 12648, pp. 178–206. Springer (2021). https://doi.org/10.1007/978-3-030-72019-3_7
Das, A., DeYoung, H., Mordido, A., Pfenning, F.: Nested session types. ACM Trans. Program. Lang. Syst. 44(3), 19:1–19:45 (2022). https://doi.org/10.1145/3539656
Das, A., Pfenning, F.: Rast: A language for resource-aware session types. Log. Methods Comput. Sci. 18(1) (2022). https://doi.org/10.46298/lmcs-18(1:9)2022
De Bruijn, N.G.: Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with application to the Church-Rosser theorem. In: Indagationes Mathematicae. vol. 75, pp. 381–392. Elsevier (1972). https://doi.org/10.1016/1385-7258(72)90034-0
The FreeST programming language. https://freest-lang.github.io/ (2019)
Gapeyev, V., Levin, M.Y., Pierce, B.C.: Recursive subtyping revealed: functional pearl. In: ICFP. pp. 221–231. ACM (2000). https://doi.org/10.1145/351240.351261
Gauthier, N., Pottier, F.: Numbering matters: first-order canonical forms for second-order recursive types. In: ICFP. pp. 150–161. ACM (2004). https://doi.org/10.1145/1016850.1016872
Gay, S.J.: Bounded polymorphism in session types. MSCS 18(5), 895–930 (2008). https://doi.org/10.1017/S0960129508006944
Gay, S.J., Hole, M.: Subtyping for session types in the pi calculus. Acta Informatica 42(2-3), 191–225 (2005). https://doi.org/10.1007/s00236-005-0177-z
Gay, S.J., Poças, D., Vasconcelos, V.T.: The different shades of infinite session types. In: FoSSaCS. LNCS, vol. 13242, pp. 347–367. Springer (2022). https://doi.org/10.1007/978-3-030-99253-8_18
Gay, S.J., Thiemann, P., Vasconcelos, V.T.: Duality of session types: The final cut. In: PLACES. EPTCS, vol. 314, pp. 23–33 (2020). https://doi.org/10.4204/EPTCS.314.3
Gay, S.J., Vasconcelos, V.T.: Linear type theory for asynchronous session types. J. Funct. Program. 20(1), 19–50 (2010). https://doi.org/10.1017/S0956796809990268
Girard, J.Y.: Interprétation fonctionnelle et élimination des coupures de l’arithmétique d’ordre supérieur. Ph.D. thesis, Éditeur inconnu (1972)
Girard, J.: Linear logic. Theor. Comput. Sci. 50, 1–102 (1987). https://doi.org/10.1016/0304-3975(87)90045-4
Glew, N.: A theory of second-order trees. In: ESOP. LNCS, vol. 2305, pp. 147–161. Springer (2002). https://doi.org/10.1007/3-540-45927-8_11
Griffith, D.E.: Polarized substructural session types. Ph.D. thesis, University of Illinois at Urbana-Champaign (2016). https://doi.org/10.2172/1562827
Hindley, J.R., Seldin, J.P.: Introduction to Combinators and Lambda-Calculus. Cambridge University Press (1986)
Hinze, R.: Polytypic values possess polykinded types. Sci. Comput. Program. 43(2-3), 129–159 (2002). https://doi.org/10.1016/S0167-6423(02)00025-4
Honda, K.: Types for dyadic interaction. In: CONCUR. LNCS, vol. 715, pp. 509–523. Springer (1993). https://doi.org/10.1007/3-540-57208-2_35
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: ESOP. LNCS, vol. 1381, pp. 122–138. Springer (1998). https://doi.org/10.1007/BFb0053567
Hopcroft, J.E., Karp, R.M.: A linear algorithm for testing equivalence of finite automata. Tech. rep., Cornell University (1971)
Im, H., Nakata, K., Park, S.: Contractive signatures with recursive types, type parameters, and abstract types. In: ICALP. LNCS, vol. 7966, pp. 299–311. Springer (2013). https://doi.org/10.1007/978-3-642-39212-2_28
Jančar, P.: Short decidability proof for DPDA language equivalence via 1st order grammar bisimilarity. CoRR abs/1010.4760 (2010), http://arxiv.org/abs/1010.4760
Jančar, P.: Bisimilarity on basic process algebra is in 2-ExpTime (an explicit proof). Log. Methods Comput. Sci. 9(1) (2012). https://doi.org/10.2168/LMCS-9(1:10)2013
Keizer, A.C., Basold, H., Pérez, J.A.: Session coalgebras: A coalgebraic view on session types and communication protocols. In: ESOP. LNCS, vol. 12648, pp. 375–403. Springer (2021). https://doi.org/10.1007/978-3-030-72019-3_14
Kiefer, S.: BPA bisimilarity is EXPTIME-hard. Inf. Process. Lett. 113(4), 101–106 (2013). https://doi.org/10.1016/j.ipl.2012.12.004
Kobayashi, N., Pierce, B.C., Turner, D.N.: Linearity and the pi-calculus. ACM Trans. Program. Lang. Syst. 21(5), 914–947 (1999). https://doi.org/10.1145/330249.330251
Korenjak, A.J., Hopcroft, J.E.: Simple deterministic languages. In: SWAT. pp. 36–46. IEEE Computer Society (1966). https://doi.org/10.1109/SWAT.1966.22
Kozen, D., Silva, A.: Practical coinduction. Math. Struct. Comput. Sci. 27(7), 1132–1152 (2017). https://doi.org/10.1017/S0960129515000493
Lange, J., Yoshida, N.: Characteristic formulae for session types. In: TACAS. LNCS, vol. 9636, pp. 833–850. Springer (2016). https://doi.org/10.1007/978-3-662-49674-9_52
Lindley, S., Morris, J.G.: Talking bananas: structural recursion for session types. In: ICFP. pp. 434–447. ACM (2016). https://doi.org/10.1145/2951913.2951921
Milner, R.: Functions as processes. Math. Struct. Comput. Sci. 2(2), 119–141 (1992). https://doi.org/10.1017/S0960129500001407
Padovani, L.: Context-free session type inference. ACM Trans. Program. Lang. Syst. 41(2), 9:1–9:37 (2019). https://doi.org/10.1145/3229062
Pierce, B.C.: Types and programming languages. MIT Press (2002)
Puntigam, F.: Non-regular process types. In: Euro-Par. LNCS, vol. 1685, pp. 1334–1343. Springer (1999). https://doi.org/10.1007/3-540-48311-X_189
Ravara, A., Vasconcelos, V.T.: Behavioural types for a calculus of concurrent objects. In: Euro-Par. LNCS, vol. 1300, pp. 554–561. Springer (1997). https://doi.org/10.1007/BFb0002782
Reynolds, J.C.: Towards a theory of type structure. In: Programming Symposium. LNCS, vol. 19, pp. 408–423. Springer (1974). https://doi.org/10.1007/3-540-06859-7_148
Sénizergues, G.: The equivalence problem for deterministic pushdown automata is decidable. In: ICALP. LNCS, vol. 1256, pp. 671–681. Springer (1997). https://doi.org/10.1007/3-540-63165-8_221
Sénizergues, G.: L(A) = L(B)? decidability results from complete formal systems. In: ICALP. LNCS, vol. 2380, p. 37. Springer (2002). https://doi.org/10.1007/3-540-45465-9_4
Solomon, M.H.: Type definitions with parameters. In: POPL. pp. 31–38. ACM Press (1978). https://doi.org/10.1145/512760.512765
Stirling, C.: Decidability of DPDA equivalence. Theor. Comput. Sci. 255(1-2), 1–31 (2001). https://doi.org/10.1016/S0304-3975(00)00389-3
Stirling, C.: Deciding DPDA equivalence is primitive recursive. In: ICALP. Lecture Notes in Computer Science, vol. 2380, pp. 821–832. Springer (2002). https://doi.org/10.1007/3-540-45465-9_70
Südholt, M.: A model of components with non-regular protocols. In: SC. LNCS, vol. 3628, pp. 99–113. Springer (2005). https://doi.org/10.1007/11550679_8
Takeuchi, K., Honda, K., Kubo, M.: An interaction-based language and its typing system. In: PARLE. LNCS, vol. 817, pp. 398–413. Springer (1994). https://doi.org/10.1007/3-540-58184-7_118
Thiemann, P., Vasconcelos, V.T.: Context-free session types. In: ICFP. pp. 462–475. ACM (2016). https://doi.org/10.1145/2951913.2951926
Toninho, B., Caires, L., Pfenning, F.: Dependent session types via intuitionistic linear type theory. In: PPDP. pp. 161–172. ACM (2011). https://doi.org/10.1145/2003476.2003499
Toninho, B., Caires, L., Pfenning, F.: Higher-order processes, functions, and sessions: A monadic integration. In: ESOP. LNCS, vol. 7792, pp. 350–369. Springer (2013). https://doi.org/10.1007/978-3-642-37036-6_20
Toninho, B., Yoshida, N.: On polymorphic sessions and functions: A tale of two (fully abstract) encodings. ACM Trans. Program. Lang. Syst. 43(2), 7:1–7:55 (2021). https://doi.org/10.1145/3457884
Tov, J.A.: Practical programming with substructural types. Ph.D. thesis, Northeastern University (2012)
Vasconcelos, V.T.: Fundamentals of session types. Inf. Comput. 217, 52–70 (2012). https://doi.org/10.1016/j.ic.2012.05.002
Walker, D.: Advanced Topics in Types and Programming Languages, chap. Substructural Type Systems, pp. 3–44. The MIT Press (2005)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Poças, D., Costa, D., Mordido, A., Vasconcelos, V.T. (2023). System \(F^\mu _\omega \) with Context-free Session Types. In: Wies, T. (eds) Programming Languages and Systems. ESOP 2023. Lecture Notes in Computer Science, vol 13990. Springer, Cham. https://doi.org/10.1007/978-3-031-30044-8_15
Download citation
DOI: https://doi.org/10.1007/978-3-031-30044-8_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-30043-1
Online ISBN: 978-3-031-30044-8
eBook Packages: Computer ScienceComputer Science (R0)





 type operator in a type language.
type operator in a type language.






 , then
, then
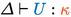 .
. and
and
 , then
, then
 and
and
 .
. for some
for some
 . Furthermore, if
. Furthermore, if
 , then
, then
 .
.

 . Normalisation
. Normalisation
 is represented as
is represented as
 and
and
 is a shorthand for type
is a shorthand for type
 .
. , then there exists
, then there exists
 s.t.
s.t.
 and
and
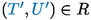 ;
; , then there exists
, then there exists
 s.t.
s.t.
 and
and
 .
. for
for
 a fresh nonterminal symbol with a production
a fresh nonterminal symbol with a production
 as well as
as well as
 for each
for each  .
. for
for
 a fresh symbol with a single production
a fresh symbol with a single production
 .
. :
:
 for
for
 a fresh nonterminal symbol with a single production
a fresh nonterminal symbol with a single production
 .
. for
for
 a fresh symbol with a production
a fresh symbol with a production
 .
. one of
one of
 ,
,
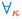 ,
,
 ,
,
 :
:
 for a fresh nonterminal
for a fresh nonterminal
 with a production
with a production
 for each
for each  for
for
 fresh with productions
fresh with productions
 and
and
 .
.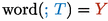 for
for
 a fresh symbol with a production
a fresh symbol with a production
 .
. .
. for
for
 a fresh symbol with productions
a fresh symbol with productions
 and
and
 .
. , then
, then
 .
. , then
, then
 for
for
 a fresh nonterminal symbol. Let
a fresh nonterminal symbol. Let
 . Then
. Then
 has a production
has a production
 for each production
for each production
 .
. then there exists
then there exists
 such that
such that
 and
and
 .
. then there exists
then there exists
 such that
such that
 and
and
 .
. in rule
in rule  no longer has transitions);
no longer has transitions); with
with
 on the right-hand side of rules
on the right-hand side of rules  like the other constants in rule
like the other constants in rule  in
in  .
. ;
;  ;
; 
 has an arity
has an arity
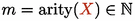 .
. is an expression; if
is an expression; if
 and
and
 are expressions, then so is
are expressions, then so is
 . Whenever
. Whenever  is called a constant.
is called a constant. is an expression over
is an expression over  , written as
, written as
 , where
, where
 and the variables in
and the variables in
 must be taken from
must be taken from
 .
.


 and
and
 , then
, then
 .
. and
and
 , then
, then
 .
. and
and
 , then
, then
 .
. where
where
 is not a
is not a
 or a
or a
 and
and
 ,
,
 ,
,
 ,
,
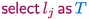 ,
,
 ,
,
 ;
; where
where
 in not a
in not a
 and
and
 ,
,
 ,
,
 ,
,
 ,
,
 ;
; and
and
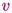 is not of the form
is not of the form
 ;
; and
and
 or
or
 with
with  or
or
 or
or
 or
or
 or
or
 and
and
 is not an endpoint
is not an endpoint
 ;
; and
and
 ;
; and
and
 ,
,
 ,
,
 .
.