Geometric Construction of the Covering Manifold

Abstract

In this chapter, we provide a geometric construction of a manifold extending a given Galois cover to a wreath product, using composita and fiber products. For this to be possible, a certain assumption on the homology, previously called (∗), needs to be strengthened to a new condition (∗∗) (equivalent in most cases). To motivate and use this new condition, we first recall the connection between homology of a quotient and coinvariants. Apart from geometric tools, the construction is also based on the vanishing of certain group cohomology, which is used to prove the existence of certain isometries of manifolds. In the final section, we give a universal property of the wreath product in relation to coverings of manifolds, just like there is such a universal property in the theory of Galois extensions of fields.

In this chapter, we provide a geometric construction of a manifold extending a given Galois cover to a wreath product, using composita and fiber products. For this to be possible, a certain assumption on the homology, previously called (∗), needs to be strengthened to a new condition (∗∗) (equivalent in most cases). To motivate and use this new condition, we first recall the connection between homology of a quotient and coinvariants. Apart from geometric tools, the construction is also based on the vanishing of certain group cohomology, which is used to prove the existence of certain isometries of manifolds. In the final section, we give a universal property of the wreath product in relation to coverings of manifolds, just like there is such a universal property in the theory of Galois extensions of fields.

1 From Quotient to Submodule

If ℓ is a prime number coprime to |G|, by Maschke’s theorem, any short exact sequence of F _ℓ[G]-modules splits, and condition (∗) from Theorem 6.4.1 is equivalent to

$$\displaystyle \begin{aligned} (\ast \ast) \ (\operatorname{Ind}_{H_1}^G \mathbf{1}) \otimes_{\mathbf{Z}} {\mathbf{F}}_\ell \ \mathit{is \ an} \ {\mathbf{F}}_\ell[G]\mathit{-submodule \ of} \ \operatorname{H}_1(M,{\mathbf{F}}_\ell). \end{aligned}$$

2 Homology of a Quotient as Coinvariants

We recall the following tool from invariant theory, see, e.g. [21, II §2]. If R is a commutative ring (for us, R is Z, Q or F _ℓ), H a finite group, and $\mathscr M$ is a (left) R[H]-module, its coinvariants are defined as the R-module $\mathscr M_H:= \mathscr M / I \mathscr M$ where I is the kernel of the augmentation map $R[H] \rightarrow R \colon \sum k_h h \mapsto \sum k_h$. An explicit description is given by

$$\displaystyle \begin{aligned} I \mathscr M = \langle h(x)-x \colon h \in H, x \in \mathscr M \rangle \end{aligned}$$

(by linearly, it suffices to let x run over a set of generators of $\mathscr M$). Denote the projection map by

$$\displaystyle \begin{aligned} \underline{\text{t}}_R \colon \mathscr M \rightarrow \mathscr M_H = \mathscr M / I \mathscr M. \end{aligned} $$

(7.1)

When R is clear from the context, we will leave it out of the notation and simply write $\underline {\text{t}}$ for this map.

This map is particularly easy if $\mathscr M = \bigoplus R[H] x_i$ is free as an R[H]-module with generators x _i; then $\mathscr M_H = \bigoplus R x_i$ with the obvious map, i.e.,

$$\displaystyle \begin{aligned} \underline{\text{t}}_R \colon \bigoplus R[H] x_i \rightarrow \bigoplus Rx_i \colon \sum_i \sum_h k_h h x_i \mapsto \sum_i \left(\sum_h k_h\right) x_i,\end{aligned} $$

(7.2)

cf. [21, (2.3)].

One may use “transfer” to prove the following (the case of a free action is also in [21, II.(2.4)]).

Lemma 7.2.1 ([16, III.2.4])

If H is a finite group of isometries of a closed smooth manifold M with quotient map

$$\displaystyle \begin{aligned} q \colon M \rightarrow H \backslash M, \end{aligned}$$

and the order of H is coprime to the characteristic of the field K, then the first K-homology of the quotient, $\operatorname {H}_1(H \backslash M,K)$ , is isomorphic to the coinvariants $\operatorname {H}_1(M,K)_H$ of the first K-homology of M, and under this identification, the map q _∗ that q induces on the first homology groups is the map $\underline {\mathit{\text{t}}}_K$ from (7.1), i.e., we have a diagram

3 Geometric Construction

We refer back to the situation of diagram (6.10), and keep our assumption that F _ℓ is a field of order coprime to |G|. By condition (∗∗), we have a decomposition of F _ℓ[G]-modules

$$\displaystyle \begin{aligned} \operatorname{H}_1(M,{\mathbf{F}}_\ell) = \mathscr N \oplus V \cong \bigoplus {\mathbf{F}}_\ell \omega_i \oplus V \end{aligned}$$

(for some F _ℓ[G]-submodule V ), where the G-action on $\mathscr N$ is given in terms of the permutation of cosets as gω _i = ω _g(i), with the convention that i = 1 corresponds to the trivial H ₁-coset in G. We also let

$$\displaystyle \begin{aligned} V':=\bigoplus_{i \geq 2} {\mathbf{F}}_\ell \omega_i \end{aligned}$$

denote the vector space complement of F _ℓ ω ₁ in $\mathscr N$.

The quotient map q ₁: M → M ₁ = H ₁∖M induces a surjective map

$$\displaystyle \begin{aligned} q_{1*} \colon \operatorname{H}_1(M,{\mathbf{F}}_\ell) \rightarrow \operatorname{H}_1(M_1,{\mathbf{F}}_\ell), \end{aligned}$$

and we define $\omega _1^{\prime }:=q_{1*}(\omega _1)$.

Let Γ₁ denote the subgroup Γ₁ ≤ Γ₀ for which $M_1 = \Gamma _1 \backslash \widetilde M$.

Lemma 7.3.1

Suppose ℓ is coprime to |G| and condition (∗) (equivalently, (∗∗)) holds. Then we have a well-defined and commutative diagram:

(7.3)

where

• ι is the embedding of Γ in Γ ₁;

• r ₁: C ⁿ → C, (k ₁, …, k _n)↦k ₁ is projection onto the first coordinate;

• φ ₀ is defined by

  $$\displaystyle \begin{aligned} \varphi_0 \colon \operatorname{H}_1(M_1,{\mathbf{F}}_\ell) \xrightarrow{\cong} {\mathbf{F}}_\ell \omega_1^{\prime} \oplus W \$\rightarrow {\mathbf{F}}_\ell \cong C \\ k_1 \omega^{\prime}_1 + w \$\mapsto k_1 \qquad (k_1 \in {\mathbf{F}}_\ell, w \in W). \end{aligned} $$

  with W := q _1∗(V ⊕ V ′) a complementary vector space to ${\mathbf {F}}_\ell \omega _1^{\prime }$ in $\operatorname {H}_1(M_1,{\mathbf {F}}_\ell )$.

Proof

To see that this is well defined and the right square commutes, we need that $\omega _1^{\prime }$ is linear independent of W = q _1∗(V ⊕ V ′); so suppose that there are a ₁, a ₂ ∈F _ℓ such that $a_1 \omega _1^{\prime } + a_2 q_{1*}(v) = 0$ for some v ∈ V ⊕ V ′. This means that

$$\displaystyle \begin{aligned} a_1 \omega_1 + a_2 v \in \ker(q_{1*}). \end{aligned} $$

(7.4)

By Lemma 7.2.1, the kernel of q _1∗ is equal to the kernel of $\underline {\text{t}}_{{\mathbf {F}}_\ell }$, and by definition this kernel is spanned by elements h ₁(ω _i) − ω _i (i = 1, …, n) and h ₁(v) − v for v ∈ V  and h ₁ ∈ H ₁. Now

• for any h ₁ ∈ H ₁ ≤ G, $h_1(\omega _i)-\omega _i=\omega _{h_1(i)}-\omega _i$; if i = 1, this element is zero, since that index corresponds to the trivial conjugacy class of H ₁ in G, whereas if i ≠ 1, this element belongs to V ′, since then also h ₁(i) ≠ 1;

• since $\mathscr N \oplus V$ is a decomposition as F _ℓ[G]-modules, h ₁(v) − v ∈ V  for all v ∈ V  and all h ₁ ∈ H ₁. □

It follows that $\ker (q_{1*}) \subseteq V \oplus V'$, and by (7.4), a ₁ ω ₁ ∈ V ⊕ V ′. Since ω ₁ is linearly independent from V ⊕ V ′, we conclude that a ₁ = 0, as desired. This guarantees that if $\omega = \sum k_i \omega _i + v \in \operatorname {H}_1(M,{\mathbf {F}}_\ell )$ with v ∈ V  (so φ(ω) = (k ₁, …, k _n)), then $q_{1*}(\omega ) = k_1 \omega ^{\prime }_1 + w \in \operatorname {H}_1(M_1,{\mathbf {F}}_\ell )$ with w ∈ W, so

$$\displaystyle \begin{aligned} \varphi_0(q_{1*}(\omega)) = k_1 = r_1(\varphi(\omega)).\end{aligned}$$

Just like we defined $\Gamma =\ker \Psi$ in (6.11), we now set

$$\displaystyle \begin{aligned} \Gamma_1^{\prime} := \ker \chi_0 \vartriangleleft \Gamma_1 \ \mbox{and }\ M_1^{\prime}:= \Gamma_1^{\prime} \backslash \widetilde M \ \mbox{with covering map }\ q_1^{\prime} \colon M_1^{\prime} \rightarrow M_1. \end{aligned} $$

(7.5)

The following lemma describes the relationship between the group $\Gamma =\ker \Psi$ used in Chap. 6, and $\Gamma ^{\prime }_1:=\ker \chi _0$, the group used in this chapter.

Lemma 7.3.2

Suppose ℓ is coprime to |G| and condition (∗) (equivalently, (∗∗)) holds. The group $\Gamma '=\ker \Psi$ can be expressed in terms of the group $\Gamma _1^{\prime }=\ker \chi _0$ and a set $\{\overline g_1,\dots ,\overline g_n\}$ of lifts of {g ₁, …, g _n} to Γ ₀ , as $\Gamma ' = \Gamma ^{\prime }_{\mathrm {new}}$ , where

$$\displaystyle \begin{aligned} \Gamma^{\prime}_{\mathrm{new}} := \bigcap_{i=1}^n \overline g_i \Gamma_1^{\prime} \overline g_i^{-1} \cap \Gamma= \bigcap_{i=1}^n (\Gamma \cap \overline g_i \Gamma_1^{\prime} \overline g_i^{-1}) = \bigcap_{i=1}^n \overline g_i (\Gamma \cap \Gamma_1^{\prime}) \overline g_i^{-1}.\end{aligned} $$

(7.6)

Proof

The equalities in (7.6) follow since Γ is normal in Γ₀. It remains to prove $\Gamma ^{\prime }_{\mathrm {new}} = \ker \Psi$. Notice that it follows from diagram (7.3) that

$$\displaystyle \begin{aligned} \Gamma_1^{\prime} \cap \Gamma = \ker \chi_0 \cap \Gamma = \{\gamma \in \Gamma \mid r_1 \circ \Psi(\gamma) = 0 \} = \Psi^{-1}( \{0\} \times C^{n-1} ). \end{aligned} $$

(7.7)

Since Ψ is surjective, this implies $\Psi (\Gamma _1^{\prime } \cap \Gamma ) = \{0\} \times C^{n-1}.$ Since by definition

$$\displaystyle \begin{aligned} \Phi(g_i)(\{0\} \times C^{n-1}) = C^{i-1} \times \{0\} \times C^{n-i}, \end{aligned}$$

from diagram (6.12), we conclude that

$$\displaystyle \begin{aligned} \Psi(\overline g_i (\Gamma_1^{\prime} \cap \Gamma) \overline g_i^{-1}) = \Phi(g_i) \Psi(\Gamma_1^{\prime} \cap \Gamma) = C^{i-1} \times \{0\} \times C^{n-i}, \end{aligned} $$

(7.8)

and therefore

$$\displaystyle \begin{aligned} \Psi(\Gamma^{\prime}_{\mathrm{new}}) \subseteq \bigcap\limits_i C^{i-1} \times \{0\} \times C^{n-i} = \{0\}, \end{aligned}$$

so $\Gamma ^{\prime }_{\mathrm {new}} \subseteq \ker \Psi$.

To prove the reverse inclusion, assume that Ψ(γ) = 0 for some γ ∈ Γ. Then by diagram (6.12) we also have $\Psi (\gamma _0^{-1} \gamma \gamma _0) = 0$ for any γ ₀ ∈ Γ₀, so

$$\displaystyle \begin{aligned} \gamma_0^{-1} \gamma \gamma_0 \in \Psi^{-1}(0) \subseteq \Psi^{-1}( \{0\} \times C^{n-1} ) \stackrel{(7.7)}{=} \Gamma_1^{\prime} \cap \Gamma. \end{aligned}$$

Therefore $\gamma \in \gamma _0 (\Gamma _1^{\prime } \cap \Gamma ) \gamma _0^{-1}$ for all γ ₀, showing that $\gamma \in \Gamma ^{\prime }_{\mathrm {new}}$, so $\ker \Psi \subseteq \Gamma ^{\prime }_{\mathrm {new}}$. □

Remark 7.3.3

Standard expressions for the kernel of the restriction and induction of representations (see, e.g., [54, Lemma 5.11]) allow one to give a representation-theoretic description of $\Gamma ^{\prime }_{\mathrm {new}}$. Namely, let $\widetilde \chi _0$ denote the linear character on Γ₁ given by $\widetilde \chi _0(\gamma )= e^{2\pi i \chi _0(\gamma )/\ell }$ where χ ₀ is as in diagram (7.3). Then, with $\ker \widetilde \chi _0 = \ker \chi _0 = \Gamma _1^{\prime }$, we have

$$\displaystyle \begin{aligned} \ker \operatorname{Res}_\Gamma^{\Gamma_0} \operatorname{Ind}_{\Gamma_1}^{\Gamma_0} \widetilde \chi_0 = \Gamma \cap \ker \operatorname{Ind}_{\Gamma_1}^{\Gamma_0} \widetilde \chi_0 = \Gamma \cap \bigcap_{\gamma_0 \in \Gamma_0} \gamma_0 \ker(\widetilde \chi_0) \gamma_0^{-1} = \Gamma^{\prime}_{\mathrm{new}}. \end{aligned}$$

We now perform the following 2-step geometric construction:

• (a) For g ∈ G, “twist” the cover q ₁: M → M ₁ by defining $q_1^g \colon M \rightarrow M_1$ by x↦q ₁(g ⁻¹ x), and set

  $$\displaystyle \begin{aligned} M_g^{\prime\prime}:= M_1^{\prime} \times_{M_1,q_1^g} M; \end{aligned}$$

  corresponding to the following diagram:

  

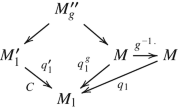  (7.9)

  The two different M in the diagram are in fact identical, but the maps to M ₁ are different.

• (b) Iteratively construct the fiber product

  $$\displaystyle \begin{aligned} M^{\prime}_{\mathrm{new}} := M^{\prime\prime}_{g_1} \times_M M^{\prime\prime}_{g_2} \times_M \dots \times_M M^{\prime\prime}_{g_n}, \end{aligned} $$

  (7.10)

  where {g ₁, …, g _n} is the chosen set of representatives for G∕H ₁; this is presented in the following diagram:

  

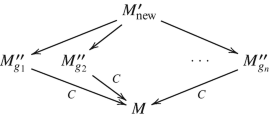  (7.11)

We will prove that this manifold $M^{\prime }_{\mathrm {new}}$ is the same as M′, the one constructed in the previous chapter.

Proposition 7.3.4

Suppose ℓ is coprime to |G| and condition (∗) (equivalently, (∗∗)) holds.

• (i) The fiber product $M^{\prime }_{\mathrm {new}}$ in (7.10) is represented as

  $$\displaystyle \begin{aligned} M^{\prime}_{\mathrm{new}} = \big\{ (x_1,\dots,x_n,x) \$\in M_1^{\prime} \times \cdots M_1^{\prime} \times M \mid \notag \\ \$q_1^{\prime}(x_i) = q_1(g_i^{-1}x), \ i =1,\dots,n \big\}, \end{aligned} $$

  (7.12)

  and in these coordinates, the projection $M^{\prime }_{\mathrm {new}} \to M^{\prime \prime }_{g_i}$ is given by

  $$\displaystyle \begin{aligned} M^{\prime}_{\mathrm{new}} \ni (x_1,x_2,\dots,x_n,x) \mapsto (x_i,x) \in M^{\prime\prime}_{g_i}. \end{aligned}$$

  $M^{\prime }_{\mathrm {new}}$ is a connected manifold and corresponds to the subgroup $\Gamma ^{\prime }_{\mathrm {new}}$ , so that in fact $M^{\prime }_{\mathrm {new}} = M'$.

• (ii) Geometrically, the action of $\widetilde G$ on $M^{\prime }_{\mathrm {new}}$ is expressed as follows in the coordinates used in (7.12): there exists an isometry $\iota \colon M^{\prime }_{\mathrm {new}} \rightarrow M^{\prime }_{\mathrm {new}}$ that conjugates the action of $\widetilde G$ into

  • $\underline {c}=(c_i) \in C^n \le \widetilde G$ acts componentwise on each factor $M^{\prime \prime }_{g_i}$ , i.e.,

    $$\displaystyle \begin{aligned} \iota^{-1} \underline{c} \iota \cdot (x_1,x_2,\dots,x_n,x) = (c_1 x_1,\dots,c_n x_n,x); \end{aligned} $$

    (7.13)

  • $g \in G \le \widetilde G$ acts on $M^{\prime }_{\mathrm {new}}$ by

    $$\displaystyle \begin{aligned} \iota^{-1} g \iota \cdot (x_1,x_2,\dots,x_n,x) = (x_{g^{-1}(1)},x_{g^{-1}(2)},\dots,x_{g^{-1}(n)},gx), \end{aligned} $$

    (7.14)

    where g ⁻¹(i) is defined, as before, via $g^{-1} g_i \in g_{g^{-1}(i)}H_1$ . Colloquially, this means that, up to an isometry, in diagram (7.11), g act naturally on the “base” manifold M, while the points in the various $M^{\prime \prime }_{g_j}$ above a given point in M are permuted across these different manifolds in the same way as g ⁻¹ permutes the cosets G∕H ₁.

Proof

Since the group homomorphism χ ₀: Γ₁ → C in diagram (7.3) is surjective, $\Gamma _1^{\prime } := \ker \chi _0 \vartriangleleft \Gamma _1$ is of index ℓ in Γ₁, and $q_1^{\prime } \colon M_1^{\prime } \rightarrow M_1$ is a C-Galois cover.

• (a) Since M ₁ is a manifold, the compositum is described as

  $$\displaystyle \begin{aligned} M_g^{\prime\prime} = \{ (x_1,x) \in M^{\prime}_1 \times M \colon q_1^{\prime}(x_1) = q_1(g^{-1} x) \}. \end{aligned}$$

  Since the degrees of the covers $q_1^{\prime } \colon M_1^{\prime } \rightarrow M_1$ and q ₁: M → M ₁ are coprime, Lemma 2.3.2 implies that $M^{\prime \prime }_g$ is connected and equal to the compositum. As in (6.5), the action of g ⁻¹ on M ₀ and M ₁ corresponds to the action on Γ₀ and the subgroup $\Gamma _1^{\prime }$ by conjugation with $\overline g^{-1}$, where $\overline g$ is a lift of g to Γ₀. Hence the corresponding group is the intersection $\Gamma _g^{\prime \prime }:=\Gamma \cap \overline g \Gamma _1^{\prime } \overline g^{-1}$, i.e., $M_g^{\prime \prime }=\Gamma _g^{\prime \prime } \backslash \widetilde M$. By Lemma 2.3.3 and coprimality of the degree, the covering $M_g^{\prime \prime } \rightarrow M$ is C-Galois.

• (b) Since M is a manifold, the underlying set of the fiber product is indeed the set theoretic fiber product in (7.12). We next argue that $M^{\prime }_{\mathrm {new}}$ is connected, agrees with the compositum, and indeed corresponds to the group $\Gamma ^{\prime }_{\mathrm {new}}$ (and hence Γ′) in (7.6), i.e., $M^{\prime }_{\mathrm {new}}=M'$. This will finish the proof of (i). To see the connectedness, we use induction with respect to the number of factors. So suppose we have already proven that $M_{g_1}^{\prime \prime } \times _M \dots M_{g_{N-1}}^{\prime \prime } \rightarrow M$ is a connected C ^N−1-cover corresponding to the group $\bigcap \limits _{i=1}^{N-1} \overline g_i (\Gamma \cap \Gamma _1^{\prime }) \overline g_i^{-1}$. By Lemma 2.3.2, the product with the next factor $M_{g_N}^{\prime \prime }$ is connected if and only if

  $$\displaystyle \begin{aligned} \Gamma = \langle \bigcap_{i=1}^{N-1} \overline g_i (\Gamma \cap \Gamma_1^{\prime}) \overline g_i^{-1}, \overline g_N (\Gamma \cap \Gamma_1^{\prime}) \overline g_N^{-1} \rangle. \end{aligned} $$

  (7.15)

  To prove this, we notice that is true after applying Ψ, using (7.8): the image of left hand side is C ⁿ, and the image of the right hand side is the subgroup of C ⁿ spanned by {0}^N−1 × C ^n−N and C ^N−1 ×{0}× C ^n−N, which equals the whole of C ⁿ. Hence Eq. (7.15) is true up to $\ker \Psi$, and from Lemma 7.3.2, it follows that $\ker \Psi$ is contained in both the left hand side and the right hand side of the equality, proving that (7.15) holds on the nose.

To prove (ii), note that $M^{\prime }_{\mathrm {new}} \to M$ is a C ⁿ-Galois cover by Lemma 2.3.3, with one copy of C acting componentwise on each factor $M^{\prime \prime }_{g_i}$, and this is the same as the action of C ⁿ on M′. The claim about the action of $g \in G \leq \widetilde G$ can be proven as follows: the action of G on M′ is given by considering G as a subgroup of $\widetilde G$, and as such it acts by isometries on M _new = M′. We know that, in the geometric representation (7.12) for $M^{\prime }_{\mathrm {new}}$,

$$\displaystyle \begin{aligned} g \underline{x} = \underline{y} \mbox{ with } \underline{x}=(x_1,\dots,x_n,x), \underline{y}= (y_1,\dots,y_n,y) \end{aligned}$$

for some unique $y_i \in M_1^{\prime }$ and y ∈ M with $q_1^{\prime }(y_i) \stackrel {\mathrm {(I)}}{=} q_1(g_i^{-1}y).$ We only need to determine what y _i and y are. Since the action of G on M is as given, $y\stackrel {\mathrm {(II)}}{=}gx$. Recall also that $g^{-1} g_i = g_{g^{-1}(i)}h_{g,i}$ for some h _g,i ∈ H ₁. In particular, with q ₁: M → M ₁ the covering with group H ₁, for x ∈ M we have $q_1((g^{-1}g_i)^{-1} x) \stackrel {\mathrm {(III)}}{=}q_1 (g_{g^{-1}(i)}^{-1} x).$ We collect this information to compute

$$\displaystyle \begin{aligned} q_1^{\prime}(y_i) \stackrel{\mathrm{(I)}}{=} q_1(g_i^{-1}y) \stackrel{\mathrm{(II)}}{=}q_1(g_i^{-1} g x) = q_1((g^{-1}g_i)^{-1} x) = q_1 (g_{g^{-1}(i)}^{-1} x) \stackrel{\mathrm{(III)}}{=}q_1^{\prime}(x_{g^{-1}(i)}). \end{aligned}$$

Since $q_1^{\prime } \colon M_1^{\prime } \rightarrow M_1$ is a C-cover, this shows that $y_i = c_i x_{g^{-1}(i)}$ for some $\underline {c} = (c_i) \in C^n$, that a priori depends on g and $\underline {x}$, i.e., it is a map

$$\displaystyle \begin{aligned} \underline{c} \colon G \times M' \rightarrow C^n. \end{aligned}$$

Let us first prove that it does not depend x ∈ M′. Denote the dependency on $\underline {x}$ by $\underline c( \underline {x})$. Let d(⋅, ⋅) denote the distance on a manifold induced from the Riemannian metric. Since C acts properly discontinuously on $M_1^{\prime }$ there is a δ > 0 such that, for any two elements c, c′∈ C and $x \in M_1^{\prime }$, if d(cx, c′x) < δ, then c′ = c. If $\underline {x}'$ is at distance ε from $\underline {x}$ in M′, then so is $g \underline {x}$ from $g \underline {x}'$, and hence so is $c_i( \underline {x}) x_{g^{-1}(i)}$ from $c_i( \underline {x}') x^{\prime }_{g^{-1}(i)}$ for all i. Hence

$$\displaystyle \begin{aligned} d(c_i(\underline{x})\$x_{g^{-1}(i)}, c_i(\underline{x}')x_{g^{-1}(i)}) \\ \$\leq d(c_i(\underline{x})x_{g^{-1}(i)}, c_i(\underline{x}')x^{\prime}_{g^{-1}(i)}) + d(c_i(\underline{x}')x^{\prime}_{g^{-1}(i)}, c_i(\underline{x}')x_{g^{-1}(i)}) \\ \$= d(c_i(\underline{x})x_{g^{-1}(i)}, c_i(\underline{x}')x^{\prime}_{g^{-1}(i)}) + d(x^{\prime}_{g^{-1}(i)}, x_{g^{-1}(i)}) \leq 2 \varepsilon, \end{aligned} $$

(the equality in the above formula holds since $c_i( \underline {x}')$ is an isometry) and thus $c_i( \underline {x}) = c_i( \underline {x}')$ as soon as $\underline {x}$ and $\underline {x}'$ are at distance < δ∕2. We conclude that $\underline c( \underline {x})$ is locally constant in $\underline {x}$, and since M′ is connected, $\underline {c}$ is actually independent of $\underline {x}$. so that we have a map

$$\displaystyle \begin{aligned} \underline{c} \colon G \rightarrow C^n. \end{aligned} $$

(7.16)

Now denote the dependence on g by $\underline {c}(g)$. We will prove that this is a cocycle; note that we write the group operation on C ⁿ multiplicatively. We observe that for two elements g, h ∈ G,

$$\displaystyle \begin{aligned} (c_i(gh) x_{(gh)^{-1}(i)}, gh x) \$ = gh \underline{x} = g(c_i(h) x_{h^{-1}(i)}, hx) \\ \$= (c_i(g) c_{g^{-1}(i)}(h) x_{h^{-1} g^{-1}(i)}, gh x), \end{aligned} $$

so $\underline {c}(gh) = \underline {c}(g) \underline {c}(h)^g$, where the action of g on $\underline {c}=(c_i)$ is given by $\underline {c}^g:=(c_{g^{-1}(i)})$. This shows that the map $\underline {c}$ in Eq. (7.16) is a cocycle from G to C ⁿ, and the corresponding first group cohomology class lies in $\operatorname {H}^1(G,C^n)$. Since |G| and |C ⁿ| = ℓ ⁿ are coprime, the latter cohomology group is zero [21, III.(10.1)], proving that $\underline {c}$ is a coboundary, i.e., there exists $\underline {v} \in C^n$ (independent of g) such that $\underline {c}(g) = \underline {v}^{-1} \underline {v}^g = (v_i^{-1} v_{g^{-1}(i)})$. Consider the isometry

$$\displaystyle \begin{aligned} \iota \colon M^{\prime}_{\mathrm{new}} \rightarrow M^{\prime}_{\mathrm{new}} \colon \underline{x} = (x_i,x) \mapsto (v_i^{-1} x_i, x). \end{aligned}$$

Now

$$\displaystyle \begin{aligned} \iota^{-1} g \iota(\underline{x}) = \iota^{-1} (c_i(g) v_{g^{-1}(i)}^{-1} x_{g^{-1}(i)}, gx) = \iota^{-1} (v_i^{-1} x_{g^{-1}(i)}, gx) = (x_{g^{-1}(i)},gx), \end{aligned}$$

as was claimed. Note also that conjugating by ι commutes with the action of C ⁿ, so it does not change that action. □

Remark 7.3.5

The action of $\widetilde G$ on $M_{\mathrm {{new}}}^{\prime }$ ties up with the group theoretical construction from the previous chapter, as follows. The group $\widetilde G \cong \Gamma _0 / \Gamma '$ acts naturally on $M' = \Gamma ' \backslash \widetilde M$ via

$$\displaystyle \begin{aligned} (\gamma_0 \Gamma') \cdot (\Gamma'\widetilde x) = \Gamma' \cdot (\gamma_0 \widetilde x). \end{aligned} $$

(7.17)

The explicit identification between M′ and $M_{\mathrm {{new}}}^{\prime }$ is given by the map

$$\displaystyle \begin{aligned} M' = \Gamma' \backslash \widetilde M \ni \Gamma' \widetilde x \mapsto (\Gamma_1^{\prime} \overline g_1^{-1}\widetilde x,\dots,\Gamma_1^{\prime}\overline g_n^{-1} \widetilde x,\Gamma \widetilde x) =: (x_1,\dots,x_n,x) \in M_{\mathrm{{new}}}^{\prime}, \end{aligned} $$

(7.18)

where {g _i H ₁} represent the cosets of H ₁ in G and $G \to \Gamma _0: g \mapsto \overline g$ is a section such that we have $\overline e_G = e_{\Gamma _0}$, $\overline {g^{-1}} = \overline g^{-1}$ and $\overline g \Gamma ' = \jmath (g)$ with the homomorphism ȷ : G → Γ₀∕ Γ′ representing the splitting of (6.14). The action of $\widetilde G \cong \Gamma _0/\Gamma '$, transferred from M′ to $M_{\mathrm {{new}}}^{\prime }$ is then

$$\displaystyle \begin{aligned} (\gamma_0 \Gamma') \cdot (\Gamma_1^{\prime} \overline g_1^{-1}\widetilde x,\dots,\Gamma_1^{\prime}\overline g_n^{-1} \widetilde x, \Gamma \widetilde x) = (\Gamma_1^{\prime}\overline g_1^{-1} \gamma_0 \widetilde x,\dots,\Gamma_1^{\prime}\overline g_n^{-1}\gamma_0 \widetilde x, \Gamma \gamma_0 \widetilde x). \end{aligned} $$

(7.19)

Let c ∈ Γ be an element satisfying Ψ(c) = e ₁ and set $c_i := \overline g_i c \overline g_i^{-1} \in \Gamma$, as in Sect. 6.3. Utilising the diagrams (6.12) and (7.3), we see that $c_i \in \overline g_j \Gamma _1^{\prime } \overline g_j^{-1}$ for all j ≠ i. Thus, (7.19) implies

$$\displaystyle \begin{aligned} \begin{array}{rcl} (c_i \Gamma') \cdot (x_1,\dots,x_n,x) \$ =\$\displaystyle (\Gamma_1^{\prime}\overline g_1^{-1} c_i \widetilde x,\dots,\Gamma_1^{\prime}\overline g_n^{-1} c_i \widetilde x, \Gamma c_i \widetilde x) \\ \$ =\$\displaystyle (\Gamma_1^{\prime}\overline g_1^{-1} \widetilde x, \dots, \underbrace{\Gamma_1^{\prime} c \overline g_i^{-1} \widetilde x}_{i\text{-th entry}}, \Gamma_1^{\prime}\overline g_n^{-1} \widetilde x, \Gamma \widetilde x).{} \end{array} \end{aligned} $$

(7.20)

Let g ∈ G; by definition, we have $\overline g^{-1} \overline g_i \Gamma _1^{\prime } = \overline g_{g^{-1}(i)} c^{- k_i(g)} \Gamma _1^{\prime }$ for some k _i(g) modulo ℓ. This implies that

$$\displaystyle \begin{aligned} \begin{array}{rcl} (\overline g \Gamma') \cdot (x_1,\dots,x_n,x) \$ \stackrel{(7.19)}{=}\$\displaystyle (\Gamma_1^{\prime} \overline g_1^{-1} \overline g \widetilde x, \dots, \Gamma_1^{\prime} \overline g_n^{-1} \overline g \widetilde x, \Gamma \overline g \widetilde x) \\ \$ =\$\displaystyle (\Gamma^{\prime}_1 c^{k_1(g)} \overline g_{g^{-1}(1)} \widetilde x,\dots,\Gamma^{\prime}_1 c^{k_n(g)} \overline g_{g^{-1}(n)} \widetilde x, \Gamma \overline g \widetilde x) \\ \$ \stackrel{(7.20)}{=}\$\displaystyle (c_1^{k_1(g)} \cdots c_n^{k_n(g)}\Gamma') \cdot (x_{g^{-1}(1)},\dots,x_{g^{-1}(n)},g \cdot x). \end{array} \end{aligned} $$

Now $g \mapsto (c_i^{k_i(g)}\Gamma ')_{i=1}^n$ is a cocycle from G to C ⁿ =  Γ∕ Γ′, and since $\operatorname {H}^1(G,C^n)=0$, there exists (m ₁, …, m _n) with $k_i(g) = m_{g^{-1}(i)}-m_i$ (modulo ℓ). Using the commutativity of the elements c _i Γ′, this implies that if we set $c_0 := \prod _{i=1}^n c_i^{m_i}$, then

$$\displaystyle \begin{aligned} (c_0 \jmath(g) c_0^{-1}) \cdot (x_1,\dots,x_n,x) = (x_{g^{-1}(1)},\dots,x_{g^{-1}(n)},g \cdot x) \end{aligned}$$

for all g ∈ G and all $(x_1,\dots ,x_n,x) \in M_{\mathrm {{new}}}^{\prime }$. This shows that a copy of G in $\widetilde G \cong \Gamma _0 / \Gamma '$, namely $c_0 \jmath (G) c_0^{-1}$, acts on $M_{\mathrm {{new}}}^{\prime }$ via permutation of the first n entries. In other words, it is possible to conjugate the subgroup G in $\widetilde G$ to realise the specific action (7.14) on $M_{\mathrm {{new}}}^{\prime }$.

4 Universal Property of the Wreath Product

The appearance of the wreath product in our constructions becomes less of a surprise given the following universal property, showing that the minimal Galois cover that “contains” a G-cover and a C-cover as in our situation arises from this wreath product (the analogous result in the theory of field extensions is well known, compare [37, 13.7]).

Proposition 7.4.1

Let G and C denote finite groups with C cyclic of prime order ℓ not dividing the order of G. Suppose that we are given Riemannian manifolds $M,M_1,M_1^{\prime }$ and a developable Riemannian orbifold M ₀ such that M → M ₀ is G-Galois with subcover M ₁ → M ₀ , and $M_1^{\prime } \rightarrow M_1$ is C-Galois. If N → M ₀ is a Galois cover of minimal degree admitting Riemannian covers N → M and $N \rightarrow M_1^{\prime }$ , then the Galois group G′ of N over M ₀ is the wreath product $\widetilde G:=C^n \rtimes G$ , where n is the degree of the cover M ₁ → M ₀ (see Figure (7.21).)

(7.21)

Proof

Writing the manifolds $M_0,M,M_1,M_1^{\prime },N$ as quotients of he universal cover $\widetilde M_0$ of M ₀ by the respectively group $\Gamma _0,\Gamma , \Gamma _1, \Gamma _1^{\prime }, \Gamma _N$, the defining properties of N imply that it is the normal closure of the compositum of $M_1^{\prime }$ and M over M ₀, and hence

$$\displaystyle \begin{aligned} \Gamma_N = \bigcap_{\gamma_0 \in \Gamma_0} \gamma_0 ( \Gamma \cap \Gamma_1^{\prime}) \gamma_0^{-1}. \end{aligned}$$

First of all, for g ∈ G, choose one element $\overline g \in \Gamma _0$ that maps to g ∈ Γ₀∕ Γ≅G. We claim that

$$\displaystyle \begin{aligned} \Gamma_N = \bigcap_{i=1}^n \Gamma_{g_i} \mbox{ where } \Gamma_{g_i} := \overline g_i ( \Gamma \cap \Gamma_1^{\prime}) {\overline g_i}^{-1}, \end{aligned}$$

for {g _i} a set of coset representatives for H ₁ in G. Indeed, for any γ ₀ ∈ Γ₀ we can write $\gamma _0 = \overline g_i \gamma _1$ for some i ∈{1, …, n} and some γ ₁ ∈ Γ₁, since the cosets of H ₁≅ Γ₁∕ Γ in G≅ Γ₀∕ Γ are g ₁ H ₁, …, g _n H ₁ and the cosets of Γ₁ in Γ₀ are therefore $\overline g_1 \Gamma _1,\dots , \overline g_n \Gamma _1$. The statement now follows from the fact that γ ₀ ∈ Γ₀ must lie in one of these cosets $\overline g_i \Gamma _1$; since both Γ and $\Gamma _1^{\prime }$ are normal in Γ₁, we have

$$\displaystyle \begin{aligned} \gamma_0 (\Gamma \cap \Gamma_1^{\prime} ) \gamma_0^{-1} \$ = (\overline g_i \gamma_1) (\Gamma \cap \Gamma_1^{\prime}) (\overline g_i \gamma_1)^{-1} = \overline g_i \gamma_1 (\Gamma \cap \Gamma_1^{\prime}) \gamma_1^{-1} \overline g_i^{-1} \\ \$= \overline g_i (\Gamma \cap \Gamma_1^{\prime}) \gamma_1 \gamma_1^{-1} \overline g_i^{-1} = \overline g_i (\Gamma \cap \Gamma_1^{\prime}) \overline g_i^{-1}. \end{aligned} $$

Now since Γ is normal in Γ₀, Γ ≥ Γ_N, and we find an exact sequence

$$\displaystyle \begin{aligned} 1 \rightarrow \Gamma/\Gamma_N \rightarrow \Gamma_0 / \Gamma_N \rightarrow \Gamma_0 / \Gamma \cong G \rightarrow 1. \end{aligned}$$

The natural map $\varphi \colon \Gamma \rightarrow \prod \limits _{i=1}^n \Gamma / \Gamma _{g_i}$ has kernel $\bigcap \limits _{i=1}^n \Gamma _{g_i} = \Gamma _N$. Next, $\Gamma / \Gamma _{g_i} \cong C$ since the index is the prime number ℓ. Finally, we claim that φ is surjective. For this, it suffices to find for every i an element γ _i ∈ Γ with

$$\displaystyle \begin{aligned} \varphi(\gamma_i) = e_i=(0,\dots,0,1,0,\dots,0) \in C^n. \end{aligned}$$

Since C is cyclic of prime order, every non-zero element is a generator, and it suffices to choose $\gamma _i \in ( \bigcap \limits _{j \neq i}\Gamma _{g_j}) \setminus \Gamma _{g_i}$. This is possible since the reasoning in the first paragraph of this proof shows that the latter set is non-empty. In the end, we find a sequence

$$\displaystyle \begin{aligned} 1 \rightarrow C^n \rightarrow \Gamma_0/\Gamma_N \rightarrow G \rightarrow 1 \end{aligned}$$

where G acts on C ⁿ by permuting the factors like it permutes the cosets of H ₁, and this finishes the proof. □

Remark 7.4.2

In our setup, the universality property says the following: if we search for the “easiest possible” twisted Laplace operator on M ₁, meaning associated to the Laplace operator on some prime order cyclic cover of M ₁, we necessarily arrive at a diagram of the form (5.6).

Project

Assuming condition (∗∗), one can now give the following alternative construction of diagram (5.6) used in the main Theorem 6.4.1: perform the above two step construction of $M^{\prime }_{\mathrm {new}}$ and define an action of $\widetilde G$ on $M^{\prime }_{\mathrm {new}}$ using the right hand side of Eqs. (7.13) and (7.14). Prove directly that this manifold satisfies the required properties.