Keywords

1 Introduction

The term “chaos” covers a rather broad class of phenomena showing random-like behaviors at a first glance, even if they are generated by deterministic systems. This kind of processes is used to denote phenomena which are of a purely stochastic nature, such as the behavior of a waft of smoke or ocean turbulence, or the dynamic of molecules inside a vessel filled with gas, among many others [25]. However, chaotic system behaviors are easily mistaken for random noises given they share the property of long term unpredictable irregular behavior and broad band spectrum.

A classical topic in studying real world phenomena is to distinguish then between chaotic and random dynamics [18]. Deterministic chaotic systems are necessarily nonlinear, and conventional statistical procedures are insufficient for their analysis [39]. If the output of a deterministic chaotic system is analysed with these approaches, it will be erroneously recognised as the result of a random process. Therefore, characterizing the irregular behavior that can be caused either by deterministic chaos or by randon processes is challenging because of the surprising similarity that deterministic chaotic and random signals often show. Thus, it is still an open problem to distinguish among these two types of phenomena [25].

Deterministic chaos and its applications can be observed in control theory, computer science, physics, biology, and many other fields [18]. The interest in studying chaotic systems arises indeed when the theme of chaos reaches a high interdisciplinary level involving not only mathematicians, physicians and engineers but also biologists, economists and scientists from different areas. Several research works have shown that order could arise from disorder in various fields, from biological systems to condensed matter, from neuroscience to artificial neural networks [1]. In these cases, disorder often indicates both non-organized patterns and irregular behavior, whereas order is the result of self-organization and evolution, and often arises from a disorder condition or from the presence of dissymmetries. Gros [19] discusses the origin of self-organization where, leveraging from various key points from evolutionary theory and biology, it emphasizes the idea that life exists at the edge of chaos. Other examples in which the concept of stochastic driven procedures leads to ordered results are, e.g., Monte Carlo and evolutionary optimization [39], together with stochastic resonance in which the presence of noise improves the transmission of information [14].

The discovery of the phenomenon of deterministic chaos has brought about the need to identify manifestations of this phenomenon also in experimental data. Research on this line has focused so far on exploring the properties of cause and effect of chaotic phenomena, and also on using deterministic chaotic processes as instruments to improve other systems. This article focuses on the latter, and in particular on exploiting chaos for the improvement of heuristic optimization [32]. The goal consists on evaluating to performance between chaotic and random dynamics within a metaheuristic algorithm, showing the use of chaos in the inner optimization process, and focussing the attention on how chaos supports the birth of order from disorder also in this field [38]. This means to investigate the effects of the introduction of either deterministic chaotic or random sequences in a complex optimization routine. For this purpose, in particular, in this work we focus on Variable Neighbourhood Search (VNS), a popular explorative metaheuristic for combinatorial optimization problems based on dynamic changes of the neighbourhood structure in the solution space during the search process [21]. To compare the performance between a VNS procedure that runs using chaotic signals and that of a traditional random-based VNS, we consider as use case a set of labelling graph problems, i.e. the labelled spanning tree and forest problems. These problems are formulated on an undirected labelled graph, and consist on selecting the subset of labels such that the subgraph generated by these labels has an optimal spanning tree or forest. This family of problems has many real-world applications in different fields, such as in data compression, telecommunications network design, and multimodal transportation systems [9, 10, 12, 13]. For example, in multimodal transportation systems there are often circumstances where it is needed to guarantee a complete service between the terminal nodes of the network by using the minimum number of provider companies. This situation can be modelled as a labelling graph problem, where each edge of the input graph is assigned a label, denoting a different company managing that link, and one wants to obtain a spanning tree of the network using the minimum number of labels. This spanning tree will reduce the construction cost and the overall complexity of the network.

The effects of using chaos in VNS on this family of combinatiorial optimization problems are evaluated, aiming at disentangling the improvement in the optimization power due to the inclusion of a deterministic chaotic map within the VNS approach, one of the most popular metaheuristic used for tackling this class of problems. For the task, as it will be shown next, different popular one-dimensional chaotic maps are considered. The rest of the paper is structured as follows. Section 2 provides an overview of the background literature, while Sect. 3 presents the considered labelling graph problems used as testbench. Section 4 describes the VNS methodology implemented for this family of problems. Section 5 describes how we used chaos in VNS and the deterministic chaotic maps considered in our experiments. Section 6 shows the obtained empirical results and findings, while in Sect. 7 we provide our main conclusions.

2 Related Work

The active use of chaos has been recently widely investigated in the literature [18, 25]. The link between chaos and randomness has been largely investigated in several works (see e.g. [20, 26, 31] among others). Particularly interesting results have arisen in computer systems and algorithms, where chaos has been observed in the dynamics of algorithmic routines [24] and evolutionary algorithms [38, 39]. The latter is a topic of great interest, linked to the work presented in this paper. Chaos indeed has been used to substitute pseudo-random number generators in a variety of heuristic optimization procedures. The use of chaos inside evolutionary optimization is discussed in [27, 38], where it is thoroughly evaluated whether pure chaotic sequences improve the performance of evolutionary strategies. Davendra et al. [15] use with success a chaos driven evolutionary algorithm for PID control, while El-Shorbagy et al. [17] propose a chaos-based evolutionary algorithm for nonlinear programming problems. Hong et al. [22] propose a chaotic Genetic Algorithm for cyclic electric load forecasting; for the same problem, Dong et al. [16] introduce a hybrid seasonal approach using a chaotic Cuckoo Search algorithm together with a Support Vector Regression model. Another example on the use of chaos in a Genetic Algorithm is present in [28], with an application for the solution of a chip mapping problem. Senkerik et al. [33, 34] discuss the impact of chaos on Differential Evolution, powering the algorithm by a multi-chaotic framework used for parent selection and population diversity. Pluhacek et al. [29, 30] has widely explored the use of deterministic chaos inside Particle Swarm Optimization. Hong et al. [23] introduce a novel chaotic Bat Algorithm for forecasting complex motion of floating platforms. Chen et al. [6] propose a Whale Optimization Algorithm with a chaos-based mechanism relying on quasi-opposition for global optimization problems. In [40], instead, an improved Artificial Fish Swarm Algorithm based on chaotic search and feedback strategy has been described. Wang et al. [36] recently present an improved Grasshopper Optimization Algorithm using an adaptive chaotic strategy to further improve the comprehensive ability of grasshopper swarms in the early exploration and later development, and apply the algorithm to pattern synthesis of linear array in RF antenna design.

We do not attempt to hide the fact that, in certain ways, the field has been progressing in a way that seems to us less useful, and sometimes even harmful, to the development of the field in general. For example, many of the contributions that appear in the new literature, in our opinion do appear rather marginal additions to a list of relevant and widely accepted metaheuristics [35]. Nevertheless, it can be stated that, based on the listed and further other research papers in the literature, several contributions have shown the value that chaos appears to provide as an additional tool for heuristic optimization routines. It is evident the increasingly rising attention of the research community towards the hybridization of modern optimization algorithms and chaotic dynamics.

To the best of our knowledge, however, no attempts have been made on the use of chaos within the Variable Neighbourhood Search algorithm. We want to fill this gap, and, therefore, in this paper we use chaos to try to improve the VNS metaheuristic, testing it through different chaotic functions. As shown next, we evaluate the performance of the impact of a chaotic version of VNS on a set of labelling graph problems, used as testbench, to a non-chaotic version of the same algorithm.

3 The Labelled Spanning Tree and Forest Problems

In this paper we scratch a chaotic version of VNS, aimed to achieve further improvements to a classic, random-based VNS implementation tackling two classical labelling graph problems, namely the Minimum Labelling Spanning Tree (MLST) [4] and the k-Labelled Spanning Forest (kLSF) [3] problems. Variants exist (see e.g. [8, 10]), but these two problems are maybe the most prominent and general of this family. They are defined on a labelled graph, that is an undirected graph, \(G=(V,E,L)\), where V is its set of nodes and E is the set of edges that are labelled on the set L of labels.

The MLST problem [4] consists on, given a labelled input graph \(G=(V,E,L)\), getting a spanning tree with the minimum number of labels; i.e., the aim is to find the labelled spanning tree \(T^*=(V,E^*,L^*)\) of the input graph that minimizes the size of label set \(|L^*|\).

Instead, the kLSF problem [3] is defined as follows. Given a labelled input graph \(G=(V,E,L)\) and an integer positive value \(\bar{k}\), find a labelled spanning forest \(F^*=(V,E^*,L^*)\) of the input graph having the minimum number of connected components with the upper bound \(\bar{k}\) for the number of labels to use, i.e. \(\text {min} |Comp(G^*)|\) with \(|L^*| \le \bar{k}\).

Therefore in both problems, the matter is to find an optimal set of labels \(L^*\). Since a solution to the MLST problem would be a solution also to the kLSF problem if the obtained solution tree would not violate the limit \(\bar{k}\) on the used number of labels, it is easily deductable that the two problems are deeply correlated. Given the subset of labels \(L^* \subseteq L\), the labelled subgraph \(G^*=(V,E^*,L^*)\) may contain cycles, but each of them can be arbitrarily break by eliminating edges in polynomial time until a forest, or a tree, is obtained.

The NP-hardness of the MLST and kLSF problems has been proved in [4] and in [3], respectively. Therefore any practical solution approach to both problems requires heuristics. Several optimization algorithms to the MLST problem have been approached in the literature [2, 37], showing in several cases the particular suitability of the VNS heuristic [9, 11, 12]. For the kLSF problem, in [3] a Genetic Algorithm and the Pilot Method metaheuristics have been proposed. In particular, in [7, 13], some metaheuristics based on Greedy Randomized Adaptive Search Procedure and Variable Neighbourhood Search have been designed, obtaining high-quality results in most cases and showing the effectivenes of the VNS approach [13]. Given VNS has demonstrated to be a promising strategy for this class of problems, we have chosen it as a benchmark for testing the use of chaos inside the VNS metaheuristic. Nevertheless, note that the approach can be easily adapted and generalised to other optimization problems where the solution space consists of subsets of a reference set, such as feature subset selection problems or a variety of location problems.

4 Variable Neighbourhood Search

Variable Neighbourhood Search (VNS) is an explorative metaheuristic for combinatorial optimization problems based on dynamic changes of the neighbourhood structure of the solution space during the search process [21]. The guiding principle of VNS is that a local optimum with respect to a given neighbourhood may not be locally optimal with respect to another neighbourhood. Therefore VNS looks for new solutions in increasingly distant neighbourhoods of the current solution, jumping only if a better solution than the current best solution is found [21]. The process of changing neighbourhoods when no improvement occurs is aimed at producing a progressive diversification.

figure a

Given a labelled graph \(G = (V,E,L)\) with n vertices, m edges, and \(\ell \) labels, each solution is encoded by a binary string [9], i.e. \(C = (c_1, c_2 ,\ldots , c_{\ell })\) where

$$\begin{aligned} c_i= \left\{ \begin{array}{ll} 1 &{} \quad \text {if label }i\text { is in solution }C\\ 0 &{} \quad \text {otherwise}\\ \end{array} \right. \qquad (\forall i=1,\ldots ,\ell ).\end{aligned}$$
(1)

Denote with \(N_{k}(C)\) the neighbourhood space of the solution C, and with \(k_{\text {max}}\) the maximum size of the neighbourhood space. In order to impose a neighbourhood structure on the solution space S, comprising all possible solutions, the distance considered between any two such solutions \(C_1, C_2 \in S\), is the Hamming distance [9, 12]:

$$\begin{aligned} \rho (C_1,C_2)=|C_1-C_2|=\sum _{i=1}^{\ell }\lambda _i\end{aligned}$$
(2)

where \(\lambda _i = 1\) if label i is included in one of the solutions but not in the other, and 0 otherwise, \(\forall i = 1,..., \ell \). Then, given a solution C, its kth neighbourhood, \(N_k(C)\), is considered as all the different sets having a Hamming distance from C equal to k labels, where \(k = 1, 2,\ldots , k_{\text {max}}\), and \(k_{\text {max}}\) is the maximum dimension of the shaking. In a more formal way, the kth neighbourhood of a solution C is defined as \(N_k(C) = \{S \subset L: \rho (C,S) = k\}\), where \(k = 1,...,k_{\text {max}}.\)

For illustrative purpose and a better comprehension, in Algorithm 1 is described the VNS implementation for the MLST problem [9, 12]. The VNS solution approach for the kLSF problem is very akin [7, 13] and only differ from the fact that an upper bound \(\bar{k}\) for the number of labels has to be imposed, and that a forest instead of a spanning tree has to be considered for halting the algorithm. Note that given a subset of labels \(L^* \subseteq L\), the labelled subgraph \(G^*=(V,E^*,L^*)\) may contain cycles, but they can arbitrarily break each of them by eliminating edges in polynomial time until a forest or a tree is obtained.

figure b

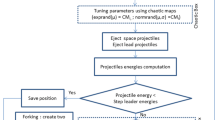
Algorithm 1 starts from an initial feasible solution C generated at random and lets parameter k vary during the execution. In the successive shaking phase (Shaking phase(\(N_k(C)\)) procedure, see Algorithm 2) a random solution \(C'\) is selected within the neighbourhood \(N_k(C)\) of the current solution C. This is done by randomly adding further labels to C, or removing labels from C, until the resulting solution has a Hamming distance equal to k with respect to C [9]. Addition and deletion of labels at this stage have the same probability of being chosen. For this purpose, a random number is selected between 0 and 1 (\(rnd \leftarrow random[0,1]\)). If this number is smaller than 0.5, the algorithm proceeds with the deletion of a label from C. Otherwise, an additional label is included at random in C from the set of unused labels \((L-C)\). The procedure is iterated until the number of addition/deletion operations is exactly equal to k [12].

figure c

The successive local search (Local search(\(C'\)) procedure, see Algorithm 3) consists of two steps [9]. In the first step, since deletion of labels often gives an infeasible incomplete solution, additional labels may be added in order to restore feasibility. In this case, addition of labels follows the criterion of adding the label with the minimum number of connected components. Note that in case of ties in the minimum number of connected components, a label not yet included in the partial solution is chosen at random within the set of labels producing the minimum number of components (i.e. \(u\in S\) where \(S = \{\ell \in (L-C'):\) min \(Comp(C'\cup \{\ell \})\}\)). Then, the second step of the local search tries to delete labels one by one from the specific solution, whilst maintaining feasibility [9, 12].

After the local search phase, if no improvements are obtained (\(|C'| \ge |C|\)), the neighbourhood structure is increased (\(k \leftarrow k + 1\)) giving a progressive diversification (\(|N_1(C)|< |N_2(C)|< ... < |N_{k_{\text {max}}}(C)|\)), where \(k_{\text {max}} \leftarrow (|C|+|C|/3)\) from [9, 12]. Otherwise, the algorithm moves to the improved solution (\(C\leftarrow C'\)) and sets the first neighbourhood structure (\(k \leftarrow 1\)). Then the procedure restarts with the shaking and local search phases, continuing iteratively until the user termination conditions are met.

5 Using Chaos in VNS

Chaos is a non-periodic, long-term behavior in a deterministic system that exhibits sensitive dependence on initial conditions, and is a common nonlinear phenomenon in our lives [25]. The dynamic properties of chaos can be summarised as following [40]:

  1. 1.

    “Sensitive dependence to Initial Conditions (SIC)”: Chaos is highly sensitive to the initial value.

  2. 2.

    “Certainty”: Chaos is produced by a certain iterative formula.

  3. 3.

    “Ergodicity”: Chaos can go through all states in certain ranges without repetition.

In general, the most important defining property of chaotic variables is the first one, which requires that trajectories originating from very nearly identical initial conditions diverge at an exponential rate [28]. Pseudorandomness and ergodicity are other important dynamic characteristics of a chaotic structure, which ensure that the track of a chaotic variable can travel ergodically over the whole space of interest.

Chaos is similar to randomness. The variation of the chaotic variable has indeed an inherent property in spite of the fact that it looks like a disorder. Edward Lorenz irregularity in a toy model of the weather displayed first chaotic or strange attractor in 1963. It was mathematically defined as randomness generated by simple deterministic systems. A deterministic structure can have no stochastic (probabilistic) parameters. Therefore chaotic systems are not at all equal to noisy systems driven by random processes. The irregular behavior of the chaotic systems arises from intrinsic nonlinearities rather than noise [25].

Several experimental studies have shown already the benefits of using chaotic signals rather than random signals [18], although a general rule can not be drawn yet [32]. Chaos has been used as a novel addition to optimization techniques to help escaping from local optima, and chaos-based searching algorithms have aroused intense interests [32, 39].

As from the second property of chaos just listed above, one-dimensional noninvertible maps are the simplest systems with capability of generating chaotic dynamics. They are capable of providing simple deterministic chaotic signals, that we can use inside our VNS procedure (Algorithm 1) in place of the pseudo-random number generation occurring in the shaking phase (Algorithm 2). Here the chaotic mapping of a shaking \(N_k(\cdot )\) to an incumbent solution, C, includes the following major steps:

  1. 1.

    Variable C in the solution space is mapped to the chaotic space, by using a deterministic chaotic map chosen by the user.

  2. 2.

    Using the selected chaotic dynamics, select the kth chaotic variable from the generating map.

  3. 3.

    The chaotic variable is then mapped back to the solution space, producing the next solution \(C'\).

Please note that after this step, in case of an infeasible incomplete solution is obtained, additional labels may be added in order to restore feasibility, following the criterion of adding the label with the minimum number of connected components with respect to the incumber solution \(C'\).

In the following we briefly depict some well-known one-dimensional chaotic maps that we employ in our experiments. For more in-depth descriptions, the reader in referred to [5, 32].

Logistic map

The logistic map is a chaotic polynomial map. It is often cited as an example of how complex behavior can arise from a very simple nonlinear dynamical equation. This map is defined by:

$$\begin{aligned} x_{n+1}=f(\mu ,x_n)=\mu x_n(1-x_n), 0<\mu \le 4 \end{aligned}$$
(3)

in which \(\mu \) is a control parameter, and x is the variable. Since Eq. (3) represents a deterministic dynamic system, it seems that its long-term behavior can be predicted.

Tent Map

In mathematics, the tent map is an iterated function, in the shape of a tent, forming a discrete-time dynamical system. It takes a point \(x_n\) on the real line and maps it to another point, according to:

$$\begin{aligned} x_{n+1} = {\left\{ \begin{array}{ll} \mu x_n &{} \text {if }x_n < 1/2\\ \mu (1-x_n) &{} \text {otherwise,} \end{array}\right. } \end{aligned}$$
(4)

where \(\mu \) is a positive real constant. The tent map and the logistic map are topologically conjugate, and thus the behavior of the two maps is in this sense identical under iteration.

Bernoulli Shift Map

The Bernoulli shift (Bshift) map belongs to class of piecewise linear maps which consist of a number of piecewise linear segments. This map is a particularly simple example, consisting of two linear segments to model the active and passive states of the source. It is defined as follows:

$$\begin{aligned} x_{n+1} = {\left\{ \begin{array}{ll} \dfrac{x_n}{1-\lambda } &{} \text {if }0< x_n < (1-\lambda )\\ \dfrac{x_n-(1-\lambda )}{\lambda } &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$
(5)

5.1 Sine Map

The sine map is described by the following equation:

$$\begin{aligned} x_{n+1}= \frac{\alpha }{4} \sin {(\pi x_n)}, \end{aligned}$$
(6)

where \(0 < \alpha \le 4\). This map has qualitatively the same shape as the logistic map. Such maps are also called unimodal chaotic maps.

Circle map

The circle map [22] is represented by

$$\begin{aligned} x_{n+1}= x_{n}+b - \frac{a}{2\pi } \sin {(2\pi x_n)}, \end{aligned}$$
(7)

where a can be interpreted as a strength of nonlinearity, and b as an externally applied frequency. The circle map exhibits very unexpected behavior as a function of these parameters; with \(a = 0.5\) and \(b = 0.2\), it generates chaotic sequences in (0, 1).

Iterative Chaotic Map with Infinite Collapses

The iterative chaotic map with infinite collapses (ICMIC) is defined by:

$$\begin{aligned} x_{n+1}= \sin (\alpha /x_n), \end{aligned}$$
(8)

where \(\alpha \in (0, \infty )\) is an adjustable parameter.

6 Experimental Results

We show here our computational experience on the use of chaos within the VNS methodology for the considered labelling graph problems. We examine the VNS implementation using pseudo-random number generation in the shaking phase (Rand), and the same VNS model including the different deterministic chaotic maps in the shaking step, denoted respectively with: Logistic, Tent, Bshift, Sine, Circle, and ICMIC. To test the performance and the efficiency of the algorithms, we run an experimental evaluation on a set of labelled graphs having numbers of vertices \(|V| = 100\), 200, 300, 400, 500, 1000, labels \(|L|=0.25\,V|\), \(0.5\,V|\), |V|, \(1.25\,V|\), and edges \(|E|=(|V|-1)/|V|\). These are the well-known benchmark instances in the literature taken from [9, 11, 12] for the MLST literature, and from [7, 13] for the kLSF problem. All the considered instances are available upon request from the authors. For each combination of |V| and |L|, ten different problem instances are generated; the parameter \(\bar{k}\) for the kLSF is determined experimentally as \(\lfloor |V| /2^j \rfloor \), where j is the smallest value such that the generated instances do not report a single connected solution when solved with maximum vertex covering [3]. The algorithms have been implemented in C++ under the Microsoft Visual Studio 2015 framework, and all the computations run on an Intel Quad-Core i7 64-bit microprocessor at 2.30 GHz with 32 GB RAM.

For each dataset, solution quality is evaluated as the average objective function value (i.e. the number of labels of the solution for the MLST problem, or the number of connected components for the kLSF problem) among the 10 problem instances. As in [9, 12, 13], a maximum allowed CPU time of 1 hour has been chosen as stopping condition for all the VNS algorithms. Selection of the maximum allowed CPU time as the stopping criterion is made in order to have a fair and direct comparison between the different VNS implementations with respect to the quality of their solutions. All the algorithms run until the maximum CPU time is reached and, in each case, the best solution is recorded, along with the total number of iterations required to obtain such best solution.

Fig. 1.
figure 1

Bar chart of the objective function values obtained by the different VNS variants for solving the MLST problem instances (left) and the kLSF problem instances (right).

Full size image

We show in Fig. 1 the bar chart of the sum of the objective function values obtained by the different VNS variants for the MLST problem instances (left) and for the kLSF problem instances (right). The results show that the deterministic chaotic maps perform well in the considered instances for both problems, with the exception of Sine and Circle that appear to not bring a real improvement over that classical VNS with pseudo-random number generation. The best results are obtained when using the ICMIC map, reaching the best solutions in both problems. Fine results are also reached, respectively, by the Tent, Logistic, and Bshift maps, which follow immediately after ICMIC and clearly outperform Rand.

Fig. 2.
figure 2

Bar chart of the total number of iterations required by the different VNS variants for solving the MLST problem instances (left) and the kLSF problem instances (right).

Full size image

We also compare the total number of iterations at which the best solutions are obtained when executing VNS with each of the discussed chaotic maps, and show the relative bar chart in Fig. 2. We see a consistent drop with respect to the number of iterations required by all the VNS variants using the chaotic maps, meaning that they are able to converge earlier with respect to Rand. Looking at the figure, the best performance in terms of total number of iterations is obtained by Sine for both problems, immediately followed by the ICMIC map, and by the Logistic and Tent maps, afterwards. However, although Sine is faster than the other chaotic maps, it does not show top performance with respect to the objective function values (Fig. 1), meaning it is more prone to get stuck into local optima. Instead, looking at Bshift and Circle, they appear to be sometimes slower than the other employed maps. Nevertheless, summarizing, as seen already with respect to solution quality, it is again evident the value of using the chaotic maps in VNS, given all the chaotic VNS variants always outperform Rand with respect to the required number of iterations.

7 Conclusions

This paper introduces the novel idea of combining the two concepts of chaotic sequences and Variable Neighbourhood Search (VNS). Different popular one-dimensional chaotic maps have been considered, and they have been injected into the shaking phase of the VNS algorithm in place of classical pseudo-random number generation. The chaotic VNS variants have been tested on a family of labelling graph problems, namely the Minimum Labelling Spanning Tree (MLST) problem and the k-Labelled Spanning Forest (kLSF) problem. In order to evaluate the effectiveness of the chaotic maps in reaching the best solution for the considered problems, objective function values and total number of iterations required by the different VNS implementations have been computed upon a set of problem instances commonly used in the literature. Simulation results on this set of benchmarks indicate that searching efficiency of the VNS algorithm improves when using the one-dimensional chaotic maps within the shaking phase. The proposed chaotic variants work quite better than the classical VNS algorithms using randomness for the two problems introduced in previous works.

Summarizing, although preliminary, the obtained results look encouraging, showing an overall validity of the employed methodology. The achieved VNS optimization strategy using chaos seems to be highly promising for both labelling graph problems. The experiments carried out confirm the efficiency, lower number of iterations, and scalability of the chaotic VNS implementations. Ongoing investigation will consist in performing a thorough statistical analysis of the resulting chaotic VNS strategies against the best algorithms in the literature for these problems, in order to better quantify and qualify the improvements obtained. Further investigation will deal also with the application of chaotic variants of VNS to other optimization problems.