Pathways Through Pressure-Driven Percolation in Salt Rock

Abstract

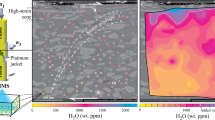
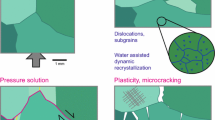
Under undisturbed conditions and in the absence of significant impurities or intercalations (e.g. anhydrite) rock salts are considered to be tight against fluid or gas pressures, which stems from their crystalline structure composed of strongly viscoplastic, impermeable salt grains grown together at their grain boundaries (Minkley et al. 2013, 2015).

3.1 Hydro-Mechanical Properties of Salt Rocks and the Concept of Pressure-Driven Percolation

Under undisturbed conditions and in the absence of significant impurities or intercalations (e.g. anhydrite) rock salts are considered to be tight against fluid or gas pressures, which stems from their crystalline structure composed of strongly viscoplastic, impermeable salt grains grown together at their grain boundaries (Minkley et al. 2013, 2015). Thus, its small natural porosity of 0.1–1% consists mainly of isolated brine pockets as evidenced e.g. by microscopic investigations of thin salt slivers. There are however stress- and pressure-conditions under which this hydraulically inactive flow network of connected grain boundaries can be opened. Then—and only then—a significant increase in macroscopic permeability can be observed due the creation of a connected flow path by opening the grain boundaries for permeation (Fig. 3.1).

Fig. 3.1

Percolation of a colored solution on grain boundaries in hydro-mechanically coupled triaxial compression tests on salt specimen

The conditions for such an increase in permeability can be classified into two principle mechanisms:

• damage induced creation of internal fractures by deviatoric loading

• pressure-driven opening of grain-boundaries by an applied fluid/gas pressure

The first item describes the creation of flow paths by damaging the salt due to loading above its threshold for damage initiation (the so-called dilatancy boundary). The second mechanism—which is the main focal point of this study—describes the ability of fluids and gases to “open” the initially impermeable grain boundaries when the applied pressure becomes higher than the normal stresses acting on them. The attacking pressure thereby allows the medium to push its way into the grain boundaries and creates a connected flow path structure. Since this formation of a flow network occurs only after exceeding a certain threshold related to stress and pressure, this effect has been termed “pressure-driven-percolation” in the field of salt mechanics. In the assessment of barrier integrity in salt mining—i.e. the preservation of aforementioned sealing capacity of the salt units—these two mechanisms have lead to the development of two associated criteria for their evaluation (Kock et al. 2012):

• Dilatancy criterion

• Minimum principle stress criterion (MPS)

The dilatancy criterion describes the amount of mechanical damage the salt material has experienced, while the MSP compares the acting minimum principle stress with a theoretically attacking fluid pressure, e.g. a column of groundwater above the salt top or the gas pressure within a salt cavern. While the dilatancy criterion is typically more relevant for the assessment of damage at the contour of underground drifts and caverns (the excavation disturbed zone—EDZ), the MSP generally has a more far-reaching impact since the large-scale stress redistributions around a salt mine may reach far into the salt, potentially threatening its capacity as a hydraulic protection layer. It is important to note, that the minimum principle stress criterion is not the result of a hydro-mechanical modeling, but solely a stress- and pressure-based assessment of a given stress-state from a geomechanical modeling. As such it must be ensured, that it is applied at the most unfavorable state of the modeled system.

Fig. 3.2

Highly anisotropic percolation in salt rocks perpendicular to the least compressive stress under true triaxial compression (Kamlot 2009)

Additionally, the MSP is conservative in the sense that it only considers the scalar quantity of the least compressive stress. In reality, numerous laboratory hydro-mechanically coupled percolation studies have shown that the pressure-driven percolation is a highly oriented process, where the fluid generally percolates in a plane perpendicular to the least compressive stress (Kamlot 2009) (Fig. 3.2). Therefore it is possible that the MSP becomes too conservative, when the minimum principle stress may be lower than the attacking fluid pressure, but the direction of the stress field is such that this does not lead to a loss of the hydraulic protection capacity of the salt layer.

Based on the previous considerations, the idea suggests itself to model the pressure-driven percolation as a diffusion process using a dynamic, full permeability tensor based on the fluid pressures and the stress tensor. However, this seemingly simple idea of modeling highly anisotropic diffusion leads to a number of numerical challenges in this and also in other scientific fields. The subsequent section will therefore outline the principle idea and the arising problems more detailed, before proposing a mesh-free numerical approach taken from the field of magneto-hydrodynamics in astrophysics.

3.2 Development of a Mesh-Free Percolation Model Inspired by Magneto-Hydrodynamics

3.2.1 Numerical Challenges in Modeling Highly Anisotropic Permeation

Most geomechanical codes capable of modeling a Darcy-type porous diffusion use finite-volume techniques (Moukalled et al. 2016), where the fluid resides in control volumes and each of these volumes may exchange fluid with its neighbors. By solving a balance equation and, the flow rates between those elements are determined and the corresponding changes in saturation and/or pressure are calculated. In order to determine the pressure gradient between to connected volumes i and j, a so-called two-point flux approximation (TPFA) is made (Aavatsmark 2002):

$$ \mathbf {\nabla } p_{ij} = \frac{p_j - p_i}{d_{ij}}\textbf{e}_{ij} $$

This widely-used approximation is one of the main reason for excessive numerical (i.e. false) diffusion when a highly anisotropic permeability tensor is used. For anisotropic permeability tensors, this approximation only yields accurate results when the directions of the element connection vectors ($\textbf{e}_{ij})$ are aligned with the Eigenvectors of that particular permeability tensor, i.e. its principle directions. Assuming that the permeability tensor is not constant and may change its principle directions (as it is proposed here by coupling it to the fluid pressure and stress tensor) this condition will never be met in the simulations. The introduced numerical error is of order n(0), meaning it is inherently tied to the model structure and does not converge away with increasing mesh resolution. It leads to numerical instabilities and implausible results including:

• violation of non-negativity (may yield negative temperatures in numerical modelings of anisotropic temperature distributions (Sharma and Hammett 2007))

• violation of the maximum principle (in a closed system, the method may yield e.g. higher fluid pressures than the ones it started with) (Gao and Wu 2013)

Even though this numerical problem is known for decades and the literature shows numerous correction approaches in a wide spectrum of applications from thermal propagation to astrophysics, it is still the default approximation in many—if not all—established geomechanical codes. In the context of geomechanical barrier integrity not correcting for this problem leads to uncontrolled numerical diffusion, since the anisotropic fluid distribution will not stay stable and inevitably fill the whole model domain, thus rendering the approach useless for the evaluation of a hydraulic barrier.

3.2.2 Basic Approach and Formulation

In order to discretize the problem, a choice has to be made on how to discretize the model domain volume into a set of cells or particles i with coordinates $\boldsymbol{x}_i$. Instead of using a typical mesh e.g. of interconnected hexahedra or Voronoi elements, the approach formulated by Hopkins et al. (Hopkins 2015, 2016) considers a mesh-free alternative. A differential volume $d^3\boldsymbol{x}$ at coordinate $\boldsymbol{x}$. This differential volume can then be partitioned fractionally among its nearest particles by using a weighting function W depending on the distance $\boldsymbol{x}-\boldsymbol{x}_i$ and a “kernel size” $h(\boldsymbol{x})$, thereby associating a fraction $\Psi _i(\boldsymbol{x})$ of the volume $d^3\boldsymbol{x}$ with particle i:

$$ \Psi _i(\boldsymbol{x}) = \frac{1}{\omega (\boldsymbol{x})}W(\boldsymbol{x}-\boldsymbol{x}_i,h(\boldsymbol{x})) $$

$$ \omega (\boldsymbol{x}) = \sum _j(\boldsymbol{x}-\boldsymbol{x}_i,h(\boldsymbol{x})) $$

$W(\boldsymbol{x}-\boldsymbol{x}_i,h(\boldsymbol{x}))$ can be any continuous, symmetric and compactly supported function. Its absolute value is irrelevant due to the normalization. This type of model discretization therefore conceptually sits somewhere between a Voronoi tessellation and smooth-particle hydrodynamics. Hopkins et al. (Hopkins 2015) show, that this partition of unity discretization makes it possible to formulate the balance equation of property $\boldsymbol{U}$ for a given particle i with associated volume $V_i$ as a Godunov-type finite-volume equation:

$$ \frac{d}{dt}(V_i\boldsymbol{U_i})+\sum _j \boldsymbol{F}_{ij}\cdot \boldsymbol{A}_{ij} = 0 $$

with the “fluxes” $\boldsymbol{F}_{ij}$ in or out of an effective face area $\boldsymbol{A}_{ij}$.

Another crucial advantage of this method is the fact that that type of discretization easily allows for a second-order accurate approximation of the gradient of any property f as a least-squares fit over all points in the kernel region, which effectively makes it a type of multi-point flux approximation method (MFPA):

$$ (\nabla f)_i^\alpha = \sum _j (f_j-f_i) (\boldsymbol{W}_i^{-1})^{\alpha \beta }(\boldsymbol{x}_j-\boldsymbol{x}_i)^\beta \omega _j(\boldsymbol{x}_i) $$

$$ \boldsymbol{W}_i^{\alpha \beta } = \sum _j (\boldsymbol{x}_j-\boldsymbol{x}_i)^\alpha (\boldsymbol{x}_j-\boldsymbol{x}_i)^\beta \omega _j(\boldsymbol{x}_i) $$

Is it important to note, that this gradient estimator is second-order accurate for an arbitrary particle configuration and therefore particularly suited for the mesh-free method. While the method proposed in Hopkins (2015) is constructed for very general hydrodynamics applications and leads to solving the associated Riemann problem, we now differ from the original formulation by transferring the general notion to the field of diffusion in porous media. In a simple explicit time-stepping scheme, we calculate the fluxes $F_{ij}$ between each particle and its associated “neighbors” by evaluating the approximated gradient at the midway point between each particle and summing these contributions.

$$ F_{ij}=\frac{1}{\mu }(\boldsymbol{K}\cdot \mathbf {\nabla } p_{ij})\cdot \boldsymbol{A_{ij}} $$

In order to stabilize the anisotropic diffusion equation, this flux is compared to the direct two-point flux

$$ F^{direct}_{ij}= \frac{1}{\mu }\left[ \boldsymbol{K}\cdot \left( \frac{p_j - p_i}{d_{ij}}\textbf{e}_{ij}\right) \boldsymbol{A_{ij}}\right] $$

Using this direct flux, the final flux $\tilde{F}_{ij}$ is given by

$$ \tilde{F}_{ij}={\left\{ \begin{array}{ll} 0 &{} \text {if } \text {sgn}(F^{direct}_{ij}\cdot F_{ij}) \text { and } |F^{direct}_{ij}|>2\cdot |F_{ij}|\\ F_{ij} &{} \text {otherwise} \end{array}\right. } $$

Additionally, a basic saturation concept is introduced, giving each particle a porosity value and ensuring, that no flow can occur out of an unsaturated zone by multiplying the calculated flow rate with an empirical saturation function as $s_ij$ used in the geomechanical modeling codes of Itasca (Itasca 2022a, b):

$$ s_{ij}=s^2\cdot (3-2s) $$

where s is the saturation of the zone where the fluid is coming from (upwind scheme). Using this approach the volumetric flow rate $\dot{Q}_i$ for particle i is

$$ \dot{Q}_i = \sum _j \tilde{F}_{ij}\cdot s_{ij} $$

If the saturation at particle i is less than 1, this flow rate is used to update the saturation by

$$ s_i(t+\Delta t) = s_i(t)+\frac{\cdot {Q}_i}{n_i\cdot V_i}\cdot \Delta t $$

with porosity $n_i$ and associated volume $V_i$. If the particle is already fully saturated, the associated pressure $p_i$ is updated instead using the fluid bulk modulus $B_{fluid}$:

$$ p_i(t+\Delta t) = p_i(t)+\frac{B_{fluid}\cdot {Q}_i}{n_i\cdot V_i}\cdot \Delta t $$

This algorithm was implemented as a Python module in FLAC3D, since this is the framework exposing the relevant internal variables of the corresponding numerical FLAC3D model in order to have access to the corresponding stresses and strains from the mechanical calculations of the salt behavior. In a staggered approach, the time-dependent mechanical problem is solved iteratively by FLAC3D for a given amount of time before the new stress tensor field is then given to the newly developed Python module for the anisotropic fluid flow calculation for the same timespan (albeit obviously using a different timestep for the fluid flow calculations). Although it is has experienced some optimizations, the Python implementation is—by nature of the interpreted programming language—much slower than a comparable C++ implementation using HPC-ready sparse matrix library would be. This would however need to be encapsulated again as a Python module in order to continue to work in conjunction with the FLAC3D software. Such efforts were tested in principle with the framework of this project and are (in addition to optimizations of the numerical structure itself) a potential field of improvement for future work. Together with the dynamic calculation of the local permeability tensor based on the stress tensor and the fluid pressure (see Sect. 3.3.3), we will subsequently refer to the new Mesh-Free Percolation technique as the MFP-approach.

3.3 Validation in Analytical Test Cases and Idealized Percolation Situations

In order to demonstrate the capabilities of the new method and also show the unphysical numerical problems arising in standard implementations, a number of test cases have been assembled as a benchmark for the modeling of highly anisotropic porous flow. These examples and their comparative results are discussed hereafter and may aid in validation and verification for similar methods in the context of geomechanical percolation processes.

3.3.1 Diffusion of a 1D-Step Function in Different Constant Permeability Fields

In order to validate the basic diffusion capabilities, a 1D-step function is initialized in a constant isotropic permeability field (3.3) with a pressure $p = 1$ MPa on the left half and zero pressure on the right half of the model. The mesh has been created deliberately in a tilted fashion (with respect to the orientation of the quadratic elements) in order to create the most unfavorable condition for the subsequent analysis with an anisotropic permeability. For the isotropic permeability k in the first modeling, the pressure step will diffuse and soften the transition with time given by the analytical solution for the pressure profile $p_{x,t}$ for a given time t:

$$ p(x,t>0)=\frac{p}{2}+\frac{p}{2}\text {Erf}\left[ {\frac{x-x_0}{4\kappa t}}\right] $$

with

$$ \kappa =\frac{B_{fluid}\cdot K}{n\mu } $$

where n is the rock porosity and $\mu$ the viscosity of the flowing medium. Figure 3.3 shows the pressure profile for a time of t $=$ 600 s using the new MFP-approach in comparison with the native FLAC3D fluid logic. As to be expected, both codes are in good agreement with the analytical solution for the isotropic case.

Fig. 3.3

Model setup and mesh for the 1D isotropic diffusing step validation example (top) and the modeling results of the resulting pressure profile for different approaches (bottom) showing good agreement with the analytical solution

In the second step, we now assign a anisotropic permeability, which is only nonzero in the vertical direction ($k_x = 0 m^2$). Therefore, the numerical simulation should keep the initial step function perfectly intact, since there should be no flow into the x-direction. Again we examine the pressure profiles for both codes in Fig. 3.4 for a time of t $=$ 12000 s. It can be clearly seen, that the MFP-approach coincides with the analytical (${=}$initial) pressure profile, while the FLAC3D model exhibits the numerical errors discussed in the previous sections: The fluid front does not stay stable and move into the x-direction while also showing higher pressures than the initial condition on the left side and negative pressures on the right hand side. This is a clear example of the undesired effects using lower-order flow approximations in highly anisotropic settings and is therefore proposed as a first and simple validity check for anisotropic approaches on porous flow.

Fig. 3.4

Resulting pressure profiles for the 1D anisotropic diffusing step function, which should stay perfectly immobile. The MHD approach successfully captures this, while the standard two-point flux-approximation implemented in FLAC3D fails to keep the fluid front stable and also exhibits numerical problems

3.3.2 The Diffusing Ring Problem

Another numerically challenging example for highly anisotropic flow is the so-called diffusing ring. Following the description in Hopkins et al., we initialize a purely azimuthal pressure field in a 2D cubic box. With cylindrical coordinates centered on the origin we initialize $p(t=0)=p_0(\exp {-(1/2)[(r-r_0)^2/\delta r_0^2+\phi ^2/\delta \phi _0^2]})$ with $p0=$,$r_0=$ and $\phi _0=$. Since the permeability field is purely azimuthal, the pressure should then only diffuse along a ring-shape around the center. For short times, this problem has an exact solution:

$$ p(t>0)=p_0(\exp {-(1/2)[(r-r_0)^2/\delta r_0^2+\phi ^2/\delta \phi ^2]}) $$

with

$$ \delta \phi ^2(r,t)=\delta \phi _0^2 + 2Kr^{-2}t $$

At later times, the diffusion from both sides of the ring intersects and there is no longer an exact solution. Again we test this problem setup using the MFP-approach and the native FLAC3D implementation. As an example of the modeling results, Fig. 3.5 shows the pressure distribution along the annulus after a short time (t $=$ 60 s) in comparison to the original distribution. Even for this very short time, it can be seen that the MFP-results are again in good agreement with the analytical solution, while the FLAC3D results is already starting to deviate noticeably.

Fig. 3.5

Resulting pressure profiles for the 1D anisotropic diffusing step function, which should stay perfectly immobile. The MHD approach successfully captures this, while the standard two-point flux-approximation implemented in FLAC3D fails to keep the fluid front stable and also exhibits numerical problems

For longer times, the pressure distribution wraps around as to be expected and stays fairly stable in the MFP modeling, while it again exhibits strong numerical diffusion in the FLAC3D implementation, eventually filling and equalizing the pressure in the whole domain. Therefore, this second—more elaborate—numerical example has confirmed the shortcomings of the default methods and the capabilities of the MFP-approach to accurately model this challenging setup.

3.3.3 Inclusion of Pressure- and Stress-Dependent Anisotropic Diffusion

So far, the presented results were carried out for constant permeability problems with different boundary conditions and setups with the intent to verify the basic capabilities of the proposed method to accurately model anisotropic fluid flow. At this point we now include the mechanisms described in the introductory section in order to model the pressure-driven percolation in salt rocks.

In its principle axes, we formulate the anisotropic diffusivity tensor K in the following way:

$$ K=\begin{bmatrix} k_{2} + k_{3} &{} 0 &{} 0\\ 0 &{} k_1 + k_3 &{} 0 \\ 0 &{} 0 &{} k_1 + k_2 \end{bmatrix} $$

with

$$ k_i = {\left\{ \begin{array}{ll} A(p+\sigma _i) \text { for } p > \sigma _i \\ 0 \text { otherwise} \end{array}\right. } $$

where $\sigma _i$ are the principle stresses and p is the fluid pressure. By this construction, e.g. a pressure p exceeding the minimum principle stress $\sigma _3$ will lead to an increase in permeability in the directions of $\sigma _1$ and $\sigma _2$, i.e. the fluid may move in a plane perpendicular to the principle stress $\sigma _3$.

Using this straightforward approach we can then test its functionality by modeling fluid injection tests in a cubic sample subjected to different stress conditions similar to the ones described in Kamlot (2009). On the purely cartesian mesh ($20 \times 20 \times 20$ elements), we initialize a fluid pressure of p in the center of the model, whose stress state is given by $\sigma _1 = \sigma _2$ = 11 MPa and $\sigma _3$ $=$ 9 MPa. The given stress field was again deliberately chosen to lead to an unfavorably inclined fluid flow forming an angle of 45$^\circ$ against the principle axes of the mesh. Since the initial fluid pressure is below the minimum principle stress in the sample, there should be no flow occurring until the fluid pressure—which is increased stepwise—reaches and exceeds that mininum principle stress.

Fig. 3.6

45$^{\circ }$ degrees inclined pressure-driven percolation modeling with strong numerical diffusion and invalid pressures (holes) in the default FLAC3D implementation and stable percolation in the novel MHD approach

As expected, the initialized fluid stays stable until it exceeds the minimum principle stress. Upon exceeding the percolation front develops in the expected inclined orientation and is—most importantly—stable with respect to potential erroneous numerical diffusion in the direction of $\sigma _3$ (Fig. 3.6). Therefore, the proposed method is capable of both modeling both constant anisotropies as well as with the additional interaction of a spatially varying stress- and pressure-dependent permeability tensor.

Fig. 3.7

Location of the test site in the mining field Springen (left) and construction of the large-scale 60 m borehole with 1.35 m diameter between mining levels (right)

3.3.4 Application on a Large-Scale in Situ Borehole Pressurization Test in a Salt Mine

A numerical recalculation of a large-scale in situ test was to be performed in order to demonstrate the capabilities and accuracy of the new approach. In this in-situ test, a 60 m long borehole with a diameter of 1,35 m was drilled between to mining levels of a salt mine and additionally monitored by a seismic array (Fig. 3.7). The borehole was cemented in the lower part, leaving a 40 m high cylindrical cavity which was then pressurized with gas. In accordance with the expected stress field, the salt borehole was gas-tight until the gas pressures reached a level above the minimum principle stress at the lower end of the borehole. The thereby created percolation front started in the bottom part of the borehole (at the cement plug) and progressed in a nearly horizontal plane above the underground mine drifts (Fig. 3.8), which was to be replicated by the newly developed method. The hydro-mechanically coupled calculations of the percolation reaction in response to the stepwise increase of borehole pressure successfully confirm the in situ observations. Using the novel MHD-approach, the modeled borehole is tight against the attacking gas pressure until the minimum principle stress is exceeded, which happens first in the lowest part of the borehole (Fig. 3.9). The direction of the percolation plane is oriented perpendicular to the smallest compressive stress and therefore initially nearly horizontally aligned. The percolation front in the in situ—test eventually hit a almost perfectly horizontal weakness plane and is therefore slightly more localized, which is not included in this modeling. However, the new method has shown to be well suited to model the pressure- and stress-tensor-dependent salt percolation process both in laboratory and in situ scale remarkably well.

Fig. 3.8

Pressure steps of the in situ—test (top left) and AE-measurement (setup top right) of the percolation front after the 68 bar pressure step in side (bottom left) and top view (bottom right)

Fig. 3.9

Modeled percolation front starting to develop only after exceeding the necessary percolation pressure and permeating perpendicular to the least compressive stress