Abstract
The Cryptocurrency Volatility Index (CVI index) has been introduced to estimate the 30-day future volatility of the cryptocurrency market. In this article, we introduce a new Deep Neural Network with an attention mechanism to forecast future values of this index. We then look at the stability and performance of our proposed model against the benchmark models widely used for time series prediction. The results show that our proposed model performs well when compared to popular methods such as traditional Long Short Term Memory, Temporal Convolution Network, and other statistical methods like Simple Moving Average, Random Forest and Support Vector Regression. Furthermore, we show that the well-known Simple Moving Average method, while it has its own advantages, has the weak spot when dealing with time series with large fluctuations.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The success of the cryptocurrency market can be seen through the constant increase in total market capitalization, going from 20 billion USD at the beginning of 2017 to over 3 trillion USD in 2021, and in the number of investors joining the community starting from 65 million in mid-2020 to over 300 million at the end of 2021. One reason for this expansion is due to the large gains that cryptocurrencies (especially Bitcoin) can bring to investors, thanks to dramatic fluctuations in prices [12]. Furthermore, unlike the stock market, the cryptocurrency market has much fewer restrictions, allowing investors to complete a transaction quickly and freely [38]. Unfortunately, the ease of trading in cryptocurrency makes it very vulnerable to external factors such as news of financial developments, the movement of other assets and even the statements from influencers [17, 29]. As a consequence, compared to traditional markets such as stocks, bonds and commodities, the volatility of the cryptocurrency market tends to be extremely high [39]. This can lead to large fluctuations, for instance, a study conducted by Alexander et al. revealed that the losses of cryptocurrencies can reach 70% within one day [9]. Thus, the understanding of the volatility of the cryptocurrency market is essential to reduce the investment risk as well as to open opportunities to predict market’s movements and gain profits.
Due to the demand to measure the volatility of the cryptocurrency market, the Cryptocurrency Volatility Index (CVI index) has been launched. This is defined as a measure of the 30-day future fluctuation degree of the price of the entire cryptocurrency market using the Black-Scholes option pricing model. In this way, an index that fluctuates between 0 and 200 is developed, such that 200 will indicate the maximum level of implied volatility in the market whilst a value of zero indicates the lowest volatility [10]. This index is intended to prevent investors from putting themselves at risk by modifying their trading strategy in line with different values of CVI. The higher the CVI value is, the greater the risks are but also the greater the potential return is.
The usefulness of the CVI index is the main motivation behind this work. Specifically, our objective is to answer the following research question:
-
Is it possible to predict with accuracy the future value of the CVI index using neural networks?
We examine data from 10 cryptocurrencies which act as input features. Furthermore, we use the CVI index time series as labels for our prediction task. All time series span from 10/11/2017 to 12/01/2022. The details of this dataset are described in Sect. 3. Regarding the prediction model, we utilize Long Short Term Memory (LSTM), which is suitable for time series-related problems [16, 18], to extract these input features, followed by a Multilayer Perceptron (MLP) which allows the synthesis of the information extracted from the previous stage, the outputs of this stage being the predicted CVI values. Moreover, instead of using only the output from the last LSTM cell, which might lead to the losses of valuable information from earlier input data points, we use all outputs from the entire sequence of LSTM cells that are weighted according to their level of importance. We use a technique named Attention mechanism [41] for this weighing and name this novel neural network method AT-LSTM-MLP.
The remainder of this paper is organized as follows. Section 2 discusses related works. Section 3 introduces the dataset used in our experiments. Section 4 describes our AT-LSTM-MLP model and an outline of appropriate hyperparameters and specifications required to run experiments. Section 5 shows empirical results followed by an analysis learned from experiments. Section 6 gives conclusions for the article.
2 Related Works
Throughout the history of financial markets, there have been a number of prediction methods used to predict the future price and implied volatility of different assets such as stocks, bonds and cryptocurrencies.
Simple methods based on statistical learning frameworks have been found to show good performance in many studies, e.g. Simple Moving Average (SMA) [2], Support Vector Regression (SVR) [11] and Random Forest (RF) [32]. The advantages of these statistical methods are that they are easy to implement, thus, the time complexity is significantly low and they tend to work well with different datasets. That is why these methods are often used as benchmark models to verify the efficiency of other methods even though there is a superiority from more recent methods [23, 30].
Another commonly used method is GARCH, typically used to estimate the volatility of a time series such as stocks, bonds, market indices and recently, cryptocurrencies [7]. The first to use the GARCH model was Abdelhamid to estimate the volatility of different stocks circulating in the stock exchange of Casablanca at that time [13]. With time, there have been many variants of GARCH models proposed to optimize the prediction problem corresponding to a specific time series [4, 20]. Until now, although the global financial market has changed considerably (i.e. more people invested, more investment options, etc.), the performance of GARCH-type models still seems to be good. The study [28] showed that the volatility of world currencies, namely the GBP, CAD, AUD, CHF and the JPY is effectively predicted by using a GARCH-type model called IGARCH. On the other hand, CGARCH and TGARCH models work well with major cryptocurrencies such as Bitcoin, Litecoin and Ripple. All the time series were observed from October 2015 to November 2019. For a longer period from 2010 to 2020, GARCH and a simpler corresponding model ARCH have also been successfully used to form variance equations for highly-capitalized cryptocurrencies [5].
Neural Networks were first introduced in 1944 by McCullough and Pitts from the University of Chicago [25]. Since then, they have been applied to many different areas from healthcare services [15] to daily utility applications [42] and entertainment purposes [40]. In Finance, there is an increasing tendency to use RNNs to understand the operation of financial markets [1]. This is because they tend to work very well with time series data and are often integrated into prediction-related problems [18, 31]. LSTM [14], a version of Recurrent Neural Networks, appears to be dominant because of its ability to recollect longer so that information in the architecture can travel deeper. In [27], Aditi et al. made a comparison between Polynomial Regression, RNN, LSTM and ARIMA [6] for Bitcoin price fluctuation prediction. To do the experiment, the authors used a dataset of a combination between daily close price, volume and social media-related information such as Google Trend index, tweets’ emotions as well as the number of posts on Twitter containing the keyword “Bitcoin”. Out of four methods, LSTM outperformed the others with an accuracy of approximately 83%. Elsewhere, the information about Bitcoin blockchain technology has also been exploited to predict the future price. Specifically, Suhwan et al. investigated the performance of different Deep Learning models for estimating Bitcoin prices one day ahead [19]. In this study, 30 features were collected with one of them being daily closing price of Bitcoin and the rest being about blockchain specifications such as the average block size, the relative measure of difficulty in finding a new block, the total number of blockchain wallets created, etc. The results showed that LSTM slightly outperformed Multi-layer perceptrons and a pre-trained model ResNet. Another common Neural Network architecture is Convolution Neural Network (CNN), widely applied to analyze image data [35]. Recently, this type of Neural Network has been incorporated into financial research and has achieved certain successes. In particular, the authors in [3] used CNN as a part of their model to predict the future Bitcoin volatility and named it Temporal Convolution Network (TCN). Moreover, CNN can be incorporated into a LSTM model to improve the efficiency of the prediction. A method introduced in [24] for the prediction of Bitcoin, Ethereum and Ripple prices on the following hour combined three different Deep Learning models, including LSTM, Bidirectional LSTM and CNN, then used a statistical method such as Support Vector Regression or k-Nearest Neighbour to average the weighted output of each single model. It was confirmed that this practice helped improve the performance compared to individual models. In general, a large variety of methods for future volatility prediction exist in both traditional and cryptocurrency markets that use RNNs. All of these methods show an outperformance compared to GARCH-type models [16, 23].
3 Dataset
In order to answer our research question, we have chosen 77 digital currencies that meet the following three criteria:
-
(i) Large market capitalization: The market capitalization is greater than 1 million USD.
-
(ii) Long historical time series: The number of trading days is greater than 1000.
-
(iii) Few missing values: The percentage of missing values is less than 10%.
Furthermore, we use the CVI Index, which we have introduced in the previous section acting as labels for our proposed prediction model. The dataset used in this work was collected from two different sources: for cryptocurrencies’ historical data, we downloaded time series’ closing prices on the open financial website Yahoo! Finance; for CVI Index, the data was collected from the website Investing.com. All time series are collected day by day.
However, the trading schedule of each cryptocurrency is different, resulting in inconsistency across the entire dataset. Due to the difference in trading dates, if we attempted to use all the historical time series, we might end up with an empty dataset. For this reason, we chose 10 out of 77 cryptocurrencies that are widely known and have the longest historical data, the ultimate input features comprise BTC, ETH, BCH, ADA, XRP, DOGE, LINK, LTC, XLM and ETC. Each of them has 1537 data points starting from 10/11/2017 until 12/1/2021. When it comes to our labels, CVI Index begins on 31/3/2019 and ends on the same day as the other time series, the total number of data points is 1019. Subsequently, after merging all available data together (10 cryptocurrency time series and CVI time series), we have a 1019 data point dataset that consists of 10 cryptocurrencies acting as input features and CVI index acting as labels.
Since the original input features were collected daily from closing prices, it is necessary to convert this type of data into daily volatility:
-
Step 1: Calculating daily return of each cryptocurrency by using daily closing prices: \(y_t = log \left( \frac{Close_t}{Close_{t-1}}\right) \). Where \(y_t\), \(Close_t\) are daily return, close price at timestamp t, respectively.
-
Step 2: Calculating daily volatility from daily return, as suggested by Fernando et al [33]: \(\sigma _t = \sqrt{\frac{1}{5}\varSigma _{i=0}^4y^2_{t-i}}\). Where \(\sigma _t\) is realized volatility at timestamp t.
4 Methodology
4.1 Attention Based-Deep Neural Network (AT-LSTM-MLP)
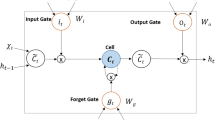
We create a novel Neural Network by combining 2 different types of Neural Network models, Long Short Term Memory [14] and Multilayer Perceptron (MLP) [22] and adding Attention Mechanism to weight the degree of importance for each LSTM cell. A diagram for this architecture is shown in Fig. 1.
AT-LSTM-MLP model. \(x_k\) refers to time series values at timestamp k, \(k = \left( 1,2,\dots , T\right) \), \(x^l\) refers to time series values of \(l^{th}\) input feature, \(l = \left( 1,2,\dots , n\right) \). The model comprises 2 parts: Long Short Term Memory with Attention Mechanism and Multilayer Perceptron. The output of the model are future predicted CVI indices.
Our proposed architecture (AT-LSTM-MLP) takes advantage of the outstanding characteristics not only of LSTM but also Attention Mechanism by using the weighted outputs of all LSTM cells from the sequence. These LSTM outputs will go to a Multilayer Perceptron where the future CVI index is predicted at the end. The process can be described as follows:
Firstly, we determine the shape of input data, each row is one timestamp while each column is one input feature. In our defined formula, we set T as the number of timestamps and n as the number of input features. We use the matrix form below as an input of our model:
Secondly, we move this input forward to a sequence of LSTM cells where each single LSTM cell (\(f_t\)) takes one row of the input (\(x_t\)) sequentially with the number of LSTM cells equal to the number of rows. The output at this phase is a set of hidden states at each LSTM cell \(\left( h_1, h_2, \ldots , h_T\right) \): \( h_t = f_t \left( x_t,h_{t-1}\right) \). Since LSTM takes the previous hidden state as an input argument, we set as default that the original hidden state (\(h_o\)) is zero, meaning that there no information from the time series revealed to the first LSTM cell. The hidden states \(\left( h_1, h_2, h_3, \dots , h_T\right) \) then go through the self-attention mechanism. The output at this stage, denoted as s, is obtained by the following mathematical equations:
where W and u are training parameters, \(a_1, a_2, \dots , a_n\) are Softmax coefficients. The Eq. 2a can be interpreted as a representation of a Fully Connected layer once each hidden state is passed to this layer in order to be embedded in a new vector space. We define an alignment function named score to measure how important each embedded hidden state \(u_t\) is. Theoretically, score can be any function depending on the research questions. In this work, we choose a straightforward function \(score\left( u_k,u \right) = u_k^T u\). This function will return a scalar value for each corresponding embedded hidden state. We use Softmax function to map the original values to a probability distribution where all the components add up to 1, the larger input components will correspond to larger probabilities. The last Eq. 2c is a weighted sum of all considered hidden states as well as the output of this attention mechanism.
Thirdly, the process continues moving to a Multilayer Perceptron with the predicted CVI index \(y_{CVI}\) obtained at the end: \(y_{CVI} = MLP\left( s\right) \).
4.2 Training Parameters and Implementation of Our Proposed Model
Our aim is to predict one-day future CVI index using 10 input features, which are 10 cryptocurrency time series. We run our proposed model on Tesla K80 GPU with memory size of 12 GB. We take the last 20% of the dataset for test set in order to evaluate the model’s performance, while the remaining data is used for training. All trainable parameters we initialize randomly following normal distribution with mean of 0. We built the model and ran all mentioned methods using Pytorch [34]. The details for the model specifications are described in Table 1, the optimal value according to each specification is shown in bold. We note that Mean Absolute Error is chosen as the loss function for our model. This is due to the lowest errors in the test set which were calculated using this metric.
4.3 Training Parameters and Implementation of Benchmark Models
The performance of our new method is verified by comparing with the following five different techniques:
1) Simple Moving Average [37]
We run the Simple Moving Average method for various window sizes according to the Autocorrelation plot. From this, we noticed 30 spikes outside of the blue area and thus statistically significant. Since a small change in the window sizes could lead to a small difference among the results, we do not use all possible window sizes. Instead, we choose window sizes = 2, 3, 4, \(\ldots \), 10, 15, 20, 25 and 30.
2) Support Vector Regression [26]
We use the Radial Basis Function kernel (RBF kernel) to find the optimal hyperplane for this regression problem because our data is clearly non-linear [36]. The regularization parameter is set to 1.0 to achieve a lower generalization error. To capture the shape of the data efficiently, we choose Gamma coefficient \(\gamma \) = 0.1, which is a parameter attached to the RBF kernel. All observations in the train set are put into SVR to estimate the most optimal solution for future prediction.
3) Random Forest [21]
We tested different possible values for the number of Decision Trees and found that 100 gives the best result. At each internal node of a Decision tree, we randomly choose three input features to consider when looking for the best split. The optimal feature will be chosen based on Variance Reduction technique. The minimum number of samples required to split an internal node is 2, the minimum number of samples at one leaf is 1. We use the average operation to synthesize the results of all Decision Trees. All observations in the train set are put into RFm to estimate the most optimal solution for future prediction.
4) Standard Long Short Term Memory [14]
This model comprises 20 LSTM cells with the size of hidden state being 1. We use the hidden state of the last LSTM cell as the output of the model. We train this model in 7000 epochs with a learning rate of 0.005. The other parameters used in this model are similar to our original model AT-LSTM-MLP.
5) Temporal Convolution Network [3]
From our original model, we replace the LSTM block with a TCN block. As each input of this model has 10 features and 20 timestamps, we set a kernel with a length of 5 and the number of channels of 10 to slide on the input. We choose dilation = 2. We train this model in 5000 epochs with a learning rate of 0,001. The other parameters used in this model are similar to AT-LSTM-MLP.
5 Empirical Results and Analysis
We measure the error of the methods through three different metrics: MAE, RMSE, and SMAPE [8]. For methods when results vary at every single run, we run each model 10 times, then get the mean \(\mu \) and standard deviation \(\sigma \) from all single results to give the final figure that is represented as \(\mu \pm \sigma \). For static methods, such as Simple Moving Average and Support Vector Regression, we run them once and consider the result as the final result.
Table 2 shows the results of our proposed model and four other models used for comparison. AT-LSTM-MLP, which is our model, outperforms other methods with RMSE, MAE, and SMAPE of \(2.24 \pm 0.17\), \(1.62 \pm 0.09\), \(1.76 \pm 0.10\), respectively. LSTM comes into second place with errors at more than double comparing to AT-LSTM-MLP. Whereas, the three remaining methods show poor results as the predicted values are too far from real values. These results give an answer to our research question that AT-LSTM-MLP can predict the future value of the CVI index well.
Table 3 show the results of SMA with different sizes of sliding window. In general, we can conclude that SMA works well with the data. However, the accuracy seems to fall off gradually as the sliding window size increases, the first sliding window sizes perform better than all other benchmarks with the exception of our method (AT-LSTM-MLP). SMA with sliding window size of 2 yields the best result of 2.02, 2.63, and 2.16 in MAE, RMSE, and SMAPE, respectively. This performance indicates the weakness of the SMA method. Particularly, SMA only works well with stable data, i.e. when the difference between time stamps within a sliding time window is small.
An illustration of predicted and real values using AT-LSTM-MLP and benchmark models is shown in Fig. 2 (only methods with good performance are illustrated).
6 Conclusions
We have built a novel Deep Neural Network by combining Long Short Term Memory, Multilayer Perceptron and Attention mechanism, named AT-LSTM-MLP. Our goal is to predict the day-ahead CVI index using ten long-series cryptocurrencies with large market capitalization. By comparing our proposed method with five benchmark models in three different metrics, we show that AT-LSTM-MLP performs better than the others. Moreover, we also indicate the main weakness of SMA: it only works well with stable data, when the difference between time stamps within a sliding time window is small.
The results from this study contribute to literature on the cryptocurrency market with some useful tools and information that aim to helping the investors in making decisions in investment. We believe that our method can be applied to other prediction tasks that involve time series because of its good performance.
References
Saeed, M.: An introduction to recurrent neural networks and the math that powers them (2021)
Abu Bakar, N., Rosbi, S., Uzaki, K.: Forecasting cryptocurrency price movement using moving average method: a case study of Bitcoin cash. J. Adv. Res. 7(12), 609–614 (2019)
Akbiyik, E., Erkul, M., Kaempf, K., Vasiliauskaite, V., Antulov-Fantulin, N.: Ask “who”, not “what”: Bitcoin volatility forecasting with Twitter data. arXiv preprint arXiv:2110.14317 (2021)
Ali, G.: EGARCH, GJR-GARCH, TGARCH, AVGARCH, NGARCH, IGARCH and APARCH models for pathogens at marine recreational sites. J. Stat. Econ. Methods 2(3), 57–73 (2013)
Almansour, B., Alshaterand, M., Almansour, A.: Performance of ARCH and GARCH models in forecasting cryptocurrency market volatility. Ind. Eng. Manag. Syst. 20(2), 130–139 (2021)
Ariyo, A., Adewumi, A., Ayo, C.: Stock price prediction using the ARIMA model. In: 2014 UKSim-AMSS 16th International Conference on Computational Modelling, Simulation, pp. 106–112. IEEE (2014)
Bhowmik, R., Wang, S.: Stock market volatility and return analysis: a systematic literature review. Entropy 22(5) (2020)
Botchkarev, A.: Performance metrics (error measures) in machine learning regression, forecasting and prognostics: properties and typology. arXiv preprint arXiv:1809.03006 (2018)
Brauneis, A., Mestel, R.: Price discovery of cryptocurrencies: Bitcoin and beyond. Econ. Lett. 165, 58–61 (2018)
Briefing, C.: What is the crypto volatility index (CVI)? (2021)
Dash, R.K., Nguyen, T., Sharma, A., Cengiz, K., Sharma, A.: Fine-tuned support vector regression model for stock predictions. Neural Comput. Appl. (2021)
Dong, F., Xu, Z., Zhang, Y.: Bubbly Bitcoin. Econ. Theory 1–43 (2021)
El Bouhadi, A.: Conditional volatility of most active shares of Casablanca stock exchange. Econometrica 50(1) (1982)
Graves, A.: Long short-term memory. In: Graves, A. (ed.) Supervised Sequence Labelling with Recurrent Neural Networks. SCI, vol. 385, pp. 37–45. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-24797-2_4
Han, C., Rundo, L., Murao, K., Noguchi, T.: MADGAN: unsupervised medical anomaly detection GAN using multiple adjacent brain MRI slice reconstruction. BMC Bioinform. 22(31) (2021)
Hu, Y., Ni, J., Wen, L.: A hybrid deep learning approach by integrating LSTM-ANN networks with GARCH model for copper price volatility prediction. Physica A 557 (2020)
Huynh, T.: When Elon Musk changes his tone, does Bitcoin adjust its tune? Comput. Econ. (2022)
Jay, P., Kalariya, V., Parmar, P., Tanwar, S., Kumar, N., Alazab, M.: Stochastic neural networks for cryptocurrency price prediction. Blockchain-Enabled Trustworthy Syst. 8 (2020)
Ji, S., Kim, J., Im, H.: A comparative study of Bitcoin price prediction using deep learning. Mathematics 7(10), 898 (2019)
Katsiampa, P.: Volatility estimation for Bitcoin: a comparison of GARCH models. Econ. Lett. 158, 3–6 (2017)
Khaidem, L., Saha, S., Dey, S.R.: Predicting the direction of stock market prices using random forest. Appl. Math. Finan. (2016)
Krogh, A.: What are artificial neural networks? Nat. Biotechnol. 26(2), 195–197 (2008)
Liu, Y.: Novel volatility forecasting using deep learning-long short term memory recurrent neural networks. Expert Syst. Appl. 132, 99–109 (2019)
Livieris, I., Pintelas, E., Stavroyiannis, S., Pintelas, P.: Ensemble deep learning models for forecasting cryptocurrency time-series. Algorithms 13(5) (2020)
McCulloch, W., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 5(4), 115–133 (1943)
Meesad, P., Rasel, R.I.: Predicting stock market price using support vector regression. In: 2013 International Conference on Informatics, Electronics and Vision (ICIEV), pp. 1–6 (2013)
Mittal, A., Dhiman, V., Singh, A., Prakash, C.: Short-term Bitcoin price fluctuation prediction using social media and web search data. In: 2019 Twelfth International Conference on Contemporary Computing (IC3), pp. 1–6. IEEE (2019)
Naimy, V., Haddad, O., Fernández-Avilés, G., El Khoury, R.: The predictive capacity of GARCH-type models in measuring the volatility of crypto and world currencies. PLoS One 16(1) (2021)
Nguyen, A.P.N., Mai, T.T., Bezbradica, M., Crane, M.: The cryptocurrency market in transition before and after Covid-19: an opportunity for investors? Entropy 24(9), 1317 (2022)
Nguyen, H.V., Naeem, A., Wichitaksorn, N., Pears, R.: A smart system for short-term price prediction using time series models. Comput. Electr. Eng. 76, 339–352 (2019)
Nguyen-Pham, N.A., Nguyen, T.: An efficient hybrid mechanism with LSTM neural networks in application to stock price forecasting. In: Knowledge Innovation Through Intelligent Software Methodologies, Tools and Techniques: Proceedings of the 19th International Conference on New Trends in Intelligent Software Methodologies, Tools and Techniques (SoMeT_20), vol. 327, p. 447 (2020)
Park, J.S., Sung Cho, H., Sung Lee, J., Chung, K.I., Kim, J.M., Kim, D.J.: Forecasting daily stock trends using random forest optimization. In: 2019 International Conference on ICT Convergence (ICTC), pp. 1152–1155 (2019)
Pérez-Cruz, F., Afonso-Rodriguez, J.A., Giner, J.: Estimating GARCH models using support vector machines. Quant. Finan. 3(3), 163 (2003)
PyTorch: PyTorch Tutorials (2022). https://pytorch.org/tutorials/
Quach, B.M., Dinh, V.C., Pham, N., Huynh, D., Nguyen, B.T.: Leaf recognition using convolutional neural networks based features. Multimed. Tools Appl. 1–25 (2022)
Ramedani, Z., Omid, M., Keyhani, A., Shamshirband, S., Khoshnevisan, B.: Potential of radial basis function based support vector regression for global solar radiation prediction. Renew. Sust. Energ. Rev. 39, 1005–1011 (2014)
Raudys, A., Pabarskaite, Z.: Optimising the smoothness and accuracy of moving average for stock price data. Technol. Econ. Dev. Econ. 24(3), 984–1003 (2018)
Reiff, N.: What are the advantages of paying with Bitcoin? (2021)
Rogojanu, A., Badea, L.: The issue of competing currencies. Theor. Appl. Econ. 590(1), 103–114 (2014)
Silver, D., et al.: Mastering chess and shogi by self-play with a general reinforcement learning algorithm. arXiv preprint arXiv:1712.01815 (2017)
Tixier, A.: Notes on deep learning for NLP. Computer Science Department (DaSciM team), École Polytechnique, Palaiseau, France (2018)
Zhang, X., Zhou, Y., Wang, J., Lu, X.: Personal interest attention graph neural networks for session-based recommendation. Entropy 23(11) (2021)
Acknowledgements
The authors Martin Crane, Marija Bezbradica wish to acknowledge the support, in part, from the Science Foundation Ireland under Grant Agreement No. 13/RC/2106_P2 at the ADAPT SFI Research Centre at DCU. ADAPT, the SFI Research Centre for AI-Driven Digital Content Technology, is funded by the Science Foundation Ireland through the SFI Research Centres Programme. The author An P. N. Nguyen wishes to acknowledge the support from Dublin City University’s Research Committee and research grants from Science Foundation Ireland Centre for Research Training in Artificial Intelligence under grant number 18/CRT/6223.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this paper
Cite this paper
Nguyen, A.P.N., Crane, M., Bezbradica, M. (2023). Cryptocurrency Volatility Index: An Efficient Way to Predict the Future CVI. In: Longo, L., O’Reilly, R. (eds) Artificial Intelligence and Cognitive Science. AICS 2022. Communications in Computer and Information Science, vol 1662. Springer, Cham. https://doi.org/10.1007/978-3-031-26438-2_28
Download citation
DOI: https://doi.org/10.1007/978-3-031-26438-2_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-26437-5
Online ISBN: 978-3-031-26438-2
eBook Packages: Computer ScienceComputer Science (R0)