Keywords

1 Introduction

When making decisions, fisheries managers almost always assume that the parameters of the growth function are statistically identified and temporally stable. While many data-rich fisheries have performed well in recent years, fisheries with little to no data still account for more than 80% of global harvest (Costello et al., 2012). When currently unassessed fisheries begin to accumulate data, there will no doubt be attempts to manage these fisheries using standard statistical methods. If the growth function’s parameters are not well identified in the available data, then there may be fundamental problems that are unlikely to be solved by changes in institutions and management objectives such as those suggested by the recent Pew Oceans Commission and the US Commission on Oceans Policy. This paper looks at the intrinsic difficulties involved in estimating fishery growth parameters, where the parameters of a time-invariant function are poorly estimated from a short sample of fishery and fishery-independent data.

The standard natural resource economics textbook treatments of how to optimally manage a fishery implicitly assume that biologists have delivered to them the “true” underlying parameters of a stable biological growth function (Gordon, 1954; Smith, 1969; Fisher, 1981; Berck & Perloff, 1984; Clark, 1990; Hartwick & Olewiler, 1998; Perman et al., 2003; Tietenberg & Lewis, 2018). Indeed, most economic analysis is done as if there is not even a random element to changes in fish stocks. While this has allowed economists to concentrate on the “economic” part of the management problem, serious issues arise if the underlying biological parameters upon, which decisions are being made, are substantially wrong. Indeed, the basic theme of this paper is that the estimates of the biological parameters will usually be sufficiently far from their true values in such a manner that economists cannot ignore the implications of this issue in providing policy advice.

To be sure, economists have not completely ignored the issue of uncertainty, although “relative” neglect is probably a fair assessment. Much of this neglect stems from a perceived division of labor between biologists and economists and a line of work begun by Reed (1979). Reed’s work suggested that if one simply tacked on a random term to the current period of growth, then the optimal policy was still the deterministic constant escapement rule of Gordon (1954). The reason is that if the error term was i.i.d. with an expected value of zero and observable, then it was optimal to adjust to each shock by setting harvests to keep the stock size constant. Clark and Kirkwood (1986) examine Reed’s framework under the more realistic assumption that contemporaneously there is measurement error in the stock size. Using a Bayesian framework, they find that a constant escapement rule is no longer optimal and that optimal stock size can be smaller or larger than in Reed’s case. Clark and Kirkwood maintain the assumption that the parameters of the growth function are known.Footnote 1

There has a been renewed interest in looking at uncertainty, some of which is stimulated by a provocative biologically oriented paper by Roughgarden and Smith (1996), which argued that the large amount of uncertainty in biological modeling calls for the use of some variant of the precautionary principle in fisheries management. This has led some economists, most notably Sethi et al. (2005), to reexamine the uncertainty issue.Footnote 2 Sethi et al. use three independent sources of uncertainty, growth, stock size measurement, and harvest implementation, each modeled as a contemporaneous error term. In this sense, Sethi et al. encompasses the Reed, Clark, and Kirkwood results and the more formal parts of Roughgarden and Smith. They find that uncertainty with respect to stock size measurement matters the most. In particular, they find constant escapement rules that attempt to hold the stock size at the level that maximizes sustainable yield and, which often characterize fisheries management, lead to substantially lower profit and a higher probability that the fish stock being managed will go extinct, compared to management under the adaptive policy they find to be optimal.

Sethi et al. (2005) suggest that uncertainty is more important than economists previously thought but at its heart is still a stable deterministic growth function with contemporaneous uncorrelated i.i.d. error terms added to the growth, stock measurement, and harvest equations. There are two other interesting possibilities to explore. The first is that the system is not stable over time in the sense of having clear time series dynamics either in the deterministic (Carson et al., 2009) or stochastic (Costello, 2000; Costello et al., 2001) part of the model. The second feature explored in this paper is the possibility that the system is stable but the parameters being used for policy purposes are fundamentally different from the true ones.Footnote 3

The precautionary principle has many flavors but provides few specific decision rules. One common practice is to reduce quotas to some fraction of MSY such that good estimates of the growth function parameters still play a critical role.Footnote 4 The other common practice is to suggest setting aside marine protected areas to prevent a fish stock from being wiped out (Lauck et al., 1998). But even when marine protected areas are in place, the remaining fishing grounds are likely to require some form of management tied to the biological state of the fishery to reduce the probability of collapse.

Operational application of the precautionary principle faces many difficulties (Sunstein, 2005; Randall, 2011). It should not simply always ban activities that have associated risks that are poorly quantified and have the potential for high levels of harm, as its proponents often believe. Meaningful trade-offs will need to be made. Further, the decision-making framework should move toward the ordinary risk management framework as better information about the originally difficult to quantify risks becomes available. Grant and Quiggin (2013) provide a perspective on the precautionary principle that emphasizes inductive reasoning about possible risks which they term “bound awareness.” The procedure put forward in this paper is in the spirit of their work in that it advances a heuristic decision rule that reduces the possibility of “unfavorable surprises” while engaging in active experimentation that progressively helps to improve the parameter estimates of the fisheries growth model.

Section 2 of this paper will introduce the basic model and in-sample simulation framework. Section 2 includes a discussion of some of the fisheries biology literature on estimating growth equations. This literature shows that even simple Gordon-Shaefer logistic growth models typically produce poor estimates and that there has been a tendency to move toward ever more complicated models that improve in-sample – but typically not out-of-sample – forecasting ability. Economists have paid surprisingly little attention to the technical estimation problems that biologists have long faced. Various shades of macroeconomic modeling and forecasting issues come to mind here (Hamilton, 1994). The fundamental problem is that errors are propagated through a nonlinear dynamic system, with the issue being exacerbated by a high degree of correlation between many variables, imperfect observability of some key variables, and a relatively short time series available on which to estimate model parameters.

While the parameters of the growth equation are technically identified, they are often only weakly identified because of the typical lack of substantial variation in the stock size and because of the tightly coupled relationship between the growth rate and the carrying capacity. In samples of the size often used for the purpose, parameter estimates may be almost arbitrarily far from their true values and the property of asymptotic consistency of little practical import. This under identification becomes even more troublesome if one allows various economic factors associated with catch per unit of effort measurements to be correlated with the unobserved random shocks, as seems likely.

Section 3 will describe estimation results for the parameter values used for growth rate, carrying capacity and stock size in the fisheries example in Perman et al. (2003), a popular graduate textbook. However, the results are not unique to this specification. Our example shows a frightening degree of parameter dispersion; even with almost 30 periods of data, some of the parameter estimates still display considerable bias.

Section 3 continues by simulating the traditional management practice of using estimated parameter values to determine catch. This is adaptive in the sense that it uses estimates of maximum sustainable yield (MSY)Footnote 5 updated with accumulated harvest and stock data. This is done repeatedly with different draws on the vector of random error. This allows us to trace out various outcome distributions. Specifically, we focus on average catch and frequency of collapse.

Section 4 introduces a simple rule-of-thumb scheme that forsakes an effort at formal estimation of the growth function parameters. This is similar to the direction that some of the macroeconomic literature has taken when the true model parameters are unknown (Brock et al., 2007). There is also an earlier strand in the agricultural economics literature (Rausser & Hochman, 1979), which suggests that optimizing decision rules coupled with highly nonlinear stochastic natural systems can be too complicated to be practically implemented and that they may be dominated by simple transparent rules that condition on a few observables. This rationale is also reflected in the popular Taylor rule approach to monetary policy for central banks (Orphanides, 2008).

Optimal stochastic control feedback rules may also be dominated by simple conditioning rules simply because of an inability to properly specify and estimate the system. Here, rather than assuming that the parameters of the growth function are known or even knowable, we make the much weaker assumption than is typical and assume only that the growth function is stable and is single-peaked. Our rule of thumb looks at the changes in stock and catch over two periods to determine which side of the peak one is on and takes a step toward it. Because there is a true stochastic component to growth, it is always possible to take a step in the wrong direction. Essentially, this is an adaptive gradient pursuit method, which is always on average moving in the correct direction. We show that this precautionary rule of thumb can lower the likelihood of collapse. When traditional management is combined with an initial period of precautionary management, future estimates converge to the truth more quickly and the likelihood of collapse is again lower.

The paper concludes in Sect. 5 with remarks on using precaution and statistics in fisheries that are only beginning to receive funding for assessment.

2 Model and Simulation Framework

The standard textbook fisheries example is the Gordon-Schaefer model with a logistic growth equation (Clark, 1990; Perman et al., 2003). The growth equation is usually represented as:

$$ G\left({X}_t\right)=r{X}_t\left(1\hbox{--} {X}_t/K\right), $$
(1)

where G(Xt) is the net natural growth in the fish stock at time t, Xt, r is the growth rate, and K is the carrying capacity. Xt + 1 = Xt + G(Xt) – Ft, where Ft is the quantity of fish harvested. A sustainable yield occurs where Ft = G(Xt). Maximizing sustainable yield (MSY), which is the explicit or implicit objective written into much fisheries legislation, occurs when the population is set at ½ K and is equal to rK/4. Adding an economic actor such as a rent maximizing sole owner shifts the MSY formulation of stock size a bit higher or lower to take account of how costs depend on stock size (stock size larger than MSY and increasing as degree of dependence increases) and the magnitude of the positive discount rate (stock size smaller than MSY and decreasing as discount rate increases). The optimal harvest size, though, is still typically driven to a large degree by the underlying MSY biology, as these two factors often roughly offset each other. What is crucial for the argument we advance is the dependence of current policies on knowing K to set the optimal stock size and rK to set the optimal harvest. Similar dependence exists for most of the other growth functions commonly used in making fisheries management decisions, so the conceptual issues can all be well illustrated using the logistic function. Further, we note that, while the Gordon-Shaefer logistic growth model can be criticized for not being realistic enough to fit empirical data, it is an entirely different matter if we generate data as if that model were true and then try to fit it. Now, the Gordon-Shaefer logistic model with stock assumed to be observable represents the best case of having to fit only two parameters relative to the available time dimension of the dataset.Footnote 6 While our simple model has but a single species and ignores spatial/temporal heterogeneity, the complications that arise from accounting for these factors make estimation all the more difficult and consequently reinforce the case for precaution when estimates are used to inform management.

The main problem is that K in the logistic growth equation is fundamentally under-identified, unless r is known (and to a lesser degree vice versa for r unless K is known). The main reason is that, unless there is substantial variation in Xt, then observing Xt and G(Xt) only identifies the ratio r/K. Since fisheries managers often try to hold Xt constant, which is optimal for MSY with i.i.d. environmental shocks to the growth equation (Reed, 1979), little variation in Xt is generally observed. Under-identification of K and r is not a new argument. Hilborn and Walters (1992) develop it at some length, but the argument does not seem to have permeated thinking in the economics literature on fisheries management. Instead, one sees explorations of other sources of uncertainty.

This fundamental under-identification of the parameters of the growth equation has a counterpart in the environmental valuation literature. There, it is well-known that – because observed conditions do not vary sufficiently – one must induce experimental variation (often in a stated preference context) in attributes such as cost in order to statistically identify the parameters of interest with enough precision to be useful for policy purposes. In the fisheries context, this would require intentionally encouraging very large swings in G(Xt) by setting different harvest levels in order to learn about r and K. This is unlikely to happen, as it would be fought in either direction by different interest groups.

Hilborn and Walters (1992) note that, in many empirical fishing models, because of the statistical imprecision in parameter estimates, K is set to the largest observed stock size (usually estimated via sampling or some other method). This, of course, technically resolves the statistical identification problem. However, the other parameter estimates can now be grossly wrong as a consequence and, hence, may result in policy prescriptions that are grossly wrong. In particular, assuming a value of K, which is too small, will result in an estimate of r that is too large and a recommendation to set Xt too low, which can be potentially disastrous.

Here, fishery data are simulated according to Eq. (1), including a uniformly distributed catch variable, Ft, and a normally distributed additive disturbance term, εt. This yields a linear estimating equation: Xt + 1 – Ft = rXt – (r/K)Xt2 + εt. The policy parameter of MSY = rK/4 is easily recovered from the linear regression results from the estimating equation. For notational compactness, define β1 and β2 as the respective coefficients from the linear regression. A consistentFootnote 7 estimate of the maximum of the growth curve is then given by:

$$ {\textrm{MSY}}_{\textrm{OLS}}=\frac{{\left({\beta}_1-1\right)}^2}{-4{\beta}_2} $$
(2)

This completes the model and in-sample simulation framework. The next section describes the performance of a fishery managed using OLS estimates obtained from simulated data. We then proceed to compare these statistical decisions under identical draws from the error terms to the performance of heuristic management.

3 Statistical Management

Parameter estimates are calculated by simulating sample data according to the model outlined in the previous section. The harvest data for the in-sample period are a uniformly distributed fraction of the fish stock that can be thought of as exogenously varying fishing effort. While many fishery datasets might exhibit a “one-way trip” of depletion (Hilborn & Walters, 1992), this tends to “rig the game” in the sense that parameter estimates are less precise, and probability of collapse is higher. For this reason, the in-sample data simulations use uniform fishing variability to give estimation the best chance of success. Figure 1 displays average parameter estimates for each regression coefficient and MSY over 10,000 simulations for 200 periods each. The regression coefficients are consistent for their true values and converge smoothly. The small-sample bias in the regression coefficients leads to some problematic behavior in the estimates of the policy variable; estimates of MSY are consistent but exhibit a much less regular approach to the true value, with many spikes, some quite large, along the path to convergence. This fits with empirical under-identification as described above (Kenny, 1979).

Fig. 1
Three graphs. a, Graph of Beta hat subscript 1 versus estimate of 1+ hat r denotes a downward curve above a linear line. b. Graph of Beta hat subscript 2 versus estimate of negative r hat over K indicates an upward curve below a linear line. c. Graph of M hat S Y versus estimate of M hat S Y fluctuates above the linear line with 2 sharp peaks.

Consistency of estimates

Full size image

The simulations above confirm that estimates implied by Eq. (2) are consistent. Using these estimates for policy is a different matter. Figure 2 demonstrates the performance of a statistical management regime that allows harvesting of the estimated value for MSY beginning at period 30.Footnote 8 When statistical management begins, catches immediately increase and the rate of collapse (stock reaching zero) increases, rising to nearly 90% by the 100th period. While there may exist discount rates for which this catch profile is supported as optimal, the fact remains that most fishery management legislation contains a mandate to prevent collapse of the resource. Statistical management, even for a correctly specified model with unrealistically high-quality data, performs poorly.

Fig. 2
Two graphs. a, the graph plots M S Y hat and expected catch, the dots for M S Y hat lie at 0 till 10, rise to 0.08 at 10, and fall gradually, the line for catch reaches 0.04 at 30 and decreases thereafter. b, the dots in the graph gradually rise from 0 to 85 between 0 and 100 which represent the percent of trials collapsed. Approximated values.

Statistical management

Full size image

4 Heuristic Precaution

What is the manager to do in the face of unreliable estimates of MSY in the given sample? A first thought might be to introduce a reduction to MSY, but it is not obvious how to make such a reduction that is not an arbitrary “fudge factor.” This section presents a modest suggestion: discard all but recent data. A “rule-of-thumb” management program using only the most recent three periods’ stock and catch data can perform a rudimentary gradient search for the stock which yields MSY. The motivation for the gradient search is that much can be learned from three periods about the current position of the stock. Presume only that G(Xt) has a unique global maximum value greater than zero and G(Xt) = 0 for Xt = 0 and Xt = 0 for some unknown K > 0. The goal is to set catch levels to send the stock level to that which maximizes the growth function. If the noise term is reasonably small and stock and catch values are known, then G(Xt) = (Xt – 1 – Xt) – Yt – 1, approximately. Therefore, at time period s and given data: {Ys, Ys – 1, Ys – 2, Xs, Xs – 1, Xs – 2}, we can rewrite to obtain our estimates of the realized growth in the previous two periods:

G(Xs – 1) = (Xs – Xs – 1) – Ys – 1 and G(Xs – 2) = (Xs – 1 – Xs – 2) – Ys – 2. We now have four cases, two of which are informative:

  1. 1.

    Xs – 1 > Xs and G(Xs – 1) > G(Xs): This implies that the single peak occurs at some X greater than Xs.

  2. 2.

    Xs – 1 < Xs and G(Xs – 1) < G(Xs): This is not enough information to determine the location of the peak.

  3. 3.

    Xs – 1 < Xs and G(Xs – 1) > G(Xs): This implies that the single peak occurs at some X greater than Xs.

  4. 4.

    Xs – 1 > Xs and G(Xs – 1) < G(Xs): This is not enough information to determine the location of the peak.

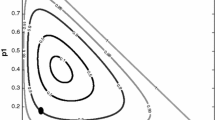
Three realizations of the stock and growth values are sufficient to describe two values lying on the underlying growth function. Figure 3 summarizes these four cases outlined above.

Fig. 3
Four graphs plot four different cases based on the relationship between X subscript s minus 1 and X subscript s, and G of X subscript s minus 1 and G of X subscript s. Graphs a and b have one single peak curve on a slanting distribution curve. Graphs c and d have one single peak curve on a distribution curve. Two points are marked on the meeting point each.

The four possibilities for 2 points for any single-peaked growth curve

Full size image

The rule-of-thumb decision rule makes use of the implications of each case above. In the informative cases 1 and 2, the rule increases or decreases the harvest by a factor, γ, assigned arbitrarily to be 5 in simulations below. To summarize, the rule of thumb sets period s catch as follows for each of the four cases:

  1. 1.

    Set Ys = (1 − γ)Ys−1

  2. 2.

    Set Ys = Ys−1

  3. 3.

    Set Ys = (1 + γ)Ys−1

  4. 4.

    Set Ys = Ys−1

Any precautionary preference would be concerned with the probability of stock collapse. Many management plans contain statements mandating a maintenance of stocks at or near that which yields MSY, coupled with a mandate to prevent the stock from crashing and to prevent the stock from dropping below some threshold as in Lee (2003). The rule of thumb decreases the probability of stock collapse.

Figures 4, 5, 6, and 7 present averages of 100,000 trials for 100 periods for managing a fishery under different regimes. Figure 4 shows the baseline of OLS statistical management beginning at period 15. Figures 5 and 6 show the results of preceding OLS statistical management by 15 and 30 years (respectively) of rule-of-thumb (gradient) management. Figure 7 shows the results of using our rule-of-thumb heuristic approach for the entire 85-year period of active management displayed. In every case, statistical management is dominated by our simple heuristic rule. Most strikingly, our rule-of-thumb gradient approach maintains high average catch levels; at the same time, the longer it is used relative to the standard OLS statistical management regime, the lower the probability of a fishery collapse.

Fig. 4
Two graphs. a, the graph plots M S Y hat and expected catch, the dots for M S Y hat lie at 0 till 10, rise to 0.08 at 10, and fall gradually, the line for catch reaches 0.05 at 15 and decreases thereafter. b, the dots in the graph gradually rise from 0 to 85 between 0 and 100 which represent the percent of trials collapsed. Approximated values.

Pure statistical management with delay

Full size image
Fig. 5
Two graphs titled Begin the rule of thumb at t = 15, O L S at t = 30. a, the dots for M S Y hat lie at 0, then go to 0.08 at 10 and fall thereafter and the line for catch increases to 0.03 between 20 and 30 and decreases after 31. b, the dots in the graph gradually rise from 0 to 80 between 0 and 100 which represent the percent of trials collapsed. Approximated values.

Mixed management, short horizon

Full size image
Fig. 6
Two graphs titled Begin rule of thumb at t = 15, O L S at t = 45, the dots for M S Y hat lies at 0 till10, go to 0.07 at 10, and decreases thereafter and the line for catch almost lies at 0.01 except two growths between 20 and 30, and at 45. b, the dots in the graph gradually rise from 0 to 60 between 0 and 100 which represent the percent of trials collapsed. Approximated values.

Mixed management, long horizon

Full size image
Fig. 7
Two graphs titled Begin rule of thumb at t = 15, O L S at t = 100, the dots for M S Y hat lies at 0 till 10, go to 0.07 at 10, and decreases thereafter and the line for catch almost lies at 0.01 except two growths between 20 and 30. b, the dots in the graph gradually rise from 0 to 21 between 0 and 100 which represent the percent of trials collapsed. Approximated values.

Pure heuristic management with delay

Full size image

The results suggest that it is unlikely that small samples of fishery independent data contain much payoff-relevant information. The rule of thumb outperforms decisions based on the entire sample. It is important to remember that OLS is correctly specified for this model, and the disturbance terms are normally distributed and i.i.d., a rosy situation indeed. The model is simple, but any change to the model to increase realism will only make the bio-econometrician’s task more difficult, as there is no more realistic growth model with fewer than two parameters.

5 Concluding Remarks

Fisheries in the developing world are plagued by myriad difficulties. Property rights are insecure. Ecosystems are degraded. Data are missing and, of necessity, the parameter estimates upon which fisheries management decisions are made must be wrong. Statistical estimates are never the true parameter values. Economists have largely ignored this issue. Indeed, most theoretical and applied work has taken the parameter estimates from biologists and treated them as truth. When economists have considered uncertainty, it is typically in the form of random environmental shocks to recruitment from the growth equation. In the simplest cases, i.i.d. error terms allow the appropriate adjustment in each time period. Sethi et al. (2005) have shown that other forms of error, such those resulting from having to measure stock size, can create much more substantial problems for managing fisheries. Our work extends the list of problems by emphasizing statistical uncertainty in the parameter estimates when only relatively short time series data are available – a situation that characterizes many fisheries.

In the simple Gordon-Shaefer model, measurement error in the main biological parameters – growth rate, carrying capacity, and maximum sustainable yield – tends to be fairly large. In part that is because the regression model has two covariates, stock size and stock size squared, which tend to be highly correlated. This high correlation is made much worse by the usual management practice of trying to maintain stock size at a specific level. The typical error in the parameter estimates increases rapidly in the underlying unexplained variance. More complex (and realistic) models, either in terms of more parameters or more complex error structures, are likely to create even worse statistical properties for the estimates used. This paper gives the game away to the bio-econometrician; estimation is made as simple as possible. The functional form is the one used to generate the data; the error component is generated independently and has low variance. Further, both catch and stock are assumed observable. This paper shows that there is little gain (if any) to using the full, but still quite small, sample typically available for most fisheries. Throwing out 90% of the sample and using a heuristic are better.

Increasing the number of parameters will almost surely make the problem worse. Some readers may argue that real stock assessments rely on fishery-independent data and that our results only reinforce the importance of that source of information. Fisheries are multidimensional dynamic systems and data on variables beyond catch and stock levels (such as length-frequency and length-at-age) may improve estimates, but only if the out-of-sample predictive information they provide grows at a rate substantially larger than the number of extra parameters that must be fit. That is because the fundamental nature of the problem is the propagation of measurement error in the parameters in a nonlinear optimization model.

One of the immediate results of our framework is that under- or overestimating the allowable catch by the same amount does not result in symmetric errors. Overestimation leads to higher catches now and, of necessity, fewer fish later, including substantially increasing the risk that the fishery collapses. For any given over- and underestimate of the allowable catch, there is typically a discount rate that would make one indifferent. Environmentalists and fishers, however, are likely to disagree on the discount rate. The social discount rate is also likely to be lower than the private discount rate. This discount rate story as a source of conflict is not new, but what is new is the interaction between the level of parameter uncertainty and the discount rate. Uncertainty amplifies the policy variance implied by differing discount rates. Reducing the level of uncertainty can be Pareto-improving for all groups and can reduce (but not eliminate) the degree of conflict. This insight may be useful in implementing more practical variants of the precautionary principle.

Given the poor performance of the standard statistical estimates of the relevant biological parameters and the fact that either over- or underestimation of allowable catch can reduce welfare, it is useful to ask if there is any way to improve the situation. Because the problem is essentially one of high collinearity and small sample size, one possibility is to limit the range of either the carrying capacity or growth rate parameters. Interesting opportunities for doing this appear to be available, particularly with the recent biological work on estimating historical population stocks before large-scale commercial fishing (Jackson et al., 2001). A Bayesian framework (Geweke, 1986; Gelman et al., 2003; Walters & Ludwig, 1994) is natural. Pinning down a reasonable narrow range for one of these parameters could add a great deal of stability to the estimate of allowable catch.

Our framework suggests a different way of dealing with the issue. It may be generally applicable to situations where there is considerable uncertainty about the underlying biological growth function, other than the assumption that it is single peaked. Our rule-of-thumb decision simply tests which side of the peak one is likely to be on, using very limited information, and then pursues it using a conservative step size. Since there are stochastic shocks, it is always possible to move in the wrong direction on any particular step. On average, though, one moves in the correct direction. This simple approach works reasonably well in the sense of being fairly close to using the growth function parameters estimated in the standard way when the parametric modeling being fit was the correct one. Further, there are clearly more sophisticated adaptive gradient pursuit methods that could be explored than the simple rule-of-thumb approach in this paper; such methods may be more statistically efficient while maintaining a large degree of robustness. Another logical step would be to look at the performance of different adaptive gradient pursuit methods when the underlying parametric model being fit was the incorrect one, so that there was both specification and parameter estimation error, as is likely to be the case in realistic empirical applications. Our current framework shows promise for cautious adaptive management as a path to implementing management guided by a precautionary principle. Finally, we have assumed the usual biological management strategy of setting an overall catch limit. It would be useful to see how our proposed method interacts with the use of landing fees (Weitzman, 2002) or individual transferable quotas (Squires et al., 1995).