Keywords

1 Introduction

The modelling under location uncertainty (LU) setting has shown to provide consistent physical representations of fluid dynamics [10, 12]. This representation introduces a random component to describe the unresolved flow components. This enables to consider less dissipative systems than the classical large-scale counterparts. Nevertheless, the ability of such a model to represent faithfully the uncertainties associated to the actual unresolved small scales highly depends on the definition of the random component and on its evolution along time. Unsurprisingly, stationarity/time-varying and homogeneity/inhomogeneity characteristics have strong influences on the results [1, 2]. Another important aspect concerns the ability to include in the noise representation a stationary drift component associated to the temporal mean of the high-resolution fluctuations. As shown in this paper such stationary drift can be elegantly introduced in the noise through Girsanov theorem. Yet, large-scale persistent components associated to the high resolution fluctuations are not strictly stationary and slowly varying quasi-periodic components might be important to include. To that purpose we devise a noise generation scheme relying on the dynamic mode decomposition [13]. Such a decomposition or other related techniques aiming to provide a spectral representation of the Koopman operator [11] will allow us to represent the noise as a superposition of random and deterministic harmonics oscillators. The first ones are attached to the fast components whereas the latter represent the slow fluctuations components. As demonstrated in Sect. 4, this strategy brings us a very efficient technique for ocean double-gyres configuration.

2 Modelling Under Location Uncertainty

In this section, we briefly review the LU setting and the associated random QG model that will be used for the numerical evaluations.

2.1 Stochastic Flow

The evolution of Lagrangian particle trajectory (X t) under LU is described by the following stochastic differential equation (SDE):

$$\displaystyle \begin{aligned} \mathrm{d} \boldsymbol{X}_t (\boldsymbol{x}) = \boldsymbol{v} \big( \boldsymbol{X}_t (\boldsymbol{x}), t \big)\, \mathrm{d} t + \boldsymbol{\sigma} \big( \boldsymbol{X}_t (\boldsymbol{x}), t \big)\, \mathrm{d} \boldsymbol{B}_t,\ \quad \boldsymbol{X}_0 (\boldsymbol{x}) = \boldsymbol{x} \in \mathcal{D}, \end{aligned} $$
(1)

where v denotes the time-smooth resolved velocity that is both spatially and temporally correlated, σdB t stands for the fast oscillating unresolved flow component (also called noise in the following) that is only correlated in space, and \(\mathcal {D} \subset \mathbb {C}^d\) (d =  2 or 3) is a bounded spatial domain.

We now give the mathematical definitions of the noise. In the following, let us fix a finite time T < ∞ and the Hilbert space \(H = (L^2 (\mathcal {D}))^d\) with the inner product \(\left \langle {\boldsymbol {f}, \boldsymbol {g}} \right \rangle _{\scriptscriptstyle H} = \int _{\scriptscriptstyle \mathcal {D}} (\boldsymbol {f}^{\dagger } \boldsymbol {g}) (\boldsymbol {x})\, \mathrm {d} \boldsymbol {x}\) and the norm \(\|\boldsymbol {f}\|{ }_{\scriptscriptstyle H} = \left \langle {\boldsymbol {f}, \boldsymbol {f}} \right \rangle _{\scriptscriptstyle H}^{1/2}\), where •† stands for transpose-conjugate operation. Then, {B t}0≤t≤T is an H-valued cylindrical Brownian motion (see definition in [4]) on a filtered probability space \((\varOmega , \mathcal {F}, \{\mathcal {F}_t\}_{\scriptscriptstyle 0\leq t \leq T}, \mathbb {P})\), with the covariance operator diag(I d) (where I d is an d-dimensional vector of identity operators). For each (ω, t) ∈ Ω × [0, T] constraining, σ(⋅, t)[•] to be a (random) Hilbert-Schmidt integral operator on H with a bounded matrix kernel σ̆ = (σ̆ij)i,j=1,…,d such that

$$\displaystyle \begin{aligned} \boldsymbol{\sigma} (\boldsymbol{x}, t)\, \boldsymbol{f} = \int_{\mathcal{D}} \breve{\boldsymbol{\sigma}} (\boldsymbol{x}, \boldsymbol{y}, t) \boldsymbol{f} (\boldsymbol{y})\, \mathrm{d} \boldsymbol{y},\ \quad \boldsymbol{f} \in H,\ \quad \boldsymbol{x} \in \mathcal{D} . \end{aligned} $$
(2a)

Its adjoint operator σ ∗(⋅, t)[•] satisfying \(\left \langle {\boldsymbol {\sigma } (\boldsymbol {\cdot }, t) \boldsymbol {f}, \boldsymbol {g}} \right \rangle _{\scriptscriptstyle H} = \left \langle {\boldsymbol {f}, \boldsymbol {\sigma }^* (\boldsymbol {\cdot }, t) \boldsymbol {g}} \right \rangle _{\scriptscriptstyle H}\) reads:

$$\displaystyle \begin{aligned} \boldsymbol{\sigma}^* (\boldsymbol{x}, t)\, \boldsymbol{g} = \int_{\mathcal{D}} \breve{\boldsymbol{\sigma}}^{\dagger} (\boldsymbol{x}, \boldsymbol{y}, t) \boldsymbol{g} (\boldsymbol{y})\, \mathrm{d} \boldsymbol{y},\ \quad \boldsymbol{g} \in H,\ \quad \boldsymbol{x} \in \mathcal{D} . \end{aligned} $$
(2b)

The composite operator σ(⋅, t)σ ∗(⋅, t)[•] is trace class on H and admits eigenfunctions ξ n(⋅, t) with eigenvalues λ n(t) satisfying \(\sum _{n \in \mathbb {N}} \lambda _n (t) < + \infty \). The noise can then be equally defined by the spectral decomposition:

$$\displaystyle \begin{aligned} \boldsymbol{\sigma} (\boldsymbol{x}, t)\, \mathrm{d} \boldsymbol{B}_t = \sum_{n \in \mathbb{N}} \lambda_n^{1/2} (t) \boldsymbol{\xi}_n (\boldsymbol{x}, t)\, \mathrm{d} \beta_n (t), \end{aligned} $$
(3)

where β n are independent standard Brownian motions. In addition, we assume that the operator-space-valued process {σ(⋅, t)[•]}0≤t≤T is stochastically integrable, i.e. \(\mathbb {P} \big [ \int _0^T \sum _{n \in \mathbb {N}} \lambda _n (t)\, \mathrm {d} t < +\infty \big ] = 1\). From [4], the stochastic integral \(\{ \int _0^t \boldsymbol {\sigma } (\boldsymbol {\cdot }, s)\, \mathrm {d} \boldsymbol {B}_s \}_{\scriptscriptstyle 0\leq t \leq T}\) is a continuous square integrable H-valued martingale, hence a centered Gaussian process, \(\mathbb {E}_{\scriptscriptstyle \mathbb {P}} [\int _0^t \boldsymbol {\sigma } (\boldsymbol {\cdot }, s)\, \mathrm {d} \boldsymbol {B}_s] = \boldsymbol {0}\), of bounded variance, \(\mathbb {E}_{\scriptscriptstyle \mathbb {P}} \big [ \| \int _0^t \boldsymbol {\sigma } (\boldsymbol {\cdot }, s)\, \mathrm {d} \boldsymbol {B}_s \|{ }_{\scriptscriptstyle H}^2 \big ] < +\infty \). Moreover, the joint quadratic variation process of the noise, evaluated at the same point \(\boldsymbol {x} \in \mathcal {D}\), is given by

$$\displaystyle \begin{aligned} &\Big\langle \int_0^{\cdot} \boldsymbol{\sigma} (\boldsymbol{x}, s)\, \mathrm{d} \boldsymbol{B}_s, \int_0^{\cdot} \boldsymbol{\sigma} (\boldsymbol{x}, s)\, \mathrm{d} \boldsymbol{B}_s \Big\rangle_t = \int_0^t \boldsymbol{a} (\boldsymbol{x}, s)\, \mathrm{d} s \end{aligned} $$
(4a)
$$\displaystyle \begin{aligned} & \boldsymbol{a} (\boldsymbol{x}, t) = \int_{\mathcal{D}} \breve{\boldsymbol{\sigma}} (\boldsymbol{x}, \boldsymbol{y}, t) \breve{\boldsymbol{\sigma}}^{\dagger} (\boldsymbol{y}, \boldsymbol{x}, t)\, \mathrm{d} \boldsymbol{y} = \sum_{n \in \mathbb{N}} \lambda_n (t) \big( \boldsymbol{\xi}_n \boldsymbol{\xi}_n^{\dagger} \big) (\boldsymbol{x}, t) . \end{aligned} $$
(4b)

We remark that real-valued noise can be achieved by adding the constraint that both eigenfunctions, eigenvalues and the standard Brownian motions in (3) are organised in complex-conjugated pairs. In that case, its joint quadratic variation process is real-valued as well.

The previous formulations consist of only a zero-mean and temporally uncorrelated noise. However, this might not be enough and including a mean or time-correlated component of the unresolved velocity field could be of crucial importance to obtain a relevant model. For instance, the eddy parametrization proposed by [15] is decomposed into a deterministic mean term and a stochastic term of zero-mean. For the double-gyre circulation configuration, the considered deterministic parametrization allows to reproduce the eastwards jet for the coarse-resolution model, while the additional stochastic terms enhance the gyres circulation and improves the flow variability. Similarly, the random-forcing model proposed by [3] consists in a space-time correlated stochastic process to enhance the jet extension. The slow modes of the sub-grid scales can be provided by adequate high-pass filtering of high-resolution data on the coarse grid. We aim in this work at investigating the incorporation of such slow components within the LU framework. However, the derivation of LU models [10, 12, 1] relies on the martingale properties of the centered noise and we need hence to properly handle non centred Brownian terms. The Girsanov transformation [4] provides a theoretical tool that fully warrants such a superposition: by a change of the probability measure, the composed noise can be centered with respect to a new probability measure while the additional drift term appears, which pulls back time-correlated sub-grid-scale components into the dynamical system. The associated mathematical description is given as follows. Let Γ t be an H-valued \(\mathcal {F}_t\)-predictable process satisfying the Novikov condition, \(\mathbb {E}_{\scriptscriptstyle \mathbb {P}} \big [ \exp (\frac {1}{2} \int _0^{\scriptscriptstyle T} \|\boldsymbol {\varGamma }_t\|{ }_{\scriptscriptstyle H}^2\, \mathrm {d} t ) \big ] < +\infty \), then the process \(\{ \boldsymbol {\widetilde {B}}_t := \boldsymbol {B}_t + \int _0^t \boldsymbol {\varGamma }_s\, \mathrm {d} s\}_{\scriptscriptstyle 0 \leq t \leq T}\) is an H-valued cylindrical Wiener process on \((\varOmega , \mathcal {F}, \{\mathcal {F}_t\}_{\scriptscriptstyle 0 \leq t \leq T}, \widetilde {\mathbb {P}})\) with Radon-Nikodym derivative

$$\displaystyle \begin{aligned} \frac{\mathrm{d} \widetilde{\mathbb{P}}}{\mathrm{d} \mathbb{P}} = \exp \Big( - \int_0^T \left\langle {\boldsymbol{\varGamma}_t, \mathrm{d} \boldsymbol{B}_t} \right\rangle _{\scriptscriptstyle H} - \frac{1}{2} \int_0^T \|\boldsymbol{\varGamma}_t\|{}_{\scriptscriptstyle H}^2\, \mathrm{d} t \Big) . \end{aligned} $$
(5a)

In this case, the SDE (1) under the probability measure \(\widetilde {\mathbb {P}}\) reads:

$$\displaystyle \begin{aligned} \mathrm{d} \boldsymbol{X}_t = \big( \boldsymbol{v} (\boldsymbol{X}_t, t) - \boldsymbol{\sigma} (\boldsymbol{X}_t, t) \boldsymbol{\varGamma}_t \big)\, \mathrm{d} t + \boldsymbol{\sigma} (\boldsymbol{X}_t, t)\, \mathrm{d} \boldsymbol{\widetilde{B}}_t . \end{aligned} $$
(5b)

In the present work, we shall consider rather this modified stochastic flow defined on \((\varOmega , \mathcal {F}, \{\mathcal {F}_t\}_{\scriptscriptstyle 0 \leq t \leq T}, \widetilde {\mathbb {P}})\) with \(\mathbb {E}_{\scriptscriptstyle \widetilde {\mathbb {P}}} [\boldsymbol {\sigma } \mathrm {d} \boldsymbol {\widetilde {B}}_t] = \boldsymbol {0}\) as the physical solution. Hereafter, σΓ t is referred to as the Girsanov drift.

2.2 Stochastic QG Model

The evolution law of a random tracer (function) Θ transported along the stochastic flow, Θ(X t+δt, t + δt) = Θ(X t, t), is derived by [10, 1]. Under the probability measure \(\widetilde {\mathbb {P}}\), this can be described by the following stochastic partial differential equation (SPDE), namely

$$\displaystyle \begin{aligned} \mathbb{D}_t \varTheta &:= \mathrm{d}_t \varTheta + (\boldsymbol{\widetilde{v}}^{\star}\, \mathrm{d} t + \boldsymbol{\sigma} \mathrm{d} \boldsymbol{\widetilde{B}}_t) \boldsymbol{\cdot} \boldsymbol{\nabla} \varTheta - \frac{1}{2} \boldsymbol{\nabla} \boldsymbol{\cdot} (\boldsymbol{a} \boldsymbol{\nabla} \varTheta)\, \mathrm{d} t = 0 {} \end{aligned} $$
(6a)
$$\displaystyle \begin{aligned} \boldsymbol{\widetilde{v}}^{\star} &:= \boldsymbol{v} - \frac{1}{2} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{a} + \boldsymbol{\sigma}^* (\boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\sigma}) - \boldsymbol{\sigma} \boldsymbol{\varGamma} , {} \end{aligned} $$
(6b)

In this SPDE, the first term dt Θ(x) := Θ(x, t + δt) − Θ(x, t) stands for the (forward) increment of Θ at a fixed point \(\boldsymbol {x} \in \mathcal {D}\); the second term describes the tracer’s advection by an effective drift \(\boldsymbol {\widetilde {v}}^{\star }\) and the noise \(\boldsymbol {\sigma } \mathrm {d} \boldsymbol {\widetilde {B}}_t\); the last term depicts the tracer’s diffusion through the noise quadratic variation a. The effective drift (6b) ensues from (i) the noise inhomogeneity, (ii) the possible unresolved flow divergence and (iii) the statistical correction due to the change of probability measures, respectively.

The derivation of the stochastic geophysical models under the LU framework follows exactly the same path as the deterministic derivation, together with a proper scaling of the noise and its amplitude. In particular, a continuously stratified QG model under LU has been derived by [12, 9] using an asymptotic approach. With horizontally moderate and vertically weak noises (see definitions in [12, 9]), the governing equations under the probability measure \(\widetilde {\mathbb {P}}\) read:

$$\displaystyle \begin{aligned} &\hspace{-3pt}\underline{\text{Evolution of potential vorticity (PV):}} \\ &\hspace{-3pt}\mathbb{D}_t q = \sum_{i=1,2} \mathrm{J} \Big( (\widetilde{u}^{\star})^i\, \mathrm{d} t + (\sigma \mathrm{d} \widetilde{B}_t)^i, u^i \Big) - \Big( \frac{1}{2} \boldsymbol{\nabla} \boldsymbol{\cdot} \big( \partial_{x_i}^{\perp} \boldsymbol{a} \boldsymbol{\nabla} u^i \big) + \beta \partial_{x_i} a_{i2} \Big)\, \mathrm{d} t, {} \end{aligned} $$
(7a)
$$\displaystyle \begin{aligned} &\hspace{-3pt}\underline{\text{From PV to streamfunction:}} \\ &\hspace{-3pt}\nabla^2 \psi + \partial_z \Big( \frac{f_0^2}{N^2} \partial_z \psi \Big) = q - \beta y, {} \end{aligned} $$
(7b)
$$\displaystyle \begin{aligned} &\underline{\text{Incompressible constraints:}} \\ &\boldsymbol{u} = \boldsymbol{\nabla}^{\perp} \psi,\ \quad \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\sigma} \mathrm{d} \boldsymbol{\widetilde{B}}_t = \boldsymbol{\nabla} \boldsymbol{\cdot} (\boldsymbol{\widetilde{u}}^{\star} - \boldsymbol{u}) = 0 {}. \end{aligned} $$
(7c)

Here, ∇ = [∂ x, ∂ y]T, ∇ ⊥ = [−∂ y, ∂ x]T, \(\nabla ^2 = \partial _{xx}^2 + \partial _{yy}^2\) denote two-dimensional operators and J(f, g) = ∂ x f∂ y g − ∂ x g∂ y f stands for the Jacobian operator. The vector fields \(\boldsymbol {u}, \boldsymbol {\sigma } \mathrm {d} \boldsymbol {\widetilde {B}}_t\) and the tensor field a are two-dimensional (2D) horizontal quantities. The horizontal effective drift is defined as \(\boldsymbol {\widetilde {u}}^{\star } := \boldsymbol {u} - \boldsymbol {\nabla } \boldsymbol {\cdot } (\boldsymbol {a} / 2) - \boldsymbol {\sigma } \boldsymbol {\varGamma }\). The scalar fields q and ψ represent the PV and the streamfunction. In Eq. (7b), N 2 = −(g∕ρ 0)∂ z ρ is the Brunt-Väisälä (or buoyancy) frequency with g the gravity value, ρ 0 the background density, ρ the density anomaly, and f 0 + βy is the Coriolis parameter under a beta-plane approximation. As shown in [1], one important characteristic of the random model (7) is that it conserves the total energy of the resolved flow (under natural boundary condition) for any realization (i.e. pathwise). This property highlights a strong relation between the classical deterministic model and the stochastic formulation.

3 Numerical Parameterization of Unresolved Flow

Data-driven approaches are presented in this section to estimate the spatial correlation functions of the unresolved flow component based on the spectral decomposition (3). In practice, we work with a finite set of functions to represent the small-scale Eulerian velocity fluctuations rather than with the Lagrangian particles trajectory. We first review the empirical orthogonal functions (EOF) method for which the noise covariance is assumed quasi-stationary. We then propose an approach relying on the dynamic mode decomposition (DMD) to account for the temporal behavior of the spatial correlations.

3.1 EOF-Based Method

In the following, let {u HR(x, t i)}i=1,…,N be the set of velocity snapshots provided by a high-resolution (HR) simulation. We first build the spatial local fluctuations u f(x, t i) of each snapshot on the coarse-grid points. In particular, for the QG system (7), one can first perform a high-pass filtering with a 2D Gaussian convolution kernel G on each HR streamfunction ψ HR, to obtain the streamfunction fluctuations, ψ f(x, t i) = ((I −G) ⋆ ψ HR)(x, t i) (only for the coarse-grid points x). Then, the geostrophic velocity fluctuations can be derived by \(\boldsymbol {u}_f = \boldsymbol {\nabla }^{\perp }_{\scriptscriptstyle \text{LR}} \psi _f\). We next centre the data set by \(\boldsymbol {u}_f^{\prime } = \boldsymbol {u}_f - \overline {\boldsymbol {u}_f}^t\) (with \(\overline {\bullet }^t\) the temporal mean) and perform the EOF procedure [9] to get a set of orthogonal temporal modes {α m}m=1,…,N and orthonormal spatial modes {ϕ m}m=1,…,N satisfying

$$\displaystyle \begin{aligned} \boldsymbol{u}_f^{\prime} (\boldsymbol{x}, t_i) = \sum_{m=1}^{N} \alpha_m (t_i) \boldsymbol{\phi}_m (\boldsymbol{x}),\ \quad \overline{\alpha_m \alpha_n}^t = \lambda_m \delta_{m,n} . \end{aligned} $$
(8)

Truncating the modes (with M ≪ N) and rescaling by a small-scale decorrelation time τ, the stationary noise and its quadratic variation can be build by

$$\displaystyle \begin{aligned} \boldsymbol{\sigma} (\boldsymbol{x}) \mathrm{d} \boldsymbol{\widetilde{B}}_t = \sqrt{\tau} \sum_{m=1}^M \sqrt{\lambda_m} \boldsymbol{\phi}_m (\boldsymbol{x})\, \mathrm{d} \beta_m (t),\ \quad \boldsymbol{a} (\boldsymbol{x}) = \tau \sum_{m=1}^M \lambda_m \boldsymbol{\phi}_m (\boldsymbol{x}) \boldsymbol{\phi}_m^{\scriptscriptstyle T} (\boldsymbol{x}) . \end{aligned} $$
(9)

Note that this time scale τ is used to match the fact that the noise in (5b) has the physical dimension of a length. In practice, we often consider the coarse-grid simulation timestep Δt LR. In addition, the Girsanov drift is set to be \(\boldsymbol {\sigma } (\boldsymbol {x}) \boldsymbol {\varGamma }_t = \overline {\boldsymbol {u}_f}^t (\boldsymbol {x})\). It means that the Girsanov drift here is the projection of the temporal mean of the sub-grid scales onto the EOFs, i.e. \(\boldsymbol {\sigma } (\boldsymbol {x}) \boldsymbol {\varGamma }_t = \sum _{m=1}^N \gamma _m \boldsymbol {\phi }_m (\boldsymbol {x})\) with \(\gamma _m = \langle \overline {\boldsymbol {u}_f}^t, \boldsymbol {\phi }_m \rangle _{\scriptscriptstyle H}\) satisfying \(\sum _{m=1}^N \gamma _m^2 < + \infty \).

3.2 DMD-Based Method

The DMD algorithm [13] seeks a spectral decomposition of the best-fit linear operator A that relates the two snapshots:

$$\displaystyle \begin{aligned} \boldsymbol{u}^{\prime}_f (\boldsymbol{x}, t_{i+1}) \approx \boldsymbol{A} \boldsymbol{u}^{\prime}_f (\boldsymbol{x}, t_{i}) . \end{aligned} $$
(10a)

Applying the exact DMD procedure proposed by [14], the corresponding spectral expansion in continuous time reads

$$\displaystyle \begin{aligned} \boldsymbol{u}^{\prime}_f (\boldsymbol{x}, t) = \sum_{m=1}^N b_m \exp \big( (\sigma_m + \mathrm{i}\, \omega_m) t \big) \boldsymbol{\varphi}_m (\boldsymbol{x}), \end{aligned} $$
(10b)

where \(\boldsymbol {\varphi }_m (\boldsymbol {x}) \in \mathbb {C}^d\) are the DMD modes (eigenvectors of A) associated to the DMD eigenvalues \(\mu _m \in \mathbb {C}\), \(\sigma _m = \log (|\mu _m|) / \varDelta t_{\scriptscriptstyle \text{d}} \in \mathbb {R}\) are the modes growth rate (with Δt s = t i+1 − t i the sampling step of data), \(\omega _m = \arg (\mu _m) / \varDelta t_s \in \mathbb {R}\) are the modes frequencies (with i the imaginary unit) and \(b_m \in \mathbb {C}\) are the modes amplitudes. In practice, our data set of velocity fluctuations is real valued, hence the DMD modes (also eigenvalues and amplitudes) are two-by-two complex conjugates, i.e. \(\boldsymbol {\varphi }_{\scriptscriptstyle 2 p} = \overline {\boldsymbol {\varphi }}_{\scriptscriptstyle 2p-1}\ (p=1,\ldots ,N/2)\).

We next propose to split the total set of DMD modes into two subsets, \(\mathcal {M}^c\) and \(\mathcal {M}^r\), to select separately adequate fast and slow modes for the noise (from \(\mathcal {M}^r\)) and the Girsanov drift (from \(\mathcal {M}^c\)), respectively, according to the following analysis of frequencies and amplitudes:

$$\displaystyle \begin{aligned} \mathcal{M}^c &= \Big\{ m \in [1, N]\ \Big|\ |\mu_m| \approx 1,\ |\omega_m| \leq \frac{\pi}{\tau_c},\ |b_m| \geq C \Big\}, {} \end{aligned} $$
(11a)
$$\displaystyle \begin{aligned} \mathcal{M}^r &= \Big\{ m \in [1, N]\ \Big|\ |\mu_m| \approx 1,\ |\omega_m| > \frac{\pi}{\tau_c},\ |b_m| \geq C \Big\}, {} \end{aligned} $$
(11b)

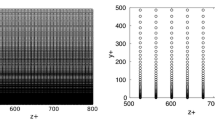
where τ c is a temporal-separation-scale that can be estimated by the spatial mean of the autocorrelation functions of data and C denotes an empirical cutoff of amplitudes. The DMD modes that are neither included in \(\mathcal {M}^c\) nor in \(\mathcal {M}^r\) are discarded. An example of spectrum and amplitudes of the selected DMD modes is shown in Fig. 1. In order to avoid spurious effects associated with the non-orthogonality of DMD modes, their amplitudes are rescaled such that the reconstructed data corresponds to an orthogonal projection onto the subspace spanned by the modes in \(\mathcal {M}^c\) or \(\mathcal {M}^r\). In particular, we propose to rescale those truncated DMD modes as follows:

  1. (i)

    Construct the Gramian \(\boldsymbol {G} = (g_{m,n})_{\scriptscriptstyle m,n \in \mathcal {M}^c}\) with \(g_{m,n} = \left \langle {\boldsymbol {\varphi }_m, \boldsymbol {\varphi }_n} \right \rangle _{\scriptscriptstyle H}\);

    Fig. 1
    figure 1

    Illustration of the selections of DMD modes used for the noise (orange) and the Girsanov drift (blue)

    Full size image
  2. (ii)

    Inverse the Gramian \(\boldsymbol {G}^{-1} := (g_{m,n}^{-1})_{\scriptscriptstyle m,n \in \mathcal {M}^c}\) and derive the dual set of the truncated DMD modes by \(\boldsymbol {\varphi }_m^* = \sum _{\scriptscriptstyle n \in \mathcal {M}^c} g_{m,n}^{-1} \boldsymbol {\varphi }_n\);

  3. (iii)

    Project the initial state of data on the dual set of modes to update the amplitudes: \(\boldsymbol {\phi }_m := \langle \boldsymbol {u}^{\prime }_f (\boldsymbol {\cdot }, t_1), \boldsymbol {\varphi }_m^* \rangle _{\scriptscriptstyle H}\, \boldsymbol {\varphi }_m\).

Such procedure holds separately for the DMD modes of \(\mathcal {M}^c\) and \(\mathcal {M}^r\). Finally, the noise and the correction drift can be defined as

$$\displaystyle \begin{aligned} \boldsymbol{\sigma} (\boldsymbol{x}, t) \mathrm{d} \boldsymbol{\widetilde{B}}_t &= \sqrt{\tau} \sum_{m \in \mathcal{M}^r} \exp (\mathrm{i}\, \omega_m t) \boldsymbol{\phi}_m (\boldsymbol{x})\, \mathrm{d} \beta_m (t) , \end{aligned} $$
(12a)
$$\displaystyle \begin{aligned} \boldsymbol{\sigma} (\boldsymbol{x}, t) \boldsymbol{\varGamma}_t &= \overline{\boldsymbol{u}_f}^t (\boldsymbol{x}) + \sum_{m \in \mathcal{M}^c} \exp (\mathrm{i}\, \omega_m t) \boldsymbol{\phi}_m (\boldsymbol{x}) , {} \end{aligned} $$
(12b)

In particular, we assume that each pair of the complex Brownian motions are conjugates (\(\beta _{\scriptscriptstyle 2 p} = \overline {\beta }_{\scriptscriptstyle 2 p - 1}\)) and their real and imaginary parts are independent. As such, both noise \(\boldsymbol {\sigma } \mathrm {d} \boldsymbol {\widetilde {B}}_t\) and correction drift σΓ t are real-valued fields. In addition, the joint quadratic variation of such noise remains stationary:

$$\displaystyle \begin{aligned} \boldsymbol{a} (\boldsymbol{x}) = \tau \sum_{m \in \mathcal{M}^r} \boldsymbol{\phi}_m (\boldsymbol{x}) \boldsymbol{\phi}_m^{\dagger} (\boldsymbol{x}) . \end{aligned} $$
(12c)

In a similar way as in the EOF-based method, we could also construct the Girsanov drift by the projection of the RHS of (12b) onto the DMD modes. As we have dropped the unstable DMD modes, one can show that the predictability and the Novikov condition (presented in Sect. 2) of Γ hold in this case.

4 Numerical Experiments

In this section, we present some numerical results of the stochastic QG system (7). The objective consists to improve the variability of large-scale models defined on coarse grids. To that end, a high-resolution deterministic reference model (REF) is first simulated and compared to several coarse-resolution models: the benchmark deterministic model (DET), two stochastic models with an EOF-based noise (STO-EOF) and a DMD-based noise (STO-DMD).

4.1 Configurations

In this study, we consider a vertically discretized QG dynamical core proposed in [8] and extended in the stochastic setting [9]. This model consists in n isopycnal layers with constant thickness H k and density ρ k in each layer k. In this case, the prognostic variables such as ψ in (7) are assumed to be layer-averaged quantities. Homogeneous Dirichlet boundary conditions have been imposed for the term f 0 ∂ z ψ∕N 2 in (7b) at the ocean surface and bottom. Moreover, external forcing and numerical dissipation are included in the evolution of PV (7a): the Ekman pumping \(\vec {\nabla }^{\perp } \boldsymbol {\cdot } \boldsymbol {\tau }\) due to the wind stress τ over ocean surface boundary, a linear drag − (f 0 η ek∕2)∇2 ψ n at ocean bottom with a very thin thickness η ek, and a biharmonic dissipation − A 4∇4(∇2 ψ k) in each layer with uniform coefficient A 4. In particular, we consider here a finite box ocean driven by an idealized (stationary and symmetric) wind stress \(\boldsymbol {\tau } = [-\tau _0 \cos (2\pi y)/L_y, 0]^{\scriptscriptstyle T}\). A mixed horizontal boundary condition is used for the k-th layer streamfunction: \(\psi _k |{ }_{\partial \mathcal {A}} = f_k (t)\) and \(\partial _n^2 \psi _k |{ }_{\partial \mathcal {A}} = - (\alpha _{\text{bc}}/\varDelta x) \partial _n \psi _k |{ }_{\partial \mathcal {A}}\) (same for the 4-th order derivative). Here, \(\mathcal {A}\) denotes the 2D area, f k is a time-dependent function constrained by mass conservation [7], Δx stands for the horizontal resolution and α bc is a nondimensional coefficient associated to the slip conditions [7]. A quiescent initial condition is used for the REF, whereas a spin-up condition downsampled from REF (after 90-years integration) is adopted for all the coarse-resolution models. The common parameters for all the simulations are listed in Table 1, whereas resolution dependant parameters are presented separately in Table 2. Both EOF and DMD modes are calibrated from the REF data during 40 years (after the spin-up) with a 5-days sampling step. As for the numerical discretization, a conservative flux form [9] together with a stochastic Leapfrog scheme [5] is adopted for the evolution of PV (7a). The inversion of the modified Helmholtz equation (7b) is carried out with a discrete sine transform method [7].

Table 1 Common parameters for all the models. The buoyancy frequency N 2 in (7b) is approximated by \(g_{k+0.5}^{\prime }/(H_k + H_{k+1})/2\) on the interface between layers k and k + 1
Full size table
Table 2 Values of grid varying parameters. The energy proportion captured by the truncated EOF modes are given in the bracket. For DMD method, the first number stands for the size of \(\mathcal {M}^c\) (11a) whereas the latter is the one of \(\mathcal {M}^r\) (11b)
Full size table

Snapshots of the surface PV provided by the different simulations are shown in Fig. 2. The dynamics of REF (5 km) model is mainly characterized by a meandering eastward jet with adjacent recirculations, which results from the most active mesoscale eddies effect through baroclinic instability. However, this effect cannot be properly resolved once the horizontal resolution exceeds the baroclinic deformation radius maximum (39 km here). For instance, the DET (80 km) simulation generates only a smooth symmetric field. On the other hand, both STO-EOF and STO-DMD models are able to reproduce the eastward jet on the coarse mesh (80 km) by including the non-linear effects carried both by the unresolved noise and the correction drift. In particular, the STO-DMD model produces a stronger meridional perturbation along the jet and is able to capture some of the large-wave structures predicted by the REF model. The improvements brought by these random models will be diagnosed and analyzed more precisely in the following.

Fig. 2
figure 2

Snapshots of surface PV provided by different simulations after 60-years integration. The black arrows are the interpolated geostrophic velocities

Full size image

4.2 Diagnostics

We first compare the long-term mean (over a 100-years interval) of the kinetic energy (KE) spectrum for both coarse models at different resolutions (40, 80, 120 km). As shown in Fig. 3, introducing only a dissipation mechanism like the biharmonic viscosity in the DET coarse models leads to an excessive decrease of the resolved KE compared to the REF model. Both STO-EOF and STO-DMD models at different resolutions, recover a given amount of lost energy over all wavenumbers. In particular, the STO-DMD models provide higher KE backscattering at large scales and better spectrum slope in the inertial-range than the stationary unresolved models. This seems to highlight the importance of the non-stationary characteristic of the noise and Girsanov drift.

Fig. 3
figure 3

Temporal mean of vertically integrated KE spectra for the different models

Full size image

We then quantify the temporal variability (over the same 100-years interval) predicted by the different coarse models. In this work, we adopt the following three global metrics. The first one is the root-mean-square error (RMSE) between the standard deviation of the streamfunction of a coarse model (denoted by σ[ψ M]) and the subsampled high-resolution one (denoted by σ[ψ R]), \(\|\sigma [\psi ^{\scriptscriptstyle \text{M}}] - \sigma [\psi ^{\scriptscriptstyle \text{R}}]\|{ }_{\scriptscriptstyle L^2 (\mathcal {D})}\), where \(\mathcal {D} = \mathcal {A} \times [-H, 0]\) and H stands for the total depth of the ocean basin. The second criterion is the Gaussian relative entropy (GRE) [6] which assesses in a single measure the mean and variance reconstruction:

$$\displaystyle \begin{aligned} \hspace{-6pt}\text{GRE} = \frac{1}{|\mathcal{D}|} \int_{\mathcal{D}} \frac{1}{2} \left(\! \frac{\big( \overline{\psi^{\scriptscriptstyle\text{M}}}^t - \overline{\psi^{\scriptscriptstyle\text{R}}}^t \big)^2}{\sigma^2 [\psi^{\scriptscriptstyle\text{M}}]} + \frac{\sigma^2 [\psi^{\scriptscriptstyle\text{R}}]}{\sigma^2 [\psi^{\scriptscriptstyle\text{M}}]} - 1 - \log \Big( \frac{\sigma^2 [\psi^{\scriptscriptstyle\text{R}}]}{\sigma^2 [\psi^{\scriptscriptstyle\text{M}}]} \Big) \!\right)\, \mathrm{d} \boldsymbol{x}. \end{aligned} $$
(13)

It is clear that a coarse model of high variability will have low RMSE and GRE, whereas a poor variability will lead to a large RMSE and GRE. The last metric measures the eddy kinetic energy (EKE), \((\rho _0/2) \|\boldsymbol {u}'\|{ }_{\scriptscriptstyle (L^2(\mathcal {D}))^2}^2\), where \(\boldsymbol {u}' := (I - \mathcal {F}_t) [\boldsymbol {u}]\) is the eddy velocity filtered out through a 2-years low-pass filter \(\mathcal {F}_t\) at every point in space. For comparison reason, we show here only the time average of this metric (\(\overline {\text{EKE}}\)) for the different models.

These three criteria are shown in Fig. 4 as bar plots. The DET models show very high RMSE and GRE with a very low order of EKE, meaning that they produce poor variability along time and failed to represent the eddies effect. Compared to the STO-EOF, the STO-DMD models enable to increase significantly the internal variability and the eddy energy. Moreover, these improvements are resolution-aware. As shown in Table 2, under a similar level of captured energy, the STO-DMD models require much less modes than the STO-EOF, which reduces first the memory cost. Then, in terms of computational cost at each step, the former consists in generating less Gaussian variables than the latter, and reduces hence as well the dimension of the matrix-vector multiplication for the spectral decomposition (3).

Fig. 4
figure 4

Comparison of variability measures for different coarse models. The y-axis of the last two figures are in \(\log \)-scales

Full size image

4.3 Discussion

In order to distinguish the contribution of the correlated Girsanov drift and the uncorrelated noise, three additional benchmark runs (at resolution 80 km) have been further performed and compared to the proposed STO-DMD model, they are (i) STO-DMD without any correlation drift (i.e. σΓ t = 0); (ii) STO-DMD only with \(\boldsymbol {\sigma } \boldsymbol {\varGamma }_t = \overline {\boldsymbol {u}_f}^t\); (iii) a simplified deterministic version of the proposed STO-DMD model, denoted as DET-DMD, which only encodes the (full) correlated drift σΓ t into the DET model. We remark that for the two first runs the DMD modes used for the correlated drift in the previous stochastic model are now included into the noise component. As shown in Fig. 5, run (i) fails to reproduce the eastwards jet on the coarse mesh, whereas the other runs succeed. However, run (ii) produces similar results as the STO-EOF model (see Fig. 2) with a lower improvement of variability, and run (iii) captures more waves than the others, yet leads to a reduction of the jet magnitude compared to the proposed STO-DMD model. In particular, by comparing the KE spectra of the different runs, Fig. 6 illustrates that the simplified DET-DMD model allows to produce backscattering of KE from small to large scales, and the proposed STO-DMD enhances this result with significantly higher KE at large-scales. We observe a consistent conclusion for the EKE budget (see Fig. 6). These comparisons demonstrate that the both correlated drift (σΓ t) and the uncorrelated noise (\(\boldsymbol {\sigma } \mathrm {d} \boldsymbol {\widetilde {B}}_t\)) contribute on the prediction of large-scale patterns and on the improvement of the variability of the large-scale models.

Fig. 5
figure 5

Snapshots of surface PV provided by different simulations after 60-years integration. These four figures (from left to right) correspond to the benchmark runs (i), (ii), (iii) and the proposed STO-DMD model

Full size image
Fig. 6
figure 6

Comparison of KE spectra and layered EKE (only horizontally integrated) for different coarse models

Full size image

5 Conclusions

The proposed stochastic parameterization has been successfully implemented in a well established QG dynamical core. Different noises defined from high-resolution data have been considered. An additional correction drift ensuing from a change of probability measure has been introduced. This non-intuitive term seems quite important in the reproduction of the eastward jet within the wind-driven double-gyre circulation. Furthermore, the DMD procedure has been adopted to represent the quasi-periodic dynamic of the unresolved flow. The resulting random model enables us to improve the intrinsic variability of the large-scale resolved flow.