Spinor Methods

Abstract

This chapter is an introduction to spinors and spinor algebra methods and their application in spin dynamics. Spinors and their manipulation are introduced, first, together with a number of properties of interest for the calculation of spin transport in special devices such as Siberian snakes, spin rotators, and in beam lines in general, and for the calculation as well of the effects of depolarizing resonances in cyclic accelerators. Practical application to spin transport follows. Spinor eigenvectors are introduced and applied to the calculation of stable spin precession direction in cyclic accelerators. Spin motion near integer and intrinsic resonances is derived using these techniques, and allows reproducing results obtained in the previous chapter.

This manuscript has been authored by Brookhaven Science Associates, LLC under Contract No. DE-SC0012704 with the U.S. Department of Energy. The United States Government and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes.

3.1 Introduction

This lecture is based on several of the founding theoretical papers and earlier lectures regarding spinor methods in spin dynamics. Publications used to prepare these notes include A. Chao’s 2000 USPAS lecture [1], Courant-Ruth’s 1980 BNL report [2], Montague’s 1984 article [3], Tkatchenko-Niem’s 1993 Saturne report, [4] and textbooks by S.Y. Lee [5] and Conte and MacKay [6].

This list is not exhaustive, however it is believed to be a sound starting point for further exploration and advanced knowledge, beyond the present brief theoretical introduction to spinor methods.

3.2 Spinors

In dealing with Thomas-BMT equation of spin motion for spin-½ particles in Chap. 2, spin was considered a classical quantity (by resorting to the principle of correspondence), handled under the form of a 3-vector in real space, $\mathbf S = \left ( \begin {array}{c} S_{{s} } \\[-.7ex] S_{{x}} \\[-.7ex] S_{{y}} \end {array} \right )$(in the reference frame defined in Fig. 2.5).

An alternate method to describe spin motion uses their spinor representation: a complex 2-vector

$$\displaystyle \begin{aligned} \psi= \left( \begin{array}{c} \psi_1 \\ \psi_2 \end{array} \right)\end{aligned}$$

manipulated using spinor algebra: a 2 × 2 rotation matrix algebra.

The complex components ψ₁ and ψ₂ of a spinor represent the respective probabilities of the +½ and −½ spin states (spin angular momentum S = ±ħ∕2). The normalization condition for the spinors reads

Two-dimensional spinors will be addressed here, for spin ½ particles. The treatment for 3-dimensional spinors, spin 1 particles, can be found for instance in Ref. [6].

3.3 Pauli Matrices

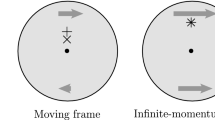
The wanting frame in this chapter is represented in Fig. 3.1.

Fig. 3.1

The moving frame (Serret-Frénet frame). Note that it is left-handed, for convenience (whereas a right-handed frame was considered in Chap. 2, Fig. 2.5)

A spinor matrix algebra has 4 basis elements:

• the identity matrix $I = \left ( \begin {array}{ccc} 1 & ~ & 0 \\[-.7ex] 0 && 1 \end {array} \right )$, and

• Pauli matrices: $\sigma _{{x}} = \left ( \begin {array}{ccc} 0 & ~ & 1 \\[-.7ex] 1 && 0 \end {array} \right )$, $\sigma _{{s} } = \left ( \begin {array}{ccc} 0 & ~ & -i \\[-.7ex] i && 0 \end {array} \right )$, $\sigma _{{y}} = \left ( \begin {array}{ccc} 1 & ~ & 0 \\[-.7ex] 0 && -1 \end {array} \right )$.

Indices relate to the frame axes, this is addressed below.

Moving from a spinor 2-vector representation, $\psi = \left ( \begin {array}{c} \psi _1 \\ \psi _2 \end {array} \right )$, to a classical 3-vector $\mathbf S= \left ( \begin {array}{c} S_{{x}} \\[-.7ex] S_{{s} } \\[-.7ex] S_{{y}} \end {array} \right )$, goes as follows.

Define a 3-vector $\mathbf \sigma = \left ( \begin {array}{c} \sigma _{{x}} \\[-.7ex] \sigma _{{s} } \\[-.7ex] \sigma _{{y}} \end {array} \right )$, take Hermitian conjugate of ψ, then

(3.1)

Note the expected $|\mathbf S|{ }^2 = S_{{x}}^2 + S_{{s} }^2 + S_{{y}}^2 = 1,$ as comes out with some algebra.

Pauli Matrix Properties

A variety of properties are resorted to in manipulating spinors, which will be used in particular in various calculations to come, as follows:

wherein the suffix i stands for indifferently x, s or y.

$$\displaystyle \begin{aligned} \sigma_{{x}} \sigma_{{s} } = -\sigma_{{s} } \sigma_{{x}} = i \sigma_{{y}}; \ \sigma_{{s} } \sigma_{{y}} = -\sigma_{{y}} \sigma_{{s} } = i \sigma_{{x}}; \ \sigma_{{y}} \sigma_{{x}} = -\sigma_{{x}} \sigma_{{y}} = i \sigma_{{s} }\end{aligned}$$

$$\displaystyle \begin{aligned} \mathrm{vector}\ \mathrm{product:} \ \mathbf \sigma \times \mathbf \sigma \equiv \left( \begin{array}{c} \sigma_{{x}} \\[-.7ex] \sigma_{{s} } \\[-.7ex] \sigma_{{y}} \end{array} \right) \times \left( \begin{array}{c} \sigma_{{x}} \\[-.7ex] \sigma_{{s} } \\[-.7ex] \sigma_{{y}} \end{array} \right) = 2i\mathbf \sigma \end{aligned}$$

A real-space 3-vector $\mathbf \omega = \left ( \begin {array}{c} \omega _{{x}} \\[-.7ex] \omega _{{s} } \\[-.7ex] \omega _{{y}} \end {array} \right )$ can be represented by a 2 × 2 Hermitian matrix:

$$\displaystyle \begin{aligned} \mathbf \sigma \cdot \mathbf \omega = \mathbf \omega \cdot \mathbf \sigma = \omega_{{x}}\sigma_{{x}} + \omega_{{s} }\sigma_{{s} } + \omega_{{y}}\sigma_{{y}} = \left( \begin{array}{cc} \omega_{{y}} & \omega_{{x}} -i \omega_{{s} } \\ \omega_{{x}} +i \omega_{{s} } & -\omega_{{y}} \end{array} \right)\end{aligned}$$

with the following properties:

$$\displaystyle \begin{aligned} {det}|\mathbf \sigma \cdot \mathbf \omega| = -\omega^2; \quad (\mathbf \sigma \cdot \mathbf \omega)^n = \Bigg\{ \begin{array}{ll} \omega^n \, I & \mathrm{if}\ \mathrm{n}\ \mathrm{even}\\ \omega^{n-1} (\mathbf \sigma \cdot \mathbf \omega ) & \mathrm{if}\ \mathrm{n}\ \mathrm{odd}\\ \end{array} \quad (|\mathbf \omega|=\omega)\end{aligned}$$

$$\displaystyle \begin{aligned} (\mathbf \sigma \cdot \mathbf \omega_a)(\mathbf \sigma \cdot \mathbf \omega_b) = I (\mathbf \omega_a\cdot \mathbf \omega_b) + i\mathbf \sigma \cdot (\mathbf \omega_a\times \mathbf \omega_b).\end{aligned}$$

3.4 Spin Transport

3.4.1 An Optical Element

An optical element may be represented by a 2 × 2 matrix (noted T, here). The transport of a spinor through that element writes

$$\displaystyle \begin{aligned} \psi_f = T(f\leftarrow i)\, \psi_i {}\end{aligned} $$

(3.2)

with ψ_i and ψ_f the spinor respectively before and after the element.

Assume that the matrix T describes a spinor rotation by an angle ϕ ω, with $\mathbf \omega = \left ( \begin {array}{c} \omega _{{x}} \\[-.7ex] \omega _{{s} } \\[-.7ex] \omega _{{y}} \end {array} \right )$the precession vector. T can thus be written under either one of the following different forms:

$$\displaystyle \begin{aligned} \begin{array}{rcl} T = e^{\textstyle \frac{i}{2}\, (\mathbf \omega \cdot \mathbf \sigma ) \, \phi} \\ = I\, \cos \dfrac{\omega \phi}{2} + i\, \left( \dfrac{\mathbf \omega}{\omega}\cdot \mathbf \sigma \right)\, \sin \dfrac{\omega \phi}{2} \\ = t_0 I + i t_{{x}}\sigma_{{x}} + i t_{{s} } \sigma_{{s} }+ i t_{{y}}\sigma_{{y}} \\ = \left( \begin{array}{cc} t_0 +i t_{{y}} & t_{{s} } +i t_{{x}} \\ -t_{{s} } +i t_{{x}} & t_0 -i t_{{y}} \end{array} \right) {} \end{array} \end{aligned} $$

(3.3)

The coefficients t_0,x,s,y introduced here satisfy

$$\displaystyle \begin{aligned} t_0 = \cos \dfrac{\omega \phi}{2}, \ t_{{x}} = \dfrac{\omega_{{x}}}{\omega} \sin \dfrac{\omega \phi}{2}, \ t_{{s} } = \dfrac{\omega_{{s} }}{\omega} \sin \dfrac{\omega \phi}{2}, \ t_{{y}} = \dfrac{\omega_{{y}}}{\omega} \sin \dfrac{\omega \phi}{2} {}\end{aligned} $$

(3.4)

Note the properties:

Examples

• 1. In a uniform vertical field B = B_y y, over an orbital section [θ₁, θ₂],

  • spins precess around B ∥y

  • by an angle ϕ = Gγ(θ₂ − θ₁) (as (θ₂ − θ₁) is the trajectory deviation),

    thus

    $$\displaystyle \begin{aligned} \phi\, \mathbf \omega = G\gamma (\theta_2-\theta_1) \left(\begin{array}{c} 0\\[-.7ex] 0\\[-.7ex] 1 \end{array} \right) \quad \!\mathrm{so}\ \mathrm{that}\! \quad \phi\, \mathbf \omega \cdot \mathbf \sigma = G\gamma (\theta_2-\theta_1)\left(\begin{array}{c} 0\\[-.7ex] 0\\[-.7ex] 1 \end{array} \right)\cdot \left( \begin{array}{c} \sigma_{{x}} \\[-.7ex] \sigma_{{s} } \\[-.7ex] \sigma_{{y}} \end{array} \right)= G\gamma (\theta_2-\theta_1) \sigma_{{y}}\end{aligned}$$

    yielding (Eqs. 3.2 and 3.3)

    $$\displaystyle \begin{aligned} \psi(\theta_2)= e^{\textstyle\frac{i}{2}\, G\gamma (\theta_2-\theta_1) \sigma_{{y}}} \psi(\theta_1)\end{aligned}$$

    and finally

    $$\displaystyle \begin{aligned} T(\theta_2 \leftarrow \theta_1)=e^{\textstyle\frac{i}{2}\, G\gamma (\theta_2-\theta_1) \sigma_{{y}}}\end{aligned}$$

• 2. Over one turn along the closed orbit in a perfect ring, in the moving frame, (θ₂ − θ₁) = 2π, thus

  $$\displaystyle \begin{aligned} \psi(\theta_2)\ =\ e^{\textstyle\frac{i}{2}\, G\gamma \, 2\pi \sigma_{{y}}} \psi(\theta_1) \ =\ e^{\textstyle\frac{i}{2}\, 2\pi u_{\mathrm{sp}}\sigma_{{y}}} \psi(\theta_1),\end{aligned}$$

  so that

  $$\displaystyle \begin{aligned} T_{\mathrm{1-turn}}=e^{\textstyle\frac{i}{2}\, 2\pi u_{\mathrm{sp}}\sigma_{{y}}}\end{aligned}$$

  wherein

  $$\displaystyle \begin{aligned} 2\pi u_{\mathrm{sp}}=2\pi G\gamma\ \mathrm{is}\ \mathrm{the}\ \mathrm{spin}\ \mathrm{precession}\ \mathrm{angle}\ \mathrm{over}\ (\theta_2-\theta_1)=2\pi,\end{aligned}$$
  $$\displaystyle \begin{aligned} u_{\mathrm{sp}} = \mathrm{spin}\ \mathrm{tune.}\end{aligned}$$

3.4.2 Transpose to 3D Space

Transposing spinor 2-vector transport through an optical element, namely,

$$\displaystyle \begin{aligned} \psi_f = T(f\leftarrow i)\, \psi_i\end{aligned}$$

to 3D space spin 3-vector transport, using the coefficients t₀, t_x, t_s, t_y of the 2 × 2 T-matrix (Eqs. 3.3 and 3.4), writes

(3.5)

with S_i and S_f the spin 3-vectors respectively at entrance and exit of the optical element.

3.4.3 Rotations About the Moving Frame Axes

Consider a rotation by an angle ϕ around the x axis, noting $\mathbf \omega = \mathbf n_x=\left ( \begin {array}{c} 1\\[-.7ex] 0\\[-.7ex] 0\end {array}\right )$ the unit x-rotation vector. Thus ω ⋅σ = σ_x. This x-axis spinor rotation is represented by the matrix (Eq. 3.3)

$$\displaystyle \begin{aligned} T_{\mathrm{{x}-rot}}= e^{\textstyle \frac{i}{2}\, (\mathbf n_x \cdot \mathbf \sigma ) \, \phi} = e^{\textstyle \frac{i}{2}\, \sigma_{{x}} \, \phi} = I\, \cos \dfrac{\phi}{2} + i\, \sigma_{{x}}\, \sin \dfrac{ \phi}{2} = t_0 I + it_{{x}}\sigma_{{x}}\end{aligned}$$

$$\displaystyle \begin{aligned} = \left( \begin{array}{ccc} \cos \frac{\phi}{2} & i\sin \frac{\phi}{2} \\ {} i\sin \frac{\phi}{2} & \cos \frac{\phi}{2} \end{array} \right) {} \end{aligned} $$

(3.6)

Transpose to the 3D space rotation matrix M_x using the t_0,x,s,y coefficient notation (Eq. 3.5), this gives

$$\displaystyle \begin{aligned} M_{\mathrm{{x}}\mathrm{-rot}} = \left( \begin{array}{ccc} t_0^2 + t_{{x}}^2 & 0 & 0 \\ 0 & t_0^2 - t_{{x}}^2 & 2t_0t_{{x}} \\ 0 & -2t_0t_{{x}} & t_0^2 - t_{{x}}^2 \end{array} \right) \, =\, \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \phi & \sin \phi \\ 0 & - \sin \phi & \cos \phi \end{array} \right) \end{aligned}$$

which is the expected form for a ϕ angle rotation around the x axis.

Repeat the Previous Calculation for the s-Axis and y-Axis Rotations

An s-axis spinor rotation is represented by the matrix

$$\displaystyle \begin{aligned} T_{\mathrm{s} -\mathrm{rot}} = e^{\textstyle \frac{i}{2}\, (\mathbf n_{{s} }\cdot \mathbf \sigma ) \, \phi} = e^{\textstyle \frac{i}{2}\, \sigma_{{s} } \, \phi} = I \cos \dfrac{\phi}{2} + i\, \sigma_{{s} }\, \sin \dfrac{\phi}{2} = t_0 I + it_{{s} }\sigma_{{s} }\end{aligned}$$

$$\displaystyle \begin{aligned} = \left( \begin{array}{ccc} \cos \frac{\phi}{2} & \sin \frac{\phi}{2} \\ -\sin \frac{\phi}{2} & \cos \frac{\phi}{2} \end{array} \right) {} \end{aligned} $$

(3.7)

Transpose to 3D space to get $M_{\mathrm {s}} -\mathrm {rot} = \left (\begin {array}{ccc} \cos \phi & 0& \sin \phi \\[-.7ex] 0 & 1 & 0 \\[-.7ex] - \sin \phi & 0& \cos \phi \end {array} \right )$

A y-axis spinor rotation is represented by the matrix

$$\displaystyle \begin{aligned} T_{\mathrm{y}-\mathrm{rot}} = e^{\textstyle \frac{i}{2}\, (\mathbf n_{{y}}\cdot \mathbf \sigma ) \, \phi} = e^{\textstyle \frac{i}{2}\, \sigma_{{y}} \, \phi} = I \cos \dfrac{\phi}{2} + i\, \sigma_{{y}}\, \sin \dfrac{\phi}{2} = t_0 I + it_{{y}}\sigma_{{y}}\end{aligned}$$

$$\displaystyle \begin{aligned} = \left( \begin{array}{ccc} e^{\textstyle i\frac{\phi}{2}} & 0 \\ 0 & e^{\textstyle -i \frac{\phi}{2}}\end{array} \right) {} \end{aligned} $$

(3.8)

Transpose to 3D space to get $M_{\mathrm {y}}-\mathrm {rot} = \left (\begin {array}{ccc} \cos \phi & \sin \phi & 0 \\[-.7ex] - \sin \phi & \cos \phi & 0 \\[-.7ex] 0 & 0 & 1 \end {array} \right )$

3.4.4 ϕ-Rotation About an Arbitrary Axis

Let $\mathbf n =\left ( \begin {array}{c} n_{{x}}\\ n_{{s} } \\ n_{{y}} \end {array}\right )$ be the rotation axis. The spinor rotation matrix writes

$$\displaystyle \begin{aligned} T_{\mathrm{n-rot}} = e^{\textstyle \frac{i}{2}\, (\mathbf n \cdot \mathbf \sigma ) \, \phi} =I\, \cos \dfrac{\phi}{2} + i\, (\mathbf n \cdot \mathbf \sigma)\, \sin \dfrac{\phi}{2} = \left( \begin{array}{ccc} \cos \frac{\phi}{2} + in_{{y}} \sin \frac{\phi}{2} & (in_{{x}} + n_{{s} })\sin \frac{\phi}{2} \\ (in_{{x}} - n_{{s} }) \sin \frac{\phi}{2} & \cos \frac{\phi}{2} - in_{{y}} \sin \frac{\phi}{2} \end{array} \right)\end{aligned}$$

3.4.5 Transport Through a Sequence of Optical Elements

Given the respective 2 × 2 spinor transport matrices T₁ (1st element) and T₂ (2nd element), and spinor states ψ_i and ψ_f respectively before the first and after the second element, the transport writes

$$\displaystyle \begin{aligned} \psi_f= T_2 \ T_1 \,\psi_i = e^{\textstyle\frac{i}{2}\, (\mathbf \omega_2 \cdot \mathbf \sigma) \, \phi_2} \, e^{\textstyle\frac{i}{2}\, (\mathbf \omega_1 \cdot \mathbf \sigma) \, \phi_1}\ \psi_i.\end{aligned}$$

$$\displaystyle \begin{aligned} =\Big[ \cos \dfrac{\omega_2 \phi_2}{2} + i\, \left( \dfrac{\mathbf \omega_2}{\omega_2}\cdot \mathbf \sigma \right)\, \sin \dfrac{\omega_2 \phi_2}{2}\Big] \Big[ \cos \dfrac{\omega_1 \phi_1}{2} + i\, \left( \dfrac{\mathbf \omega_1}{\omega_1}\cdot \mathbf \sigma \right)\, \sin \dfrac{\omega_1 \phi_1}{2}\Big]\end{aligned}$$

The Pauli matrix properties and other aforementioned rules can be applied to expand this product. Alternatively, use the t₀, t_x, t_s, t_y coefficient notation (Eq. 3.3), which gives

$$\displaystyle \begin{aligned} \begin{array}{rcl} & T_2\ T_1 = (I t_{2,o} + i\sigma_{{x}} t_{2,x} + i\sigma_{{s} } t_{2,{s} } + i \sigma_{{y}} t_{2,{y}}) (I t_{1,o} + i\sigma_{{x}} t_{1,x} + i\sigma_{{s} } t_{1,{s} } + i \sigma_{{y}} t_{1,{y}}) \\ & = I ( t_{2,o} t_{1,o} - t_{2,{x}} t_{1,{x}} - t_{2,{s} } t_{1,{s} } - t_{2,{y}} t_{1,{y}} ) \\ & +i\sigma_{{x}} ( t_{2,o} t_{1,{x}} + t_{2,{x}} t_{1,o} - t_{2,{s} } t_{1,{y}} + t_{2,{y}} t_{1,{s} } ) \\ & +i\sigma_{{s} } ( t_{2,o} t_{1,{s} } + t_{2,{x}} t_{1,{y}} + t_{2,{s} } t_{1,o} - t_{2,{y}} t_{1,{x}} ) \\ & +i\sigma_{{y}} ( t_{2,o} t_{1,{y}} - t_{2,{x}} t_{1,{s} } + t_{2,{s} } t_{1,{x}} + t_{2,{y}} t_{1,o} ) {} \end{array} \end{aligned} $$

(3.9)

This generalizes to N optical elements:

$$\displaystyle \begin{aligned} \psi_f= T_N \times \ldots \times T_2 \times T_1 \ \psi_i {} \end{aligned} $$

(3.10)

Example: A Local Field Error in an Otherwise Perfect Ring

It has been shown that, for a y-axis spin precession by an angle ϕ = Gγ(θ₂ − θ₁) over an orbital section (θ₂ − θ₁) in uniform field,

$$\displaystyle \begin{aligned} \psi(\theta_2)= T(\theta_2 \leftarrow \theta_1) \psi(\theta_1) \, , \qquad T(\theta_2 \leftarrow \theta_1)= e^{\textstyle\frac{i}{2}\, G\gamma (\theta_2-\theta_1) \sigma_{{y}}}\end{aligned}$$

Now, add a local field error

• at orbital azimuth θ_e,

• causing spin to precess locally by angle ϕ_e around direction n_e, so that

  $$\displaystyle \begin{aligned} T_{\mathrm{error}} = e^{\textstyle\frac{i}{2} (\mathbf n_e\cdot \mathbf \sigma)\phi_e}.\end{aligned}$$

  Thus, by virtue of the transport through a sequence of optical elements, the spinor transport matrix around the ring (θ₁ = 0, θ₂ = 2π, 0 < θ_e < 2π) writes

  $$\displaystyle \begin{aligned} T_{\mathrm{1-turn}} = T(2\pi \leftarrow \theta_e) \ T_{\mathrm{error}} \ T(\theta_e \leftarrow 0)\end{aligned}$$
  $$\displaystyle \begin{aligned} = e^{\textstyle\frac{i}{2}\, G\gamma (2\pi -\theta_e) \sigma_{{y}}}\ e^{\textstyle\frac{i}{2} (\mathbf n_e\cdot \mathbf \sigma)\phi_e}\ e^{\textstyle\frac{i}{2}\, G\gamma \theta_e \sigma_{{y}}}\end{aligned}$$

3.4.6 Precession Angle and Axis, from the 2 × 2 Spinor Map

As seen earlier (Eq. 3.3), from the known quantities

$$\displaystyle \begin{aligned} \mathrm{precession}\ \mathrm{angle} \ \omega\phi \qquad \mathrm{and} \quad \mathrm{precession}\ \mathrm{vector} \ \dfrac{\mathbf \omega}{\omega}\end{aligned}$$

the 2×2 spinor transport matrix can be written

$$\displaystyle \begin{aligned} T = e^{\textstyle \frac{i}{2}\, (\mathbf \omega \cdot \mathbf \sigma ) \, \phi} \ = I\, \cos \dfrac{\omega \phi}{2} + i\, ( \dfrac{\mathbf \omega}{\omega}\cdot \mathbf \sigma )\, \sin \dfrac{\omega \phi}{2}\end{aligned}$$

Now, conversely, if T is a spinor map, then

$$\displaystyle \begin{aligned} \mathrm{the}\ \mathrm{precession}\ \mathrm{angle}\ \omega\phi \ \mathrm{satisfies} \quad \cos \dfrac{\omega \phi}{2} = \dfrac{1}{2}\, tr(T),\end{aligned}$$

$$\displaystyle \begin{aligned} \mathrm{and}\ \mathrm{the}\ \mathrm{precession}\ \mathrm{vector}\ \mathrm{is} \quad \mathbf \omega = \dfrac{-i}{2 \sin\dfrac{\omega \phi}{2}}\, tr( T\, \mathbf \sigma) = \dfrac{-i}{2\sin\dfrac{\omega \phi}{2}}\, \left( \begin{array}{c} tr(T \sigma_{{x}}) \\ {} tr(T \sigma_{{s} } ) \\ {} tr(T \sigma_{{y}} ) \end{array} \right).\end{aligned}$$

Precession Vector Demonstrate this latter relationship.

With the material introduced so far, the problem “Low Energy Spin Rotator” of Sect. 2.4 can be solved using spinor methods, this is the object of Exercise 3.7 (Sect. 3.7).

3.5 Periodic Structures

From what precedes, with T_1−turn the 1-turn spinor map of a planar, defect free periodic structure, and ν_sp = ωϕ∕ 2π the spin tune, one gets

$$\displaystyle \begin{aligned} \cos \pi u_{\mathrm{sp}} = \dfrac{1}{2}\, tr(T_{\mathrm{1-turn}}) {} \end{aligned} $$

(3.11)

whereas the stable precession vector satisfies

$$\displaystyle \begin{aligned} \mathbf n = \dfrac{-i}{2\sin \pi u_{\mathrm{sp}}}\, tr( T_{\mathrm{1-turn}}\, \mathbf \sigma) {} \end{aligned} $$

(3.12)

3.5.1 Eigenvectors

Note T(θ + 2π ← θ) = T_1−turn the 1-turn spinor transport matrix at orbital angle θ (note that it can be transported at arbitrary observation azimuth θ using Eqs. 3.9 and 3.10). Let Λ(θ) be the 2-vector eigenvector, this property writes

$$\displaystyle \begin{aligned} \Lambda (\theta+2\pi) = T_{\mathrm{1-turn}}\ \Lambda(\theta) \qquad (\mathrm{this}\ \mathrm{is}\ \mathrm{the}\ \mathrm{periodicity}\ \mathrm{condition})\end{aligned}$$

or equivalently

$$\displaystyle \begin{aligned} (T_{\mathrm{1-turn}} -\lambda I) \Lambda =0 \qquad \mathrm{eigenvalue}\ \mathrm{equation}\end{aligned}$$

The two eigenvalues λ_± satisfy

$$\displaystyle \begin{aligned} det(T_{\mathrm{1-turn}} -\lambda I) = \lambda^2 -\lambda \,tr(T) + det(T)=0\end{aligned}$$

wherein (Eq. 3.3) $Tr(T)=2\,t_0 = 2 \cos \dfrac {\omega \phi }{2}$, det(T) = 1. This yields

$$\displaystyle \begin{aligned} \lambda_{\pm} \quad = \quad t_0 \pm i \sqrt{1-t_0^2} \quad = \quad \cos \dfrac{\omega \phi}{2} \pm i\, \sin \dfrac{\omega \phi}{2} \quad = \quad e^{\textstyle \pm i \dfrac{\omega \phi}{2} },\end{aligned}$$

with ωϕ the spin precession angle over a turn. The eigenvectors result, namely,

$$\displaystyle \begin{aligned} \Lambda_{\pm}= \left( \begin{array}{c} it_{{y},\mathrm{1-turn}}\ \mp \sqrt{1-t_{0,\mathrm{1-turn}}^2} \\{}-t_{{s} ,\mathrm{1-turn}} + it_{{x},\mathrm{1-turn}} \end{array} \right)\end{aligned}$$

This result can be transposed to real space 3-vector, using (Eq. 3.1)

which yields

$$\displaystyle \begin{aligned} \mathbf n_{\pm} = \frac{(\pm)}{\sqrt{1- t^2_{0,\mathrm{1-turn}}}} \left( \begin{array}{c} t_{{x},\mathrm{1-turn}} \\ t_{{s} ,\mathrm{1-turn}} \\ t_{{y},\mathrm{1-turn}} \end{array} \right) = \frac{(\pm)}{\omega} \left( \begin{array}{c} \omega_{{x}} \\ \omega_{{s} } \\ \omega_{{y}} \end{array} \right) {} \end{aligned} $$

(3.13)

With the material introduced so far, the problem “Synchronized Torque” of Sect. 2.4 can be solved using spinor methods, this is the object of Exercise 3.7 (Sect. 3.7).

3.5.2 Differential Equation of Spin Motion

Using spinors, the differential equation of spin motion writes

$\dfrac {d\psi }{d\theta } = \dfrac {i}{2} (\mathbf \Omega \cdot \mathbf \sigma ) \psi$  $\Leftrightarrow \quad \dfrac {d \mathbf S}{d\theta }=\mathbf S \times \mathbf \Omega$ Following an oft-met notation θ here denotes the trajectory deviation angle (velocity vector precession angle), not the orbital angle; dθ = 0 in field-free sections.

If the precession vector Ω does not depend on θ the spinor form is readily integrated:

This represents a spin rotation around Ω, by an angle ϕ =  Ω(θ₂ − θ₁).

In a perfect ring, flat orbit, in the moving frame,

$$\displaystyle \begin{aligned} \mathbf \Omega = \left( \begin{array}{c} 0\\[-.7ex] 0 \\[-.7ex] G\gamma\end{array} \right) \quad \mathrm{so}\ \mathrm{that} \quad \mathbf \Omega \cdot \mathbf \sigma = G\gamma\, \sigma_{{y}}\end{aligned}$$

• which denotes a vertical rotation axis—this is what σ_y signifies,

• with precession angle ϕ = Gγ(θ₂ − θ₁) over the interval [θ₁, θ₂].

If θ₂ − θ₁ = 2π the particle completes a full revolution, ϕ ∕ 2π = Gγ is the number of spin precessions per turn, “spin tune”,

$$\displaystyle \begin{aligned} u_{\mathrm{sp}} = G\gamma\end{aligned}$$

3.6 Spin Motion Near an Isolated Resonance

Spin motion satisfies

$$\displaystyle \begin{aligned} \dfrac{d \mathbf S}{d\theta}=\mathbf S \times \mathbf \Omega\end{aligned}$$

In the presence of perturbing fields the precession axis is no longer vertical, namely,

$$\displaystyle \begin{aligned} \mathbf \Omega = \left( \begin{array}{c} \xi_R \\[-.7ex] -\xi_I \\[-.7ex] -G\gamma \end{array} \right)\end{aligned}$$

with horizontal components Ω_x and Ω_s as detailed in Eqs. 2.14, 2.15, Chap. 2; note that the opposite sign of the Ω_y component stems from the choice of clockwise reference frame rotation along the reference orbit, there (Fig. 2.5), versus anti-clockwise here (Fig. 3.1).

Reformulated in terms of spinors the equation of motion writes

$$\displaystyle \begin{aligned} \dfrac{d\psi}{d\theta} \ =\ \dfrac{i}{2} (\mathbf \Omega \cdot \mathbf \sigma) \psi \ =\ \dfrac{i}{2} (\xi_R \sigma_{{x}} - \xi_I \sigma_{{s} } - G\gamma \sigma_{{y}})\, \psi = \dfrac{i}{2} \left(\begin{array}{cc} -G\gamma & \xi \\ \xi^* & G\gamma \end{array} \right)\psi\end{aligned}$$

Develop the resonance strength in Fourier series:

Move into the Gγ_n-frequency precessing frame; this change of variable has the merit of yielding a differential equation with constant coefficient,

$$\displaystyle \begin{aligned} \psi\! =e\! ^{\textstyle -\dfrac{i}{2}G\! \gamma_n \theta \sigma_{{y}}} \phi \!= \!\left(I\cos\dfrac{G\!\gamma_n \, \theta}{2} -i\sigma_{{y}} \sin \dfrac{G\!\gamma_n \, \theta}{2} \right)\phi\end{aligned}$$

Hence the new form

$$\displaystyle \begin{aligned} \dfrac{d\phi}{d\theta} = \dfrac{i}{2} \Big[ \epsilon_R \sigma_{{x}} - \epsilon_I \sigma_{{s} } - (G\gamma - G\gamma_n ) \sigma_{{y}} \Big] \phi = \dfrac{i}{2} (\mathbf \omega \cdot \mathbf \sigma) \phi \quad \Big[ \mathbf \omega = \left( \begin{array}{c} \epsilon_R \\[-.7ex] -\epsilon_I \\[-.7ex] -\delta_n \end{array} \right), \delta_n=G\gamma - G\!\gamma_n \Big],\end{aligned}$$

which can readily be integrated,

Back to the orbital frame:

$$\displaystyle \begin{aligned} \psi(\theta_2)= e^{\textstyle -\dfrac{i}{2}G\! \gamma_n \theta_2 \sigma_{{y}}} e^{\textstyle \dfrac{i}{2}(\mathbf \omega \cdot \mathbf \sigma) (\theta_2 -\theta_1)} e^{\textstyle \dfrac{i}{2}G\! \gamma_n \theta_1 \sigma_{{y}}} \psi(\theta_1)\end{aligned}$$

Introduce the t_0,x,s,y coefficient notation, note that $\omega =\sqrt {|\epsilon _n|{ }^2 + \delta _n^2}$; after some algebra (using Eqs. 3.3 and 3.9) the spinor transport matrix in the moving frame comes out [4],

$$\displaystyle \begin{aligned} T(\theta_2 \leftarrow \theta_1)= {} \end{aligned} $$

(3.14)

$$\displaystyle \begin{aligned} I \left( \cos \frac{G\! \gamma_n(\theta_2-\theta_1)}{2}\, \cos \frac{\omega (\theta_2-\theta_1)}{2} - \frac{\delta_n}{\omega}\sin \frac{G\! \gamma_n(\theta_2-\theta_1)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} \right) \end{aligned}$$

$$\displaystyle \begin{aligned} +i\sigma_{{x}} \left( \frac{\epsilon_R}{\omega}\cos \frac{G\! \gamma_n (\theta_1+\theta_2)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} +\frac{\epsilon_I}{\omega} \sin \frac{G\! \gamma_n (\theta_1+\theta_2)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} \right) \end{aligned}$$

$$\displaystyle \begin{aligned} +i\sigma_{{s} } \left( -\frac{\epsilon_I}{\omega}\cos \frac{G\! \gamma_n (\theta_1+\theta_2)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} +\frac{\epsilon_R}{\omega} \sin \frac{G\! \gamma_n (\theta_1+\theta_2)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} \right) \end{aligned}$$

$$\displaystyle \begin{aligned} +i\sigma_{{y}} \left( -\frac{\delta_n}{\omega}\cos \frac{G\! \gamma_n(\theta_2-\theta_1)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} - \sin \frac{G\! \gamma_n(\theta_2-\theta_1)}{2}\, \sin \frac{\omega (\theta_2-\theta_1)}{2} \right) \end{aligned}$$

From this mapping it can be seen that the spin precession features a double frequency:

• Gγ_n on the high frequency side—tens to hundreds of units, in high energy proton rings for instance,

• and $\omega =\sqrt {|\epsilon _n|{ }^2 + \delta _n^2}$ on the low frequency side near resonance (δ_n → 0), with resonance strength |𝜖_n| < 1 as in existing installations.

3.6.1 Case of an Integer Resonance, G γ_n = integer

In the expression for T(θ₂ ← θ₁) (Eq. 3.14) take

• θ₁ = 0, θ₂ = 2πm with m=number of turns,

• G γ_n=integer thus $\cos {}(G\! \gamma _n m \pi )=\pm 1$ and $\sin {}(G\! \gamma _n m \pi )=0.$

This results in:

$$\displaystyle \begin{aligned} T_{\mathrm{m-turn}} = \pm \left( I \, \cos m\omega \pi + \ i\sigma_{{x}} \dfrac{\epsilon_R}{\omega} \sin m\omega \pi \ - i\sigma_{{s} } \dfrac{\epsilon_I}{\omega} \sin m\omega \pi \ - i\sigma_{{y}} \dfrac{\delta_n}{\omega} \sin m\omega \pi \right)\end{aligned}$$

Note that with Gγ_n=integer, the Gγ_n frequency component vanishes, the ω frequency only is left.

Transpose to 3D space using the t_0,x,s,y notation, that yields for the spin vector after m turns [4],

$$\displaystyle \begin{aligned} \begin{array}{rcl} & \mathbf S(m) = \\ & \left( \begin{array}{ccccc} 2\dfrac{\epsilon_R^2}{\omega^2} \sin^2(m\omega \pi)+ \cos{}(2m\omega \pi) &\displaystyle &\displaystyle -2\dfrac{\epsilon_R \epsilon_I}{\omega^2} \sin^2(m\omega \pi)-\dfrac{\delta_n}{\omega} \sin{}(2m\omega \pi) &\displaystyle &\displaystyle -2\dfrac{\epsilon_R \delta_n}{\omega^2} \sin^2(m\omega \pi)+\dfrac{\epsilon_I}{\omega} \sin{}(2m\omega \pi) \\ -2\dfrac{\epsilon_R \epsilon_I}{\omega^2} \sin^2(m\omega \pi)+\dfrac{\delta_n}{\omega} \sin{}(2m\omega \pi) & &\displaystyle 2\dfrac{\epsilon_I^2}{\omega^2} \sin^2(m\omega \pi)+ \cos{}(2m\omega \pi) &\displaystyle &\displaystyle 2\dfrac{\epsilon_I \delta_n}{\omega^2} \sin^2(m\omega \pi)+\dfrac{\epsilon_R}{\omega} \sin{}(2m\omega \pi) \\ -2\dfrac{\epsilon_R \delta_n}{\omega^2} \sin^2(m\omega \pi)-\dfrac{\epsilon_I}{\omega} \sin{}(2m\omega \pi) & &\displaystyle 2\dfrac{\epsilon_I \delta_n}{\omega^2} \sin^2(m\omega \pi)-\dfrac{\epsilon_R}{\omega} \sin{}(2m\omega \pi) &\displaystyle &\displaystyle 2\dfrac{\delta_n^2}{\omega^2} \sin^2(m\omega \pi)+ \cos{}(2m\omega \pi) \end{array} \right) \, \mathbf S(0) \end{array} \end{aligned} $$

Spins precess at a frequency $\omega =\sqrt {|\epsilon _n|{ }^2 + \delta _n^2}$, around a 3-vector which can be obtained by averaging over turns (an average denoted $\overline {*}$), namely

$$\displaystyle \begin{aligned} \overline{\mathbf S} = \left( \begin{array}{c} \overline{ S_{{x}} } \\ \overline{ S_{{s} } } \\ \overline{ S_{{y}} } \end{array} \right) = \left( \begin{array}{ccccc} \dfrac{\epsilon_R^2}{\omega^2} && -\dfrac{\epsilon_R \epsilon_I}{\omega^2} && -\dfrac{\epsilon_R \delta_n}{\omega^2} \\ {} -\dfrac{\epsilon_R \epsilon_I}{\omega^2} && \dfrac{\epsilon_I^2}{\omega^2} && \dfrac{\epsilon_I \delta_n}{\omega^2} \\ {} -\dfrac{\epsilon_R \delta_n}{\omega^2} && \dfrac{\epsilon_I \delta_n}{\omega^2} && \dfrac{\delta_n^2}{\omega^2} \end{array} \right) \, \mathbf S(0) {}\end{aligned} $$

(3.15)

Polarization $| \overline { \mathbf S} |$ depends on the initial spin vector S(0). In particular if S(0) = (0, 0, ∓1), along the vertical axis, Eq. 3.15 yields the polarization vector (Fig. 3.2)

$$\displaystyle \begin{aligned} \overline{ \mathbf S } = \dfrac{\pm \delta_n}{|\epsilon_n|{}^2 + \delta_n^2} \left( \begin{array}{c} \epsilon_R \\ -\epsilon_I \\ -\delta_n \end{array} \right)\end{aligned}$$

It can be verified that $\overline {\mathbf S}$ is aligned on the periodic spin precession direction, as follows. Set m=1 in the m-turn matrix T_m−turn

$$\displaystyle \begin{aligned} T_{1-turn} =\pm \big( I \cos \omega\pi + i\sigma_{{x}} \dfrac{\epsilon_R}{\omega} \sin \omega\pi - i\sigma_{{s} } \dfrac{\epsilon_I}{\omega} \sin \omega\pi - i\sigma_{{y}} \dfrac{\delta_n}{\omega} \sin \omega\pi \big)\end{aligned}$$

Fig. 3.2

Spins S(m) precess at frequency ω around the local, fixed, spin closed orbit n₀

This provides (Eq. 3.4) the coefficients $t_{0}=\cos \omega \pi$, $t_{{x}}=\frac {\epsilon _R}{\omega }\sin \omega \pi$, $t_{{s} }=-\frac {\epsilon _I}{\omega }\sin \omega \pi$, $t_{{y}}=-\frac {\delta _n}{\omega }\sin \omega \pi$ used in defining the eigenvectors n₀ (Eq. 3.13), so yielding

$$\displaystyle \begin{aligned} \mathbf n_0 = \dfrac{(\pm)}{\sqrt{|\epsilon_n|{}^2+\delta_n^2}} \left( \begin{array}{c} \epsilon_R \\ - \epsilon_I \\ - \delta_n \end{array} \right)\end{aligned}$$

Far from the resonance:

$$\displaystyle \begin{aligned} |\delta_n|=|G\gamma - G\!\gamma_n| \rightarrow \infty \ \mathrm{thus}\ n_{{x}} \mathrm{and}\ n_{{s} } \rightarrow 0, \ n_{{y}} \rightarrow 1,\quad \mathbf n_0 \parallel \mathbf y\end{aligned}$$

beam polarization is vertical. On the resonance:

$$\displaystyle \begin{aligned} |\delta_n|=0 \ \mathrm{thus}\ n_{{y}}=0, \quad \mathbf n_0 \perp \mathbf y,\end{aligned}$$

beam polarization lies in the (x,s) plane, along a direction $\left ( \begin {array}{c} \epsilon _R \\ -\epsilon _I \end {array} \right )$which depends on the observation azimuth θ.

3.6.2 Case of an Intrinsic Resonance, G γ_n = integer ± ν_y

In the expression for T(θ₂ ← θ₁) (Eq. 3.14) substitute

$$\displaystyle \begin{aligned} \theta_1 = 0, \quad \theta_2=2\pi m;\end{aligned}$$

This yields [4]

$$\displaystyle \begin{aligned} \begin{array}{rcl} & T_{\mathrm{m-turn}} = I ( \cos mG\! \gamma_n\pi\, \cos m\omega \pi - \frac{\delta_n}{\omega}\sin mG\! \gamma_n\pi\, \sin m\omega \pi ) \\ & +i\sigma_{{x}} ( \frac{\epsilon_R}{\omega}\cos mG\! \gamma_n\pi\, \sin m\omega \pi +\frac{\epsilon_I}{\omega} \sin mG\! \gamma_n\pi\, \sin m\omega \pi ) \\ & +i\sigma_{{s} } ( -\frac{\epsilon_I}{\omega}\cos mG\! \gamma_n\pi\, \sin m\omega \pi +\frac{\epsilon_R}{\omega} \sin mG\! \gamma_n\pi\, \sin m\omega \pi ) \\ & +i\sigma_{{y}} ( -\frac{\delta_n}{\omega}\cos mG\! \gamma_n\pi\, \sin m\omega \pi - \sin mG\! \gamma_n\pi\, \cos m\omega \pi ) {} \end{array} \end{aligned} $$

(3.16)

Regarding the precession motion of the spin vector S, inspection of the T_m−turn matrix shows that (Fig. 3.3)

• spin vectors S precess at frequency ω around the eigenvector n_±,

  Fig. 3.3

  

  Spins S(m) precess at frequency ω around the eigenvector vector n, which itself precesses around the vertical axis at frequency Gγ

• while n_± precesses around the vertical axis at a frequency Gγ_n;

• the S_x and S_s components of S oscillate

  • with an average zero value:

    $$\displaystyle \begin{aligned} <S_{{x}}>_{\mathrm{turn}}=0 \quad \mathrm{and} \quad <S_{{s} }>_{\mathrm{turn}}=0\end{aligned}$$

    by contrast with the integer resonance case,

  • at a frequency ω (precession frequency around n_±),

  • modulated by a frequency Gγ_n (precession of n_± around the vertical);

• the vertical component of S, S_y, oscillates at frequency ω around an average which is S(0)-dependent, namely

  $$\displaystyle \begin{aligned} \begin{array}{rcl} & S_{{y}} = -\left(2\frac{\epsilon_R \delta_n}{\omega^2} \sin^2(m\omega \pi)+\frac{\epsilon_I}{\omega} \sin{}(2m\omega \pi) \right) S_{{x}}(0) \\ & + \left(2\frac{\epsilon_I \delta_n}{\omega^2} \sin^2(m\omega \pi)-\frac{\epsilon_R}{\omega} \sin{}(2m\omega \pi) \right) S_{{s} }(0) + \left(2\frac{\delta_n^2}{\omega^2} \sin^2(m\omega \pi)+ \cos{}(2m\omega \pi) \right) S_{{y}}(0) \end{array} \end{aligned} $$

  • thus a polarization state (the average over turns)

    $$\displaystyle \begin{aligned} \overline{\mathbf S} = \dfrac{\delta_n}{|\epsilon_n|{}^2 + \delta_n^2} \left( \begin{array}{c} 0 \\ 0 \\ -\epsilon_R S_{{x}}(0) + \epsilon_I S_{{s} }(0) + \delta_n S_{{y}}(0) \end{array} \right)\end{aligned}$$

  • and note: the vertical component < S_y >  has the same value as in the case of an integer resonance (Eq. 3.15).

The spin precession vector is obtained from the 1-turn spinor transport matrix, as follows.

Take an arbitrary turn, θ₁ = 2πm, and θ₂ = θ₁ + 2π, thus (Eq. 3.17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} & T_{\mathrm{1-turn}}= I \Big( \cos G\! \gamma_n \pi\, \cos \omega \pi - \frac{\delta_n}{\omega}\sin G\! \gamma_n \pi\, \sin \omega \pi \Big) \\ & +i\sigma_{{x}} \Big( \frac{\epsilon_R}{\omega}\cos G\! \gamma_n \pi (2m+1)\, \sin \omega \pi +\frac{\epsilon_I}{\omega} \sin G\! \gamma_n \pi (2m+1)\, \sin \omega \pi \Big) \\ & +i\sigma_{{s} } \Big( -\frac{\epsilon_I}{\omega}\cos G\! \gamma_n \pi (2m+1)\, \sin \omega \pi +\frac{\epsilon_R}{\omega} \sin G\! \gamma_n \pi (2m+1)\, \sin \omega \pi \Big) \\ & +i\sigma_{{y}} \Big( -\frac{\delta_n}{\omega}\cos G\! \gamma_n \pi\, \sin \omega \pi - \sin G\! \gamma_n \pi\, \sin \omega \pi \Big) {} \end{array} \end{aligned} $$

(3.17)

the eigenvector is obtained from the 1-turn matrix, for the record (Eq. 3.13)

$$\displaystyle \begin{aligned} \mathbf n_{\pm} = \frac{(\pm)}{\sqrt{1- t^2_{0,\mathrm{1-turn}}}} \left( \begin{array}{c} t_{{x},\mathrm{1-turn}} \\ t_{{s} ,\mathrm{1-turn}} \\ t_{{y},\mathrm{1-turn}} \end{array} \right) \end{aligned}$$

with the following properties:

• its vertical component is ∝ t_y, thus constant (independent of m, Eq. 3.17),

• as a consequence n_± precesses around the y axis with frequency Gγ_n;

• its x and s components oscillate with frequency Gγ_n.

Example: Proximity of Gγ = 0 − ν_y Intrinsic Resonance in the AGS Booster

The AGS injector ring (AGS Booster) is described in Chap. 14 which may be referred to for details. Polarized helion particles are considered, G = −4.184153. The vertical tune is set to ν_y = 4.82, resonance occurs at Gγ = −4.82.

Given the betatron amplitude considered here, the resonance strength (Eq. 2.35) takes the value |𝜖_n| = 0.00132.

Consider Fig. 3.4:

• the slow S_y component oscillation with ± 1 amplitude occurs on resonance. The frequency satisfies ω⁻¹ = 755 turns, measured from the turn-by-turn record. This value of ω coincides with the resonance strength |𝜖_n| = 0.001324 as δ_n = 0;

  Fig. 3.4

  

  Helion spin precession at Gγ = −ν_y in the AGS Booster, observed turn-by-turn at some azimuth around the ring. The vertical spin component S_y oscillates slowly (solid sinusoids), frequency ω ≪ 1; three different distances to the resonance are plotted, δ_n = 0 (0), δ_n = |𝜖_n| (1) and 2|𝜖_n| (2). Full amplitude occurs on the resonance. The oscillation of S_x and S_s components (dots) is fast, frequency Gγ_n = 4.82, and modulated, modulation frequency $\omega = \sqrt {\delta _n^2 + |\epsilon _n|{ }^2} = |\epsilon _n|$ here, on resonance

• two additional slow S_y oscillations are displayed, for respective distances to the resonance δ_n = |𝜖_n| and δ_n = 2|𝜖_n| (smallest amplitude). Their frequencies satisfy $\omega = \sqrt {\delta _n^2 + |\epsilon _n|}$, this can be checked from the number of turns per oscillation.

• rapid oscillations in the graph concern the S_x and S_s components, frequency is Gγ_n = 4.82, the case δ_n = 0 is represented here, S_x and S_s oscillations are modulated at the frequency of the S_y component oscillation, ω = |𝜖_n|.

3.7 Homework

In the following two exercises, the questions addressed in the Exercises 1 and 3 of Chap. 2 (Sect. 2.3) via numerical simulations, are treated using spinors.

Exercise 1: Low Energy Spin Rotator

• 1.a Give the spinor representation of the Wien filter rotator of Exercise 1 in Chap. 2 (Sect. 2.3).

• 1.b Check consistency (spin precession angle, precession axis) with the numerical simulation results of question 2 in that exercise.

Solution 1.a: The spinor rotation matrix is ( Ω ⋅σ)ϕ with Ωϕ the spin rotation angle.

The 2 × 2 transfer matrix is

$$\displaystyle \begin{aligned} T = e^{\textstyle \dfrac{i}{2}(\mathbf \Omega\cdot \mathbf \sigma)\phi} = I\, \cos \dfrac{\Omega \phi}{2} + i\, ( \dfrac{\mathbf \Omega}{\Omega}\cdot \mathbf \sigma )\, \sin \dfrac{\Omega \phi}{2}\end{aligned}$$

$\mathbf \Omega = \left ( \begin {array}{c} \Omega _{X} \\ {} \Omega _{Y} \\ {} \Omega _{Z} \end {array} \right ) \equiv \left ( \begin {array}{c} 0 \\ {} 0 \\ {} \Omega _{Z} \end {array} \right )$ as both E and B result in a precession around the vertical (Z) axis.

Thus Ω ⋅σ = Ω_Z σ_Z, | Ω_Z| = | Ω|, $T = e^{\textstyle \dfrac {i}{2}\Omega _Z\, \phi \, \sigma _Z} = I\, \cos \dfrac {\Omega _Z \phi }{2} + i\, \sigma _Z\, \sin \dfrac {\Omega _Z \phi }{2}$

$$\displaystyle \begin{aligned} = \cos \dfrac{\Omega_Z \phi}{2} \, \left( \begin{array}{ccc} 1 & ~ & 0 \\[-.7ex] 0 && 1 \end{array} \right) + i \sin \dfrac{\Omega_Z \phi}{2} \, \left( \begin{array}{ccc} 1 & ~ & 0 \\[-.7ex] 0 && -1 \end{array} \right) = \left( \begin{array}{ccc} e^{\textstyle i\dfrac{\Omega_Z \phi}{2}} & ~ & 0 \\0 && e^{\textstyle -i\dfrac{\Omega_Z \phi}{2}} \end{array} \right)\end{aligned}$$

With precession angle Ω_Zϕ = π∕2, $\dfrac {\Omega _Z \phi }{2}=\pi /4$, one gets $e^{\textstyle \pm i\dfrac {\Omega _Z \phi }{2}}=\dfrac {1\pm i}{\sqrt {2}}$, thus

$$\displaystyle \begin{aligned} T = \left( \begin{array}{ccc} \dfrac{1+i}{\sqrt{2}} & ~ & 0 \\ 0 && \dfrac{1 - i}{\sqrt{2}} \end{array} \right)\end{aligned}$$

Transform to real 3D space using , this yields the expected π∕2 angle Z-rotation matrix

$$\displaystyle \begin{aligned} M_{\mathrm{x}} \, =\, \left(\begin{array}{ccc} 0 & 1 & 0 \\ -1 & 0 & 1 \\ 0 & 0 & 1 \end{array} \right)\end{aligned}$$

Apply to initial $\mathbf S_i = \left ( \begin {array}{c} 1 \\[-.7ex] 0 \\[-.7ex] 0 \end {array} \right )$, this yields the expected

$$\displaystyle \begin{aligned} \mathbf S_f = M\, \mathbf S_i = \left( \begin{array}{c} 0 \\[-.7ex] -1 \\[-.7ex] 0 \end{array} \right)\end{aligned}$$

1.b: Numerical checks with tracking simulation outcomes are straight forward.

Exercise 2: Synchronized Torque

• 2.a Give the spinor representation of the solenoid spin rotator of Exercise 2 in Chap. 2 (Sect. 2.3).

• 2.b Give the spinor representation of the ring including the solenoid spin rotator.

• 2.c Find the spin tune. Compare with the numerical outcomes of Exercise 2 in Chap. 2.

• 2.d Deduce the spin closed orbit vector at the solenoid, and the spin tune.

Solution 2.a: The solenoid causes a s-rotation of angle ϕ_s, it is thus represented by the matrix (with n_s a unit vector along the s-axis)

$$\displaystyle \begin{aligned} T_{\mathrm{spinR}} = e^{\textstyle \dfrac{i}{2}\, (\mathbf n_s\cdot \mathbf \sigma )\phi_s} = e^{\textstyle \dfrac{i}{2}\, \sigma_s\phi_s} = I\cos\dfrac{\phi_s}{2} + i \sigma_s \sin \dfrac{\phi_s}{2} = \left( \begin{array}{ccc} \cos \frac{\phi_s}{2} & \sin \frac{\phi_s}{2} \\ -\sin \frac{\phi_s}{2} & \cos \frac{\phi_s}{2} \end{array} \right)\end{aligned}$$

which expectedly coincides with the s-axis spinor rotation matrix (Eq. 3.7).

2.b: The ring with ϕ_s torque is represented by the spinor matrix

$$\displaystyle \begin{aligned} T_{\mathrm{ring}} = e^{\textstyle \dfrac{i}{2}\, (\mathbf n_y\cdot \mathbf \sigma )G\gamma\, 2\pi} \ e^{\textstyle \dfrac{i}{2}\, (\mathbf n_s\cdot \mathbf \sigma )\phi_s} = (I\cos G\gamma\pi + i \sigma_y \sin G\gamma\pi) \, (I\cos\dfrac{\phi_s}{2} + i \sigma_s \sin \dfrac{\phi_s}{2}) \end{aligned}$$

thus, given − σ_yσ_s = iσ_x,

$$\displaystyle \begin{aligned} T_{\mathrm{ring}}=I\cos G\gamma\pi\ \cos\dfrac{\phi_s}{2} + i \sigma_x \sin G\gamma\pi \ \sin \dfrac{\phi_s}{2}+ i \sigma_s \sin \dfrac{\phi_s}{2} \ \cos G\gamma\pi + i \sigma_y \ \sin G\gamma\pi \ \cos\dfrac{\phi_s}{2} \end{aligned}$$

Under explicit 2 × 2 matrix form: this is also simply the product of y-axis and s-axis spinor rotations, namely

$$\displaystyle \begin{aligned} T_{\mathrm{ring}} = \left( \begin{array}{ccc} e^{\textstyle iG\gamma \pi} & 0 \\ 0 & e^{\textstyle -i G\gamma \pi} \end{array} \right) \left( \begin{array}{ccc} \cos \frac{\phi_s}{2} & \sin \frac{\phi_s}{2} \\ -\sin \frac{\phi_s}{2} & \cos \frac{\phi_s}{2} \end{array} \right) = \left( \begin{array}{ccc} e^{\textstyle iG\gamma \pi} \cos \frac{\phi_s}{2}& e^{\textstyle iG\gamma \pi} \sin \frac{\phi_s}{2} \\ -e^{\textstyle -iG\gamma \pi} \sin \frac{\phi_s}{2} & e^{\textstyle -i G\gamma \pi} \cos \frac{\phi_s}{2} \end{array} \right)\end{aligned}$$

2.c: The spin tune satisfies:  $\cos \pi u _{\mathrm {sp}} = \frac {1}{2}\mathrm {Tr}(T_{\mathrm {ring}}) = \cos G\gamma \pi \, \cos \frac {\phi _s}{2}$, so

$$\displaystyle \begin{aligned} \mathrm{frac}(u_{\mathrm{sp}}) = \pm \frac{1}{\pi}\, \mathrm{acos}\big( \cos G\gamma \pi \ \cos \frac{\phi_s}{2}\big)\end{aligned}$$

Numerically:

$$\displaystyle \begin{aligned} \mathrm{case}\ \mathrm{E=200}\,\mathrm{keV,} \ G\gamma=1.793229, \ \phi_s=\dfrac{\pi}{6} \ \Rightarrow \ \mathrm{frac}(u_{\mathrm{sp}}) = 0.220656\end{aligned}$$

$$\displaystyle \begin{aligned} \mathrm{case}\ \mathrm{E=370.0825}\,\mathrm{MeV,} \ G\gamma=2, \ \phi_s=\dfrac{\pi}{6} \ \Rightarrow \ \mathrm{frac}(u_{\mathrm{sp}}) = 0.08333\end{aligned}$$

$$\displaystyle \begin{aligned} \mathrm{case}\ \mathrm{E=370.0825}\,\mathrm{MeV,} \ G\gamma=2.5, \ \phi_s=\dfrac{\pi}{6} \ \Rightarrow \ \mathrm{frac}(u_{\mathrm{sp}}) = 0.5\end{aligned}$$

All three cases are in accord with the numerical simulation results of Exercise 2 in Chap. 2.

2.d: The spin closed orbit, or periodic spin vector, can be obtained by taking the t_i components from the form (slide 7) T_ring = t₀I + iσ_xt_x + iσ_st_s + iσ_yt_y, namely

$$\displaystyle \begin{aligned} \mathbf n_{\pm} = \left( \begin{array}{c} \pm \dfrac{t_{{x},\mathrm{1-turn}}}{\sqrt{1- t^2_{0,\mathrm{1-turn}}}} \\ \pm \dfrac{t_{{s} ,\mathrm{1-turn}}}{\sqrt{1- t^2_{0,\mathrm{1-turn}}}} \\ \pm \dfrac{t_{{y},\mathrm{1-turn}}}{\sqrt{1- t^2_{0, \mathrm{1-turn}}}} \end{array} \right)\end{aligned}$$

Thus T_ring as obtained above yields

$$\displaystyle \begin{aligned} t_0 = \cos G\gamma\pi\ \cos\dfrac{\phi_s}{2} \quad \rightarrow \quad \sqrt{1- t^2_{0, \mathrm{1-turn}}} =\sin \pi u_{sp}\end{aligned}$$

and

$$\displaystyle \begin{aligned} t_x= \sin G\gamma\pi \ \sin \dfrac{\phi_s}{2}, \ t_y = \sin \dfrac{\phi_s}{2} \ \cos G\gamma\pi, \ t_z =\sin G\gamma\pi \ \cos\dfrac{\phi_s}{2} \end{aligned}$$

so that

$$\displaystyle \begin{aligned} \mathbf n_{\pm} =\pm \left( \begin{array}{c} \sin G\gamma\pi \ \sin \dfrac{\phi x_s}{2}/ \sin \pi u_{\mathrm{sp}}\\ \cos G\gamma\pi \ \sin \dfrac{\phi_s}{2}/ \sin \pi u_{\mathrm{sp}} \\ \sin G\gamma\pi \ \cos \dfrac{\phi_s}{2}/ \sin \pi u_{\mathrm{sp}} \end{array}\right).\end{aligned}$$

Numerically

$$\displaystyle \begin{aligned} \mathrm{case}\ \mathrm{E=200}\,\mathrm{keV,} , \quad \mathbf n_{\pm} =\pm \left( \begin{array}{c} 0.3225386 \\ -0.2449867 \\ -0.91430318 \end{array}\right)\end{aligned}$$

$$\displaystyle \begin{aligned} \mathrm{case}\ \mathrm{E=108.4116}\,\mathrm{MeV,} , \quad \mathbf n_{\pm} =\pm \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right)\end{aligned}$$

$$\displaystyle \begin{aligned} \mathrm{case}\ \mathrm{E=370.0825}\,\mathrm{MeV,} , \quad \mathbf n_{\pm} =\pm \left( \begin{array}{c} 0 \\ 0.258819 \\ 0.96592 \end{array}\right)\end{aligned}$$

to be compared with the numerical results for the spin closed orbit vector at the origin of the optical sequence in Exercise 2.d, Chap. 2.