On the Use of Machine Learning for Subgrid Scale Filtered Density Function Modelling in Large Eddy Simulations of Combustion Systems

Abstract

The application of machine learning algorithms to model subgrid-scale filtered density functions (FDFs), required to estimate filtered reaction rates for Large Eddy Simulation (LES) of chemically reacting flows, is discussed in this chapter. Three test cases, i.e., a low-swirl premixed methane-air flame, a MILD combustion of methane-air mixtures, and a kerosene spray turbulent flame, are presented. The scalar statistics in these test cases may not be easily represented using the commonly used presumed shapes for modeling FDFs of mixture fraction and progress variable. Hence, the use of ML methods is explored. Particularly, deep neural network (DNN) to infer joint FDFs of mixture fraction and progress variable is reviewed here. The Direct Numerical Simulation (DNS) datasets employed to train the DNNs in each test case are described. The DNN performances are shown and compared to typical presumed probability density function (PDF) models. Finally, this chapter examines the advantages and caveats of the DNN-based approach.

1 Introduction

Increasingly stringent regulations on pollutants emissions from fossil fuel combustion are demanding for novel combustion technologies which can have high fuel flexibility, increased efficiency and low emissions. Moreover, a significant adoption of renewable technologies in future years is expected to reduce carbon footprint and meet the long-term objective of CO$_2$ neutrality. Nevertheless, combustion-based energy technologies will play a role in the future (or low-carbon) energy mix as discussed in the chapter “Introduction”. Hence, combustion research is called in to provide solutions to the expected challenges arising from issues related to fuel flexibility and improving efficiency with pollutants reduction. Current combustion studies focus on aspects such as development, validation and uncertainty quantification of new models, and involve either experiments or numerical simulations, or both. A collection of these studies represents a massive amount of data that can be leveraged to achieve significant progress in combustion science. Utilising this data has thus become a new challenge and research opportunity. Data-driven techniques such as machine learning (ML) have demonstrated their abilities to extract information from massive data and assist in developing novel models which can be leveraged for technology development.

Machine learning techniques allow us to have statistical inference, for some unknown quantities of interest, with reasonably accuracy and confidence by carefully training the algorithms using representative data. Since the 1990s, ML has regained increasing attention and achieved outstanding results in many areas (Jordan and Mitchell 2015), including science, technology, manufacturing, finance, education, health care, and many more. Combustion science is not an exception to this trend, there are many studies demonstrating successful use of ML for combustion and some of these studies date almost 30 years back. Christo and coworkers (Christo et al. 1995, 1996b, a) first employed a machine learning algorithm, namely the Artificial Neural Network (ANN), in the 1990s to deal with chemistry tabulation for turbulent combustion simulations. These works involved training an ANN to obtain changes in the composition of several reactive scalars rather than using the conventional direct integration of the relevant equations. Satisfactory results suggested that the ANN was able to provide, with computational efficiency, the chemical kinetics information required for turbulent combustion simulations. The computational efficiency was mainly noted to come from memory saving. The subsequent studies extended this novel approach to more complex chemical systems (Blasco et al. 1998, 1999; Chen et al. 2000), where multiple ANNs were proposed for different subdomains of the large composition space. The valuable time saving achieved by ANN compared with traditional methods was presented. The recent advances on ML applied to chemical kinetics are discussed in chapters “Machine Learning Techniques in Reactive Atomistic Simulations” and “Machine Learning for Combustion Chemistry” with different perspectives.

Blasco et al. (2000) employed two different ANNs, namely the Self-Organising Map (SOM) and the Multi-layer Perceptron (MLP), to estimate the thermochemical states during a combustion simulation. The SOM was used to partition the thermochemical space into subdomains, while several MLPs were trained on each subdomain to predict the evolution of the thermochemical space in time. These early explorations identify a general route to utilise the ANN for chemistry tabulation approaches, although their generality was limited due to the similarity between training and testing cases. Consequently, later studies focused on developing ANNs for a wider range of combustion conditions.

Sen et al. trained ANNs using unsteady flame-turbulence-vortex interaction cases and subsequently used them for Large Eddy Simulations (LES) of syngas/air flames quite successfully (Sen and Menon 2009; Ali Sen and Menon 2010; Sen et al. 2010). Zhou et al. demonstrated successful application of the ANN to turbulent premixed flames by including 1D laminar premixed flame cases at different turbulent intensities while training the ANN (Zhou et al. 2013). A wider range of combustion conditions were also considered in later studies by including non-premixed laminar flamelets (Chatzopoulos and Rigopoulos 2013) to include local extinction and reignition (Franke et al. 2017) and non-adiabatic conditions (Wan et al. 2020, 2021) in the training data sets. Furthermore, randomising the non-premixed flamelets before using them as training data sets were shown to improve the generality of the ANN and helped to capture the behaviour of turbulent premixed flames quite well (Readshaw et al. 2021; Ding et al. 2021). Also, other techniques were explored to improve the generalisation level of ANN: Chi et al. (2021) trained the ANN on-the-fly during a simulation, whereas An et al. (2020) trained their ANN using data from Reynolds-averaged Navier–Stokes (RANS) simulations of hydrogen/carbon monoxide/kerosene/air mixture in a rocket combustion chamber and tested it for LES.

Further to the chemical kinetics use, another application of the ANN focuses on replacing the traditional flamelet look-up table, which requires a large memory. The general procedure is to set thermochemical scalars, which are the basis of the look-up table, as the input of the ANN and to infer the tabulated values. This reduces the memory requirement significantly since only the weights and bias(es) of the ANN need to be saved. A first successful application was demonstrated in Flemming et al. (2005) by building ANNs having the mixture fraction, its variance and its scalar dissipation rate as inputs and mass fractions as outputs, and using them in LES of the Sandia flame D. This was extended in Kempf et al. (2005) and Emami and Fard (2012) to estimate scalar mass fraction variations in a turbulent CH$_4$/H$_2$/N$_2$ jet diffusion flame. The optimisation of the ANN architecture, in terms of number of hidden layers and neurons per layer, was also explored to improve the predictive accuracy of LES of the Sydney bluff-body swirl-stabilised methane-hydrogen flame (Ihme et al. 2006, 2008, 2009).

The use of ANN for inferring multi-dimensional flamelet library is also explored in recent studies. Owoyele et al. proposed a grouped multi-targets ANN approach to model 4D and 5D flamelet libraries respectively for a n-dodecane spray flame, under conditions of the Spray A flame from the Engine Combustion Network (ECN), and methyl decanoate combustion in a compression ignition engine (Owoyele et al. 2020). Ranade et al. (2021) trained a SOM-MLP method on a 4D Probability Density Function (PDF) table and used it for RANS and LES of the DLR-A turbulent jet diffusion flame. These works showed that the ANN yielded good accuracy at reduced computational costs with low storage space requirements. Similarly, Zhang et al. (2020) extended the application of the SOM-MLP algorithm to the Flamelet Generated Manifolds (FGM) model by using species mass fractions in mixture fraction-progress variable space as training data. This ANN approach was successfully used in RANS calculations and LES of ECN Spray H flame to explore the detailed spray combustion process. More comprehensive reviews of the applications of ML in combustion research can be found in Zheng et al. (2020), Zhou et al. (2022) and Ihme et al. (2022).

Presumed PDF shapes are typically used along with tabulated chemistry approaches. The PDF of relevant scalars such as mixture fraction and progress variable are used to compute averaged temperature, density, species mass fractions, and the relevant reaction rates. These quantities can be stored in a look-up table with the first two moments of the above scalars as controlling variables. Although widely employed in several past studies, presumed PDF or Filtered Density Function (FDF), in the context of LES, approaches may not accurately represent the scalar statistical behaviour under several conditions, such as extinction and reignition, combustion among multiple streams, multi-regime burners, and multi-phase reacting flows. The FDFs having shapes different to the regular distributions such as Gaussian or $\beta$-function can be also observed prominently in Moderate or Intense Low-oxygen Dilution (MILD) combustion. This combustion mode features broadly distributed reaction zones rather than conventional flamelet-like structures, with strong interactions between autoigniting and propagating fronts. Therefore, it may not be satisfactory to use conventional PDFs/FDFs models to predict reaction rates, and advanced data-driven techniques like machine learning may be a suitable alternative for improving the accuracy. De Frahan et al. (2019) compared the performance of three different machine learning techniques, viz., random forests, which is a traditional ensemble methods, deep neural networks (DNNs), and conditional variational autoencoder (CVAE), multiple hidden layers between which is also know as generative learning, to infer marginal FDFs of reaction progress variable in a swirling methane/air premixed flame and showed that DNN is superior compared to the other two techniques. The DNN is an ANN with multiple hidden layers between input and output. Yao et al. (2020) built an MLP to obtain the mixture fraction marginal FDF for LES of turbulent spray flames and observed an order of magnitude improvement compared to those of the traditional presumed FDF approaches. Chen et al. (2021) employed a DNN to predict the joint FDF of mixture fraction and progress variable in MILD combustion conditions and showed that the DNN is generally able to capture the complex FDF behaviours and their variations with excellent accuracy, outperforming other presumed FDF models.

This chapter aims to provide an overview of recent studies employing deep neural networks (interchangeably referred to as DNN, ANN or MLP hereafter) to infer subgrid-scale FDFs and reaction rates needed for LES of turbulent combustion under conventional and MILD conditions. A review of the Direct Numerical Simulation (DNS) data used to train these DNNs is also given. The chapter is structured as follows. A recap of the treatment of FDFs in LES of turbulent combustion systems is provided in Sect. 2. The DNS cases used as training datasets for the DNNs are described in Sect. 3. The characteristics of the DNNs employed for the different combustion cases are illustrated in Sect. 4. The main results in terms of FDF and reaction rate predictions are discussion in Sect. 5. The conclusions are summarised in Sect. 6.

2 FDF Modelling

The filtered reaction rate appearing in the transport equation for a species filtered mass fraction or reaction progress variable needs a closure model and recent developments in various closure models are described in the book (Swaminathan et al. 2022) and review papers (Veynante and Vervisch 2002; Pitsch 2006). Earlier chapters of this book discuss the potential application of ML techniques to some of the reaction rate closures. In the presumed PDF approach, the filtered reaction rate is modelled as an integral of the product of a conditional reaction rate and a FDF (see Eq. 6). The mixture fraction and the reaction progress variable are typically used as conditioning variables to signify the role of mixing and flame propagation on reaction rate (Bradley et al. 1998; Ihme and Pitsch 2008a). The conditional reaction rate may be estimated using one of the methods developed in past studies and these methods used canonical flames for chemistry tabulation, e.g., flamelet-generated manifolds (van Oijen and de Goey 2002), flame prolongation of intrinsic low dimensional manifold (Gicquel et al. 2000), conditional source term estimation method (Jin et al. 2008), or the solution of conditionally filtered equations for species mass fractions and energy via the conditional moment closure method (Klimenko and Bilger 1999).

The subgrid variations in the conditioning variables about their filtered values are represented by the filtered density function (FDF). The FDF can generally be obtained by solving its transport equations using various approaches, e.g., Lagrangian particles (Pope 1985), Eulerian stochastic fields (Jones and Kakhi 1998), and multi-environment (Fox 2003). However, these approaches are computationally expensive and thus using a presumed FDF can be chosen (Pitsch 2006; Pope 2013) to save computational costs. This presumed FDF approach will need only the statistical moments, usually the mean and variance, of the key variables (mixture fraction, progress variable, flame stretch/straining, heat loss, etc., depending on the physical scenario of interest) to be transported and it is therefore much more economical.

The $\beta$-PDF (Cook and Riley 1994) is the most commonly used presumed FDF in LES of turbulent flames (Raman et al. 2005; Navarro-Martinez et al. 2005; Ihme and Pitsch 2008b; Chen et al. 2017), and it usually provides a good approximation of a conserved scalar distribution. The Favre-averaged FDF of the mixture fraction Z with a presumed $\beta$-distribution is calculated as

$$\begin{aligned} \widetilde{P}_{\beta }(\xi ;\widetilde{Z},\widetilde{\sigma ^2_Z}) = \frac{\Gamma (a+b)}{\Gamma (a)\Gamma (b)}\;\xi ^{a-1}\left( 1-\xi \right) ^{b-1}, \end{aligned}$$

(1)

where $\xi$ is the sample space variable for Z, $\widetilde{Z}$ is the filtered mixture fraction and $\widetilde{\sigma ^2_Z} \equiv \widetilde{Z''}=(Z-\widetilde{Z})^2$ is the mixture fraction subgrid variance. The parameters of the $\Gamma$ function are $a = \widetilde{Z} \left( 1/\widetilde{g_Z} - 1\right)$ and $b = \left( 1 - \widetilde{Z} \,\right) \left( 1/\widetilde{g_Z} - 1\right)$. The segregation factor is $\widetilde{g_Z} = \widetilde{\sigma ^2_Z} ~/ \left( \widetilde{Z} (1-\widetilde{Z}) \right)$. The Favre-filtered FDF of the progress variable, $\widetilde{P}_{\beta }(\eta ;\widetilde{c}, \widetilde{\sigma ^2_{c}})$, can also be presumed to follow a $\beta$ distribution and obtained in a similar manner using $\widetilde{c}$ and $\widetilde{\sigma ^2_{c}}\equiv \widetilde{c''}=(c-\widetilde{c})^2$. The joint FDF of $\xi$ and $\eta$ can be modelled as

$$\begin{aligned} \widetilde{P}\left( \xi , \eta \right) = \widetilde{P}_{\beta }\left( \xi ;\widetilde{Z},\widetilde{\sigma ^2_Z}\right) \widetilde{P}_{\beta }\left( \eta ;\widetilde{c},\widetilde{\sigma ^2_{c}}\right) , \end{aligned}$$

(2)

assuming that there is a weak correlation between the subgrid fluctuations of Z and c. Such assumption has been widely accepted for LES of conventional combustion (Pitsch 2006; Veynante and Vervisch 2002). However, stronger subgrid correlations of scalars fluctuations can occur in MILD combustion (Minamoto et al. 2014) and hence the above assumption may not applicable universally. Other analytical distributions have been considered in past studies (Grout et al. 2009; Darbyshire and Swaminathan 2012; Linse et al. 2014). Darbyshire and Swaminathan (2012) proposed a correlated joint PDF model using the Plackett copula (Plackett 1965) to include the covariance of Z and c in RANS calculations. The covariance, $\widetilde{\sigma }_{Zc}$, written as $\widetilde{\sigma }_{Zc} =\widetilde{{ }\left( Z-\widetilde{Z}\right) \left( c-\widetilde{c}\right) }$ is used in the copula method to obtain a joint PDF from the univariate marginal distributions, $\widetilde{P}_{\beta }(Z)$ and $\widetilde{P}_{\beta }(c)$. For non-zero values of $\widetilde{\sigma }_{Zc}$, the correlated joint PDF is calculated as

$$\begin{aligned} \widetilde{P}\left( Z,c\right) = \frac{\theta \,\widetilde{P}_{\beta }(Z)\widetilde{P}_{\beta }(c)\left( \mathscr {A}-2\mathscr {B} \right) }{\left( \mathscr {A}^2 - 4\theta \mathscr {B} \right) ^{3/2}}, \end{aligned}$$

(3)

with

$$\begin{aligned} \mathscr {A} = 1+(\theta -1)\left[ \widetilde{{\mathscr {C}}}_{\beta }(Z) +\widetilde{{\mathscr {C}}}_{\beta }(c)\right] , \end{aligned}$$

(4)

and

$$\begin{aligned} \mathscr {B} = (\theta -1) \widetilde{{\mathscr {C}}}_{\beta }(Z) \widetilde{{\mathscr {C}}}_{\beta }(c), \end{aligned}$$

(5)

where $\widetilde{{\mathscr {C}}}_{\beta }$ is the $\beta$ cumulative distribution function (CDF) and $\theta$ is the odds ratio calculated using a Monte Carlo approach (Ruan et al. 2014). The copula method has been used in RANS calculations of stratified premixed and lifted jet flames (Ruan et al. 2014; Chen et al. 2015) showing improved prediction of the lift-off height with respect to the double-$\beta$ PDF given in Eq. (2).

In presumed-FDF approaches, the subgrid reaction rate is obtained as

$$\begin{aligned} \overline{\dot{\omega }} = \int _0^1 \int _0^1 \langle \dot{\omega }|Z,c\rangle P\left( Z, c; \; \widetilde{Z},\widetilde{\sigma ^2_{Z}},\widetilde{c},\widetilde{\sigma ^2_{c}} \right) \;\;dZ \;dc, \end{aligned}$$

(6)

and this approach reduces the computational cost significantly for LES by using presumed FDF in the above equation. However, the presumed FDF shapes obtained using classical functions, for example bimodal delta function, may not be fully satisfactory for situations such as (i) MILD combustion conditions, (ii) when there are evaporating droplets, and (iii) when the burnt or burning mixture is inhomogeneous leading to significant statistical correlation between Z and c (Chen et al. 2018). To overcome these issues, machine learning algorithms are employed to construct predictive models for the scalar PDFs/FDFs in recent studies. A deep neural network (DNN), among other ML techniques tested, was shown to be better than a joint $\beta$-function model in inferring subgrid FDFs in a swirling methane-air premixed flame (de Frahan et al. 2019). This behaviour was also demonstrated for MILD combustion (Chen et al. 2021) and turbulent spray flames (Yao et al. 2020). These tests were conducted using respective direct numerical simulation (DNS) datasets. DNS can be seen as a virtual experiment resolving all the relevant length and time scales without turbulence modelling. Thus, it is a powerful tool for investigating combustion models. It is quite straightforward to obtain filtered quantities from DNS data by applying appropriate filtering operations (Pope 2000) and these can be used as input to ML algorithms such as DNN. The data extraction and its processing prior to using them for DNN training are important steps which can play a role to improve accuracy and generality of the neural networks. Details about these steps, along with the main features of the cases studied in de Frahan et al. (2019), Chen et al. (2021) and Yao et al. (2020), are discussed in the following sections. Details on the respective DNS cases can be found in those studies as the objective here is on the use of ML techniques.

3 DNS Data Extraction and Manipulation

Three combustion cases are considered in this chapter: a low-swirl premixed methane-air flame investigated in de Frahan et al. (2019), methane-air combustion under MILD conditions studied in Chen et al. (2021), and a turbulent kerosene spray flame used in Yao et al. (2020). The corresponding DNS setups and data preparation procedures are described next.

3.1 Low-Swirl Premixed Flame

The DNS dataset considered by de Frahan et al. is a snapshot of a quasi-stationary simulation of an experimental low-swirl, premixed methane-air burner (Day et al. 2012). In this setup, a nozzle imposes a low swirl to a CH$_4$/air mixture with fuel-air equivalence ratio $\phi = 0.7$ at the inflow. The nozzle region is surrounded by a co-flow of cold air. A lifted premixed flame with its partially burnt mixture reacting with co-flow air in downstream locations was observed in the experiments. The presence of this multi-regime burning introduces challenges for modeling the joint FDF of mixture fraction and progress variable. Training ML models with such DNS dataset has additional advantages such as using diverse subsets as training data, avoiding overfitting, and increasing the opportunities for model generalisation. The training sets were constructed by selecting different subvolumes, indicated by $\mathcal {V}$ as in Fig. 1, spanning from premixed combustion region to downstream zone containing mixing of premixed combustion products with co-flow air. de Frahan et al. (2019) used a single time snapshot at $t = 0.0626$ s from the DNS to demonstrate the capabilities of ML for FDF modelling. In the context of LES, the FDF at a given point and time can be extracted by applying fine-grained filtering to DNS or experimental data at a given instant (Pope 1990). In each subvolume, sample moments and the associated FDF were thus obtained by using a discrete box filter:

$$\begin{aligned} \overline{\psi }(x,y,z) = \frac{1}{n_f^3}\sum _{i=-n_f/2}^{n_f/2}\sum _{j=-n_f/2}^{n_f/2}\sum _{k=-n_f/2}^{n_f/2}\psi (x+i\Delta x,y+j\Delta x,z+k\Delta x), \end{aligned}$$

(7)

where $\psi$ is the quantity of interest, $n_f$ is the number of points in the discrete box filter, $\overline{\Delta }= 32\Delta x$ is the filter size, and $\Delta x =100\,\upmu$m is the smallest spatial cell size in the DNS (six times smaller than the laminar flame thickness). Four sample moments of the joint FDF, i.e., $\widetilde{Z}$, $\widetilde{\sigma }^2_Z$, $\widetilde{c}$, $\widetilde{\sigma }^2_c$, which are Favre-filtered mixture fraction, its subgrid scale (SGS) variance, progress variable and its SGS variance, were extracted for each subvolume. The filter size was chosen to be representative of typical LES filter scale (Pitsch 2006) and to ensure adequate samples to construct FDF. These filters were spaced equidistant of $8\Delta x$, leading to 58800 FDFs for each subvolume. The mixture fraction Z was defined using nitrogen mass fraction so that it took a value of 1 in the burner stream and 0 in the co-flow air. The progress variable, varying between 0 and 0.21, was defined using mass fractions of CO$_2$, CO, H$_2$O and H$_2$ as $c = Y_{\text {CO2}} + Y_{\text {CO}} + Y_{\text {H2O}} + Y_{\text {H2}}$. The density-weighted FDFs of Z and c were constructed using 64 bins in Z space and 32 bins in c space, which gives a vector of 2048 values to describe a single joint FDF. The conditional means of the reaction rate $\langle \dot{\omega }|Z,c\rangle$ were also extracted for each sample with an identical discretisation.

Fig. 1

Illustration of data generation procedure for $\mathcal {V}_5$

Prior to training, the sample moments were independently centered by subtracting the median and scaled by dividing the data by the range between the 25th and 75th quantiles. It is known that appropriate centring and scaling are generally beneficial for ML algorithms (Goodfellow et al. 2016). According to the authors this centring and scaling were robust to outliers. The samples from a volume $\mathcal {V}_i$ were randomly split among two distinct datasets: a training dataset, $\mathcal {D}_i^t$, and a validation dataset, $\mathcal {D}_i^v$, comprising 5% of the total samples, as illustrated in Fig. 1.

3.2 MILD Combustion

The MILD combustion DNS dataset of Doan et al. (2018) was used to study the application of DNN for inferring subgrid FDF in MILD combustion by Chen et al. (2021). A cube of size $L_x \times L_y \times L_z = 10 \times 10 \times 10$ mm was used to conduct DNS of turbulent combustion of inhomogeneous methane-air mixtures diluted with exhaust gases. A spatial resolution of $\delta x\approx 20$ $\upmu$m obtained using 512 points distributed uniformly in each direction was observed to be sufficient to resolve the turbulent and chemical length scales of interest as described in Doan et al. (2018). The simulation was run for 1.5 flow-through time $\tau _f$, defined in Minamoto and Swaminathan (2015). Further detail on the DNS procedure and datasets can be found in Doan et al. (2018). Three cases, viz., AZ1, AZ2 and BZ1, with different mixing length scales and dilution levels were considered for the DNN training. The conditioning variables for the FDF analyses were the Bilger mixture fraction (Bilger 1976) and a temperature-based reaction progress variable, $c_T$, defined as

$$\begin{aligned} c_T = \frac{T - T_u}{T_b(Z) - T_u}, \end{aligned}$$

(8)

where $T_u$ is 1500 K and the value of burnt mixture temperature $T_b$ depends on Z and it can be obtained using MILD Flame Element (MIFE) laminar calculations (Minamoto and Swaminathan 2014). Favre-filtered fields were extracted from the DNS by applying a low-pass box filter. For example, the Favre-filtered mixture fraction $\widetilde{Z}$ was obtained as:

$$\begin{aligned} \widetilde{Z}({\boldsymbol{x}}, t) = \frac{1}{\overline{\rho }({\boldsymbol{x}}, t)} \int _{{\boldsymbol{x}}-\frac{\Delta }{2}}^{{\boldsymbol{x}}+\frac{\Delta }{2}} \rho \left( {\boldsymbol{x}'},t \right) \; Z \left( {\boldsymbol{x}'}, t \right) \;\; d{\boldsymbol{x}'} , \end{aligned}$$

(9)

where $\overline{\,\cdot \,}$ and $\widetilde{\,\cdot \,}$ denote the Reynolds and Favre filtering respectively, $\rho$ is the mixture density and $\Delta$ is the filter width. The position vectors are ${\boldsymbol{x}}$ and ${\boldsymbol{x}'}$. The subgrid variance was obtained as

$$\begin{aligned} \widetilde{\sigma ^2_Z}({\boldsymbol{x}},t)= \frac{1}{\overline{\rho }({\boldsymbol{x}},t)} \int _{{\boldsymbol{x}}-\frac{\Delta }{2}}^{{\boldsymbol{x}}+\frac{\Delta }{2}} \rho \left( {\boldsymbol{x}'},t \right) \left[ Z \left( {\boldsymbol{x}'},t \right) - \widetilde{Z}\left( {\boldsymbol{x}},t \right) \right] ^2 \;\; d{\boldsymbol{x}'}. \end{aligned}$$

(10)

Similarly, the $\widetilde{c}_T$ and $\widetilde{\sigma ^2_{c_T}}$ fields were calculated as above. The Z-$c_T$ joint FDF was then computed as

$$\begin{aligned} \widetilde{P}(\xi ,\eta ;{\boldsymbol{x}}, t) = \frac{1}{\overline{\rho }({\boldsymbol{x}}, t)} \int _{{\boldsymbol{x}}-\frac{\Delta }{2}}^{{\boldsymbol{x}}+\frac{\Delta }{2}} \rho \left( {\boldsymbol{x}'}, t \right) \; \delta \left[ \xi - Z\left( {\boldsymbol{x}'}, t \right) \right] \delta \left[ \eta - c_T\left( {\boldsymbol{x}'}, t\right) \right] \;\; d{\boldsymbol{x}'} , \end{aligned}$$

(11)

where $\xi$ and $\eta$ were the sample-space variables of Z and $c_T$ respectively, $\delta [\cdot ]$ is the Dirac delta function. The discrete FDFs were obtained for a given point in a given DNS snapshot by binning the Z and $c_T$ samples in the corresponding filtering subspace with 35 non-uniform bins in Z space (clustered around the stoichiometric value) and 31 uniform bins in $c_T$ space. The subgrid-scale covariance, $\widetilde{\sigma }_{Z c_T}$, also used by the copula model, was computed as

$$\begin{aligned} \begin{aligned} \widetilde{\sigma _{Zc_T}}({\boldsymbol{x}},t) = \frac{1}{\overline{\rho }({\boldsymbol{x}},t)} \int _{{\boldsymbol{x}}-\frac{\Delta }{2}}^{{\boldsymbol{x}}+\frac{\Delta }{2}} \rho ({\boldsymbol{x}'},t)&\left[ Z({\boldsymbol{x}'},t)-\widetilde{Z}({\boldsymbol{x}},t) \right] \\&\times \left[ c_T({\boldsymbol{x}'},t)-\widetilde{c_T}({\boldsymbol{x}},t) \right] \;\; d{\boldsymbol{x}'}. \end{aligned} \end{aligned}$$

(12)

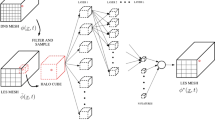
The filtered scalar fields $\widetilde{Z}$, $\widetilde{c_T}$, $\widetilde{\sigma _{Z}^2}$, $\widetilde{\sigma _{c_T}^2}$ and $\widetilde{\sigma _{Zc_T}}$ formed the DNN input matrix $\textbf{X}$. The unfiltered $\rho$, Z and $c_T$ fields were used to obtain the Favre filtered FDFs required for the target matrix $\textbf{Y}$. The procedure is shown schematically in Fig. 2 for a snapshot of case AZ1. The filtered fields are presented in 2D with the thin DNS grid-lines for visual clarity. The indices i, j and k pertain to the x, y and z directions in 3D space, respectively, and are assigned to each “LES filter cube” indicated by a red box in Fig. 2. The total number of samples taken in each direction is $n_\textrm{cube}$. The effects of filter size were also investigated by considering a range of filter sizes relevant to typical LES. The filter sizes were normalized using the thermal thickness of the stoichiometric MIFE, $\delta ^{\text {st}}_{\text {th}}=1.6$ mm. A filter size of $\Delta = 80 \delta x$ corresponded to $\Delta ^+ = \Delta /\delta ^{\text {st}}_{\text {th}} = 1$. The extracted matrices $\textbf{X}$ and $\textbf{Y}$ were flattened to be two-dimensional, with as many rows as the number of samples and as many columns as the number of features. The input matrix $\textbf{X}$ had 5 columns, while the target matrix $\textbf{Y}$ had 1085 columns, obtained from the discretisation step mentioned above.

Fig. 2

Schematic demonstration of the construction of the DNN input and target matrices (Chen et al. 2021)

Centring and scaling of the input matrix $\textbf{X}$ were performed as follows: each column vector, having $n_\textrm{cube}^3$ elements, was centred by subtracting its mean and scaled by dividing by its standard deviation. Centring and scaling were not applied to the output matrix $\textbf{Y}$. However, to address the issue of having unbounded values of the FDFs, the discrete density function values were considered. As such, every number in $\textbf{Y}$ varied between 0 and 1, and the sum of the elements in each target row is equal to 1.

Subsequent to the scaling procedures, a dimensionality reduction technique like Principal Component Analysis (PCA), discussed in chapter “Reduced-Order Modeling of Reacting Flows Using Data-Driven Approaches” was used to identify and remove the outliers in the training data. Two types of outliers, viz., leverage and orthogonal, Verdonck et al. (2009) were determined and discarded. Details about the identification and removal step are provided in Chen et al. (2021). Once leverage and orthogonal outliers were removed from the dataset, the DNN training was then performed on the remaining observations as discussed in the following Sect. 4.2.

3.3 Spray Combustion

Carrier-phase DNS (CP-DNS) data of turbulent spray flames were used to build a deep learning training database for mixture fraction FDF predictions. In carrier-phase DNS, the flow field is resolved with a point source approximation for the droplets, thus all relevant scales of the fluid phase are resolved except the boundary layers around individual particles. The governing equations of the gas phase are solved in the Eulerian framework and coupled with a Lagrangian solver for displacement, size, and temperature of the droplets. An equilibrium state of the liquid and the vapor at the interface was assumed. A full description of the governing equations is provided in Yao et al. (2020). The computational domain is a rectangular box, discretised by a mesh with 192$\times$128$\times$128 cells having $\delta _{\textrm{DNS}}$ = 100 $\upmu$m. This grid size ensured a sufficient resolution of the small scale structures of the flow field (Pope 2000), whereas a finer resolution could compromise the point particle assumptions of the liquid phase. Kerosene droplets (treated as single-component C$_{12}$H$_{23}$) were randomly injected into humid air, representative of experimental (Khan et al. 2007; Wang et al. 2018) and numerical (Wright et al. 2005; Giusti et al. 2018) setups. A homogeneous isotropic turbulent velocity field, calculated by a modified von Karman spectrum (Wang et al. 2019) was imposed at the inlet. The progressive kerosene droplet evaporation led to an ignitable mixture that promoted a statistically planar turbulent partially premixed flame. Further downstream, the hot post-flame temperatures led to reduced turbulence levels due to higher viscosity and a sudden evaporation of remaining droplets that could penetrate the flame. This lack of homogeneity and the presence of a source term for the mixture fraction are prone to make the existing FDF models (O’Brien and Jiang 1991; Cook and Riley 1994) inaccurate.

Fig. 3

Simulation setup of CP-DNS (solid points: droplets; the gas phase is colored by temperature) and an LES filter box (Yao et al. 2020)

Filter boxes were used for post-processing of CP-DNS data to group several DNS cells into one LES cell. A filter box example is shown in Fig. 3 along with the DNS domain and setup, and the simulated temperature contour. The mixture fraction FDF $P(\eta )$ was computed from DNS data using a mixture fraction binning, with a bin size of 0.01 for all DNS cells lying within a specific LES cell. Favre filtering was used to extract LES quantities that were employed as input variables for the ANN. According to Klimenko and Bilger (1999), the following input quantities were found to have an effect on the mixing statistics and were thus considered: mixture fraction $\xi$, eddy viscosity $\nu _t$, turbulence dissipation rate $\epsilon _t$, diffusion coefficient D, density $\rho$, spray evaporation rate $J_m$, relative velocity between the droplet and the surrounding gas $U_d$ and droplet number density C. The turbulence dissipation rate was replaced by the more easily available strain rate $|S_{ij} |$. All the DNN inputs were filtered and Favre averaged. Therefore, the input features are commonly accessible in a typical LES of spray combustion. Moreover, Wang et al. concluded in their study that these parameters sufficiently characterize the mixture fraction FDF in turbulent spray flames. To ensure the reliability of the DNN for a reasonable range of LES meshes, the authors investigated the following LES filter sizes: $(\Delta _\textrm{LES})^3=(8\delta _\textrm{DNS})^3$, $(\Delta _\textrm{LES})^3=(16\delta _\textrm{DNS})^3$, $(\Delta _\textrm{LES})^3=(32\delta _\textrm{DNS})^3$. The final database is a combination of data samples with different $\Delta _\textrm{LES}$. The performance of the DNN for data samples using different LES filter boxes were assessed. The output target was set to be a placeholder of 60 elements covering $\xi$ in [0, 0.6], as $\xi _{max}\le$ 0.6 in the the spray flame simulations. To avoid that the binning procedure could lead to empty bins, especially for small $\Delta _\textrm{LES}$, missing values were replaced by interpolated values computed by Stineman interpolation method, which is widely used in statistics to deal with the missing values as it preserves the monotonicity of data and prevents introducing spurious oscillations (Stineman 1980). It was found that the commonly used zero-padding operation, which fills in blank data with zeros, is not applicable as the DNN would be misled and learn erroneous patterns. A total of 18 simulation cases were run to form the full database for training and validation purposes. The validation (test) dataset consisted of five simulation cases, resulting in a test/train ratio of about 0.38. These datasets included parameter ranges that approximate conditions to be expected in real spray flames and were used for the a priori validation presented in Sect. 5.

To recap, the three studies selected several DNS cases to construct a heterogeneous training set. If only one DNS case was available then several subdomains within the DNS domain were selected. Chen et al. (2021) considered one additional DNN input feature, i.e., the scalar covariance, to the input set chosen by de Frahan et al. (2019). Yao et al. (2020) chose different DNN input features specifically for spray combustion. No scaling was adopted by Yao et al., whereas two different scaling methods were implemented in the other studies. Only Chen et al. adopted an outlier removal by using a dimensional reduction technique. Discrete density functions, bounded between 0 and 1, were the DNN target in de Frahan et al. (2019) and Chen et al. (2021) while Yao et al. (2020) considered probability density function values. The review of these studies shows that no unique algorithm needs to be adopted to prepare the input data for a ML model. The only common goal that needs to be pursued is to construct an input dataset that is as heterogeneous as possible to increase the generalisation, also known as transfer learning, of the trained ML models. The similarities and differences of the DNNs used in these three studies are discussed next.

4 Deep Neural Networks for Subgrid-Scale FDFs

A standard neural network consists of many simple connected functional units, called neurons. Each neuron receives an input which is processed through activation functions to produce an output. Multiple neurons can be combined to form fully connected networks, which are called artificial neural networks (ANNs) since they mimic the neuron arrangements in the human brain. Feed-forward networks, also called multi-layer perceptrons (MLPs), are classic ANN structures, and they are composed of layers of neurons, where a weighted output from one layer is the input to the next layer. The first layer of the MLP accepts a vector as input and the elements of this vector are known as features. The final output of the MLP is the target quantity of interest. The layer providing the final MLP output is called output layer, while the other layers in the network are called hidden layers. In a mathematical perspective (Goodfellow et al. 2016), the MLP defines a mapping from the input $\boldsymbol{x}$ to the output $\boldsymbol{y}=f(\boldsymbol{x},\boldsymbol{\theta })$, where the parameters $\boldsymbol{\theta }$ are the trainable network parameters. Each neuron is a functional unit that is generally described by

$$\begin{aligned} \boldsymbol{y} = \phi (\boldsymbol{x}^T\boldsymbol{\omega }+\boldsymbol{b}), \end{aligned}$$

(13)

where $\boldsymbol{\omega }$ and $\boldsymbol{b}$ are the weights and bias vector, and $\phi$ is the activation function (see Sect. 2.3.7.2, Chap. 2, this volume), which provides great flexibility to ANNs by introducing non-linearity to an otherwise linear relationship between input and output. There are several activation functions and some of these will be introduced and described later. The weight $\boldsymbol{\omega }$ is a matrix of the size $k\times m$, whereas the bias $\boldsymbol{b}$ is a vector of m elements. For each layer, k is the number of inputs received from the preceding layer and m is the number of neurons in the current layer. $\boldsymbol{\omega }$ and $\boldsymbol{b}$ contains the trainable parameters of the network. The training of ANNs pursues the objective of minimizing a target loss function

$$\begin{aligned} \mathcal {L}(\boldsymbol{x},\boldsymbol{\omega }) = \mathscr {G}(f(\boldsymbol{x},\boldsymbol{\omega })-f^*), \end{aligned}$$

(14)

where $\mathscr {G}$ is any measure of the difference between the modeled value f and the real value $f^*$. The most commonly used loss functions are the mean absolute error (MAE) and the mean squared error (MSE). Nonlinear optimization methods, such as backward propagation (Rumelhart et al. 1986), are used to identify the network weights that minimize the error between predictions and labeled training data. The training step gives the optimized set of weights. The MLP is a design that is suitable for regression problems, whereas other types of ANNs, such as Convolutional Neural Network (CNN) and Recurrent Neural Network (RNN), have been extensively used in processing image data and time series problems, etc., see Sect. 2.3.7.2 (Chap. 2, this volume), for further detail. A schematic of the MLP architecture with input, hidden, and output layers is shown in Fig. 4 as an example.

Fig. 4

A schematic of 3-layer MLP architecture

4.1 Low-Swirl Premixed Flame

A feed-forward fully connected DNN with three, two hidden and an output, layers was trained by de Frahan et al. (2019) to predict the joint subfilter FDF of mixture fraction and progress variable. There were 256 and 512 neurons in the two hidden layers and neurons had a leaky rectified linear unit activation function (LeakyReLU): 

$$\begin{aligned} y_i = {\left\{ \begin{array}{ll} ~~x_i &{} \text {if } x_i\ge 0 \\ ~~\alpha x_i &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(15)

where $x_i$ is the weighted sum of the neuron input, $y_i$ is its output, and $\alpha$, usually equal to 0.01, is the slope. A LeakyReLU activation function avoids mapping negative input to zero values unlike its parent function ReLU having $\alpha = 0$. A large weight update during training can yield the summed input to be always negative regardless of the network input. A neuron featuring a ReLU function will then output a zero value leading to the dying ReLU case, in which the neuron neither activates a gradient-based optimization nor adjust its weights. Furthermore, similar to the vanishing gradients problem, the learning can be slow while training ReLU networks stumbling on constant zero gradients. The leaky rectifier allows for a small, non-zero gradient when the unit is saturated and not active. Additionally, each hidden layer is followed by a batch normalization layer (Ioffe and Szegedy 2015) and this technique has been widely used to build deep networks as it leads to speed and performance improvements. It applies the following function:

$$\begin{aligned} y_i = \gamma \frac{x_i - \mu _x}{\sqrt{\sigma _x^2 + \epsilon }} + \delta \end{aligned}$$

(16)

where $x_i$ and $y_i$ are the i-th elements of the layer input and output vectors respectively. These vectors are of size n having a mean and variance of $\mu _x = 1/n\sum _{i=1}^n x_i$ and $\sigma _x^2 = 1/n\sum _{i=1}^n(x_i - \mu _x)^2$. A small real number $\epsilon$ is used to maintain numerical stability. Both $\gamma$ and $\delta$ are learning parameter vectors of size n and they are updated iteratively during training for optimization purposes. de Frahan et al. (2019) chose $\epsilon = 10^{-5}$ and a moving average of $\mu _x$ and $\sigma _x$ computed during training with a decay of 0.1 (or, equivalently, momentum of 0.9).

The DNN inputs are the four moments of the joint FDF, viz., $\widetilde{Z}$, $\widetilde{\sigma ^2_Z}$, $\widetilde{c}$, and $\widetilde{\sigma ^2_c}$ whereas the outputs are a total of 2048 FDF values obtained from the discretisation of the joint FDF of mixture fraction Z and progress variable c as described in Sect. 3.1. Thus, an output layer having 2048 neurons, as many as the number of outputs, was considered in de Frahan et al. (2019). The output layer features a softmax activation function:

$$\begin{aligned} y_i = \frac{\exp (x_i)}{\sum _{i=1}^n\exp (x_i)} \end{aligned}$$

(17)

where $x_i$ and $y_i$ are defined as for Eq. 16. This type of activation function ensures that $\sum _{i=1}^ny_i=1$ and $y_i\in [0,1]$ $\forall \; i$. The loss function used was the binary cross entropy between the target y and the prediction $\hat{y}$ and this function is

$$\begin{aligned} {\mathcal {L}}(\hat{y},y) = \frac{1}{n}\sum _{i=1}^n\left( y_i\log \hat{y}_i + \left( 1 - y_i \right) \log \left( 1 - \hat{y}_i \right) \right) , \end{aligned}$$

(18)

representing a proper metric for measuring the difference between two probability distributions. The total number of trainable parameters was 1.1 M. The training was performed over 500 epochs, i.e., 500 training loops through the entire training data. For each epoch, the training data is fully shuffled and divided into batches with 64 training samples per batch. All trainable parameters are updated after each epoch. A split of 95/5% between training and validation samples was applied on the entire dataset. The loss function is computed on the validation samples which are not part of the training process. Thus, the validation loss is the true indicator of the ANN’s performance and provides hints regarding its generality. It is a common practice to track the losses during both training and validation steps continuously to check if the losses are decreasing over each epoch by studying learning curves (a plot of loss vs epoch number). These learning curves can be used to diagnose an underfit, overfit, or well-fit model and whether the training or validation datasets are not representative of the problem domain. A good ANN training gives loss curves that decreases continuously until a plateau is reached where the difference between the training and validation losses is small. de Frahan et al. (2019) chose Adam optimizer (Kingma and Ba 2014), which is a gradient descent algorithm, with an initial learning rate of $10^{-4}$. The learning rate is a dimensionless parameter that determines the step size of the stochastic gradient descent used to adjust the weights, $\mathbf {\boldsymbol{\omega }}$. The Adam optimizer is more sophisticated than traditional stochastic gradient descent by having a per-parameter learning rate, which can also be adapted during the training (Kingma and Ba 2014).

4.2 MILD Combustion

Chen et al. (2021) used a feed-forward fully connected DNN to infer the joint FDF of mixture fraction and progress variable. This DNN is similar to the one employed by de Frahan et al. (2019) and can be summarized as follows:

• linear hidden layer with 5 input features and bias, LeakyReLU activation function with $\alpha = 0.01$, and 256 output features;

• batch normalization layer with 256 input and output features, and momentum equal to 0.9;

• linear hidden layer with 256 input features and bias, LeakyReLU activation function with $\alpha = 0.01$, and 512 output features;

• batch normalization layer with 512 input and output features, and momentum equal to 0.9;

• linear output layer with 512 input features and bias, softmax activation function, and 1085 output features.

Thus, the two hidden layers had 256 and 512 fully connected neurons, where LeakyReLU activation functions were applied. Each hidden layer was followed by a batch normalization layer. The output layer contained 1085 neurons featuring a softmax activation function. The loss function used was the binary cross entropy given in Eq. 18 along with Adam optimizer with an initial learning rate of $10^{-4}$. The model was trained for maximum 1000 epochs with batch size of 256 training samples. The ANN features were the four moments of the joint FDF and the outputs were a total of 1085 FDF values. A split of 80/20% between training and validation samples was applied on the entire dataset containing about 28000 filtered DNS boxes. An early stopping method, by using a predefined number of epochs, was used for the training to avoid overfitting. An overfitted ANN will have a validation loss that decreases for the first several epochs but increases subsequently (Goodfellow et al. 2016).

4.3 Spray Flame

Yao et al. (2020) used an MLP with four hidden layers and 500 neurons per layer to infer the Favre-filtered FDF of the mixture fraction in spray flames. As noted in Sect. 3.3, the input quantities were $\widetilde{\xi }$, $\widetilde{\nu }_t$, $\widetilde{|S_{ij} |}$, $\widetilde{ D}$, $\overline{\rho }$, spray evaporation rate $\widetilde{J_m}$, relative velocity between the droplet and the surrounding gas $\widetilde{U}_d$, and droplet number density $\widetilde{C}$. The output was a vector with 60 elements since the FDF of the mixture fraction $P(\eta )$ (where $\eta$ is the sample space variable for the mixture fraction $\xi$) was obtained as described in Sect. 3.3. The activation function $\phi (z) = \max (0,z)$ applied in each layer was the ReLU. A traditional stochastic gradient descent algorithm was used to minimize the mean absolute error, which was the loss function. A total of 18 DNS cases were run to form the full datasets for the training and validation steps. The validation (test) dataset consisted of five cases, resulting in a test/train ratio of $\sim$0.38. An early stopping criterion was imposed for the training process. This ANN was also trained on the conditional scalar dissipation rate $\langle N|\xi =\eta \rangle$, which is another interesting application.

5 Main Results

5.1 FDF Predictions and Generalisation

An overview of the ML model performance in each of the test cases is discussed in this section. The FDF predictions provided by ML and analytical models were assessed a priori using the FDFs obtained from the DNS cases.

5.1.1 Premixed Flame

Three different ML models, i.e., random forest (RF), conditional variational autoencoder (CVAE), and DNN, were trained by de Frahan and coworkers using filtered DNS data from the subvolume $\mathcal {V}_3$ of the low-swirl premixed flame, i.e., the algorithms were trained on $\mathcal {D}^t_3$, and the metrics were evaluated on $\mathcal {D}^v_3$ (see Fig. 1). Figure 5 compares the marginal FDFs P(Z) and P(c) obtained using the three ML models, $\beta$-function model and DNS result for $\mathcal {V}_3$ for three different values (low, medium, and high) of the Jensen-Shannon divergence (JSD), which measures the similarity of two probability distributions, $Q_1 = Q^\textrm{DNS}(n)$ and $Q_2 = Q^\textrm{model}(n)$. The JSD is given by

$$\begin{aligned} \text {J}(Q_1||Q_2) = \frac{1}{2}\sum _{n=1}^{N} \Bigg \{ Q_1(n)~{\ln }\left[ \frac{Q_1(n)}{Q_2(n)}\right] +~ Q_2(n)~{\ln }\left[ \frac{Q_2(n)}{Q_1(n)}\right] \Bigg \} \end{aligned}$$

(19)

The JSD divergence is symmetric, i.e., $J(Q_1||Q_2)=J(Q_2||Q_1)$, and mathematically bounded between 0 and $\ln (2)$, with 0 indicating $Q_1 = Q_2$. The JSD for the three samples shown in Fig. 5 were computed by considering the FDFs extracted from the DNS of the premixed flame and those obtained by the $\beta -\beta$ analytical model. It can be seen from Fig. 5 that the $\beta -\beta$ analytical model is unable to capture more complex FDF shapes, such as bimodal distributions, as also confirmed by high JSD values. Thus, the need for more accurate models is motivated. Accurate predictions can be expected for $J(P||P_m)<0.3$, whereas predictions with $J(P||P_m)>0.6$ exhibit incorrect median values and overall shapes.

Fig. 5

Marginal FDF for low, mid-range, and high Jensen-Shannon divergence values for the $\beta -\beta$ PDF model. Red solid line is for RF model, green dashed line is for DNN model, blue dash-dotted line is for CVAE model, orange short dashed line is for $\beta -\beta$ model and black solid line is the DNS result (de Frahan et al. 2019)

The abilities of the three ML models to infer the subgrid FDF in regions other than $\mathcal {D}^t_3$ was also assessed because DNS results showed that the FDF in downstream locations were significantly different from those for $\mathcal {V}_3$. So, the ML models were trained using (1) $\mathcal {D}^t_3$ data (volume centered at z $=$ 0.0775 m), (2) data from $\mathcal {D}^t_5$ (volume centered at z $=$ 0.1025 m) and (3) data collected from the odd-numbered volumes $\mathcal {D}^t = \cup _{i=1, 3,5,7,9}D^t_i$. The training data in the last case were representative of the entire computational domain. It was found that the models trained using data from a single volume were unable to infer the FDF in other volumes which was indicated by the high 90th percentile ($J_{90}$) of all the Jensen–Shannon divergences errors. The ML models trained using the odd-numbered volumes (test 3 above) gave $J_{90} < 0.2$ for the entire physical domain although only 4% of the DNS data from the entire computational domain was used for the training. Among the three ML modes, DNN yielded the lowest errors. The analytical $\beta -\beta$ model had $J_{90}$ values which were almost twice of that for the ML models. The sample marginal FDFs of mixture fraction and progress variable for 3 different values of Jensen-Shannon divergences computed for the DNN model are shown in Fig. 6 and it is clear that the bimodal distributions are also captured quite well by the ML models.

Fig. 6

Marginal FDF for median and high Jensen-Shannon divergence values for models trained on $\mathcal {D}^t = \cup _{i=1, 3,5,7,9}D^t_i$. Red solid line is for RF, green dashed line is for DNN, blue dash-dotted line is for CVAE, orange short dashed line is for $\beta -\beta$ model, and black solid line is for DNS (de Frahan et al. 2019)

Another generalisation test was conducted by using validation data generated from a different time snapshot of the DNS ($t = 0.059$ s). For this case, the DNN model trained on $\mathcal {D}^t = \cup _{i=1, 3,5,7,9}D^t_i$ provided reasonable $J_{90}$ values, although slightly higher than those obtained for the validation data from the same time snapshot of the training data. The $\beta -\beta$ model provided similar errors in both cases but three times higher than those of the DNN model. These generalisation tests demonstrated that the learned models are able to generalize temporally, as well as spatially. The results reported in this subsection suggest that it is important to use the training data covering the expected range of physical processes for which the ML is to be applied.

5.1.2 MILD Combustion

For the MILD combustion cases, the FDFs provided by DNN, $\beta -\beta$ and copula models are presented and compared to the DNS FDFs in Figs. 7, 8 and 9 for cases AZ1, AZ2 and BZ1 respectively. The DNN model significantly outperforms both analytical models and its prediction agrees very well with the DNS data for the different cases. As a general observation, the DNN captures the non-regular shapes of the marginal FDF of the progress variable quite well where the analytical models given by the $\beta$ function and copula give Gaussian-like distributions. This difference has important implications for the reaction rate modelling as one shall see later in Sect. 5.2. For the mixture fraction, however, all models give good results but only the DNN is able to capture the asymmetry of the FDF which can be seen clearly in Fig. 9b and  9d for case BZ1. These results indicate promising capabilities of the DNN to predict the complex subgrid scalar statistics in MILD combustion.

Fig. 7

Case AZ1: comparison of joint and marginal FDFs from DNS and models for filter sizes of $\Delta ^+ = 0.5$ in (a) and (b), $\Delta ^+ = 1$ in (c) and (d), and $\Delta ^+ = 1.5$ in (e) and (f) (Chen et al. 2021)

Fig. 8

Case AZ2: comparison of joint and marginal FDFs from DNS and models for filter sizes of $\Delta ^+ = 0.5$ (Chen et al. 2021)

Fig. 9

Case BZ1: comparison of joint and marginal FDFs from DNS and models for filter sizes of $\Delta ^+ = 0.5$ in (a) and (b), and $\Delta ^+ = 1.0$ in (c) and (d) (Chen et al. 2021)

It was noted by Chen et al. (2021) that the FDFs extracted directly using the instantaneous snapshots of DNS are random variables containing subgrid statistical information, as also pointed out in Pitsch (2006) and Pope (1985). The instantaneous FDFs present certain levels of randomness due to the unsteady nature of single realisations. This randomness is removed to a good extent if the training data for ML are selected over many DNS realisations at a statistically stationary state. Therefore, following several experimental studies (Wang et al. 2007; Tong 2001; Cai et al. 2009), the instantaneous FDFs obtained from the DNS were conditioned on the resolved scalars, $\widetilde{Z}$ and $\widetilde{c_T}$, and then ensemble-averaged. A quantitative comparison of the conditionally averaged FDFs was then performed. Two variables, $\widetilde{Z}$ and $\widetilde{c_T}$, were considered as the number of available DNS samples was not sufficient to perform a statistically meaningful averaging on the four statistical moments used as ANN inputs. The resolved mixture fraction and progress variable were chosen so that the selected samples were located in the reaction zone ($\widetilde{c_T} \approx 0.5$). Figures 10 and 11 show the conditional FDFs, $\left\langle \widetilde{P}(Z,c_T)\,\big |\,\widetilde{Z},\widetilde{c_T} \right\rangle$, for cases AZ1 and BZ1 respectively and the values of the conditioning variables are given in the figure captions. The DNN accurately reproduces the conditional joint and both marginal FDFs. It also captures the significant changes in the FDF shape with the varying filter size, especially for the progress variable. For case AZ1, both the $\beta$ and copula models overpredict the peak when $\Delta ^+ \le 1$ for both Z and $c_T$ distributions. However, for $\Delta ^+ = 1.5$, the overall prediction is good for $\widetilde{P}(Z)$ and the peak of $\widetilde{P}(c_T)$ is also close to the DNS value although the shape is not captured. Similar results were reported for cases AZ2 also. For case BZ1, the mixture fraction distribution is predicted fairly well by all models for different $\Delta ^+$ values. However, both analytical models fail to predict the bimodal-plateau shape of $\widetilde{P}(c_T)$, which is typical of MILD combustion but seen seldom in conventional flames.

Fig. 10

Case AZ1: comparison of joint and marginal FDFs from DNS and models for a and b $\Delta ^+ = 0.5$, $\widetilde{Z} = 0.007$, $\widetilde{c_T} = 0.45$; c and d $\Delta ^+ = 1$, $\widetilde{Z} = 0.0066$, $\widetilde{c_T} = 0.43$; and e and f $\Delta ^+ = 1.5$, $\widetilde{Z} = 0.0064$, $\widetilde{c_T} = 0.39$ (Chen et al. 2021)

Fig. 11

Case BZ1: comparison of joint and marginal FDFs from DNS and models for a and b $\Delta ^+ = 0.5$, $\widetilde{Z} = 0.00034$, $\widetilde{c_T} = 0.48$; and c and d $\Delta ^+ = 1$, $\widetilde{Z} = 0.0036$, $\widetilde{c_T} = 0.46$ (Chen et al. 2021)

The JSD values were also calculated using Eq. (19), for the DNN and the two analytical models which confirmed the observations made using Figs. 7, 8, 9, 10 and 11. The JSD values provided by the DNN were much lower than those for the $\beta$ and copula models. Improved predictions and lower JSD values were observed for all the models by increasing the filter size and this improvement was particularly significant for the DNN having $J_{90} < 0.05$. The DNN model performed equally well for Z and $c_T$.

To check for generalisation capability, the DNN was further validated using data which were not included in the learning/training step. The training and validation datasets included snapshots taken from $t = \tau _f$ to $1.2\tau _f$, where $\tau _f$ is the flow-through time, but the test data were taken using snapshots taken between $1.4\tau _f$ and $1.5\tau _f$. Substantial variations in the MILD combustion behaviour were observed among these snapshots (see Doan et al. 2018 for details). Hence, a robustly trained DNN is attractive if it can accurately infer a quantity of interest (here, FDF) for scenarios that have not been explicitly seen during the training process. The PDFs of the JSD values for the self-predictions (i.e., predictions performed on the training datasets) and unknown-predictions of the FDF are shown in Fig. 12. A filter size of $\Delta ^+ = 1$ was used for all cases. As indicated in Fig. 12, the DNN provides a similar level of accuracy when unseen test data points are fed to the model. More than $80\%$ of the JSD values are smaller than 0.05. The advantage of using DNN as FDF model is still unaffected since the majority of JSD values were larger than 0.1 for the $\beta$ and copula FDF models. A slightly worse performance was achieved by the DNN when the training data came from cases AZ1 and BZ1, and the validation was done on case AZ2. The JSD results obtained from this new test with the self-predictions for $\Delta ^+ = 0.5$ indicated that the overall performance was still good although the JSD distribution shifted towards higher JSD values. Further improvement on predictions is expected to be achieved if more datasets with different scenarios are included in the training.

Fig. 12

Comparison of Jansen-Shannon divergence for DNN self- and unknown-predictions of FDF of a progress variable and b mixture fraction. The filter size for all cases is $\Delta ^+ = 1.0$ (Chen et al. 2021)

5.1.3 Spray Flame

Yao et al. (2020) visually compared the FDF predicted by ANN and $\beta$-function model with the DNS values for one of the validation cases (CX1). Moreover, the data samples of this case were divided into three different groups characterized by filter size $\Delta _{\textrm{LES}}$, to compute the sensitivity of the trained ANN model to LES grid sizes. The LES cells were selected randomly for a given $\widetilde{\xi }$ ranging from fuel-lean to fuel-rich conditions. The stoichiometric mixture fraction value is $\widetilde{\xi }_{st} = 0.068$.

Figure 13 compares FDF computed using ANN and $\beta$-function with DNS results for two filtered mixture fraction values and three $\Delta _{\textrm{LES}}$. There is no marked differences in the ANN prediction for different $\Delta _{\textrm{LES}}$. The ANN predictions of $\widetilde{P}(\eta )$ are in excellent agreement with the DNS results, including the peak value and its location. The FDF is skewed towards the lean side ($\eta < \xi _{st}$) for $\widetilde{\xi } = 0.05$ whereas it is stretched towards the rich side for $\widetilde{\xi } = 0.10$, and even a bimodal behaviour appears at larger filter sizes. The $\beta$-function does not seem to represent the FDFs well and numerical issues can arise when the mean is close to zero or unity with small SGS variance (Kronenburg et al. 2000).

Fig. 13

Validation of ANN predictions of $\widetilde{P}(\eta )$ with DNS results for different LES grid sizes. The results are shown for $\widetilde{\xi } = 0.05$ (top) and $\widetilde{\xi } = 0.1$ (bottom) (Yao et al. 2020)

5.2 Reaction Rate Predictions

The filtered reaction rate inferred by the ML models were also assessed against DNS results by de Frahan et al. (2019) for their premixed flame and by Chen et al. (2021) for the MILD combustion cases. The ML models used by de Frahan et al. inferred the unconditional filtered reaction rates $\overline{\dot{\omega }}$, which are computed according to Eq. 6, and are shown in Fig. 14. Significant over predictions were observed for the $\beta -\beta$ model. The comparisons of the conditional reaction rates are also shown in Fig. 14.

Fig. 14

Reaction rate $\overline{\dot{\omega }}$ inferred by the ML models trained on $\mathcal {D}^t = \cup _{i=1, 3,5,7,9}D^t_i$. Red squares and solid line are for RF model, green diamonds and dashed line are for DNN, blue circles and dash-dotted line are for CVAE, orange pentagons and short dashed line are for $\beta -\beta$ model, and black solid line is for DNS result (de Frahan et al. 2019)

The reaction rate in the transport equation for the filtered temperature-based progress variable, $\overline{\dot{\omega }}_{c_T}$, can be computed using

$$\begin{aligned} \overline{\dot{\omega }}_{c_T}(\boldsymbol{x},t) = \int _0^1\int _0^1\langle \dot{\omega }_{c_{T}}\rangle {\widetilde{P}}(Z,c_T;\boldsymbol{x},t) \;\;dZ \;\;dc_T, \end{aligned}$$

(20)

where the joint FDF $\widetilde{P}\left( Z,c_T\right)$ is obtained through the ANN in the MILD combustion cases investigated by Chen et al. (2021). The symbol $\langle \dot{\omega }_{c_T}(\boldsymbol{x},t)\rangle = \langle \dot{\omega }_{c_T}(\boldsymbol{x},t)/\rho (\boldsymbol{x},t)|Z, c_T\rangle$ is defined as the doubly conditional mean reaction rate obtained from the DNS data. The instantaneous reaction rate of $c_T$ is defined as $\dot{\omega }_{c_T} = \dot{q}/[c_p(T_b-T_u)]$, with $\dot{q}$ and $c_p$ being the volumetric heat release rate and specific heat capacity of the mixture respectively. The conditional averages are computed using samples collected over the entire computational domain, see Sect. 3.2, and all the snapshots available ($\approx 60$) to achieve good statistical convergence. The authors verified that the doubly conditional mean rates have negligible variations in time and space, supporting the assumption of many turbulent combustion models (viz., flamelets, see Bradley et al. 1990; Fiorina et al. 2003; Pierce and Moin 2004; van Oijen et al. 2016; and conditional moment-based methods, see Klimenko and Bilger 1999; Steiner and Bushe 2001) that the conditional means have small temporal and spatial variations if appropriate conditioning variables are used. The target filtered reaction rate $\overline{\dot{\omega }}_{c_T}^{m-DNS}$ was obtained by computing both the conditional mean reaction rate and the FDF in Eq. 20 directly from the DNS data. The scatter plots of $\overline{\dot{\omega }}_{c_T}^{m-DNS}$ and the reaction rates computed using FDFs obtained through $\beta$, copula and DNN models are presented in Fig. 15 for one of the DNS cases (AZ1) investigated in Chen et al. (2021). The qualitative behaviours and the trends were found to be similar for the other two cases. Although all models give reasonable predictions, the DNN outperforms the analytical models for all filter sizes. Moreover, the DNN predictions generally exhibit good symmetry about the diagonal, indicating a bias towards neither under- nor over-prediction, while the scatters for both the $\beta$ and copula models are asymmetric. As $\Delta ^+$ increases, the DNN prediction improves considerably whereas the performance of the analytical models does not follow this trend with the filter size. For both the $\beta$ and copula models, a trend in the off-diagonal samples moving from under-predictions at small $\Delta ^+$ to over-predictions at larger $\Delta ^+$ can be seen.

Fig. 15

Scatter plot of $\overline{\dot{\omega }}_{c_T}^{m-DNS}$ and $\overline{\dot{\omega }}_{c_T}$ (in kg/m³/s) modelled using different FDF models (denoted using different markers) for case AZ1. The results for different filter sizes are also shown (Chen et al. 2021)

6 Conclusions and Prospects

The application of ML algorithms to infer subgrid-scale filtered density functions (FDFs) in three test cases, i.e., swirling premixed flame, MILD and spray combustion, have been discussed in this chapter. Particularly, the promising results provided by deep neural networks (DNNs) for accurately inferring the FDFs have been shown. DNNs are generally able to capture the complex FDF behaviours and their variations with great accuracy across various combustion scenarios, turbulent and thermochemical conditions, and LES filter sizes. This can be achieved by manipulating the input data (extracted from DNS of these three cases), changing the network architecture, and tuning the network hyperparameters (e.g., learning rate, batch size). It has been shown that if the DNN training dataset is heterogeneous, i.e., it contains different possible outcomes of the quantities of interest, the DNN can handle unknown inputs quite well, suggesting a good model robustness. Thus, the DNN can be applied as a black-box model to other cases. By contrast, analytical models such as the $\beta$-function and copula models in most cases show their limitations quite clearly.

Although the above observations demonstrate the potential of DNN-based FDF modelling in combustion, several challenges remain and require further investigations. Searching for an optimal combination of the DNN hyperparameters can be highly time-consuming and computationally expensive. For example, an exhaustive grid search, looping through all combinations of layers and neurons to find an optimum, is not an easy task and may require cloud computing services (Yao et al. 2020). Moreover, due to the black-box nature of ML models, it is often hard to debug them to a satisfying level or improve them substantially after such a level is reached. This shifts the attention to the preprocessing of training data, which can be a daunting and time-consuming task, as mentioned in Chen et al. (2021). The lack of physical constraints in the training of ML models is yet another issue, and research is ongoing to develop physics-informed ML models that can respect physical laws and increase the interpretability and generalisation capability of ML models.

If DNNs are to replace combustion models, the overhead of retrieving predictions can also be of concern and counterbalance the observed savings in storage requirement. The overhead associated with the use of DNNs is highly machine-dependent and also network size-dependent. A posteriori LES studies need to quantify the computational times required by the DNN inference of FDFs and mean reaction rates. High inference times could hinder the development of in-situ capabilities, where the ML model is trained during the simulation, which can mitigate the risk of extrapolation. The latter can be reduced by also combining ML training and applications with uncertainty quantification or sensitivity analysis approaches that can effectively verify the performance of the ML model, provide a level of confidence in its predictions, guarantee that it does not violate physics laws and promote its more comprehensive application.

Machine Learning has induced notable advancements in combustion science. It has been effectively used for finding hidden patterns under large amounts of data, exploring and visualising high-dimensional input spaces, deriving complex mapping from inputs and outputs, and reducing computational cost and memory occupation (Zhou et al. 2022). However, many challenges and hence research opportunities are left to be addressed, and the development of physics-based ML approaches is just the starting point of a scientific paradigm shift that will bring new insights in combustion science with the help of big data. The combination of ML and combustion will provide solutions to daunting problems and enhance the understanding and deployment of novel combustion processes and technologies, which will shape a cleaner and sustainable future energy arena.