Abstract
The medium- and long-term projections of global climate models show the effects of global warming will be most pronounced in cold climate areas, especially in the high latitudes of the Northern Hemisphere. The consequences could involve a higher probability of global natural disasters and a higher uncertainty as to plant response to climate risk. In this chapter, we describe life under a cold climate, particularly in relation to forest ecosystems, species distribution, and local conditions in the Northern Hemisphere. We analyze recent climate trends and how the ongoing and future climate changes can affect the sensitivity of conifer species, the most common tree form in the boreal regions. We combine experimental data and theoretical process-based simulations involving tree-ring width, tree-ring density, and wood anatomy. This combined approach permits assessing a longer tree-ring record that overlaps with direct instrumental climate observations. The latter are currently experiencing the divergence problem in which tree-ring growth has diverged from the trends of the main climatic drivers. Given that most process-based models are multidimensional, the parameterization described in this chapter is key for obtaining reliable tree growth simulations connected with a site-specific climate, tree species, and the individual trajectory of tree development. Our approach combining experimental and theoretical approaches in xylogenesis is of interest to forest ecologists, physiologists, and wood anatomists.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1 Cold Climates and Terrestrial Ecosystems: Definitions and Examples
The Earth’s climate can be classified on the basis of various criteria, and many classification systems have been proposed, including the aridity index, the Holdridge life zone classification, and the respective climate classifications of Alisov, Berg, Köppen, and Lauer (Critchfield, 1966). Because climate is a major controlling factor of biological ecosystems, climate classification is closely correlated with biome distributions. Of the climate classifications, the Köppen system is one of the most widely applied (Beck et al., 2018). This approach, based on the thresholds and seasonality of monthly surface air temperatures and precipitation, divides the Earth’s climates into 5 main classes and 30 subgroups (i.e., subclusters). The extensive use of Köppen’s system relates to climate being long recognized as a major driver of global vegetation distributions (Beck et al., 2018; Vaganov et al., 2006; Woodward & Williams, 1987; Yang et al., 2017). Therefore, from the Köppen system, we can identify four main groups of boreal/subboreal climates in the Northern Hemisphere: subarctic (boreal), wet continental, hemiboreal, and cold semiarid climate (Fig. 11.1).

Modified from Beck et al. (2018), CC BY license
Main classes of cold climates and the representative Köppen climate classification subtypes: subarctic or boreal (Dfc, Dwc, Dsc, Dfd, Dwd, and Dsd), wet continental (Dsa, Dsb, Dwa, Dwb, Dfa, Dfb), hemiboreal (Dfb, Dsb), and cold semiarid climate (ET).
In the Northern Hemisphere, boreal forests represent 65% of the land area covered by vegetation, and a significant portion of that distribution is dominated by conifer species (about 70% of the forests). Cold climate conditions characterize these ecosystems, and the associated main conifer species are very sensitive to climatic conditions. Therefore, coniferous trees are of particular interest to the scientific community as the study of their climate sensitivity offers insight into plant physiology and ecology, particularly concerning tree-ring growth response to climatic forcing (Briffa et al., 1998; D’Arrigo et al., 2006, 2008; Esper & Frank, 2009; Kirdyanov et al., 2020; Rossi et al., 2013, 2016; Tumajer et al., 2021a; Vaganov et al., 1999, 2011).
2 Recent Trends in Climate and Their Influence on the Seasonal Growth of Trees
The interest in climate change is driven by the extraordinary contemporary changes in the Earth’s climate system. These changes are manifested by the globally increasing surface air temperature, albeit with regional differences (IPCC, 2007, 2014). Increasing concentrations of atmospheric greenhouse gases, in particular CO2, are driving this warming. Two periods in global CO2 concentrations are evident in the twentieth-century record: increasing concentrations at a relatively low rate (pre-1960s) and a heightened annual increase in CO2 concentrations since (IPCC, 2007, 2014; Jones et al., 2001; Thorne et al., 2003). This increase is also reflected by rising mean temperatures, which are most striking in the Northern Hemisphere (IPCC, 2007, 2014; Jones, 2002; Jones et al., 2001; Jones & Briffa, 1992). This recent temperature uptick, relative to the earlier, more stable temperature pattern (known as the hockey stick temperature record), can be attributed to the anthropogenic-related greenhouse gas and land-use changes (IPCC, 2007; Jones et al., 2001).
Medium- and long-term global climate projections show that warming will be most pronounced at higher latitudes, especially in the Northern Hemisphere (IPCC, 2007). In scenario B1 (one of the lower projections of increased greenhouse gases), global temperatures are projected to increase by 0.8 °C in 2020–2029, whereas this increase will be 2 °C in 2090–2099 IPCC, 2007. In colder climate regions, the projected increase for 2020–2029 and 2090–2099 is 1–2.5 °C and 3–4.5 °C, respectively. The most conservative scenario A2 projects a 4–6.5 °C increase at high latitudes by 2090–2099.
These projections of warming lead to numerous questions. How will the current and projected climate change affect forest ecosystems, particularly those in cold climates? What are the mechanisms of such impacts? Have similar changes occurred in the past, and how did they affect tree-ring growth? How might such changes affect the development of forest ecosystems in the future?
The answers to these questions are complex and ambiguous and require undertaking the following dendroecological and dendrophysiological tasks:
-
identify meaningful statistical relationships between climate factors and interannual and intra-annual tree-ring growth (Briffa et al., 2002; Fritts, 1976; Rossi et al., 2008a, 2008b, 2013);
-
identify the functional mechanisms of climate and woody plant growth interactions and then develop adequate process-based tree growth models (Guiot et al., 2014; Vaganov et al., 1999, 2006);
-
forecast these changes taking into account anthropogenic influences and analyze the effect of these changes on forest ecosystems (Briffa et al., 2008; Charney et al., 2016; He et al., 2018a).
The main source of information required to accomplish these tasks is derived from tree rings, which record information related to various environmental factors, including climate (Anchukaitis et al., 2012; Briffa et al., 2002; Vaganov et al., 1999, 2006). Most tree species in cold regions are extremely sensitive to climate (Kirdyanov et al., 2003; Rossi et al., 2016; Shishov et al., 2016), and climatic factors account for 40–70% of the variability observed in the anatomical traits of tree rings (Vaganov et al., 2006). The successful resolution of these tasks requires using different (preferably independent) tree-ring characteristics, each recording specific (and different) information about tree growth patterns and the environmental factors affecting these patterns (Arzac et al., 2019; Gennaretti et al., 2017a; Puchi et al., 2019). This research commonly analyzes tree growth based on tree-ring width (Briffa et al., 2002; Cook & Kairiukstis, 1990; Fritts, 1976). Complementary tree-ring traits are also highly useful when analyzing the seasonal growth patterns of boreal trees. Vaganov et al., (1999, 2006, 2011) found a strong positive correlation between the temperature at different periods of the growing season—in particular at the start of the growing season—and cell size, cell wall thickness, and maximum density in the rings of larch collected from northern Eurasia. The relationship between coniferous tree-ring structural parameters and climate has also been analyzed for various regions of the globe. The use of complementary independent tree-ring traits—derived from those already being used via mathematical and statistical transformations—leads to novel information about the tree environment (Briffa et al., 2008).
Dendroclimatic analyses, using temperature-sensitive tree-ring chronologies obtained from a network of dendroclimatic monitoring stations distributed across the high latitudes of northern Eurasia and North America, indicate a heterogeneous response of woody plant growth to temperature increases (Briffa et al., 1998; D’Arrigo et al., 2008). Spatiotemporal analyses of long tree-ring chronologies from the mid to high latitudes of the Northern Hemisphere have revealed a distortion in the relationship between positive temperature trends and observed tree-ring growth after the 1960s in some regions where temperature is the principal growth-limiting factor (Briffa et al., 1998; Büntgen et al., 2021; D’Arrigo et al., 2006, 2008; Driscoll et al., 2005; Esper & Frank, 2009; Kirdyanov et al., 2020). This distortion, known as the divergence problem, reflects a change in tree growth with warmer summer temperatures.
Understanding and resolving this problem is critical for developing adequate statistical models for reconstructing climatic variables from dendrochronological data (Briffa et al., 1998).
A possible cause of this divergence may be the temperature-dependent drought stress of woody plants, which is particularly pronounced for fast-growing trees (Barber et al., 2000). This conclusion derives from a comparative analysis of dendrochronological data with a climate index representing a linear combination of temperature and precipitation (Barber et al., 2000). Another hypothesis for the divergence problem is a decrease in tree-ring growth when the temperature reaches a physiological threshold, thereby limiting growth (Hoch & Körner, 2003; Wilmking et al., 2004). Moreover, the current warming in the Northern Hemisphere is unprecedented over the last 2000 years (IPCC, 2007, 2014). Combining data from measurements of tree-ring width and maximum tree-ring density with simulations using the process-based tree-ring growth Vaganov-Shashkin model (VS-model) (Vaganov et al., 2006) has demonstrated a relationship between the decline in the sensitivity of trees and a positive trend in winter precipitation in subarctic Siberia between 1960 and 1995 (Vaganov et al., 1999). This observation led to the hypothesis of a shift in the start of the tree growth season to later dates because of a delayed melting of snow cover and, consequently, a decreased sensitivity of the trees to temperature change (Vaganov et al., 1999). A shift in temperature as a factor limiting tree-ring growth has also been observed in Alaska (Lloyd & Fastie, 2002). Finally, a most recent hypothesis proposes that the significant discrepancy between the annual growth of temperature-sensitive woody plants and summer temperature can be explained by the nonlinear dynamics of a low-frequency component of incoming solar radiation, which is closely correlated with the concentration of aerosol elements in the atmosphere at high latitudes in the Northern Hemisphere (Fig. 11.2; Büntgen et al., 2021; Kirdyanov et al., 2020).

Reproduced with permission from John Wiley and Sons from Kirdyanov et al. (2020)
Measured (green) and simulated boreal tree-ring width (TRW) indices a without (red line with smoothing) and b with (black line with smoothing) dimming that includes the low-frequency component of incoming solar radiation in the process-based forward model (VS-lite).
Most of the abovementioned methods for estimating trends of a nonclimatic nature share a distortion (over- or underestimation) of the true index values of the dendrochronological series under selected conditions (Melvin, 2004). This distortion is pronounced at the ends of time series (Melvin, 2004) and is characteristic of a power law, polynomial approximations of degree P (P ≤ 5) (Cook & Kairiukstis, 1990), as well as the commonly used low-frequency cubic spline (Melvin, 2004). Such inconsistencies can significantly alter both the statistical response function of woody plants to principal climatic factors (Melvin, 2004) and likely the tree-ring simulations based on various process-based tree-ring models (Guiot et al., 2014). Another reason for the divergence may relate to a sampling bias (Brienen et al., 2012; Duchesne et al., 2019).
However, the causes may be much more complex, combining the interaction of limiting and accelerating growth factors. The large number of noncontradictory hypothesesFootnote 1 relating to the same problem indicates that all information contained in the characteristics of the tree ring cannot be extracted correctly on the basis of mathematical and statistical approaches used in dendrochronology, dendrophysiology, and wood anatomy. Therefore, there is a need to develop new theoretical tools (models), tested with direct high-quality measurements and experimental analyses, that can adequately assess the influence of external factors on the growth of woody plants.
3 Experimental Analysis of Tree-Ring Growth in Cold Climates
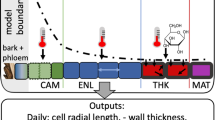
Tree growth and survival are severely affected by climate, having significant consequences on their contribution to forest dynamics and carbon fluxes (Frank et al., 2015). Tree-ring structure depends on a complex cell formation process following successive phases of development (Rathgeber et al., 2016), controlled by external and internal factors occurring during the growing season (Dengler, 2001). Thus, in conifers, different cell development phases lead to intraseasonal changes in the anatomical characteristics of tracheids during the growing season, from wide and thin-walled earlywood cells to narrow and thick-walled latewood cells (Fig. 11.3). Moreover, each type of cell has different functions. Thus, earlywood cells ensure efficient sap transport, whereas latewood cells favor mechanical stability (Björklund et al., 2017). The ratio between earlywood and latewood is critical for maintaining the balance between the structure and function of the xylem and plays a crucial role in tree water–carbon interactions (Domec & Gartner, 2002).

Reproduced from Arzac et al. (2018a) with permission from Elsevier
Diagram of a Pinus sylvestris xylem cross section indicating parameters including the cell diameter in the earlywood (DEW), the transition zone (DTW), latewood (DLW), maximum cell wall thickness (CWTm), and tracheidograms of the cell diameter (solid black line) and cell wall thickness (dashed black line). The limits of the 2010 tree ring are identified (between the vertical dashed blue lines) as are the earlywood, transition wood, and latewood zones (vertical dashed black lines).
The intraseasonal change in xylem morphology might be driven by the need for structural reinforcement by latewood (Sperry et al., 2006), photoperiod (Gyllenstrand et al., 2007), or changes in water availability (Olano et al., 2012) throughout the growing season. In addition, the low availability of carbohydrates in the cambium at the beginning of the growing season allows a longer period for cell enlargement and limited wall deposition, whereas at the end of the growing season, a higher availability results in cells having a smaller lumen and wider walls (Cartenì et al., 2018). In temperature-sensitive regions, temperature can control cell production and radial cell expansion (Vaganov et al., 1999). Moreover, secondary wall thickening and the formation of latewood cells are also driven by temperature, as reflected by the strong correlation between maximum latewood density and summer temperature (Vaganov et al., 1999).
Because different cells are formed during distinct periods over the growing season, they encode the environmental information during their formation on a weekly to a seasonal basis (Bryukhanova et al., 2013; Kirdyanov et al., 2003; Vaganov et al., 1999). Thus, tree-ring structure depends highly on the timing and magnitude of the climatic events and conditions occurring during the cell developmental phases (Castagneri et al., 2017; Rathgeber, 2017), thereby being relevant when extracting the environmental information encoded in the tree rings. A full tree ring encodes information at an annual resolution (showing interannual variability from ring to ring). Earlywood and latewood parts of a tree ring encode the seasonal or intra-annual variability, and xylem cell traits encode environmental information at a weekly resolution. Moreover, xylem cell traits, such as cell size, wall thickness, and the wall-to-lumen ratio, can present different detailed seasonal information depending on their position within the ring and be used to identify the principal factors controlling tree growth or to reconstruct past climatic conditions (Fonti & Jansen, 2012; Vaganov, 1990). Understanding the specific climatic factors affecting tree-ring formation is essential to assess the impact of changing climatic seasonality on tree-ring structure and functioning.
Ongoing climate change will likely have diverse impacts on the various tree-ring sectors and functions depending on the seasonality of the changes. For example, when trees experience drought conditions, they reduce transpiration to protect their tissues from extensive water loss and avoid hydraulic failure (Irvine et al., 1998). However, these physiological responses affect the capacity of the tree to photoassimilate atmospheric carbon and maintain the turgor pressure of the growing cell, which modifies the amount, size, structure (Fonti et al., 2010; Steppe et al., 2015), and functioning of a forming tree ring; this response represents an important legacy for future tree performance, e.g., biomass production and resilience capacity (Anderegg et al., 2015). Moreover, changes in climate conditions may also influence the phenological patterns of tree growth via a lengthening or shortening of the growing season, with important consequences for forest productivity (Arzac et al., 2021a).
In cold regions, the tree growing season spans late spring to late summer, whereas trees remain dormant in autumn and winter. The onset of tree growth requires a minimum temperature threshold, which generally occurs somewhere between April and June, depending on the forest’s location and sufficient soil moisture to maintain the process over the growing season (Kramer, 1964). Therefore, the temperature before xylogenesis (early spring) would be expected to promote an earlier onset of growth and larger growth rings. Low temperatures are also linked to the production of smaller cells (Zhirnova et al., 2020) and a limited carbon assimilation, resulting in important ecological consequences globally. Warming trends affect the stability and diversity of global forest ecosystems at various spatiotemporal scales. However, temperature is not the only factor controlling tree growth in cold environments. Although late spring and early summer temperatures are considered as the main drivers of boreal forest growth, soil moisture availability is likely to become a critical factor even in the coldest environments (Arzac et al., 2018b, 2019; Tabakova et al., 2020).
Reduced summer precipitation and increased temperatures will favor increased transpiration (Babushkina et al., 2015); this scenario will reduce turgor pressure, which eventually induces the formation of smaller and thicker latewood-like cells. Climatic factors constraining tree growth in temperate and boreal environments shift along a gradient, passing from water shortages, limiting growth at lower altitudes/latitudes, to colder temperatures limiting growth at higher latitudes (Babst et al., 2013; Hellmann et al., 2016). Therefore, temperature is a main limiting factor controlling tree growth in cold environments (Vaganov et al., 2006). Studies carried out on contrasting environmental conditions, e.g., high-elevation sites in the Mediterranean region and permafrost sites in northern Siberia, have shown the relevant effect of water availability later in the growing season (Arzac et al., 2016, 2019).
Various techniques can be applied (von Arx et al., 2016) to evaluate the effect of climate on tree growth and tree-ring structure. These approaches can investigate at the cellular to tree-ring level and include the in situ monitoring of intra-annual dynamics of wood formation using dendrometers. Measuring ring width and earlywood and latewood width require the xylem structure in the wood sample to be clearly visible. The widths of the tree ring, earlywood, and latewood are then usually measured by direct observation of the wood samples by using specialized tree-ring measurement systems, e.g., LinTab and Velmex, or by measuring digitized wood samples, e.g., CooRecorder/CDendro, and WinDENDRO. However, if the study aims to obtain more detailed information on xylem cell traits, quantitative wood anatomical (QWA) methods are applied (von Arx et al., 2016). QWA involves the production and analysis of thin histological preparations of wooden material, thereby allowing the study of many parameters in the xylem and also cambial activity. QWA methods follow a series of successive steps, including (1) microsection preparation (sectioning, staining, fixation); (2) the digitizing of anatomical sections, e.g., using a slide scanner or a camera mounted on an optical microscope; and (3) the measurements of the cell structures by specialized software, e.g., ROXAS, WinCELL, and AutoCellRow (Dyachuk et al., 2020; von Arx et al., 2016). Finally, in the case of in situ monitoring of the intra-annual dynamics of wood formation, dendrometers provide automatic measurements of changes in stem diameter at various temporal scales.
Typically, dendrochronological studies assess the effect of climate conditions on tree growth by correlating tree-ring width indices (or other parameters) with meteorological data, e.g., temperature, precipitation, cloudiness, soil moisture, and/or wind, at a daily or monthly resolution. Such analyses determine the main environmental factors—and the role of the magnitude and timing of these factors—controlling tree growth and structure. Although the first steps to unveil climate effects are relatively simple, e.g., response functions, the subsequent statistical analyses are now quite sophisticated and can include a large number of diverse parameters to obtain a more comprehensive understanding of the mechanisms involved in tree-ring formation. For example, general additive mixed models identify differences between the various tree-ring parameters as a function of several variables, including site location, tree age, and target year (Zuur et al., 2009). Because this type of statistical model provides a broader view of the parameters controlling tree growth, they are increasingly applied to dendrochronological studies. In addition, modeling tree-ring growth as a theoretical approach is commonly used to simulate cell growth rates, determine ring structure and cell phenology, evaluate the effect of climatic limiting factors, and forecast tree growth under future climate scenarios.
Significant warming trends affect the phenology and physiology of trees and the geographical distribution of different types of boreal forests (Barber et al., 2000; Cuny et al., 2015; Menzel et al., 2006). Warmer temperatures also likely trigger an earlier onset of growth because of more favorable conditions in usually cold climate regions (He et al., 2018a; Menzel et al., 2006; Yang et al., 2017). These changes are reflected in tree rings and xylem structure; for example, increased tree radial growth of Pinus sylvestris L. has been observed in stands from western to eastern Siberia (Tabakova et al., 2020). Arzac et al. (2019) obtained similar results in central Yakutia, in which the ring width and latewood width of Larix cajanderi Mayr and P. sylvestris have increased over the recent decades in response to warmer temperatures. Nevertheless, the climate sensitivity of P. sylvestris could decrease because of changes in climate seasonality; thus, in southern Siberia, current climate seasonality changes positively impact both the hydraulic efficiency (by increasing the diameter of the earlywood cells) and the latewood width of wood produced (Arzac et al., 2018a).
In terms of xylem structure, seasonal variations in climate have clearly affected xylem cell differentiation, and therefore, total ring structure (Cuny & Rathgeber, 2016). Thus, favorable temperatures at the beginning of the growing season may contribute to the extension of cambial activity during the formation of earlywood (Rossi et al., 2013), whereas low temperatures at the end of the growing season constrain cell wall deposition during the formation of latewood (Cuny & Rathgeber, 2016; Zhirnova et al., 2020). Beyond the critical role of temperature for tree growth, precipitation signals are very strong at critical tree growth stages for both earlywood and latewood (Babushkina et al., 2018).
4 Tree-Ring Process-Based Models as Tools for Analyzing Climate Influence on Long-Term Tree-Ring Growth
One of the main objectives of dendrochronology and wood anatomy is the study of the year-to-year variability in the qualitative and quantitative characteristics of tree-ring growth and the identification of environmental factors that determine this variability over the long term, i.e., up to several decades, throughout the cold climate boreal zone (Vaganov et al., 2006, 2011). Seasonal direct observations of the xylogenesis of conifers and the appropriate statistical analysis are unique sources of information for understanding the processes occurring during the formation of tree rings (Vaganov et al., 2006). The direct and experimental observations of tree-ring formation contribute significantly to a deeper understanding of tree growth response to environmental conditions (Rossi et al., 2008a, 2008b, 2013). However, this kind of analysis often requires weekly monitoring, sampling, and measuring; this requirement is extremely labor intensive and generally unfeasible over vast territories. Without belittling the experimental and theoretical significance of direct observations of the xylogenesis of conifers, unfortunately such data in most cases can cover only a few seasons (2–4 years), with rare exceptions. Even 15-year xylogenesis observations (Buttò et al., 2020) do not ensure that, during the analysis, a long-term phenomenon, e.g., the divergence problem, does not occur (Kirdyanov et al., 2020). Moreover, the network of xylogenesis observations is significantly inferior to the spatial network of dendrochronological data, which covers the main forest biomes of the boreal zone.
Thus, estimating the differentiation time of cambium and xylem by process-based modeling is a possible tool that adequately extrapolates local xylogenesis analyses over widespread territories (Guiot et al., 2014). Given the significant increase in the quantity of tree-ring (including anatomical wood) data, there is an ongoing need to develop methods and software able to automatically identify and process all forms of biological information obtained from tree rings. Performing an adequate simulation of tree-ring cell structure makes it possible to separate the climate-driven component from other external (e.g., forest fires, insect outbreaks, snow avalanches) and internal (e.g., seasonal hormone variability, age-dependent trends) factors in tree-ring growth and understand the principal processes during the formation of tree rings over the long term (Shishov et al., 2021; Vaganov et al., 2006).
Process-based models describe tree growth on the basis of climate forcing and local nonclimatic environments, such as tree competition, insect outbreaks, and fires (Guiot et al., 2014). These multidimensional models can describe nonlinear interactions between tree growth and environments. In most processed-based tree growth models, climate variables are considered the primary global drivers of spatiotemporal growth variability (Guiot et al., 2014; Misson, 2004; Ogée et al., 2009; Peters et al., 2021; Vaganov et al., 2006). These models are useful for understanding the growth processes under investigation and finding new patterns reflecting the interaction of environmental factors with biological processes occurring within woody plants.
For example, the model MAIDEN (Modeling and Analysis In DENdroecology) and its modification MAIDENiso simulate annual tree-ring increments, carbon and oxygen isotope compositions based on daily CO2 atmospheric concentrations, precipitation, and minimum and maximum air temperatures. These models evaluate carbon assimilation and allocation within various global forest stands, including those in cold climate regions (Gennaretti et al., 2017a; Lavergne et al., 2017; Rezsöhazy et al., 2020). Two modifications exist for MAIDEN: one developed for Mediterranean forests (Gea-Izquierdo et al., 2015) and one for boreal tree species (Gennaretti et al., 2017a, 2017b). This model can estimate daily photosynthesis and allocate the daily available carbon and stored nonstructural carbohydrates to different pools, i.e., leaves, roots, stem.
The stem growth and wood formation model of Drew and Downes (2015) is a potential candidate for use in cold climate conditions. The model uses CABALA-estimated daily variables—daily minimum and maximum leaf water potential, carbohydrate allocated to stem, stand density, tree height, and crown length (Battaglia et al., 2004)—as inputs to predict tracheid size, cell wall thickness, and microfiber angles in a cell on the basis of cambial activity and carbohydrate balance (Drew & Downes, 2015). Growth is limited by the daily osmotic potential of cell growth; this parameter links cell wall turgor, water, and carbohydrate balance. From these cell simulations, the model can estimate wood density. The model distinguishes between radial and longitudinal cell expansion.
One of the most modern and comprehensive models is the turgor-driven growth model of Peters et al. (2021), which estimates the growth dynamics of most tree tissues. The model has already been tested successfully along an elevation gradient involving different climate conditions. In this model, tissue development is limited by water balance and depends on cell growth. In turn, cell growth is limited by the water and temperature balance and depends on the turgor of cell walls. The variables required as inputs to the model are tree-specific allometric characteristics, hourly tree physiological measurements, and micrometeorological data and parameters. Incorporating these variables disentangles reversible, i.e., daily shrinkage and swelling as a result of water transport, from irreversible diameter growth (Peters et al., 2021).
The Vaganov-Shashkin tree-ring simulation model (VS-model) is one of the most applied model. This model is often used because of the minimal requirements for inputs and has already been used in various environments from warm semiarid and temperate conditions (Anchukaitis et al., 2006; Evans et al., 2006; Jevšenak et al., 2021; Touchan et al., 2012; Tumajer et al., 2021a, 2021b) to cold climates (Belousova et al., 2021; Buttò et al., 2020; He et al., 2017, 2018b; Popkova et al., 2018; Shishov et al., 2016; Tychkov et al., 2019; Vaganov & Shashkin, 2000; Vaganov et al., 2006, 2011; Yang et al., 2017). As a significant simplification of the VS-model, the VS-lite version accepts monthly temperature and precipitation data and offers the best choice for estimating a nonlinear tree-ring response to changing climate on a global scale (Tolwinski-Ward et al., 2011, 2013). However, the VS-lite is not formally a process-based model; it can be considered as a mathematical operator having some biological basis that effectively estimates a monthly-scale nonlinear relationship between climatic and dendrochronological data sets (Guiot et al., 2014).
Below we consider some of the issues concerning the tree-ring growth simulations in a cold climate that are common to most process-based models, using the VS-model, which we use as an example.
The VS-model is based on several assumptions (Vaganov et al., 2006):
The main target of external (climatic) influence is the cambial zone, the zone of actively dividing cells. The external influence affects the linear growth rate of cambial cells (and the cell cycle).
The main external factors affecting the growth rate of cambial cells are daily average temperature, day length (closely correlated with solar irradiation), and soil moisture. Day length is determined by latitude, solar declination, and day of the year.
The tree-ring growth rate is positively correlated with the number of new cells in the enlargement zone and their sizes. Therefore, the growth rate variations predetermine mainly the anatomical characteristics of the tracheids being formed, i.e., radial diameter. The principle of limiting factors—Liebig’s principle; Ebelhar et al. (2008)—is used to estimate the growth rate.
The model simulates only climatically induced tree-ring width and structural variations. Therefore, the model can insulate climatic forcing from other local environmental effects, i.e., fires, insect outbreaks.
The basic algorithm of the VS-model (Fig. 11.4) involves the input of daily climatic data (temperature, precipitation, and solar irradiation), the calculation of integral tree-ring growth rate G from the climatic data, and estimation of cell production (number of cells formed during the growing season) and their radial sizes by the integral (environmental) tree-ring growth rate G.
The principal factors affecting the growth rate, i.e., air temperature, soil moisture, and day length, are used as inputs to the model. The cell production and their radial sizes are estimated on the basis of the integral (or environmental; see Anchukaitis et al. 2020) growth rate values at each time step (day of the year) t, which are calculated using the principle of limiting factors:
where \(G\left(t\right)\) is the integral growth rate, \({g}_{I}\left(t\right),{g}_{T}\left(t\right),{g}_{W}\left(t\right)\) are the partial growth rates dependent on day length (solar irradiance) I, temperature T, and soil water content W, respectively.
The model estimates the daily water balance on the basis of the accumulated precipitation in the soil (with or without snowmelt), transpiration (temperature-dependent), and runoff (Thornthwaite & Mather, 1955). Day length (or incoming sunlight) is determined by the model according to the latitude at which the meteorological station or dendrochronological site is located (Vaganov et al., 2006). The number of cells formed per growing season and their sizes are then calculated on the basis of the integral (environmental) growth rate (Anchukaitis et al., 2020; Belousova et al., 2021; Shishov et al., 2021).
5 Theoretical Interactions in the Climate–Tree Growth System in Cold Climates
The VS-model was developed to estimate the climate signal (component) in tree rings (Vaganov et al., 2006). Generally, trees growing in extreme conditions are very sensitive to climate; thus, climate can explain up to 60–65% of annual tree-ring variability measured over decades. The percentage of explained variance can vary depending on location (Fig. 11.5). The distance between the southern MIN and northern PlatPO Siberian sites is about 2,200 km; the explained variance varies from 36 to 50%, respectively. The percentage of explained variance also depends on tree species and microclimates (Buttò et al., 2020; Popkova et al., 2020; Yang et al., 2017).

Reprinted by permission from Springer Nature from Tychkov et al. (2019)
The observed tree-ring chronology (solid black line) and simulated chronology (solid gray line) a for 1936–2009 at the MIN site (southern forest–steppe of central Siberia) and b for 1950–2009 at the PlatPO site (taiga of central Siberia). Average index for tree-ring growth and standard deviation are included (dashed horizontal lines).
Another important specificity of cold climates is tree phenology, particularly cambium activity, which can be estimated effectively over the long-term by the VS-model (He et al., 2018b; Jevšenak et al., 2021; Tumajer et al., 2021a; Yang et al., 2017). Relative to more temperate conditions, the period of ring formation is shorter in cold climates; the cambium of conifer species is active between 180 and 240 days per year in semiarid Mediterranean Tunisia (Touchan et al., 2012) or Spain (Tumajer et al., 2021b) and just during 50–65 days per year in the extreme cold forest–tundra region of northern Yakutia, Russia (unpublished data). In both cases, ring cells pass through all stages of xylogenesis.
Moreover, the VS-model simulation can also reveal long-term trends in cambium phenology. For example, the period of cambium activity has become longer because of climate warming in the cold semiarid part of the Tibetan Plateau (Yang et al., 2017) and, as a result, significant negative (positive) shifts have been observed at the onset (end) of the growing season (Fig. 11.6).

Reproduced with permission from Yang et al. (2017)
Cambium phenology in a cold semiarid area of the Tibetan Plateau, northwestern China; a the average onset of the growing season (SoS) and b end of the growing season (EoS) for 1960–2014, as obtained using the VS-model. Dashed lines indicate linear trends for 1960–2014 (black line), 1982–2014 (red line), and 1960–1981 (blue line). Error bars indicate the standard deviation among the 20 composite sites. Significant (P < 0.01) advancing (delaying) trends in SoS (EoS) were detected for the periods 1960–2014 and 1982–2014. During 1960–1981, however, a nonsignificant (P > 0.05) trend was identified.
Although most tree species are very sensitive to seasonal temperature variations in cold climates (Cook & Kairiukstis, 1990), this sensitivity can change over the growing season, i.e., two conifer species located in the same cold habitat can vary in their respective response to a similar temperature and moisture regime (Fig. 11.7). Spruce growth is always limited by temperature (Fig. 11.7b); however, soil moisture becomes a critical component controlling tree-ring growth in the middle of the growing season for larch, even in permafrost conditions (Fig. 11.7a).

Reprinted from Shishov et al. (2016) with permission from Elsevier
Typical patterns of partial growth rates dependent on solar irradiance GrE(t) (black dotted line), soil moisture GrW(t) (dashed gray line), and temperature GrT(t) (solid black line) between 1950 and 2009 for two northern Siberia taiga sites with a Siberian larch (Larix gmelinii (Rupr.)) and b Siberian spruce (Picea obovata Ledeb.) trees. The growth rates are fitted by a negative exponentially weighted smoothing. The lowest partial growth rate represents the most limiting factor for each day of the year.
Finally, because of the high percentage of explained variance in tree rings in cold climates (Briffa, 2000; Briffa et al., 1998; Vaganov et al., 1999) and the climate-oriented outputs of the VS-model (Anchukaitis et al., 2020; Vaganov et al., 2006), it is possible to effectively reconstruct the long-term seasonal cambial kinetics and their timing (Popkova et al., 2018; Shishov et al., 2021). This is also possible for temperate habitats, where trees are less sensitive to thermal conditions (Tumajer et al., 2021a). Generally, cold climate trees show less seasonal cell production than trees in temperate climate environments (Vaganov et al., 2006).
6 Model Parameterization and Calibration Features
The main problem for most process-based models is the large number of model parameters that must be reasonably re-estimated for each habitat. Therefore, an adequate parameterization of the models is needed using appropriate experimental (ecobiological) and theoretical (mathematical) approaches. First, the obtained values of the model parameters should be reasonably interpreted by the nature of processes involved in the model (Shishov et al., 2016; Tychkov et al., 2019) and direct field observations (Buttò et al., 2020; Jevšenak et al., 2021; Tumajer et al., 2021a, 2021b). Second, even the most sophisticated mathematical optimizations, i.e., Bayesian approaches (Anchukaitis et al., 2020), or differential evolution (Kirdyanov et al., 2020) in a multidimensional parameter space cannot ensure that mathematically optimal parameters providing the best fit between the observed and simulated tree-ring growth are not artificial. To resolve these issues, we suggest using a two-step parameterization procedure: (1) visual (manual or semiautomatic) parameterization (Shishov et al., 2016) to obtain reasonable initial values of the model parameters that are ecobiologically interpreted; and (2) mathematical multidimensional optimization limited by the neighborhood of the obtained parameter values.
The visual parameterization approach described here could be applied to most process-based models. The new version of the model is VS-oscilloscope-online (http://vs-web.sfu-kras.ru:8080/), analogous in nature to a physical oscilloscope (Fig. 11.8). The VS-oscilloscope models (visualizes) the nonlinear tree-ring growth response to climate variability while assessing the contribution of each climatic variable (temperature or soil moisture) to the daily variability of seasonal dynamics of tree-ring formation (Tumajer et al., 2021a).
VS-oscilloscope-online is a web-graphical interface software based on Lazarus code (Shishov et al., 2016; Tychkov et al., 2019) with the potential use of the MATLAB version of the VS-model (Anchukaitis et al., 2020). The web-designed tree-ring simulation system can be considered as a cross-platform application; therefore, the VS-model can be used on computers regardless of the installed operating system (e.g., Windows, Linux, Mac iOS).
The basic idea of the visual parameterization (VS-oscilloscope) is to select the optimal parameter values to achieve a maximum correlation and synchronicity from a visual assessment of the synchrony between the simulated growth curve and the actual tree-ring chronology (Shishov et al., 2016).
The values of all parameters are fixed (or held constant), and only one parameter is modified, e.g., Tmin, the minimum temperature for the onset of tree-ring formation or first cambial cell division (Vaganov et al., 2006). Changing the position of the bottom Tmin to the right (left) increases (decreases) the value of this parameter in degrees (°C), which is then used to estimate the growth rate. Changing the position of the bottom for the analyzed parameter leads to a recalculation of the simulated growth curve, accounting for the parameter’s new value (Fig. 11.8b, right panel).
The VS-oscilloscope’s virtual display (Fig. 11.8b, right panel) shows the actual tree-ring chronology downloaded from a *.crn file (red line), the new simulated growth curve (blue), and the previous modeled curve (green). Iterations with new parameter values are performed until the maximum correlation between the growth curve and tree-ring chronology is obtained. The procedure is repeated for all parameters of the VS-model (Shishov et al., 2016).
The VS-oscilloscope control unit interface contains two tabs for inputting raw data (Fig. 11.8a) and adjusting growth parameter values (Fig. 11.8b). Raw data containing daily values of temperature and cumulative precipitation and values of initial tree-ring chronology, latitude, longitude, and tree species are loaded using a special ASCII format. The VS-oscilloscope-online operates with 19 parameters associated with the local conditions of the woody plant growth. According to the VS-model algorithm (Fig. 11.4), the parameters can be divided into two groups: those essential for calculating the integral growth rate of tree rings (19 parameters) and those necessary to determine cambial activity (17 parameters). The values of 19 parameters can be changed manually in the Model Parameterization panel (Fig. 11.8b, left panel).
If the user has questions while using the VS-oscilloscope-online, they can use the web link Click Me to access a ZIP archive of an input data example and user guide (Fig. 11.8a). When the application has finished, the best model obtained by the optimal parameter settings is saved by the system and downloaded in *.csv, *.dat, or *.xlsx format as a ZIP archive (Fig. 11.8b, use the Best Result and Download Files links).
When the calculations are completed, several files are created: (1) a chronology file (e.g., crns.*), which contains the simulated growth index (Model), actual tree-ring chronologies for the study area (Crn), Z-scores of simulated (NMOD) and actual (NCRN) chronologies, the number of days when the minimum temperature for growth start is reached (Tmin), the day of the year when a growing season starts (SoS) and ends (EoS) (2) a growth rate file (e.g., rates.*), having a table containing dates of the year (Date), days of the year (Day), an integral growth rate (Gr, relative units), a partial growth rate (GrW, relative units) dependent on soil moisture, a partial growth rate (GrT, relative units) dependent on temperature, a partial growth rate (GrW, relative units) dependent on soil moisture, and a partial growth rate (GrE, relative units) dependent on solar irradiance, daily temperature (Tem, °C), daily precipitation (Prec, mm), estimated soil moisture Sm (v/v), and daily transpiration (Tr, mm).
These output data can be used to analyze long-term trends in cambium phenology (Yang et al., 2017), seasonal tree-ring growth patterns dependent on climatic variability (Buttò et al., 2020; He et al., 2017; Jevšenak et al., 2021; Tychkov et al., 2019), and seasonal cambium kinetics due to the cambium block of the VS-model (Anchukaitis et al., 2020; Belousova et al., 2021; Shishov et al., 2021; Tumajer et al., 2021a).
This parameterization procedure allows us to assess the impact of each individual climatic factor (temperature, soil moisture, and solar irradiance) on tree-ring growth and interactively control the intervals of valid model parameter values on the basis of available direct observations of the physical processes described by the growth simulation model (Vaganov et al., 2006). Such approaches provide a better understanding of the growth process of tree rings and greatly facilitate working with the multidimensional VS-model.
The main goal of any parameterization is to obtain the best fit of the simulated values to the observed direct measurements by selecting certain parameter values of the model. At the same time, in the context of tree-ring modeling, the selected parameters should not conflict with the biological principles of growth and field parameters obtained for the different environmental conditions of the studied forest stands (Buttò et al., 2020; Tumajer et al., 2021b; Tychkov et al., 2019). Solving this problem by the direct mathematical optimization of multidimensional parameter space is problematic, given the high probability of attaining a local optimum that generates artificial outcomes (Evans et al., 2006; Tolwinski-Ward et al., 2013).
Along with the Bayesian approach (Anchukaitis et al., 2020; Tolwinski-Ward et al., 2013), the differential evolution (DE) approach is a good candidate and is one of the fastest optimization methods (Price et al., 2005). The basic concept of DE is to obtain optimal values for multidimensional, real-valued functions of parameters on the basis of genetic mutations of a specially generated parameter set (see Storn & Price, 1997 for more details). Moreover, DE does not use the gradient of the problem being optimized; thus, DE does not require the optimization problem to be differentiable, as required by classic optimization methods such as gradient descent and quasi-Newton methods. Thus, DE can be applied to a wide suite of process-based tree-ring models. This optimization is already incorporated into the VS-lite and VS-models (Kirdyanov et al., 2020; Tumajer et al., 2021b).
Following the above-described two-step parameterization procedure will significantly limit the risk of obtaining inadequate model parameters; therefore, theoretical (simulated) tree-ring growth patterns under climatic forcing will be more reliable.
7 Conclusions
In the last decades, the Earth’s climate, particularly in the higher latitudes of the Northern Hemisphere, has changed markedly as increases in average annual temperatures are melting glaciers and raising global sea levels (IPCC, 2007, 2014). In addition to warming, there is also an imbalance in natural systems, leading to changes in rainfall patterns, temperature anomalies, and an increased frequency of extreme events, such as hurricanes, floods, and droughts (Anderegg et al., 2015; IPCC, 2007, 2014). According to the medium- and long-term projections of global climate models, the effects of global warming will be most pronounced in areas characterized by cold climates, especially in the high latitudes of the Northern Hemisphere (IPCC, 2007, 2014). The consequences of this warming include a higher probability of global natural disasters, greater uncertainty in plant response to climate (IPCC, 2007, 2014), and decreased diversity in many forest ecosystems (Anderegg et al., 2015). The experimental and theoretical study of tree rings and their formation is a key source of information for revealing nonlinear relationships between climatic factors and seasonal tree-ring growth. These studies contribute to a better understanding of forest ecosystem processes and how they are affected by global climate change (Vaganov et al., 2006, 2011). Moreover, a greater understanding of the tree-ring growth processes is essential when developing adequate models for reconstructing climatic variables from dendrochronological data (Esper & Frank, 2009). Conifers are particularly sensitive to climatic conditions and are of special interest for studying the nonlinear response of tree growth to climatic influences in cold climates (Rossi et al., 2013, 2016; Vaganov et al., 1999, 2006).
The most effective research combines experimental approaches, including wood anatomy data of tree rings (Fonti et al., 2010) and the respective advanced statistical analyses (Babst et al., 2013; Cuny et al., 2013), with theoretical process-based simulations (Anchukaitis et al., 2020; Cuny et al., 2015; Gennaretti et al., 2017a; Peters et al., 2021; Vaganov et al., 2006) capable of extending experimentation over the long-term to ensure an overlap with direct instrumental climate observations (Briffa et al., 1998). Given that most process-based models are multidimensional and involve many parameters (Guiot et al., 2014), parameterization is a crucial issue for obtaining reliable tree growth simulations connected with local climate and species and the individual trajectory of tree development (Tychkov et al., 2019). Accordingly, we have detailed the example of the two-step parameterization procedure of the VS-model, which can be used in most models. The potential of tree-ring growth simulations can be applied to various research fields, including tree phenology, forest management, and carbon cycle analysis through the annual estimation of the absolute volume of woody biomass of forest ecosystems (Vaganov et al., 2006).
Notes
- 1.
There is a well-known theorem in mathematical logic that holds that it is not possible to prove the contradictory nature of a hypothesis within the framework of the theory in which it is put forward.
References
Anchukaitis, K. J., Evans, M. N., Kaplan, A., et al. (2006). Forward modeling of regional scale tree-ring patterns in the southeastern United States and the recent influence of summer drought. Geophysical Research Letters, 33(4), L04705. https://doi.org/10.1029/2005GL025050.
Anchukaitis, K. J., Breitenmoser, P., Briffa, K. R., et al. (2012). Tree rings and volcanic cooling. Nature Geoscience, 5(12), 836–837. https://doi.org/10.1038/ngeo1645.
Anchukaitis, K. J., Evans, M. N., Hughes, M. K., et al. (2020). An interpreted language implementation of the Vaganov-Shashkin tree-ring proxy system model. Dendrochronologia, 60, 125677. https://doi.org/10.1016/j.dendro.2020.125677.
Anderegg, W. R. L., Hicke, J. A., Fisher, R. A., et al. (2015). Tree mortality from drought, insects, and their interactions in a changing climate. New Phytologist, 208(3), 674–683. https://doi.org/10.1111/nph.13477.
Arzac, A., Garcia-Cervigon, A. I., Vicente-Serrano, S. M., et al. (2016). Phenological shifts in climatic response of secondary growth allow Juniperus sabina L. to cope with altitudinal and temporal climate variability. Agricultural and Forest Meteorology, 217, 35–45. https://doi.org/10.1016/j.agrformet.2015.11.011.
Arzac, A., Babushkina, E., Fonti, P., et al. (2018a). Evidences of wider latewood in Pinus sylvestris from a forest-steppe of Southern Siberia. Dendrochronologia, 49, 1–8. https://doi.org/10.1016/j.dendro.2018.02.007.
Arzac, A., Rozas, V., Rozenberg, P., et al. (2018b). Water availability controls Pinus pinaster xylem growth and density: A multi-proxy approach along its environmental range. Agricultural and Forest Meteorology, 250–251, 171–180. https://doi.org/10.1016/j.agrformet.2017.12.257.
Arzac, A., Popkova, M., Anarbekova, A., et al. (2019). Increasing radial and latewood growth rates of Larix cajanderi Mayr. and Pinus sylvestris L. in the continuous permafrost zone in Central Yakutia (Russia). Annals of Forest Science, 76(4), 96. https://doi.org/10.1007/s13595-019-0881-4.
Arzac, A., Tabakova, M. A., Khotcinskaia, K., et al. (2021a). Linking tree growth and intra-annual density fluctuations to climate in suppressed and dominant Pinus sylvestris L. trees in the forest-steppe of Southern Siberia. Dendrochronologia, 67, 125842. https://doi.org/10.1016/j.dendro.2021.125842.
Arzac, A., Tychkov, I., Rubtsov, A., et al. (2021b). Phenological shifts compensate warming-induced drought stress in southern Siberian Scots pines. European Journal of Forest Research, 140(6), 1487–1498. https://doi.org/10.1007/s10342-021-01412-w.
Babst, F., Poulter, B., Trouet, V., et al. (2013). Site- and species-specific responses of forest growth to climate across the European continent. Global Ecology and Biogeography, 22(6), 706–717. https://doi.org/10.1111/geb.12023.
Babushkina, E. A., Vaganov, E. A., Belokopytova, L. V., et al. (2015). Competitive strength effect in the climate response of Scots pine radial growth in south-central Siberia forest-steppe. Tree-Ring Research, 71(2), 106–117. https://doi.org/10.3959/1536-1098-71.2.106.
Babushkina, E. A., Belokopytova, L. V., Kostyakova, T. V., et al. (2018). Earlywood and latewood features of Pinus sylvestris in semiarid natural zones of South Siberia. Russian Journal of Ecology, 49, 209–217. https://doi.org/10.1134/S1067413618030013.
Barber, V. A., Juday, G. P., & Finney, B. P. (2000). Reduced growth of Alaskan white spruce in the twentieth century from temperature-induced drought stress. Nature, 405, 668–673. https://doi.org/10.1038/35015049.
Battaglia, M., Sands, P., White, D., et al. (2004). CABALA: A linked carbon, water and nitrogen model of forest growth for silvicultural decision support. Forest Ecology and Management, 193, 251–282. https://doi.org/10.1016/j.foreco.2004.01.033.
Beck, H. E., Zimmermann, N. E., McVicar, T. R., et al. (2018). Present and future Koppen-Geiger climate classification maps at 1-km resolution. Science Data, 5, 180214. https://doi.org/10.1038/sdata.2018.214.
Belousova, D. A., Shishov, V. V., Babushkina, E. A., et al. (2021). VS-cambium-developer: A new approach to modeling the functioning of the cambial zone of conifers under the influence of environmental factors. Russian Journal of Ecology, 52(5), 358–367. https://doi.org/10.1134/S1067413621050040.
Björklund, J., Seftigen, K., Schweingruber, F., et al. (2017). Cell size and wall dimensions drive distinct variability of earlywood and latewood density in Northern Hemisphere conifers. New Phytologist, 216, 728–740. https://doi.org/10.1111/nph.14639.
Brienen, R. J. W., Gloor, E., & Zuidema, P. A. (2012). Detecting evidence for CO2 fertilization from tree ring studies: The potential role of sampling biases. Global Biogeochemical Cycles, 26(1), GB1025. https://doi.org/10.1029/2011GB004143.
Briffa, K. R. (2000). Annual climate variability in the Holocene: Interpreting the message of ancient trees. Quaternary Science Reviews, 19, 87–105. https://doi.org/10.1016/S0277-3791(99)00056-6.
Briffa, K. R., Schweingruber, F. H., Jones, P. D., et al. (1998). Reduced sensitivity of recent tree-growth to temperature at high northern latitudes. Nature, 391, 678–682. https://doi.org/10.1038/35596.
Briffa, K. R., Osborn, T. J., Schweingruber, F. H., et al. (2002). Tree-ring width and density data around the Northern Hemisphere: Part 1, local and regional climate signals. The Holocene, 12, 737–757. https://doi.org/10.1191/0959683602hl587rp.
Briffa, K. R., Shishov, V. V., Melvin, T. M., et al. (2008). Trends in recent temperature and radial tree growth spanning 2000 years across northwest Eurasia. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences, 363(1501), 2269–2282. https://doi.org/10.1098/rstb.2007.2199.
Bryukhanova, M. V., Kirdyanov, A. V., Prokushkin, A. S., et al. (2013). Specific features of xylogenesis in Dahurian larch, Larix gmelinii (Rupr.) Rupr., growing on permafrost soils in Middle Siberia. Russian Journal of Ecology, 44, 361–366. https://doi.org/10.1134/S1067413613050044.
Büntgen, U., Kirdyanov, A. V., Krusic, P. J., et al. (2021). Arctic aerosols and the ‘divergence problem’ in dendroclimatology. Dendrochronologia, 67, 125837. https://doi.org/10.1016/j.dendro.2021.125837.
Buttò, V., Shishov, V., Tychkov, I., et al. (2020). Comparing the cell dynamics of tree-ring formation observed in microcores and as predicted by the Vaganov-Shashkin model. Frontiers in Plant Science, 11, 1268. https://doi.org/10.3389/fpls.2020.01268.
Cartenì, F., Deslauriers, A., Rossi, S., et al. (2018). The physiological mechanisms behind the earlywood-to-latewood transition: A process-based modeling approach. Frontiers in Plant Science, 9(July), 1053. https://doi.org/10.3389/fpls.2018.01053.
Castagneri, D., Fonti, P., von Arx, G., et al. (2017). How does climate influence xylem morphogenesis over the growing season? Insights from long-term intra-ring anatomy in Picea abies. Annals of Botany, 119(6), 1011–1020. https://doi.org/10.1093/aob/mcw274.
Charney, N. D., Babst, F., Poulter, B., et al. (2016). Observed forest sensitivity to climate implies large changes in 21st century North American forest growth. Ecology Letters, 19(9), 1119–1128. https://doi.org/10.1111/ele.12650.
Cook, E. R., & Kairiukstis, L. A. (1990). Methods of dendrochronology: Applications in the environmental sciences (p. 394). Dordrecht, Netherlands: Springer.
Critchfield, H. (1966). General climatology. Prentice Hall Inc.
Cuny, H. E., & Rathgeber, C. B. K. (2016). Xylogenesis: Coniferous trees of temperate forests are listening to the climate tale during the growing season but only remember the last words! Plant Physiology, 171(1), 306–317. https://doi.org/10.1104/pp.16.00037.
Cuny, H. E., Rathgeber, C. B. K., Kiessé, T. S., et al. (2013). Generalized additive models reveal the intrinsic complexity of wood formation dynamics. Journal of Experimental Botany, 64(7), 1983–1994. https://doi.org/10.1093/jxb/ert057.
Cuny, H. E., Rathgeber, C. B. K., Frank, D., et al. (2015). Woody biomass production lags stem-girth increase by over one month in coniferous forests. Nature Plants, 1(11), 15160. https://doi.org/10.1038/nplants.2015.160.
D’Arrigo, R., Wilson, R., & Jacoby, G. (2006). On the long-term context for late twentieth century warming. Journal of Geophysical Research, 111, D03103. https://doi.org/10.1029/2005JD006352.
D’Arrigo, R., Wilson, R., Liepert, B., et al. (2008). On the “divergence problem” in northern forests: A review of the tree-ring evidence and possible causes. Global and Planetary Change, 60, 289–305. https://doi.org/10.1016/j.gloplacha.2007.03.004.
Dengler, N. G. (2001). Regulation of vascular development. Journal of Plant Growth Regulation, 20(1), 1–13. https://doi.org/10.1007/s003440010008.
Domec, J. C., & Gartner, B. L. (2002). How do water transport and water storage differ in coniferous earlywood and latewood? Journal of Experimental Botany, 53, 2369–2379. https://doi.org/10.1093/jxb/erf100.
Drew, D. M., & Downes, G. (2015). A model of stem growth and wood formation in Pinus radiata. Trees, 29, 1395–1413. https://doi.org/10.1007/s00468-015-1216-1.
Driscoll, W. W., Wiles, G. C., D’Arrigo, R. D., et al. (2005). Divergent tree growth response to recent climatic warming, Lake Clark National Park and Preserve, Alaska. Geophysical Research Letters, 32, L20703. https://doi.org/10.1029/2005GL024258.
Duchesne, L., Houle, D., Ouimet, R., et al. (2019). Large apparent growth increases in boreal forests inferred from tree-rings are an artefact of sampling biases. Scientific Reports, 9(1), 6832. https://doi.org/10.1038/s41598-019-43243-1.
Dyachuk, P., Arzac, A., Peresunko, P., et al. (2020). AutoCellRow (ACR)—A new tool for the automatic quantification of cell radial files in conifer images. Dendrochronologia, 60, 125687. https://doi.org/10.1016/j.dendro.2020.125687.
Ebelhar, S. A., Chesworth, W., & Paris, Q. (2008). Law of the minimum. In W. Chesworth (Ed.), Encyclopedia of soil science (pp. 431–437). Springer.
Esper, J., & Frank, D. (2009). Divergence pitfalls in tree-ring research. Climatic Change, 94(3), 261. https://doi.org/10.1007/s10584-009-9594-2.
Evans, M. N., Reichert, B. K., Kaplan, A., et al. (2006). A forward modeling approach to paleoclimatic interpretation of tree-ring data. Journal of Geophysical Research, 111(G3), G03008. https://doi.org/10.1029/2006JG000166.
Fonti, P., & Jansen, S. (2012). Xylem plasticity in response to climate. New Phytologist, 195, 734–736. https://doi.org/10.1111/j.1469-8137.2012.04252.x.
Fonti, P., von Arx, G., Garcia-Gonzalez, I., et al. (2010). Studying global change through investigation of the plastic responses of xylem anatomy in tree rings. New Phytologist, 185(1), 42–53. https://doi.org/10.1111/j.1469-8137.2009.03030.x.
Frank, D., Reichstein, M., Bahn, M., et al. (2015). Effects of climate extremes on the terrestrial carbon cycle: Concepts, processes and potential future impacts. Global Change Biology, 21(8), 2861–2880. https://doi.org/10.1111/gcb.12916.
Fritts, H. C. (1976). Tree rings and climate. London: Academic Press.
Gea-Izquierdo, G., Guibal, F., Joffre, R., et al. (2015). Modelling the climatic drivers determining photosynthesis and carbon allocation in evergreen Mediterranean forests using multiproxy long time series. Biogeosciences, 12(12), 3695–3712. https://doi.org/10.5194/bg-12-3695-2015.
Gennaretti, F., Gea-Izquierdo, G., Boucher, E., et al. (2017a). Ecophysiological modeling of photosynthesis and carbon allocation to the tree stem in the boreal forest. Biogeosciences, 14, 4851–4866. https://doi.org/10.5194/bg-14-4851-2017.
Gennaretti, H., Naulier, S., & Bégin, A. (2017b). Bayesian multiproxy temperature reconstruction with black spruce ring widths and stable isotopes from the northern Quebec taiga. Climate Dynamics, 49(11–12), 4107–4119. https://doi.org/10.1007/s00382-017-3565-5.
Guiot, J., Boucher, E., & Gea-Izquierdo, G. (2014). Process models and model-data fusion in dendroecology. Frontiers in Ecology and Evolution, 2, 1–12 https://doi.org/10.3389/fevo.2014.00052.
Gyllenstrand, N., Clapham, D., Kallman, T., et al. (2007). A Norway spruce FLOWERING LOCUS T homolog is implicated in control of growth rhythm in conifers. Plant Physiology, 144, 248–257. https://doi.org/10.1104/pp.107.095802.
He, M., Shishov, V., Kaparova, N., et al. (2017). Process-based modeling of tree-ring formation and its relationships with climate on the Tibetan Plateau. Dendrochronologia, 42, 31–41. https://doi.org/10.1016/j.dendro.2017.01.002.
He, M., Yang, B., Shishov, V., et al. (2018a). Relationships between wood formation and cambium phenology on the Tibetan plateau during 1960–2014. Forests, 9(2), 1–13. https://doi.org/10.3390/f9020086.
He, M., Yang, B., Shishov, V., et al. (2018b). Projections for the changes in growing season length of tree-ring formation on the Tibetan Plateau based on CMIP5 model simulations. International Journal of Biometeorology, 62(4), 631–641. https://doi.org/10.1007/s00484-017-1472-4.
Hellmann, L., Agafonov, L., Ljungqvist, F. C., et al. (2016). Diverse growth trends and climate responses across Eurasia’s boreal forest. Environmental Research Letters, 11(7), 074021. https://doi.org/10.1088/1748-9326/11/7/074021.
Hoch, G., & Körner, C. (2003). The carbon charging of pines at the climatic treeline: A global comparison. Oecologia, 135, 10–21. https://doi.org/10.1007/s00442-002-1154-7.
Intergovernmental Panel on Climate Change (IPCC). (Ed.). (2007). Climate Change 2007: Synthesis report. Contribution of Working Groups I, II and III to the fourth assessment report of the Intergovernmental Panel on Climate Change (p. 104). Geneva: IPCC.
Intergovernmental Panel on Climate Change (IPCC) (Ed.). (2014). Climate Change 2014: Synthesis report. Contribution of Working Groups I, II and III to the fifth assessment report of the Intergovernmental Panel on Climate Change (p. 151). Geneva: IPCC.
Irvine, J., Perks, M. P., Magnani, F., et al. (1998). The response of Pinus sylvestris to drought: Stomatal control of transpiration and hydraulic conductance. Tree Physiology, 18(6), 393–402. https://doi.org/10.1093/treephys/18.6.393.
Jevšenak, J., Tychkov, I., Gričar, J., et al. (2021). Growth-limiting factors and climate response variability in Norway spruce (Picea abies L.) along an elevation and precipitation gradients in Slovenia. International Journal of Biometeorology, 65(2), 311–324. https://doi.org/10.1007/s00484-020-02033-5.
Jones, P. D. (2002). Changes in climate and variability over the last 1000 years. International Geophysics, 83, 133–142. https://doi.org/10.1016/S0074-6142(02)80162-0.
Jones, P. D., & Briffa, K. R. (1992). Global surface air temperature variations during the twentieth century: Part 1, Spatial, temporal and seasonal details. The Holocene, 2, 165–179. https://doi.org/10.1177/095968369200200208.
Jones, P. D., Osborn, T. J., & Briffa, K. R. (2001). The evolution of climate over the last millennium. Science, 292(5517), 662–667. https://doi.org/10.1126/science.1059126.
Kirdyanov, A., Hughes, M., Vaganov, E., et al. (2003). The importance of early summer temperature and date of snow melt for tree growth in the Siberian Subarctic. Trees, 17(1), 61–69. https://doi.org/10.1007/s00468-002-0209-z.
Kirdyanov, A. V., Krusic, P. J., Shishov, V. V., et al. (2020). Ecological and conceptual consequences of Arctic pollution. Ecology Letters, 23(12), 1827–1837. https://doi.org/10.1111/ele.13611.
Kramer, P. (1964). The role of water in wood formation. In M. Zimmermann (Ed.), The formation of wood in forest trees (pp. 519–532). New York: Academic Press.
Lavergne, A., Gennaretti, F., Risi, C., et al. (2017). Modelling tree ring cellulose δ18O variations in two temperature-sensitive tree species from North and South America. Climate of the Past, 13, 1515–1526. https://doi.org/10.5194/cp-13-1515-2017.
Lloyd, A. H., & Fastie, C. L. (2002). Spatial and temporal variability in the growth and climate response of treeline trees in Alaska. Climatic Change, 52, 481–509. https://doi.org/10.1023/A:1014278819094.
Melvin, T. (2004). Historical growth rates and changing climatic sensitivity of boreal conifers. Ph.D. thesis, University of East Anglia.
Menzel, A., Sparks, T. H., Estrella, N., et al. (2006). European phenological response to climate change matches the warming pattern. Global Change Biology, 12(10), 1969–1976. https://doi.org/10.1111/j.1365-2486.2006.01193.x.
Misson, L. (2004). MAIDEN: A model for analyzing ecosystem processes in dendroecology. Canadian Journal of Forest Research, 34(4), 874–887. https://doi.org/10.1139/x03-252.
Ogée, J., Barbour, M. M., Wingate, L., et al. (2009). A single-substrate model to interpret intra-annual stable isotope signals in tree-ring cellulose. Plant, Cell and Environment, 32, 1071–1090. https://doi.org/10.1111/j.1365-3040.2009.01989.x.
Olano, J., Eugenio, M., Garcia-Cervigon, A. I., et al. (2012). Quantitative tracheid anatomy reveals a complex environmental control of wood structure in continental Mediterranean climate. International Journal of Plant Sciences, 173(2), 137–149. https://doi.org/10.1086/663165.
Peters, R. L., Steppe, K., Cuny, H. E., et al. (2021). Turgor—A limiting factor for radial growth in mature conifers along an elevational gradient. New Phytologist, 229, 213–229. https://doi.org/10.1111/nph.16872.
Popkova, M. I., Vaganov, E. A., Shishov, V. V., et al. (2018). Modeled tracheidograms disclose drought influence on Pinus sylvestris tree-rings structure from Siberian forest-steppe. Frontiers in Plant Science, 9(August), 1144. https://doi.org/10.3389/fpls.2018.01144.
Popkova, M. I., Shishov, V. V., Vaganov, E. A., et al. (2020). Contribution of xylem anatomy to tree-ring width of two larch species in permafrost and non-permafrost zones of Siberia. Forests, 11, 1343. https://doi.org/10.3390/f11121343.
Price, K., Storn, R. M., & Lampinen, J. A. (2005). Differential evolution. Berlin, Heidelberg: Springer.
Puchi, P. F., Castagneri, D., Rossi, S., et al. (2019). Wood anatomical traits in black spruce reveal latent water constraints on the boreal forest. Global Change Biology, 26(3), 1767–1777. https://doi.org/10.1111/gcb.14906.
Rathgeber, C. B. K. (2017). Conifer tree-ring density inter-annual variability—anatomical, physiological and environmental determinants. New Phytologist, 216(3), 621–625. https://doi.org/10.1111/nph.14763.
Rathgeber, C. B. K., Cuny, H. E., & Fonti, P. (2016). Biological basis of tree-ring formation: A crash course. Frontiers in Plant Science, 7(734). https://doi.org/10.3389/fpls.2016.00734.
Rezsohazy, J., Goosse, H., Guiot, J., et al. (2020). Application and evaluation of the dendroclimatic process-based model MAIDEN during the last century in Canada and Europe. Climate of the Past, 16, 1043–1059. https://doi.org/10.5194/cp-16-1043-2020.
Rossi, S., Deslauriers, A., Anfodillo, T., et al. (2008a). Age-dependent xylogenesis in timberline conifers. New Phytologist, 177(1), 199–208. https://doi.org/10.1111/j.1469-8137.2007.02235.x.
Rossi, S., Deslauriers, A., Gricar, J., et al. (2008b). Critical temperatures for xylogenesis in conifers of cold climates. Global Ecology and Biogeography, 17(6), 696–707. https://doi.org/10.1111/j.1466-8238.2008.00417.x.
Rossi, S., Anfodillo, T., Cufar, K., et al. (2013). A meta-analysis of cambium phenology and growth: Linear and non-linear patterns in conifers of the northern hemisphere. Annals of Botany, 112(9), 1911–1920. https://doi.org/10.1093/aob/mct243.
Rossi, S., Anfodillo, T., Čufar, K., et al. (2016). Pattern of xylem phenology in conifers of cold ecosystems at the Northern Hemisphere. Global Change Biology, 22(11), 3804–3813. https://doi.org/10.1111/gcb.13317.
Shishov, V. V., Tychkov, I. I., Popkova, M. I., et al. (2016). VS-oscilloscope: A new tool to parameterize tree radial growth based on climate conditions. Dendrochronologia, 39, 42–50. https://doi.org/10.1016/j.dendro.2015.10.001.
Shishov, V. V., Tychkov, I. I., Anchukaitis, K. J., et al. (2021). A band model of cambium development: Opportunities and prospects. Forests, 12(10), 1361.
Sperry, J. S., Hacke, U. G., & Pittermann, J. (2006). Size and function in conifer tracheids and angiosperm vessels. American Journal of Botany, 93(10), 1490–1500. https://doi.org/10.3732/ajb.93.10.1490.
Steppe, K., Sterck, F., & Deslauriers, A. (2015). Diel growth dynamics in tree stems: Linking anatomy and ecophysiology. Trends in Plant Science, 20(6), 335–343. https://doi.org/10.1016/j.tplants.2015.03.015.
Storn, R., & Price, K. (1997). Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11, 341–359. https://doi.org/10.1023/A:1008202821328.
Tabakova, M., Arzac, A., Martinez, E., et al. (2020). Climatic factors controlling Pinus sylvestris radial growth along a transect of increasing continentality in southern Siberia. Dendrochronologia, 62, 125709. https://doi.org/10.1016/j.dendro.2020.125709.
Thorne, P. W., Jones, P. D., Tett, S. F. B., et al. (2003). Probable causes of late twentieth century tropospheric temperature trends. Climate Dynamics, 21, 573–591. https://doi.org/10.1007/s00382-003-0353-1.
Thornthwaite, C. W., & Mather, J. R. (1955). The water balance (p. 104). Centerton: Laboratory of Climatology, Drexel Institute of Technology.
Tolwinski-Ward, S. E., Evans, M. N., Hughes, M. K., et al. (2011). Erratum to: An efficient forward model of the climate controls on interannual variation in tree-ring width. Climate Dynamics, 36(11), 2441–2445. https://doi.org/10.1007/s00382-011-1062-9.
Tolwinski-Ward, S. E., Anchukaitis, K. J., & Evans, M. N. (2013). Bayesian parameter estimation and interpretation for an intermediate model of tree-ring width. Climate of the Past, 9(4), 1481–1493. https://doi.org/10.5194/cp-9-1481-2013.
Touchan, R., Shishov, V. V., Meko, D. M., et al. (2012). Process based model sheds light on climate sensitivity of Mediterranean tree-ring width. Biogeosciences, 9(3), 965–972. https://doi.org/10.5194/bg-9-965-2012.
Tumajer, J., Kašpar, J., Kuželová, H., et al. (2021a). Forward modeling reveals multidecadal trends in cambial kinetics and phenology at treeline. Frontiers in Plant Science, 12(32), 613643. https://doi.org/10.3389/fpls.2021.613643.
Tumajer, J., Shishov, V. V., Ilyin, V. A., et al. (2021b). Intra-annual growth dynamics of Mediterranean pines and junipers determines their climatic adaptability. Agricultural and Forest Meteorology, 311, 108685. https://doi.org/10.1016/j.agrformet.2021.108685.
Tychkov, I. I., Sviderskaya, I. V., Babushkina, E. A., et al. (2019). How can the parameterization of a process-based model help us understand real tree-ring growth? Trees, 33(2), 345–357. https://doi.org/10.1007/s00468-018-1780-2.
Vaganov, E. A. (1990). The tracheidogram method in tree-ring analysis and its application. In E. Cook & L. Kairiukstis (Eds.), Methods of dendrochronology (pp. 63–76). Dordrecht: Springer.
Vaganov, E. A., & Shashkin, A. V. (2000). The growth and structure of annual rings [in Russian]. Novosibirsk: Nauka Publishing House.
Vaganov, E. A., Hughes, M. K., Kirdyanov, A. V., et al. (1999). Influence of snowfall and melt timing on tree growth in subarctic Eurasia. Nature, 400, 149–151. https://doi.org/10.1038/22087.
Vaganov, E. A., Hughes, M. K., & Shashkin, A. V. (2006). Growth dynamics of conifer tree rings: Images of past and future environments (p. 357). Berlin, Heidelberg: Springer.
Vaganov, E. A., Anchukaitis, K. J., & Evans, M. N. (2011). How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. In M. K. Hughes, T. W. Swetnam, & H. F. Diaz (Eds.), Dendroclimatology: Progress and prospects (pp. 37–75). Dordrecht: Springer.
von Arx, G., Crivellaro, A., Prendin, A. L., et al. (2016). Quantitative wood anatomy–Practical guidelines. Frontiers in Plant Science, 7, 781. https://doi.org/10.3389/fpls.2016.00781.
Wilmking, M., Juday, G. P., Barber, V. A., et al. (2004). Recent climate warming forces contrasting growth responses of white spruce at treeline in Alaska through temperature thresholds. Global Change Biology, 10, 1724–1736. https://doi.org/10.1111/j.1365-2486.2004.00826.x.
Woodward, F. I., & Williams, B. G. (1987). Climate and plant distribution at global and local scales. Vegetatio, 69, 189–197. https://doi.org/10.1007/BF00038700.
Yang, B., He, M., Shishov, V., et al. (2017). New perspective on spring vegetation phenology and global climate change based on Tibetan Plateau tree-ring data. Proceedings of the National Academy of Sciences of the United States of America, 114(27), 6966–6971. https://doi.org/10.1073/pnas.1616608114.
Zhirnova, D. F., Babushkina, E. A., Belokopytova, L. V., et al. (2020). To which side are the scales swinging? Growth stability of Siberian larch under permanent moisture deficit with periodic droughts. Forest Ecology and Management, 459, 117841. https://doi.org/10.1016/j.foreco.2019.117841.
Zuur, A., Ieno, E., Walker, N., et al. (2009). Mixed effects models and extensions in ecology with R. New York: Springer.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Shishov, V.V., Arzac, A., Popkova, M.I., Yang, B., He, M., Vaganov, E.A. (2023). Experimental and Theoretical Analysis of Tree-Ring Growth in Cold Climates. In: Girona, M.M., Morin, H., Gauthier, S., Bergeron, Y. (eds) Boreal Forests in the Face of Climate Change. Advances in Global Change Research, vol 74. Springer, Cham. https://doi.org/10.1007/978-3-031-15988-6_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-15988-6_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-15987-9
Online ISBN: 978-3-031-15988-6
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)