Keywords

1 Introduction

During my doctoral studies, I mainly focused on reflection seismology problems. As the name suggests, reflection seismology processes seismic waves reflected by the subsurface features like faults, sediment layers, and rock bodies. Intrinsically, reflection seismology is a collection of inverse problems [4, 18]. Additionally, given the dimensionality of the datasets, the costs related to acquisitions and processing, and the scarcity of ground truth, its tasks are often hard to solve and thus very challenging.

Advanced problems are ill-posed, which means that the solution is not unique, and are ill-conditioned, which means that small errors in the data result in dramatic changes in the solution [19]. These aspects and computational issues make the inverse problem theory long to be considered fulfilled.

For excellent physical reasons, seismic spectra imply that single-experiment data are insufficient for imaging purposes. This observation explains why seismic surveys are multi experiment [18]. The redundant data and the nonlinear nature of the modeling functions motivated the study of supervised deep learning imaging techniques. Although it is strongly based on statistical methods, machine learning has the particular focus on making decisions in an automated manner. In other words, it intrinsically aims at merging data processing with human interpretation. In exploration geophysics, solutions to inverse problems must fulfill some physical constraints, as they must be interpreted. In this sense, geophysicists are studying how to embed ML-generated features into traditional inversion schemes. Vice versa, physical constraints have been applied to machine learning scheme for lithofacies segmentation [11], data processing [14] and inversion problems [5]. Additionally, in [6] human interpretation methods are integrated into a CNN scheme.

Generative models were also proposed to precondition the inversion, under the assumption that CNNs can extract high-level features from data. This is the case of the so-called Deep Prior paradigm, initially developed for super-resolution, denoising, and inpainting of natural images [21].

In the light of these considerations, my research focused on understanding the advantages, and drawbacks, of machine learning methods for addressing geophysical inverse problems. To this end, the present brief is organized as follows. In Sect. 2, I first introduce a seismic imaging technique, the Reverse Time Migration (RTM), whose least-squares solution I address by means of generative networks [15]. Such architectures are a powerful tool for enhancing seismic images, but they lack physical information. Thus, I propose to change paradigm. In Sect. 3 I develop a Deep Prior interpolation scheme for seismic data [12]. In Sect. 4 I deploy convolutional autoencoders to detect buried landmine on radar data [3]; a CNN learns the secure soil features, thus failing to reconstruct signatures from possible threats. Finally, I draw my conclusions and devise a pathway for future research.

2 RTM Image Enhancement Through GANs

Reverse Time Migration (RTM) is a wave-equation-based imaging technique that represents the state-of-the-art industrial technology for depth imaging [23]. The goal of RTM is to image the reflectivity of the Earth subsurface from reflection data [2]:

$$\begin{aligned} \textbf{d}=F\left( \textbf{m}\right) + \textbf{n}, \end{aligned}$$
(1)

where \(\textbf{d}\) are the observed scattered data, \(\textbf{m}\) is the reflectivity model, F is a forward modeling operator and \(\textbf{n}\) is an additive noise.

Usually, the reflectivity image is computed as:

$$\begin{aligned} \textbf{m}= \textbf{B}'\textbf{d}, \end{aligned}$$
(2)

where \(\textbf{B}\) is the Born linear approximation of F that leverages finite difference Green’s functions, and \('\) represents the adjoint operator (i.e., the conjugate transpose).

To overcome limitations such as spatial aliasing, limited aperture, and non-uniform illumination, Least-Squares Reverse Time Migration (LS-RTM) was proposed to invert the forward modeling operator through iterative algorithms [17] in a least-squares sense:

$$\begin{aligned} \hat{\textbf{m}}= \mathop {\mathrm {arg\,min}}\limits _\textbf{m}\left\Vert \textbf{d}-\textbf{B}\textbf{m}\right\Vert _2^2+ \lambda R\left( \textbf{m}\right) , \end{aligned}$$
(3)

where R is a proper regularizing operator that imposes a-priori information or desired features on the resulting solution (e.g., it can enforce solution sparsity, smoothness, etc., depending on the result on the desired goal).

2.1 Generative Adversarial Networks

We can split the least-squares problem into two different problems: a standard imaging operator followed by a post-processing operator. In particular, we can invert the model-data relationship (1) as

$$\begin{aligned} F^{-1}=\mathcal {G} \circ B', \end{aligned}$$
(4)

where \(\mathcal {G}\) is a mapping operator (i.e., a post-processing machine) that transforms the migrated \(\textbf{m}=\textbf{B}'\textbf{d}\) into the desired image \(\bar{\textbf{m}}\).

I propose to use a convolutional neural network (CNN) as a general-purpose post-processing tool after RTM to produce images as if more sophisticated algorithms generated them. Specifically, I devise a Generative Adversarial Network (GAN), which is a class of CNNs that have been proposed in [8] to learn deep representations using a small training dataset. To achieve the goal of a realistic generation, they are trained singularly.

In supervised training, the generator \(\mathcal {G}\) minimizes a distance between the generated and reference images. In GANs, the generator is flanked by a fellow discriminator \(\mathcal {D}\), which is a binary classifier trained to discriminate whether its input is a pristine image or generated by its mate. At the same time, \(\mathcal {G}\) is trained to obtain the desired output from a given input and fool \(\mathcal {D}\). Therefore, \(\mathcal {D}\) can be seen as a regularizer driving \(\mathcal {G}\) to output realistic images. More formally, we can write the adversarial loss as the sum of two components. \(\textbf{m}\) and \(\bar{\textbf{m}}\) being the input and the ground truth vectors, respectively, the first term, referred to as the generator loss, is often defined as the \(\ell _2\)-norm of the error introduced by the generator:

$$\begin{aligned} \mathcal {L}_\mathcal {G} = \left\Vert \mathcal {G}(\textbf{m}) - \bar{\textbf{m}} \right\Vert _2^2, \end{aligned}$$
(5)

it forces the generated model to be similar to the target. As second term, we define the discriminator loss starting from a query image \(\hat{\textbf{m}}\) as

$$\begin{aligned} \mathcal {L}_\mathcal {D} = \log \mathcal {D}(\hat{\textbf{m}}, \bar{\textbf{m}}) + \log \left( 1 - \mathcal {D}(\hat{\textbf{m}}, \mathcal {G}(\textbf{m})) \right) , \end{aligned}$$
(6)

which measures how likely the generator is able to fool the discriminator in terms of binary cross-entropy. Finally, these two terms are added together to form the GAN loss:

$$\begin{aligned} \mathcal {L}= \mathcal {L}_\mathcal {G} + \lambda \mathcal {L}_\mathcal {D}, \end{aligned}$$
(7)

where the parameter \(\lambda \) balances the two contributions.

2.2 Experimental Results

Let us consider a fast track project: we desire high quality migrated images, but we have no resources to perform RTM over the entire data. We could perform a fine migration over a subset of the available dataset, and a faster migration (e.g., with subsampled data) over the whole dataset. Then, we train a GAN to refine the coarsely migrated images, and finally, we can deploy it over the entire coarse dataset.

Input images \(\textbf{m}\) have been generated by migrating 10 equispaced sources and 80 equispaced receivers covering the whole acquisition surface. The target images \(\bar{\textbf{m}}\) have been migrated from 200 sources and 800 receivers.

The training was performed for 300 epochs; nonetheless, the net converged after 50 epochs approximately. The parameter \(\lambda \) was set to 0.1. Once the training is completed, the time required to create an output image of the network was about 2 min, almost entirely dedicated to migration with the coarse geometry, while a fine geometry would require 40 min.

It is interesting that results are pretty promising on the test image, showing that the proposed solution does not simply overfit the training set but can generalize. Nevertheless, a few details are lost on the test set. It is worth noticing a channel around the center of the target patch shown in Fig. 1, which is missing in the output and barely present in the coarse input. To increase the quality of the generated images, we would like to add physical information to the CNN training.

Fig. 1
figure 1

Input \(\textbf{m}\) (a), output \(\hat{\textbf{m}}\) (b) and desired \(\bar{\textbf{m}}\) (c) patches from the test set

Full size image

3 Seismic Data Interpolation Through Deep Priors

Let us consider an ideal densely and regularly sampled three-dimensional cube of seismic data. This data cube represents the true model we aim at estimating through interpolation. Without loss of generality, we can represent ideal data as a vector \(\bar{\textbf{m}}\). We can think of the observed seismic data \(\textbf{d}\) as generated by a linear sampling operator \(\textbf{S}\) applied to \(\bar{\textbf{m}}\). Therefore, we can define the interpolation problem as the inversion of

$$\begin{aligned} \textbf{d}=\textbf{S}\bar{\textbf{m}}. \end{aligned}$$
(8)

Within the Deep Prior paradigm [21], the standard inverse problem cost function

$$\begin{aligned} J(\textbf{m}) = \left\Vert \textbf{S}\textbf{m}- \textbf{d}\right\Vert _2^2 \end{aligned}$$
(9)

is recast as finding the set of parameters \({\boldsymbol{\theta }}\) which minimizes

$$\begin{aligned} J({\boldsymbol{\theta }}) = \left\Vert \textbf{S}f_{{\boldsymbol{\theta }}}(\textbf{z}) - \textbf{d}\right\Vert _2^2, \end{aligned}$$
(10)

where \(\textbf{z}\) is a noise realization and \({\boldsymbol{\theta }}\) the parameters of the CNN \(f_{{\boldsymbol{\theta }}}\).

Once the optimum set of parameters \({\boldsymbol{\theta }}^*\) has been computed, the inverted model is simply the output of such optimized network:

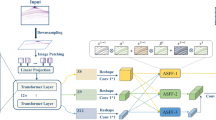
$$\begin{aligned} \hat{\textbf{m}}=f_{{\boldsymbol{\theta }}^*}\left( \textbf{z}\right) . \end{aligned}$$
(11)

Figure 2 helps visualizing the deep prior scheme adopted for interpolation. The convolutional autoencoder \(f_{{\boldsymbol{\theta }}}\) is optimized by computing the loss function over the actual known traces only; no ground truth is required. As a byproduct, it also generates missing traces.

In the inversion process, the CNN implicitly assumes the role of prior information that exploits correlations in the data to learn their inner structure. Therefore, choosing a specific CNN architecture is critical for a suitable and well-performing solution.

Fig. 2
figure 2

Seismic data interpolation in the Deep Prior paradigm

Full size image

3.1 Experimental Results

In this example, the desired shot gather is obtained via FD acoustic propagation over a 3D extension of the Marmousi model, depicted in the top-right pane of Fig. 3. It comprises 175 crosslines and 100 inlines; the sampling interval is 10m. The wavelet is a Ricker centered in 15 Hz; the recording time is 3.5 s. The top-left pane shows the input decimated data, obtained by randomly deleting 90% of the traces. Interpolation is performed with a modified version of the Multi-Resolution U-Net architecture [10], employing 2D kernels (thus processing slices of the volume) and 3D kernels. The interpolation results are shown in the bottom left and right panes, respectively. The 3D convolutions are the right choice to extract relevant information from the decimated volume; however, the computational cost is much higher than the 2D case.

Fig. 3
figure 3

Deep Priors interpolation of pre-stack seismic data. Top: input coarse data and desired dense data; bottom: interpolated data through 2D and 3D kernels, respectively

Full size image

3.2 Tackle Aliasing with Event Dips

Deep Priors have shown effective reconstruction performance when resolving irregular sampling. However, such techniques do not optimally perform when facing aliased data. A viable way to improve the performance is to drive the solution according to the events slopes.

Specifically, I first estimate a low-pass version of the data considering as

$$\begin{aligned} J\left( {\boldsymbol{\theta }}\right) = \left\Vert \textbf{S}f_{{\boldsymbol{\theta }}} \left( \textbf{z}\right) - \textbf{L} \textbf{d}\right\Vert _2^2, \end{aligned}$$
(12)

\(\textbf{L}\) being a second order Butterworth low-pass filter applied trace-by-trace, thus removing alias effects that could badly impact on standard Deep Prior inversion. Then, I estimate the slope angles \(\boldsymbol{\phi }\) through the structure tensor algorithm [22], to build the directional Laplacian operator \(\overrightarrow{\nabla }_{\boldsymbol{\phi }}\) [9]. The latter is employed to regularize the inversion of the full-band seismic data:

$$\begin{aligned} J({\boldsymbol{\theta }}) = \left\Vert \textbf{S}f_{{\boldsymbol{\theta }}}(\textbf{z}) - \textbf{d}\right\Vert _2^2 + \varepsilon \textbf{w}^2 \left\Vert \overrightarrow{\nabla }_{\boldsymbol{\phi }}f_{{\boldsymbol{\theta }}}(\textbf{z}) \right\Vert _2^2, \end{aligned}$$
(13)

where \(\textbf{w}\) is the vector that collects the anisotropy of the estimated gradient square tensor for each data sample [22], and it can be interpreted as a confidence measure of the estimated slopes. Notice that, as the optimization goes on, the interpolated data can be used to produce a better estimate of the data slopes, updating \(\overrightarrow{\nabla }_{\boldsymbol{\phi }}\) at runtime.

Fig. 4
figure 4

Interpolation results on synthetic linear events: input decimated data, target complete data, output of Deep Prior optimization with and without the proposed regularization. Above, the data; below, the corresponding FK spectra

Full size image

I compare the interpolation results with and without the proposed regularizer on a synthetic dataset of 4 linear events with different dips. Three events are mildly steep, while the fourth event has been designed to produce aliasing effects. This example is simple yet particularly challenging due to the slope of the events. The desired data are depicted in the second column of Fig. 4. I build a regular binary mask for simulating the decimation by keeping one trace over 3, as depicted in the first column. The network is optimized for 3000 iterations to fit the low-passed data (12). Then, the slopes are estimated, and the regularized optimization is performed for 7000 iterations with \(\varepsilon =5\).

The results of Deep Prior optimization when minimizing the regularized (13) and the standard data fitting (10) are reported in the third and fourth columns, respectively. Standard Deep Prior optimization could not resolve the aliasing of the steeper event, while the regularized results are more homogeneous. This effect is evident also in the spectra depicted in the fourth column, where we can notice a residual aliasing pattern; it has been mitigated by regularization.

4 CNN Landmine Detection

Landmines have been massively deployed in a vast amount of countries all over the world. According to the United Nations, the \(99.6\%\) of mines and unexploded ordnance must be safely removed from an area to consider it landmine-free. The majority of modern landmines are mainly composed of plastic materials, significantly reducing the efficacy of metal detectors. A suitable alternative is the Ground Penetrating Radar (GPR), as it is capable of detecting even small dielectric changes in the subsurface.

The 2D image \(\textbf{V}(t, x)\) whose coordinates are the reflection time t and the inline axis x is called B-scan. By concatenating Y consecutive B-scans, we sample the soil also in the crossline axis y, thus obtaining the volume \(\textbf{V}(t,x,y)\). If the y-th B-scan has been acquired over a buried target, we associate the binary label \(l(y)=1\); if it has been acquired over a target-free area, we label it with \(l(y)=0\). The buried object detection problem we aim at solving consists in taking the volume \(\textbf{V}(t,x,y)\) as input, and producing a label \(\hat{l}(y)\) for each B-scan.

Instead of a naive supervised binary classification scheme, let us train a convolutional autoencoder on patches of mine-free B-scans by minimizing the MSE between the input volume \(\textbf{v}_i\) and the autoencoder output \(\hat{\textbf{v}}_i\). Once the training has converged, we can state that the CNN has learned how to reconstruct background soil information correctly. When a volume of soil \(\textbf{V}\) is to be analyzed, it is split into sub-blocks \(\textbf{v}_i\) and the anomaly metrics depicted in Fig. 5 is computed as:

$$\begin{aligned} e_i = \left\Vert \mathcal {E}(\textbf{v}_i) - \mathcal {E}(\mathcal {D}(\mathcal {E}(\textbf{v}_i))\right\Vert _2^2. \end{aligned}$$
(14)

Then, all \(e_i\) values are merged into a volumetric anomaly mask \(\textbf{E}\) of the same size of \(\textbf{V}\). Finally, the label \(\hat{l}(y)\) is computed by hard-thresholding the maximum value of \(\textbf{E}(t,x,y)\) with a global value \(\varGamma \).

Fig. 5
figure 5

The proposed anomaly detection scheme

Full size image

4.1 Experimental Results

To compare against other methods proposed in the literature, I consider a simple detector that uses the maximum value of the B-scan energy, a standard constant false alarm rate (CFAR) technique [1], a model-based method [7], a computer vision approach [20] and two CNN-based methods [13, 16]. I evaluated my technique employing Receiver Operating Characteristic (ROC) curve, which represents the probability of correct detection (i.e., correctly finding a threat) and probability of false detection (i.e., detecting objects in clear areas) by spanning all possible values of the threshold \(\Gamma \). Each point of a ROC curve is obtained by comparing the ground truth l(y) with \(\hat{l}(y)\) binarized with respect to threshold \(\Gamma \). In a real scenario, traces generated by a single landmine can be observed in multiple B-scans. We consider a misdetection every time we miss a single B-scan. Therefore all presented results can then be considered a lower bound on the performance of the proposed method.

As depicted in Fig. 6, the proposed anomaly detector achieves the best Area Under the Curve (AUC) score. It is worth noticing that, along with the method proposed by my colleagues in [13], the proposed autoencoder is able to achieve a \(\textrm{TPR}_{\textrm{FPR}=0}\) near 0.9, which is highly desirable in a demining system.

Fig. 6
figure 6

ROC curves of the proposed landmine anomaly detector compared with state-of-the-art solutions

Full size image

5 Conclusions

Convolutional Neural Networks (CNNs) are an uprising tool to leverage data patterns, especially when acquisition campaigns produce redundant datasets as in Exploration Geophysics. In many physical applications, however, the data features extracted by convolutional layers are not sufficient to describe the complex phenomena that we aim to invert. This consideration suggests that a-priori domain information should also be inserted in machine learning schemes.

In this brief, I presented three different machine learning paradigms applied to imaging, interpolation, and interpretation tasks. First, I study the Generative Adversarial Networks (GANs) as a tool to refine Reverse Time Migration (RTM) images. This supervised network produces very good results but it lacks of physical information on the geological features it processes. Then, I described how Deep Priors could be relevant to seismic data interpolation. While producing state-of-the-art results, this method cannot solve the intrinsic spectral incompleteness of seismic traces, especially in the presence of aliased data, for which I proposed a slope-informed regularization term. Finally, I show how learning patterns can be employed in an anomaly detection scheme for spotting landmines in Ground Penetrating Radar (GPR) data. The learning ability of a CNN is leveraged to discriminate safe background soil images and buried threats signatures. Such a scheme is based on a single class training, thus relaxing the requirements, and costs, of collecting datasets.

In the last years, a considerable number of architectures have been proposed for improving human-level tasks. A general trend is to go for deeper, heavier, and more complex ensemble models. It is worth noticing that this race does not guarantee better results. Therefore, extra care should be spent studying new problem-setting approaches rather than problem-solving ones.