Abstract
This chapter is dedicated to the monotonicity formula for the boundary adjusted energy introduced by Weiss in [52]. Precisely, for every Λ ≥ 0 and every u ∈ H 1(B 1).
You have full access to this open access chapter, Download chapter PDF
This chapter is dedicated to the monotonicity formula for the boundary adjusted energy introduced by Weiss in [52]. Precisely, for every Λ ≥ 0 and every u ∈ H 1(B 1) we define
where we recall that Ωu := {u > 0}. In particular, we have
This chapter is organized as follows:
In Sect. 9.1 we prove several preliminary results for the Weiss’ boundary adjusted energy, which hold for a general Sobolev function u defined on an open set \(D\subset \mathbb {R}^d\). In particular, in Lemma 9.1 we prove that the function \((x_0,r)\mapsto W_\Lambda (u_{x_0,r})\) is continuous (where it is defined), where we recall that \(u_{x_0,r}(x):=\frac 1ru(x_0+rx)\); in Lemma 9.2, we compute the derivative of \(W_\Lambda (u_{x_0,r})\) with respect to r and we prove that
where \(z_{x_0,r}\) is the one-homogeneous extension defined in Lemma 9.2 while the deviation \(\mathcal D(u_{x_0,r})\) is defined as
and measures at what extent the function is not one-homogeneous (see Lemma 9.3) and controls the oscillation of u from scale to scale, which is measured by the norm \(\|u_{x_0,r}-u_{x_0,s}\|{ }_{L^2(\partial B_1)}\). Finally, in Proposition 9.4, as a direct consequence of the Weiss formula (Lemma 9.2), we obtain that, if u is a (local) minimizer of \(\mathcal F_\Lambda \) in D, then the Weiss energy \(W(u_{x_0,r})\) is monotone increasing in r.
In Sect. 9.2 we introduce the notion of stationary free boundary, that is, the free boundary ∂ Ωu ∩ D of a function \(u:D\to \mathbb {R}\), which is stationary for the functional \(\mathcal F_\Lambda \) with respect to internal perturbations with vector fields compactly supported in D. In Lemma 9.5, we compute the variation of the energy \(\mathcal F_\Lambda \) with respect to a compactly supported vector field \(\xi \in C^\infty _c(D;\mathbb {R}^d)\), which is simply defined as
where \(u_t:D\to \mathbb {R}\) is defined through the identity u t(x + tξ(x)) = u(x). We say that a function is stationary (see Definition 9.7), if the first variation is zero with respect to any vector field, that is, if
In Lemma 9.6 we show that if u is a minimizer of \(\mathcal F_\Lambda \) in D, then it is stationary in D. Then, in Lemma 9.8, we prove that every stationary function satisfies an equipartition-of-the-energy identity; in Lemma 9.9, we prove that the equipartition of the energy is sufficient for the monotonicity of the Weiss energy. In particular, the monotonicity formula holds for stationary free boundaries. The result of Sect. 9.2 are fundamental for the proof of Theorem 1.9, but we do not need them in the proof of Theorem 1.4, where we can use directly Proposition 9.4.
In Sect. 9.3 we give the sufficient conditions for the homogeneity of the blow-up limits of a function \(u:D\to \mathbb {R}\) (Lemma 9.10). We then apply this result to minimizers of \(\mathcal F_\Lambda \) (Proposition 9.12), but we will also use it in the context of Theorem 1.9. This is why the exposition contains the intermediate Lemma 9.11.
In Sect. 9.4 we prove that the only one-homogeneous global solutions in dimension two are the half-plane solutions (see Proposition 9.13). In particular, this means that d ∗≥ 3.
In Sect. 9.5 we give another proof of the fact that the minimizers of \(\mathcal F_\Lambda \) are viscosity solutions (Proposition 7.1). Our main result is Proposition 9.18, which applies to minimizers of \(\mathcal F_\Lambda \), but also in the context of Theorem 1.9.
Finally, in Sect. 9.6, we use the Weiss monotonicity formula to relate the energy density
of a minimizer u of \(\mathcal F_\Lambda \), to the Lebesgue density
of the set Ωu, at every point of the free boundary x 0 ∈ ∂ Ωu (Lemma 9.20). Moreover, we characterize the regular part of the free boundary Reg(∂ Ωu) in terms of the energy and the Lebesgue densities (Lemma 9.22). We will not use the results from Sect. 9.6 in the proofs of Theorems 1.2, 1.4, 1.9 and 1.10, but they remain an interesting application of the monotonicity formula and the homogeneity of the blow-up limits and were used, for instance, in the analysis of the vectorial free boundaries (see [41]).
9.1 The Weiss Boundary Adjusted Energy
Let u ∈ H 1(B r(x 0)) be a given function on the ball \(B_r(x_0)\subset \mathbb {R}^d\) and consider the rescaling
We notice that the different terms of the energy W Λ have the following scaling properties:
Thus, we have
In particular, since u is a Sobolev function, the function \((x_0,r)\mapsto W_\Lambda (u_{x_0,r})\) is continuous, where it is defined. We give the precise statement in the following lemma.
Lemma 9.1 (Continuity of the Function \((x_0,r)\mapsto W_\Lambda (u_{x_0,r})\))
Let D be a bounded open set in \(\mathbb {R}^d\) and let u ∈ H 1(D). Let δ > 0 and let D δ be the set
Then, the function
is continuous.
Proof
The continuity of the terms
follows by the fact that if \(f:D\to \mathbb {R}\) is a function in L 1(D), then the map
is continuous, which in turn follows by the dominated convergence theorem. In order to prove the continuity of the function
we consider the sequence to (x n, r n) ∈ D δ × (0, δ) converging to a point (x 0, r 0) ∈ D δ × (0, δ). We first notice that reasoning as above, we have
Next, we notice that \(u_{x_n,r_n}\) converges weakly in H 1(B 1) to \(u_{x_0,r_0}\). In fact, for any \(\phi \in C^\infty _c(B_1)\) we have
Now, since the norm of \(u_{x_n,r_n}\) converges to the norm of \(u_{x_0,r_0}\), we get that
By the trace inequality, we have that
which concludes the proof. □
Lemma 9.2 (Derivative of the Weiss’ Energy)
Let D be a bounded open set in \(\mathbb {R}^d\) and let u ∈ H 1(D). Let x 0 ∈ D and δ = dist(x 0, ∂D). Then, the function Φ u(x 0, ⋅) is differentiable almost everywhere on (0, δ) and for (almost) every r ∈ (0, δ), we have
where \(z_{x_0,r}:B_1\to \mathbb {R}\) is the one-homogeneous extension of \(u_{x_0,r}\) in B 1:
Proof
Without loss of generality we can assume x 0 = 0. We recall that u r := u 0,r.
We first notice that the function r↦| Ωu ∩ B r| is differentiable almost everywhere and that for almost every r ∈ (0, δ) we have
which can be written as
In fact, we have
Thus, (9.2) implies that it is sufficient to prove (9.1) in the case Λ = 0.
As above, we notice that the function \(\displaystyle r\mapsto \int _{B_r}|\nabla u|{ }^2\,dx\) is differentiable almost-everywhere and that we have
In order to deal with the boundary term, we first compute
Thus, we have
Now, we notice that for every r such that u r = z r ∈ H 1(∂B 1), we can write the function \(z_r:B_1\to \mathbb {R}\) in polar coordinates ρ ∈ (0, 1], \(\theta \in \mathbb S^{d-1}\) as z r(ρ, θ) = ρ z r(1, θ) and we have
Now, putting together (9.3), (9.4) and (9.5), we get that
which concludes the proof. □
We now define the deviation \(\mathcal D\) as
Thus, (9.1) can be written as
In the next lemma we show that the deviation \(\mathcal D(u_{x_0,r})\) controls the oscillation of u.
Lemma 9.3 (The Deviation Controls the Oscillation of the Blow-Up Sequence)
Let D be a bounded open set in \(\mathbb {R}^d\) and let u ∈ H 1(D). Let x 0 ∈ D and δ = dist(x 0, ∂D). Then, for almost every 0 < r < R < δ, we have
In particular, if \(\mathcal D(u_{x_0,s})=0\) for every s ∈ (0, δ), then the function \(u_{x_0,\delta }:B_1\to \mathbb {R}\) is one-homogeneous, that is
Proof
We set for simplicity, x 0 = 0 and \(u_r:=u_{x_0,r}\). For any x ∈ ∂B 1, we have
Integrating over the sphere ∂B 1 and using the Cauchy-Schwarz inequality, we obtain
which concludes the proof. □
We conclude this subsection with the following proposition.
Proposition 9.4 (Weiss Monotonicity Formula)
Let D be a bounded open set in \(\mathbb {R}^d\) and let u ∈ H 1(D) be a minimizer of \(\mathcal F_\Lambda \) in D. Let x 0 ∈ D and \(\delta _{x_0}=\mathit{\text{dist}}(x_0,\partial D)\) . Then the function \(r\mapsto W_\Lambda (u_{x_0,r})\) is non-decreasing on the interval \((0,\delta _{x_0})\).
Proof
By Lemma 9.2 we have that
Now, since \(u_{x_0,r}\) is a minimizer of \(\mathcal F_\Lambda \) in B 1 and since by definition \(z_{x_0,r}=u_{x_0,r}\) on ∂B 1, we get that \(\displaystyle \frac {\partial }{\partial r}W_\Lambda (u_{x_0,r})\ge 0\), which concludes the proof. □
9.2 Stationary Free Boundaries
In this section we introduce the notion of a stationary free boundary (Definition 9.7) and we prove a monotonicity formula for the Weiss energy (Proposition 9.9).
Lemma 9.5 (First Variation of the Energy)
Suppose that \(D\subset \mathbb {R}^d\) is a bounded open set and that u ∈ H 1(D). Let \(\xi \in C^\infty _c(D ;\mathbb {R}^d)\) be a given vector field with compact support in D and let Ψ t be the diffeomorphism
Then,
-
(i)
for t small enough, Ψ t : D → D is a diffeomorphism and setting \(\Phi _t:=\Psi _t^{-1}\) , the function u t := u ∘ Φ t is well-defined and belongs to H 1(D);
-
(ii)
the function t↦∫D|∇u t|2 dx is differentiable at t = 0 and
$$\displaystyle \begin{aligned} \frac{\partial}{\partial t}\Big\vert_{t=0}\int_{D}|\nabla u_t|{}^2\,dx= \int_{D}\left(-2\nabla u\cdot D\xi \nabla u+ |\nabla u|{}^2\mathrm{div}\,\xi\,\right)dx; \end{aligned}$$ -
(iii)
the function \(\displaystyle t\mapsto |\Omega _{u_t}\cap D|\) is differentiable at t = 0 and
$$\displaystyle \begin{aligned} \frac{\partial}{\partial t}\Big\vert_{t=0}|\Omega_{u_t}\cap D|= \int_{\Omega_u\cap D}\mathrm{div}\,\xi\,dx. \end{aligned}$$ -
(iv)
if Ω u is open, if ∂ Ω u is a C 2 regular in D and if u ∈ C 2( Ω u), then
$$\displaystyle \begin{aligned} \frac{\partial}{\partial t}\Big\vert_{t=0}\int_{D}|\nabla u_t|{}^2\,dx\! & =\!-\int_{\partial\Omega_u} \!\!\xi\cdot \nu\,|\nabla u|{}^2\,d\mathcal{H}^{d-1}\qquad \mathit{\text{and}}\\ \frac{\partial}{\partial t}\Big\vert_{t=0}|\Omega_{u_t}\cap D|\! & =\!\int_{\partial\Omega_u}\!\!\xi\cdot \nu\,d\mathcal{H}^{d-1}\,, \end{aligned} $$where ν(x) is the exterior normal to ∂ Ω at the point x ∈ ∂ Ω.
Proof
The first claim follows by the fact that ξ is smooth and compactly supported in D. Thus, we start directly by proving (ii). We use the conventions
for general \(u:\mathbb {R}^d\to \mathbb {R}\) and \(\Phi :\mathbb {R}^d\to \mathbb {R}^d\), so that
In our case u t = u ∘ Φt, by the change of variables y = Φt(x) (thus, x = Ψt(y)), we get
We now notice that
and we calculate
which concludes the proof of (ii).
In order to prove (iii), we notice that
This means that  , and so, we can compute
, and so, we can compute

which proves (iii).
We now prove (iv). Assume that u is C 2 in the open set Ωu. Then, setting ξ = (ξ 1, …, ξ d) and using the convention for summation over the repeating indices, we compute
Integrating by parts we obtain
Since u = 0 on ∂ Ωu and positive in Ωu, we have that ∇u = ν|∇u|. Thus,
which proves the first part of the claim (iv). The second part of (iv) follows by a simple integration by parts in Ωu. □
As a consequence of Lemma 9.5 we obtain that for every \(\Lambda \in \mathbb {R}\), u ∈ H 1(D) and vector field \(\xi \in C^\infty _c(D;\mathbb {R}^d)\) we can define the first variation of \(\mathcal F_\Lambda \) at u in the direction ξ as

Lemma 9.6 (The Minimizers have Zero First Variation)
Let D be a bounded open set in \(\mathbb {R}^d\) and let u ∈ H 1(D) be a minimizer of \(\mathcal F_\Lambda \) in D. Then,
If, moreover, ∂ Ω u is C 2 smooth in D, then
Proof
The first part of the statement follows directly by Lemma 9.5. In order to prove the second part, we notice that in the case when ∂ Ωu is smooth, we have
for every vector field \(\xi \in C^\infty _c(D;\mathbb {R}^d)\). This implies (9.7). □
Definition 9.7 (Stationary Free Boundaries)
Let \(D\subset \mathbb {R}^d\) be a bounded open set and u ∈ H 1(D) be a non-negative function such that
Then, we say that the function u and the free boundary ∂ Ωu are stationary for \(\mathcal F_\Lambda \).
As a consequence of Lemma 9.6 we obtain the following.
Lemma 9.8 (Equipartition of the Energy)
Suppose that D is a bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) is a non-negative function which is stationary for \(\mathcal F_\Lambda \) (in the sense of Definition 9.7). Then, for every x 0 ∈ D and every 0 < r < dist(x 0, ∂D), we have
where we recall that \(u_{x_0,r}(x)=\frac 1ru(x_0+rx)\) and that \(z_{x_0,r}\) is the one-homogeneous extension of \(u_{x_0,r}\) in B 1 , that is, \(z_{x_0,r}(x)=|x|u_{x_0,r}\big ({x}/{|x|}\big )\).
Proof
Without loss of generality, we assume that x 0 = 0. For every ε > 0, we consider a function \(\phi _{\varepsilon }\in C^\infty _c(B_r)\) such that

Taking the vector field ξ ε(x) = xϕ ε(x) we get that
Thus, the stationarity of u impies that

which passing to the limit as ε → 0 implies that

Since Δu = 0 on Ωu, we have that
which together with (9.9) implies (9.8). □
Proposition 9.9 (Monotonicity Formula for Stationary Free Boundaries)
Suppose that D is a bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) is a non-negative function which is stationary for \(\mathcal F_\Lambda \) (in the sense of Definition 9.7). Let x 0 ∈ D and \(\delta _{x_0}=\mathrm {dist}\,(x_0,\partial D)\) . Then the function \(r\mapsto W_\Lambda (u_{x_0,r})\) is non-decreasing on the interval \((0,\delta _{x_0})\) and we have
Proof
9.3 Homogeneity of the Blow-Up Limits
In this section, we use the Weiss’ monotonicity formula to prove that the blow-up limits of u are one-homogeneous functions. The most general result is given in Lemma 9.10. We then prove the homogeneity of the blow-up limits of stationary functions (Lemma 9.11) and the homogeneity of the blow-up limits of minimizers of \(\mathcal F_\Lambda \) (Proposition 9.12).
Lemma 9.10
Suppose that D is a bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) is a non-negative function. Let x 0 ∈ D and \(\delta _{x_0}=\mathrm {dist}\,(x_0,\partial D)\) . Let r n → 0 be an infinitesimal sequence and let \(u_n:=u_{r_n,x_0}\in H^1(B_1)\) . Suppose that
-
(a)
the limit
$$\displaystyle \begin{aligned} L:=\lim_{r\to0}W_\Lambda(u_{r,x_0}), \end{aligned}$$exists and is finite;
-
(b)
u n converges strongly in H 1(B 1) to a function u ∞∈ H 1(B 1);
-
(c)
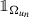 converges strongly in L
1(B
1) to
converges strongly in L
1(B
1) to
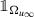 ;
; -
(d)
u ∞ is stationary for \(\mathcal F_\Lambda \) in B 1.
Then u ∞ is one-homogeneous.
Proof
Without loss of generality, we suppose that x 0 = 0 and we write \(u_{r,x_0}=u_r\). We set for simplicity v := u ∞. By the hypothesis (a), we have that,
On the other hand, the strong convergence of u
n and  implies that
implies that
where we recall that \(\displaystyle v_s(x)=\frac 1s v(sx)\). This implies that
and, by Proposition 9.9, we obtain that
which, by Lemma 9.3, gives that v is one-homogeneous. □
Lemma 9.11 (Homogeneity of the Blow-Up Limits)
Suppose that D is a bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) is a non-negative function which is stationary for \(\mathcal F_\Lambda \) (in the sense of Definition 9.7). Let x 0 ∈ D ∩ ∂ Ω u , r n → 0 be an infinitesimal sequence and \(u_n:=u_{r_n,x_0}\in H^1(B_1)\) . Suppose that
-
(a)
u n converges strongly in H 1(B 1) to a function u ∞∈ H 1(B 1);
-
(b)
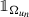 converges strongly in L
1(B
1) to
converges strongly in L
1(B
1) to
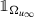 .
.
Then u ∞ is one-homogeneous.
Proof
Since u is stationary, Lemma 9.9 implies that the function \(r\mapsto W_\Lambda (u_{x_0,r})\) is non-decreasing in r. Thus, the limit
does exist and so the hypothesis (a) of Lemma 9.10 is fulfilled. Now, the strong convergence of u
n and  to u
∞ and
to u
∞ and  in B
1, and the definition of the first variation \(\delta \mathcal F_\Lambda (\cdot ,D)\) imply that u
∞ is also stationary in B
1. Thus, hypothesis (d) of Lemma 9.10 is also fulfilled and, so the claim follows by Lemma 9.10. □
in B
1, and the definition of the first variation \(\delta \mathcal F_\Lambda (\cdot ,D)\) imply that u
∞ is also stationary in B
1. Thus, hypothesis (d) of Lemma 9.10 is also fulfilled and, so the claim follows by Lemma 9.10. □
Proposition 9.12 (Homogeneity of the Blow-Up Limits)
Suppose that D is a bounded open set in \(\mathbb {R}^d\) and u ∈ H 1(D) is a non-negative function and a local minimizer of \(\mathcal F_\Lambda \) in D. Let x 0 ∈ D. Then every blow-up limit \(u_0\in \mathcal {B}\mathcal {U}_u(x_0)\) is one-homogeneous.
Proof
By Lemma 9.6, every minimizer of \(\mathcal F_\Lambda \) is stationary for \(\mathcal F_\Lambda \). Moreover, by Proposition 6.2, we have that the conditions (a) and (b) of Lemma 9.11 are fulfilled. This concludes the proof. □
9.4 Regularity of the Free Boundaries in Dimension Two
The main result of this section is the following.
Proposition 9.13 (One-Homogeneous Global Minimizers in Dimension Two)
Let \(z:\mathbb {R}^2\to \mathbb {R}\) be a one-homogeneous global minimizer of \(\mathcal F_\Lambda \) in \(\mathbb {R}^2\) . Then, there is \(\nu \in \mathbb {R}^2\) such that
In particular, we obtain that the critical dimension d ∗ is at least 3 (see Definition 1.5).
The proof of Proposition 9.13 is based on the following lemma.
Lemma 9.14
Let \(z\in H^1_{loc}(\mathbb {R}^d)\) be a continuous and non-negative one-homogeneous function in \(\mathbb {R}^d\) . Then,
if and only if, the trace \(c=z|{ }_{\partial B_1}\in H^1(\partial B_1)\) is such that
Proof
The proof follows simply by writing the Laplacian in polar coordinates. In fact, we have that z(r, θ) = rc(θ) and
which concludes the proof of Lemma 9.14. □
Proof of Proposition 9.13
Let z(r, θ) = rc(θ) and let \(\Omega _c\subset \mathbb S^1\) be the set {c > 0}. Since c is continuous (see Sect. 3), we have that Ωc is open and so it is a countable union of disjoint arcs (which we identify with segments on the real line). Notice that \(\Omega _c\neq \mathbb S^1\) since z(0) = 0 and z minimizes locally \(\mathcal F_\Lambda \) (the local minimizers cannot have isolated zeros, for instance, by the density estimates from Sect. 5.1). Now, Lemma 9.14 implies that on each arc \(\mathcal I\subset \Omega _c\), the trace c is a solution of the PDE
Thus, up to a translation \(\mathcal I=(0,\pi )\) and c(θ) is a multiple of \(\sin \theta \) on \(\mathcal I\). Thus, Ωc is a union of disjoint arcs, each one of length π. Thus, these arcs can be at most two. Now, by Lemma 2.9 and the fact that 0 ∈ ∂ Ωz, we get that | Ωz ∩ B 1| < |B 1| = π and so, \(\mathcal {H}^1(\Omega _c)<2\pi \). This means that Ωc is an arc of length π and that z is of the form z(x) = a (x ⋅ ν), for some constant a > 0. Since z is a local minimizer in \(\mathbb {R}^d\) and ∂ Ωz is smooth, Lemma 6.11 implies that \(a=\sqrt {\Lambda }\), which concludes the proof. □
9.5 The Optimality Condition on the Free Boundary: A Monotonicity Formula Approach
The aim of this subsection is to give an alternative proof to the fact that the (local) minimizers of \(\mathcal F_\Lambda \) are viscosity solutions to the problem
The main result of the subsection is Proposition 9.18, which can be applied not only to minimizers, but also to measure constrained minimizers (see Theorem 1.9 and Sect. 11). It can also be applied to a large class of problems in which a monotonicity formula does hold. In fact, the proof is quite robust and can be applied to almost-minimizers (see for instance [46]) and to vectorial problems (see [41]), for which the construction of competitors is typically more involved. The proof of Proposition 9.18 is based on the following two lemmas. Before we give the two statements, we recall that, for any d ≥ 2, we identify the (d − 1)-dimensional sphere \(\mathbb S^{d-1}\) with the boundary of the unit ball ∂B 1 in \(\mathbb {R}^d\). In particular, we will use the notation
Lemma 9.15
Suppose that \(c\in H^1(\mathbb S^{d-1})\) is a continuous non-negative and non-constantly-vanishing function, satisfying the following conditions:
-
(a)
\(\Omega _c\subset \mathbb S^{d-1}_+\) , where as usual Ω c := {c > 0};
-
(b)
\(\Delta _{\mathbb S} c+(d-1)c=0\) in Ω c.
Then, \(\Omega _c=\mathbb S^{d-1}_+\) and there is a constant α > 0 such that
Lemma 9.16
Suppose that \(c\in H^1(\mathbb S^{d-1})\) is a continuous non-negative function, satisfying the following conditions:
-
(a)
\(\mathbb S^{d-1}_+\subset \Omega _c=\{c>0\}\);
-
(b)
\(\Delta _{\mathbb S} c+(d-1)c=0\) in Ω c.
Then, c is given by one of the following functions:
-
(i)
c(x) = α(x ⋅ e d)+ , where α > 0 is a positive constant;
-
(ii)
c(x) = α(x ⋅ e d)+ + β(x ⋅ e d)− , where α > 0 and β > 0.
In the proofs of Lemmas 9.15 and 9.16 we will use the following well-known result, whose proof we the leave to the reader.
Lemma 9.17 (Variational Characterization of the Principal Eigenvalue)
Let \(\Omega \subset \mathbb S^{d-1}\) be a connected open subset of the unit sphere. Let \(\phi \in H^1_0(\Omega )\) be a given non-zero function. Then, the following are equivalent:
-
(i)
ϕ > 0 in Ω, ∫Ω ϕ 2 dθ = 1 , and there is λ ≥ 0 for which ϕ solves the PDE
$$\displaystyle \begin{aligned} -\Delta_{\mathbb S}\phi=\lambda\phi\quad \mathit{\text{in}}\quad \Omega\; \end{aligned}$$in the usual weak sense:
$$\displaystyle \begin{aligned} \int_\Omega\nabla_\theta\phi\cdot\nabla_\theta \eta\,d\theta=\lambda \int_\Omega\phi \eta\,d\theta\quad \mathit{\text{for every}}\quad \eta\in H^1_0(\Omega); \end{aligned}$$ -
(ii)
ϕ is the unique (up to a sign) solution of the variational problem
$$\displaystyle \begin{aligned} {} \min\Big\{\int_\Omega|\nabla_\theta \psi|{}^2\,d\theta\ :\ \psi\in H^1_0(\Omega),\ \int_\Omega \psi^2\,d\theta=1\Big\}. \end{aligned}$$
Proof of Lemma 9.15
Since the linear functions are one-homogeneous and harmonic in \(\mathbb {R}^d\), we have that the function
defined on the sphere solves the equation
In particular, setting \(\displaystyle \alpha _d:=\left (\int _{\mathbb S^{d-1}}\phi _1^2\,d\theta \right )^{-1}\), we get that α d ϕ 1 is the unique minimizer of
On the other hand, \(c\in H^1_0(\mathbb S^{d-1}_+)\) and solves the equation \(-\Delta _{\mathbb S}c=(d-1)c\) in Ωc. Thus,
which means that (up to a multiplicative constant) c is a solution of the same problem. Thus, the uniqueness of ϕ 1 gives the claim. □
Proof of Lemma 9.16
Let \(\widetilde \Omega _c\) be the connected component of Ωc containing \(\mathbb S^{d-1}_+\); and let \(\widetilde c\) be the restriction of c to \(\widetilde \Omega _c\). Thus, \(\widetilde \Omega _c=\{\widetilde c>0\}\) and \(\widetilde c\) solves the PDE
Thus, \(\tilde c\) is the unique minimizer of
Thus, reasoning as in the proof of Lemma 9.15, we get that \(\widetilde \Omega _c=\mathbb S^{d-1}_+\) and that there is a constant α > 0 such that
We now consider two cases. If Ωc has only one connected component, then \(\Omega _c=\widetilde \Omega _c\) and \(c=\widetilde c\), which concludes the proof. If Ωc has more than one connected components, then  is non-empty and is contained in the half-sphere
is non-empty and is contained in the half-sphere
Thus, applying Lemma 9.15, we get that the restriction of c on  should be of the form β(θ ⋅ e
d)−, for some positive constant β, which concludes the proof. □
should be of the form β(θ ⋅ e
d)−, for some positive constant β, which concludes the proof. □
Proposition 9.18
Suppose that \(D\subset \mathbb {R}^d\) is a bounded open set and that u ∈ H 1(D) is a continuous non-negative function such that:
-
(a)
u is harmonic in Ω u = {u > 0}.
-
(b)
Ω u satisfies the upper density bound
$$\displaystyle \begin{aligned} \limsup_{r\to0}\frac{|\Omega_u\cap B_r(x_0)|}{|B_r|}<1\qquad \mathit{\text{for every}}\qquad x_0\in\partial\Omega_u\cap D. \end{aligned}$$ -
(c)
For every x 0 ∈ D ∩ ∂ Ω u and every infinitesimal sequence r n → 0, there is a subsequence (that we still denote by r n ) such that the blow-up sequence \(u_{r_n,x_0}\) converges uniformly in B 1 to a blow-up limit \(u_0:B_1\to \mathbb {R}\) ( \(u_0\in \mathcal {B}\mathcal {U}_u(x_0)\) ).
-
(d)
Every blow-up limit \(\mathcal {B}\mathcal {U}_u(x_0)\ni u_0:B_1\to \mathbb {R}\) is a one-homogeneous non-identically-zero function, which is stationary for the functional \(\mathcal F_\Lambda \).
Then u satisfies the optimality condition
in viscosity sense.
Proof
Suppose first that the function φ touches u from below in x 0 ∈ ∂ Ωu and assume that x 0 = 0. Consider the blow-up sequences
as r n → 0, the condition (c) implies that, up to a subsequence, we have
the convergence being uniform in B 1. In particular, since u n are harmonic in \(\Omega _{u_n}\), the uniform convergence of u n to u 0 implies that also u 0 is harmonic on \(\Omega _{u_0}\).
Notice that, as φ is smooth, we have φ 0(x) = ξ ⋅ x, where the vector \(\xi \in \mathbb {R}^d\) is precisely the gradient ∇φ(0). Without loss of generality we may assume that ξ = Ae d for some constant A ≥ 0, thus
Moreover, we can assume that A > 0 since otherwise the inequality \(|\nabla \varphi |\le \sqrt {\Lambda }\) holds trivially.
Now, since u 0 ≥ φ 0, we obtain that u 0 > 0 on the set {x d > 0}. Thus, u 0 is a 1-homogeneous harmonic function on the cone {u 0 > 0}⊃{x d > 0}. By Lemma 9.16, there are only two possibilities:
The second case is ruled out since it contradicts (b). Thus,
Now, the stationarity of u 0 (condition (d)) and Lemma 9.5 imply that \(\alpha =\sqrt {\Lambda }\). By the inequality u 0 ≥ φ 0, we get that \(\sqrt {\Lambda }\ge A\).
Suppose now that φ touches u from above at a point x 0 and assume that x 0 = 0. Again, we consider the blow-up limits U 0 and φ 0 defined in (9.11) and we assume that φ 0 is given by (9.12). Since u 0 is not identically zero (assumption (d)), we get that a > 0. Since u 0 ≤ φ 0 we have that the set {u 0 > 0} is contained in the half-space {x d > 0}. By the one-homogeneity of u 0 and Lemma 9.15 we obtain that necessarily {u 0 > 0} = {x d > 0}. Thus, u 0 is of the form (9.13) for some α > 0. Now, the stationarity of u 0 implies that necessarily \(\alpha =\sqrt {\Lambda }\) and, since u 0 ≤ φ 0, we get that \(|\nabla \varphi (0)|=A\ge \sqrt {\Lambda }\), which concludes the proof. □
9.6 Energy and Lebesgue Densities
In this section, we prove that if u is a (local) minimizer of \(\mathcal F_\Lambda \), then at every boundary point x 0 ∈ ∂ Ωu the Lebesgue density of the set Ωu is well-defined. Moreover, we characterize the regular part of the free boundary in terms of the Lebesgue density. Most of the ideas in this section come from [41], where we used a similar characterization of the regular part of the vectorial free boundaries. In the case of the one-phase problem, we will not use this result in the proofs of neither of the Theorems 1.2, 1.4, 1.9 nor 1.10; we give it here only for the sake of completeness. The precise statement is the following:
Proposition 9.19
Suppose that \(D\subset \mathbb {R}^d\) is a bounded open set and that u ∈ H 1(D) is a non-negative function, a local minimizer of \(\mathcal F_\Lambda \) in D. Then, the limit
Thus, we can write
The regular and the singular parts of the free boundary are given by
Moreover, for every γ ∈ [1∕2, 1), we have
Proof
The claims (9.14), (9.15) and (9.17) follow directly by Lemma 9.20 below. The claim (9.16), follows by Lemma 9.22. □
Lemma 9.20 (Energy and Lebesgue Densities)
Suppose that \(D\subset \mathbb {R}^d\) is a bounded open set and that u ∈ H 1(D) is a continuous non-negative function such that:
-
(a)
For every x 0 ∈ D and every infinitesimal sequence r n → 0, there is a subsequence (that we still denote by r n ) such that:
-
\(u_n:=u_{r_n, x_0}\) converges strongly in H 1(B 1) to a function \(u_0:B_1\to \mathbb {R}\);
-
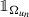 converges in L
2(B
1) to
converges in L
2(B
1) to
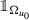 .
.
(As usual, we say that u 0 is a blow-up limit of u, and we note \(u_0\in \mathcal {B}\mathcal {U}_u(x_0)\) .)
-
-
(b)
Every blow-up limit \(\mathcal {B}\mathcal {U}_u(x_0)\ni u_0:B_1\to \mathbb {R}\) is a one-homogeneous non-identically-zero function such that Δu 0 = 0 in \(\Omega _{u_0}\cap B_1\).
-
(c)
For every x 0 ∈ ∂ Ω u ∩ D, the limit
$$\displaystyle \begin{aligned} \Theta(u, x_0):=\lim_{r\to0}W_\Lambda(u_{r,x_0})\,, \end{aligned}$$does exist.
Then, for every x 0 ∈ ∂ Ω u ∩ D, we have that
Moreover, for every \(u_0\in \mathcal {B}\mathcal {U}_{u}(x_0)\) , we have that
Proof
We first notice that (b) implies that
Let x 0 ∈ ∂ Ωu ∩ D and the infinitesimal sequence r n → 0 be given. Then, by (a), up to a subsequence, \(u_{r_n,x_0}\) converges to a blow-up limit u 0. Using (c) and then again (a), we get
On the other hand, the strong H 1(B 1) convergence of \(u_{r_n,x_0}\) to u 0 implies that
Then, we have
which concludes the proof. □
In the proof of Lemma 9.22, we will use the following result.
Theorem 9.21 (The Spherical Caps Minimize λ 1 on the Sphere)
For any (quasi-)open spherical set \(\Omega \subset \mathbb S^{d-1}\) we define the first eigenvalue λ 1( Ω) as
For every open set \(\Omega \subset \mathbb S^{d-1}\) such that \(\mathcal {H}^{d-1}(\Omega )\le \frac 12 d\omega _d\) we have that
with equality if and only if, up to a rotation, \(\Omega =\mathbb S^{d-1}_+\).
Lemma 9.22 (Characterization of the Regular Part of the Free Boundary)
Suppose that \(D\subset \mathbb {R}^d\) is a bounded open set and that u ∈ H 1(D) is as in Lemma 9.20 . Then,
Moreover,
if and only if, every blow-up limit \(u_0\in \mathcal {B}\mathcal {U}_u(x_0)\) is of the form
In particular, if u is a minimizer of \(\mathcal F_\Lambda \) in D, then \(Reg(\partial \Omega _u)=\Omega _u^{({1}/{2})}\) in D.
Proof
Suppose that x 0 ∈ ∂ Ωu ∩ D and let
Let r n → 0 be an infinitesimal sequence. Then, by the assumption Lemma 5.1 (a), up to extracting a subsequence, we can suppose that \(u_{r_n,x_0}\) converges to a blow-up limit \(u_0:\mathbb {R}^d\to \mathbb {R}\). By the hypothesis Lemma 5.1 (b), we get that u 0 is one-homogeneous and harmonic in \(\Omega _{u_0}\cap B_1\). This implies that, on the sphere ∂B 1, u 0 solves the PDE
Thus, Theorem 9.21 implies that
which by the homogeneity of u 0 gives that
Now, the convergence of \(\Omega _{u_{r_n,x_0}}\) to \(\Omega _{u_0}\) implies that
which concludes the proof of the lower bound (9.18). In the case of equality γ = 1∕2, we have that \(u_0\Big |{ }_{\partial B_1}\) is precisely the first eigenvalue on the half-sphere \(\mathbb S_{d-1}^+\), whose one-homogeneous extension is precisely (9.19). □
References
D. Mazzoleni, S. Terracini, B. Velichkov, Regularity of the optimal sets for some spectral functionals. Geom. Funct. Anal. 27(2), 373–426 (2017)
E. Russ, B. Trey, B. Velichkov, Existence and regularity of optimal shapes for elliptic operator with drift. Calc. Var. PDE 58(6), 199 (2019)
G.S. Weiss, Partial regularity for a minimum problem with free boundary. J. Geom. Anal. 9(2), 317–326 (1999)
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2023 The Author(s)
About this chapter
Cite this chapter
Velichkov, B. (2023). The Weiss Monotonicity Formula and Its Consequences. In: Regularity of the One-phase Free Boundaries. Lecture Notes of the Unione Matematica Italiana, vol 28. Springer, Cham. https://doi.org/10.1007/978-3-031-13238-4_9
Download citation
DOI: https://doi.org/10.1007/978-3-031-13238-4_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-13237-7
Online ISBN: 978-3-031-13238-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


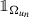 converges strongly in L
1(B
1) to
converges strongly in L
1(B
1) to
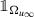 ;
;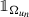 converges strongly in L
1(B
1) to
converges strongly in L
1(B
1) to
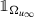 .
.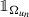 converges in L
2(B
1) to
converges in L
2(B
1) to
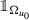 .
.